Nonuniform Alikhanov Linearized Galerkin Finite Element Methods for Nonlinear Time-Fractional Parabolic Equations

Abstract

The solutions of the nonlinear time fractional parabolic problems usually undergo dramatic changes at the beginning. In order to overcome the initial singularity, the temporal discretization is done by using the Alikhanov schemes on the nonuniform meshes. And the spatial discretization is achieved by using the finite element methods. The optimal error estimates of the fully discrete schemes hold without certain time-step restrictions dependent on the spatial mesh sizes. Such unconditionally optimal convergent results are proved by taking the global behavior of the analytical solutions into account. Numerical results are presented to confirm the theoretical findings.

1 Introduction

In this paper, we consider the nonuniform Alikhanov FEMs for solving nonlinear time fractional parabolic equations (TFPEs):

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _t^\alpha u-\Delta u=g(u),&{} \text {in }\Omega \times (0,T], \\ u(x,0)=u_0(x) , &{} \text {in }\Omega ,\\ u(x,t)=0, &{} \text {on }\partial \Omega \times (0,T], \end{array}\right. \end{aligned}$$

(1.1)

where $\Omega \subset \mathbb {\mathbb {R}}^d$, ($d=2$ or 3) is a bounded and convex (smooth) polygon in $\mathbb {\mathbb {R}}^2$ (or polyhedron in $\mathbb {\mathbb {R}}^3$ ), u(x, t) is an unknown function defined in $\Omega \times [0,T]$, and $g(u)\in C^2(\mathbb {\mathbb {R}})$ is a nonlinear function. Here, $\partial _t^\alpha u$ denotes the Caputo fractional derivative of order $\alpha$, defined by

$$\begin{aligned} \partial _t^\alpha u=\int _{0}^{t} w_{1-\alpha }(t-s)u'(s)ds,~~~0<\alpha <1, \end{aligned}$$

where $\Gamma (\cdot )$ is the common Gamma function and $w_{1-\alpha }(t)=\frac{t^{-\alpha }}{\Gamma (1-\alpha )}$. TFPEs are widely used to describe different natural phenomena involving some anomalous transport mechanism. The typical models include the time fractional Allen–Cahn equation, the time fractional fokker planck equation, the time fractional fisher equations and so on [1, 2].

In the past several decades, different numerical schemes are developed to numerically solve the TFPBs, including finite different methods [3,4,5,6,7], spectral methods [8, 9] and so on [10,11,12,13]. Since the typical solutions of TFPEs have the initial layers, the implication of the direct L1-type methods, BDF convolution quadrature methods lead some possible loss of accuracy [14]. To overcome the initial difficulties, M. Stynes et al. applied the L1-scheme on the graded meshes to solve the linear time fractional problems [15] and obtained the optimal error estimates of the fully discrete schemes. Cao et al. studied the corrected implicit-explicit schemes for the nonlinear fractional equations with nonsmooth solutions [16]. Jin et al. considered the corrected BDF convolution quadrature [17]. More about the topic, we refer readers to the recent papers [18,19,20,21,22,23,24,25,26].

In this study, we present an effective numerical scheme for solving the TFPEs. The numerical scheme is constructed as follows. The time discretization is done by using the Alikhanov scheme on the nonuniform meshes, taking global behavior of the analytical solutions into account. The spatial discretization is done by using the Galerkin FEMs. The nonlinear term is approximated by using the Newton linearized methods. Then, we obtain the unconditionally optimal error estimates of the fully discrete and linearized scheme. Such unconditional results imply that the error estimate holds without any time-step restrictions dependent on the spatial mesh sizes. We believe that this paper is the first to get the unconditional convergence results of Alikhanov formula on the general nonuniform meshes.

The key proof of the unconditional convergence results is the temporal-spatial error splitting argument, which has a successful application in analysis of numerical schemes for two- and three-dimensional PDEs of parabolic type [27,28,29,30,31]. However, the previous results are obtained by using the uniform meshes or graded meshes. The proof of the present results is much more technical due to the use of the nonuniform meshes and the non-locality of the problem. On one hand, the local truncation error is expressed in a discrete convolution form. We need to consider the effect of the errors at different time level. On the other hand, we have to estimate the boundedness of some nonlocal operator and the numerical solutions involving different time levels.

The rest of this paper is organized as follows. In Sect. 2, we propose a linearized nonuniform Alikhanov FEM for solving the problem (1.1) and present our main results. In Sect. 3, a discrete fractional Grönwall type inequality and the time-spatial splitting methods are used to obtain the error estimates. In Sect. 4, numerical tests are done to verify our theoretical findings. Finally, we give some conclusions in Sect. 5.

2 The Nonuniform Alikhanov Formula and Main Results

In this section, we present the fully discrete numerical schemes for solving problem (1.1) and the convergence results of the schemes.

Let $\mathcal {T}_h$ be a conforming and shape regular simplicial triangulation or tetrahedra of $\Omega$, and let $h=\max _{K\in \mathcal {T}_h}\{\text {diam}\ K\}$ be the mesh size. Denote $V_h$ by the finite-dimensional subspace of $H_0^1(\Omega )$, which consists of continuous piecewise polynomials of degree r ($r\ge 1$) on $\mathcal {T}_h$. Let time step $\tau _k = t_k-t_{k-1}, t_{k-\theta }=(1-\theta )t_k+\theta t_{k-1},0=t_0<t_1<t_2<\cdots <t_N,\theta \in [0,1)$, where N is an integer. Denote the step size ratios $\rho _k:=\tau _k/\tau _{k+1}$ and the maximum step size $\tau :=\max _{1\le k\le N}\tau _k$. For a sequence of functions{$\omega ^n$}, we write

$$\begin{aligned} \omega ^{n,\theta }=(1-\theta )\omega ^n+\theta \omega ^{n-1},~~~\nabla _{\tau }\omega ^n=\omega ^n-\omega ^{n-1},~~1\le n\le N,~~\theta =\frac{\alpha }{2}. \end{aligned}$$

(2.1)

The nonuniform Alikhanov approximation to Caputo’s fractional derivative at $t_{n-\theta }$ is defined by

$$\begin{aligned} (\partial _t^\alpha \phi )^{n-\theta }= & {} \int _{0}^{t_{n-\theta }}w_{1-\alpha }(t_{n-\theta }-s)\phi '(s)ds\\= & {} \sum _{k=1}^{n-1}\int _{t_{k-1}}^{t_k}w_{1-\alpha }(t_{n-\theta }-s)\phi '(s)ds+\int _{t_{n-1}}^{t_{n-\theta }}w_{1-\alpha }(t_{n-\theta }-s)\phi '(s)ds\\\approx & {} \sum _{k=1}^{n-1}\int _{t_{k-1}}^{t_k}w_{1-\alpha }(t_{n-\theta }-s)(\Pi _{2,k}\phi )'(s)ds\\&+\int _{t_{n-1}}^{t_{n-\theta }}w_{1-\alpha }(t_{n-\theta }-s)(\Pi _{1,n} \phi )'(s)ds, \end{aligned}$$

where $\Pi _{2,k}\phi$ means the quadratic interpolate at $t_{k-1},t_{k}$ and $t_{k+1}$, and $\Pi _{1,k}\phi$ denoted as the linear interpolate with the nodes $t_{k-1},t_{k}$. Omit the truncation error, the nonuniform Alikhanov formula is given by

$$\begin{aligned} (D_{\tau }^{\alpha }\phi )^{n-\theta }:= & {} \sum _{k=1}^{n-1}\int _{t_{k-1}}^{t_k}w_{1-\alpha }(t_{n-\theta }-s)\left[ \frac{\nabla _{\tau } \phi ^k}{\tau _k}+\frac{2(s-t_{k-1/2})}{\tau _k(\tau _k+\tau _{k+1})}(\rho _k\nabla _{\tau }\phi ^{k+1}-\nabla _{\tau }\phi ^k)\right] ds\nonumber \\&+\int _{t_{n-1}}^{t_{n-\theta }}w_{1-\alpha }(t_{n-\theta }-s)\frac{\nabla _{\tau }\phi ^n}{\tau _n}ds\nonumber \\= & {} \tilde{a}_0^{(n)}\nabla _{\tau }\phi ^n+\sum _{k=1}^{n-1}(\tilde{a}_{n-k}^{(n)}\nabla _{\tau }\phi ^k+\rho _k\tilde{b}_{n-k}^{(n)}\nabla _{\tau }\phi ^{k+1}-\tilde{b}_{n-k}^{(n)}\nabla _{\tau }\phi ^k)\nonumber \\= & {} A_{0}^{(n)}\nabla _{\tau }\phi ^n+\sum _{k=1}^{n-1}A_{n-k}^{(n)}\nabla _{\tau }\phi ^k, \end{aligned}$$

(2.2)

where the discrete coefficients $\tilde{a}_{n-k}^{(n)}$ and $\tilde{b}_{n-k}^{(n)}$ are

$$\begin{aligned} \tilde{a}_{0}^{(n)}= & {} \frac{1}{\tau _n}\int _{t_{n-1}}^{t_{n-\theta }}w_{1-\alpha }(t_{n-\theta }-s)ds,~~~ \tilde{a}_{n-k}^{(n)}=\frac{1}{\tau _k}\int _{t_{k-1}}^{t_k}w_{1-\alpha }(t_{n-\theta }-s)ds,\\ \tilde{b}_{n-k}^{(n)}= & {} \frac{2}{\tau _k(\tau _k+\tau _{k+1})}\int _{t_{k-1}}^{t_k}(s-t_{k-\frac{1}{2}})w_{1-\alpha }(t_{n-\theta }-s)ds, \end{aligned}$$

and

$$\begin{aligned} A_{n-k}^{(n)}=\left\{ \begin{array}{ll} \tilde{a}_{0}^{(n)}+\rho _{n-1}\tilde{b}_{1}^{(n)}, &{} k=n, \\ \tilde{a}_{n-k}^{(n)}+\rho _{k-1}\tilde{b}_{n-k+1}^{(n)}-\tilde{b}_{n-k}^{(n)} , &{} 2\le k\le n-1,\\ \tilde{a}_{n-1}^{(n)}-\tilde{b}_{n-1}^{(n)}, &{}k=1. \end{array}\right. \end{aligned}$$

The Newton linearized nonuniform Alikhanov Galerkin FEM is to find $U_h^n\in V_h$ such that, for $n=1,2,\ldots ,N$,

$$\begin{aligned}&\Big ((D_{\tau }^{\alpha }U_h)^{n-\theta },v\Big )+\Big (\nabla U_h^{n,\theta },\nabla v\Big )\nonumber \\&\quad -\Big (g(U_h^{n-1})+(1-\theta )g_1(U_h^{n-1})(U_h^n-U_h^{n-1}),v\Big )=0~~~~~\forall v\in V_h, \end{aligned}$$

(2.3)

where $g_1(U_h^{n-1})=\frac{\partial }{\partial u}g\big |_{u=U_h^{n-1}}$.

The typical solutions of the nonlinear time fractional problems have an initial layer, which are widely described by (see. e.g., [21])

$$\begin{aligned} \Vert u_{t}^{(m)}\Vert _{L^{\infty }(0,T;H^{r+1})}\le C(1+t^{\sigma -m}),~~~m=0,1,2,3,~~\sigma \in (0,1)\cup (1,2),~~r=1,2,\nonumber \\ \end{aligned}$$

(2.4)

where C is a constant.

Remark 2.1

As pointed out in [14, 15], if the initial condition $u_0(x)\in H^{r+1}(\Omega )\cap H_0^1(\Omega )$ for each t and the nonlinear term is Lipschitz continuous, then problem (1.1) has a unique solution u such that

$$\begin{aligned} u \in C^\alpha ([0, T ]; L_2(\Omega )) \cap C([0, T ]: H^{r+1}(\Omega )\cap H_0^1(\Omega )). \end{aligned}$$

It implies that $\sigma =\alpha$ in most references. For the assumption $\sigma \in (0,\alpha )$, we refer readers to [32, 33]. Suppose that the solution is smoother, i.e., $\sigma >\alpha$, some additional hypothesis should be added (see [15]). This is quite restrictive. Just to make the current analysis extendable, we assume that $\sigma \in (0,1)\cup (1,2)$.

To capture the initial singularities, we have some restrictions on the temporal stepsizes, i.e., we assume that there exists a constant $C_\gamma >0$, independent of k, and a fixed $\gamma \ge 1$ such that

$$\begin{aligned}&\tau _k\le C_\gamma \tau \min \{1,t_k^{1-1/\gamma }\}~, 1\le k\le N, t_k\le C_\gamma t_{k-1}~~ \text { and} \nonumber \\&\quad ~~\tau _k/t_k\le C_\gamma \tau _{k-1}/t_{k-1},~~2\le k\le N. \end{aligned}$$

(2.5)

Here and below, we always assume (2.4) and (2.5) hold whenever they are refereed.

Now, we present optimal error estimates of the fully discrete schemes and leave the main proof to the next sections.

Theorem 2.1

Suppose that $u_0\in H^{r+1}(\Omega )\bigcap H_0^1(\Omega )$ and the nonlinear time fractional problem (1.1) has a unique solution, satisfying $u(\cdot ,t)\in H^{r+1}(\Omega )\bigcap H_0^1(\Omega )$. Then, there exist positive constants $\tau _0$ and $h_0$, such that when $\tau \le \tau _0$ and $h<h_0$, the $r-$degree finite element system defined in (2.3) has a unique solution $U_h^m$, $m=1,2,3,\ldots , N$, satisfying

$$\begin{aligned} \Vert u^m-U_h^m\Vert _{L^2}\le C_0(\tau ^{\min \{\gamma \sigma ,2\}}+h^{r+1}), \end{aligned}$$

(2.6)

where $u^m=u(\cdot ,t_m)$ and $C_0$ is a positive constant independent of $\tau$ and h.

Remark 2.2

The assumption (2.5) is necessary due to the initial layer. A typical example satisfying (2.5) is the graded meshes, i.e, for a given interval $[0,T_0]$, we let

$$\begin{aligned} t_k=T_0\left( \frac{k}{N_0}\right) ^\gamma ,~~~k =0,1,\cdots , N_0, \end{aligned}$$

where $N_0$ is a positive integer.

Remark 2.3

At present, there are some convergence results of the nonuniform Alikhanov time discretization for time-fractional problems. In [34], Liao et al. presented the error convolution structure and a global consistency analysis of the nonuniform Alikhanov approximation. They also obtained a sharp L2-norm error estimate for the linear reaction-subdiffusion problems. In [26], Chen and Martin showed that the scheme attains second-order convergence for the linear time-fractional diffusion problem. The analysis in [26] followed a completely different line of attack. In our manuscript, the convergence results rely heavily on the discrete Grönwall inequality in [21] and the error convolution structure in [34]. However, the emphasis is quite different from the previous investigations on linear problems. In order to get convergence results for high-dimensional nonlinear problems, the boundedness of numerical solutions in the maximum norm is usually required. For this, one may apply the inverse inequality, which may lead to certain space-time restriction condition $\tau =\mathcal {O}(h^p)$ (p is a constant). The main contribution of the present paper is to get the optimal error estimates by removing the restrictions. We believe that this paper is the first to get the results on the Alikhanov scheme for the nonlinear problems. The results imply that the numerical solutions are bounded without placing any condition on the relative sizes of the temporal and spatial meshes. Then the error estimates hold without certain time-step restrictions dependent on the spatial mesh size.

3 Proof of the Main Results

In this section, we focus on the proof of the main results.

3.1 Preparation

Some properties of $A_{n-k}^{(n)}$ will play an important role in the proof. They are proved in [7, 34]. Here we list them.

A1.:

The discrete kernels are monotone, i.e., $0<A_{k-1}^{(n)}\le A_{k-2}^{(n)},~~2\le k\le n\le N$.

A2.:

Let $\pi _A=\frac{11}{4}$. It holds that $A_{n-k}^{(n)}\ge \frac{1}{\pi _A\tau _k}\int _{t_{k-1}}^{t_k}w_{1-\alpha }(t_n-s)ds,~~~1\le k\le n\le N.$

A3.:

There exists a constant $\rho >0$ such that the step size ratio $\rho _k\le \rho ,~~~1\le k\le N-1$.

Thanks to the properties of the coefficients, one can get the following lemmas.

Lemma 3.1

[21] Let

$$\begin{aligned} P_{0}^{(n)}:=\frac{1}{A_{0}^{(n)}},~~P_{n-j}^{(n)}:=\frac{1}{A_{0}^{(j)}}\sum _{k=j+1}^{n}(A_{k-j-1}^{(k)}-A_{k-j}^{(k)})P_{n-k}^{(n)},~~1\le j\le n-1. \end{aligned}$$

(3.1)

Then, it holds

$$\begin{aligned} \sum _{j=1}^{n}P_{n-j}^{(n)}w_{1-\alpha }(t_j)\le \pi _A,~~~~~~1\le n\le N, \end{aligned}$$

and

$$\begin{aligned} \sum _{j=1}^{n}P_{n-j}^{(n)}\le t_n^{\alpha }\pi _A\Gamma (2-\alpha ). \end{aligned}$$

(3.2)

Lemma 3.2

[21] For any sequence $\{v^n\}_{n=0}^{N}$, it holds

$$\begin{aligned} \frac{1}{2}\sum _{k=1}^{n}A_{n-k}^{(n)}\nabla _{\tau }(\Vert v^k\Vert ^2)\le \big <v^{n,\theta },(D_{\tau }^{\alpha }v)^{n-\theta }\big >,~~~for~~1\le n\le N. \end{aligned}$$

(3.3)

Lemma 3.3

[21] Suppose the nonnegative sequences $\{v^n,\xi ^n\}_{n=0}^{N}$ satisfy

$$\begin{aligned} \sum _{k=1}^{n}A_{n-k}^{(n)}\nabla _{\tau }(v^k)^2\le \lambda _1(v^n)^2+\lambda _2(v^{n-1})^2+v^{n,\theta }(\xi ^n+\eta ) ~~~n\ge 1. \end{aligned}$$

(3.4)

Then, it holds

$$\begin{aligned} v^n\le 2E_{\alpha }(2\max (1,\rho )\pi _A\lambda t_n^{\alpha })\left[ v^0+\max _{1\le k\le n}\sum _{j=1}^{k}P_{k-j}^{(k)}\xi ^j+\pi _A\Gamma (2-\alpha )t_n^\alpha \eta \right] , \end{aligned}$$

(3.5)

where $\tau _n$ satisfies $\max _{1\le n\le N}\tau _n\le (2\pi _A\Gamma (2-\alpha )\lambda )^{-\frac{1}{\alpha }}$, $\lambda =\lambda _1+\lambda _2$, and $E_\alpha (z)=\sum _{k=0}^{\infty }\frac{z^k}{\Gamma (1+k\alpha )}$ is the Mittag-Leffler function.

Lemma 3.4

[34] Suppose that $v\in C^3((0,T])$ and there exists a constant $C_v>0$ such that

$$\begin{aligned} |v'''(t)|\le C_v(1+t^{\sigma -3}),~~~~~for~~~0\le t\le T. \end{aligned}$$

Then, it holds that

$$\begin{aligned} \sum _{j=1}^{n}P_{n-j}^{(n)}|\Upsilon _1^{j}|\le C_v\left( \frac{\tau _1^\sigma }{\sigma }+{\max _{2\le k\le n}t_k^{\sigma -(3-\alpha )/\gamma }}\tau ^{3-\alpha }\right) , \end{aligned}$$

where $\Upsilon _1^n=\frac{1}{\Gamma (1-\alpha )}\int _{0}^{t_{n-\theta }}\frac{v'(s)}{(t-s)^\alpha }ds-(D_{\tau }^{\alpha }v(t))^{n-\theta }.$

Lemma 3.5

([34], Lemma 3.8) Suppose that ${v\in C^2((0,T])}$ with $\Vert v''(t)\Vert _{H^2}\le C_\nu (1+t^{\sigma -2})$, where $\sigma \in (0,1)\cup (1,2)$. Then, it holds that

$$\begin{aligned} \sum _{j=1}^{n}P_{n-j}^{(n)}|\Upsilon _2^{j,\theta }|\le C_v(\tau _1^{\sigma +\alpha }/\sigma +t_n^{\alpha }\max _{2\le k\le n}t_{k-1}^{\sigma -2}\tau _k^2),~~~~~1\le n\le N, \end{aligned}$$

(3.6)

where $\Upsilon _2^{n,\theta }=\Delta v(t_{n-\theta })-\Delta v^{n,\theta }$ for $1\le n\le N$.

Lemma 3.6

Assume that $\nu \in C^2((0,T])$ satisfies $|\nu '(t)|\le C_\nu (1+t^{\sigma -1}), ~~{\sigma \in (0,1)\cup (1,2)}$ and $g\in C^2(\mathbb {R})$ is a nonlinear function. Denote $\nu ^n=\nu (t_n)$ and $R_\nu ^n=g(\nu ^{n-\theta })-g(\nu ^{n-1})-g_1(\nu ^{n-1})(\nu ^{n-\theta }-\nu ^{n-1}), 1\le n\le N$, $\theta \in [0,1)$ then

$$\begin{aligned} \sum _{j=1}^{n}P_{n-j}^{(n)}|R_\nu ^j|\le {2} C_\nu (\tau _1^{2\sigma +\alpha }+t_n^\alpha \max _{2\le k\le n}\tau _k^2t_{k-1}^{2(\sigma -1)}),~~~1\le n\le N. \end{aligned}$$

Proof

Applying Taylor expansion, it holds that, for any $0<s<1,$

$$\begin{aligned} R_\nu ^j= & {} \frac{(1-\theta )^2}{2}(\nu ^j-\nu ^{j-1})^2g''(\nu ^{j-1}+s(\nu ^{j-\theta }-v^{j-1}))\\\le & {} \frac{(1-\theta )^2C_{g1}}{2}\left( \int _{t_{j-1}}^{t_j}|\nu '(t)|dt\right) ^2, \end{aligned}$$

where $C_{g1}$ is a constant dependent on g. By using the condition of $\nu (t)$ and fundamental inequality $(a+b)^2\le 2(a^2+b^2)$, we get

$$\begin{aligned} |R_\nu ^1|\le C_\nu \left[ \int _{0}^{t_1}(1+t^{\sigma -1})dt\right] ^2\le {2}C_\nu \left( \tau _1^2+\frac{\tau _1^{2\sigma }}{\sigma ^2}\right) , \end{aligned}$$

and

$$\begin{aligned} |R_\nu ^j|\le C_\nu [\int _{t_{j-1}}^{t_j}(1+t^{\sigma -1})dt]^2\le {2}C_\nu (\tau _j^2+\tau _j^2t_{j-1}^{2(\sigma -1)}),~~~2\le j\le N, \end{aligned}$$

which further gives that

$$\begin{aligned} \sum _{j=1}^{n}P_{n-j}^{(n)}|R_\nu ^j|\le & {} P_{n-1}^{(n)}|R_\nu ^1|+\sum _{j=2}^{n}P_{n-j}^{(n)}|R_\nu ^j|\\\le & {} \Gamma (2-\alpha )\pi _A\tau _1^\alpha |R_\nu ^1|+\max _{2\le k\le n}|R_\nu ^{k,\theta }|\sum _{j=1}^{n}P_{n-j}^{(n)}\\\le & {} {2}C_\nu [\tau _1^{\alpha +2\sigma }+\max _{2\le k\le n}t_n^\alpha (\tau _k^2+\tau _k^2t_{k-1}^{2\sigma -2})], \end{aligned}$$

which finishes the proof. $\square$

Let $R_h$ : $H_0^1(\Omega )\rightarrow V_h$ be Ritz projection operator satisfying

$$\begin{aligned} (\nabla (u-R_h u), \nabla \omega )=0, \quad \forall \omega \in V_h. \end{aligned}$$

(3.7)

By classical FEM theory [35], we can find that for any $v\in H^s(\Omega )\cap H_0^1(\Omega )$,

$$\begin{aligned} \Vert v-R_h v\Vert _{L^2}+h\Vert \nabla (v-R_h v)\Vert _{L^2}\le C_{\Omega } h^s\Vert v\Vert _{H^s}, \quad 1\le s\le r+1. \end{aligned}$$

(3.8)

To prove Theorem 2.1, we need to introduce the following time-discrete system

$$\begin{aligned} (D_{\tau }^{\alpha }U)^{n-\theta }=\Delta U^{n,\theta }+g(U^{n-1})+g_1(U^{n-1})(1-\theta )(U^n-U^{n-1}),~~~~~n=1,2,\ldots ,N,\nonumber \\ \end{aligned}$$

(3.9)

with initial and boundary conditions

$$\begin{aligned} U^n(x)= & {} 0,~~~~~~~~~~~x\in \partial \Omega , \quad n=1,2,3,\ldots , N, \end{aligned}$$

(3.10)

$$\begin{aligned} U^0(x)= & {} u_0(x),~~~~~~x\in \Omega . \end{aligned}$$

(3.11)

We split the errors into two terms, i.e.,

$$\begin{aligned} \Vert u^n-U_h^n \Vert \le \Vert u^n-U^n\Vert +\Vert U^n-U_h^n\Vert :=\Vert e^n\Vert +\Vert U^n-U_h^n\Vert , \end{aligned}$$

(3.12)

where $u^n~:=u(\cdot , t_n)$. Then, we will show the numerical solutions are bounded without any certain time-step restrictions dependent on the spatial mesh sizes.

3.2 Analysis of the Time-Discrete System

In this subsection, we focus on the error estimates of time discrete systems.

Considering $t=t_{n-\theta }$ in first equation of (1.1) and $u^{n-\theta }:=u(t_{n-\theta })$, we have

$$\begin{aligned} (D_{\tau }^{\alpha }u)^{n-\theta }-\Delta u^{n,\theta }-\big [g(u^{n-1})+g_1(u^{n-1})(1-\theta )(u^n-u^{n-1})\big ]=P^n, \end{aligned}$$

(3.13)

where

$$\begin{aligned} P^n= & {} (D_{\tau }^{\alpha }u)^{n-\theta } - D_{t_{n-\theta }}^{\alpha }u+\Delta u(t_{n-\theta }) - \Delta u^{n,\theta }+g(u^{n-\theta })\nonumber \\&-\big [g(u^{n-1})+g_1(u^{n-1})(1-\theta )(u^n-u^{n-1})\big ]. \end{aligned}$$

(3.14)

Subtracting (3.9) from (3.13), we have

$$\begin{aligned} (D_{\tau }^{\alpha }e)^{n-\theta }-\Delta e^{n,\theta }-r^{n,\theta }=P^n, \end{aligned}$$

(3.15)

where $e^n:=u^n-U^n$ and

$$\begin{aligned} r^{n,\theta }= & {} g(u^{n-1})+g_1(u^{n-1})(1-\theta )(u^n-u^{n-1})-g(U^{n-1})\nonumber \\&-g_1(U^{n-1})(1-\theta )(U^n-U^{n-1})\nonumber \\= & {} g(u^{n-1})-g(U^{n-1})+g_1(u^{n-1})(1-\theta )u^n-g_1(u^{n-1})(1-\theta )u^{n-1}\nonumber \\&-g_1(U^{n-1})(1-\theta )U^n+g_1(U^{n-1})(1-\theta )U^{n-1}\nonumber \\= & {} g(u^{n-1})-g(U^{n-1})+(1-\theta )g_1(u^{n-1})u^n-(1-\theta )g_1(U^{n-1})u^n\nonumber \\&+(1-\theta )g_1(U^{n-1})u^n-(1-\theta )g_1(U^{n-1})U^n\nonumber \\&+(1-\theta )g_1(U^{n-1})U^{n-1}-(1-\theta )g_1(u^{n-1})U^{n-1}\nonumber \\&+(1-\theta )g_1(u^{n-1})U^{n-1}-(1-\theta )g_1(u^{n-1})u^{n-1}. \end{aligned}$$

(3.16)

Meanwhile, it holds that

$$\begin{aligned} \Delta u=\partial _t^\alpha u-g(u), \end{aligned}$$

and

$$\begin{aligned} \Delta U^{n,\theta }=(D_{\tau }^{\alpha }U)^{n-\theta }-g(U^{n-1})-g_1(U^{n-1})(1-\theta )(U^n-U^{n-1}).\end{aligned}$$

Then, we have, for $n=1,2,\cdots ,N,$

$$\begin{aligned} \Delta e^{n,\theta }= & {} \int _{0}^{t_{n-\theta }}w_{1-\alpha }(t_{n-\theta }-s)u'(s)ds -(D_{\tau }^{\alpha }U)^{n-\theta } \\&-g(u^{n,\theta })+ g(U^{n-1})+g_1(U^{n-1})(1-\theta )(U^n-U^{n-1}). \end{aligned}$$

Noting that $u^n=U^n=0$ as $x\rightarrow \partial \Omega$, it holds that

$$\begin{aligned} \int _{0}^{t_{n-\theta }}w_{1-\alpha }(t_{n-\theta }-s)u'(x,s)ds =(D_{\tau }^{\alpha }U)^{n-\theta } =0,~~~~~~ x\rightarrow \partial \Omega , \end{aligned}$$

and

$$\begin{aligned}&g(u^{n-\theta })- g(U^{n-1})-g_1(U^{n-1})(1-\theta )(U^n-U^{n-1})\\&\quad =g(u^{n-1})-g(U^{n-1})=g'(0)(u^{n-1}-U^{n-1})\\&\quad =0,~~~~~~ x\rightarrow \partial \Omega . \end{aligned}$$

Therefore,

$$\begin{aligned} \Delta e^{n,\theta } =0, ~~~~~~x\rightarrow \partial \Omega . \end{aligned}$$

(3.17)

Theorem 3.1

The semi-discrete system (3.9)–(3.11) has a unique solution $U^m$ and there exists a positive $\tau _1^*$ such that, when $\tau \le \tau _1^*$,

$$\begin{aligned}&\Vert e^m\Vert _{H^2}\le C_1^*\tau ^{\min \{\sigma \gamma ,2\}}, \end{aligned}$$

(3.18)

$$\begin{aligned}&\Vert U^m\Vert _{H^2}+\Vert (D_{\tau }^{\alpha }U)^{m-\theta }\Vert _{H^2}\le C_1^{**}, \end{aligned}$$

(3.19)

where $m=1,2,\ldots ,N$ and $C_1^*,C_1^{**}$ are two positive number independent of $\tau$ and h.

Proof

Noting that at each time level, system (3.9) is a linear elliptic equation. The existence and uniqueness of the solution $U^n$ can be obtained obviously. Next, we prove the main results by using the mathematical induction. Firstly, we can check that the estimation holds for $m=0$. Now, we suppose that (3.18) holds for $0\le m\le n-1$. Then, we have, for $m\le n-1$,

$$\begin{aligned} \Vert U^m\Vert _{L^\infty }\le & {} \Vert u^m\Vert _{L^\infty }+\Vert e^m\Vert _{L^\infty }\\\le & {} \Vert u^m\Vert _{L^\infty }+C_{\Omega }\Vert e^m\Vert _{H^2}\\\le & {} \Vert u^m\Vert _{L^\infty }+C_{\Omega }C_1^*\tau ^{\min \{\sigma \gamma ,2\}}\\\le & {} K_1, \end{aligned}$$

where $\tau \le \tilde{\tau }_1=(C_{\Omega }C_1^*)^{-\frac{1}{\min \{\sigma \gamma ,2\}}}$ and here and below

$$\begin{aligned} K_1:=\max _{1\le n\le N}\Vert u^n\Vert _{L^{\infty }}+1. \end{aligned}$$

Together with $g\in C^2(\mathbb {\mathbb {R}})$, there exists a positive constant $C_L$ independent of $\tau$ such that

$$\begin{aligned} \Vert g_1(u^{n-1})\Vert _{L^2}\le & {} C_L, \end{aligned}$$

(3.20)

$$\begin{aligned} \Vert g(U^{n-1})-g(u^{n-1})\Vert _{L^2}\le & {} C_L\Vert e^{n-1}\Vert _{L^2}, \end{aligned}$$

(3.21)

$$\begin{aligned} \Vert g_1(U^{n-1})-g_1(u^{n-1})\Vert _{L^2}\le & {} C_L\Vert e^{n-1}\Vert _{L^2}. \end{aligned}$$

(3.22)

Now we start to estimate the error for $m=n$. Taking inner with $e^{n,\theta }$ both sides in Eq. (3.15) and using Cauchy–Schwarz inequality, we arrive

$$\begin{aligned} ((D_{\tau }^{\alpha }e)^{n-\theta },e^{n,\theta })\le \Vert e^{n,\theta }\Vert _{L^2}\Vert r^{n,\theta }\Vert _{L^2}+\Vert P^n\Vert _{L^2}\Vert e^{n,\theta }\Vert _{L^2}. \end{aligned}$$

(3.23)

Substituting (3.20)–(3.22) into (3.16), we get

$$\begin{aligned} \Vert r^n\Vert _{L^2}\le & {} C_L\Big [\Vert e^{n-1}\Vert _{L^2}+(1-\theta )\Vert u^n\Vert _{L^\infty }\Vert e^{n-1}\Vert _{L^2}+(1-\theta )\Vert e^n\Vert _{L^2}\nonumber \\&+(1-\theta )\Vert U^{n-1}\Vert _{L^\infty }\Vert e^{n-1}\Vert _{L^2}+(1-\theta )\Vert e^{n-1}\Vert _{L^2}\Big ]\nonumber \\\le & {} \big [C_L+(1-\theta )C_L K_1+K_1 C_L(1-\theta )+C_L(1-\theta )\big ]\Vert e^{n-1}\Vert _{L^2}\nonumber \\&+(1-\theta )C_L\Vert e^n\Vert _{L^2}\nonumber \\\le & {} C_1(\Vert e^{n-1}\Vert _{L^2}+\Vert e^n\Vert _{L^2}), \end{aligned}$$

(3.24)

where $C_1$ is a positive constant only depending on $C_L,K_1,\theta$.

Substituting (3.24) into (3.23) and applying $(a+b)^2\le 2(a^2+b^2)$ with Young’s inequality, we have

$$\begin{aligned} ((D_{\tau }^{\alpha }e)^{n-\theta },e^{n,\theta })\le & {} \Vert e^{n,\theta }\Vert ^2_{L^2}+\frac{1}{4}\Vert r^{n,\theta }\Vert ^2_{L^2}+\Vert P^n\Vert _{L^2}\Vert e^{n,\theta }\Vert _{L^2}\nonumber \\\le & {} 2(1 - \theta )^2\Vert e^n\Vert ^2_{L^2} + 2\theta ^2\Vert e^{n-1}\Vert ^2_{L^2} + \frac{C_1^2}{2}(\Vert e^{n-1}\Vert ^2_{L^2} + \Vert e^n\Vert ^2_{L^2})\\&+\Vert P^n\Vert _{L^2}\Vert e^{n,\theta }\Vert _{L^2}\\\le & {} [2\theta ^2+\frac{C_1^2}{2}]\Vert e^{n-1}\Vert ^2_{L^2} + [2(1-\theta )^2 + \frac{C_1^2}{2}]\Vert e^n\Vert ^2_{L^2} + \Vert P^n\Vert _{L^2}\Vert e^{n,\theta }\Vert _{L^2}\\\le & {} C_2\Vert e^{n-1}\Vert ^2_{L^2}+C_3\Vert e^n\Vert ^2_{L^2}+\Vert P^n\Vert _{L^2}\Vert e^{n,\theta }\Vert _{L^2}, \end{aligned}$$

where $C_2=2\theta ^2+\frac{C_1^2}{2},C_3=2(1-\theta )^2+\frac{C_1^2}{2}$. Recall Lemma 3.2, the inequality above further implies

$$\begin{aligned} \frac{1}{2}\sum _{k=1}^{n}A_{n-k}^{(n)}\nabla _{\tau }\Vert e^k\Vert ^2_{L^2}\le C_2\Vert e^{n-1}\Vert ^2_{L^2}+C_3\Vert e^n\Vert ^2_{L^2}+\Vert P^n\Vert _{L^2}\Vert e^{n,\theta }\Vert _{L^2}. \end{aligned}$$

Applying the discrete Grönwall inequality in Lemmas 3.3–3.6, we have there exists a $\tilde{\tau }_2 ~(0<\tilde{\tau }_2\le (2\pi _A\Gamma (2-\alpha )(C_2+C_3))^{-\frac{1}{\alpha }}$ such that

$$\begin{aligned} \Vert e^n\Vert _{L^2}\le & {} 4E_\alpha (4\max (1,\rho )\pi _A(C_2+C_3)t_n^\alpha )\max _{1\le k\le n}\sum _{j=1}^{k}P_{k-j}^{(k)}\Vert P^j\Vert _{L^2}\nonumber \\\le & {} 4E_\alpha (4\max (1,\rho )\pi _A(C_2+C_3) t_n^\alpha )\max _{1\le k\le n}\sum _{j=1}^{k}P_{k-j}^{(k)}\Vert P^j\Vert _{L^2}\nonumber \\\le & {} 4E_\alpha (4\max (1,\rho )\pi _A(C_2+C_3) t_n^\alpha )C_\nu \left( \frac{\tau _1^\sigma }{\sigma } + {\max _{2\le k\le n}t_k}^{\sigma - \frac{3-\alpha }{\gamma }}\tau ^{3 - \alpha } + \frac{\tau _1^{\sigma +\alpha }}{\sigma }\nonumber \right. \\&\left. +t_n^\alpha \max _{2\le k\le n}t_{k-1}^{\sigma -2}\tau _k^2 + \tau _1^{2\sigma +\alpha }+t_n^\alpha \max _{2\le k\le n}t_{k-1}^{2(\sigma -1)}\tau _k^2\right) \nonumber \\\le & {} C_4\left( \frac{\tau _1^\sigma }{\sigma } + {\max _{2\le k\le n}t_k}^{\sigma - \frac{3-\alpha }{\gamma }}\tau ^{3 - \alpha } + t_n^\alpha \max _{2\le k\le n}t_{k-1}^{\sigma -2}\tau _k^2 + t_n^\alpha \max _{2\le k\le n}t_{k-1}^{2(\sigma -1)}\tau _k^2\right) ,\nonumber \\ \end{aligned}$$

(3.25)

where $C_4=4 C_\nu E_\alpha (4\max (1,\rho )\pi _A(C_2+C_3) t_n^\alpha )$ is a positive constant independent of $n,\tau$ and h. In addition, denote $\zeta =\min \{2,\sigma \gamma \}$, we have for $2\le k\le n$,

$$\begin{aligned} t_{k-1}^{\sigma -2}\tau _k^2\le & {} C_\gamma t_k^{\sigma -2}\tau _k^2\le C_\gamma t_k^{\sigma -2}\tau _k^{2-\zeta }\left( \tau \min \{1,t_k^{1-\frac{1}{\gamma }}\}\right) ^\zeta \nonumber \\\le & {} C_\gamma t_{k}^{\sigma -2}\tau _k^{2-\zeta }\tau ^\zeta t_k^{\zeta -\frac{\zeta }{\gamma }}\nonumber \\\le & {} C_\gamma t_k^{\sigma -\frac{\zeta }{\gamma }}(\tau _k/t_k)^{2-\zeta }\tau ^{\zeta }. \end{aligned}$$

(3.26)

Therefore,

$$\begin{aligned} \Vert e^n\Vert _{L^2}\le C_4[C_\gamma \tau ^{\sigma \gamma }+C_\gamma t_n^{\alpha +\sigma -\frac{\zeta }{\gamma }}(\tau _k/t_k)^{2-\zeta }\tau ^{\zeta }]\le C_4C_\gamma T^{\alpha +\sigma -\frac{\zeta }{\gamma }}\tau ^{\zeta }=C_5\tau ^{\min \{\sigma \gamma ,2\}},\nonumber \\ \end{aligned}$$

(3.27)

where $C_5=C_4 C_\gamma T^{\alpha +\sigma -\frac{\zeta }{\gamma }}$.

Similarly, multiplying by $-\Delta e^{n,\theta }$ and $\Delta ^2 e^{n,\theta }$ in (3.15), respectively, integrating it over $\Omega$ and using Cauchy–Schwarz inequality and the condition of boundary value (3.11), we have, there exist two constant $\tilde{C}_2$ and $\tilde{C}_3$, such that

$$\begin{aligned} ((D_{\tau }^{\alpha }\nabla e)^{n-\theta },\nabla e^{n,\theta })\le \Vert \nabla P^n\Vert _{L^2}\Vert \nabla e^{n,\theta }\Vert _{L^2}+{ \tilde{C}_2}\Vert \nabla e^n\Vert ^2_{L^2}+{ \tilde{C}_3}\Vert \nabla e^{n-1}\Vert ^2_{L^2}, \end{aligned}$$

(3.28)

and

$$\begin{aligned} ((D_{\tau }^{\alpha }\Delta e)^{n-\theta },\Delta e^{n,\theta })\le \Vert \Delta P^n\Vert _{L^2}\Vert \Delta e^{n,\theta }\Vert _{L^2}+{ \tilde{C}_2}\Vert \Delta e^n\Vert ^2_{L^2}+{ \tilde{C}_3}\Vert \Delta e^{n-1}\Vert ^2_{L^2}, \end{aligned}$$

(3.29)

where we have noted (3.17).

By Lemmas 3.2 and 3.3 , there exists a positive constant ${\tilde{\tau }_3}$, when $\tau \le {\tilde{\tau }_3}$, such that

$$\begin{aligned} \Vert \nabla e^n\Vert _{L^2}\le 4E_\alpha (2\max (1,\rho )\pi _A{\lambda } t_n^\alpha )\max _{1\le k\le n}\sum _{j=1}^{k}P_{k-j}^{(k)}\Vert \nabla P^j\Vert _{L^2}, \end{aligned}$$

and there exists a positive constant ${\tilde{\tau }_4}$, when $\tau \le {\tilde{\tau }_4}$, such that

$$\begin{aligned} \Vert \Delta e^n\Vert _{L^2}\le 4E_\alpha (2\max (1,\rho )\pi _A{\lambda } t_n^\alpha )\max _{1\le k\le n}\sum _{j=1}^{k}P_{k-j}^{(k)}\Vert \Delta P^j\Vert _{L^2}, \end{aligned}$$

where the constant $\lambda$ is independent of $\tau$ and h.

Together with Lemmas 3.2–3.4, we obtain

$$\begin{aligned}&\Vert \nabla e^n\Vert _{L^2}\le C_6 \tau ^{\min \{\sigma \gamma ,2\}}, \end{aligned}$$

(3.30)

$$\begin{aligned}&\Vert \Delta e^n\Vert _{L^2}\le C_7 \tau ^{\min \{\sigma \gamma ,2\}}. \end{aligned}$$

(3.31)

Now, by (3.27), (3.30) and (3.31), we get, when $\tau \le {\tilde{\tau }_5}=\min \{{\tilde{\tau }_1,\tilde{\tau }_2,\tilde{\tau }_3,\tilde{\tau }_4}\}$,

$$\begin{aligned} \Vert e^n\Vert _{H^2}\le & {} \sqrt{\Vert e^n\Vert ^2_{L^2}+\Vert \nabla e^n\Vert ^2_{L^2}+\Vert \Delta e^n\Vert ^2_{L^2}}\\\le & {} \sqrt{C_5+C_6+C_7}\tau ^{\min \{\sigma \gamma ,2\}}\\\le & {} C_c\tau ^{\min \{\sigma \gamma ,2\}}, \end{aligned}$$

which further implies that

$$\begin{aligned} \Vert U^n\Vert _{H^2}\le \Vert u^n\Vert _{H^2}+\Vert e^n\Vert _{H^2}\le \Vert u^n\Vert _{H^2}+C_c\tau ^{\min \{\sigma \gamma ,2\}}\le K_1, \end{aligned}$$

when $\tau \le {\tilde{\tau }}_6= C_c^{-\frac{1}{\min \{\sigma \gamma ,2\}}}$. Taking $\tau _1^*=\min \{{\tilde{\tau }_1,\tilde{\tau }_2,\tilde{\tau }_3,\tilde{\tau }_4,\tilde{\tau }_5,\tilde{\tau }_6}\}$, we conclude that the result (3.18) holds for $m=n$.

Using the definition of $(D_{\tau }^{\alpha }v)^{n-\theta }$, we arrive that

$$\begin{aligned} \Vert (D_{\tau }^{\alpha }e)^{n-\theta }\Vert _{H^2}\le & {} A_0^{(n)}\Vert e^n\Vert _{H^2}+\sum _{k=1}^{n-1}(A_{n-k}^{(n)}-A_{n-k-1}^{(n)})\Vert e^k\Vert _{H^2}-A_{n-1}^{(n)}\Vert e^0\Vert _{H^2}\\\le & {} \left[ A_0^{(n)}+\sum _{k=1}^{n-1}(A_{n-k}^{(n)}-A_{n-k-1}^{(n)})\right] C_1^*\tau ^{\min \{\sigma \gamma ,2\}}\\\le & {} A_0^{(n)}C_1^*\tau ^{\min \{\sigma \gamma ,2\}}\\\le & {} \frac{24\tau _n^{-\alpha }}{11\Gamma (2-\alpha )}C_1^*\tau ^{\min \{\sigma \gamma ,2\}}, \end{aligned}$$

where $A_0^{(n)}\le \tilde{a}_{0}^{(n)}+\rho _{n-1}\tilde{b}_{1}^{(n)}\le \frac{24}{11\tau _n}\int _{t_{n-1}}^{t_n} w_{1-\alpha }(t_n-s)ds$ is used under the condition A3 and the proof can be found in Theorem 2.2 of reference [34].

Therefore

$$\begin{aligned} \Vert (D_{\tau }^{\alpha } U)^{n-\theta }\Vert _{H^2}\le \Vert (D_{\tau }^{\alpha }u)^{n-\theta }\Vert _{H^2}+\Vert (D_{\tau }^{\alpha }e)^{n-\theta }\Vert _{H^2}\le C_1^{**}, \end{aligned}$$

the mathematical induction is closed, which completes the proof. $\square$

3.3 Analysis of Spatial-Discrete System

In this subsection, we aim to get the boundedness of the numerical solutions. Firstly, by Theorem 3.1 and $\Vert R_h \upsilon \Vert _{L^\infty }\le C_{\Omega }\Vert \upsilon \Vert _{H^2}$ for any $\upsilon \in H^2(\Omega )$, we can obtain $\Vert R_h U^n\Vert _{L^{\infty }}$ is bounded. Therefore, we define

$$\begin{aligned} K_2=\max _{1\le n\le N}\Vert R_h U^n\Vert _{L^{\infty }}+1. \end{aligned}$$

(3.32)

The weak form of Eq. (3.9) can be written as

$$\begin{aligned} ((D_{\tau }^{\alpha }U)^{n-\theta },v)= & {} (\Delta U^{n,\theta },v) \nonumber \\&+ (g(U^{n-1}) + g_1(U^{n-1})(1-\theta )(U^n-U^{n-1}),v),~\forall v\in H_0^1,\nonumber \\ \end{aligned}$$

(3.33)

where $n=1,2,\ldots ,N$.

Let

$$\begin{aligned} U^n-U_h^n=U^n-R_h U^n+R_h U^n-U_h^n=U^n-R_h U^n+\vartheta _h^n,\quad n=0,1,2,\ldots , N. \end{aligned}$$

Subtracting (2.3) from (3.33) and using (3.7), we have

$$\begin{aligned}&((D_{\tau }^{\alpha }\vartheta _h)^{n-\theta },v)+(\nabla \vartheta _h^{n,\theta },\nabla v)-(R_2^n,v)\nonumber \\&\quad =-((D_{\tau }^{\alpha }(U^n-R_h U^n))^{n-\theta },v), ~~~for~~v\in V_h, \end{aligned}$$

(3.34)

where

$$\begin{aligned} R_2^n= & {} g(U^{n-1}) + g_1(U^{n-1})(1-\theta )(U^n-U^{n-1})\nonumber \\&-[g(U_h^{n-1})+g_1(U_h^{n-1})(1-\theta )(U_h^n - U_h^{n-1})]. \end{aligned}$$

(3.35)

Theorem 3.2

Let $U^m$ and $U_h^m$ be the solutions of (3.33) and (2.3), respectively. Then, for $m=1,2,3,\ldots , N$, there exists $\tau _2^*>0$, $h_1^*>0$ such that, when $\tau \le \tau _2^*$, $h\le h_1^*$,

$$\begin{aligned}&\Vert \vartheta _h^m\Vert _{L^2}\le h^{\frac{11}{6}}, \end{aligned}$$

(3.36)

$$\begin{aligned}&\Vert U_h^m\Vert _{L^{\infty }}\le K_2. \end{aligned}$$

(3.37)

Proof

As the fact that the coefficient matrix of the resulting equation is diagonally dominant when taking sufficiently small $\tau$, the solution of the Eq. (3.33) exists and is unique. Next, we still prove (3.36) by mathematic induction. Since $U_h^0=R_h u_0$, we have (3.36) holds for $m=0$.

Now, suppose that (3.36) holds for $m=1,\cdots ,n-1$. We will show the result holds for $m=n$. By the assumption and (3.32), we have

$$\begin{aligned} \Vert U_h^m\Vert _{L^{\infty }}\le & {} \Vert R_h U^m\Vert _{L^{\infty }}+\Vert R_h U^m-U_h^m\Vert _{L^{\infty }}\nonumber \\\le & {} \Vert R_h U^m\Vert _{L^{\infty }}+C_{\Omega }h^{-\frac{d}{2}}\Vert R_h U^m-U_h^m\Vert _{L^2}\nonumber \\\le & {} \Vert R_h U^m\Vert _{L^{\infty }}+C_{\Omega }h^{-\frac{d}{2}}h^{\frac{11}{6}}\nonumber \\\le & {} \Vert R_h U^m\Vert _{L^{\infty }}+1\nonumber \\\le & {} K_2, \end{aligned}$$

(3.38)

for $d=2,3$ and $h\le h_1=C_{\Omega }^{-\frac{6}{11-3d}}.$

With the similar approach of processing $r^n$, we can obtain that

$$\begin{aligned} R_2^n= & {} g(U^{n-1}) - g(U_h^{n-1})+(1-\theta )g_1(U^{n-1})(U^n-U^{n-1})\\&-\, (1 - \theta )g_1(U_h^{n-1})(U_h^n-U_h^{n-1})\\= & {} g(U^{n-1}) - g(U_h^{n-1}) + (1 - \theta )[g_1(U^{n-1})U^n - g_1(U_h^{n-1})U^n\\&+\, g_1(U_h^{n-1})U^n - g_1(U_h^{n-1})U_h^n]\\&-(1 - \theta )[g_1(U^{n-1})U^{n-1} - g_1(U_h^{n-1})U^{n-1} + g_1(U_h^{n-1})U^{n-1} - g_1(U_h^{n-1})U_h^{n-1}]\\= & {} g(U^{n-1}) - g(U_h^{n-1}) + (1-\theta )[g_1(U^{n-1}) - g_1(U_h^{n-1})]U^n\\&+\, (1-\theta )g_1(U_h^{n-1})(U^n-U_h^n)\\&-\, (1-\theta )[g_1(U^{n-1})-g_1(U_h^{n-1})]U^{n-1}-(1-\theta )g_1(U_h^{n-1})(U^{n-1}-U_h^{n-1}). \end{aligned}$$

Considering the boundedness of $\Vert U^n\Vert _{H^2}, \Vert U_h^{n-1}\Vert _{L^{\infty }}$ and $g\in C^2(\mathbb {R})$, we can see that, there exists a positive constant $C_g$ dependent on $C_1^*, K_2, C_{\Omega }$ such that

$$\begin{aligned} \Vert g_1(U_h^{n-1})\Vert _{L^2}\le & {} C_g, \end{aligned}$$

(3.39)

$$\begin{aligned} \Vert g(U^{n-1})-g(U_h^{n-1})\Vert _{L^2}\le & {} C_g\Vert U^{n-1}-U_h^{n-1}\Vert _{L^2}, \end{aligned}$$

(3.40)

$$\begin{aligned} \Vert g_1(U^{n-1})-g_1(U_h^{n-1})\Vert _{L^2}\le & {} C_g\Vert U^{n-1}-U_h^{n-1}\Vert _{L^2}, \end{aligned}$$

(3.41)

which further implies that

$$\begin{aligned} \Vert R_2^n\Vert _{L^2}\le & {} 2C_g(K_1+1)\Vert U^{n-1}-U_h^{n-1}\Vert _{L^2}+C_g\Vert U^n-U_h^n\Vert _{L^2}\nonumber \\\le & {} 2C_g(K_1+1)(\Vert U^{n-1} - R_h U^{n-1}\Vert _{L^2} + \Vert \vartheta _h^{n-1}\Vert _{L^2})\nonumber \\&+\, C_g(\Vert U^n - R_h U^n\Vert _{L^2} + \Vert \vartheta _h^n\Vert _{L^2})\nonumber \\\le & {} 2C_g(K_1+1)(C_\Omega K_1h^2+\Vert \vartheta _h^{n-1}\Vert _{L^2})+C_g(C_\Omega K_1h^2+\Vert \vartheta _h^{n}\Vert _{L^2})\nonumber \\\le & {} C_K h^2+2C_g(K_1+1)\Vert \vartheta _h^{n-1}\Vert _{L^2}+C_g\Vert \vartheta _h^{n}\Vert _{L^2}. \end{aligned}$$

(3.42)

Here $C_K$ is a positive constant independent of n but dependent on $K_1, C_g, C_{\Omega }$. Taking $v=\vartheta _h^{n,\theta }$ in Eq. (3.34), we obtain

$$\begin{aligned} ((D_{\tau }^{\alpha }\vartheta _h)^{n-\theta },\vartheta _h^{n,\theta }) + (\nabla \vartheta _h^{n,\theta },\nabla \vartheta _h^{n,\theta }) - (R_2^n,\vartheta _h^{n,\theta })+((D_{\tau }^{\alpha }(U-R_h U))^{n-\theta },\vartheta _h^{n,\theta })=0. \end{aligned}$$

Notice that $\Vert \nabla \vartheta _h^{n,\theta }\Vert ^2_{L^2}\ge 0$ , we have

$$\begin{aligned} ((D_{\tau }^{\alpha }\vartheta _h)^{n-\theta },\vartheta _h^{n,\theta })\le \Vert R_2^n\Vert _{L^2}\Vert \vartheta _h^{n,\theta }\Vert _{L^2}+\Vert (D_{\tau }^{\alpha }(U-R_h U))^{n-\theta }\Vert _{L^2}\Vert \vartheta _h^{n,\theta }\Vert _{L^2}. \end{aligned}$$

(3.43)

Substituting (3.42) into (3.43) and using Lemma 3.2, the above inequality further gives that

$$\begin{aligned} \frac{1}{2}\sum _{k=1}^{n}A_{n-k}^{(n)}\nabla _\tau \Vert \vartheta _h^n\Vert ^2_{L^2}\le & {} \Vert R_2^n\Vert _{L^2}\Vert \vartheta _h^{n,\theta }\Vert _{L^2}+\Vert (D_{\tau }^{\alpha }(U-R_h U))^{n-\theta }\Vert _{L^2}\Vert \vartheta _h^{n,\theta }\Vert _{L^2}\\\le & {} C_Kh^2\Vert \vartheta _h^{n,\theta }\Vert _{L^2}+2C_g(K_1+1)\Vert \vartheta _h^{n-1}\Vert _{L^2}\Vert \vartheta _h^{n,\theta }\Vert _{L^2}\\&+C_g\Vert \vartheta _h^{n}\Vert _{L^2}\Vert \vartheta _h^{n,\theta }\Vert _{L^2} + \Vert (D_{\tau }^{\alpha }(U - R_h U))^{n-\theta }\Vert _{L^2}\Vert \vartheta _h^{n,\theta }\Vert _{L^2}\\\le & {} C_{10}\Vert \vartheta _h^{n-1}\Vert ^2_{L^2}+C_{11}\Vert \vartheta _h^n\Vert ^2_{L^2}+C_K h^2\Vert \vartheta _h^{n,\theta }\Vert _{L^2}\\&+\Vert (D_{\tau }^{\alpha }(U-R_h U))^{n-\theta }\Vert _{L^2}\Vert \vartheta _h^{n,\theta }\Vert _{L^2}\\\le & {} C_{10}\Vert \vartheta _h^{n-1}\Vert ^2_{L^2} + C_{11}\Vert \vartheta _h^n\Vert ^2_{L^2} \\&+ (C_K + C_\Omega \Vert (D_{\tau }^{\alpha }U)^{n-\theta }\Vert _{H^2})h^2\Vert \vartheta _h^{n,\theta }\Vert _{L^2}, \end{aligned}$$

where $C_{10}=2C_g(K_1+1)+\frac{C_g\theta }{2}, C_{11}=C_g(K_1+1)(1-\theta )+\frac{C_g(2-\theta )}{2}$.

Applying the inequality (3.19), Lemma 3.3 and $U_h^0=R_h u^0$, we arrive

$$\begin{aligned} \Vert \vartheta _h^n\Vert _{L^2}\le & {} 2E_{\alpha }(4\max (1,\rho )\pi _A(C_{10}+C_{11})t_n^\alpha )[\Vert \vartheta _h^0\Vert _{L^2}\\&+2\pi _A\Gamma (2-\alpha )t_n^\alpha ( C_k+ C_{\Omega }K_1) h^2]\\\le & {} 4E_{\alpha }(4\max (1,\rho )\pi _A(C_{10}+C_{11})t_n^\alpha )[\pi _A\Gamma (2-\alpha )T^\alpha ( C_k+C_\Omega C_1^{**})]h^2\\\le & {} h^{\frac{11}{6}}, \end{aligned}$$

where $h\le h_2=[4E_{\alpha }(4\max (1,\rho )\pi _A{(C_{10}+C_{11})}t_n^\alpha )(\pi _A\Gamma (2-\alpha )T^\alpha (C_k+C_\Omega C_1^{**}))]^{-\frac{1}{6}}$.

Furthermore,

$$\begin{aligned} \Vert U_h^n\Vert _{L^{\infty }}\le \Vert R_h U^n\Vert _{L^{\infty }}+\Vert \vartheta _h^n\Vert _{L^{\infty }}\le \Vert R_h U^n\Vert _{L^{\infty }}+C_{\Omega }h^{-d/2}h^{\frac{11}{6}}\le K_2. \end{aligned}$$

Then, (3.36) and (3.37) hold for $m=n$. The mathematical induction is done and the proof is completed. $\square$

3.4 Optimal Error Estimates

In Sect. 3.3, the boundedness of $\Vert U_h^n\Vert _{L^\infty }$ is obtained without certain time-step restrictions dependent on the spatial mesh sizes. Thanks to the results, we are ready to get the unconditionally optimal error estimates.

The weak form of Eq. (3.13) satisfies

$$\begin{aligned}&((D_{\tau }^{\alpha }u)^{n-\theta },v) - (\Delta u^{n,\theta },v) - (g(u^{n-1})\nonumber \\&\quad +g_1(u^{n-1})(1-\theta )(u^n-u^{n-1}),v) = (P^n,v), ~~\forall {v}\in V_h. \end{aligned}$$

(3.44)

Denote

$$\begin{aligned} u^n-U_h^n=u^n-{R_h u^n+R_h u^n-U_h^n}={u^n-R_h u^n}+\eta _h^n,\quad n=0,1,2,\ldots , N.\nonumber \\ \end{aligned}$$

(3.45)

Subtracting (3.44) from (2.3) gives

$$\begin{aligned} ((D_{\tau }^{\alpha } \eta _h)^{n-\theta },v)+(\nabla \eta _h^{n,\theta },\nabla v)-(R_3^n,v)=(P^n,v)+(R_4^n,v), \end{aligned}$$

(3.46)

where

$$\begin{aligned} R_3^n= & {} g(u^{n-1})+g_1(u^{n-1})(1-\theta )(u^n-u^{n-1})\\&-\,[g(U_h^{n-1})+g_1(U_h^{n-1})(1-\theta )(U_h^n-U_h^{n-1})] \end{aligned}$$

and

$$\begin{aligned} R_4^n=(D_{\tau }^{\alpha }(u-R_h u))^{n-\theta }. \end{aligned}$$

By (3.37),

$$\begin{aligned} \Vert R_3^n\Vert _{L^2}\le & {} \Vert g(u^{n-1})+g_1(u^{n-1})(1-\theta )(u^n-u^{n-1})\nonumber \\&-\, [g(U_h^{n-1})+g_1(U_h^{n-1})(1-\theta )(U_h^n-U_h^{n-1})]\Vert _{L^2}\nonumber \\\le & {} \Vert g(u^{n-1})-g(U_h^{n-1})\Vert _{L^2}+(1-\theta )[~\Vert (g_1(u^{n-1})-g_1(U_h^{n-1}))u^n\Vert _{L^2}\nonumber \\&+\, \Vert g_1(U_h^{n-1})(u^n-U_h^n)\Vert _{L^2}]+(1-\theta )[\Vert g_1(u^{n-1})(u^n-U_h^{n-1})\Vert _{L^2}\nonumber \\&+\, \Vert (g_1(u^{n-1})-g_1(U_h^{n-1}))U_h^{n-1}\Vert _{L^2}]\nonumber \\\le & {} C_{12}(\Vert u^n-U_h^n\Vert _{L^2}+\Vert u^{n-1}-U_h^{n-1}\Vert _{L^2})\nonumber \\\le & {} C_{12}(C_{\Omega }\Vert u^n\Vert _{r+1}h^{r+1}+\Vert \eta _h^n\Vert _{L^2}+C_{\Omega }\Vert u^{n-1}\Vert _{r+1}h^{r+1}+\Vert \eta _h^{n-1}\Vert _{L^2})\nonumber \\\le & {} C_{12}(\Vert \eta _h^{n-1}\Vert _{L^2}+\Vert \eta _h^n\Vert _{L^2}+C_{\Omega }h^{r+1}), \end{aligned}$$

(3.47)

where $C_{12}$ is a constant dependent on u and g.

Substituting $v=\eta _h^{n,\theta }$ into (3.46) and using Cauchy–Schwarz inequality, we derive

$$\begin{aligned} ((D_{\tau }^{\alpha }\eta _h)^{n-\theta },\eta _h^{n,\theta })\le & {} \Vert R_3^n\Vert _{L^2}\Vert \eta _h^{n,\theta }\Vert _{L^2}+\Vert P^n\Vert _{L^2}\Vert \eta _h^{n,\theta }\Vert _{L^2}+\Vert R_4^n\Vert _{L^2}\Vert \eta _h^{n,\theta }\Vert _{L^2}\nonumber \\\le & {} C_{12}\left[ \theta + \frac{(1-\theta )^2}{2}+(1-\theta )\right] \Vert \eta _h^{n-1}\Vert ^2_{L^2}\nonumber \\&+\, C_{12}\left[ \frac{(1-\theta )^2}{2} + (1 - \theta )\right] \Vert \eta _h^n\Vert ^2_{L^2}\nonumber \\&+\, C_{12}C_\Omega h^{r+1}\Vert \eta _h^{n,\theta }\Vert _{L^2}+\Vert P^n\Vert _{L^2}\Vert \eta _h^{n,\theta }\Vert _{L^2}+\Vert R_4^n\Vert _{L^2}\Vert \eta _h^{n,\theta }\Vert _{L^2}\nonumber \\\le & {} \frac{3C_{12}}{2}(\Vert \eta _h^n\Vert ^2_{L^2}+\Vert \eta _h^{n-1}\Vert ^2_{L^2})+C_{12}C_{\Omega }h^{r+1}\Vert \eta _h^{n,\theta }\Vert _{L^2}\nonumber \\&+\, \Vert P^n\Vert _{L^2}\Vert \eta _h^{n,\theta }\Vert _{L^2}+\Vert R_4^n\Vert _{L^2}\Vert \eta _h^{n,\theta }\Vert _{L^2}. \end{aligned}$$

(3.48)

Together with the regularity of exact solution u, we get

$$\begin{aligned} \max _{1\le k\le n}\sum _{j=1}^{k}P_{k-j}^{(k)}\Vert R_4^j\Vert _{L^2}\le & {} \max _{1\le k\le n}\sum _{l=1}^{k}\sum _{j=l}^{k}P_{k-j}^{(k)}A_{j-l}^{(j)}\Vert \nabla _\tau (u^l-R_h u^l)\Vert _{L^2}\\\le & {} \max _{1\le k\le n}\sum _{l=1}^{k}\Vert \nabla _\tau (u^l-R_h u^l)\Vert _{L^2}\\\le & {} \max _{1\le k\le n}\sum _{l=1}^{k}\int _{t_{l-1}}^{t_l}\Vert (u-R_h u)'(t)\Vert _{L^2}dt\\\le & {} C_\Omega h^{r+1}\int _{0}^{t_n}\Vert u'(t)\Vert _{H^{r+1}}dt\le C_\Omega (t_n+t_n^\sigma ) h^{r+1}. \end{aligned}$$

By Lemmas 3.3, 3.4 and 3.6, there exists a positive constant $\tau _3^*$, when $\tau \le \tau _3^*$, it holds

$$\begin{aligned} \Vert \eta _h^n\Vert _{L^2}\le & {} 4E_\alpha (2\max (1,\rho )\pi _A3C_{12}t_n^\alpha )[\Vert \eta _h^0\Vert _{L^2}+\max _{1\le k\le n}\sum _{j=1}^{k}P_{k-j}^{(k)}(\Vert P^j\Vert _{L^2}+\Vert R_4^j\Vert _{L^2})\\&+\, \pi _A\Gamma (2-\alpha )t_n^\alpha C_{12}C_{\Omega }h^{r+1}]\\\le & {} 4E_\alpha (6\max (1,\rho )\pi _AC_{12}t_n^\alpha )[C_{12}C_{\Omega }h^{r+1}+C_p\tau ^{\min \{\sigma \gamma ,2\}}]\\\le & {} C_{13}(h^{r+1}+\tau ^{\min \{\sigma \gamma ,2\}}), \end{aligned}$$

where $C_{13}=4E_\alpha (6\max (1,\rho )\pi _AC_{12}t_n^\alpha )(C_{12}C_\Omega +C_p)$.

With (3.8), the above inequality further implies that

$$\begin{aligned} \Vert u^n-U_h^n\Vert _{L^2}\le \Vert u^n-R_h u^n\Vert _{L^2}+\Vert R_h u^n-U_h^n\Vert _{L^2}\le (C_\Omega C+C_{13})(\tau ^{\min \{\sigma \gamma ,2\}}+h^{r+1}),\nonumber \\ \end{aligned}$$

(3.49)

for $1\le n\le N$. Therefore, (2.6) holds when $\tau \le \tau _0 = \min \{\tau _1^*,\tau _2^*,\tau _3^*\},h \le h_0 = h_1^*$ and $C_0\ge C_\Omega C + C_{13}$. This completes the proof of the Theorem 2.1.

4 Numerical Experiments

In this section, we present several numerical examples to confirm the theoretical results. In the numerical experiments, the interval [0,T] is divided into two parts $[0,T_0]\cup [T_0,T]$, where $T_0:=2^{-\gamma }$. In the interval $[0,T_0]$, we let $t_n=(n/N_0)^\gamma T_0$ for $0\le n\le N_0$, where $N_0:=\lceil \frac{\gamma N}{2^\gamma -1+\gamma }\rceil$. The smoothly graded meshes are applied in the first part $[0,T_0]$ and a uniform is used in the interval $[T_0,T]$.

Example 1

Consider the two-dimensional time-fractional Fisher’s equation, which are widely used in heat and mass transfer, ecology and physiology [2].

$$\begin{aligned} \partial _t^\alpha u-\Delta u-u(1-u)=g,~~~~~~~~~~~x\in \Omega ,~~0<t<1, \end{aligned}$$

(4.1)

where $\Omega =[0,1]^2$. The initial condition and the source term g are chosen correspondingly to the exact solution

$$\begin{aligned} u=(1+t^\sigma )x^2(1-x)^3y^2(1-y)^3. \end{aligned}$$

Table 1 The errors and orders with $\sigma =\alpha =0.4,\gamma =2/\sigma$ (Example 4.1)

Table 2 The errors and orders with $\sigma =\alpha =0.6,\gamma =2/\sigma$ (Example 4.1)

Table 3 The errors and orders with $\sigma =\alpha =0.8,\gamma =2/\sigma$ (Example 4.1)

Fig. 1

2D problem:   $L^2$-errors of linear element approximations with fixed $\tau$ by changing spatial mesh sizes

Fig. 2

2D problem:   $L^2$-errors of quadratic element approximations with fixed $\tau$ by changing spatial mesh sizes

Fig. 3

3D problem:   $L^2$-errors of quadratic element approximations with fixed $\tau$ by changing spatial mesh sizes ($\alpha =0.6$)

To verify the numerical errors and convergence orders in temporal and spatial direction, the $L^2$-norm of the error is computed with $\sigma =\alpha$ and $\sigma \gamma =2$ for different $\alpha$ and $N=\lceil M^{(r+1)/2}\rceil$ with $M=10,20,40,80$. Here, M means uniform triangular partition with $M+1$ nodes in each direction. That is to say, we choose $M=N$ with linear finite element methods (L-FEMs) and $N=\lceil M^{3/2}\rceil$ for Q-FEMs, respectively. The numerical errors are shown in Tables 1, 2 and 3, respectively. It can be clearly seen that all convergence results agree with theoretical findings.

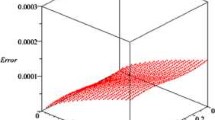
At the same time, the unconditional convergence can be confirmed by taking $\tau =1/5,1/10,1/20,1/40$ with L-FEMs and Q-FEMs. We plot the numerical results in Figs. 1 and 2, respectively. We can see that the errors tend to be a constant. The numerical results indicate that the error estimates hold without certain time-step restrictions dependent on the spatial mesh sizes.

Example 2

Consider the three-dimensional time fractional Allen–Cahn equation,

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle _0^C D_t^\alpha u-\Delta u-u(1-u^2)=g,&{}x\in \Omega ,~~0<t<1,\\ u(x,0)=u_0(x),&{}x\in \Omega ,\\ u=0,&{}x\in \partial \Omega , \end{array}\right. \end{aligned}$$

(4.2)

where $\Omega = [0,1]^3$, g is chosen correspondingly to the exact solution

$$\begin{aligned} u=(1+t^\sigma )\sin (\pi x)\sin (\pi y)\sin (\pi z). \end{aligned}$$

Table 4 The errors and orders in temporal and spatial direction with linear element ($\sigma =\alpha ,\gamma =2/\sigma$) (Example 4.2)

We solve problem (4.2) by using L-FEMs with $M=N$. The numerical results and the convergence orders are given in Table 4. Figure 3 illustrates that the errors tend to a constant, which implies that the conditional time steps are not needed.

5 Conclusions

In this paper, a linearized nonuniform Alkihanov FEM is proposed to solve TFPE effectively. Optimal error estimates of the fully discrete scheme are obtained. Such convergence results hold without certain time-step restrictions dependent on the spatial mesh sizes.