Error Estimates of Mixed Finite Element Methods for Time-Fractional Navier–Stokes Equations

Abstract

This paper studies the Galerkin finite element approximation of time-fractional Navier–Stokes equations. The discretization in space is done by the mixed finite element method. The time Caputo-fractional derivative is discretized by a finite difference method. The stability and convergence properties related to the time discretization are discussed and theoretically proven. Under some certain conditions that the solution and initial value satisfy, we give the error estimates for both semidiscrete and fully discrete schemes. Finally, a numerical example is presented to demonstrate the effectiveness of our numerical methods.

1 Introduction

Let $\varOmega \subset \mathbf {R}^2$ be a bounded and connected polygonal domain. We consider the following Navier–Stokes equations with a time fractional differential operator

$$\begin{aligned} \left\{ \begin{array}{ll} cD^{\alpha }_tu-\nu \triangle u+u\cdot \nabla u+\nabla p=f,\ \ \quad &{}\text {in}\ \ \quad \varOmega \times [0, T],\\ \nabla \cdot u=0,\ \ \quad &{}\text {in}\ \ \quad \varOmega \times [0, T],\\ u(x,0)=u_{0},\ \ \quad &{}\text {in}\ \ \quad \varOmega \\ u=0,\ \ \quad &{}\text {on}\ \ \quad \partial \varOmega \times [0, T],\\ \end{array}\right. \end{aligned}$$

(1)

where $\alpha \in (0,1)$ is a fixed number and $cD^{\alpha }_t$ is the Caputo fractional derivative(see Definition 2.1), $u=(u_1,u_2)$ represents the velocity field, $\nu >0$ is the viscosity coefficient, p is the associated pressure, $u_0$ is the initial velocity and $f=(f_1,f_2)$ is an external force.

The considered problem (1) is referred to as time-fractional Navier–Stokes equations (TFNSE for short) thereafter, which have many physical applications in many fields such as turbulence, heterogeneous flows and materials, viscoelasticity and electromagnetic theory. Particularly when $\alpha =1$, the problem (1) reduces to the classical Navier–Stokes equations, numerical approximations of which have been studied by many authors [2, 7–10, 12–14, 16–27, 29–32, 34, 35, 40–43]. At the same time, for the time-fractional Navier–Stokes equations like (1), Carvalho-Neto and Planas [28] have proved the existence, uniqueness, decay, and regularity properties of mild solutions to TFNSE. Momani and Odibat [33] have discussed the analytical solution of a time-fractional Navier–Stokes equations by Adomian decomposition method in a tube. However, to the best of our knowledge, numerical analysis of such problems for time-fractional Navier–Stokes equations is missing in the literature. Therefore, this article aims to fill the gap and investigate the strong approximations of TFNSE like (1).

Recently, fractional calculus have attracted enough attention, because of its non-local property of fractional derivative(and integrals). As a result, a number of numerical techniques for fractional differential equations have been developed and their stability and convergence have been investigated, see e.g. [3–6, 11, 15, 37–39]. Jin et al. [4], by using piecewise linear functions, have studied two semidiscrete approximation schemes for the homogeneous time-fractional diffusion equation. Zeng et al. [15] have studied the second-order accurate schemes for the time-fractional diffusion equation with unconditional stability. Two fully discrete schemes are firstly proposed for the time-fractional sub-diffusion equation with space discretized by finite element and time discretized by the fractional linear multistep methods. Jiang and Ma [37] have proposed high-order methods for solving time-fractional partial differential equations. The proposed high-order method is based on high-order finite element method for space and finite difference method for time. Lin and Xu [38] have proposed the finite difference scheme in time and Legendre spectral methods in space for the numerical solution of time-fractional diffusion equation. Liu et al. [39] have discussed the numerical solutions of a time-fractional fourth-order reaction-diffusion problem with a nonlinear reaction term, which is based on a finite difference approximation in time direction and finite element method in spatial direction.

Our aim is to obtain strong convergence error estimates for both semidiscrete and fully discrete schemes for the problem (1). The discretization in space is done by the mixed finite element method. The main difficulty in the error analysis about space discretization stems from the term of fractional derivative $cD^{\alpha }_t$ which makes the methods of energy type estimate and parabolic duality argument no more applicable. Following the idea of Heywood and Rannacher [25], firstly the velocity is split into two parts by introducing a linearized discrete problem with solution $v_h$. In particular, by defining certain approximations $S_hu$ of the solution of (1), the role of which is similar to that of a Ritz projection in treating the heat equation, using the Laplace transform techniques, as well as combing the propertied of the operator $\overline{E}_h$ with the bilinear operator $B(\cdot , \cdot )$, we derive the error estimate for the velocity. The time Caputo-fractional derivative is discretized by a finite difference method. The stability and convergence properties related to the time discretization are discussed and theoretically proven.

The structure of this paper is as follows: In Sect. 2, we introduce basic notations, give the definitions of the Caputo fractional differential operator and Mittag-Leffler function. In Sect. 3, we discuss the weak formulation, describe the semidiscrete Galerkin approximations about space and establish the error estimate for the velocity. In Sect. 4, we present several lemmas which play a crucial role in the proof of our main results. By discretizing the time-fractional derivative, we derive the fully discrete scheme for (1) and then give the error estimate for the fully discrete scheme. Finally, in Sect. 5, a numerical example is presented to demonstrate the effectiveness of our numerical methods.

2 Preliminaries

Throughout the paper, we denote as C a constant that may not be of the same form from one occurrence to another, even in the same line. In this section, we introduce basic notations, give the definitions of Mittag-Leffler function and the Caputo fractional differential operator.

We use the standard notation $H^s(\varOmega ), \Vert \cdot \Vert _s, (\cdot , \cdot )_s, s\ge 0$ for the Sobolev spaces, the standard Sobolev norm and inner product, respectively. When $s=0$, $L^2(\varOmega )$ is written instead of $H^0(\varOmega )$, the $L^2$-inner product and $L^2$-norm are separately denoted by $(\cdot , \cdot )$ and $\Vert \cdot \Vert$. For the mathematical setting of problem (1), the following spaces

$$\begin{aligned} X=H_0^1(\varOmega )^2,\ \ \ \ Y=L^2(\varOmega )^2,\ \ \ \ M=L_0^2(\varOmega )=\left\{ q\in L^2(\varOmega ):\int _{\varOmega } qdx=0\right\} , \end{aligned}$$

are introduced. Next, let the closed subset V of X be given by

$$\begin{aligned} V=\{v\in X, \text {div}\ v=0\}, \end{aligned}$$

and denote by H the closed subset of Y, i.e.,

$$\begin{aligned} H=\left\{ v\in Y, \text {div}\ v=0, v\cdot n|_{\partial \varOmega }=0\right\} . \end{aligned}$$

Moreover, we define the continuous bilinear forms $a(\cdot ,\cdot )$ and $d(\cdot ,\cdot )$ on $X\times X$ and $X\times M$, respectively, by

$$\begin{aligned} a(u,\phi )=\nu \left( \nabla u, \nabla \phi \right) , \ \ \forall u,v\in X,\ \ d(\phi ,p)=(\text {div}\phi , p), \ \ \forall \phi \in X ,\quad \forall p\in M, \end{aligned}$$

and a bilinear operator $B(\cdot ,\cdot )$ on $X\times X$ by

$$\begin{aligned} B(u,v)=(u\cdot \nabla )v+\frac{1}{2}(\text {div}u)v,\ \quad \forall u,v\in X. \end{aligned}$$

At the same time, a trilinear form $b(\cdot ,\cdot ,\cdot )$ on $X\times X\times X$ is introduced by

$$\begin{aligned} b(u,v,w)=(u\cdot \nabla v,w),\ \ u, v, w\in X, \end{aligned}$$

which has the following properties(cf.,[25, 35]):

$$\begin{aligned} b(u,v,w)= & {} -b(u,w,v),\ \ b(u,v,v)=0,\ \ \quad \forall u,v,w\in X,\\ \Vert b(u,v,w)\Vert\le & {} M\Vert \nabla u\Vert \Vert \nabla v\Vert \Vert \nabla w\Vert , \ \ \quad \forall u,v,w\in X. \end{aligned}$$

For the readers convenience, we recall the definitions of Mittag-Leffler function and the Caputo fractional differential operator. We shall use extensively the Mittag-Leffler function $E_{\alpha ,\beta }(z)$ [1] defined by

$$\begin{aligned} E_{\alpha ,\beta }(z)=\sum \limits _{k=0}^{\infty }\frac{z^k}{\varGamma (k\alpha +\beta )}, \quad z\in \mathbb {C}, \end{aligned}$$

where $\varGamma (.)$ is the standard Gamma function defined as

$$\begin{aligned} \varGamma (z)=\int _0^\infty t^{z-1}e^{-t}\mathrm {d}t, \quad \mathfrak {R}(z)>0. \end{aligned}$$

Definition 1

[1] Let $\alpha \in (0,1)$, the expression

$$\begin{aligned} cD^{\alpha }_tu(t)=\frac{1}{\varGamma (1-\alpha )}\int _0^t(t-s)^{-\alpha }\frac{d}{ds}u(s)\mathrm {d}s \end{aligned}$$

is called the Caputo fractional derivative of order $\alpha$ of the function u.

3 Space Semi-discretization

In this section, we will give the weak formulation of (1), describe the semidiscrete Galerkin approximations and then derive the error estimates for the velocity about space discretization. From now on, we denote by h with $0<h<1$ a real positive discretization parameter tending to zero.

3.1 Semidiscrete Fractional Navier–Stokes Equations

With the notations in Sect. 2, the variational formulation of (1) is as follows: find $(u,p)\in (X,M)$ for all $t\in [0,T]$ such that for all $(\phi ,q)\in (X,M)$

$$\begin{aligned} \left\{ \begin{array}{ll} \left( cD^{\alpha }_tu,\phi \right) +a(u,\phi )+b(u,u,\phi )-d(\phi ,p)+d(u,q)=(f,\phi ),\\ u(x,0)=u_{0}. \end{array}\right. \end{aligned}$$

(2)

We introduce the finite element subspace $(X_h,M_h)$ of $(X,M), Y_h\subset Y$ and define the subspace $V_h$ of $X_h$ given by

$$\begin{aligned} V_h=\{v_h\in X_h, \text {div}v_h=0\}. \end{aligned}$$

We assume that the couple $(X_h, M_h)$ satisfies the discrete LBB(or named inf-sup) condition

$$\begin{aligned} \sup \limits _{v_h\in X_h}\frac{\left( \varphi _h, \text {div} v_h\right) }{\Vert v_h\Vert _1}\ge \beta \Vert \varphi _h\Vert , \quad \forall \varphi _h\in M_h, \end{aligned}$$

(3)

where $\beta >0$ is a constant.

Let $P_h:Y\rightarrow V_h$ denotes the $L^2$-orthogonal projection defined by

$$\begin{aligned} \left( P_hv,v_h\right) =(v,v_h),\ \ v\in Y,\ \ v_h\in V_h. \end{aligned}$$

The operator $\overline{E}_h(t)$ is introduced by

$$\begin{aligned} \overline{E}_h(t)v_h=\sum \limits _{j=1}^\infty t^{\alpha -1}E_{\alpha ,\alpha }\left( -\lambda _j^h t^\alpha \right) \left( v,\varphi _j^h\right) \varphi _j^h,\ \ v_h\in X_h, \end{aligned}$$

(4)

where $\{\lambda _j^h\}_{j=1}^{N}$ and $\{\varphi _j^h\}_{j=1}^{N}$ are respectively the eigenvalues and the eigenfunctions of the discrete Laplace operator $-\varDelta _h$ defined by $-(\varDelta _h\psi , \chi )=(\nabla \psi , \nabla \chi ),\ \ \forall \psi , \chi \in X_h.$

For later use, we need the regularity result which is related to the operator $\overline{E}_h(t)$ and collect the result in the next lemma.

Lemma 1

[3] Let $\overline{E}_h(t)$ be defined by (4) and $\psi \in X_h$. Then it holds that

$$\begin{aligned} \Vert \overline{E}_h(t)\psi \Vert _p\le \left\{ \begin{array}{ll} Ct^{-1+\alpha (1+\frac{q-p}{2})}\Vert \psi \Vert _q, &{} p-2\le q\le p,\\ Ct^{-1+\alpha }\Vert \psi \Vert _q, &{} p<q. \end{array} \right. \end{aligned}$$

(5)

The discrete analogue of weak formulation (2) now reads as follows: find $(u_h,p_h)\in (X_h,M_h)$ such that for all $(\phi _h,q_h)\in (X_h,M_h)$,

$$\begin{aligned} \left( cD^{\alpha }_tu_h,\phi _h\right) +a(u_h,\phi _h)+b\left( u_h,u_h,\phi _h\right) -d(\phi _h,p_h)+d(u_h,q_h)=(f,\phi _h), \end{aligned}$$

(6)

with $u_h(0)=P_hu_{0}$.

For the discrete approximation, it is straightforward to verify that the trilinear term $b(u_h,v_h,w_h)$ enjoys the following properties (cf. [41]):

$$\begin{aligned} b\left( u_h,v_h,w_h\right)= & {} -b(u_h,w_h,v_h),\ \ b(u_h,v_h,v_h)=0,\ \ \quad \forall u_h, v_h, w_h\in X_h,\end{aligned}$$

(7)

$$\begin{aligned} \Vert b\left( u_h,v_h,w_h\right) \Vert\le & {} c_0\Vert \nabla u_h\Vert \Vert \nabla v_h\Vert \Vert \nabla w_h\Vert , \ \ \quad \forall u_h, v_h, w_h\in X_h. \end{aligned}$$

(8)

3.2 Error Estimate for the Velocity

With $V_h$ as above, we now introduce an equivalent Galerkin formulation. Find $u_h\in V_h$ such that $u_h(0)=P_hu_{0}$ and for $t>0$

$$\begin{aligned} \left( cD^{\alpha }_tu_h,\phi _h\right) +a(u_h,\phi _h)+b(u_h,u_h,\phi _h)=(f,\phi _h),\ \ \forall \phi _h\in V_h. \end{aligned}$$

(9)

Theorem 1

(Error estimate for space discretization) Let u and $u_h$ be the solutions of (2) and (9), respectively. We suppose that the solution $\{u,p\}$ of (2) satisfies the following regularity condition: $\sup \limits _{t\in [0,T]}\{\Vert u\Vert _2+\Vert \nabla p\Vert \} \le C$, then the following estimate holds

$$\begin{aligned} \Vert u-u_h\Vert \le Ch^2. \end{aligned}$$

We firstly dissociate the non-linearity by introducing an intermediate solution $v_h$. Let $v_h$ be a finite element Galerkin approximation to a linearised time-fractional Navier-Stokes equation satisfying

$$\begin{aligned} \left( cD^{\alpha }_tv_h,\phi _h\right) +a(v_h,\phi _h)+b(u,u,\phi _h)=(f,\phi _h),\ \ \forall \phi _h\in V_h, \end{aligned}$$

(10)

with $v_h(0)=P_hu_{0}$.

Subsequently, the error is split as

$$\begin{aligned} e:=u-u_h=(u-v_h)+(v_h-u_h)=\xi +\eta . \end{aligned}$$

Note that $\xi$ is the error committed by approximating a linearized(Stokes) problem and $\eta$ represents the error due to the presence of the nonlinearity in the equation.

Below, the estimate for $\xi$ is derived. Firstly $\xi$ is split into two parts $\zeta$, the estimate of which is given, and $\theta$. Because of the presence of the term of fractional derivative $cD^{\alpha }_t$, the methods of energy type estimate and parabolic duality argument for $\theta$ are no more suitable. By making use of the Laplace transform techniques and the property of analytic contraction semigroup that the Stokes operator $A_h$ generates, we derive the error estimate for the $\xi$.

Lemma 2

We suppose that the solution $\{u,p\}$ of   (2) satisfies the following regularity condition: $\sup \limits _{t\in [0,T]}\{\Vert u\Vert _2+\Vert \nabla p\Vert \} \le C$, then for $\xi =u-v_h$, we have the following estimate

$$\begin{aligned} \Vert \xi \Vert \le Ch^2. \end{aligned}$$

Proof

Subtracting (10) from (2), the equation in $\xi$ is written as

$$\begin{aligned} \left( cD^{\alpha }_t\xi ,\phi _h\right) +a(\xi ,\phi _h)=(p, \nabla \cdot \phi _h),\ \ \phi _h\in V_h. \end{aligned}$$

We now decompose $\xi$ as

$$\begin{aligned} \xi :=(u-S_hu)+(S_hu-v_h)=\zeta +\theta , \end{aligned}$$

where $S_hu$ is given by (4.52), [25]. Lemma 4.7, [25] tells us that

$$\begin{aligned} \Vert u-S_hu\Vert +h\Vert u-S_hu\Vert _1\le Ch^2. \end{aligned}$$

In order to complete the estimate for $\xi$, we only need to estimate $\theta$. The equation in $\theta$ reads as

$$\begin{aligned} \left( cD^{\alpha }_t\zeta ,\phi _h\right) +\left( cD^{\alpha }_t\theta ,\phi _h\right) +a(\zeta , \phi _h)+a(\theta ,\phi _h)=(p,\nabla \cdot \phi _h),\ \ \forall \phi _h\in V_h. \end{aligned}$$

Making use of the definition of $S_hu$, that is, $a(\zeta , \phi _h)=(p,\nabla \cdot \phi _h)$, then the above equation can be simplified as

$$\begin{aligned} \left( cD^{\alpha }_t\theta ,\phi _h\right) +a(\theta ,\phi _h)=-\left( cD^{\alpha }_t\zeta ,\phi _h\right) ,\ \ \forall \phi _h\in V_h. \end{aligned}$$

Let $A=-\nu \varDelta$ and $A_h$ is the discrete analogue of A, there holds

$$\begin{aligned} cD^{\alpha }_t\theta + A_h\theta =-cD^{\alpha }_t\zeta ,\ \ \theta (0)=0. \end{aligned}$$

Taking the Laplace transform on both sides of the above equation, we recover

$$\begin{aligned} z^\alpha \hat{\theta }(z)+A_h\hat{\theta }(z)=-z^\alpha \hat{\zeta }(z). \end{aligned}$$

Therefore,

$$\begin{aligned} \hat{\theta }(z)=-(z^\alpha I+A_h)^{-1}z^\alpha \hat{\zeta }(z). \end{aligned}$$

Because the Stokes operator $A_h$ generates an analytic contraction semigroup [44] and then there exists a constant c which depends only on $\phi$ and $\alpha$ such that

$$\begin{aligned} \Vert \left( z^\alpha I+A_h\right) ^{-1}\Vert \le cz^{-\alpha },\ \ \forall z\in \varSigma _\phi , \end{aligned}$$

where $\varSigma _\theta =\{z\in \mathbb {C}:|\text{ arg } z|\le \phi \}$.

So there holds

$$\begin{aligned} \Vert \left( z^\alpha I+A_h\right) ^{-1}z^\alpha \Vert \le c. \end{aligned}$$

Using the inverse Laplace transform yields

$$\begin{aligned} \Vert \theta \Vert \le c\Vert \zeta \Vert =c\Vert u-S_hu\Vert \le Ch^2. \end{aligned}$$

By the triangle inequality, we have

$$\begin{aligned} \Vert \xi \Vert \le \Vert \zeta \Vert +\Vert \theta \Vert \le Ch^2, \end{aligned}$$

which completes the proof. $\square$

Subsequently, we give the main result in this section. By making use of the properties of the operator $\overline{E}_h$ and the standard duality arguments, the methods of which are different from classical Navier-Stokes equations, we derive the error estimate for the velocity.

Proof of Theorem 1

Since $e=u-u_h=(u-v_h)+(v_h-u_h)=\xi +\eta$ and the estimate of $\xi$ is known from Lemma 2, it is enough to estimate $\eta$. From (9) and (10), the equation for $\eta$ becomes

$$\begin{aligned} \left( cD^{\alpha }_t\eta ,\phi _h\right) +a(\eta ,\phi _h)+b(u,u,\phi _h)-b(u_h,u_h,\phi _h)=0, \end{aligned}$$

with $\eta (0)=0$.

Equivalently, the above equation can be recast as

$$\begin{aligned} cD^{\alpha }_t\eta +A\eta +B(u,u)-B(u_h,u_h)=0,\ \ \eta (0)=0. \end{aligned}$$

By Duhamel’s principle(cf.[36]) and Lemma 1, one can derive that

$$\begin{aligned} \Vert \eta \Vert= & {} \left\| \int _0^t\overline{E}_h(t-s)\left( B(u,u)-B(u_h,u_h)\right) ds\right\| \nonumber \\\le & {} \int _0^t\Vert A_h^{1/2}\overline{E}_h(t-s)A_h^{-1/2}\left( B(u,u)-B(u_h,u_h)\right) \Vert ds\nonumber \\\le & {} \int _0^t(t-s)^{-1+\alpha /2}\Vert A_h^{-1/2}\left( B(u,u)-B(u_h,u_h)\right) \Vert ds. \end{aligned}$$

(11)

Thus it is enough to estimate $\Vert A_h^{-1/2}(B(u,u)-B(u_h,u_h))\Vert$. We proceed by the standard duality arguments, using the splitting

$$\begin{aligned} B(u,u)-B(u_h,u_h)=B(u,e)+B(e,u_h). \end{aligned}$$

By the triangle inequality it yields

$$\begin{aligned} \Vert A_h^{-1/2}\left( B(u,u)-B(u_h,u_h)\right) \Vert \le \Vert B(u,e)\Vert _{-1}+\Vert B(e,u_h)\Vert _{-1}, \end{aligned}$$

(12)

so that the proof is reduced to estimate each of the above negative norms on the right-hand side. Using the skew-symmetry property (7) and noticing $\text {div} u=0$, one obtains for the first term:

$$\begin{aligned} \Vert B(u,e)\Vert _{-1}= & {} \sup \limits _{\Vert \phi \Vert =1}\left| -((u\cdot \nabla )\phi ,e)-\frac{1}{2}((\nabla \cdot u)\phi ,e)\right| \\\le & {} \sup \limits _{\Vert \phi \Vert =1}\left( \Vert e\Vert \Vert u\Vert _{\infty }\Vert \phi \Vert _1+\Vert e\Vert \Vert \nabla \cdot u\Vert _{L^4}\Vert \phi \Vert _{L^4}\right) \\\le & {} C\Vert e\Vert . \end{aligned}$$

Regarding the other term in (12), we derive

$$\begin{aligned} \Vert B(e,u_h)\Vert _{-1}= & {} \sup \limits _{\Vert \phi \Vert =1}\left| \frac{1}{2}((e\cdot \nabla )u_h,\phi )-\frac{1}{2}((e\cdot \nabla )\phi ,u_h)\right| \\\le & {} \sup \limits _{\Vert \phi \Vert =1}\left( \Vert e\Vert \Vert \nabla u_h\Vert _{L^4}\Vert \phi \Vert _{L^4}+\Vert e\Vert \Vert \phi \Vert _1\Vert u_h\Vert _{\infty }\right) \\\le & {} C\Vert e\Vert , \end{aligned}$$

where, in the last inequality, we have used the Sobolev’s imbeddings $\Vert \phi \Vert _{L^4}\le C\Vert \phi \Vert _1$ and the regularity condition of the solution $u_h$.

It is obvious that there holds

$$\begin{aligned} \Vert A_h^{-1/2}\left( B(u,u)-B(u_h,u_h)\right) \Vert \le C\Vert e\Vert . \end{aligned}$$

(13)

Substituting (13) into (11), it is show that

$$\begin{aligned} \Vert \eta \Vert \le C\int _0^t(t-s)^{-1+\alpha /2}\Vert u(s)-u_h(s)\Vert ds. \end{aligned}$$

By fractional Gronwall’s lemma [45], a use of the triangle inequality with Lemma 2 completes the rest of the proof. $\square$

4 Full Discretization

In this section, we will give the discretization of time Caputo-fractional derivative by a finite difference method, as well as the stability and convergence properties related to the time discretization. By collecting the convergence results for the space discretization and for the time discretization, the error estimate for fully discrete scheme of (1) has been obtained.

The time-fractional derivative $cD^{\alpha }_tu$ is discretized by the first-order backward Euler scheme. We suppose $t_n=n\triangle t, n=0, 1 ,\ldots , N ,$ in which $\triangle t=\frac{T}{N}$ denotes the step of time. Then the time-fractional derivative in Eq. (1) at time point $t=t_{n+1}$ can be approximated as [38]

$$\begin{aligned} cD^{\alpha }_tu= & {} \frac{1}{\varGamma (1-\alpha )}\int _0^{t_{n+1}}\frac{\partial u(x,s)}{\partial s}\frac{ds}{(t_{n+1}-s)^{\alpha }}\nonumber \\= & {} \frac{1}{\varGamma (2-\alpha )}\sum _{j=0}^nb_j\frac{u\left( x,t_{n+1-j}\right) -u(x,t_{n-j})}{(\varDelta t)^\alpha }+r^{n+1}_{\varDelta t}, \end{aligned}$$

(14)

where $b_j=(j+1)^{1-\alpha }-j^{1-\alpha }$. The coefficients $b_j$ possess the following properties:

• (1) $b_j>0, j=0, 1, 2, \ldots , n$,

• (2) $1=b_0>b_1>b_2>\ldots >b_n, b_n\rightarrow 0$ as $n\rightarrow \infty$,

• (3) $\sum _{j=0}^n(b_j-b_{j+1})+b_{n+1}=1$.

Let

$$\begin{aligned} L_t^\alpha u_h\left( x,t_{n+1}\right) :=\frac{1}{\varGamma (2-\alpha )}\sum _{j=0}^nb_j\frac{u_h\left( x,t_{n+1-j}\right) -u_h(x,t_{n-j})}{(\varDelta t)^\alpha }, \end{aligned}$$

then $cD^{\alpha }_tu_h=L_t^\alpha u_h(x,t_{n+1})+r^{n+1}_{\varDelta t}$, where

$$\begin{aligned} r^{n+1}_{\varDelta t}\le c_u\varDelta t^{2-\alpha }. \end{aligned}$$

(15)

And $c_u$ depends on the the second derivative of u in time.

Using $L_t^\alpha u_h(x,t_{n+1})$ as an approximation of $cD^{\alpha }_tu_h$ in the Eq. (6), then we will get the fully discrete scheme of (1): find $(u_h^{n+1},p_h^{n+1})\in (X_h,M_h)$ such that for all $(\phi _h,q_h)\in (X_h,M_h)$,

$$\begin{aligned}&\left( u_h^{n+1},\phi _h\right) +a_0a\left( u_h^{n+1},\phi _h\right) +a_0b\left( u_h^{n+1},u_h^{n+1},\phi _h\right) -a_0d\left( \phi _h,p_h^{n+1}\right) \nonumber \\&\quad +\,a_0d\left( u_h^{n+1},q_h\right) =(1-b_1)\left( u_h^n,\phi _h\right) +\sum _{j=1}^{n-1}\left( b_j-b_{j+1}\right) \left( u_h^{n-j},\phi _h\right) \nonumber \\&\quad +\,b_n\left( P_hu^0,\phi _h\right) +a_0\left( f^{n+1},\phi _h\right) , \end{aligned}$$

(16)

where $a_0=\varGamma (2-\alpha )\triangle t^\alpha$, $f^{n+1}$ is the value of f at point $t_{n+1}$.

Following [38], it will be useful to define the error term $r^{n+1}$ by

$$\begin{aligned} r^{n+1}:=a_0\left( cD^{\alpha }_tu_h-L_t^\alpha u_h(x,t_{n+1})\right) . \end{aligned}$$

(17)

Using (15), the error term $r^{n+1}$ becomes

$$\begin{aligned} |r^{n+1}|=\varGamma (2-\alpha )\triangle t^\alpha |r^{n+1}_{\triangle t}|\le C\triangle t^2. \end{aligned}$$

(18)

The stability analysis for the full discrete problem is given in the following lemma.

Lemma 3

The full discrete scheme (16) is unconditionally stable for $0<\triangle t<T,$ and

$$\begin{aligned} \Vert u_h^{n+1}\Vert \le \left( \Vert P_hu^0\Vert +a_0\sum _{j=1}^{n+1}\Vert f^j\Vert \right) \end{aligned}$$

(19)

holds.

Further, we have

$$\begin{aligned} \sqrt{a_0}\Vert \nabla u_h^{n+1}\Vert \le \left( \Vert P_hu^0\Vert +a_0\sum _{j=1}^{n+1}\Vert f^j\Vert \right) . \end{aligned}$$

(20)

Proof

Mathematical induction is used to prove the lemma. When $\mathrm{n}=0$, the formulation (16) can be written as

$$\begin{aligned}&\left( u_h^1,\phi _h\right) +a_0a\left( u_h^1,\phi _h\right) +a_0b\left( u_h^1,u_h^1,\phi _h\right) -a_0d\left( \phi _h,p_h^1\right) +a_0d\left( u_h^1,q_h\right) \nonumber \\&\quad =\left( P_hu^0,\phi _h\right) + a_0\left( f^1,\phi _h\right) . \end{aligned}$$

(21)

Taking $\phi _h=u_h^1\in X_h$ and $q_h=p_h^1\in M_h$ in (21) and making use of the property (7) of $b(u_h,v_h,w_h)$, there holds

$$\begin{aligned} \left( u_h^1,u_h^1\right) +a_0a\left( u_h^1,u_h^1\right) =\left( P_hu^0,u_h^1\right) +a_0\left( f^1,u_h^1\right) . \end{aligned}$$

Using the coercivity of $a(u_h^1,u_h^1)$ and Schwarz inequality yield

$$\begin{aligned} \Vert u_h^1\Vert ^2\le \Vert P_hu^0\Vert \Vert u_h^1\Vert +a_0\Vert f^1\Vert \Vert u_h^1\Vert , \end{aligned}$$

that is,

$$\begin{aligned} \Vert u_h^1\Vert \le \Vert P_hu^0\Vert +a_0\Vert f^1\Vert . \end{aligned}$$

Suppose $\phi _h=u_h^j\in X_h, q_h=p_h^j\in M_h$, we have

$$\begin{aligned} \Vert u_h^{j}\Vert \le \left( \Vert P_hu^0\Vert +a_0\sum _{i=1}^{j}\Vert f^i\Vert \right) ,\ \ \quad j=2, 3, \ldots , n. \end{aligned}$$

(22)

Next, setting $\phi _h=u_h^{n+1}\in X_h$ and $q_h=p_h^{n+1}\in M_h$ in (16), and using the property (7) of $b(u_h,v_h,w_h)$, one arrives at

$$\begin{aligned}&\left( u_h^{n+1},u_h^{n+1}\right) +a_0a\left( u_h^{n+1},u_h^{n+1}\right) =(1-b_1)\left( u_h^n,u_h^{n+1}\right) \\&\quad +\sum _{j=1}^{n-1}\left( b_j-b_{j+1}\right) \left( u_h^{n-j},u_h^{n+1}\right) +b_n\left( P_hu^0,u_h^{n+1}\right) +a_0\left( f^{n+1},u_h^{n+1}\right) . \end{aligned}$$

Using the property of the coercivity of $a(u_h^{n+1},u_h^{n+1})$ and Schwarz inequality once again, we deduce

$$\begin{aligned}&\Vert u_h^{n+1}\Vert ^2\le (1-b_1)\Vert u_h^n\Vert \Vert u_h^{n+1}\Vert +\sum _{j=1}^{n-1}\left( b_j-b_{j+1}\right) \Vert u_h^{n-j}\Vert \Vert u_h^{n+1}\Vert \\&\quad +b_n\Vert P_hu^0\Vert \Vert u_h^{n+1}\Vert +a_0\Vert f^{n+1}\Vert \Vert u_h^{n+1}\Vert , \end{aligned}$$

which can be simplified as

$$\begin{aligned} \Vert u_h^{n+1}\Vert \le (1-b_1)\Vert u_h^n\Vert +\sum _{j=1}^{n-1}\left( b_j-b_{j+1}\right) \Vert u_h^{n-j}\Vert +b_n\Vert P_hu^0\Vert +a_0\Vert f^{n+1}\Vert . \end{aligned}$$

Hence, by using the inductive hypothesis (22), we get

$$\begin{aligned} \Vert u_h^{n+1}\Vert \le \left( (1-b_1)+\sum _{j=1}^{n-1}\left( b_j-b_{j+1}\right) +b_n\right) \left( \Vert P_hu^0\Vert +a_0\sum _{j=1}^{n}\Vert f^{n}\Vert \right) +a_0\Vert f^{n+1}\Vert . \end{aligned}$$

Making use of the properties of the coefficients $b_j$, we obtain

$$\begin{aligned} \Vert u_h^{n+1}\Vert \le \left( \Vert P_hu^0\Vert +a_0\sum _{j=1}^{n+1}\Vert f^j\Vert \right) , \end{aligned}$$

which is (19).

The proof of (20) is similar to the proof of (19) by mathematical induction. Hence, we can omit it. The proof is completed. $\square$

The following lemma will play an important role in proving the error estimate about the time discretization.

Lemma 4

Let $\nu >0$ is the viscosity coefficient and $c_0$ is defined by (8). Suppose that

$$\begin{aligned} \sum _{j=1}^n\Vert f^j\Vert +\frac{1}{a_0}\Vert P_hu_0\Vert \le \frac{\nu }{\sqrt{a_0}c_0}, \end{aligned}$$

(23)

then we have

$$\begin{aligned} a\left( e^n,e^n\right) +b\left( e^n,u_h^n,e^n\right) \ge 0, \end{aligned}$$

where $a_0=\varGamma (2-\alpha )\triangle t^\alpha , e^n=u_h(t_n)-u_h^n$.

Proof

Under the assumption of (23), there holds

$$\begin{aligned} \frac{1}{\sqrt{a_0}}\Vert P_hu^0\Vert +\sqrt{a_0}\sum _{j=1}^{n}\Vert f^j\Vert \le \frac{\nu }{c_0}. \end{aligned}$$

By making use of (20), we know that

$$\begin{aligned} \Vert u_h^n\Vert _1\le \frac{\nu }{c_0}, \end{aligned}$$

in other words,

$$\begin{aligned} \nu -c_0\Vert u_h^n\Vert _1\ge 0. \end{aligned}$$

Besides, using the coercivity of $a(e^{n},e^{n})$ and the property (8) of b, we obtain

$$\begin{aligned} a\left( e^n,e^n\right) +b\left( e^n,u_h^n,e^n\right)\ge & {} \left( \nu -c_0\Vert u_h^n\Vert _1\right) \Vert e^n\Vert _1^2\\\ge & {} 0. \end{aligned}$$

The proof of the lemma is completed. $\square$

Remark 1

The condition (23) means that it requires a small initial data and small time step size.

The error analysis for the solution of the semi-discrete problem about time is discussed in the following theorem.

Theorem 2

(Error estimate for time discretization) Let $u_h(t_n)$ be the solution of (6), $\{u_h^n\}_{n=1}^N$ be the time-discrete solution of (16). Under the assumption of Lemma 4, then we have the following error estimate

$$\begin{aligned} \Vert u_h(t_n)-u_h^n\Vert \le CT^\alpha \varDelta t^{2-\alpha }, n=1, 2, \ldots , N. \end{aligned}$$

The proof of Theorem 2 needs the following lemma.

Lemma 5

Under the assumption of Theorem 2, we have

$$\begin{aligned} \Vert u_h(t_n)-u_h^n\Vert \le Cb^{-1}_{n-1}\varDelta t^2, n=1,2,\ldots ,N. \end{aligned}$$

Proof

Let $e^n=u_h(t_n)-u_h^n, \tilde{e}^n=p_h(t_n)-p_h^n.$

For $n=0$, by combining (6), (16) and (17), the error equation can be read as

$$\begin{aligned}&\left( e^1,\phi _h\right) +a_0a\left( e^1,\phi _h\right) +a_0b\left( e^1,u_h^1,e^1\right) -a_0d\left( \phi _h,\tilde{e}^1\right) +a_0d\left( e^1,q_h\right) \nonumber \\&\quad =\left( e^0,\phi _h\right) +\left( r^1,\phi _h\right) . \end{aligned}$$

Taking $\phi _h=e^1\in X_h$ and $q_h=\tilde{e}^1\in M_h$ in the above equation and noting $e^0=0$, we obtain

$$\begin{aligned} \left( e^1,e^1\right) +a_0a\left( e^1,e^1\right) +a_0b\left( e^1,u_h^1,e^1\right) =\left( r^1,e^1\right) . \end{aligned}$$

By Lemma 4 and Schwarz inequality, we get

$$\begin{aligned} \Vert e^1\Vert \le \Vert r^1\Vert . \end{aligned}$$

This together with (18), gives

$$\begin{aligned} \Vert u_h-u_h^1\Vert \le C b_0^{-1}\varDelta t^2. \end{aligned}$$

Suppose $\Vert u_h-u_h^n\Vert \le C b_{n-1}^{-1}\varDelta t^2$ for $n=1, 2, 3, \ldots , s.$ Next we prove $n=s+1$. By combining (6), (16) and (17), the error equation can be written as

$$\begin{aligned}&\left( e^{n+1},\phi _h\right) +a_0a\left( e^{n+1},\phi _h\right) +a_0b\left( e^{n+1},u_h^{n+1},e^{n+1}\right) -a_0d\left( \phi _h,\tilde{e}^{n+1}\right) \nonumber \\&\quad +a_0d\left( e^{n+1},q_h\right) =(1-b_1)\left( e^{n},\phi _h\right) +\sum _{j=1}^{n-1}\left( b_j-b_{j+1}\right) \left( e^{n-j},\phi _h\right) \nonumber \\&\quad +b_n(e^0,v)+\left( r^{n+1},\phi _h\right) . \end{aligned}$$

(24)

Let $\phi _h=e^{n+1}\in X_h, q_h=\tilde{e}^{n+1}\in M_h$ in the Eq. (24), then we have

$$\begin{aligned}&\left( e^{n+1},e^{n+1}\right) +a_0a\left( e^{n+1},e^{n+1}\right) +a_0b\left( e^{n+1},u_h^{n+1},e^{n+1}\right) =(1-b_1)\left( e^{n},e^{n+1}\right) \\&\quad +\sum _{j=1}^{n-1}\left( b_j-b_{j+1}\right) \left( e^{n-j},e^{n+1}\right) +b_n\left( e^0,e^{n+1}\right) +\left( r^{n+1},e^{n+1}\right) . \end{aligned}$$

By Lemma 4 and Schwarz inequality, we deduce

$$\begin{aligned} \Vert e^{n+1}\Vert ^2\le & {} (1-b_1)\Vert e^{n}\Vert \Vert e^{n+1}\Vert +\sum _{j=1}^{n-1}\left( b_j-b_{j+1}\right) \Vert e^{n-j}\Vert \Vert e^{n+1}\Vert \\&+\Vert r^{n+1}\Vert \Vert e^{n+1}\Vert . \end{aligned}$$

By the induction assumption, the fact that $b_j^{-1}/b_{j+1}^{-1}<1$ for all non-negative integer j and the properties of $b_j$, it can be written as

$$\begin{aligned} \Vert e^{n+1}\Vert\le & {} (1-b_1)\Vert e^{n}\Vert +\sum _{j=1}^{n-1}\left( b_j-b_{j+1}\right) \Vert e^{n-j}\Vert +\Vert r^{n+1}\Vert \\\le & {} \left[ (1-b_1)b_{n-1}^{-1}+\sum _{j=1}^{n-1}\left( b_j-b_{j+1}\right) b_{n-j-1}^{-1}\right] C\varDelta t^2+C\varDelta t^2\\\le & {} \left[ (1-b_1)+\sum _{j=1}^{n-1}\left( b_j-b_{j+1}\right) +b_n\right] C b_{n}^{-1}\varDelta t^2\\= & {} C b_{n}^{-1}\varDelta t^2. \end{aligned}$$

The proof is completed. $\square$

Proof of Theorem 2

As in the way of [38], by the definition of $b_n$, it can be obtained that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }n^{-\alpha }b_{n-1}^{-1}= & {} \lim \limits _{n\rightarrow \infty }\frac{n^{-\alpha }}{n^{1-\alpha }-(n-1)^{1-\alpha }}\\= & {} \lim \limits _{n\rightarrow \infty }\frac{n^{-1}}{1-(1-\frac{1}{n})^{1-\alpha }}\\= & {} \frac{1}{(1-\alpha )}. \end{aligned}$$

Introduce a function $\varPsi (x):=x^{-\alpha }/(x^{1-\alpha }-(x-1)^{1-\alpha })$. Since $\varPsi ^{\prime }(x)\ge 0$ for $\forall x\ge 1$, therefore $\varPsi (x)$ is increasing about x for all $x>1$. This means that $n^{-\alpha }b_{n-1}^{-1}$ increasingly tends to $1/(1-\alpha )$ as $1<n\rightarrow \infty$. It is to be noted that $n^{-\alpha }b^{-1}_{n-1}=1$ for $n=1$, hence it can be written as

$$\begin{aligned} n^{-\alpha }b^{-1}_{n-1}\le \frac{1}{(1-\alpha )},\ \ n=1, 2, \ldots , N. \end{aligned}$$

For all n such that $n\triangle t\le T$, we obtain

$$\begin{aligned} \Vert u_h(t_n)-u_h^n\Vert\le & {} Cb^{-1}_{n-1}\triangle t^2\\= & {} Cn^{-\alpha }b^{-1}_{n-1}n^\alpha \triangle t^{2-\alpha +\alpha }\\\le & {} C\frac{1}{1-\alpha }(n\triangle t)^\alpha (\triangle t)^{2-\alpha }\\\le & {} CT^\alpha (\triangle t)^{2-\alpha }. \end{aligned}$$

The proof is completed. $\square$

Next we will give the error estimate for the fully discrete scheme by collecting the convergence results for the space discretization and for the time discretization.

Theorem 3

(Error estimate for fully discrete scheme) Let $\{u(t_n)\}_{t\in [0,T]}$ be the solution of (1) and let $\{u_h^n\}_{n=1}^{N}$ be the solution of the scheme (16) with $T=N\triangle t$. Under the assumption of Lemma 4, then there is $C>0$ such that

$$\begin{aligned} \Vert u(t_n)-u_h^n\Vert \le C(h^2+T^\alpha \varDelta t^{2-\alpha }). \end{aligned}$$

Proof

The proof follows from Theorem 1 and Theorem 2 by the triangle inequality. We are no longer to repeat here. $\square$

Table 1 The errors and space convergence rates for u with fixed time step $\varDelta t=1/500$

5 Numerical Example

In order to demonstrate the effectiveness of our numerical methods, a numerical example is presented. The main purpose is to check the convergence behavior of the numerical solution with respect to the time step $\varDelta t$ and the space step h used in the calculation.

We consider the following fractional burger equation

$$\begin{aligned} D_t^{\alpha }u-u_{xx}+uu_x= & {} f(x,t),\ \ x\in \varOmega ,\ \ t\in [0,1],\\ u(0,t)= & {} u(1,t)=0,\ \ t\in [0,1],\\ u(x,0)= & {} 0,\ \ x\in \varOmega , \end{aligned}$$

in which $\varOmega =[0,1],$ and the source term f is chosen as

$$\begin{aligned} \frac{2}{\varGamma (3-\alpha )}t^{2-\alpha }\text {sin}(\pi x)+\pi ^2 t^2\text {sin}(\pi x)+\pi t^4\text {sin}(\pi x)\text {cos}(\pi x). \end{aligned}$$

Then the exact solution is $t^2 \text {sin}(\pi x)$.

We compute the errors in $L^2$ discrete norm. And all the numerical results in the tables below are evaluated at T=1. The spatial and temporal meshes are taken uniform. The finite element method using piecewise-linear polynomials is used for the space and the scheme for time described in previous sections is used in the example.

Table 2 The errors and time convergence rates for u with fixed space step $h=1/800$

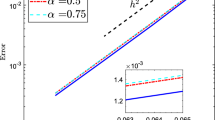
For the $0<\alpha <1$ case, the theoretical convergence order is $O(h^2+\varDelta t^{2-\alpha })$. In Table 1, for a fixed time step $\varDelta t=1/500$ and some different spatial meshes, we can see the orders of convergence for u in $L^2$-norms are close to 2 which are accord with the spatial convergence order $O(h^2)$. In Table 2, it shows that the errors between the exact solution and numerical solution and the convergence orders about $\triangle t$ with different $\alpha$ values for a fixed spatial step $h=1/800$. The numerical results are consistent with our theoretical results in Theorem 3.