The Temporal Second Order Difference Schemes Based on the Interpolation Approximation for the Time Multi-term Fractional Wave Equation

Abstract

In this paper, two temporal second-order schemes are derived and analyzed for the time multi-term fractional diffusion-wave equation based on the order reduction technique. The weighted average at two time levels is applied to the discretization of the spatial derivative, in which the weight coefficient corresponds to the optimal point for the time discretization. The two difference schemes are proved to be uniquely solvable. The stability and convergence are rigorously investigated utilizing the energy method. In addition, a fast difference scheme is also presented. The applicability and the accuracy of the schemes are demonstrated by several numerical experiments.

1 Introduction

Recently, the fractional differential equations (FDES) have attracted more and more attention, which can simulate many physical and chemical processes more accuracy than the classical integer-order differential equations. FDES have been frequently used to solve many application problems [1,2,3,4,5,6,7]. The time fractional sub-diffusion and diffusion-wave equation are obtained from the classical diffusion or wave equation by replacing the first or second order time derivative by a fractional derivative of order $\alpha$ with $0< \alpha < 1$ or $1< \alpha < 2$, respectively. In practice, many processes can be described by the multi-term FDES, such as the underlying processes with loss [8], viscoelastic damping [9], oxygen delivery through a capillaryto tissues [10], the anomalous diffusion in highly heterogeneous aquifers and complex viscoelastic materials [11].

In particular, the multi-term time-fractional diffusion-wave equations can successfully describe the power-law frequency dependence in a continuous time random walk model [12].

For most fractional differential equations, it is very difficult to get the exact solutions. Many researchers have proposed various kinds of numerical methods for solving fractional differential equations [13,14,15]. Much work has been done numerically on the time diffusion-wave equations. For the approximation of the fractional derivative with order $\alpha \in (1,2)$, Oldham and Spanier proposed the first-order GL formula based on the Grünwald-Letnikov derivative [16]. Sun and Wu [17] derived L1 formula using linear interpolation technique which keeps $(3-\alpha )$-order accuracy. Later, the L1 formula was used for solving the problem with diffusion-wave property [18,19,20], and the derived numerical schemes obtain $(3-\alpha )$-order accuracy in time. Zhao et al. [21] proposed a second-order formula using high-order interpolation for the variable-order fractional derivative with the order between 1 and 2, and applied the formula for solving wave propagation problem. Sun et al. [22] explored the L2-$1_\sigma$ formula for the fractional diffusion-wave problem and obtained the second-order scheme both in time and in space. Dehghan et al. [23] proposed a high-order numerical scheme to solve the space-time tempered fractional diffusion-wave equation. They employ the fourth-order technique to approximate the Riesz fractional derivative and a second-order approximation for the tempered fractional integral. The convergence order of the proposed method is $O(\tau ^2+h^4).$ Ghazizadeh et al. [24] constructed a generalized MacCormack scheme and a fully implicit scheme for solving the fractional Cattaneo equation. The stability of the former scheme was analyzed using the Von Neumann stability criterion. The scheme keeps second-order spatial rate of convergence and ($1 + \alpha$)-order temporal rate of convergence, where $\alpha \in (1, 2)$ is the order of fractional derivative. Li and Cao [25] presented an unconditional stable scheme with convergence order of O($\tau ^{3-\alpha } + h^2$) for the 1D Cattaneo equation. Vong et al. [26] derived a fourth order finite difference scheme for the 1D generalized fractional Cattaneo equation combining L1 approximation for the time fractional derivative and compact difference scheme for the second-order space derivative. The stability and convergence were proved in the maximum norm by the energy method.

There are many numerical methods for multi-term fractional diffusion equation, such as Galerkin finite element [27], finite difference method [28, 38], spectral method [29], and so on. Some research work on multi-term time fractional diffusion-wave equation has been made. In [30], Salehi applied a meshless collocation method to solve the multi-term time fractional diffusion-wave equation in two dimensions. The Caputo time fractional derivatives are approximated by a scheme of order $O(\tau ^{3-\alpha }), \alpha \in (1, 2).$ Abdel-Rehim et al. [31] gave the simulations of the approximation solutions of time-fractional wave, forced wave (shear wave), and damped wave equations. The Von-Neumann stability conditions are also considered and discussed for these models. Liu [32] established a strong maximum principle for fractional diffusion equations with multiple Caputo derivatives in time, and investigate a related inverse problem of practical importance. Bhrawy and Zaky [33] proposed a shifted Jacobi tau method for both temporal and spatial discretizations for multi-term time-space fractional differential equation with Dirichlet boundary conditions. Dehghan et al. [34] constructed a high order difference scheme and Galerkin spectral technique for the numerical solution of multi-term time fractional partial differential equations. The proposed methods are based on a finite difference scheme in time, which have $(3-\alpha )$ order accuracy.

Ren and Sun [35] proposed some efficient numerical schemes to solve one-dimensional and two-dimensional multi-term time fractional diffusion-wave equation, by combining the compact difference approach for the spatial discretisation and an L1 approximation for the multi-term time Caputo fractional derivatives. Liu et al. [36] proposed a finite difference scheme for solving a two-term time-fractional wave-diffusion equation. Brunner et al. [37] introduced an artificial boundary and found the exact and approximate artificial boundary conditions for the time-fractional diffusion-wave equation on a two-dimensional unbounded spatial domain, which leads to a problem on a bounded computational domain.

It is noted that the above methods for multi-term fractional diffusion-wave equation are obtained mainly by applying directly the techniques which are used to handle the single-term fractional diffusion-wave equation, including L1 formula and GL formula. L1 formula can only achieve $3-\alpha$ order accuracy which is a little lower. Although GL formula can obtain 2 order accuracy, it requires the continuous zero-extension of the solution when $t<0.$

In [38], the authors proposed a numerical formula to approximate the multi-term Caputo fractional derivatives of order $\alpha _r$ ($0<\alpha _r\le 1$) at the super-convergent point. The formula can achieve at least second-order accuracy at this point. And some effective difference schemes for solving the time multi-term fractional sub-diffusion equation and the time distributed-order sub-diffusion equation, respectively, are presented along with the theoretical analysis on the solvability, stability and convergence.

Motivated by the novel idea proposed in [38] and combining with the order reduction method, we will present two temporal second-order accuracy difference schemes based on the interpolation approximation for the time multi-term fractional wave equation. The unconditional stability and convergence of the proposed difference schemes in $L_\infty$ norm are proved, and the convergence order of the two difference schemes is $O(\tau ^2+h^2)$ and $O(\tau ^2+h^4),$ respectively.

Most difference schemes for time fractional differential equations require storing the solution at all previous time steps for use and huge computational cost. Nowadays some efforts have been made to develop efficient fast numerical methods for the Caputo derivative. Jiang et al. [39] proposed a fast evaluation of Caputo fractional derivative based on the L1 formula which employed the sum-of-exponentials (SOE) approximation to the kernel function $t^{-1-\alpha }.$ The fast algorithm keeps the accuracy of $O(\tau ^{2-\alpha })$ and reduces the computational complexity significantly. Yan et al. [40] proposed a fast ${\mathcal {F}}L2$-$1_\sigma$ formula for the Caputo fractional derivative combining the L2-$1_\sigma$ formula with SOE approximation. The formula has high accuracy and reduces the storage and computational cost. We will develop a fast difference scheme by combining ${\mathcal {F}}L2$-$1_\sigma$ formula with the method of the order reduction for time fractional diffusion wave equation.

In this paper, consider the following time multi-term fractional wave equation

$$\begin{aligned}&\sum _{r=0}^m \lambda _r\ {}_0^CD_t^{\alpha _r} u(x,t)=u_{xx}(x,t)+f(x,t),\quad 0<x<L,~0<t\le T, \end{aligned}$$

(1.1)

$$\begin{aligned}&u(0,t)=0,\quad u(L,t)=0,\quad 0< t\le T, \end{aligned}$$

(1.2)

$$\begin{aligned}&u(x,0)=w_1(x),\quad u_t(x,0)=w_2(x),\quad 0\le x\le L, \end{aligned}$$

(1.3)

where $\lambda _0, \lambda _1, \ldots , \lambda _m$ are some positive constants, $1< \alpha _m< \alpha _{m-1}< \cdots < \alpha _0\le 2$ and at least one of $\alpha _i$’s belongs to (1, 2), ${}_0^CD_t^\alpha f(t)$ is the Caputo fractional derivative defined by

$$\begin{aligned} {}_0^CD_t^\alpha f(t)=\frac{1}{\Gamma (2-\alpha )}\int _0^t \frac{f''(s)}{(t-s)^{\alpha -1}}ds. \end{aligned}$$

This paper is arranged as follows. In Sect. 2, some useful notations and lemmas are introduced. A temporal and spatial second order difference scheme is presented for time multi-term fractional diffusion wave equation in Sect. 3. The stability and convergence of the difference scheme are discussed. Sect. 4 constructs a temporal second order and spatial fourth-order compact difference scheme. The stability and convergence of the compact difference scheme are also shown. In Sect. 5, a fast second-order difference scheme is presented for the time multi-term fractional diffusion wave equation. In Sect. 6, two numerical examples are demonstrated to verify the theoretical results. The paper ends with a brief conclusion in Sect. 7.

2 Preliminary

Denote

$$\begin{aligned} \gamma _r=\alpha _r-1, \quad 0\le r\le m \end{aligned}$$

and

$$\begin{aligned} F(\sigma )=\sum _{r=0}^m\frac{\lambda _r}{\Gamma (3-\gamma _r)}\sigma ^{1-\gamma _r} \left[ \sigma -\big (1-\frac{\gamma _r}{2}\big )\right] \tau ^{2-\gamma _r},\quad \sigma \ge 0. \end{aligned}$$

It is easy to know that $0< \gamma _m< \gamma _{m-1}< \cdots < \gamma _0\le 1.$

Lemma 2.1

[38] The equation $F(\sigma )=0$ has a unique positive root $\sigma ^*\in {[}a,b],$ where $a=1-\frac{\gamma _0}{2},~b=1-\frac{\gamma _m}{2}.$

If $m=0,$ the root of $F(\sigma )=0$ is $\sigma ^*=1-\frac{\gamma _0}{2}.$ If $m\ge 1,$ the root $\sigma ^*$ of $F(\sigma )=0$ can be obtained by the Newton iteration method.

Lemma 2.2

[38] For $m\ge 1,$ the Newton iteration sequence $\{\sigma _k\}_{k=0}^{\infty },$ generated by

$$\begin{aligned} \left\{ \begin{array}{l} \sigma _{k+1}=\sigma _k-\frac{F(\sigma _k)}{F^\prime (\sigma _k)},\quad k=0, 1, 2, \ldots ,\\ \sigma _0=b,\end{array}\right. \end{aligned}$$

(2.1)

is monotonically decreasing and convergent to $\sigma ^*.$

For simplicity in writing hear and after, let $\sigma =\sigma ^*.$ For $0< \gamma <1,$ a sequence $\{c_n^{(k+1,\gamma )}\}$ defined in [41] is introduced in the following.

$$\begin{aligned} a_0^{(\gamma )}= & {} \sigma ^{1-\gamma },~ a_l^{(\gamma )} =(l+\sigma )^{1-\gamma }-(l-1+\sigma )^{1-\gamma },~ l\ge 1, \\ b_l^{(\gamma )}= & {} \frac{1}{2-\gamma }[(l+\sigma )^{2-\gamma } -(l-1+\sigma )^{2-\gamma }] -\frac{1}{2}[(l+\sigma )^{1-\gamma } +(l-1+\sigma )^{1-\gamma }],~ l\ge 1. \end{aligned}$$

For $k=0$

$$\begin{aligned} c_0^{(k+1,\gamma )}=a_0. \end{aligned}$$

(2.2)

For $k\ge 1$

$$\begin{aligned} c_n^{(k+1,\gamma )}=\left\{ \begin{array}{ll} a_0^{(\gamma )}+b_1^{(\gamma )},&{}\quad n=0,\\ a_n^{(\gamma )}+b_{n+1}^{(\gamma )}-b_n^{(\gamma )}, &{}\quad 1\le n\le k-1,\\ a_k^{(\gamma )}-b_k^{(\gamma )},&{}\quad n=k. \end{array}\right. \end{aligned}$$

(2.3)

Denote

$$\begin{aligned} \hat{c}_n^{(k+1)}=\sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\gamma _r}}{\Gamma (2-\gamma _r)}c_n^{(k+1,\gamma _r)},\quad n=0,1,\ldots ,k \end{aligned}$$

and

$$\begin{aligned} \hat{b}_n=\sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\gamma _r}}{\Gamma (2-\gamma _r)}b_n^{(\gamma _r)},\quad n=0,1,\ldots ,k. \end{aligned}$$

The properties of the coefficients $\{\hat{c}_n^{(k)}\}$ and $\{\hat{b}_n\}$ will be stated in the following two lemmas.

Lemma 2.3

[38] Given any non-negative integer m and positive constants $\lambda _0, \lambda _1, \ldots , \lambda _m,$ for any $\gamma _i\in (0,1], i=0,1,\ldots ,m,$ it holds

$$\begin{aligned} \hat{c}_1^{(k+1)}>\hat{c}_2^{(k+1)}>\cdots>\hat{c}_{k-2}^{(k+1)}>\hat{c}_{k-1}^{(k+1)}>\sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\gamma _r}}{\Gamma (2-\gamma _r)}\cdot \frac{1-\gamma _r}{2}(k-1+\sigma )^{-\gamma _r}. \end{aligned}$$

In addition, there exists a $\tau _0>0,$ such that

$$\begin{aligned} (2\sigma -1)\hat{c}_0^{(k+1)}-\sigma \hat{c}_1^{(k+1)}>0, \end{aligned}$$

when $\tau \le \tau _0,~n=2,3,\ldots ,$ and

$$\begin{aligned} \hat{c}_0^{(k+1)}>\hat{c}_1^{(k+1)}. \end{aligned}$$

Lemma 2.4

[22] The sequences $\{\hat{c}_n^{(k)}\}$ and $\{\hat{b}_n\}$ satisfy

$$\begin{aligned} \hat{c}_n^{(k+1)} =\left\{ \begin{array}{l} \hat{c}_n^{(k)},\quad 0\le n\le k-2,\\ \hat{c}_{n}^{(k)}+\hat{b}_{n+1},\quad n=k-1. \end{array}\right. \end{aligned}$$

In addition

$$\begin{aligned} \sum _{n=1}^k\hat{c}_n^{(k+1)}\le \sum _{r=0}^m\lambda _r\ \frac{3\tau ^{-\gamma _r}}{2\Gamma (2-\gamma _r)}(k+\sigma )^{1-\gamma _r} \end{aligned}$$

and

$$\begin{aligned} \sum _{n=1}^k\hat{b}_n\le \sum _{r=0}^m\lambda _r\ \frac{\gamma _r\tau ^{-\gamma _r}}{2\Gamma (3-\gamma _r)}(k+\sigma )^{1-\gamma _r}. \end{aligned}$$

Take two positive integers M, N and let $h=\frac{L}{M}, \tau =\frac{T}{N}.$ Denote $x_i=ih, t_k=k\tau ,$$\Omega _{h}=\big \{ x_{i}~|~0\le i\le M\big \},\quad \Omega _{\tau }=\big \{t_{k}~|~ 0\le k\le N\big \}$ and $t_{k+\sigma }=t_k+\sigma \tau .$

If $w=\{w^k~|~0\le k\le N\}$ is a grid function defined on $\Omega _\tau ,$ denote

$$\begin{aligned} \delta _tw^{\frac{1}{2}}= & {} \frac{1}{\tau }(w^1-w^0),\\ D_{\hat{t}}w^k= & {} \frac{1}{2\tau }\big [(2\sigma +1)w^{k+1}-4\sigma w^k+(2\sigma -1)w^{k-1}\big ],~1\le k\le N-1 \end{aligned}$$

and

$$\begin{aligned} w^{k+\sigma }=\sigma w^{k+1}+(1-\sigma ) w^k. \end{aligned}$$

Let

$$\begin{aligned} \mathcal {U}_h=\{u~|~u=(u_0,\ldots ,u_M),u_0=u_M=0\}. \end{aligned}$$

For $u\in \mathcal {U}_h$, introduce the following notations

$$\begin{aligned} \delta _xu_{i+\frac{1}{2}}= & {} \frac{1}{h}(u_{i+1}-u_i), \quad \delta _x^2u_{i}=\frac{1}{h^2}(u_{i+1}-2u_i+u_{i-1}),\\ \mathcal {A} u_i= & {} \frac{1}{12}(u_{i-1}+10u_i+u_{i+1}). \end{aligned}$$

For any $u,v\in \mathcal {U}_h,$ the inner products and norms are defined by

$$\begin{aligned} (u,v)= & {} h\sum _{i=1}^{M-1}u_iv_i,\quad (\delta _xu, \delta _xv)= h\sum _{i=0}^{M-1}\left( \delta _xu_{i+\frac{1}{2}}\right) \left( \delta _xv_{i+\frac{1}{2}}\right) , \quad \langle u, v \rangle _{\mathcal {A}}=(u, \mathcal {A}v), \\ \Vert u\Vert= & {} \sqrt{(u,u)},\quad \Vert \delta _x u\Vert =\sqrt{(\delta _xu, \delta _xu)}, \quad \Vert u\Vert _{\mathcal {A}}=\sqrt{\langle u, u \rangle _{\mathcal {A}}} , \quad \Vert u\Vert _\infty =\max _{0\le i\le M}|u_i|. \end{aligned}$$

Lemma 2.5

[38] Suppose $f\in C^3([0,T]),$ for any $\gamma _i\in (0,1], i=0,1,\ldots ,m$ and $\gamma _0>\gamma _1>\cdots >\gamma _m,$ then it holds

$$\begin{aligned} \sum _{r=0}^m\lambda _r\ {}_0^CD_t^{\gamma _r}f(t_{k+\sigma }) =&\sum _{n=0}^{k}\Big (\sum _{r=0}^m\lambda _r \ \frac{\tau ^{-\gamma _r}}{\Gamma (2-\gamma _r)} c_n^{(k+1,\gamma _r)}\Big )\big [f(t_{k-n+1})-f(t_{k-n})\big ] +O(\tau ^{3-\gamma _0})\\ =&\sum _{n=0}^{k}\hat{c}_{k-n}^{(k+1)}\big [f(t_{n+1})-f(t_{n})\big ] +O(\tau ^{3-\gamma _0}). \end{aligned}$$

Lemma 2.6

[22] Suppose $f\in C^3([0,T]).$ It holds

$$\begin{aligned} D_{\hat{t}}f(t_k)&\equiv \frac{1}{2\tau }\big [(2\sigma +1)f(t_{k+1}) -4\sigma f(t_k)+(2\sigma -1)f(t_{k-1})\big ]\\&=\frac{df}{dt}(t_{k+\sigma })+O(\tau ^2),~k\ge 1. \end{aligned}$$

Lemma 2.7

[38] Suppose $\langle \cdot ,\cdot \rangle _*$ is an inner product on $\mathcal {U}_h,$$\Vert \cdot \Vert _*$ is a norm deduced by the inner product. For any grid functions $v^0,v^1,\ldots ,v^{k+1}\in \mathcal {U}_h,$ we have the following inequality

$$\begin{aligned} \Big \langle \sum _{n=0}^k\hat{c}_{k-n}^{(k+1)}(v^{n+1}-v^{n}), v^{k+\sigma }\Big \rangle _*\ge \frac{1}{2}\sum _{n=0}^k \hat{c}_{k-n}^{(k+1)}\big (\Vert v^{n+1}\Vert _*^2-\Vert v^n\Vert _*^2\big ). \end{aligned}$$

Lemma 2.8

[22] For any grid functions $u^0,u^1,\ldots ,u^{N}\in \mathcal {U}_h$, we have the following inequality

$$\begin{aligned} \big (D_{\hat{t}}u^{k}, u^{k+\sigma }\big )\ge \frac{1}{4\tau }(E^{k+1}-E^{k}),~k\ge 1, \end{aligned}$$

with

$$\begin{aligned} E^{k+1}=(2\sigma +1)\Vert u^{k+1}\Vert ^2-(2\sigma -1)\Vert u^k\Vert ^2 +(2\sigma ^2+\sigma -1)\Vert u^{k+1}-u^{k}\Vert ^2,~k\ge 0. \end{aligned}$$

(2.4)

In addition, it holds

$$\begin{aligned} E^{k+1}\ge \frac{1}{\sigma }\Vert u^{k+1}\Vert ^2,~k\ge 0. \end{aligned}$$

(2.5)

Lemma 2.9

[43] For any $u\in \mathcal {U}_h,$ we have

$$\begin{aligned} \Vert u\Vert _\infty \le \frac{\sqrt{L}}{2}\Vert \delta _x u\Vert ,\quad \Vert u\Vert \le \frac{L}{\sqrt{6}}\Vert \delta _x u\Vert , \end{aligned}$$

and

$$\begin{aligned} \frac{2}{3}\Vert u\Vert ^2\le \Vert u\Vert _{\mathcal {A}}^2\le \Vert u\Vert ^2,\quad \Vert \mathcal {A}u\Vert \le \Vert u\Vert . \end{aligned}$$

Lemma 2.10

[42] Assume the grid function $\{w^k~|~0\le k\le N\}$ is a nonnegative sequence and satisfies the inequality

$$\begin{aligned} w^k\le A+\tau B \sum _{p=1}^{k} w^p,\quad 0\le k\le N, \end{aligned}$$

where A, B are nonnegative constants. Then, when $\tau \le \frac{1}{2B},$ we have

$$\begin{aligned} w^k\le A\exp (2Bk\tau ),~0\le k\le N. \end{aligned}$$

3 A Second-Order Difference Scheme in Time and Space

3.1 The Derivation of the Difference Scheme

Now, combining the super-convergence approximation [38] with the order reduction method, we construct the difference scheme for the problem (1.1)–(1.3).

Let $\gamma _r=\alpha _r-1,~0\le r\le m$ and

$$\begin{aligned} v(x,t)= u_t(x,t). \end{aligned}$$

(3.1)

Then

$$\begin{aligned} \frac{\partial ^{\alpha _r} u }{\partial t^{\alpha _r}}(x,t)=&\frac{1}{\Gamma (2-{\alpha _r})}\int _0^t \frac{\partial ^2 u}{\partial s^2}(x,s) \frac{1}{(t-s)^{{\alpha _r}-1}}ds\nonumber \\ =&\frac{1}{\Gamma (1-\gamma _r)}\int _0^{t} \frac{\partial v}{\partial s}(x,s) \frac{1}{(t-s)^{\gamma _r}}ds\nonumber \\ =&\frac{\partial ^{\gamma _r} v }{\partial t^{\gamma _r}}(x,t). \end{aligned}$$

(3.2)

It follows from (3.1) that

$$\begin{aligned} (u_{xx})_t=v_{xx}. \end{aligned}$$

Then, Eqs. (1.1)–(1.3) are equivalent to the following equation

$$\begin{aligned}&\sum _{r=0}^m \lambda _r\ {}_0^CD_t^{\gamma _r} v(x,t)=u_{xx}(x,t)+f(x,t),\quad 0<x<L,~0<t\le T, \end{aligned}$$

(3.3)

$$\begin{aligned}&\frac{\partial }{\partial t}\Big (\frac{\partial ^2u}{\partial x^2}\Big ) =\frac{\partial ^2v}{\partial x^2},\quad x\in (0,L),~t\in (0,T], \end{aligned}$$

(3.4)

$$\begin{aligned}&u(x,0)=w_1(x),~v(x,0)=w_2(x),\quad x\in [0,L], \end{aligned}$$

(3.5)

$$\begin{aligned}&u(0,t)=0,~u(L,t)=0,\quad t\in (0,T], \end{aligned}$$

(3.6)

$$\begin{aligned}&v(0,t)=0,~v(L,t)=0,\quad t\in (0,T]. \end{aligned}$$

(3.7)

Suppose $u(x,t)\in C^{4,4}_{x,t}([0,L]\times [0, T]).$ Define the grid functions

$$\begin{aligned} U_i^k=u(x_i,t_k),\quad V_i^k=v(x_i,t_k),\quad 0\le i\le M,\quad 0\le k\le N. \end{aligned}$$

Considering (3.3) at the point $(x_i,t_{k+\sigma }),$ we have

$$\begin{aligned} \sum _{r=0}^m \lambda _r\ {}_0^CD_t^{\gamma _r} v(x_i,t_{k+\sigma })=u_{xx}(x_i,t_{k+\sigma })+f(x_i,t_{k+\sigma }),\quad 1\le i\le M-1,~0\le k\le N-1. \end{aligned}$$

(3.8)

Using Lemma 2.5, we obtain

$$\begin{aligned}&\sum _{r=0}^m \lambda _r\ {}_0^CD_t^{\gamma _r} v(x_i,t_{k+\sigma }) =\sum _{n=0}^{k}\hat{c}_{k-n}^{(k+1)}\big (V_i^{n+1}-V_i^{n}\big ) +O(\tau ^{3-\gamma _0}),\nonumber \\&\quad 1\le i\le M-1,~0\le k\le N-1. \end{aligned}$$

(3.9)

By Taylor expansion, it yields

$$\begin{aligned} u_{xx}(x_i,t_{k+\sigma })&=\sigma u_{xx}(x_i,t_{k+1}) +(1-\sigma )u_{xx}(x_i,t_{k})+O(\tau ^2)\nonumber \\&=\sigma \delta _x^2U_i^{k+1}+(1-\sigma ) \delta _x^2U_i^{k}+O(\tau ^2+h^2),\nonumber \\&=\delta _x^2U_i^{k+\sigma }+O(\tau ^2+h^2),\quad 1\le i \le M-1,~0\le k\le N-1. \end{aligned}$$

(3.10)

Substituting (3.9) and (3.10) into (3.8), we get

$$\begin{aligned} \sum _{n=0}^{k}\hat{c}_{k-n}^{(k+1)}\big (V_i^{n+1}-V_i^{n}\big ) =\delta _x^2U_i^{k+\sigma }+f_i^{k+\sigma }+R_i^{k+\sigma },\quad 1\le i \le M-1,~0\le k\le N-1, \end{aligned}$$

(3.11)

where $f_i^{k+\sigma }=f(x_i,t_{k+\sigma })$ and there exists a constant $c_0$ such that

$$\begin{aligned} {|}R_i^{k+\sigma }|\le c_0(\tau ^2+h^2),\quad 1\le i\le M-1,\quad 0\le k \le N-1. \end{aligned}$$

(3.12)

Considering Eq. (3.4) at the points $(x_i,t_{\frac{1}{2}})$ and $(x_i,t_{k+\sigma })$, respectively, we have

$$\begin{aligned} (u_{xx})_t\left( x_i,t_{\frac{1}{2}}\right) =v_{xx}\left( x_i,t_{\frac{1}{2}}\right) , ~1\le i\le M-1 \end{aligned}$$

(3.13)

and

$$\begin{aligned} (u_{xx})_t(x_i,t_{k+\sigma })=v_{xx}(x_i,t_{k+\sigma }), ~1\le i\le M-1,~ 1\le k\le N-1. \end{aligned}$$

(3.14)

By Taylor expansion, it follows from (3.13) that

$$\begin{aligned} \delta _t\delta _x^2U_i^{\frac{1}{2}}=\delta _x^2V_i^{\frac{1}{2}} +r_i^{\frac{1}{2}},~ 1\le i\le M-1. \end{aligned}$$

(3.15)

By Lemma 2.6 and Taylor expansion, it follows from (3.14) that

$$\begin{aligned} D_{\hat{t}}\delta _x^2U_i^k= \delta _x^2V_i^{k+\sigma } +r_i^{k+\sigma },~ 1\le i\le M-1,~ 1\le k\le N-1. \end{aligned}$$

(3.16)

There exists a constant $c_1$ such that

$$\begin{aligned} |r_i^{\frac{1}{2}}|\le&c_1 (\tau ^2+h^2), \quad 1\le i\le M-1, \end{aligned}$$

(3.17)

$$\begin{aligned} |r_i^{k+\sigma }|\le&c_1 (\tau ^2+h^2),\quad 1\le i \le M-1,\quad 1\le k\le N-1. \end{aligned}$$

(3.18)

In addition, noticing (3.4)–(3.6), we obtain

$$\begin{aligned} U_i^0=&w_1(x_i),~V_i^0=w_2(x_i), ~1\le i\le M-1, \end{aligned}$$

(3.19)

$$\begin{aligned} U_0^k=&0,~U_M^k=0,~0\le k\le N, \end{aligned}$$

(3.20)

$$\begin{aligned} V_0^k=&0,~V_M^k=0,~0\le k\le N. \end{aligned}$$

(3.21)

Omitting the small terms in (3.11), (3.15) and (3.16) and noticing (3.19), (3.21) and we construct the difference scheme for the problem (1.1)–(1.3) as follows

$$\begin{aligned}&\sum _{n=0}^{k}\hat{c}_{k-n}^{(k+1)}(v_i^{n+1}-v_i^{n}) =\delta _x^2u_i^{k+\sigma }+f_i^{k+\sigma },\quad 1\le i\le M-1,~0\le k\le N-1, \end{aligned}$$

(3.22)

$$\begin{aligned}&\delta _t\delta _x^2u_i^{\frac{1}{2}} =\delta _x^2v_i^{\frac{1}{2}},~ 1\le i\le M-1, \end{aligned}$$

(3.23)

$$\begin{aligned}&D_{\hat{t}}\delta _x^2u_i^k= \delta _x^2v_i^{k+\sigma },~ 1 \le i\le M-1,~1\le k\le N-1, \end{aligned}$$

(3.24)

$$\begin{aligned}&u_i^0=w_1(x_i),~v_i^0=w_2(x_i),~1\le i\le M-1, \end{aligned}$$

(3.25)

$$\begin{aligned}&u_0^k=0,~u_M^k=0,~0\le k\le N, \end{aligned}$$

(3.26)

$$\begin{aligned}&v_0^k=0,~v_M^k=0,~0\le k\le N. \end{aligned}$$

(3.27)

3.2 The Unique Solvability of the Difference Scheme

Theorem 3.1

The difference Scheme (3.22)–(3.27) is uniquely solvable.

Proof

Denote $u^k=(u_0^k,u_1^k,\ldots ,u_M^k),~v^k=(v_0^k,v_1^k, \ldots ,u_M^k).$

(1) For $k=0$, we can obtain the system of linear algebraic equations about the unknowns $u^1$ and $v^1$ from (3.22), (3.23), (3.26) and (3.27). Considering its homogenous system, we have

$$\begin{aligned}&\hat{c}_0^{(1)}v_i^1=\sigma \delta _x^2u_i^1,\quad 1\le i\le M-1, \end{aligned}$$

(3.28)

$$\begin{aligned}&\frac{1}{\tau }\delta _x^2u_i^1=\frac{1}{2}\delta _x^2v_i^1, \quad 1\le i\le M-1, \end{aligned}$$

(3.29)

$$\begin{aligned}&u_0^1=0,~u_M^1=0,~v_0^1=0,~v_M^1=0. \end{aligned}$$

(3.30)

Solving $\delta _x^2u_i^1$ from (3.29) and substituting the result into (3.28), we obtain

$$\begin{aligned} \hat{c}_0^{(1)}v_i^1=\frac{\sigma \tau }{2}\delta _x^2v_i^1, \quad 1\le i\le M-1, \end{aligned}$$

(3.31)

Taking the inner product of (3.31) with $v^{1}$ and using the summation by parts, we get

$$\begin{aligned} \hat{c}_0^{(1)}\Vert v^1\Vert ^2+\frac{\sigma \tau }{2}\Vert \delta _xv^1\Vert ^2=0. \end{aligned}$$

It implies that

$$\begin{aligned} v_i^1=0,\quad 1\le i\le M-1. \end{aligned}$$

Then, it follows from (3.28) that

$$\begin{aligned} \delta _x^2u_i^1=0,\quad 1\le i\le M-1. \end{aligned}$$

(3.32)

Taking the inner product of (3.32) with $u^1$ and noticing (3.30), it yields

$$\begin{aligned} \Vert \delta _xu^1\Vert =0,\quad \le k\le N-1. \end{aligned}$$

Then we get

$$\begin{aligned} u_i^1=0,\quad 1\le i\le M-1. \end{aligned}$$

(2) For $k (1\le k\le N-1),$ suppose that $\{u^{k-1},~v^{k-1}, u^k , v^{k}\}$ have been determined, then we get a linear system of equations with respect to $u^{k+1}$ and $v^{k+1}$ from (3.22), (3.24), (3.26) and (3.27).

Consider the corresponding homogeneous system

$$\begin{aligned}&\hat{c}_0^{(k+1)}v_i^{k+1}=\sigma \delta _x^2u_i^{k+1}, \quad 1\le i\le M-1, \end{aligned}$$

(3.33)

$$\begin{aligned}&\frac{2\sigma +1}{2\sigma \tau }\delta _x^2u_i^{k+1} =\delta _x^2v_i^{k+1},\quad 1\le i\le M-1, \end{aligned}$$

(3.34)

$$\begin{aligned}&u_0^{k+1}=0,~u_M^{k+1}=0, \end{aligned}$$

(3.35)

$$\begin{aligned}&v_0^{k+1}=0,~v_M^{k+1}=0. \end{aligned}$$

(3.36)

Solving $\delta _x^2u_i^{k+1}$ from (3.34) and substituting the result into (3.33), it yields

$$\begin{aligned} \hat{c}_0^{(k+1)}v_i^{k+1}=\frac{2\sigma ^2\tau }{2\sigma +1} \delta _x^2v_i^{k+1},\quad 1\le i\le M-1. \end{aligned}$$

(3.37)

Taking the inner product of (3.37) with $v^{k+1}$ and using the summation by parts, we obtain

$$\begin{aligned} \hat{c}_0^{(k+1)}\Vert v^{k+1}\Vert ^2+\frac{2\sigma ^2\tau }{2\sigma +1} \Vert \delta _xv^{k+1}\Vert ^2=0, \end{aligned}$$

which yields that

$$\begin{aligned} v_i^{k+1}=0,\quad 1\le i\le M-1. \end{aligned}$$

Consequently, it follows from (3.33) that

$$\begin{aligned} \delta _x^2u_i^{k+1}=0,~1\le i\le M-1. \end{aligned}$$

(3.38)

Taking the inner product of (3.38) with $u^{k+1},$ we have

$$\begin{aligned} \Vert \delta _xu^{k+1}\Vert =0. \end{aligned}$$

Then it yields

$$\begin{aligned} u_i^{k+1}=0,\quad 1\le i\le M-1. \end{aligned}$$

According to the induction principle, this completes the proof. $\square$

3.3 The Stability and Convergence of the Difference Scheme

Firstly, we present the priori estimate of the difference Scheme (3.22)–(3.27). The proof is divided into two steps, which correspond to the case $k=0$ and $k\ge 1.$

Theorem 3.2

Suppose $\{p_i^k~|~0\le i\le M,~0\le k\le N\}$ and $\{q_i^k~|~0\le i\le M,~0\le k\le N\}$ satisfy

$$\begin{aligned}&\sum _{n=0}^k\hat{c}_{k-n}^{(k+1)}(q_i^{n+1}-q_i^{n}) =\delta _x^2p_i^{k+\sigma }+f_i^{k+\sigma },\quad 1\le i\le M-1,~0\le k\le N-1, \end{aligned}$$

(3.39)

$$\begin{aligned}&\delta _t\delta _x^2p_i^{\frac{1}{2}}=\delta _x^2q_i^{\frac{1}{2}} +g_i^{\frac{1}{2}},\quad 1\le i\le M-1, \end{aligned}$$

(3.40)

$$\begin{aligned}&D_{\hat{t}}\delta _x^2p_i^{k}=\delta _x^2q_i^{k+\sigma } +g_i^{k+\sigma },\quad 1\le i\le M-1,~1\le k\le N-1, \end{aligned}$$

(3.41)

$$\begin{aligned}&p_i^0=w_1(x_i),~q_i^0=w_2(x_i),\quad 1\le i\le M-1, \end{aligned}$$

(3.42)

$$\begin{aligned}&p_0^k=0,~p_M^k=0,~q_0^k=0,~q_M^k=0,~0\le k\le N, \end{aligned}$$

(3.43)

where $w_1(x_i)=0,~w_2(x_i)=0$ for $i=0,M.$ Then there exists a constant $\tau _0$ such that the following inequality holds when $\tau \le \tau _0,$

$$\begin{aligned} \Vert \delta _xp^k\Vert ^2\le c_2\exp \Big (\frac{4\sigma L^2}{3}T\Big )G_k ,\quad \tau \sum _{n=1}^{k}\Vert q^n\Vert ^2\le c_3G_k,~ 0\le k\le N. \end{aligned}$$

where $c_2$ and $c_3$ are two constants and

$$\begin{aligned} G_k&=\Vert \delta _xp^0\Vert ^2+\Vert \delta _x^2p^0\Vert ^2+\Vert q^0\Vert ^2 +\Vert \delta _xq^0\Vert ^2+\Vert f^\sigma \Vert ^2+\Vert g^{\frac{1}{2}}\Vert ^2\\&\quad +\tau \sum _{l=1}^{k-1}\Vert f^{l+\sigma }\Vert ^2 +\tau \sum _{l=1}^{k-1}\Vert g^{l+\sigma }\Vert ^2. \end{aligned}$$

Proof

Step1. When $k=0$, the system is as follows

$$\begin{aligned}&\hat{c}_0^{(1)}(q_i^{1}-q_i^0)=\sigma \delta _x^2p_i^{1} +(1-\sigma )\delta _x^2p_i^{0}+f_i^{\sigma },~1\le i\le M-1, \end{aligned}$$

(3.44)

$$\begin{aligned}&\delta _t\delta _x^2p_i^{\frac{1}{2}}=\delta _x^2q_i^{\frac{1}{2}} +g_i^{\frac{1}{2}},~1\le i\le M-1, \end{aligned}$$

(3.45)

$$\begin{aligned}&p_i^0=w_1(x_i),~q_i^0=w_2(x_i),\quad 1\le i\le M-1, \end{aligned}$$

(3.46)

$$\begin{aligned}&p_0^1=0,~p_M^1=0,~q_0^1=0,~q_M^1=0 \end{aligned}$$

(3.47)

with $p_0^0=0,~p_M^0=0,~q_0^0=0,~q_M^0=0.$

(I) Taking the inner product of (3.44) with $q^1,$ we have

$$\begin{aligned} \hat{c}_0^{(1)}\Vert q^{1}\Vert ^2=\hat{c}_0^{(1)}(q^0,q^1) -\sigma \big (\delta _xp^{1},\delta _xq^1\big )+(1-\sigma ) (\delta _x^2p^0,q^1)+(f^\sigma ,q^1). \end{aligned}$$

(3.48)

Taking the inner product of (3.45) with $-2\sigma p^1$ and by the summation by parts, it yields

$$\begin{aligned} \frac{2\sigma }{\tau }\Vert \delta _xp^1\Vert ^2 =\frac{2\sigma }{\tau } (\delta _xp^0,\delta _xp^1)+\sigma (\delta _xq^1,\delta _xp^1) +\sigma (\delta _xq^0,\delta _xp^1)-2\sigma (g^{\frac{1}{2}},p^1).\nonumber \\ \end{aligned}$$

(3.49)

Adding (3.48) with (3.49) and using Young inequality and Lemma 2.9, we obtain

$$\begin{aligned}&\hat{c}_0^{(1)}\Vert q^{1}\Vert ^2+\frac{2\sigma }{\tau }\Vert \delta _xp^1\Vert ^2\nonumber \\&\quad \le \hat{c}_0^{(1)}(q^0,q^1)+(1-\sigma )(\delta _x^2p^0,q^1) +(f^\sigma ,q^1)\nonumber \\&\qquad +\frac{2\sigma }{\tau }(\delta _xp^0,\delta _xp^1) +\sigma (\delta _xq^0,\delta _xp^1)-2\sigma (g^{\frac{1}{2}},p^1)\nonumber \\&\quad \le \Big (\frac{\hat{c}_0^{(1)}}{3}\Vert q^1\Vert ^2 +\frac{3\hat{c}_0^{(1)}}{4}\Vert q^0\Vert ^2\Big ) +\Big (\frac{\hat{c}_0^{(1)}}{3}\Vert q^1\Vert ^2 +\frac{3(1-\sigma )^2}{4\hat{c}_0^{(1)}}\Vert \delta _x^2p^0\Vert ^2\Big )\nonumber \\&\qquad +\Big (\frac{\hat{c}_0^{(1)}}{3}\Vert q^1\Vert ^2 +\frac{3}{4\hat{c}_0^{(1)}}\Vert f^\sigma \Vert ^2\Big ) +\Big (\frac{\sigma }{3\tau }\Vert \delta _xp^1\Vert ^2 +\frac{3\sigma }{\tau }\Vert \delta _xp^0\Vert ^2\Big ) \nonumber \\&\qquad +\Big (\frac{\sigma }{3\tau }\Vert \delta _xp^1\Vert ^2 +\frac{3\sigma \tau }{4}\Vert \delta _xq^0\Vert ^2\Big ) +\Big (\frac{\sigma }{3\tau }\Vert \delta _xp^1\Vert ^2 +\frac{L^2\sigma }{2}\tau \Vert g^{\frac{1}{2}}\Vert ^2\Big ). \end{aligned}$$

(3.50)

It follows that

$$\begin{aligned} \Vert \delta _xp^1\Vert ^2&\le 3\Vert \delta _xp^0\Vert ^2+\frac{3\hat{c}_0^{(1)}\tau }{4\sigma }\Vert q^0\Vert ^2 +\frac{3(1-\sigma )^2\tau }{4\hat{c}_0^{(1)}\sigma } \Vert \delta _x^2p^0\Vert ^2+\frac{3\tau }{4\hat{c}_0^{(1)} \sigma }\Vert f^\sigma \Vert ^2\nonumber \\&\quad +\frac{3\tau ^2}{4}\Vert \delta _xq^0\Vert ^2+\frac{L^2}{2}\tau ^2 \Vert g^{\frac{1}{2}}\Vert ^2. \end{aligned}$$

(3.51)

(II) It follows from (3.45) that

$$\begin{aligned} \delta _x^2p_i^1=\delta _x^2p_i^0+\tau \delta _x^2q_i^{\frac{1}{2}}+\tau g_i^{\frac{1}{2}},\quad 1\le i\le M-1. \end{aligned}$$

(3.52)

Substituting (3.52) into (3.44), we have

$$\begin{aligned} \hat{c}_0^{(1)}(q_i^{1}-q_i^0)=\delta _x^2p_i^0+\sigma \tau \delta _x^2q_i^{\frac{1}{2}}+f_i^\sigma +\sigma \tau g_i^{\frac{1}{2}},\quad 1\le i\le M-1. \end{aligned}$$

(3.53)

Taking the inner product of (3.53) with $q^\frac{1}{2},$ we obtain

$$\begin{aligned} \hat{c}_0^{(1)}\left( q^{1}-q^0,q^\frac{1}{2}\right) =\left( \delta _x^2p^0,q^\frac{1}{2}\right) +\sigma \tau \left( \delta _x^2q^{\frac{1}{2}}, q^\frac{1}{2}\right) +\left( f^\sigma ,q^\frac{1}{2}\right) +\sigma \tau \left( g^{\frac{1}{2}},q^\frac{1}{2}\right) . \end{aligned}$$

By the summation by parts and Young inequality $ab\le \frac{a^2}{2\varepsilon }+\frac{\varepsilon b^2}{2} \ \big (\hbox {taking}\ \varepsilon =\frac{3}{\hat{c}_0^{(1)}}\big )$, it yields

$$\begin{aligned}&\frac{\hat{c}_0^{(1)}}{2}(\Vert q^{1}\Vert ^2-\Vert q^{0}\Vert ^2)\nonumber \\&\quad =\Big (\delta _x^2p^{0},q^\frac{1}{2}\Big ) -\sigma \tau \Vert \delta _xq^{\frac{1}{2}}\Vert ^2 +\Big (f^\sigma ,q^\frac{1}{2}\Big ) +\sigma \tau \Big (g^{\frac{1}{2}},q^\frac{1}{2}\Big )\nonumber \\&\quad \le \Big (\frac{1}{2\varepsilon }\Vert \delta _x^2p^0\Vert ^2 +\frac{\varepsilon }{2}\Vert q^{\frac{1}{2}}\Vert ^2\Big ) +\Big (\frac{1}{2\varepsilon }\Vert f^\sigma \Vert ^2 +\frac{\varepsilon }{2}\Vert q^{\frac{1}{2}}\Vert ^2\Big ) + \Big (\frac{1}{2\varepsilon }\Vert \sigma \tau g^\frac{1}{2}\Vert ^2+\frac{\varepsilon }{2} \Vert q^{\frac{1}{2}}\Vert ^2\Big )\nonumber \\&\quad \le \Big (\frac{\hat{c}_0^{(1)}}{6}\Vert q^{\frac{1}{2}}\Vert ^2 +\frac{3}{2\hat{c}_0^{(1)}}\Vert \delta _x^2p^0\Vert ^2\Big ) +\Big (\frac{\hat{c}_0^{(1)}}{6}\Vert q^{\frac{1}{2}}\Vert ^2 +\frac{3}{2\hat{c}_0^{(1)}}\Vert f^\sigma \Vert ^2\Big ) \nonumber \\&\qquad +\Big (\frac{\hat{c}_0^{(1)}}{6}\Vert q^{\frac{1}{2}}\Vert ^2 +\frac{3\sigma ^2\tau ^2}{2\hat{c}_0^{(1)}} \Vert g^{\frac{1}{2}}\Vert ^2\Big )\nonumber \\&\quad \le \frac{\hat{c}_0^{(1)}}{4}\Vert q^1\Vert ^2 +\frac{\hat{c}_0^{(1)}}{4}\Vert q^0\Vert ^2+\frac{3}{2\hat{c}_0^{(1)}} \Vert \delta _x^2p^0\Vert ^2 +\frac{3}{2\hat{c}_0^{(1)}}\Vert f^\sigma \Vert ^2 +\frac{3\sigma ^2\tau ^2}{2\hat{c}_0^{(1)}}\Vert g^{\frac{1}{2}}\Vert ^2 . \end{aligned}$$

(3.54)

From (3.54), we obtain

$$\begin{aligned} \Vert q^1\Vert ^2\le 3\Vert q^0\Vert ^2+\frac{6}{(\hat{c}_0^{(1)})^2}\Vert \delta _x^2p^0\Vert ^2 +\frac{6}{(\hat{c}_0^{(1)})^2}\Vert f^\sigma \Vert ^2+\frac{6\sigma ^2\tau ^2}{(\hat{c}_0^{(1)})^2}\Vert g^{\frac{1}{2}}\Vert ^2. \end{aligned}$$

(3.55)

Step 2. When $k\ge 1,$ taking the inner product (3.39) with $q^{k+\sigma }$, we obtain

$$\begin{aligned} \left( \sum _{n=0}^k\hat{c}_{k-n}^{(k+1)}(q^{n+1}-q^{n}),q^{k+\sigma }\right) =\Big (\delta _x^2p^{k+\sigma },q^{k+\sigma }\Big ) +\Big (f^{k+\sigma },q^{k+\sigma }\Big ),~1\le k\le N-1. \end{aligned}$$

(3.56)

By Lemma 2.7 and Lemma 2.4, we have

$$\begin{aligned}&\left( \sum _{n=0}^k\hat{c}_{k-n}^{(k+1)}(q^{n+1}-q^{n}),q^{k+\sigma }\right) \ge \frac{1}{2}\sum _{n=0}^k\hat{c}_{k-n}^{(k+1)}\big (\Vert q^{n+1}\Vert ^2 -\Vert q^{n}\Vert ^2\big )\nonumber \\&\quad =\frac{1}{2}\left( \sum _{n=1}^{k+1}\hat{c}_{k-n+1}^{(k+1)}\Vert q^{n}\Vert ^2 -\sum _{n=1}^{k}\hat{c}_{k-n}^{(k)}\Vert q^{n}\Vert ^2-\hat{b}_k\Vert q^1\Vert ^2 -\hat{c}_{k}^{(k+1)}\Vert q^0\Vert ^2\right) ,\nonumber \\&\qquad 1\le k\le N-1. \end{aligned}$$

(3.57)

Using Young inequality, for any $\varepsilon >0$, it holds

$$\begin{aligned} \Big |\Big (f^{k+\sigma },q^{k+\sigma }\Big )\Big |\le \varepsilon \Vert q^{k+\sigma }\Vert ^2+\frac{1}{4\varepsilon } \Vert f^{k+\sigma }\Vert ^2. \end{aligned}$$

(3.58)

Substituting (3.57) and (3.58) into (3.56), it yields

$$\begin{aligned}&\frac{1}{2}\left( \sum _{n=1}^{k+1}\hat{c}_{k-n+1}^{(k+1)}\Vert q^{n}\Vert ^2 -\sum _{n=1}^{k}\hat{c}_{k-n}^{(k)}\Vert q^{n}\Vert ^2-\hat{b}_k\Vert q^1\Vert ^2 -\hat{c}_{k}^{(k+1)}\Vert q^0\Vert ^2\right) \nonumber \\&\quad \le \Big (\delta _x^2p^{k+\sigma },q^{k+\sigma }\Big ) +\varepsilon \Vert q^{k+\sigma }\Vert ^2+\frac{1}{4\varepsilon } \Vert f^{k+\sigma }\Vert ^2,\quad 1\le k\le N-1. \end{aligned}$$

(3.59)

Taking the inner product (3.41) with $-p^{k+\sigma }$, we get

$$\begin{aligned} -\Big (D_{\hat{t}}\delta _x^2p^{k},p^{k+\sigma }\Big ) =-\Big (\delta _x^2q^{k+\sigma },p^{k+\sigma }\Big ) -\Big (g^{k+\sigma },p^{k+\sigma }\Big ),\quad 1\le k\le N-1. \end{aligned}$$

(3.60)

Using Lemma 2.8, it yields

$$\begin{aligned} -\Big (D_{\hat{t}}\delta _x^2p^{k},p^{k+\sigma }\Big ) =\Big (D_{\hat{t}}\delta _xp^{k},\delta _xp^{k+\sigma }\Big ) \ge \frac{1}{4\tau }(F^{k+1}-F^k), \end{aligned}$$

(3.61)

where

$$\begin{aligned} F^{k+1}=(2\sigma +1)\Vert \delta _xp^{k+1}\Vert ^2-(2\sigma -1) \Vert \delta _xp^k\Vert ^2+(2\sigma ^2+\sigma -1)\Vert \delta _xp^{k+1} -\delta _xp^{k}\Vert ^2 \end{aligned}$$

(3.62)

and

$$\begin{aligned} F^{k+1}\ge \frac{1}{\sigma } \Vert \delta _xp^{k+1}\Vert ^2,~k\ge 0. \end{aligned}$$

(3.63)

By Cauchy-Schwarz inequality, we have

$$\begin{aligned} \Big |-\Big (g^{k+\sigma },p^{k+\sigma }\Big )\Big |\le \frac{1}{2}\Vert g^{k+\sigma }\Vert ^2+\frac{1}{2}\Vert p^{k+\sigma }\Vert ^2, \quad 1\le k\le N-1. \end{aligned}$$

(3.64)

Substituting (3.61) and (3.64) into (3.60), it yields

$$\begin{aligned} \frac{1}{4\tau }(F^{k+1}-F^k)\le -\Big (\delta _x^2q^{k+\sigma }, p^{k+\sigma }\Big ) +\frac{1}{2}\Vert g^{k+\sigma }\Vert ^2 +\frac{1}{2}\Vert p^{k+\sigma }\Vert ^2,\quad 1\le k\le N-1. \end{aligned}$$

(3.65)

Adding (3.59) with (3.65), we obtain

$$\begin{aligned}&\frac{1}{2}\left( \sum _{n=1}^{k+1}\hat{c}_{k-n+1}^{(k+1)}\Vert q^{n}\Vert ^2 -\sum _{n=1}^{k}\hat{c}_{k-n}^{(k)}\Vert q^{n}\Vert ^2-\hat{b}_k\Vert q^1\Vert ^2 -\hat{c}_{k}^{(k+1)}\Vert q^0\Vert ^2\right) +\frac{1}{4\tau }(F^{k+1}-F^k)\nonumber \\&\quad \le \varepsilon \Vert q^{k+\sigma }\Vert ^2+\frac{1}{4\varepsilon } \Vert f^{k+\sigma }\Vert ^2 +\frac{1}{2}\Vert g^{k+\sigma }\Vert ^2+\frac{1}{2} \Vert p^{k+\sigma }\Vert ^2,\quad 1\le k\le N-1. \end{aligned}$$

(3.66)

Denote

$$\begin{aligned} H^{k+1}=2\tau \sum _{n=1}^{k+1}\hat{c}_{k-n+1}^{(k+1)}\Vert q^{n}\Vert ^2+F^{k+1}. \end{aligned}$$

Then, (3.66) can be rewritten as

$$\begin{aligned} H^{k+1}&\le H^k+2\tau \hat{b}_k\Vert q^1\Vert ^2+ 2\tau \hat{c}_{k}^{(k+1)}\Vert q^0\Vert ^2 +4\tau \varepsilon \Vert q^{k+\sigma }\Vert ^2+\frac{\tau }{\varepsilon } \Vert f^{k+\sigma }\Vert ^2 \nonumber \\&\quad +2\tau \Vert g^{k+\sigma }\Vert ^2+2\tau \Vert p^{k+\sigma }\Vert ^2\nonumber \\ \le&H^1+2\tau \sum _{n=1}^{k}\hat{b}_n\Vert q^1\Vert ^2+2\tau \sum _{n=1}^{k} \hat{c}_{n}^{(k+1)}\Vert q^0\Vert ^2 +8\tau \varepsilon \sum _{n=1}^{k+1}\Vert q^{n} \Vert ^2+\frac{\tau }{\varepsilon }\sum _{n=1}^{k}\Vert f^{n+\sigma }\Vert ^2\nonumber \\&\quad +2\tau \sum _{n=1}^{k}\Vert g^{n+\sigma }\Vert ^2+4\tau \sum _{n=1}^{k+1}\Vert p^{n}\Vert ^2, \quad 1\le k\le N-1. \end{aligned}$$

(3.67)

By Lemma 2.3, (3.62) and (3.63), when $\tau \le \tau _0,$ we have

$$\begin{aligned} H^{k+1}\ge \left( \sum _{r=0}^m\lambda _r\frac{(1-\gamma _r)T^{-\gamma _r}}{\Gamma (2-\gamma _r)}\right) \tau \sum _{n=1}^{k+1}\Vert q^{n}\Vert ^2 +\frac{1}{\sigma }\Vert \delta _xp^{k+1}\Vert ^2,\quad 1\le k\le N-1 \end{aligned}$$

(3.68)

and

$$\begin{aligned} H^1=2\tau \hat{c}_0^{(1)}\Vert q^1\Vert ^2+F^1\le 2\tau \hat{c}_0^{(1)}\Vert q^1\Vert ^2 +(4\sigma ^2+4\sigma -1) \Vert \delta _xp^1\Vert ^2+(4\sigma ^2-1)\Vert \delta _xp^0\Vert ^2. \end{aligned}$$

(3.69)

Substituting (3.68) and (3.69) into (3.67), it yields

$$\begin{aligned}&\left( \sum _{r=0}^m\lambda _r\frac{(1-\gamma _r) T^{-\gamma _r}}{\Gamma (2-\gamma _r)}\right) \tau \sum _{n=1}^{k+1} \Vert q^{n}\Vert ^2+\frac{1}{\sigma }\Vert \delta _xp^{k+1}\Vert ^2\nonumber \\&\quad \le 2\tau \hat{c}_0^{(1)}\Vert q^1\Vert ^2 +(4\sigma ^2+4\sigma -1) \Vert \delta _xp^1\Vert ^2+(4\sigma ^2-1)\Vert \delta _xp^0\Vert ^2 +2\tau \sum _{n=1}^{k}\hat{b}_n\Vert q^1\Vert ^2\nonumber \\&\qquad +2\tau \sum _{n=1}^{k}\hat{c}_{n}^{(k+1)}\Vert q^0\Vert ^2 +8\tau \varepsilon \sum _{n=1}^{k+1}\Vert q^{n}\Vert ^2 +\frac{\tau }{\varepsilon }\sum _{n=1}^{k}\Vert f^{n+\sigma }\Vert ^2\nonumber \\&\qquad +2\tau \sum _{n=1}^{k}\Vert g^{n+\sigma }\Vert ^2 +4\tau \sum _{n=1}^{k+1}\Vert p^{n}\Vert ^2. \end{aligned}$$

(3.70)

Taking $\varepsilon =\frac{1}{16}\Big (\sum \limits _{r=0}^m\lambda _r \frac{(1-\gamma _r)T^{-\gamma _r}}{\Gamma (2-\gamma _r)}\Big )$ and using Lemma 2.4, (3.51) and (3.55), we have

$$\begin{aligned} \Vert \delta _xp^{k+1}\Vert ^2&\le 4\sigma \tau \sum _{n=1}^{k+1}\Vert p^{n}\Vert ^2+c_2G_{k+1}\\&\le \frac{2L^2\sigma }{3}\tau \sum _{n=1}^{k+1} \Vert \delta _xp^{n}\Vert ^2+c_2G_{k+1},\quad 1\le k\le N-1, \end{aligned}$$

where $c_2$ is a constant.

By Lemma 2.10, it follows that

$$\begin{aligned} \Vert \delta _xp^{k+1}\Vert ^2\le&c_2 \exp \Big (\frac{4\sigma L^2}{3}T\Big )G_{k+1},\quad 1\le k\le N-1. \end{aligned}$$

(3.71)

Substituting (3.71) into (3.70), there exists a constant $c_3$ such that

$$\begin{aligned} \tau \sum _{n=1}^{k+1}\Vert q^{n}\Vert ^2\le&c_3G_{k+1},\quad 1\le k\le N-1. \end{aligned}$$

This completes the proof. $\square$

Theorem 3.2 implies the following theorem.

Theorem 3.3

The solution of the difference scheme (3.22)–(3.27) is unconditionally stable with respect to the initial values $w_1, w_2$ and the right hand side function f.

Proof

Suppose $\{\theta _i^k\,|\,0\le i\le M,~0\le k\le N\}$ and $\{z_i^k\,|\,0\le i\le M,~0\le k\le N\}$ be the solution of

$$\begin{aligned}&\sum _{n=0}^{k}\hat{c}_{k-n}^{(k+1)}(\theta _i^{n+1}-\theta _i^{n}) =\delta _x^2z_i^{k+\sigma }+f_i^{k+\sigma }+\xi _i^k,\quad 1\le i\le M-1,~0\le k\le N-1, \end{aligned}$$

(3.72)

$$\begin{aligned}&\delta _t\delta _x^2z_i^{\frac{1}{2}}=\delta _x^2\theta _i^{\frac{1}{2}}, ~ 1\le i\le M-1, \end{aligned}$$

(3.73)

$$\begin{aligned}&D_{\hat{t}}\delta _x^2z_i^k= \delta _x^2\theta _i^{k+\sigma }, ~ 1\le i\le M-1,~1\le k\le N-1, \end{aligned}$$

(3.74)

$$\begin{aligned}&z_i^0=w_1(x_i)+\eta _{1i},~\theta _i^0=w_2(x_i) +\eta _{2i},~1\le i\le M-1, \end{aligned}$$

(3.75)

$$\begin{aligned}&z_0^k=0,~z_M^k=0,~0\le k\le N, \end{aligned}$$

(3.76)

$$\begin{aligned}&\theta _0^k=0,\theta _M^k=0,~0\le k\le N. \end{aligned}$$

(3.77)

Denote

$$\begin{aligned} \nu _i^k=\theta _i^k-v_i^k,\quad \mu _i^k=z_i^k-u_i^k,\quad 0\le i \le M, 0\le k\le N. \end{aligned}$$

Subtracting (3.72)–(3.77) from (3.21)–(3.27), we get the perturbation error equations

$$\begin{aligned}&\sum _{n=0}^{k}\hat{c}_{k-n}^{(k+1)}(\nu _i^{n+1}-\nu _i^{n}) =\delta _x^2\mu _i^{k+\sigma }+\xi _i^k,\quad 1\le i\le M-1,~0\le k\le N-1,\\&\delta _t\delta _x^2\mu _i^{\frac{1}{2}}=\delta _x^2 \nu _i^{\frac{1}{2}}, \quad 1\le i\le M-1,\\&D_{\hat{t}}\delta _x^2\mu _i^k= \delta _x^2 \nu _i^{k+\sigma },\quad 1\le i\le M-1,\quad 1\le k\le N-1,\\&\mu _i^0=\eta _{1i},\quad \nu _i^0=\eta _{2i},\quad 1\le i\le M-1,\\&\mu _0^k=0,\quad \mu _M^k=0,\quad 0\le k\le N,\\&\nu _0^k=0,\nu _M^k=0,\quad 0\le k\le N. \end{aligned}$$

By Theorem 3.2, we obtain

$$\begin{aligned} \Vert \delta _x\mu ^k\Vert ^2\le \kappa _1\exp \left( \frac{4\sigma L^2}{3}T\right) Q_k,\quad \tau \sum _{n=1}^{k}\Vert \nu ^n\Vert ^2\le \kappa _2Q_k,~ 0\le k\le N, \end{aligned}$$

where $\kappa _1$ and $\kappa _2$ are two constants and

$$\begin{aligned} Q_k=\Vert \delta _x\eta _1\Vert ^2+\Vert \delta ^2_x\eta _1\Vert ^2 +\Vert \eta _2\Vert ^2+\Vert \delta _x\eta _2\Vert ^2+\Vert \xi ^1\Vert ^2 +\tau \sum _{l=2}^{k-1}\Vert \xi ^l\Vert ^2. \end{aligned}$$

The proof ends. $\square$

Next, we give the convergence of the scheme (3.22)–(3.27). We have the following theorem.

Theorem 3.4

Suppose the problem (3.3)–(3.7) has a unique smooth solution and $\{u_i^k, v_i^k\;|\;0\le i \le M,~0\le k\le N\}$ is the solution of the difference scheme (3.22)–(3.27). Then when $\tau \le \tau _0$, there exists a constant $C_1$ such that

$$\begin{aligned} \Vert e^k\Vert _\infty \le C_1(\tau ^2+h^2),~\tau \sum _{n=1}^{k}\Vert \rho ^n\Vert \le C_1(\tau ^2+h^2),~ 0\le k\le N. \end{aligned}$$

Proof

Let

$$\begin{aligned} \rho _i^k=V_i^k-v_i^k,\quad e_i^k=U_i^k-u_i^k,~0\le i \le M,~0\le k\le N. \end{aligned}$$

Subtracting (3.22)–(3.27) from (3.11), (3.15), (3.16), (3.19)–(3.21), respectively, we obtain the error equations as follows

$$\begin{aligned}&\sum _{n=0}^{k}\hat{c}_{k-n}^{(k+1)}(\rho _i^{n+1}-\rho _i^{n}) =\delta _x^2e_i^{k+\sigma }+R_i^{k+\sigma },\quad 1\le i\le M-1, \quad 0\le k\le N-1, \end{aligned}$$

(3.78)

$$\begin{aligned}&\delta _t\delta _x^2e_i^{\frac{1}{2}}=\delta _x^2\rho _i^{\frac{1}{2}} +r_i^{\frac{1}{2}},\quad 1\le i\le M-1, \end{aligned}$$

(3.79)

$$\begin{aligned}&D_{\hat{t}}\delta _x^2e_i^k= \delta _x^2\rho _i^{k+\sigma } +r_i^{k+\sigma },\quad 1\le i\le M-1,\quad 1\le k\le N-1, \end{aligned}$$

(3.80)

$$\begin{aligned}&e_i^0=0,\quad \rho _i^0=0,\quad 1\le i\le M-1, \end{aligned}$$

(3.81)

$$\begin{aligned}&e_0^k=0,\quad e_M^k=0,\quad 0\le k\le N, \end{aligned}$$

(3.82)

$$\begin{aligned}&\rho _0^k=0,\quad \rho _M^k=0,\quad 0\le k\le N. \end{aligned}$$

(3.83)

Using Theorem 3.2 and noticing (3.12), (3.17) and (3.18), we can obtain

$$\begin{aligned} \Vert \delta _xe^k\Vert ^2\le c_4(\tau ^2+h^2)^2, \quad \tau \sum _{n=1}^{k} \Vert \rho ^n\Vert ^2\le c_4(\tau ^2+h^2)^2,\quad 0\le k\le N, \end{aligned}$$

where $c_4$ is a constant.

It follows from Lemma 2.9 and Cauchy-Schwarz inequality that

$$\begin{aligned} \Vert e^k\Vert _\infty \le C_1(\tau ^2+h^2),\quad \tau \sum _{n=1}^{k} \Vert \rho ^n\Vert \le C_1(\tau ^2+h^2),\quad 0\le k\le N, \end{aligned}$$

where $C_1=\max \{\sqrt{c_4T},\frac{\sqrt{c_4 L}}{2}\}.$ The proof ends. $\square$

4 A Fourth-Order Difference Scheme in Space

4.1 The Derivation of the Difference Scheme

Suppose $u(x,t)\in C_{x,t}^{6,4}([0,L]\times [0,T]).$

Considering (3.3) at the point $(x_i,t_{k+\sigma }),$ we obtain

$$\begin{aligned} \sum _{r=0}^m \lambda _r\ {}_0^CD_t^{\gamma _r} v(x_i,t_{k+\sigma })=u_{xx}(x_i,t_{k+\sigma })+f(x_i,t_{k+\sigma }),\quad 1\le i\le M-1,\quad 0\le k\le N-1. \end{aligned}$$

Using Lemma 2.5 and Taylor expansion, we obtain

$$\begin{aligned}&\sum _{n=0}^{k}\hat{c}_{k-n}^{(k+1)}\big (V_i^{n+1}-V_i^{n}\big ) =\sigma u_{xx}(x_i,t_{k+1})+(1-\sigma )u_{xx}(x_i,t_{k}) +f_i^{k+\sigma }+O(\tau ^2),\nonumber \\&\quad 0\le i\le M,\quad 0\le k\le N-1. \end{aligned}$$

(4.1)

Acting the averaging operator $\mathcal {A}$ on both sides of (4.1) and using Taylor expansion, we have

$$\begin{aligned}&\sum _{n=0}^{k}\hat{c}_{k-n}^{(k+1)}\big (\mathcal {A}V_i^{n+1} -\mathcal {A}V_i^{n}\big ) =\sigma \mathcal {A} u_{xx}(x_i,t_{k+1}) +(1-\sigma )\mathcal {A}u_{xx}(x_i,t_{k})\nonumber \\&\qquad +\mathcal {A}f(x_i,t_{k+\sigma })+O(\tau ^2)\nonumber \\&\quad =\delta _x^2U_i^{k+\sigma }+\mathcal {A}f_i^{k+\sigma } +S_i^{k+\sigma },\nonumber \\&\qquad 1\le i\le M-1,\quad 0\le k\le N-1, \end{aligned}$$

(4.2)

where there exists a constant $c_5$ such that

$$\begin{aligned} {|}S_i^{k+\sigma }|\le c_5(\tau ^2+h^4),\quad 1\le i\le M-1, \quad 0\le k\le N-1, \end{aligned}$$

(4.3)

Considering Eq. (3.4) at the points $(x_i,t_{\frac{1}{2}})$ and $(x_i,t_{k+\sigma }),$ we have

$$\begin{aligned} u_{xxt}\left( x_i,t_{\frac{1}{2}}\right) =v_{xx} \left( x_i,t_{\frac{1}{2}}\right) , \quad 0\le i\le M \end{aligned}$$

(4.4)

and

$$\begin{aligned} u_{xxt}(x_i,t_{k+\sigma })=v_{xx}(x_i,t_{k+\sigma }), \quad 0\le i\le M,\quad 1\le k\le N-1. \end{aligned}$$

(4.5)

Acting $\mathcal {A}$ on Eqs. (4.4) and (4.6), we get

$$\begin{aligned} \mathcal {A}u_{xxt}\left( x_i,t_{\frac{1}{2}}\right) =\mathcal {A}v_{xx} \left( x_i,t_{\frac{1}{2}}\right) , \quad 1\le i\le M-1 \end{aligned}$$

(4.6)

and

$$\begin{aligned} \mathcal {A}u_{xxt}(x_i,t_{k+\sigma })=\mathcal {A}v_{xx}(x_i,t_{k+\sigma }), \quad 1\le i\le M-1,\quad 1\le k\le N-1. \end{aligned}$$

(4.7)

Using Taylor expansion and Lemma 2.6, it yields

$$\begin{aligned} \delta _t\delta _x^2U_i^{\frac{1}{2}}=\delta _x^2V_i^{\frac{1}{2}} +s_i^{\frac{1}{2}},\quad 1\le i\le M-1 \end{aligned}$$

(4.8)

and

$$\begin{aligned} D_{\hat{t}}\delta _x^2U_i^k= \delta _x^2V_i^{k+\sigma } +s_i^{k+\sigma },\quad 1\le i\le M-1,\quad 1\le k\le N-1, \end{aligned}$$

(4.9)

where there exists a constant $c_6$ such that

$$\begin{aligned} |s_i^{\frac{1}{2}}|\le&c_6 (\tau ^2+h^4),\quad 1\le i\le M-1, \end{aligned}$$

(4.10)

$$\begin{aligned} {|}s_i^{k+\sigma }|\le&c_6 (\tau ^2+h^4),\quad 1\le i\le M-1. \end{aligned}$$

(4.11)

Noticing the initial and boundary conditions, we get

$$\begin{aligned} U_i^0=&w_1(x_i),\quad V_i^0=w_2(x_i), \quad 1\le i\le M-1, \end{aligned}$$

(4.12)

$$\begin{aligned} U_0^k=&0,\quad U_M^k=0,\quad 0\le k\le N, \end{aligned}$$

(4.13)

$$\begin{aligned} V_0^k=&0,\quad V_M^k=0,\quad 0\le k\le N. \end{aligned}$$

(4.14)

Omitting the small terms in (4.2), (4.8) and (4.9) ans noticing (4.12)–(4.14), we construct the difference scheme for the problem (1.1)–(1.3) as follows

$$\begin{aligned}&\sum _{n=0}^{k}\hat{c}_{k-n}^{(k+1)}(\mathcal {A}v_i^{n+1}-\mathcal {A}v_i^{n}) =\delta _x^2u_i^{k+\sigma }+\mathcal {A}f_i^{k+\sigma },\quad 1\le i\le M-1,\quad 0 \le k\le N-1, \end{aligned}$$

(4.15)

$$\begin{aligned}&\delta _t\delta _x^2u_i^{\frac{1}{2}}=\delta _x^2v_i^{\frac{1}{2}},\quad 1 \le i\le M-1, \end{aligned}$$

(4.16)

$$\begin{aligned}&D_{\hat{t}}\delta _x^2u_i^k= \delta _x^2v_i^{k+\sigma },\quad 1\le i \le M-1,\quad 1\le k\le N-1, \end{aligned}$$

(4.17)

$$\begin{aligned}&u_i^0=w_1(x_i),\quad v_i^0=w_2(x_i),\quad 1\le i\le M-1, \end{aligned}$$

(4.18)

$$\begin{aligned}&u_0^k=0,\quad u_M^k=0,\quad 0\le k\le N, \end{aligned}$$

(4.19)

$$\begin{aligned}&v_0^k=0,\quad v_M^k=0,\quad 0\le k\le N. \end{aligned}$$

(4.20)

We know $u^0$ and $v^0$ from (4.18)–(4.20). Solving $\delta _x^2u_i^1$ from (4.16) and then substituting the result into (4.15) with the superscript $k=0$ yield a tri-diagonal system of linear algebraic equations about $v^1.$ After $v^1$ is obtained, then $u^1$ can be got easily. Now suppose $\{u^{l}, v^l\,|\, 0\le l\le k\}$ have been determined. Then, we solve $\delta _x^2 u_i^{k+1}$ from (4.16) and substitute it into (4.15) to obtain a tri-diagonal system of linear algebraic equations about $v^{k+1}.$ When $v^{k+1}$ is obtained, it is an easy work to get $u^{k+1}$ by solving (4.16). We see that only two tri-diagonal systems of linear algebraic equations need be solved at each time level and the double weep method can be used.

4.2 The Unique Solvability of the Difference Scheme

Theorem 4.1

The difference Scheme (4.15)–(4.20) is uniquely solvable.

Proof

(1) For $k=0$, from (4.15), (4.16), (4.19) and (4.20), we can get the linear system of equations with respect to $u^1$ and $v^1.$ Considering its homogenous system, we have

$$\begin{aligned}&\hat{c}_0^{(1)}\mathcal {A}v_i^1=\sigma \delta _x^2u_i^1,\quad 1\le i\le M-1, \end{aligned}$$

(4.21)

$$\begin{aligned}&\frac{1}{\tau }\delta _x^2u_i^1=\frac{1}{2}\delta _x^2v_i^1,\quad 1\le i\le M-1, \end{aligned}$$

(4.22)

$$\begin{aligned}&u_0^1=0,\quad u_M^1=0,\quad v_0^1=0,\quad v_M^1=0. \end{aligned}$$

(4.23)

Solving $\delta _x^2u_i^1$ from (4.22) and substituting the result into (4.21), then taking the inner product of the obtained equality with $v^{1},$ it yields

$$\begin{aligned} \hat{c}_0^{(1)}\Vert v^1\Vert _{\mathcal {A}}^2=\frac{\sigma \tau }{2}(\delta _x^2v^1, v^{1}) =-\frac{\sigma \tau }{2}\Vert \delta _xv\Vert ^2. \end{aligned}$$

It follows that

$$\begin{aligned} v_i^1=0,\quad 1\le i\le M-1. \end{aligned}$$

Then, from (4.21), it yields

$$\begin{aligned} \delta _x^2u_i^1=0,\quad 1\le i\le M-1. \end{aligned}$$

(4.24)

Taking the inner product of (4.24) with $u^1,$ we get

$$\begin{aligned} \Vert \delta _xu^{1}\Vert =0. \end{aligned}$$

Thus we have

$$\begin{aligned} u_i^1=0,\quad 1\le i\le M-1. \end{aligned}$$

(2) Suppose that $\{u^{k-1},\ v^{k-1},u^{k},\ v^{k}\}$ have been determined, then we get a linear system of equations with respect to $u^{k+1}$ and $v^{k+1}$ from (4.15), (4.17), (4.19) and (4.20). Consider the corresponding homogeneous system

$$\begin{aligned}&\hat{c}_0^{(k+1)}\mathcal {A}v_i^{k+1}=\sigma \delta _x^2u_i^{k+1},\quad 1\le i\le M-1, \end{aligned}$$

(4.25)

$$\begin{aligned}&\delta _x^2u_i^{k+1}=\frac{2\sigma \tau }{2\sigma +1} \delta _x^2v_i^{k+1},\quad 1\le i\le M-1, \end{aligned}$$

(4.26)

$$\begin{aligned}&u_0^{k+1}=0,\quad u_M^{k+1}=0, \end{aligned}$$

(4.27)

$$\begin{aligned}&v_0^{k+1}=0,\quad v_M^{k+1}=0. \end{aligned}$$

(4.28)

Substituting (4.26) into (4.25) and then taking the inner product of the obtained equality with $v^{k+1}$, we obtain

$$\begin{aligned} \hat{c}_0^{(k+1)}\Vert v^{k+1}\Vert _{\mathcal {A}}^2 +\frac{2\sigma ^2\tau }{2\sigma +1}\Vert \delta _xv^{k+1}\Vert ^2=0. \end{aligned}$$

It implies that

$$\begin{aligned} v_i^{k+1}=0,\quad 1\le i\le M-1. \end{aligned}$$

Then, it follows from (4.25) that

$$\begin{aligned} \delta _x^2u_i^{k+1}=0,\quad 1\le i\le M-1. \end{aligned}$$

(4.29)

Taking the inner product of (4.29) with $u^{k+1}$, it yields

$$\begin{aligned} \Vert \delta _xu^{k+1}\Vert =0. \end{aligned}$$

Consequently, we get

$$\begin{aligned} u_i^{k+1}=0,\quad 1\le i\le M-1. \end{aligned}$$

The proof ends. $\square$

4.3 The Stability and Convergence of the Difference Scheme

Next, we investigate the stability and convergence of the difference scheme. The following theorem presents the prior estimate on the difference scheme (4.15)–(4.20).

Theorem 4.2

Suppose $\{p_i^k|0\le i\le M,\quad 0\le k\le N\}$ and $\{q_i^k|0\le i\le M,\quad 0\le k\le N\}$ satisfy

$$\begin{aligned}&\sum _{n=0}^k\hat{c}_{k-n}^{(k+1)}(\mathcal {A}q_i^{n+1} -\mathcal {A}q_i^{n})=\delta _x^2p_i^{k+\sigma } +\mathcal {A}f_i^{k+\sigma },\quad 1\le i\le M-1,\quad 0\le k\le N-1, \end{aligned}$$

(4.30)

$$\begin{aligned}&\delta _t\delta _x^2p_i^{\frac{1}{2}}=\delta _x^2q_i^{\frac{1}{2}} +g_i^{\frac{1}{2}},\quad 1\le i\le M-1, \end{aligned}$$

(4.31)

$$\begin{aligned}&D_{\hat{t}}\delta _x^2p_i^{k}=\delta _x^2q_i^{k+\sigma } +g_i^{k+\sigma },\quad 1\le i\le M-1,\quad 1\le k\le N-1, \end{aligned}$$

(4.32)

$$\begin{aligned}&p_i^0=w_1(x_i),\quad q_i^0=w_2(x_i),\quad 1\le i\le M-1, \end{aligned}$$

(4.33)

$$\begin{aligned}&p_0^k=0,\quad p_M^k=0,\quad q_0^k=0,\quad q_M^k=0,\quad 0\le k\le N, \end{aligned}$$

(4.34)

where $w_1(x_i)=0,\quad w_2(x_i)=0$ for $i=0,M.$ Then when $\tau \le \tau _0,$ it holds that

$$\begin{aligned} \Vert \delta _xp^k\Vert ^2\le c_7\exp \Big (\frac{4\sigma L^2}{3}T\Big )L_k ,\quad \tau \sum _{n=1}^{k}\Vert q^n\Vert ^2\le c_8L_k,\quad 0\le k\le N. \end{aligned}$$

where $c_7$ and $c_8$ are two constants and

$$\begin{aligned} L_k&=\Vert \delta _xp^0\Vert ^2+\Vert \delta _x^2p^0\Vert ^2+\Vert q^0\Vert ^2 +\Vert \delta _xq^0\Vert ^2+\Vert \mathcal {A}f^\sigma \Vert ^2+\Vert g^{\frac{1}{2}}\Vert ^2\\&\quad +\tau \sum _{l=1}^{k-1}\Vert f^{l+\sigma }\Vert _\mathcal {A}^2 +\tau \sum _{l=1}^{k-1}\Vert g^{l+\sigma }\Vert ^2. \end{aligned}$$

Proof

Step 1. When $k=0$, the system is as follows

$$\begin{aligned}&\hat{c}_0^{(1)}(\mathcal {A}q_i^{1}-\mathcal {A}q_i^0)=\sigma \delta _x^2p_i^{1}+(1-\sigma )\delta _x^2p_i^{0} +\mathcal {A}f_i^{\sigma },\quad 1\le i\le M-1, \end{aligned}$$

(4.35)

$$\begin{aligned}&\delta _t\delta _x^2p_i^{\frac{1}{2}}=\delta _x^2q_i^{\frac{1}{2}} +g_i^{\frac{1}{2}},\quad 1\le i\le M-1, \end{aligned}$$

(4.36)

$$\begin{aligned}&p_i^0=w_1(x_i),\quad q_i^0=w_2(x_i),\quad 1\le i\le M-1, \end{aligned}$$

(4.37)

$$\begin{aligned}&p_0^1=0,\quad p_M^1=0,\quad q_0^1=0,\quad q_M^1=0 \end{aligned}$$

(4.38)

with $p_0^0=0,\quad p_M^0=0,\quad q_0^0=0,\quad q_M^0=0.$

(I) Taking the inner product of (4.35) with $q^1,$ we obtain

$$\begin{aligned} \hat{c}_0^{(1)}\Vert q^{1}\Vert _{\mathcal {A}}^2=\hat{c}_0^{(1)}(\mathcal {A}q^0,q^1) -\sigma \big (\delta _xp^{1},\delta _xq^1\big )+(1-\sigma )(\delta _x^2p^0,q^1) +(\mathcal {A}f^\sigma ,q^1). \end{aligned}$$

Taking the inner product of (4.36) with $-2\sigma p^1,$ we arrive at

$$\begin{aligned} \frac{2\sigma }{\tau }\Vert \delta _xp^1\Vert ^2 =\frac{2\sigma }{\tau }(\delta _xp^0,\delta _xp^1) +\sigma (\delta _xq^1,\delta _xp^1) +\sigma (\delta _xq^0,\delta _xp^1)-2\sigma \left( g^{\frac{1}{2}},p^1\right) . \end{aligned}$$

Similar to the derivation of (3.51)and noticing $\Vert \mathcal {A}q^0\Vert \le \Vert q^0\Vert$, it yields

$$\begin{aligned} \Vert \delta _xp^1\Vert ^2&\le 3\Vert \delta _xp^0\Vert ^2 +\frac{3\tau }{4\hat{c}_0^{(1)}\sigma }\Vert q^0\Vert ^2 +\frac{3(1-\sigma )^2\tau }{4\hat{c}_0^{(1)}\sigma } \Vert \delta _x^2p^0\Vert ^2+\frac{3\tau }{4\hat{c}_0^{(1)}\sigma } \Vert \mathcal {A}f^\sigma \Vert ^2\nonumber \\&\quad +\frac{3\tau ^2}{4}\Vert \delta _xq^0\Vert ^2+\frac{L^2}{2}\tau ^2 \Vert g^{\frac{1}{2}}\Vert ^2. \end{aligned}$$

(4.39)

(II) It follows from (4.36) that

$$\begin{aligned} \delta _x^2p_i^1=\delta _x^2p_i^0+\tau \delta _x^2q_i^{\frac{1}{2}}+\tau g_i^{\frac{1}{2}},\quad 1\le i\le M-1. \end{aligned}$$

(4.40)

Substituting (4.40) into (4.35), we have

$$\begin{aligned} \hat{c}_0^{(1)}(\mathcal {A}q_i^{1}-\mathcal {A}q_i^0)=\delta _x^2p_i^0 +\sigma \tau \delta _x^2q_i^{\frac{1}{2}} +\mathcal {A}f_i^\sigma +\sigma \tau g_i^{\frac{1}{2}},\quad 1\le i\le M-1. \end{aligned}$$

(4.41)

Taking the inner product of (4.41) with $q^\frac{1}{2},$ we obtain

$$\begin{aligned} \hat{c}_0^{(1)}\left( \mathcal {A}q^{1}-\mathcal {A}q^0, q^\frac{1}{2}\right) =\left( \delta _x^2p^0, q^\frac{1}{2}\right) +\sigma \tau \left( \delta _x^2q^{\frac{1}{2}}, q^\frac{1}{2}\right) +\left( \mathcal {A}f^\sigma , q^\frac{1}{2}\right) +\sigma \tau \left( g^{\frac{1}{2}}, q^\frac{1}{2}\right) . \end{aligned}$$

By Cauchy-Schwarz inequality and Lemma 2.9, it follows that

$$\begin{aligned}&\frac{\hat{c}_0^{(1)}}{2}(\Vert q^{1}\Vert _{\mathcal {A}}^2 -\Vert q^{0}\Vert _{\mathcal {A}}^2)\\&\quad \le \frac{\hat{c}_0^{(1)}}{9}\Vert q^{\frac{1}{2}}\Vert ^2 +\frac{9}{4\hat{c}_0^{(1)}}\Vert \delta _x^2p^0\Vert ^2 +\frac{\hat{c}_0^{(1)}}{9}\Vert q^{\frac{1}{2}}\Vert ^2 +\frac{9}{4\hat{c}_0^{(1)}}\Vert \mathcal {A}f^\sigma \Vert ^2 +\frac{\hat{c}_0^{(1)}}{9}\Vert q^{\frac{1}{2}}\Vert ^2\\&\qquad +\frac{9\sigma ^2\tau ^2}{4\hat{c}_0^{(1)}}\Vert g^{\frac{1}{2}}\Vert ^2\\&\quad \le \frac{\hat{c}_0^{(1)}}{4}\Vert q^1\Vert _{\mathcal {A}}^2 +\frac{\hat{c}_0^{(1)}}{4}\Vert q^0\Vert _{\mathcal {A}}^2 +\frac{9}{4\hat{c}_0^{(1)}}\Vert \delta _x^2p^0\Vert ^2 +\frac{9}{4\hat{c}_0^{(1)}}\Vert \mathcal {A}f^\sigma \Vert ^2 +\frac{9\sigma ^2\tau ^2}{4\hat{c}_0^{(1)}}\Vert g^{\frac{1}{2}}\Vert ^2. \end{aligned}$$

Then, noticing $\Vert q^0\Vert _{\mathcal {A}}\le \Vert q^0\Vert ,$ we get

$$\begin{aligned} \Vert q^1\Vert _{\mathcal {A}}^2\le 3\Vert q^0\Vert ^2+\frac{9}{(\hat{c}_0^{(1)})^2} \Vert \delta _x^2p^0\Vert ^2 +\frac{9}{(\hat{c}_0^{(1)})^2}\Vert \mathcal {A}f^\sigma \Vert ^2 +\frac{9\sigma ^2\tau ^2}{(\hat{c}_0^{(1)})^2}\Vert g^{\frac{1}{2}}\Vert ^2. \end{aligned}$$

(4.42)

By $\Vert q^1\Vert \le \frac{3}{2}\Vert q^1\Vert _{\mathcal {A}}$, we obtain

$$\begin{aligned} \Vert q^1\Vert \le \frac{3}{2}\left[ 3\Vert q^0\Vert ^2+\frac{9}{(\hat{c}_0^{(1)})^2} \Vert \delta _x^2p^0\Vert ^2 +\frac{9}{(\hat{c}_0^{(1)})^2}\Vert \mathcal {A}f^\sigma \Vert ^2 +\frac{9\sigma ^2\tau ^2}{(\hat{c}_0^{(1)})^2}\Vert g^{\frac{1}{2}}\Vert ^2\right] . \end{aligned}$$

Step 2. When $k\ge 1,$ taking the inner product (4.30) with $q^{k+\sigma }$, we obtain

$$\begin{aligned}&\left( \sum _{n=0}^k\hat{c}_{k-n}^{(k+1)}(\mathcal {A}q^{n+1} -\mathcal {A}q^{n}),q^{k+\sigma }\right) =\Big (\delta _x^2p^{k+\sigma },q^{k+\sigma }\Big )\nonumber \\&\quad +\Big (\mathcal {A}f^{k+\sigma },q^{k+\sigma }\Big ),\quad 1\le k\le N-1. \end{aligned}$$

(4.43)

By Lemma 2.7 and Lemma 2.4, we have

$$\begin{aligned}&\left( \sum _{n=0}^k\hat{c}_{k-n}^{(k+1)}(\mathcal {A}q^{n+1} -\mathcal {A}q^{n}),q^{k+\sigma }\right) \ge \frac{1}{2}\sum _{n=0}^k \hat{c}_{k-n}^{(k+1)}\big (\Vert q^{n+1}\Vert _{\mathcal {A}}^2 -\Vert q^{n}\Vert _{\mathcal {A}}^2\big )\nonumber \\&\quad = \frac{1}{2}\left( \sum _{n=1}^{k+1}\hat{c}_{k-n+1}^{(k+1)} \Vert q^{n}\Vert _{\mathcal {A}}^2 -\sum _{n=1}^{k}\hat{c}_{k-n}^{(k)} \Vert q^{n}\Vert _{\mathcal {A}}^2-\hat{b}_k\Vert q^1\Vert _{\mathcal {A}}^2 -\hat{c}_{k}^{(k+1)}\Vert q^0\Vert _{\mathcal {A}}^2\right) ,\nonumber \\&\qquad 1\le k\le N-1. \end{aligned}$$

(4.44)

Using Young’s inequality, for any $\varepsilon >0$, it holds

$$\begin{aligned} \Big |\Big (\mathcal {A}f^{k+\sigma },q^{k+\sigma }\Big )\Big |\le \Vert f^{k+\sigma }\Vert _\mathcal {A}\cdot \Vert q^{k+\sigma }\Vert _\mathcal {A} \le \varepsilon \Vert q^{k+\sigma }\Vert _{\mathcal {A}}^2 +\frac{1}{4\varepsilon }\Vert f^{k+\sigma }\Vert _{\mathcal {A}}^2. \end{aligned}$$

(4.45)

Substituting (4.44) and (4.45) into (4.43), it yields

$$\begin{aligned}&\frac{1}{2}\left( \sum _{n=1}^{k+1}\hat{c}_{k-n+1}^{(k+1)}\Vert q^{n} \Vert _{\mathcal {A}}^2 -\sum _{n=1}^{k}\hat{c}_{k-n}^{(k)}\Vert q^{n} \Vert _{\mathcal {A}}^2-\hat{b}_k\Vert q^1\Vert _{\mathcal {A}}^2 -\hat{c}_{k}^{(k+1)}\Vert q^0\Vert _{\mathcal {A}}^2\right) \nonumber \\&\quad \le \Big (\delta _x^2p^{k+\sigma },q^{k+\sigma }\Big ) +\varepsilon \Vert q^{k+\sigma }\Vert _{\mathcal {A}}^2+\frac{1}{4\varepsilon } \Vert f^{k+\sigma }\Vert _\mathcal {A}^2,\quad 1\le k\le N-1. \end{aligned}$$

(4.46)

Taking the inner product (4.32) with $-p^{k+\sigma }$, we get

$$\begin{aligned} -\Big (D_{\hat{t}}\delta _x^2p^{k},p^{k+\sigma }\Big )= -\Big (\delta _x^2q^{k+\sigma },p^{k+\sigma }\Big ) -\Big (g^{k+\sigma },p^{k+\sigma }\Big ),\quad 1\le k\le N-1. \end{aligned}$$

Similarly to the derivation of (3.65), it yields

$$\begin{aligned} \frac{1}{4\tau }(F^{k+1}-F^k)\le -\Big (\delta _x^2q^{k+\sigma }, p^{k+\sigma }\Big ) +\frac{1}{2}\Vert g^{k+\sigma }\Vert ^2+\frac{1}{2} \Vert p^{k+\sigma }\Vert ^2,\quad 1\le k\le N-1, \end{aligned}$$

(4.47)

where $F^{k+1}$ is defined by (3.62).

Adding (4.46) with (4.47), we obtain

$$\begin{aligned}&\frac{1}{2}\left[ \sum _{n=1}^{k+1}\hat{c}_{k-n+1}^{(k+1)} \Vert q^{n}\Vert _{\mathcal {A}}^2 -\sum _{n=1}^{k}\hat{c}_{k-n}^{(k)} \Vert q^{n}\Vert _{\mathcal {A}}^2-\hat{b}_k\Vert q^1\Vert _{\mathcal {A}}^2 -\hat{c}_{k}^{(k+1)}\Vert q^0\Vert _{\mathcal {A}}^2\right] +\frac{1}{4\tau }(F^{k+1}-F^k)\nonumber \\&\quad \le \varepsilon \Vert q^{k+\sigma }\Vert _{\mathcal {A}}^2 +\frac{1}{4\varepsilon }\Vert f^{k+\sigma }\Vert _\mathcal {A}^2 +\frac{1}{2}\Vert g^{k+\sigma }\Vert ^2+\frac{1}{2} \Vert p^{k+\sigma }\Vert ^2,\quad 1\le k\le N-1. \end{aligned}$$

(4.48)

Denote

$$\begin{aligned} J^{k+1}=2\tau \sum _{n=1}^{k+1}\hat{c}_{k-n+1}^{(k+1)} \Vert q^{n}\Vert _{\mathcal {A}}^2+F^{k+1}. \end{aligned}$$

Then (4.48) can be rewritten as

$$\begin{aligned} J^{k+1}&\le J^k+2\tau \hat{b}_k\Vert q^1\Vert _{\mathcal {A}}^2 + 2\tau \hat{c}_{k}^{(k+1)}\Vert q^0\Vert _{\mathcal {A}}^2 +4\tau \varepsilon \Vert q^{k+\sigma }\Vert _{\mathcal {A}}^2 +\frac{\tau }{\varepsilon }\Vert \mathcal {A}f^{k+\sigma }\Vert ^2\nonumber \\&\quad +2\tau \Vert g^{k+\sigma }\Vert ^2+2\tau \Vert p^{k+\sigma }\Vert ^2\nonumber \\&\le J^1+2\tau \sum _{n=1}^{k}\hat{b}_n\Vert q^1\Vert _{\mathcal {A}}^2 +2\tau \sum _{n=1}^{k}\hat{c}_{n}^{(k+1)}\Vert q^0\Vert _{\mathcal {A}}^2 +8\tau \varepsilon \sum _{n=1}^{k+1}\Vert q^{n}\Vert _{\mathcal {A}}^2 +\frac{\tau }{\varepsilon }\sum _{n=1}^{k} \Vert f^{n+\sigma }\Vert _\mathcal {A}^2\nonumber \\&\quad +2\tau \sum _{n=1}^{k}\Vert g^{n+\sigma }\Vert ^2+4\tau \sum _{n=1}^{k+1} \Vert p^{n}\Vert ^2, \quad 1\le k\le N-1. \end{aligned}$$

(4.49)

Using Lemma 2.3, (3.62) and (3.63), when $\tau \le \tau _0,$ we obtain

$$\begin{aligned} J^{k+1}\ge \left( \sum _{r=0}^m\lambda _r\frac{(1-\gamma _r) T^{-\gamma _r}}{\Gamma (2-\gamma _r)}\right) \tau \sum _{n=1}^{k+1} \Vert q^{n}\Vert _{\mathcal {A}}^2+\frac{1}{\sigma }\Vert \delta _xp^{k+1} \Vert ^2,\quad 1\le k\le N-1 \end{aligned}$$

(4.50)

and

$$\begin{aligned} J^1=2\tau \hat{c}_0^{(1)}\Vert q^1\Vert _{\mathcal {A}}^2+F^1\le 2\tau \hat{c}_0^{(1)}\Vert q^1\Vert _{\mathcal {A}}^2 +(4\sigma ^2+4\sigma -1) \Vert \delta _xp^1\Vert ^2+(4\sigma ^2-1)\Vert \delta _xp^0\Vert ^2. \end{aligned}$$

(4.51)

Substituting (4.50) and (4.51) into (4.49), we have

$$\begin{aligned}&\left( \sum _{r=0}^m\lambda _r\frac{(1-\gamma _r) T^{-\gamma _r}}{\Gamma (2-\gamma _r)}\right) \tau \sum _{n=1}^{k+1} \Vert q^{n}\Vert _{\mathcal {A}}^2+\frac{1}{\sigma }\Vert \delta _xp^{k+1}\Vert ^2\nonumber \\&\quad \le 2\tau \hat{c}_0^{(1)}\Vert q^1\Vert _{\mathcal {A}}^2 +(4\sigma ^2+4\sigma -1)\Vert \delta _xp^1\Vert ^2+(4\sigma ^2-1)\Vert \delta _xp^0\Vert ^2 +2\tau \sum _{n=1}^{k}\hat{b}_n\Vert q^1\Vert _{\mathcal {A}}^2\nonumber \\&\qquad +2\tau \sum _{n=1}^{k}\hat{c}_{n}^{(k+1)}\Vert q^0\Vert ^2 +8\tau \varepsilon \sum _{n=1}^{k+1}\Vert q^{n}\Vert _{\mathcal {A}}^2 +\frac{\tau }{\varepsilon }\sum _{n=1}^{k}\Vert f^{n+\sigma }\Vert _\mathcal {A}^2\nonumber \\&\qquad +2\tau \sum _{n=1}^{k}\Vert g^{n+\sigma }\Vert ^2+4\tau \sum _{n=1}^{k+1} \Vert p^{n}\Vert ^2,\nonumber \\&\qquad 1\le k\le N-1 . \end{aligned}$$

(4.52)

Taking $\varepsilon =\frac{1}{16}\Big (\sum \limits _{r=0}^m\lambda _r \frac{(1-\gamma _r)T^{-\gamma _r}}{\Gamma (2-\gamma _r)}\Big )$ and using Lemma 2.4, (4.39) and (4.42), we have

$$\begin{aligned} \Vert \delta _xp^{k+1}\Vert ^2&\le 4\sigma \tau \sum _{n=1}^{k+1} \Vert p^{n}\Vert ^2+c_7L_{k+1} \le \frac{2L^2\sigma }{3}\tau \sum _{n=1}^{k+1} \Vert \delta _xp^{n}\Vert ^2+c_7L_{k+1},\quad 1\le k\le N-1, \end{aligned}$$

where $c_7$ is a constant. By Lemma 2.10, it follows that

$$\begin{aligned} \Vert \delta _xp^{k+1}\Vert ^2&\le c_7 \exp \Big (\frac{4\sigma L^2}{3}T\Big )L_{k+1},\quad 1\le k\le N-1. \end{aligned}$$

(4.53)

Substituting (4.53) into (4.52) and using Lemma 2.9, we get

$$\begin{aligned} \tau \sum _{n=1}^{k+1}\Vert q^{n}\Vert ^2\le \frac{3}{2}\tau \sum _{n=1}^{k+1}\Vert q^{n} \Vert _{\mathcal {A}}^2 \le c_8L_{k+1},\quad 1\le k\le N-1, \quad 1\le k\le N-1, \end{aligned}$$

where $c_8$ is a constant.

This completes the proof. $\square$

From the theorem above, we can obtain the stability of the difference scheme.

Theorem 4.3

The solution of the difference Scheme (4.15)–(4.20) is unconditionally stable with respect to the initial values $w_1, w_2$ and the right hand side function f.

Next, we prove the convergence of the difference Scheme (4.15)–(4.20).

Let

$$\begin{aligned} \rho _i^k=V_i^k-v_i^k,\quad e_i^k=U_i^k-u_i^k,\quad 0\le i \le M,\quad 0\le k\le N. \end{aligned}$$

Subtracting (4.15)–(4.20) from (4.2), (4.8), (4.9), (4.12)–(4.14), respectively, we get the error equations as follows

$$\begin{aligned}&\sum _{n=0}^{k}\hat{c}_{k-n}^{(k+1)}(\mathcal {A}\rho _i^{n+1} -\mathcal {A}\rho _i^{n})=\delta _x^2e_i^{k+\sigma } +S_i^{k+\sigma },\quad 1\le i\le M-1,\quad 0\le k\le N-1, \end{aligned}$$

(4.54)

$$\begin{aligned}&\delta _t\delta _x^2e_i^{\frac{1}{2}}=\delta _x^2 \rho _i^{\frac{1}{2}}+s_i^{\frac{1}{2}},\quad 1\le i\le M-1, \end{aligned}$$

(4.55)

$$\begin{aligned}&D_{\hat{t}}\delta _x^2e_i^k= \delta _x^2\rho _i^{k+\sigma } +s_i^{k+\sigma },\quad 1\le i\le M-1,\quad 1\le k\le N-1, \end{aligned}$$

(4.56)

$$\begin{aligned}&e_i^0=0,\quad \rho _i^0=0,\quad 1\le i\le M-1, \end{aligned}$$

(4.57)

$$\begin{aligned}&e_0^k=0,\quad e_M^k=0,\quad 0\le k\le N, \end{aligned}$$

(4.58)

$$\begin{aligned}&\rho _0^k=0,\quad \rho _M^k=0,\quad 0\le k\le N. \end{aligned}$$

(4.59)

Theorem 4.4

Suppose the problem (3.3)–(3.7) has a unique smooth solution and $\{u_i^k, v_i^k\;|\;0\le i \le M,~0\le k\le N\}$ is the solution of the difference Scheme (4.15)–(4.20). Then when $\tau \le \tau _0,$ there exists a constant $C_2$ such that

$$\begin{aligned} \Vert e^k\Vert _\infty \le C_2(\tau ^2+h^4),\quad \tau \sum _{n=1}^{k}\Vert \rho ^n\Vert \le C_2(\tau ^2+h^4),\quad 0\le k\le N. \end{aligned}$$

Proof

By Theorem 4.2 and noticing (4.3), (4.10) and (4.11), it yields

$$\begin{aligned} \Vert \delta _xe^k\Vert ^2\le c_9(\tau ^2+h^4)^2, \quad \tau \sum _{n=1}^{k} \Vert \rho ^n\Vert ^2\le c_9(\tau ^2+h^4)^2,\quad 0\le k\le N, \end{aligned}$$

where $c_9$ is a constant.

Using Lemma 2.3 and Cauchy-Schwarz inequality, we have

$$\begin{aligned} \Vert e^k\Vert _\infty \le C_2(\tau ^2+h^4),\quad \tau \sum _{n=1}^{k} \Vert \rho ^n\Vert \le C_2(\tau ^2+h^4),\quad 0\le k\le N, \end{aligned}$$

where $C_2=\max \{\sqrt{c_9T},\frac{\sqrt{c_9 L}}{2}\}.$ The proof ends. $\square$

5 A Fast Second-Order Difference Scheme

In this section, we present a fast difference scheme for multi-term fractional diffusion wave equation based on the ${}^\mathcal {F}L2$-$1_\sigma$ formula [40], which can reduce the computational complexity significantly.

In [39, 40], the kernel function $t^{-\alpha }$ in Caputo derivative is approximated by the sum-of-exponentials. For the given $\alpha \in (0,1),$ tolerance error $\varepsilon ,$ cut-off time step size $\hat{\tau }$ and final time T,  there is one positive integer $N_{\exp },$ exponential coefficients $s_l$ and corresponding positive weights $\omega _l,~(l=1,2,\ldots , N_{\exp })$ satisfying

$$\begin{aligned} \Big |t^{-\alpha }-\sum _{l=1}^{N_{\exp }}\omega _le^{-s_lt} \Big |\le \varepsilon ,\quad \forall t\in [\hat{\tau },T]. \end{aligned}$$

In addition, the number of exponentials has the following order

$$\begin{aligned} N_{exp}=O\Big (\log \frac{1}{\varepsilon }\Big (\log \log \frac{1}{\varepsilon } +\log \frac{T}{\hat{\tau }}\Big ) +\log \frac{1}{\hat{\tau }} \Big (\log \log \frac{1}{\varepsilon }+\log \frac{T}{\hat{\tau }}\Big )\Big ). \end{aligned}$$

The fast evaluation of Caputo derivative, ${}^\mathcal {F}L2$-$1_\sigma$ formula, is given as follows

$$\begin{aligned} {}_0^CD_t^{\gamma _r}v(t_{k+\sigma })&= {}^{\mathcal {FH}} {\mathcal {D}}_t^{\gamma _r} v^{k+\sigma }+O(\varepsilon +\tau ^2)\nonumber \\&= \sum _{l=1}^{N_{\exp }}\hat{w}_l\hat{V}_l^k +\frac{\sigma ^{1-\gamma _r}}{\tau ^{\gamma _r} \Gamma (2-\gamma _r)}(v^{k+1}-v^k)+O(\varepsilon +\tau ^2), \end{aligned}$$

where $\hat{w_l}=\frac{1}{\Gamma (1-\gamma _r)}w_l$ and $\hat{V}_l^k$ is obtained by the following recurrence relation

$$\begin{aligned} \hat{V}_l^k=e^{-s_l\tau }\hat{V}_l^{k-1}+A_l(v^k-v^{k-1})+B_l(v^{k+1}-v^k), \end{aligned}$$

with $\hat{V}_l^0=0,~(l=1,\ldots ,N_{\exp })$ and

$$\begin{aligned} A_l=\int _0^1\Big (\frac{3}{2}-s\Big )e^{-s_l\tau (\sigma +1-s)} \quad ds,\quad B_l=\int _0^1\Big (s-\frac{1}{2}\Big )e^{-s_l\tau (\sigma +1-s)}\quad ds. \end{aligned}$$

Thus, we obtain

$$\begin{aligned}&\sum _{r=0}^m \lambda _r\ {}_0^CD_t^{\gamma _r} v(t_{k+\sigma }) =\sum _{r=0}^m \lambda _r\ \left( \sum _{l=1}^{N_{\exp }}\hat{w}_l \hat{V}_l^k+\frac{\sigma ^{1-\gamma _r}}{\tau ^{\gamma _r} \Gamma (2-\gamma _r)}(v^{k+1}-v^k)\right) +O(\varepsilon +\tau ^2),\nonumber \\&\quad 1\le i\le M-1,\quad 0\le k\le N-1. \end{aligned}$$

Then, we can construct a fast second-order recursion difference scheme for Eqs. (3.3)–(3.7) as follows

$$\begin{aligned}&\sum _{r=0}^m \lambda _r\ \left( \sum _{l=1}^{N_{\exp }} \hat{w}_l\hat{V}_l^k+\frac{\sigma ^{1-\gamma _r}}{\tau ^{\gamma _r} \Gamma (2-\gamma _r)}(v_i^{k+1}-v_i^k)\right) =\delta _x^2u_i^{k+\sigma }+f_i^{k+\sigma },\nonumber \\&\quad 1\le i\le M-1,\quad 0\le k\le N-1, \end{aligned}$$

(5.1)

$$\begin{aligned}&\delta _t\delta _x^2u_i^{\frac{1}{2}}=\delta _x^2v_i^{\frac{1}{2}}, \quad 1\le i\le M-1, \end{aligned}$$

(5.2)

$$\begin{aligned}&D_{\hat{t}}\delta _x^2u_i^k= \delta _x^2v_i^{k+\sigma }, \quad 1\le i\le M-1,\quad 1\le k\le N-1, \end{aligned}$$

(5.3)

$$\begin{aligned}&u_i^0=w_1(x_i),\quad v_i^0=w_2(x_i),\quad 1\le i\le M-1, \end{aligned}$$

(5.4)

$$\begin{aligned}&u_0^k=0,\quad u_M^k=0,\quad 0\le k\le N, \end{aligned}$$

(5.5)

$$\begin{aligned}&v_0^k=0,\quad v_M^k=0,\quad 0\le k\le N, \end{aligned}$$

(5.6)

$$\begin{aligned}&\hat{V}_l^0=0,\quad 1\le l\le N_{\exp }, \end{aligned}$$

(5.7)

$$\begin{aligned}&\hat{V}_l^k=e^{-s_l\tau }\hat{V}_l^{k-1}+A_l(v_i^k-v_i^{k-1}) +B_l(v_i^{k+1}-v_i^k),\nonumber \\&\quad 1\le l\le N_{\exp }, \quad 1\le i\le M-1, \quad 1\le k\le N-1,. \end{aligned}$$

(5.8)

From (5.4)–(5.6), we know $u^0$ and $v^0.$ Solving $\delta _x^2u^1$ from (5.2) and substituting the result into (5.1) with the superscript $k=0$ then noting (5.7) achieve a tri-diagonal system of linear algebraic equations about $v^1.$ After $v^1$ is obtained, then $u^1$ can be got easily from (5.2). Now suppose $\{u^{k-1}, v^{k-1}, u^{k}, v^{k}\}$ and $\{\hat{V}_l^{k-1}\,|\, 1\le l\le N_{\exp }\}$ have been determined. Then, we solve $\delta _x^2 u^{k+1}$ from (5.3) and substitute the result and (5.8) into (5.1) to obtain a tri-diagonal system of linear algebraic equations about $v^{k+1}.$ When $v^{k+1}$ is obtained, by solving (5.3) to get $u^{k+1}.$ Simultaneously, we get $\{\hat{V}_l^k\,|\, 1\le l\le N_{\exp }\}$ from (5.8). We find that only two tri-diagonal systems of linear algebraic equations need be solved at each time level and the double weep method can be used.

The determination of $\{u^{k+1}, v^{k+1}\}$ and $\{\hat{V}_l^{k}\,|\, 1\le l\le N_{\exp }\}$ is only dependent on $\{u^{k-1}, v^{k-1},$$u^{k}, v^{k}\}$ and $\{\hat{V}_l^{k-1}\,|\, 1\le l\le N_{\exp }\}.$ We only need store the values at two time levels. This reduces the storage and computational cost significantly.

The analysis of the stability and convergence of the difference scheme (5.1)–(5.8) is too long, which we omit here.

6 Numerical Experiments

In this section, we provide two numerical examples. The first example is to demonstrate the accuracy of the difference scheme (3.22)–(3.27) and the scheme (4.15)–(4.20). A comparison with the difference scheme based on L1 formula is also presented. The second example is to compare the difference scheme (3.22)–(3.27) with the fast difference scheme (6.1)–(6.3), which shows that the fast difference scheme can reduce the CPU time greatly.

Denote

$$\begin{aligned} E(h,\tau )= & {} \max _{0\le k\le N}\Vert U^k-u^k\Vert _\infty , \\ \mathrm{Order}_{\tau }= & {} \mathrm{log}_{2}(E(h,2\tau )/E(h,\tau )),\quad \mathrm{Order}_{h}=\mathrm{log}_{2}(E(2h,\tau )/E(h,\tau )). \end{aligned}$$

Example 6.1

In (1.1)–(1.3), take $T=1$, $[0,L]=[0,\pi ].$ Consider the problem (1.1)–(1.3) with the source term

$$\begin{aligned} f(x,t)=\left( \sum _{r=0}^{2}\frac{24\lambda _rt^{4-\alpha _r}}{\Gamma (5-\alpha _r)}+t^{4}\right) \sin x \end{aligned}$$

and the initial the boundary values

$$\begin{aligned} u(0,t)=0,~u(1,t)=0,\quad u(x,0)=0,~u_t(x,0)=0. \end{aligned}$$

The problem has an exact solution

$$\begin{aligned} u(x,t)=t^{4}\sin x. \end{aligned}$$

With different values of $\lambda _0, \lambda _1, \lambda _2$ and $\alpha _0, \alpha _1, \alpha _2,$ the difference scheme (3.22)–(3.27) and the scheme (4.15)–(4.20) will be used to numerically solve this problem, respectively.

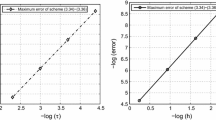
Firstly, we examine the numerical accuracy in time. Taking the fixed and sufficiently small h,  the maximum errors and convergence orders are shown in Table 1. From Table 1, one can see that both difference schemes can achieve the second-order accuracy in time. The computational results are in a good agreement with theoretical results.

Secondly, the numerical accuracy of the difference scheme (3.22)–(3.27) and the scheme (4.15)–(4.20) in space is tested. We fix the temporal step size $\tau =\frac{1}{5000}$, Table 2 presents the maximum errors and convergence orders for the different space step sizes. From Table 2, we can find that, the second-order convergence of the difference schemes (3.22)–(3.27) and the fourth-order convergence of the scheme (4.15)–(4.20) in space are verified, respectively.

Table 1 Maximum errors and convergence orders of the two difference schemes in time

Table 2 Maximum errors and convergence orders of the two difference schemes in space ($N=5000$)

Next, we show the efficiency of proposed difference scheme comparing with the difference scheme based on L1 formula. The difference scheme for the problem (1.1)–(1.3) based on L1 formula is as follows [27]:

$$\begin{aligned}&\sum _{r=0}^m\frac{\tau ^{1-\alpha _r}}{\Gamma (3-\alpha _r)} \left[ a^{(\alpha _r)}_0\delta _tu_i^{k+\frac{1}{2}} - \sum _{n=1}^{k-1}\Big (a^{(\alpha _r)}_{k-n-1} -a^{(\alpha _r)}_{k-n}\Big )\delta _tu_i^{n+\frac{1}{2}} -a^{(\alpha _r)}_{k-1}w_2(x_i)\right] \nonumber \\&\quad =\delta _x^2u_i^{k+\frac{1}{2}}+f_i^{k+\frac{1}{2}},\quad ~1\le i \le M-1,~1\le k\le N-1, \end{aligned}$$

(6.1)

$$\begin{aligned}&u_i^0=w_1(x_i),\quad 1\le i\le M-1, \end{aligned}$$

(6.2)

$$\begin{aligned}&u_0^k=0,~u_M^k=0,~0\le k\le N, \end{aligned}$$

(6.3)

where $\delta _tu^{k+\frac{1}{2}}=\frac{u^{k+1} -u^{k}}{\tau },\quad a^{(\alpha _r)}_0=1,\quad a^{(\alpha _r)}_l=(l+1)^{2-\alpha _r} -l^{2-\alpha _r}.$

Table lists the errors and the orders of the scheme (3.22)–(3.27) and the scheme (6.1)–(6.3). For the different temporal step sizes $\frac{1}{40},~\frac{1}{80},~\frac{1}{160}$ and $\frac{1}{320},$ we choose the spatial step sizes by $h=\tau ^{\frac{1}{2}\min {\{2-\gamma _r\}}}$ for the scheme (6.1)–(6.3) and $h=\tau$ for the scheme (3.22)–(3.27). From Table 3, we can see the scheme (6.1)–(6.3) has $\min {\{2-\gamma _r\}}$ order accuracy, while the scheme (3.22)–(3.27) can achieve 2-order accuracy. It shows that the scheme (3.22)–(3.27) is more efficient than the scheme (6.1)–(6.3).

Table 3 Maximum errors and convergence orders of the two difference schemes

Example 6.2

In (1.1)–(1.3), take $T=1$, $[0,L]=[0,\pi ].$ Consider the problem (1.1)–(1.3) with the source term

$$\begin{aligned} f(x,t)=\left( \sum _{r=0}^{2}\lambda _r\frac{\Gamma (3+\alpha _0)}{\Gamma (3+\alpha _0-\alpha _r)}t^{2+\alpha _0-\alpha _r} +t^{2+\alpha _0}\right) \sin x \end{aligned}$$

and the initial and boundary values

$$\begin{aligned} u(0,t)=0,~u(1,t)=0,\quad u(x,0)=0,~u_t(x,0)=0. \end{aligned}$$

The problem has an exact solution

$$\begin{aligned} u(x,t)=t^{2+\alpha _0}\sin x. \end{aligned}$$

Table 4 Numerical errors and convergence orders of the difference scheme (5.1)–(5.6) in time with $M=1000$ and $(\lambda _0, \lambda _1, \lambda _2)=(3,2,1),$$(\alpha _0,\alpha _1,\alpha _2)=(4/3,5/4,6/5)$ for Example 6.2

Table 5 Numerical errors and convergence orders of two difference schemes in space with $N=5000$ and $(\lambda _0, \lambda _1, \lambda _2)=(3,2,1),$$(\alpha _0,\alpha _1,\alpha _2) =(4/3,5/4,6/5)$ for Example 6.2

From Table 4 and Table 5, we can see that the difference scheme (5.1)–(5.6) can achieve second order accuracy both in time and in space. We take $\varepsilon =10^{-10}$ and $\hat{\tau }=\sigma \tau$ in the simulation. The CPU time for both schemes are also shown in Table 5 which verifies the efficiency of the scheme (5.1)–(5.6). From Table 5, we find the difference scheme (5.1)–(5.6) can reduce the computational cost significantly.

7 Conclusion

Motivated by the idea in [38], we propose two temporal second-order accuracy difference schemes at the super-convergence point by the order reduction technique for time multi-term fractional diffusion wave equation. The schemes based on the interpolation approximation can achieve higher-order accuracy than L1 formula and more efficient than GL formula which requires continuous zero-extension of the solution when $t<0.$ The unconditional stability and convergence of the two schemes are proved rigorously by the energy method. We also present a fast difference scheme which can reduce the computational cost significantly. The numerical examples are presented to verify the theoretical results.