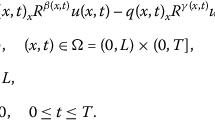The Temporal Second Order Difference Schemes Based on the Interpolation Approximation for Solving the Time Multi-term and Distributed-Order Fractional Sub-diffusion Equations

Abstract

In this article, a special point is found for the interpolation approximation of the linear combination of multi-term fractional derivatives. The derived numerical differentiation formula can achieve at least second order accuracy. Then the formula is used to numerically solve the time multi-term and distributed-order fractional sub-diffusion equations. Several unconditionally stable and convergent difference schemes are presented. The stability and convergence of the difference schemes are discussed. Some numerical examples are provided to show the efficiency of the proposed difference schemes.

1 Introduction

In recent years, the fractional calculus has been greatly developed and many related books appeared, such as [1,2,3,4] and so on. The definitions of fractional derivatives are diverse, among which the Riemann–Liouville fractional derivative and the Caputo fractional derivative are most favorable ones. The time-fractional derivatives are usually defined in the Caputo sense, while the space-fractional derivatives are often described in the Riemann–Liouville sense. These two fractional derivatives are closely connected with some initial values. The Riesz fractional derivative which is commonly employed to define the space-fractional derivative, can also be regarded as that in the Riemann–Liouville sense. Many processes in physics, finance, engineering, chemistry, acoustics etc. can be modelled by the fractional differential equation (FDE). The analytical solutions of most fractional differential equations (FDEs) are not explicit, therefore, some effective numerical techniques for solving FDEs become necessary and important.

Fractional derivatives, which have been used to describe various materials and processes with memory and hereditary properties, are nonlocal with long memory and weak singular kernels. It brings a surprising challenge in both the theory research and numerical approximation. Particularly for the time-fractional problems, all the information on the previous time levels is required when the time-fractional derivative is considered on the current time level. Therefore, to develop the effective numerical differentiation formula to approximate the fractional derivative is fundamental in designing the numerical algorithms for solving FDEs. The direct numerical approximation for the one-term fractional derivative has been well studied in literatures. One of the typical approximation formulae is termed as “G–L approximation”, which is arising from the equivalence of the Riemann–Liouville fractional derivative and the Grünwald–Letnikov derivative for a wide class of functions. This approximation formula was considered as early as in 1970 s in the book [1] by Oldham and Spanier. The G–L approximation and the computation of coefficients were further discussed by Lubich in [5] and in the book [2] by Podlubny. Then many scholars have made a series of work along this routine. The applications of the G–L approximation for the time-fractional derivatives have been widely studied. Here we only mention a few part of works. Chen et al. [6] proposed an implicit difference scheme for a fractional partial differential equation (FPDE) describing sub-diffusion using the first-order G–L approximation formula. A variable-order anomalous subdiffusion equation was further numerically considered still using the first-order G–L approximation formula in [7]. Gao et al. [8] constructed an effective difference scheme with the second-order accuracy in time for solving the time-fractional sub-diffusion equation based on certain super-convergence of the first-order G–L approximation formula. Ding and Li [9] gave a mixed spline method for reaction-subdiffusion equations based on the G–L approximation for the involved time-fractional derivatives. Yuste and Acedo [10] presented an explicit difference method for fractional diffusion equations with the G–L approximation for the time-fractional Riemann–Liouville derivatives. The G–L approximation formula is also utilized to approximate the space-fractional derivative. Meerschaert and Tadjeran [11] investigated finite difference approximations for fractional advection-dispersion flow equations. Using the first-order G–L approximation formula to approximate the $\alpha$-th order ($1<\alpha \leqslant 2$) Riemann–Liouville space-fractional derivative, the derived difference scheme was unstable, thus, a shifted first-order G–L approximation formula was developed in [11]. To improve the numerical accuracy, Tian et al. [12] presented some weighted and shifted G–L approximation formulae for the Riemann–Liouville fractional derivative and illustrated applications in solving space-fractional diffusion equations in one and two dimensions.

It is worth mentioning that the standard G–L approximation coincides with the first-order Lubich’s method [5]. Some higher-order approximations with the similar form to the standard G–L approximation were also developed by Lubich in [5].

The other class of the approximation formulae for fractional derivatives is based on the interpolation approximation. One of the well known formulae is called the L1 formula, which is derived from a piecewise linear interpolation approximation for the function f in the $\alpha$-th order ($0<\alpha \leqslant 1$) Caputo fractional derivative $_0^CD_t^\alpha f(t)$. The exact numerical accuracy of this formula is proved to be $(2-\alpha )$-th order for the function $f\in C^2([0,t])$ [13, 14]. This formula has been widely used to construct the numerical method for solving the time-fractional differential equation. Langlands and Henry [15] presented an implicit difference method for the fractional diffusion equation by the mean of the L1 formula. Sun and Wu [13] developed implicit difference schemes for solving time-fractional diffusion-wave equations based on the L1 formula for approximating the time-fractional derivatives. Lin and Xu [14] considered a numerical method for the time-fractional diffusion equation with a finite difference discretization in time based on the L1 formula and Legendre spectral methods in space. Brunner et al. [16] applied the L1 formula for time-fractional derivatives and the adaptive spatial basis selection approach for the space derivative to carry out some numerical simulations for 2D fractional subdiffusion problems. By the same numerical approximation for the time-fractional derivative, Pang and Sun [17] proposed high order finite difference methods in space for solving time-space fractional diffusion equations. With the purpose of improving the numerical accuracy to approximate the Caputo fractional derivative, Gao et al. [18] gave a new numerical differentiation formula, called L1-2 formula, based on the piecewise quadratic interpolation approximation for the function f in the $\alpha$-th order ($0<\alpha \leqslant 1$) Caputo fractional derivative $_0^CD_t^\alpha f(t)$, except on the first small interval. The applications of the L1-2 formula into solving the time-fractional differential equation were also illustrated. It seems to be a challenge to strictly prove the stability and convergence of the proposed schemes until now. Alikhanov [19] derived a new numerical differentiation formula, called the L2-$1_{\sigma }$ formula, to approximate the Caputo fractional derivative at a special point. And the time second-order difference schemes for fractional diffusion equations and for the time-space fractional differential equation based on the L2-$1_{\sigma }$ formula were developed and analyzed in [19] and [20], respectively. The modified L1 methods were developed and used to obtain the Crank–Nicolson method for the time-fractional subdiffusion equation in [21].

All the above mentioned work is devoted to the numerical approximation of the one-term fractional derivative. However, the multi-term FDE has been proved to be valuable models for describing many processes in practice, such as the oxygen delivery through a capillary to tissues [22], viscoelastic damping [23], the underlying processes with loss [24], the anomalous diffusion in highly heterogeneous aquifers and complex viscoelastic materials [25] and in rheology [26]. In particular, the multi-term time-fractional diffusion-wave equations can successfully describe the power-law frequency dependence in a continuous time random walk model [27].

To find accurate and efficient numerical algorithms for multi-term FDEs becomes an active research undertaking recently. Some research work on this subject has been made, for example, the iterative method [22, 28], a Haar wavelet collocation method in [23], a method of separating variables [29], the Galerkin finite element method [25] and the method using generalized triangular function operational matrices [30]. It is well known that the finite difference method is simple and easy to be implemented. Some of the existing finite difference methods for solving multi-term FDEs can be found. In [27], the multi-term time-fractional differential equation was firstly written as an equivalent system of single-term equations and then, two fractional predictor-corrector methods were used to solve the equivalent system. Ren and Sun [31] investigated the finite difference method for solving multi-term time-fractional sub-diffusion equations, where each time-fractional derivative was discretized using the L1 formula. By a similar technique, Ye et al. [32] handled the time-fractional derivatives in the reduced multi-term problem from the time-distributed order differential equation. Alikhanov [33] studied numerical solutions of the multi-term variable-distributed order diffusion equation with the help of L1 formula for the approximation of time-fractional derivatives. Wang and Vong [34] explored the finite difference approximation for a two-term time-fractional sub-diffusion equation with a weighted and shifted G–L approximation formula for the involved time-fractional derivatives. The smooth extension of solutions to the half-line in time was required. Gao et al. [35,36,37,38] discussed the finite difference method for solving time-distributed diffusion equations using the G–L or weighted and shifted G–L approximation for time-fractional derivatives. The smooth extension of solutions was also essential.

It is noted that the direct numerical treatment of the multi-term fractional derivative has not gained a great development until now. The existing main approaches to the multi-term fractional derivative are direct applications of the techniques which are used to handle the single-term fractional derivative, mainly including the L1 approximation [31,32,33] and the G–L approximation [34,35,36,37,38]. The disadvantage of the former approach lies in the lower order of numerical accuracy, while the latter one requires the continuous zero-extension of solutions when $t<0$.

The major contribution of this work concentrates on the derivation of a higher accurate interpolation approximation for a linear combination of the multi-term fractional derivatives in the Caputo sense, whose orders belong to the interval [0, 1]. To the authors’ knowledge, this higher accurate interpolation approximation for the multi-term fractional derivatives has not been covered in the published literatures. Then some temporal second-order difference schemes for solving time multi-term and distributed-order fractional sub-diffusion equations are proposed based on the presented higher accurate interpolation approximation.

The outline of this work is as follows. Section 2 is devoted to the derivation of a higher accurate interpolation approximation for the linear combination of multi-term fractional derivatives. A special point is found to be a unique root of a nonlinear equation, which can be obtained by the Newton iterative method. An effective numerical differentiation formula to approximate the linear combination of multi-term fractional derivatives at this point is established and its numerical accuracy is analyzed. In the following two sections, applications of this numerical differentiation formula into solving the multi-term time-fractional sub-diffusion equation and the time distributed-order sub-diffusion equation are illustrated, respectively. Some effective difference schemes are developed and the unique solvability, unconditional stability and convergence are also discussed. In Sect. 5, several numerical experiments are carried out to investigate the computational efficiency of the proposed numerical algorithms. The last section contains some concluding remarks on this work.

2 The Higher Accurate Interpolation Approximation for the Linear Combination of Multi-term Fractional Derivatives

Consider

$$\begin{aligned} \sum _{r=0}^m\lambda _r\ {}_0^CD_t^{\alpha _r}f(t), \end{aligned}$$

(2.1)

where $\lambda _0, \lambda _1, \ldots , \lambda _m$ are some positive constants, $0 \leqslant \alpha _m< \alpha _{m-1}< \cdots < \alpha _0\leqslant 1$ and at least one of $\alpha _i$’s belongs to (0, 1), ${}_0^CD_t^\alpha f(t)$ is the Caputo fractional derivative defined by

$$\begin{aligned} {}_0^CD_t^\alpha f(t)=\left\{ \begin{aligned}&f(t)-f(0),\quad \alpha =0,\\&\frac{1}{\Gamma (1-\alpha )}\int _0^t f^{\prime }(s)(t-s)^{-\alpha }{\mathrm {d}}s,\quad \alpha \in (0, 1),\\&f'(t),\quad \alpha =1. \end{aligned}\right. \end{aligned}$$

For $m=0,$ Alikhanov [19] has found a special point for the interpolation approximation of the Caputo fractional derivative based on the work [18] and derived a numerical differentiation formula to approximate the Caputo fractional derivative at this point with the numerical accuracy of order $3-\alpha _0$ uniformly. It is pertinent to ask what about for a linear combination (2.1) of the multi-term fractional derivatives? Is there a point at which one can achieve a higher accurate interpolation approximation for (2.1)? It is precisely the starting point of our present work.

To this end, some preparation work is firstly done.

2.1 Some Interpolation Polynomials

Let $\tau$ be the step size. Denote $t_n=n\tau , n=0,1,2,\ldots .$

Suppose $f\in C^3[0,t_n].$ Let $L_{2,k}(s)$ be a quadratic polynomial on $[t_{k-1}, t_{k+1}]$ satisfying

$$\begin{aligned} L_{2,k}(t_{k-1})=f(t_{k-1}),\quad L_{2,k}(t_k)=f(t_k),\quad L_{2,k}(t_{k+1})=f(t_{k+1}),\quad 1\leqslant k\leqslant n-1. \end{aligned}$$

Denote

$$\begin{aligned} t_{k-\frac{1}{2}}=\left( k-\frac{1}{2}\right) \tau ,\quad \delta _tf\left( t_{k-\frac{1}{2}}\right) =\frac{f(t_k)-f(t_{k-1})}{\tau }. \end{aligned}$$

Then

$$\begin{aligned}&f(s)-L_{2,k}(s)=\frac{1}{6}f^{\prime \prime \prime }(\eta _k)(s-t_{k-1})(s-t_k)(s-t_{k+1}),\quad \nonumber \\&s\in [t_{k-1}, t_{k+1}],\ \eta _k\in (t_{k-1}, t_{k+1});\nonumber \\ L^\prime _{2,k}(s)&=\delta _tf\left( t_{k-\frac{1}{2}}\right) \frac{t_{k+\frac{1}{2}}-s}{\tau }+\delta _tf\left( t_{k+\frac{1}{2}}\right) \frac{s-t_{k-\frac{1}{2}}}{\tau }, \quad s\in [t_{k-1}, t_{k+1}]. \end{aligned}$$

(2.2)

Let $L_{1,n}(s)$ be a linear polynomial on $[t_{n-1}, t_{n}]$ satisfying

$$\begin{aligned} L_{1,n}(t_{n-1})=f(t_{n-1}),\quad L_{1,n}(t_{n})=f(t_{n}). \end{aligned}$$

Then

$$\begin{aligned} f(s)-L_{1,n}(s)= & {} \frac{1}{2} f^{\prime \prime }(\xi _n)(s-t_{n-1})(s-t_{n}),\quad s\in [t_{n-1}, t_{n}],\ \xi _n\in (t_{n-1}, t_{n});\\ L_{1,n}^\prime (s)= & {} \delta _tf(t_{n-\frac{1}{2}}),\quad s\in [t_{n-1}, t_{n}] \end{aligned}$$

and

$$\begin{aligned}&f^\prime (s)-L_{1,n}^\prime (s)\nonumber \\&\quad =f^\prime (s)-\delta _t f\left( t_{n-\frac{1}{2}}\right) \nonumber \\&\quad =\big [f^\prime (s)-f^\prime \left( t_{n-\frac{1}{2}}\right) \big ]+\big [f^\prime \left( t_{n-\frac{1}{2}}\right) -\delta _t f\left( t_{n-\frac{1}{2}}\right) \big ]\nonumber \\&\quad =\big [f^{\prime \prime }\left( t_{n-\frac{1}{2}}\right) \left( s-t_{n-\frac{1}{2}}\right) +\frac{1}{2}f^{\prime \prime \prime }\left( {\hat{\eta }}_n\right) \left( s-t_{n-\frac{1}{2}}\right) ^2\big ]-\frac{1}{24}\tau ^2 f^{\prime \prime \prime }\left( \tilde{\eta }_n\right) ,\nonumber \\&\quad s\in [t_{n-1}, t_{n}],\ \hat{\eta }_n, \tilde{\eta }_n\in (t_{n-1}, t_{n}). \end{aligned}$$

(2.3)

With the recalling of the above interpolation polynomials, we now turn to the derivation of a higher accurate interpolation approximation for (2.1).

2.2 The Higher Accurate Interpolation Approximation

Denote

$$\begin{aligned} F(\sigma )=\sum _{r=0}^m\frac{\lambda _r}{\Gamma (3-\alpha _r)}\sigma ^{1-\alpha _r}\big [\sigma -\left( 1-\frac{\alpha _r}{2}\right) \big ]\tau ^{2-\alpha _r},\quad \sigma \geqslant 0. \end{aligned}$$

Let

$$\begin{aligned} a=\min _{0\leqslant r\leqslant m}\left\{ 1-\frac{\alpha _r}{2}\right\} ,\quad b=\max _{0\leqslant r\leqslant m}\left\{ 1-\frac{\alpha _r}{2}\right\} . \end{aligned}$$

It is easy to know that

$$\begin{aligned} a=1-\frac{1}{2}\max _{0\leqslant r\leqslant m}\{\alpha _r\}=1-\frac{\alpha _0}{2}\geqslant \frac{1}{2},\quad b=1-\frac{1}{2}\min _{0\leqslant r\leqslant m}\{\alpha _r\}=1-\frac{\alpha _m}{2}\leqslant 1. \end{aligned}$$

Lemma 2.1

The equation $F(\sigma )=0$ has a unique positive root $\sigma ^*\in [a,b].$

Proof

If $m=0,$ it is apparent that the equation $F(\sigma )=0$ has a unique root $\sigma ^*=1-\frac{\alpha _0}{2}.$

Now, we suppose $m\geqslant 1.$ If $0\leqslant \sigma \leqslant a,$ then $F(\sigma )\leqslant F(a)<0.$ If $\sigma \geqslant b,$ then $F(\sigma )\geqslant F(b)>0.$ When $\sigma \in [a, b],$ we have

$$\begin{aligned} F^\prime (\sigma )=\sum _{r=0}^m\frac{\lambda _r}{\Gamma (2-\alpha _r)}\sigma ^{-\alpha _r}[\sigma -\frac{1}{2}(1-\alpha _r)]\tau ^{2-\alpha _r}>0. \end{aligned}$$

Thus, the equation $F(\sigma )=0$ has a unique positive root $\sigma ^*\in [a,b].$ $\square$

Lemma 2.2

For $m\geqslant 1,$ the Newton iteration sequence $\{\sigma _k\}_{k=0}^{\infty },$ generated by

$$\begin{aligned} \left\{ \begin{array}{l} \sigma _{k+1}=\sigma _k-\frac{F(\sigma _k)}{F^\prime (\sigma _k)},\quad k=0, 1, 2, \ldots ,\\ \sigma _0=b,\end{array}\right. \end{aligned}$$

(2.4)

is monotonically decreasing and convergent to $\sigma ^*.$

Proof

In view of the proof for the above lemma, we have $F(a)< 0, F(b)>0$ and $F^\prime (\sigma )>0$ when $\sigma \in [a, b].$ In addition, when $\sigma \in [a, b],$ we have

$$\begin{aligned}&F^{\prime \prime }(\sigma )=\sum _{r=0}^m\frac{\lambda _r}{\Gamma (1-\alpha _r)}\sigma ^{-\alpha _r-1}\left( \sigma +\frac{1}{2}\alpha _r\right) \tau ^{2-\alpha _r}>0. \end{aligned}$$

Noticing

$$\begin{aligned} F(\sigma _0)F^{\prime \prime }(\sigma _0)>0, \end{aligned}$$

then the Newton iteration sequence $\{\sigma _k\}_{k=0}^{\infty }$ generated by (2.4) is monotonically decreasing and convergent to $\sigma ^*$ [39]. $\square$

From now on, for simplicity in writing, we denote $\sigma =\sigma ^*,$ which means that this $\sigma \in [\frac{1}{2}, 1)$ satisfying $F(\sigma )=0.$

Denote $t_{n-1+\sigma }=(n-1+\sigma )\tau$ and consider ${}_0^CD_t^\alpha f(t_{n-1+\sigma })$ for any $\alpha \in [0,1].$

If $n=1,$ then

$$\begin{aligned} {}_0^CD_t^\alpha f(t_{n-1+\sigma })=\frac{1}{\Gamma (1-\alpha )}\int _{t_0}^{t_\sigma } f^{\prime }(s)(t_\sigma -s)^{-\alpha }{\mathrm {d}}s. \end{aligned}$$

If $n\geqslant 2,$ then

$$\begin{aligned} {}_0^CD_t^\alpha f(t_{n-1+\sigma })= & {} \frac{1}{\Gamma (1-\alpha )}\Bigg [\sum _{k=1}^{n-1}\int _{t_{k-1}}^{t_k} f^{\prime }(s)(t_{n-1+\sigma }-s)^{-\alpha }{\mathrm {d}}s\nonumber \\&+\,\int _{t_{n-1}}^{t_{n-1+\sigma }} f^{\prime }(s)(t_{n-1+\sigma }-s)^{-\alpha }{\mathrm {d}}s\Bigg ]. \end{aligned}$$

For the case with $\alpha =0$ or $\alpha =1,$ the above two equalities can be understood in the limit sense.

The next theorem will give a numerical differentiation formula to approximate (2.1) at the point $t=t_{n-1+\sigma }$ and reveal its numerical accuracy.

Theorem 2.1

Suppose $f\in C^3([t_0,t_n]).$ Let

$$\begin{aligned} Df(t_{n-1+\sigma })\equiv & {} \sum _{r=0}^m\lambda _r\ {}_0^CD_t^{\alpha _r}f(t_{n-1+\sigma })\\= & {} \sum _{r=0}^m \frac{\lambda _r}{\Gamma (1-\alpha _r)}\Bigg [\sum _{k=1}^{n-1}\int _{t_{k-1}}^{t_k}f^{\prime }(s)(t_{n-1+\sigma }-s)^{-\alpha _r}{\mathrm {d}}s\\&+\int _{t_{n-1}}^{t_{n-1+\sigma }}f^{\prime }(s)(t_{n-1+\sigma }-s)^{-\alpha _r}{\mathrm {d}}s\Bigg ] \end{aligned}$$

and

$$\begin{aligned} {\mathcal {D}}f(t_{n-1+\sigma })\equiv & {} \sum _{r=0}^m\frac{\lambda _r}{\Gamma (1-\alpha _r)}\Bigg [\sum _{k=1}^{n-1}\int _{t_{k-1}}^{t_k}L_{2,k}^{\prime }(s)(t_{n-1+\sigma }-s)^{-\alpha _r}{\mathrm {d}}s\\&+\int _{t_{n-1}}^{t_{n-1+\sigma }}L_{1,n}^{\prime }(s)(t_{n-1+\sigma }-s)^{-\alpha _r}{\mathrm {d}}s\Bigg ]. \end{aligned}$$

Then, we have

$$\begin{aligned} |Df(t_{n-1+\sigma })-{\mathcal {D}}f(t_{n-1+\sigma })|\leqslant M\sum _{r=0}^m \frac{\lambda _r}{\Gamma (2-\alpha _r)}\cdot \Big (\frac{1-\alpha _r}{12}+\frac{\sigma }{6}\Big ) \sigma ^{-\alpha _r}\tau ^{3-\alpha _r}, \end{aligned}$$

(2.5)

where $M=\displaystyle \max _{t_0\leqslant s\leqslant t_{n}}|f^{\prime \prime \prime }(s)|.$

Proof

It is easy to know that

$$\begin{aligned}&Df(t_{n-1+\sigma })-{\mathcal {D}}f(t_{n-1+\sigma })\nonumber \\&\quad =\sum _{r=0}^m\frac{\lambda _r}{\Gamma (1-\alpha _r)}\sum _{k=1}^{n-1}\int _{t_{k-1}}^{t_k}\big [f^{\prime }(s)-L_{2,k}^\prime (s)\big ](t_{n-1+\sigma }-s)^{-\alpha _r} {\mathrm {d}} s\nonumber \\&\qquad +\sum _{r=0}^m \frac{\lambda _r}{\Gamma (1-\alpha _r)}\int _{t_{n-1}}^{t_{n-1+\sigma }}\big [f^{\prime }(s)-L_{1,n}^\prime (s)\big ](t_{n-1+\sigma }-s)^{-\alpha _r}{\mathrm {d}} s. \end{aligned}$$

(2.6)

Since

$$\begin{aligned} A&\equiv \sum _{k=1}^{n-1}\int _{t_{k-1}}^{t_k}\big [f^{\prime }(s)-L_{2,k}^\prime (s)\big ](t_{n-1+\sigma }-s)^{-\alpha _r}{\mathrm {d}}s\nonumber \\&=\sum _{k=1}^{n-1}\Big \{\left. [f(s)-L_{2,k}(s)](t_{n-1+\sigma }-s)^{-\alpha _r}\right| _{s=t_{k-1}}^{t_k}\nonumber \\&\quad -\int _{t_{k-1}}^{t_k}\left[ f(s)-L_{2,k}(s)\right] \alpha _r(t_{n-1+\sigma }-s)^{-\alpha _r-1}{\mathrm {d}}s\Big \}\nonumber \\&=-\sum _{k=1}^{n-1}\int _{t_{k-1}}^{t_k}\left[ f(s)-L_{2,k}(s)\right] \alpha _r(t_{n-1+\sigma }-s)^{-\alpha _r-1}{\mathrm {d}}s \end{aligned}$$

and using (2.2), we get $|f(s)-L_{2,k}(s)|\leqslant \frac{1}{12}M\tau ^3$ for $s\in [t_{k-1},t_{k+1}]$ and hence

$$\begin{aligned} |A|\leqslant & {} \sum _{k=1}^{n-1}\int _{t_{k-1}}^{t_k}|f(s)-L_{2,k}(s)| \alpha _r(t_{n-1+\sigma }-s)^{-\alpha _r-1}{\mathrm {d}}s\nonumber \\\leqslant & {} \frac{1}{12}M\tau ^3\sum _{k=1}^{n-1}\int _{t_{k-1}}^{t_k} \alpha _r(t_{n-1+\sigma }-s)^{-\alpha _r-1}{\mathrm {d}}s\nonumber \\= & {} \frac{1}{12}M\tau ^3\int _{t_{0}}^{t_{n-1}} \alpha _r(t_{n-1+\sigma }-s)^{-\alpha _r-1}{\mathrm {d}}s\nonumber \\= & {} \frac{1}{12}M\tau ^3\big [(t_{n-1+\sigma }-t_{n-1})^{-\alpha _r}-(t_{n-1+\sigma }-t_0)^{-\alpha _r}\big ]\nonumber \\\leqslant & {} \frac{1}{12}M\tau ^3 \cdot (\sigma \tau )^{-\alpha _r}\nonumber \\= & {} \frac{1}{12}M\sigma ^{-\alpha _r}\tau ^{3-\alpha _r}. \end{aligned}$$

(2.7)

For the second term on the right hand of (2.6), according to (2.3), we have

$$\begin{aligned} B\equiv & {} \sum _{r=0}^m \frac{\lambda _r}{\Gamma (1-\alpha _r)}\int _{t_{n-1}}^{t_{n-1+\sigma }}\big [f^{\prime }(s)-L_{1,n}^\prime (s)\big ](t_{n-1+\sigma }-s)^{-\alpha _r}{\mathrm {d}}s\nonumber \\= & {} \sum _{r=0}^m \frac{\lambda _r}{\Gamma (1-\alpha _r)}\int _{t_{n-1}}^{t_{n-1+\sigma }}\bigg [f^{\prime \prime }\left( t_{n-\frac{1}{2}}\right) \left( s-t_{n-\frac{1}{2}}\right) +\frac{1}{2}f^{\prime \prime \prime }({\hat{\eta }}_n)\left( s-t_{n-\frac{1}{2}}\right) ^2\nonumber \\&-\frac{1}{24}\tau ^2 f^{\prime \prime \prime }(\tilde{\eta }_n)\bigg ](t_{n-1+\sigma }-s)^{-\alpha _r}{\mathrm {d}}s\\= & {} f^{\prime \prime }\left( t_{n-\frac{1}{2}}\right) \sum _{r=0}^m\frac{\lambda _r}{\Gamma (1-\alpha _r)}\int _{t_{n-1}}^{t_{n-1+\sigma }}\left( s-t_{n-\frac{1}{2}}\right) \left( t_{n-1+\sigma }-s\right) ^{-\alpha _r}{\mathrm {d}}s\nonumber \\&+\sum _{r=0}^m \frac{\lambda _r}{\Gamma (1-\alpha _r)}\int _{t_{n-1}}^{t_{n-1+\sigma }} \bigg [\frac{1}{2}f^{\prime \prime \prime }\left( {\hat{\eta }}_n\right) \left( s-t_{n-\frac{1}{2}}\right) ^2 -\frac{1}{24}\tau ^2 f^{\prime \prime \prime }\left( \tilde{\eta }_n\right) \bigg ]\left( t_{n-1+\sigma }-s\right) ^{-\alpha _r}{\mathrm {d}} s. \end{aligned}$$

Noticing $F(\sigma )=0,$ we know that

$$\begin{aligned}&\sum _{r=0}^m \frac{\lambda _r}{\Gamma (1-\alpha _r)}\int _{t_{n-1}}^{t_{n-1+\sigma }}(s-t_{n-\frac{1}{2}})(t_{n-1+\sigma }-s)^{-\alpha _r}{\mathrm {d}}s\\&\quad =\sum _{r=0}^m\frac{\lambda _r}{\Gamma (1-\alpha _r)}\int _{0}^{\sigma \tau }\left[ \left( \sigma -\frac{1}{2}\right) \tau -\xi \right] \xi ^{-\alpha _r}{\mathrm {d}}\xi \\&\quad =\sum _{r=0}^m\frac{\lambda _r}{\Gamma (3-\alpha _r)}\sigma ^{1-\alpha _r}\bigg [\sigma -\left( 1-\frac{\alpha _r}{2}\right) \bigg ]\tau ^{2-\alpha _r}\\&\quad =F(\sigma )\\&\quad =0. \end{aligned}$$

Therefore,

$$\begin{aligned} B= & {} \sum _{r=0}^m\frac{\lambda _r}{\Gamma (1-\alpha _r)}\int _{t_{n-1}}^{t_{n-1+\sigma }}\bigg [\frac{1}{2}f^{\prime \prime \prime }\left( {\hat{\eta }}_n\right) \left( s-t_{n-\frac{1}{2}}\right) ^2-\frac{1}{24}\tau ^2 f^{\prime \prime \prime }(\tilde{\eta }_n)\bigg ]\\&\times \left( t_{n-1+\sigma }-s\right) ^{-\alpha _r}{\mathrm {d}}s. \end{aligned}$$

Consequently,

$$\begin{aligned} |B|&\leqslant \frac{1}{6} M\sum _{r=0}^m\frac{\lambda _r}{\Gamma (1-\alpha _r)}\cdot \frac{\sigma ^{1-\alpha _r}}{1-\alpha _r}\tau ^{3-\alpha _r}. \end{aligned}$$

(2.8)

Substituting (2.7) and (2.8) into (2.6), we get

$$\begin{aligned} |Df(t_{n-1+\sigma })-{\mathcal {D}}f(t_{n-1+\sigma })|\leqslant M\sum _{r=0}^m \frac{\lambda _r}{\Gamma (1-\alpha _r)}\cdot \bigg (\frac{1}{12}+\frac{1}{6}\cdot \frac{\sigma }{1-\alpha _r}\bigg ) \sigma ^{-\alpha _r}\tau ^{3-\alpha _r}. \end{aligned}$$

This completes the proof of the theorem.$\square$

2.3 Properties of Coefficients in the Numerical Differentiation Formula

In this subsection, we will rewrite the derived numerical differentiation formula more explicitly and discuss some useful properties of coefficients in this formula. To this end, for $\alpha \in [0, 1],$ denote

$$\begin{aligned} a_0^{(\alpha )}= & {} \sigma ^{1-\alpha },\quad a_l^{(\alpha )}=(l+\sigma )^{1-\alpha }-(l-1+\sigma )^{1-\alpha },\quad l\geqslant 1,\\ b_l^{(\alpha )}= & {} \frac{1}{2-\alpha }\left[ (l+\sigma )^{2-\alpha }-(l-1+\sigma )^{2-\alpha }\right] -\frac{1}{2}\left[ (l+\sigma )^{1-\alpha }+(l-1+\sigma )^{1-\alpha }\right] ,\ l\geqslant 1. \end{aligned}$$

When $n=1,$ denote

$$\begin{aligned} c_0^{(n,\alpha )}=a_0^{(\alpha )}; \end{aligned}$$

When $n\geqslant 2,$ denote

$$\begin{aligned} c_k^{(n,\alpha )}={\left\{ \begin{array}{ll}a_0^{(\alpha )}+b_1^{(\alpha )},&{}\quad k=0,\\ a_k^{(\alpha )}+b_{k+1}^{(\alpha )}-b_k^{(\alpha )},&{}\quad 1\leqslant k\leqslant n-2,\\ a_k^{(\alpha )}-b_k^{(\alpha )},&{}\quad k=n-1.\end{array}\right. } \end{aligned}$$

In particular, when $\alpha =1,$ $c_0^{(n,\alpha )}=1,\ c_k^{(n,\alpha )}=0,\ 1\leqslant k\leqslant n-1;$ When $\alpha =0,$ $c_0^{(n,\alpha )}=\sigma ,\ c_k^{(n,\alpha )}=1,\ 1\leqslant k\leqslant n-1.$

Now the derived numerical differentiation formula can be written explicitly as follows:

$$\begin{aligned} {\mathcal {D}}f(t_{n-1+\sigma })=\sum _{k=0}^{n-1}\Bigg (\sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)}c_k^{(n,\alpha _r)}\Bigg )\big [f(t_{n-k})-f(t_{n-k-1})\big ]. \end{aligned}$$

(2.9)

Denote

$$\begin{aligned} \hat{c}_k^{(n)}=\sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)}c_k^{(n,\alpha _r)},\quad k=0,1,\ldots ,n-1. \end{aligned}$$

The next two lemmas will state some properties of the coefficients $\{\hat{c}_k^{(n)}\}$.

Lemma 2.3

Given any non-negative integer m and positive constants $\lambda _0, \lambda _1, \ldots , \lambda _m,$ for any $\alpha _i\in [0,1], i=0,1,\ldots ,m,$ where at least one of $\alpha _i$’s belongs to (0, 1),  it holds

$$\begin{aligned} \hat{c}_1^{(n)}>\hat{c}_2^{(n)}>\cdots>\hat{c}_{n-2}^{(n)}>\hat{c}_{n-1}^{(n)}>\sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)}\cdot \frac{1-\alpha _r}{2}(n-1+\sigma )^{-\alpha _r}.\end{aligned}$$

(2.10)

Proof

If $m=0,$ the conclusion has been obtained in [19]. Now, we suppose $m\geqslant 1.$ For any $\alpha _r\in (0,1),$ we have [19]

$$\begin{aligned} c_1^{(n,\alpha _r)}>c_2^{(n,\alpha _r)}>\cdots> c_{n-2}^{(n,\alpha _r)}>c_{n-1}^{(n,\alpha _r)}>\frac{1-\alpha _r}{2}(n-1+\sigma )^{-\alpha _r}. \end{aligned}$$

(2.11)

In particular, if $\alpha _r=0,$ we have

$$\begin{aligned} c_1^{(n,\alpha _r)}=c_2^{(n,\alpha _r)}=\cdots =c_{n-1}^{(n,\alpha _r)}=1>\frac{1-0}{2}(n-1+\sigma )^{-0}; \end{aligned}$$

(2.12)

If $\alpha _r=1,$ we have

$$\begin{aligned} c_1^{(n,\alpha _r)}=c_2^{(n,\alpha _r)}=\cdots =c_{n-1}^{(n,\alpha _r)}=0\geqslant \frac{1-1}{2}(n-1+\sigma )^{-1}; \end{aligned}$$

(2.13)

Combining with (2.11)–(2.13) and noticing that at least one of $\alpha _i$’s belongs to (0, 1),  we can get the required conclusion (2.10). $\square$

Lemma 2.4

Given any non-negative integer m and positive constants $\lambda _0, \lambda _1, \ldots , \lambda _m,$ for any $\alpha _i\in [0,1], i=0,1,\ldots ,m,$ where at least one of $\alpha _i$’s belongs to (0, 1),  then there exists a number $\tau _0>0,$ such that

$$\begin{aligned} (2\sigma -1)\hat{c}_0^{(n)}-\sigma \hat{c}_1^{(n)}>0 \end{aligned}$$

(2.14)

when $\tau \leqslant \tau _0, n=2,3,\ldots$ and hence

$$\begin{aligned} \hat{c}_0^{(n)}>\hat{c}_1^{(n)}. \end{aligned}$$

(2.15)

Proof

If $m=0,$ the proof can be found in [19]. Now, we suppose $m\geqslant 1$ and hence $\sigma \in (\frac{1}{2},1).$ When $n\geqslant 3,$ for each $\alpha _r\in [0,1],$ we have

$$\begin{aligned}&(2\sigma -1){c}_0^{(n,\alpha _r)}-\sigma {c}_1^{(n,\alpha _r)}\\&\quad =(2\sigma -1)\left( a_0^{(\alpha _r)}+b_1^{(\alpha _r)}\right) -\sigma \left( {a}_1^{(\alpha _r)}+b_2^{(\alpha _r)}-b_1^{(\alpha _r)}\right) \\&\quad =-\frac{s_r(2+\sigma )-\sigma }{2}(2+\sigma )^{1-\alpha _r}+\frac{(4\sigma ^2+3\sigma -1)s_r-4\sigma ^2+\sigma }{2\sigma }(1+\sigma )^{1-\alpha _r}\\&\qquad -\frac{3\sigma -1}{2}(s_r-1)\sigma ^{1-\alpha _r}, \end{aligned}$$

where $s_r=\frac{\sigma }{1-\alpha _r/2}, r=0,1,\ldots ,m.$

With the help of

$$\begin{aligned} (2+\sigma )^{1-\alpha _r}&=(1+\sigma )^{1-\alpha _r}\Big (1+\frac{1}{1+\sigma }\Big )^{1-\alpha _r}\\&\leqslant (1+\sigma )^{1-\alpha _r}\left( 1+\frac{1-\alpha _r}{1+\sigma }\right) \\&=(1+\sigma )^{1-\alpha _r}\frac{\sigma s_r+2\sigma }{s_r(1+\sigma )}, \end{aligned}$$

further we have

$$\begin{aligned}&(2\sigma -1){c}_0^{(n,\alpha _r)}-\sigma {c}_1^{(n,\alpha _r)}\nonumber \\&\quad \geqslant \frac{1}{2}\left[ \Big (3\sigma ^2+5\sigma +2-\frac{1}{\sigma }\Big ) s_r+\frac{2\sigma ^2}{s_r}-5\sigma ^2-7\sigma +1\right] (1+\sigma )^{-\alpha _r}\nonumber \\&\qquad -\frac{3\sigma -1}{2}( s_r-1)\sigma ^{1-\alpha _r}. \end{aligned}$$

(2.16)

Taking into account that

$$\begin{aligned} \sum \limits _{r=0}^{m}\lambda _r\frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)}\sigma ^{1-\alpha _r}(s_r-1)=\frac{2}{\tau ^2}F(\sigma )=0 \end{aligned}$$

and denoting

$$\begin{aligned} f_\sigma (t)=\Big (3\sigma ^2+5\sigma +2-\frac{1}{\sigma }\Big )t+\frac{2\sigma ^2}{t}-5\sigma ^2-7\sigma +1, \quad \sigma \in (1/2,1), \end{aligned}$$

from (2.16), we get

$$\begin{aligned}&(2\sigma -1)\hat{c}_0^{(n)}-\sigma \hat{c}_1^{(n)}\nonumber \\&\quad =\sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)}\left[ (2\sigma -1){c}_0^{(n,\alpha _r)}-\sigma {c}_1^{(n,\alpha _r)}\right] \nonumber \\&\quad \geqslant \frac{1}{2}\sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)}f_{\sigma }(s_r)(1+\sigma )^{-\alpha _r}-\frac{3\sigma -1}{2}\sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)}\sigma ^{1-\alpha _r}(s_r-1)\nonumber \\&\quad =\frac{1}{2}\sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)}f_{\sigma }(s_r)(1+\sigma )^{-\alpha _r}\nonumber \\&\quad =\frac{1}{2}\lambda _0\ \frac{\tau ^{-\alpha _0}}{\Gamma (2-\alpha _0)}f_{\sigma }( s_0)(1+\sigma )^{-\alpha _0}+\frac{1}{2}\sum _{r=1}^m\lambda _r\ \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)}f_{\sigma }( s_r)(1+\sigma )^{-\alpha _r}. \end{aligned}$$

(2.17)

Since $s_0=\frac{\sigma }{1-\alpha _0/2}>1$ and

$$\begin{aligned} f_\sigma ( s_0)>f_\sigma (1)=\frac{(2\sigma -1)(1-\sigma )}{\sigma }>0, \end{aligned}$$

from (2.17), it follows

$$\begin{aligned}&(2\sigma -1)\hat{c}_0^{(n)}-\sigma \hat{c}_1^{(n)}\nonumber \\&\quad >\frac{1}{2}\lambda _0\frac{\tau ^{-\alpha _0}}{\Gamma (2-\alpha _0)}(1+\sigma )^{-\alpha _0}\left[ f_\sigma (1) +\sum \limits _{r=1}^{m}\lambda _r\frac{\tau ^{\alpha _0-\alpha _r}\Gamma (2-\alpha _0)}{\lambda _0\Gamma (2-\alpha _r)}f_\sigma (s_r)(1+\sigma )^{\alpha _0-\alpha _r}\right] \nonumber \\&\quad =\frac{1}{2}\lambda _0\frac{\tau ^{-\alpha _0}}{\Gamma (2-\alpha _0)}(1+\sigma )^{-\alpha _0}\left[ f_\sigma (1)+O(\tau ^{\alpha _0-\alpha _1})\right] . \end{aligned}$$

(2.18)

Since $\alpha _0-\alpha _1>0,$ there exists a number $\tau _0>0,$ such that $f_\sigma (1)+O(\tau ^{\alpha _0-\alpha _1})\geqslant 0$ when $\tau \leqslant \tau _0.$ Thus, we can get the inequality (2.14) when $n\geqslant 3.$

If $n=2,$ we have

$$\begin{aligned}&(2\sigma -1){c}_0^{(2,\alpha _r)}-\sigma {c}_1^{(2,\alpha _r)}\nonumber \\&\quad =(2\sigma -1)\left( a_0^{(\alpha _r)}+b_1^{(\alpha _r)}\right) -\sigma \left( {a}_1^{(\alpha _r)}-b_1^{(\alpha _r)}\right) \nonumber \\&\quad \geqslant (2\sigma -1)\left( a_0^{(\alpha _r)}+b_1^{(\alpha _r)}\right) -\sigma \left( {a}_1^{(\alpha _r)}+b_2^{(\alpha _r)}-b_1^{(\alpha _r)}\right) . \end{aligned}$$

(2.19)

Then multiplying (2.19) by $\lambda _r\ \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)}$ and summing up for r from 0 to m, using the previous result when $n\geqslant 3,$ it is easy to know that $(2\sigma -1)\hat{c}_0^{(2)}-\sigma \hat{c}_1^{(2)}>0$ when $\tau \leqslant \tau _0.$ That is, the inequality (2.14) is true when $\tau \leqslant \tau _0,$ $n=2,3, \ldots$ .

From (2.14), we can immediately arrive at (2.15) when $\tau \leqslant \tau _0$ since $\sigma \in (\frac{1}{2},1).$ $\square$

From Theorem 2.1, one can know that the numerical accuracy of ${\mathcal {D}}f(t_{n-1+\sigma })$ to approximate the value of the linear combination (2.1) of multi-term Caputo fractional derivatives at the point $t_{n-1+\sigma }$ is at least second order if $f\in C^3[0,t_n].$ In the aftermentioned part, based on Theorem 2.1, we aim to develop some high order accurate difference schemes for solving the multi-term time-fractional sub-diffusion equation and the time distributed-order sub-diffusion equation, respectively.

3 Difference Schemes for the Multi-term Fractional Sub-diffusion Equation

Consider the following problem

$$\begin{aligned}&\sum _{r=0}^m\lambda _r \; {}_0^CD_t^{\alpha _r}u(x,t)=u_{xx}(x,t)+f(x,t),\quad 0<x<L,\ 0<t\leqslant T, \end{aligned}$$

(3.1)

$$\begin{aligned}&u(0,t)=0, \quad u(L,t)=0,\quad 0\leqslant t\leqslant T,\end{aligned}$$

(3.2)

$$\begin{aligned}&u(x,0)=u_0(x),\quad 0<x<L. \end{aligned}$$

(3.3)

Take two positive integers M and N. Denote $h=L/M, \tau =T/N, x_i=ih\;(0\leqslant i\leqslant M), t_n=n\tau \;(0\leqslant n\leqslant N),$ $\Omega _h=\{x_i\;|\; 0\leqslant i\leqslant M\}.$

Let

$$\begin{aligned} \mathcal {V}_h=\big \{v\;|\; v=(v_0, v_1, \ldots , v_{M-1}, v_M), v_0=0, v_M=0\big \}. \end{aligned}$$

Suppose $v, w\in \mathcal {V}_h.$ Introduce the following notations

$$\begin{aligned}&\delta _xv_{i-\frac{1}{2}}=\frac{1}{h}(v_i-v_{i-1}),\quad \delta _x^2v_i=\frac{1}{h^2}(v_{i-1}-2v_i+v_{i+1}),\\&(v,w)=h\sum _{i=1}^{M-1}v_iw_i,\quad \langle v,w \rangle =h\sum _{i=1}^{M}\left( \delta _x v_{i-\frac{1}{2}}\right) \left( \delta _x w_{i-\frac{1}{2}}\right) ,\\&\Vert v\Vert =\sqrt{(v, v)},\quad |v|_1=\sqrt{\langle v,v \rangle },\quad \Vert v\Vert _\infty =\max _{1\leqslant i\leqslant M-1}|v_i|. \end{aligned}$$

For any $v\in \mathcal {V}_h,$ we have [40, 41]

$$\begin{aligned} \Vert v\Vert _\infty \leqslant \frac{\sqrt{L}}{2}|v|_1. \end{aligned}$$

(3.4)

Based on Lemmas 2.3 and 2.4, the following lemma is true.

Lemma 3.1

[19, 40] Let $\mathcal {V}$ be an inner product space and $(\cdot , \cdot )$ is the inner product with the induced norm $\Vert \cdot \Vert .$ For $v^0, v^1, \cdots , v^n\in \mathcal {V} ,$ we have

$$\begin{aligned}&\sum _{k=0}^{n-1}\hat{c}_k^{(n)}\big (v^{n-k}-v^{n-k-1}, \sigma v^n+(1-\sigma )v^{n-1}\big )\\&\quad \geqslant \frac{1}{2}\sum _{k=0}^{n-1}\hat{c}_k^{(n)}\big (\Vert v^{n-k}\Vert ^2-\Vert v^{n-k-1}\Vert ^2\big ),\ n=1, 2, \ldots . \end{aligned}$$

Remark

Lemma 3.1 is vital for the analysis of the following difference schemes.

Denote

$$\begin{aligned} U_i^n= & {} u(x_i,t_n),\quad 0\leqslant i\leqslant M, 0\leqslant n\leqslant N;\qquad f_i^{n-1+\sigma }=f(x_i,t_{n-1+\sigma }),\\ 0\leqslant & {} i\leqslant M, 1\leqslant n\leqslant N. \end{aligned}$$

3.1 A Difference Scheme for (3.1)–(3.3)

Suppose $u(x,t)\in C^{(4,3)}([0,L]\times [0,T]).$

Considering (3.1) at the point $(x_i,t_{n-1+\sigma }),$ we have

$$\begin{aligned}&\sum _{r=0}^m\lambda _r\ {}_0^CD_t^{\alpha _r}u(x_i,t_{n-1+\sigma })\nonumber \\&\quad =u_{xx}(x_i,t_{n-1+\sigma })+f(x_i,t_{n-1+\sigma }),\quad 1\leqslant i\leqslant M-1, 1\leqslant n\leqslant N. \end{aligned}$$

(3.5)

Using (2.9) and Theorem 2.1, we get

$$\begin{aligned}&\sum _{r=0}^m\lambda _r\ {}_0^CD_t^{\alpha _r}u(x_i,t_{n-1+\sigma })\nonumber \\&\quad =\sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)} \sum _{k=0}^{n-1}c_k^{(n,\alpha _r)}\big (U_i^{n-k}-U_i^{n-k-1}\big )+O(\tau ^{3-\alpha _0}). \end{aligned}$$

(3.6)

In addition, it holds that

$$\begin{aligned} u_{xx}(x_i,t_{n-1+\sigma })&=\sigma u_{xx}(x_i,t_{n}) +(1-\sigma ) u_{xx}(x_i,t_{n-1})+O(\tau ^2)\nonumber \\&=\delta _x^2(\sigma U_i^n+(1-\sigma )U_i^{n-1})+O(\tau ^2+h^2). \end{aligned}$$

(3.7)

Substituting (3.6) and (3.7) into (3.5), we obtain

$$\begin{aligned}&\sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)} \sum _{k=0}^{n-1}c_k^{(n,\alpha _r)}\big (U_i^{n-k}-U_i^{n-k-1}\big )\nonumber \\&\quad =\delta _x^2(\sigma U_i^n+(1-\sigma )U_i^{n-1})+f_i^{n-1+\sigma }+R_i^n, \quad 1\leqslant i\leqslant M-1, 1\leqslant n\leqslant N \end{aligned}$$

(3.8)

and there exists a constant $c_1$ such that

$$\begin{aligned} |R_i^n|\leqslant c_1(\tau ^2+h^2),\quad 1\leqslant i\leqslant M-1, 1\leqslant n\leqslant N. \end{aligned}$$

(3.9)

Omitting the small term $R_i^n$ in (3.8) and noticing the initial-boundary conditions

$$\begin{aligned}&U_0^n=0, \quad U_M^n=0,\quad 0\leqslant n\leqslant N, \end{aligned}$$

(3.10)

$$\begin{aligned}&U_i^0=u_0(x_i),\quad 1\leqslant i\leqslant M-1, \end{aligned}$$

(3.11)

we construct a difference scheme for (3.1)–(3.3) as follows

$$\begin{aligned}&\sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)} \sum _{k=0}^{n-1}c_k^{(n,\alpha _r)}\big (u_i^{n-k}-u_i^{n-k-1}\big )\nonumber \\&\quad =\delta _x^2(\sigma u_i^n+(1-\sigma )u_i^{n-1})+f_i^{n-1+\sigma }, \quad 1\leqslant i\leqslant M-1, 1\leqslant n\leqslant N,\end{aligned}$$

(3.12)

$$\begin{aligned}&u_0^n=0, \quad u_M^n=0,\quad 0\leqslant n\leqslant N,\end{aligned}$$

(3.13)

$$\begin{aligned}&u_i^0=u_0(x_i),\quad 1\leqslant i\leqslant M-1. \end{aligned}$$

(3.14)

Denote

$$\begin{aligned} u^n=(u_0^n, u_1^n, u_2^n, \ldots , u_{M-1}^n, u_M^n). \end{aligned}$$

Theorem 3.1

The difference scheme (3.12)–(3.14) is uniquely solvable.

Proof

By (3.13) and (3.14), the value of $u^0$ is determined. If $\{u^{k}\;|\; 0\leqslant k\leqslant n-1\}$ has been determined, then we get a linear system of equations with respect to $u^n.$ Consider the corresponding homogeneous system:

$$\begin{aligned}&\sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)} c_0^{(n,\alpha _r)}u_i^{n}=\sigma \delta _x^2u_i^n, \quad 1\leqslant i\leqslant M-1,\end{aligned}$$

(3.15)

$$\begin{aligned}&u_0^n=0, \quad u_M^n=0. \end{aligned}$$

(3.16)

Multiplying (3.15) by $hu_i^n$ and summing up for i from 1 to $M-1,$ then using (3.16), we obtain

$$\begin{aligned} \sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)} c_0^{(n,\alpha _r)}\Vert u^{n}\Vert ^2=\sigma h\sum _{i=1}^{M-1}(\delta _x^2u_i^n)u_i^n=-\sigma |u^n|_1^2. \end{aligned}$$

Consequently,

$$\begin{aligned} \Vert u^n\Vert =0, \end{aligned}$$

which gives $u^n=0$ in view of (3.16). This completes the proof.$\square$

A prior estimate on the difference scheme (3.12)–(3.14) is stated as follows.

Theorem 3.2

Let $\{u^n\;|\; 0\leqslant n\leqslant N\}$ be the solution of the difference scheme (3.12)–(3.14). Then we have

$$\begin{aligned} |u^n|_1^2\leqslant |u^0|_1^2+ \frac{1}{\displaystyle \sum _{r=0}^m\frac{\lambda _r}{T^{\alpha _r}\Gamma (1-\alpha _r)}}\max _{1\leqslant l\leqslant n}\Vert f^{l-1+\sigma }\Vert ^2,\quad 1\leqslant n\leqslant N, \end{aligned}$$

(3.17)

where

$$\begin{aligned} \Vert f^{l-1+\sigma }\Vert ^2=h\sum _{i=1}^{M-1}(f_i^{l-1+\sigma })^2. \end{aligned}$$

Proof

Making an inner product of (3.12) with $-\delta _x^2\big (\sigma u^n+(1-\sigma )u^{n-1}\big )$ on both sides, we have

$$\begin{aligned}&\sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)} \sum _{k=0}^{n-1}c_k^{(n,\alpha _r)}\big (u^{n-k}-u^{n-k-1}, -\delta _x^2(\sigma u^n+(1-\sigma )u^{n-1})\big )\nonumber \\&\quad =-\big ( \delta _x^2(\sigma u^n+(1-\sigma )u^{n-1}),\delta _x^2(\sigma u^n+(1-\sigma )u^{n-1})\big )\nonumber \\&\qquad -\big (f^{n-1+\sigma }, \delta _x^2(\sigma u^n+(1-\sigma )u^{n-1})\big )\nonumber \\&\quad \leqslant -\left\| \delta _x^2(\sigma u^n+(1-\sigma )u^{n-1})\right\| ^2+\left\| \delta _x^2(\sigma u^n+(1-\sigma )u^{n-1})\right\| ^2\nonumber \\&\qquad +\frac{1}{4}\left\| f^{n-1+\sigma }\right\| ^2, \quad 1\leqslant n\leqslant N. \end{aligned}$$

(3.18)

Using Lemma 3.1 and noticing (3.13), we know

$$\begin{aligned}&\sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)} \sum _{k=0}^{n-1}c_k^{(n,\alpha _r)}\big (u^{n-k}-u^{n-k-1}, -\delta _x^2(\sigma u^n+(1-\sigma )u^{n-1})\big )\nonumber \\&\quad =\sum _{k=0}^{n-1}\hat{c}_k^{(n)}\big <u^{n-k}-u^{n-k-1}, \sigma u^n+(1-\sigma )u^{n-1}\big >\nonumber \\&\quad \geqslant \frac{1}{2}\sum _{k=0}^{n-1} \hat{c}_k^{(n)}\big (|u^{n-k}|_1^2-|u^{n-k-1}|_1^2\big ). \end{aligned}$$

(3.19)

Substituting (3.19) into (3.18), we get

$$\begin{aligned} \frac{1}{2}\sum _{k=0}^{n-1} \hat{c}_k^{(n)}\big (|u^{n-k}|_1^2-|u^{n-k-1}|_1^2\big )\leqslant \frac{1}{4}\Vert f^{n-1+\sigma }\Vert ^2,\quad 1\leqslant n\leqslant N, \end{aligned}$$

or

$$\begin{aligned}&\hat{c}_0^{(n)}|u^{n}|_1^2\leqslant \sum _{k=1}^{n-1}\big (\hat{c}_{k-1}^{(n)}-\hat{c}_k^{(n)}\big )|u^{n-k}|_1^2+\hat{c}_{n-1}^{(n)}|u^{0}|_1^2+\frac{1}{2}\Vert f^{n-1+\sigma }\Vert ^2,\quad 1\leqslant n\leqslant N.\nonumber \\ \end{aligned}$$

(3.20)

Noticing

$$\begin{aligned} \hat{c}_{n-1}^{(n)}\geqslant \sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)}\cdot \frac{1-\alpha _r}{2}(n-1+\sigma )^{-\alpha _r}\geqslant \frac{1}{2}\sum _{r=0}^m\frac{\lambda _r}{T^{\alpha _r}\Gamma (1-\alpha _r)}, \end{aligned}$$

(3.21)

it follows from (3.20) that

$$\begin{aligned} \hat{c}_0^{(n)}|u^{n}|_1^2\leqslant&\sum _{k=1}^{n-1}\big (\hat{c}_{k-1}^{(n)}-\hat{c}_k^{(n)}\big ) |u^{n-k}|_1^2\nonumber \\&+\,\hat{c}_{n-1}^{(n)}\left( |u^{0}|_1^2+\frac{1}{2}\cdot \frac{2}{\displaystyle \sum _{r=0}^m\frac{\lambda _r}{T^{\alpha _r}\Gamma (1-\alpha _r)}}\Vert f^{n-1+\sigma }\Vert ^2\right) ,\quad 1\leqslant n\leqslant N. \end{aligned}$$

The induction method applied to the above inequality will produce (3.17). This completes the proof.$\square$

Theorem 3.2 reveals the unconditional stability of the difference scheme (3.12)–(3.14) with respect to the initial value and the inhomogeneous term f. The next result is about the convergence of this scheme.

Theorem 3.3

Let $\{u^n\;|\; 0\leqslant n\leqslant N\}$ be the solution of the difference scheme (3.12)–(3.14) and

$$\begin{aligned} e_i^n=U_i^n-u_i^n, \quad 0\leqslant i\leqslant M, 0\leqslant n\leqslant N. \end{aligned}$$

Then we have

$$\begin{aligned} \Vert e^n\Vert _\infty \leqslant \frac{c_1L}{2} \sqrt{ \frac{1}{\displaystyle \sum _{r=0}^m\frac{\lambda _r}{T^{\alpha _r}\Gamma (1-\alpha _r)}}}\; (\tau ^2+h^2),\quad 1\leqslant n\leqslant N. \end{aligned}$$

(3.22)

Proof

Subtracting (3.12)–(3.14) from (3.8), (3.10)–(3.11), respectively, we obtain the error equations as follows

$$\begin{aligned}&\sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)} \sum _{k=0}^{n-1}c_k^{(n,\alpha _r)}\big (e_i^{n-k}-e_i^{n-k-1}\big )\nonumber \\&\quad =\delta _x^2(\sigma e_i^n+(1-\sigma )e_i^{n-1})+R_i^n, \quad 1\leqslant i\leqslant M-1, 1\leqslant n\leqslant N, \end{aligned}$$

(3.23)

$$\begin{aligned}&e_0^n=0, \quad e_M^n=0,\quad 0\leqslant n\leqslant N,\end{aligned}$$

(3.24)

$$\begin{aligned}&e_i^0=0,\quad 1\leqslant i\leqslant M-1. \end{aligned}$$

(3.25)

Applying (3.9) and the stability inequality (3.17), we have

$$\begin{aligned} |e^n|_1^2\leqslant&|e^0|_1^2+ \frac{1}{\displaystyle \sum _{r=0}^m\frac{\lambda _r}{T^{\alpha _r}\Gamma (1-\alpha _r)}}\max _{1\leqslant l\leqslant n}\Vert R^{l}\Vert ^2\\ \leqslant&\frac{1}{\displaystyle \sum _{r=0}^m\frac{\lambda _r}{T^{\alpha _r}\Gamma (1-\alpha _r)}} \big [c_1(\tau ^2+h^2)\big ]^2L,\quad 1\leqslant n\leqslant N. \end{aligned}$$

Noting (3.4), we obtain

$$\begin{aligned} \Vert e^n\Vert _\infty \leqslant \frac{\sqrt{L} }{2}|e^n|_1\leqslant \frac{c_1L}{2} \sqrt{ \frac{1}{\displaystyle \sum _{r=0}^m\frac{\lambda _r}{T^{\alpha _r}\Gamma (1-\alpha _r)}}}\;(\tau ^2+h^2),\quad 1\leqslant n\leqslant N. \end{aligned}$$

This completes the proof.$\square$

3.2 The Extension to the 2D Problem

The idea for solving the 1D problem (3.1)–(3.3) can be directly extended to handle the 2D problem. Now we will briefly discuss this issue. To this end, consider the problem

$$\begin{aligned}&\sum _{r=0}^m\lambda _r \; {}_0^CD_t^{\alpha _r}u(x,y,t)=\Delta u(x,y,t)+f(x,y,t),\quad (x,y)\in \Omega ,\ 0<t\leqslant T,\end{aligned}$$

(3.26)

$$\begin{aligned}&u(x,y,t)=0, \quad (x,y)\in \partial \Omega ,\ 0\leqslant t\leqslant T,\end{aligned}$$

(3.27)

$$\begin{aligned}&u(x,y,0)=u_0(x,y),\quad (x,y)\in \Omega , \end{aligned}$$

(3.28)

where $\Omega =[0,L_1]\times [0,L_2], \partial \Omega$ is the boundary of $\Omega ,$ $\Delta u=u_{xx}+u_{yy}$ is the Laplacian operator, $u_0(x,y)$ and f(x, y, t) are given functions.

The mesh partition is firstly given as $\{(x_i, y_j)\;|\;0\leqslant i\leqslant M_1, 0\leqslant j\leqslant M_2\}$ with $x_i=ih_1, y_j=jh_2,$ where $h_1=L_1/M_1, h_2=L_2/M_2$ and $M_1, M_2$ are two positive integers.

Let

$$\begin{aligned} \omega= & {} \{(i,j)\;|\;1\leqslant i\leqslant M_1-1, 1\leqslant j\leqslant M_2-1\},\quad \partial \omega =\{(i,j)\;|\;(x_i, y_j)\in \partial \Omega \},\\ \bar{\omega }= & {} \omega \cup \partial \omega ,\quad \mathcal {U}_h=\{u\;|\;u=\{u_{ij}\;|\;(i,j)\in \bar{\omega }\}\}. \end{aligned}$$

For any $u\in \mathcal {U}_h,$ define

$$\begin{aligned} \delta _x^2u_{ij}= & {} \frac{1}{h_1^2}(u_{i-1,j}-2u_{ij}+u_{i+1,j}),\quad \delta _y^2u_{ij}=\frac{1}{h_2^2}(u_{i,j-1}-2u_{ij}+u_{i,j+1}),\\ \Delta _h u_{ij}= & {} \delta _x^2u_{ij}+\delta _y^2u_{ij}. \end{aligned}$$

Denote

$$\begin{aligned} U_{ij}^n= & {} u(x_i,y_j,t_n),\quad (i,j)\in \bar{\omega },\ 0\leqslant n\leqslant N;\quad f_{ij}^{n-1+\sigma }=f(x_i, y_j, t_{n-1+\sigma }),\\ (i,j)\in & {} \bar{\omega },\ 1\leqslant n\leqslant N. \end{aligned}$$

Suppose $u(x,y,t)\in C^{(4,4,3)}(\bar{\Omega }\times [0,T]).$ Considering Eq. (3.26) at the point $(x_i, y_j, t_{n-1+\sigma }),$ we have

$$\begin{aligned} \sum _{r=0}^m\lambda _r\ {}_0^CD_t^{\alpha _r}u(x_i, y_j, t_{n-1+\sigma })=\Delta u(x_i, y_j, t_{n-1+\sigma })+f_{ij}^{n-1+\sigma },\quad (i,j)\in \omega ,\ 1\leqslant n\leqslant N. \end{aligned}$$

(3.29)

Using Theorem 2.1 and (2.9), we obtain

$$\begin{aligned}&\sum _{r=0}^m\lambda _r\ {}_0^CD_t^{\alpha _r}u(x_i, y_j, t_{n-1+\sigma })\nonumber \\&\quad =\sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)} \sum _{k=0}^{n-1}c_k^{(n,\alpha _r)}\big (U_{ij}^{n-k}-U_{ij}^{n-k-1}\big )+O(\tau ^{3-\alpha _0}). \end{aligned}$$

(3.30)

Moreover, it is easy to know that

$$\begin{aligned} \Delta u(x_i, y_j, t_{n-1+\sigma })&=\sigma \Delta u(x_i, y_j, t_{n}) +(1-\sigma )\Delta u(x_i, y_j, t_{n-1})+O(\tau ^2)\nonumber \\&=\Delta _h(\sigma U_{ij}^n+(1-\sigma )U_{ij}^{n-1})+O(\tau ^2+h_1^2+h_2^2). \end{aligned}$$

(3.31)

Inserting (3.30) and (3.31) into (3.29) yields

$$\begin{aligned}&\sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)} \sum _{k=0}^{n-1}c_k^{(n,\alpha _r)}\big (U_{ij}^{n-k}-U_{ij}^{n-k-1}\big )\nonumber \\&\quad =\Delta _h(\sigma U_{ij}^n+(1-\sigma )U_{ij}^{n-1})+f_{ij}^{n-1+\sigma }+S_{ij}^n, \quad (i,j)\in \omega ,\ 1\leqslant n\leqslant N\quad \end{aligned}$$

(3.32)

and there is a positive constant $c_2$ such that

$$\begin{aligned} |S_{ij}^n|\leqslant c_2(\tau ^2+h_1^2+h_2^2),\quad (i,j)\in \omega ,\ 1\leqslant n\leqslant N. \end{aligned}$$

(3.33)

Omitting the small term $S_{ij}^n$ in (3.32), replacing $U_{ij}^n$ by its numerical one $u_{ij}^n$ and noticing the exact initial-boundary value conditions (3.27)–(3.28), we can get the following difference scheme for solving (3.26)–(3.28):

$$\begin{aligned}&\sum _{r=0}^m\lambda _r\ \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)} \sum _{k=0}^{n-1}c_k^{(n,\alpha _r)}\big (u_{ij}^{n-k}-u_{ij}^{n-k-1}\big )\nonumber \\&\quad =\Delta _h(\sigma u_{ij}^n+(1-\sigma )u_{ij}^{n-1})+f_{ij}^{n-1+\sigma }, \quad (i,j)\in \omega ,\ 1\leqslant n\leqslant N, \end{aligned}$$

(3.34)

$$\begin{aligned}&u_{ij}^n=0, \quad (i,j)\in \partial \omega ,\ 0\leqslant n\leqslant N,\end{aligned}$$

(3.35)

$$\begin{aligned}&u_{ij}^0=u_0(x_i,y_j),\quad (i,j)\in \omega . \end{aligned}$$

(3.36)

Using the discrete energy method, the difference scheme (3.34)–(3.36) can be shown to be uniquely solvable, unconditionally stable and convergent with the order of $O(\tau ^2+h_1^2+h_2^2).$

The application of the numerical differentiation formula (2.9) into solving the time distributed-order fractional sub-diffusion equation will be illustrated in the following section.

4 Difference Schemes for the Time Distributed-Order Fractional Sub-diffusion Equation

Consider the 1-D time distributed-order fractional sub-diffusion problem

$$\begin{aligned}&\int _0^1w(\alpha )\;{}_0^CD_t^\alpha u(x,t){\mathrm {d}}\alpha =u_{xx}(x,t)+f(x,t),\quad 0<x<L, 0<t\leqslant T,\end{aligned}$$

(4.1)

$$\begin{aligned}&u(0,t)=0,\quad u(L,t)=0,\quad 0\leqslant t\leqslant T,\end{aligned}$$

(4.2)

$$\begin{aligned}&u(x,0)=u_0(x),\quad 0<x<L, \end{aligned}$$

(4.3)

where

$$\begin{aligned} w(\alpha )\geqslant 0,\quad \int _0^1w(\alpha ){\mathrm {d}}\alpha =w_0>0. \end{aligned}$$

Divide the integral interval [0, 1] into 2J-subintervals with $\Delta \alpha =\frac{1}{2J}$ and $\alpha _l=l\Delta \alpha , l=0, 1, 2, \ldots , 2J.$

For the numerical approximation of the distributed integral, we need the following lemma.

Lemma 4.1

(The composite Simpson formula) [39] Let $s(\alpha )\in C^{4}([0, 1]).$ Then we have

$$\begin{aligned} \int _0^1s(\alpha ){\mathrm {d}}\alpha =\Delta \alpha \sum _{l=0}^{2J}d_ls(\alpha _l)-\frac{\Delta \alpha ^4}{180} s^{(4)}(\eta ),\quad \eta \in (0,1), \end{aligned}$$

where

$$\begin{aligned} d_l= \left\{ \begin{array}{ll} \frac{1}{3},&{}\quad l=0,\; 2J,\\ &{} \\ \frac{2}{3},&{}\quad l=2,\; 4,\; \ldots ,\; 2J-4,\; 2J-2, \\ &{} \\ \frac{4}{3},&{}\quad l=1,\; 3,\; \ldots ,\; 2J-3,\; 2J-1. \end{array} \right. \end{aligned}$$

Using the above lemma, we have

$$\begin{aligned} \int _0^1w(\alpha )\;{}_0^CD_t^\alpha u(x,t){\mathrm {d}}\alpha =\Delta \alpha \sum _{r=0}^{2J}d_rw(\alpha _r)\ {}_0^CD_t^{\alpha _r} u(x,t)+O(\Delta \alpha ^4). \end{aligned}$$

(4.4)

Denote $m=2J,$ $\lambda _r=d_r w(\alpha _r)\Delta \alpha .$

Suppose $u(x,t)\in C^{(4,3)}([0,L]\times [0,T]).$

Considering (4.1) at the point $(x_i,t_{n-1+\sigma })$ and using (4.4), we have

$$\begin{aligned}&\sum _{r=0}^m\lambda _r \ {}_0^CD_t^{\alpha _r} u(x_i,t_{n-1+\sigma })=u_{xx}(x_i,t_{n-1+\sigma })+f(x_i,t_{n-1+\sigma })+O(\Delta \alpha ^4),\nonumber \\&\quad 1\leqslant i\leqslant M-1, 1\leqslant n\leqslant N. \end{aligned}$$

(4.5)

We construct the following difference scheme for (4.1)–(4.3):

$$\begin{aligned}&\sum _{r=0}^m\lambda _r \frac{\tau ^{-\alpha _r}}{\Gamma (2-\alpha _r)} \sum _{k=0}^{n-1}c_k^{(n,\alpha _r)}\big (u_i^{n-k}-u_i^{n-k-1}\big )\nonumber \\&\quad =\delta _x^2(\sigma u_i^n+(1-\sigma )u_i^{n-1})+f_i^{n-1+\sigma }, \quad 1\leqslant i\leqslant M-1, 1\leqslant n\leqslant N,\end{aligned}$$

(4.6)

$$\begin{aligned}&u_0^n=0, \quad u_M^n=0,\quad 0\leqslant n\leqslant N,\end{aligned}$$

(4.7)

$$\begin{aligned}&u_i^0=u_0(x_i),\quad 1\leqslant i\leqslant M-1. \end{aligned}$$

(4.8)

The truncation error of (4.6) is $O(\Delta \alpha ^4+\tau ^2+h^2).$

We can show that the difference scheme (4.6)–(4.8) is uniquely solvable, unconditionally stable and convergent with the convergence order of $O(\Delta \alpha ^4+\tau ^2+h^2)$ in $L_\infty$ norm.

Remark

The idea can be directly applied to handle the 2D time distributed-order sub-diffusion problem. We skip the details here due to the limitation of the article in length.

5 Numerical Examples

In this section, we are devoted to some numerical illustration on the theoretical results in the previous sections. Firstly, the higher accurate numerical differentiation formula (2.9) to approximate the time multi-term fractional derivatives $Df(t)=\sum _{r=0}^m\lambda _r\ {}_0^CD_t^{\alpha _r}f(t)$ at the special point $t_{n-1+\sigma }$ is verified. Then the applications of this numerical formula into solving the time multi-term fractional sub-diffusion equation and the time distributed-order sub-diffusion equation are numerically illustrated, respectively.

Example 5.1

Take $T=1, m=2, (\lambda _0, \lambda _1, \lambda _2)=(3,2,1),$ $f(t)=t^4.$ Then

$$\begin{aligned} Df(t_{n-1+\sigma })=\sum _{r=0}^m\lambda _r\ {}_0^CD_t^{\alpha _r}f(t)|_{t=t_{n-1+\sigma }}=\sum _{r=0}^m\lambda _r\cdot \frac{\Gamma {(5)}}{\Gamma {(5-\alpha _r)}}t^{4-\alpha _r}_{n-1+\sigma }. \end{aligned}$$

Denote

$$\begin{aligned} \mathrm{Emax(\tau )}=\max _{1\leqslant n\leqslant N}|Df(t_{n-1+\sigma })-{\mathcal {D}}f(t_{n-1+\sigma })|, \end{aligned}$$

where N is the temporal step number such that $N\tau =T=1$ with $\tau$ the temporal step size. Define the numerical convergence order by

$$\begin{aligned} \mathrm{Order}=\log _2\frac{\mathrm{Emax}(\tau )}{\mathrm{Emax}(\tau /2)}. \end{aligned}$$

Table 1 lists the maximum numerical errors and convergence orders of the numerical differentiation formula (2.9) to approximate the time multi-term fractional derivatives $\sum _{r=0}^m\lambda _r\ {}_0^CD_t^{\alpha _r}f(t)$ at the special point $t_{n-1+\sigma }$ $(1\leqslant n\leqslant N).$ In addition, for each pair of orders of multi-term fractional derivatives and different step sizes $\tau ,$ the calculated value of $\sigma$ is also displayed in this table. From the table, one can see that the numerical convergence orders of (2.9) can achieve $O(\tau ^{3-\alpha _0}),$ which is in a good agreement with theoretical results.

Table 1 Numerical errors and convergence orders of numerical formula (2.9) to approximate the time multi-term fractional derivatives $\sum _{r=0}^m\lambda _r\ {}_0^CD_t^{\alpha _r}f(t)$ at the point $t_{n-1+\sigma }$

Example 5.2

In (3.1)–(3.3), take $T=1, L=\pi , m=2,$ $f(x,t)=\Big [24\sum _{r=0}^m \lambda _rt^{4-\alpha _r}/\Gamma (5-\alpha _r)+t^4\Big ]\sin x,$ $u_0(x)=0.$

The analytical solution of this example is given by $u(x,t)=t^4\sin x.$

Denote

$$\begin{aligned} \mathrm{err}(h,\tau )= & {} \max _{0\leqslant i\leqslant M,0\leqslant n\leqslant N}|u(x_i,t_n)-u_i^n|, \quad \mathrm{order}_t=\log _2\frac{\mathrm{err}(h,\tau )}{\mathrm{err}(h,\tau /2)},\\ \mathrm{order}_x= & {} \log _2\frac{\mathrm{err}(h,\tau )}{\mathrm{err}(h/2,\tau )}. \end{aligned}$$

With several sets of values of $\lambda _0, \lambda _1, \ldots , \lambda _m$ and $\alpha _0, \alpha _1, \ldots , \alpha _m$, the difference scheme (3.12)–(3.14) will be employed to numerically solve this example. Firstly, the numerical accuracy of this scheme in time will be verified. Taking the sufficiently small step size h and varying step size $\tau ,$ the numerical errors and numerical convergence orders will be listed in Table 2. The computational results in Table 2 confirm the second-order convergence of the difference scheme (3.12)–(3.14) in time.

Table 2 Numerical errors and convergence orders of the difference scheme (3.12)–(3.14) in time for solving Example 5.2 ($M=1000$)

Next, the numerical accuracy of the difference scheme (3.12)–(3.14) in space for solving this example will be examined. Numerical results of this scheme under different step sizes in space will be calculated and the numerical errors, as well as the numerical convergence orders will be recorded in Table 3, from which, one can find that, the second-order convergence of the difference scheme (3.12)–(3.14) in space can be achieved. The numerical results are in accord with the expected ones.

Table 3 Numerical errors and convergence orders of the difference scheme (3.12)–(3.14) in space for solving Example 5.2 ($N=2000$)

Example 5.3

In (4.1)–(4.3), take $T=1/2, L=\pi ,$ $w(\alpha )=\Gamma (5-\alpha ),$ $u_0(x)=0,$ $f(x,t)=t^3\big [24(t-1)/\log t+t\big ]\sin x.$

The analytical solution of this example is also given by $u(x,t)=t^4\sin x.$

Denote

$$\begin{aligned} \mathrm{Err}(h,\tau ,\Delta \alpha )= & {} \max _{0\leqslant i\leqslant M, 0\leqslant n\leqslant N}|u(x_i,t_n)-u_i^n|, \quad \mathrm{Order}_{\tau }=\log _2\frac{\mathrm{Err}(h,\tau ,\Delta \alpha )}{\mathrm{Err}(h,\tau /2,\Delta \alpha )},\\ \mathrm{Order}_{h}= & {} \log _2\frac{\mathrm{Err}(h,\tau ,\Delta \alpha )}{\mathrm{Err}(h/2,\tau ,\Delta \alpha )}, \mathrm{Order}_{\Delta \alpha }=\log _2\frac{\mathrm{Err}(h,\tau ,\Delta \alpha )}{\mathrm{Err}(h,\tau ,\Delta \alpha /2)}. \end{aligned}$$

This example will be numerically calculated by the presented difference scheme (4.6)–(4.8).

In the first run, with the fixed and sufficiently small step sizes h and $\Delta \alpha$ and varying the step size $\tau ,$ this example is calculated and numerical errors as well as the convergence orders are recorded in Table 4. From Table 4, the second-order convergence of the scheme in time can be observed.

Table 4 Numerical errors and convergence orders of the difference scheme (4.6)–(4.8) in time for solving Example 5.3 ($M=2000, J=100$)

Now, the numerical experiments are carried out for this example with the purpose of verifying the numerical accuracy of the difference scheme (4.6)–(4.8) in space. In Table 5, the computational results are given for different spatial step sizes when the mesh grid is fixed to be $\tau =1/2000$ and $\Delta \alpha =1/200$ for the difference scheme (4.6)–(4.8). From the results in Table 5, we can conclude that the convergence order of the difference scheme (4.6)–(4.8) in space is two, which is in accordance with the expected results.

Table 5 Numerical errors and convergence orders of the difference scheme (4.6)–(4.8) in space for solving Example 5.3 ($N=1000, J=100$)

Moreover, we will illustrate that the difference scheme (4.6)–(4.8) is fourth-order convergent in distributed order. When the step size $\Delta \alpha$ is reduced by half, the numerical errors are decreasing by a factor of 16,  where the step sizes $\tau$ and h are fixed to be sufficiently small to ensure that the dominated errors are produced from the numerical approximation of distributed integral. The results are displayed in Table 6, from which, the desirable fourth-order convergence in distributed order of this scheme can be read off evidently.

Table 6 Numerical errors and convergence orders of the difference scheme (4.6)–(4.8) in distributed order for solving Example 5.3 ($N=10,000, M=2000$)

The next example is devoted to examining the efficiency of the proposed difference schemes for solving the problem without enough smoothness of the extended solution at the initial point if zero extension to the domain $t<0$ is made. Let’s take a multi-term fractional differential equation as example.

Example 5.4

In (3.1)–(3.3), take $T=1, L=\pi , m=2,$ $f(x,t)=\Big [\sum _{r=0}^m \lambda _rt^{1-\alpha _r}E_{1,2-\alpha _r}(t)+\exp (t)\Big ]\sin (x),$ $u_0(x)=\sin (x),$ where $E_{\alpha ,\beta }(z)$ is the Mittag-Leffler function defined by

$$\begin{aligned} E_{\alpha ,\beta }(z)=\sum _{k=0}^{\infty }\frac{z^k}{\Gamma {(\alpha k+\beta )}}. \end{aligned}$$

The analytical solution of this example is given by $u(x,t)=\exp (t)\sin (x).$

Noticing $\lim _{t\rightarrow 0+}\frac{\partial ^k u}{\partial t^k}(x,t)\not \equiv 0, k=0,1,2,\ldots \ ,$ the analytical solution can not be continuously zero extended to the domain with $t<0,$ hence, the direct application of the weighted and shifted Grünwald–Letnikov approximation in [12, 34] can not produce the ideal computational results to approximate the multi-term time-fractional derivatives in (3.1). With the help of the close relationship between the Caputo fractional derivative and Riemann–Liouville fractional derivative [2]

$$\begin{aligned} {}_0^CD_t^{\alpha }f(t)={}_0^{RL}D_t^{\alpha }[f(t)-f(0)], \quad 0<\alpha <1, \end{aligned}$$

we can transform Eq. (3.1) into the equivalent form in the Riemann–Liouville sense as

$$\begin{aligned} \sum _{r=0}^m\lambda _r \; {}_0^{RL}D_t^{\alpha _r}[u(x,t)-u(x,0)]=u_{xx}(x,t)+f(x,t),\quad 0<x<L,\ 0<t\leqslant T, \end{aligned}$$

(5.1)

where the $\alpha$-th order Riemann–Liouville fractional derivative ${}_0^{RL}D_t^{\alpha }f(t)$ is defined by

$$\begin{aligned} {}_0^{RL}D_t^{\alpha }f(t)=\frac{1}{\Gamma (1-\alpha )}\frac{{\mathrm {d}}}{{\mathrm {d}}t}\int _0^t(t-s)^{-\alpha }f(s){\mathrm {d}}s,\quad 0<\alpha <1. \end{aligned}$$

With the weighted and shifted Grünwald–Letnikov (WSGL) approximation proposed in [12, 34] for time Riemann–Liouville fractional derivatives in (5.1) and the second-order approximation for the spatial derivative, we can construct a difference scheme for solving (3.1)–(3.3) as follows:

$$\begin{aligned}&\sum _{r=0}^m\lambda _r\ \tau ^{-\alpha _r} \sum _{k=0}^{n}w_k^{(\alpha _r)}(u_i^{n-k}-u_i^0)=\delta _x^2u_i^n+f_i^n, \quad 1\leqslant i\leqslant M-1, 1\leqslant n\leqslant N, \end{aligned}$$

(5.2)

$$\begin{aligned}&u_0^n=0, \quad u_M^n=0,\quad 0\leqslant n\leqslant N,\end{aligned}$$

(5.3)

$$\begin{aligned}&u_i^0=u_0(x_i),\quad 1\leqslant i\leqslant M-1, \end{aligned}$$

(5.4)

with

$$\begin{aligned} w_0^{(\alpha _r)}=\big (1+\frac{\alpha _r}{2}\big )g_0^{(\alpha _r)}, \quad w_k^{(\alpha _r)}=\big (1+\frac{\alpha _r}{2}\big )g_k^{(\alpha _r)}-\frac{\alpha _r}{2}g_{k-1}^{(\alpha _r)}, \ k\geqslant 1 \end{aligned}$$

and

$$\begin{aligned} g_0^{(\alpha _r)}=1, \quad g_k^{(\alpha _r)}=\Big (1-\frac{\alpha _r+1}{k}\Big )g_{k-1}^{(\alpha _r)},\ k\geqslant 1. \end{aligned}$$

Table 7 displays the computational results when the above difference scheme (5.2)–(5.4) is used to solve this example. Only the case with $(\lambda _0, \lambda _1, \lambda _2)=(3,2,1)$ and $(\alpha _0,\alpha _1,\alpha _2)=(2/3,1/2,1/3)$ is shown for simplicity. From this table, one can find that only the first order convergence of this scheme in time is exhibited even for this example with the smooth solution. Motivated by the idea of fractional linear multistep methods (FLMMs) [5, 42], some correction terms can be added into the scheme to take into account the asymptotic behavior of the function u(x, t) near the origin $t=0.$ In view of the form of the analytical solution in this example, one correction term can be added to modify the above scheme and get the following improved difference scheme:

$$\begin{aligned}&\sum _{r=0}^m\lambda _r\ \Big [\tau ^{-\alpha _r} \sum _{k=0}^{n}w_k^{(\alpha _r)}(u_i^{n-k}-u_i^0)+w_{n,\alpha _r}(u_i^1-u_i^0)\Big ]=\delta _x^2u_i^n+f_i^n,\nonumber \\& \quad 1\leqslant i\leqslant M-1, 1\leqslant n\leqslant N,\end{aligned}$$

(5.5)

$$\begin{aligned}&u_0^n=0, \quad u_M^n=0,\quad 0\leqslant n\leqslant N,\end{aligned}$$

(5.6)

$$\begin{aligned}&u_i^0=u_0(x_i),\quad 1\leqslant i\leqslant M-1, \end{aligned}$$

(5.7)

where the starting weights $\{w_{n,\alpha _r}\}$ are chosen such that

$$\begin{aligned} {}_0^{RL}D_t^{\alpha _r} t|_{t=t_n}=\tau ^{-\alpha _r}\sum _{k=0}^nw_k^{(\alpha _r)}t_{n-k}+w_{n,\alpha _r}t_1, \quad 1\leqslant n\leqslant N. \end{aligned}$$

Some simple calculations give

$$\begin{aligned} w_{n,\alpha _r}=\tau ^{-\alpha _r}\Big [\frac{n^{1-\alpha _r}}{\Gamma (2-\alpha _r)}-\sum _{k=0}^n kw_{n-k}^{(\alpha _r)}\Big ]. \end{aligned}$$

The second-order convergence of the improved scheme (5.5)–(5.7) in time can be observed from the computational results in Table 7.

Table 7 Numerical errors and convergence orders of the scheme (5.2)–(5.4) and the scheme (5.5)–(5.7) in time with $M=10,000$, $(\alpha _0,\alpha _1,\alpha _2)=(2/3,1/2,1/3)$ and $(\lambda _0, \lambda _1, \lambda _2)=(3,2,1)$ for solving Example 5.4 using the WSGL approximation

The higher accurate interpolation approximation presented in this work will be directly effective for this problem. To illustrate this point, firstly, in Table 8, the computational errors and numerical convergence orders in time are listed, from which, one can find that the difference scheme (3.12)–(3.14) yields the numerical convergence order close to two for solving this non-zero initial value problem.

Table 8 Numerical errors and convergence orders of the difference scheme (3.12)–(3.14) in time for solving Example 5.4 with $M=10,000,$ $(\alpha _0,\alpha _1,\alpha _2)=(2/3,1/2,1/3)$ and $(\lambda _0, \lambda _1, \lambda _2)=(3,2,1)$

Secondly, we aim to measure the numerical accuracy of the difference scheme (3.12)–(3.14) in space for solving this example. Table 9 collects the computational errors and numerical accuracy using this difference scheme. The numerical results from Table 9 are consistent with the expected accuracy $O(h^2)$ for the difference scheme (3.12)–(3.14) in space.

Table 9 Numerical errors and convergence orders of the difference scheme (3.12)–(3.14) in space for solving Example 5.4 with $N=2000,$ $(\alpha _0,\alpha _1,\alpha _2)=(2/3,1/2,1/3)$ and $(\lambda _0, \lambda _1, \lambda _2)=(3,2,1)$

Fig. 1

The convergence orders of the scheme (3.34)–(3.36) obtained for Example 5.5 with $(\alpha _0,\alpha _1,\alpha _2)=(\frac{1}{3}, \frac{1}{4}, \frac{1}{5})$ [left in time; right in space ($h_1=h_2\equiv h$)]

The last example is designed for the 2D problem (3.26)–(3.28) to test the computational efficiency of the corresponding difference scheme.

Example 5.5

In (3.26)–(3.28), take $T=1, L_1=L_2=\pi , m=2,$ $u_0(x,y)=0$ and $f(x,y,t)=\Big [24\sum _{r=0}^m \frac{\lambda _r}{\Gamma {(5-\alpha _r)}}t^{4-\alpha _r}+2t^4\Big ]\sin x\sin y.$

The analytical solution is given by $u(x,y,t)=t^4\sin x\sin y.$

The numerical solutions with $(\alpha _0,\alpha _1,\alpha _2)=(\frac{1}{3}, \frac{1}{4}, \frac{1}{5})$ will be calculated. Figure 1 gives graphs of errors by the scheme (3.34)–(3.36) as a function of the mesh size, where the slopes reflect the convergence orders of the scheme (3.34)–(3.36) in time and in space, respectively. In the left panel, we choose $h_1=h_2=\pi /500$ and the slope is nearly two, which is the numerical convergence order of the scheme (3.34)–(3.36) in time. While in the right panel, the mesh size $\tau =1/2000$ is chosen and the slope is also nearly two, which is in accord with the theoretical convergence order of the scheme (3.34)–(3.36) in space.

To further illustrate the efficiency of the proposed difference scheme (3.34)–(3.36), Fig. 2 shows the surface of solutions at $t=1$ with the mesh step sizes $\tau =1/40, h_1=h_2=\pi /40.$ The good agreement of numerical solutions with the exact solutions can be clearly seen.

Fig. 2

The solution surfaces at $t=1$ with $(\alpha _0,\alpha _1,\alpha _2)=(\frac{1}{3}, \frac{1}{4}, \frac{1}{5})$ and $\tau =1/40, h_1=h_2=\pi /40$ [left the exact solution; right the numerical solution by the scheme (3.34)–(3.36)]

6 Conclusion

A special point of interpolation approximation to a linear combination of multi-term Caputo fractional derivatives of order $\alpha _r$ ($0<\alpha _r\leqslant 1$) is given by finding the root of an equation, which is one of the major contributions of the present work since the derived numerical differentiation formula can achieve over second-order accuracy to approximate the value of the multi-term Caputo fractional derivatives at this point. The strict error analysis of the differentiation formula is given by Theorem 2.1. Compared with the previous related works, where the L1 approximation or the WSGL approximation was used to discretize each term of multi-term Caputo fractional derivatives at $t=t_n$ [40], the higher accurate interpolation approximation developed in the present work is more meaningful because of the higher-order numerical accuracy than the L1 approximation and no extra requirements on the extension of the solutions to the domain outside the computational domain or some correction works even for the smooth problems like that using WSGL approximation. Then some effective difference schemes for solving the time multi-term fractional sub-diffusion equation and the time distributed-order sub-diffusion equation, respectively, are developed along with the investigation on the solvability, stability and convergence analysis. Numerical experiments verify the efficiency of the proposed difference schemes. We can easily obtain the spatial fourth order difference schemes for the time multi-term fractional sub-diffusion equation and the time distributed-order sub-diffusion equation.

In the future work, the higher accurate interpolation approximation to a linear combination of multi-term Caputo fractional derivatives of order $\alpha _r$ ($1<\alpha _r\leqslant 2$) will be taken into account.