1 Introduction

Many mesh generation and a posteriori adaptation strategies for the finite element method (FEM) are motivated by the reduction of interpolation errors over the mesh elements to be generated or refined. For linear finite elements, there is a long tradition of both a priori and a posteriori error estimates that aid the FEM practitioner. However, when one moves to (straight-sided) high-order FEM, there are fewer estimates available. Finally, when one considers curvilinear high-order elements with curved sides and faces, which are crucial in correctly aligning the mesh with an underlying geometry, results are even more sparse.

Curvilinear elements are obtained through the use of a geometric mapping from a reference element to the desired element in physical Cartesian space (i.e., world-space). The mapping is typically defined in an isoparametric or subparametric manner using a subset of the same polynomial basis functions that are used to represent the approximated solutions. However, in using this approach, an issue that has always bothered FEM practitioners is the question of how the choice of the geometric mapping functions impacts on the approximation properties of those elements in world-space, i.e., in the natural coordinate system of interest. Botti [1] was among the first to quantify the impact of polynomial mapping functions on the quality of the solution—providing a proof on the order of convergence in an integral norm of an FEM projection operator for quadrilateral elements as a function of elemental polynomial (enrichment) order p and mapping polynomial order q.

Many of the contemporary results for bounding the error in finite element interpolation, including [1], have been derived from the Bramble-Hilbert lemma [2]. In their paper, Bramble and Hilbert explicitly mention that this lemma can replace the “standard” Taylor series technique. This approach, however, does not naturally translate to an understanding of a “good” high-order finite element from the perspective of interpolation error, owing to the lack of a constructive proof. This aspect was addressed by Dupont and Scott [3], who were able to provide a constructive proof of the lemma using a Taylor series expansion. Arnold et al. [4] proved error bounds for straight-sided quadrilateral finite elements by extending the Bramble-Hilbert lemma. Dekel and Lavitan [5], however, argued that the main drawback of their proof is that the constant associated with the order of convergence depends on a “chunkiness parameter”, which blows up as a triangle becomes very thin. In order to accommodate this drawback, a quasi-uniform mesh is assumed in which the parameter is uniformly bounded. Dekel and Leviatan [5] provided a constructive proof for the lemma that showed that the interpolated polynomial in a star-shaped domain obeys the bounds for a straight-sided finite element.

A key drawback of approaches based on the Bramble-Hilbert lemma, in our view, is that these results lead to bounds that are defined in an integral manner and therefore do not offer much insight into how the geometric mapping can be changed in order to reduce the interpolation error. We note that from a practical perspective, the mapping relies on a distribution of points in the reference and Cartesian elements, alongside a set of Lagrange interpolants. Although there is a rich body of literature relating to the effects of the distribution of points in the reference element, the placement of the points in the Cartesian element and how this pertains to the interpolation error are far less well-understood.

In earlier work [6], we highlighted how a first-principles approach, using a Taylor series expansion of the function to be interpolated, leads to a pointwise bound on the interpolation error for second-order straight-sided triangular elements. This bound, at a point in the high-order element, is proportional to the sum of the product of its distance from a high-order node of the triangle with the value of the corresponding shape function. This node-based approach gives FEM and adaptive mesh refinement (AMR) practitioners a method through which nodes can be moved and placed optimally in order to reduce the interpolation error of a given function.

In this paper, we show how this approach can be extended to derive interpolation error bounds that are applicable for any valid (i.e., non self-intersecting) finite element mesh at a polynomial order p and mapping order q. In particular, we highlight that the bound is again dependent on the position of the mesh nodes, and thus our work provides a tighter bound than Lebesgue function-based bounds, but with an assumption on the bounds on high-order derivatives of the function we interpolate. This paper can be viewed as an extension of [5] in the context of the high-order, curved finite elements and as an extension of [1] with constructive proofs for an interpolation version of the theorems stated in their paper. We also consider triangular elements due to their nearly ubiquitous nature in the FEM, as opposed to the quadrilaterals investigated in [1].

As we prove our results from first principles using the Taylor series, it becomes possible to define the quality of a high-order, curved element and to optimally place nodes within a triangle to minimize the error bounds. This approach also enables us to analyze the effect of anisotropy on the error bounds. The proofs presented in this paper are considerably simpler than Bramble-Hilbert lemma-based proofs in earlier work in that they do not require extensive knowledge of functional analysis. We believe that the biggest impact of this paper will be in AMR for engineering applications in which high-order meshes are used.

We conclude with a brief overview of the structure of this paper. In Sect. 2, we reproduce the result of [1] in terms of the order of convergence of solutions under h-refinement, but under the \(L^\infty \) norm instead of the \(L^2\) norm. We then outline the bounds in terms for both the interpolation of a function and its derivatives. In Sect. 3, we present a number of numerical experiments to validate the order of convergence for triangular elements, and examine the tightness of the bounds in the context of anisotropic mesh refinement. Since the research and application of high-order FEM are still relatively nascent, the scope for future research in this field is large. We will indicate future research directions in Sect. 4, including the study of conditioning of stiffness matrices, node placement, and error estimation techniques for high-order polynomial interpolation.

2 Interpolation Error Bound

In this section, we derive error bounds for the piecewise interpolation error of p-th order triangular elements with a q-th order reference-to-physical space mapping for a function and its derivative. The proofs for the error bounds closely follow the techniques employed by Johnson [7] and our previous paper [6].

2.1 Overview

We begin by providing a brief mathematical framework of the interpolation problem. Let \(K^e\) denote a triangular element belonging to the conformal mesh of a domain \(\varOmega \subset \mathbb {R}^2\), so that \(\varOmega = \bigcup _e K^e\) and \(K^e \cap K^f = \emptyset \) if \(e\ne f\). This mesh is then combined with an appropriate high-order polynomial expansion on each element, so that discrete solutions of a given PDE will belong to the space

$$\begin{aligned} \mathcal {D}^p(\varOmega ) = \{ v\in L^2(\varOmega ) \ |\ v|_{K^e}\in \mathbb {P}^p(K^e) \}, \end{aligned}$$

where \(L^2(\varOmega )\) denotes the space of square integrable functions on \(\varOmega \) and

$$\begin{aligned} \mathbb {P}^p(K^e) = \mathrm {span} \left\{ x_1^i x_2^j\ |\ (x_1,x_2) \in K^e,\ 0\le i\le p,\ 0\le i+j \le p \right\} \end{aligned}$$

is the polynomial space of total degree p on \(K^e\), which is spanned by \(N(p) = \tfrac{1}{2}(p+1)(p+2)\) basis functions.

This paper focuses on a key part of both the numerical solution of a PDE and applications in AMR: the polynomial interpolation of a known function \(u:\varOmega \rightarrow \mathbb {R}\) to obtain a discrete approximation \(u_h \in \mathcal {D}^p(\varOmega )\). This process can be viewed as the application of a projection \(\pi \) so that \(u_h = \pi u\), and can be defined in a number of ways depending on the desired outcome: for example in [1], \(\pi \) is an \(L^2\) projection. Here however, in order to provide constructive proofs, we consider \(\pi \) to be the result of a \(L^\infty \) interpolation operator, which we will define in the following section with the aide of a reference element. The intent of this work is to obtain convergence properties and bounds on the pointwise interpolation error \(\Vert u-u_h\Vert _{L^\infty }\) by assuming sufficient regularity of u so as to apply Taylor’s theorem. To this end, we therefore consider functions \(u\in C_b^k(\varOmega )\) that are bounded and k-times continuously differentiable for sufficiently large k, so that \(\pi : C_b^k(\varOmega )\rightarrow \mathcal {D}^p(\varOmega )\).

2.2 Reference-to-World Mapping

In order to facilitate the definition of a basis spanning \(\mathcal {D}^p(K^e)\) on each element, we consider a reference triangle

$$\begin{aligned} K = \{ (\xi _1,\xi _2)\ |\ \xi _i\in [-1,1], \xi _1+\xi _2\le 0 \} \end{aligned}$$

and define a basis on K. To assist in the definition of \(\pi \), we consider the commonly-used basis of total degree p Lagrange interpolants \(\lambda _k(\xi )\), so that a function \(f:K\rightarrow \mathbb {R}\) with \(f\in \mathcal {D}^p(K)\) can be written as

$$\begin{aligned} f(\xi ) = \sum _{k=1}^{N(p)} \hat{f}_k \lambda _k(\xi ), \end{aligned}$$

where \(\{ \hat{\xi }_i \}_{i=1}^{N(p)} \subset K\) denotes a distribution of solvent points within the reference element and \(\lambda _i(\hat{\xi }_j) = \delta _{ij}\), where \(\delta _{ij}\) is the Kronecker delta. In this setting, the interpolation operator \(\pi \) can then be viewed as the mapping such that, for an arbitrary function \(v:\varOmega \rightarrow \mathbb {R}\), \(\pi v\) is the unique polynomial such that \(\pi v(\hat{\xi }_k) = v(\hat{\xi }_k)\) for each k and

$$\begin{aligned} \pi v(\xi ) = \sum _{k=1}^{N(p)} v(\hat{\xi }_k) \lambda _k(\xi ). \end{aligned}$$
(1)

To translate this basis on K to a basis on any given element \(K^e\), we require the definition of a diffeomorphism \(\chi ^e:K\rightarrow K^e\) between the reference and physical space element to define a basis over the world-space element that involves polynomials in the reference space. An important aspect of this high-order finite element setting is that each element \(K^e\) is generally assumed to be curvilinear. This allows, for example, the mesh elements that touch the domain boundary to be curved so that the mesh accurately represents the underlying geometry. This is particularly important in the context of, for example, fluid dynamics problems. Here, an accurate representation of the geometry is critical in the accurate prediction of important flow features such as separation and recirculation, which define key aspects of the fluid’s behaviour.

To define the reference-to-physical space mapping and to enable the use of curved elements, we typically choose to employ the use of mappings that draw from a subset of the basis functions defined on K. That is, we suppose that \(\chi ^e = (\chi ^e_1,\chi ^e_2)\in [\mathbb {P}^q(K)]^2\) for some polynomial order \(q \le p\), where if \(q=p\) the mapping is referred to as isoparametric, if \(q<p\) it is subparametric and if \(q>p\) it is superparametric. Each coordinate of a given point \(x =(x_1,x_2) \in K^e\) can be expressed as a function of the mapping from a point \(\xi \in K\), which in turn is written as a polynomial

$$\begin{aligned} x_k = \chi ^e_k(\xi ) = \sum _{i,j=0}^{i+j\le q} \alpha _{ij,k} \xi _1^i\xi _2^j, \end{aligned}$$
(2)

where \(\alpha _{ij,k}\) are constants depending on the element \(K^e\). Hereafter, \(x\in \varOmega \) will denote coordinates in the physical Cartesian space and \(\xi \in K\) in the reference triangle.

Fig. 1
figure 1

Notation showing reference-to-world mappings \(\chi ^e\) from the reference element K to a physical element \(K^e\), where the nodes correspond to an order of \(p=3\). The distributions of nodal coordinates are denoted by \(\hat{\xi }_k\in K\) and \(\hat{x}_k\in K^e\)

Full size image

Since we consider Lagrange interpolants as our particular basis on K, another way to define this mapping explicitly is through the definition of nodal points \(\{ \hat{x}_k = ((\hat{x}_k)_1, (\hat{x}_k)_2) \}_{k=1}^{N(q)}\subset K^e\) on each element. This then yields

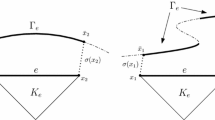
$$\begin{aligned} x_k = \chi ^e_k(\xi ) = \sum _{i=1}^{N(q)} (\hat{x}_i)_k \lambda _i(\xi ) \end{aligned}$$

so that under this mapping, the reference points \(\hat{\xi }_k\) map onto the physical elemental nodes \(\hat{x}_k\). Figure 1 shows a visual representation of this setting. Throughout this paper we make the assumption followed in [8], that \(\chi ^e\) has a positive Jacobian determinant for every \(\xi \in K\) for every element \(K^e\) in the mesh, and its inverse is smooth.

Finally, we note in particular that the distributions of nodes \(\hat{\xi }_k\) in relation to their interpolation properties on K is a very well-studied topic, as described in e.g. [8]. Generally, the goal of such points is to minimise the Lebesgue constant of \(\pi \), leading to distributions such as those proposed by Hesthaven [9]. However, the effect of the distribution of \(\hat{x}_k\) on the interpolation operator is far less well-understood in the context of curvilinear elements. This is the key aim of this paper and the results of the following two sections.

2.3 Convergence Order

Our first goal is to determine the order of the interpolation error \(\Vert u-\pi u\Vert _{L^\infty }\) in terms of the element size h; that is, we wish to determine the integer k such that \(\Vert u-\pi u\Vert _{L^\infty }\le ~C|h^k|\) for some constant C. This then determines the order of convergence under h-refinement (reduction of element size). For straight sided elements, it is a standard result that \(k=p+1\). However when a reference-to-physical space mapping of order q is introduced, Botti [1] determined that \(k=\lfloor {p/q}\rfloor +1\) in the \(L^2\) norm through the use of the Bramble-Hilbert lemma. In this section, we highlight how the same result under the \(L^\infty \) norm can be recovered in a first-principles setting, under the assumption of sufficient regularity of u.

Theorem 1

The interpolation error \(\Vert u-\pi u\Vert _{L^\infty }\) is of order \(k = \lfloor p/q\rfloor +1\), so that \(\Vert u-\pi u\Vert _{L^\infty }\le C|h^k|\) for a constant C.

Proof

We begin with a Taylor series expansion of the true solution u in world-space around an arbitrary world-space point \(x^*\in K^e\) where the size of \(K^e\) is bounded by h [7]. In a standard Taylor expansion, this is represented in terms of a power series

$$\begin{aligned} \sum _{0\le |\alpha |\le p} \frac{(x-x^*)^\alpha }{\alpha !}\partial ^\alpha u(x^*) + D_{p+1}(\zeta ), \end{aligned}$$

where \(\alpha \) is a 2-tuple multi-index and D is a remainder term of polynomial order \(p+1\) depending on a point \(\zeta \) lying on the line segment between x and \(x^*\). However, for the coming analysis, since we have explicit expressions for \(x_1\) and \(x_2\) in terms of \(\xi _1\) and \(\xi _2\) through the mapping \(\chi ^e\), consider a rearrangement of this series in terms of monomials, so that

$$\begin{aligned} u(x) = \sum _{i,j=0}^{i+j\le p} a_{ij} x_1^i x_2^j + D_{p+1}(\zeta ). \end{aligned}$$
(3)

In this form, \(a_{ij}\) are summations of constants which depend on \(x^*\) and the partial derivatives of u up to order \(i+j\) evaluated at \(x^*\).

Before proceeding further, to help clarify the coming argument, we first outline the relationship between the true solution u and its representation in world-space \(K^e\) and reference-space K. Recall that these spaces are related through the polynomial mapping \(\chi ^e:K\rightarrow K^e\). The true solution u can therefore either be viewed as a function in the world-space element \(K^e\), or alternatively in the reference element K through the mapping \(v := u \circ \chi ^e\). However, we note that since \((\chi ^e)^{-1}\) is not necessarily polynomial, the interpolation operator \(\pi u\) (with respect to x) is a smooth, but not necessary polynomial, function. Hence when we interpolate in world space we are not forming an interpolating polynomial (in world space) but an interpolating function. We therefore opt to consider u in its mapped coordinate v, under which the interpolation \(\pi v\) is a polynomial function, and leverage the fact that \(\Vert u-\pi u \Vert _{L^\infty } = \Vert v-\pi v\Vert _{L^\infty }\).

To achieve this, we apply the mapping (2) to Eq. (3) to obtain the expression

$$\begin{aligned} v(\xi ) = \sum _{i,j=0}^{i+j\le p} \left( a_{ij} \left[ \sum _{k,l=0}^{k+l\le q} \alpha _{kl,1} \xi _1^k\xi _2^l \right] ^i \left[ \sum _{k,l=0}^{k+l\le q} \alpha _{kl,2} \xi _1^k\xi _2^l \right] ^j \right) + D_{p+1}(\zeta ), \end{aligned}$$
(4)

which allows us to “view” the function u(x) as defined in Eq. (3) on the reference element, which we denote by \(v(\xi )\).

Now let \(\pi v\) denote the polynomial interpolant of v, which we note is a polynomial of total degree p in \(\xi \). In this case, \(\pi v\) is a summation of monomials \(\xi _1^i\xi _2^j\) such that \(i+j\le p\). We note from Eq. (4) that under the application of \(\chi ^e\), the interpolation error \(v(\xi )-\pi v(\xi )\) now contains monomials up to order pq, which is greater than the remainder term of order \(p+1\) for all \(q>1\). We therefore determine the order of convergence as the minimum value of \(i+j\) such that monomials inside the inner summations are of order less than or equal to \(p+1\), since these are the only values that can be supported under the expansion of total degree p.

Finally then, we consider the maximum value of each inner summation where \(k+l=q\). This choice of k and l for a given p and q have corresponding leading-order monomials \(\xi _1^{ik}\xi _2^{il}\xi _1^{jk}\xi _2^{jl}\) of total degree \(q(i+j)\). The convergence order is therefore given by the minimum integer \(n = i+j\) such that \(qn \ge p+1\), which is clearly given by \(n = \lfloor p/q \rfloor +1\). \(\square \)

2.4 Bounds on Interpolation Error

We now consider the effects of the projection operator and its impact on the interpolation error. Considering an expansion in terms of Lagrange interpolants from Eq. (1), we aim to construct an expression of \(v(\hat{\xi }_k)\) which includes the mapping terms so that an explicit bound can be constructed on \(\pi v(\xi )\). One such representation would be given by substituting \(\hat{\xi }_k\) into Eq. (4); however this would then yield a monomial expansion in terms of \(\hat{\xi }_k\) which is difficult to manipulate. Instead, we start by examining a slightly different Taylor expansion than the one utilised for u(x) in Eq. (3). Namely, we consider the expansion evaluated at a world-space nodal position \(x_k = \chi ^e(\hat{\xi }_k)\) around a general position \(x\in K^e\), giving

$$\begin{aligned} u(x_k) = u(x) + \sum _{i,j=1}^{i+j\le p} \tilde{a}_{ij}x_1^ix_2^j + D_{p+1}(\tilde{\zeta }). \end{aligned}$$

In the above expression, we have used a similar technique as before to amalgamate terms involving \(x_k\) into the constants \(\tilde{a}_{ij}\), which we note are different from the \(a_{ij}\) terms in Eq. (3). Additionally, \(\tilde{\zeta }\) is a point on the line segment connecting x and \(x_k\). The mapping function can then be substituted into the above expression, yielding

$$\begin{aligned} v(\hat{\xi }_k) = v(\xi ) + \left( \sum _{i,j=1}^{0<(i+j)\le pq} b_{ij,k}\xi _1^i\xi _2^j\right) + D_{p+1}(\tilde{\zeta }), \end{aligned}$$

where, as before, v denotes the composition of u and the inverse mapping \((\chi ^e)^{-1}\). By substituting the above into the polynomial expansion of Eq. (1) we obtain

$$\begin{aligned} \pi v(\xi ) = \sum _{k=1}^{N(p)} \lambda _k(\xi )\left[ v(\xi ) + \left( \sum _{i,j=1}^{0<(i+j)\le pq} b_{ij,k} \xi _1^i\xi _2^j\right) + D_{p+1}(\tilde{\zeta })\right] . \end{aligned}$$
(5)

As has been shown for linear interpolation over a triangle [7] and for quadratic interpolation over a triangle [6], we will show that the following lemma holds true for shape functions associated with polynomial interpolation of a solution over a triangle so as to reduce the equation above.

Lemma 1

$$\begin{aligned} \sum _{k=1}^{N(p)} \lambda _k(\xi )= & {} 1 \end{aligned}$$
(6)
$$\begin{aligned} \sum _{k=1}^{N(p)} \lambda _k(\xi )\left( \sum _{i,j=1}^{0<(i+j)\le p} b_{ij,k}\xi _1^i\xi _2^j\right)= & {} 0. \end{aligned}$$
(7)

Note that the summation terminates when \((i+j) = p\), not when \((i+j) = pq\).

Proof

Just as it has been obtained by Johnson [7] and in our previous paper [6], the proof of the lemma is obtained by constructing appropriate polynomial functions w for every point in the domain K. To show Eq. (6), let \(w(\xi ) = c\) be a constant function. Then clearly \(w = \pi w\), giving \(c = \pi w(\xi ) = \sum _i\lambda _i(\xi ) w(\xi ) = c\sum _i\lambda _i(\xi )\) and \(\sum _i \lambda _i(\xi ) = 1\). To show Eq. (7) for known values of partial derivatives (up to p-th order) of a function at a given point, a p-th order polynomial function w can be constructed such that the polynomial’s value and partial derivatives are identical to the original function. Moreover, this is exactly evaluated by the interpolation technique. Since we can construct these functions at any point, for every point in the domain, Eq. (7) holds. \(\square \)

By substituting the lemma above into Eq. (5) and rearranging the terms, we obtain

$$\begin{aligned} \pi v(\xi )-v(\xi ) = \sum _{k=1}^{N(p)} \lambda _k(\xi )\left( \sum _{(i,j)}^{(i+j)>p} b_{ij,k} \xi _1^i\xi _2^j + D_{p+1}(\tilde{\zeta })\right) . \end{aligned}$$

This again highlights that the error is bounded by coefficients of \(\xi _i\xi _j\), where \(i+j>p\). Furthermore, since we assume that v has sufficient regularity, we may take an explicit form of \(D_{p+1}\) so as to obtain a bound on the interpolation error as in [6], which leads to the following theorem:

Theorem 2

The interpolation error \(|u(x)-\pi u(x)|\) over \(K^e\) obeys the inequality

$$\begin{aligned} | u(x)-\pi u(x) | \le \frac{c}{(p+1)!}\sum _{i=1}^{N(p)} |\lambda ^e_i(x)| \Vert x-\hat{x}_i\Vert _2^{p+1} \end{aligned}$$
(8)

where c is the upper bound on the \((p+1)\)-th derivative of u, \(\Vert \cdot \Vert _2\) is the Euclidean norm on \(\mathbb {R}^2\) and \(\lambda ^e_i = \lambda _i\circ (\chi ^e)^{-1}\).

Note that in the above statement, there is no explicit appearance of the mapping order q. Upon first glance therefore, it might be inferred that the interpolation error scales at order \(p+1\) based on the term \(\Vert x-\hat{x}_i\Vert _2^{p+1}\), which lies in contradiction of Theorem 1. However, we note that q does appear implictly and nontrivially in the definition of the shape functions \(\lambda _i^e\), since these are defined using the reference-to-world mapping \(\chi ^e\). We will further investigate the validility and tightness of this bound numerically in Sect. 3.2.

3 Numerical Experiments

In this section, we perform a number of numerical experiments to validate the theory of the previous section. In Sect. 3.1, we consider a series of convergence tests on uniformly-refined grids of geometric orders up to \(q=6\) and validate the order of convergence as \(\lfloor p/q \rfloor + 1\), as proven in Theorem 1. In Sect. 3.2, we examine the error bound on the interpolation error and investigate the tightness of the bound derived in Theorem 2 in the context of anisotropic grids.

3.1 Validation of Convergence Order

In this section, we provide a validation of the convergence order result proven in Theorem 1 and in [1]. In these tests, we consider the interpolation of the smooth function \(u(x) = \sin (\pi x)\sin (\pi y)\) onto a polynomial space of degree six. For geometry orders \(1\le q\le 6\), we then construct a series of h-refined triangular meshes and examine the order of convergence for each refinement respectively, comparing it to the theoretical result. Our methodology is therefore a significant expansion from the results presented in [1], given that the domain adopts triangular elements as opposed to quadrilaterals, and we observe the theoretical results across a broader range of geometry orders than the quadratic orders considered in [1].

Fig. 2
figure 2

High-order structured mesh using \(N=5\) subdivisions at geometry order \(q=3\). The original, straight-sided mesh is shown on the left. On the right we see the resulting curvilinear mesh once the perturbation process is applied, which is used for convergence testing. Colouring of the curved mesh denotes the magnitude of the scaled Jacobian of \(\nabla \chi ^e\) for each element (Color figure online)

Full size image

The starting point for this series of tests is a square domain \(\varOmega \) with corners at \((x,y) = (1,1)\) and (3, 3) respectively. We generate a series of structured, straight-sided triangular meshes of equal size through the subdivision of each side of \(\varOmega \) into N equally-sized segments, so that the element size \(h=2/N\), as shown in the left hand image of Fig. 2. We consider subdivisions in the range \(10^0\le N\le 10^2\) so that the coarsest mesh consists of two triangles and the finest of \(2\times 10^4\) triangles. To generate meshes at each geometry order q, we first generate a straight-sided high-order mesh so that each edge of the triangle consists of \(q+1\) points lying on a line segment. The \(q-1\) edge-interior nodes of each triangle are then shifted by a small, random amount in the edge-normal direction. This is done in an alternating fashion, so that neighbouring edge nodes use both the interior-facing and exterior-facing normal directions. This process then guarantees the mesh is of the desired order q. The interior nodes locations are then calculated through a standard Gordon-Hall blending, and the perturbation is reduced appropriately at higher orders so as to ensure that every mesh is valid. An example of these high-order meshes can be seen in the right-hand image of Fig. 2, which shows an \(N=5\) subdivided mesh at geometry order \(q=3\). This figure also shows the validity and randomised nature of the mesh by visualising the scaled Jacobian

$$\begin{aligned} J_s^e = \frac{\min _{\xi \in K}\left\{ \det \nabla \chi ^e(\xi )\right\} }{\max _{\xi \in K}\left\{ \det \nabla \chi ^e(\xi )\right\} } \end{aligned}$$

associated with each element \(K^e\), with reference-to-physical space map \(\chi ^e\). In particular \(J_s^e\) is positive across the mesh, so that every element is valid.

Fig. 3
figure 3

Interpolation error \(\Vert u-\pi u \Vert _{L^\infty }\) for the function \(u(x_1,x_2) = \sin (\pi x_1)\sin (\pi x_2)\) and its sixth-order polynomial interpolant \(\pi u\) (Color figure online)

Full size image

We use the Nektar++ spectral/hp element framework [10] to perform the polynomial interpolation \(\pi u\) at an order of \(p=6\) of the function u. This is performed on every mesh generated at different subdivisions N and geometry orders q. Figure 3 shows the interpolation error recorded in each case, where the error is sampled using \(N(20) = 231\) points within each element in order to obtain an accurate representation of the error. We note that this error saturates at a small value of around \(10^{-13}\), as seen in the results of \(q=1\) and \(q=2\), past which further h-refinement does not lead to reduction in the error.

The results show a clear trend in a reduction of convergence order as q is increased in a ‘fan’ of error curves, in line with the theoretical results of the previous section. In particular, convergence rates obtained through a simple linear regression are calculated as 1.86, 1.91, 1.89, 3.01, 4.31 and 6.45 for \(q=6\) to \(q=1\) respectively, which align well with the theoretical order of \(\lfloor p/q\rfloor +1\).

From these results we can therefore conclude that the geometry order has a significant impact of the order of convergence for even moderate polynomial orders. For example, using even the smallest amount of curvature (i.e. \(q=2\)) leads to a reduction of convergence order of nearly a factor of two.

3.2 Examination of Error Bounds

In this section, we present results that show the correlation between the derived error bound of Eq. (8) and the actual interpolation error for various smooth functions. To highlight the usefulness of these bounds for adaptive mesh refinement, in which grids tend to be refined in an anisotropic fashion, we adjust our methodology to observe the interpolation error and bound on a sequence of grids that are constructed at various levels of anisotropy.

3.2.1 Generation of Straight-Sided Anisotropic Grids

In order to generate anisotropic meshes that form the starting point of these experiments, we consider a regular straight-sided triangulation of the same square domain \(\varOmega \) with corners at (1, 1) and (3, 3) as in the previous section. We initially consider a grid with \(N=5\) equally-sized elements along each edge of the square, as shown in Fig. 4a. The grid is then deformed into one that is anisotropic (as in Fig. 4b) by transforming each coordinate of the triangular vertices according to a one-dimensional function \(g_f:[1,3]\rightarrow [1,3]\). This is defined analytically as

$$\begin{aligned} g_f(x) = f^{-1}\left[ \tfrac{1}{2}(f(3)-f(1))(x-1)+f(1)\right] , \end{aligned}$$

where \(f:[1,3]\rightarrow \mathbb {R}\) is a smooth, invertible, strictly increasing function that controls the spacing of the elements. Under this definition, the endpoints of the domain are preserved since \(g_f(1) = 1\) and \(g_f(3) = 3\), but the spacing of element edges grows according to f. An example of this process for \(f(x) = x^4\) is shown in Fig. 4. Additionally, it is important to note that \(g_f\) is only applied to the three linear vertices of each triangle and not to the high-order nodes—these are constructed after the mesh is deformed.

Fig. 4
figure 4

Illustration of grid generation process under the deformation map g with \(f(x) = x^4\). Undeformed mesh on the left hand side and deformed grid on the right hand side. High-order nodes are constructed after deformation and are shown at order \(p=5\). a Initial undeformed grid. b Deformed anisotropic grid

Full size image
Table 1 The error bounds and the actual interpolation error over a domain with meshes of varying polynomial order p
Full size table
Table 2 The error bounds and the actual interpolation error over a domain with meshes of varying polynomial order p
Full size table
Table 3 The error bounds and the actual interpolation error over a domain with meshes of varying polynomial order p
Full size table
Table 4 The error bounds and the actual interpolation error over a domain with curved meshes of varying polynomial order p
Full size table
Table 5 The error bounds and the actual interpolation error over a domain with curved meshes of varying polynomial order p
Full size table
Table 6 The error bounds and the actual interpolation error over a domain with curved meshes of varying polynomial order p
Full size table

3.2.2 Methodology

In the experiments that follow, we aim to measure the interpolation error of various smooth functions u(x) at polynomial orders \(p \le 5\), along with the error bounds of Eq. (8) derived in the previous section. The error between u and its resulting interpolant \(\pi u\) is calculated using a 10-th order set of high-order nodes within each element in order to obtain an accurate value of the error. The upper bound on the \((p+1)\)-th derivative of u, represented as c in Eq. (8), is calculated at the same set of points. Finally, in order to assess the asymptotic properties of the tightness of the bound according to the anisotropic nature of the meshes, we report the \(L^\infty \) error and bound in only the smallest element of the mesh.

We consider meshes generated through the choice of \(f(x) = x^n\) for \(1\le n \le 4\) which leads to a series of increasingly anisotropic meshes. Additionally, we consider two non-polynomial mappings \(f(x) = \sin (\pi x/10)\) and \(f(x) = \exp (x)\). For the experiments below, two orders of geometry are considered. We first perform experiments for straight-sided meshes on which \(q=1\), so as to recover the ‘classical’ result that convergence order is dictated by the \((p+1)\)-th order derivatives. We then consider meshes at order \(q=2\), which are constructed in a similar manner to Sect. 3.1 by slightly perturbing the mid point of all the interior edges. This results in a mesh where every element is curved. Since the perturbation is small, the elements remain valid (i.e. the determinant of the Jacobian is greater than 0 at all points inside every element).

3.2.3 Results for \(q=1\)

In Table 1, we compare the error bounds and the interpolation error for the function \(u(x) = \sin (x\pi /10) + \sin (y\pi /10)\) when it is being interpolated on the meshes described above. The results clearly indicate a monotonic relationship between the theoretical interpolation error bound and the actual error. We also verified that the bounds were respected for every point for which the error was sampled. In most cases, for high-order expansions, as the error bounds increase, the interpolation error also increases. For a given \(p-\)order expansion, the ratio (as computed from the columns in the table) of the bound and the error is nearly a constant. We also see that the bounds are “tighter” for the lower-order expansions than they are for higher-order expansions, i.e., the ratio of the error to the bound was close to one for lower-order expansions then the higher-order expansions.

Table 2 provides the results for interpolation of the function \(u(x) = e^x + e^y\). The error is a larger value here because the function values themselves are larger, and they grow faster than the previous function, but the trends are identical. The bounds and error reduce as the order of expansion grows, and the monotonic relationship between them is maintained.

Finally, Table 3 shows the results for the polynomial function \(x^6 + x^5 + x^4 + 4x^3 + x^2 + x + y^6 + y^5 + y^4 + 4y^3 + y^2 + y\). The bounds and the error are much closer to each other because the growth of the function is limited in a polynomial function due to its vanishing seventh derivative. The trend is identical to the previous two cases.

3.2.4 Results for \(q=2\)

We now consider the interpolation of the same functions as in the section above, but at an increased geometric order of \(q=2\). To avoid superparametric mappings where \(q > p\), we consider polynomial orders \(p>1\). The results from the experiments are reported in Tables 4, 5 and 6. The observed results are consistent with those obtained for the linear meshes above, where again the ratios of actual error and the error bounds are nearly constant for a given order p. Consequently, the theoretical error bound and the actual error are asymtotically related. We also see that the bounds are “tighter” for lower-order expansions than for higher-order expansions.

3.2.5 Summary

Our results show that the theoretical error bound and the actual error are asymptotically related, i.e., when the theoretical bounds are large or small, the actual error is also large or small, respectively. The theoretical bounds are functions of the appropriate derivatives of the function being interpolated. Thus, our paper shows that the appropriate derivative ought to be used to estimate the interpolation error and adaptively refine the mesh. The algorithm that should be to used refine the mesh, however, is an entirely different problem. Currently, mesh refinement algorithms tend to use estimates for the Hessian to drive refinement of the mesh as these are reasonably straightforward to compute, as seen in, for example, Ref. [11]. Our results, on the other hand, along with other previous work in this area (such as [6, 12]), highlight that higher-order derivatives should be used to refine the mesh.

4 Conclusion and Future Work

We have provided an alternative derivation from first principles, using a Taylor series expansion, for the interpolation error bounds for curvilinear finite elements. Specifically, we have demonstrated the effect of reference-to physical mapping on the order of convergence of the interpolation error under h-refinement. We characterized and visualized the error bounds for certain types of curved high-order elements. We have shown its implications on adaptive refinement of high-order meshes through carefully designed numerical experiments. Our results indicate that the \((\lfloor p/q\rfloor +1)\)-th order partial derivative should direct adaptation for p-th order finite element meshes for q-th order geometries..

As mentioned in Sects. 1 and 2, node placement in a high-order element is typically dictated by Lebesgue constant minimization. This approach assumes that the properties of the function being interpolated are unknown. In engineering applications, however, partial derivatives can be estimated through sophisticated techniques [13,14,15,16,17]. Thus, minimization of our error bounds is likely to produce an element whose error bounds are smaller. For some applications, such as in solid mechanics, the derivatives of the solution are more important than the solution itself. In such cases, too, minimization of our error bounds is likely to be ideal. Future research efforts should be carried out to determine suitable node placement using our error bounds.

Our bounds can be modified for Hermite finite elements in which even the partial derivatives of the solution of PDEs are computed directly from the FEM. A study of error bounds and their effect on the AMR for such meshes will be interesting for both researchers and engineers. We note that it is relatively difficult to adapt Bramble-Hilbert lemma-based proofs for anisotropic functions and Hermite elements. As the Taylor series proof is based on first principles, and it directly incorporates the use of shape functions, all the objective can be achieved relatively easily for any type of element and function.

Finally, we note that there has been little effort to characterize the conditioning of the stiffness matrix as a function of the (geometric) curvature of a triangle for high-order elements. Several open problems in the area need to addressed for the high-order FEM to be used for engineering applications, and in theory our perspective on the error bounds facilitates this type of study.