1 Introduction

High-order methods of computational fluid dynamics (CFD) are proven useful in many aspects which can achieve low-dissipation results, e.g., the discontinuous Galerkin methods (DG) [1,2,3,4,5,6,7,8]. However, the total numerical error of using a high-order method can be affected by the approximation error of surface geometries, e.g., see reference [7, 8], where using curved elements are shown to be necessary to eliminate the unphysical entropy wake in DG solvers. So curved elements are widely used in the high-order CFD community and considering the curvature of surface elements is the minimum requirement of achieving high-fidelity, high-order accurate simulations, especially on coarse grids. However, for practical applications, such a requirement is usually not met. In most of the cases, only straight-sided meshes are provided while the CAD files are inaccessible, so that mesh curving has to be considered if high-quality solutions are pursued with high-order methods.

In this paper, a 3-D curved mesh generator is prescribed for converting linear elements to quadratic elements, which is required by most high-order methods, especially DG. To recover curvature from the provided linear mesh, cubic Bézier surfaces [9, 10] are reconstructed upon the numerical approximation of nodal normals.

Successive curved mesh refinement is also realized by inquiring the middle nodes of the edges and faces of the reconstructed quadratic elements. The mesh curving and refinement are applied to the DLR-F6 configuration [11].

2 Mesh Curving

In this section, mesh curving strategies are studied based on the cubic Bézier surface reconstruction [9, 10]. A discontinuous Galerkin flow solver with the physical orthogonal basis [1,2,3,4,5,6] is used for assessing the solution quality with approximated curved boundaries. Finally, the mesh curving is applied to the DLR-F6 configuration.

2.1 Cubic Bézier Surface

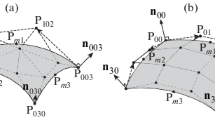
In the first mesh curving strategy, we consider the mesh curving problem under the framework of cubic Bézier surface reconstruction [9, 10]. In most cases, the surface mesh only consists of triangles and/or quadrilaterals. Correspondingly, the cubic Bézier triangle and quadrilateral are used, as illustrated in Fig. 1a, b.

Fig. 1
figure 1

Cubic Bézier surface. (a) Triangle. (b) Quadrilateral

Full size image

Compared with linear elements, extra mid-edge points (such as p m1, p m2, p m3 in Fig. 1a, b) are needed to be computed with the cubic Bézier curves for defining the quadratic elements. In this section, we outline the theory of cubic Bézier Surface firstly. Without loss of generality, considering a n-order of Bézier curve in the form of

$$\displaystyle \begin{aligned} \mathbf{B}(t) = \sum_{i=0}^{n} {\mathbf{b}}_{i,n} (t)\, {\mathbf{P}}_i,\quad t \in [ 0, 1 ], \end{aligned} $$
(1)

where P i is the ith control node of the Bézier curve, B(t) is the resulting parametric curve and term b i,n(t) is called the Bernstein basis polynomials which may be written as

$$\displaystyle \begin{aligned} {\mathbf{b}}_{i,n} (t) = \binom{n}{k} \, t^i \, {(1-t)}^{(n-i)}, \quad i = 1,\dotsc, n \end{aligned} $$
(2)

Note that t 0 = 1, (1 − t)0 = 1 for any t value, and that the binomial coefficient \(\binom {n}{k}\) is defined as

$$\displaystyle \begin{aligned} \binom{n}{k} = \frac{n!}{k!(n-k)!} \end{aligned} $$
(3)

The first and last control nodes coincide with the end points of the edge, so only the two internal control nodes are computed. The derivative of the Bézier curve with a respect to t is actually a tangential vector T:

$$\displaystyle \begin{aligned} \mathbf{T} (t) = {\mathbf{B}}^\prime(t) = n \cdot \sum_{i=0}^{n-1} ({\mathbf{P}}_{i+1}-{\mathbf{P}}_i) \cdot {\mathbf{b}}_{i,n-1} (t) {} \end{aligned} $$
(4)

The cubic Bézier curve with n = 3 is shown in Fig. 1a. This triangle consists of the three corner nodes P 300, P 030, P 003, and the three computed surface normals n 300, n 030, and n 003. To reconstruct the cubic Bézier curve for each edge of the triangle, for instance on the edge P 003 →P 300, the tangential vector is computed as (4) where T(0) and T(1) must be in the same vector direction.

$$\displaystyle \begin{aligned} \begin{aligned} \mathbf{T}(0) = {\mathbf{P}}_{300} - {\mathbf{P}}_{003} - (({\mathbf{P}}_{300} - {\mathbf{P}}_{003}) \cdot {\mathbf{n}}_{030}) \, {\mathbf{n}}_{030} \\ \mathbf{T}(1) = {\mathbf{P}}_{300} - {\mathbf{P}}_{003} - (({\mathbf{P}}_{300} - {\mathbf{P}}_{003}) \cdot {\mathbf{n}}_{300}) \, {\mathbf{n}}_{300} \end{aligned} \end{aligned} $$
(5)

By solving (5), the control nodes are expressed as

$$\displaystyle \begin{aligned} \begin{aligned} & {\mathbf{P}}_{0} = {\mathbf{P}}_{003} \\ & {\mathbf{P}}_{1} = {\mathbf{P}}_{102} = (2 {\mathbf{P}}_{003} + {\mathbf{P}}_{300} - (({\mathbf{P}}_{300} - {\mathbf{P}}_{003}) \cdot {\mathbf{n}}_{030}) \, {\mathbf{n}}_{030})/3 \\ & {\mathbf{P}}_{2} = {\mathbf{P}}_{201} = (2 {\mathbf{P}}_{300} + {\mathbf{P}}_{003} + (({\mathbf{P}}_{300} - {\mathbf{P}}_{003}) \cdot {\mathbf{n}}_{300}) \, {\mathbf{n}}_{300})/3 \\ & {\mathbf{P}}_{3} = {\mathbf{P}}_{300} \end{aligned} \end{aligned} $$
(6)

With the cubic Bézier curve formula (1) defined by (6), the middle node of each edge can be computed by taking t = 0.5. For both six-node triangle and eight-node quadrilateral, not mid-face nodes exist, thus the reconstruction is actually done on edges but not surfaces. The same procedure can be applied to all the edges on the wall surfaces. Finally, the curved elements can be output into a mesh file for high-order solvers.

2.1.1 Calculation of Surface Normals

The cubic Bézier surface is defined by the nodal coordinates and normals, so only the normals are required. The normal n i at the ith node is calculated by the inverse-distance weighting (IDW) [12] of its N surrounding surface normals as in (7), where r j is the distance from the ith node to its jth neighboring surface center.

$$\displaystyle \begin{aligned} \omega_i = \frac {{r_i}^{-2}} {\sum_{j=1}^{N} {r_j}^{-2}}, \qquad \mathbf{{n}}_{i} = \sum_{j=1}^{N} \omega_j \mathbf{{n}}_{j} {} \end{aligned} $$
(7)

IDW satisfies \(\sum _{j=1}^{N} \omega _j =1\) and it is thus linear preserving. And, IDW also produces nonlinear interpolation when the scalar vectors are distributed nonlinearly. One of the greatest advantages of using IDW is that the interpolated normals can be bounded by the maximum and minimum of the data points. Thus, the safety of normal reconstruction is enhanced without introducing any dangerous new extremum.

The normals are then computed for all the wall nodes which are the most significant parts causing the geometric error. At each node, a single normal is computed despite that its surrounding surface cells could be on different patches. When the node is at the intersection of multiple patches, the computed normal is not well defined. The order of mesh curving should be conducted firstly on the symmetric wall, then the solid wall and followed by the far-field boundary surfaces. By doing this the normal singularity can be partially removed. The remaining singular normals probably have bad vector directions which differ greatly to their surrounding computed normals. So the angle α between two end-point normals of an edge is thus can be used as a measure of singularity.

A threshold angle control strategy for avoiding the singularity is tested effective in which the edges with the singular angle α ≥ 30 ∼60° are kept straight and the midpoints are obtained by geometric averages of end-point nodes while all other edges are recovered to curves. While the volume mid-edge nodes are simply obtained by geometric averages of end-point nodes. Note that the entire algorithm is fully automatically without human inventions.

2.1.2 Numerical Tests for the Mesh Curving

In this section, the mesh curving strategies are firstly tested for the numerical solutions of the inviscid Euler equations by a high-order discontinuous Galerkin flow solver [1, 2]. Smooth inviscid flows past a sphere are computed which admits a symmetric flow pattern and a constant entropy across the computational domain in theory, so that the error due to curved mesh approximations can be computed quantitatively.

Both the linear mesh and the curved method are tested, which show that the unphysical wake flow produced by using the linear grids is greatly improved by using the curved mesh, see also [7, 8]. In this test, the fourth-order DG is used for spatial discretization and a fast first-order exponential time integration (EXP1) [4] with CFL = 103 is used for the steady-state time marching. Figure 2 presents the steady-state residual convergences of the linear and curved meshes. It is so obvious that meaningful high-order accurate solutions can be obtained only if the curved mesh is employed, while the convergence of the linear mesh shows stagnation due to the production of unphysical wakes, as shown in Fig. 3. The error is measured quantitatively with the entropy variable which has an exact value for smooth inviscid flows. The entropy error is defined as

$$\displaystyle \begin{aligned} E_{L_2 \left(\varOmega \right)} \left(s\right) := \sqrt{ \frac{1}{|\varOmega|} {\displaystyle \int_\varOmega {\left( \frac{s}{ s_0} \right)}^2 \mathrm{d} {V} - 1 }} {} \end{aligned} $$
(8)

where Ω is the cell element and |Ω| is the cell volume. s := P∕ρ γ is the entropy, P the pressure and ρ the density. s 0 is the exact entropy value of the free stream. In Fig. 2 (left), it is observed that a steady-state convergence cannot be realized with the linear mesh. The entropy error with the linear mesh stagnates at 10−3.42, while the one with the curved mesh converged at 10−5.32, as shown in Fig. 2 (right). So the curve mesh reconstruction does help on reducing the errors induced by the geometry approximations. In Fig. 3 (left), large entropy errors with the linear mesh occur in the wake flow region due to the straight-sided surface approximations and the flow symmetry is broken as shown in the pressure contour of Fig. 4 (left) which is unphysical. In contrast, using the recovered curved mesh indeed gives theoretically consistent results along with the fourth-order discontinuous Galerkin methods, in which the pressure contour is symmetric, as shown in Fig. 4 (right) and the local entropy error \(S_{err}:=P/\rho ^\gamma -P_0/\rho _0^\gamma \) is much smaller than the linear one, see Figs. 3 (left) and 2 (right). This case shows that using the mesh curving method is indeed helpful in reducing the errors produced by the linear surface approximations.

Fig. 2
figure 2

Smooth flow past a sphere: convergence history of the density residuals \(\lg \| R(\rho _n) \|{ }_2\) with the curved mesh (left) and the linear mesh (right). Rapid convergence can be achieved by using the curved mesh while the unphysical wake flow with the linear mesh leads to residual stagnation

Full size image
Fig. 3
figure 3

Smooth flow past a sphere: comparison of entropy error with the curved mesh (left) and the linear mesh (right). The local entropy error \(S_{err}:=P/\rho ^\gamma -P_0/\rho _0^\gamma \). The linear-element approximation of curved surface induces a large entropy wake

Full size image
Fig. 4
figure 4

Smooth flow past a sphere: comparison of pressure contours with the curved mesh (left) and the linear mesh (right). The result of the linear mesh gives a unphysical wake flow pattern

Full size image
Fig. 5
figure 5

DLR-F6 configuration: computed nodal normals; normal (blue), edge (black)

Full size image
Fig. 6
figure 6

DLR-F6 configuration: marking uncurved edges with red spheres

Full size image
Fig. 7
figure 7

DLR-F6 configuration: marking uncurved edges with the red sphere

Full size image
Fig. 8
figure 8

DLR-F6 configuration: successive curved mesh refinements. Number of cells: 1,345,335 (left), 10,791,182 (middle), 86,500,468 (right)

Full size image

Next, the mesh curving strategies are applied to a three-dimensional complex geometry: DLR-F6 configuration. The surface hybrid grids of DLR-F6 has 34,676 nodes, 54,804 linear elements, and 11,150 linear edges. First, nodal normals are computed according to Sect. 2.1.1. In Fig. 5, the computed normals at each node are shown in blue. Then by applying the mesh curving using the Cubic Bézier surface reconstruction with setting α = 60°, 98.6% of 11,150 edges are converted to curves and 161 edges are kept straight. The uncurved, straight edges are marked with red spheres and are shown in Fig. 6. From which we can see that most of the edges are converted to curves except four tiny regions which contain uncurved edges. Zoom-in views of these four regions are shown in Fig. 7, where the straight edges are marked with red spheres and the curved edges are denoted by multiple black nodes. Finally, the curved surface mesh is shown in the left one of Fig. 8, which is also used for curved mesh refinements in Sect. 3.

3 Curved Mesh Refinement

In this section, a curved mesh refinement tool is developed based on the mesh curving developed in Sect. 2. Global mesh refinements are realized by inquiring curved mesh information such as the midpoints of edges and faces. Edge- and face-based arrays are thus created for storing newly generated middle nodes of edges and faces without duplicating the node storage. A convention of elemental node numbering has to be defined to form subcell topologies which can be chosen arbitrarily but must be consistent during mesh refinements. The full procedure mesh refinement algorithm is shown in Algorithm 1 in details.

Algorithm 1 Curved mesh refinement

This quadratic elements refinement process is iteratively called with storing an internal mesh file for each refinement level. Note that only the initialization stage requires the participation of cubic Bézier curves and the refinement levels greater than two use the shape function interpolations for saving computational cost. The resulting quadratic elements approximate the curvature of cubic Bézier surfaces but are immediately compatible with traditional finite element solvers.

In the quadratic elements approximation, the mapping from reference coordinate ( ξ, η ) ∈ [ ( 0, 1 ), ( 0, 1 ) ] to physical coordinate x on a triangle is defined as \({\mathbf {{x}}=\sum \nolimits _{i = 1}^6 {{N}_i \, \mathbf {{x}}_i}\ }\) where ζ = 1 − ξ − η. For a quadrilateral, the reference coordinate is ( ξ, η ) ∈ [ (  − 1, 1 ), (  − 1, 1 ) ] while \({\mathbf {{x}}=\sum \nolimits _{i = 1}^8 {N_i \, \mathbf {{x}}_i}\ }\). The middle points of edges can be computed easily instead of using Bézier curves. The shape functions of the quadratic surface elements are listed in Table 1. In the step 13 of Algorithm 1, the quadratic children cells are computed by computing the mid-edge points using the shape functions of Table 1. In the step 12, according to [13], there are three ways of conducting tetrahedron splitting. Among all the splitting possibilities, we split the tetrahedron with choosing the shortest average edge length of the new children cells.

Table 1 Quadratic surface elements
Full size table

The mesh refinement method is applied to the DLR-F6 configuration used for the mesh curving in Sect. 2.1.2. Two levels of successive mesh refinements are applied. The resulting meshes are shown in Fig. 8 with volume cell number 1,345,335, 10,791,182 and 86,500,468, from left to right. The zoom-in views of the inlet of the nacelle are displayed in Fig. 9, from which we can see that the feature of the high-curvature surface of the inlet is smoothly captured for each level of curved mesh refinement. Because the mesh curving is only conducted on the boundaries, the mesh refinement results in linear volume elements away from the boundaries. It deserves a future study to spread the mesh curving effects from boundaries to the whole computational domain.

Fig. 9
figure 9

DLR-F6 configuration: zoom-in views of the nacelle grids. The high-curvature surfaces are smoothly approximated with the curved mesh refinements

Full size image

4 Conclusion

Mesh curving and refinement algorithms applied to high-order discontinuous Galerkin methods are presented. The mesh curving algorithm uses the cubic Bézier surface/curves reconstruction to recover curvature from the provided linear mesh, thus, can upgrade a linear mesh to a quadratic one. Comparing with other mesh curving techniques [14,15,16], the current strategy is much easier to implement while does not require surface fitting. Moreover, it supports both hybrid element types curving and also global curved mesh refinement. Numerical tests demonstrate that by using curved elements along with the high-order methods, unphysical entropy errors can be significantly reduced. The mesh curving and refinement can be applied to three-dimensional geometries, such as the DLR-F6 configuration, as shown in the paper.

Finally, even if the mesh curving and refinement approaches turned out to be robust, further research is needed to increase the accuracy of the curved surface approximation. Moreover, the feature sharping/feature detection and volume elements curving algorithms need to be further investigated, especially for more complex geometries.