Abstract
We present a second order energy stable numerical scheme for the two and three dimensional Cahn–Hilliard equation, with Fourier pseudo-spectral approximation in space. A convex splitting treatment assures the unique solvability and unconditional energy stability of the scheme. Meanwhile, the implicit treatment of the nonlinear term makes a direct nonlinear solver impractical, due to the global nature of the pseudo-spectral spatial discretization. We propose a homogeneous linear iteration algorithm to overcome this difficulty, in which an \(O(s^2)\) (where s the time step size) artificial diffusion term, a Douglas–Dupont-type regularization, is introduced. As a consequence, the numerical efficiency can be greatly improved, since the highly nonlinear system can be decomposed as an iteration of purely linear solvers, which can be implemented with the help of the FFT in a pseudo-spectral setting. Moreover, a careful nonlinear analysis shows a contraction mapping property of this linear iteration, in the discrete \(\ell ^4\) norm, with discrete Sobolev inequalities applied. Moreover, a bound of numerical solution in \(\ell ^\infty \) norm is also provided at a theoretical level. The efficiency of the linear iteration solver is demonstrated in our numerical experiments. Some numerical simulation results are presented, showing the energy decay rate for the Cahn–Hilliard flow with different values of \(\varepsilon \).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this article we consider an efficient numerical implementation of a second order accurate and energy stable scheme for the Cahn–Hilliard equation. For any \(\phi \in H^1 (\Omega )\), with \(\Omega \subset R^d\) (\(d=2\) or \(d=3\)), the energy functional is given by (see [8] for a detailed derivation):
in which a positive constant \(\varepsilon \) stands for the parameter of the interface width. In turn, the Cahn–Hilliard equation becomes the \(H^{-1}\) conserved gradient flow of the energy functional (1):
with a periodic boundary condition imposed for both the phase field \(\phi \) and the chemical potential \(\mu \). As a result of a simple calculation, the following energy dissipation law is available: \(d_t E (t)=-\int _{\Omega } |\nabla \mu |^2 \,d {\varvec{x}}\le 0\). Furthermore, the equation is mass conservative: \(\int _\Omega \partial _t \phi \, d{\varvec{x}}= 0\).
The numerical approximation to the CH equation has been extensively studied; see the related references [1, 3, 20–23, 25, 26, 29, 37, 40–43, 52], etc. In particular, the energy stability becomes one research focus in recent years, due to its importance to the long time numerical simulation. Among the energy stable numerical approaches, the convex splitting idea, originated by Eyre’s pioneering work [24], has attracted more and more attentions. This approach treats the convex part implicitly and the concave part explicitly; as a result, the unique solvability and unconditional energy stability could be established at a theoretical level. Its extensive applications to a wide class of gradient flows have been available; see the related works for the phase field crystal (PFC) equation and the modified version [4, 5, 39, 49, 50, 53], epitaxial thin film growth models [10, 12, 46, 48], non-local Cahn–Hilliard model [33, 34], the Cahn–Hilliard–Hele–Shaw (CHHS) and related models [11, 14, 15, 28, 51], etc.
Both first and second order (in time) convex splitting approximations have been extensively studied for these gradient flows. In particular, a great advantage of the second order temporal splitting over the standard first order one has been demonstrated by various numerical experiments, in terms of numerical efficiency and accuracy. For the Cahn–Hilliard equation (2), a second order convex splitting scheme has been reported in a recent article [36], based on the modified version of the Crank–Nicholson temporal approximation. This numerical scheme enjoys many advantages over the standard second order temporal approximations [2, 17, 29, 47], in particular in terms of the unconditional energy stability and an unconditionally unique solvability. Also see another recent finite element work [16] for the related analysis.
Meanwhile, it is observed that, for most convex splitting numerical works in the existing literature, a local spatial discretization is used, such as the finite difference or finite element approximation; there has been no reported numerical scheme which combines the convex splitting (in time) for the Cahn–Hilliard-type gradient flow and a spatial approximation with a global nature, such as the spectral or pseudo-spectral method. The key reason for this subtle fact is that, the convex splitting scheme usually treats the nonlinear term implicitly, since the nonlinear part corresponds to the convex part of the Ginzburg–Landau energy functional. In turn, an efficient nonlinear solver is needed for this implicit treatment. Moreover, a well-known fact shows that, highly efficient nonlinear finite difference and finite element solvers have been available, such as nonlinear multi-grid or nonlinear conjugate solvers; the local nature of these spatial discretization has greatly simplified the numerical efforts to develop these solvers. On the other hand, the development of a nonlinear solver with spectral or pseudo-spectral solver turns out to be much more challenging. This makes a convex splitting scheme with spectral/pseudo-spectral spatial approximation very difficult to implement.
In this paper, we propose a linear iteration algorithm to implement the second order convex splitting scheme for the CH equation (2), with a Fourier pseudo-spectral spatial discretization. This algorithm introduces a second order accurate \(O (s^2)\) artificial diffusion term in the form of Douglas–Dupont regularization. And also, the diffusion power may be a fractional number, dependent on the discrete Sobolev embedding from \(H^\alpha \) into \(L^4\). A key point of the linear iteration is that, although the numerical scheme itself is highly nonlinear, we treat the nonlinear term explicitly at each iteration stage. Therefore, the numerical difficulty associated with the nonlinear solver and the global nature of pseudo-spectral approximation is overcome. Moreover, by a careful nonlinear analysis and using a subtle estimate of the functional bound for the nonlinear terms, a contraction mapping property (in a discrete \(\ell ^4\) norm) is theoretically justified if the parameter associated with the artificial diffusion coefficient is greater than a given constant, and this constant will be discussed in detail. In other words, the highly nonlinear numerical scheme can be very efficiently solved by such a linear iteration algorithm, and a geometric convergence rate is assured for this linear iteration under the given constraint. Similar to the linear iteration algorithm reported in [12] for the no-slope-selection epitaxial thin film growth model, the linear operator involved in the scheme, denoted as \({\mathcal {L}}\), is positive definite with constant coefficients, and it can be efficiently inverted at the discrete level by FFT or other existing fast linear solvers.
The leading order energy stability indicates a uniform in time \(H^1\) bound at a discrete level. In addition, we demonstrate a discrete version of an \(\ell ^\infty (0,T;H^2)\) bound of the numerical solution, and this bound is independent of the final time T. Such a bound is based on a discrete \(\ell ^\infty (0,T; H^2) \cap \ell ^2 (0,T; H^4)\) energy estimate for the numerical scheme, with the help of repeated applications of discrete Hölder inequality and Sobolev inequalities in the Fourier pseudo-spectral space. In comparison with a recent work [36], where a similar analysis for the finite difference scheme is performed, the nonlinear analysis and Sobolev inequality are more involved in the pseudo-spectral scheme reported in this article. Moreover, as an application of three-dimensional Sobolev inequality, a uniform in time \(\ell ^\infty \) bound (in the maximum norm) of the numerical solution is derived. Because of this estimate, a cut-off approach for the numerical solution is not needed in our work, compared to a few existing ones [47].
The rest of the manuscript is organized as follows. In Sect. 2 we present the numerical scheme. First we review the Fourier pseudo-spectral approximation in space and recall a second order convex splitting scheme for the Cahn–Hilliard equation (2) with unconditional energy stability and unique solvability, as reported in [16, 36]. Then we propose an \(O (s^2)\) artificial diffusion term in the form of a Douglas–Dupont-type regularization, and a linear iteration algorithm to implement it. We demonstrate that the unconditional energy stability is preserved for such an addition of artificial diffusion. In particular, we prove that the corresponding linear iteration algorithm is assured to be a contraction mapping under a condition for the artificial diffusion constant. Subsequently, the \(\ell ^\infty \) bound of the numerical solution is provided in Sect. 3. In Sect. 4 we present some numerical simulation results. We offer our concluding remarks in Sect. 5.
2 The Numerical Scheme
2.1 Fourier Pseudo-Spectral Approximations
The Fourier pseudo-spectral method, a discrete variable representation (DVR) method, is also referred as the Fourier collocation spectral method. It is closely related to the Fourier spectral method, but complements the basis by an additional pseudo-spectral basis, which allows to represent functions on a quadrature grid. This simplifies the evaluation of certain operators, and can considerably speed up the calculation when using fast algorithms such as the fast Fourier transform (FFT); see the related descriptions in [6, 13, 32, 38].
To simplify the notation in our pseudo-spectral analysis, we assume that the domain is given by \(\Omega = (0,1)^3\), \(N_x = N_y = N_z =: N\in {\mathbb {N}}\) and \(N \cdot h = 1\). We further assume that N is odd:
The analyses for more general cases are a bit more tedious, but can be carried out without essential difficulty. The spatial variables are evaluated on the standard 3D numerical grid \(\Omega _N\), which is defined by grid points \((x_i, y_j, z_k)\), with \(x_i = i h\), \(y_j=jh\), \(z_k = k h\), \(0 \le i , j, k \le 2K +1\). This description for three-dimensional mesh (\(d=3\)) can here and elsewhere be trivially modified for the two-dimensional case (\(d=2\)).
We define the grid function space
Given any periodic grid functions \(f,g\in {\mathcal {G}}_N\), the \(\ell ^2\) inner product and norm are defined as
The zero-mean grid function subspace is denoted \(\mathring{{\mathcal {G}}}_N := \left\{ f\in {\mathcal {G}}_N \; \big | \; \langle f, 1\rangle =: \overline{f} = 0\right\} \). For \(f\in {\mathcal {G}}_N\), we have the discrete Fourier expansion
where
are the discrete Fourier coefficients. The collocation Fourier spectral first and second order derivatives of f are defined as
The differentiation operators in the y and z directions, \(\mathcal{D}_y\), \(\mathcal{D}_y^2\), \(\mathcal{D}_z\) and \(\mathcal{D}_z^2\) can be defined in the same fashion. In turn, the discrete Laplacian, gradient and divergence operators are given by
at the point-wise level. It is straightforward to verify that
See the derivations in the related references [6, 9, 30], et cetera.
In addition, we introduce the discrete fractional operator \((-\Delta _N)^\gamma \), for any \(\gamma >0\), via the formula
for a grid function f with the discrete Fourier expansion as (5). Similarly, for a grid function f of (discrete) mean zero—i.e., \(f\in \mathring{{\mathcal {G}}}_N\)—a discrete version of the operator \((-\Delta )^{-\gamma }\) may be defined as
Observe that, in this way of defining the inverse operator, the result is a periodic grid function of zero mean, i.e, \((-\Delta _N)^{-\gamma } f\in \mathring{{\mathcal {G}}}_N\).
Detailed calculations show that the following summation-by-parts formulas are valid (see the related discussions in [10, 12, 31, 32]): for any periodic grid functions \(f,g\in {\mathcal {G}}_N\),
Similarly, the following summation-by-parts formula is also available: for any \(\gamma \ge 0\),
We define \(\Vert f \Vert _{H_N^\gamma } := \Vert ( - \Delta _N )^{\frac{\gamma }{2}} f \Vert _2\).
Since the Cahn–Hilliard equation (2) is an \(H^{-1}\) gradient flow, we need a discrete version of the norm \(\Vert \cdot \Vert _{H^{-1}}\) defined on \(\mathring{{\mathcal {G}}}_N\). To this end, for any \(f\in \mathring{{\mathcal {G}}}_N\), we define
Similar to (14), the following summation-by-parts formula may be derived:
In addition to the standard \(\ell ^2\) norm, we also introduce the \(\ell ^p\), \(1\le p <\infty \), and \(\ell ^\infty \) norms for a grid function \(f\in {\mathcal {G}}_N\):
For any periodic grid function \(\phi \in {\mathcal {G}}_N\), the discrete Cahn–Hilliard energy is defined as
The following two lemmas will play important roles in the contraction mapping analysis and the maximum norm analysis in the later sections.
Lemma 2.1
Suppose \(d=2\) or 3, \(\alpha _0\in (0,1)\), and \(\gamma _1,\gamma _2 >0\). For any periodic grid function with zero mean, \(f\in \mathring{{\mathcal {G}}}_N\), we have,
for some constant \(C_0>0\) that only depends on \(\alpha _0\) and d, and some constant \(C_1>0\) that only depends on d.
Lemma 2.2
Suppose \(d=2\) or 3. For any \(f\in \mathring{{\mathcal {G}}}_N\), we have
for some \(C_2>0\) that only depends on d.
The proofs will be provided in “Appendices 1 and 2”, respectively. Observe that (20) and (21) are discrete versions of the standard Sobolev embeddings from \(H^{\alpha _0}\) into \(L^4\) and \(H^2\) into \(L^\infty \), respectively, both of which are needed in the nonlinear analysis.
It is well-known that the existence of aliasing error in the nonlinear terms poses a serious challenge in the numerical analysis of Fourier pseudo-spectral schemes, and we need some tools to quantify this error. To this end, we introduce a periodic extension of a grid function and a Fourier collocation interpolation operator.
Definition 1
Suppose that the grid function \(f\in {\mathcal {G}}_N\) has the discrete Fourier expansion (5). Its spectral extension into the trigonometric polynomial space \({\mathcal {P}}_K\) (the space of trigonometric polynomials of degree at most K) is defined as
We write \(S_N(f) = f_S\) and call \(S_N:{\mathcal {G}}_N \rightarrow {\mathcal {P}}_K\) the spectral interpolation operator. Suppose \(g\in C_\mathrm{per}(\Omega ,{\mathbb {R}})\). We define the grid projection \(Q_N: C_\mathrm{per}(\Omega ,{\mathbb {R}})\rightarrow {\mathcal {G}}_N\) via
The resultant grid function may, of course, be expressed as a discrete Fourier expansion:
We define the de-aliasing operator \(R_N :C_\mathrm{per}(\Omega ,{\mathbb {R}}) \rightarrow {\mathcal {P}}_K\) via \(R_N := S_N(Q_N)\). In other words,
Finally, for any \(g\in L^2(\Omega ,{\mathbb {R}})\), we define the (standard) Fourier projection operator \(P_N:L^2(\Omega ,{\mathbb {R}}) \rightarrow {{\mathcal {P}}}_K\) via
where
are the (standard) Fourier coefficients.
Remark 2.3
Note that, in general, for \(g\in C_\mathrm{per}(\Omega ,{\mathbb {R}})\), \(P_N(g) \ne R_N(g)\), and, in particular,
However, if \(g\in {\mathcal {P}}_K\) to begin with, then \(\hat{g}_{\ell ,m,n} = \widehat{Q_N(g)}_{\ell ,m,n}^N\). In other words, \(R_N :{\mathcal {P}}_K \rightarrow {\mathcal {P}}_K\) is the identity operator.
To overcome a key difficulty associated with the \(H^m\) bound of the nonlinear term obtained by collocation interpolation, the following lemma is introduced.
Lemma 2.4
Suppose that m and K are non-negative integers, and, as before, assume that \(N = 2K+1\). For any \(\varphi \in \mathcal{P}_{mK}\) in \({\mathbb {R}}^d\), we have the estimate
for any non-negative integer r.
The case of \(r=0\) was proven in Weinan E’s earlier papers [18, 19]. The case of \(r \ge 1\) was analyzed in a recent article by Gottlieb and Wang [32].
2.2 The Second-Order Convex Splitting Scheme
A second order accurate convex splitting scheme for the CH equation (2) was reported in [36], with a centered difference approximation in space. If the spatial discretization is replaced by the Fourier pseudo-spectral method, the numerical scheme is formulated as follows: given \(\phi ^m,\phi ^{m-1}\in {\mathcal {G}}_N\), find \(\phi ^{m+1}\), \(\mu ^{m+1/2} \in {\mathcal {G}}_N\) such that
where \(s = T/M\). For simplicity, on the initial step we assume \(\phi ^{-1} \equiv \phi ^0\).
Following a similar argument as in [36], the unique solvability and unconditional energy stability for this numerical scheme can be straightforwardly established. On the other hand, there are severe numerical challenges associated with the practical implementation of (26)–(29), due to the implicit treatment of the nonlinear term \(\chi (\phi ^{m+1},\phi ^m )\). If a spatial discretization of a local nature, such as the finite difference approximation, is taken, this issue could be handled by some well-developed multi-grid solvers; see the related discussions in [4, 39, 51, 53], et cetera. However, the global nature of the Fourier pseudo-spectral method makes a direct numerical implementation of this nonlinear scheme extremely challenging.
To overcome this difficulty, we add an \(O (s^2)\) artificial diffusion term to (26), and come up with the following alternate second order numerical scheme:
The values of A and \(\alpha \) will be specified later.
Before proceeding into further analysis, we make an observation. It is clear that the numerical solution of the fully discrete second order scheme (30) is mass-conserving at the discrete level: if \(\overline{\phi ^{m-1}} = \overline{ \phi ^m } = \phi _\mathrm{av}\), then \(\overline{\phi ^{m+1}} = \phi _\mathrm{av}\). We will assume that \(|\phi _\mathrm{av}|\le 1\), as is standard.
Proposition 2.5
For any \(A\ge 0\) and any \(\alpha \ge 0\) the scheme (30) is second order accurate in time, i.e., its local truncation error is \(O\left( s^2\right) \); it is unconditionally uniquely solvable, and it is unconditionally strongly energy stable, with respect to the discrete energy
i.e., \({\mathcal {E}}_N (\phi ^{m+1},\phi ^m) \le {\mathcal {E}}_N (\phi ^m,\phi ^{m-1})\), for any \(n\ge 1\), and any \(s>0\).
Proof
The order of accuracy the can be verified by Taylor expansions, assuming sufficient regularity. We omit the details for brevity. For the unique solvability, we note that scheme (30) could be rewritten as
where
Note that the constant \(\mu ^{m+1/2}_\mathrm{av}\) must be added for compatibility, so that
The unconditional unique solvability of (32)–(33) can be proved by observing the strict convexity of the following functional over the affine hyperplane \({\mathcal {A}} := \left\{ \phi \in {\mathcal {G}}_N \; \big | \; \overline{\phi } = \phi _\mathrm{av} \right\} \):
It is often easier to shift the hyperplane \({\mathcal {A}}\) to the linear space \(\mathring{{\mathcal {G}}}_N\) through a simple affine change of variables. See [15, 39], for example, for more details.
For the energy stability analysis, we take a discrete inner product of (30) with \((-\Delta _N)^{-1} (\phi ^{m+1} - \phi ^m)\), and make use of the following identities and inequalities:
and
Then we arrive at
so that an unconditional stability with respect to the modified discrete energy (31) is established. \(\square \)
Remark 2.6
We can obtain an equivalent statement of energy stability, which will be useful for some purposes, using the following identity:
Remark 2.7
We note that the modified energy (31) is strongly stable, i.e., \({\mathcal {E}}_N (\phi ^{m+1},\phi ^m) \le {\mathcal {E}}_N (\phi ^m,\phi ^{m-1})\). Meanwhile, for the original energy \(E_N (\phi )\), such a strong stability is not available at a theoretical level. On the other hand, since the modified energy contains \(E_N (\phi )\) and a non-negative modified term, we are able to derive the weak stability of the original energy functional:
by taking \(\phi ^{-1} \equiv \phi ^0\). In other words, the original energy functional is always bounded by the initial energy value.
In addition to the second order convex splitting approaches, there have been a few related works with second-order in time approximations for the CH equation in recent years. A semi-discrete second-order scheme for a family of Cahn–Hilliard-type equations was proposed in [54], with applications to diffuse interface tumor growth models. An unconditional energy stability was proved, by taking advantage of a (quadratic) cut-off of the double-well energy and artificial stabilization terms. And also, their scheme turns out to be linear, which is another advantage. However, a convergence analysis is not available in their work.
A careful examination of several second-order in time numerical schemes for the CH equation is presented in [35]. An alternate variable is used in the numerical design, denoted as a second order approximation to \(v=\phi ^2-1\). A linearized, second order accurate scheme is derived as the outcome of this idea, and an unconditional energy stability is established in a modified version. However, such an energy stability is applied to a pair of numerical variables \((\phi , v)\), and an \(H^1\) stability for the original physical variable \(\phi \) has not been justified. As a result, the convergence analysis is not available for this numerical approach.
In comparison, with the weak stability (40) available for the original energy functional, we are able to derive a uniform-in-time \(H^1\) and \(H^2\) bound of the numerical solution presented in this article, namely (66) and (73) in Sect. 3. These estimates play an essential role in the convergence analysis for the proposed numerical scheme.
With all these observations, we note many advantages of the proposed second order convex splitting approach over the second order temporal approximations reported in the existing literature, in particular in terms of the energy stability for the original phase variable \(\phi \) and the convergence analysis.
2.3 A Homogeneous Linear Iteration (HLI) Algorithm
Although the unconditional energy stability and unique solvability of (30) have been established, implementation of the scheme is clearly a challenge due to the combination of strong nonlinearity and the global nature of the pseudo-spectral discretization. In this section, we propose a linear iteration method to solve the scheme, and prove that the iteration always converges to the unique solution of (30) if the splitting parameter A is chosen judiciously.
Based on (32)–(33), we rewrite the scheme (30) in an equivalent form:
where
and
Note that \({\mathcal {L}}\) is a positive, linear, homogeneous (constant coefficient) operator.
Now, we propose the following homogeneous linear iteration (HLI) method to solve the scheme (41): given \(\phi ^m, \phi ^{m-1}, \psi ^k\in {\mathcal {G}}_N\), find the unique periodic solution, \(\psi ^{k+1}\in {\mathcal {G}}_N\), that satisfies
where the mass compatibility constant must now take the form
Observe that the mass compatibility ensures that the right hand side of (42) is of mean zero, a necessary condition for solvability. Here k stands for the HLI index, not the time step index. The method is initialized via \(\psi ^0 := \phi ^m\). Clearly, \(\psi = \phi ^{m+1}\) is the unique fixed point solution:
2.4 A Contraction Mapping Property
First, we derive a uniform in time \(\Vert \cdot \Vert _4\) bound of the exact solution for the numerical scheme (30). By Proposition 2.5, the energy bound (40) is available. Meanwhile, the following inequality is observed: for any \(f\in {\mathcal {G}}_N\),
since \(\frac{1}{8} | f |^4 - \frac{1}{2} | f |^2 + \frac{1}{2} \ge 0\) holds at a point-wise level. A combination with the discrete energy (18) implies that, for all \(n\ge 1\),
We now prove that the linear fixed point iteration (42) must converge to the unique fixed point, provided that A is sufficiently large.
Theorem 2.8
By choosing \(\alpha =\frac{1}{2}\) for \(d=2\), and \(\alpha =\frac{3}{4}\) for \(d=3\), the linear iteration (42) is a contraction mapping in the discrete \(\left\| \, \cdot \, \right\| _4\) norm, provided that
with the constants \(C_0\), \(C_1\) and \(C_4\) given by (19), (20) and (46), respectively.
Proof
Let \(\psi \) denote the unique periodic solution to (41) and define the iteration error at each stage via
where \(\psi ^k\) is the \(k^\mathrm{th}\) iterate generated by the HLI method (42). First, we observe that the solution created by (42) at each iteration stage has the same discrete average as \(\phi ^m\), namely,
The iteration error, therefore, always has zero (discrete) mean: \(\overline{e^k} =0\).
Since \(\psi ^0 := \phi ^m\), and \(\psi = \phi ^{m+1}\), by the preliminary bound (46), we obtain an estimate for the initial error in the discrete \(\left\| \, \cdot \, \right\| _4\) norm:
Subtracting (42) from (41) yields
Taking a discrete inner product with \(e^{k+1}\) – and using the fact that \(\overline{e^{k+1}} = 0\) – leads to
in which the summation-by-parts formulas (13) and (14) were used in the first step, and a discrete Hölder inequality was applied at the last step.
To proceed further in the nonlinear analysis, we make the following a priori assumption at the iteration stage k:
We now show that this same bound will be recovered at the next iteration stage. With this assumption, we get a bound of \(\psi ^k\) in the discrete \(\Vert \cdot \Vert _4\) norm:
Going back to (52), we arrive at the following estimate:
Moreover, since \(\overline{e^k} =0\) for any k, we apply (19) (in Lemma 2.1) and get
which in turn yields
where \(C_5\) is defined in (47). Meanwhile, an application of the discrete Sobolev inequality (20) leads to
Substitution into (58) yields
or, equivalently,
As a result, a contraction is assured under the condition that
or, equivalently,
Clearly, we are justified in our a priori assumption (53), since
provided condition (62) is enforced. This finishes the proof. \(\square \)
Remark 2.9
At each iteration stage, the operator \(\mathcal{L}\) defined in (41) is positive, linear, and homogeneous and can be inverted efficiently using the Fast Fourier Transform (FFT). We note that the operators \((\Delta _N)^{-1}\) and \((-\Delta _N)^\alpha \) (with a non-integer value of \(\alpha \)) do not pose any difficulty in the numerical implementation, since all the operators share exactly the same Fourier eigenfunctions; only a slight modification of the eigenvalues is needed in the computations.
Remark 2.10
As an observation in the contraction mapping analysis, the purpose of the choice of a non-zero value for the parameter \(\alpha \) is to make sure that the continuous “embedding” from \(\left( {\mathcal {G}}_N, \Vert \, \cdot \, \Vert _{H_N^\alpha }\right) \) into \(\left( {\mathcal {G}}_N, \Vert \, \cdot \, \Vert _4\right) \) is valid, independent of N. On the other hand, an increasing value of \(\alpha \) usually amplifies the Douglas–Dupont regularization, which in turn leads to increasing local truncation error. In practical computations, we can take \(\alpha =0\). For instance, with \(\alpha =0\), the following choice
would, formally, lead to a contraction. Since the maximum norm of the solution for the typical Cahn–Hilliard model is of O (1), we are able to take an O (1) value of A, combined with \(\alpha = 0\), in practical computations, as presented in Sect. 4. However, this argument is only intuitive, and a firm theoretical justification is not available.
Remark 2.11
In a recent work [12], a similar linear iteration was proposed and analyzed for the epitaxial thin film growth without slope selection. In particular, a universal bound of \(\frac{5}{4}\) was established for the constant A associated with the Douglas–Dupont regularization, to ensure a contraction mapping property for the HLI proposed in [12]. In comparison, the lower bound for constant A in Theorem 2.8 is related to the discrete Sobolev constant \(C_1\) and the uniform in time \(\Vert \cdot \Vert _4\) bound \(C_4\) (dependent on the initial data), given by estimates (20) and (46), respectively. The key reason for this subtle fact is that the higher order derivatives of the nonlinear terms in the no-slope selection thin film model automatically have an \(L^\infty \) bound, as a universal constant 1, so that a universal lower bound for A is available. In contrast, for the nonlinear numerical scheme (30), where the nonlinear terms have a polynomial structure, an \(L^\infty \) bound of their derivatives are not directly valid.
On the other hand, we observe that the lower bound of constant A (given by Theorem 2.8) does not have a singular dependence on \(\varepsilon \), since \(C_1\) and \(C_4\) do not. This constant could be taken to be O (1) in practical computations.
3 A Maximum Norm Estimate of the Numerical Solution
A uniform-in-time \(H^1\) bound of the numerical solution (30) is available at a discrete level, as a result of the energy stability given by Proposition 2.5. A combination of (40) and (45) yields, for all \(n\ge 0\),
Now, consider \(\phi _S^n:= S_N(\phi ^m)\), where \(S_N\) is the spectral interpolation operator defined in (22). Since \(\phi _S^n\in {\mathcal {P}}_K\), it follows that
Since \(\overline{\phi ^m}=\phi _\mathrm{av}\) (discrete average), it also follows by a simple calculation that \(\overline{\phi _S^n}=\phi _\mathrm{av}\) (continuous average). Using the continuous Poincaré inequality,
for all \(n \ge 0\), with \(\beta _0 = | \phi _\mathrm{av}|\).
Lemma 3.1
Suppose that \(\phi ^\ell \in {\mathcal {G}}_N\), \(\ell = 0,1 , \cdots , M\) are the unique solutions to the scheme (30). The following estimate is valid: for any \(0\le m \le M-1\),
for some positive constants \(C_7,\cdots , C_{10}\) that are independent of s and m.
Proof
We observe that \(\chi (\phi ^{m+1} , \phi ^m)\) is the point-wise interpolation of a continuous function \(\chi (\phi _S^{m+1} , \phi _S^m)\). As a consequence of Lemma 2.4 and the fact that \(\chi (\phi _S^{m+1} , \phi _S^m) \in \mathcal{P}_{L}\), with \(L = 3\cdot K\), we conclude that
Furthermore, a repeated application of the Hölder inequality shows that
Meanwhile, the uniform in time \(H^1\) estimate (66), combined with the 3-D Sobolev inequality, and the Gagliardo-Nirenberg type inequalities, indicates that
for \(\ell = m, m+1\). A combination of (68), (69), and the equality \(\left\| \Delta ^2 \phi _S^\ell \right\| _{L^2} = \left\| \Delta _N^2 \phi ^\ell \right\| _{2}\) leads to the result. \(\square \)
Using estimates (66) and (67), we can now derive a discrete \(\ell ^\infty (0,T;H^2)\) estimate of the numerical solution. The following proposition is the main result of this section.
Theorem 3.2
We assume an initial data \(\phi ^0 \in H^4_\mathrm{per}(\Omega )\). For any \(A\ge 0\) and any \(\alpha \in [0,1)\), the following bound is valid for the numerical solution given by the approximation scheme (30):
where \(s\cdot M = T\) and \(C_{11} >0\) is a constant independent of h, s, and T, provided that the time step size satisfies the restriction
where \(C_{12}>0\) is the constant associated with the discrete elliptic regularity, \(\Vert \Delta _N f \Vert _2 \le C_{12} \Vert \Delta _N^2 f \Vert _2\). The right hand side of estimate (74) is independent of T.
Proof
Taking the discrete inner product of (30) with \(\Delta _N^2 \phi ^{m+1}\) gives
An application of summation-by-parts using periodic boundary conditions indicates that
The concave diffusion term could be similarly handled:
for any \(\beta > 0\), in which the following inequality has been applied in the last step:
for \(\ell = m, m-1\). Meanwhile, the bi-harmonic diffusion term can be treated in a more straightforward way:
The estimate for the right hand side of (75) is similar to that of the concave diffusion term. First, we will need the following weighed Sobolev inequality:
for any \(\beta >0\), where \(C_{14}>0\) depends on A, \(\beta \), and \(C_6\). Then, using the last inequality, along with the summation-by-parts formula (14) and the Cauchy inequality
Using estimate (67), we arrive at
for any \(\beta >0\), with \(C_{15} = C_{15}(\beta ,C_7,\cdots ,C_{10})>0\).
A combination of (75), (76), (77), (79), (81), and (82) yields
under a standard assumption \(A \ge 1\). Choosing \(\beta = \frac{1}{40} \varepsilon ^2\) fixes the constant term, and we have
where \(C_{16} >0\) is a fixed constant that depends on \(\varepsilon ^{-1}\) to some positive power. With an addition of \(\frac{7\varepsilon ^2}{16} \Vert \Delta _N^2 \phi ^m \Vert _2^2\) to both sides, this inequality becomes
We now introduce a modified “energy”:
The last estimate now takes the form
On the other hand, by performing a similar analysis as in (3.32) – (3.33) in reference [36], the following estimate is valid:
provided that the constraint (74) is satisfied. Note that (74) is not so restrictive, since the bound on the right-hand-side will typically be greater than 1. Then we arrive at
An application of induction with the last estimate (see reference [36]) indicates that
The following observation is made
for some \(C_{17}>0\) that is independent of T and s, using \(\phi ^{-1}\equiv \phi ^0\) and the fact that \(G^0\) is bounded independently of h by consistency. To conclude, we employ the elliptic regularity
and this finishes the proof of Proposition 3.2. \(\square \)
Remark 3.3
This analysis follows a similar idea as in the recent work [36], in which the second order convex splitting temporal approximation is combined with the centered difference in space. On the other hand, due to the Fourier pseudo-spectral spatial approximation in (30), we are able to bound the nonlinear inner product with the help of Lemma 2.4. In turn, this approach avoids an application of discrete version of Hölder inequality and Sobolev embedding. This subtle difference greatly simplifies the estimate presented in Theorem 3.2.
Remark 3.4
A detailed examination of (90) reveals an asymptotic decay of the contribution coming from the term \(G^0\), which is essentially the \(H^2\) norm of the initial data \(\phi ^0\).
In addition, we observe the following Sobolev inequality
where the first estimate is based on the fact that \(\phi ^m\) is the point-wise interpolation of its continuous extension \(\phi _S^m\). This gives the \(\ell ^\infty (0,T; \ell ^\infty )\) bound of the numerical solution.
Remark 3.5
Similar to the \(H^2\) estimate given by Theorem 3.2, the \(\left\| \, \cdot \, \right\| _\infty \) bound (93) for the numerical solution is final time independent. There have been limited theoretical works to derive an \(L^\infty \) bound of the numerical solution for the Cahn–Hilliard equation; see [3] for the analysis of a first-order numerical scheme applied to the CH equation with a logarithmic energy. On the other hand, for a second-order scheme for the CH model with a nonlinear polynomial energy, estimate (93) is the first such result if a pseudo-spectral approximation is taken in space.
Remark 3.6
A detailed derivation shows that the global in time \(\left\| \, \cdot \, \right\| _\infty \) bound, \(C C_{11}\) in (93), depends singularly on \(\varepsilon ^{-m_0}\), where \(m_0\) is some positive integer. Meanwhile, a well-known theoretical analysis presented by L. Caffarelli [7] gives an \(\varepsilon \)-independent \(L^\infty \) bound for the CH equation, at the PDE level, provided that a cut-off is applied to the energy. For the standard CH energy (1), in which the polynomial part is given by \(\frac{1}{4} \phi ^4 - \frac{1}{2} \phi ^2\) without a cut-off, the availability of an \(\varepsilon \)-independent \(L^\infty \) bound of the solution is still an open problem, at both the PDE and numerical levels.
Remark 3.7
A careful examination reveals that, the stability estimate for the modified energy (31) and the weak stability (40) for the original energy functional are valid for any \(A \ge 0\), due to the convex splitting nature of the temporal discretization. In turn, the uniform in time \(H^1\) and \(H^2\) bound for the numerical solution, namely (65) and (73), respectively, could be derived in the same manner, even if \(A =0\). In other words, the Douglas–Dupont-type regularization term does not play any essential role in the proof of Theorem 3.2, and the estimate (73) holds even if the artificial regularization term is removed.
On the other hand, the primary purpose to introduce the Douglas–Dupont-type regularization term is to facilitate the numerical implementation of the highly nonlinear scheme (30). With an addition of this regularization term, the linear iteration algorithm (42) could be efficiently applied, and the contraction mapping property of such an iteration is theoretically justified in Theorem 2.8, provided that the parameter A satisfies (47).
We point out that, with the uniform-in-time \(H^2\) bound (73) available for the numerical solution, we are able to establish a local in time convergence analysis for the proposed scheme. This analysis follows a very similar form as Theorem 4.1 in [36]; the details are skipped for simplicity and are left to interested readers.
Theorem 3.8
Given initial data \(\psi \in C^{m+6}_\mathrm{per}(\Omega )\), suppose the unique solution \(\phi _e(x,y,z,t)\) for the Cahn–Hilliard equation (2) is of regularity class
Define the error grid function \(\tilde{\phi }_{i,j,k}^\ell := \Phi _{i,j,k}^\ell - \phi _{i,j,k}^\ell \), where \(\phi _{i,j,k}^\ell \) is the numerical solution of the proposed scheme (30). Consequently, provided s is sufficiently small, for all positive integers \(\ell \), such that \(s \cdot \ell \le T\), we have
where \(C = C(\varepsilon ,T)>0\) is independent of s and h.
Remark 3.9
For the consistency, we note that the numerical scheme (30) has an \(O (s^2)\) local truncation error. On the other hand, if we rewrite (30) in an equivalent form: \(\phi ^{m+1}-\phi ^m = s \Delta _N \tilde{\mu }^{m+1/2}\), the local truncation error becomes \(O (s^3)\), since we have multiplied by s on both sides. In the convergence analysis and error estimate, a well-known fact implies that, although only an \(O(s^3)\) local truncation error has contributed to the numerical error function—the difference between the numerical and exact solutions—at each time step, its accumulation in time leads to an \(O (s^2)\) convergence rate.
Remark 3.10
With the \(O (s^2 + h^m)\) consistency at hand, the key point to establish the convergence analysis is to obtain a bound of the numerical solution in certain functional norm. The uniform in time \(H^2\) bound (73) and the \(\Vert \cdot \Vert _\infty \) bound (93) enable us to derive the desired \(H^2\) convergence result, namely (95).
Remark 3.11
Other than the nonlinear convex splitting approach, the idea of linear convex splitting has also attracted a great deal of attentions in recent years. For example, the following linear convex splitting scheme for the CH equation was considered in Feng, Tang and Yang [27]:
with \(f (x) = x^3 - x\). Energy stability may be rigorously proven for such linear splitting schemes, provided that \(\beta \ge \beta _0\), where \(\beta _0 \sim \varepsilon ^{-n_0}\), for some integer value of \(n_0\). A theoretical justification of the value for \(\beta \) has been provided in more recent works [44, 45].
For this linear splitting scheme, the energy stability will yield the desired bound for the numerical solution, and a full order convergence analysis is expected to be available.
Remark 3.12
In addition to the linear splitting scheme (96), its combination with the spectral deferred correction (SDC) method has also been studied in [27], to achieve higher order temporal accuracy. For the SDC method, an immediate observation is that the energy stability is not directly available any more, due to the Picard iteration nature involved in the numerical algorithm. In turn, any further numerical analysis for the SDC method becomes very challenging, due to the lack of energy stability estimate. Instead, one may think about an alternate approach, the linearized stability analysis for the numerical scheme. This challenging problem will be considered in our future works.
4 Numerical Simulation Results
4.1 Algebraic Convergence of the HLI Algorithm
In this subsection we present some numerical tests to support the theoretical convergence for the proposed homogeneous linear iteration (HLI) algorithm (42). Different values of the diffusion coefficient \(\varepsilon \) and the time step size s are used to compare the convergence rates for the linear iteration. We take the following exact profile for the phase variable:
over the domain \(\Omega = (0,1)^2\). Making this the exact solution requires that we manufacture appropriate values for \(\phi ^m\) and F in (33). In Fig. 1 we plot the iteration error \(\left\| e^k \right\| _2\) versus k, where \(e^k := \psi ^k-\psi \), as in Theorem 2.8, with a fixed \(N =128\). We expect to and, in fact, do see a finite saturation of the iteration error in the figure. As expected, the saturation levels differ for different values of the parameters. Naturally, a larger value of N will allow for smaller saturation levels in each case, but at the cost of more computation.
Discrete \(\Vert \cdot \Vert _2\) norm of the error for the linear iteration versus the iteration stage k, with a fixed choice \(A=1\). a Dependence of the convergence rate on the diffusion parameter \(\varepsilon \), with \(s=0.01\), \(A=1\); b dependence of the convergence rate on the time step size s, with \(\varepsilon =0.1\), \(A=1\)
For the first test, the results for which are reported in Fig. 1a, we fix \(s=0.01\) and \(A=1\) and vary \(\varepsilon \): \(\varepsilon =1\) and \(\varepsilon =0.1\). It is clear that the linear iteration error reaches a saturation after certain iteration stages. We observe that the convergence rate for the linear iteration increases with an increasing value of \(\varepsilon \), which in turn implies that numerical implementation of the linear iteration algorithm (42) becomes more challenging with a smaller diffusion coefficient \(\varepsilon \). This result matches with our theoretical analysis in proof of Theorem 2.8. Also note, that each iteration of the linear iteration method reduces the iteration by roughly a constant amount, which is not surprising since we have a pure contraction of the error.
For the second test, the results for which are reported in Fig. 1b, we fix \(\varepsilon =0.1\), \(A=1\) and vary s: \(s=10^{-2}\) and \(s=10^{-3}\). Similarly, the linear iteration error reaches a saturation after certain iteration stages. The convergence rate for the linear iteration increases with a decreasing value of s. These results likewise match with our theoretical analysis in the proof of Theorem 2.8.
Based on these experiment data, we usually take six to ten iteration stages within each time step in the practical numerical simulations, by setting \(10^{-10}\) as the tolerance of iteration error.
4.2 Convergence of the Proposed Numerical Scheme
In this subsection we perform a numerical accuracy check for the fully discrete second order scheme (30). The two-dimensional computational domain is set to be \(\Omega = (0,1)^2\), and the exact profile for the phase variable is given by
To make \(\Phi \) satisfy the original PDE (2), we have to add an artificial, time-dependent forcing term. The linear iteration (42) is applied to solve the nonlinear system associated with the proposed second order scheme (30) for (2). We compute solutions with grid sizes \(N=64\) to \(N=640\) in increments of 64, and the errors are reported at the final time \(T=1\). Two parameters for the diffusion coefficient are used: \(\varepsilon =0.5\) and \(\varepsilon =0.1\). The time step is determined by the linear refinement path: \(s = 0.5 h\), where h is the spatial grid size. Figure 2 shows the discrete \(\Vert \cdot \Vert _1\), \(\Vert \cdot \Vert _2\) and \(\Vert \cdot \Vert _\infty \) norms of the errors between the numerical and exact solutions. A clear second order temporal accuracy is observed in all cases.
Discrete \(\Vert \cdot \Vert _1\), \(\Vert \cdot \Vert _2\) and \(\Vert \cdot \Vert _\infty \) numerical errors at \(T=1.0\) plotted versus N for the fully discrete second order scheme (30), with the linear iteration algorithm (42) applied. The time step size is set to be \(s = 0.5 h\). The data lie roughly on curves \(CN^{-2}\), for appropriate choices of C, confirming the full second-order accuracy of the scheme. Left: With the diffusion parameter \(\varepsilon =0.5\); Right: with the diffusion parameter \(\varepsilon =0.1\)
Meanwhile, we note that the numerical errors displayed in Fig. 2 are dominated by the temporal error, since the Fourier spectral accuracy makes the spatial numerical error almost negligible, in comparison with the \(O (s^2)\) temporal accuracy. To investigate the spatial accuracy in an appropriate way, we rewrite the forcing term associated with the substitution of the exact profile (98) into the original PDE (2), so that the temporal discretization errors are exactly canceled in the equation and only the spatial discretization errors are kept. With such an external force term, we compute solutions with grid sizes \(N=24\) to \(N=96\) in increments of 8, and the errors are reported at the final time \(T=0.5\), with a fixed time step size \(s=0.01\). The discrete numerical errors (in \(\Vert \cdot \Vert _1\), \(\Vert \cdot \Vert _2\) and \(\Vert \cdot \Vert _\infty \) norms) are presented in Fig. 3, with the same diffusion parameters as in Fig. 2: \(\varepsilon =0.5\) and \(\varepsilon =0.1\). The spatial spectral accuracy is apparently observed for both cases. And also, a saturation of spectral accuracy appears with an increasing N, due to finite machine precision.
Discrete \(\Vert \cdot \Vert _1\), \(\Vert \cdot \Vert _2\) and \(\Vert \cdot \Vert _\infty \) numerical errors at \(T=0.5\) plotted versus N for the proposed numerical scheme (30), combined with the linear iteration algorithm (42). The external force term is rewritten to make the temporal numerical error exactly cancel, so that only the spectrally accurate spatial error is observed. The time step size is fixed as \(s = 0.01\). Left: With the diffusion parameter \(\varepsilon =0.5\); Right: with the diffusion parameter \(\varepsilon =0.1\)
4.3 Coarsening Processes and Energy Dissipation in Time
In this subsection we present a numerical simulation result of a physics example. With the assumption that the interface width is in a much smaller scale than the domain size, i.e., \(\varepsilon \ll \min \left\{ L_x,L_y\right\} \), one is interested in how properties associated with the solution to (2) scale with time. In particular, the energy dissipation law has attracted a great deal of attentions, and a formal analysis indicates a lower decay bound as \(t^{-1/3}\). Meanwhile, it is noted that the rate quoted as the lower bound is typically observed for the averaged values of the energy quantity. A numerical prediction of this scaling law turns out to be very challenging, since a large time scale simulation has to be performed. To adequately capture the full range of coarsening behaviors, numerical simulations for the coarsening process require short- and long-time accuracy and stability, in addition to high spatial accuracy for small values of \(\varepsilon \).
We compare the numerical simulation result with the predicted coarsening rate, using the proposed second order scheme (30) combined with the linear iteration algorithm (42) for the Cahn–Hilliard flow (2). The diffusion parameter is taken to be \(\varepsilon =0.02\). For the domain we take \(L_x = L_y = L= 12.8\) and \(h = L /N\), where h is the uniform spatial step size. For such a value of \(\varepsilon \), our numerical experiment has shown that \(N=512\) is sufficient to resolve the small structures in the solution.
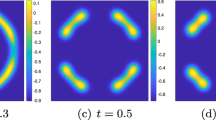
For the temporal step size s, we use increasing values of s in the time evolution. In more detail, \(s = 0.004\) on the time interval [0, 400], \(s = 0.04\) on the time interval [400, 6000], and \(s=0.16\) on the time interval [6000, 20,000]. Whenever a new time step size is applied, we initiate the two-step numerical scheme by taking \(\phi ^{-1} = \phi ^0\), with the initial data \(\phi ^0\) given by the final time output of the last time period. Both the energy stability and second order numerical accuracy have been theoretically assured by our arguments in Proposition 2.5, Theorem 3.8, respectively. Figure 4 presents time snapshots of the phase variable \(\phi \) with \(\varepsilon =0.02\). A significant coarsening process is clearly observed in the system. At early times many small structures are present. At the final time, \(t=20{,}000\), a single interface structure emerges, and further coarsening is not possible.
The long time characteristics of the solution, especially the energy decay rate, are of interest to material scientists. Recall that, at the space-discrete level, the energy, \(E_N\) is defined via (18). Figure 5 presents the log–log plot for the energy versus time, with the given physical parameter \(\varepsilon =0.02\). The detailed scaling “exponent” is obtained using least squares fits of the computed data up to time \(t=400\). A clear observation of the \(a_e t^{b_e}\) scaling law can be made, with \(a_e = 8.1095\), \(b_e=-0.3445\). In other words, an almost perfect \(t^{-1/3}\) energy dissipation law is confirmed by our numerical simulation.
Log–log plot of the temporal evolution the energy \(E_N\) for \(\varepsilon =0.02\). The energy decreases like \(t^{-1/3}\) until saturation. The red lines represent the energy plot obtained by the simulations, while the straight lines are obtained by least squares approximations to the energy data. The least squares fit is only taken for the linear part of the calculated data, only up to about time \(t=400\). The fitted line has the form \(a_e t^{b_e}\), with \(a_e = 8.1095\), \(b_e=-0.3445\) (Color figure online)
In addition, we provide another numerical simulation result to demonstrate the energy dissipation law versus time, with a different physical parameter \(\varepsilon =0.03\); all other set-up are kept the same. For this physical parameter \(\varepsilon \), we compute the Cahn–Hilliard flow up to a final time \(T=6000\), when the saturation state is clearly observed. The log–log plot for the energy is presented in Fig. 6. Again, the least squares approximation (up to time \(t=400\)) is applied to calculate the scaling “exponent”, and a scaling law of \(a_e t^{b_e}\), with \(a_e = 9.8286\), \(b_e=-0.3118\), is obtained by the numerical results. This scaling law also matches the \(t^{-1/3}\) law very well. And also, it is remarkable to note that a smaller value of \(\varepsilon =0.02\) leads to a scaling law closer to the \(t^{-1/3}\) prediction.
Log–log plot of the temporal evolution the energy \(E_N\) for \(\varepsilon =0.03\), with the same set-up as in Fig. 5. The least squares fit is only taken for the linear part of the calculated data, only up to about time \(t=400\). The fitted line has the form \(a_e t^{b_e}\), with \(a_e = 9.8286\), \(b_e=-0.3118\) (Color figure online)
5 Summary and Remarks
In this paper we have presented an unconditionally energy stable second-order numerical scheme for the Cahn–Hilliard equation (2), with the Fourier pseudo-spectral approximation in space. The temporal discretization follows the second order convex splitting reported in a recent article [36], while the global nature of the Fourier pseudo-spectral scheme makes a direct nonlinear solver not feasible. In turn, we introduce an \(O(s^2)\) artificial diffusion term, a Douglas–Dupont-type regularization, and a contraction mapping property of the proposed linear iteration (in a discrete \(\Vert \cdot \Vert _4\) norm) is justified at a theoretical level. An addition of this regularization does not affect the unconditional unique solvability and unconditional energy stability of the scheme. In addition to the leading order \(H^1\) estimate indicated by the energy stability, we establish a uniform in time \(H^2\) bound for the numerical solution, by performing an \(\ell ^\infty (0,T; H^2) \cap \ell ^2 (0,T; H^4)\) analysis at a discrete level. As a result of this \(H^2\) estimate, a discrete maximum bound is also available for the numerical solution.
This linear iteration algorithm demonstrates an efficient approach to implement a highly nonlinear scheme. The nonlinear system can be decomposed as an iteration of purely linear solvers, which can be very efficiently implemented with the help of FFT in a Fourier spectral set-up. The numerical simulation experiments showed that the second order scheme, combined with the linear iteration algorithm, is able to produce accurate long time numerical results with a reasonable computational cost. In particular, the energy dissipation rate given by our numerical simulation indicates an almost perfect match with the theoretical \(t^{-1/3}\) prediction, which is remarkable.
References
Aristotelous, A., Karakasian, O., Wise, S.M.: A mixed discontinuous Galerkin, convex splitting scheme for a modified Cahn–Hilliard equation and an efficient nonlinear multigrid solver. Discrete Contin. Dyn. Sys. B 18, 2211–2238 (2013)
Aristotelous, A., Karakasian, O., Wise, S.M.: Adaptive, second-order in time, primitive-variable discontinuous Galerkin schemes for a Cahn–Hilliard equation with a mass source. IMA J. Numer. Anal. 35, 1167–1198 (2015)
Barrett, J., Blowey, J.: Finite element approximation of the Cahn–Hilliard equation with concentration dependent mobility. Math. Comput. 68, 487–517 (1999)
Baskaran, A., Hu, Z., Lowengrub, J., Wang, C., Wise, S.M., Zhou, P.: Energy stable and efficient finite-difference nonlinear multigrid schemes for the modified phase field crystal equation. J. Comput. Phys. 250, 270–292 (2013)
Baskaran, A., Lowengrub, J., Wang, C., Wise, S.: Convergence analysis of a second order convex splitting scheme for the modified phase field crystal equation. SIAM J. Numer. Anal. 51, 2851–2873 (2013)
Boyd, J.: Chebyshev and Fourier Spectral Methods. Dover, New York, NY (2001)
Caffarelli, L., Muler, N.: An \(L^\infty \) bound for solutions of the Cahn–Hilliard equation. Arch. Rational Mech. Anal. 133, 129–144 (1995)
Cahn, J.W., Hilliard, J.E.: Free energy of a nonuniform system. i. interfacial free energy. J. Chem. Phys. 28, 258–267 (1958)
Canuto, C., Quarteroni, A.: Approximation results for orthogonal polynomials in Sobolev spaces. Math. Comp. 38, 67–86 (1982)
Chen, W., Conde, S., Wang, C., Wang, X., Wise, S.M.: A linear energy stable scheme for a thin film model without slope selection. J. Sci. Comput. 52, 546–562 (2012)
Chen, W., Liu, Y., Wang, C., Wise, S.M.: An optimal-rate convergence analysis of a fully discrete finite difference scheme for Cahn–Hilliard–Hele–Shaw equation. Math. Comput., (2016). Published online: http://dx.doi.org/10.1090/mcom3052
Chen, W., Wang, C., Wang, X., Wise, S.M.: A linear iteration algorithm for energy stable second order scheme for a thin film model without slope selection. J. Sci. Comput. 59, 574–601 (2014)
Cheng, K., Feng, W., Gottlieb, S., Wang, C.: A Fourier pseudospectral method for the “Good“ Boussinesq equation with second-order temporal accuracy. Numer. Methods Partial Differ. Equ. 31(1), 202–224 (2015)
Collins, C., Shen, J., Wise, S.M.: An efficient, energy stable scheme for the Cahn–Hilliard–Brinkman system. Commun. Comput. Phys. 13, 929–957 (2013)
Diegel, A., Feng, X., Wise, S.M.: Convergence analysis of an unconditionally stable method for a Cahn–Hilliard–Stokes system of equations. SIAM J. Numer. Anal. 53, 127–152 (2015)
Diegel, A., Wang, C., Wise, S.M.: Stability and convergence of a second order mixed finite element method for the Cahn–Hilliard equation. IMA J. Numer. Anal. (2016). doi:10.1093/imanum/drv065
Du, Q., Nicolaides, R.: Numerical analysis of a continuum model of a phase transition. SIAM J. Numer. Anal. 28, 1310–1322 (1991)
Weinan, E.: Convergence of spectral methods for the Burgers equation. SIAM J. Numer. Anal. 29, 1520–1541 (1992)
Weinan, E.: Convergence of Fourier methods for Navier–Stokes equations. SIAM J. Numer. Anal. 30, 650–674 (1993)
Elliot, C.M., Stuart, A.M.: The global dynamics of discrete semilinear parabolic equations. SIAM J. Numer. Anal. 30, 1622–1663 (1993)
Elliott, C.M., French, D.A., Milner, F.A.: A second-order splitting method for the Cahn–Hilliard equation. Numer. Math. 54, 575–590 (1989)
Elliott, C.M., Garcke, H.: On the Cahn–Hilliard equation with degenerate mobility. SIAM J. Math. Anal. 27, 404 (1996)
Elliott, C.M., Larsson, S.: Error estimates with smooth and nonsmooth data for a finite element method for the Cahn–Hilliard equation. Math. Comp. 58, 603–630 (1992)
Eyre, D.: Unconditionally gradient stable time marching the Cahn-Hilliard equation. In: Bullard, J.W., Kalia, R., Stoneham, M., Chen, L.Q. (eds.) Computational and Mathematical Models of Microstructural Evolution, volume 53, pages 1686–1712, Warrendale, PA, USA, (1998). Materials Research Society
Feng, X.: Fully discrete finite element approximations of the Navier–Stokes–Cahn-Hilliard diffuse interface model for two-phase fluid flows. SIAM J. Numer. Anal. 44, 1049–1072 (2006)
Feng, X., Prohl, A.: Error analysis of a mixed finite element method for the Cahn–Hilliard equation. Numer. Math. 99, 47–84 (2004)
Feng, X., Tang, T., Yang, J.: Long time numerical simulations for phase-field problems using \(p\)-adaptive spectral deferred correction methods. SIAM J. Sci. Comput. 37, A271–A294 (2015)
Feng, X., Wise, S.M.: Analysis of a fully discrete finite element approximation of a Darcy–Cahn–Hilliard diffuse interface model for the Hele-Shaw flow. SIAM J. Numer. Anal. 50, 1320–1343 (2012)
Furihata, D.: A stable and conservative finite difference scheme for the Cahn–Hilliard equation. Numer. Math. 87, 675–699 (2001)
Gottlieb, D., Orszag, S.A.: Numerical Analysis of Spectral Methods, Theory and Applications. SIAM, Philadelphia, PA (1977)
Gottlieb, S., Tone, F., Wang, C., Wang, X., Wirosoetisno, D.: Long time stability of a classical efficient scheme for two dimensional Navier–Stokes equations. SIAM J. Numer. Anal. 50, 126–150 (2012)
Gottlieb, S., Wang, C.: Stability and convergence analysis of fully discrete Fourier collocation spectral method for 3-d viscous Burgers’ equation. J. Sci. Comput. 53, 102–128 (2012)
Guan, Z., Lowengrub, J.S., Wang, C., Wise, S.M.: Second-order convex splitting schemes for nonlocal Cahn–Hilliard and Allen–Cahn equations. J. Comput. Phys. 277, 48–71 (2014)
Guan, Z., Wang, C., Wise, S.M.: A convergent convex splitting scheme for the periodic nonlocal Cahn–Hilliard equation. Numer. Math. 128, 377–406 (2014)
Guillén-González, F., Tierra, G.: Second order schemes and time-step adaptivity for Allen–Cahn and Cahn–Hilliard models. Comput. Math. Appl. 68(8), 821–846 (2014)
Guo, J., Wang, C., Wise, S.M., Yue, X.: An \(H^2\) convergence of a second-order convex-splitting, finite difference scheme for the three-dimensional Cahn-Hilliard equation. Commu. Math. Sci. 14, 489–515 (2016)
He, Y., Liu, Y., Tang, T.: On large time-stepping methods for the Cahn–Hilliard equation. Appl. Numer. Math. 57(4), 616–628 (2006)
Hesthaven, J., Gottlieb, S., Gottlieb, D.: Spectral Methods for Time-dependent Problems. Cambridge University Press, Cambridge, UK (2007)
Hu, Z., Wise, S., Wang, C., Lowengrub, J.: Stable and efficient finite-difference nonlinear-multigrid schemes for the phase-field crystal equation. J. Comput. Phys. 228, 5323–5339 (2009)
Kay, D., Welford, R.: Efficient numerical solution of Cahn–Hilliard–Navier Stokes fluids in 2d. SIAM J. Sci. Comput. 29, 2241–2257 (2007)
Kay, D., Welford, Richard: A multigrid finite element solver for the Cahn–Hilliard equation. J. Comput. Phys. 212, 288–304 (2006)
Khiari, N., Achouri, T., Ben Mohamed, M.L., Omrani, K.: Finite difference approximate solutions for the Cahn-Hilliard equation. Numer. Meth. PDE 23, 437–455 (2007)
Kim, J.S., Kang, K., Lowengrub, J.S.: Conservative multigrid methods for Cahn–Hilliard fluids. J. Comput. Phys. 193, 511–543 (2003)
Li, D., Qiao, Z.: Stabilized times schemes for high accurate finite differences solutions of nonlinear parabolic equations. J. Sci. Comput., (2016). Submitted and in review
Li, D., Qiao, Z., Tang, T.: Characterizing the stabilization size for semi-implicit Fourier-spectral method to phase field equations. SIAM J. Numer. Anal. (2016). Accepted and in press
Shen, J., Wang, C., Wang, X., Wise, S.M.: Second-order convex splitting schemes for gradient flows with Ehrlich–Schwoebel type energy: application to thin film epitaxy. SIAM J. Numer. Anal. 50, 105–125 (2012)
Shen, J., Yang, X.: Numerical approximations of Allen–Cahn and Cahn–Hilliard equations. Discrete Contin. Dyn. Sys. A 28, 1669–1691 (2010)
Wang, C., Wang, X., Wise, S.M.: Unconditionally stable schemes for equations of thin film epitaxy. Discrete Contin. Dyn. Sys. A 28, 405–423 (2010)
Wang, C., Wise, S.M.: Global smooth solutions of the modified phase field crystal equation. Methods Appl. Anal. 17, 191–212 (2010)
Wang, C., Wise, S.M.: An energy stable and convergent finite-difference scheme for the modified phase field crystal equation. SIAM J. Numer. Anal. 49, 945–969 (2011)
Wise, S.M.: Unconditionally stable finite difference, nonlinear multigrid simulation of the Cahn–Hilliard–Hele–Shaw system of equations. J. Sci. Comput. 44, 38–68 (2010)
Wise, S.M., Kim, J.S., Lowengrub, J.S.: Solving the regularized, strongly anisotropic Chan–Hilliard equation by an adaptive nonlinear multigrid method. J. Comput. Phys. 226, 414–446 (2007)
Wise, S.M., Wang, C., Lowengrub, J.S.: An energy stable and convergent finite-difference scheme for the phase field crystal equation. SIAM J. Numer. Anal. 47, 2269–2288 (2009)
Wu, X., van Zwieten, G.J., van der Zee, K.G.: Stabilized second-order convex splitting schemes for Cahn–Hilliard models with application to diffuse-interface tumor-growth models. Inter. J. Numer. Methods Biomed. Eng. 30, 180–203 (2014)
Acknowledgments
The authors thank Wenbin Chen, Xiaoming Wang and the anonymous reviewers for their valuable comments and suggestions. This work is supported in part by the NSF DMS-1418689 (C. Wang), NSF DMS-1418692 (S. Wise), NSFC 11271281 (X. Yue), and the fund of China Scholarship Council 201408515169 (K. Cheng). The first author also thanks University of Massachusetts Dartmouth, for support during his visit.
Author information
Authors and Affiliations
Corresponding author
Appendices
Proof of Lemma 2.1
For a 3-D grid function f with its discrete Fourier expansion as (5), an application of discrete Parseval equality gives
with \(\lambda _{\ell , m, n} = 4 \pi ^2 ( \ell ^2 + m^2 + n^2 )\). This in turn yields
A similar calculation also gives
By making comparison between (101) and (102), we conclude that (19) is a direct consequence of the following application of Young’s inequality:
with \(C^*\) only dependent on \(\alpha _0\) and \(\Omega \).
For the proof of (20), a discrete version of Sobolev embedding from \(H^{\alpha _0}\) into \(\ell ^4\), we have to utilize the continuous extension of f, given by (22). For simplicity of presentation, we focus our analysis in the 2-D case; for the 3-D grid function, the analysis could be carried out in a similar, yet more tedious way. And also, \(\Vert \cdot \Vert \) is denoted as the standard \(L^2\) norm for a continuous function.
We denote the following grid function
A direct calculation shows that
Note that both norms are discrete in the above identity. Moreover, we assume the grid function g has a discrete Fourier expansion as
and denote its continuous version as
With an application of the Parseval equality at both the discrete and continuous levels, we have
On the other hand, we also denote
The reason for \(H \in \mathcal{P}_{2K}\) is because \(f_N \in \mathcal{P}_{K}\). We note that \(H \ne G\), since \(H \in \mathcal{P}_{2K}\), while \(G \in \mathcal{P}_{K}\), although H and G have the same interpolation values on at the numerical grid points \((x_i, y_j)\). In other words, g is the interpolation of H onto the numerical grid point and G is the continuous version of g in \(\mathcal{P}_{K}\). As a result, collocation coefficients \(\hat{g}_c^N\) for G are not equal to \(\hat{h}^N\) for H, due to the aliasing error. In more detail, for \(- K \le \ell , m \le K\), we have the following representations:
With an application of Cauchy inequality, it is clear that
Meanwhile, an application of Parseval’s identity to the Fourier expansion (109) gives
Its comparison with (108) indicates that
with the estimate (111) applied. Meanwhile, since \(H (x,y) = \left( f_N (x,y) \right) ^2\), we have
Therefore, a combination of (105), (113) and (114) results in
For the continuous function \(f_N (x,y)\), we have the following estimate in Sobolev embedding (in 2-D):

Then we arrive at
This finishes the proof of (20) for \(d=2\).
The 3-D case could be analyzed in the same fashion, and the details are skipped for the sake of brevity. The proof of Lemma 2.1 is completed.
Proof of Lemma 2.2
For any grid function \(f\in {\mathcal {G}}_N\), we recall its continuous extension, \(f_S = S_N(f)\in {\mathcal {P}}_K\), as defined in (22). Since f is the point-wise grid interpolation of \(f_S\), we have
For the smooth function \(f_S\), applying the 3-D Sobolev inequality associated to the embedding \(H^2\hookrightarrow L^\infty \) and elliptic regularity, we have
Subsequently, the maximum norm estimate (21) is a direct consequence of the following identities:
This finishes the proof of Lemma 2.2.
Rights and permissions
About this article
Cite this article
Cheng, K., Wang, C., Wise, S.M. et al. A Second-Order, Weakly Energy-Stable Pseudo-spectral Scheme for the Cahn–Hilliard Equation and Its Solution by the Homogeneous Linear Iteration Method. J Sci Comput 69, 1083–1114 (2016). https://doi.org/10.1007/s10915-016-0228-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-016-0228-3