High Order Finite Difference Methods for the Wave Equation with Non-conforming Grid Interfaces

Abstract

We use high order finite difference methods to solve the wave equation in the second order form. The spatial discretization is performed by finite difference operators satisfying a summation-by-parts property. The focus of this work is on numerical treatments of non-conforming grid interfaces and non-conforming mesh blocks. Interface conditions are imposed weakly by the simultaneous approximation term technique in combination with interface operators, which move discrete solutions between grids at an interface. In particular, we consider an interpolation approach and a projection approach with corresponding operators. A norm-compatible condition of the interface operators leads to energy stability for first order hyperbolic systems. By imposing an additional constraint on the interface operators, we derive an energy estimate of the numerical scheme for the second order wave equation. We carry out eigenvalue analyses to investigate the additional constraint and its relation to stability. In addition, a truncation error analysis is performed, and discussed in relation to convergence properties of the numerical schemes. In the numerical experiments, stability and accuracy properties of the numerical scheme are further explored, and the practical usefulness of non-conforming grid interfaces and mesh blocks is discussed in two practical examples.

1 Introduction

For wave propagation problems, the computational domain is often large compared with the wavelength, and waves travel for a long time. It has been shown that high order accurate discretizations in time and space are more efficient to solve these problems on smooth domains [9, 15]. Although it is straightforward to derive high order finite difference stencils in the interior of the computational domain, it is challenging to derive boundary closures in a stable and accurate way. For long time simulations, it is also desirable that the discretization is strictly stable [10, p. 129] so that the numerical solution only exhibits growth originated from the differential equation. A successful candidate of high order finite differences is the summation-by-parts simultaneous approximation term (SBP-SAT) method [5, 30]. An SBP operator [17] approximates a spatial derivative, and mimics integration-by-parts via its associated norm. The SAT method [3] is used to impose boundary conditions and grid interface conditions weakly.

Traditionally, the wave equation is written as a first order hyperbolic system, and is then solved by well-developed methods for such systems. However, there are various drawbacks in doing so [16]. For example, new variables are introduced in the system. This not only leads to more computational work, but also requires a careful derivation of the boundary conditions for the new variables. Therefore, it is desirable to solve directly the wave equation in the second order form. The SBP-SAT scheme has been used to solve the wave equation in the second order in [1, 22] for different boundary conditions, and in [21] for a discontinuous medium. In [31], the method is extended to handle complex geometries and heterogeneous media. Stability of the numerical scheme is proved by the energy method, and such a scheme is often termed as energy stable.

For a wave that travels in an inhomogeneous medium, the wave speed varies in space. The frequency of a wave is given by initial and boundary data, and any present interior forcing. To resolve a given frequency, the corresponding wavelength is proportional to the wave speed. A reduction in the wave speed confined to a subset of the physical domain yields a wave with a shorter wavelength localized in that subset. In [11, 15], the accuracy of a numerical solution to a Cauchy problem is stated in terms of the number of grid points per wavelength. For computational efficiency it is important that a fine mesh is used in the subset that constitutes the slower medium, and a coarse mesh elsewhere.

To achieve this, we can partition the computational domain into blocks, where the mesh sizes are constant in each block but differ in different blocks. Though there are conforming strategies [13], it is more natural that the partitioning results in non-conforming grid interfaces with hanging nodes, or even non-conforming mesh blocks. Suitable interface conditions are then imposed to couple adjacent mesh blocks and yield a well-posed problem. Many techniques for the numerical treatment of interface conditions have been proposed. In [27], an energy conserving discretization of the elastic wave equation in the second order formulation is presented. The finite difference operators satisfy the principle of SBP, and the grid interface with a 1:2 refinement ratio is handled by using ghost points. Stability is proved by the energy method, but the convergence rate of the numerical scheme is limited to two.

Besides the ghost point approach, the SAT method can be used for the numerical coupling of grid interfaces, for example for the advection-diffusion equation in [4] and the wave equation in [21]. In [20], norm-compatible interpolation operators are constructed to handle non-conforming grid interfaces, and the Euler equations are used as the model problem. The norm-compatible condition leads to an energy estimate for first order hyperbolic systems, and also for the Schrödinger equation [26]. The interpolation error of the norm-compatible interpolation operators [20] is of the same order as the truncation error of the SBP operators. In the numerical experiments, it is shown that the convergence rate of the numerical scheme applied to the Euler equations is not lowered by using the interpolation operators, compared with the case with only conforming grid interfaces. To use the interpolation operators presented in [20], the mesh refinement ratio is fixed to 1:2 and the mesh blocks must be conforming.

Recently, a general purpose methodology for coupling non-conforming grid interfaces as well as non-conforming mesh blocks was developed in [14]. This technique uses projection operators to move a discrete finite difference solution to piecewise polynomial functions in a subspace of a Hilbert space where the coupling is done. The wave equation in the first order system formulation is used as a model problem. Stability is proved by the energy method, and the numerical experiments demonstrate that the convergence rate is high order though slightly lower than when conforming grid interfaces were used. The projection operators allow for a very flexible configuration of meshing in the sense that grid interfaces and mesh blocks do not need to be conforming. Similarly to the interpolation operators, the projection operators satisfy a norm-compatible condition that is essential for the stability proof to hold.

In this paper, we focus on numerical treatments of non-conforming grid interfaces for the wave equation in the second order form in the framework of the SBP-SAT methodology. In particular, stability and accuracy properties of the resulting methods are investigated. We have found that in contrast to first order hyperbolic systems, the norm-compatible condition is not sufficient for energy stability. The second and fourth order accurate interpolation operators in [20] and projection operators in [14] satisfy an additional condition. We give a stability proof by the energy method for those cases. For higher order accurate operators, the additional condition is not satisfied, and we cannot prove stability. In fact, numerical experiments show that the sixth and eighth order accurate schemes based on the interpolation operators are unstable in several settings, while no unphysical growth is observed for the higher order accurate schemes with the projection operators. An eigenvalue analysis of the spatial operators support these observations.

Local mesh refinement reduces the number of grid points significantly in computations. To achieve full efficiency, the numerical scheme must also be accurate enough. It is desirable that the convergence rate is not depressed by using non-conforming grid interfaces and mesh blocks. Even though this is in most cases true for first order hyperbolic systems, the situation for second order equations is less favourable. By a truncation error analysis, we show that the truncation error near the corners of mesh blocks connected by the non-conforming grid interfaces is two orders larger than that with conforming grid interfaces. The large truncation error is localized at only a few grid points in a two dimensional space, and its effect to the convergence rate may therefore be weakened. In fact, the numerical experiments show that the convergence rate with a non-conforming grid interface is only one order lower than the corresponding case with a conforming grid interface. In addition, we give some practical examples to compare the numerical schemes with interpolation operators and projection operators. We have found that in certain cases it is beneficial to use non-conforming grid interfaces, albeit the accuracy reduction.

The structure of this paper is as follows. In Sect. 2, the SBP-SAT methodology is introduced. We then discuss stability and accuracy properties of the numerical coupling based on interpolation operators in Sect. 3, and projection operators in Sect. 4. Numerical experiments are carried out in Sect. 5 including the eigenvalue analyses for stability, convergence verifications for accuracy and two practical examples of problems with a complex geometry. We conclude and mention future work in Sect. 6.

2 Preliminaries

We begin with the preliminaries that will be used in the discussion of the SBP-SAT method. Let $w_1(x)$ and $w_2(x)$ be two real-valued functions in L$_2[0,1]$. An inner product is defined by $(w_1,w_2)=\int _0^1w_1w_2dx$, with a corresponding norm $\Vert w_1\Vert ^2=(w_1,w_1)$. The computational domain [0, 1] is discretized by $N+1$ equidistant grid points

$$\begin{aligned} x_i=ih,\quad i=0,1,\ldots ,N, \text { where } h=\frac{1}{N}. \end{aligned}$$

With any fixed N, a grid function can be represented by a vector and an operator can be represented by a matrix. Throughout this paper, we use an operator and a matrix interchangeably when there is no ambiguity.

2.1 SBP Finite Difference Operators

To solve the wave equation with constant coefficients in a rectangular domain, an SBP finite difference operator approximating second derivative $\partial ^2 /\partial x^2$ is needed. In this paper, we use the operators constructed in [19, 23], and defined as follows.

Definition 1

A difference operator $D_2=H^{-1}(-M+BS)$ approximating second derivative $\partial ^2 /\partial x^2$ is an explicit narrow diagonal second derivative SBP operator, if H is diagonal and positive definite, M is symmetric positive semi-definite, $B = \text {diag} (-1, 0,\ldots , 0, 1)$, the first and last row of S is a one sided approximation of $\partial /\partial x$ at the boundary and the interior stencil width of $D_2$ is minimal.

The diagonal positive definite matrix H defines the SBP norm, and it has the interior weight h and special boundary weights. A difference operator is explicit if no system of equations is needed to solve when computing difference approximations, i.e. compact Padé-type schemes are not considered here. The concept narrow is introduced in [24], which means that the interior finite difference stencil width is minimal. To derive an energy estimate for the SBP-SAT scheme for the wave equation with a Dirichlet boundary condition or an interface condition at a material heterogeneity, the following lemma, which is often referred to as the borrowing trick [1, 21, 31], is essential:

Lemma 1

The matrix M in the diagonal norm SBP operators $D_2$ constructed in [19, 23] can be written as

$$\begin{aligned} M=h\alpha (BS)^TBS+\tilde{M}, \end{aligned}$$

where h is the grid spacing, $\alpha$ is a constant independent of h, the matrices B and S are the same as in Definition 1, and $\tilde{M}$ is symmetric positive semi-definite.

The values of $\alpha$ are computed in [21] for the second, fourth and sixth order accurate SBP operators $D_2$. We use the same technique to compute the values of $\alpha$ for the eighth and tenth order cases, and list them in Table 1.

Table 1 $\alpha$ Values

When a complex geometry is present, a curvilinear grid can be used to resolve the geometrical features. In this case, even if the original equation has only constant coefficients, the transformed equation has second derivative terms with variable coefficients, and mixed derivative terms [29]. For this reason, there is a need of SBP operators $D_1$ approximating first derivative $\partial /\partial x$ and $D_2^{(b)}=H^{-1}(-M^{(b)}+B^{(b)}S)$ approximating second derivative $\partial /\partial x (b(x)\partial /\partial x)$ with $b(x)>0$. To derive an energy estimate for stability, it is important that $D_1$ and $D_2^{(b)}$ are associated with the same norm. In addition, when a mixed derivative term is present $D_1$ and $D_2^{(b)}$ must be compatible. Compatibility [24] means that $M^{(b)}$ can be written as $M^{(b)}=D_1^THB^{(b)}D_1+R^{(b)}$ where $R^{(b)}$ is symmetric positive semi-definite. In this case, $D_2^{(b)}$ is essentially equal to applying $D_1$ twice plus a small dissipative term. In this paper, we use the compatible SBP operators $D_1$ constructed in [28] and $D_2^{(b)}$ constructed in [18]. In the special case $b(x)\equiv 1$, $D_2^{(b)}$ in [18] coincides with the corresponding constant coefficient SBP operators $D_2$ in [23].

The accuracy of SBP operators are often termed as 2p, meaning that the truncation error is $\mathcal {O}(h^{2p})$ in the interior. To satisfy the SBP property, the truncation error near the boundary increases. For all the SBP operators we use, near the boundary the truncation error is $\mathcal {O}(h^{p})$. For $S\approx \frac{d}{dx}$ at the boundary, the truncation error is $\mathcal {O}(h^{p+1})$. Compatible SBP operators $D_1$ and $D_2$ are constructed in [28] and [23] for $p=1,2,3,4$. The operators $D_1$ and $D_2$ are further extended to tenth order accuracy in [19], but they are not compatible. The operators $D_2^{(b)}$ in [18] have accuracy $p=1,2,3$. The construction of $D_2^{(b)}$ requires the solution of a large system of nonlinear equations, which is very involved when the accuracy order is high. The borrowing trick for $D_2^{(b)}$ is presented in [31].

3 Non-conforming Grid Interfaces Handled by Interpolation Operators

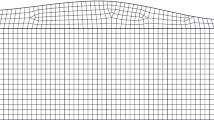
The numerical coupling of conforming grid interfaces by the SAT method for the wave equation is discussed in [31]. Our aim in this section is to generalize the scheme to also couple non-conforming grid interfaces by using interpolation operators. Figure 1a, b show two examples of non-conforming grid interfaces in conforming mesh blocks. To begin with, we consider a grid interface with a coarse grid on one side and a fine grid on the other side. We denote the interpolation operators by $I_{F2C}$ and $I_{C2F}$, with the subscripts F2C and C2F referring to fine to coarse and coarse to fine, respectively.

Fig. 1

Conforming mesh blocks with non-conforming grid interfaces. a Two mesh blocks, b four mesh blocks

A key concept, norm-compatible, is important because it enables interpolating solutions across the interface while preserving the SBP property.

Definition 2

Let $H_C$ and $H_F$ denote the SBP norms corresponding to the coarse grid and the fine grid on an interface of two mesh blocks. We call the interpolation operators $I_{F2C}$ and $I_{C2F}$ norm-compatible if

$$\begin{aligned} H_{F}I_{C2F}=(H_{C}I_{F2C})^T. \end{aligned}$$

(1)

We will also make use of the following definition when proving stability by the energy method.

Definition 3

Let $H_C$ and $H_F$ denote the SBP norms corresponding to the coarse grid and the fine grid on an interface of two mesh blocks. We call the interpolation operators $I_{F2C}$ and $I_{C2F}$ norm-contracting if the matrices

$$\begin{aligned} \Xi _C:=H_{C}(I_{C}-I_{F2C}I_{C2F}) \text { and } \Xi _F:= H_{F}(I_{F}-I_{C2F}I_{F2C}) \end{aligned}$$

are symmetric positive semi-definite. $I_{C}$ and $I_{F}$ are identity matrices.

Norm-compatible interpolation operators for the grid interface with mesh refinement ratio 1:2 are constructed in [20]. The construction of interpolation operators with other refinement ratios (1:4, 1:8, $\ldots$) is possible by the same technique. The interpolation operators do not interpolate exactly, instead they mimic the accuracy property of the diagonal norm SBP operators. For $p=1,2,3,4$, the interpolation error is $\mathcal {O}(h^{2p})$ in the interior of the interface, but near the ends of the interface the interpolation error increases to $\mathcal {O}(h^{p})$. Though the accuracy is reduced near the ends of the interface, the number of grid points with the large interpolation error $\mathcal {O}(h^p)$ is independent of h. We call them 2pth order accurate interpolation operators, and when used together with 2pth order accurate SBP operators the scheme is also termed as 2pth order accurate, even though the local truncation error of the semi-discretized equation may not be $\mathcal {O}(h^{2p})$ or $\mathcal {O}(h^{p})$. Here, h is used to denote the magnitude of the mesh sizes for the sake of a simplified notation. In Sect. 3.1.2, we perform a truncation error analysis based on the interpolation accuracy and relate it to the convergence rate of the scheme.

For the norm-contracting condition in Definition 3, it is straightforward to show that $\Xi _C$ and $\Xi _F$ are symmetric by using the norm-compatible condition in Definition 2. However, the positive semi-definiteness is not a built-in constraint in the construction process of the interpolation operators. In Sect. 5.1, we perform an eigenvalue analysis and show that only the second and fourth order accurate interpolation operators constructed in [20] are norm-contracting. However, the eigenvalue analysis of the spatial operator in Sect. 5.1 seems to suggest, see Table 3, that the scheme with the sixth other accurate interpolation operators is stable, indicating that the norm-contracting condition is sufficient but not necessary for stability.

3.1 The Wave Equation with a Non-conforming Grid Interface

The wave equation in the second order form in two space dimensions is

$$\begin{aligned} U_{tt}=U_{xx}+U_{yy}, \end{aligned}$$

(2)

in a domain $\varOmega =[0,1]^2$ and $0\le t\le t_f$. We assume that the initial conditions and boundary conditions are compatible smooth functions with compact support. As a consequence, the true solution U is also smooth. The numerical scheme and analysis in this section are valid with an additional forcing function in (2), although we do not include it for a sake of simplified notations.

In the numerical scheme, we use subscripts x and y to distinguish variables in different spatial directions, and L and R to distinguish variables in different mesh blocks. In addition, bold letters are used to denote the operators in two space dimensions, which are obtained from the corresponding one dimensional operators through the Kronecker product $\varvec{A_x}=A_x\otimes I_y$ and $\varvec{A_y}=I_x\otimes A_y$, where $I_x$ and $I_y$ are identity matrices.

The computational domain is partitioned into two conforming mesh blocks $\varOmega _L$ and $\varOmega _R$ with a grid interface at $x=0.5, y\in [0,1]$. A coarse mesh in $\varOmega _L$ has $n_{xL}\times n_{yL}$ grid points and a fine mesh $\varOmega _R$ has $n_{xR}\times n_{yR}$ grid points. The equality $n_{yR}=2n_{yL}-1$ yields a 1:2 mesh refinement ratio across the interface illustrated in Fig. 1a. Since the true solution is smooth, the proper interface conditions are continuity of the solution and continuity of first normal derivative across the grid interface.

For a simplified notation, we define the matrices Table 2 that are used to pick up solutions along grid interfaces. In each of those matrices, all elements are zero except one element equal to one. The sizes along with the positions of the nonzero element are listed in the second and third column of Table 2. Note that $E_{LR}=E_{RL}^T$.

Table 2 Matrices that are used to pick up solutions on the interface

Next, Eq. (2) is discretized by the SBP finite difference operators in space and the non-conforming grid interface conditions are imposed weakly by the SAT method and interpolation operators. Since the focus here is the numerical treatment of grid interface conditions, we omit the penalty terms for the boundary conditions, which can be constructed as in [22]. The semi-discretized equation corresponding to (2) reads:

$$\begin{aligned}&u_{tt}=\varvec{D_{2xL}}u+\varvec{D_{2yL}}u+SAT_{u1}+SAT_{u2}+SAT_{\partial u}, \end{aligned}$$

(3a)

$$\begin{aligned}&v_{tt}=\varvec{D_{2xR}}u+\varvec{D_{2yR}}v+SAT_{v1}+SAT_{v2}+SAT_{\partial v}, \end{aligned}$$

(3b)

where

$$\begin{aligned} \begin{aligned}&SAT_{u1}=\frac{1}{2}\varvec{H_{xL}^{-1}S_{xL}^T}(\varvec{E_{0L}}u-(E_{LR}\otimes I_{F2C}) v), \\&SAT_{u2}=-\tau \varvec{H_{xL}^{-1}}(\varvec{E_{0L}}u-(E_{LR}\otimes I_{F2C}) v), \\&SAT_{\partial u}=-\frac{1}{2}\varvec{H_{xL}^{-1}}(\varvec{E_{0L}S_{xL}}u- (E_{LR}\otimes I_{F2C}) \varvec{S_{xR}}v), \end{aligned} \end{aligned}$$

(4)

and

$$\begin{aligned} \begin{aligned}&SAT_{v1}=-\frac{1}{2}\varvec{H_{xR}^{-1}S_{xR}^T}(\varvec{E_{0R}v-}(E_{RL}\otimes I_{C2F}) u), \\&SAT_{v2}=-\tau \varvec{H_{xR}^{-1}}(\varvec{E_{0R}v-}(E_{RL}\otimes I_{C2F}) u), \\&SAT_{\partial v}=\frac{1}{2}\varvec{H_{xR}^{-1}}(\varvec{E_{0R}S_{xR}}v- (E_{RL}\otimes I_{C2F}) \varvec{S_{xL}}u). \end{aligned} \end{aligned}$$

(5)

Here, u and v are grid functions in $\varOmega _L$ and $\varOmega _R$ with elements organized column-wise. In Eq. (3a), both $SAT_{u1}$ and $SAT_{u2}$ impose weakly the continuity of the solution across the grid interface, and $SAT_{\partial u}$ imposes weakly the continuity of the first normal derivative. The term $\varvec{S_{xL}^T}$ in $SAT_{u1}$ makes the semi-discretization symmetric with respect to the SBP norms. The penalty parameter $\tau$ in $SAT_{u2}$ controls the strength of the weak enforcement, and its value is determined by the energy method. The penalty terms in Eq. (3b) are constructed in a similar way.

If the grids are conforming, we replace the interpolation operators in (4) and (5) by identity matrices, and recover the numerical scheme in [31] for conforming interface problems.

3.1.1 Stability Analysis by the Energy Method

In the stability analysis below, the norm-contracting property of the interpolation operators is used to derive an energy estimate. The same interpolation operators are used for the Schrödinger equation in [26], but for that case the norm-contracting property is not needed for energy stability. For the Euler equations, the norm-contracting property is not needed when the standard SBP operators are used for the discretization, but needed when upwind SBP operators are used [20].

Theorem 1

If the interpolation operators $I_{F2C}$ and $I_{C2F}$ are norm-compatible and norm-contracting, then the semi-discretization (3) is stable for any $\tau$ such that

$$\begin{aligned} \tau \ge \max \left( \frac{1}{2\alpha h_{xL}}, \frac{1}{2\alpha h_{xR}}\right) . \end{aligned}$$

Proof

Multiplying Eq. (3a) by $u_t^T(H_{xL}\otimes H_{yL})$ and Eq. (3b) by $v_t^T(H_{xR}\otimes H_{yR})$ from the left, and using the equality $E_{LR}=E_{RL}^T$ and the norm-compatible condition in Definition 2, we obtain

$$\begin{aligned}&\frac{d}{dt} \left( u_t^T (H_{xL}\otimes H_{yL})u_t+v_t^T(H_{xR}\otimes H_{yR})v_t\right) \nonumber \\&\quad =\frac{d}{dt} \left( -u^T (M_{xL}\otimes H_{yL})u + u^T (E_{0L}S_{xL}\otimes H_{yL}) u - \tau u^T (E_{0L}\otimes H_{yL}) u\right. \nonumber \\&\quad \quad -\,v^T (M_{xR}\otimes H_{yR}) v - v^T (E_{0R}S_{xR}\otimes H_{yR}) v - \tau v^T (E_{0R}\otimes H_{yR}) v \nonumber \\&\quad \quad -\,u^T (S_{xL}^T E_{LR}\otimes H_{yL} I_{F2C}) v + v^T (S_{xR}^TE_{RL}\otimes H_{yR}I_{C2F}) u \nonumber \\&\quad \quad \left. +\, 2\tau u^T (E_{LR}\otimes H_{yL}I_{F2C}) v -u^T (H_{xL}\otimes M_{yL}) u -v^T (H_{xR}\otimes M_{yR}) v\right) . \end{aligned}$$

(6)

Since the penalty terms for the boundary conditions are omitted, the B matrix of $D_2$ in Definition 1 is adjusted accordingly: the nonzero element corresponding to the omitted boundary condition is changed to zero. Next, the following equality is obtained by moving all terms on the right hand side of (6) to the left

$$\begin{aligned} \frac{d}{dt}\mathcal {E_H^W}=0, \end{aligned}$$

(7)

where

$$\begin{aligned} \mathcal {E_H^W}= & {} u_t^T(H_{xL}\otimes H_{yL})u_t+v_t^T (H_{xR}\otimes H_{yR})v_t \nonumber \\&+\,u^T (M_{xL}\otimes H_{yL}) u - u^T (E_{0L}S_{xL}\otimes H_{yL}) u + \tau u^T (E_{0L}\otimes H_{yL}) u \nonumber \\&+\,v^T (M_{xR}\otimes H_{yR}) v + v^T (E_{0R}S_{xR}\otimes H_{yR}) v + \tau v^T (E_{0R}\otimes H_{yR}) v \nonumber \\&+\,u^T (S_{xL}^T E_{LR}\otimes H_{yL} I_{F2C}) v - v^T (S_{xR}^TE_{RL}\otimes H_{yR}I_{C2F}) u \nonumber \\&-\,2\tau u^T (E_{LR}\otimes H_{yL}I_{F2C}) v+u^T (H_{xL}\otimes M_{yL}) u +v^T (H_{xR}\otimes M_{yR}) v. \end{aligned}$$

(8)

It remains to show that $\mathcal {E_H^W}\ge 0$ for all u and v. In this case, $\mathcal {E_H^W}$ is a discrete energy of the semi-discretized Eq. (3). Since the interpolation operators are norm-contracting, it follows that

$$\begin{aligned} u^T (E_{0L}\otimes H_{yL}) u\ge & {} u^T (E_{0L}\otimes H_{yL}I_{F2C}I_{C2F}) u \\= & {} u^T (E_{0L}\otimes I_{C2F}^TH_{yR}I_{C2F}) u \\= & {} ((E_{0L}\otimes I_{C2F}) u)^T (I_{xL}\otimes H_{yR}) ((E_{0L}\otimes I_{C2F}) u). \end{aligned}$$

Consequently, we have for u:

$$\begin{aligned} u^T (E_{0L}\otimes H_{yL}) u\ge & {} \frac{1}{2} u^T (E_{0L}\otimes H_{yL}) u\nonumber \\&+\, \frac{1}{2}((E_{0L}\otimes I_{C2F}) u)^T (I_{xL}\otimes H_{yR}) ((E_{0L}\otimes I_{C2F}) u), \end{aligned}$$

(9)

and for $\varvec{v}$:

$$\begin{aligned} v^T (E_{0R}\otimes H_{yR}) v\ge & {} \frac{1}{2} v^T (E_{0R}\otimes H_{yR}) v\nonumber \\&+\, \frac{1}{2}((E_{0R}\otimes I_{F2C}) v)^T (I_{xR}\otimes H_{yL}) ((E_{0R}\otimes I_{F2C}) v). \end{aligned}$$

(10)

In addition, Lemma 1 gives:

$$\begin{aligned} \begin{aligned}&M_{xL}=\tilde{M}_{xL}+h_{xL}\alpha (E_{0L}S_{xL})^T (E_{0L}S_{xL}), \\&M_{xR}=\tilde{M}_{xR}+h_{xR}\alpha (E_{0R}S_{xR})^T (E_{0R}S_{xR}), \end{aligned} \end{aligned}$$

(11)

where $\tilde{M}_{xL}$ and $\tilde{M}_{xR}$ are symmetric positive semi-definite matrices. We then substitute (9), (10) and (11) to (8), and obtain

$$\begin{aligned} \mathcal {E_H^W} \ge \Upsilon _1+\Upsilon _2+\Upsilon _3, \end{aligned}$$

where

$$\begin{aligned} \Upsilon _1= & {} u_t^T(H_{xL}\otimes H_{yL})u_t+v_t^T(H_{xR}\otimes H_{yR})v_t+u^T (\tilde{M}_{xL}\otimes H_{yL}) u \\&+\, v^T (\tilde{M}_{xR}\otimes H_{yR}) v+ u^T (H_{xL}\otimes M_{yL}) u + v^T (H_{xR}\otimes M_{yR}) v,\\ \Upsilon _2= & {} h_{xL}\alpha (\varvec{E_{0L}S_{xL}}u)^T \varvec{H_{yL}} (\varvec{E_{0L}S_{xL}}u) \\&-\, (\varvec{E_{0L}S_{xL}}u)^T \varvec{H_{yL}} (\varvec{E_{0L}}u-(E_{LR}\otimes I_{F2C}) v) \\&+\, \frac{\tau }{2}(\varvec{E_{0L}} u-(E_{LR}\otimes I_{F2C}) v)^T \varvec{H_{yL}} (\varvec{E_{0L}} u-(E_{LR}\otimes I_{F2C}) v),\\ \Upsilon _3= & {} h_{xR}\alpha (\varvec{E_{0R}S_{xR}}v)^T \varvec{H_{yR}} (\varvec{E_{0R}S_{xR}}v) \\&-\, (\varvec{E_{0R}S_{xR}}v)^T \varvec{H_{yR}} ((E_{RL}\otimes I_{C2F}) u-\varvec{E_{0R}}v) \\&+\, \frac{\tau }{2}((E_{RL}\otimes I_{C2F}) u-\varvec{E_{0R}} v)^T \varvec{H_{yR}} ((E_{RL}\otimes I_{C2F}) u-\varvec{E_{0R}} v). \end{aligned}$$

Since $\tilde{M}_{xL}$ and $\tilde{M}_{xR}$ are positive semi-definite, it follows $\Upsilon _1\ge 0$. We also need to make sure that $\Upsilon _2\ge 0$ and $\Upsilon _3\ge 0$. Consider $\Upsilon _2$ first and let

$$\begin{aligned} a=\varvec{E_{0L}S_{xL}}u \quad \text {and}\quad b= \varvec{E_{0L}} u-(E_{LR}\otimes I_{F2C})v, \end{aligned}$$

then

$$\begin{aligned} \Upsilon _2 = h_{xL}\alpha a^T \varvec{H_{yL}} a-a \varvec{H_{yL}} b+ \frac{\tau }{2} b^T \varvec{H_{yL}} b. \end{aligned}$$

(12)

We apply Young’s inequality

$$\begin{aligned} a\varvec{H_{yL}}b\le \frac{\delta }{2} a^T \varvec{H_{yL}} a+\frac{1}{2\delta }b^T \varvec{H_{yL}} b \end{aligned}$$

to the second term in (12) with $\delta =2h_{xL}\alpha$, and obtain

$$\begin{aligned} \Upsilon _2\ge \frac{\tau }{2} b^T \varvec{H_{yL}} b-\frac{1}{4h_{xL}\alpha }b^T \varvec{H_{yL}} b \end{aligned}$$

To have $\Upsilon _2\ge 0$, we need $\tau /2\ge 1/(4h_{xL}\alpha )$, which implies $\tau \ge 1/(2h_{xL}\alpha )$. In the same way, we find that to have $\Upsilon _3\ge 0$ it requires $\tau \ge 1/(2h_{xR}\alpha )$. Therefore, for any

$$\begin{aligned} \tau \ge \max \left( \frac{1}{2\alpha h_{xL}}, \frac{1}{2\alpha h_{xR}}\right) , \end{aligned}$$

we have $\mathcal {E_H^W}\ge 0$ and an energy estimate is obtained so that (3) is stable. $\square$

If the mesh size is the same in the x and y directions, then $h_{xR}=\frac{1}{2}h_{xL}$ and

$$\begin{aligned} \tau \ge \frac{1}{\alpha h_{xL}} \end{aligned}$$

results in an energy estimate.

Although there is no upper bound for the parameter $\tau$ from the energy analysis, it is not good to choose a very large value because then a small time step must be used for stability.

3.1.2 Convergence Rate

We discuss the accuracy property of (3) by analyzing the truncation error of (3a). Equation (3b) can be analyzed in a similar way. The truncation errors of the SBP operators $\varvec{D_{2xL}}$ and $\varvec{D_{2xR}}$ are both $\mathcal {O}(h^{2p})$ in the interior and $\mathcal {O}(h^p)$ near the interface. In the first penalty term $SAT_{u1}$ in Eq. (4), the truncation error is dominated by an interpolation error $\mathcal {O}(h^p)$ located at the corners of mesh blocks connected by the non-conforming grid interface. Due to the $h^{-1}$ factor in both $\varvec{H_{x}^{-1}}$ and $\varvec{S_{xL}^T}$, the largest truncation error of $SAT_{u1}$ is therefore $\mathcal {O}(h^{p-2})$ and is localized at a few grid points. Similarly, we find that the largest truncation errors of $SAT_{u2}$ and $SAT_{\partial u}$ are $\mathcal {O}(h^{p-2})$ and $\mathcal {O}(h^{p-1})$, and are localized at a few grid points. The number of such grid points is independent of mesh sizes. Consequently, the dominated truncation error of the semi-discretization (3a) is $\mathcal {O}(h^{p-2})$ localized at a finite number of grid points.

In [32], the convergence of the SBP-SAT discretization of the second order wave equation in one space dimension with a grid interface is analyzed. The result is that if the penalty parameter is chosen strictly larger than the limit value required for stability, the truncation error $\mathcal {O}(h^p)$ localized at a few grid points near the grid interface results in an error $\mathcal {O}(h^{p+1})$ in the solution for $p=1$, and an error $\mathcal {O}(h^{p+2})$ for $p\ge 2$. In other words, we gain one order in convergence if $p=1$ and two orders if $p\ge 2$.

In our case, the spatial dimension is two and there is the possibility of another gain in convergence. That is, the number of grid points with truncation error $\mathcal {O}(h^{p-2})$ is finite and independent of mesh sizes. Hence, the H-norm (equivalent to the standard L$_2$ norm in finite dimension) of this truncation error is $\mathcal {O}(h^{p-1})$, and is one order higher than the pointwise truncation error. Therefore, we can hope to get an extra gain in convergence comparing with the corresponding one dimensional case.

By a convergence test in Sect. 5, we find that the extra gain is one order, which gives a total gain of two orders for $p=1$ and three orders for $p\ge 2$. That is, the truncation error $\mathcal {O}(h^{p-2})$ localized at a few grid points results in an error $\mathcal {O}(h^{p})$ in the solution for $p=1$, and an error $\mathcal {O}(h^{p+1})$ for $p\ge 2$. To obtain this convergence rate, it is important to note that the penalty parameter must be strictly larger than the value required for stability.

Comparing with the case with only conforming grid interfaces, the convergence rate obtained in our numerical experiments is one order lower. Even though a non-conforming grid interface allows for a local mesh refinement, the loss of accuracy may attenuate its efficiency in practice. To overcome the accuracy reduction by the non-conforming grid interfaces, we have tried to build interpolation operators with error $\mathcal {O}(h^{2p})$ in the interior and error $\mathcal {O}(h^{p+1})$ near the ends of the interface, based on both diagonal and block norm SBP operators by using the symbolic software MAPLE and the approach presented in [20]. However, we could not find a solution to the resulting system of equations.

Fig. 2

Non-conforming mesh blocks with T-junction interfaces

3.2 An Extension to T-junction Interfaces

So far, we have only considered conforming mesh blocks as shown in Fig. 1a, b. The grid at the interface between the two mesh blocks on the left in Fig. 1b is conforming. It is then in many cases desirable not to consider it as a grid interface, but to use the mesh shown in Fig. 2a instead, where the interface forms a T-junction and the mesh blocks become non-conforming. This is because SBP operators have a larger truncation error near the grid interface than in the interior. The usage of redundant grid interfaces results in additional errors in the solution. Moreover, avoiding T-junction interfaces may lead to a bad partitioning of the computational domain with many unnecessary mesh blocks. However, one has to deal with an extra difficulty: near the interface intersection point in Fig. 2a, the SBP norm in the vertical direction has the interior weights in the left mesh block, and the boundary weights in the two mesh blocks on the right. As a consequence, the norm-compatible condition is violated and no energy estimate can be derived.

In [25], T-junction operators are constructed to make the SBP norms compatible at a T-junction interface, and are used in the numerical scheme of solving the advection equation and the Schrödinger equation in the SBP-SAT framework. Stability is proved by the energy method, but it comes with the cost that the T-junction operators introduce an extra contribution to the truncation error of $\mathcal {O}(h^{p-1})$ for the advection equation and $\mathcal {O}(h^{p-2})$ for the Schrödinger equation. Such errors occur even there is no hanging nodes in the mesh, though they are only localized at a few grid points near the T-junction intersection point. The T-junction operators in [25] can also be used together with the interpolation operators to handle non-conforming grid interfaces. One constraint for the T-junction operators is that the interface intersection point must be a grid point in all involved mesh blocks, for example a close-up T-junction interface in Fig. 2b. It is not straightforward to handle the T-junction interface shown in Figure 2c by the same technique. This kind of problem can be handled by the projection operators, which are used in this paper and discussed in Sect. 4.

4 Non-conforming Grid Interfaces and Mesh Blocks Handled by Projection Operators

In [14], a new methodology of handling grid interfaces is introduced. In contrast to the interpolation operators which are based on a direct interpolation technique, the new methodology is based on a projection method. The highlights are that there is no strict requirement on the mesh refinement ratio, and the mesh blocks do not need to be conforming.

To illustrate how the projection method works, we consider again the mesh $\varOmega$ shown in Figure 1a, and denote $y_L$ in $\varOmega _L$ and $y_R$ in $\varOmega _R$ the grids on the interface. In addition, $z_L$ and $z_R$ denote the discrete finite difference solutions on $y_L$ and $y_R$. In a general setting, eight projection operators are used to move $z_L$ and $z_R$ between the two grids on the interface. Firstly, the discrete finite difference solution $z_L$ is projected by a projection operator $P_{f2p}^L$ to a piecewise polynomial function on the grid $y_L$. By a piecewise polynomial function on a grid, we mean that the function is a polynomial in each grid interval between any two adjacent grid points, but is not necessarily continuous at any grid point. The associated mass matrix $M^L$ on $y_L$ is diagonal positive definite since orthogonal polynomials are used as the basis functions. Next, the glue grid y with the mass matrix $M^g$ is defined as the grid that consists of the grid points on both $y_L$ and $y_R$. The projection operator $P_{p2g}^L$ is used to project the piecewise polynomial function from $y_L$ to y, and is viewed as a basis transformation between polynomial spaces. Similarly, $P_{p2f}^L$ and $P_{g2p}^L$ are projection operators in the reversed direction corresponding to $P_{f2p}^L$ and $P_{p2g}^L$, respectively. $P_{f2p}^R$, $P_{p2f}^R$, $P_{p2g}^R$ and $P_{g2p}^R$ are the corresponding projection operators for the grid $y_R$. For a more detailed discussion, we refer to the theory in §2 and the illustration in Figure 2.2 in [14].

When using the projection operators, the penalty terms for the interface coupling are constructed on the glue grid. To this end, we define the operators

$$\begin{aligned} P_{f2g}^L=P_{p2g}^L P_{f2p}^L\quad \quad P_{f2g}^R=P_{p2g}^R P_{f2p}^R \end{aligned}$$

(13)

and

$$\begin{aligned} P_{g2f}^L=P_{p2f}^LP_{g2p}^L\quad \quad P_{g2f}^R=P_{p2f}^R P_{g2p}^R \end{aligned}$$

(14)

that project the discrete finite difference solution directly to the glue grid, and vice versa. The operators $P_{f2g}^{L/R}$ and $P_{g2f}^{L/R}$ have a projection error $\mathcal {O}(h^{2p})$ in the interior and $\mathcal {O}(h^p)$ near the ends of the interface with $p=1,2,3,4,5$.

As described in Sect. 3, the interpolation operators interpolate between two finite difference grids. The projection operators, on the other hand, project between a finite difference grid and a glue grid. The projection operators in [14] satisfy an analog of the norm-compatible condition in Definition 2.

Definition 4

Let $P_{f2g}$ and $P_{g2f}$ be projection operators projecting between a finite difference grid and a glue gird. They are called norm-compatible if

$$\begin{aligned} H P_{g2f}=(M^g P_{f2g})^T, \end{aligned}$$

(15)

where H is the diagonal SBP norm on the finite difference grid and $M^g$ is the diagonal mass matrix on the glue grid.

4.1 The Wave Equation with a Non-Conforming Grid Interface

We start by considering a non-conforming grid interface with conforming mesh blocks, and define

$$\begin{aligned} I_{L2R}= P_{g2f}^R P_{f2g}^L \text { and } I_{R2L}= P_{g2f}^L P_{f2g}^R. \end{aligned}$$

(16)

The operator $I_{L2R}$ projects the discrete finite difference solution from the grid on the left to the grid on the right, and $I_{R2L}$ projects in the other direction. Therefore, $I_{L2R}^p$ and $I_{R2L}^p$ in (16) can be used to impose grid interface conditions in the same way as the interpolation operators discussed in Sect. 3. In addition, $I_{L2R}^p$ and $I_{R2L}^p$ have similar accuracy property as the interpolation operators in [20]. For energy stability, we need the following lemma.

Lemma 2

If the projection operators in (13) and (14) are norm-compatible according to Definition 4, then the operators $I_{L2R}$ and $I_{R2L}$ defined in (16) satisfy

$$\begin{aligned} H_{R}I_{L2R}=(H_{L}I_{R2L})^T, \end{aligned}$$

where $H_L$ and $H_R$ are the diagonal SBP norms at the grids on the left and on the right of the interface, respectively. In this case, $I_{L2R}$ and $I_{R2L}$ are norm-compatible according to Definition 2.

Proof

The proof follows in a direct calculation by using (16) and Definition 4.

$$\begin{aligned} H_{R}I_{L2R}= & {} H_{R}P_{g2f}^R P_{f2g}^L=\big (M^g P_{f2g}^R\big )^T P_{f2g}^L \\= & {} \big (\big (P_{f2g}^L\big )^T M^g P_{f2g}^R\big )^T=\big (H_{L} P_{g2f}^L P_{f2g}^R\big )^T=\big (H_{L}I_{R2L}\big )^T. \end{aligned}$$

$\square$

We have the following theorem for the stability of the scheme using projection operators to handle a non-conforming grid interface.

Theorem 2

Consider the semi-discretization (3) with $I_{C2F}$ and $I_{F2C}$ replaced by $I_{L2R}$ and $I_{R2L}$ in (16). If $I_{L2R}$ and $I_{R2L}$ defined in (16) are norm-compatible and norm-contracting, then the semi-discretization is stable for any $\tau$ such that

$$\begin{aligned} \tau \ge \max \left( \frac{1}{2\alpha h_{xL}}, \frac{1}{2\alpha h_{xR}}\right) . \end{aligned}$$

The proof of Theorem 2 follows in the same way as for Theorem 1. In Sect. 5.1, we provide an eigenvalue analysis to examine if the operators $I_{L2R}$ and $I_{R2L}$ are norm-contracting. The accuracy discussion in Sect. 3.1.2 is also valid for the schemes with the operators $I_{L2R}$ and $I_{R2L}$. However, the interpolation operators $I_{C2F}(I_{F2C})$ are not the same as $I^p_{L2R}(I^p_{R2L})$ in (16). The latter one has a wider stencil.

In the construction procedure of the interpolation operators and projection operators, one gets a system of linear equations after imposing stability and accuracy requirements. The solution of the linear system has a few free parameters. There are different ways to tune those free parameters. In [20], the free parameters are used to minimize the coefficients of the leading interpolation error in L$_2$ norm, while in [14] the free parameters are used to minimize the distance between nearest eigenvalues of $P_{p2f}P_{f2p}$ for a finite difference grid of size 64. The choice of tuning free parameters has no influence on the theoretical order of accuracy, but may have an impact on whether the operators are norm-contracting and the practical accuracy. The comparison between the interpolation operators and projection operators is made in more detail in the numerical experiments in Sect. 5.

4.2 The Wave Equation with a T-junction Interface

The projection technique is very flexible to handle grid interfaces in the sense that we are free to choose the interface structure, the mesh refinement ratio and the accuracy of the diagonal norm SBP operators. In [14], the authors also couple the SBP finite difference method with the discontinuous Galerkin method, inspired by the relation between the discontinuous Galerkin spectral element method and the SBP-SAT finite difference method [7].

If a T-junction interface is present in the mesh, for example in Fig. 2, we cannot use $I_{L2R}^p$ and $I_{R2L}^p$ in a direct way. This is because near the junction point the SBP norm has the interior weights on one side while boundary weights on the other side, and no energy estimate can be obtained. To overcome the instability, the coupling is done on the glue grid. (This reduces to use $I_{L2R}^p$ and $I_{R2L}^p$ in (16) directly when there is no T-junction interface in the mesh.) That is, we project finite difference solutions to the glue grid, compute the penalty terms there, and project them back to the finite difference grids. In this way, we avoid the instability caused by the SBP norms since the penalty terms are computed on the common glue grid.

For completeness, in “Appendix 1”, we derive an SBP-SAT finite difference discretization of the wave equation (2) on the mesh shown in Fig. 2a by using the projection operators to handle the T-junction interface. The energy analysis for the scheme is also given in “Appendix 1”.

5 Numerical Experiments

In this section, numerical experiments are performed to compare the schemes with the interpolation operators [20] and the projection operators [14], and verify their stability and accuracy properties. Moreover, we also give two practical examples to study local mesh refinement by solving the wave equation on a domain with a complex geometry.

The diagonal norm SBP operators used in the numerical experiments can be found in [28] for $D_1\approx \partial /\partial x$ and in [23] for $D_2\approx \partial ^2/\partial x^2$ up to eighth order accuracy. The corresponding operators of tenth order accuracy can be found in [19]. The SBP operators approximating second derivative with variable coefficient are in [18] up to sixth order accuracy.

The L$_2$ error and maximum error are computed as the norm of the difference between the exact solution $u^{ex}$ and the numerical solution $u^h$ according to

$$\begin{aligned}&\Vert u^h-u^{ex}\Vert _{\text {L}_2}=\sqrt{h^d(u^h-u^{ex})^T(u^h-u^{ex})}, \\&\Vert u^h-u^{ex}\Vert _{\infty }=\max |u^h-u^{ex}|, \end{aligned}$$

where d is the spatial dimension of the equation. The convergence rate is computed by

$$\begin{aligned} q=\log \left( \frac{\Vert u^h-u^{ex}\Vert }{\Vert u^{2h}-u^{ex}\Vert }\right) \bigg / \log \left( \frac{1}{2}\right) . \end{aligned}$$

5.1 Stability Study

We begin with an eigenvalue analysis to determine if the interpolation operators in [20] and projection operators in [14] are norm-contracting. The computational domain is $x\in [-1,1]$ and $y\in [0,1]$ with a grid interface at $x=0$. In the left domain the number of grid points is 26 in both x and y directions, while in the right domain the number of grid points is 51 in both x and y directions. The mesh refinement ratio is 1:2 across the grid interface, which makes both the interpolation operators and projection operators applicable. The matrices $\Xi _L$ and $\Xi _R$, constructed as in Definition 3, are symmetric, so they have real eigenvalues. We denote $k_L$ and $k_R$ the smallest eigenvalue of $\Xi _L$ and $\Xi _R$, scaled by the mesh size:

$$\begin{aligned} k_L=\min (\text {eig}(\Xi _L))/h_{yL} \quad k_R=\min (\text {eig}(\Xi _R))/h_{yR}. \end{aligned}$$

In Table 3, we list $k_L$ and $k_R$ for the interpolation operators and the projection operators in Column three and four, respectively. The second and fourth order accurate interpolation operators are norm-contracting with errors up to machine precision. For the second order accurate case, we can prove that $k_L,k_R\ge 0$ independent of h, because $\Xi _L$ is diagonally dominant and $\Xi _R$ can be transformed to a diagonally dominant matrix without changing the signs of the eigenvalues. For the sixth and eighth order cases, the interpolation operators are not norm-contracting. The difference between these two cases is that $k_L$ and $k_R$ for the eighth order case are about two magnitudes larger than $k_L$ and $k_R$ for the sixth order case in absolute value. When increasing the number of grid points, the values of $k_L$ and $k_R$ remain unchanged.

The projection operators are norm-contracting in the second and fourth order accurate cases as well. The sixth, eighth and tenth order accurate projection operators are not norm-contracting, but the values of $k_L$ and $k_R$ are a few magnitude smaller than those for the sixth order accurate interpolation operators in absolute value, and they approach slightly to zero as the mesh is refined.

Table 3 IO: interpolation operators, PO: projection operators

Another way of analyzing stability through numerical experiments is to write the semi-discretized equation (3) as a system of ordinary differential equations

$$\begin{aligned} \varvec{z_{tt}=Qz+F}, \end{aligned}$$

(17)

where $\varvec{Q}$ is the discretization operator including the interface and outer boundary treatment, and $\varvec{F}$ contains the outer boundary data. It is stable if the eigenvalues of $\varvec{Q}$ are real and non-positive. We have computed the eigenvalues of $\varvec{Q}$ by using the same mesh as for the computation of $k_L$ and $k_R$. All the eigenvalues are real. In Table 3, the largest eigenvalue of $\varvec{Q}$ (without any mesh size scaling) is shown in Column five and six for the schemes with the interpolation operators and projection operators, respectively.

The numerical scheme with interpolation operators is stable for the second and fourth order cases, which agrees with the stability analysis in Theorem 1. Though we cannot derive an energy estimate for the sixth order accurate scheme, the eigenvalue analysis shows that for this particular setting the scheme is stable. In addition, we find that the largest eigenvalue of Q does not change with a refined mesh. The scheme is not stable for the eighth order case, since the largest eigenvalue of Q is positive and grows when the mesh is refined. The numerical schemes with the projection operators are stable for all cases even though only second and fourth order accurate projection operators are norm-contracting. Moreover, the largest eigenvalue of Q does not change with a refined mesh. The eigenvalue analysis indicates that the norm-contracting property implies stability, but is not necessary.

5.2 Accuracy Study

In this section, the convergence of the SBP-SAT method applied to the wave equation (2) with a non-conforming grid interface and non-conforming mesh blocks is investigated. The analytical solution to (2) is manufactured, which means that a closed form is chosen and is used to obtain the initial and boundary data. At the outer boundaries, Dirichlet boundary condition is imposed weakly by the SAT method as described in [22]. The penalty parameter $\tau$ is chosen 1.5 times its limit value required by stability for both interface and boundary treatment.

5.2.1 A Non-conforming Grid Interface

In the first numerical experiment, the computational domain is $[-1,1]\times [0,1]$ where a grid interface is located at $x=0,\ y\in [0,1]$. In the grid refinement level $r=0$, the numbers of grid points in the left block and right block are $26\times 26$ and $51\times 51$. The mesh sizes are halved in both x and y directions when r is increased by one. In this setting, the grid refinement ratio is 1:2, and both the interpolation operators and the projection operators are applicable for the numerical treatment of interface conditions. We choose the final time $T=2$, and use the fourth order Runge–Kutta method as the time integrator with the step size in time chosen so small that the temporal error is negligible compared with the spatial error.

The manufactured solution to (2) is chosen to be

$$\begin{aligned} U(x,y,t)=\cos (5x+1)\cos (5y+2)\cos (5\sqrt{2}t+3). \end{aligned}$$

(18)

Fig. 3

Convergence test for the case with a non-conforming grid interface. a Interpolation operators, b projection operators

In Fig. 3a, the L$_2$ error of the solution computed by the SBP-SAT scheme with the interpolation operators is plotted versus the number of grid points in the x direction in the left block. The time step is $\Delta t=0.1h$. The convergence rates in $\hbox {L}_2$ norm are about 1, 3 and 4 for the second, fourth and sixth order schemes, respectively. Though the sixth order accurate scheme lacks a stability proof, it seems that for this particular setting the scheme is stable and exhibits the expected convergence rate. Instability occurs when using the eighth order accurate scheme.

The corresponding results with the projection operators are plotted in Fig. 3b. The convergence rate in L$_2$ norm is about one for the second order accurate scheme, and $p+1$ for the fourth, sixth, eighth and tenth order accurate schemes. We note that though we cannot derive an energy estimate for the sixth, eighth and tenth order accurate cases, the schemes are stable and converge as expected. The time step is $\Delta t=0.1h$ for $2p=2,4,6$. With this time step, the tenth order accurate scheme yields slightly lower convergence rate than expected, and the result shown in Fig. 3b is obtained with $\Delta t=0.05h$. The eighth order accurate scheme is a special one, since with $\Delta t=0.05h$ it is even unstable. To obtain the result in Fig. 3b, $\Delta t=0.025h$ is used as the time step, which indicates that the eighth order accurate semi-discretized equation is stiff. This is not surprising because the $\alpha$ value in the borrowing trick is very small for the eighth order accurate case, which in return leads to a very large $\tau$ value in the penalty term that increases stiffness. Moreover, the error obtained with the eighth order accurate scheme is larger than the error obtained with the sixth order accurate scheme, except for the finest mesh refinement level.

From Fig.3a, b, it is also observed that the errors are similar to each other for the schemes of the same order of accuracy with interpolation operators and projection operators.

5.2.2 A T-junction Interface

Next, we consider the computational domain $[-1,1]^2$ that is divided into three mesh blocks as shown in Fig. 2a. The interfaces are located at $x=0,y\in [-1,1]$ and $y=0,x\in [0,1]$. In the grid refinement level $r=0$, the numbers of grid points in Block 1 (left), Block 2 (top-right) and Block 3 (bottom-right) are $28\times 51$, $27\times 25$ and $51\times 50$, respectively. The mesh sizes are halved in both x and y directions when r is increased by one. This partitioning and meshing result in a highly non-conforming grid interface with a close-up shown in Fig. 2c. The interface conditions are imposed weakly by the SAT method with the projection operators. To test convergence, (18) is used as the analytical solution. The computational results are shown in Fig. 4.

Fig. 4

Convergence test for the case with a T-junction, highly non-conforming interface

Clearly, $(p+1)$th convergence rate in L$_2$ norm is obtained for $p=2,3,4,5$ and first order convergence rate is obtained for $p=1$. Here, we observe again that the schemes higher than fourth order accuracy are stable even though we cannot derive an energy estimate.

5.3 Some Practical Examples

In many applications, the frequency of the present wave is given by initial and boundary data, and internal forcing functions. The wavelength of a wave is determined by the ratio between the wave speed of the material in which the wave is traveling and the frequency of the wave. The accuracy of a numerical solution can be stated in terms of how many grid points per wavelength are used to resolve the present waves [15]. For waves with a fixed frequency content, a reduction in wave speed confined to a subset of the physical domain yields waves of a shorter wavelength localized in that subset. For accuracy it is therefore necessary to refine the grid to compensate for the shorter present wavelengths. For computational efficiency it is important that this refinement is done only in the subset that constitutes the slower medium, since it is only in the slower medium that wavelengths are reduced. As an example, Fig. 5 shows the scattering and diffraction of an acoustic time-harmonic plane wave impinging on a circular region of a slower material, the wavelength is seen to be reduced inside the circular region.

Fig. 5

An example of an acoustic time-harmonic plane wave impinging on a circular inclusion, where the wavelength is much smaller inside the circular inclusion than that outside

Geometrical features of the physical domain such as a curved boundary or an internal cavity introduces a local radius of curvature. A small local radius of curvature compared with the present wavelengths can imply difficulties when generating a computational grid. As an example, Fig. 6a shows the scattering of an acoustic time-harmonic plane wave impinging on a circular cavity of a radius of curvature smaller than the wave length of the incoming and scattered waves. A part of the grid used to represent the wave field is shown as an inset, where it is seen in Fig. 6b that the quality of the grid is impaired as the grid spacing gets unnecessarily small close to the cavity.

Fig. 6

An example of an acoustic time-harmonic plane wave impinging on a circular cavity with a grid, where close to the cavity the grid size in the azimuthal direction is much smaller than that in the radial direction. a A circular cavity, b a close-up of the mesh near the cavity

In the preceding experiments it has been verified that using interpolation operators [20] and projection operators [14] to patch together the computational grid in a multi-block fashion yields a stable discretization, the convergence rate, however, was seen to be reduced. In the following experiments we give examples of the practical benefit of using interpolation operators and projection operators in a region with a slower wave speed or a geometrical feature of a small radius of curvature, albeit the reduction in order of accuracy. In particular, we will consider experiments involving acoustic waves impinging on a circular cavity and a circular inclusion of a differing material.

The numerical method used to solve the acoustic wave equation in the following experiments is based on the SBP-SAT scheme described in [31]. The geometrical features are handled by using a multi-block strategy to decompose the physical domain into blocks, where each block allows for a mapping to curvilinear coordinates. In [31] the blocks that constitute the domain are discretized by using conforming grids and patched together by the SAT method. In this paper we allow for non-conforming grids by implementing interpolation operators as well as projection operators into the handling of the multi-block interfaces.

The following numerical experiments use two different two dimensional domains:

• $\mathcal {D}_1$: An acoustic plane with a circular cavity of radius a.

• $\mathcal {D}_2$: An acoustic plane with a circular inclusion of radius a.

The geometries of the domains are handled by decomposing each domain in a multi-block fashion, and a curvilinear grid is used in each domain to resolve the curved boundaries. The blocks are then patched together to compound the entire domain. A detailed description of how these two grids are constructed is presented in “Appendix 2”.

5.3.1 A Circular Cavity

In this numerical experiment, we consider a domain of an infinite homogeneous medium with wave speed $c > 0$. A circular cavity of radius $a=1$ is centered at the origin. Let a plane harmonic wave $u_I=e^{i(\omega t-\gamma x)}, \gamma =\omega /c$ propagate in that domain and impinge on the cavity. A scattered wave $u_S$ is generated when the incident wave hits the cavity, and the total displacement $u_I+u_S$ satisfies the wave equation. On the boundary of the cavity a homogeneous Neumann boundary condition

$$\begin{aligned} \frac{\partial }{\partial n}(u_I + u_S) = 0, \text {on}\ x^2+y^2 = 1 \end{aligned}$$

is imposed. Here $\frac{\partial }{\partial n}$ denotes the normal derivative on the boundary of the cavity. A detailed derivation of an analytical solution to this problem is found in [8, §7].

Fig. 7

Computational domain of the circular cavity experiment. a N-partitioning, b T-partitioning

We take $\omega =2\pi$ and $c=2.5$, which give a wavelength of 2.5. The computational domain $\mathcal {D}_1$ is chosen to be the rectangle $[-25.5,11.7]\times [-11.7,11.7]$ with the cavity centered at the origin. Two ways of partitioning the domain are considered, namely the N-partitioning and the T-partitioning shown in Fig.  7a and 7b, respectively. In the N-partitioning approach, we only use conforming gird interfaces and conforming mesh blocks. The cavity is surrounded by four blocks that constitute the square $[-11.7,11.7]^2$, which is attached to a rectangular domain on its left hand side. The numbers of grid points on each edge are shown in Fig. 7a, and are chosen so that approximately 20 grid points per wavelength are used in the discretization. In this setting, the mesh is of bad quality since the mesh size near the cavity is significantly smaller than the mesh size near the outer boundaries. To overcome this drawback, we propose the T-partitioning where the cavity is surrounded by a small square block $[-1.3,1.3]^2$. Here, all the grid interfaces are also conforming but a T-junction interface is present at $x=-11.7$ with the intersection points marked by the dots. Again we choose the mesh size so that there are approximately 20 grid points per wavelength, and here it is only over-resolved in the small block $[-1.3,1.3]^2$. The T-partitioning results in a mesh of 54903 grid points. The number of grid points with the N-partitioning is about doubled to 109867.

Fig. 8

Relative maximum error of the numerical experiment with the circular cavity. a Fourth order accurate scheme, b sixth order accurate scheme

We employ the fourth and sixth order SBP-SAT method to propagate the wave for ten temporal periods with the T-junction interface handled by the projection operators [14], and show the recorded relative maximum errors in Fig. 8a, b. The relative maximum error is computed as the maximum error scaled by the maximum absolute value of the analytical solution in space and time. In both cases, the relative maximum error with the T-partitioning is about three times larger than that with the N-partitioning. The is not surprising because the mesh with the T-partitioning has less grid points than the mesh with the N-partitioning, and the corresponding scheme with the T-partitioning has one order lower convergence rate than that of the N-partitioning. It does not seem to improve the efficiency by using T-junction interfaces for this case.

Although using T-junction interfaces introduces a larger error in the solution, it could be beneficial for a problem with a more complex geometry. For example, if there are several cavities in the domain, an N-partitioning that only allows conforming mesh blocks would produce a large number of small mesh blocks. With a higher order accurate scheme, the boundary stencil gets wider and the number of grid points in each direction must be large enough in every mesh block. It is therefore over-resolved in those small mesh blocks and results in a suboptimal performance of the numerical scheme, and T-junction interfaces could be desirable.

5.3.2 A Circular Inclusion

Consider a circular domain of radius $a=1$ embedded in an infinite surrounding medium of differing material with wave speed c. Let the wave speed $c'$ of the circular domain be such that $c'<c$ and let an incoming time-harmonic plane wave $u_I(x,y,t) = e^{i(\omega t - \gamma x)}, \gamma =\frac{\omega }{c}$ travel in the x-direction and impinge on the circular inclusion. The resulting field consists of the incoming wave $u_I$, as well as the scattered and diffracted waves $u_S$ and $u_D$, respectively. The conditions at the interface of the circular inclusion are

$$\begin{aligned} \begin{aligned}&u_I + u_S = u_D,\\&c \frac{\partial }{\partial n}\left( u_I + u_S\right) = c' \frac{\partial }{\partial n} u_D, \end{aligned} \text {on}\ x^2 + y^2 = 1, \end{aligned}$$

(19)

where $\frac{\partial }{\partial n}$ denotes the normal derivative on the interface. Since $c'<c$, the short wavelength occurs inside the circular domain. An analytical expression for the solution is given in [2, p. 667].

Fig. 9

Computational domain of the circular inclusion experiment: solid lines are the boundary, dashed lines are the conforming interfaces, and the dashed-dot lines in red are either conforming or non-conforming interfaces (Color figure online)

In the numerical experiments we take $\omega = 2 \pi$, $c=1$ and $c' = 1/10$, which give a wavelength of 1 and 1 / 10 outside and inside the circular inclusion, respectively. To resolve the geometric features, the computational domain is decomposed into 10 conforming blocks as shown in Fig. 9. We set the length of the side of the square block outside the circular inclusion to $2D = 2.6$, and set the length of the side of the square inside the circular inclusion to $2d = 0.7\sqrt{2}$. Both square blocks are centered at the origin. The Cartesian block $[-5.9,-1.3]\times [-1.3,1.3]$ is then attached to the left of this representation. Firstly, we only use conforming grid interfaces with the numbers of grid points in each block given in Table 4. The resolution outside the circular inclusion is about 16 and 51 points per wavelength in the horizontal and vertical direction, respectively. Inside the circular inclusion the waves are resolved by about 10 grid points per wavelength in both directions. Hence, the waves are significantly over-resolved in the vertical direction outside the inclusion, which leads to a suboptimal distribution of grid points.

To amend the over-resolution, we partition the computational domain in the same way as above but use non-conforming interfaces denoted by the red dashed-dot line in Fig. 9. The non-conforming grid interfaces with refinement ration 1:2 are handled by the interpolation and projection operators. The numbers of grid points in each block are chosen as in Table 5. Now the resolution is reduced to about 26 grid points per wavelength in the vertical direction outside the circular inclusion. The interface conditions (19) are imposed numerically with the SAT technique and at outer boundaries the exact solution is injected at all times. In [6], the SBP finite difference method applied to the wave equation with the injection method to impose the Dirichlet boundary condition is proved to be stable.

Table 4 Number of grid points with conforming grid interfaces

Table 5 Number of grid points with non-conforming grid interfaces

Fig. 10

Relative maximum error of the numerical experiment with the circular inclusion. a Fourth order accurate scheme, b sixth order accurate scheme

The solution is propagated numerically for 10 temporal periods by the SBP-SAT method and the relative maximum error is recorded at each time step. In Fig. 10a, b we plot the recorded relative maximum error as functions of time. Here we see that the errors are similar in both cases. The grid with conforming interfaces has 46460 grid points, whereas the grid with non-conforming interfaces has 38710 grid points. The smallest grid size is determined by the resolution inside the circular inclusion, for this reason the time step $\Delta t = 4 \times 10^{-4}$ for the sixth order SBP-SAT method and $\Delta t = 5 \times 10^{-4}$ for the fourth order SBP-SAT method are the same for both grids. We conclude that even though the formal order of accuracy is lowered by using blocks with non-conforming interfaces it can be a beneficial strategy within the SBP-SAT framework when the physical domain contains regions that require a higher density of grid points. We also note that for more complex multi-block domains consisting of a larger number of blocks the benefits of using blocks with non-conforming grid interfaces are expected to increase.

In the experiment with the sixth order SBP-SAT scheme with the interpolation operators, the numerical solution blows up quickly, which indicates that the scheme is unstable. The corresponding scheme with the projection operators is stable. According to the stability analysis in Sect. 5.1, for the sixth order accurate scheme neither the interpolation operator nor the projection operator is norm-contracting. If the smallest eigenvalue of $\Xi _{L/R}$ is non-negative, then an energy estimate is obtained and ensures stability. The smallest eigenvalue of $\Xi _{L/R}$ scaled by the mesh size is in the magnitude of $-10^{-1}$ for the sixth order accurate interpolation operator, and $-10^{-5}$ for the sixth order accurate projection operator. The violation of norm-contracting condition for the projection operator is much weaker than for the interpolation operator.

6 Conclusion and Outlook

In this work, high order accurate SBP finite difference operators are used to discretize the wave equation in the second order form on a block-structured mesh. Adjacent mesh blocks are patched together by imposing suitable interface conditions via the SAT technique. The emphasis is placed on the numerical treatment of non-conforming grid interfaces by the interpolation operators and projection operators, which are also compared in terms of the stability and accuracy properties. In contrast to first order hyperbolic equation, energy stability of the scheme for the second order wave equation introduces an additional condition on the numerical treatment of non-conforming grid interfaces. This condition is satisfied for the second and fourth order accurate cases, and an energy estimate is derived. For higher order accurate schemes, the additional stability condition is violated. We show by the eigenvalue analysis that the violation is stronger with interpolation operators than with projection operators. Unphysical growth is observed in the numerical experiments with high order interpolation operators, whereas with projection operators the scheme is stable in all the experiments we have conducted.

We have also performed a truncation error analysis and an investigation of the convergence property for the scheme, which indicates that the convergence rate is one order lower than that in the corresponding case with conforming grid interfaces and mesh blocks. We present two practical examples of problems with a complex geometry: a circular cavity and a circular inclusion, where we show that it could be beneficial to use non-conforming grid interfaces or mesh blocks.

For high order accurate interpolation operators and projection operators, there are free parameters left in the construction process. It is desirable to tune the free parameters so that the additional stability condition is satisfied. However, the resulting nonlinear problem seems difficult to solve. To overcome the accuracy reduction, more accurate interpolation operators or new ways of imposing interface conditions are needed.

Appendices

Appendix 1

We use L, $R^1$ and $R^2$ as subscripts or superscripts to distinguish variables in the left, bottom-right and top-right blocks in the mesh shown in Fig. 2a. The grid functions u, $v_1$ and $v_2$ are the numerical solution vectors in $\varOmega _L$, $\varOmega _{R^1}$ and $\varOmega _{R^2}$, respectively. The mesh blocks are non-conforming, and the grid interfaces can be non-conforming as well. Furthermore, there is no strict restriction on the mesh refinement ratio.

1.1 Semi-discretization

In the following, we construct the penalty terms for the numerical treatment of the T-junction interface conditions. The penalty terms for the outer boundaries are omitted. The semi-discretized equation reads

$$\begin{aligned} \begin{aligned} u_{tt}&=\varvec{D_{2xL}+D_{2yL}}u+SAT_{u1}+SAT_{u2}+SAT_{\partial u}, \\ \begin{pmatrix} v_1 \\ v_2 \end{pmatrix}_{tt}&=\varvec{\begin{pmatrix} D_{2xR^1}+D_{2yR^1} &{}\, \\ \,&{}\quad D_{2xR^2}+D_{2yR^2} \end{pmatrix}}\begin{pmatrix} {v_1} \\ {v_2} \end{pmatrix}+SAT_{v1}+SAT_{v2}+SAT_{\partial v}, \end{aligned} \end{aligned}$$

(20)

where

$$\begin{aligned} \begin{aligned}&SAT_{u1}=\frac{1}{2}\varvec{H_{xL}^{-1}S_{xL}^T}\left( \varvec{E_{0L}}u- \varvec{I_{R2L}}\begin{pmatrix} v_1 \\ v_2 \end{pmatrix} \right) , \\&SAT_{u2}=-\tau \varvec{H_{xL}^{-1}}\left( \varvec{E_{0L}}u- \varvec{I_{R2L}}\begin{pmatrix} v_1 \\ v_2 \end{pmatrix} \right) , \\&SAT_{\partial u}=-\frac{1}{2}\varvec{H_{xL}^{-1}}\left( \varvec{E_{0L}S_{xL}}u-\varvec{I_{R2L}} \begin{pmatrix} \varvec{S_{xR^1}} &{}\, \\ \,&{}\quad \varvec{S_{xR^2}} \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \end{pmatrix}\right) , \\&\varvec{I_{R2L}}=(E_{0L}\otimes P_{g2f}^L) \varvec{I_{v_1v_2}^u} \begin{pmatrix} E_{LR^1}\otimes P_{f2g}^{R^1} &{}\, \\ \,&{}\quad E_{LR^2}\otimes P_{f2g}^{R^2} \end{pmatrix}, \end{aligned} \end{aligned}$$

(21)

and

$$\begin{aligned} \begin{aligned}&SAT_{v1}=-\frac{1}{2}\begin{pmatrix} \varvec{H_{xR^1}^{-1}S_{xR^1}^T} &{} \\ &{} \varvec{H_{xR^2}^{-1}S_{xR^2}^T} \end{pmatrix}\left( \begin{pmatrix} \varvec{E_{0R^1}} &{}\, \\ \,&{}\quad \varvec{E_{0R^2}} \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \end{pmatrix} - \varvec{I_{L2R}}u \right) , \\&SAT_{v2}=-\tau \begin{pmatrix} \varvec{H_{xR^1}^{-1}} &{} \\ &{} \varvec{H_{xR^2}^{-1}} \end{pmatrix}\left( \begin{pmatrix} \varvec{E_{0R^1}} &{}\, \\ \,&{}\quad \varvec{E_{0R^2}} \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \end{pmatrix} - \varvec{I_{L2R}}u \right) , \\&SAT_{\partial v}=\frac{1}{2}\begin{pmatrix} \varvec{H_{xR^1}^{-1}} &{}\, \\ \,&{}\quad \varvec{H_{xR^2}^{-1}} \end{pmatrix}\left( \begin{pmatrix} \varvec{E_{0R^1}S_{xR^1}} &{}\, \\ \,&{}\quad \varvec{E_{0R^2}S_{xR^2}} \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \end{pmatrix} - \varvec{I_{L2R}S_{xL}}u \right) , \\&\varvec{I_{L2R}}=\begin{pmatrix} E_{R^1L}\otimes P_{g2f}^{R^1} &{}\, \\ \,&{}\quad E_{R^2L}\otimes P_{g2f}^{R^2} \end{pmatrix} \varvec{I_u^{v_1v_2}} (E_{0L}\otimes P_{f2g}^L). \end{aligned} \end{aligned}$$

(22)

The elements in the matrices $\varvec{I_{v_1v_2}^u}$ and $\varvec{I_u^{v_1v_2}}$ are either zero or one. These two matrices are used to pick up the solution along the interface and put it in the right place for coupling.

1.2 Energy Analysis

We note that there is a similarity between the semi-discretization (20) and (3). Comparing the penalty terms in (21) with the penalty terms in (4), the difference is that $E_{LR}\otimes I_{F2C}$ in (4) is replaced by $\varvec{I_{R2L}}$ in (21). Similarly, $E_{RL}\otimes I_{C2F}$ in (5) is replaced by $\varvec{I_{L2R}}$ in (22). As a consequence, the energy analysis for (20) follows in the same way as in Theorem 1, if the corresponding norm-compatible condition (Definition 2) and the norm-contracting condition (Definition 3) are satisfied.

For the T-junction interface in consideration, the norm-compatible condition is

$$\begin{aligned} \begin{pmatrix} H_{yR^1}P_{g2f}^{R^1} &{}\, \\ \,&{}\quad H_{yR^2}P_{g2f}^{R^2} \end{pmatrix}P_{f2g}^L=\left( H_{yL}P_{g2f}^L\begin{pmatrix} P_{f2g}^{R^1} &{} \,\\ \,&{}\quad P_{f2g}^{R^2} \end{pmatrix}\right) ^T, \end{aligned}$$

(23)

and the norm-contracting condition is that the matrices

$$\begin{aligned} \begin{aligned}&H_{yL}\left( I_{yL}-P_{g2f}^L\begin{pmatrix} P_{f2g}^{R^1} &{}\, \\ \,&{}\quad P_{f2g}^{R^2} \end{pmatrix}\begin{pmatrix} P_{g2f}^{R^1} &{}\, \\ \,&{}\quad P_{g2f}^{R^2} \end{pmatrix}P_{f2g}^L\right) ,\\&\begin{pmatrix} H_{yR^1} &{}\, \\ \,&{}\quad H_{yR^2} \end{pmatrix}\left( \begin{pmatrix} I_{yR^1} &{}\, \\ \,&{}\quad I_{yR^2} \end{pmatrix}-\begin{pmatrix} P_{g2f}^{R^1} &{}\, \\ \,&{}\quad P_{g2f}^{R^2} \end{pmatrix}P_{f2g}^L P_{g2f}^L\begin{pmatrix} P_{f2g}^{R^1} &{}\, \\ \,&{}\quad P_{f2g}^{R^2} \end{pmatrix}\right) \end{aligned} \end{aligned}$$

(24)

are symmetric positive semi-definite. It is straightforward to prove (23) by using (15) in Definition 4, so (23) is satisfied for all the projection operators in [14]. However, the validation of the norm-contracting property relies on eigenvalue analyse. We have performed an eigenvalue analysis for the particular mesh setting used in Sect. 5.2.2, and found that the norm-contracting condition is satisfied for the second and fourth order accurate cases. The validation remains with a refined mesh.

Appendix 2

We give a detailed description for the construction of the two grids used in the efficiency studies in Sect. 5.3. A general block $\mathcal {B}_i$ of a decomposition has four boundaries defined by the parametrized curves

$$\begin{aligned} \begin{aligned}&\mathcal {C}_{iS} = \left( x_{iS}(\xi ),y_{iS}(\xi )\right) ,\quad \mathcal {C}_{iN} = \left( x_{iN}(\xi ),y_{iN}(\xi )\right) ,\\&\mathcal {C}_{iW} = \left( x_{iW}(\eta ),y_{iW}(\eta )\right) , \quad \mathcal {C}_{iE} = \left( x_{iE}(\eta ),y_{iE}(\eta )\right) , \end{aligned} \end{aligned}$$

where $0\le \xi \le 1, 0\le \eta \le 1$. $\mathcal {C}_{iS}$ and $\mathcal {C}_{iN}$ describe one pair of opposing sides and $\mathcal {C}_{iW}$ and $\mathcal {C}_{iE}$ the other pair. Let $\mathcal {P}_{iSW}$ denote the point of intersection between the curves $\mathcal {C}_{iS}$ and $\mathcal {C}_{iW}$ e.t.c. A bijection $(x,y) = \mathcal {T}_i(\xi ,\eta )$ from the unit square $\mathcal {S} = [0,1]^2$ to the block $\mathcal {B}_i$ of the decomposition is given by the transfinite interpolation [12] as

$$\begin{aligned} \mathcal {T}_i(\xi ,\eta )= & {} (1-\eta ) \mathcal {C}_{iS} + \eta \mathcal {C}_{iN} + (1-\xi ) \mathcal {C}_{iW} + \xi \mathcal {C}_{iE}\\&-\,\xi \eta \mathcal {P}_{iNE} - \xi (1-\eta ) \mathcal {P}_{iSE} - \eta (1-\xi ) \mathcal {P}_{iNW} - (1-\xi )(1-\eta )\mathcal {P}_{iSW}. \end{aligned}$$

The unit square $\mathcal {S}$ is discretized by the points

$$\begin{aligned} \begin{aligned}&\xi _j = j h_{\xi }, h_{\xi } = 1/(N_{i\xi }-1), \quad j = 0, \dots , N_{i\xi }-1,\\&\eta _k = k h_{\eta }, h_{\eta } = 1/(N_{i\eta }-1), \quad k = 0, \dots , N_{i\eta }-1, \end{aligned} \end{aligned}$$

where $N_{i\xi }$ and $N_{i\eta }$ are integers determining the number of grid points in the spatial directions of the discretization of the block $\mathcal {B}_i$. The corresponding grid points are computed as

$$\begin{aligned} (x_j,y_k) = \mathcal {T}_i(\xi _j,\eta _k). \end{aligned}$$

We now give details on how the grids in $\mathcal {D}_1 - \mathcal {D}_2$ are constructed. $\mathcal {D}_1$ represents a circular cavity in an infinite surrounding medium. We construct the computational grid such that the cavity of radius a is centered inside a square of side 2D. This is done by introducing four blocks $\mathcal {B}^{(1)}_1$–$\mathcal {B}^{(1)}_4$. The bounding curves of block $\mathcal {B}^{(1)}_1$ are given by

$$\begin{aligned} \begin{aligned}&\mathcal {C}^{(1)}_{1S} = a\left( \xi \sqrt{2} - 1/\sqrt{2}, \sqrt{1-(\xi \sqrt{2} - 1/\sqrt{2})^2}\right) ,\\&\mathcal {C}^{(1)}_{1N} = \left( D, 2D \xi - D\right) ,\\&\mathcal {C}^{(1)}_{1W} = \left( -\eta (D-a/\sqrt{2}) - a/\sqrt{2}, \eta (D-a/\sqrt{2}) + a/\sqrt{2}\right) ,\\&\mathcal {C}^{(1)}_{1E} = \left( \eta (D-a/\sqrt{2}) + a/\sqrt{2}, \eta (D-a/\sqrt{2}) + a/\sqrt{2}\right) . \end{aligned} \end{aligned}$$

The bounding curves of the remaining blocks $\mathcal {B}^{(1)}_2$–$\mathcal {B}^{(1)}_4$ that constitute the square with the cavity at the center are obtained via rotation by a factor $\pi /2$,

$$\begin{aligned} \mathcal {C}^{(1)}_{ij} = \mathcal {C}^{(1)}_{i-1j} \begin{bmatrix} \cos {\pi /2}&\quad -\sin {\pi /2}\\ \sin {\pi /2}&\quad \cos {\pi /2}\end{bmatrix},\quad i = 2,3,4,\ \ j = S,N,W,E. \end{aligned}$$

The domain $\mathcal {D}_1$ can now be represented by attaching the grid representing the cavity to one or more Cartesian blocks.

The circular inclusion of $\mathcal {D}_2$ is decomposed into five blocks $\mathcal {B}^{(2)}_1$–$\mathcal {B}^{(2)}_5$. The block $\mathcal {B}^{(2)}_1$ is a square at the center of the circular inclusion with corners at the points $(\pm ad,\pm ad), 0 < d < \sqrt{2}/2$ defined by the bounding curves,

$$\begin{aligned} \begin{aligned}&\mathcal {C}^{(2)}_{1S} = a\left( 2d \xi -d, -d\right) ,\ \mathcal {C}^{(2)}_{1N} = a\left( 2d\xi -d, d\right) ,\\&\mathcal {C}^{(2)}_{1W} = a\left( -d, 2d\eta -d\right) ,\ \mathcal {C}^{(2)}_{1E} = a\left( d, 2d\eta -d\right) . \end{aligned} \end{aligned}$$

Here a is the radius of the circular inclusion. The block $\mathcal {B}^{(2)}_2$ is defined by its bounding curves,

$$\begin{aligned} \begin{aligned}&\mathcal {C}^{(2)}_{2S} = \mathcal {C}^{(2)}_{1N},\\&\mathcal {C}^{(2)}_{2N} = \mathcal {C}^{(1)}_{1S},\\&\mathcal {C}^{(2)}_{2W} = a\left( -\eta (\sqrt{2}/2-d)-d, \eta (\sqrt{2}/2-d) + d\right) ,\\&\mathcal {C}^{(2)}_{2E} = a\left( \eta (\sqrt{2}/2-d) + d, \eta (\sqrt{2}/2-d) + d\right) . \end{aligned} \end{aligned}$$

The bounding curves of the remaining blocks $\mathcal {B}^{(2)}_3$–$\mathcal {B}^{(2)}_5$ that constitute the circular inclusion of $\mathcal {D}_2$ are obtained via rotations by a factor $\pi /2$ as in (6). The inclusion is then centered inside a square of side 2D by attaching it to the blocks $\mathcal {B}^{(1)}_1$–$\mathcal {B}^{(1)}_4$ above. The circular inclusion is now the union of the nine blocks $\mathcal {B}^{(1)}_1$–$\mathcal {B}^{(1)}_4$ and $\mathcal {B}^{(2)}_1$–$\mathcal {B}^{(2)}_5$. The domain $\mathcal {D}_2$ can now be represented by attaching the grid representing the inclusion to one or more Cartesian blocks.