Constrained TV$_p$-$\ell _2$ Model for Image Restoration

Abstract

The popular total variation (TV) model for image restoration (Rudin et al. in Phys D 60(1–4):259-268, 1992) can be formulated as a Maximum A Posteriori estimator which uses a half-Laplacian image-independent prior favoring sparse image gradients. We propose a generalization of the TV prior, referred to as TV$_p$, based on a half-generalized Gaussian distribution with shape parameter p. An automatic estimation of p is introduced so that the prior better fits the real images’ gradient distribution; we will show that, in general, the estimated p value does not necessarily require to be close to zero. The restored image is computed by using an alternating directions methods of multipliers procedure. In this context, a novel result in multivariate proximal calculus is presented which allows for the efficient solution of the proposed model. Numerical examples show that the proposed approach is particularly efficient and well suited for images characterized by a wide range of gradient distributions.

1 Introduction

Image restoration refers to the recovery of a clean sharp image from a noisy, and potentially blurred, observation. In this paper, we consider the problem of restoring images corrupted by known blur and additive white Gaussian noise. Without loss of generality, we consider grayscale images with a square $d \times d$ domain. Let $u \in {\mathbb R}^{d^2}$ be the unknown clean image concatenated into a column vector, $K \in {\mathbb R}^{d^2 \times d^2}$ be a known linear blurring operator and $n \in {\mathbb R}^{d^2}$ be an unknown realization of the random noise process, which we assume additive white Gaussian with zero mean. The discrete model of the image degradation process which relates the observed corrupted image $g \in {\mathbb R}^{d^2}$ to the clean image u can be expressed as follows:

$$\begin{aligned} g \,\;{=}\;\, K u \,\;{+}\;\, n. \end{aligned}$$

(1)

Given K and g, our goal is to solve the inverse problem of recovering an as accurate as possible estimate $u^{*}$ of the clean image u, which is known as non-blind deconvolution or deblurring. Since the blurring operator is typically very ill-conditioned or even singular, some sort of regularization is required in order to get meaningful estimates.

The following regularization approach, representing the well known TV-$\ell _2$ or ROF model [23], is largely used:

$$\begin{aligned} u^{*} \;{\leftarrow }\; \mathrm {arg} \min _{u \in {\mathbb R}^{d^2}} \left\{ \, \mathrm {TV}(u) + \frac{\mu }{2} \, \Vert K u - g \Vert _2^2 \, \right\} , \end{aligned}$$

(2)

where TV(u) denotes the discrete TV semi-norm of image u defined as

$$\begin{aligned} \mathrm {TV}(u) \,\;{:=}\;\, \sum _{i=1}^{d^2} \Vert (\nabla u)_i \Vert _2 \, , \end{aligned}$$

(3)

and $( \nabla u)_i := (D_{x,i} u,D_{y,i} u)$ denotes the discrete gradient of u at pixel i and $D_{x,i}$, $D_{y,i}$ represent the i th rows of the x- and y-directional finite difference operators $D_x, D_y \in {\mathbb R}^{d^2 \times d^2}$.

Model (2–3) has been recognized as a successful image restoration model, especially for sparse gradient images, that is it reconstructs very well piecewise-constant images.

The TV seminorm is the $\ell _1$ norm of the image gradient magnitude, and the minimization of the $\ell _1$ norm is known to promote sparsity in its argument. Recently, there has been interest in employing nonconvex $\ell _p$ quasinorms with $0<p<1$ for sparsity exploiting image reconstruction, which is potentially more effective than $\ell _1$, but it results in nonconvex optimization problems, see [26].

In this paper we will consider the more general formulation

$$\begin{aligned} u^{*} \;{\leftarrow }\; \mathrm {arg} \min _{u \in {\mathbb R}^{d^2}} \left\{ \, \mathrm {TV}_p(u) + \frac{\mu }{2} \Vert K u - g \Vert _2^2 \, \right\} , \end{aligned}$$

(4)

where the TV$_p$ regularization term is given by:

$$\begin{aligned} \mathrm {TV}_p(u) \,\;{:=}\;\, \sum _{i=1}^{d^2} \Vert (\nabla u)_i \Vert _2^p, \end{aligned}$$

(5)

with $p>0$.

Under the discrepancy principle [8], the unconstrained model in (4–5) can be formulated as the following constrained optimization problem:

$$\begin{aligned} u^* \,\;{\leftarrow }\;\, \mathrm {arg} \min _{u \in {\mathcal {S}}} \mathrm {TV}_p(u), \end{aligned}$$

(6)

with the feasible set defined as

$$\begin{aligned} {\mathcal {S}} \;{=}\; \left\{ \, u \in {\mathbb R}^{d^2}{:}\;\, \Vert K u - g \Vert _2 \;{\le }\; \tau \sigma d \, \right\} , \end{aligned}$$

(7)

where $\tau >0$ is a pre-determined scalar parameter controlling the standard deviation of the residue image $K u - g$. In the following we will refer to (5–7) as the proposed TV$_p$-$\ell _2$ model.

The benefit of the constrained form (6–7) with respect to the unconstrained form (4) is twofold: first, the parameter $\sigma$ in (7), representing the standard deviation of noise corrupting the observed image g, can be more naturally estimated than the regularization parameter $\mu$ in (4), see [32]; second, this form is more convenient for assessing p-dependence of the reconstructed images independently on $\mu$, see [26]. Actually, as we will discuss later, in our proposal the parameter p is automatically estimated from the observed image.

We notice that the TV$_p$ regularizer in (5) differs from the proposals in [17, 33], and [15] for which the regularization term is not a function of the $\ell _2$-norm of the gradient, but of the absolute value of first/second-order differences. The latter approach gives raise to an anisotropic regularization. As observed in [19], even though rotational invariance is not well defined in the discrete setting, the former choice yields image restorations of better quality than the latter. In [15], for example, the restoration models incorporate $\ell _p$normbased analysis priors, applying linear operators to u, and $p=0.5$ is used only in the numerical experiments.

In [19, 21] and [26] the TV$_p$ regularizer is instead considered in the context of image reconstruction and restoration. In [19] an interesting investigation on the properties of minimizers of generic nonconvex nonsmooth functionals is carried out, and two minimization methods are presented which, however, differ significantly from our proposal. The popular iteratively reweighted norm (IRN) method is proposed in [21] for minimizing the so called generalized total variation (TV) functional, which can include the TV$_p$ regularizer. Both [19] and [21] minimize unconstrained functionals in the form (4). In [26] the regularizer (5) is called TpV and applied in the context of image reconstruction.

However, the three mentioned proposals essentially rely on a fixed p value with $0<p<1$ for exploiting gradient sparsity. On the contrary, we will propose not only an efficient algorithm for the constrained minimization problem involving the regularizer in (5), but, supported by the MAP formulation presented, we are also able to provide a probabilistically founded procedure for the automatic estimate of the parameter p.

In order to solve the TV$_p$-$\ell _2$ model we propose an efficient minimization method based on the ADMM strategy. The ADMM is stable, efficient and in particular faster than most of the state-of-the-art algorithms for solving optimization problems [3, 29].

In [16] an ADMM-based iteratively reweighted algorithm is proposed for the solution of a hybrid variational deblurring model, which considers the hyper-Laplacian distributions of the first and second order derivatives. With respect to our proposal in [16] the case $p>1$ is not considered, p is empirically chosen, the algorithm is substantially different, and above all, the regularization term corresponds to the anisotropic TV as defined in [26], instead of the isotropic TV as considered in our model.

The rest of the paper is organized as follows. In Sect. 2 we motivate the choice of the TV$_p$ regularizer and corresponding estimate of the p shape parameter via MAP approach. In Sect. 3 we illustrate the overall ADMM-based algorithm used to solve the proposed constrained TV$_p$-$\ell _2$ model. In Sect. 4 we present a novel result in proximal calculus used for the solution of the critical ADMM optimization subproblem associated with the auxiliary variable representing the image gradient. In Sect. 5 we report experimental results evaluating the performance of the proposed model. In Sect. 6 we draw conclusions.

2 Motivations Via MAP Estimator

A commonly used paradigm for image restoration is the probabilistic MAP approach [13]: the restored image is obtained by maximizing the posterior probability of the unknown clean image u given the observed image g and the blurring operator K, considered as a deterministic parameter. In formulas:

$$\begin{aligned}&u^{*} \,\;{\leftarrow }\;\, \arg \max _{u \in {\mathbb R}^{d^2}} \, \Pr (u|g;K) \nonumber \\&\quad \; \;{\leftarrow }\; \arg \min _{u \in {\mathbb R}^{d^2}} \, \left\{ -\log \Pr (g|u;K) -\log \Pr (u) \right\} , \end{aligned}$$

(8)

where (8) follows by applying the Bayes’ rule, by dropping the evidence term $\Pr (g)$ since it does not depend on u, and by reformulating the maximization as a minimization of the negative logarithm of the posterior. The two terms $\Pr (g|u;K)$ and $\Pr (u)$ represent the likelihood and the prior, respectively [10]. The likelihood term encodes information on the noise model and forces closeness of the estimate $u^{*}$ to the observation g according to such model. The prior term embodies prior knowledge on the unknown clean image u, typically in the form of smoothness constraints.

In case of additive, zero-mean, independent identically distributed (or white) Gaussian noise, the likelihood term takes the following form:

$$\begin{aligned} \Pr (g|u;K) \;{=}\, \prod _{i=1}^{\,d^2} \frac{1}{\sqrt{2 \pi }\sigma } \exp \left( - \frac{(K u - g)_i^2}{2\sigma ^2} \right) \,{=}\, \frac{1}{W} \, \exp \left( - \frac{\left\| K u - g \right\| _2^2}{2 \sigma ^2} \right) , \end{aligned}$$

(9)

where $\sigma$ is the noise standard deviation, $x_i$ and $\Vert x \Vert _2$ denote the ith component and the $\ell _2$-norm of vector x, respectively, and W is a constant term depending on $\sigma$ but not on u.

For what concerns the prior, a common choice is to model the unknown image u as a Markov random field (MRF) [9], such that the image can be characterized by its Gibbs prior distribution, whose general form is:

$$\begin{aligned} \Pr (u) \;{=}\; \frac{1}{Z} \, \prod _{i=1}^{\,d^2} \, \exp \big ( - \alpha \, V_{c_i} (u) \big ) \;{=}\; \frac{1}{Z} \, \exp \bigg ( - \alpha \sum _{i=1}^{d^2} V_{c_i} (u) \bigg ), \end{aligned}$$

(10)

where $\alpha > 0$ is the MRF parameter, $\{c_i\}_{i=1}^{d^2}$ is the set of all cliques (a clique is a set of neighboring pixels) for the MRF, $V_{c_i}$ is the potential function defined on the clique $c_i$ and Z is the partition function, that is a function not depending on u which allows for the normalization of the prior.

Choosing as potential function at the generic ith pixel the magnitude of the discrete gradient at the same pixel, i.e. $V_{c_i}(u) := \Vert (\nabla u)_i \Vert _2$, the Gibbs prior in (10) reduces to the popular TV prior:

$$\begin{aligned} \Pr (u) \;{=}\; \frac{1}{Z} \, \exp \bigg ( - \alpha \sum _{i=1}^{d^2} \Vert (\nabla u)_i \Vert _2 \bigg ). \end{aligned}$$

(11)

Using the TV prior in (11) can be regarded as implicitly assuming that the gradient magnitude at each pixel of the unknown clean image, $\Vert \nabla u \Vert _2$, follows a half-Laplacian (or exponential) distribution, whose probability density function (pdf) is given by:

$$\begin{aligned} \Pr (x;\alpha ) \;{=}\; \left\{ \, \begin{array}{ll} \alpha \exp (-\alpha \, x) &{} \;\; \mathrm {for}\;\; x \ge 0 \\ 0 &{} \;\; \mathrm {for}\; \; x < 0 \end{array} \right. , \end{aligned}$$

(12)

where $\alpha > 0$ is called the scale parameter of the distribution.

Replacing the Gaussian likelihood (9) and the TV prior (11) into the MAP inference formula (8), one gets:

$$\begin{aligned}&u^{*} \leftarrow \arg \min _{u \in {\mathbb R}^{d^2}} \left\{ - \ln \Bigg [ \, \frac{1}{W} \, \exp \left( - \frac{\left\| K u - g \right\| _2^2}{2 \sigma ^2} \right) \Bigg ] \right. \nonumber \\&\qquad \qquad \qquad \qquad \quad \left. - \ln \Bigg [ \, \frac{1}{Z} \, \exp \Bigg ( - \alpha \sum _{i=1}^{d^2} \Vert (\nabla u)_i \Vert _2 \Bigg ) \Bigg ]\right\} . \end{aligned}$$

(13)

Dropping the constant terms in (13) and setting $\mu = 1 / (\alpha \sigma ^2)$, one obtains model (2–3).

However, the half-Laplacian pdf in (12) for gradient magnitudes, implicitly assumed by the TV-$\ell _2$ model, can be too stringent and yield unsatisfactory reconstructions. More precisely, both in case of images characterized by heavy tailed gradient distributions, such as photographic and textured images, and even for images with sparse gradients, the unique degree of freedom embodied by the scale parameter $\alpha$ in the TV prior (11) does not allow for accurate modeling of the actual gradients distribution of the image to be restored.

Some evidence of this problem is given in Fig. 1, where three images characterized by different gradient distributions are shown together with the associated normalized histograms of gradient magnitudes. The superimposed dashed green lines, which represent the half-Laplacian pdfs that best fit the histograms, show how the half-Laplacian distribution does not possess enough flexibility to suitably model these images.

Fig. 1

Top row the three images barbara (left), cameraman (center) and geometric (right). Center row the associated normalized histograms of gradient magnitudes together with the best fitting half-Laplacian distribution (dashed green line) and hGGD (solid red line). Bottom row zoomed details (Color figure online)

In order to tackle this problem, we propose to replace the one-parameter half-Laplacian distribution in (12) for gradient magnitudes with the more flexible two-parameters generalized Gaussian distribution (GGD); see [27, 30, 34] for parametric GGD estimation and [6] for an application of GGD for modelling a reference gradient distribution.

More precisely, since gradient magnitudes are clearly not negative, we consider a half-GGD (hGGD), whose pdf takes the form:

$$\begin{aligned} \Pr (x;\alpha ,p) \;{=}\; \left\{ \begin{array}{ll} \frac{\alpha \, p}{\varGamma (1/p)} \, \exp \big ( - ( \alpha \, x \, )^p \big ) &{} \;\; \mathrm {for}\;\; x \ge 0 \\ 0 &{} \;\; \mathrm {for}\;\; x < 0 \end{array} \right. , \end{aligned}$$

(14)

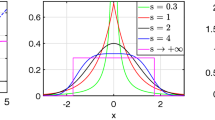
where $\alpha >0$ is the scale parameter, $p>0$ is the shape parameter and $\varGamma$ denotes the Gamma function. This family of distributions covers a wider spectrum of pdfs including half-Laplacian ($p=1$), half-Gaussian ($p = 2$), and uniform ($p \rightarrow \infty$) distributions. In Fig. 2 we illustrate the pdfs of hGGD for a few different values of the shape parameter p when keeping a fixed value $m_2 = 1$ of the second noncentral (or raw) moment, which for the hGGD in (14) takes the form:

$$\begin{aligned} m_2= & {} \int _{-\infty }^{+\infty } x^2 \Pr (x;\alpha ,p) \, dx \,\;{=}\;\, \frac{\alpha \, p}{\varGamma (1/p)} \int _{0}^{+\infty } x^2 \exp \big ( - ( \alpha \, x \, )^p \big ) \, dx \nonumber \\= & {} \frac{\varGamma (3/p)}{\alpha ^2\varGamma (1/p)}. \end{aligned}$$

(15)

By setting $m_2 = 1$, from (15) we have that $\alpha = \sqrt{\varGamma (3/p) / \varGamma (1/p)}$, so that for each considered p value in Fig. 2, namely $p = 0.7, 1, 2, 100$, the associated $\alpha$ value is univocally defined.

Fig. 2

The pdfs of hGGD for different values of the shape parameter p and $m_2 = 1$

In Fig. 1 the superimposed solid red lines represent the hGGDs that best fit the real gradient distributions of the three given images. These distributions derive from (14) by choosing an optimal estimated parameter p as suggested in [27] and briefly summarized at the end of this Section. It is evident from Fig. 1 that the hGGD holds the potential to model gradient magnitudes of images better than the half-Laplacian distribution.

Assuming the hGGD pdf in (14) for gradient magnitudes at each pixel corresponds to choosing the following TV$_p$ Gibbs prior for the unknown clean image u:

$$\begin{aligned} \Pr (u) \;{=}\; \frac{1}{Z} \, \exp \bigg ( - \theta \, \sum _{i=1}^{d^2} \Vert (\nabla u)_i \Vert _2^p \, \bigg ), \end{aligned}$$

(16)

where $\theta = \alpha ^p$. Replacing the Gaussian likelihood (9) and the TV$_p$ prior (16) into the MAP inference formula (8), we obtain a generalization of the TV-$\ell _2$ model (2–3) given by model (5–7).

Estimating the shape parameter p of a hGGD is thus a crucial issue, as a suitably chosen p allows to adapt the prior to the particular image context. In fact, in the image deblurring context, the parameter p does not necessarily need to be close to zero neither lower than one, but, instead, has to guarantee the hGGD which best represents the actual gradient distribution of the particular image to be restored.

We conclude this section by introducing a brief review of the Global Convergence Method (GCM) proposed in [27] for the estimation of the shape parameter p of a GGD model and then verifying how this procedure can be seamlessly used for the estimation of the shape parameter of a hGGD. The usefulness of this estimate will be demonstrated in Sect. 5, where the usage of the estimated shape parameter $p\,$ will provide a substantial improvement of the image restoration results. For an extended review of theoretically and practically comparisons of estimation methods we refer the reader to [34].

As stated in [27], given a random variable X which is distributed according to a zero-mean GGD, the random variable Y defined as

$$\begin{aligned} Y \;{:=}\; | \, \alpha \, X \, |^p \;{=}\; \alpha ^p \, | X |^p \end{aligned}$$

(17)

is gamma-distributed, such that (see equation (2) in [27]) the ratio between the second-order moment and the squared first-order moment of Y is given by:

$$\begin{aligned} \displaystyle { \frac{E \big [ \, Y^2 \, \big ]}{\left( E \big [ \, Y \, \big ] \right) ^2} } \,\;{=}\;\, \displaystyle { \frac{E \left[ \, \alpha ^{2p} \, | \, X \, |^{2p} \, \right] }{\left( E \left[ \, \alpha ^p \, | \, X \, |^p \, \right] \right) ^2} } \,\;{=}\;\, \displaystyle { \frac{E \left[ \, | \, X \, |^{2p} \, \right] }{\left( E \left[ \, | \, X \, |^p \, \right] \right) ^2} } \,\;{=}\;\, p + 1, \end{aligned}$$

(18)

where $E[\,\cdot \,]$ denotes the expectation operator. The following function of the shape parameter p, referred to as shape function, has thus been proposed in [27]:

$$\begin{aligned} Z(p) \,\;{:=}\;\, \displaystyle { \frac{E\left[ \,|X|^{2p}\,\right] }{\left( E\left[ \,|X|^{p}\,\right] \right) ^2} } - (1 + p), \end{aligned}$$

(19)

then the author demonstrates (see Theorem 1 and Theorem 2 in [27]) that the shape equation

$$\begin{aligned} Z(p) \,\;{=}\;\, 0 \end{aligned}$$

(20)

has a unique global root in $]0,+\infty [$ which is equal to the true shape parameter value, and that this root can be obtained by the Newton–Raphson iterative algorithm starting from any initial guess.

Since the true shape parameter value is clearly unknown, the above shape function and shape equation cannot be used in practice. Hence, an empirical (or sample-based) shape function is introduced in [27]:

$$\begin{aligned} Z_m(p) \,\;{:=}\;\, \displaystyle { \frac{\frac{1}{m}\sum _{i=1}^m |x_i|^{2p}}{\left( \frac{1}{m}\sum _{i=1}^m |x_i|^{p}\right) ^2} } - (1 + p), \end{aligned}$$

(21)

where $\{ x_i\}_{i=1}^m$ represents a set of observed samples from the GGD to be estimated. In Theorem 3 of [27] the author proves that the sample-based shape equation

$$\begin{aligned} Z_m(p) \,\;{=}\;\, 0 \end{aligned}$$

(22)

has a unique global root (with probability tending to 1) and that this root tends to the true shape parameter in probability, that is the root of (22) is a consistent estimator of the true shape parameter. Finally, Theorem 4 of [27] demonstrates that the Newton–Raphson functional iteration:

$$\begin{aligned} p^{k+1} = p^k - \frac{Z_m(p^k)}{Z_m^{\prime }(p^k)}, \end{aligned}$$

(23)

where

$$\begin{aligned} Z_m^{\prime }(p)= & {} \frac{\left( \frac{2}{m}\sum _{i=1}^m |x_i|^{2p}\log |x_i|\right) \left( \frac{1}{m}\sum _{i=1}^m |x_i|^{p}\right) ^2}{\left( \frac{1}{m}\sum _{i=1}^m |x_i|^{p}\right) ^4} \nonumber \\&- \frac{\left( \frac{1}{m}\sum _{i=1}^m |x_i|^{p}\log |x_i|\right) \left( \frac{1}{m}\sum _{i=1}^m |x_i|^{2p}\right) \left( \frac{2}{m}\sum _{i=1}^m |x_i|^{p}\right) }{\left( \frac{1}{m}\sum _{i=1}^m |x_i|^{p}\right) ^4}-1, \end{aligned}$$

(24)

converges (with probability tending to 1) to the unique global root of (22) starting from any initial guess.

In our case, we need to estimate the shape parameter of a hGGD. Let X denote a GGD-distributed random variable, then the associated hGGD random variable $\widetilde{X}$ is defined in terms of (i.e., as a function of) X as follows:

$$\begin{aligned} \widetilde{X} \;{:=}\; | X |. \end{aligned}$$

(25)

Hence, the analogous $\widetilde{Y}$ of the variable Y in (17) is given by:

$$\begin{aligned} \widetilde{Y} \;{=}\; \left| \, \alpha \, \widetilde{X} \, \right| ^p \;{=}\; \alpha ^p \, \widetilde{X}^p \;{=}\; \alpha ^p \, | \, X^p \, | \;{=}\; Y. \end{aligned}$$

(26)

It follows from (26) that the GCM estimation formulas (21–24) can be used to estimate the shape parameter $p\,$ of a hGGD.

3 Applying ADMM to the Proposed Model

Constrained problems are in general much more difficult to solve than unconstrained ones [35] as discussed in the introduction. Recently, Chan et al. [3] successfully adapted the ADMM strategy for solving the constrained TV-$\ell _2$ model. In the following we introduce a suitable variant of the basic ADMM approach to solve the proposed constrained minimization problem in (5–6) with the feasible set ${\mathcal {S}}$ defined in (7).

Towards this aim, we first introduce two auxiliary variables t and r to reformulate it into the following equivalent form:

$$\begin{aligned} \{ u^{*},t^*,r^* \}&\;{\leftarrow } \; \mathrm {arg} \min _{u,t,r} \, \left\{ \, \sum _{i=1}^{d^2} \Vert \, t_i \, \Vert _2^p \;{+}\;\, \imath _{{\mathcal {B}}} (r) \right\} \nonumber \\ \mathrm {s.t.}\, :&\;\;\; t = D u , \, r = Ku - g, \end{aligned}$$

(27)

where $D = (D_x;D_y) \in {\mathbb R}^{2d^2 \times d^2}$, $t_i = (D_{x,i} u;D_{y,i} u) \in {\mathbb R}^2$, and $\imath _{{\mathcal {B}}}$ is the indicator function of the feasible set ${\mathcal {B}}$ for the variable r defined as

$$\begin{aligned} {\mathcal {B}} \,\;{=}\; \left\{ \, r \in {\mathbb R}^{d^2} {:}\;\, \Vert r \Vert _2 \;{\le }\; \tau \sigma d \, \right\} , \end{aligned}$$

(28)

with the convention that $\imath _{{\mathcal {B}}}(r)$ takes the value 0 for $r \in {\mathcal {B}}$ and $+\infty$ otherwise [2].

The auxiliary variable t is introduced to transfer the discrete gradient operator $(\nabla u)_i$ out of the possibly non-differentiable non-convex term $\Vert \, \cdot \, \Vert _2^p$. The variable r plays the role of the restoration residue $K u - g$ within the discrepancy principle-based constraint (7) so that the simpler constraint (28) is now imposed on r.

To solve (27), we define the augmented Lagrangian functional

$$\begin{aligned} \mathcal {L}(u,t,r;\lambda _t,\lambda _r)= & {} \sum _{i=1}^{d^2} \Vert \, t_i \, \Vert _2^p \;{+}\; \imath _{{\mathcal {B}}} (r) \nonumber \\&\;{-}\, \langle \, \lambda _{t} \, , \, t - D u \, \rangle \,\;{+}\;\, \frac{\beta _t}{2} \, \Vert \, t - D u \, \Vert _2^2 \nonumber \\&\;{-}\, \langle \, \lambda _{r} \, , \, r - (Ku - g) \, \rangle \,\;\;\;{+}\;\, \frac{\beta _r}{2} \, \Vert \, r - (Ku - g) \, \Vert _2^2 \, , \end{aligned}$$

(29)

where $\beta _t, \beta _r > 0$ are scalar penalty parameters and $\lambda _t$, $\lambda _r$ are the vectors of Lagrange multipliers, $\lambda _t \in Q$, $\lambda _r, \in V$ with $V = {\mathbb R}^{d^2}$, $Q = {\mathbb R}^{2 d^2}$.

Solving (27) is thus equivalent to search for the solutions of the following saddle point problem:

$$\begin{aligned} \mathrm {Find}&\;\, (x^*;\lambda ^*) \;\;{\in }\;\; X \times \Lambda \nonumber \\ \mathrm {s.t.}&\; \mathcal {L}(x^*;\lambda ) \,\;{\le }\;\, \mathcal {L}(x^*;\lambda ^*) \,\;{\le }\;\, \mathcal {L}(x;\lambda ^*) \nonumber \\&\; \forall \, (x;\lambda ) \;\;\;{\in }\;\; X \times \Lambda , \end{aligned}$$

(30)

with $\mathcal {L}$ defined in (29) and where, for simplicity of notations, we set $x = (u,t,r)$, $\lambda = (\lambda _t,\lambda _r)$, $X = V \times Q \times V$ and $\Lambda = Q \times V$.

Starting at $u = u^k$, $r = r^k$, $\lambda _t = \lambda _t^k$, and $\lambda _r = \lambda _r^k$, the ADMM iterative scheme [2] applied to the solution of (27) reads as follows:

$$\begin{aligned}&t^{k+1} \;{\leftarrow }\;\;\,\, \mathrm {arg} \, \min _{t \in Q} \; \mathcal {L}\left( u^k,t,r^k;\lambda _t^k,\lambda _r^k\right) \end{aligned}$$

(31)

$$\begin{aligned}&r^{k+1} \;{\leftarrow }\;\;\,\, \mathrm {arg} \, \min _{r \in V} \; \mathcal {L}\left( u^k,t^{k+1},r;\lambda _t^k,\lambda _r^k\right) \end{aligned}$$

(32)

$$\begin{aligned}&u^{k+1} \;{\leftarrow }\;\;\,\, \mathrm {arg} \, \min _{u \in V} \; \mathcal {L}\left( u,t^{k+1},r^{k+1};\lambda _t^k,\lambda _r^k\right) \end{aligned}$$

(33)

$$\begin{aligned}&\left( \begin{array}{c} \lambda _t^{k+1} \\ \lambda _r^{k+1} \end{array} \right) \;{\leftarrow }\;\; \left( \, \begin{array}{l} \lambda _t^{k} \,\,\;{-}\;\,\, \gamma \, \beta _t \, \big ( \, t^{k+1} \,\;\;{-}\;\, D u^{k+1} \, \big ) \\ \lambda _r^{k} \,\,\;{-}\;\, \gamma \, \beta _r \big ( \, r^{k+1} \;\;{-}\;\, (Ku^{k+1} - g)\, \big ) \end{array} \, \right) , \end{aligned}$$

(34)

where $\gamma$ is a relaxation parameter chosen in the interval $(0,(\sqrt{5} + 1) / 2)$ , as analyzed in [3].

In the following subsections we show in detail how to solve the three minimization sub-problems (31–33) for the variables t, r and u, respectively, then we present the overall iterative ADMM-based minimization algorithm. The minimization sub-problem (31) for the variable t requires a proximal calculus result which will be given in Sect. 4.

3.1 Solving the Sub-problem for t

Given the definition of the augmented Lagrangian functional in (29), the minimization sub-problem for t in (31) can be written as follows:

$$\begin{aligned}&t^{k+1} \;{\leftarrow }\; \mathrm {arg} \, \min _{t \in Q}\, \left\{ \, \sum _{i=1}^{d^2} \left\| t_i \right\| _2^p \;{-}\; \langle \lambda ^k_t , t - D u^k \rangle \;{+}\; \frac{\beta _t}{2} \left\| t - D u^k \right\| _2^2 \,\right\} \nonumber \\&\quad \quad \;{\leftarrow }\; \mathrm {arg} \, \min _{t \in Q}\, \left\{ \, \sum _{i=1}^{d^2} \left\| t_i \right\| _2^p \;{+}\; \frac{\beta _t}{2} \left\| t - \left( D u^k + \frac{1}{\beta _t} \lambda ^k_t \right) \right\| _2^2 \,\right\} \nonumber \\&\quad \quad \;{\leftarrow }\; \mathrm {arg} \, \min _{t \in Q}\, \; \sum _{i=1}^{d^2} \left\{ \left\| t_i \right\| _2^p \;{+}\; \frac{\beta _t}{2} \left\| t_i - \left( \left( D u^k \right) _i + \frac{1}{\beta _t} \left( \lambda ^k_t \right) _i \right) \right\| _2^2 \right\} . \end{aligned}$$

(35)

Note that in (35) the minimized functional is written in explicit component-wise form, with $\left( D u^k \right) _i, \left( \lambda ^k_t \right) _i \in {\mathbb R}^2$ denoting the discrete gradient and the Lagrange multipliers at pixel i, respectively. The minimization in (35) is thus equivalent to the following $d^2$ 2-dimensional problems:

$$\begin{aligned} t^{k+1}_i {\leftarrow }\; \mathrm {arg} \min _{t_i \in {\mathbb R}^2} \left\{ \, \left\| t_i \right\| _2^p \;{+}\; \frac{\beta _t}{2} \left\| t_i - q^k_i \right\| _2^2 \,\right\} , \quad i = 1, \ldots , d^2, \end{aligned}$$

(36)

with the constant vectors $q^k_i \in {\mathbb R}^2$ defined as

$$\begin{aligned} q^k_i \,\;{:=}\;\, \left( D u^k \right) _i + \frac{1}{\beta _t} \left( \lambda ^k_t \right) _i, \quad i = 1, \ldots , d^2. \end{aligned}$$

(37)

The solution of (36) is obtained based on Proposition 1 reported in Sect. 4, that is:

$$\begin{aligned} t_i^{k+1} \;{=}\;\, \xi _i^{k+1} \, q_i^k \, , \quad i = 1, \ldots , d^2, \end{aligned}$$

(38)

where, in particular, the shrinkage coefficients $\,\xi _i^{k+1} \in [0 , 1], \;\, i = 1,\ldots ,d^2 ,\,$ are computed according to statement (50) of Proposition 1. The overall computational cost of this subproblem is linear in the number of pixels $d^2$.

In the context of proximal calculus, (36) can be formulated as

$$\begin{aligned} t^{k+1}_i {\leftarrow }\; \mathrm {prox}_{\beta _t f}(q^k_i), \quad i = 1, \ldots , d^2 \,, \end{aligned}$$

(39)

where $\mathrm {prox}_{\beta _t f}: {\mathbb R}^2 \rightarrow {\mathbb R}^2$ denotes the proximal operator of the function $f(t_i)=\left( \sqrt{t_{i,1}^2+t_{i,2}^2}\right) ^p, t_i \in {\mathbb R}^2$. The solution for the proximal operator (39) will be provided in Sect. 4.

3.2 Solving the Sub-problem for r

Given the definition of the augmented Lagrangian functional in (29), the minimization sub-problem for r in (32) is as follows:

$$\begin{aligned}&r^{k+1} \;{\leftarrow }\;\; \mathrm {arg} \, \min _{r \in {\mathcal {B}}}\, \left\{ \,{-}\, \left\langle \lambda ^k_r , r - \left( K u^k - g \right) \right\rangle \;{+}\; \frac{\beta _r}{2} \left\| r - \left( K u^k - g \right) \right\| _2^2 \,\right\} \nonumber \\&\quad \;{\leftarrow }\;\; \mathrm {arg} \, \min _{r \in {\mathcal {B}}}\, \left\{ \, \frac{\beta _r}{2} \left\| r - \left( K u^k - g + \frac{1}{\beta _r} \lambda ^k_r \right) \right\| _2^2 \;\right\} . \end{aligned}$$

(40)

Recalling that $\beta _r > 0$, the solution of (40) is thus given by a simple Euclidean projection of the $d^2$-dimensional vector

$$\begin{aligned} q^k \,\;{:=}\;\, K u^k - g + \frac{1}{\beta _r} \lambda ^k_r \end{aligned}$$

(41)

onto the feasible set ${\mathcal {B}}$ defined in (28). Since ${\mathcal {B}}$ is nothing else but the $l_2$-ball with radius $\rho = \tau \sigma d$, such a projection can be easily obtained as follows:

$$\begin{aligned} r^{k+1} \,\;{=}\;\, \min \left\{ \, \rho \, , \, \left\| q^k \right\| _2 \, \right\} \frac{q^k}{\left\| q^k \right\| _2}, \end{aligned}$$

(42)

where $0 \cdot ( 0 / 0) = 0$ is assumed. The computational complexity of this sub-problem is clearly linear in the number of pixels $d^2$.

3.3 Solving the Sub-problem for u

The minimization sub-problem for u in (33) can be re-written as follows:

$$\begin{aligned} u^{k+1}&{\leftarrow }&\mathrm {arg} \min _{u \in V}\, \left\{ \,{-}\, \left\langle \lambda ^k_{t} , t^{k+1} - D u \right\rangle \;{+}\; \frac{\beta _t}{2} \left\| t^{k+1} - D u \right\| _2^2 \right. \nonumber \\&\left. \,{-}\, \left\langle \lambda ^k_{r} , r^{k+1} - \left( K u - g \right) \right\rangle \;{+}\; \frac{\beta _r}{2} \left\| r^{k+1} - \left( K u - g \right) \right\| _2^2 \,\right\} \nonumber \\&{\leftarrow }&\mathrm {arg} \, \min _{u \in V}\, \left\{ \,{+}\, \left\langle \lambda ^k_{t} , D u \right\rangle \;{+}\; \frac{\beta _t}{2} \left\| t^{k+1} - D u \right\| _2^2 \right. \nonumber \\&\left. \,{+}\, \left\langle \lambda ^k_{r} , K u \right\rangle \;{+}\; \frac{\beta _r}{2} \left\| r^{k+1} - \left( K u - g \right) \right\| _2^2 \,\right\} , \end{aligned}$$

(43)

where in (43) we omitted the constant terms. Problem (43) is a quadratic minimization problem whose first-order optimality conditions read as follows:

$$\begin{aligned} D^T \lambda ^k_t - \beta _t D^T \left( t^{k+1} - D u \right) + K^T \lambda ^k_r - \beta _r K^T \left( r^{k+1} - \left( K u - g \right) \right) = 0 \end{aligned}$$

(44)

that is

$$\begin{aligned} \left( \beta _t D^T D + \beta _r K^T K \right) u = - D^T \lambda ^k_t + \beta _t D^T t^{k+1} - K^T \lambda ^k_r + \beta _r K^T \left( r^{k+1} + g \right) \end{aligned}$$

(45)

which reduces to the linear system

$$\begin{aligned} \left( D^T D + \frac{\beta _r}{\beta _t} K^T K \right) u = D^T \left( t^{k+1} - \frac{1}{\beta _t} \lambda ^k_t \right) + \frac{\beta _r}{\beta _t} K^T \left( r^{k+1} - \frac{1}{\beta _r} \lambda ^k_r + g \right) . \end{aligned}$$

(46)

The $d^2 \times d^2$ linear system in (46) is solvable if the coefficient matrix has full-rank, that is if the following condition holds:

$$\begin{aligned} \mathrm {Ker}\left( D^T D \right) \;{\cap }\; \mathrm {Ker}\left( K^T K \right) \;{=}\; \{ 0 \}, \end{aligned}$$

(47)

where $\mathrm {Ker}(M)$ denotes the null space of the matrix M and 0 is the $d^2$-dimensional null vector. In image restoration, condition (47) is typically satisfied. In fact, K represents a blurring operator, which is a low-pass filter, whereas the regularization matrix D is usually a difference operator and, hence, is a high-pass filter.

In case that (47) is satisfied, the coefficient matrix in (46) is symmetric positive definite and, typically, is highly sparse. Hence, the linear system in (46) can be solved quite efficiently by the iterative (preconditioned) Conjugate Gradient method. Moreover, under appropriate assumptions about the solution u near the image boundary, the linear system can be solved even more efficiently. For example, under periodic boundary conditions for u both $D^T D$ and $K^T K$ are block circulant matrices with circulant blocks, so that the coefficient matrix in (46) can be diagonalized by the 2D discrete Fourier transform (FFT implementation). However, it is well known that imposing periodic boundary conditions leads to ringing effects in the solution u due to artificially introduced image discontinuities. The use of more natural reflective and anti-reflective boundary conditions in image deblurring has been considered in [20] and [7], respectively. With these choices, no artificial discontinuities near the image boundary are introduced, hence higher quality solutions can be obtained. As illustrated in [20] and [7], under reflective and anti-reflective boundary conditions the coefficient matrix in (46) can be diagonalized by the 2D discrete cosine and sine transforms (FCT and FST implementations), respectively. Provided that the penalty parameters $\beta _t$ and $\beta _r$ are kept fixed for all the ADMM iterations, the coefficient matrix in (46) does not change and it can be diagonalized once for all at the beginning. Therefore, at each ADMM iteration the linear system (46) can be solved by one forward FFT/FCT/FST and one inverse FFT/FCT/FST, each at a cost of $O(d^2 \log d)$.

Finally, we notice that, in image restoration, the requirement for non-negativity of the solution u is sometimes imposed. Such a constraint can be integrated in the sub-problem for u, for example, by following the non-negative quadratic programming strategy proposed in [25] and used, e.g., in [22].

3.4 ADMM Iterative Scheme

To solve the proposed constrained TV$_p$-$\ell _2$ optimization problem in (6–7), or equivalently the split problem in (27), we use the efficient iterative ADMM-based scheme reported in Algorithm 1. The efficiency comes from using a novel proximal operator to solve the subproblem for t, as explained in Sect. 4.

In the field of image and signal processing the ADMM has been one of the most powerful and successful methods for solving various convex or nonconvex optimization problems. In convex settings, numerous convergence results have been established for ADMM as well as its varieties, see for example [12] and references therein. In particular, convergence results cover the proposed TV$_p$-$\ell _2$ model in the special case of $p \ge 1$.

However, for $p < 1$ the ADMM is under nonconvex settings, where there have been a few studies on the convergence properties. To the best of our knowledge, existing convergence analysis of ADMM for nonconvex problems is very limited to particular classes of problems and under certain conditions of the dual step size [11].

Nevertheless, the ADMM works extremely well for various applications involving nonconvex objectives, and this is a practical justification of its wide use.

4 Result on the Proximal Minimization

The proximal operator for solving the L$_p$ non-convex minimization problem for univariate functions was computed in [14] by both the look-up table (LUT) approach and an analytic approach for two specific values of p. However, these approaches cannot be trivially extended to the multidimensional case and general p. In [36] the authors introduce a generalization of soft-thresholding proximal operator for univariate functions and general p and they simply apply it element-wise to the solution of an anisotropic TV. However, the proximal operator (39) cannot be reduced to an element-wise computation of proximal operator of univariate functions thus the proximal operator needs an ad hoc demonstration. Nevertheless we should remark that the proposition below generalizes the result in [36], which corresponds to set the problem dimensionality to $m=1$.

Proposition 1

Let $\beta > 0$, $0 < p < 2$ and $q \in {\mathbb R}^m$ with $m \ge 1$ be given constants. Then, the proximal operator of the m-variate function $f(x)=\left( \Vert x \Vert _2 \right) ^p, x \in {\mathbb R}^m,$ defined as the m-dimensional minimization problem

$$\begin{aligned} x^* \leftarrow prox_{\beta f}(q):= \mathrm {arg} \min _{x \in {\mathbb R}^m} \left\{ \, \phi (x) \;{=}\; \left\| x \right\| _2^p \;{+}\; \frac{\beta }{2} \left\| x - q \right\| _2^2 \,\right\} \end{aligned}$$

(48)

is given by

$$\begin{aligned} x^* \,\;{=}\;\, \xi ^* q \, , \;\;\, \mathrm {where} \;\; \xi ^* \, {\in } \; [0,1] \end{aligned}$$

(49)

with

(50)

where we set

$$\begin{aligned}&\alpha \,\;{:=}\;\, \beta \, \Vert q \Vert _2^{2-p}, \end{aligned}$$

(51)

$$\begin{aligned}&\bar{\alpha } \,\;{:=}\;\, \displaystyle { \frac{\left( 2-p \right) ^{2-p}}{\left( 2-2p \right) ^{1-p}} } \, , \quad \quad \bar{\xi } \,\;{:=}\;\, 2 \, \displaystyle { \frac{1 - p}{2 - p} } \, . \end{aligned}$$

(52)

Proof

In the following, we prove separately the proposition statement in (49) and the four cases (a), (b), (c), (d) of the proposition statement in (50).

Fig. 3

Geometric representation of problem (48) in the 2-dimensional case

Proof of statement (49)

To allow for a clearer understanding of the proof, in Fig. 3 we give a geometric representation of problem (48) in the 2-dimensional case ($m = 2$). First, we prove that the solution $x^*$ of (48) lies on the closed half-line Oq with origin at the m-dimensional null vector O and passing through q, represented in solid red in Fig. 3a. To this purpose, we demonstrate that for every point z not lying on Oq there always exists a point $z^*$ on Oq such that $\phi (z) - \phi (z^*) > 0$. In particular, we define $z^*$ as the intersection point between the half-line Oq and the ($m-1$)-dimensional sphere with center in O and passing through z, depicted in solid blue in Fig.  3a. Noting that $\Vert z^*\Vert _2 = \Vert z \Vert _2$ by construction, we can thus write:

$$\begin{aligned} \phi (z) - \phi (z^*)= & {} \Vert z \Vert _2^p - \Vert z^* \Vert _2^p + \frac{\beta }{2} \left( \Vert z - q \Vert _2^2 - \Vert z^* - q \Vert _2^2 \right) \nonumber \\= & {} \frac{\beta }{2} \left( \Vert z \Vert _2^2 + \Vert q \Vert _2^2 - 2 \, \langle \, z \, , \, q \rangle - \Vert z^* \Vert _2^2 - \Vert q \Vert _2^2 + 2 \, \langle \, z^* \, , \, q \rangle \right) \nonumber \\= & {} \beta \left\langle z^* - z , q \right\rangle \nonumber \\= & {} \beta \left\| z^* - z \right\| _2 \left\| q \right\| _2 cos\left( \widehat{O \, z^* z} \right) >0. \end{aligned}$$

(53)

Hence, the solution $x^*$ of (48) lies on the closed half-line Oq, i.e. $x^* = \xi ^* q$, $\xi ^* \ge 0$. We notice that for $m=1$ the above part of the proof is not necessary.

We now prove that the solution $x^*$ of (48) lies inside the segment [Oq], represented in solid red in Fig. 3b. Towards this aim, by replacing $x = \xi q$, $\xi \ge 0$ we reduce the original m-dimensional minimization problem in (48) to the following equivalent 1-dimensional problem:

$$\begin{aligned}&\xi ^* {\leftarrow }\; \mathrm {arg} \min _{\xi \ge 0} \left\{ \, \left\| \xi q \right\| _2^p \;{+}\; \frac{\beta }{2} \left\| \xi q - q \right\| _2^2 \,\right\} \nonumber \\&\quad {\leftarrow }\; \mathrm {arg} \min _{\xi \ge 0} \left\{ \, \left\| q \right\| _2^p \xi ^p \;{+}\; \frac{\beta }{2} \left\| q \right\| _2^2 \left( \xi - 1 \right) ^2 \,\right\} \nonumber \\&\quad {\leftarrow }\; \mathrm {arg} \min _{\xi \ge 0} \left\{ \, \xi ^p \;{+}\; \frac{\beta }{2} \left\| q \right\| _2^{2-p} \left( \xi - 1 \right) ^2 \,\right\} \nonumber \\&\quad {\leftarrow }\; \mathrm {arg} \min _{\xi \ge 0} \left\{ \, f(\xi ) \;{=}\; \xi ^p \;{+}\; \frac{\alpha }{2} \left( \xi ^2 - 2\xi \right) \,\right\} , \end{aligned}$$

(54)

where in (54) we omitted the constant terms in $f(\xi )$, and $\alpha$ is defined in (51).

We demonstrate that for every point z lying on the half-line Oq but outside the segment [Oq], i.e. $z = \xi _z q$ with $\xi _z > 1$, there always exists a point $z^* = \xi _{z^*} q$ on [Oq] with $\xi _{z^*} \le 1$ such that $f(\xi _z) - f(\xi _{z^*}) > 0$. In particular, it suffices to choose $z^* = q$, that is $\xi _{z^*} = 1$, as illustrated in Fig. 3b. We obtain:

$$\begin{aligned} f(\xi _z) - f(\xi _{z^*}) \,\;{=}\;\, f(\xi _z) - f(1) \,\;{=}\;\, \left( \xi _z^p \;{-}\; 1 \right) \;{+}\; \frac{\alpha }{2} \left( \xi _z - 1 \right) ^2. \end{aligned}$$

(55)

Since $\xi _z > 1$ by construction and $p > 0$ by hypothesis, clearly the two terms $\left( \xi _z^p - 1\right)$ and $\left( \xi _z - 1\right)$ are both positive and cause the expression in (55) to be positive. Hence, the solution $x^* = \xi ^* q$ of the original minimization problem (48) lies in the segment [Oq], i.e. $0 \le \xi ^* \le 1$.

As a consequence of previous demonstration, we can rewrite the initial problem (48) as

$$\begin{aligned} \xi ^* {\leftarrow }\; \mathrm {arg} \min _{0 \le \xi \le 1} \, f(\xi ) \; , \end{aligned}$$

(56)

where, for future references, the first and second order derivatives are given by:

$$\begin{aligned} f'(\xi )= & {} p \, \xi ^{p-1} + \alpha \left( \xi - 1 \right) , \end{aligned}$$

(57)

$$\begin{aligned} f''(\xi )= & {} p \, (p - 1) \, \xi ^{p-2} + \alpha . \end{aligned}$$

(58)

$\square$

Proof of case a) of statement (50)

If $\Vert q \Vert _2 = 0$, that is q is the m-dimensional null vector, the objective function $\phi (x)$ minimized in (48) depends on x only through its $l_2$-norm $\Vert x \Vert _2$. Hence, the minimizers will be all the vectors $x^*$ belonging to the $(m-1)$-dimensional sphere $\Vert x \Vert _2 = r^*$, with radius $r^* \ge 0$ given by the solution of the constrained 1-dimensional problem obtained from (48) by setting $q = 0$ and $r = \Vert x \Vert _2$, that is

$$\begin{aligned} r^* \;{=}\; \mathrm {arg} \min _{r \ge 0} \left\{ \, r^p \;{+}\; \frac{\beta }{2} r^2 \,\right\} . \end{aligned}$$

(59)

Since $\beta > 0$ and $p > 0$ by hypothesis, the function minimized in (59) is continuous and strictly increasing for $r \ge 0$, hence it admits the unique global minimum at $r^* = 0$ and the solution of the original problem (48) is $x^* = 0$. $\square$

Proof of case b) of statement (50)

If $\Vert q \Vert _2 > 0$ and $p = 1$, problem (56) simplifies to:

$$\begin{aligned} \xi ^* {\leftarrow }\; \mathrm {arg} \min _{0 \le \xi \le 1} \left\{ \, f(\xi ) \;{=}\; \frac{\alpha }{2} \, \xi ^2 \;{+}\; \left( 1 - \alpha \right) \xi \,\right\} , \end{aligned}$$

(60)

with $\alpha = \beta \Vert q \Vert _2$ a strictly positive coefficient ($\beta > 0$ by hypothesis). The function $f(\xi )$ minimized in (60) represents a strictly convex parabola passing through the origin and having its unconstrained global minimum at the abscissa of its vertex:

$$\begin{aligned} \xi _{v} \;{=}\; 1 - \frac{1}{\alpha }. \end{aligned}$$

(61)

Therefore, after noting that $\xi _{v} < 1 \;\, \forall \alpha > 0$, for what concern the constrained minimization in (60) we have two cases:

$$\begin{aligned} \xi ^* \;{=}\; \left\{ \begin{array}{lll} \xi _v &{} \; \mathrm {if} \; &{} \xi _v > 0 \\ 0 &{} \; \mathrm {if} \; &{} \xi _v \le 0 \end{array} \right. \;\, , \;\; \mathrm {that} \; \mathrm {is:} \quad \; \xi ^* \;{=}\; \max \left\{ 1 - \frac{1}{\alpha } \, , \, 0 \right\} . \end{aligned}$$

(62)

$\square$

Proof of case c) of statement (50)

If $\Vert q \Vert _2 > 0$ and $1 < p < 2$, then the coefficient $\alpha$ defined in (51) and the term $p (p - 1)$ are both strictly positive; hence, the second derivative $f''(\xi )$ in (58) is strictly positive for $0 < \xi \le 1$ and tends to $+\infty$ as $\xi$ tends to $0^+$, so that the minimized function $f(\xi )$ in (56) is strictly convex. For what concern the sign of the first derivative $f'(\xi )$ defined in (57) we can write:

$$\begin{aligned} f'(\xi ) \lesseqqgtr 0 \;\;\, \mathrm {for} \;\; g_1(\xi ) \lesseqqgtr g_2(\xi ) \, , \;\; \mathrm {with} \;\; g_1(\xi ) = \xi ^{p-1}, \;\; g_2(\xi ) = \displaystyle {\frac{\alpha }{p}} \left( 1 - \xi \right) . \end{aligned}$$

(63)

We note that $g_1(\xi )$ is a power function with exponent $0 < p - 1 < 1$; hence, for every $1 < p < 2$, $g_1(\xi )$ is a continuous, strictly increasing and strictly concave function passing through the points (0,0) and (1,1). $g_2(\xi )$ represents a bundle of straight lines passing through the point (1,0) with negative angular coefficient $-\alpha / p$. In Fig. 4 we show $g_1(\xi )$ and $g_2(\xi )$ for $p = 1.5$ and for two different values $\alpha _1 < \alpha _2$ of $\alpha$, together with the associated objective functions $f(\xi )$ minimized in (56). Clearly, $g_1(\xi )$ and $g_2(\xi )$ admit a unique intersection point with abscissa $0 < \xi ^* < 1$ for every $1 < p < 2$ and $\alpha > 0$, hence $\xi ^*$ is the unique root of equation $f'(\xi ) = 0$. Moreover, since $f(\xi )$ is strictly convex, $\xi ^*$ is the abscissa of the global minimum of $f(\xi )$. $\square$

Fig. 4

Case c) of statement (50). Plot of $g_1(\xi )$ and $g_2(\xi )$ defined in (63) for $p = 1.5$ and for two different values $\alpha _1 < \alpha _2$ of $\alpha$ (left) and plot of the associated minimized functions $f(\xi )$ defined in (56) (right). Red asterisks indicate global minimums of the minimized functions (Color figure online)

Proof of case d) of statement (50)

If $\Vert q \Vert _2 > 0$ and $0 < p < 1$, then $p (p - 1) < 0$, the second derivative $f''(\xi )$ satisfies

$$\begin{aligned} f''(\xi ) \lesseqqgtr 0 \quad \mathrm {for} \quad \xi \lesseqqgtr \xi _{inf} \, , \quad \mathrm {with} \quad \xi _{inf} \;{=}\; \displaystyle { \left( \frac{p \, (1 - p)}{\alpha } \right) ^{\textstyle {\frac{1}{2-p}}}}. \end{aligned}$$

(64)

It can be easily demonstrated that the inflection point at $\xi = \xi _{inf}$ lies inside the considered optimization domain $0 < \xi < 1$ if and only if the following condition on $\alpha$ holds:

$$\begin{aligned} \alpha \,\;{>}\;\, p \, (1 - p). \end{aligned}$$

(65)

If (65) does not hold, $f(\xi )$ does not admit any local minimum in $0 < \xi < 1$. On the contrary, if (65) holds then $f(\xi )$ may admit a local minimum in $\xi _{inf} \le \xi < 1$.

For what concern the first derivative $f'(\xi )$, we notice how the considerations expressed in (63) for the case $1 < p < 2$ are still formally valid, the only substantial difference being in the power function $g_1(\xi )$ having here negative exponent $-1 < p - 1 < 0$. In Fig. 5a we show $g_1(\xi )$ and $g_2(\xi )$ for $p = 0.5$ and for five different $\alpha$ values, and in Fig. 5b–f we depict the associated objective functions $f(\xi )$ to be minimized in (56) where $\hat{\alpha }$ and $\bar{\alpha }$ are defined in (66) and (68), respectively.

We can distinguish the following cases depending on $\alpha$:

• If $\alpha < \hat{\alpha }$ then $g_1(\xi ) > g_2(\xi ) \; \forall \xi$, that is, according to (63), $f'(\xi ) > 0 \; \forall \xi$ thus the global minimum is at $\xi ^* = 0$. See Fig. 5b.

• If $\alpha = \hat{\alpha }$ then $g_1(\xi ) > g_2(\xi )$ everywhere but at $\hat{\xi }$ where $g_1(\xi )$ and $g_2(\xi )$ intersect, that is $f'(\hat{\xi }) = 0$. Therefore, $f(\xi )$ is increasing and presents a stationary point of inflection at $\hat{\xi }$; the global minimum is again at $\xi ^* = 0$. See Fig. 5c. It can be easily demonstrated that:

  $$\begin{aligned} \hat{\alpha } \;{=}\; p \, \frac{\left( 2-p \right) ^{2-p}}{\left( 1-p \right) ^{1-p}} \; , \quad \; \hat{\xi } \;{=}\; \frac{1-p}{2-p} \; , \quad \; f(\hat{\xi }) \;{=}\; \frac{1}{2} \, \left( 1-p \right) ^{1+p} \left( 2-p \right) ^{1-p}. \end{aligned}$$

  (66)

• If $\alpha > \hat{\alpha }$, then $g_1(x)$ and $g_2(x)$ intersect in two points of abscissae $\xi _1$ and $\xi _2$ with $0 < \xi _1 < \hat{\xi } < \xi _2 < 1$; see Fig. 5a. Hence, recalling (63), $f(\xi )$ has two stationary points in ]0, 1[: a local maximum at $\xi = \xi _1$ and a local minimum at $\xi = \xi _2$, where $\xi _1$ and $\xi _2$ are the two roots of the nonlinear equation $f'(\xi )=0$. The local minimum of $f(\xi )$ at $\xi _2$ is a global minimum if and only if $f(\xi _2) < f(0) = 0$. Such a point can be obtained by solving the following system of two nonlinear equations in the two unknowns $\alpha$ and $\xi$:

  $$\begin{aligned} \left\{ \begin{array}{lclcl} f(\xi ) &{} {=} &{} \xi ^p + \displaystyle {\frac{\alpha }{2}} \left( \xi ^2 - 2 \xi \right) &{} \,\;{=}\;\, &{} 0 \\ f'(\xi ) &{} {=} &{} p \, \xi ^{p-1} + \alpha \left( \xi - 1 \right) &{} \,\;{=}\;\, &{} 0 \end{array} \right. \; , \end{aligned}$$

  (67)

  that admits the unique solution:

  $$\begin{aligned} \bar{\alpha } \;{=}\; \displaystyle { \frac{\left( 2-p \right) ^{2-p}}{\left( 2-2 p \right) ^{1-p}} } \; , \quad \quad \bar{\xi } \;{=}\; 2 \, \displaystyle { \frac{1-p}{2-p} } \end{aligned}$$

  (68)

• If $\hat{\alpha } < \alpha < \bar{\alpha }$, with $\hat{\alpha }$ given in (66) and $\bar{\alpha }$ given in (68), then $f(\xi _2(\alpha )) > f(0) = 0$. Hence, the global minimum is again at $\xi ^* = 0$. See Fig. 5d.

• If $\alpha = \bar{\alpha }$, then the minimized function $f(\xi )$ assumes the global minimum $f(\xi ^*) = 0$ both at $\xi = 0$ and at $\xi = \bar{\xi }$, with $\bar{\xi }$ defined in (68). See Fig 5e.

• If $\alpha > \bar{\alpha }$, then the local minimum is the global minimum, that is $\xi ^* = \xi _2(\alpha )$. Therefore, $\xi ^*$ can be obtained by searching for the unique root of $f'(\xi ) = 0$ in $]\bar{\xi },1[$. See Fig. 5f.

This proves case d) of the proposition statement in (50). $\square$

Fig. 5

Case d) of statement (50). Plot of $g_1(\xi )$ and $g_2(\xi )$ defined in (63) for $p = 0.5$ and for five different $\alpha$ values a, and the associated minimized function $f(\xi )$ b–f. a $g_1(\xi )$ and $g_2(\xi )$, b $f(\xi )$ for $\alpha < \hat{\alpha }$, c $f(\xi )$ for $\alpha = \hat{\alpha }$, d $f(\xi )$ for $\hat{\alpha }<{\alpha }<{\bar{\alpha }}$, e $f(\xi )$ for ${\alpha }={\bar{\alpha }}$, f $f(\xi )$ for ${\alpha } > {\bar{\alpha }}$

In the case d) of statement (50), the result of the proposition allows us to limit the interval of application of the root-finder algorithm to $]\bar{\xi },1[$, which in practice let us to obtain a sufficiently accurate approximation of the root by performing just one iteration of Newton-Raphson method.

The generic Newton–Raphson iteration is as follows:

$$\begin{aligned} \xi _{k+1} \;{=}\; \xi _k - \frac{ f'\left( \xi _k\right) }{ f''\left( \xi _k\right) } \;{=}\; \xi _k - \frac{ p \xi _k^{p-1} + \alpha \left( \xi _k - 1\right) }{ p \left( p-1 \right) \xi _k^{p-2} + \alpha } \;{=}\; \frac{ p \left( p-2 \right) \xi _k^{p-1} + \alpha }{ p \left( p-1 \right) \xi _k^{p-2} + \alpha }. \end{aligned}$$

(69)

It can be easily demonstrated that starting from $\xi _0 = 1$ (within the domain of attraction of the root) the iteration in (69) converges with quadratic rate to the local minimum.

As previously stated, experiments demonstrated that one iteration yields sufficiently accurate solutions. Hence, the approximate solution $\xi ^*$ is obtained as follows:

$$\begin{aligned} \xi ^* \;{=}\; \frac{ p \left( p-2 \right) + \alpha }{ p \left( p-1 \right) + \alpha }. \end{aligned}$$

(70)

5 Experimental Results

In this section, we evaluate the performance of the proposed constrained TV$_p$-$\ell _2$ model in (6–7) when applied to the restoration of gray-scale images synthetically corrupted by blur and additive zero-mean white Gaussian noise. The performance will be evaluated in terms of both accuracy of the obtained restorations and efficiency of the proposed ADMM-based minimization scheme reported in Algorithm 1.

The blurred signal-to-noise ratio (BSNR) and the Improved signal-to-noise ratio (ISNR) are used to measure the quality of the observed degraded images g and of the restored images $u^*$, respectively. They are defined as follows:

$$\begin{aligned} \mathrm {BSNR}(g,u)= & {} 10\log _{10}\frac{ \Vert Ku - E\left[ Ku \right] \Vert _2^2}{\Vert g - Ku \Vert _2^2}\,\text{ dB }, \\ \mathrm {ISNR}(u^*,g,u)= & {} 10\log _{10}\frac{\Vert g-u\Vert _2^2}{\Vert u^*-u\Vert _2^2}\,\text{ dB }, \end{aligned}$$

where u denotes the uncorrupted image. The ISNR quantity provides a quantitative measure of the improvement in the quality of the restored image: a high ISNR value indicates that $u^*$ is an accurate approximation of u. The standard deviation $\sigma$ of the additive noise is univocally related to the BSNR as follows:

$$\begin{aligned} \sigma = \sqrt{{\Vert K u - E[K u] \Vert _2^2}/(d^2 10^{\mathrm {BSNR}/10})}. \end{aligned}$$

(71)

As approximate solution $u^*$ of the image restoration problem, solved by ADMM-based iterative scheme reported in Algorithm 1, we consider $u^k$ obtained as soon as the relative difference between two successive iterates satisfies

$$\begin{aligned} e^k:= \Vert u^k - u^{k-1} \Vert _{2} \;{/}\; \Vert u^{k-1}\Vert _{2} \,\;{<}\;\,10^{-4}, \end{aligned}$$

(72)

or after a maximum number of 500 iterations.

In Algorithm 1 we used for all the examples the same parameter value $\tau = 1$ in the discrepancy principle-based constraint (7) such that, at convergence, the standard deviation of the restoration residual $Ku^* - g$ is forced to be exactly equal to the noise standard deviation $\sigma$.

The experiments were performed under Windows 7 in MATLAB on a HP G62 Notebook PC with an Intel(R) Core(TM) i3 CPU M350 @2.27GHz processor and 4GB of RAM.

Example 1: the benefit of the parameter $\mathbf {p}$. In this experiment, we show how the proposed automatic estimate of the parameter p for the TV$_p$ regularizer in (5) provides image restorations of better quality than setting $p=1$, which corresponds to the classical TV-$\ell _2$ functional [23, 31], implemented as constrained model using Algorithm 1.

In particular, we applied a Gaussian blur with a kernel characterized by the two parameters band and sigma: the former parameter specifies the half-bandwidth of the Toeplitz blocks in the blur matrix, the latter the standard deviation of the Gaussian point spread function. The larger the sigma is, the stronger the blur effect is, and, consequently, the worst the ill-conditioning of the blur matrix will be. The kernel is generated through the MATLAB command fspecial(’Gaussian’,band,sigma). Finally, each blurred image has been corrupted with zero-mean white Gaussian noise of different levels.

The shape parameter p for the hGGD distribution (14) of the gradient magnitudes has been estimated by the GCM described in Sect. 1, that is by solving the non-linear equation (22). The Newton–Raphson method in (23) is started using as initial guess the value 0.8; for all the experiments we got empirically the convergence.

The three uncorrupted images mandrill ($d=512$), barbara ($d=512$) and geometric ($d=256$), present different gradient distributions (hGGD) characterized by a p value obtained by applying the GCM algorithm to the images u, which are $p_u=1.28$ for mandrill, $p_u=0.67$ for barbara and $p_u=0.22$ for geometric. Clearly, the uncorrupted images are in practice not available, hence the automatic procedure GCM is applied also to the available degraded images g after carrying out a few iterations (less than 5 for the considered examples) of the TV-$\ell _2$ algorithm, which removes most of the spurious gradients introduced by degradations. The obtained estimate of p is denoted by $p_g$.

Table 1 Example 1. ISNR values obtained by restoring the image barbara corrupted by Gaussian blur with $\texttt {band}\,=\,5$, $\texttt {sigma}\,=\,1.0$, and additive Gaussian noise yielding BSNR = 40

To show how the automatically estimated value of p corresponds to a nearly optimal restoration result, in Table 1 we report the ISNR values obtained by applying Algorithm 1 with different p values in the range [0.2,1.5] to the barbara test image corrupted by Gaussian blur with $\texttt {band}=5$, $\texttt {sigma}=1.0$, and additive white Gaussian noise yielding BSNR = 40. The $p_u$ value 0.67 corresponds to the best restoration result, and an estimate $p_g=0.7$ seems to be a good compromise for practical image restorations.

We evaluate quantitatively the robustness of the p estimation with respect to the noise level, keeping a fixed Gaussian blur ($\texttt {band}=5$, $\texttt {sigma}=1.0$). Table 2 shows the resulting ISNR values for increasing noise levels, with BSNRs ranging from 40 to 20. The restoration results of TV$_p$-$\ell _2$ with $p_u$ and $p_g$ are similar and both outperform the TV-$\ell _2$ algorithm.

Table 2 Example 1. ISNR values obtained by restoring the images mandrill, barbara and geometric corrupted by fixed Gaussian blur ($\texttt {band}=5$, $\texttt {sigma}=1.0$) and additive zero-mean white Gaussian noise with increasing level

Figure 6b shows the blurred and noisy image for the restoration of the image barbara. The restored results by both methods are shown in Fig. 6c, d, the corresponding zoomed details are illustrated in Fig. 6e, and the associated ISNR values are reported in the second row of Table 2.

Fig. 6

Example 1. Restoration results obtained by TV-$\ell _2$ c and TV$_p$-$\ell _2$ with estimated $p = p_g = 0.71$ d on the test image barbara a corrupted by Gaussian blur with $\texttt {band}=5$, $\texttt {sigma}=1.0$ and additive zero-mean white Gaussian noise yielding BSNR = 30 b. The small rectangular-contoured regions in a, b, c, d are zoomed in e. a Original,b corrupted (BSNR = 30), c restored by TV$_p$-$\ell _2$ (ISNR = 1.77) d restored by TV$_p$-$\ell _2$ (ISNR = 2.44), e from left to right, zoomed details of original, corrupted, TV$-\ell _2$, TV$_p$-$\ell _2$ images.

From Table 2, we observe that the ISNR values of the restored images by the proposed method TV$_p$-$\ell _2$ are always better than those obtained by TV-$\ell _2$, by using both the $p_u$ and the $p_g$ values. The benefits of the appropriate gradient distribution are more significant for smaller noise levels. Moreover, for the mandrill restoration, which corresponds to $p>1$, the performance gain is modest.

Example 2: convex versus nonconvex restorations. For the restoration of images characterized by very sparse gradients, such as piecewise-constant images, nonconvex regularizers hold the potential for better restorations than convex models.

In this example, we compare the proposed TV$_p$-$\ell _2$ model with the convex TV-$\ell _2$ model and with a state-of-the-art nonconvex model proposed in [19], whose software is made available by the authors [18]. The nonconvex rational prior used in [20] depends on a parameter $\alpha$ which has the same role of the parameter p for TV$_p$ in tuning nonconvexity of the model. The model will be referred to as FNNMM. Since the authors did not provide any procedure to estimate $\alpha$, we used the suggested value $\alpha =0.5$ for all the experiments.

We compared the results of the three algorithms when applied to the two $200 \times 200$ purely geometric images square and rectangles depicted in Figs. 7a and 8a, respectively. We chose these two geometric images in order to better highlight some of the beneficial capabilities of nonconvex models. The superimposed colored segments represent cross-sections that will be analyzed in Figs. 7i, j and 8i, j.

Fig. 7

Example 2. Restoration results obtained by TV-$\ell _2$ c, FNNMM d and TV$_p$-$\ell _2$ with estimated $p = 0.37$ e on the test image square a corrupted by Gaussian blur with $\texttt {band}=15$, $\texttt {sigma}=3.5$ and additive white Gaussian noise yielding BSNR = 30 b. a Original, b corrupted (BSNR = 30), c TV-$\ell _2$ (ISNR = 16.02), d FNNMM (ISNR = 17.70), e TV$_p$-$\ell _2$ (ISNR = 31.15), f restoration error of TV-$\ell _2$, g restoration error of FNNMM, h restoration error of TV$_p$-$\ell _2$ (Color figure online)

Fig. 8

Example 2. Restoration results obtained by TV-$\ell _2$ c, FNNMM d and TV$_p$-$\ell _2$ with estimated $p = 0.27$ e on the test image rectangles a corrupted by Gaussian blur with $\texttt {band}=15$, $\texttt {sigma}=3.5$ and additive white Gaussian noise yielding BSNR = 30 b. a Original, b corrupted (BSNR = 30), c TV-$\ell _2$ (ISNR = 13.26), d FNNMM (ISNR = 14.67), e TV$_p$-$\ell _2$ (ISNR = 23.98), f restoration error of TV-$\ell _2$, g restoration error of FNNMM, h restoration error of TV$_p$-$\ell _2$

The degraded images shown in Figs. 7b and 8b have been synthetically generated from the uncorrupted images by first applying a Gaussian blur with kernel of parameters band = 15 and sigma = 3.5, and then adding zero-mean white Gaussian noise yielding a BSNR = 30.

It is well-known that, among convex models, TV-$\ell _2$ has the potential to yield satisfactory restoration results since it allows the solution to have edges. In particular, piecewise constant functions such as those represented by the considered square and rectangles images are particularly prone to be well restored by TV-$\ell _2$. However, TV-$\ell _2$ also possesses some undesirable effects, such as the loss of image contrast [28], the smearing of textures [4], and the staircase effect [1]. A thorough mathematical justification of these drawbacks can be found in [5, 28]. As shown in [20], nonconvex models provide solutions that tend to have better quality and partially solve these problems.

For example, as discussed in [28], the TV of a feature is directly proportional to its boundary size, so that one way of minimizing the TV of that feature would be to reduce its boundary size, in particular by smoothing corners. This effect is well visible in Fig. 7, where the considered cross section passes through the corners of the white square thus highlighting the better ability of nonconvex TV$_p$-$\ell _2$ and FNNMM models in restoring the correct shape of the square in correspondence of the corners with respect to the convex TV-$\ell _2$ model (see the zoomed detail in Fig. 7j).

As observed in [28], the loss of contrast is inversely proportional to the local features scale. Figure 8a represents rectangles of different sizes which can be seen as features at different scales. The image restored by TV-$\ell _2$ shown in Fig. 8c presents a loss of contrast which is more significant for the smallest-scale features. The smoothed-out portions of the restored image are well visible in Fig. 8f which represents the error image, given at each pixel by the absolute value of the gray level difference between the uncorrupted and the restored images. Figure 8i, j highlight the contrast loss problem by plotting a horizontal cross section of the rectangles image.

We also apply TV$_p$-$\ell _2$ model to the rectangles image where we chose the value of p according to the GCM procedure described in Sect. 1 applied to the uncorrupted image in Fig. 8a. From Fig. 8f–j we observe how the TV$_p$-$\ell _2$ model is more contrast-preserving with respect to both the convex TV-$\ell _2$ and the nonconvex FNNMM models.

To provide more evidence of the benefits of using nonconvex versus convex regularizers, in Table 3 we report the ISNR values obtained by the three algorithms on the square and rectangles images for different noise levels yielding BSNR = 40,30,20. Results in Table 3 confirm the improvement in restoration quality provided by the considered nonconvex TV$_p$-$\ell _2$ and FNNMM models with respect to the convex TV-$\ell _2$ model. Moreover, we notice how the proposed TV$_p$-$\ell _2$ approach significantly outperforms FNNMM for BSNR = 40,30, whereas the two algorithms compete for BSNR = 20. We can conclude that the obtained benefits are related both to the automatic selection of the p parameter, and to the different nonconvex regularizer used in the model.

Table 3 Example 2. ISNR values obtained by restoring the images square and rectangles corrupted by fixed Gaussian blur with $\texttt {band}=15$, $\texttt {sigma}=3.5$ and additive zero-mean white Gaussian noise of increasing level (i.e. decreasing BSNR)

We notice that, as expected, the estimated p values of the hGGD shape parameter for the two considered purely geometric images square and rectangles are very small, which leads to a strongly nonconvex TV$_p$-$\ell _2$ model. Hence, we conclude this example presenting an empirical investigatiion on the numerical convergence of the proposed ADMM-based minimization scheme for the nonconvex case ($p < 1$).

Towards this aim, in Fig. 9 we report some convergence plots concerning the case BSNR = 40 (first row of Table 3) for both the square (left column) and rectangles (right column) test images.

Fig. 9

Example 2. Empirical convergence related to the case BSNR = 40 (first row of Table 3). a Test image square, b test image rectangles

In particular, the plots in the first, second and third row of Fig. 9 represent the logarithm of the relative change of the iterates $e^k$ defined in (72), the values of the TV$_p$ functional defined in (5), and the values of the standard deviation of the restoration residual, respectively, versus the iteration index k for the first 4000 iterations of Algorithm 1. The plots in the first row of Fig. 9 show that for both the test images the iterates $u^k$ computed by Algorithm 1 converge to some limit, whereas the plots in the second row demonstrate that, as expected from theory, the approached limits correspond to some global/local minimum of the nonconvex nonsmooth TV$_p$ functional. Moreover, plots in the third row of Fig. 9 show that the standard deviations of the residuals converge quite quickly towards the limit values 0.7612 and 0.8837 for square and rectangles, respectively. More precisely, the latter values correspond to the residual standard deviations prescribed by the discrepancy principle-based formula (7) with $\tau =1$.

Finally, we observe that the ISNR values obtained at convergence after 4000 iterations are equal to 52.90 for square and 46.68 for rectangles which both outperform the ISNR values in Table 3.

Example 3: computational efficiency. In this example, experimental results are given to evaluate computational efficiency of the proposed TV$_p$-$\ell _2$ ADMM-based minimization procedure reported in Algorithm 1. In particular, we compare our algorithm TV$_p$-$\ell _2$ with $p = 1$ (hereinafter called OUR) with a good candidate state-of-the-art method for the solution of the constrained TV-$\ell _2$ model presented in [32], that we will name CW in the following. In particular, in [32] the authors proposed a primal-dual approach, and demonstrated that it is more efficient than other existing algorithms for the solution of the same model.

For the comparison, we followed the same procedure as in [32] and considered the same three image restoration problems: in the first problem, the point spread function is a $9 \times 9$ uniform blur and the additive Gaussian noise variance is $\sigma ^2 = 0.56^2$; in the second and third problems, the $15 \times 15$ point spread function is given by $h_{i,j} = 1 /(1+i^2+j^2)$ with $i,j = -7,\ldots ,7$ and the noise variances are $\sigma ^2 = 2$ and $\sigma ^2 = 8$, respectively. These three types of corruptions have been applied to the two $256 \times 256$ test grayscale images cameraman and lena.

The proposed algorithm OUR has been applied using the following parameters setting: $\beta _t = 10$, $\beta _r = 1000$, $\gamma = 1.618$. For the CW approach we used the same parameter values used in [32], that is the primal and dual step-sizes are set to $s = 1$, $t = 1/16$. We stopped the iterations of both the algorithms as soon as the relative change criterion (72) was satisfied.

The MATLAB source code for CW has been provided us by the authors of [32].

For the two test images cameraman and lena, in Fig. 10 we plot the ISNR values (top) and the negative logarithm of the relative change e (bottom), defined as in (72), versus the CPU time. From the plots, we observe that OUR algorithm outperforms CW algorithm in terms of speed-accuracy tradeoff. In particular, the top rows of Fig. 10a, b show that OUR algorithm approximately halves the computational time required to satisfy the stopping criterion with respect to the state-of-the-art CW algorithm. Furthermore, the plots on the bottom rows of Fig. 10a, b outline that the efficiency gain increases with the decreasing of the tolerance used in the stopping criterion.

Fig. 10

Example 3. ISNR (top row) and negative logarithm of relative change (bottom row) versus CPU time (in seconds) for cameraman a and lena b images. The images are corrupted by $9 \times 9$ uniform blur with noise of variance $\sigma ^2 = 0.56^2$ (first column), and blur with $15 \times 15$ point spread function given by $h_{i,j} = 1 / (1 + i^2 + j^2)$ with noise of variance $\sigma ^2 = 2$ (second column) and $\sigma ^2 = 8$ (third column), respectively. a Cameraman, b lena

6 Conclusion

We presented a constrained variational model for the restoration of images corrupted by blur and additive white Gaussian noise. The proposed TV$_p$-$\ell _2$ model extends the well-known TV-$\ell _2$ model by adopting a parametrized hGGD prior for image gradients which generalizes the half-Laplacian distribution assumed by TV-$\ell _2$. An automatic estimation of the parameter p has been introduced to exploit the great flexibility offered by the hGGD in matching gradient distributions in real images. To solve the proposed model, a novel efficient minimization algorithm based on the ADMM strategy has been presented which is supported by a novel result in multivariate proximal calculus.

Experiments demonstrate both the good performance of the proposed model in terms of restoration accuracy, and the computational efficiency of the presented minimization procedure. Theoretical demonstrations of these improvements will be further investigated in future work.