Automatic fidelity and regularization terms selection in variational image restoration

Abstract

This paper addresses the study of a class of variational models for the image restoration inverse problem. The main assumption is that the additive noise model and the image gradient magnitudes follow a generalized normal (GN) distribution, whose very flexible probability density function (pdf) is characterized by two parameters—typically unknown in real world applications—determining its shape and scale. The unknown image and parameters, which are both modeled as random variables in light of the hierarchical Bayesian perspective adopted here, are jointly automatically estimated within a Maximum A Posteriori (MAP) framework. The hypermodels resulting from the selected prior, likelihood and hyperprior pdfs are minimized by means of an alternating scheme which benefits from a robust initialization based on the noise whiteness property. For the minimization problem with respect to the image, the Alternating Direction Method of Multipliers (ADMM) algorithm, which takes advantage of efficient procedures for the solution of proximal maps, is employed. Computed examples show that the proposed approach holds the potential to automatically detect the noise distribution, and it is also well-suited to process a wide range of images.

1 Introduction

In this paper, we are interested in the restoration of images undergoing a degradation process of the form

$$\begin{aligned} b \,\;{=}\;\, {{\mathsf {K}}}u + e, \quad \; e \;\, \text {realization}\;\text {of}\;\,E, \end{aligned}$$

(1.1)

where the matrix ${{\mathsf {K}}}\in {{\mathbb {R}}}^{n\times n}$, representing the discretized linear blurring operator, is a large severely ill-conditioned and possibly rank-deficient matrix, and $u,b,e\in {{\mathbb {R}}}^n$ are vectorized forms of the discrete sought uncorrupted image, observed degraded image and additive noise image, respectively. The n-variate random vector $\,E$ models the inherently probabilistic nature of noise corruption, and its pdf $\,\text {Pr}_E(e): {{\mathbb {R}}}^n \rightarrow {{\mathbb {R}}}_+$, with ${{\mathbb {R}}}_{+}$ denoting the set of non-negative real numbers, represents the largest information one can hope to possess about the unknown noise realization e in (1.1).

Determining the uncorrupted image u from the observed degraded image b is a discrete linear inverse problem and the more information is available on the image degradation process (1.1) and on the characteristics of the sought image u, the higher the chances for an accurate estimate $u^*$ will be.

In this paper, we address the restoration of images undergoing (1.1) under the assumption that the noise corruption is independently and identically distributed (IID) with zero-mean generalized normal (GN) pdf, in short IIDGN, with unknown pdf parameters. The class of zero-mean IIDGN noises is larger than it may seem at a first glance. In fact, as detailed in the paper, the zero-mean GN pdf is a flexible family of distributions characterized by two parameters, a scale and a shape parameter. It contains some popular noise distributions such as, e.g. the normal, Laplace, hyper-Laplace (or impulsive) and, as a limiting case, uniform distributions.

In order to tackle the considered ill-posed inverse problem, we adopt a variational framework where the image restoration task is recast as the problem of seeking an estimate $u^*$ of the original u among the minimizers of a suitable cost functional $J:{{\mathbb {R}}}^n \rightarrow {{\mathbb {R}}}$. The typical variational model for image restoration reads

(1.2)

where the functionals R and F and the positive real scalar $\mu$ are referred to as regularization term, fidelity term and regularization parameter, respectively. In particular, R encodes prior information or beliefs available on the sought image u, while F measures the likelihood of any u given the knowledge of the observed data b and of the observation (or degradation) process, namely of the blur matrix and the noise distribution. Finally, the regularization parameter $\mu$ allows to balance solution regularity and trust in the data and is of crucial importance for obtaining good quality restorations.

It is quite well known—and it will be demonstrated in the paper—that whenever, in accordance with our assumption, the additive noise realization e in (1.1) is drawn from an IIDGN noise distribution having zero-mean, shape parameter $q \in {{\mathbb {R}}}_{++}$ and standard deviation $\sigma _r \in {{\mathbb {R}}}_{++}$—with ${{\mathbb {R}}}_{++}={{\mathbb {R}}}_{+}\setminus \left\{ 0\right\}$—the most suitable choice for F from a Bayesian probabilistic perspective is the so-called $\hbox {L}_q$ fidelity term, namely

$$\begin{aligned} F(u;{{\mathsf {K}}},b) \,\;{=}\;\, \text {L}_q(u;{{\mathsf {K}}},b) \,\;{:}{=}\, \left\| r(u;{{\mathsf {K}}},b) \right\| _q^q , \quad \; r(u;{{\mathsf {K}}},b) \,\,{:}{=}\,\, {{\mathsf {K}}}u - b \;\, {\in } \; {{\mathbb {R}}}^n , \end{aligned}$$

(1.3)

where $\,r(u;{{\mathsf {K}}},b)\,$ represents the restoration residual image.

For what concerns R, the choice of modeling the sought image u by a Markov random field (MRF) but with a special Gibbs prior which, in analogy with the considered noise distributions, is of zero-mean IIDGN type with shape parameter $p \in {{\mathbb {R}}}_{++}$ and standard deviation $\sigma _g \in {{\mathbb {R}}}_{++}$, leads to the class of so-called $\hbox {TV}_p$ regularizers, namely

$$\begin{aligned} R(u) \,\;{=}\;\, \text {TV}_p(u) \,\;{:}{=}\; \left\| g(u) \right\| _p^p ,\; g(u) \,\,{:}{=}\, \left( \left\| ({{{\mathsf {D}}}} u)_1 \right\| _2, \ldots , \left\| ({{{\mathsf {D}}}} u)_n \right\| _2 \right) ^T {\in } \; {{\mathbb {R}}}_+^n \, ,\qquad \end{aligned}$$

(1.4)

where g(u) represents the vector of image gradient magnitudes, the matrix ${{\mathsf {D}}}\,{\in }\, {{\mathbb {R}}}^{2n \times n}$ is defined by ${{\mathsf {D}}}\;{:}{=}\; \left( {{\mathsf {D}}}_h^T,{{\mathsf {D}}}_v^T\right) ^T$ with ${{\mathsf {D}}}_h,{{\mathsf {D}}}_v \in {{\mathbb {R}}}^{n \times n}$ coefficient matrices of finite difference operators discretizing the first-order horizontal and vertical partial derivatives of image u, respectively, and where, with a little abuse of notation, $({{\mathsf {D}}}u)_i {:}{=} \big ( ({{\mathsf {D}}}_h u)_i,({{\mathsf {D}}}_v u)_i\big ) \in {{\mathbb {R}}}^2$ indicates the discrete gradient of $\,u$ at pixel i.¹

Despite the fixed choice of the gradient as the ‘inner’ linear operator, the model proposed in this paper is general and other linear operators might be chosen as well, such as, e.g., higher-order differential operators or any transform operator. Indeed, the $\hbox {TV}_p$ class of regularizers in (1.4) is large enough to model effectively the features of a sufficiently wide set of images, ranging from piecewise constant to smooth images.

Replacing (1.3) and (1.4) into (1.2), one obtains the class of $\hbox {TV}_p$–$\hbox {L}_q$ variational models for image restoration, which read

(1.5)

The class of $\hbox {TV}_p$–$\hbox {L}_q$ models contains some very popular members such as, e.g. the TV-$\hbox {L}_2$ [27], TV-$\hbox {L}_1$ [15, 19] and, as a limiting case, TV-$\hbox {L}_{\infty }$ models [16]—where TV stands for $\hbox {TV}_1$ and represents the standard Total Variation semi-norm - but it is ‘larger’ than its renowned members and the two free shape parameters p, q hold the potential for changing the functional form of the objective $J_{p,q}$ so as to deal effectively with wider sets of target images and of noise corruptions.

However, selecting manually or also by heuristic approaches the triplet $(p,q,\mu )$ of shape and regularization parameters yielding optimal or even only good quality restorations, so as to fully exploit the $\hbox {TV}_p$–$\hbox {L}_q$ model potentialities, is a very hard task. In this paper, we propose an effective fully automatic approach for selecting $(p,q,\mu )$ based on a hierarchical Bayesian formulation of the problem and on MAP estimation.

1.1 Related work

Strategies for the automatic selection of only the regularization parameter $\mu$ have been proposed in literature for few fixed values of the shape parameters p, q.

For $p\,{=}\,q\,{=}\,2$, the $\hbox {TV}_p$–$\hbox {L}_q$ model reduces to a standard Tikhonov-regularized least-squares problem. For this class of quadratic models, many heuristic approaches have been proposed for automatically selecting $\mu$, such as, e.g., L-curve [10] and generalized cross-validation (GCV) [18]; on the other hand, several methods exploiting the information on the noise corruption have been designed. Among these, we mention the discrepancy principle (DP) [5, 24, 25], which can be adopted whenever the noise level is assumed to be known, and the residual whiteness principle (RWP) [2], consisting in selecting $\mu$ which minimizes the residual normalized auto-correlation.

The automatic DP and GCV strategies have been extended to the TV-$\hbox {L}_2$ model in [31, 32] and the former has been applied in [21] to the larger class of $\hbox {TV}_p$–$\hbox {L}_2$ models. Recently, a fully automatic selection strategy for $\mu$ based on the RWP has been proposed [22] for a wide class of R-$\hbox {L}_2$ models, with R a set of (convex) regularizers containing the $\hbox {TV}_p$ terms with $p \ge 1$.

The problem of estimating the regularization parameter and, more in general, the parameters arising in the regularization term R(u), has been extensively discussed within a Bayesian framework. The probabilistic paradigm relies on the well-established connection between the classical variational regularizer and the prior probability density function (pdf), encoding information or beliefs available a priori on u. The presence of unknown or poorly known parameters in the prior, i.e. in the regularizer, accounts for the lack of meaningful and/or precise prior information which prevents from designing a fully determined prior distribution. The original information can be thus enriched relying on two main strategies, namely empirical and hierarchical Bayesian techniques. Empirical methods aim to select the unknown parameters by exploiting the information encoded in the data b, i.e. in the likelihood pdf—see, e.g., the recent works [17, 29] and references therein. On the other hand, hierarchical approaches overcome the uncertainty in the prior by layering it and introducing additional priors on the parameters, referred to as hyperpriors [13, 26]. The hierarchical formulation has been employed for the automatic selection of the sole $\mu$ in presence of $\hbox {L}_2$ fidelity term and $\hbox {TV}_p$ regularizers with $p=2$ ([23]), $p=1$ ([4]) and $p\in [1,2]$ ([3]). For sparse recovery problems, more advanced hierarchical models have been proposed in [9, 11, 12, 14], where the authors introduced locally varying zero-mean conditionally Gaussian priors with unknown variances for which gamma and Generalized Gamma (GG) hyperpriors have been considered; the space-variant parameters resulting in the penalty term, which is coupled with the $\hbox {L}_2$ fidelity term, are automatically estimated based on an iterative alternating scheme for the MAP formulation.

Besides the former strategies, that can be classified as heuristic or based on deterministic information, and the latter Bayesian approaches, we also mention a hybrid line of research aimed at selecting the functional form of the regularizer [6,7,8, 20, 21], but only coupled with the $\hbox {L}_2$ data term. More specifically, the variational models of interest are derived based on a probabilistic MAP formulation. However, the regularizer parameters are not recast in a Bayesian framework and their estimation is carried out either once for all in a preliminary phase [21] or as a Maximum Likelihood step interlaced with the iterations of the minimization algorithm [6,7,8, 20].

To the best of authors’ knowledge, the joint automatic selection of the regularization parameter $\mu$ and the shape parameters p, q of the $\hbox {TV}_p$–$\hbox {L}_q$ class of models has not been dealt with before either in an empirical or hierarchical Bayesian perspective.

1.2 Contribution

In this paper, we present a fully automatic approach stemming from a Bayesian modeling of the image restoration inverse problem when the acquisition process is as in (1.1) under the assumption of zero-mean IIDGN noise corruption with unknown scale and shape parameters. The noise-related likelihood and the assumed Markovian prior lead to the $\hbox {TV}_p-\hbox {L}_q$ class of variational models, whereas the inclusion of informative hyperpriors on the free parameters of the likelihood and the prior, which represents the key conceptual contribution of this work, provides a probabilistically grounded and transparent machinery for automatically selecting all the free parameters $\mu ,p,q$ in the $\hbox {TV}_p-\hbox {L}_q$ model. This framework gives rise to two different hypermodels, one following a fully hierarchical Bayesian paradigm, the other taking advantage of the interaction between the introduced hyperpriors and the Residual Whiteness Principle (RWP) [22]. We also propose an automatic, efficient strategy for initializing—i.e., setting once for all from the observed degraded image b before starting the restoration—the hyperpriors based on a recent approach presented in [22] for different purposes.

From a numerical point of view, we address the minimization of a cost function of both the sought image u and the hyperparameter vector $\theta := (\sigma _g,p,\sigma _r,q)$. The function is non-convex jointly in $(u,\theta )$, hence disjoint sets of global minimizers may exist and, more importantly, the iterative minimization algorithm might get trapped in bad local minimizers. We propose an alternating minimization (AM) approach which, coupled with choosing the output of the hyperpriors initialization as the initial iterate, converges towards good quality solutions. For the minimization problem with respect to u, the classical ADMM algorithm is enriched with efficient and robust procedures for the solution of the proximal maps arising in the resulting sub-problems.

The proposed approach provides valuable benefits from different perspectives:

• (i) From an applicative point of view, the automatic selection of the free parameters $p,\,q,\,\mu$ in the $\hbox {TV}_p$–$\hbox {L}_q$ models allows to apply the proposed framework to the restoration of a wide spectrum of images corrupted by different IIDGN noises.

• (ii) On the numerical side, the proposed initialization strategy allows for a stable recovery of u and $\theta$, despite non-convexity of the objective function.

• (iii) Finally, from a modeling perspective the proposed hierarchical framework can be easily extended to other classes of parametrized variational models, also aimed at solving inverse imaging problems different from restoration (such as, e.g., image inpainting, super-resolution and computed tomography reconstruction) and characterized by general—i.e. rectangular and/or singular—forward linear operators ${{\mathsf {K}}}$. Moreover, the proposed approach can be generalized by replacing the first order difference matrix ${{\mathsf {D}}}$ in the regularizer R with a matrix ${{\mathsf {L}}}$ representing, e.g., higher order difference operators or a generic transform operator. In fact, the only condition required by all theoretical derivations in this paper is that the null spaces of the forward operator ${{\mathsf {K}}}$ and the regularization operator ${{\mathsf {L}}}$ have trivial intersection.

The paper is organized as follows. In Sect. 2, we introduce useful definitions and properties and we detail the hierarchical MAP formulation for the model of interest. Then, in Sect. 3 we design suitable hyperpriors for the unknown parameters and introduce the two proposed hypermodels, whose numerical solution is addressed in Sect. 4. In Sect. 5, our method is extensively tested on different images. Finally, we conclude with some outlook for future research in Sect. 6.

2 The proposed model by probabilistic Bayesian formulation

In this section, we first motivate and then illustrate in detail the proposed approach. In particular, after introducing some notations and recalling some useful preliminaries, we derive the proposed variational model by recasting in fully probabilistic terms the image restoration inverse problem (1.1) under the assumption of additive zero-mean IIDGN noise corruption with unknown scale and shape parameters.

2.1 Notations and preliminaries

In the paper, we indicate random variables and their realizations by capital letters and their corresponding lower case letters, e.g. X and x, and we denote by $\hbox {Pr}_X$, $\eta _X$, $m_X$ and $\sigma _X$ the pdf, mean, mode and standard deviation of random variable X, respectively; we will omit the subscript X when not necessary. The characteristic function $\chi _S$ of a set S is defined by $\chi _S(x) = 1$ if $x\in S$, 0 otherwise, whereas the indicator function $\iota _S$ is defined by $\iota _S(x) = 0$ if $x\in S$, $+\infty$ otherwise. We thus have $\iota _S(x) = -\ln \chi _S(x)$. We denote by $0_n$ the n-dimensional column vector of all zeros.

In what follows, we recall few well-known definitions and in Proposition 2.1 we also introduce a function $\phi$ arising in the paper—for the proof we rely on [1].

Proposition 2.1

The gamma function $\varGamma : {{\mathbb {R}}}_{++} \rightarrow {{\mathbb {R}}}$, the log-gamma function

$\varLambda : {{\mathbb {R}}}_{++} \rightarrow {{\mathbb {R}}}$ and the function $\phi :{{\mathbb {R}}}_{++}\rightarrow {{\mathbb {R}}}$ defined by

$$\begin{aligned} \varGamma (x) \,{=}\, \int _0^{+\infty } t^{x-1} e^{-t} d t, \; \varLambda (x) \,{=}\, \ln \varGamma (x) \, , \;\,\phi (x) \,{:}{=}\, \sqrt{ \varGamma (1/x) \,/\, \varGamma (3/x) }\,, \qquad \end{aligned}$$

(2.1)

satisfy the following properties:

$$\begin{aligned}&\varGamma , \varLambda , \phi \in C^{\infty }\left( {{\mathbb {R}}}_{++} \right) \,,\; \varGamma \;\,\text {is} \;\,\text {strongly}\;\text {convex},\;\, \varLambda \;\,\text {is}\;\, \text {convex},\;\\&\lim _{x \searrow 0} \varGamma (x) \;{=}\; \lim _{x \searrow 0} \varLambda (x) \;{=}\; \lim _{x \nearrow \infty } \varGamma (x) =\lim _{x \nearrow \infty } \varLambda (x) \;{=}\; {+}\infty , \\&\;\lim _{x \searrow 0} \phi (x) \;{=}\; 0, \;\, \lim _{x \nearrow \infty } \phi (x) \;{=}\; \sqrt{3}. \end{aligned}$$

Definition 2.1

(Generalized Normal distribution) A scalar random variable X is generalized normal-distributed with mean $\eta \in {{\mathbb {R}}}$, standard deviation $\sigma \in {{\mathbb {R}}}_{++}$ and shape parameter $s \in {{\mathbb {R}}}_{++}$, denoted by $X \sim GN(\eta ,\sigma ,s)$, if its pdf has the form

$$\begin{aligned} \text {Pr}_X(x) \,{=}\, \text {Pr}_{GN}\left( x|\eta ,\sigma ,s\right) \,{:}{=}\, \frac{1}{2 \,\sigma } \frac{s}{\varGamma (1/s) \, \phi (s)} \, \exp \left( - \left| \frac{x-\eta }{\sigma \, \phi (s)} \right| ^s \right) \!, \quad x \;{\in }\; {{\mathbb {R}}},\qquad \end{aligned}$$

(2.2)

with $\varGamma$ and $\phi$ functions defined in (2.1). In particular, for any fixed $\eta \in {{\mathbb {R}}}$, $\sigma \in {{\mathbb {R}}}_{++}$, the pdf in (2.2) converges pointwise to a uniform distribution as $s \rightarrow +\infty$, namely

$$\begin{aligned} \lim _{s \rightarrow +\infty } \text {Pr}_{GN}(x|\eta ,\sigma ,s) \,\;{=}\;\, \big (1/(2 \sqrt{3}\,\sigma )\big )\, \chi _{\,[0,\sqrt{3} \sigma ]} \left( \left| x - \eta \right| \right) . \end{aligned}$$

Definition 2.2

(Generalized Gamma distribution) A scalar random variable X is generalized gamma-distributed with mode $m \in {{\mathbb {R}}}_{++}$ and shape parameters $d \in (1,+\infty )$, $s \in {{\mathbb {R}}}_{++}$, denoted by $X \sim GG(m,d,s)$, if its pdf has the form

$$\begin{aligned}&\text {Pr}_X(x) \,{=}\, \text {Pr}_{GG}\left( x|m,d,s\right) \nonumber \\&{:=}\, \frac{s}{m \, \varGamma (d/s)} \left( \frac{d-1}{s}\right) ^{d/s} \left( \frac{x}{m}\right) ^{d-1} \exp \left( -\frac{d-1}{s} \, \left( \frac{x}{m}\right) ^{s}\right) \,,\qquad \end{aligned}$$

(2.3)

with $\varGamma$ and $\phi$ functions defined in (2.1).

In Fig. 1 we report the graphs of some of the introduced functions and pdfs. In particular, the middle panel shows the large flexibility of the GN family, hence the large potential capability of the considered class of $\hbox {TV}_p$–$\hbox {L}_q$ models in dealing effectively with images—shape parameter p - and noises—shape parameter q—of very different type. Finally, in the next subsection we report the analysis of the Maximum Likelihood Esimation (MLE) strategy for the unknown parameters of a zero-mean GN distribution, which will be useful for our discussion.

Fig. 1

From left to right, plots of functions $\varGamma ,\varLambda ,\phi$ defined in (2.1), of the GN pdf in (2.2) for $\eta = 0$, $\sigma = 1$ and some different values of the shape parameter s, of the GG pdf in (2.3) for $m = 1$, $d = 2$ and some different values of parameter s

2.1.1 ML estimation of the unknown parameters of a zero-mean GN distribution

Let $\,X \sim GN(0,\sigma ,s)$ with unknown scale and shape parameters $\sigma ,s \in {{\mathbb {R}}}_{++}$, and let $\,x = (x_1,\ldots ,x_n) \,\,{\in }\,\, {{\mathbb {R}}}^n$ be a vector of n independent realizations of X. According to the ML estimation approach, $\sigma$ and s can be selected by maximizing the likelihood $\text {Pr}(x\mid \sigma ,s) = \prod _{i=1}^n\text {Pr}_{GN}(x_i\mid 0,\sigma ,s)$ or, equivalently, minimizing its negative logarithm. Recalling the GN pdf definition in (2.2), after some manipulations we have

(2.4)

where $\,\varGamma (1+1/s) = (1/s)\,\varGamma (1/s)$. It comes from Proposition 2.1 that $G \in C^{\infty }({{\mathbb {R}}}_{++}^2)$ for any $x \in {{\mathbb {R}}}^n$ and that, for any fixed $s \in {{\mathbb {R}}}_{++}$, G is strictly convex and coercive in $\sigma$. By imposing $\partial G / \partial \sigma = 0$ and then replacing back into (2.4), it is a matter of simple algebra to verify that the ML estimates $\,\sigma ^{\text {ML}},s^{\text {ML}}$ in (2.4) are given by

(2.5)

(2.6)

Estimates $\sigma ^{\text {ML}},s^{\text {ML}}$ exist if (2.5) admits solutions. We note that $f^{\text {ML}} \in C^{\infty }({{\mathbb {R}}}_{++})$ and

(2.7)

where the Stirling’s series $\ln \varGamma (1/s) = (1/s)\ln (1/s)-s+\ln \sqrt{2\pi s} + O(s)$ has been used in (2.7). Hence, if $\Vert x\Vert _0=n$, either the global minimizer(s) $s^{\text {ML}} \in {{\mathbb {R}}}_{++}$ or a global infimizer is at $s^{\text {ML}}=+\infty$. We can accept this latter scenario, as it indicates that samples are drawn from a uniform pdf, with $\sigma ^{\text {ML}} = \Vert x\Vert _{\infty } / \sqrt{3}$. Then, if $0<\Vert x\Vert _0<n$, function f in (2.5) is unbounded below as $\lim _{s\rightarrow 0}f^{\text {ML}}(s) = -\infty$. This can be avoided by constraining $s \in [\,{\underline{s}},+\infty )$, ${\underline{s}} \in {{\mathbb {R}}}_{++}$, as we will do in the paper. Finally, if $\Vert x\Vert _0=0$ then $\lim _{s\rightarrow 0}f^{\text {ML}}(s) = \lim _{s\rightarrow +\infty }f^{\text {ML}}(s)=-\infty$. However, this degenerate configuration, which arises when X follows a delta distribution, can be easily detected.

2.2 Model derivation by hierarchical Bayesian formulation and MAP estimation

A widely used approach for the derivation of variational models aimed at solving inverse problems consists in the fully probabilistic Bayesian formulation of the problem followed by a MAP estimation of the sought unknowns. The adoption of a Bayesian perspective requires to interpret all the unknowns involved in the image formation model (1.1) as random variables and the MAP estimation approach consists in deriving and then maximizing the posterior pdf of such unknowns. In order to get an analytical form for the posterior, we derive the expression of the likelihood from the probabilistic characteristics of the measurement model (1.1), assume a form for the prior and, eventually, for the hyperprior, and finally apply the Bayes’ rule [13, 28].

Under our assumption that the additive noise in (1.1) is zero-mean IIDGN with the pair of scale-shape parameters given by $\theta _L := (\sigma _r,q) \in {{\mathbb {R}}}_{++}^2$, and recalling the definition of the residual image $r(u;{{\mathsf {K}}},b)$ in (1.3), the likelihood pdf takes the form

$$\begin{aligned} \text {Pr}(b|u,\theta _L) \,\;{=}\;\, \left( \frac{1}{2 \sigma _r} \frac{q}{\varGamma (1/q) \, \phi (q)} \right) ^n \exp \left( - \left\| \, \frac{1}{\sigma _r \phi (q)} \, r(u;{{\mathsf {K}}},b) \, \right\| _q^q \right) . \end{aligned}$$

(2.8)

Modeling the unknown image u as a MRF with a Gibbs prior of IIDGN type with the pair of scale-shape parameters given by $\theta _P := (\sigma _g,p) \in {{\mathbb {R}}}_{++}^2$, and recalling the definition of the gradient norms vector g(u) in (1.4), the prior pdf takes the form

$$\begin{aligned} \text {Pr}(u|\theta _P) \,\;{=}\;\, \left( \frac{1}{2 \sigma _g} \frac{p}{\varGamma (1/p) \, \phi (p)} \right) ^n \exp \left( - \left\| \, \frac{1}{\sigma _g \phi (p)} \, g(u) \, \right\| _p^p \right) . \end{aligned}$$

(2.9)

Here, the so-called hyperparameter vector $\theta =(\theta _P,\theta _L)\in {{\mathbb {R}}}_{++}^4$ containing the free parameters of the likelihood and prior pdfs is unknown and has to be estimated jointly with the uncorrupted image u. The posterior pdf of $(u,\theta )$ given the data b reads

$$\begin{aligned} \text {Pr}(u,\theta |b)&= \text {Pr}(u,\theta _P,\theta _L|b) \,{=}\, \text {Pr}(b|u,\theta _P,\theta _L) \, \text {Pr}(u,\theta _P,\theta _L) \,\, / \,\, \text {Pr}(b) \end{aligned}$$

(2.10)

$$\begin{aligned}&= \text {Pr}(b|u,\theta _P,\theta _L) \, \text {Pr}(u|\theta _P,\theta _L) \, \text {Pr}(\theta _P,\theta _L) \,\, / \,\, \text {Pr}(b) \nonumber \\&= \text {Pr}(b|u,\theta _L) \, \text {Pr}(u|\theta _P) \, \text {Pr}(\theta _P,\theta _L) \,\, / \,\, \text {Pr}(b) \, , \end{aligned}$$

(2.11)

where (2.10) comes from applying the Bayes’ rule and (2.11) from considering that b and $\theta _P$ are conditionally independent given u—hence $\text {P}(b|u,\theta _P,\theta _L)=\text {P}(b|u,\theta _L)$—and that u and $\theta _L$ are conditionally independent given $\theta _P$ - hence $\text {P}(u|\theta _P,\theta _L)=\text {P}(u|\theta _P)$.

Among the viable strategies explored in the literature and that could be applied here to extract meaningful information from the posterior—such as, e.g., the conditional mean or the minimum mean square error—we select as representative of $\text {Pr}(u,\theta |b)$, according to the MAP approach, its mode, so that the joint estimates $(u^*,\theta ^*)$ of the target image and the (prior and likelihood) hyperparameters are obtained by maximizing the posterior or, equivalently, minimizing its negative logarithm $- \ln \text {Pr}(u,\theta |b)$:

(2.12)

where (2.12) comes from (2.11) and from dropping the constant evidence term $\text {Pr}(b)$. The MAP approach presents significative advantages in terms of computational efficiency. However, we point out that when the cost function in (2.12) is non-convex, the minimization algorithm may get trapped in bad local minima. Here, the typical downsides of MAP are held back by the design of a suitable initial guess—see Sect. 4.1—which increases the algorithmic robustness.

Replacing (2.8) for the likelihood and (2.9) for the prior into the MAP inference formula (2.12), dropping the constants, rearranging and, then, recalling Definitions  (1.3) and (1.4) of the $\hbox {L}_q$ fidelity and the $\hbox {TV}_p$ regularizer, respectively, we obtain:

(2.13)

where the hyperprior term $\,-\ln \text {Pr}(\theta )\,$ will be made explicit in the next section, while the prior+likelihood function $\,{J_0}: {{\mathbb {R}}}^n {\times }\, {{\mathbb {R}}}_{++}^4 \,{\rightarrow }\; {{\mathbb {R}}}\,$ reads

$$\begin{aligned} \quad J_{0}\left( u,\theta \right) \,\,\;{=}\;\,\,&n \ln \left[ \, \varGamma (1{+}1/p)\,\phi (p)\,\sigma _g \, \right] \;{+}\; \left( \phi (p) \, \sigma _g\right) ^{-p} \,\, \text {TV}_p(u) \nonumber \\ \,\,\;{+}\;\,\,&n \ln \left[ \, \varGamma (1{+}1/q)\,\phi (q)\,\sigma _r \, \right] \,\!\,\!\;{+}\; \left( \phi (q) \, \sigma _r\right) ^{-q} \,\,\,\! \text {L}_q(u;{{\mathsf {K}}},b) \nonumber \\ \,\,\;{=}\;\,\,&G\left( \sigma _g,p,g(u)\right) \;{+}\; G\left( \sigma _r,q,r(u)\right) \, . \end{aligned}$$

(2.14)

In (2.14) we wrote the prior and likelihood terms in the same compact way based on function G defined in (2.4), with $x = g(u)$ or $x = r(u)$—see definitions in (1.3)–(1.4)—regarded here as a third independent variable instead of a fixed parameter.

If no hyperpriors are considered or, equivalently, a flat (uniform) prior for the hyperparameter vector $\theta$ is used so that the term $\,-\ln \text {Pr}(\theta )\,$ in (2.13) is constant, then the proposed model (2.13)–(2.14) reduces to minimizing the function $J_{0}$ only, jointly with respect to u and $\theta$.

However, it is easy to prove that $J_{0}$ is unbounded below, hence it does not admit global minimizers. In fact, for u a constant image, such that $\text {TV}(u) = 0$, $J_{0}$ tends to $\,-\infty$ as $\sigma _g$ tends to 0. This represents a fatal weakness of the no-hyperprior model and indicates the necessity to introduce some hyperprior on $\theta$.

3 Design of suitable hyperpriors

In this section, we define suitable hyperpriors $\text {Pr}(\theta )$ for the proposed Bayesian MAP variational model (2.13)–(2.14). In particular, we design the hyperpriors with the threefold aim of (i) adjusting the fatal intrinsic weakness of the no-hyperprior model, (ii) allowing for an efficient solution and (iii) maximizing the beneficial effect of the hyperprior on the variational model solutions, i.e. on the quality of the attained restored images. The latter aim will be pursued by exploiting the peculiarities of the preliminary estimates provided by the initialization approach described in Sect. 4.1.

First, we rewrite the hyperprior $\text {Pr}(\theta )$ in the following equivalent form

$$\begin{aligned} \text {Pr}(\theta ) \,\;{=}\;\, \text {Pr}\left( \sigma _g,p,\sigma _r,q\right) \,\;{=}\;\, \text {Pr}\left( \sigma _g,\sigma _r|p,q\right) \text {Pr}(p,q) \, . \end{aligned}$$

(3.1)

In order to let the shape parameters to be selected in a fully free and automatic manner, we adopt a flat (uniform) hyperprior on the joint variable (p, q) over the set $B=B_p\times B_q \subset {\overline{{{\mathbb {R}}}}}_{++}^2$, with $B_p=[\,{\underline{p}},+\infty ]$, $B_q=[\,{\underline{q}},+\infty ]$ and ${\overline{{{\mathbb {R}}}}}_{++}={{\mathbb {R}}}_{++}\cup \{+\infty \}$:

$$\begin{aligned} \text {Pr}(p,q) \;{=}\; \varrho \, \chi _B(p,q) \;{=}\; \varrho \, \chi _{B_p}(p) \chi _{B_q}(q)\,, \; \forall \, (p,q) \in {{\mathbb {R}}}^2_{++}\,,\;\varrho \in {{\mathbb {R}}}_{++}\,. \end{aligned}$$

(3.2)

Notice that we admit $q=+\infty$—corresponding to a uniform noise - and $p=+\infty$—which describes very peculiar configurations of the gradient magnitudes. In addition, as a general rule, ${\underline{p}},\,{\underline{q}}$ are set in order to allow non-convex $\hbox {TV}_p$–$\hbox {L}_q$ models, i.e. ${\underline{p}},{\underline{q}}<1$, which are known to be preferable in terms of sparsity promotion, and at the same time to avoid strongly non-convex configurations, i.e. ${\underline{p}},{\underline{q}}\ge 0.5$, thus lowering the risk of getting stuck in local minima. Finally, notice that $-\ln \text {Pr}(p,q)=\iota _{B}(p,q)$.

For what concerns the GN standard deviations $\sigma _g,\,\sigma _r$, two different approaches are discussed here. The first strategy is based on a fully hierarchical paradigm according to which $\sigma _g$ and $\sigma _r$ are modeled as independent random variables conditioned on p and q, respectively. In other words, the joint hyperprior in (3.1) takes the form

$$\begin{aligned} \text {Pr}(\sigma _g,\sigma _r\mid p,q)= \text {Pr}(\sigma _g\mid p)\,\text {Pr}(\sigma _r \mid q)\,. \end{aligned}$$

(3.3)

For both $\sigma _g\mid p$ and $\sigma _r\mid q$ we adopt GG hyperpriors—see definition (2.3)—with modes $m_{g}$ and $m_{r}$ and shape parameters $d_{g},p$ and $d_{r},q$, respectively:

$$\begin{aligned} \text {Pr}(\sigma _g\mid p) = \text {Pr}_{GG}(\sigma _g \mid m_g,d_g,p)\,,\quad \text {Pr}(\sigma _r\mid q) = \text {Pr}_{GG}(\sigma _r \mid m_r,d_r,q)\,. \end{aligned}$$

(3.4)

The family of GG distributions contains many notable distributions, such as, e.g., the gamma distribution for $p,q=1$. In a number of recent works, the gamma and, more in general, the GG pdfs have been adopted as hyperpriors for the unknown variances of zero-mean Gaussian distributions used to model the entries of an assumed sparse signal [9, 11, 12, 14]. More specifically, the authors there exploit the heavy tail structure of the GG pdfs as it guarantees the realizations of outliers corresponding to the few non-zero entries of the signal. Here, our perspective is slightly different; in fact, we rely on a robust initialization for the parameters $\sigma _g,\sigma _r$ that will be used to set the modes $m_g,m_r$. As a result, the parameters $d_g,d_r$ will be fixed in order to tighten the GG pdfs around their modes, thus limiting the outcome of outliers. Hence, the choice of GG hyperpriors has to be interpreted here as a natural and—as explained next—advantageous way to constrain the unknown parameters within a small interval of the positive real line on which we rely with high confidence. More specifically, the advantage of a GG hyperprior is related to computational efficiency. In fact, as it will be illustrated in Sect. 4.2.2, this choice allows for independently updating the four hyperparameters $p,\sigma _g,q,\sigma _r$ along the iterations of the proposed alternating minimization scheme, with explicit closed-form expressions for the scale parameters $\sigma _g, \sigma _r$.

By plugging (3.4) into (3.3), then (3.3) and (3.2) into (3.1), and finally taking the negative logarithm, the negative log-hyperprior takes the following compact form

$$\begin{aligned} - \ln \text {Pr}(\theta ) \,\;{=}\;\, H(\sigma _g,p\,;\,m_g,d_g) \,\;{+}\;\, H(\sigma _r,q\,;\,m_r,d_r) \,\;{-}\;\,\ln \rho \, , \end{aligned}$$

(3.5)

with the (parametric) function $\,H(\sigma ,s;m,d): {{\mathbb {R}}}_{++}^2 \rightarrow {{\mathbb {R}}}$ defined by

$$\begin{aligned} H\!\left( \sigma ,s\,;\,m,d\right) \!{=}\ln \left( \frac{\sigma }{s} \varGamma \left( \frac{d}{s}\right) \right) \!{+} \frac{d}{s}\ln \frac{s}{d{-}1}{-}d\,\ln \frac{\sigma }{m}\!{+}\frac{d{-}1}{s}\left( \frac{\sigma }{m}\right) ^s{+}\iota _{B}(s),\qquad \end{aligned}$$

(3.6)

where the last term $\,\iota _{B}(s)$, $\,B$ being either $B_p$ or $B_q$, accounts for the assumed constraints on the shape parameters p, q. Finally, replacing into (2.13) the expressions of $J_0$ in (2.14) and of $- \ln \text {Pr}(\theta )$ in (3.5), our (first) complete hypermodel reads

(3.7)

where we dropped the constant $-\ln \rho$, we omitted the dependence of J on the constant parameters $m_g,d_g,m_r,d_r$, and function $T(\sigma ,s,x;m,d): {{\mathbb {R}}}_{++}^2 \times {{\mathbb {R}}}^n \rightarrow {{\mathbb {R}}}$ reads

$$\begin{aligned} T(\sigma ,s,x;m,d) \,\;{:}{=}\;\, G(\sigma ,s,x) \,\;{+}\;\, H(\sigma ,s\,;\,m,d) \, , \end{aligned}$$

with functions G and H defined in (2.4) and (3.6), respectively.

As detailed in Sect. 4, problem (3.7), to which we refer as the $\hbox {H}_1$–$\hbox {TV}_p$–$\hbox {L}_q$ hypermodel, can be solved by means of a very efficient strategy, which relies also on the existence of closed-form expressions for the unknowns $\sigma _g$, $\sigma _r$. However, as reported in Sect. 5, $\hbox {H}_1$–$\hbox {TV}_p$–$\hbox {L}_q$ does not perform well on natural images characterized by textures and details at different scales. More specifically, the estimates of the GN shape parameters p, q are of good quality, while the scale parameters $\sigma _g,\sigma _r$ are more likely to be misestimated, thus yielding a significant over-smoothing in the restorations.

To overcome this weakness, we introduce a second hypermodel $\hbox {H}_2$–$\hbox {TV}_p$–$\hbox {L}_q$ which follows the outlined hierarchical Bayesian paradigm for obtaining the estimates $\,u^*$, $p^*$, $q^*$, $\sigma _r^*$, whereas $\sigma _g^*$ is computed according to a bilevel optimization framework based on the RWP, so as to hold back the downsides of $\hbox {H}_1$–$\hbox {TV}_p$–$\hbox {L}_q$. In formulas:

(3.8)

(3.9)

(3.10)

In particular, in (3.9) the cost function J is the same defined in (3.7) for the first hypermodel $\hbox {H}_1$–$\hbox {TV}_p$–$\hbox {L}_q$ but with $\sigma _g$ regarded here as a free parameter. The residual whiteness function ${\mathscr {W}}: {{\mathbb {R}}}^n \rightarrow {{\mathbb {R}}}$ in (3.10) is the one introduced in [22] and leads to the function $W(\sigma ) = ({\mathscr {W}} \circ {\tilde{r}})(\sigma ): {{\mathbb {R}}}_{++} \rightarrow {{\mathbb {R}}}$ whose explicit expression will be given in Sect. 4.1. The numerical examples in Sect. 5 will confirm the gain in terms of robustness attained with the introduction of this second hypermodel $\hbox {H}_2$–$\hbox {TV}_p$–$\hbox {L}_q$.

4 The numerical solution algorithm

We now present an effective iterative method for the numerical solution of the proposed variational hypermodels in (3.7) and in (3.8)–(3.10), whose main steps are summarized in Algorithm 1. The initialization strategy, which is common to the two approaches, is detailed in Sect. 4.1, while the u- and $\theta$-update steps are discussed in Sects. 4.2 and 4.3, respectively. The algorithm relies on an alternating minimization (AM) scheme for which we do not provide a theoretical proof of convergence. However, in the numerical section we show clear empirical evidence of the good convergence behaviour of the scheme. For the algorithm to be determined, we make the standard (and reasonable) assumption that the null spaces of matrices ${{\mathsf {K}}}$ and ${{\mathsf {D}}}$ have trivial intersection.

4.1 Robust initialization

Computing in a fully automatic and efficient manner an acceptable-quality initial estimate $u^{(0)}$ of u under the general assumption of IIDGN noise corruption with unknown scale and shape parameters is a hard task. However, it is of vital importance not only for setting suitable hyperprior parameters but also for the success of the alternating minimization scheme outlined in Algorithm 1, which can get trapped in bad local minimizers as the joint optimization problem in $(u,\theta )$ is non-convex. Recently, a strategy for automatically selecting the regularization parameter of regularized least-square models for restoring images corrupted by additive white Gaussian noise has been proposed [22]. It is based on the RWP, i.e. on maximizing the whiteness of the restoration residual. The core block of this approach is applying the strategy to Tikhonov-regularized least-square (in short TIK–$\hbox {L}_2$) quadratic models.

The $\hbox {TV}_p$–$\hbox {L}_q$ model with $p = q = 2$ is a particular TIK–$\hbox {L}_2$ model, hence, also motivated by the fact that the noise whiteness property exploited by the RWP holds for any considered IIDGN noise corruption (note that IID property implies whiteness), we use the strategy in [22] for computing our initial estimate $u^{(0)}$. In formulas:

(4.1)

with value $\,\mu _W\,$ automatically selected by minimizing the whiteness measure function

$W: {{\mathbb {R}}}_{++} \,{\rightarrow }\; {{\mathbb {R}}}_+$ defined in [22]. Formally, $\mu _W$ is obtained by solving the 1-d problem

(4.2)

with $\,\epsilon _i,\eta _i,\zeta _i \in {{\mathbb {R}}}_+$, $i = 1,\ldots ,n$, defined in terms of the known quantities b, ${{\mathsf {K}}}$, ${{\mathsf {D}}}$ [22]. Tests in Sect. 5.1 will confirm robustness of the RWP-based strategy in (4.1)–(4.2) when applied to images of different type corrupted by different IIDGN noises. Given $u^{(0)}$, an initial estimate $\theta ^{(0)}=(\theta _P^{(0)},\theta _L^{(0)})$ is obtained by applying the MLE procedure in Sect. 2.1.1 to the data sets $\,g(u^{(0)}) \in {{\mathbb {R}}}_{++}^n$ for $\theta _P^{(0)}$ and $r(u^{(0)}) \in {{\mathbb {R}}}^n$ for $\theta _L^{(0)}$, respectively, with functions g, r defined in (1.3)–(1.4). More precisely, first we compute $p^{(0)}$ and $q^{(0)}$ by solving (2.5) with $x=g(u^{(0)})$ and $x=r(u^{(0)})$, respectively. The existence of solutions is guaranteed as we search for $p^{(0)},q^{(0)}$ within the domains $B_p=[\,{\underline{p}},+\infty ]$, $B_q=[\,{\underline{q}},+\infty ]$, ${\underline{p}},{\underline{q}} \in {{\mathbb {R}}}_{++}$, introduced in Sect. 3. Then, $\sigma _g^{(0)},\sigma _r^{(0)}$ are obtained via (2.6) with $\,s^*=p^{(0)},\, x=g(u^{(0)})\,$ and $\,s^*=q^{(0)}, \,x=r(u^{(0)})$, respectively. Finally, $\sigma _g^{(0)}$, $\sigma _r^{(0)}$ are used to set the modes of the GG hyperpriors on $\sigma _g$, $\sigma _r$ for the first hypermodel and on the sole $\sigma _r$ for the second one, whereas the two parameters $d_{r},d_{g}$, accounting for the standard deviations of the GG hyperpriors, are set manually.

4.2 Alternating scheme for $\hbox {H}_1$–$\hbox {TV}_p$–$\hbox {L}_q$

Here, we discuss the u- and $\theta$-updates for $\hbox {H}_1$–$\hbox {TV}_p$–$\hbox {L}_q$ in the left side of Algorithm 1.

4.2.1 Minimization with respect to u

Recalling the definition of $J(u,\theta )$ in (3.7), the u-update step for $\hbox {H}_1$–$\hbox {TV}_p$–$\hbox {L}_q$ reads

(4.3)

(4.4)

where (4.4) comes from (4.3) by simple manipulations, by recalling definitions (1.3), (1.4) and by introducing the (current) regularization parameter $\mu ^{(k)} \,{\in }\, {{\mathbb {R}}}_{++}\!$ with

$$\begin{aligned} \mu ^{(k)} \,\;{:}{=}\;\, \big ( \sigma _g^{(k)} \phi \big (p^{(k)}\big ) \big )^{p^{(k)}} \big ( \sigma _r^{(k)} \phi \big (q^{(k)}\big ) \big )^{-q^{(k)}} \! . \end{aligned}$$

(4.5)

In order to lighten the notation, in the rest of this section we drop the (outer) iteration index superscripts (k) and indicate by ${\hat{u}}$—in place of $u^{(k+1)}$—the sought solution. However, to avoid confusion, the (inner) iterations of the numerical algorithm proposed in the following for solving (4.4) are denoted by a different index j.

In Proposition 4.1, whose proof comes easily from Lemma 5.1 and Proposition 5.2 in [6] and from well-known arguments of convex analysis, we study $J_{p,q}$ in (4.4).

Proposition 4.1

If the null spaces of matrices ${{\mathsf {K}}}$ and ${{\mathsf {D}}}$ have trivial intersection, then for any $(\mu ,p,q) \in {{\mathbb {R}}}_{++}^3$ the function $\,J_{p,q}$ in (4.4) is continuous, bounded below by zero and coercive, hence it admits global minimizers. If $p,q \ge 1$, then $\,J_{p,q}$ is also convex, hence it admits a convex compact set of global minimizers. Finally, if $p,q \ge 1$ and $pq > 1$, then $\,J_{p,q}$ is strictly convex, hence it admits a unique global minimizer.

We solve (4.4) by means of an ADMM-based approach. First, we resort to the variable splitting strategy and rewrite (4.4) in the equivalent linearly constrained form

(4.6)

where $\,t\in {{\mathbb {R}}}^{2n}$ and $\,r \in {{\mathbb {R}}}^n$ are the newly introduced variables and where we define $\,t_i \;{:}{=}\; \left( ({{\mathsf {D}}}_h u)_i,({{\mathsf {D}}}_v u)_i\right) ^T {\in }\; {{\mathbb {R}}}^2$.

The augmented Lagrangian function for (4.6) reads

$$\begin{aligned} {\mathscr {L}}(u,t,r,\lambda _t,\lambda _r) \,{=}\,&\sum _{i=1}^n \left\| t_i \right\| _2^{p} \,{+}\, \mu \left\| r \right\| _{q}^{q} \,{-}\, \langle \, \lambda _t \, , \, t - {{\mathsf {D}}}u \, \rangle \,{+}\, (\beta _t/2) \,\, \Vert \, t - {{\mathsf {D}}}u \, \Vert _2^2 \nonumber \\ \,{-}\,&\langle \, \lambda _r \, , \, r - \left( {{\mathsf {K}}}u - b\right) \, \rangle \,{+}\, (\beta _r/2) \, \Vert \, r - \left( {{\mathsf {K}}}u - b\right) \, \Vert _2^2, \end{aligned}$$

(4.7)

where $\,\beta _t, \beta _r \in {{\mathbb {R}}}_{++}$ are penalty parameters and $\lambda _t \in {{\mathbb {R}}}^{2n}$, $\lambda _r \in {{\mathbb {R}}}^{n}$ are the vectors of Lagrange multipliers associated with the set of $2n+n$ linear constraints in (4.6).

Upon suitable initialization, and for any $j\ge 0$, the j-th iteration of the standard ADMM applied to computing a saddle-point of ${\mathscr {L}}$ defined in (4.7) reads as follows:

(4.8)

(4.9)

(4.10)

The sub-problem for u in (4.8) is a linear system which—under the assumption that the null spaces of ${{\mathsf {K}}}$ and ${{\mathsf {D}}}$ have trivial intersection—is solvable as the coefficient matrix is symmetric positive definite. Adopting periodic boundary conditions for u, ${{\mathsf {D}}}^{T}{{\mathsf {D}}}$ and ${{\mathsf {K}}}^{T}{{\mathsf {K}}}$ are block-circulant with circulant blocks matrices that can be diagonalized by the 2D discrete Fourier transform. The solution is thus obtained at the cost of $O(n\ln n)$ operations by using the 2D fast Fourier transform implementation.

The two remaining sub-problems for variables t and r in (4.9)–(4.10) can both be split into n independent (2-dimensional and 1-dimensional, respectively) minimization problems taking the form of proximity operators, in formula:

(4.11)

Hence, solving both sub-problems for t and r reduces to computing the proximal operator of the parametric function $f_s(x) := ||x||_2^s, \; s \in {{\mathbb {R}}}_{++}$, with $x \in {{\mathbb {R}}}^z, \; z \in \{1,2\}$.

We remark that in the proposed AM approach—see Algorithm 1—the parameters p and q are automatically estimated at each outer iteration k, hence both p and q can assume whichever real positive value. We thus need a reliable and efficient strategy for computing the proximal map of $f_s$ for any $s \in {{\mathbb {R}}}_{++}$. For the sake of better readability, here we only summarize the content of the derived results, which are rather technical and, for this reason, are reported in the Appendix. In particular, in Proposition A.1, we extend to the case $s > 2$ the results in Proposition 1 of [21], which in their turn extended to the z-d case the 1-d results presented in [33] for $s < 1$. We can conclude that, for any $s,\gamma \in {{\mathbb {R}}}_{++}$, $\hbox {prox}_{f_s}^{\gamma }$ takes the form of a shrinkage operator, such that (4.11) reads

$$\begin{aligned} t_i^{(j+1)} \;{=}\;\, \xi _{p,i}^* \,\, y_{p,i}^{(j)} \, , \quad \;\;\, r_i^{(j+1)} \;{=}\;\, \xi _{q,i}^* \,\, y_{\,\,q,i}^{(j)} \, , \quad \;\;\, i = 1,\ldots ,n \, , \end{aligned}$$

(4.12)

where, depending on p, q, the shrinkage factors $\xi _{p,i}^*$, $\xi _{q,i}^*$ in (4.12) can either be expressed in closed-form or be the unique solution of a non-linear equation—see Proposition A.1. For this latter case, in Corollary A.1 we prove that the Newton–Raphson scheme with suitable initialization can be applied with guarantee of convergence.

4.2.2 Minimization with respect to $\theta$

Based on the definition of our cost function $J(u,\theta )$ in (3.7), the $\theta$-update reads

where $\{\sigma ^{\text {MAP}},s^{\text {MAP}}\}$, either coinciding with $\theta _P^{(k+1)}$ or with $\theta _L^{(k+1)}$, is obtained as

(4.13)

with $x=g(u^{(k+1)})$ for $\theta _P^{(k+1)}$ and $x=r(u^{(k+1)})$ for $\theta _L^{(k+1)}$, and where functions G and H are defined in (2.4) and in (3.6), respectively. The MAP superscript indicates that (4.13) can be regarded as a MAP estimation problem for $(\sigma ,s)$, which reduces to the MLE problem (2.4) when the selected hyperprior is a uniform pdf. In analogy with the results reported for the MLE problem in Section 2.1.1, we can prove the following proposition on the existence of solutions for problem (4.13).

Proposition 4.2

Let $T(\cdot ;x,m,d):{{\mathbb {R}}}_{++}^2\rightarrow {{\mathbb {R}}}$ be the cost function of problem (4.13), $x\in {{\mathbb {R}}}^n$ and $m\in {{\mathbb {R}}}_{++},d\in (1,+\infty )$. Then, $T\in C^{\infty }({{\mathbb {R}}}_{++}^2)$. Furthermore, the minimizers of T can be obtained as

with $B{=}[{\underline{s}},+\infty ]$, ${\underline{s}}\in {{\mathbb {R}}}_{++}$, $\alpha {:}{=}(n-d+1)/n$, $\beta {:}{=}(d-1)/n$, $\sigma _{\text {ML}}$ given in (2.7) and

$$\begin{aligned} \begin{aligned}&f^{\text {MAP}}(s)= n\ln [\varGamma (1{+}1/s)\phi (s)]{+}\ln [(1/d)\varGamma (1+d/s)]{+}(d/s)\ln (s/n\beta )\\&{+}(n/s)\big (\sqrt{\alpha ^2{+}4\beta m^{-s}\sigma _{\text {ML}}(s)^s}{+}\alpha \ln (({-}\alpha {+}\sqrt{\alpha ^2{+}4\beta m^{-s}\sigma _{\text {ML}}(s)^s})/(2\beta ))\big )\,. \end{aligned} \end{aligned}$$

4.3 Alternating scheme for $\hbox {H}_2$–$\hbox {TV}_p$–$\hbox {L}_q$

We now discuss the numerical solution of $\hbox {H}_2$–$\hbox {TV}_p$–$\hbox {L}_q$ defined in (3.8)–(3.10), whose main steps are outlined in the right side of Algorithm 1. The bilevel structure of the model is simply dealt with by jointly updating the unknowns u and $\sigma _g$. More precisely, after the initialization step, at each outer AM iteration we first update for $(u,\sigma _g)$ and then for $(p,q,\sigma _r)$. The former update is carried out by solving problem (4.3)–(4.4) for different values of $\sigma _g$. For each considered $\sigma _g$, we compute the whiteness measure W as in (4.2), and select as updated $u^{(k+1)},\,\sigma _g^{(k+1)}$ the ones for which W is the smallest. The latter update is performed by means of the procedure outlined in Sect. 4.2.2 for q and $\sigma _r$, while $p^{(k+1)}$ is sought as a solution of problem (2.4) constrained to the domain $B_p$ with $\sigma _g=\sigma _g^{(k+1)}$ and $x=g(u^{(k+1)})$.

5 Computed examples

In this section, we assess the performance of the proposed fully automatic variational hypermodel in its two versions $\hbox {H}_1$–$\hbox {TV}_p$–$\hbox {L}_q$ in (3.7) and $\hbox {H}_2$–$\hbox {TV}_p$–$\hbox {L}_q$ in (3.8)–(3.10), solved by the iterative approaches outlined in Algorithm 1. After defining the experimental setting, in Sect. 5.1 we evaluate the robustness of the initialization approach described in Sect. 4.1, then the two hypermodels are extensively tested and compared in Sect. 5.2. Finally, the performance of the $\hbox {H}_2$–$\hbox {TV}_p$–$\hbox {L}_q$ hypermodel is evaluated in absolute terms in Sect. 5.3, also by comparing it with some popular (not fully automatic) competitors.

In order to highlight the great flexibility of the proposed fully automatic image restoration approach, we consider four test images characterized by very different properties; see Fig. 2.

Fig. 2

Original test images ${\bar{u}}$: qrcode ($256\times 256$, ${\bar{p}}=0.7$, ${\bar{\sigma }}_g=0.2408$), sinusoid ($200\times 200$, ${\bar{p}}=98$, ${\bar{\sigma }}_g=0.0348$), peppers ($256 \times 256$, ${\bar{p}}=0.72$, ${\bar{\sigma }}_g=0.1008$), skyscraper ($256\times 256$, ${\bar{p}}=0.7$, ${\bar{\sigma }}_g=0.1572$)

In particular, qrcode is a purely geometric, piecewise constant image, sinusoid a prototypical smooth image, peppers a piecewise smooth image and skyscrapers, the most difficult to be dealt with, is made by a mixture of piecewise constant, smooth and textured components. For each (uncorrupted) test image ${\bar{u}}$, we also report the quantities ${\bar{p}}$, $\bar{\sigma _g}$, representing the “target” values of the shape and scale parameters of the underlying GN prior pdf. These values are obtained by applying the MLE procedure for GN pdf parameters outlined in Sec. 2.1.1 to the data set $\,x = (\Vert ({{\mathsf {D}}}{\bar{u}})_1 \Vert _2,\ldots ,\Vert ({{\mathsf {D}}}{\bar{u}})_n \Vert _2)$, namely the gradient norms of the target uncorrupted image ${\bar{u}}$, where, here and in the following experiments, the s estimation problem—with $s=p,q$—is addressed via gridsearch; ${\bar{p}},{\bar{\sigma }}_g$ will serve as reference values with which to compare the obtained estimates $p^*,\sigma _g^*$. The ${\bar{p}}$ value ranges from 0.7 for the piecewise constant image qrcode to 98 for the smooth image sinusoid. The overbar notation is also used to indicate the true values ${\bar{q}}$, $\bar{\sigma _r}$ of the shape and scale parameters of the GN likelihood pdf  (i.e., of the IIDGN noise pdf).

In the experiments, all test images have been corrupted by space-invariant Gaussian blur defined by a 2D discrete convolution kernel generated using the Matlab command fspecial(’gaussian’,band,sigma) with parameters $\texttt {band}\,{=}\,5\ \text {and}\ \texttt {sigma}\,{=}\,1.$ In particular, band represents the side length (in pixels) of the square support of the kernel, whereas sigma is the standard deviation of the circular, zero-mean, bivariate Gaussian pdf representing the kernel in the continuous setting. We assume periodic boundary conditions for image ${\bar{u}}$, hence the blur matrix ${{\mathsf {K}}}\in {{\mathbb {R}}}^{n \times n}$ is block-circulant with circulant blocks and can be diagonalized in ${\mathbb {C}}$ by the 2D discrete Fourier transform, thus allowing fast multiplication and storage saving. In accordance with the considered degradation model (1.1), after applying ${{\mathsf {K}}}$ to ${\bar{u}}$, the blurred image ${{\mathsf {K}}}{\bar{u}}$ is additively corrupted by IIDGN noise realizations $e \in {\mathbb {R}}^n$ from GN pdfs with standard deviation ${\bar{\sigma }}_r\,{=}\,0.1$ and different shape parameters ${\bar{q}}$, ranging from 0.5, which is the case of a strongly impulsive GN noise, to $+\infty$, namely uniform noise, passing through the two notable intermediate values ${\bar{q}}=1$ and ${\bar{q}}=2$ associated with Laplacian and Gaussian noises, respectively. The blur- and noise-corrupted images $\,b = {{\mathsf {K}}}{\bar{u}} \,{+}\, e\,$ are shown in the first column of Fig. 4 for qrcode and sinusoid corrupted by uniform noise and in the first rows of Figs. 5 and 6 for peppers and skyscraper degraded by impulsive, Laplacian, Gaussian and uniform noises.

The quality of the obtained restored images $u^*$ versus the associated true images ${\bar{u}}$ has been assessed by means of two scalar measures, the Improved Signal-to-Noise Ratio (ISNR), $\text {ISNR}(b,{\bar{u}},u^*) := 10\log _{10}\left( \Vert b-{\bar{u}}\Vert _2^2/\Vert u^*-{\bar{u}}\Vert _2^2\right)$, and the Structural Similarity Index (SSIM) [30]. The larger the ISNR and SSIM values, the higher the restoration quality. For all tests, both the outer AM scheme iterations and the inner ADMM iterations are stopped as soon as $\delta _{u}^{(k)} \,{:}{=}\, \big \Vert u^{(k)} {-}\, u^{(k-1)} \big \Vert _{2}/\big \Vert u^{(k-1)}\big \Vert _{2} <10^{-5}$, $k \in {\mathbb {N}} \setminus \{0\}$, and the ADMM penalty parameters $\beta _t$, $\beta _r$ have been set manually.

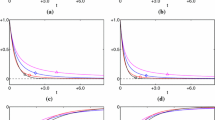
5.1 Robustness evaluation of the RWP-based Tikhonov initialization

We analyze experimentally the automatic Tikhonov initialization approach outlined in Sec. 4.1 and based on the RWP. In particular, it is of crucial importance to show that the approach is effective for the wide range of images and noises considered. To this aim, in Fig. 3 we graphic, for all test images and some different ${\bar{q}}$ values, the whiteness measure function $W(\mu )$ in (4.2), but reparameterized as a function of the scalar quantity $\tau (\mu ) \;{:}{=}\; {\hat{\sigma }}_r(\mu )/{\bar{\sigma }}_r$, where ${\bar{\sigma }}_r$ is the true noise standard deviation and ${\hat{\sigma }}_r(\mu ) \;{:}{=}\; \Vert \, {{\mathsf {K}}}\,\! u_{\,\text {Tik}}(\mu ) \,{-}\, b \, \Vert _2 \,/\, \sqrt{n}$ represents its $\mu$-dependent estimate based on the solution $u_{\,\text {Tik}}(\mu )$ of the TIK–$\hbox {L}_2$ model in (4.1). Plotting W as a function of $\tau (\mu )$ (instead of $\mu$) helps in detecting immediately the quality of the estimate $u^{(0)}$ in terms of associated discrepancy. In each plot of Fig. 3, the dashed colored vertical lines represent the optimal $\,\tau _W := \tau (\mu _W) = {\hat{\sigma }}_r(\mu _W)/{\bar{\sigma }}_r$ values selected according to the RWP (global minimizers of $W(\tau )$), while the black vertical line at $\tau =1$ corresponds to a perfect estimate ${\hat{\sigma }}_r$ of ${\bar{\sigma }}_{r}$.

In analogy to what observed in [22], where the same study has been done only for $q=2$, first we notice that the RWP tends to slightly under-estimate the true standard deviation ${\bar{\sigma }}_{r}$. In general, this circumstance has already been proved to be preferable since it leads to restorations with higher ISNR and SSIM values [7, 22]. More important—if not crucial—to the purpose of this work, one can notice from Fig. 3 that, for each test image, the function W presents approximately the same behavior and, hence, optimal $\tau _W$ value, for any different ${\bar{q}}$ value. This reflects the expected power of the RWP which, relying on the residual whiteness property, allows to deal equally well with IID noises having very different distributions, like, e.g., the hyper-Laplacian, Laplacian, Gaussian and uniform distributions considered here.

In Table 1 we report the ISNR and SSIM values associated with the initialized image $u^{(0)} = u_{\text {Tik}}(\mu _W)$ as well as the hyperparameter estimates $p^{(0)}$, $q^{(0)}$, $\sigma _{r}^{(0)}$, $\sigma _{g}^{(0)}$ for all test images and noise shape parameters ${\bar{q}}\in \{0.5,1,2,+\infty \}$. We note that $q^{(0)}$ is a good approximation of the shape parameter ${\bar{q}}$ of the true underlying noise distribution, while $p^{(0)}$ is a less accurate estimate of the target value ${\bar{p}}$.

Fig. 3

Tikhonov initialization. Whiteness measure function W in (4.2)—as function of $\tau (\mu )$—for the four test images corrupted by blur and additive IIDGN noises of standard deviation ${\bar{\sigma }}_r = 0.1$ for some different values of the noise shape parameter ${\bar{q}}$

Table 1 Tikhonov initialization

5.2 Comparative performance evaluation of the two variational hypermodels

We now evaluate the accuracy of the results obtainable by the two proposed hypermodels in (3.7) and (3.8)–(3.10), solved via the iterative schemes in Algorithm 1. We remark that, once for all after the initialization phase, for the $\hbox {H}_1$–$\hbox {TV}_p$–$\hbox {L}_q$ hypermodel the modes $m_g,m_r$ of the two GG hyperpriors are set equal to the estimates $\sigma _g^{(0)}$, $\sigma _r^{(0)}$, respectively, while the shape parameters $d_{g}$, $d_r$ are set manually in order to fix the standard deviation of the two GG hyperpriors to $10^{-3}$. For $\hbox {H}_2$–$\hbox {TV}_p$–$\hbox {L}_q$ hypermodel, only $\sigma _r$ and $d_{r}$ are set in this way, as $\sigma _g$ is automatically selected based on the RWP.

In Table 2 we report the obtained quantitative results, i.e. the ISNR and SSIM values of the restored images $u^*$ and the estimated hyperparameters $\,p^*$, $q^*$, $\sigma _g^*$, $\sigma _r^*$ where, for each test, the highest ISNR and SSIM values are in boldface. We also show the (percentage) variations $\,\varDelta \text {ISNR}$ and $\varDelta \text {SSIM}$ with respect to the ISNR and SSIM values achieved after the initialization phase (see Table 1).

Table 2 The two variational hypermodels

On the piecewise constant qrcode and the smooth sinusoid test images, the two hypermodels perform similarly well, as evidenced by the reported ISNR and SSIM values. The improvements $\,\varDelta \text {ISNR}$ and $\varDelta \text {SSIM}$ are remarkable on both images and for all noise corruptions, with those on qrcode being an order of magnitude larger. This difference is explained by considering that the initial image $u^{(0)}$ is attained by means of a quadratically-regularized model - which is particularly suitable for smooth images like sinusoid—hence $u^{(0)}$ for sinusoid is already of good quality. Since the two hypermodels perform similarly on qrcode and sinusoid for all noise types, in Fig. 4 we only show some visual results in the case of IIDGN uniform noise (${\bar{q}} = +\infty$). More specifically, we report the image $u^{(0)}$ computed by the Tikhonov initialization (second column), the output $u^*$ of the $\hbox {H}_1$–$\hbox {TV}_p$–$\hbox {L}_q$ model (third column), and the absolute error images for $u^{(0)}$ and $u^*$ (fourth and fifth columns, respectively), scaled by a factor of 10 to facilitate the visualization. As already indicated by the values reported in Table 2, the improvement of $u^*$ with respect to $u^{(0)}$ is particularly significant for the qrcode test image.

The similarity in the performance of the two hypermodels does not hold anymore when natural images such as peppers and skyscraper are processed. In fact, as reported in Table 2, the ISNR and SSIM for $\hbox {H}_1$–$\hbox {TV}_p$–$\hbox {L}_q$ are significantly lower than for $\hbox {H}_2$-$\hbox {TV}_p$-$\hbox {L}_q$, with ISNR values also lower than those achieved after the initialization phase (see the negative $\varDelta$ISNR values). The estimated noise standard deviations $\sigma _r^*$ for $\hbox {H}_1$-$\hbox {TV}_p$-$\hbox {L}_q$ are in fact significantly larger than the true value ${\bar{\sigma }}_r$ and thus correspond to over-smoothed restored images $u^*$—see second rows of Figs. 5 and 6, where we show the visual results for peppers and skyscraper. The estimation errors are also reflected in the histograms of the residual images shown in the third rows of Figs. 5 and 6, where the pdfs corresponding to the Tikhonov initialization (dashed magenta lines) are closer to the true ones (solid green lines) when compared to the pdfs resulting from the overall $\hbox {H}_1$–$\hbox {TV}_p$–$\hbox {L}_q$ approach (dashed red lines). On the other hand, one can notice from Table 2 and from the forth and fifth rows of Figs. 5 and 6 that the estimated noise standard deviations for $\hbox {H}_2$–$\hbox {TV}_p$–$\hbox {L}_q$ result to be closer to the true value ${\bar{\sigma }}_r = 0.1$ and high-quality restorations are attained.

Fig. 4

From left to right: data corrupted by IIDGN with ${\bar{q}}=+\infty$, output of TIK–$\hbox {L}_2$, restoration by $\hbox {H}_1$–$\hbox {TV}_p$–$\hbox {L}_q$ and absolute errors (x10) for qrcode and sinusoid

The observed behavior is motivated by the fact that adopting the $\hbox {H}_2$–$\hbox {TV}_p$–$\hbox {L}_q$ hypermodel can be equivalently interpreted as a way to set a hyperprior on the regularization parameter $\mu$ in the $\hbox {TV}_p$–$\hbox {L}_q$ model (1.3)–(1.5), with $\mu$ expressed as in (4.5). This guarantees a more direct monitoring of the balancing between the regularization and fidelity terms. We also remark that the mentioned balancing is particularly delicate when the selected regularizer is not expected to be flexible enough to model the actual image properties, as in the case of peppers and skyscrapers test image that would certainly benefit from using a more sophisticated regularizer.

As a result of this comparison, we can conclude that the $\hbox {H}_2$–$\hbox {TV}_p$–$\hbox {L}_q$ hypermodel is the best performing one and, hence, hereinafter we focus on it.

In Fig. 7 we provide some evidences for the good convergence behaviour of the overall alternating minimization approach outlined in Algorithm 1 for the $\hbox {H}_2$–$\hbox {TV}_p$–$\hbox {L}_q$ hypermodel. In particular, for qrcode image corrupted by blur and additive IIDGN noise with ${\bar{q}}=2$, ${\bar{\sigma }}_r = 0.1$, we monitor the hyperparameter vector $\theta ^{(k)}$ and the restoration quality measures $\text {ISNR}\big (u^{(k)}\big )$, $\text {SSIM}\big (u^{(k)}\big )$ along the outer iterations of Algorithm 1. The reported values for iteration index $k=0$ correspond to the outputs $u^{(0)}$, $\theta ^{(0)}$ of the Tikhonov initialization. We note that all the monitored quantities stabilize after very few iterations, even in this experiment where not only the cost function J is jointly non-convex in u and the hyperparameters but also its restriction to u (minimized by ADMM) becomes non-convex after the first outer iteration—in fact, $p^{(k)} < 1$ for $k \ge 1$.

Fig. 5

Hypermodels on peppers. From top to bottom: corrupted images, restored images by $\hbox {H}_1$–$\hbox {TV}_p$–$\hbox {L}_q$ and $\hbox {H}_2$–$\hbox {TV}_p$–$\hbox {L}_q$, and their residual histograms

Fig. 6

Hypermodels on skyscraper. From top to bottom: corrupted images, restored images by $\hbox {H}_1$–$\hbox {TV}_p$–$\hbox {L}_q$ and $\hbox {H}_2$–$\hbox {TV}_p$–$\hbox {L}_q$, and their residual histograms

Fig. 7

From left to right: trajectories of $\,p^{(k)},\,q^{(k)}$, of $\sigma _g^{(k)},\,\sigma _r^{(k)}$, accuracy measures $\text {ISNR}\big (u^{(k)}\big )$ and $\text {SSIM}\big (u^{(k)}\big )$, along the outer iterations of the AM scheme in Algorithm 1

5.3 Performance evaluation of the $\hbox {H}_2$–$\hbox {TV}_p$–$\hbox {L}_q$ hypermodel

The key novelty of the proposed method relies on the illustrated hierarchical Bayesian framework which allows to automatically pick up and use for restoration one variational model among the infinity contained in the considered $\hbox {TV}_p$–$\hbox {L}_q$ class, parametrized by the two shape parameters p, q and the regularization parameter $\mu$. This leads to a completely unsupervised restoration approach which, as evidenced by the results reported in previous section for the $\hbox {H}_2$–$\hbox {TV}_p$–$\hbox {L}_q$ hypermodel, is capable of achieving good-quality restorations for a large class of images and of noise corruptions

To the best of author’s knowledge, there not exist in literature other approaches of this type for the automatic selection of the three hyperparameters of the $\hbox {TV}_p$–$\hbox {L}_q$ class of models. Furthermore, the proposed hierarchical framework could be used for other classes of parametrized variational models as well, also larger than $\hbox {TV}_p$–$\hbox {L}_q$ or even containing $\hbox {TV}_p$–$\hbox {L}_q$ as a subset. Hence, we think it is not meaningful here to compare the results reported in previous section with those obtainable by using regularizers not belonging to the $\hbox {TV}_p$ class or, even more, fidelity terms suitable for noises other than the considered additive IIDGN class. Instead, we believe it is of crucial importance in order to validate the proposed automatic framework and evaluate its potential practical appeal, to compare its accuracy with the best results achievable by the whole class of $\hbox {TV}_p$–$\hbox {L}_q$ models and, in particular, by the most popular members of the $\hbox {TV}_p$–$\hbox {L}_q$ class, such as the TV–$\hbox {L}_2$, TV–$\hbox {L}_1$,TIK–$\hbox {L}_2$ and TIK–$\hbox {L}_1$ models.

To this aim, we carry out the following experiment, whose quantitative results are reported in Table 3. We consider the most severe test skyscraper corrupted by the same blur as in previous sections and by additive IIDGN noise with standard deviation ${\bar{\sigma }}_r = 0.1$ and shape parameter ${\bar{q}} = 3$. We run our fully automatic restoration $\hbox {H}_2$–$\hbox {TV}_p$–$\hbox {L}_q$ hypermodel and report the obtained ISNR and SSIM accuracy results in the first row of Table 3. Then, we compare these results with those achievable by a set of non-automatic meaningful $\hbox {TV}_p$–$\hbox {L}_q$ models, with a priori fixed p and q values reported in the second and third column of Table 3. In particular, for each of these tests, the regularization parameter $\mu$ of the $\hbox {TV}_p$–$\hbox {L}_q$ model has been set manually so as to achieve the highest ISNR value (shown in the fourth column of Table 3, with the associated SSIM in the fifth column) and the highest SSIM value (in the sixth column, with the associated ISNR in the last column). For a fair comparison, the considered non-automatic $\hbox {TV}_p$–$\hbox {L}_q$ models have been solved via the ADMM algorithm outlined in Sec. 4.2.1, using the same initial iterate (image $u^{(0)}$ output of the proposed Tikhonov initialization) and stopping criterion ($\delta _u^{(k)} < 10^{-5}$) as our hypermodel.

In the second row of Table 3 we report the results of using the final shape parameter estimates $p^*=0.7$ and $q^*=3.08$ provided by our hypermodel. The $\hbox {ISNR}_\text {max}$ and $\hbox {SSIM}_\text {max}$ values are slightly higher than the hypermodel but the associated SSIM and ISNR values are slightly lower. In the third row we consider the target shape parameter values ${\bar{p}}=0.7$ and ${\bar{q}}=3$ and the obtained results are very little worse than using $p^*$ and $q^*$. In the last six rows we show the results for six very popular members of the $\hbox {TV}_p$–$\hbox {L}_q$ class corresponding to $p = 1,2$, $q = 1,2,+\infty$. All the six non-automatic models perform worse than our automatic hypermodel. Finally, the results reported in the fourth row of Table 3 are the most meaningful as they clearly validate the proposed hierarchical Bayesian approach. The ${\hat{p}}$ and ${\hat{q}}$ values are in fact those providing the best results among the $\hbox {TV}_p$–$\hbox {L}_q$ class. To obtain ${\hat{p}}$ and ${\hat{q}}$, we ran the $\hbox {TV}_p$–$\hbox {L}_q$ model for a grid of different (p, q) values and then selected the pair $({\hat{p}},{\hat{q}})$ yielding the highest ISNR and the highest SSIM. The results of this experiment are shown in Fig. 8.

Table 3 Quantitative performance evaluation of the $\hbox {H}_2$–$\hbox {TV}_p$–$\hbox {L}_q$ hypermodel skyscrapers($\bar{p} = 0.7, \bar{q} = 3$)

Fig. 8

ISNR and SSIM values achieved by $\hbox {TV}_p$–$\hbox {L}_q$ model for different (p, q) values. The largest ISNR and SSIM in the red box are attained at $p=0.7$ and $q=3$

6 Conclusions

The present article discusses the introduction of a probabilistic hierarchical approach for the fully automatic solution of the image restoration inverse problem when both the noise and the image gradient magnitudes are assumed to follow a GN distribution. The joint estimation of the original image and of the unknown parameters determining the prior and the likelihood pdfs relies on the introduction of two classes of hyperpriors. The resulting hypermodels are addressed by means of an alternating minimization scheme, for which a robust initialization based on the noise whiteness property is provided. The proposed machinery leads to a completely unsupervised restoration approach which is capable of achieving good-quality restorations for a large class of images and of noise corruptions. As future work, more sophisticated regularizers enforcing the robustness of the algorithm in presence of high level of corruptions can be explored. In addition, the capability of the proposed framework to effectively address the case of mixed noise can be also investigated.

A Proofs of the results

Proposition A.1

Let $s,\gamma \in {{\mathbb {R}}}_{++}$, $z \in {\mathbb {N}}$ be given constants, let $f_s: {{\mathbb {R}}}^z \rightarrow {{\mathbb {R}}}$ be the (parametric, not necessarily convex) function defined by $f_s(x) := \Vert x\Vert _2^s$ and let $\text {prox}_{f_s}^{\gamma }: {{\mathbb {R}}}^z \rightrightarrows {{\mathbb {R}}}^z$ be the proximal operator of function $f_s$ with proximity parameter $\gamma$, defined as the z-dimensional minimization problem

Then, for any $z \in {\mathbb {N}}, \, s,\gamma \in {{\mathbb {R}}}_{++}, \, y \in {{\mathbb {R}}}^z$, $\text {prox}_{f_s}^{\gamma }$ takes the form of a shrinkage operator:

$$\begin{aligned} \text {prox}_{f_s}^{\gamma }(y) \,\;{=}\;\,\, \xi ^* \big ( s,\rho \left( s,\gamma ,\Vert y\Vert _2\right) \big ) \, y \, , \;\;\,\text {with}\;\,\,\, \xi ^*\!: \, {{\mathbb {R}}}_{++} {\times } \,\, {{\mathbb {R}}}_+ \rightrightarrows \, [0,1) \, , \end{aligned}$$

and with function

$$\begin{aligned}&\rho : \, {{\mathbb {R}}}_{++}^2 {\times }\,\,\! {{\mathbb {R}}}_+ \rightarrow {{\mathbb {R}}}_+ \;\;\, defined \;\, by \;\;\;\, \rho (s,\gamma ,\Vert y\Vert _2) \\&\qquad {=}\;\, \left\{ \begin{array}{lll} \displaystyle { (\gamma /s) \Vert y\Vert _2^{2-s} \quad \text {if}\;\,\,\Vert y\Vert _2 \,{>}\; 0 \, , } \\ \displaystyle { 0 \qquad \qquad \qquad \!\! \text {if}\;\,\,\Vert y\Vert _2 \,{=}\; 0 \, , } \end{array} \right. \end{aligned}$$

In particular, for any $z \in {\mathbb {N}}$, the shrinkage coefficient function $\xi ^*(s,\rho )$ satisfies:

$$\begin{aligned} \begin{array}{llcl} s \;{>}\; 0, &{}\!\!\! \,\rho \;{=}\; 0 &{} \!\!\!{\Longrightarrow }\!\!\! &{} \xi ^*(s,\rho ) \,\;{=}\;\, 0 \, , \\ s \;{\le }\; 1, &{}\!\!\! \,\rho \;{<}\; {\bar{\rho }}(s) &{} \!\!\!{\Longrightarrow }\!\!\! &{} \xi ^*(s,\rho ) \,\;{=}\;\, 0 \, , \\ s \;{\le }\; 1, &{}\!\!\! \,\rho \;{=}\; {\bar{\rho }}(s) &{} \!\!\!{\Longrightarrow }\!\!\! &{} \xi ^*(s,\rho ) \,\;{\in }\; \{ 0, {\bar{\xi }}(s) \} \, , \\ s \;{\le }\; 1, &{}\!\!\! \,\rho \;{>}\; {\bar{\rho }}(s) &{} \!\!\!{\Longrightarrow }\!\!\! &{} \xi ^*(s,\rho ) \,\;{=}\;\, \text {unique sol. in}\,\;({\bar{\xi }}(s),1)\;\text {of}\;\, h(\xi ;s,\rho ) \;{=}\; 0 \, , \\ s \;{>}\; 1, &{}\!\!\! \,\rho \;{>}\; 0 &{} \!\!\!{\Longrightarrow }\!\!\! &{} \xi ^*(s,\rho ) \,\;{=}\;\, \text {unique sol. in}\,\quad \;\,(0,1)\;\text {of}\;\, h(\xi ;s,\rho ) \;{=}\; 0 \, , \end{array} \end{aligned}$$

(A.1)

with functions ${\bar{\rho }}: (0,1] \rightarrow [1,\infty )$, ${\bar{\xi }}: (0,1] \rightarrow [0,1)$, and $h: (0,1] \rightarrow {{\mathbb {R}}}$ defined by

$$\begin{aligned} {\bar{\rho }}(s) \,{=}\, \frac{(2-s)^{2-s}}{s \, (2-2s)^{1-s}} \, , \quad {\bar{\xi }}(s) \,{=}\, 2\,\frac{1-s}{2-s} \, , \quad h(\xi ;s,\rho ) \,{=}\, \xi ^{s-1} {+}\, \rho \left( \xi {-} 1 \right) \, . \end{aligned}$$

(A.2)

Finally, the function $\,\xi ^*$ exhibits the following regularity and monotonicity properties:

$$\begin{aligned} \begin{array}{c} \xi ^* \;{\in }\; C^{\infty }(S), \;\; S \;{=}\; S_0 \cup S_1, \;\;\, S_0 \;{=}\; (0,1]\,{\times }\,({\bar{\rho }}(s),\infty ), \; S_1 \;{=}\; (1,\infty )\,{\times }\,{{\mathbb {R}}}_{++} , \quad \\ \displaystyle { \frac{\partial \xi ^*}{\partial s}(s,\rho ) \;{>}\; 0 \, , \quad \frac{\partial \xi ^*}{\partial \rho }(s,\rho ) \;{>}\; 0 \, , \quad \forall \, (s,\rho ) \,\;{\in }\; S \, . } \end{array} \end{aligned}$$

(A.3)

Proof

The proof of (A.1)–(A.2) comes easily from Proposition 1 in [21], as (A.1)–(A.2) is there proved for $s<2$, but the proof of case c) in that proposition can be seamlessly extended to cover the case $s \ge 2$.

To prove (A.3), first we notice from (A.1)–(A.2) that $\xi ^*(s,\rho ) \,{\in }\, (0,1) \; \forall \, (s,\rho ) \,{\in }\, S$ and introduce the function $\,f\,{:}\;\, S_f \rightarrow {{\mathbb {R}}}$, $\,S_f = (0,1) \,{\times }\, S \;{\subset }\; {{\mathbb {R}}}_{++}^3$, defined by $\,f(\xi ,s,\rho ) \,{:}{=}\, h(\xi ;s,\rho )$ ${=}\; \xi ^{s-1} + \rho \, (\xi -1)$, $\forall \, (\xi ,s,\rho ) \,{\in }\, S_f$. The function f clearly satisfies

$$\begin{aligned} f \,{\in }\, C^{\infty }(S_f) \, , \quad \; \frac{\partial f}{\partial \xi } (\xi ,s,\rho )= (s-1) \, \xi ^{s-2} + \rho \;{=}\; 0 \;\; \text {for}\;\, s \,{<}\, 1 \;{\wedge }\; \xi ^{s-2} \,{=}\, \rho / (1-s) . \end{aligned}$$

We now demonstrate by contradiction that that if $s < 1$ then $\xi ^{s-2} \ne \rho /(1-s)$ for any $(\xi ,s,\rho ) \in S_f$. In fact, according to the definition of set $S_f$ given above, we have that $\xi > {\bar{\xi }}(s)$ and $\rho > {\bar{\rho }}(s)$ for $s<1$, with functions ${\bar{\xi }},{\bar{\rho }}$ defined in (A.2). But we have

$$\begin{aligned}&\xi \,\;{>}\;\, {\bar{\xi }}(s) \,\,\;{\Longleftrightarrow }\;\,\, \xi ^{s-2} \,{<}\, \left( {\bar{\xi }}(s)\right) ^{s-2}\\&\,{\Longleftrightarrow }\;\, \frac{\rho }{1-s} \,{<}\, \left( 2 \, \frac{1-s}{2-s} \right) ^{s-2} \,{\Longleftrightarrow }\;\, \rho \,\;{<}\;\, \frac{s}{2} \, {\bar{\rho }}(s) \, . \end{aligned}$$

Hence, $\,\partial f / \partial \xi \ne 0 \;\, \forall \, (\xi ,s,\rho ) \in S_f$ and it follows form the implicit function theorem that, for any $(s,\rho ) \in S$, the shrinkage coefficient $\xi ^* \in (0,1)$ is given by the infinitely many times differentiable function of $(s,\rho )$, denoted $\xi ^*(s,\rho )$, solution of equation

$$\begin{aligned} f\left( \xi ^*(s,\rho ),s,\rho \right) = 0 \,\;\;{\Longleftrightarrow }\;\; \left( \xi ^*(s,\rho )\right) ^{s-1} + \rho \, \left( \xi ^*(s,\rho ) - 1\right) = 0 \, . \end{aligned}$$

(A.4)

Taking the partial derivatives of both sides of (A.4) with respect to s and $\rho$, and recalling that for any function $\,c(x) \;{=}\; w(x)^{a(x)}$ with $\,w(x) \;{>}\; 0 \;\, \forall \, x \in {{\mathbb {R}}}$, it holds that

$$\begin{aligned} c'(x) \,{=}\, c(x) \left[ \, a'(x) \ln w(x) + a(x) w'(x) / w(x) \, \right] \,, \end{aligned}$$

after simple manipulations we have

$$\begin{aligned}&\frac{\partial }{\partial s} f\left( \xi ^*(s,\rho ),s,\rho \right) \;{=}\; 0 \,{\Longleftrightarrow }\, \frac{\partial \xi ^*}{\partial s}(s,\rho ) \,{=}\, \frac{ - \left( \xi ^*(s,\rho )\right) ^{s-1} \, \ln \, \xi ^*(s,\rho ) }{ (s-1) \left( \xi ^*(s,\rho )\right) ^{s-2} + \rho } \, , \qquad \quad \end{aligned}$$

(A.5)

$$\begin{aligned}&\frac{\partial }{\partial \rho } f\left( \xi ^*(s,\rho ),s,\rho \right) \;{=}\; 0 \,{\Longleftrightarrow }\, \frac{\partial \xi ^*}{\partial \rho }(s,\rho ) \,\;{=}\;\, \frac{ 1 - \xi ^*(s,\rho ) }{ \;\, (s-1) \left( \xi ^*(s,\rho )\right) ^{s-2} + \rho \;} \, . \qquad \quad \end{aligned}$$

(A.6)

Since $\,(s,\rho ) \in S \,\;{\Longrightarrow }\;\, \rho > 0, \, \xi ^*(s,\rho ) \in (0,1)$, then both the numerators in the definitions of $\partial \xi ^* / \partial s$ and $\partial \xi ^* / \partial \rho$ in (A.5)–(A.6) are positive quantities. The denominator in (A.5)–(A.6) is also clearly positive for $s \ge 1$; for $s<1$ it is positive for

$$\begin{aligned} \left( \xi ^*(s,\rho )\right) ^{2-s} \,{>}\;\, (1-s)/\rho \,\;{\Longleftarrow }\; \left( \xi ^*(s,\rho )\right) ^{2-s} \,{>}\;\, (1-s)/{\bar{\rho }}(s) \,\;{=}\;\, (s/2) \, \left( {\bar{\xi }}(s)\right) ^{2-s}\,, \end{aligned}$$

which is always verified since $\,\xi ^*(s,\rho ) \;{>}\; {\bar{\xi }}(s)$ for $s<1$. This proves (A.3). $\square$

Corollary A.1

Under the setting of Proposition A.1, let $(s,\rho ) \in S$. Then, the Newton–Raphson iterative scheme applied to the solution of $h(\xi ;s,\rho ) = 0$, namely

$$\begin{aligned} \xi _{k+1} \,\;{=}\;\,\, \xi _k - \frac{h\left( \xi _k;s,\rho \right) }{h'\left( \xi _k;s,\rho \right) } \,\;{=}\;\,\, \frac{ \rho \;{+}\; (s-2) \, \xi _k^{s-1} }{ \rho \;{+}\; (s-1) \, \xi _k^{s-2} } \, , \;\;\;\; k \;{=}\; 1,2,\ldots , \end{aligned}$$

(A.7)

converges to $\xi ^*(s,\rho )$ if the initial iterate $\xi _0$ is chosen, dependently on $s,\rho$, as follows:

$$\begin{aligned} \begin{array}{llcl} s \;{\le }\; 1, &{} \rho \;{>}\; {\bar{\rho }}(s) &{} {\Longrightarrow } &{} \xi _0 \;\;{\in }\;\, \big [ {\bar{\xi }}(s),1 \big ] \, , \\ s \;{\in }\; (1,2), &{} \rho \;{>}\; 2-s &{} {\Longrightarrow } &{} \xi _0 \;\;{\in }\;\, (0,1] \, , \\ s \;{\in }\; (1,2), &{} \rho \;{\le }\; 2-s &{} {\Longrightarrow } &{} \xi _0 \;\;{\in }\;\, \big ( 0,\xi ^*(s,\rho ) \big ] \, , \\ s \;{\ge }\; 2 &{} \rho \;{>}\; 0 &{} {\Longrightarrow } &{} \xi _0 \;\;{\in }\;\, [0,1] \, . \end{array} \end{aligned}$$

(A.8)

Hence, based on (A.3), $\xi _0$ for computing $\xi ^*(s,\rho )$ by (A.7) can be chosen among the solutions $\xi ^*({\tilde{s}},\rho )$ for different s values according to the following strategy:

$$\begin{aligned} \begin{array}{llcl} s \;{\le }\; 1, &{} \rho \;{>}\; {\bar{\rho }}(s) &{} {\Longrightarrow } &{} \xi _0 \;\;{=}\;\, \xi ^*({\tilde{s}},\rho ), \;\; {\tilde{s}} \;{\ge }\; s \, , \\ s \;{\in }\; (1,2), &{} \rho \;{>}\; 2-s &{} {\Longrightarrow } &{} \xi _0 \;\;{=}\;\, \xi ^*({\tilde{s}},\rho ), \;\; {\tilde{s}} \;{>}\; 1 \, , \\ s \;{\in }\; (1,2), &{} \rho \;{\le }\; 2-s &{} {\Longrightarrow } &{} \xi _0 \;\;{=}\;\, \xi ^*({\tilde{s}},\rho ), \;\; {\tilde{s}} \;{\in }\; (1,s] \, , \\ s \;{\ge }\; 2 &{} \rho \;{>}\; 0 &{} {\Longrightarrow } &{} \xi _0 \;\;{=}\;\, \xi ^*({\tilde{s}},\rho ), \;\; {\tilde{s}} \;{>}\; 0 \, . \end{array} \end{aligned}$$

(A.9)

Proof

According to Proposition A.1, for any given pair $(s,\rho ) \in S$, the shrinkage coefficient $\xi ^*(s,\rho )$ is given by the unique root of nonlinear equation $h(\xi ;s,\rho ) = 0$ in the open interval $({\bar{\xi }}(s),1)$ for $s\le 1$, (0, 1) for $s>1$. Convergence of the Newton–Raphson method applied to finding such roots depends on the initial guess as well as on the first- and second-order derivatives of the function h, which read

$$\begin{aligned} h'(\xi ;s,\rho ) \,\;{=}\;\, (s-1) \, \xi ^{s-2} + \rho \, , \quad \; h''(\xi ;s,\rho ) \,\;{=}\;\, (s-1)(s-2) \, \xi ^{s-3} \, . \end{aligned}$$

In particular, it is immediate to verify that $h \;{\in }\, C^{\infty }\left( (0,1]\right)$ for any $(s,\rho ) \in S$ and that, depending on s, the function h and its derivatives $h',h''$ satisfy

$$\begin{aligned}&\left\{ \begin{array}{l} s \;{<}\; 1 \\ \rho \;{>}\; {\bar{\rho }}(s) \end{array} \right. \nonumber \\&\quad {\Rightarrow }\left\{ \begin{array}{l} h \,{\in }\, C^{\infty } \left( \left[ {\bar{\xi }}(s),1\right] \right) , \;\, h\!\left( {\bar{\xi }}(s)\right) \,{=}\, \frac{s}{2-s}\left( {\bar{\rho }}(s)-\rho \right) \,{<}\, 0, \;\, h(1) \,{=}\, 1, \quad \\ h'\!\left( {\bar{\xi }}(s)\right) {=}\, \rho \,{+}\, \frac{s}{2}{\bar{\rho }}(s), \;\,h'(1) \,{=}\, \rho \,{+}\, s \,{-}\,\! 1, \;\,h'(\xi ),h''(\xi ) \,{>}\, 0 \; \forall \xi \,{\in }\, [{\bar{\xi }}(s),1], \end{array} \right. \quad \nonumber \\&\left\{ \begin{array}{l} s \;{\in }\, (1,\!2) \\ \rho \;{>}\; 0 \end{array} \right. \nonumber \\&\quad {\Rightarrow }\left\{ \begin{array}{l} h \,{\in }\, C^0\big ([0,1]\big ) \,{\cap }\, C^{\infty }\big ((0,1]\big ), \;\, h(0) \,{=}\, {-}\rho \,{<}\, 0, \;\, h(1) \,{=}\, 1, \;\, h'(0^+) \,{=}\,\! {+}\infty , \quad \\ h'(1) \,{=}\, \rho \,{+}\, s \,{-}\,\! 1, \;\, h'(\xi ) \,{>}\, 0 \;\, \forall \xi \,{\in }\, (0,1], \;\, h''(\xi ) \,{<}\, 0 \;\, \forall \xi \,{\in }\, (0,1], \end{array} \right. \quad \nonumber \\&\left\{ \begin{array}{l} s \;{>}\, 2 \\ \rho \;\!{>}\; 0 \end{array} \right. \nonumber \\&\quad {\Rightarrow }\left\{ \begin{array}{l} h \,{\in }\, C^1\big ([0,1]\big ) \,{\cap }\, C^{\infty }\big ((0,1]\big ), \;\, h(0) \,{=}\, {-}\rho \,{<}\, 0, \;\, h(1) \,{=}\, 1, \;\, h'(0) \,{=}\, \rho , \quad \\ h'(1) \,{=}\, \rho \,{+}\, s \,{-}\,\! 1, \;\, h'(\xi ) \,{>}\, 0 \;\, \forall \xi \,{\in }\, [0,1], \;\, h''(\xi ) \,{>}\, 0 \;\, \forall \xi \,{\in }\, (0,1], \end{array} \right. \end{aligned}$$

Properties of $\,h,h',h''$ for $s\,{<}\,1 \,{\wedge }\, \rho \,{>}\,{\bar{\rho }}(s)$ indicate that in this case the iterative scheme (A.7) is guaranteed to converge to the unique root $\xi ^*(s,\rho )$ of $h(\xi ;s,\rho ) = 0$ in the open interval $({\bar{\xi }}(s),1)$ if $\xi _0 \in \big [\xi ^*(s,\rho ),1]$. But, since it can be proved (we omit the proof for shortness) that setting $\xi _0 = {\bar{\xi }}(s)$ the first iteration of (A.7) yields $\xi _1 \in \big [\xi ^*(s,\rho ),1\big )$, then (A.7) converges under the milder condition $\xi _0 \in [{\bar{\xi }}(s),1]$.

Properties of $\,h,h',h''$ for $s\,{\in }\,(1,2) \,{\wedge }\, \rho \,{>}\,0$ lead to the convergence condition $\xi _0 \,{\in }\, \big (0,\xi ^*(s,\rho )\big ]$ for (A.7), with $\xi _0 \,{=}\, 0$ excluded since $h'(0^+) \,{=}\; {+}\infty \;{\Longrightarrow }\; \xi _k \,{=}\, 0 \;\, \forall k$. It can be proved that setting $\xi _0 = 1$, then (A.7) yields $\xi _1 \in \big (0,\xi ^*(s,\rho )\big ]$ if and only if $\rho \,{>}\, 2-s$. Hence, for $\rho \,{>}\, 2-s$ we have the milder convergence condition $\xi _0 \,{\in }\, (0,1]$.

Properties of $\,h,h',h''$ for $s\,{>}\,2 \;{\wedge }\; \rho \,{>}\,0$ indicate that (A.7) is guaranteed to converge to the desired $\,\xi ^*(s,\rho )\,$ if $\,\xi _0 \,{\in }\, \big [\xi ^*(s,\rho ),1]$. However, as it is easy to prove that $\xi _0\,{=}\,0$ in (A.7) yields $\xi _1\,{=}\,1$, then (A.7) converges for any $\xi _0\,{\in }\,[0,1]$ in this case.

This completes the proof of (A.8), whereas (A.9) comes easily from (A.8) and from the monotonicity properties of function h given in (A.3).$\square$

Proof of Proposition 4.2

Based on Proposition 2.1, the function T is infinitely differentiable. Hence, we impose a first order optimality condition on T with respect to $\sigma$:

$$\begin{aligned} \frac{\partial T}{\partial \sigma } = (n-d{+}1)/\sigma -s(\phi (s))^{-s}\Vert x\Vert _s^s(1/\sigma )^{s+1}+(d{-}1)m^{-s}\sigma ^{s-1}=0\,.\qquad \end{aligned}$$

(A.10)

Equation (A.10) admits the following closed-form solution:

$$\begin{aligned} \sigma ^{\text {MAP}}(s) = m\,\left[ \left( -\alpha +\sqrt{\alpha ^2+4\beta m^{-s} (\sigma ^{\text {ML}})^{s}}\right) /(2\beta )\right] ^{1/s}\,, \end{aligned}$$

(A.11)

where the expression of $\sigma ^{\text {ML}}(s)$ is given in (2.7). Note that (A.11) can be further manipulated so as to give

$$\begin{aligned}&\sigma ^{\text {MAP}}(s) = m\alpha ^{1/s}[(-1+\sqrt{1+c(s)})/(2\beta )]^{1/s}\,,\nonumber \\&\quad \text {with}\quad c(s):=4(\beta /\alpha ^2) (m\phi (s))^{-s}(s/n)\Vert x\Vert _s^s\,. \end{aligned}$$

(A.12)

It is easy to verify that the second derivative of T with respect to $\sigma$ computed at $\sigma ^{\text {MAP}}(s)$ is strictly positive, hence the stationary point in (A.10) is a minimum. Finally, plugging (A.12) into the expression of function T in (4.13), after a few simple manipulations, the s estimation problem takes the form:

Based on Proposition 2.1, it is easy to verify that $f^{\text {MAP}}\in C^{\infty }(B)$ and that the following limits hold:

$$\begin{aligned} \lim _{s\rightarrow +\infty } f_1(s)= n\ln \sqrt{3} - \ln d \in {{\mathbb {R}}}\,,\quad \lim _{s\rightarrow +\infty } \Vert x\Vert _s/(m\phi (s)) = \Vert x\Vert _{\infty } / (m\sqrt{3}) =: \nu \,. \end{aligned}$$

Depending on $\nu$, the three following scenarios arise:

• (a) $\nu =1$. Based on the properties of function $\phi$ and $\Vert \cdot \Vert _{\infty }$, $\nu$ tends to 1 from the right. If $\nu \rightarrow 1^+$ slower than $s\rightarrow +\infty$, case (a) leads to case (c), otherwise, $c(s)\sim O(s)$ and $f_2(s)$ vanish so that $f^{\text {MAP}}(s)$ tends to a finite value when s goes to $+\infty$.

• (b) $\nu < 1$.

  For large s, the first term in $f_2(s)$ vanishes, while for the logarithmic term we consider the Maclaurin series expansion of $\sqrt{1+c(s)}$, so that:

  $$\begin{aligned}&\lim _{s\rightarrow +\infty } f_2(s) = \lim _{s\rightarrow +\infty } (n\alpha /s)[\ln (\alpha /(2\beta ))+\ln (-1+1+(1/2)c(s)+o(c(s)))]\\&\quad =\lim _{s\rightarrow +\infty } (n\alpha /s) \ln ((1/2)c(s)) = \lim _{s\rightarrow +\infty } (n\alpha /s)\ln (2(\beta /\alpha ^2)(s/n)) \nonumber \\&\qquad + (n\alpha )\ln \nu = n\alpha \ln \nu \in {{\mathbb {R}}}\,. \end{aligned}$$

  Therefore, function $f^{\text {MAP}}(s)$ tends to a finite value when $s\rightarrow +\infty$.

• (c) $\nu > 1$. For large s, we have $(n\alpha /s)\ln (-1+\sqrt{1+c(s)})\sim (n\alpha /s)\ln \sqrt{c(s)}\rightarrow k\in {{\mathbb {R}}}_{+}$ as $s\rightarrow + \infty$. Hence:

  $$\begin{aligned} \lim _{s\rightarrow +\infty } f_2(s) = \lim _{s\rightarrow +\infty } (n\alpha /s)\sqrt{1+c(s)} + k = + \infty \longrightarrow \lim _{s\rightarrow +\infty }f^{\text {MAP}}(s)=+\infty . \end{aligned}$$

We conclude that $f^{\text {MAP}}$ admits either a finite minimizer, that can be plugged into (A.11) thus returning $\sigma ^{\text {MAP}}$, or $s^{\text {MAP}}=+\infty$, i.e. the samples in x are drawn from a uniform distribution with $\sigma ^{\text {MAP}}=m\nu$. $\square$