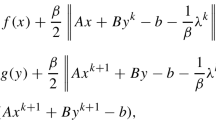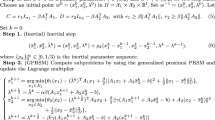1 Introduction

The split feasibility problem (SFP), which was first introduced by Censor and Elfving [12] to model phase retrieval problems, models a variety of inverse problems. Its recent applications to the medical treatment of intensity-modulated radiation therapy and medical imaging reconstruction [7, 11, 13, 15–17] have inspired more studies theoretically and practically.

The mathematical formulation of SFP is indeed a feasibility problem that amounts to finding a point \(x^*\in {\mathbb {R}}^n\) with the property

$$\begin{aligned} x^*\in {\mathcal {C}}\quad \text {and}\quad Ax^*\in {\mathcal {Q}}, \end{aligned}$$
(1.1)

where \({\mathcal {C}}\) and \({\mathcal {Q}}\) are nonempty, closed and convex subsets of \({\mathbb {R}}^n\) and \({\mathbb {R}}^m\), respectively, and \(A: {\mathbb {R}}^n\rightarrow {\mathbb {R}}^m\) is a linear operator.

It is known that SFP (1.1) includes a variety of real-world inverse problems as special cases. For instance, when \({\mathcal {Q}}=\{b\}\) is singleton, SFP (1.1) is reduced to the classical convexly constrained linear inverse problem, that is, finding a point \(x^*\in {\mathbb {R}}^n\) such that

$$\begin{aligned} x^*\in {\mathcal {C}}\quad \text {and}\quad Ax^*=b. \end{aligned}$$
(1.2)

This problem has extensively been studied in the literature (see [29, 30, 45, 48, 51] and the references therein). Due possibly to the unclear structure of the general constraint set \({\mathcal {Q}}\), SFP (1.1) has however been received much less attention than its special case (1.2). As a matter of fact, certain algorithms that work for (1.2) seemingly have no straightforward counterparts for SFP (1.1). For instance, it still remains unclear whether the dual approach for (1.2) proposed in [45] (see also [48]) can be extended to SFP (1.1).

The SFP (1.1) can be solved by optimization algorithms since it is equivalent to the constrained minimization problem:

$$\begin{aligned} \min _{x\in C}\;f(x):=\frac{1}{2}\Vert Ax-P_{{\mathcal {Q}}}Ax\Vert ^2. \end{aligned}$$
(1.3)

[Here \(P_{{\mathcal {Q}}}\) is the projection onto \({\mathcal {Q}}\) (see (2.1)).] Among the existing algorithms for SFP (1.1), the CQ algorithm introduced by Byrne [7, 8] is the most popular; it generates a sequence \(\{x^k\}\) through the recursion process:

$$\begin{aligned} x^{k+1}=P_{{\mathcal {C}}}\left( x^k-A^{\top }\left( Ax^k-P_{{\mathcal {Q}}}Ax^k\right) \right) . \end{aligned}$$

This is indeed the gradient-projection algorithm applied to the minimization problem (1.3) (it is also a special case of the proximal forward-backward splitting method [24]). Recent improvements of the CQ algorithm with relaxed stepsizes and projections can be found in [26, 46, 55, 57, 60].

It is often the case that SFP (1.1) and (1.2) are ill-posed, due to possible ill-conditionedness of A. As a result, regularization must be reinforced. In fact, for the past decades, regularization techniques have successfully been used for solving (1.2), in particular, the unconstrained case of \({\mathcal {C}}={\mathbb {R}}^n\); see [30, 32, 39, 49] and the references therein. Regularization methods for SFP (1.1) have however been quite a recent topic; see [10, 14, 55, 58] where the classical Tikhonov regularization [51] is used to promote stability of solutions. In contrast with Tikhonov’s regularization, the \(\ell _1\)-norm regularization for (1.2) has been paid much more attention recently, due to the fact that the \(\ell _1\)-norm induces sparsity of solutions [6, 22, 27, 31, 56]. A typical example is the lasso [50] (also known as basis pursuit denoising [22]) which is the minimization problem:

$$\begin{aligned} \min _{x\in {\mathbb {R}}^n}\frac{1}{2}\Vert Ax-b\Vert ^2+\sigma \Vert x\Vert _1, \end{aligned}$$
(1.4)

where \(b\in {\mathbb {R}}^m\) and \(\sigma >0\) is a regularization parameter.

The \(\ell _1\)-norm regularization of SFP (1.1) is the following constrained minimization problem:

$$\begin{aligned} \min _{x\in {\mathbb {R}}^n}\left\{ \;\Vert x\Vert _1\;|\;x\in {\mathcal {C}}\;\;\text {and}\;\;Ax\in {\mathcal {Q}}\right\} , \end{aligned}$$
(1.5)

which can also be recast as

$$\begin{aligned} \min _{x\in {\mathcal {C}}}\; \frac{1}{2}\Vert Ax-P_{{\mathcal {Q}}}(Ax)\Vert ^2+\sigma \Vert x\Vert _1. \end{aligned}$$
(1.6)

Notice that the lasso (1.4), the basis pursuit (BP) and basis pursuit denoising (BPDN) of Chen et al. [22] (see also [9, 27, 31, 53, 56]) are special cases of (1.5) and (1.6).

Compared with (1.4), the \(\ell _1\)-regularized SFP (1.6) has been received much less attention. In fact, as far as we have noticed, (1.6) has been considered only in [38], in which certain properties of the solution set of (1.6) were discussed, leaving algorithmic approaches unattached.

The main purpose of this paper is to introduce an implementable splitting algorithm for solving the \(\ell _1\)-regularized SFP (1.6) via the technique of alternating direction method of multipliers (ADMM) [33] in the framework of variational inequalities. Towards this we use the trick of variable splitting to rewrite (1.6) as

$$\begin{aligned} \begin{array}{cl} \displaystyle \min _{x,z} &{} f(x)+\sigma \Vert z\Vert _1 \\ \hbox {s.t.}&{} x=z,\;x\in {\mathcal {C}},\;z\in {\mathbb {R}}^n,\end{array}\; \end{aligned}$$
(1.7)

where f(x) is defined as in (1.3). Now ADMM, which has been widely used in the areas of variational inequalities, compressive sensing, image processing, and statistical learning (cf. [2, 6, 19, 21, 35, 36, 40, 56, 59]), works for (1.7) as follows: Given the k-th iterate \({\mathbf {w}}^k:=(x^k,z^k,\lambda ^k)\in {\mathcal {C}}\times {\mathbb {R}}^n\times {\mathbb {R}}^n\); the \((k+1)\)-th iterate \({\mathbf {w}}^{k+1}:=(x^{k+1},z^{k+1},\lambda ^{k+1})\) is obtained by solving three subproblems

figure a

where \(\{\lambda ^k\}\) is a sequence of Lagrangian multipliers and \(\gamma >0\) is a penalty parameter for violation of the linear constraints. The advantage of ADMM lies in its full exploiture of the separability structure of (1.7). Nevertheless, the subproblem (1.9) may not be easy enough to get solved due to the existence of the constraint set \({\mathcal {C}}\). To overcome this difficulty we will combine the techniques of linearization of ADMM and the proximal point algorithm [41] to propose a new algorithm, Algorithm 1 in Sect. 3. The main contribution of this paper is to prove the global convergence of this algorithm and apply it to solve image deblurring problems.

The rest of this paper is structured as follows. In Sect. 2, we summarize some basic notation, definitions and properties that will be useful for our subsequent analysis. In Sect. 3, we analyze the subproblems of ADMM for (1.7) and propose an implementable algorithm by incorporating the ideas of linearization and the proximal point algorithm into the new algorithm. Then, we prove global convergence of the proposed algorithm under some mild conditions. In Sect. 4, numerical experiments on image deblurring problems are carried out to verify the efficiency and reliability of our algorithm. Finally, concluding remarks are included in Sect. 5.

2 Preliminaries

In this section, we summarize some basic notation, concepts and well known results that will be useful for further discussions in subsequent sections.

Let \({\mathbb {R}}^n\) be an n-dimensional Euclidean space. For any two vectors \(x, y\in {\mathbb {R}}^n\), \(\left\langle x,\;y\right\rangle \) denotes the standard inner product. Furthermore, for a given symmetric and positive definite matrix M, we denote by \(\Vert x\Vert _M=\sqrt{\left\langle x, M x\right\rangle }\) the M-norm of x. For any matrix A, we denote \(\Vert A\Vert \) as its matrix 2-norm.

Throughout this paper, we denote by \(\iota _{\varOmega }\) the indicator function of a nonempty closed convex set \(\varOmega \), i.e.,

$$\begin{aligned} \iota _\varOmega (x):=\left\{ \begin{array}{ll} 0, &{}\;\; \text {if}\;\; x\in \varOmega , \\ +\infty , &{}\;\; \text {if}\;\; x\notin \varOmega .\end{array} \right. \end{aligned}$$

The projection operator \(P_{\varOmega ,M}\) from \({\mathbb {R}}^n\) onto the nonempty closed convex set \(\varOmega \) under M-norm is defined by

$$\begin{aligned} P_{\varOmega ,M}[x]:=\arg \min \left\{ \;\Vert y-x\Vert _M\;\;|\;\;{y\in \varOmega }\;\right\} , \quad x\in {\mathbb {R}}^n. \end{aligned}$$
(2.1)

For simplicity, let \(P_{\varOmega }\) be the projection operator under Euclidean norm. It is well-known that the projection \(P_{\varOmega ,M}\) (in \(\varOmega \)) can be characterized by the relation

$$\begin{aligned} \left\langle u-P_{\varOmega ,M}[u],\; M\left( v-P_{\varOmega ,M}[u]\right) \right\rangle \le 0, \quad u \in {\mathbb {R}}^n, \quad v \in \varOmega . \end{aligned}$$

(The proof is available in any standard optimization textbook, such as [5, p. 211].) Next we introduce Moreau’s notion [42] of proximity operators which extends the concept of projections.

Definition 2.1

Let \(\varphi :{\mathbb {R}}^n\rightarrow {\mathbb {R}}\cup \{+\infty \}\) be a proper, lower semicontinuous and convex function. The proximity operator of \(\varphi \), denoted by \(\mathbf{prox}_\varphi \), is defined as an operator from \({\mathbb {R}}^n\) into itself and given by

$$\begin{aligned} \mathbf{prox}_\varphi (x)=\mathop {\hbox {arg min}}\limits _{y\in {\mathbb {R}}^n} \left\{ \varphi (y) +\frac{1}{2}\Vert x-y\Vert ^2 \right\} ,\quad x\in {\mathbb {R}}^n. \end{aligned}$$
(2.2)

It is clear that \(P_{\varOmega }=\mathbf{prox}_\varphi \) when \(\varphi =\iota _{\varOmega }\). Moreover, if we denote by \(\mathbf{I}\) the identity operator on \({\mathbb {R}}^n\), then \(\mathbf{prox}_\varphi \) and \((\mathbf{I}-\mathbf{prox}_\varphi )\) share the same nonexpansivity of \(P_\varOmega \) and \((\mathbf{I}-P_\varOmega )\). The reader is referred to [23, 24, 42] for more details.

Definition 2.2

Let \(\varphi :{\mathbb {R}}^n\rightarrow {\mathbb {R}}\cup \{+\infty \}\) be a proper, lower semicontinuous and convex function. The subdifferential of \(\varphi \) is the set-valued operator \(\partial \varphi :{\mathbb {R}}^n\rightarrow 2^{{\mathbb {R}}^n}\), given by, for \(x\in {\mathbb {R}}^n\),

$$\begin{aligned} \partial \varphi (x):=\left\{ \; \zeta \in {\mathbb {R}}^n\; | \; \varphi (y) \ge \varphi (x) +\left\langle y-x,\;\zeta \right\rangle ,\quad y\in {\mathbb {R}}^n\;\right\} . \end{aligned}$$

According to the above two definitions, the minimizer in the definition (2.2) of \(\mathbf{prox}_\varphi (x)\) is characterized by the inclusion

$$\begin{aligned} 0\in \partial \varphi (\mathbf{prox}_\varphi (x)) + \mathbf{prox}_\varphi (x) - x. \end{aligned}$$

Definition 2.3

A set-valued operator T from \({\mathbb {R}}^n\) to \(2^{{\mathbb {R}}^n}\) is said to be monotone if

$$\begin{aligned} \left\langle x_1-x_2,\;x_1^*-x_2^* \right\rangle \ge 0,\quad x_1,\;x_2\in {\mathbb {R}}^n,\;\; x_1^*\in T(x_1),\;x_2^*\in T(x_2). \end{aligned}$$

A monotone operator is said to be maximal monotone if its graph is not properly contained in the graph of any other monotone operator.

It is well-known [47] that the subdifferential operator \(\partial \varphi \) of a proper, lower semicontinuous and convex function \(\varphi \) is maximal monotone.

Definition 2.4

Let \(g:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\) be a convex and differentiable function. We say that its gradient \(\nabla g\) is Lipschitz continuous with constant \(L>0\) if

$$\begin{aligned} \Vert \nabla g(x_1)-\nabla g(x_2)\Vert \le L \Vert x_1-x_2\Vert ,\quad x_1,\;x_2\in {\mathbb {R}}^n. \end{aligned}$$

Notice that the gradient of the function f defined in (1.6) is \(\nabla f=A^\top (\mathbf{I}-P_\varOmega )A \). It is easily seen that \(\nabla f\) is monotone and Lipschitz continuous with constant \(\Vert A\Vert ^2\), i.e.,

$$\begin{aligned} \Vert \nabla f(x_1) - \nabla f(x_2)\Vert \le \Vert A\Vert ^2\Vert x_1-x_2\Vert ,\quad x_1,\;x_2\in {\mathbb {R}}^n. \end{aligned}$$
(2.3)

3 Algorithm and Its Convergence Analysis

We are aimed in this section to invent a new algorithm, Algorithm 1 below, and prove its global convergence under certain mild conditions.

3.1 Algorithm

We begin with more analysis on the algorithm (1.8)–(1.9). The subproblem (1.9) is a constrained optimization problem which might not be easy enough to be solved efficiently. To make ADMM implementable for some constrained models, it is suggested directly linearizing the constrained subproblem [i.e., (1.9)] [18, 20, 52]. Clearly, an immediate benefit is that the solutions to the subproblems can be represented explicitly. It is noteworthy that direct linearization on ADMM must often be imposed strong conditions (e.g., strict convexity) for global convergence. Notice that the linearization on ADMM yields an approximate function involving a proximal term. Since the proximal point algorithm (PPA) [41] is one of the most powerful solvers in optimization, which not only provides a unified algorithmic framework including ADMM as its special case [28], but also, as Parikh and Boyd [44] emphasized, works under extremely general conditions, we combine the ideas of linearization on ADMM and PPA to propose an implementable splitting algorithm which has easier subproblems with closed-form solutions and shares similar convergence results to the PPA’s. More concretely, our idea is that we first add a proximal term to the subproblem (1.8), and the resulting subproblem has a closed-form solution via the shrinkage operator. We then linearize the function f at the latest iterate \(x^k\) in such a way that the subproblem (1.9) is simple enough to possess a closed-form expression. Following these two steps, we get an intermediate Lagrangian multiplier via (1.10).

Taking a revisit on the linearization procedure, we see that the resulting subproblem is essentially a one-step approximation of ADMM, which might not be the best output for the next iterate. Accordingly, we add a correction step with lower computational costs to update the output of the linearized ADMM (LADMM) for the purpose of compensating the approximation errors caused by linearization. A notable feature is that the correction-step can improve the numerical performance in terms of taking fewer iterations than LADMM, in addition to relaxing the conditions for global convergence and inducing a strong convergence result as [4].

Basing upon the above analysis, we will design an algorithm that inherits the advantages of ADMM and PPA. Our algorithm is a two-stage method, consisting of a prediction step and a correction step. Below, we mainly state the details of the prediction step. First, we generate the predictor \({\widetilde{z}}^k\) via

$$\begin{aligned} {\widetilde{z}}^k = \mathop {\hbox {arg min}}\limits _{z\in {\mathbb {R}}^n} \left\{ \sigma \Vert z\Vert _1+\frac{\gamma }{2}\left\| x^k-z-\frac{\lambda ^k}{\gamma }\right\| ^2+\frac{\rho _2}{2}\left\| z-z^k\right\| ^2\right\} , \end{aligned}$$
(3.1)

where \(\rho _2\) is a positive constant. The reason of imposing an proximal term \(\frac{\rho _2}{2}\left\| z-z^k\right\| ^2\) is to regularize the z-related subproblem. Besides, we can further derive a stronger convergence result theoretically with the help of such proximal term. Obviously, (3.1) can be rewritten as

$$\begin{aligned} {\widetilde{z}}^k=\mathop {\hbox {arg min}}\limits _{z\in {\mathbb {R}}^n} \left\{ \sigma \Vert z\Vert _1 + \frac{\gamma +\rho _2}{2}\left\| z-\frac{1}{\gamma +\rho _2}\left( \gamma x^k-\lambda ^k+\rho _2 z^k\right) \right\| ^2\right\} . \end{aligned}$$

Consequently, using the shrinkage operator [24, 56], we can solve the last minimization and express \({\widetilde{z}}^k\) in closed-form as

$$\begin{aligned} {\widetilde{z}}^k={{\mathrm{\text {shrink}}}}\left( \omega ^k,\;\frac{\sigma }{\gamma +\rho _2}\right) \quad \text {with}\quad \omega ^k:=\frac{1}{\gamma +\rho _2}\left( \gamma x^k-\lambda ^k+\rho _2 z^k\right) . \end{aligned}$$
(3.2)

Recall that the shrinkage operator ‘\({{\mathrm{\text {shrink}}}}(\cdot ,\cdot )\)’ is defined by

$$\begin{aligned} {{\mathrm{\text {shrink}}}}(w,\mu ):=\text {sign}(w)\odot \max \left\{ 0,|w|-\mu \right\} ,\qquad w\in {\mathbb {R}}^n,\;\mu >0, \end{aligned}$$
(3.3)

where the ‘sign’, ‘\(\max \)’, and the absolute value function ‘\(|\cdot |\)’ are component-wise, and ‘\(\odot \)’ denotes the component-wise product.

For the x-related subproblem, the minimization subproblem (1.9) is not simple enough to have closed-form solution due to the nonlinearity of the function f. We may treat the nonlinearity of f by linearization. As a matter of fact, given \(\left( x^k,{\widetilde{z}}^k,\lambda ^k\right) \), we linearize f at \(x^k\) to get an approximate subproblem of (1.9), that is,

$$\begin{aligned} {\widetilde{x}}^k&=\mathop {\hbox {arg min}}\limits _{x\in {\mathcal {C}}}\left\{ \left\langle \nabla f\left( x^k\right) ,\;x-x^k \right\rangle + \frac{\rho _1}{2}\left\| x-x^k\right\| ^2+\frac{\gamma }{2}\left\| x-{\widetilde{z}}^k-\frac{\lambda ^k}{\gamma } \right\| ^2\right\} \nonumber \\&=P_{{\mathcal {C}}}\left[ \frac{1}{\rho _1+\gamma }\left( \rho _1 x^k+\gamma {\widetilde{z}}^k+\lambda ^k -\nabla f\left( x^k\right) \right) \right] , \end{aligned}$$
(3.4)

where \(\rho _1\) is a suitable constant for approximation. With a pair of predictors \(({\widetilde{x}}^k,{\widetilde{z}}^k)\), we generate the last predictor of \(\lambda \) via

$$\begin{aligned} \widetilde{\lambda }^k=\lambda ^k-\gamma \left( {\widetilde{x}}^k-{\widetilde{z}}^k\right) . \end{aligned}$$
(3.5)

Finally, with the predictor \({\widetilde{{\mathbf {w}}}}^k=\left( {\widetilde{x}}^k,{\widetilde{z}}^k,\widetilde{\lambda }^k\right) \), we update the next iterate with a correction step to compensate the approximation errors caused by the linearization of ADMM. This correction step together with the proximal regularization further relaxes the convergence requirements and improves the numerical performance (see Sect. 4).

Before presenting the splitting algorithm, for the sake of convenience, we denote \(\eta _1(x,{\widetilde{x}}):=\nabla f(x) -\nabla f({\widetilde{x}})\), \(I_n\) the n-dimensional identity matrix, and

$$\begin{aligned} {\mathbf {w}}:=\left( \begin{array}{c}x \\ z\\ \lambda \end{array}\right) ,\quad M:=\left( \begin{array}{ccc}(\rho _1+\gamma )I_n &{}\quad 0 &{}\quad 0 \\ 0&{}\quad \rho _2I_n &{}\quad 0 \\ 0&{}\quad 0&{}\quad \frac{1}{\gamma }I_n\end{array}\right) \quad \text {and}\quad \eta ({\mathbf {w}},{\widetilde{{\mathbf {w}}}}):=\left( \begin{array}{c} \eta _1(x,{\widetilde{x}}) \\ 0 \\ 0\end{array}\right) . \end{aligned}$$
(3.6)

Then, the corresponding algorithm is described formally in Algorithm 1.

figure b

Remark 3.1

It is worth pointing out that Algorithm 1 is not limited to solve the \(\ell _1\)-norm regularized SFP. When we use a general regularizer \(\varphi (z)\) instead of \(\sigma \Vert z\Vert _1\) in subproblem (3.1), then (3.1) amounts to

$$\begin{aligned} {\widetilde{z}}^k=\mathop {\hbox {arg min}}\limits _{z\in {\mathbb {R}}^n} \left\{ \varphi (z) + \frac{\gamma +\rho _2}{2}\left\| z-\frac{1}{\gamma +\rho _2}\left( \gamma x^k-\lambda ^k+\rho _2 z^k\right) \right\| ^2\right\} . \end{aligned}$$

By invoking the definition of the proximity operator given in (2.2), the above scheme can be rewritten as

$$\begin{aligned} {\widetilde{z}}^k=\mathbf{prox}_{\frac{1}{\gamma +\rho _2}\varphi }\left( \omega ^k\right) \quad \text {with}\quad \omega ^k:=\frac{1}{\gamma +\rho _2}\left( \gamma x^k-\lambda ^k+\rho _2 z^k\right) . \end{aligned}$$

Therefore, Algorithm 1 is easily implementable as long as the above proximity operator has explicit representation. We refer the reader to [23] for more details of proximity operators.

Remark 3.2

The direction \({\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \) defined by (3.10) apparently involves the matrix inverse of M. This is however not a computational worry since M is a block scalar matrix and its inverse is trivially obtained.

Remark 3.3

Even if we deal with the special case of \({\mathcal {Q}}:=\{b\}\) in the ADMM algorithm (1.8)–(1.10), the second subproblem (1.9) is still not easy to solve under the assumption \({\mathcal {C}}\ne {\mathbb {R}}^n\) or \(A\ne I_n\). When we further consider special cases \({\mathcal {C}}\subset {\mathbb {R}}^n_{+}\), an interesting work [61] showed that the resulting problem can be recast as

$$\begin{aligned} \begin{array}{cl} \displaystyle \min _{x,z} &{} \sigma \left( z^\top e\right) + \frac{1}{2}\Vert Ax-b\Vert ^2 \\ \hbox {s.t.}&{} x=z,\;x\in {\mathbb {R}}^n,\;z\in {\mathcal {C}},\end{array}\; \end{aligned}$$
(3.11)

where \(e:=(1,1,\ldots ,1)^\top \). Accordingly, applying ADMM to (3.11) yields an implementable algorithm such that all subproblems have closed-form solutions. However, for general settings on \({\mathcal {C}}\) and \({\mathcal {Q}}\), we can not directly formulate \(\Vert z\Vert _1\) as \((z^\top e)\) and the nonlinearity of \(f(x)=\frac{1}{2}\Vert Ax-P_{{\mathcal {Q}}}(Ax)\Vert ^2\) also results in a subproblem without explicit representation. Comparatively speaking, our formulation for (1.6) and linearization are more suitable for general convex sets \({\mathcal {C}}\) and \({\mathcal {Q}}\).

3.2 Convergence Analysis

In this section we prove the global convergence of Algorithm 1. We begin with stating a fundamental fact derived from the first-order optimality condition, that is, problem (1.7) is equivalent to the variational inequality (VI) of finding a vector \({\mathbf {w}}^*\in \varOmega \) with the property

$$\begin{aligned} \left\langle {\mathbf {w}}-{\mathbf {w}}^*,\;F\left( {\mathbf {w}}^*\right) \right\rangle \ge 0,\quad {\mathbf {w}}\in \varOmega , \end{aligned}$$
(3.12a)

with

$$\begin{aligned} {\mathbf {w}}:=\left( \begin{array}{c}x \\ z\\ \lambda \end{array}\right) ,\quad F({\mathbf {w}}):=\left( \begin{array}{c} \nabla f(x) - \lambda \\ \zeta + \lambda \\ x-z\end{array} \right) \quad \text {and}\quad \varOmega :={\mathcal {C}}\times {\mathbb {R}}^n\times {\mathbb {R}}^n, \end{aligned}$$
(3.12b)

where \(\zeta \in \partial (\sigma \Vert \cdot \Vert _1)(z)\). The global convergence of Algorithm 1 will be established within the VI framework.

Lemma 3.1

Suppose that \({\mathbf {w}}^*\) is a solution of (3.12). Then, we have

$$\begin{aligned} \left\langle {\mathbf {w}}^k-{\mathbf {w}}^*,\;M{\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \right\rangle \ge \phi \left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) . \end{aligned}$$
(3.13)

Proof

First, the iterative scheme (3.4) can be easily recast into a VI, that is,

$$\begin{aligned} \left\langle x-{\widetilde{x}}^k,\; \nabla f\left( x^k\right) +\left( \rho _1+\gamma \right) \left( {\widetilde{x}}^k-x^k \right) +\gamma x^k -\gamma {\widetilde{z}}^k-\lambda ^k \right\rangle \ge 0,\quad x\in {\mathcal {C}}. \end{aligned}$$

Using (3.5) and rearranging terms of the above inequality yields

$$\begin{aligned} \left\langle x-{\widetilde{x}}^k,\; \nabla f\left( {\widetilde{x}}^k\right) -\widetilde{\lambda }^k+\left( \rho _1+\gamma \right) \left( {\widetilde{x}}^k-x^k\right) +\eta _1\left( x^k,{\widetilde{x}}^k\right) \right\rangle \ge \gamma \left\langle x-{\widetilde{x}}^k,\;{\widetilde{x}}^k-x^k\right\rangle , \end{aligned}$$
(3.14)

where \(\eta _1\left( x^k,{\widetilde{x}}^k\right) \) is given in (3.6).

Similarly, it follows from (3.1) and, respectively, (3.5) that

figure c

where \(\zeta ^k\in \partial \left( \sigma \Vert \cdot \Vert _1\right) \left( z^k\right) \). Upon summing up (3.14)–(3.16), we can rewrite it into a compact form as follows

$$\begin{aligned} \left\langle {\mathbf {w}}-{\widetilde{{\mathbf {w}}}}^k,\; F\left( {\widetilde{{\mathbf {w}}}}^k\right) - M{\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \right\rangle \ge \gamma \left\langle {\widetilde{z}}^k-{\widetilde{x}}^k+x-z,\;{\widetilde{x}}^k-x^k \right\rangle ,\quad {\mathbf {w}}\in \varOmega . \end{aligned}$$
(3.17)

Setting now \({\mathbf {w}}:={\mathbf {w}}^*\) in the above inequality and noticing the fact that \(x^*=z^*\), we get

$$\begin{aligned} \left\langle {\mathbf {w}}^*-{\widetilde{{\mathbf {w}}}}^k,\; F\left( {\widetilde{{\mathbf {w}}}}^k\right) - M{\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \right\rangle \ge \left\langle \widetilde{\lambda }^k-\lambda ^k,\;{\widetilde{x}}^k-x^k \right\rangle . \end{aligned}$$

Equivalently,

$$\begin{aligned} \left\langle {\widetilde{{\mathbf {w}}}}^k-{\mathbf {w}}^*,\; M{\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \right\rangle \ge \left\langle {\widetilde{{\mathbf {w}}}}^k-{\mathbf {w}}^*,\; F\left( {\widetilde{{\mathbf {w}}}}^k\right) \right\rangle + \left\langle \widetilde{\lambda }^k-\lambda ^k,\;{\widetilde{x}}^k-x^k \right\rangle . \end{aligned}$$
(3.18)

Since f and \(\sigma \Vert \cdot \Vert _1\) are convex functions, it is easy to derive that the function F defined in (3.12) is monotone. It turns out that

$$\begin{aligned} \left\langle {\widetilde{{\mathbf {w}}}}^k-{\mathbf {w}}^*,\; F\left( {\widetilde{{\mathbf {w}}}}^k\right) \right\rangle \ge \left\langle {\widetilde{{\mathbf {w}}}}^k-{\mathbf {w}}^*,\; F\left( {\mathbf {w}}^*\right) \right\rangle \ge 0. \end{aligned}$$

This together with (3.18) further implies that

$$\begin{aligned} \left\langle {\widetilde{{\mathbf {w}}}}^k-{\mathbf {w}}^*,\; M{\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \right\rangle \ge \left\langle \widetilde{\lambda }^k-\lambda ^k,\;{\widetilde{x}}^k-x^k \right\rangle . \end{aligned}$$

The desired inequality (3.13) now immediately follows from the above inequality and the definition of \(\phi \left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \) given by (3.9). \(\square \)

Indeed, the above result implies that \(-{\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \) is a descent search direction of the unknown distance function \(\frac{1}{2}\Vert {\mathbf {w}}-{\mathbf {w}}^*\Vert ^2_M\) at the point \({\mathbf {w}}={\mathbf {w}}^k\). Below, we show that the stepsize defined by (3.8) is reasonable. To see this we define two functions

$$\begin{aligned} {\mathbf {w}}^{k+1}(\alpha ):={\mathbf {w}}^k-\alpha {\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \end{aligned}$$
(3.19)

and

$$\begin{aligned} \varTheta (\alpha ):=\Vert {\mathbf {w}}^k-{\mathbf {w}}^*\Vert ^2_M-\Vert {\mathbf {w}}^{k+1}(\alpha )-{\mathbf {w}}^*\Vert _M^2. \end{aligned}$$
(3.20)

Note that the function \(\varTheta (\alpha )\) may be viewed as the progress-function to measure the improvement obtained at the k-th iteration of Algorithm 1. We need to maximize \(\varTheta (\alpha )\) for seeking an optimal improvement.

Lemma 3.2

Suppose that \({\mathbf {w}}^*\) is a solution of (3.12). Then we have

$$\begin{aligned} \varTheta (\alpha )\ge q(\alpha ), \end{aligned}$$
(3.21)

where

$$\begin{aligned} q(\alpha )=2\alpha \phi \left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) - \alpha ^2 \Vert {\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \Vert _M^2. \end{aligned}$$

Proof

It follows from (3.19) and (3.20) that

$$\begin{aligned} \varTheta (\alpha )&=\Vert {\mathbf {w}}^k-{\mathbf {w}}^*\Vert ^2_M-\Vert {\mathbf {w}}^{k+1}(\alpha )-{\mathbf {w}}^*\Vert _M^2 \\&=\Vert {\mathbf {w}}^k-{\mathbf {w}}^*\Vert ^2_M-\Vert {\mathbf {w}}^k-\alpha {\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) -{\mathbf {w}}^*\Vert _M^2\\&=2\alpha \left\langle {\mathbf {w}}^k-{\mathbf {w}}^*,\;M{\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \right\rangle - \alpha ^2 \Vert {\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \Vert _M^2 \\&\ge 2\alpha \phi \left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) - \alpha ^2 \Vert {\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \Vert _M^2, \end{aligned}$$

where the last inequality follows from Lemma 3.1. \(\square \)

Since \(q(\alpha )\) is a quadratic function of \(\alpha \), it is easy to find that \(q(\alpha )\) attains its maximum value at the point

$$\begin{aligned} \alpha _k:=\frac{\phi \left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) }{\Vert {\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \Vert _M^2}. \end{aligned}$$
(3.22)

It then turns out that, for any relaxation factor \(\tau >0\),

$$\begin{aligned} \varTheta (\tau \alpha _k)&\ge 2\tau \alpha _k \phi \left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) - \tau ^2\alpha _k^2 \Vert {\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \Vert _M^2 \\&= \tau (2-\tau )\alpha _k \phi \left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) . \end{aligned}$$

To ensure that an improvement can be obtained at each iteration, we should limit \(\tau \in (0,2)\) so that the right-hand side in the above relation is positive. However, we suggest to choose \(\tau \in [1,2)\) for fast convergence in practice (see Sect. 4).

Lemma 3.3

Suppose that \(\rho _1\ge \Vert A\Vert ^2\). Then, the step size \(\alpha _k\) defined by (3.8) is bounded away below from zero; that is, \(\inf _{k\ge 1}\alpha _k\ge \alpha _{\min }>0\) for some positive constant \(\alpha _{\min }\).

Proof

An appropriate application of the Cauchy–Schwartz inequality

$$\begin{aligned} 2\left\langle {\mathbf {a}},{\mathbf {b}}\right\rangle \le \kappa \Vert {\mathbf {a}}\Vert ^2 + \frac{1}{\kappa }\Vert {\mathbf {b}}\Vert ^2, \quad {\mathbf {a}},\ {\mathbf {b}}\in {\mathbb {R}}^n, \ \kappa >0 \end{aligned}$$

implies that

$$\begin{aligned} \left\langle \widetilde{\lambda }^k-\lambda ^k,\;{\widetilde{x}}^k-x^k\right\rangle \le \frac{1}{2\gamma }\Vert \widetilde{\lambda }^k-\lambda ^k\Vert ^2 +\frac{\gamma }{2}\Vert {\widetilde{x}}^k-x^k\Vert ^2. \end{aligned}$$

Consequently, it follows from (3.9) and (3.10) that

$$\begin{aligned} \phi \left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right)&=\left\langle {\mathbf {w}}^k-{\widetilde{{\mathbf {w}}}}^k,\; M{\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \right\rangle + \left\langle \widetilde{\lambda }^k-\lambda ^k,\;{\widetilde{x}}^k-x^k \right\rangle \nonumber \\&\ge \left( \rho _1+\frac{\gamma }{2}\right) \Vert {\widetilde{x}}^k-x^k\Vert ^2 +\rho _2\Vert {\widetilde{z}}^k-z^k\Vert ^2\nonumber \\&\quad +\frac{1}{2\gamma }\Vert \widetilde{\lambda }^k-\lambda ^k\Vert ^2 -\left\langle x^k-{\widetilde{x}}^k,\;\eta _1\left( x^k,{\widetilde{x}}^k\right) \right\rangle \nonumber \\&\ge \left( \rho _1-\Vert A\Vert ^2+\frac{\gamma }{2}\right) \Vert {\widetilde{x}}^k-x^k\Vert ^2 +\rho _2\Vert {\widetilde{z}}^k-z^k\Vert ^2+\frac{1}{2\gamma }\Vert \widetilde{\lambda }^k-\lambda ^k\Vert ^2 \nonumber \\&\ge C_{\min } \Vert {\widetilde{{\mathbf {w}}}}^k-{\mathbf {w}}^k\Vert ^2, \end{aligned}$$
(3.23)

where the second inequality follows from the Cauchy–Schwartz inequality and the Lipschitz continuity of \(\nabla f\), and the last inequality from the introduction of the constant \(C_{\min }:=\min \left\{ \frac{\gamma }{2},\;\rho _2,\;\frac{1}{2\gamma }\right\} .\)

On the other hand, it follows again from the Cauchy–Schwartz inequality and monotonicity of \(\nabla f\) that

$$\begin{aligned} \Vert {\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \Vert ^2_M&= \left\langle {\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) ,\;M{\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \right\rangle \nonumber \\&=\Vert {\mathbf {w}}^k-{\widetilde{{\mathbf {w}}}}^k\Vert _M^2-2\left\langle x^k-{\widetilde{x}}^k,\;\eta _1\left( x^k,{\widetilde{x}}^k\right) \right\rangle +\frac{1}{\rho _1+\gamma }\Vert \eta _1\left( x^k,{\widetilde{x}}^k\right) \Vert ^2 \nonumber \\&\le \left( \rho _1 + \gamma + \frac{\Vert A\Vert ^4}{\rho _1+\gamma }\right) \Vert x^k-{\widetilde{x}}^k\Vert ^2 + \rho _2\Vert z^k-{\widetilde{z}}^k\Vert ^2+\frac{1}{\gamma }\Vert \lambda ^k-\widetilde{\lambda }^k\Vert ^2 \nonumber \\&\le C_{\max } \Vert {\mathbf {w}}^k-{\widetilde{{\mathbf {w}}}}^k\Vert ^2, \end{aligned}$$
(3.24)

where \(C_{\max }:=\max \left\{ \frac{(\rho _1 + \gamma )^2 +\Vert A\Vert ^4}{\rho _1+\gamma },\;\rho _2,\;\frac{1}{\gamma } \right\} \). Thus, combining (3.23) and (3.24) immediately yields

$$\begin{aligned} \alpha _k\ge \frac{C_{\min }}{C_{\max }}=:\alpha _{\min }>0. \end{aligned}$$

The assertion of this lemma is proved. \(\square \)

Theorem 3.1

Suppose that \(\rho _1\ge \Vert A\Vert ^2\) and let \({\mathbf {w}}^*\) be an arbitrary solution of (3.12). Then the sequence \(\{{\mathbf {w}}^k\}\) generated by Algorithm 1 satisfies the following property

$$\begin{aligned} \Vert {\mathbf {w}}^{k+1}-{\mathbf {w}}^*\Vert ^2_M\le \Vert {\mathbf {w}}^k-{\mathbf {w}}^*\Vert ^2_M -\tau (2-\tau )\alpha _{\min }C_{\min }\Vert {\mathbf {w}}^k-{\widetilde{{\mathbf {w}}}}^k\Vert ^2. \end{aligned}$$
(3.25)

Proof

From (3.7), (3.22) and (3.23) together with Lemmas 3.1 and 3.3, it follows that

$$\begin{aligned} \Vert {\mathbf {w}}^{k+1}-{\mathbf {w}}^*\Vert ^2_M&=\Vert {\mathbf {w}}^k-\tau \alpha _k {\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) -{\mathbf {w}}^*\Vert ^2_M \nonumber \\&=\Vert {\mathbf {w}}^k-{\mathbf {w}}^*\Vert ^2_M - 2\tau \alpha _k \left\langle {\mathbf {w}}^k-{\mathbf {w}}^*,\;M{\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \right\rangle + \tau ^2 \alpha _k^2\Vert {\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \Vert _M^2 \\&\le \Vert {\mathbf {w}}^k-{\mathbf {w}}^*\Vert ^2_M -2\tau \alpha _k \phi \left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) + \tau ^2 \alpha _k^2\Vert {\mathbf {d}}\left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \Vert _M^2 \\&=\Vert {\mathbf {w}}^k-{\mathbf {w}}^*\Vert ^2_M -\tau (2-\tau )\alpha _k \phi \left( {\mathbf {w}}^k,{\widetilde{{\mathbf {w}}}}^k\right) \\&\le \Vert {\mathbf {w}}^k-{\mathbf {w}}^*\Vert ^2_M -\tau (2-\tau )\alpha _{\min }C_{\min }\Vert {\mathbf {w}}^k-{\widetilde{{\mathbf {w}}}}^k\Vert ^2. \end{aligned}$$

We obtained the desired result. \(\square \)

Theorem 3.2

Suppose that \(\rho _1\ge \Vert A\Vert ^2\). Then, the sequence \(\{{\mathbf {w}}^k\}\) generated by Algorithm 1 is globally convergent to a solution of VI (3.12).

Proof

Let \({\mathbf {w}}^*\) be a solution of (3.12). It is immediately clear from (3.25) that

$$\begin{aligned} \Vert {\mathbf {w}}^{k+1}-{\mathbf {w}}^*\Vert ^2_M\le \Vert {\mathbf {w}}^k-{\mathbf {w}}^*\Vert ^2_M\le \cdots \le \Vert {\mathbf {w}}^0-{\mathbf {w}}^*\Vert ^2_M. \end{aligned}$$
(3.26)

That is, the sequence \(\{\Vert {\mathbf {w}}^k-{\mathbf {w}}^*\Vert _M\}\) is decreasing. In particular, the sequence \(\{{\mathbf {w}}^k\}\) is bounded and the

$$\begin{aligned} \lim _{k\rightarrow \infty } \Vert {\mathbf {w}}^k-{\mathbf {w}}^*\Vert _M\quad \mathrm{exists}. \end{aligned}$$
(3.27)

By rewriting (3.25) as

$$\begin{aligned} \tau (2-\tau )\alpha _{\min }C_{\min }\Vert {\mathbf {w}}^k-{\widetilde{{\mathbf {w}}}}^k\Vert ^2\le \Vert {\mathbf {w}}^k-{\mathbf {w}}^*\Vert ^2_M-\Vert {\mathbf {w}}^{k+1}-{\mathbf {w}}^*\Vert ^2_M , \end{aligned}$$

we immediately conclude that

$$\begin{aligned} \lim _{k\rightarrow \infty } \Vert {\mathbf {w}}^k-{\widetilde{{\mathbf {w}}}}^k\Vert =0. \end{aligned}$$
(3.28)

It turns out that \(\lim _{k\rightarrow \infty } \Vert x^k-{\widetilde{x}}^k\Vert =0\) and that the sequences \(\{{\mathbf {w}}^k\}\) and \(\{{\widetilde{{\mathbf {w}}}}^k\}\) have the same cluster points. To prove the convergence of the sequence \(\{{\mathbf {w}}^k\}\), let \(\{{\mathbf {w}}^{k_j}\}\) be a subsequence of \(\{{\mathbf {w}}^{k}\}\) that converges to some point \({\mathbf {w}}^{\infty }\); hence, the subsequence \(\{{\widetilde{{\mathbf {w}}}}^{k_j}\}\) of \(\{{\widetilde{{\mathbf {w}}}}^{k}\}\) also converges to \({\mathbf {w}}^{\infty }\).

Now taking the limit as \(j\rightarrow \infty \) over the subsequence \(\{k_j\}\) in (3.17) and using the continuity of F, we arrive at

$$\begin{aligned} \left\langle {\mathbf {w}}-{\mathbf {w}}^{\infty },\; F({\mathbf {w}}^{\infty })\right\rangle \ge 0,\quad {\mathbf {w}}\in \varOmega . \end{aligned}$$

Namely, \({\mathbf {w}}^{\infty }\) solves VI (3.12).

Finally, substituting \({\mathbf {w}}^{\infty }\) for \({\mathbf {w}}^*\) in (3.27) and using the fact that \(\Vert {\mathbf {w}}^k-{\mathbf {w}}^{\infty }\Vert _M\) is convergent, we conclude that

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert {\mathbf {w}}^{k}-{\mathbf {w}}^{\infty }\Vert _M= \lim _{j\rightarrow \infty }\Vert {\mathbf {w}}^{k_j}-{\mathbf {w}}^{\infty }\Vert _M=0. \end{aligned}$$

This proves that the full sequence \(\{{\mathbf {w}}^{k}\}\) converges to \({\mathbf {w}}^{\infty }\). \(\square \)

4 Numerical Experiments

The development of implementable algorithms tailored for \(\ell _1\)-norm regularized SFP [(even if for its special case of (1.2)] is in infant stage. Our main goal here is not to investigate the competitiveness of this approach with other algorithms, but simply to illustrate the reliability and the sensitivity with respect to some involved parameters of the presented method. Certainly, we also report some results to support our motivation by comparing Algorithm 1 (abbreviated as ‘ISM’) with ADMM and the straightforward linearized ADMM (we use “LADMM” for short) corresponding to (3.2), (3.4) and (3.5). Specifically, we demonstrate the application of the three algorithms to an image deblurring problem and report some preliminary numerical results to achieve the aforementioned goals.

All codes were written by Matlab 2010b and run on a Lenovo desktop computer with Intel Pentium Dual-Core processor 2.33GHz and 2Gb main memory.

The problem under test here is a wavelet-based image deblurring problem, which is a special case of (1.5) with a box constraint \({\mathcal {C}}\) and \({\mathcal {Q}}:=\{b\}\). More concretely, the model for this problem can be formulated as:

$$\begin{aligned} \min _x\;\left\{ \;\sigma \Vert Wx\Vert _1+\frac{1}{2}\Vert Ax-b\Vert ^2\;\Big |\;x\in {\mathcal {C}}\; \right\} , \end{aligned}$$
(4.1)

where b represents the (vectorized) observed image, the matrix \(A:=BW\) consists of a blur operator B and an inverse of a three stage Haar wavelet transform W, and the set \({\mathcal {C}}\) is a box area in \({\mathbb {R}}^{n}\). Indeed, if the image is considered with double precision entries, then the pixel values lie in \({\mathcal {C}}:=[0,1]\), and an 8-bit gray-scale image corresponds to \({\mathcal {C}}:=[0,255]\). Notice that the unconstrained alternative of (4.1), i.e., \({\mathcal {C}}:={\mathbb {R}}^n\), is more popular in the literature (see, for instance, [1, 3, 37]). However, as shown in [18, 20, 34, 43], more precise restoration, especially for binary images, may occur by absorbing an additional box constraint \({\mathcal {C}}\) into the model. In this section, we are concerned with the constrained model (4.1) and investigate the behavior of Algorithm 1 for this problem.

In these experiments, we adopt the reflective boundary condition and set the regularization parameter \(\sigma \) as 2e\(-\)5. We test eight different images, which were scaled into the range between 0 and 1, i.e., \({\mathcal {C}}:=[0,1]\), and corrupted in the same way used in [3]. More specifically, each image was degraded by a Gaussian blur of size \(9\times 9\) and standard deviation 4 and corrupted by adding an additive zero-mean white Gaussian noise with standard deviation \(10^{-3}\). The original and degraded eight images are listed in Figs. 1 and 2, respectively.

Fig. 1
figure 1

Original images. Left to right, top to bottom shape.jpg (\(128\times 128\)); chart.tiff (\(256\times 256\)); satellite (\(256\times 256\)); church (\(256\times 256\)); barbara (\(512\times 512\)); lena (\(512\times 512\)); man (\(512\times 512\)); boat (\(512\times 512\))

Full size image
Fig. 2
figure 2

Observed images

Full size image

We first define the usual signal-to-noise ratio (SNR) in decibel (dB) to measure the quality of the recovered image, i.e.,

$$\begin{aligned} \mathrm{SNR}:=20\log _{10}\frac{\Vert x\Vert }{\Vert \tilde{x}-x\Vert }, \end{aligned}$$

where x is a clean image and \(\tilde{x}\) is a restored image. Clearly, a larger SNR value means that we restored a better image. Without loss of generality, we use

$$\begin{aligned} \frac{\Vert x^{k+1}-x^k\Vert }{\Vert x^k\Vert }\le \mathrm{tol} \end{aligned}$$
(4.2)

to be the stopping criterion throughout the experiments. Throughout, we report the number of iterations (Iter.); computing time in seconds (Time), and SNR values (SNR).

We first investigate the numerical behavior of our ISM for (4.1). Notice that the global convergence of our ISM is built up under the assumption \(\rho _1\ge \Vert A\Vert ^2\). We thus set \(\rho _1=1.5\Vert A\Vert ^2\) throughout the experiments. Below, we test ‘chart.tiff’ image and investigate the performance of the rest of parameters involved in our method. For the relaxation parameter \(\tau \), we set \(\gamma =0.02\), \(\rho _2=0.01\), and test three cases of \(\tau =\{1.0\), 1.4, \(1.8\}\). For the penalty parameter \(\gamma \), we take \(\tau =1.8\), \(\rho _2=0.01\) and then consider four cases of \(\gamma =\{0.1\), 0.02, 0.001, \(0.0001\}\). Finally, we set \(\tau =1.8\) and \(\gamma =0.02\) to investigate the performance of \(\rho _2\) with \(\rho _2=\{1\), 0.05, 0.1, \(0.01\}\). For each case, we plot the evolution of SNR with respect to iterations in Fig. 3.

Fig. 3
figure 3

Numerical performance of our ISM with different parameters

Full size image

It can be easily seen from the first plot in Fig. 3 that larger \(\tau \) performs better than the smaller ones, which also supports the theoretical analysis in Sect. 3 [see Lemma 3.2 and (3.22)]. From the last two plots in Fig. 3, however, smaller \(\gamma \) and \(\rho _2\) bring better performance relatively. Indeed, we can choose \(\rho _2=0\) due to \(\eta ({\mathbf {w}},{\widetilde{{\mathbf {w}}}})\) defined in (3.6) can be simplified as \(\eta _1(x,{\widetilde{x}})\). Of course a suitable \(\rho _2>0\) may have benefits for stable performance in certain applications, because \(\frac{\rho _2}{2}\Vert z-z^k\Vert ^2\) serves a similar role as Tikhonov regularization. Though we can not demonstrate (possibly impossible, indeed) the best choices of the parameters for all problems, the results in Fig. 3 provide a direction for us to choose them empirically.

According to the above data, we now take \(\tau =1.8\), \(\gamma =0.02\), \(\rho _2=0.01\) and report the numerical results of our ISM under different stopping tolerances ‘tol’. More specifically, we set four different tolerances \(\text {tol}=\{10^{-3}\), \(5\times 10^{-4}\), \(10^{-4}\), \(5\cdot 10^{-5}\}\) in (4.2) and summarize the corresponding results in Table 1.

Table 1 Numerical performance of ISM under different tolerances ‘tol’
Full size table

The data in Table 1 show that the number of iterations is increasing significantly when we set a smaller tolerance ‘tol’. However, our method is still efficient for the case of \(\mathrm{tol}\ge 5\times 10^{-4}\). More importantly, our ISM is easily implementable due to its simple subproblems.

Table 2 Numerical comparison (tol = \(10^{-5}\))
Full size table
Fig. 4
figure 4

Recovered images by the three methods. From top to bottom: ISM, LADMM and ADMM

Full size image

Hereafter, we turn to compare ISM with LADMM and ADMM showing the necessity of linearization and correction step. For the parameters involved in LADMM and ADMM, we follow the same settings of ISM, that is, \(\rho _1=1.5\Vert A\Vert ^2\) for LADMM and \(\gamma =0.02\) for both LADMM and ADMM. Here, we set the tolerance as \(\mathrm{tol}=10^{-5}\) and reported the corresponding results in Table 2. Note that the subproblem (1.9) of ADMM does not have closed-form solution. We thus implemented the projected Barzilai–Borwein method in [25] to pursuit an approximate solution to this problem and allow a maximal number of 30 for the inner loop. Accordingly, we also report the inner iteration (denoted by “InIt.”) of ADMM in Table 2. The recovered images are listed in Fig. 4.

As shown in Table 2, we can see that ADMM requires fewest iterations to recover a satisfactory image. However, ADMM needs a time-consuming inner loop to pursuit an approximate solution such that ADMM takes more computing time than ISM and LADMM, which can be clearly seen from the number of inner iterations. Thus, the linearization is necessary for the problem under consideration. Comparing ISM and LADMM, we can see that ISM takes fewer iterations to get higher SNR than LADMM, but more computing time. This supports that our correction step can improve the performance of ISM in terms of iterations. Since the correction step requires to compute \(\eta _1(x^k,{\widetilde{x}}^k)\), ISM needs one more discrete cosine transform and its inverse, which thus takes more computing time than LADMM. From the recovered images in Fig. 4, the three methods can recover desirable images. In summary, all experiments in this section verify the efficiency and reliability of our ISM.

5 Conclusions

We have considered the \(\ell _1\)-norm regularized SFP, which is an extension of the timely \(\ell _1\)-norm regularized linear inverse problems, but has been received much less attention. Due to the nondifferentiability of \(\ell _1\)-norm regularizer, many traditional iterative methods in the literature of SFP can not be directly applied to the \(\ell _1\)-regularized model. Therefore, we have proposed a splitting algorithm, which exploits the structure of the problem such that its subproblems are simple enough to have closed-form solutions under the assumptions that projections onto the sets \({\mathcal {C}}\) and \({\mathcal {Q}}\) are readily computed. Our preliminary numerical results have supported the idea of the application of \(\ell _1\)-norm regularization to SFP, and verified the reliability and efficiency of Algorithm 1. Recently, an extension of SFP, i.e., multiple-set split feasibility problem (MSFP), has been received considerable attention, e.g., see [13, 54, 62, 63]. Therefore, to investigate the application of \(\ell _1\)-norm regularization to MSFP and the applicability of the proposed algorithm to the regularized MSFP is our future work. On the other hand, as stated in [38], larger regularization parameter \(\sigma \) in (1.6) will yields sparser solutions, and it is difficult to choose \(\sigma \) that fits well for all problems. Thus, how to choose a suitable \(\sigma \) automatically in algorithmic implementation is also our further investigation.