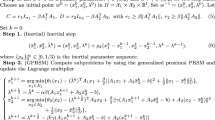A Partially Inertial Customized Douglas–Rachford Splitting Method for a Class of Structured Optimization Problems

Abstract

In this paper, we are concerned with a class of structured optimization problems frequently arising from image processing and statistical learning, where the objective function is the sum of a quadratic term and a nonsmooth part, and the constraint set consists of a linear equality constraint and two simple convex sets in the sense that projections onto simple sets are easy to compute. To fully exploit the quadratic and separable structure of the problem under consideration, we accordingly propose a partially inertial Douglas–Rachford splitting method. It is noteworthy that our algorithm enjoys easy subproblems for the case where the underlying two simple convex sets are not the whole spaces. Theoretically, we establish the global convergence of the proposed algorithm under some mild conditions. A series of computational results on the constrained Lasso and constrained total-variation (TV) based image restoration demonstrate that our proposed method is competitive with some state-of-the-art first-order solvers.

1 Introduction

We consider a class of structured optimization problems as follows:

$$\begin{aligned} \min _{x,y}&\quad f(x)+ g(y) \nonumber \\ \text {s.t.}&\quad Ax+By=b, \nonumber \\&\quad x\in {\mathcal {X}},y\in {\mathcal {Y}}, \end{aligned}$$

(1.1)

where f(x) is in particular specified as a quadratic function, i.e., $f(x)=\frac{1}{2}\Vert Kx-d\Vert ^2$ with $K\in {{\mathbb {R}}}^{m_1\times n_1}$ and $d\in {{\mathbb {R}}}^{m_1}$; $g:{{\mathbb {R}}}^{n_2}\rightarrow {{\mathbb {R}}}$ is a continuous closed convex (usually assumed to be nonsmooth) function; $A\in {{\mathbb {R}}}^{m_2\times n_1} \text { and }B\in {{\mathbb {R}}}^{m_2\times n_2}$ are given matrices; $b\in {{\mathbb {R}}}^{m_2}$ is a given vector; both $\mathcal X\subset {{\mathbb {R}}}^{n_1}$ and ${\mathcal {Y}}\subset {{\mathbb {R}}}^{n_2}$ are simple closed convex sets in the sense that projections onto them are very easy (e.g., nonnegative orthant, spheroidal or box areas). Throughout this paper, we assume that the solution set of problem (1.1) is nonempty. Besides, it is noteworthy that although we restrict the later theoretical discussion to the case of model (1.1) with vector variables, all our results actually are applicable to the case with matrix variables.

The main reason that we focus on model (1.1) with a specific quadratic term is its fruitful applications in the areas of image processing, machine learning, and statistical analysis. Generally speaking, the quadratic part f(x) often serves as a data-fidelity term and the nonsmooth part g(y) usually represents a regularization term to promote some special structure (e.g., sparsity and low-rankness) of solutions. Below, we just list three motivating examples which are special cases of model (1.1).

• Constrained TV-based image restoration. The pixels constrained TV-based image restoration model (see [29, 39]) takes the form of

  $$\begin{aligned} \min _{x\in {\mathcal {B}}} \left\{ \frac{1}{2}\Vert Kx-d\Vert ^2 + \mu \Vert |\varvec{D} x|\Vert _1\right\} , \end{aligned}$$

  (1.2)

  where d is an observed image; $K\in {{\mathbb {R}}}^{n\times n}$ represents a degraded operator with $n=n_1\times n_2$ being the total number of pixels; $\varvec{D}$ is the discrete gradient operator (see [42] for more details); $\mathcal {B}=[\textbf{l},\textbf{u}]$ is a box area in ${{\mathbb {R}}}^n$ (e.g., $\mathcal {B}=[0,1]^n$ and $[0,255]^n$ for double precision and 8-bit gray-scale images, respectively); $\mu$ is a positive trade-off parameter between the data-fidelity and regularization term. Clearly, introducing an auxiliary variable y to the TV regularization term immediately leads to the following reformulation:

  $$\begin{aligned} \min _{x,y} \left\{ \frac{1}{2}\Vert Kx-d\Vert ^2+\mu \Vert |y|\Vert _1 ~~\big \vert ~~ \varvec{D} x-y=0,~ x\in {\mathcal {B}},~y\in {{\mathbb {R}}}^n\times {{\mathbb {R}}}^n\right\} , \end{aligned}$$

  (1.3)

  which is a special case of the generic model (1.1) with settings $g(y)=\mu \Vert |y|\Vert _1$, $A=\varvec{D}$, $B=-I$, $\mathcal X={\mathcal {B}}$, and ${\mathcal {Y}}={{\mathbb {R}}}^n\times {{\mathbb {R}}}^n$.

• Constrained Lasso. The constrained Lasso problem is an extension of the standard Lasso problem [43] with an extra constraint. Mathematically, it can be expressed as

  $$\begin{aligned} \min _{x\in {\mathcal {X}}} \left\{ \frac{1}{2}\Vert Kx-d\Vert ^2+\mu \Vert x\Vert _1\right\} , \end{aligned}$$

  (1.4)

  where $d\in {{\mathbb {R}}}^l$ is an observed vector; $K\in {{\mathbb {R}}}^{l\times n}$ is a design or dictionary matrix; $\mu$ is a positive constant controlling the degree of sparsity and ${\mathcal {X}}\subset {{\mathbb {R}}}^n$ is an extra constraint. For example, the nonnegative constraint, the ball constraint, the sum-to-zero constraint and so on [25]. Such a model has been applied to hyperspectral unmixing [36], classification [17], economics [47], and face recognition [18]. Like model (1.2), we can also rewrite (1.4) as a special instance of (1.1) by introducing an additional variable y to the $\ell _1$-norm regularization term, i.e.,

  $$\begin{aligned} \min _{x,y} \left\{ \frac{1}{2}\Vert Kx-d\Vert ^2+\mu \Vert y\Vert _1 ~~\big \vert ~~ x-y=0,~x\in {\mathcal {X}},~y\in {{\mathbb {R}}}^n\right\} . \end{aligned}$$

  (1.5)

• Nuclear-norm-regularized least squares. A fundamental matrix completion model is the so-called nuclear-norm-regularized least squares problem (e.g., see [16, 37, 44]), which has the form of

  $$\begin{aligned} \min _{X\in \mathcal {B}} \left\{ \frac{1}{2}\Vert \mathcal {K}(X)-M\Vert _F^2 +\mu \Vert X\Vert _*\right\} , \end{aligned}$$

  (1.6)

  where $\mathcal {K}$ can be regarded as a linear sampling operator; M is an observed incomplete or corrupted matrix; $\Vert \cdot \Vert _F$ denotes the standard Frobenius norm; $\Vert \cdot \Vert _*$ is the nuclear norm (i.e., the sum of all singular values) promoting the low-rankness of a matrix; $\mu >0$ is a trade-off parameter; $\mathcal {B}$ is a box area (e.g., [1, 5] and $[-10,10]$, respectively) usually serving as a range of ratings in recommendation systems such as the classic Netflix problem [5] and Jester Joke problem [27]. Like models (1.2) and (1.4), we reformulate model (1.6) as

  $$\begin{aligned} \min _{X,Y} \left\{ \frac{1}{2}\Vert \mathcal {K}(X)-M\Vert _F^2+\mu \Vert Y\Vert _*~~\vert ~~{X-Y=0},~X\in \mathcal {B},~Y\in {{\mathbb {R}}}^{m\times n}\right\} . \end{aligned}$$

  (1.7)

  It is clear that (1.7) is also a special case of model (1.1) with matrix variables.

To solve model (1.1), one of the most popular solvers is the so-called alternating direction method of multipliers (ADMM) proposed in [24, 26], which, for given the k-th iterate $(y^k,\lambda ^k)$, updates the next iterate via

where $\lambda ^k\in {{\mathbb {R}}}^{m_2}$ is the Lagrangian multiplier, $\beta >0$ is a penalty parameter, and $\gamma \in (0,(1+\sqrt{5})/2)$ is a relaxation factor. Actually, the great success of ADMM in statistical learning is owing to its easy subproblems when applying to some nonsmooth optimization models without extra simple convex sets, such as Lasso and basis pursuit (see [10] and references therein for more applications). In other words, ADMM efficiently exploits the great virtue of some nonsmooth functions being simple enough in the sense that their associated proximal operators enjoy closed-form solutions. However, when revisiting the iterative scheme of ADMM for (1.1), we observe that both subproblems, i.e., (1.8a) and (1.8b), are constrained optimization problems due to the appearance of $\mathcal {X}$ and $\mathcal {Y}$. Consequently, (1.8a) and (1.8b) have no closed-form solutions, even when f and g are simple enough to possess explicit proximal operators (e.g., $\Vert \cdot \Vert _1$ and $\Vert \cdot \Vert _*$), and $\mathcal {X}$ and $\mathcal {Y}$ are simple enough with cheap projections (e.g., nonnegative orthant and box areas). Indeed, the appearance of general matrices A and B (i.e., A and B are not identity matrices) also makes both subproblems (1.8a) and (1.8b) lose their closed-form solutions for some cases such as $f(\cdot )=\Vert \cdot \Vert _1$ and $f(\cdot )=\Vert \cdot \Vert _*$. In these situations, we usually need to call some optimization solvers to find approximate solutions of (1.8a) and (1.8b), thereby causing more computing time for large-scale problems than those methods with easy subproblems. e.g., see numerical results in [29, 34, 35, 46]. We here emphasize that there exist closed-form solutions to the subproblems of linearized ADMM when the objective functions are differentiable. However, there are many cases where the objective functions are not necessarily differentiable. Therefore, to make (1.8a) and (1.8b) easy to be solved, Han et al. [29] introduced a so-named customized Douglas–Rachford splitting method (CDRSM) to find solutions of (1.1) with general convex objective functions, where they showed that such an algorithm can successfully circumvent constrained subproblems so that it has easier subproblems than ADMM in some cases. A series of numerical experiments in [29, 33] verified that CDRSM performs better than ADMM for some constrained optimization problems.

To accelerate speed of first-order optimization methods, inertial (a.k.a., extrapolation) technique originally proposed in [40] is one of the most popular strategies in the literature. Recently, many efficient inertial-type splitting algorithms have been developed, e.g., inertial forward-backward algorithm [3, 9, 38], inertial Peaceman-Rachford splitting algorithm [20, 21], inertial ADMM [7, 15, 28], inertial Douglas–Rachford splitting method [2, 8], to name just a few. Like ADMM (1.8), however, these accelerated splitting algorithms still fail to maximally exploit the favorable structure (e.g., simple convex sets $\mathcal {X}$ and $\mathcal {Y}$ and separability of the objective) of (1.1). For example, when directly applying the inertial Douglas–Rachford splitting method [2, 8], we can see from [29] that both variables x and y are treated as a one-block variable, thereby resulting in a coupled subproblem so that the algorithm is not easy enough to implement. Therefore, we aim to introduce an implementable Douglas–Rachford splitting method equipped with an inertial acceleration step for solving model (1.1). Generally speaking, the quadratic part f(x) often serves as a data-fidelity term, which usually dominates the objective function of (1.1) in many real-world applications, since the trade-off parameter in g(y) (e.g., the $\mu$ in (1.2), (1.4) and (1.6)) usually is small. In other words, the quadratic term plays a more important role in the process of solving model (1.1). Accordingly, we in this paper propose a partially inertial Douglas–Rachford splitting method for problem (1.1), where we only consider the inertial acceleration to the quadratic term related variable and Lagrangian multiplier. Since our algorithm is based on the CDRSM [29], our proposed inertial variant of CDRSM fully exploits the separable structure of the objective function, thereby enjoying much easier subproblems than ADMM and the original Douglas–Rachford splitting method (DRSM). Moreover, some numerical experiments on constrained Lasso and image deblurring show that our proposed algorithm has expected promising numerical behaviors.

The rest of this paper is organized as follows. In Sect. 2, we recall some basic results of maximal monotone operators and list two equivalent reformulations of model (1.1). In Sect. 3, we first present our new algorithm (see Algorithm 1) and then establish the global convergence under some mild conditions. In Sect. 4, we conduct some numerical experiments to verify that the embedded inertial technique can really accelerate the CDRSM for solving problem (1.1). Finally, we complete this paper with drawing some concluding remarks in Sect. 5.

2 Preliminaries

In this section, we summarize some basic concepts and well-known results that will be used in the subsequent analysis. Also, we recall two equivalent reformulations of problem (1.1).

Let ${{\mathbb {R}}}^n$ be an n-dimensional Euclidean space equipped with the standard Euclidean norm, i.e., $\Vert x\Vert =\sqrt{x ^\top x}$ for any $x\in {{\mathbb {R}}}^n$, where the superscript ‘$^\top$’ represents the transpose of a vector or matrix. For any matrix M, we denote $\Vert M\Vert$ as its matrix 2-norm.

Let $P_{\Omega }[\cdot ]$ denote the projection operator onto $\Omega$ under the Euclidean norm, i.e.,

$$\begin{aligned} P_{\Omega }[x]:=\arg \min \{\Vert x-y\Vert ~|~y\in \Omega \}. \end{aligned}$$

(2.1)

The following properties with respect to the projection operator are fundamental in the literature and their proof can be found in [6, 12, 22].

Lemma 1

Let $\Omega$ be a nonempty closed convex subset of ${{\mathbb {R}}}^n$ and $P_{\Omega }[\cdot ]$ be the projection operator onto $\Omega$ defined in (2.1). Then we have

$$\begin{aligned} \left(u-P_{\Omega }[u]\right) ^\top \left(v-P_{\Omega }[u]\right)\le 0,\quad \forall u\in {{\mathbb {R}}}^n,~~\forall v\in \Omega . \end{aligned}$$

(2.2)

Lemma 2

For any $x,y\in {{\mathbb {R}}}^n$, and $\tau \in {{\mathbb {R}}}$, we have the following identity

$$\begin{aligned} \Vert \tau x+(1-\tau )y\Vert ^2=\tau \Vert x\Vert ^2+(1-\tau )\Vert y\Vert ^2- \tau (1-\tau )\Vert x-y\Vert ^2. \end{aligned}$$

(2.3)

Hereafter, we recall a lemma which will be used for global convergence analysis.

Lemma 3

( [11]) Let $\{x^k\}$ be a sequence in ${{\mathbb {R}}}^n$ and ${\mathcal {D}}$ be a nonempty set of ${{\mathbb {R}}}^n$. Suppose that

• (i). $\lim _{k\rightarrow +\infty } \Vert x^k-x\Vert$ exists for all $x\in {\mathcal {D}}$;

• (ii). every cluster point of $\{x^k\}$ belongs to ${\mathcal {D}}$.

Then, the sequence $\{x^k\}$ converges to a point in ${\mathcal {D}}$.

Definition 1

A set-valued map $T:{{\mathbb {R}}}^n\rightarrow 2^{{{\mathbb {R}}}^n}$ is said to be monotone if

$$\begin{aligned} (u_1-u_2) ^\top (v_1-v_2)\ge 0,\quad \forall u_1,~u_2\in {{\mathbb {R}}}^n,~v_1\in T(u_1),~v_2\in T(u_2). \end{aligned}$$

Definition 2

For a convex function $f:{{\mathbb {R}}}^n\rightarrow {{\mathbb {R}}}$, its subdifferential at x is the set-valued operator given by

$$\begin{aligned} \partial f(x)=\{\xi ~|~f(y)\ge f(x)+\xi ^\top (y-x),\quad \forall y\in {\textbf {dom}}f\}, \end{aligned}$$

where $\xi$ is called a subgradient of f at x, and ${\textbf {dom}}f$ is the effective domain of f.

Below, we recall two equivalent reformulations for problem (1.1) that will be useful for algorithmic design and convergence analysis. Let $\lambda \in {{\mathbb {R}}}^{m_2}$ be the Lagrange multiplier associated to the linear constraints of (1.1). Then, the classical variational inequality (VI for short) characterization of (1.1) can be stated as finding a vector $w^*\in {\mathcal {W}}$ such that

$$\begin{aligned} (w-w^*) ^\top F(w^*)\ge 0, \quad \forall w\in {\mathcal {W}}, \end{aligned}$$

(2.4a)

where $w:=(x,y,\lambda ),~{\mathcal {W}}:={\mathcal {X}}\times \mathcal Y\times {{\mathbb {R}}}^{m_2}$ and

$$\begin{aligned} F(w):=\{(\nabla f(x)-A ^\top \lambda ,~\zeta -B ^\top \lambda ,~Ax+By-b)~\vert ~\zeta \in \partial g(y)\}. \end{aligned}$$

(2.4b)

Clearly, it is well-known from [41] that the underlying mapping F(w) defined in VI (2.4) is monotone. Moreover, note that the nonempty assumption on the solution set of problem (1.1) implies the nonemptiness of the solution set (denoted by ${\mathcal {W}}^*$ throughout this paper) of VI (2.4). Alternatively, it also follows from [23, page 3] that VI (2.4) can be further reformulated as finding a zero point of the sum of two maximal monotone operators, i.e., finding $w^*\in \mathcal {W}$ such that

$$\begin{aligned} 0\in F(w^*)+{\mathcal {N}}_{{\mathcal {W}}}(w^*), \end{aligned}$$

(2.5)

where ${\mathcal {N}}_{{\mathcal {W}}}(\cdot )$ is the normal cone of ${\mathcal {W}}$ defined as

For any $\beta >0$, we let

$$\begin{aligned} \mathscr {E}(w,\beta )=w-P_{{\mathcal {W}}}[w-\beta F(w)]. \end{aligned}$$

(2.6)

Then, we have the following proposition.

Proposition 1

The vector $w^*\in {\mathcal {W}}^*$ is a solution of VI (2.4) if and only if $\Vert \mathscr {E}(w^*,\beta )\Vert =0$ for any $\beta >0$.

3 The Algorithm and Its Convergence Analysis

In this section, we first elaborate our proposed partially inertial CDRSM for solving (1.1). Then, we prove its global convergence under some mild conditions.

3.1 Algorithm

Before stating our new algorithm, we first recall the general scheme of DRSM for solving (2.5) (see [30, 32, 45]), which, for given the k-th iterate $w^k$, reads as

$$\begin{aligned} w^{k+1} = (I+\beta F)^{-1}\{w^k+\beta F(w^k)-\gamma \mathscr {E}(w^k,\beta )\}, \end{aligned}$$

(3.1)

where $(I+\beta F)^{-1}$ represents the standard resolvent operator and $\gamma \in (0,2)$ is a relaxation factor. Accordingly, by using the notations of F and w given in (2.4b), the iterative scheme (3.1) can be specified as finding $w^{k+1}\in \mathcal W$ and $\zeta ^{k+1}\in \partial g(y^{k+1})$ such that

Clearly, we can see from (3.2) that both (3.2a) and (3.2b) are unconstrained minimization problems, which are in general easier than ADMM’s subproblems, i.e., (1.8a) and (1.8b), as long as the projections onto $\mathcal {X}$ and $\mathcal {Y}$ are simple enough with explicit representations. However, such an algorithm is not easy to implement due to the coupled variables $(x^{k+1},y^{k+1},\lambda ^{k+1})$. In other words, the straightforward application of DRSM does not fully exploit the separability of the objective function. Actually, it can be easily seen from (3.2) that the main difficulty to implement such an algorithm is owing to the appearance of $\lambda ^{k+1}$ in (3.2a) and (3.2b). Hence, Han et al. [29] first made a prediction on $\lambda$, and slightly modified the updating schemes on $x^{k+1}$, $y^{k+1}$ and $\lambda ^{k+1}$. Consequently, they introduced the so-called CDRSM for (1.1). Inspired by the inertial acceleration idea, we in this paper propose a partially inertial CDRSM (denoted by ICDRSM) to accelerate the original CDRSM for solving (1.1). It is remarkable that our ICDRSM approaches the original CDRSM when the inertial parameters approaches zero.

To present our ICDRSM, for notational simplicity, we below denote

$$\begin{aligned} {\bar{u}}^k:=({\tilde{x}}^k,{\bar{\lambda }}^k,\beta ),\quad \bar{v}^k:=(y^k,{\bar{\lambda }}^k,\beta ),\quad {\bar{w}}^k:=(\tilde{x}^k,y^k,{\bar{\lambda }}^k,\beta ), \end{aligned}$$

(3.3)

and consequently,

With the above preparations, details of the proposed ICDRSM for (1.1) can be described in Algorithm 1.

Algorithm 1

A partially inertial CDRSM for (1.1).

3.2 Convergence Analysis

In this subsection, we establish the global convergence of Algorithm 1. For notational convenience, we let

$$\begin{aligned} z_1:=x+\beta \nabla f(x),~ z_2:=y+\beta \zeta ,~ \textbf{z}:=\begin{pmatrix} z_1\\ z_2\\ \lambda \end{pmatrix} ~ \text {and} ~ \mathscr {D}({\bar{w}}^k):=\begin{pmatrix} \mathscr {E}_x({\bar{u}}^k)\\ \mathscr {E}_y({\bar{v}}^k)\\ \mathscr {E}_{\lambda }({\bar{w}}^k) \end{pmatrix}, \end{aligned}$$

(3.13)

where $\nabla f(x)=K ^\top (Kx-d)$ and $\zeta \in \partial g(y)$. For convenience, we further denote

$$\begin{aligned} \tilde{z}_1:=\tilde{x}+\beta \nabla f(\tilde{x}),~ \tilde{\textbf{z}}:=\begin{pmatrix} \tilde{z}_1\\ z_2\\ \tilde{\lambda } \end{pmatrix}. \end{aligned}$$

(3.14)

The following lemma clarifies the relationship between $\mathscr {D}({\bar{w}}^k)$ and a solution of the VI problem (2.4).

Lemma 4

If $\mathscr {D}({\bar{w}}^k)=0$ for any $\beta >0$, then the vector $w^{k+1}=(x^{k+1},y^{k+1},\lambda ^{k+1})$ is a solution of VI (2.4).

Proof

From the notation of $\mathscr {D}({\bar{w}}^k)$ in (3.13), we know that $\mathscr {D}({\bar{w}}^k)=0$ implies

$$\begin{aligned} \Vert \mathscr {E}_x({\bar{u}}^k)\Vert =\Vert \mathscr {E}_y(\bar{v}^k)\Vert =\Vert \mathscr {E}_{\lambda }({\bar{w}}^k)\Vert =0. \end{aligned}$$

(3.15)

Then, by substituting (3.15) into (3.4) and combining with (3.6), we have

$$\begin{aligned} \mathscr {E}_3({\tilde{x}}^k,y^k,\beta )=0, \end{aligned}$$

which immediately implies that

$$\begin{aligned} \mathscr {E}({\tilde{x}}^k,y^k,{\bar{\lambda }}^k,\beta )=0. \end{aligned}$$

(3.16)

Hence, by invoking Proposition 1, the relation (3.16) means that $({\tilde{x}}^k,y^k,{\bar{\lambda }}^k)$ is a solution of VI (2.4). Consequently, it follows from the optimality conditions of (3.7) and (3.8) and the update scheme (3.9) that $x^{k+1}={\tilde{x}}^k$, $y^{k+1}=y^k$, and $\lambda ^{k+1}={\tilde{\lambda }}^k$, which, together with the fact that $({\tilde{x}}^k,y^k,{\bar{\lambda }}^k)$ is a solution, means that $(x^{k+1},y^{k+1},\lambda ^{k+1})$ is also a solution of VI (2.4). This completes the proof. $\square$

Lemma 5

Suppose that $w^*\in {\mathcal {W}}^*$ is an arbitrary solution of (2.4). Then the sequence $\{{\tilde{\textbf{z}}}^k\}$ generated by Algorithm 1 satisfies

$$\begin{aligned} ({\tilde{\textbf{z}}}^k-\textbf{z}^*)^\top \mathscr {D}(\bar{w}^k)\ge \varphi ({\bar{w}}^k),\quad k\ge 1, \end{aligned}$$

where $\textbf{z}^*, {\tilde{\textbf{z}}}^k, \mathscr {D}({\bar{w}}^k)$ and $\varphi ({\bar{w}}^k)$ are defined in (3.13),(3.14) and (3.11), respectively.

Proof

Since $w^*=(x^*,y^*,\lambda ^*)\in {\mathcal {W}}^*$ and $\zeta ^*\in \partial g(y^*)$, it follows from (2.4) that

$$\begin{aligned} (x'-x^*) ^\top \left(\nabla f(x^*)-A ^\top \lambda ^*\right)\ge 0,\quad \forall x'\in {\mathcal {X}}, \end{aligned}$$

(3.17)

and

$$\begin{aligned} (y'-y^*) ^\top \left(\zeta ^*-B ^\top \lambda ^*\right)\ge 0,\quad \forall y'\in {\mathcal {Y}}. \end{aligned}$$

Then, by setting $x'=P_{{\mathcal {X}}}[{\tilde{x}}^k-\beta (\nabla f(\tilde{x}^k)-A ^\top {\bar{\lambda }}^k)]={\tilde{x}}^k-\mathscr {E}_x({\bar{u}}^k)$ in (3.17), we have

$$\begin{aligned} \left({\tilde{x}}^k-\mathscr {E}_x({\bar{u}}^k)-x^*\right) ^\top \left(\nabla f(x^*)-A ^\top \lambda ^*\right)\ge 0. \end{aligned}$$

(3.18)

On the other hand, by setting $\Omega :={\mathcal {X}}$, $u:=\tilde{x}^k-\beta (\nabla f({\tilde{x}}^k)-A ^\top {\bar{\lambda }}^k)$, and $v:=x^*$ in (2.2), we have

$$\begin{aligned} \left(\mathscr {E}_x({\bar{u}}^k)-\beta (\nabla f({\tilde{x}}^k)-A ^\top {\bar{\lambda }}^k)\right) ^\top \left(x^*-{\tilde{x}}^k+\mathscr {E}_x(\bar{u}^k)\right)\le 0. \end{aligned}$$

(3.19)

Multiplying inequality (3.18) by $\beta$ and summing (3.18) and (3.19), it follows from $\nabla f(x)=K^\top (Kx-d)$ that

$$\begin{aligned} \left({\tilde{x}}^k-x^*-\mathscr {E}_x({\bar{u}}^k)\right) ^\top \left(\mathscr {E}_x({\bar{u}}^k)-\beta K ^\top K({\tilde{x}}^k-x^*)+\beta A ^\top ({\bar{\lambda }}^k-\lambda ^*)\right)\ge 0. \end{aligned}$$

Rearranging the above inequality leads to

$$\begin{aligned}&({\tilde{z}}_1^k-z_1^*) ^\top \mathscr {E}_x(\bar{u}^k)+\beta ({\tilde{\lambda }}^k-\lambda ^*) ^\top A\left(\tilde{x}^k-x^*-\mathscr {E}_x({\bar{u}}^k)\right) \nonumber \\ \ge&\Vert \mathscr {E}_x({\bar{u}}^k)\Vert ^2+\beta ({\tilde{x}}^k-x^*) ^\top K ^\top K({\tilde{x}}^k-x^*)+\beta ({\tilde{\lambda }}^k-{\bar{\lambda }}^k) ^\top A\left({\tilde{x}}^k-x^*-\mathscr {E}_x({\bar{u}}^k)\right)\nonumber \\ \ge&\Vert \mathscr {E}_x(\bar{u}^k)\Vert ^2+\beta ({\tilde{\lambda }}^k-{\bar{\lambda }}^k) ^\top A\left(\tilde{x}^k-x^*-\mathscr {E}_x({\bar{u}}^k)\right), \end{aligned}$$

(3.20)

where the second inequality comes from the fact that $K ^\top K$ is a positive semi-definite matrix.

Similarly, we can also obtain

$$\begin{aligned}&(z_2^k-z_2^*) ^\top \mathscr {E}_y(\bar{v}^k)+\beta ({\tilde{\lambda }}^k-\lambda ^*) ^\top B\left(y^k-y^*-\mathscr {E}_y({\bar{v}}^k)\right)\nonumber \\&\quad \quad \quad \quad \quad \quad \quad \quad \ge \Vert \mathscr {E}_y(\bar{v}^k)\Vert ^2+\beta ({\tilde{\lambda }}^k-{\bar{\lambda }}^k) ^\top B\left(y^k-y^*-\mathscr {E}_y({\bar{v}}^k)\right). \end{aligned}$$

(3.21)

By adding (3.20) and (3.21), it follows from the notation of $\mathscr {E}_{\lambda }({\bar{w}}^k)$ in (3.4c) that

$$\begin{aligned} \begin{pmatrix} {\tilde{z}}_1^k-z_1^*\\ z_2^k-z_2^*\\ {\tilde{\lambda }}^k-\lambda ^* \end{pmatrix} ^\top \begin{pmatrix} \mathscr {E}_x({\bar{u}}^k)\\ \mathscr {E}_y({\bar{v}}^k)\\ \mathscr {E}_{\lambda }({\bar{w}}^k) \end{pmatrix} \ge \Vert \mathscr {E}_x({\bar{u}}^k)\Vert ^2+\Vert \mathscr {E}_y(\bar{v}^k)\Vert ^2+({\tilde{\lambda }}^k-{\bar{\lambda }}^k) ^\top \mathscr {E}_{\lambda }({\bar{w}}^k). \end{aligned}$$

Consequently, we conclude the assertion of this lemma by using the notations ${\textbf{z}}^*,~{\tilde{\textbf{z}}}^k$, $\mathscr {D}(\bar{w}^k)$ and $\varphi ({\bar{w}}^k)$ given by (3.11), (3.13) and (3.14), respectively. $\square$

By invoking the first-order optimality condition of subproblems (3.7) and (3.8) with the notations $z_1,z_2$ in (3.13), we obtain

$$\begin{aligned} z_1^{k+1}={\tilde{z}}^k_1-\gamma \alpha _k \mathscr {E}_x(\bar{u}^k)\quad \text {and}\quad z_2^{k+1}= z^k_2-\gamma \alpha _k \mathscr {E}_y({\bar{v}}^k). \end{aligned}$$

Note that, from the notations of ${\textbf{z}}^{k+1}, {\tilde{\textbf{z}}}^{k}$ and $\mathscr {D}({\bar{w}}^k)$ defined in (3.13) and (3.14), the iterative scheme (3.7)-(3.9) then can be recast into the compact form:

$$\begin{aligned} {\textbf{z}}^{k+1}={\tilde{\textbf{z}}}^k-\gamma \alpha _k\mathscr {D}(\bar{w}^k). \end{aligned}$$

(3.22)

Thus, if $\varphi ({\bar{w}}^k)$ is nonnegative, Lemma 5 implies that $-\mathscr {D}({\bar{w}}^k)$ is a descent direction of the distance function $\frac{1}{2}\Vert {\textbf{z}}-{\textbf{z}}^*\Vert ^2$ at ${\tilde{\textbf{z}}}^k$. Then, in this sense, $\alpha _k$ plays the role of “step size”, and $\gamma$ can be viewed as a relaxed factor. In the following lemma, we will prove the sequence $\{\alpha _k\}$ generated by Algorithm 1 is bounded below.

Lemma 6

Assume that $\beta \in (0,\sqrt{2}/{c})$. For the step size $\alpha _k$ given by (3.10), there exists a constant $\alpha _{\min }>0$ such that

$$\begin{aligned} \alpha _k\ge \alpha _{\min },\quad \forall k\ge 0. \end{aligned}$$

Proof

For any two vectors $a,b\in {{\mathbb {R}}}^m$, we have the inequality

$$\begin{aligned} 2a ^\top b\le \delta \Vert a\Vert ^2+1/\delta \Vert b\Vert ^2,\quad \delta >0. \end{aligned}$$

(3.23)

Hence, applying (3.23) to the last term of (3.11), for any $\delta >0$, we have

$$\begin{aligned} ({\tilde{\lambda }}^k-{\bar{\lambda }}^k) ^\top \mathscr {E}_{\lambda }(\bar{w}^k)&=\Vert {\tilde{\lambda }}^k-{\bar{\lambda }}^k\Vert ^2-\beta ({\tilde{\lambda }}^k-{\bar{\lambda }}^k) ^\top \left(A\mathscr {E}_x({\bar{u}}^k)+B\mathscr {E}_y({\bar{v}}^k)\right) \nonumber \\&\ge (1-\delta )\Vert {\tilde{\lambda }}^k-{\bar{\lambda }}^k\Vert ^2-\frac{\beta ^2}{2\delta }\left(\Vert A\mathscr {E}_x(\bar{u}^k)\Vert ^2+\Vert B\mathscr {E}_y({\bar{v}}^k)\Vert ^2\right)\nonumber \\&\ge (1-\delta )\Vert {\tilde{\lambda }}^k-{\bar{\lambda }}^k\Vert ^2-\frac{\beta ^2c^2}{2\delta }\left(\Vert \mathscr {E}_x(\bar{u}^k)\Vert ^2+\Vert \mathscr {E}_y({\bar{v}}^k{)}\Vert ^2\right), \end{aligned}$$

(3.24)

where $c:=\max \{\Vert A\Vert ,\Vert B\Vert \}$. By substituting (3.24) into (3.11) and setting $\delta :={\beta c}/{\sqrt{2}}$, we deduce

$$\begin{aligned} \varphi ({\bar{w}}^k)&\ge (1-\delta )\Vert {\tilde{\lambda }}^k-{\bar{\lambda }}^k\Vert ^2+\frac{2\delta -\beta ^2c^2}{2\delta }\left(\Vert \mathscr {E}_x(\bar{u}^k)\Vert ^2+\Vert \mathscr {E}_y({\bar{v}}^k{)}\Vert ^2\right)\nonumber \\&=\left(1-\frac{\beta c}{\sqrt{2}}\right)\left(\Vert {\tilde{\lambda }}^k-{\bar{\lambda }}^k\Vert ^2+\Vert \mathscr {E}_x(\bar{u}^k)\Vert ^2+\Vert \mathscr {E}_y({\bar{v}}^k{)}\Vert ^2\right)\nonumber \\&\ge 0, \end{aligned}$$

(3.25)

where the last inequality comes from the condition $\beta \in (0,\sqrt{2}/{c})$.

On the other hand,

$$\begin{aligned} \psi ({\bar{w}}^k)&\le \Vert \mathscr {E}_x({\bar{u}}^k)\Vert ^2+\Vert \mathscr {E}_y(\bar{v}^k)\Vert ^2+2\Vert {\tilde{\lambda }}^k-{\bar{\lambda }}^k\Vert ^2+2\beta ^2\left(\Vert A\mathscr {E}_x(\bar{u}^k)\Vert ^2+\Vert B\mathscr {E}_y({\bar{v}}^k)\Vert ^2\right)\nonumber \\&\le c'\left(\Vert {\tilde{\lambda }}^k-{\bar{\lambda }}^k\Vert ^2+\Vert \mathscr {E}_x(\bar{u}^k)\Vert ^2+\Vert \mathscr {E}_y({\bar{v}}^k)\Vert ^2\right), \end{aligned}$$

(3.26)

where $c':=\max \{2,~1+4\beta ^2\Vert A\Vert ^2,~1+4\beta ^2\Vert B\Vert ^2\}.$ By the definition of $\alpha _k$ given in (3.10), it immediately follows from (3.25) and (3.26) that

$$\begin{aligned} \alpha _k=\frac{\varphi ({\bar{w}}^k)}{\psi (\bar{w}^k)}\ge \frac{\sqrt{2}-\beta c}{\sqrt{2}c'}=:\alpha _{\min }>0 \end{aligned}$$

holds under the condition $\beta \in (0,\sqrt{2}/c)$. The proof is completed. $\square$

By the definitions of $z_1$ and ${\tilde{z}}_1$ in (3.13) and (3.14), it then follows from $\nabla f(x)=K^\top (Kx-d)$ that

$$\begin{aligned} \tilde{z}_1^k&= \tilde{x}^k+\beta K^\top \left(K\tilde{x}^k-d\right)\\&= x^k+\beta K^\top \left(K{x}^k-d\right)+\tau \left(I+\beta K^\top K\right)\left(x^k-x^{k-1}\right) \\&= z_1^k+\tau \left(z_1^k-z_1^{k-1}\right). \end{aligned}$$

Consequently, by denoting $\varvec{p}=(z_1,\lambda )$ as a subvector of $\textbf{z}=(z_1,z_2,\lambda )$ for notational brevity, it then follows from the above equality and iterative scheme (3.5) that

$$\begin{aligned} \tilde{\varvec{p}}^{k}=\varvec{p}^k+\tau (\varvec{p}^k-\varvec{p}^{k-1}). \end{aligned}$$

(3.27)

Theorem 1

Suppose that $\beta \in (0,\sqrt{2}/c)$. Then the sequence $\{w^k\}$ generated by Algorithm 1 converges to a solution of VI (2.4).

Proof

It follows from (3.22) that

$$\begin{aligned} \Vert {\textbf{z}}^{k+1}-{\textbf{z}}^*\Vert ^2&=\Vert \tilde{\textbf{z}}^k-\gamma \alpha _k\mathscr {D}({\bar{w}}^k)-\textbf{z}^*\Vert ^2\nonumber \\&=\Vert \tilde{\textbf{z}}^k-\textbf{z}^*\Vert ^2-2\gamma \alpha _k(\tilde{\textbf{z}}^k-\textbf{z}^*) ^\top \mathscr {D}(\bar{w}^k)+\gamma ^2\alpha _k^2\Vert \mathscr {D}({\bar{w}}^k)\Vert ^2\nonumber \\&\le \Vert \tilde{\textbf{z}}^k-\textbf{z}^*\Vert ^2-2\gamma \alpha _k\varphi (\bar{w}^k)+\gamma ^2\alpha _k^2\Vert \mathscr {D}({\bar{w}}^k)\Vert ^2\nonumber \\&=\Vert \tilde{\textbf{z}}^k-\textbf{z}^*\Vert ^2-\gamma (2-\gamma )\alpha _k^2\Vert \mathscr {D}(\bar{w}^k)\Vert ^2\nonumber \\&=\Vert \tilde{\textbf{z}}^k-\textbf{z}^*\Vert ^2-\frac{2-\gamma }{\gamma }\Vert \textbf{z}^{k+1}-\tilde{\textbf{z}}^k\Vert ^2, \end{aligned}$$

(3.28)

where the first inequality is due to Lemma 5 and the third equality follows from (3.10), (3.12) and (3.13). By invoking (2.3), it follows from (3.27) that

$$\begin{aligned} \Vert \tilde{\varvec{p}}^k-\varvec{p}^*\Vert ^2&=\Vert \varvec{p}^k-\varvec{p}^*+\tau (\varvec{p}^k-\varvec{p}^{k-1})\Vert ^2\nonumber \\&=(1+\tau )\Vert \varvec{p}^k-\varvec{p}^*\Vert ^2-\tau \Vert \varvec{p}^{k-1}-\varvec{p}^*\Vert ^2+\tau (1-\tau )\Vert \varvec{p}^k-\varvec{p}^{k-1}\Vert ^2. \end{aligned}$$

(3.29)

For any $\rho >0$, we have

$$\begin{aligned}&\Vert \varvec{p}^{k+1}-\tilde{\varvec{p}}^k\Vert ^2=\Vert \varvec{p}^{k+1}-\varvec{p}^k-\tau (\varvec{p}^k-\varvec{p}^{k-1})\Vert ^2\nonumber \\&\ge \Vert \varvec{p}^{k+1}-\varvec{p}^k\Vert ^2+\tau ^2\Vert \varvec{p}^k-\varvec{p}^{k-1}\Vert ^2+\tau \left(-\rho \Vert \varvec{p}^{k+1}-\varvec{p}^k\Vert ^2 -\frac{1}{\rho }\Vert \varvec{p}^k-\varvec{p}^{k-1}\Vert ^2\right), \end{aligned}$$

(3.30)

where the last inequality follows from the fact that $2a^\top b\ge -\frac{1}{t}\Vert a\Vert ^2-t\Vert b\Vert ^2$ for any $a,b\in \mathbb {R}^n$ and $t>0$. Recalling the definition of ${\tilde{\textbf{z}}}$ in (3.14) and substituting (3.29) and (3.30) into (3.28), we arrive at

$$\begin{aligned}{} & {} \Vert \varvec{p}^{k+1}-\varvec{p}^*\Vert ^2-(1+\tau )\Vert \varvec{p}^k-\varvec{p}^*\Vert ^2 +\tau \Vert \varvec{p}^{k-1}-\varvec{p}^*\Vert ^2+\Vert z_2^{k+1}-z_2^*\Vert ^2-\Vert z_2^{k}-z_2^*\Vert ^2\nonumber \\{} & {} \le \frac{(2-\gamma )(\rho \tau -1)}{\gamma }\Vert \varvec{p}^{k+1}-\varvec{p}^k\Vert ^2+s\Vert \varvec{p}^k -\varvec{p}^{k-1}\Vert ^2-\frac{2-\gamma }{\gamma }\Vert z_2^{k+1}-z_2^k\Vert ^2, \end{aligned}$$

(3.31)

where

$$\begin{aligned} s:=\tau (1+\tau )+\frac{\tau (2-\gamma )(1-\rho \tau )}{\gamma \rho }. \end{aligned}$$

Setting $\rho =\frac{(2-2\gamma )\tau ^2-\gamma \tau -\gamma +2}{2(2-\gamma )\tau }$, there exists ${\bar{\tau }}\in (0,1)$ such that $\rho >0$ for any $\tau \in (0,{\bar{\tau }})$ and $\rho \tau <1$ by simple validation. Combining with $\gamma \in \left(\frac{2\tau ^2+2}{2\tau ^2+\tau +1},\frac{2\tau +2}{2\tau +1}\right)\subset (1,2)$, it is clear that $s\ge 0$ holds.

For convenience, we define the sequence $\{\Phi _k\}$ by

$$\begin{aligned} \Phi _k:=\Vert \varvec{p}^k-\varvec{p}^*\Vert ^2-\tau \Vert \varvec{p}^{k-1}-\varvec{p}^*\Vert ^2+\Vert z_2^k-z_2^*\Vert ^2+s\Vert \varvec{p}^k-\varvec{p}^{k-1}\Vert ^2 \end{aligned}$$

for all $k\ge 1$. Then, we have

$$\begin{aligned} \Phi _{k+1}-\Phi _k= & {} \Vert \varvec{p}^{k+1}-\varvec{p}^*\Vert ^2-(1+\tau )\Vert \varvec{p}^{k}-\varvec{p}^*\Vert ^2 +\tau \Vert \varvec{p}^{k-1}-\varvec{p}^*\Vert ^2\\{} & {} +\Vert z_2^{k+1}-z_2^*\Vert ^2-\Vert z_2^k-z_2^*\Vert ^2+s\Vert \varvec{p}^{k+1}-\varvec{p}^{k}\Vert ^2-s\Vert \varvec{p}^k-\varvec{p}^{k-1}\Vert ^2. \end{aligned}$$

Using (3.31) yields

$$\begin{aligned} \Phi _{k+1}-\Phi _k\le \left(\frac{(2-\gamma )(\rho \tau -1)}{\gamma }+s\right)\Vert \varvec{p}^{k+1} -\varvec{p}^k\Vert ^2-\frac{2-\gamma }{\gamma }\Vert z_2^{k+1}-z_2^k\Vert ^2. \end{aligned}$$

By the definitions of $\rho$ and s, we have

$$\begin{aligned} \begin{aligned} \frac{(2-\gamma )(\rho \tau -1)}{\gamma }+s =\frac{1+\tau }{2\gamma }\frac{[(2\tau +1)\gamma -2(\tau +1)][(2\tau ^2-\tau +1)\gamma -2(1-\tau )^2]}{(2\tau ^2+\tau +1)\gamma -2(\tau ^2+1)}<0, \end{aligned} \end{aligned}$$

where the inequality is due to the selection of $\gamma$ in Algorithm 1. Thus there exists a constant $\delta >0$ such that $\delta <{\text {min}}\left\{ \frac{(2-\gamma )(1-\rho \tau )}{\gamma }-s,\frac{2-\gamma }{\gamma }\right\}$, then

$$\begin{aligned} \Phi _{k+1}-\Phi _{k}\le -\delta \Vert {\textbf{z}}^{k+1}-{\textbf{z}}^k\Vert ^2. \end{aligned}$$

(3.32)

Hence, the sequence $\{\Phi _k\}$ is monotonically nonincreasing, and in particular for all $k\ge 0$,

$$\begin{aligned} \Vert \varvec{p}^k-\varvec{p}^*\Vert ^2-\tau \Vert \varvec{p}^{k-1}-\varvec{p}^*\Vert ^2\le \Phi _k\le \Phi _1. \end{aligned}$$

Consequently, it follows that

$$\begin{aligned} \Vert \varvec{p}^k-\varvec{p}^*\Vert ^2\le \tau ^k\Vert \varvec{p}^0-\varvec{p}^*\Vert ^2+\Phi _1\sum _{i=0}^{k-1} \tau ^i\le \tau ^k\Vert \varvec{p}^0-\varvec{p}^*\Vert ^2+\frac{\Phi _1}{1-\tau }, \end{aligned}$$

(3.33)

which implies that $\{\varvec{p}^k\}$ is bounded due to the fact $\tau \in (0,1)$. Hence, the sequence $\{\varvec{z}^k\}$ is also bounded, where $\{z_2^k\}$ is bounded from the monotonicity of $\{\Phi _k\}$. Combining (3.32) and (3.33), we have

$$\begin{aligned} \delta \sum _{i=1}^{k}\Vert {\textbf{z}}^{i+1}-\textbf{z}^i\Vert ^2\le \Phi _1-\Phi _{k+1}\le \Phi _1+\tau \Vert \varvec{p}^k-\varvec{p}^*\Vert ^2 \le \tau ^{k+1}\Vert \varvec{p}^0-\varvec{p}^*\Vert ^2{+\frac{\Phi _1}{1-\tau }}, \end{aligned}$$

which shows that

$$\begin{aligned} \sum _{k=0}^{+\infty } \Vert {\textbf{z}}^{k+1}-\textbf{z}^k\Vert ^2<+\infty . \end{aligned}$$

(3.34)

Thus we have $\lim _{k\rightarrow +\infty } \Vert {\textbf{z}}^{k+1}-{\textbf{z}}^k\Vert =0$. By the definition of ${\tilde{\textbf{z}}}^k$, (3.27) and triangle inequality, we have

$$\begin{aligned} \Vert {\textbf{z}}^{k+1}-{\tilde{\textbf{z}}}^k\Vert \le \Vert \textbf{z}^{k+1}-{\textbf{z}}^k\Vert +\tau \Vert \varvec{p}^{k}-\varvec{p}^{k-1}\Vert , \end{aligned}$$

which means that $\lim _{k\rightarrow +\infty } \Vert \textbf{z}^{k+1}-{\tilde{\textbf{z}}}^k\Vert =0$. Recalling (3.22), we further obtain

$$\begin{aligned} \lim _{k\rightarrow +\infty } \mathscr {D}({\bar{w}}^k)=0. \end{aligned}$$

Then, using Lemma 4 leads to

$$\begin{aligned} \lim _{k\rightarrow +\infty } \mathscr {E}(w^k,\beta )=0. \end{aligned}$$

(3.35)

On the other hand, the sequence $\{w^k\}$ is bounded due to the boundedness of $\{{{\textbf{z}}}^k\}$. Then the sequence $\{w^k\}$ has at least one cluster point $w^{\infty }=(x^{\infty },y^{\infty },\lambda ^{\infty })$ and $\{w^{k_j}=(x^{k_j},y^{k_j},\lambda ^{k_j})\}$ be the corresponding subsequence converging to $w^{\infty }$. Thus, taking limit along this subsequence in (3.35) together with the continuity of $\mathscr {E}(w,\beta )$ with respect to w, we immediately obtain

$$\begin{aligned} \Vert \mathscr {E}(w^{\infty },\beta )\Vert ^2=\Vert \mathscr {E}(\lim _{j\rightarrow \infty }w^{k_j},\beta ) \Vert ^2=\lim _{j\rightarrow \infty }\Vert \mathscr {E}(w^{k_j},\beta )\Vert ^2=0. \end{aligned}$$

According to Proposition 1, the above fact means that $w^{\infty }$ is a solution of VI (2.4). Finally, applying Lemma 3 with setting ${\mathcal {D}}={\mathcal {W}}^*$, we conclude that the sequence $\{w^k\}$ generated by Algorithm 1 converges to $w^{\infty }$, a solution of VI (2.4). The proof is completed. $\square$

4 Numerical Experiments

In this section, we shall conduct the numerical performance of the proposed ICDRSM (i.e., Algorithm 1) to verify that the inertial technique can really improve the efficiency of solving (1.1), when comparing with some state-of-the-art benchmark solvers, including the classical ADMM (see (1.8)), inertial ADMM (denoted by “IADMM”) in [15], the primal-dual method in [13] (denoted by “PDM”) and inertial PDM (denoted by “IPDM”) in [14], and the original CDRSM proposed in [29]. All the codes are written by Matlab R2021a and all the numerical experiments are conducted on a 64-bit PC with an Intel(R) Core(TM) i5-8265U CPU @ 1.6GHz with 8GB RAM.

4.1 Constrained Lasso

In this subsection, we conduct the numerical performance of the proposed ICDRSM for solving the following ball-constrained Lasso problem

$$\begin{aligned} \min _{\Vert x\Vert \le 1} \left\{ F(x):=\frac{1}{2}\Vert Kx-d\Vert ^2+\mu \Vert x\Vert _1\right\} , \end{aligned}$$

(4.1)

which is a special case of (1.4). Here, we consider the reformulation given by (1.5). Therefore, applying our ICDRSM (i.e., Algorithm 1) to (1.5), the x- and y-subproblems (i.e., (3.7) and (3.8)) can be specified as

where ‘${\text {Shrink}}_\beta \left(\cdot \right)$’ is the soft-shrinkage operator given by

$$\begin{aligned} {\text {Shrink}}_\beta (\cdot ):=\max \{\Vert \cdot \Vert -\beta ,0\}\frac{\cdot }{\Vert \cdot \Vert }. \end{aligned}$$

(4.2)

Here, we should notice that the subgradient $\zeta ^{k+1}$ of $\mu \Vert y\Vert _1$ at $y^{k+1}$ can be updated by

$$\begin{aligned} \zeta ^{k+1}:=\frac{1}{\beta }\left(\omega ^k_y-y^{k+1}\right). \end{aligned}$$

Note that CDRSM shares similar subproblems with ICDRSM, we omit its details here for brevity. When applying ADMM to (1.5), the iterative scheme (1.8) reads as

To implement the PDM [13] to solve (4.1), we first reformulate (4.1) as a saddle point problem, i.e.,

$$\begin{aligned} \min _{\Vert x\Vert \le 1}\max _{y\in {\mathcal {Y}}_{\infty }} \left\{ y ^\top x+\frac{1}{2\mu }\Vert Kx-d\Vert ^2\right\} , \end{aligned}$$

(4.4)

where ${\mathcal {Y}}_{\infty }:=\{y~\vert ~\Vert y\Vert _{\infty }\le 1\}$. Then, the iterative scheme of PDM solving (4.4) is specified as

Apparently, the main difficulties of ADMM and PDM for solving (4.1) come from their x-subproblems, i.e., (4.1) and (4.1), where the nonnegative constraint makes their x-subproblems lose closed-form solutions. As suggested by [29], we employ the projected Barzilai-Borwein method (PBBM) in [4, 19] to find approximate solutions of (4.1) and (4.1). Before the formal simulation, we investigated the numerical sensitivity of the maximum inner iterations of PBBM to the performance of those algorithms that need PBBM, where we considered five cases by setting the largest number of inner iterations as $\{10,20,30,40,50\}$. The results showed that ADMM and PDM equipped with 20 performed slightly better than the other settings in many cases. Therefore, we empirically choose 20 as the maximum number of inner iterations for the following experiments.

Below, we conduct the numerical performance of the above six algorithms on synthetic data. In our experiments, we test four scenarios for $(m,n)=\{(1000,3000)$, (3000, 5000), (5000, 8000), $(8000,10000)\}$. Here, we first generate $K \in {{\mathbb {R}}}^{m\times n}$ in a random way such that its components satisfy independent and identical standard normal distribution. Then, we construct the observed vector d via $d = K\hat{x} + \epsilon$, where $\epsilon \in N(0, 0.01\cdot I_m)$ and $\hat{x}$ in $\ell _2$ unit ball is a sparse random vector with 0.2n nonzeros. For the trade-off parameter $\mu$, we take it as 0.001. Now, we specify the choices of parameters to implement these algorithms. We empirically set $\tau =0.3$ for ICDRSM for the four scenarios. For IADMM and IPDM, we set inertial parameters $\tau =0.1$ for the first scenario, $\tau =0.4$ for the second and third scenarios and $\tau =0.6$ for the last scenario. We set $\gamma =\frac{1}{2}\left(\frac{2(1+\tau ^2)}{2\tau ^2+\tau +1}+\frac{2+2\tau }{1+2\tau }\right)$ and $\beta =0.0005$ for ICDRSM, $\gamma =1.6$ and $\beta =0.0005$ for CDRSM, $\beta =0.1$ and $\gamma =1.6$ for ADMM and IADMM, $\nu =0.5,~\sigma =\frac{1}{\nu }$ and $\theta =1$ for PDM and IPDM. The initial iterates for all tested methods are zero vectors $x^0=y^0=\lambda ^0=\varvec{0}_{n\times 1}$. Finally, we adopt the following residual as the stopping criterion for all methods

$$\begin{aligned} {\text {resi}} = \vert F(x^k)-F(x^*)\vert \le 5\cdot 10^{-3}, \end{aligned}$$

(4.6)

where $F(x^*)$ is the objective value of termination point obtained by running CDRSM to satisfy

$$\begin{aligned} \Vert F(x^k)-F(x^{k-1})\Vert \le 10^{-12}. \end{aligned}$$

In Table 1, we report the computing time in seconds (‘CPU’) and the number of iterations (‘It.’). Note that ADMM and PDM require an inner loop to find approximate solutions of their subproblems, we accordingly report the total inner iterations (‘InIt.’) for solving x-subproblems. For each scenario, we test 10 times and report the averaged performance. The symbol ‘–’ in Table 1 means that the computing time exceeds 20 s. It can be seen from Table 1 that all inertial methods take fewer iterations and less computing time than those without inertial acceleration. Both CDRSM and ICDRSM take more iterations than ADMM, PDM and their inertial variants. However, owing to the inner iterations for solving x-subproblems, the total computing time of CDRSM and ICDRSM is less than ADMM-like and PDM-like methods. Comparing ICDRSM with CDRSM, we can see from Table 1 that ICDRSM takes fewer iterations and less computing time than CDRSM, which support the idea of this paper that inertial technique can further improve the performance of CDRSM for separable problem (1.1).

Table 1 Numerical results for box constrained Lasso

To show more details of their numerical behaviors, we show box plots with respect to computing time of these 10 times in Fig. 1, which reports the minimum, median, and maximum computing time of four methods for solving 10 groups of random problems. We can see from Fig. 1 that CDRSM and ICDRSM are relatively stable and more efficient than ADMM and PDM. Moreover, the convergence curves shown in Figs. 2 and 3 demonstrate that ICDRSM is the fastest solver for solving ball-constrained Lasso (4.1).

Fig. 1

Box plots with respect to CPU of the six methods for solving constrained Lasso

Fig. 2

Evolution of relative errors with respect to computing time for constrained Lasso

Fig. 3

Evolution of relative errors with respect to iterations for constrained Lasso

As we all know, inertial parameter is important for inertial-type algorithms. Therefore, we are further concerned with the numerical sensitivity of the inertial parameter to the three inertial-type algorithms. In our experiments, we consider four scenarios and conduct behaviors on CPU time of the three inertial-type algorithms equipped with $\tau =\{0.0,0.1,0.2,\ldots ,0.9,0.999\}$. The bar plots are listed in Fig. 4, where the algorithmic parameters and stopping criterion are the same as the previous experiments. We can observe from Fig. 4 that, with the increase of $\tau \in [0,1)$, the CPU time required by the three algorithms decreases at first and then increases. Comparatively, ICDRSM equipped with $\tau \in [0.3,0.5]$ is more reliable, and the inertial parameter should be larger as the dimension of the problem increases for IADMM and IPDM. This experience also supports our settings of the inertial parameters in the previous experiments.

Fig. 4

Numerical sensitivity of inertial parameter $\tau =\{0.0,0.1,0.2,\ldots ,0.9,0.999\}$ in terms of CPU time for the three inertial algorithms

4.2 Constrained TV-Based Image Restoration

In this subsection, we conduct the performance of the proposed ICDRSM on solving constrained TV-based image restoration problem (1.2). Here, we also consider the separable form (1.3) of (1.2). So, applying ICDRSM to model (1.3), both subproblems (3.7) and (3.8) of ICDRSM are specified as

where $\mathscr {E}_x({\bar{u}}^k)$ and $\omega _y^k$ are defined in Algorithm 1. Theoretically, the x-subproblem (4.2) has an explicit solution. However, as shown in [31, p.43], the linear system (4.2) is often solved by the fast Fourier transform (FFT) or discrete cosine transform. In our experiments, we employ FFT to find the solution of (4.2). When applying ADMM to (1.3), the main subproblems are specified as

Like the saddle point reformulation of (1.4), we can also reformulate (1.2) as the following min-max problem

$$\begin{aligned} \min _{x\in \mathcal {B}}\max _{y\in {\mathcal {Y}}_{\infty }} \left\{ y ^\top \varvec{D} x+\frac{1}{2\mu }\Vert Kx-d\Vert ^2\right\} . \end{aligned}$$

Consequently, the iterative scheme of PDM reads as

Clearly, both x-subproblems (4.2) and (4.2) have no closed-form solution. So we also employ the aforementioned to solve it approximately. Like the previous experiments, we also investigate the numerical sensitivity of the maximum number of inner iterations to the algorithms that need to recall the PBBM. According to our numerical simulation, we empirically choose 10 as the maximum number of inner iterations for the following experiments.

In our experiments, we consider four well-tested images in the literature, i.e., ‘Cameraman.tif ($256\times 256$)’, ‘Columbia.tiff ($480\times 480$)’, ‘Crowd.tiff ($512\times 512$)’ and ‘Man.pgm ($1024\times 1024$)’. All images are first corrupted by the blurring operator with a $25\times 25$ uniform kernel and by adding the zero-white Gaussian noise with the standard derivation 0.001. In Fig. 5, we list the original and degraded images.

Fig. 5

From left to right: Cameraman.tif, Columbia.tiff, Crowd.tiff, Man.pgm. From top to bottom: original images and degraded images, respectively

Fig. 6

Evolution of SNR with respect to computing time for solving constrained TV-based image restoration problem

For the algorithmic parameters, we take $\tau =0.7,0.4,0.5$ for ICDRSM, IADMM and IPDM, respectively. And we set $\gamma =\frac{1}{2}\left(\frac{2(1+\tau ^2)}{2\tau ^2+\tau +1}+\frac{2+2\tau }{1+2\tau }\right)$ and $\beta =0.35$ for ICDRSM, $\gamma =1.6$ and $\beta =0.3$ for CDRSM, $\beta =1$ and $\gamma =1.6$ for ADMM and IADMM, $\nu =0.03$, $\sigma =\frac{1}{8\nu }$ and $\theta =1$ for PDM and IPDM. The starting points for all methods are set as zeros $x^0=y^0=\lambda ^0=\varvec{0}$. As used in the literature, we employ the signal-to-noise ratio (SNR) in the unit of dB to measure the quality of restored images. The SNR is defined by

$$\begin{aligned} \textrm{SNR}=10\log _{10}\frac{\Vert x^*\Vert ^2}{\Vert x-x^*\Vert ^2}, \end{aligned}$$

(4.10)

where $x^*$ is the original image and x represents the restored image.

In Fig. 6, we graphically show the evolution of SNR values with respect to CPU time. It is clear from Fig. 6 that ICDRSM outperforms the other five methods in terms of taking less time to recover images with higher quality.

To see more detailed performance of those methods, we also report the number of iterations, computing time, and SNR values in Table 2, where images are corrupted by blurring operator with a $21\times 21$ uniform kernel, and we take pre-set SNR values as stopping criterion. The symbol ‘–’ in Table 2 means that the number of total iterations exceeds 1000 or the computing time exceeds 20 s. As shown in Table 1, both ICDRSM and CDRSM require more iterations than ADMM-like and PDM-like methods. However, ICDRSM and CDRSM take less computing time to achieve higher SNR values than other methods. The computational results in Table 2 further verify that ICDRSM equipped with an inertial step runs faster than CDRSM for solving constrained TV-based image restoration problems.

Table 2 Numerical results for constrained TV-based image restoration

Finally, we also investigate the numerical sensitivity of the inertial parameter to these inertial-type algorithms for solving constrained TV-based image restoration problems. Here, we follow the settings used in Fig. 4, i.e., $\{\tau =0.0,0.1,0.2,\ldots ,0.9,0.999\}$. The numerical results are summarized in Fig. 7, where the algorithmic parameters are the same as the previous experiments and the stopping rules are taken as some preset SNR values, i.e., 19.5 dB, 22 dB, 19.5 dB, and 22 dB for Cameraman, Columbia, Crowd, and Man, respectively. It can be observed from Fig. 7 that $\tau =0.7$ is suitable for ICDRSM, $\tau =0.4$ is suitable for IADMM and $\tau =0.5$ is suitable for IPDM, which also supports our settings of the inertial parameters in the previous experiments.

Fig. 7

Numerical sensitivity of inertial parameter $\tau =\{0.0,0.1,0.2,\ldots ,0.9,0.999\}$ in terms of CPU time for the three inertial algorithms

5 Conclusion

In this paper, we considered a class of structured convex optimization problem, which has a separable objective function and a structured constraint. Such problems have many applications in statistical learning, machine learning, and image processing. Due to the appearance of two simple convex sets in the structured constraint, a direct application of the popular ADMM yields two constrained subproblems, thereby failing to exploit the simple structure of the two simple convex sets. Comparatively, although the so-called customized DRSM (CDRSM) proposed in [29] enjoys easier subproblems than ADMM, it does not fully make use of the quadratic term in the objective function, since such a quadratic term dominates the main minimization task. Hence, we introduced the inertial acceleration technique to the quadratic term and proposed a partially inertial CDRSM for the problem under consideration. Under mild conditions, we established its global convergence. Some preliminary numerical results also supported the idea of this paper. In the future, we will pay our attention to the theoretical convergence rate and its extension to the cases where the objective function is nonconvex or nonquadratic.