An Adaptive Multiresolution Ultra-weak Discontinuous Galerkin Method for Nonlinear Schrödinger Equations

Abstract

This paper develops a high-order adaptive scheme for solving nonlinear Schrödinger equations. The solutions to such equations often exhibit solitary wave and local structures, which make adaptivity essential in improving the simulation efficiency. Our scheme uses the ultra-weak discontinuous Galerkin (DG) formulation and belongs to the framework of adaptive multiresolution schemes. Various numerical experiments are presented to demonstrate the excellent capability of capturing the soliton waves and the blow-up phenomenon.

1 Introduction

In this paper, we develop a class of adaptive multiresolution ultra-weak discontinuous Galerkin (DG) method to solve the nonlinear Schrödinger (NLS) equations in a d-dimensional space

$$\begin{aligned} i u_t + \Delta u + f(\left| u\right| ^2)u = 0, \end{aligned}$$

(1)

where u is a complex function, and f is a smooth nonlinear real function. The Schrödinger equation is of fundamental importance in quantum mechanics, reaching out to many important applications describing the physical phenomena including nonlinear optics, semiconductor electronics, quantum fluids and plasma physics [10, 32, 43]. Numerical methods for solving the NLS equations have been investigated extensively, including finite difference [5, 24, 36, 38, 40], finite element [8, 16, 25, 45], and spectral methods [14, 34, 39], to name a few. In this paper, we consider the DG method [12, 13, 35], which is a class of finite element methods using piecewise polynomial spaces for the numerical solutions and the test functions. The last several decades have seen tremendous developments of DG methods in approximating partial differential equations (PDEs) in large part due to their distinguished advantages in handling geometry, boundary conditions and accommodating adaptivity. Various types of DG methods have been proposed to compute the NLS equations. In [45], an LDG method using alternating fluxes was developed with $L^2$ stability and the sub-optimal error estimates. An LDG method with various numerical fluxes was analyzed in [27]. An analysis of the LDG method for the NLS equation with the wave operator was carried out in [17]. The direct DG (DDG) method was applied to the Schrödinger equation in [29], and the optimal accuracy was further established in [28]. In [44], a hybridized DG (HDG) method was applied to a linear Schrödinger equation. In this paper, we use the ultra-weak DG method [9], which is a class of DG methods use repeated integration by parts for calculating higher order derivatives. The ultra-weak DG schemes include the DDG and interior penalty DG methods, and have been investigated in [7, 8] for convergence and superconvergence.

The solutions to NLS equations present solitary waves, blow-up and other localized structures. Therefore, benefits of adaptivity in simulations are self-evident [6, 26, 37]. In this paper, we consider the adaptive multiresolution approach [15, 19, 21]. By exploring the inherent mesh hierarchy and the associated nestedness of the polynomial approximation spaces, multiresolution analysis (MRA) [30] is able to accelerate the computation and avoid the need for a posteriori error indicators. MRA is closely related to popular sparse grid methods [3] for solving high-dimensional problems. It is also related to the adaptive mesh refinement (AMR) technique [2, 4], which adjusts the computational grid adaptively to track small scale features of the underlying problems and improves computational efficiency. As a continuation of our previous research on adaptive multiresolution (also called adaptive sparse grid) DG methods [19,20,21,22], this paper develops an adaptive multiresolution ultra-weak DG solver for NLS equation (1) and the coupled NLS equations. First, the Alpert’s multiwavelets are employed as the DG bases in the weak formulation, and then the interpolatory multiwavelets are introduced for efficiently computing nonlinear source which has been successfully applied to nonlinear hyperbolic conservation laws [21] and Hamilton-Jacobi equations [20]. We refer the readers to [19, 21] for more details on the background of adaptive multiresolution DG methods. Numerical experiments verify the accuracy of the methods. In particular, the adaptive scheme is demonstrated to capture the moving solitons and also the blow-up phenomenon very well.

The rest of the paper is organized as follows. In Sect. 2, we review Alpert’s multiwavelets. Section 3 describes the numerical schemes. Section 4 contains numerical examples. We make conclusions in Sect. 5.

2 MRA and Multiwavelets

In this section, we briefly review the fundamentals of MRA of DG approximation spaces and the associated multiwavelets. Two classes of multiwavelets, namely the $L^2$ orthonormal Alpert’s multiwavelets [1] and the interpolatory multiwavelets [41], are used to construct our ultra-weak DG scheme. We also introduce a set of key notations used throughout the paper by following [42].

Alpert’s multiwavelets [1] have been employed to develop a class of sparse grid DG methods for solving high dimensional PDEs [18, 42]. Considering a unit sized interval $\Omega =[0,1]$ for simplicity, we define a set of nested grids $\Omega _0,\,\Omega _1,\cdots$, for which the n-th level grid $\Omega _n$ consists of $2^n$ uniform cells

$$\begin{aligned} I_{n}^j=(2^{-n}j, 2^{-n}(j+1)], \quad j=0, \cdots , 2^n-1. \end{aligned}$$

Denote $I_{-1}=[0,1].$ The piecewise polynomial space of degree at most $k \geqslant 1$ on grid $\Omega _n$ for $n \geqslant 0$ is denoted by

$$\begin{aligned} V_n^k:=\{v: v \in P^k(I_{n}^j),\, \forall \,j=0, \cdots , 2^n-1\}. \end{aligned}$$

(2)

Observing the nested structure

$$\begin{aligned} V_0^k \subset V_1^k \subset V_2^k \subset V_3^k \subset \cdots , \end{aligned}$$

we can define the multiwavelet subspace $W_n^k$, $n=1, 2, \cdots$ as the orthogonal complement of $V_{n-1}^k$ in $V_{n}^k$ with respect to the $L^2$ inner product on [0, 1], i.e.,

$$\begin{aligned} V_{n-1}^k \oplus W_n^k=V_{n}^k, \quad W_n^k \perp V_{n-1}^k. \end{aligned}$$

By letting $W_0^k:=V_0^k$, we obtain a hierarchical decomposition $V_n^k=\bigoplus \limits_{0 \leqslant l \leqslant n} W_l^k$, i.e., an MRA of space $V_n^k$. A set of orthonormal basis can be defined on $W_l^k$ as follows. When $l=0$, the basis $v^0_{i,0}(x)$, $i=0,\cdots ,k$ are the normalized shifted Legendre polynomials in [0, 1]. When $l>0$, the Alpert’s orthonormal multiwavelets [1] are employed as the bases and denoted by

$$\begin{aligned} v^j_{i,l}(x),\quad i=0,\cdots ,k,\quad j=0,\cdots ,2^{l-1}-1. \end{aligned}$$

We then follow a tensor-product approach to construct the hierarchical finite element space in multi-dimensional space. Denote $\mathbf {l}=(l_1,\cdots ,l_d)\in \mathbb {N}_0^d$ as the mesh level in a multivariate sense, where $\mathbb {N}_0$ denotes the set of nonnegative integers, we can define the tensor-product mesh grid as $\Omega _\mathbf {l}=\Omega _{l_1}\otimes \cdots \otimes \Omega _{l_d}$ and the corresponding mesh size $h_\mathbf {l}=(h_{l_1},\cdots ,h_{l_d}).$ Based on the grid $\Omega _\mathbf {l}$, we denote $I_\mathbf {l}^\mathbf {j}=\{\mathbf {x}:x_m\in (h_mj_m,h_m(j_{m}+1)),m=1,\cdots ,d\}$ as an elementary cell, and

$$\begin{aligned} \mathbf{V}_\mathbf {l}^k:=\{\mathbf{v}: \mathbf{v}\in Q^k(I^{\mathbf {j}}_{\mathbf {l}}), \,\, \mathbf {0}\leqslant \mathbf {j}\leqslant 2^{\mathbf {l}}-\mathbf {1}\}= V_{l_1,x_1}^k\times \cdots \times V_{l_d,x_d}^k \end{aligned}$$

as the tensor-product piecewise polynomial space, where $Q^k(I^{\mathbf {j}}_{\mathbf {l}})$ represents the collection of polynomials with a degree of up to k in each dimension on cell $I^{\mathbf {j}}_{\mathbf {l}}$. If we use equal mesh refinement of size $h_N=2^{-N}$ in each coordinate direction, the grid and space will be denoted by $\Omega _N$ and $\mathbf{V}_N^k$, respectively. Based on a tensor-product construction, the multi-dimensional increment space can be defined as

$$\begin{aligned} \mathbf {W}_\mathbf {l}^k=W_{l_1,x_1}^k\times \cdots \times W_{l_d,x_d}^k. \end{aligned}$$

The basis functions in case of multi-dimensions are defined as

$$\begin{aligned} v^\mathbf {j}_{\mathbf {i},\mathbf {l}}(\mathbf {x}) := \prod _{m=1}^d v^{j_m}_{i_m,l_m}(x_m) \end{aligned}$$

(3)

for $\mathbf {l}\in \mathbb {N}_0^d$, $\mathbf {j}\in B_\mathbf {l}:= \{\mathbf {j}\in \mathbb {N}_0^d: \,\mathbf {0}\leqslant \mathbf {j}\leqslant \max (2^{\mathbf {l}-\mathbf {1}}-\mathbf {1},\mathbf {0}) \}$ and $\mathbf {1}\leqslant \mathbf {i}\leqslant \mathbf {k}+\mathbf {1}$.

By introducing the standard norms for the multi-index

$$\begin{aligned} |\mathbf {l}|_1:=\sum _{m=1}^d l_m, \qquad |\mathbf {l}|_\infty :=\max _{1\leqslant m \leqslant d} l_m, \end{aligned}$$

together with the same component-wise arithmetic operations and relations as defined in [42], we achieve the decomposition

$$\begin{aligned} \mathbf{V}_N^k= {\mathop{\mathop{\bigoplus}\limits_{|\mathbf {l}|_\infty \leqslant N}}\limits_{\mathbf {l}\in \mathbb {N}_0^d}} \mathbf {W}_\mathbf {l}^k. \end{aligned}$$

(4)

Further, by a standard truncation of $\mathbf{V}_N^k$ [18, 42], we obtain the sparse grid space

$$\begin{aligned} \hat{\mathbf{V}}_N^k= {\mathop{\mathop{\bigoplus}\limits_{|\mathbf {l}|_1 \leqslant N}}\limits_{\mathbf {l}\in \mathbb {N}_0^d}} \mathbf {W}_\mathbf {l}^k \subset \mathbf{V}_N^k. \end{aligned}$$

(5)

We skip the details about the property of the space, but refer the readers to [18, 42]. In Sect. 3, we will describe the adaptive scheme that adapts a subspace of $\mathbf{V}_N^k$ according to the numerical solution, hence offering more flexibility and efficiency.

Alpert’s multiwavelets described above are associated with the $L^2$ projection operator. For nonlinear source terms, we use the interpolatory multiwavelets based on Lagrange interpolations introduced in [41]. For details, we refer readers to [21, 41].

3 Adaptive Multiresolution DG Scheme

In this section, we present the adaptive multiresolution ultra-weak DG scheme for solving the NLS equation (1). We consider periodic boundary conditions for simplicity, while the method can be adapted to other non-periodic boundary conditions.

For illustrative purposes, we first introduce some basis notations about jumps and averages for piecewise functions defined on a grid $\Omega _N$. Denote by $\Gamma$ the union of the boundaries for all the elements in the partition $\Omega _N$. The jump and average of $q\in L^2(\Gamma )$ and $\mathbf{q} \in [L^2(\Gamma )]^d$ are defined as follows. Suppose e is an edge shared by elements $T^+$ and $T^-$, we define the unit normal vectors $\mathbf{n} ^+$ and $\mathbf{n} ^-$ on e pointing exterior to $T^+$ and $T^-$. Then,

$$\begin{aligned}{}[q]=q^- \mathbf{n} ^- + q^+ \mathbf{n} ^+, \qquad&\{ q\} = \frac{1}{2} (q^-+q^+), \\ [\mathbf{q} ] = \mathbf{q} ^- \cdot \mathbf{n} ^- + \mathbf{q} ^+ \cdot \mathbf{n} ^+ , \qquad&\{ \mathbf{q} \} = \frac{1}{2}(\mathbf{q} ^- + \mathbf{q} ^+). \end{aligned}$$

For any subspace $\mathbf{V}$ of $\mathbf{V}_N^k$, define the corresponding complex-valued finite element space

$$\begin{aligned} \mathbb {V}:=\{ v=v_1 + i v_2: v_1, v_2 \in \mathbf{V}\}. \end{aligned}$$

(6)

The semi-discrete ultra-weak DG scheme [8] for (1) is defined below. We are searching for $u_h \in \mathbb {V}$ such that for any test function $\phi _h \in \mathbb {V}$,

$$\begin{aligned} i \int _{\Omega } (u_h)_t \phi _h {\text {d}}\mathbf {x}+ \int _{\Omega } u_h \nabla ^2 \phi _h {\text {d}} \mathbf {x}&- \sum _{e\in \Gamma } \int _e \hat{u}_h [\nabla \phi _h] {\text {d}}s +\sum _{e \in \Gamma } \int _e \widetilde{\nabla u_h} \cdot [\phi _h] {\text {d}}s \nonumber+\int _{\Omega } f(|u_h|^2)u_h \phi _h {\text {d}}\mathbf {x}= 0. \end{aligned}$$

(7)

We take the following numerical fluxes:

$$\begin{aligned} \widetilde{\nabla u_h} = \{ \nabla u_h \} + \alpha _1[\nabla u_h]\mathbf{e} + \beta _1[u_h], \quad \hat{u}_h = \{u_h\} + \alpha _2[u_h]\cdot \mathbf{e} + \beta _2[\nabla u_h]. \end{aligned}$$

(8)

Here, $\alpha _1$, $\alpha _2$, $\beta _1,$ and $\beta _2$ are prescribed complex numbers that may depend on the mesh size h and $\mathbf{e}=(1,\cdots ,1)\in \mathbb {R}^d$. In this work, we numerically test two types of numerical fluxes. The first one is the alternating flux corresponding to $\alpha _1=\frac{1}{2}$, $\alpha _2=-\frac{1}{2}$ and $\beta _1=\beta _2=0$. The second one is a dissipative numerical flux [8] with $\alpha _1 = \frac{1}{2}$, $\alpha _2 = -\frac{1}{2}$, $\beta _1 = 1-i$, $\beta _2 = 1+i$.

To efficiently calculate the nonlinear term $\int _{\Omega } f(|u_h|^2)u_h \phi _h {\text {d}}\mathbf {x}$ in (7), the multiresolution Lagrange interpolation is applied [21, 41], i.e., we modified the weak formulation of ultra-weak DG as follows. We are searching for $u_h \in \mathbb {V}$ such that for any test function $\phi _h \in \mathbb {V},$

$$\begin{aligned} i \int _{\Omega } (u_h)_t \phi _h {\text {d}}\mathbf {x}+ \int _{\Omega } u_h \nabla ^2 \phi _h {\text {d}} \mathbf {x}&- \sum _{e\in \Gamma } \int _e \hat{u}_h [\nabla \phi _h] {\text {d}}s +\sum _{e \in \Gamma } \int _e \widetilde{\nabla u_h} \cdot [\phi _h] {\text {d}}s \nonumber&+\int _{\Omega } \mathcal {I}_h\left( f(|u_h|^2)u_h\right) \phi _h {\text {d}}\mathbf {x}= 0. \end{aligned}$$

(9)

To preserve the accuracy of the original DG scheme (7), Lagrange interpolation of the same order must be applied in (9). For details, see the argument in [11, 21, 23]. By applying interpolation, the unidirectional principle and fast algorithm described in [21] can be employed to further improve efficiency. In numerical experiments, we also consider the coupled nonlinear Schrödinger equations in a one-dimensional space

$$\begin{aligned}&i u_t + i \alpha u_x + u_{xx} + \beta u + \kappa v + f(\left| u\right| ^2, \left| v\right| ^2)u = 0, \end{aligned}$$

(10a)

$$\begin{aligned}&i v_t - i \alpha v_x + v_{xx} - \beta u + \kappa v + g(\left| u\right| ^2, \left| v\right| ^2)v = 0, \end{aligned}$$

(10b)

where u and v are complex functions, f and g are smooth nonlinear real functions, and $\alpha$, $\beta$, $\kappa$ are real constants. We use the same DG scheme for solving the coupled NLS equation (10) except that the first order derivatives $u_x$ and $v_x$ are treated by the standard DG scheme with upwind numerical fluxes. The details are omitted here for brevity.

For time discretization, we employ the third-order implicit-explicit (IMEX) Runge-Kutta (RK) scheme [33] to advance the semi-discrete scheme (9). Specifically, the second derivative term $u_{xx}$ is treated implicitly to avoid the severe CFL time constraint, while the nonlinear source $f(\left| u\right| ^2)u$ is treated explicitly for efficiency. The adaptive procedure follows the technique developed in [20, 21] to determine the space $\mathbf{V}$ that evolves dynamically over time. The only difference is that the first-order Euler forward and Euler backward schemes are applied for the prediction. The main idea is that based on the distinguished properties of multiwavelets, we keep track of multiwavelet coefficients, i.e., $L^2$ norms of $u_h$, as an error indicator for refining and coarsening, aiming to efficiently capture the solitons or singular solutions of (1). We also remark that other types of time discretizations, e.g., exponential time differencing (ETD) or Krylov implicit integration factor (IIF) methods, could also be applied here. The efficiencies of different types of time stepping remain to be investigated.

4 Numerical Examples

In this section, we perform numerical experiments to validate the performance of our scheme. We consider the NLS equation (1) in 1D and 2D, and the coupled NLS equation (10) in 1D, with a computational domain of $[0, 1]^d$ with $d = 1, 2$. We employ the third order IMEX RK scheme in [33]. The CFL number is to be 0.1, i.e., $\Delta t=0.1 \Delta x$, unless otherwise stated. All adaptive calculations are obtained by $k = 3$. $\text {DoF}=\text {dim}(\mathbf{V})$ refers to the number of Alperts’ multiwavelets basis function with respect to the adaptive grids.

4.1 Accuracy Test for NLS Equation

Example 1

We start with the accuracy test for the NLS equation on the domain $[0,1]^d$:

$$\begin{aligned} i u_t + \Delta u + \left| u\right| ^2 u + \left| u\right| ^4 u = 0 \end{aligned}$$

(11)

with periodic boundary conditions. The exact solution is

$$\begin{aligned} u(x,t) = \exp \left(i \left(2\pi \sum _{i=1}^dx_i - \omega t \right)\right) \end{aligned}$$

(12)

with $\omega =4d \pi ^2-2$.

We first test the accuracy of the sparse grid methods in a 2D space. The results obtained by considering $k=1,2,3$ are presented in Table 1. To ensure time accuracy, we take $\Delta t=0.1\Delta x^{4/3}$ for $k=3$. As expected, the average convergence order is between k and $k+1$.

Table 1 Example 1, accuracy test for NLS equation, $d=2$, sparse grid, $t=0.1$

We then test the accuracy of adaptive method in 2D in Table 2. We observe that it takes much less DoF with higher-order polynomial degrees than lower-order ones.

Table 2 Example 1, accuracy test for NLS equation, $d=2$. Adaptive. $t=0.1$

We also show the comparison on the error vs. the CPU time for adaptive, sparse and full grid DG methods with $k=2$ in Fig. 1. From the results, it is evident that the adaptive multiresolution method is the most efficient among the three methods in this 2D example. The sparse grid method outperforms the full grid method since the solution is smooth in this example and the sparse grid space $\hat{\mathbf {V}}_N^K$ ensures comparable accuracy to the full grid space ${\mathbf {V}}_N^K$ with reduced DoFs.

Fig. 1

Example 1: $L^2$-error vs. CPU time for adaptive, sparse and full grid ultra-weak DG methods. $d=2$, $t=0.1$, $k=2$

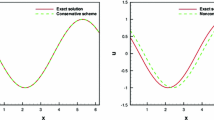
Next, we compare the performance of our numerical scheme with the alternating (conservative) and dissipative numerical fluxes. The time history of the $L^2$-error with different values of polynomial degrees k and error tolerance $\epsilon$ is shown in Fig. 2. Note that the adaptive scheme with dissipative flux and $k=1$ does not converge because the corresponding full grid DG is not consistent. In general, the two kind of numerical fluxes has the similar magnitude of errors. Since the conservative numerical flux performs better in regular DG [8], we will consider the conservative numerical flux in the following examples.

Fig. 2

Example 1: $L^2$-error vs time. $d=1$, $t=10$. $N=8$ and $\eta =\epsilon /10$. Left: conservative numerical flux; right: dissipative numerical flux

4.2 NLS Equation in 1D

Example 2

In this example, we show the soliton propagation of the NLS equation (1) in the domain [0, 1]:

$$\begin{aligned} i u_t + \frac{1}{M^2}u_{xx} + 2\left| u\right| ^2 u = 0 \end{aligned}$$

(13)

with the initial conditions corresponding to the single soliton [45]

$$\begin{aligned} u(x,0) = {{\,\mathrm{sech}\,}}(X-x_0)\exp (2i(X-x_0)) \end{aligned}$$

(14)

and the double soliton [45]

$$\begin{aligned} u(x,0) = \sum _{j=1}^2 {{\,\mathrm{sech}\,}}(X-x_j)\exp \left(\frac{1}{2}ic_j\left(X-x_j \right)\right) \end{aligned}$$

(15)

with $X=M(x-\frac{1}{2})$. Here the parameters are taken as $M=50$, $x_0=0$, $x_1=-10$, $x_2=10$, $c_1=4$ and $c_2=-4$.

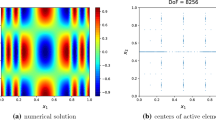
The numerical solutions and the active elements for the single soliton (14) are shown in Fig. 3. We observe that the envelope or the modulus $\left| u\right|$ are captured by our adaptive scheme quite well. The active elements are also moving with the wave peak.

Fig. 3

Example 2: 1D NLS equation, single soliton. Left: numerical solutions; right: active elements. $t=0$ and 2. $N=8$, $\epsilon =10^{-4}$, $\eta =10^{-5}$

The numerical solutions and the active elements for double solitons (15) are shown in Fig. 4. The two waves propagate in opposite directions and collide at $t=2.5$. After that, the two waves separate. Such behaviors are accurately captured by our numerical simulations. Moreover, our numerical solution does not generate symmetric active elements, which is due to the fact that the ultra-weak DG in full grid does not preserve the symmetry exactly.

Fig. 4

Example 2: 1D NLS equation, double soliton. Left: numerical solutions; right: active elements. $t=0$, 2.5 and 5. $N=8$, $\epsilon =10^{-4}$, $\eta =10^{-5}$

Example 3

In this example, we consider the bound state solution of the equation [45]

$$\begin{aligned} i u_t + \frac{1}{M^2} u_{xx} + \beta \left| u\right| ^2 u = 0 \end{aligned}$$

(16)

with an initial condition of

$$\begin{aligned} u(x,0) = {{\,\mathrm{sech}\,}}X, \end{aligned}$$

(17)

where $X= M(x-0.5), M=30$.

When $\beta = 2L^2$, it will produce a bound state of L solitons. The theoretical solution for a bound state of solitons is known [31]. If $L \geqslant 3$, small narrow structures will develop in the solution which require high mesh resolution to capture. Clearly, using a uniform mesh is far from being optimal due to such a highly localized structure. We present the numerical solutions and active elements of the bound state of solitons with $L=3,4,5$ in Figs. 5, 6 and 7. The multiscale structure of the solutions is accurately captured by our adaptive method.

Fig. 5

Example 3: bound state solution of solitons with $L=3$. Left: numerical solutions; right: active elements. $t=0$, 0.4 and 0.6. $N=9$, $k=3$, $\epsilon =10^{-4}$ and $\eta = 10^{-5}$

Fig. 6

Example 3: bound state solution of solitons with $L=4$. Left: numerical solutions; right: active elements. $t=0$, 0.4 and 0.6. $N=9, k=3$, $\epsilon =10^{-4}$ and $\eta =10^{-5}$

Fig. 7

Example 3: bound state solution of solitons with $L=5$. Left: numerical solutions; right: active elements. $t=0$, 0.4 and 0.6. $N=10, k=3$, $\epsilon =10^{-4}$ and $\eta =10^{-5}$

4.3 Coupled NLS Equation in 1D

Example 4

We show an accuracy test for the coupled NLS equation [45]

$$\begin{aligned} \left\{ \begin{array}{ll} i u_t + i \frac{\alpha }{M} u_x + \frac{1}{2M^2} u_{xx} + (\left| u\right| ^2 + \beta \left| v\right| ^2)u = 0, \\ i v_t - i \frac{\alpha }{M} v_x + \frac{1}{2M^2} v_{xx} + (\beta \left| u\right| ^2 + \left| v\right| ^2)v = 0 \end{array}\right. \end{aligned}$$

(18)

with the soliton solution

$$\begin{aligned} \left\{ \begin{array}{ll} u(x,t) = \sqrt{\frac{2a}{1+\beta } } {{\,\mathrm{sech}\,}}\left( \sqrt{2a}(X-c t)\right) \exp \left( i\left( (c-\alpha )X - \left( \frac{c^2 - \alpha ^2}{2} - a\right) t \right) \right) , \\ v(x,t) = \sqrt{\frac{2a}{1+\beta } } {{\,\mathrm{sech}\,}}\left( \sqrt{2a}(X-c t)\right) \exp \left( i\left( (c+\alpha )X - \left( \frac{c^2 - \alpha ^2}{2} - a\right) t \right) \right) , \end{array}\right. \end{aligned}$$

(19)

where $c=1, a=1, \alpha = \frac{1}{2}, \beta = \frac{2}{3}$ and $X= M(x-0.5), M=50$. The periodic boundary condition is applied in [0, 1]. The solutions are computed up to $t=1$. We take $\Delta t= \frac{0.1 M \Delta x}{\alpha }$, the maximum mesh level $N=10$, and $\eta = \epsilon /10$. The accuracy results are shown in Table 3. We can observe that the approximation with a higher polynomial degree outperforms that with a lower polynomial degree. Note that the method has saturated when $\epsilon = 10^{-4}$ for $k=1$; therefore, the error does not decay too much.

Table 3 Example 4, accuracy test for the coupled NLS equation, $d=1$. Adaptive. $t=1$

Example 5

In this example, we consider the solitary wave propagation and soliton interaction for the coupled NLS equation (18) following [45]. In this example, $\Delta t= \frac{0.1 M \Delta x}{\alpha }$.

We first take the initial condition for soliton propagation

$$\begin{aligned} \left\{ \begin{array}{ll} u(x,0) = \sqrt{\frac{2a}{1+\beta } } {{\,\mathrm{sech}\,}}\left( \sqrt{2a}X\right) \exp \left( i (c-\alpha )X \right) , \\ v(x,0) = \sqrt{\frac{2a}{1+\beta } } {{\,\mathrm{sech}\,}}\left( \sqrt{2a}X\right) \exp \left( i (c+\alpha )X \right) \end{array}\right. \end{aligned}$$

(20)

with the same parameters in Example 4 except $X= M(x-0.2), M=100$. The periodic boundary condition is used in [0, 1]. The numerical solutions and active elements at $t=0, 20$ and 50 are presented in Fig. 8. The plots of |u| and |v| are similar; thus, we only show the results of |u| here.

Fig. 8

Example 5: coupled NLS equation, single soliton. Left: numerical solutions; right: active elements. $t=0$, 20 and 50. $N=9, k=3$, $\epsilon =10^{-4}$ and $\eta =5 \times 10^{-5}$

For interaction of two solitons, we use the following initial condition:

$$\begin{aligned} \left\{ \begin{array}{ll} u(x,0) = \sum \limits_{j=1}^{2} \sqrt{\frac{2a_j}{1+\beta } } {{\,\mathrm{sech}\,}}\left( \sqrt{2a_j}X_j\right) \exp \left( i (c_j-\alpha )X_j \right) , \\ v(x,0) = \sum\limits _{j=1}^{2} \sqrt{\frac{2a_j}{1+\beta } } {{\,\mathrm{sech}\,}}\left( \sqrt{2a_j}X_j\right) \exp \left( i (c_j+\alpha )X_j \right) , \end{array}\right. \end{aligned}$$

(21)

where $c_1=1, c_2 = 0.1, a_1=1, a_2 = 0.5, \alpha = \frac{1}{2}, \beta = \frac{2}{3}$ and $X_j= M(x-0.2-x_j), M=100, x_1=0, x_2=0.25$. The periodic boundary condition is used in [0, 1]. The numerical solutions of |u| and active elements at $t=0, 20$ and 50 are presented in Fig. 9. The interaction is elastic and the solitons restore their original shapes.

Next, we consider interaction of three solitons with initial condition

$$\begin{aligned} \left\{ \begin{array}{ll} u(x,0) = \sum \limits_{j=1}^{3} \sqrt{\frac{2a_j}{1+\beta } } {{\,\mathrm{sech}\,}}\left( \sqrt{2a_j}X_j\right) \exp \left( i (c_j-\alpha )X_j \right) ,\\ v(x,0) = \sum \limits_{j=1}^{3} \sqrt{\frac{2a_j}{1+\beta } } {{\,\mathrm{sech}\,}}\left( \sqrt{2a_j}X_j\right) \exp \left( i (c_j+\alpha )X_j \right) , \end{array}\right. \end{aligned}$$

(22)

where $c_1=1, c_2 = 0.1, c_3 = -1, a_1=1.2, a_2 = 0.72, a_3 = 0.36, \alpha = \frac{1}{2}, \beta = \frac{2}{3}$ and $X_j= M(x-0.2-x_j), M=100, x_1=0, x_2=0.25, x_3 = 0.5$. The periodic boundary condition is used in [0, 1]. The numerical solutions of |u| and active elements at $t=0, 20$ and 50 are presented in Fig. 10. Notice that the three solitons restore their original shapes after the interaction.

Fig. 9

Example 5: coupled NLS equation, double solitons. Left: numerical solutions; right: active elements. $t=0$, 20 and 50. $N=9, k=3$, $\epsilon =10^{-4}$ and $\eta =4 \times 10^{-5}$

Fig. 10

Example 5: coupled NLS equation, triple solitons. Left: numerical solutions; right: active elements. $t=0$, 20 and 50. $N=9, k=3$, $\epsilon =10^{-4}$ and $\eta =4 \times 10^{-5}$

4.4 NLS Equation in 2D

Example 6

In this example, we consider the singular solutions for the 2D NLS equation

$$\begin{aligned} i u_t + \frac{1}{M^2} u_{xx} + \frac{1}{M^2} u_{yy} + \left| u\right| ^2 u = 0 \end{aligned}$$

(23)

with the initial condition [45]

$$\begin{aligned} u(x,0) = (1 + \sin X) (2 + \sin Y) \end{aligned}$$

(24)

where $X= Mx, Y=My, M=2 \pi$. Periodic boundary conditions are applied in $[0,1]^2$. Strong evidence of a singularity in finite time is obtained. The plots of |u| and active elements at $t=0$ and $t=0.108$ are shown in Fig. 11. From the results, we can observe that a singular is generated at $t=0.108$ and our method can capture the structure adaptively.

Fig. 11

Example 6: singular solutions in 2D NLS equation. Left: numerical solutions; right: active elements. $t=0$ and 0.108. $N=7, k=3$, $\epsilon =10^{-4}$ and $\eta =10^{-5}$

Example 7

In this example, we consider the 2D NLS equation (23) with the initial condition [46]

$$\begin{aligned} u(x,0) = 2.0 + 0.01\sin \left (X+\frac{\pi }{4}\right)\sin \left(Y+\frac{\pi }{4}\right), \end{aligned}$$

(25)

where $X= M(x-0.5)$, $Y=M(y-0.5)$, $M=2 \pi$. Periodic boundary conditions are applied in $[0,1]^2$. The plots of |u| and active elements at $t=0$ and $t=1.581\, 3$ are shown in Fig. 12. We can observe the blow-up phenomenon in |u| at $t=1.581\, 3$.

Fig. 12

Example 7: blow-up solution in 2D NLS equation. Left: numerical solutions; right: active elements. $t=0$ and 1.581 3. $N=7, k=3$, $\epsilon =10^{-4}$ and $\eta =10^{-5}$

Example 8

In this example, we consider the 2D NLS equation (23) with the initial condition [47]

$$\begin{aligned} u(x,0) = 6\sqrt{2}\exp (-X^2-Y^2), \end{aligned}$$

(26)

where $X= M(x-0.5)$, $Y=M(y-0.5)$ and $M=10$. Periodic boundary conditions are applied in $[0,1]^2$. The plots of |u| and active elements at $t=0$ and $t=0.04$ are shown in Fig. 13. We observe from the results that the solution blows up in the center and our method can capture the blow-up phenomenon.

Fig. 13

Example 8: single blow-up solution in 2D NLS equation. Left: numerical solutions; right: active elements. $t=0$ and 0.04. $N=9, k=3$, $\epsilon =10^{-3}$ and $\eta =10^{-4}$

5 Conclusion

In this paper, we propose an adaptive multiresolution ultra-weak DG method to solve nonlinear Schrödinger equations. The adaptive multiwavelets are applied to achieve the multiresolution. The Alpert’s multiwavelets are used to express the DG solution and the interpolatory multiwavelets are exploited to compute the nonlinear source term. Various numerical experiments are presented to demonstrate the excellent capability of capturing the soliton waves and the blow-up phenomenon. The code generating the results in this paper can be found at the GitHub link: https://github.com/JuntaoHuang/adaptive-multiresolution-DG.