Solution of the modified Yukawa–Kratzer potential under influence of the external fields and its thermodynamic properties

Abstract

The Schrödinger equation has been solved in two dimensions for the modified Yukawa–Kratzer potential (MYKP) under the influence of the magnetic field and the Aharanov–Bohm flux field (external fields). The energy eigenvalues and wave function were calculated using the parametric Nikiforov–Uvarov approach. From the resulting energy eigensolution of MYKP, we calculated energy eigenvalues for generalised Kratzer potential (GKP), modified Kratzer potential (MKP), Kratzer potential (KP), and Hellmann potential (HP). The energy values for MYKP, KP, MKP, and GKP are tabulated numerically. Under the impact of external fields, we explore different thermodynamic parameters such as partition function, mean energy, mean free (internal) energy, entropy, specific heat capacity, magnetization at finite temperature, and magnetic susceptibility at finite temperature. Plots of the effective potential, energy eigenvalues, and thermodynamic properties for various parameters were provided. The calculated numerical results for KP and HP under the effect of the magnetic field and the Aharanov–Bohm flux field are quite close to those obtained by others. In addition, MYKP also solves the Schrödinger equation using the series expansion method. It is possible to get confined state energy spectra. For distinct n,m quantum numbers for $q=1$, numerical values of energy spectra of special cases Kratzer potential for $N_2$ and CH molecules are computed, and the findings are consistent with NU method.

1 Introduction

The schrödinger equation or schrödinger type equation can be solved analytically or numerically to offer us a lot of information about a physical system. Because of their importance in statistical physics, solid-state physics, quantum field theory, and molecular physics, researchers are interested in solving these types of equations in the relativistic and non-relativistic regimes. Since the last decade, many researchers have been working to solve the diverse physical potentials in two dimensions under the influence of the magnetic field and the Aharanov–Bohm flux field for both relativistic and non-relativistic realms [1,2,3,4].

Different methods are available in the literature to solve second order differential equations, including: Nikiforov–Uvarov (NU) method [5,6,7], exact quantization rule [8,9,10,11], Qiang-Dong proper quantization rule [12, 13], the path integral method [14], asymptotic iteration method (AIM) [15], factorization method [16], Laplace transform approach [17], supersymmetric quantum mechanics (SUSYQM) [18, 19], ansatz method [20] and series expansion method [21]

Spectral features of an electron in a two-dimensional (2D) Gaussian quantum dot (GQD) investigated by Aalu [22] through the Nikiforov–Uvarov method under the combined action of magnetic field, electric field, and AB flux field. Many researchers have investigated quantum rings in the presence of an external magnetic field, observing new phenomena such as spin orbit [23], quantum hall [24], Berry’s phase [25], persistent currents [26], and the Aharonov–Bohm [27]. Ikot et al. [28] examined different thermodynamic features in the framework of superstatistics, employing the pseudoharmonic potential under the influence of external magnetic and AB fields. Ikot et al. [29] solved the screened Kratzer potential in two dimensions under the influence of the magnetic field and the Aharanov–Bohm flux field and examined various thermodynamical features. Ikhdair et al. [30, 31] investigated 2D harmonic and pseudo-harmonic oscillators in the presence of external fields and got the energy spectrum and wave function of an electron. Hamzavi et al. [32] explored the spin and pseudospin symmetry for the Killingbeck potential using a quasi-exact solution. The quark-antiquark interaction Killingbeck potential was solved using the power series technique under the effect of external fields [33, 34]. Ikhdair et al. [35] investigated non-relativistic molecular models in the presence of external magnetic fields.

Ibekwe et al. [36] analytically solved the radial Schrodinger equation with an exponential, generalised, anharmonic Cornell and created the mass spectra of the heavy quarkonium system. Theoritically Quarkonia physics now a days very important due to many available experimental states [37,38,39,40]. Using the WKB approach, Omugbe et al. [41] calculated the mass spectrum of mesons. In nuclei, atoms, molecules, and spectroscopy, as well as many other fields of physics, the accurate solution of the Schrodinger equation with some solvable potential plays an important role [42]. Obtaining analytical solutions to the radial schrödinger equation with the provided interaction potential without the use of approximation approaches is a difficult task. Ibekwe et al. [43] obtained mass spectra of heavy quarkonium for screened Kartzer potential using series expantion method. The nature of the potential model influences the applications of Schrödinger equation solutions in various circumstances [44]. AbuShady and Ezz-Alarab [45] employed an exact-analytical iteration method to study the N-radial Schrödinger equation analytically and used the results to compute the thermodynamic properties and mass of mesons. The energy eigenvalues and normalised eigen-functions of the radial SE in N-dimensional space for the quark–antiquark interaction potential were calculated analytically by Kumar and Fakir [46].

Purohit et al. [47] investigated the thermodynamic parameters of the filtered cosine Kratzar potential in the presence of a magnetic field and an Aharanov–Bohm flux field.

The modified Yukawa–Kratzer potential (MYKP) [48] solved in this study under the effect of the magnetic field and the Aharanov–Bohm flux field written as,

$$\begin{aligned} V(r)=\frac{a_1 e^{-2\alpha r}}{r^2} -\frac{a_2 e^{-\alpha r}}{r}+a+D_e-\left( \frac{A_1}{r}-\frac{A_2}{r^2}\right) \end{aligned}$$

(1)

where $A_1\equiv 2D_e r_e$, $A_2\equiv D_e r_e^2$. $r_e$ is the equilibrium bond length the interatomic distance r, $\alpha$ are the screening parameters, and $D_e$ is the dissociation energy.

In the non relativistic framework, Parmar et al. [48] achieved the solution to MYKP using the Nikiforov–Uvarov (NU) method and the SUSYQM method. They look into several thermodynamical parameters, expectation values utilising the Hellmann–Feynman theorem, and the eigensolution of the chosen dimer inferred from MYKP eigensolutions.

In this paper, we used the parametric Nikiforov–Uvarov (pNU) approach to determine the eigenspectrum of the MYKP Eq. (1) under the effect of the magnetic field $\vec {B}$ along the z direction and the Aharanov–Bohm flux field $\Phi _{AB}$ formed by a solenoid. The energy eigenvalues spectrum of the MYKP is computed numerically for various values of the magnetic field $\vec {B}$ and Aharanov–Bohm flux field $\Phi _{AB}$. By setting potential parameters, we deduced generalized Kratzer potential, modified Kratzer potential, Kratzer potential, and Hellmann potential and its energy spectrum using energy spectrum of MYKP. Different thermodynamic properties such as partition function $Z(\vec {B},\Phi _{AB},\beta )$ mean energy $U(\vec {B},\Phi _{AB},\beta )$, mean free energy $F(\vec {B},\Phi _{AB},\beta )$, entropy $S(\vec {B},\Phi _{AB},\beta )$, specific heat capacity $C_s(\vec {B},\Phi _{AB},\beta )$, magnetization $M(\vec {B},\Phi _{AB} ,\beta )$ at finite temperature and magnetic susceptibility $\chi _m(\vec {B},\Phi _{AB},\beta )$ at finite temperature for MYKP is presented. Plots of the effective potential and energy eigenvalues are also addressed with respect to $\alpha$, magnetic field $\vec {B}$, and Aharanov–Bohm flux field $\Phi _{AB}$. We also looked at graphs of thermodynamic properties vs various parameters. We used $m\rightarrow (D-2)/2+\ell$ to extend our work to D dimensions, where m and $\ell$ are magnetic and angular quantum numbers, respectively. We also used the series expansion method to solve MYKP and obtain energy spectra, which we compared to the NU method for a few dimers.

This is how the article is structured: The pNU technique is explained in Sect. 2. In Sect. 3, we presented the MYKP solution obtained under the effect of the magnetic field and the Aharanov–Bohm flux field. Section 4 presents solution of the MYKP using series expansion method and obtained thermodynamic properties. Section 5 presents the results and discussions. A brief conclusion is presented in Sect. 6.

2 Review of the parametric Nikiforov–Uvarov (pNU) method

The generalized form of the Schrödinger like second order differential equation for any potential written as [28, 49],

$$\begin{aligned} \frac{d\Psi (u)}{du^2}+\frac{g_1-g_2u}{u(1-g_3u)}\frac{d\Psi }{du}+\frac{-B_1u^2+B_2u-B_3}{ u^2(1-g_3u)^2} \Psi (u) \end{aligned}$$

(2)

From the parametric Nikiforov–Uvarov (pNU) method, the energy eigenvalues and eigen functions respectively become [28, 49]

$$\begin{aligned}&(g_{2}-g_{3})n+g_{3}n^2-(2n+1)g_{5}+(2n+1)\left( \sqrt{g_{9}}+g_{3}\sqrt{g_{8}}\right) \nonumber \\&\quad +g_{7}+2g_{3}g_{8}+2\sqrt{g_{8}g_{9}}=0 \end{aligned}$$

(3)

$$\begin{aligned}&\Psi (u)=u^{g_{12}}(1-g_3u)^{-g_{12}-\frac{g_{13}}{g_{3}}}P_n^{(g_{10}-1,(g_{11}/g_{3})-g_{10}-1)}(1-2g_3u) \end{aligned}$$

(4)

where

$$\begin{aligned}&g_{4}=(1-g_{1})/2,\quad g_{5}=(g_{2}-2g_{3})/2,\quad g_{6}=g_{5}^2+B_1,\quad g_{7}=2g_{4}g_{5}-B_2,\quad g_{8}=g_{4}^2+B_3\\&g_{9}=g_{3}g_{7}+g_{3}^2g_{8}+g_{6},\quad g_{10}=g_{1}+2g_{4}+2\sqrt{g_{8}},\quad g_{11}=g_{2}-2g_{5}+2(\sqrt{g_{9}}+g_{3}\sqrt{g_{8}})\end{aligned}$$

$$\begin{aligned} g_{12}= g_{4}+\sqrt{g_{8}}, \ \ g_{13}= g_{5}-(\sqrt{g_{9}}+g_{3}\sqrt{g_{8}}) \end{aligned}$$

(5)

for $g_3=0$,

$$\begin{aligned} \lim _{g_3\rightarrow 0} P_n^{(g_{10}-1,(g_{11}/g_{3})-g_{10}-1)}(1-2g_3u) =L_n^{g_{10}-1}(g_{11} u)\end{aligned}$$

(6)

and

$$\begin{aligned} \lim _{g_3\rightarrow 0} (1-g_3u)^{-g_{12}-\frac{g_{13}}{g_{3}}} =e^{g_{13} u} \end{aligned}$$

(7)

Equation (4) becomes

$$\begin{aligned} \Psi (u)=u^{g_{12}} e^{g_{13} u} L_n^{g_{10}-1}(g_{11} u)\end{aligned}$$

(8)

where $L_n^{g_{10}-1}(g_{11} u)$ is Laguerre polynomials.

3 Eigensolution of the MYKP with an external fields

A general formalism of the Schrödinger equation for a charged particle moving under the influence of the vector potential $\vec {A}$ written as

$$\begin{aligned} \left[ \frac{1}{2\mu }\left( \vec {p}+\frac{q}{c}\vec {A}\right) ^2+V(r)-E_{nm}\right] \psi (r,\phi )=0 \end{aligned}$$

(9)

where $\mu$-reduced mass of the system and q is the charge of the particle, $E_{nm}$ energy eigenvalues, vector momentum $\vec {p}=-i\hbar \vec {\nabla }$, c velocity of light, vector potential $\vec {A}=(A_r,A_\phi ,A_z)$, and V(r) scalar potential and wave function $\psi (r,\phi )=(2\pi r)^{-1/2} e^{im \phi } G_{nm}(r)$. For $\vec {A_r}=\vec {A_z}=0$, $\vec {A}=(0,A_1+A_2,0)$. A vector potential $\vec {A}$ can be expressed as $\vec {A}=\vec {A}_1+\vec {A}_2$ with $\vec {\nabla }\times \vec {A}_1=\vec {B}$ and $\vec {\nabla }\times \vec {A}_2=0$

where $\vec {B}$ is applied magnetic field and $\vec {A}_2$ presenting AB flux field $\Phi _{AB}$ arise due to the uniform magnetic field. Where $\vec {A}_1$ and $\vec {A}_2$ written as [50, 51]

$$\begin{aligned}&\vec {A}_1=\frac{\vec {B} e^{-\alpha r}}{1-e^{-\alpha r}}\hat{\phi }\ {\hbox {and}} \ \vec {A}_2= \frac{\Phi _{AB}}{2\pi r} \hat{\phi }\ \mathrm{therefore } \ \nonumber \\&\vec {A}=A_1+A_2=\left( \frac{\vec {B} e^{-\alpha r}}{1-e^{-\alpha r}}+\frac{\Phi _{AB}}{2\pi r}\right) \hat{\phi } \end{aligned}$$

(10)

where $\Phi _{AB}=2\pi q^{-1}$. Inserting Eqs. (1) and (10) into Eq. (9), we obtain

$$\begin{aligned} \left[ \nabla ^2-\frac{q^2}{\hbar ^2c^2} \left( \frac{\vec {B} e^{-\alpha r}}{1-e^{-\alpha r}}+\frac{\Phi _{AB}}{2\pi r}\right) ^2-\frac{1}{\hbar ^2}\left( \frac{q}{c}\vec {p}.\vec {A}+ \frac{q}{c}\vec {A}.\vec {p}\right) \right] \psi (r,\phi )-\end{aligned}$$

$$\begin{aligned} \frac{2\mu }{\hbar ^2}\left( a+D_e+\frac{a_1 e^{-2\alpha r}}{r^2}-\frac{a_2 e^{-\alpha r}}{r}-\frac{A_1}{r}+\frac{A_2}{r^2} -E_{nm} \right) \psi (r,\phi )=0 \end{aligned}$$

(11)

Using Greene–Aldrich approximation [52]

$$\begin{aligned} \frac{1}{r^2}&\approx \frac{\alpha ^2}{(1-e^{- \alpha r})^2},\ \ \Rightarrow \frac{1}{r}\approx \frac{\alpha }{(1-e^{- \alpha r})}\nonumber \\&\quad \times \frac{d^2F_{nm}(r)}{dr^2}+\left[ \left( \mu _1(E_{nm}-a-D_e)-\frac{\mu _1\alpha ^2a_1e^{-2 \alpha r}}{(1-e^{- \alpha r})^2}\right. \right. \nonumber \\&\quad \left. \left. +\frac{\mu ^{'}\alpha \left( a_2e^{- \alpha r}+A_1\right) }{(1-e^{- \alpha r})}-\frac{\mu ^{'}\alpha ^2A_2}{(1-e^{- \alpha r})^2}\right) \right] F_{nm}(r)- q_1\left( \frac{2m\alpha \vec {B} e^{- \alpha r}+q_1\vec {B^2} e^{- 2\alpha r} }{(1-e^{- \alpha r})^2} \right) \nonumber \\&F_{nm}(r)-\left[ \frac{\alpha ^2\left( m^{'^{2}}-\frac{1}{4}\right) +2q_1\alpha \vec {B}\eta e^{- \alpha r} }{(1-e^{- \alpha r})^2}\right] F_{nm}(r)=0 \end{aligned}$$

(12)

$$\begin{aligned}&\quad -\frac{d^2F_{nm}(r)}{dr^2}+V_{eff}(r)F_{nm}(r)=\mu _1(E_{nm}-a-D_e)F_{nm}(r) \end{aligned}$$

(13)

where

$$\begin{aligned} V_{eff}=\frac{\beta _1e^{- 2\alpha r}+\beta _2e^{- \alpha r}+ \beta _3}{(1-e^{- \alpha r})^2} \end{aligned}$$

(14)

and $q_1=\frac{q}{\hbar c},\ \ \mu _1=\frac{2\mu }{\hbar ^2}, \ m^{'}=m+\eta ,\ \ \eta =\frac{ \Phi _{AB} q}{2\pi \hbar c}=\frac{ \Phi _{AB} }{\Phi _o}$, flux quanta $\Phi _o=\frac{hc}{q}$

$$\begin{aligned}&\beta _1= \mu _1(\alpha ^2 a_1+\alpha a_2)+\vec {B^2} q^{'2};\ \beta _2=\mu _1\alpha (A_1-a_2)+2\alpha q_1(m+\eta );\ \nonumber \\&\beta _3=\alpha ^2\left( m^{'^{2}}-\frac{1}{4}\right) +\mu _1\alpha (\alpha A_2-A_1)\end{aligned}$$

(15)

Equation (12) can be written as

$$\begin{aligned}&\frac{d^2F_{nm}(r)}{dr^2}\nonumber \\&\quad +\left[ -\left( E_{nm}^{\prime }+\beta _1\right) e^{- 2\alpha r} +\left( 2E_{nm}^{\prime }-\beta _2\right) e^{- \alpha r} -\left( E_{nm}^{\prime }+\beta _3\right) \right] F_{nm}(r)=0\nonumber \\\end{aligned}$$

(16)

where $E_{nm}^{\prime }= -\mu _1 (E_{nm}-a-D_e)$. Now using transformation $u=e^{-\alpha r}$, we get

$$\begin{aligned}&\frac{d^2F_{nm}(u)}{du^2}+\frac{(1-u)}{u(1-u)}\frac{dF_{nm}(u)}{du}+\frac{1}{u^2(1-u)^2}\nonumber \\&\quad \times \left[ -(\varepsilon _{nm}^{2}+\xi _1)u^2 +(2\varepsilon _{nm}^{2}-\xi _2)u -(\varepsilon _{nm}^{2}+\xi _3)\right] F_{nm}(u)=0 \end{aligned}$$

(17)

$$\begin{aligned}&\varepsilon _{nm}^{2}=\frac{E_{nm}^{'}}{\alpha ^2}=-\frac{2\mu (E_{nm}-a-D_e)}{\hbar ^2\alpha ^2}; \ \nonumber \\&\xi _1=\frac{\beta _1}{\alpha ^2}=\frac{2\mu }{\hbar ^2\alpha ^2}(\alpha ^2 a_1+\alpha a_2)+\frac{q^2}{\hbar ^2 c^2\alpha ^2}\vec {B^2} \end{aligned}$$

(18)

$$\begin{aligned}&\xi _2=\frac{\beta _2}{\alpha ^2}=\frac{2\mu }{\hbar ^{2} \alpha ^{2}}(\alpha \left( A_1-a_2\right) +\frac{2\mu }{\hbar ^{2}\alpha ^{2}} \left( 2\alpha \vec {B}\right) \left( m+\eta \right) ,\nonumber \\&\xi _3=\frac{\beta _3}{\alpha ^2}= m^{'2}-\frac{1}{4}+\frac{2\mu }{\hbar ^{2} \alpha ^{2}}(\alpha ^2 A_{2}-\alpha A_1) \end{aligned}$$

(19)

Using Eqs. (3) and (5), we obtain

$$\begin{aligned} \sqrt{\varepsilon _{nm}^2+\xi _3} =-\frac{\left( n^2+n+\frac{1}{2}+(2n+1)\sqrt{\xi _1+\xi _2+\xi _3+\frac{1}{4}} +\xi _2+2\xi _3\right) }{2\left( n+\frac{1}{2}+\sqrt{\xi _1+\xi _2+\xi _3+\frac{1}{4}}\right) }\end{aligned}$$

(20)

Using Eqs. (18) and (19), we obtain

$$\begin{aligned} E_{nm}=a+D_e+\frac{ \hbar ^2\alpha ^2}{2\mu }\xi _3 -\frac{ \hbar ^2\alpha ^2}{2\mu }\left[ \frac{\xi _3-\xi _1}{2(n+\Omega )}+\frac{(n+\Omega )}{2}\right] ^2 \end{aligned}$$

(21)

$$\begin{aligned} E_{nm}&=a+D_e+\frac{\hbar ^2\alpha ^2}{2\mu } \left( m^{'2}-\frac{1}{4}\right) +\alpha ^2 A_{2}-\alpha A_1\nonumber \\&\quad -\frac{ \hbar ^2\alpha ^2}{2\mu }\left[ \frac{\frac{2\mu }{\hbar ^2}\left( A_2-a_1-\frac{\alpha A_1-a_2}{\alpha } \right) -\frac{q^2}{\hbar ^2 c^2\alpha ^2}\vec {B^2}+m^{'2}-\frac{1}{4}}{2(n+\Omega )}+\frac{(n+\Omega )}{2}\right] ^2\nonumber \\\end{aligned}$$

(22)

where

$$\begin{aligned} \Omega&=\frac{1}{2}+\sqrt{\xi _1+\xi _2+\xi _3+\frac{1}{4}}\nonumber \\&=\frac{1}{2}+\sqrt{\frac{2\mu (a_1+A_2)}{\hbar ^2}+\frac{q^2}{\hbar ^2 c^2\alpha ^2}\vec {B^2}+\frac{q}{\hbar c\alpha }2 \vec {B}m^{'}+m^{'2}}\ \end{aligned}$$

(23)

setting $m= K+1/2=\ell +\frac{(D-2)}{2}$, Eq. (22) convert into D dimensional energy eigenvalues of MYKP without an external fields reads

$$\begin{aligned} E_{n\ell }&=a+D_e+\frac{\hbar ^2\alpha ^2}{2\mu }K(K+1)+\alpha ^2 A_{2}-\alpha A_1\nonumber \\&\quad - \frac{ \hbar ^2\alpha ^2}{2\mu }\left[ \frac{\frac{2\mu }{\hbar ^2\alpha ^2}\left( \alpha ^2A_2-\alpha A_1-\alpha a_2\right) +K(K+1)]}{2(n+\Omega _1)}+\frac{(n+\Omega _1)}{2}\right] ^2 \end{aligned}$$

(24)

where

$$\begin{aligned} K=\ell +\frac{(D-3)}{2} \ \ \mathrm{and} \ \ \Omega _1=\frac{1}{2}+\sqrt{\frac{2\mu (a_1+A_2)}{\hbar ^2}+\left( K+\frac{1}{2}\right) ^2}\ \end{aligned}$$

(25)

Above Eq. (24) is exactly the same energy eigenspectrum obtained by Parmar et al. [48] for MYKP. From Eq. (4), the unnormalized wave function corresponds to the energy eigenvalues Eq. (22),

$$\begin{aligned} F_{nm}(u)=u^{\sqrt{\varepsilon _{nm}^2+\gamma _3}} (1-u)^{\Omega } \ _2F_1(-n,n+2\sqrt{\varepsilon _{nm}^2+\gamma _3}+2\Omega ,2\Omega +1;u) \end{aligned}$$

(26)

In terms of the Jacobi polynomials wave function $F_{nm}(u)$ can be expressed as

$$\begin{aligned} F_{nm}(u)=N_{n\ell } \ u^\omega (1-u)^{\Omega } P_n^{2\omega ,2\Omega -1}((1-2u); \omega =\sqrt{\varepsilon ^2+\xi _3} \end{aligned}$$

(27)

and $P_n^{\left( 2\omega ,2\Omega -1\right) }(1-2u)$ is the Jacobi polynomial which is defined as [53]

$$\begin{aligned} P_n^{\left( 2\omega ,2\Omega -1\right) }(1-2u)=\frac{\Gamma (n+2\omega +1)}{n!\Gamma (2\omega +1)} \ _2F_1(-n,n+2\omega +2\Omega ,2\omega +1;u)\end{aligned}$$

where $N_{nm}$ is normalization constant. Equations (24) and (27) is the energy spectrum and eigenfunction for MYKP respectively. Equation (26) can be written in terms of hypergeometric function as

$$\begin{aligned} F_{nm}(u)=N_{n\ell } u^\omega (1-u)^{\Omega } \frac{\Gamma (n+2\omega +1)}{n!\Gamma (2\omega +1)} \ _2F_1(-n,n+2\omega +2\Omega ,2\omega +1;u)\nonumber \\ \end{aligned}$$

(28)

Now, the total wave function becomes

$$\begin{aligned}&\psi (r,\phi )=\frac{N_{nm}}{\sqrt{r}} e^{im\phi } e^{-\alpha \omega r} (1-e^{-\alpha r})^{\Omega }\nonumber \\&\quad \frac{\Gamma (n+2\omega +1)}{n!\Gamma (2\omega +1)} \ _2F_1(-n,n+2\omega +2\Omega ,2\omega +1;e^{-\alpha r}) \end{aligned}$$

(29)

4 Solution of the MYKP using series expansion method (SEM)

From Equation (13), we consider the radial Schrodinger equation [36, 44]

$$\begin{aligned} \frac{d^2 u_{nm}(r)}{dr^2}+\frac{2}{r} \frac{du_{nm}(r)}{dr}+\left[ -E_{nl}^{'}-V_{eff}(r)\right] u_{nm}(r)=0 \end{aligned}$$

(30)

where r is internuclear separation and E denotes the energy eigenvalues of the system. We put $F_{nm}(r)= u_{nm}(r)$ and

$$\begin{aligned} V_{eff}&=\frac{1}{r^2 \alpha ^2}\left[ \beta _{1}e^{-2 \alpha r} + \beta _{2}e^{\alpha r}+ \beta _{3}\right] \end{aligned}$$

(31)

$$\begin{aligned} V_{eff}&=\frac{\beta _{1}}{r^2 \alpha ^2}-\frac{2 \beta _{1}}{r \alpha }+2 \beta _{1}-\frac{4}{3}\beta _{1}\alpha r+\frac{\beta _{2}}{r^2\alpha ^2}-\frac{\beta _{2}}{r \alpha }+\frac{\beta _{2} }{2}\nonumber \\&\quad + \frac{2}{3}\beta _{1}\alpha ^{2}r^{2}-\frac{\beta _{2}\alpha r }{6} + \frac{\beta _{3}}{r^2\alpha ^2}+\frac{\beta _{2}}{24}\alpha ^{2}r^2 \end{aligned}$$

(32)

$$\begin{aligned} V_{eff}&=\left[ \frac{2}{3}\beta _{1}+\frac{\beta _{2}}{24}\right] \alpha ^{2}r^{2}+\left[ -\frac{4}{3}\beta _{1}-\frac{\beta _{2}}{6}\right] \alpha r \nonumber \\&\quad -\frac{[2\beta _{1}+\beta _{2}]}{r \alpha }+\frac{[\beta _{1}+\beta _{2}+\beta _{3}]}{\alpha ^2 r^2 } +\left[ 2\beta _{1}+\frac{\beta _{2}}{2}\right] \end{aligned}$$

(33)

$$\begin{aligned} V_{eff}&= C_{1}r^{2}+C_{2}r-\frac{C_{3}}{r}+\frac{C_{4}}{r^{2}}+C_{5} \end{aligned}$$

(34)

where,

$$\begin{aligned} C_{1}= & {} \left[ \frac{2}{3}\beta _{1}+\frac{\beta _{2}}{24} \right] \alpha ^{2} \end{aligned}$$

(35)

$$\begin{aligned} C_{2}= & {} \left[ -\frac{4}{3}\beta _{1}-\frac{\beta _{2}}{6}\right] \alpha \end{aligned}$$

(36)

$$\begin{aligned} C_{3}= & {} \frac{2\beta _{1}+\beta _{2}}{\alpha } \end{aligned}$$

(37)

$$\begin{aligned} C_{4}= & {} \frac{\beta _{1}+\beta _{2}+\beta _{3}}{\alpha ^2} = C(C+1) \end{aligned}$$

(38)

where

$$\begin{aligned}&C=-\frac{1}{2}+\sqrt{\frac{\beta _1^2+\beta _2^2+\beta _3^2}{\alpha ^2}+\frac{1}{4}} \end{aligned}$$

(39)

$$\begin{aligned}&C_{5}= 2\beta _{1}+\frac{\beta _{2}}{2} \end{aligned}$$

(40)

$$\begin{aligned}&\frac{d^2 u_{nm}(r)}{dr^2}+\frac{2}{r} \frac{du_{nm}(r)}{dr}\nonumber \\&\quad +\left[ \varepsilon - C_{1}r^{2}-C_{2}r+\frac{C_{3}}{r}-\frac{C(C+1)}{r^{2}} \right] u_{nm}(r)=0 \end{aligned}$$

(41)

where $\varepsilon =-(E_{nl}^{'}+C_5)$ Now make an anzats wave function [36, 54]

$$\begin{aligned} u_{nm}(r)=e^{-\alpha r^{2}-\beta r} G(r) \end{aligned}$$

(42)

where $\alpha$ and $\beta$ are positive constants. Using this wave function on Eq.(41), it becomes

$$\begin{aligned}&G^{''}(r)+\left[ \left( -4\alpha -2\beta +\frac{2}{r}\right) \right] G^{'}(r)\nonumber \\&\quad +\left[ \left( 4\alpha ^{2} r-C_{1}\right) r^2+\left( 4\alpha \beta -C_{2}\right) r\right. \nonumber \\&\quad \left. +\frac{\left( C_{3}-2\beta \right) }{r}-\frac{C(C+1)}{r^2}+\left( \varepsilon -6\alpha +\beta ^{2}\right) \right] G(r)=0 \end{aligned}$$

(43)

Due to singularities in Eq. (43), the factorization wave function of the form [36, 54, 55]

$$\begin{aligned} G(r)=\sum _{n=0}^{\infty }b_{n}r^{2n+C} \end{aligned}$$

(44)

is considered suitable to solve Eq. (43). Taking the first and second derivatives of Eq. (44) and substitute alongside with Eq. (44) into our Eq. (43), we obtain

$$\begin{aligned}&\sum _{n=0}^{\infty }b_{n}\left[ (2n+C)(2n+C-1)+2(2n+C)-C(C+1)\right] r^{2n+C-2}\nonumber \\&\quad + \left[ -2\beta \left( 2n+C+1\right) +C_{3}\right] r^{2n+C-1}+\left[ -4\alpha \left( 2n+C\right) +\varepsilon +\beta ^{2}-6\alpha \right] r^{2n+C}\nonumber \\&\quad + \left( 4\alpha \beta -C_{2}\right) r^{2n+C+1}+\left( 4\alpha ^{2}-C_{1}\right) r^{2n+C+2} = 0 \end{aligned}$$

(45)

Given that r is a non-zero function, each of the terms in equation (45) is independently equal to zero. With this in mind, we may get the following relationships for each of the terms.

$$\begin{aligned}&\left( 2n+1\right) \left( 2n+C+1\right) -C-C^{2}=0 \end{aligned}$$

(46)

$$\begin{aligned}&\varepsilon =2\alpha \left( 2n+2C+3\right) -\beta ^{2} \end{aligned}$$

(47)

$$\begin{aligned}&C_{3}=2\beta \left( 2n+C+1\right) \end{aligned}$$

(48)

$$\begin{aligned}&\beta = \frac{C_{2}}{4\alpha } \end{aligned}$$

(49)

$$\begin{aligned}&C_{1}=4\alpha ^{2} \end{aligned}$$

(50)

$$\begin{aligned}&\alpha =\frac{\sqrt{C_{1}}}{2} \end{aligned}$$

(51)

Equations (47), (48), and (51) are used to obtain the energy eigenvalue expression.

$$\begin{aligned}&-(E_{nl}^{'}+C_5)=\sqrt{C_1}(2n+2C+3)-\frac{C_3^2}{4}(2n+C+1) \end{aligned}$$

(52)

$$\begin{aligned}&\mu _1(E_{nl}-a-D_e)=\sqrt{\left[ \frac{2}{3}\mu _1(\alpha ^2 a_1+\alpha a_2)+\vec {B^2} q^{'2}+\frac{\mu _1\alpha (A_1-a_2)+2\alpha q_1(m+\eta )}{24} \right] \alpha ^{2}}\nonumber \\&\quad \left( 4n+2+2\sqrt{\frac{1}{4}+\frac{\mu _1(\alpha ^2 a_1+\alpha a_2)+\mu _1\alpha (A_1-a_2)+2\alpha q_1(m+\eta )+\alpha ^2\left( m^{'^{2}}-\frac{1}{4}\right) +\mu _1\alpha (\alpha A_2-A_1)}{\alpha ^2}}\right) -\nonumber \\&\quad \frac{\left( 2\mu _1(\alpha ^2 a_1+\alpha a_2)+\beta _{2}\right) ^2}{4\alpha ^2}\nonumber \\&\quad \left( 4n+1+2\sqrt{\frac{1}{4}+\frac{\mu _1(\alpha ^2 a_1+\alpha a_2)+\mu _1\alpha (A_1-a_2)+2\alpha q_1(m+\eta )+\alpha ^2\left( m^{'^{2}}-\frac{1}{4}\right) +\mu _1\alpha (\alpha A_2-A_1)}{\alpha ^2}}\right) ^{-2}+\nonumber \\&\quad 2\mu _1(\alpha ^2 a_1+\alpha a_2)+\frac{\mu _1\alpha (A_1-a_2)+2\alpha q_1(m+\eta )}{2} \end{aligned}$$

(53)

$$\begin{aligned}&E_{nl}=a+D_e+\frac{\hbar ^2}{2\mu }\sqrt{\left[ \frac{2}{3}\beta _{1}+\frac{\beta _{2}}{24} \right] \alpha ^{2}}\left( 4n+2+2\Omega \right) -\nonumber \\&\quad \frac{\hbar ^2}{2\mu }\frac{\left( 2\beta _{1}+\beta _{2}\right) ^2}{4\alpha ^2} \left( 4n+1+2\Omega \right) ^{-2}+\frac{\hbar ^2}{2\mu }\left( 2\beta _1+\frac{\beta _2}{2}\right) \end{aligned}$$

(54)

The mass spectra of heavy quarkonium systems such as charmonium and bottomonium, which have the same flavour quark and antiqurak, are also obtained from the energy eigenvalue. The following equation is used to calculate the mass spectra.

$$\begin{aligned} M=m_{1}+m_{2}+E_{nl} \end{aligned}$$

(55)

but,

$$\begin{aligned} m_{1}=m_{2}=m_{b} \end{aligned}$$

(56)

Resulting in the expression

$$\begin{aligned} M=2m +E_{nl} \end{aligned}$$

(57)

where $m_{b}$ is the mass of the particle under investigation and $E_{nl}$ is the derived energy eigenvalues.

Substituting Eqs. (54) into (57) we obtain

$$\begin{aligned} M&=2m + a+D_e+\frac{\hbar ^2}{2\mu }\sqrt{\left[ \frac{2}{3}\beta _{1}+\frac{\beta _{2}}{24} \right] \alpha ^{2}}\left( 4n+2+2\Omega \right) \nonumber \\&\quad -\frac{\hbar ^2}{2\mu }\frac{\left( 2\beta _{1}+\beta _{2}\right) ^2}{4\alpha ^2} \left( 4n+1+2\Omega \right) ^{-2}+\frac{\hbar ^2}{2\mu }\left( 2\beta _1+\frac{\beta _2}{2}\right) \end{aligned}$$

(58)

4.1 Special cases with an external fields

4.1.1 Generalized Kratzer potential (GKP)

Setting $a_1=a_2=0$, Eq. (1) reduce into generalized Kratzer potential as [35]

$$\begin{aligned} V^{GKP}(r)=a+D_e -\left( \frac{A_1}{r}-\frac{A_2}{r^2}\right) \end{aligned}$$

(59)

Energy eigenvalues corresponds to Eq. (59) with an external fields

$$\begin{aligned} E_{nm}^{GKP}&=a+D_e+\frac{\hbar ^2\alpha ^2}{2\mu } \left( m^{'2}-\frac{1}{4}\right) +\alpha ^2 A_{2}-\alpha A_1- \frac{ \hbar ^2\alpha ^2}{2\mu }\nonumber \\&\quad \times \left[ \frac{\frac{2\mu }{\hbar ^2\alpha ^2}\left( \alpha ^2A_2-\alpha A_1\right) -\frac{q^2}{\hbar ^2 c^2\alpha ^2}\vec {B^2}+m^{'2}-\frac{1}{4}}{2(n+ \Omega ^{GKP})}+\frac{(n+ \Omega ^{GKP})}{2}\right] ^2\nonumber \\ \end{aligned}$$

(60)

where

$$\begin{aligned} \Omega ^{GKP}=\frac{1}{2}+\sqrt{\frac{2\mu A_2}{\hbar ^2}+\frac{q^2}{\hbar ^2 c^2\alpha ^2}\vec {B^2}+\frac{q}{\hbar c\alpha }2 \vec {B}m^{'}+m^{'2}}\ =\frac{1}{2} \end{aligned}$$

(61)

4.1.2 Modified Kratzer potential

Setting $a=a_1=a_2=0$, Eq. (1) convert into modified Kratzer potential as [35]

$$\begin{aligned} V^{MKP}(r)=D_e \left( \frac{r-r_e}{r}\right) ^2 \end{aligned}$$

(62)

Energy eigenvalues corresponds to Eqs. (62) from (22)

$$\begin{aligned} E_{nm}^{MKP}&=D_e+\frac{\hbar ^2\alpha ^2}{2\mu } \left( m^{'2}-\frac{1}{4}\right) +\alpha ^2 D_e r_e^2-2\alpha D_e r_e-\frac{ \hbar ^2\alpha ^2}{2\mu } \nonumber \\&\quad \times \left[ \frac{\frac{2\mu D_e}{\hbar ^2\alpha }\left( \alpha r_e^2-2 r_e\right) -\frac{q^2}{\hbar ^2 c^2\alpha ^2}\vec {B^2}+m^{'2}-\frac{1}{4}}{2(n+ \Omega ^{MKP})}+\frac{(n+ \Omega ^{MKP})}{2}\right] ^2\nonumber \\ \end{aligned}$$

(63)

where

$$\begin{aligned} \Omega ^{MKP}=\frac{1}{2}+\sqrt{\frac{\mu D_e r_e^2}{\hbar ^2}+\frac{q^2}{\hbar ^2 c^2\alpha ^2}\vec {B^2}+\frac{q}{\hbar c\alpha }2 \vec {B}m^{'}+m^{'2}}\ \end{aligned}$$

(64)

4.1.3 Kratzer potential

Setting $a_1=a_2=0$ and $a=-D_e$, Eq. (1) convert into Kratzer potential as [35]

$$\begin{aligned} V^{KP}(r)=-2D_e \left( \frac{r_e}{r}-\frac{r_e^2}{2r^2}\right) \end{aligned}$$

(65)

Energy eigenvalues corresponds to Eqs. (65) from (22)

$$\begin{aligned} E_{nm}^{KP}&=\frac{\hbar ^2\alpha ^2}{2\mu } \left( m^{'2}-\frac{1}{4}\right) +\alpha ^2 D_e r_e^2-2\alpha D_e r_e -\frac{ \hbar ^2\alpha ^2}{2\mu }\nonumber \\&\quad \times \left[ \frac{\frac{2\mu }{\hbar ^2\alpha ^2}\left( \alpha ^2D_e r_e^2-2\alpha D_e r_e\right) -\frac{q^2}{\hbar ^2 c^2\alpha ^2}\vec {B^2}+m^{'2}-\frac{1}{4}}{2(n+\Omega ^{KP})}+\frac{(n+\Omega ^{KP})}{2}\right] ^2 \end{aligned}$$

(66)

where

$$\begin{aligned} \Omega ^{KP}=\frac{1}{2}+\sqrt{\frac{\mu D_e r_e^2}{\hbar ^2}+\frac{q^2}{\hbar ^2 c^2\alpha ^2}\vec {B^2}+\frac{q}{\hbar c\alpha }2 \vec {B}m^{'}+m^{'2}}\ \end{aligned}$$

(67)

4.1.4 Hellmann potential

For $a=-D_e$, $a_2=-a_2$ and $a_1=A_2=0$, Eq. (1) covert into the Hellmann potential as [56,57,58,59,60,61]

$$\begin{aligned} V^{HP}(r)=-\frac{A_1}{r}+\frac{a_2 e^{-\alpha r}}{r} \end{aligned}$$

(68)

Energy eigenvalues corresponds to Eq. (22) with an external fields

$$\begin{aligned}&E_{nm}^{HP}=\frac{\hbar ^2\alpha ^2}{2\mu } \left( m^{'2}-\frac{1}{4}\right) -\alpha A_1 -\frac{ \hbar ^2\alpha ^2}{2\mu }\nonumber \\&\quad \left[ \frac{\frac{2\mu }{\hbar ^2\alpha }\left( a_2- A_1\right) -\frac{q^2}{\hbar ^2 c^2\alpha ^2}\vec {B^2} +\left( m^{'2}-\frac{1}{4}\right) }{2(n+\Omega ^{HP})}+\frac{(n+\Omega ^{HP})}{2}\right] ^2 \end{aligned}$$

(69)

where

$$\begin{aligned} \Omega ^{HP}=\frac{1}{2}+\sqrt{\frac{q^2}{\hbar ^2 c^2\alpha ^2}\vec {B^2}+\frac{q}{\hbar c\alpha }2 \vec {B}m^{'}+m^{'2}} \end{aligned}$$

(70)

4.2 The thermodynamic properties of the MYKP with an external fields

From the energy eigenvalues of the MYKP under influence of an external fields, we obtain the partition function $Z(\vec {B},\Phi _{AB},\beta )$ under the influence of an external fields. From partition function of the given system, we calculate mean energy $U(\vec {B},\Phi _{AB},\beta )$, mean free energy $F(\vec {B},\Phi _{AB},\beta )$, entropy $S(\vec {B},\Phi _{AB},\beta )$, specific heat capacity $C_s(\vec {B},\Phi _{AB},\beta )$, magnetization at finite temperature $(\vec {B},\Phi _{AB},\beta )$ and magnetic susceptibility $\chi _m(\vec {B},\Phi _{AB},\beta )$ at finite temperature [29] in this subsection.

Energy eigenvalues Eq. (22) reads

$$\begin{aligned} E_{nm}=L_1-\frac{\hbar ^2 \alpha ^2}{2\mu } \left[ \frac{L_2}{2(n+\Omega )}-\frac{(n+\Omega )}{2}\right] ^2 \end{aligned}$$

(71)

$$\begin{aligned} L_1&=a+D_e+\frac{\hbar ^2\alpha ^2}{2\mu } \left( m^{'2}-\frac{1}{4}\right) +\alpha ^2 A_{2}-\alpha A_1\nonumber \\ L_2&=\frac{2\mu }{\hbar ^2}\left( A_2-a_1-\frac{\alpha A_1-a_2}{\alpha } \right) -\frac{q^2}{\hbar ^2 c^2\alpha ^2}\vec {B^2}+m^{'2}-\frac{1}{4} \end{aligned}$$

(72)

Exact partition function at temperature T written as [62,63,64]

$$\begin{aligned} Z(\vec {B},\Phi _{AB},\beta )=\sum _{\upsilon =0}^{\upsilon _{max}}e^{-\beta E_{n m}} \end{aligned}$$

(73)

where $\beta =\frac{1}{kT}$, k- constant of Boltzmann and $E_{n m}$ is the energy of the $n^{\mathrm{th}}$ state. From Eqs. (71) and (73) becomes

$$\begin{aligned} Z(\vec {B},\Phi _{AB},\beta )=\sum _{n=0}^{v_m}e^{-\beta \left( L_1-\frac{\hbar ^2 \alpha ^2}{2\mu } \left[ \frac{L_2}{2(n+\Omega )}-\frac{(n+\Omega )}{2}\right] ^2\right) } \end{aligned}$$

(74)

where

$$\begin{aligned} v_m=-\Omega \pm \sqrt{L_2} \end{aligned}$$

(75)

In the classical limit, replacing the sum of Eq. (74) by an integral as [65]

$$\begin{aligned} Z(\vec {B},\Phi _{AB},\beta )=\int \limits _0^{v_m} e^{\beta \left( P_1\rho ^2+\frac{P_2}{\rho ^2}+P_3\right) } d\rho ,\quad \ \rho =n+\Omega \end{aligned}$$

(76)

where

$$\begin{aligned} P_1=\frac{\hbar ^2 \alpha ^2}{8\mu };\quad Q_2=\frac{\hbar ^2 \alpha ^2}{8\mu }L_2^2;\quad P_3=-\left( \frac{\hbar ^2 \alpha ^2}{4\mu }L_2+L_1\right) \end{aligned}$$

(77)

Employing a Maple software, we obtain $Z(\vec {B},\Phi _{AB},\beta )$ as [66]

$$\begin{aligned} Z(\vec {B},\Phi _{AB},\beta )&=\frac{1}{2} e^{\beta \left( P_1\rho ^2+P_3\right) } \sqrt{P_2\beta }\nonumber \\&\quad \times \left( \frac{2v_m e^{\frac{P_2\beta }{v_m^2}}}{ \sqrt{P_2\beta }}-\frac{2 \sqrt{\pi P_2\beta }\ {\hbox {erf}}i\left( \frac{\sqrt{P_2\beta }}{v_m}\right) }{\sqrt{P_2\beta }}-2\sqrt{\pi }\right) \end{aligned}$$

(78)

where imaginary error function ${\hbox {erf}}i$ defined as [67]

$$\begin{aligned} {\hbox {erf}}i(x)=-i \ {{\hbox {erf}}}(ix)=\frac{2}{\sqrt{\pi }}\int \limits _0^xe^{t^2}dt. \end{aligned}$$

(79)

Below mentioned thermodynamic and magnetic properties under influence of an external fields can be investigate using partition function [66] ,

• Mean energy

  $$\begin{aligned} U(\vec {B},\Phi _{AB},\beta )=-\frac{\partial }{\partial (\beta )} \mathrm{ln} Z(\vec {B},\Phi _{AB},\beta ) \end{aligned}$$

  (80)

• Mean free energy

  $$\begin{aligned} F(\vec {B},\Phi _{AB},\beta )=-k T\ \mathrm{ln} Z(\vec {B},\Phi _{AB},\beta ) \end{aligned}$$

  (81)

• Entropy

  $$\begin{aligned} S(\vec {B},\Phi _{AB},\beta )&=k \mathrm{ln} Z(\vec {B},\Phi _{AB},\beta ^{'})+k T\frac{\partial }{\partial T}\mathrm{ln} Z(\vec {B},\Phi _{AB},\beta )\nonumber \\&=k \mathrm{ln} Z(\vec {B},\Phi _{AB},\beta )-k \beta \frac{\partial }{\partial \beta }\mathrm{ln} Z(\vec {B},\Phi _{AB},\beta ) \end{aligned}$$

  (82)

• Specific heat capacity

  $$\begin{aligned} C_s (\vec {B},\Phi _{AB},\beta )&=\frac{\partial U(\vec {B},\Phi _{AB},\beta )}{\partial T}=-k \beta ^2 \frac{\partial U(\vec {B},\Phi _{AB},\beta ^{'})}{\partial \beta }\nonumber \\&=k \beta ^2 \frac{\partial ^2}{\partial \beta ^2}\mathrm{ln} Z(\beta ) \end{aligned}$$

  (83)

• Magnetization at finite temperature is written as [29, 47]

  $$\begin{aligned} M(\vec {B},\Phi _{AB},\beta )=\frac{1}{\beta Z(\vec {B},\Phi _{AB},\beta )}\frac{\partial Z(\vec {B},\Phi _{AB},\beta )}{\partial \vec {B}}\ \end{aligned}$$

  (84)

• Magnetic susceptibility at finite temperature is written as [29, 47]

  $$\begin{aligned} \chi _m(\vec {B},\Phi _{AB},\beta )=\frac{\partial M(\vec {B},\Phi _{AB},\beta )}{\partial \vec {B}}\ \end{aligned}$$

  (85)

Table 1 Spectroscopic parameters for few selected diatomic molecules

Table 2 Energy eigenvalues spectrum of the MYKP for the different n, m quantum numbers with constant values of the parameters $a=c=q=\hbar =\mu =1, a_1=a_2=-1, A_1=2, A_2=4, D_e=1.5, \alpha =0.1$

Table 3 Energy eigenvalues spectrum of the Kratzer potential for $N_2$ molecule with different n, m quantum numbers for $q=1$

Table 4 Energy eigenvalues spectrum of the Kratzer potential for $N_2$ molecule with different n, m quantum numbers for $q=1$ and comparison with numerical results in NU method and Series expansion method

Table 5 Energy eigenvalues spectrum of the Kratzer potential for CH molecule with different n, m quantum numbers for $q=1$

Table 6 Energy eigenvalues spectrum of the Kratzer potential for CH molecule with different n, m quantum numbers for $q=1$ and comparison with numerical results in NU method and Series expansion method

Table 7 Energy eigenvalues spectrum of the Hellmann potential with different n, m quantum numbers and various values of the magnetic field B for $\Phi _{AB}=0$ and parameters $q=\hbar =h=c=\mu =1$ with screening parameter $\alpha =0.01$ and $A_1=0.5, a=-0.5$

Table 8 Energy eigenvalues spectrum of the modified Kratzer potential for ScH molecule with different n, m quantum numbers and magnetic field B for $\Phi _{AB}=0$ and $q=1$

Table 9 Energy eigenvalues spectrum of the modified KP for $H_2$ molecule with different n, m quantum numbers and magnetic field $\Phi _{AB}=0$ for various values of the $\vec {B}$ and $q=1$

Table 10 Energy eigenvalues spectrum of the GKP for ScH molecule with different n, m quantum numbers and magnetic field $B=0$ for various values of the $\Phi _{AB}$,$q=1$ with $a=- 0.5$

Table 11 Energy eigenvalues spectrum of the GKP for $H_2$ molecule with different quantum numbers and magnetic field $B=0$ for various values of the $\Phi _{AB}$,$q=1$ with $a=-0.5$

5 Results and discussion

In Table 2, we calculates energy spectrum of the MYKP under effect of the magnetic field and AB flux field for the various values of the n and m quantum numbers with constant values of the other parameters. We tabulate numerical results for $\vec {B}=0,2,4,6,8$ and also for $\Phi _{AB}=2,4,6,8$. At values of $\vec {B}$ and $\Phi _{AB}$ equal to zero, degeneracy is present. Energy eigenvalues decreases with increases $\vec {B}$ and magnetic quantum number m whereas it is increase with increase $\Phi _{AB}$. Tables 3 and 4 show the energy spectrum for $N_2$ molecules for Kratzer potential, with different quantum numbers n, m for comparison with numerical results in NU and series expansion methods. Tables 5 and 6 show the similar methodology for CH molecules. Numerical results are compared with numerical results presented in Ref. [35]. In Table 7, we presented Numerical results of energy eigenspectrum for Hellmann potential under effect of an external fields. We tabulates numerical results for ScH and $H_2$ molecules for modified Kratzer potential in Tables 8 and 9. respectively. In Tables 10 and 11. we presents numerical results of the ScH and $H_2$ molecules for generalized Kratzer potential. Tabulated results are compared with numerical results presented in Ref. [47]. To calculates, energy eigenvalues of the various molecules, we used spectroscopic parameters given in Table 1.

Fig. 1

The effective MYKP $(V_{eff}(r))$ vs. a function of the interatomic distance r for the parameters as $a_2=A_1=2, A_2=4,\hbar =\mu =q=c=a=a_1=1, B=2T,\Phi _{AB}=2$ and magnetic quantum number $m=0$ with various values of screening parameter $\alpha$ as $\alpha _1=0.001, \alpha _2=0.003,\alpha _3=0.005, \alpha _4=0.05 \alpha _4=0.1$

Fig. 2

The effective MYKP $(V_{eff}(r))$ vs. a function of the interatomic distance r for the parameters as $a_2=A_1=2, A_2=4,\hbar =\mu =q=c=a=a_1=1, B=2T,\Phi _{AB}=2$ and magnetic quantum number $m=1$ with various values of screening parameter $\alpha$ as $\alpha _1=0.001, \alpha _2=0.003,\alpha _3=0.005, \alpha _4=0.05 \alpha _4=0.1$

Fig. 3

The effective MYKP $(V_{eff}(r))$ vs. a function of the interatomic distance r for the parameters as $a_2=A_1=2, A_2=4,\hbar =\mu =q=c=a=a_1=1, B=2T,\Phi _{AB}=2$ and magnetic quantum number $m=-1$ with various values of screening parameter $\alpha$ as $\alpha _1=0.001, \alpha _2=0.003,\alpha _3=0.005, \alpha _4=0.05 \alpha _4=0.1$

Fig. 4

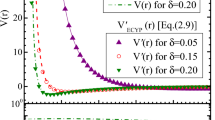
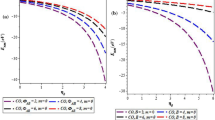
The effective MYKP$(V_{eff}(r))$ against a function of magnetic field B for the parameters as $a_2=A_1=1, A_2=2,\hbar =\mu =q=c=1, r=1,\Phi _{AB}=2$ and magnetic quantum number $m=0$ with various values of screening parameter $\alpha$ as $\alpha _1=0.001, \alpha _2=0.003,\alpha _3=0.005, \alpha _4=0.008$

Fig. 5

The effective MYKP$(V_{eff}(r))$ against a function of magnetic field B for the parameters as $a_2=A_1=1, A_2=2,\hbar =\mu =q=c=1, r=1,\Phi _{AB}=2$ and magnetic quantum number $m=1$ with various values of screening parameter $\alpha$ as $\alpha _1=0.001, \alpha _2=0.003,\alpha _3=0.005, \alpha _4=0.008$

Plots of the effective potential against interatomic distance r for various values of screening parameter $\alpha$ for $m=0$, $m=1$ and $m=-1$ presents in Figs. 1, 2 and 3 respectively. Effective potential decreases with increases r. Figures 4, 5 and 6 show the variation in effective potential with respect to magnetic field $\vec {B}$ for different values of $\alpha$ corresponds to $m=0$, $m=1$ and $m=-1$ presents respectively. Plots show effective potential increases with increases $\vec {B}$. Plots of the effective potential against $\Phi _{AB}$ for various values of screening parameter $\alpha$ for $m=0$, $m=1$ and $m=-1$ presents in Figs. 7, 8 and 9 respectively. Effective potential increases with increases $\Phi _{AB}$.

Fig. 6

The effective MYKP$(V_{eff}(r))$ against a function of magnetic field B for the parameters as $a_2=A_1=1, A_2=2,\hbar =\mu =q=c=1, r=1,\Phi _{AB}=2$ and magnetic quantum number $m=-1$ with various values of screening parameter $\alpha$ as $\alpha _1=0.001, \alpha _2=0.003,\alpha _3=0.005, \alpha _4=0.008$

Fig. 7

The effective MYKP $(V_{eff}(r))$ against a function of AB flux field $\Phi _{AB}$ for the parameters as $a_2=A_1=1, A_2=2,\hbar =\mu =q=c=1, r=1,B=2$ and magnetic quantum number $m=0$ with various values of screening parameter $\alpha$ as $\alpha _1=0.001, \alpha _2=0.003,\alpha _3=0.005, \alpha _4=0.008$

Fig. 8

The effective MYKP $(V_{eff}(r))$ against a function of AB flux field $\Phi _{AB}$ for the parameters as $a_2=A_1=1, A_2=2,\hbar =\mu =q=c=1, r=1,B=2$ and magnetic quantum number $m=1$ with various values of screening parameter $\alpha$ as $\alpha _1=0.001, \alpha _2=0.003,\alpha _3=0.005, \alpha _4=0.008$

Fig. 9

The effective MYKP $(V_{eff}(r))$ against a function of AB flux field $\Phi _{AB}$ for the parameters as $a_2=A_1=1, A_2=2,\hbar =\mu =q=c=1, r=1,B=2$ and magnetic quantum number $m=-1$ with various values of screening parameter $\alpha$ as $\alpha _1=0.001, \alpha _2=0.003,\alpha _3=0.005, \alpha _4=0.008$

Fig. 10

The energy spectrum $E_{n\ell }$ for MYKP against a function of the screening parameter ${\alpha }$ for the parameters as $a_2=A_1=2, A_2=4,\hbar =\mu =q=c=1, r=1 , B=5$ and quantum number $n=0$ with various magnetic quantum number m as $m_0=-2, m_2=-1 , m_3=0, m_4=1, m_5=2$

Fig. 11

The energy spectrum $E_{n\ell }$ for MYKP against a function of the screening parameter ${\alpha }$ for the parameters as $a_2=A_1=2, A_2=4,\hbar =\mu =q=c=1, r=1 , B=5$ and quantum number $n=1$ with various magnetic quantum number m as $m_0=-2, m_2=-1 , m_3=0, m_4=1, m_5=2$

Fig. 12

The energy spectrum $E_{n\ell }$ for MYKP against a function of the screening parameter ${\alpha }$ for the parameters as $a_2=A_1=2, A_2=4,\hbar =\mu =q=c=1, r=1 , B=5$ and quantum number $n=2$ with various magnetic quantum number m as $m_0=-2, m_2=-1 , m_3=0, m_4=1, m_5=2$

Fig. 13

The energy eigenvalues $E_{n\ell }$ for MYKP against a function of $\phi _{AB}$ for the parameters as $a_2=A_1=2, A_2=4,\hbar =\mu =q=c=1, \alpha =0.01, B=5$ and quantum number $n=0$ with various values of the magnetic quantum number m as $m_0=-2, m_2=-1 , m_3=0, m_4=1, m_5=2$

Fig. 14

The energy eigenvalues $E_{n\ell }$ for MYKP against a function of $\phi _{AB}$ for the parameters as $a_2=A_1=2, A_2=4,\hbar =\mu =q=c=1, \alpha =0.01 , B=5$ and quantum number $n=1$ with various values of the magnetic quantum number m as $m_0=-2, m_2=-1 , m_3=0, m_4=1, m_5=2$

Fig. 15

The energy eigenvalues $E_{n\ell }$ for MYKP against a function of $\phi _{AB}$ for the parameters as $a_2=A_1=2, A_2=4,\hbar =\mu =q=c=1, \alpha =0.01, B=5$ and quantum number $n=2$ with various values of the magnetic quantum number m as $m_0=-2, m_2=-1 , m_3=0, m_4=1, m_5=2$

Fig. 16

The energy spectrum $E_{n\ell }$ for MYKP with respect to a function of B for the parameters as $a_2=A_1=2, A_2=4,\hbar =\mu =q=c=1, \alpha =2 , \Phi =10$ and quantum number $n=0$ with various values of the magnetic quantum number m as $m_0=-2, m_2=-1 , m_3=0, m_4=1, m_5=2$

Fig. 17

The energy spectrum $E_{n\ell }$ for MYKP with respect to a function of B for the parameters as $a_2=A_1=2, A_2=4,\hbar =\mu =q=c=1, \alpha =2 , \Phi =10$ and quantum number $n=1$ with various values of the magnetic quantum number m as $m_0=-2, m_2=-1 , m_3=0, m_4=1, m_5=2$

Fig. 18

The energy spectrum $E_{n\ell }$ for MYKP with respect to a function of B for the parameters as $a_2=A_1=2, A_2=4,\hbar =\mu =q=c=1, \alpha =2 , \Phi =10$ and quantum number $n=2$ with various values of the magnetic quantum number m as $m_0=-2, m_2=-1 , m_3=0, m_4=1, m_5=2$

Fig. 19

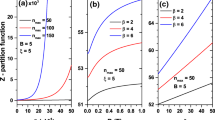
The partition function (Z) of the MYKP vs. a function of the temperature parameter $\beta$ for the parameters as $a= \hbar =\mu =q=c=m=n=1, a=5, a_1=1, a_2=2, A_1=1.5, A_2=2.25, D_e=3, \vec {B}=5T, \Phi _{AB}=20$ and $\alpha =0.9$ with various vibrational quantum number $\upsilon _{max}$ as $\upsilon _{m1}=15, \upsilon _{m2}=20, \upsilon _{m3}=25, \upsilon _{m4}=30, \upsilon _{m5}=35$ in two dimensions

Fig. 20

The partition function (Z) of the MYKP vs. a function of the magnetic field $\vec {B}$ (in Tesla) for the parameters as $a= \hbar =\mu =q=c=m=n=1, a=5, a_1=1, a_2=2, A_1=1.5, A_2=2.25, D_e=3, \upsilon _{max}=20, \Phi _{AB}=20$ and $\alpha =0.9$ with various temperature parameter $\beta$ as $\beta _1=0.1, \beta _2=0.2, \beta _3=0.3, \beta _4=0.4, \beta _5=0.5$ in two dimensions

Fig. 21

The partition function (Z) of the MYKP vs. a function of the Aharanov-Bohm flux field $\Phi _{AB}$ for the parameters as $a= \hbar =\mu =q=c=m=n=1, a=5, a_1=1, a_2=2, A_1=1.5, A_2=2.25, D_e=3, \upsilon _{max}=20, \vec {B}=5T$ and $\alpha =0.9$ with various temperature parameter $\beta$ as $\beta _1=0.1, \beta _2=0.2, \beta _3=0.3, \beta _4=0.4, \beta _5=0.5$

Fig. 22

The internal energy U of the MYKP against a function of the temperature parameter $\beta$ for the parameters as $a= \hbar =\mu =q=c=m=n=1, a=5, a_1=1, a_2=2, A_1=1.5, A_2=2.25, D_e=3, \vec {B}=5T, \Phi _{AB}=20$ and $\alpha =0.9$ with various vibrational quantum number $\upsilon _{max}$ as $\upsilon _{m1}=15, \upsilon _{m2}=20, \upsilon _{m3}=25, \upsilon _{m4}=30, \upsilon _{m5}=35$ in two dimensions

Fig. 23

The internal energy U of the MYKP against a function of the magnetic field $\vec {B}$ for the parameters as $\hbar =\mu =q=c=m=n=1, a=5, a_1=1, a_2=2, A_1=1.5, A_2=2.25, D_e=3, \upsilon _{max}=10, \Phi _{AB}=20$ and $\alpha =0.9$ with various temperature parameter $\beta$ as $\beta _1=0.08, \beta _2=0.09, \beta _3=0.8, \beta _4=0.9$ in two dimensions

Fig. 24

The internal energy U of the MYKP against a function of the Aharanov-Bohm flux field $\Phi _{AB}$ for the parameters as $\hbar =\mu =q=c=m=n=1, a=5, a_1=1, a_2=2, A_1=1.5, A_2=2.25, D_e=3, \upsilon _{max}=10, \vec {B}=10T$ and $\alpha =0.9$ with various temperature parameter $\beta$ as $\beta _1=0.2, \beta _2=0.4, \beta _3=0.6, \beta _4=0.8$ in two dimensions

Fig. 25

The free energy F of the MYKP vs. a function of the temperature parameter $\beta$ for the parameters as $\hbar =\mu =q=c=m=n=1, a=5, a_1=1, a_2=2, A_1=1.5, A_2=2.25, D_e=3, \vec {B}=10T, \Phi _{AB}=10$ and $\alpha =0.9$ with various vibrational quantum number $\upsilon _{max}$ as $\upsilon _{m1}=5, \upsilon _{m2}=10, \upsilon _{m3}=15, \upsilon _{m4}=20$ in two dimensions

Fig. 26

The free energy F of the MYKP vs.a function of the magnetic field $\vec {B}$ for the parameters as $\hbar =\mu =q=c=m=n=1, a=5, a_1=1, a_2=2, A_1=1.5, A_2=2.25, D_e=3, \upsilon _{max}=10, \Phi _{AB}=10$ and $\alpha =0.9$ with various temperature parameter $\beta$ as $\beta _1=0.2, \beta _2=0.4, \beta _3=0.6, \beta _4=0.8$ in two dimensions

Fig. 27

The free energy F of the MYKP vs. a function of the Aharanov-Bohm flux field $\Phi _{AB}$ for the parameters as $\hbar =\mu =q=c=m=n=1, a=5, a_1=1, a_2=2, A_1=1.5, A_2=2.25, D_e=3, \upsilon _{max}=10, \vec {B}=10T$ and $\alpha =0.9$ with various temperature parameter $\beta$ as $\beta _1=0.2, \beta _2=0.4, \beta _3=0.6, \beta _4=0.8$ in two dimensions

Fig. 28

The entropy S of the MYKP vs. a function of the temperature parameter $\beta$ for the parameters as $\hbar =\mu =q=c=m=n=1, a=5, a_1=1, a_2=2, A_1=1.5, A_2=2.25, D_e=3, \vec {B}=10T, \Phi _{AB}=10$ and $\alpha =0.9$ with various vibrational quantum number $\upsilon _{max}$ as $\upsilon _{m1}=5, \upsilon _{m2}=10, \upsilon _{m3}=15, \upsilon _{m4}=20$ in two dimensions

Fig. 29

The entropy S of the MYKP vs.a function of the magnetic field $\vec {B}$ for the parameters as $\hbar =\mu =q=c=m=n=1, a=5, a_1=1, a_2=2, A_1=1.5, A_2=2.25, D_e=3, \upsilon _{max}=10, \Phi _{AB}=10$ and $\alpha =0.9$ with various temperature parameter $\beta$ as $\beta _1=0.2, \beta _2=0.4, \beta _3=0.6, \beta _4=0.8$ in two dimensions

Fig. 30

The entropy S of the MYKP vs. a function of the Aharanov-Bohm flux field $\Phi _{AB}$ for the parameters as $\hbar =\mu =q=c=m=n=1, a=5, a_1=1, a_2=2, A_1=1.5, A_2=2.25, D_e=3, \upsilon _{max}=10, \vec {B}=10T$ and $\alpha =0.9$ with various temperature parameter $\beta$ as $\beta _1=0.2, \beta _2=0.4, \beta _3=0.6, \beta _4=0.8$ in two dimensions

Fig. 31

The specific heat capacity $C_v$ of the MYKP vs. a function of the temperature parameter $\beta$ for the parameters as $\hbar =\mu =q=c=m=n=1, a=5, a_1=1, a_2=2, A_1=1.5, A_2=2.25, D_e=3, \vec {B}=10T, \Phi _{AB}=10$ and $\alpha =0.9$ with various vibrational quantum number $\upsilon _{max}$ as $\upsilon _{m1}=5, \upsilon _{m2}=10, \upsilon _{m3}=15, \upsilon _{m4}=20$ in two dimensions

Fig. 32

The specific heat capacity $C_v$ of the MYKP vs.a function of the magnetic field $\vec {B}$ for the parameters as $\hbar =\mu =q=c=m=n=1, a=5, a_1=1, a_2=2, A_1=1.5, A_2=2.25, D_e=3, \upsilon _{max}=10, \Phi _{AB}=10$ and $\alpha =0.9$ with various temperature parameter $\beta$ as $\beta _1=0.02, \beta _2=0.04, \beta _3=0.06, \beta _4=0.08$ in two dimensions

Fig. 33

The specific heat capacity $C_v$ of the MYKP vs. a function of the Aharanov-Bohm flux field $\Phi _{AB}$ for the parameters as $\hbar =\mu =q=c=m=n=1, a=5, a_1=1, a_2=2, A_1=1.5, A_2=2.25, D_e=3, \upsilon _{max}=10, \vec {B}=10T$ and $\alpha =0.9$ with various temperature parameter $\beta$ as $\beta _1=0.02, \beta _2=0.04, \beta _3=0.06, \beta _4=0.08$ in two dimensions

Fig. 34

The magnetization M of the MYKP vs. a function of the temperature parameter $\beta$ for the parameters as $\hbar =\mu =q=c=m=n=1, a=5, a_1=1, a_2=2, A_1=1.5, A_2=2.25, D_e=3, \vec {B}=10T, \Phi _{AB}=10$ and $\alpha =0.9$ with various vibrational quantum number $\upsilon _{max}$ as $\upsilon _{m1}=5, \upsilon _{m2}=10, \upsilon _{m3}=15, \upsilon _{m4}=20$ in two dimensions

Fig. 35

The magnetization M of the MYKP vs.a function of the magnetic field $\vec {B}$ for the parameters as $\hbar =\mu =q=c=m=n=1, a=5, a_1=1, a_2=2, A_1=1.5, A_2=2.25, D_e=3, \upsilon _{max}=10, \Phi _{AB}=10$ and $\alpha =0.9$ with various temperature parameter $\beta$ as $\beta _1=0.02, \beta _2=0.04, \beta _3=0.06, \beta _4=0.08$ in two dimensions

Fig. 36

The magnetization M of the MYKP vs. a function of the Aharanov-Bohm flux field $\Phi _{AB}$ for the parameters as $\hbar =\mu =q=c=m=n=1, a=5, a_1=1, a_2=2, A_1=1.5, A_2=2.25, D_e=3, \upsilon _{max}=10, \vec {B}=20T$ and $\alpha =0.9$ with various temperature parameter $\beta$ as $\beta _1=0.02, \beta _2=0.04, \beta _3=0.06, \beta _4=0.08$ in two dimensions

Changes in energy eigenvalues with respect to screening parameter $\alpha$ for different values of the magnetic quantum numbers $m_0=-2$, $m_2=-1$, $m_3=0$, $m_4=1$ and $m_5=2$ for $n=0$, $n=1$ and $n=2$ presents in Figs. 10, 11 and 12 respectively. Figures show energy eigenvalues decreases with increases $\alpha$ for MYKP. Variation in energy eigenvalues corresponds to $\Phi _{AB}$ for different values of the magnetic quantum numbers $m_0=-2$, $m_2=-1$, $m_3=0$, $m_4=1$ and $m_5=2$ for $n=0$, $n=1$ and $n=2$ presents in Figs. 13, 14 and 15 respectively. Figures show energy eigenvalues decreases exponentially with increases $\Phi _{AB}$ for MYKP. Changes in energy eigenvalues corresponds to $\vec {B}$ for different values of the magnetic quantum numbers $m_0=-2$, $m_2=-1$, $m_3=0$, $m_4=1$ and $m_5=2$ for $n=0$, $n=1$ and $n=2$ presents in Figs. 16, 17 and 18 respectively. Figures indicate that energy eigenvalues decreases slowly with increases $\vec {B}$ for MYKP.

Fig. 37

The magnetic susceptibility $\chi _m$ of the MYKP vs. a function of the temperature parameter $\beta$ for the parameters as $\hbar =\mu =q=c=m=n=1, a=5, a_1=1, a_2=2, A_1=1.5, A_2=2.25, D_e=3, \vec {B}=10T, \Phi _{AB}=10$ and $\alpha =0.9$ with various vibrational quantum number $\upsilon _{max}$ as $\upsilon _{m1}=5, \upsilon _{m2}=10, \upsilon _{m3}=15, \upsilon _{m4}=20$ in two dimensions

Fig. 38

The magnetic susceptibility $\chi _m$ of the MYKP vs.a function of the magnetic field $\vec {B}$ for the parameters as $\hbar =\mu =q=c=m=n=1, a=5, a_1=1, a_2=2, A_1=1.5, A_2=2.25, D_e=3, \upsilon _{max}=10, \Phi _{AB}=10$ and $\alpha =0.9$ with various temperature parameter $\beta$ as $\beta _1=0.02, \beta _2=0.04, \beta _3=0.06, \beta _4=0.08$ in two dimensions

Fig. 39

The magnetic susceptibility $\chi _m$ of the MYKP vs. a function of the Aharanov-Bohm flux field $\Phi _{AB}$ for the parameters as $\hbar =\mu =q=c=m=n=1, a=5, a_1=1, a_2=2, A_1=1.5, A_2=2.25, D_e=3, \upsilon _{max}=10, \vec {B}=10T$ and $\alpha =0.09$ with various temperature parameter $\beta$ as $\beta _1=0.002, \beta _2=0.004, \beta _3=0.006, \beta _4=0.008$ in two dimensions

Figure 19 shows the changes of the partition function with respect to temperature parameter $\beta$ for the various values of the vibrational quantum number $\upsilon _{max}$. The relationship in this case shows the partition function increases gradually as $\beta$ increased. Changes in the partition function $Z(\vec {B},\Phi _{AB},\beta )$ corresponds to magnetic field $\vec {B}$ for different values of the $\beta$ is presents in the Fig. 20. Plots show that initially the $Z(\vec {B},\Phi _{AB},\beta )$ increases slowly as $\vec {B}$ increased and after $\vec {B}=3T$, the partition function increases an exponentially with $\vec {B}$. Figure 21 illustrates the variation of the $Z(\vec {B},\Phi _{AB},\beta )$ with AB flux field $\Phi _{AB}$ for different values of the $\beta$. It is clearly shown in these plots that the partition function decreases slowly as increasing $\Phi _{AB}$ and tends to $Z(\vec {B},\Phi _{AB},\beta )=0$ around $\Phi _{AB}=22$. In Fig. 22, we shows the behaviour of the internal energy $U(\vec {B},\Phi _{AB},\beta )$ with respect to $\beta$ for different values of the $\upsilon _{max}$. Plots show that internal energy decreases monotonically as decreasing $\beta$. Variation in internal energy $U(\vec {B},\Phi _{AB},\beta )$ corresponds to magnetic field $\vec {B}$ for various values of the $\beta$ presented in Fig. 23 We noted that $U(\vec {B},\Phi _{AB},\beta )$ initially increases and after $vec{B}=9T$ its decreases monotonically for $\beta =0.08$ and 0.09 whereas U decreases linearly as $\vec {B}$ increased for $\beta =0.8$ and 0.9. Changes in internal energy $U(\vec {B},\Phi _{AB},\beta )$ with respect to AB flux field $\Phi _{AB}$ for various values of the $\beta$ presented in Fig. 24 shows $U(\vec {B},\Phi _{AB},\beta )$ deceases initially and increases gradually after $\Phi _{AB}=6$ as $\Phi _{AB}$ increased. Variation of the free energy $F(\vec {B},\Phi _{AB},\beta )$ with varying $\beta$ corresponds to different values of the vibrational quantum number $\upsilon _{max}$ shows in Fig. 25. It is shown that free energy increases exponentially with increasing $\beta$. In Fig. 26, we shows the changes in $F(\vec {B},\Phi _{AB},\beta )$ with respect to magnetic field $\vec {B}$ for various values of the temperature parameter $\beta$. It is clearly seen that $F(\vec {B},\Phi _{AB},\beta )$ decreases gradually with increasing $\vec {B}$. In Fig. 27, we shows behaviour of the free energy $F (\vec {B},\Phi _{AB},\beta )$ with respect to AB flux field $\Phi _{AB}$ for different values of the temperature parameter $\beta$. The figure clearly indicates the $F(\vec {B},\Phi _{AB},\beta )$ decreases slowly as AB flux field increased. Figure 28 shows the changes of the entropy $S(\vec {B},\Phi _{AB},\beta )$ with respect to temperature parameter $\beta$ for different values of the vibrational quantum number $\upsilon _{max}$. We shows entropy decreases monotonically as temperature parameter increased. Behavior of the entropy $S(\vec {B},\Phi _{AB},\beta )$ corresponds to magnetic field $\vec {B}$ with various values of the temperature parameter $\beta$ shows in Fig. 29. it is clearly seen that entropy decreases gradually as increasing $\vec {B}$ for constant values of the remaining parameters. In Fig. 30, variation of the entropy $S(\vec {B},\Phi _{AB},\beta )$ with respect to AB flux field $\Phi _{AB}$ for different values of the $\beta$ is presented. Plots show entropy abruptly decreases initially and remain almost constant for $\Phi _{AB}=50$ to 65 after that it is suddenly increases as $\Phi _{AB}$ increased. We shows the behavior of the specific heat capacity $C_v(\vec {B},\Phi _{AB},\beta )$ with respect to temperature parameter $\beta$ corresponds to various values of the vibrational quantum number $\upsilon _{max}$ in Fig. 31 We noted that specific heat capacity increases as increasing temperature parameter. In Fig. 32 the variation of the specific heat capacity $C_v(\vec {B},\Phi _{AB},\beta )$ corresponds to magnetic field $\vec {B}$ for different values of the temperature parameter $\beta$ is presented. The plots show that $C_v(\vec {B},\Phi _{AB},\beta )$ decreases exponentially and $C_v(\vec {B},\Phi _{AB},\beta )$ reaches zero for all plots at $\vec {B}=2.9$ after that it is increases linearly as increasing $\beta$. Figure 33 shows the behavior of the specific heat capacity $C_v(\vec {B},\Phi _{AB},\beta )$ with respect to AB flux field $\Phi _{AB}$ for different values of the temperature parameter $\beta$. The plots show that specific heat capacity initially decreases monotonically and later increases suddenly as AB flux field increased. Variation in the magnetization $M(\vec {B},\Phi _{AB},\beta )$ at finite temperature with temperature parameter $\beta$ for various values of the vibrational quantum number $\upsilon _{max}$ presented in Fig. 34 Plots show magnetization decreases monotonically for vibrational quantum number $\upsilon _{m2}=10, \upsilon _{m3}=15, \upsilon _{m4}=20$ and for vibrational quantum number $\upsilon _{m1}=5$, magnetization almost remained constant as increasing $\beta$. Figure 35 shows changes of the magnetization $M(\vec {B},\Phi _{AB},\beta )$ at finite temperature with magnetic field $\vec {B}$ corresponds to different values of the temperature parameter $\beta$. The plots seen that magnetization increases with $\vec {B}$ increased. In Fig. 36 we shows behaviour of the magnetization $M(\vec {B},\Phi _{AB},\beta )$ at finite temperature against AB flux field $\Phi _{AB}$ for various values of the temperature parameter $\beta$. These plots show magnetization decreases with increasing $\Phi _{AB}$. Behaviour of the magnetic susceptibility $\chi _m(\vec {B},\Phi _{AB},\beta )$ at finite temperature with temperature parameter $\beta$ for various values of the vibrational quantum number $\upsilon _{max}$ is presented in Fig. 37 We observe that magnetic susceptibility increases slowly with $\beta$ increased. In Fig. 38 we shows the variation of the magnetic susceptibility $\chi _m(\vec {B},\Phi _{AB},\beta )$ at finite temperature with varying magnetic field $\vec {B}$ corresponds to different values of the $\beta$. We noted that magnetic susceptibility increases randomly with $\vec {B}$ increased. Variation in the magnetic susceptibility $\chi _m(\vec {B},\Phi _{AB},\beta )$ at finite temperature against AB flux field $\Phi _{AB}$ for different values of the temperature parameter $\beta$ is presented in Fig. 39 We notice that the magnetic susceptibility decreases slowly with increasing $\Phi _{AB}$ for temperature parameter $\beta _1=0.002$ and temperature parameter $\beta _2=0.004$ whereas the magnetic susceptibility almost remained const with increasing $\Phi _{AB}$ for temperature parameter $\beta _3=0.006$ and temperature parameter $\beta _4=0.008$.

6 Conclusions

The energy spectrum for MYKP with the magnetic field and Aharanov–Bohm flux field was obtained using the pNU approach and SEM in this study. There are special cases for the GKP, MKP, KP, and HP. The MYKP, KP, HP, MKP, and GKP numerical results are tabulated. The numerical results calculated for KP and HP are congruent with those obtained by others. There are many plots of the effective potential that correlate to interatomic distance r, magnetic field $\vec {B}$, and Aharanov–Bohm flux field $\Phi _{AB}$. The energy eigenvalues are displayed with respect to the screening parameter $\alpha$, the magnetic field $\vec {B}$, and the Aharanov-Bohm flux field $\Phi _{AB}$. We also obtained and analysed additional thermodynamic parameters such as mean energy, mean free energy, entropy, and specific heat capacity using this information. Magnetization and magnetic susceptibility at finite temperatures under the effect of external fields were also discussed. We were able to discover additional physical chemical properties in position spaces under the MYKP by using the eigenfunction of the MYKP, including Gibbs free energy, bond length, Tsallis entropy, Renyi entropy, and Fisher information entropy. This article findings may be useful in atomic-molecular physics, solid-state physics, and physical chemistry.