1 Introduction

It is a well-known fact that the Schrödinger equation (SE) describes many physical problems in different branches of physics and chemistry (Kumar and Fakir 2012; Milanovic and Ikovic 1999; Roy and Roy 2002). Generally speaking, when dealing with a particular physical system, a potential model is used, and this potential model will provide a good amount of information about the system. There are only a few potentials, such as the harmonic oscillator and hydrogen atom, for which the SE can be solved exactly (Alhaidari 2002; Serra and Lipparini 1997). In the fields of quantum physics and quantum chemistry, the most challenging task is obtaining exact, analytic solutions to the radial SE with a given interacting potential (Rani and Chand 2018; Dong and Ma 1998; Child et al. 2000; Panahi and Gavabar 2016). In particular, the arbitrary l-state solutions to the SE find some interest in chemical physics and molecular spectroscopy (Ikot et al. 2018; Rani et al. 2018). To describe the spectra of diatomic molecules, potential models like the Morse potential are generally utilised (Alavi and Rouhani 2004; Arima and Iachello 2000; Bonatsos et al. 1997). The harmonic oscillator potential is useful in many branches of physics (Monteiro et al. 1996; Rosmalen et al. 1983), and the Kratzer and pseudoharmonic potentials are intermediates between anharmonic and harmonic oscillator potentials (Bayrak et al. 2007; Berkdemir et al. 2006a; Ikhdair and Sever 2009a). The exact solution of the SE, with spherically symmetric potential, plays a vital role in nuclei, atoms, molecules and spectroscopy in many fields of modern physics. Therefore, many authors have devoted time to obtaining this exact SE solution via different analytical methods, such as point canonical transformation (PCT) (Abu-Shady 2015; De et al. 1992), the Nikifarov–Uvarov method (Ikot et al. 2011; Hassanabadi et al. 2017; Dong et al. 2003; Hassanabadi et al. 2013; Ikot et al. 2016a; Ikot and Akpabio 2011), numerical methods (Ixaru et al. 2000; Sandin et al. 2016; Hassanabadi et al. 2012), the asymptotic iterative method (AIM) (Ikot et al. 2018; Kumar and Fakir 2013; Ikhdair 2011; Ikot et al. 2014), supersymmetry quantum mechanics (SUSYQM) (Hamzavi et al. 2013; Ikot et al. 2016b), the factorisation method (Okorie et al. 2018a, b) and the Hill determinant method (Choudhury and Mondal 1995), amongst others. Due to the importance of anharmonic potentials in molecular physics, molecular spectroscopy and chemical physics, researchers have studied them in relativistic and non-relativistic regimes (Al-Jamel and Wityan 2012). Amongst many applications of the SE solution is investigating the mass spectra of heavy quarks for some special potential models. Arrays of potential models are commonly used in studying heavy quarkonium spectra. For instance, Martin, logarithmic and Cornell potentials have often been used (Al-Jamel 2011; Patel and Vinodkumar 2009a; Rai et al. 2008; Reyes et al. 2003; Zalewski 1998; Bhanot and Rudaz 1978) to investigate quark confinement. Most of these potentials consider two distinctive features of the strong interaction—asymptotic freedom and confinement (Al-Jamel 2011). The successful potential model for such systems is the one that produces its mass spectra in agreement with the experimental data, within about 20 MeV, and leptonic decay widths, within a factor of two (Al-Jamel 2018). The study of heavy quarkonium systems provides a solid understating for the quantitative test of quantum chromodynamic (QCD) theory and the standard model (Kuchin and Maksimenko 2013; Yazarloo and Mehraban 2016). Studying the wave function of the bound state of a quark and antiquark from the strong interaction between quark and antiquarks in B and D mesons gives important information about the property of strong interaction and the mechanism of heavy meson decays (Roy et al. 2012). Constructing phenomenological models by employing the basic properties of QCD is very useful for predicting the properties of hadrons, such as mass, form factors, decay widths, etc. In this context, potential models for mesons, involving potential between heavy and light quarks, have been very successful for studying hadrons and their properties (Kumar and Chand 2014). In recent years, many scientists have become interested in investigating the spectra of the above-mentioned quarks. Kumar and Fakir (2013) analytically obtained the energy eigenvalues and normalised eigenfunctions of the radial SE in N-dimensional space for the quark–antiquark interaction potential using the power series technique via a suitable ansatz to the wavefunction. Yazarloo and Mehraban (2016) studied the B and Bs mesons spectra and their decays properties within the framework of a non-relativistic potential model, using a new potential model for the interaction of mesonic systems—the Coulomb plus exponential-type potential, of the form

$$V(r) = \frac{a}{r} + be^{\alpha r} + V_{0} .$$
(1)

The authors applied the perturbation approach in their investigation. Abu-Shady et al. (2018) obtained the exact solution of the N-dimensional radial SE with the generalised Cornell potential using the Laplace’s transformation (LT) method. They deduced eigenvalues for some special cases of the generalised Cornell potential and obtained the mass spectra for the system. Maksimenko and Kuchin (2011) generated the mass spectrum of the SE for a potential comprised of the sum of a harmonic oscillator potential, a linear potential and a Coulomb potential, using the Nikiforov–Uvarov method for large and small distances between particles in the bound state; they obtained asymptotic expansions for the energy levels and wave functions. Ciftci and Kisoglu (2018) generated energy eigenvalues for an exact SE and derived the mass of a heavy quark–antiquark system (quarkonium) using the Asymptotic Iteration Method (AIM). They also tested the accuracy of their formula by comparing the eigenvalues with those obtained numerically. Furthermore, a semi-analytical formula was applied to cc, bb and cb meson systems for comparing the masses with the experimental data (Al-Oun et al. 2015). Al-Oun et al. (2015) examined characteristic heavy quarkonia (\(c\overline{c}\) and \(b\overline{b}\)) properties in the general framework of a non-relativistic potential model consisting of a Coulomb plus quadratic potential. The author determined potential parameters by simultaneously fitting the l states of both (\(c\overline{c}\) and \(b\overline{b}\)) with known experimental values. In similar development, Kuchin and Maksimenko (2013) obtained the spin-averaged mass spectra of heavy quarkonia (bb and mesons with a Cornell potential in the framework of non-relativistic SE. Rahmani et al. (2014) investigated the SE with a potential containing Coulomb, linear and quadratic terms, using the Nikiforov–Uvarov technique. They further reported the corresponding Isgur–Wise function parameters and obtained the masses, slope and curvature parameters of some heavy-light mesons. Therefore, motivated by the current advances in quark confinement, the present research introduces a generalised Cornell potential of the form

$$V\left( r \right) = ar^{2} + br - \frac{c}{r} + \frac{d}{r}\mathop e\nolimits^{ - \alpha r} + \frac{f}{{r^{2} }} + e ,$$
(2)

where a, b, c, d, e and f are potential parameters. It is to be noted that the inverse square term, \({f \mathord{\left/ {\vphantom {f {r^{2} }}} \right. \kern-0pt} {r^{2} }}\) makes the potentials more singular and produces better confinement compared to Cornell and Coulomb perturbed potentials (Rani and Chand 2018). This potential is also more general, since the Cornell potential and other quark confining potentials are embedded in it. The scheme of this presentation is as follows. Section 2studies the potential with the radial SE and presents the bound state energy eigenvalue for the potential. Section 3 presents the bound state energies of the pseudoharmonic and Kratzer potentials as special cases of the generalised energy eigenvalues. Section 4 derives the mass spectra of the heavy quarkonium systems. The results of the work are discussed in Sect. 5, and a brief conclusion is presented in Sect. 6.

2 The Radial SE with the Generalised Potential

This research considers the radial SE of the form

$$\frac{{^{{\mathop d\nolimits^{2} }} \varPsi \left( r \right)}}{{dr^{2} }} + \frac{2}{r}\frac{d\varPsi \left( r \right)}{dr} - \left[ {\frac{{l\left( {l + 1} \right)}}{{r^{2} }} + \frac{2\mu }{{\hbar^{2} }}\left( {E - V} \right)} \right]\varPsi \left( r \right) = 0 ,$$
(3)

where l is the orbital momentum quantum number; μ is the reduced mass; r is the internuclear separation; and E denotes the energy eigenvalues of the system. Substituting the generalised potential given in Eq. (2) into Eq. (3) gives

$$\left[ {\frac{{^{{\mathop d\nolimits^{2} }} }}{{dr^{2} }} + \frac{2}{r}\frac{d}{dr} - \frac{{l\left( {l + 1} \right)}}{{r^{2} }}} \right]\varPsi \left( r \right) + \left[ {\frac{2\mu }{{\hbar^{2} }}\left( {E - (ar^{2} + br - \frac{c}{r} + \frac{d}{r}\mathop e\nolimits^{ - \alpha r} + \frac{f}{{r^{2} }} + e)} \right)} \right]\varPsi \left( r \right) = 0 .$$
(4)

Taking the Taylor series expansion of the exponential term of Eq. (4) and neglecting the terms greater than \(r^{3}\)turns Eq. (4) into the following.

$$\left[ {\frac{{^{{\mathop d\nolimits^{2} }} }}{{dr^{2} }} + \frac{2}{r}\frac{d}{dr} - \frac{{l\left( {l + 1} \right)}}{{r^{2} }}} \right]\varPsi \left( r \right) + \left[ {\frac{2\mu }{{\hbar^{2} }}\left( {E - \left( {a - \frac{{d\alpha^{3} }}{6}} \right)r^{2} - \left( {b + \frac{d\alpha }{2}^{2} } \right)r + \left( {c - d} \right)\frac{1}{r} - \frac{f}{{r^{2} }} - e} \right)} \right]\varPsi \left( r \right) = 0,$$
(5)

Simplifying Eq. (5) yields

$$\left[ {\frac{{^{{\mathop d\nolimits^{2} }} }}{{dr^{2} }} + \frac{2}{r}\frac{d}{dr} - \frac{{L\left( {L + 1} \right)}}{{r^{2} }} + \frac{2\mu }{{r^{2} }}\left( {\varepsilon - Ar^{2} - Br + C\frac{1}{r}} \right)} \right]\varPsi \left( r \right) = 0 ,$$
(6)

where

$$\varepsilon = \left( {E - e} \right)\frac{2\mu }{{\hbar^{2} }},$$
(7)
$$A = \frac{2\mu }{{\hbar^{2} }}\left( {a - \frac{{d\alpha^{3} }}{6}} \right),$$
(8a)
$$B = \frac{2\mu }{{\hbar^{2} }}\left( {b + \frac{d\alpha }{2}^{2} } \right)$$
(8b)
$$C = \frac{2\mu }{{\hbar^{2} }}\left( {c - d} \right),$$
(8c)
$$L\left( {L + 1} \right) = l\left( {l + 1} \right) + \frac{2\mu }{{\hbar^{2} }}f$$
(9)
$$L = - \frac{1}{2} + \frac{1}{2}\sqrt {\left( {2l + 1} \right)^{2} + {{8\mu f} \mathord{\left/ {\vphantom {{8\mu f} {\hbar^{2} }}} \right. \kern-0pt} {\hbar^{2} }}} .$$
(10)

Using the wave function of the form, \(\varPsi \left( r \right) = \mathop e\nolimits^{{ - \alpha r^{2} - \beta r}} F\left( r \right)\), Eq. (6) becomes

$$\begin{aligned} & F^{\prime\prime}\left( r \right) + \left[ { - 4\alpha r - 2\beta + \frac{2}{r}} \right]F^{\prime}\left( r \right) \\ & \quad + \left[ {\left( {4\alpha^{2} - A} \right)r^{2} + \left( {4\alpha \beta - B} \right)r + \left( {C - 2\beta } \right)\frac{1}{r} - \frac{{L\left( {L + 1} \right)}}{{r^{2} }} + \left( {\varepsilon - 6\alpha + \beta^{2} } \right)} \right]F\left( r \right) = 0. \\ \end{aligned} .$$
(11)

Assuming the wave function for the series solution of Eq. (11) in the form

$$F(r) = \sum\limits_{n = 0}^{\infty } {a_{n} r^{2n + L} } ,$$
(12)

And substituting Eq. (12) into Eq. (11) results in the following

$$\begin{aligned} & \sum\limits_{n = 0}^{\infty } {a_{n} } \left\{ {\left[ {\left( {2n + L} \right)\left( {2n + L - 1} \right) + 2\left( {2n + L} \right) - L\left( {L + 1} \right)} \right]} \right.r^{2n + L - 2} \\ & \quad + \left[ { - 2\beta \left( {2n + L + 1} \right) + C} \right]r^{2n + L - 1} + \left[ { - 4\alpha \left( {2n + L} \right) + \varepsilon + \beta^{2} - 6\alpha } \right]r^{2n + L} \\ & \quad + \left[ {4\alpha \beta - B} \right]r^{2n + L + 1} + \left[ {4\alpha^{2} - A} \right]\left. {r^{2n + L + 2} } \right\} = 0. \\ \end{aligned} .$$
(13)

Equation (13) is a linearly independent function, each equal to zero, noting that r is a non-zero function; therefore, the coefficients of r are zeros. With this in mind, the relation for each of the terms is obtained as shown below

$$(2n + L)(2n + L + 1) - L - L^{2} = 0,$$
(14)
$$\varepsilon = 2\alpha \left( {4n + 2L + 3} \right) - \beta^{2} ,$$
(15)
$$C = 2\beta \left( {2n + L + 1} \right) ,$$
(16)
$$\alpha = \frac{\sqrt A }{2} ,$$
(17)
$$\beta = \frac{B}{4\alpha } .$$
(18)

The energy eigenvalues expressions are then obtained using Eqs. (15) and (7) as,

$$\left( {E - e} \right)\frac{2\mu }{{\hbar^{2} }} = 2\alpha \left( {4n + L + 3} \right) - \beta^{2} . .$$
(19)

By substituting the expression for L, α, β, \(A\) and \(B\), into Eq. (19), the energy eigenvalue is obtained as follows

$$\begin{aligned} E & = e + \sqrt {\frac{{\hbar^{2} \left( {6a - d\left[ {\left( {\frac{2\mu }{{\mathop \hbar \nolimits^{2} }}\left( {b + \frac{d\alpha }{2}^{2} } \right)} \right)/4\beta } \right]^{3} } \right)}}{12\mu }} \left( {4n + 2 + \sqrt {\left( {2l + 1} \right)^{2} + \frac{8\mu f}{{\hbar^{2} }}} } \right) \\ & \quad - \frac{{2\mu \left( {c - d} \right)^{2} }}{{\hbar^{2} }}\left( {4n + 1 + \sqrt {\left( {2l + 1} \right)^{2} + \frac{8\mu f}{{\hbar^{2} }}} } \right)^{ - 2} \\ \end{aligned} ,$$
(20)

where parameters \(a,b,c,d\) and \(f\) must satisfy the condition

$$c = - 2d(1 + \alpha ) + \frac{{\left[ {b + d\alpha^{2} \left( {1 + \alpha } \right)} \right]}}{2}\sqrt {\frac{{2\hbar^{2} }}{{\mu (4a + d\alpha^{4} )}}\left( {4n + 1 + \sqrt {(2l + 1)^{2} + \frac{8\mu (f + d)}{{\hbar^{2} }}} } \right)} .$$
(21)

This result is new, and, to the best of the authors’ knowledge, no study has been reported on this generalised Cornell potential and its application to mass spectra and diatomic molecules. To compute the numerical results of Eq. (20) for some selected diatomic molecules, the spectroscopic parameters are taken from Ref. Rani and Chand (2018) as given in Table 1 (Rani and Chand 2018), using the following conversion factors (Ikot et al. 2019) \(\,\,\hbar c = 1973.29\,{\text{eV}}\,{\text{and}}\,1\,{\text{a}} . {\text{m}} . {\text{u}} = 931.49408\,{\text{MeV/}}c^{ 2}\). Four diatomic molecules—CO, NO, CH and N2 (Rani and Chand 2018)—were selected and adjusted to the potential parameters as

$$a = \frac{{D_{e} }}{{r_{e}^{2} }},\,\,b = D_{e} ,\,\,c = 2D_{e} r_{e} ,\,\,d = - 2D_{e} r_{e} ,\,\,e = 2D_{e} \,\,{\text{and}}\,\,f = D_{e} r_{e}^{2} .$$
Table 1 The properties of the diatomic molecules (Rani and Chand 2018)
Full size table

Using Eq. (20) with these parameters as input, the numerical results for the four diatomic molecules of CO, NO, CH and N2 were computed. Since this result is new, and there is no available literature with which to compare this study, we rather investigate the special cases of the generalised Cornell potential which reduced to the well-known pseudoharmonic and Kratzer potentials.

3 Special Cases

The generalised Cornell potential reduces to pseudoharmonic and the Kratzer potentials, which have many applications in physics and chemistry.

3.1 The Pseudoharmonic Potential

The pseudoharmonic potential is used to study the anharmonicity of diatomic molecules and may be considered as a potential with behaviour between exactly solvable harmonic oscillator and nonlinear anharmonic models (Ussembayev 2009). This potential is used in both classical and quantum physics to describe the interaction of some diatomic molecules (Rani and Chand 2018). By adjusting the generalised Cornell potential as

$$a = \frac{{D_{e} }}{{r_{e}^{2} }},b = o,c = d = 0,e = - 2De,f = D_{e} r_{e}^{2} ,$$
(22)

The pseudoharmonic potential was obtained as

$$V(r) = \frac{{D_{e} }}{{r_{e}^{2} }}r^{2} + \frac{{D_{e} r_{e}^{2} }}{{r^{2} }} - 2D_{e} ,$$
(23)

where De represents the dissociation energy, and re is the equilibrium internuclear separation. Then, by substituting Eq. (22) into Eq. (20), the authors obtained the energy eigenvalue for the pseudoharmonic potential as

$$E_{nl} = - 2D_{e} + \sqrt {\frac{{\hbar^{2} D_{e} }}{{2\mu r_{e}^{2} }}} \left( {4n + 2 + \sqrt {\left( {2l + 1} \right)^{2} + \frac{{8\mu D_{e} r_{e}^{2} }}{{\hbar^{2} }}} } \right).$$
(24)

Equation (24) is in good agreement with that of references Rani and Chand (2018) and Ikhdair et al. (2015).

3.2 The Kratzer Potential

The Kratzer potential has been extensively used to describe molecular structures and interactions. Adjusting the values of the generalised Cornell potential parameters as

$$a = b = 0,d = o,c = 2D_{e} r_{e} ,e = D_{e} ,f = D_{e} r_{e}^{2}$$
(25)

gives the Kratzer potential as

$$V(r) = D_{e} + \frac{{D_{e} r_{e}^{2} }}{{r^{2} }} - \frac{{2D_{e} r_{e} }}{r}.$$
(26)

Using Eq. (25) in Eq. (20) provides the energy eigenvalues for the Kratzer potential as

$$E_{nl} = D_{e} - \frac{{2\mu D_{e}^{2} r_{e}^{2} }}{{\hbar^{2} }}\left( {n + \frac{1}{4}\sqrt {\left( {l + \frac{1}{2}} \right)^{2} + \frac{{2\mu D_{e} r_{e}^{2} }}{{\hbar^{2} }}} } \right)^{ - 2} .$$
(27)

Equation (27) is also in good agreement with that of references Rani and Chand (2018) and Ikhdair et al. (2015), and it can be written as

$$E_{nl} = \frac{{ - 2D_{e}^{2} r_{e}^{2} }}{{\left( {n + \frac{1}{4} + \sqrt {\left( {l + \frac{1}{2}} \right)^{2} + 2D_{e} r_{e}^{2} } } \right)^{2} }} .$$
(28)

The pseudoharmonic and Kratzer potentials have been successfully used to study the eigenvalue spectra of a class of diatomic molecules (Oyewumi et al. 2008). This research now uses results of the energy eigenvalue spectra for the pseudoharmonic and Kratzer potentials to study the four diatomic molecules of CO, NO, CH and N2. Some useful properties of these diatomic molecules are presented in Table 1 (Rani and Chand 2018). Using Table 1 alongside Eqs. (24) and (27), the authors compute the numerical values of the energy eigenvalues for the Kratzer and pseudoharmonic potentials given in Tables 2, 3, 4, 5, 6, 7, 8 and 9. In Tables 2, 3, 4 and 5, the energy spectra for the pseudoharmonic potentials of the four diatomic molecules are shown and compared with that of references Rani and Chand (2018), Ikhdair et al. (2015), Ikhdair and Sever (2009b), Arda and Sever (2012), Sever et al. (2008) and Berkdemir et al. (2006b). Also, Tables 6, 7, 8 and 9 show the energy spectra of the Kratzer potential for the four diatomic molecules for quantum numbers n and l, respectively, in comparison with those in references Rani and Chand (2018), Ikhdair et al. (2015), Ikhdair and Sever (2009b), Arda and Sever (2012), Sever et al. (2008) and Berkdemir et al. (2006b). Interestingly, the numerical results are in good agreement with those obtained in references Rani and Chand (2018), Ikhdair et al. (2015), Ikhdair and Sever (2009b), Arda and Sever (2012), Sever et al. (2008) and Berkdemir et al. (2006b).

Table 2 Numerical result of the generalised energy eigenvalues \(( {\text{GeV)}}\) for different diatomic molecules with \(a = \frac{{D_{e} }}{{r_{e}^{2} }},\,\,b = D_{e} ,\,\,c = 2D_{e} r_{e} ,\,\,d = - 2D_{e} r_{e} ,\,\,e = 2D_{e} \,\,{\text{and}}\,\,f = D_{e} r_{e}^{2}\)
Full size table
Table 3 Comparison of bound state energy eigenvalues N2 molecules \(\left( {\text{eV}} \right)\)
Full size table
Table 4 Comparison of bound state energy eigenvalues \(( {\text{eV)}}\) of CO molecules
Full size table
Table 5 Comparison of bound state energy eigenvalues \(\left( {eV} \right)\) of NO molecule
Full size table
Table 6 Comparison of bound state energy eigenvalues \(\left( {\text{eV}} \right)\) of CH molecule
Full size table
Table 7 The bound state energy eigenvalues \(( {\text{eV)}}\) of CO molecules (Kratzer)
Full size table
Table 8 Comparison of bound state energy eigenvalues \(( {\text{eV)}}\) of NO (Kratzer)
Full size table
Table 9 Comparison of bound state energy eigenvalues \(( {\text{eV)}}\) of CH (Kratzer)
Full size table

4 Mass Spectra of Heavy Quarkonium

This section derives the mass spectra of the heavy quarkonium systems, such as charmonium and bottomonium, which quarks and antiquarks of the same variety. To determine the mass spectra of the system, the approach from references Patel and Vinodkumar (2009b), Rajabi (2005) and Yu et al. (2004) is followed.

$$M = m_{1} + m_{2} + E_{nl} . ,$$
(29)

which assumes

$$m_{1} = m_{2} = m_{b} . ,$$
(30)

Resulting in the expression

$$M = 2m_{b} + E_{nl} . ,$$
(31)

where \(m_{b}\) is the mass of the particle under investigation and \(E_{nl}\) is the derived energy eigenvalues. Substituting Eq. (20) into Eq. (31) gives

$$\begin{aligned} M & = 2m + e + \sqrt {\frac{{\hbar^{2} \left( {6a - d\left[ {\left( {\frac{2\mu }{{\hbar^{2} }}\left( {b + \frac{d\alpha }{2}^{2} } \right)} \right)/4\beta } \right]^{3} } \right)}}{12\mu }} \left( {4n + 2 + \sqrt {\left( {2l + 1} \right)^{2} + \frac{8\mu f}{{\hbar^{2} }}} } \right) \\ & \quad - \frac{{2\mu \left( {c - d} \right)^{2} }}{{\hbar^{2} }}\left( {4n + 1 + \sqrt {\left( {2l + 1} \right)^{2} + \frac{8\mu f}{{\hbar^{2} }}} } \right)^{ - 2} , \\ \end{aligned} ,$$
(32)

where m is the mass of the element under consideration, and a, b, c, d, e and f are the potential parameters determined by fitting the experimental values. Applying the energy eigenvalues obtained from Eq. (20), the authors obtained an expression for mass spectra using Eq. (32) and obtained the potential parameters a, b, c, d, e and f by fitting the experimental values into the mass spectra equation and solving it simultaneously. Using the obtained potential parameters, the mass spectra of the heavy quarkonium systems (the charmonium and bottomonium) were calculated, as presented in Tables 11 and 12. These results are in good agreement with the experimental and theoretical results reported in references Kumar and Fakir (2013) and Al-Jamel and Wityan (2012). However, the present work is slightly different from the experimental and theoretical works, which can be accounted for as an approximation error.

5 Discussion of Results

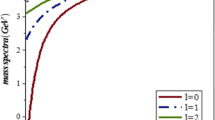
This work has introduced an exponential term into generalised anharmonic Cornell potentials and analytically solved the radial SE with the general potential, using the series expansion method. The bound state energy spectra of the SE was obtained and applied to the generalised energy to deduce the pseudoharmonic and Kratzer potentials as special cases. Suitable readjustments were also carried out on the potential parameters, and the improved results gave the pseudoharmonic and Kratzer potentials. Applying the parameters of some classes of diatomic molecules—CO, NO, CH and N2—allowed the authors to generate plots and compute the numerical values of the special cases. Figure 1 gives the shape of the generalised potential for different screening parameters; Fig. 2 gives the shape of the generalised potential for different diatomic molecules; Fig. 3 gives the shape of the pseudoharmonic potential for the above-mentioned diatomic molecules; and Fig. 4 gives the shape of the Kratzer potential for the above-mentioned diatomic molecules. A careful perusal of the graphs in Figs. 3 and 4 reveals that they follow the trend of the generalised potential graphs in Figs. 1 and 2. Figures 5 and 6 show the variation of the mass spectra with the screening parameter. It can be deduced from the graphs that the mass spectra increase as the screening parameter increases. Table 2 gives the numerical result of the generalised energy eigenvalues from Eq. (20). It may be observed in Table 2 that the quantum numbers n and l increase as the bound state energy for the different diatomic molecules increases, and this is in line with results from other works of the same kind (Ikhdair et al. 2015; Ikhdair and Sever 2009b; Arda and Sever 2012; Sever et al. 2008; Berkdemir et al. 2006b; Ikot et al. 2019). The numerical results for the special cases were computed to check the validity of the employed method in this research against methods in other, similar studies. Tables 3, 4, 5 and 6 show the energy spectra for the pseudoharmonic potential of different diatomic molecules, and Tables 7, 8, 9 and 10 display the energy spectra of the Kratzer potential for the different diatomic molecules with various principal and magnetic quantum numbers n and l, respectively. In addition, applying the energy generated from the present work, the authors generated an expression for mass spectra for the potential and obtained the potential parameters a, b, c, d, e and f by fitting the experimental values into the energy mass spectra equation and simultaneously solving it. The mass spectra of heavy quarkonium systems—specifically charmonium and bottomonium—were calculated, and the results are presented in Tables 11 and 12, respectively. Comparing the results with the experimental data and other theoretical studies (Kumar and Fakir 2013; Al-Jamel and Wityan 2012) indicated that this work’s numerical values are fractionally improved.

Fig. 1
figure 1

Shape of the generalised potential for different screening parameters

Full size image
Fig. 2
figure 2

Shape of the generalised potential for different diatomic molecules

Full size image
Fig. 3
figure 3

Shape of pseudoharmonic potential for different diatomic molecules

Full size image
Fig. 4
figure 4

Shape of Kratzer potential for different diatomic molecules

Full size image
Fig. 5
figure 5

Shape of mass spectra of Charmonium for different values of α

Full size image
Fig. 6
figure 6

Shape of mass spectra of Bottomonium for different values of α

Full size image
Table 10 Comparison of bound state energy eigenvalues \(\left( {\text{eV}} \right)\) of N2 molecule (Kratzer)
Full size table
Table 11 The mass spectrum for Charmonium with the mass \(m_{c} = 1.48\,GeV\,\alpha = 0.09,\,\,\beta = 2.001,\,\,a = 0.022,\,\,b = 0. 4 8 3,\,\,e = 1.306,\,\,d = 0. 8 9 0\,\,{\text{and}}\,\,f = 6.736\)
Full size table
Table 12 The mass spectrum for Bottomonium with the mass \(m_{b} = 4.68\,GeV\,\alpha = 0.16,\,\,\beta = 2.105,\,\,a = 0.024,\,\,b = 0. 2 4 8,\,\,e = 0.684,\,\,d = 0. 8 9 0\,\,{\text{and}}\,\,f = - \,0.213\)
Full size table

6 Conclusion

This research exactly solved the radial SE with a new, generalised, anharmonic Cornell potential using the series expansion method. The authors obtained the bound state energy spectra of the SE and deduced the pseudoharmonic and Kratzer potentials as special cases. Numerical results of the special cases were computed for the CO, NO, CH and N2diatomic molecules and were compared with results from the extant literature. In addition, we employed the energy expression of the new generalised potential to obtain its corresponding mass spectra relation and used the potential parameters to calculate the mass spectra of heavy quarkonium systems (charmonium and bottomonium). The results, when compared with the experimental data and other theoretical studies, were observed to be fractionally improved, giving more validity and reliability to the potential developed and approach used in this work. This new, generalised, anharmonic Cornell potential will be of great importance and will become a subject of interest in many fields of physics and chemistry, as it provides valuable information on the quantum mechanical system in atomic, molecule physics and chemical physics (Jia et al. 2017, 2018a, b, c, 2019; Peng et al. 2018; Jiang et al. 2019; Tang et al. 2020; Wang et al. 2019) and also opens new windows for further investigation.