1 Introduction

Recently, it has turned out that many phenomena in engineering and other areas of science can be successfully modeled by the use of fractional derivatives [1,2,3,4,5]. The motivation of this paper is to extend the application of the homotopy perturbation method [6,7,8,9,10,11] to solve the nonlinear partial differential equations with time fractional coordinate derivatives.

1.1 Background on fractional derivatives

The fractional calculus may be considered an old and yet novel topic. It is an old topic because, starting from some speculations of Leibniz (1695, 1697) and Euler (1730), it has been developed progressively up to now. However, it may be considered a novel topic as well. Only since the Seventies, the fractional calculus has been the object of specialized conferences and treatises. It is an emerging field in mathematics that has profound applications in all disciplines related to science and engineering. Some results have been reported in various books or related review articles [12,13,14]. However, we are still beginning to use this very powerful tool in many field of research. It is also a new powerful tool recently used to model complex systems with nonlinear behavior and long-term memory.

1.2 Preliminaries and notations

There are several definitions for fractional differential equations. These definitions include Grunwald–Letnikov, Riemann–Liouville, Caputo, Weyl, Marchaud, Riesz fractional derivatives, Nishimoto fractional operator, Jumarie’s definitions and so on [15, 16]. This subsection is devoted to a description of the operational properties in order to be acquainted with sufficient fractional calculus theory and enable us to follow the solutions of the problems given in this paper.

Definition 1

The Mittag–Leffler function \(E_{\alpha ,\beta }(z)\) with \(\alpha >0\), \(\beta >0\) is defined by the following series representation, valid in the whole complex plane

$$\begin{aligned} E_{\alpha ,\beta }(z)=\sum _{n=0}^{\infty }\frac{z^{n}}{\Gamma (n \alpha +\beta )},\quad z\in {\mathbb {C}}. \end{aligned}$$
(1)

For \(\beta =1\), we obtain the Mittag–Leffler function in one parameter:

$$\begin{aligned} E_{\alpha ,1}(z)=\sum _{n=0}^{\infty }\frac{z^{n}}{\Gamma (n \alpha +1)}\, {\equiv } \, E_{\alpha }(z). \end{aligned}$$
(2)

Definition 2

The Riemann–Liouville fractional integral operator of order \( \alpha \ge 0 \) of a function f is defined as

$$\begin{aligned} I^{\alpha }\xi (t)=\frac{1}{\Gamma (\alpha )} \int _{0}^{t}(t-x)^{\alpha -1}\xi (x)dx,\quad \alpha>0, \quad x>0, \end{aligned}$$
(3)

in particular \( I^{0}\xi (t)=\xi (t) \).

Definition 3

The Caputo fractional derivative of order \(\alpha \) is defined as

$$\begin{aligned} {}^CD^\alpha _{t}\xi (t)&= {\left\{ \begin{array}{ll} \frac{1}{\Gamma (m-\alpha )}\int _{0}^{t}(t -\tau )^{m-\alpha -1}\xi ^{(m)}(\tau )d\tau ,\quad \alpha> 0,\quad t > 0, &{}\quad m - 1< \alpha < m,~ m\in {\mathbb {N}},\\ \\ \displaystyle \frac{d^m}{dt^m}\xi (t), &{}\quad \alpha = m, \end{array}\right. } \end{aligned}$$
(4)

where the parameter \(\alpha \) is the order of the derivative and is allowed to be real or even complex.

With this definition, a fractional derivative would be defined for differentiable function only [1]. Recently, to overcome this limitation and in order to deal with non-differentiable functions, the following definitions was proposed by Ji Huan He [17]. This modification was successfully applied in the probability calculus, fractional Laplace problems, fractional variational equations and many other types of linear and nonlinear fractional differential equations [18].

Definition 4

The Ji Huan He’s fractional derivative of order \(\alpha \) is defined as [17]

$$\begin{aligned}&{}^HD^\alpha _{t}\xi (t)=\frac{1}{\Gamma (m-\alpha )}\frac{d^{m}}{dt^{m}}\int _{t_{0}}^{t}(\tau -t ) ^{m-\alpha -1}\nonumber \\&\quad \big (\xi _{0}(\tau )-\xi (\tau )\big )d\tau , ~\alpha> 0,~t > 0,~m - 1 < \alpha \le m,~ m\in {\mathbb {N}}. \end{aligned}$$
(5)

He [17] show that Eq. (5) for continuous and differentiable case and continuous and non-differentiable case respectively, is equivalent to

$$\begin{aligned} \frac{1}{\Gamma (m-\alpha )}\frac{d^{m}}{dt^{m}}\int _{t_{0}}^{t}(\tau -t ) ^{m-\alpha -1}\left (\sum _{i=0}^{m-1}\frac{1}{i!}(\tau -t_{0})^{i}\xi ^{(i)}(t_{0})-\xi (\tau )\right )d\tau , \end{aligned}$$
(6)

and

$$\begin{aligned} \frac{1}{\Gamma (m-\alpha )}\frac{d^{m}}{dt^{m}}\int _{t_{0}}^{t}(\tau -t ) ^{m-\alpha -1}\left (\sum _{i=0}^{m-1}\frac{(\tau -t_{0})^{i}}{\Gamma (1+i\alpha )}\xi ^{(i\alpha )}(t_{0})-\xi (\tau )\right )d\tau . \end{aligned}$$
(7)

Furthermore, He [18, 19] defined another fractional derivative in the form:

$$\begin{aligned} {}^VD^\alpha _{t}\xi (t)=\frac{1}{\Gamma (m-\alpha )}\frac{d^{m}}{dt^{m}}\int _{t_{0}}^{t}(\tau -t ) ^{m-\alpha -1}\xi (\tau )d\tau . \end{aligned}$$
(8)

The above definition of fractional derivative was introduced by the variational iteration method [20, 21]. Variational principles play an important role in physics, mathematics, and engineering science because they bring together a variety of fields, lead to novel results and represent a powerful tool of calculation. Several formulations of fractional variational principles were investigated and applied to problems of fractional dynamics. Motivated by the above results and in order to describe better the complexity of the investigated problems, recently He [22, 23] proposed a formulation of fractional variational principles with delay. For more details see [24, 25].

1.3 Fractal calculus

Fractal geometry, fractal calculus and fractional calculus have been becoming hot topics in both mathematics and engineering for non-differential solutions. Fractal theory is the theoretical basis for the fractal space-time, El Naschie’s E-infinity theory, and life science as well [26,27,28]. Fractional calculus was introduced in Newton’s time, and it has become a very hot topic in various fields, especially in mathematics and engineering for porous media, where classic mechanics becomes invalid to describe any phenomena on the porous size scale [29,30,31,32].

The fractal calculus is relatively new, it can effectively deal with kinetics, which is always called as the fractal kinetics, where the fractal time replaces the continuous time. Laurent Nottale revealed that time does be discontinuous in microphysics [33,34,35], that means that fractal kinetics takes place on very small time scale.

The fractal derivative (Hausdorff derivative) on time fractal is defined as [36,37,38]:

$$\begin{aligned} \frac{\partial T}{\partial t^{\sigma }}=\lim _{t_{B}\rightarrow x_{A}}\frac{T(t_{B})-T(t_{A})}{(t_{B})^{\sigma }-(t_{A})^{\sigma }}, \end{aligned}$$
(9)

where \( \sigma \) is the fractal dimensions of time.

A more general definition is given as follows

$$\begin{aligned} \frac{\partial ^{\tau } T}{\partial t^{\sigma }}=\lim _{t_{B}\rightarrow x_{A}}\frac{T^{\tau }(t_{B})-T^{\tau }(t_{A})}{(t_{B})^{\sigma }-(t_{A})^{\sigma }}, \end{aligned}$$
(10)

where \( \tau \) is the fractal dimensions of space.

There are other definitions for fractal derivative, and we will not discuss all definitions, because some definitions are of only mathematical interest. See [39,40,41,42,43] for more applications.

1.4 The physical understanding of the fractional derivative

He [44] showed that fractional differential equations can best describe discontinuous media, and the fractional order is equivalent to its fractional dimensions. Now consider a plane with fractal structure. The shortest path between two points A and B is not a line and we have

$$\begin{aligned} ds_{E}=k\;ds^{\alpha }, \end{aligned}$$
(11)

where \(ds_{E}\) is the actual distance between two terminal points A and B, ds is the line distance between two points, \(\alpha \) is the fractal dimension and k is a constant. Projection of the \(ds_{E}\) into the horizontal direction yields Cantor-like sets, and its length can be expressed as

$$\begin{aligned} \Delta _{x}AB=k_{x}dx^{\alpha _{x}}, \end{aligned}$$
(12)

where \(\alpha _{x}\) are the fractal dimensions of the Cantor-like sets in the horizontal direction, \(k_{x}\) is a constant.

Equation (11) means the following transform

$$\begin{aligned} s_{E}=k\;s^{\alpha }. \end{aligned}$$
(13)

Inspired by this concept of fractional derivative, we assume that the solution of the fractional differential equation can be expressed in terms of \(E_{\alpha }(t^{\alpha })\) and the Mittag–Leffler function plays a fundamental role in our study of fractional equation.

2 Homotopy perturbation method

Consider the following nonlinear differential equation, to illustrate the main ideas of the homotopy perturbation method

$$\begin{aligned} A(u)-f(r)=0, \quad r\in \Omega , \end{aligned}$$
(14)

with boundary conditions

$$\begin{aligned} B\left(u,\frac{\partial u}{\partial n}\right)=0, \quad r\in \Gamma , \end{aligned}$$
(15)

where A and B are respectively, a general differential operator and a boundary operator, f(r) is a known analytic function, \( \Gamma \) is the boundary of the domain \( \Omega \).

In general, the operator A can be divided into two parts L and N, where L is linear and N is nonlinear. Equation (14) therefore can be rewritten as follows:

$$\begin{aligned} L(u)+N(u)-f(r)=0. \end{aligned}$$
(16)

By the homotopy technique [45, 46], we construct a homotopy \( \upsilon (r,p):\Omega \times [0,1]\rightarrow {\mathbb {R}} \) which satisfies

$$\begin{aligned} {\mathcal {H}}(\upsilon ,p)=(1-p)[L(\upsilon )-L(u_{0})]+p[A(\upsilon )-f(r)]=0,\quad p\in [0,1],\quad r\in \Omega , \end{aligned}$$
(17)

or

$$\begin{aligned} {\mathcal {H}}(\upsilon ,p)=L(\upsilon )-L(u_{0})+pL(u_{0})+p[N(\upsilon )-f(r)]=0, \end{aligned}$$
(18)

where \( p\in [0,1]\) is an embedding parameter, \( u_{0} \) is an initial approximation of Eq. (14), which satisfies the boundary conditions. Obviously, from Eqs. (17) and (18), we have

$$\begin{aligned} {\mathcal {H}}(\upsilon ,0)&= L(\upsilon )-L(u_{0})=0, \end{aligned}$$
(19)
$$\begin{aligned} {\mathcal {H}}(\upsilon ,1)&= A(\upsilon )-f(r)=0, \end{aligned}$$
(20)

the changing process of p from zero to unity is just that of \( \upsilon (r,p) \) from \( u_{0}(r) \) to u(r). In topology, this is called deformation, and \( L(\upsilon )-L(u_{0}) \), \( A(\upsilon )-f(r) \) are called homotopic.

Now, assume that the solution of (17) and (18) can be expressed as:

$$\begin{aligned} \upsilon =\upsilon _{0}+p \upsilon _{1}+p^{2}\upsilon _{2}+\cdots . \end{aligned}$$
(21)

Setting \( p=1 \) results in the approximate solution of Eq. (14):

$$\begin{aligned} u=\lim _{p\rightarrow 1} \upsilon =\upsilon _{0}+\upsilon _{1}+\upsilon _{2}+\cdots . \end{aligned}$$
(22)

In these years, some rather extraordinary virtues of the homotopy perturbation method (HPM) have been exploited. The method has eliminated limitations of the traditional perturbation methods. On the other hand it can take full advantage of the traditional perturbation techniques so there has been a considerable deal of research in applying homotopy technique for solving various strongly nonlinear equations, [47,48,49,50,51] furthermore the differential operator L does not need to be linear [52].

3 Extended homtopy perturbation method

To illustrate the basic ideas of the extended homotopy perturbation method (MHPM) as a special category of new analytical methods [53] for fractional differential equations, we consider the following problem [54]

$$\begin{aligned} {}^HD_{t}^\alpha \xi (x,t) = f(\xi (x,t)),~ m - 1< \alpha < m,~m \in {\mathbb {N}},\quad t \ge 0,\quad x \in {\mathbb {R}}, \end{aligned}$$
(23)

subject to the initial and boundary conditions

$$\begin{aligned} \xi ^{(i)} (0,0) = c_i,i=0,1,\ldots ,n,~ B\left( {\xi ,\frac{{\partial \xi }}{{\partial x}},\frac{{\partial \xi }}{{\partial t}}} \right) = 0. \end{aligned}$$
(24)

Assume now that

$$\begin{aligned} f = L\xi (x,t) +(TMS)_{J} (\xi (x,t)) -g(x,t), \end{aligned}$$
(25)

where TMS is a modification of Eq. (23) which is defined in [55]:

$$\begin{aligned} (TMS)_{J}(\xi (x,t))&= ( \xi _0 (x,t)+\frac{1}{2}\xi _0 (x,t)(\xi _1 (x,t))^2) \nonumber \\&+ p \left( \xi _0 (x,t) \xi _1 (x,t) \right) + p^2 \left( \xi _0 (x,t) \xi _2 (x,t)\right) + \nonumber \\&+ \frac{1}{6}p^3 \left( (\xi _0 (x,t))^2 (\xi _3 (x,t))^2 \xi _2 (x,t)\right) + \underbrace{\ldots }_{Jtimes}, \end{aligned}$$
(26)

and L is a linear operator, g is a known analytical function and denotes the fractional derivative in the Ji Huan He sense. \(\xi \) is assumed to be a causal function of time, i. e., vanishing for \(t<0 \). Also, \(\xi ^{(i)} (x,t)\) is the ith derivative of \(\xi ,\,c_i ,\,i = 0,1,\ldots ,m - 1\) are the specified initial conditions and B is a boundary operator. In view of He’s homotopy perturbation technique, we can construct the following simple homotopy

$$\begin{aligned} {}^HD_{t}^\alpha \xi (x,t) + pf = 0,~ p \in [0,1]. \end{aligned}$$
(27)

The homotopy parameter always changes from zero to unity. In case \(p=0\), Eq. (27) becomes

$$\begin{aligned} {}^HD_{t}^\alpha \xi (x,t) = 0, \end{aligned}$$
(28)

where \(p=1\), Eq. (27) turns out to be the original fractional differential equation. In view of homotopy perturbation method, we use the homotopy parameter p to expand the solution in the following form

$$\begin{aligned} \xi _j(x,t) \approx \frac{{\xi (x,t) - \sum \limits _{i = 0}^{j - 1} {p^i \xi _i(x,t) } }}{{p^j }},~p \ne 0, \end{aligned}$$
(29)

Applying the inverse operator and considering the initial and boundary conditions, the terms of the series solution can be given by

$$\begin{aligned} \begin{array}{l} \xi _1 (x,t) = \sum \limits _{i = 0}^{n - 1} {c_i \frac{{t^i }}{{i!}},} - I_t^\alpha (L\xi _0 (x,t)) - I_t^\alpha (\xi _0 (x,t)) + I_t^\alpha g(x,t), \\ \xi _j (x,t) = - \,I_t^\alpha (L\xi _{j - 1} (x,t)) - I_t^\alpha (TMS)_{j - 1} (\xi _0 (x,t),\xi _1 (x,t),\ldots ,\xi _{j - 1} (x,t)),\,j = 2,3,\ldots . \end{array} \end{aligned}$$
(30)

Hence, we get an accurate approximate solution by adding the components of Eq. (30.

Define that \( (C({\mathbb {R}}^{2}),\Vert .\Vert ) \) is the Banach space, the space of all continuous functions on \( {\mathbb {R}}^{2}\) with the norm

$$\begin{aligned} \Vert f(x,t) \Vert = \max _{\forall x, t} \vert f(x,t) \vert . \end{aligned}$$
(31)

Definition 5

A function \( f:{\mathbb {R}}^{2}\rightarrow {\mathbb {R}} \) is said to satisfy the Lipschitz condition if there is a constant P such that

$$\begin{aligned} \vert f(X)-f(Y) \vert \le P \vert X-Y \vert , \quad \forall X, Y \in {\mathbb {R}}^2. \end{aligned}$$
(32)

The smallest constant P satisfying (32) is called a Lipschitz constant.

Theorem 1

Letfsatisfy the Lipschitz condition (32), \( M=\max _{0\le \tau \le t,0\le t \le T}\vert (t-\tau )^{\alpha -1} \vert \)and\( \gamma = [\frac{PMT}{\Gamma (\alpha )}].\frac{1}{n!} \), then the problem (23) has a unique solution\( \xi (x,t) \), whenever\( 0< \gamma <1 \).

Proof

Let y and z be two different solutions of (30) for all \( t\in [0,T] \) and \( \tau \in [0,t] \). Then,

$$\begin{aligned} y-z&= - I_t^\alpha (L y (x,t)) - I_t^\alpha (TMS)_{j - 1} (y _0 (x,t),y _1 (x,t),\ldots ,y _{j - 1} (x,t))\\&- I_t^\alpha (L z (x,t)) - I_t^\alpha (TMS)_{j - 1} (z_0 (x,t),z_1 (x,t),\ldots ,z_{j - 1} (x,t)). \end{aligned}$$

In other words

$$\begin{aligned} y-z&= - I_t^\alpha (L (y (x,t)-z(x,t)) - I_t^\alpha (TMS)_{j - 1} ((y _0 (x,t),y _1 (x,t),\ldots ,y _{j - 1} (x,t))\\&- (z_0 (x,t),z_1 (x,t),\ldots ,z_{j - 1} (x,t))). \end{aligned}$$

Hence, one will set

$$\begin{aligned} \vert y-z \vert&= \vert \frac{1}{\Gamma (\alpha )}\int _{0}^{t} (t-\tau )^{\alpha -1} L (y (x,\tau )-z(x,\tau ))d\tau \\&- \frac{1}{\Gamma (\alpha )}\int _{0}^{t} (t-\tau )^{\alpha -1}(TMS)_{j - 1} ((y _0 (x,t),y _1 (x,t),\ldots ,y _{j - 1} (x,t))\\&-(z_0 (x,t),z_1 (x,t),\ldots ,z_{j - 1} (x,t)))d\tau \vert , \end{aligned}$$

and

$$\begin{aligned} \max \vert y-z \vert \le \frac{P}{\Gamma (\alpha )}\max \int _{0}^{t}\vert (t-\tau )^{\alpha -1} \vert \vert y-z \vert d\tau . \end{aligned}$$

Consequently

$$\begin{aligned} \Vert y-z \Vert \le \left[ \frac{PMT}{\Gamma (\alpha )}\right] ^{n}. \frac{1}{n!}\Vert y-z \Vert \le \gamma \Vert y-z \Vert , \end{aligned}$$
(33)

or

$$\begin{aligned} (1-\gamma ) \Vert y-z \Vert \le 0. \end{aligned}$$
(34)

Since \( 1-\gamma \ne 0 \), then \(\Vert y-z \Vert \). Therefore \( y=z \) and this completes the proof. □

Theorem 2

Let\( \xi _{n}(x,t) \)and\( \xi (x,t) \)be defined in Banach space\( (C([0,T]),\Vert .\Vert ) \). Then, the series solution\( \lbrace \xi _{n}(x,t)\rbrace ^{\infty }_{n=1} \)defined by (30) converges to the solution of (25), if\( 0<\gamma <1 \).

Proof

Suppose that \( \lbrace s_{n} \rbrace \) is the sequence of partial sums of the series (30) and we need to show that \( s_{n}(t) \) is a Cauchy sequence in Banach space \( (C([0,T]),\Vert .\Vert ) \). For this, we consider

$$\begin{aligned} \Vert s_{n+1}(t)-s_{n}(t)\Vert = \Vert \xi _{n+1}(t)\Vert \le \gamma \Vert \xi _{n}(t)\Vert \le \gamma ^{2} \Vert \xi _{n-1}(t)\Vert \le \cdots \le \gamma ^{n+1}\Vert \xi _{0}(t) \Vert . \end{aligned}$$
(35)

Now, for every \(n,m \in N, n\ge m \) there are two arbitrary partial sums \( s_{n} \) and \( s_{m} \); by using (35) and triangle inequality successively, we have

$$\begin{aligned} \begin{array}{ll} \Vert s_{n}-s_{m}\Vert &=\Vert (s_{n}(t)-s_{n-1}(t))+ (s_{n-1}(t)-s_{n-2}(t))+\cdots + (s_{m+1}(t)-s_{m}(t))\Vert \\ & \le \Vert s_{n}-s_{n-1} \Vert +\Vert s_{n-1}-s_{n-2} \Vert +\cdots + \Vert s_{m+1}-s_{m} \Vert \\ &\le [\gamma ^{n}+\gamma ^{n-1}+\gamma ^{n-2}+\cdots + \gamma ^{m+1} ]\Vert \xi _{0}(t) \Vert \\ & \le \gamma ^{m+1}[\gamma ^{n-m-1}+\gamma ^{n-m-2}+\cdots +\gamma +1]\Vert \xi _{0}(t)\Vert \\ & \le \gamma ^{m+1}\left( \frac{1-\gamma ^{n-m}}{1-\gamma }\right) \Vert \xi _{0}(t)\Vert . \end{array} \end{aligned}$$
(36)

Since \( 0<\gamma <1 \), we have \( (1-\gamma ^{n-m})<1 \); then

$$\begin{aligned} \Vert s_{n}-s_{m} \Vert \le \frac{\gamma ^{m+1}}{(1-\gamma )}\max _{\forall t\in [0,T]} \vert \xi _{0}(t)\vert . \end{aligned}$$
(37)

Since \( \xi _{0} \) is bounded,

$$\begin{aligned} \lim _{n,m\rightarrow \infty } \Vert s_{n}(t)-s_{m}(t)\Vert =0. \end{aligned}$$
(38)

Therefore, \( s_{n}(t) \) is a Cauchy sequence in C[0, T] , so the series converges and the proof complete.□

4 Case studies in chemical phenomena

4.1 Time fractional Burgers equation

The purpose of this example is to use the MHPM for solving time-fractional Burgers equation. The fractional derivative is described in the Ji Huan He sense. In this schemes, the solutions take the form of a convergent series. The time-fractional Burgers equation with time-fractional derivative commonly used in traffic flow, acoustic transmission, shocks, boundary layer, the steepening of the waves and fluids, thermal radiation, chemical reaction, gas dynamics and many other phenomena [56].

Example 1

Consider the following time-fractional Burgers equation [56]

$$\begin{aligned} ^{H}D_{t}^{\alpha }\xi (x,t)=f(\xi (x,t)),~0<\alpha \le 1,\quad 0\le x \le 1,\quad t>0. \end{aligned}$$
(39)

where

$$\begin{aligned} f(\xi (x,t))=\xi (x,t)\frac{\partial }{\partial x}\xi (x,t)+v \frac{\partial ^{2}}{\partial x^{2}} \xi (x,t),~v \in {\mathbb {R}}. \end{aligned}$$
(40)

We solved this equation for different values of \(\alpha \) where \(\xi _{0}=\xi (x,0)=1-\tanh (\frac{x}{2v})\). By the same manipulation as Sect. 3, we get

$$\begin{aligned} \xi (x,t) = \xi _{0}+\frac{t^{\alpha }\sec h\left( \frac{x}{2v}\right) }{2v\Gamma (1+\alpha )} +\dfrac{4t^{2\alpha }\cosh ^{3} \left( \frac{x}{2v}\right) \sinh ^{4} \left( \frac{x}{2v}\right) }{v^{2}\Gamma (1+2\alpha )}+\cdots . \end{aligned}$$
(41)

Alam Khan and Ara [56] shows that the exact solution with \(\alpha =1\) is

$$\begin{aligned} \xi _{Exact}=\left( 1-\tanh \left( \frac{x-t}{2v}\right) \right) . \end{aligned}$$
(42)

According to the (26) and based on a suitable approximation of (5) the approximate solution of the problem for several values of \(t, x, v=0.5, \alpha \) and the number of iteration (NI) for the HPM and proposed method (MHPM) is represented in Table 1. In this case, acceptable agreement between \(\xi _{MHPM} (x,t)\) and \(\xi _{Exact} (x,t)\) are noticeable. In addition, Fig. 1 includes the absolute error between the exact, HPM and MHPM solution of time-fractional Burgers equation. The numerical results demonstrate the significant features, efficiency and reliability of the MHPM is more promising, convenient, and computationally attractive than other methods such HPM and the obtained results by using generalized differential transform method [56] and the references therein.

Table 1 Numerical results of Example 1 for several values of \(t, x, \alpha \)
Full size table
Fig. 1
figure 1

The absolute error between the exact, HPM and MHPM solution for Example 1

Full size image

4.2 Concentration of reactants

As we know, at a fixed temperature and in the absence of catalyst, the rate of given reaction increases with increased concentration of reactants. With increasing concentration of the reactant the number of molecules per unit volume is increased, thus the collision frequency is increased, which ultimately causes increased reaction rate.

Example 2

The concentrations of three reactants are in the form of a system of nonlinear fractional differential equations as

$$\begin{aligned} \left\{ \begin{array}{l} ^{H}D^{\alpha }\xi _{1}(x,t)=-\,0.04\xi _{1}(x,t)+0.01\xi _{2}(x,t)\xi _{3}(x,t),\\ ^{H}D^{\alpha }\xi _{2}(x,t)=-\,400\xi _{1}(x,t)-100\xi _{2}(x,t)\xi _{3}(x,t)-30000(\xi _{2}(x,t))^{2},\\ ^{H}D^{\alpha }\xi _{3}(x,t)=30(\xi _{2}(x,t))^{2}, \end{array}\right. \end{aligned}$$
(43)

where

$$\begin{aligned} \xi _{1}(0,0)=1,\quad \xi _{2}(0,0)=\xi _{3}(0,0)=0. \end{aligned}$$
(44)

Again, according to the (26) and by setting the properties of \((^{H}D^{\alpha })\) for every equation in (43) and using (44), we get the MHPM formula for concentration equations as follow

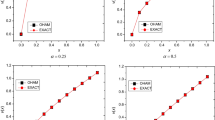
$$\begin{aligned} \left\{ \begin{array}{l} \xi _{1}(x,t) \simeq 1-\dfrac{xt^{\alpha }}{25\Gamma (1+\alpha )}+\dfrac{xt^{2\alpha }}{6253\Gamma (1+2\alpha )}-\dfrac{xt^{3\alpha }}{15625\Gamma (1+3\alpha )}, \\ \\ \xi _{2}(x,t) \simeq -\dfrac{400xt^{\alpha }}{\Gamma (1+\alpha )}+\dfrac{16xt^{2\alpha }}{6253\Gamma (1+2\alpha )}-\dfrac{480000000xt^{3\alpha }}{15625\Gamma (1+3\alpha )^{2}\Gamma (1+3\alpha )}, \\ \\ \xi _{3}(x,t) \simeq \dfrac{4800000xt^{3\alpha }}{\Gamma (1+\alpha )^{2}\Gamma (1+3\alpha )}, \end{array}\right. \end{aligned}$$
(45)

which for \(x=1\) and \(x=\alpha =1\) is the same of solution in [57, 58] respectively. Moreover, Fig. 2 depicts the approximate solutions for different values of \(\alpha \). In comparing with [57, 58] the approximations obtained by the proposed method are uniformly valid not only for small parameters, but also for very large parameters. The number of iteration is very low and the numerical outputs indicate that MHPM is easy to implement and computationally very attractive.

Fig. 2
figure 2

The plots of \( \xi _1(x,t), \xi _2(x,t),\xi _3(x,t) \), for \( \alpha =0.9\) respectively

Full size image

5 Conclusions

In this study, based on Ji Huan He’s derivative a new extended homotopy perturbation method was performed and has been successfully applied to compute the approximate solution for some of the most famous mathematical chemistry equations of fractional orders and we will try to define the way in which the structure of a complicated chemical mechanism are associated with the mathematics formula. The uniqueness of the solution and convergence analysis of the proposed method have been discussed. The rise of nonlinear terms is vital to progress in many homotopy perturbation systems. In this work, we introduced a new reliable algorithm for the calculation of these polynomials. The algorithm can be elegantly used without any need to formulas other than elementary operations. Two complicated cases of nonlinearity forms were handled by the new algorithm using only at most 6 components of the MHPM solution. In comparing with [56,57,58] the results are so promising. In the other word, in whole of defined domain the obtained results with a very low complexity of calculations imply an elegant superiority of our new method. We point out that the corresponding analytical and numerical solutions were obtained using Mathematica.