Semi-analytical solution for time-fractional diffusion equation based on finite difference method of lines (MOL)

Abstract

In this article, we apply the method of lines (MOL) for solving the time-fractional diffusion equations (TFDEs). The use of MOL yields a system of fractional differential equations with the initial value. The solution of this system could be obtained in the form of Mittag–Leffler matrix function. A direct method which computes the Mittag–Leffler matrix by applying its eigenvalues and eigenvectors analytically has been discussed. The direct approach has been applied on one-, two-, and three-dimensional TFDEs with Dirichlet, Neumann, and periodic boundary conditions as well.

1 Introduction

A wide variety of approximate methods has been investigated to solve time-dependent partial differential equations [14]. In recent years, time-fractional partial differential equations (TFPDEs) and their numerical solutions have been investigated by many researchers [4, 16,17,18,19, 27]. One way to solve TFPDEs numerically is to discretize these equations in space, by applying various techniques, but leave time variable. This way is known as Method Of Lines (MOL) [11] and converts the TFPDE to a system of fractional ordinary differential equations (FODEs) or fractional differential algebraic equations (FDAEs). In TFPDEs, it involves discretising a given differential equation in space variables while obtaining analytical solution in the time direction. For this reason, the MOL is well known as a semi-analytical method [5, 29].

In this paper, we consider the Caputo-type time-fractional diffusion equations with the initial condition as

$$\begin{aligned}& \frac{\partial ^{\alpha } U}{\partial t^{\alpha }} =a\left( \frac{\partial ^2U}{\partial x^2}+ \frac{\partial ^2U}{\partial y^2}+\frac{\partial ^2U}{\partial z^2}\right) ,\\ & \quad a,~t>0, ~0<\alpha \le 1,~ (x,y,z)\in \Omega ,\\& U(x,y,z,0)=f(x,y,z),\\ & \quad (x,y,z)\in \Omega , \end{aligned}$$

where $\Omega \subset R^3$ is an open bounded domain with smooth boundary $\partial \Omega$. In practice, the most common boundary conditions are as follows:

$$\begin{aligned}&\text{ a. } \text{ Dirichlet } ~~~~~~\qquad U=g_1,~~~~~~~~~~\qquad (x,y,z)\in \partial \Omega ,\\&\text{ b. } \text{ Neumann } ~~~\qquad \frac{\partial }{\partial n}U=g_1,~~~~~~~~\qquad (x,y,z)\in \partial \Omega ,\\&\text{ c. } \text{ Periodic } ~~ U(L,t)=U(-L,t),~~ \frac{\partial }{\partial n}U(L,t)=\frac{\partial }{\partial n}U(-L,t),\\ & \quad L\in \partial \Omega _{1/2},-L\in \partial \Omega -\partial \Omega _{1/2}, \end{aligned}$$

where $\partial \Omega _{1/2}$ denotes the half of the $\partial \Omega$.

MOL converts the time-fractional diffusion equation to a system of FODEs with the initial values. The solution of this system could be obtained in the form of Mittag–Leffler (ML) matrix function. ML function is a general form of exponential function. Various techniques to the matrix exponential function are generated through rational, Pad$\acute{\mathrm {e}}$ approximations and scaling and squaring method [13, 21, 23, 26, 28, 31]. However, these techniques are not efficient to computing the Mittag–Leffler matrix function. Obtaining the iterative method for this type of matrix function such as ones utilized for matrix exponential function is not effective. Some efficient methods have been recently presented to compute ML functions and ML matrix functions as well. The Krylov subspace methods for ML matrix functions have been presented by Moret and Novati [22]. The numerical evaluation of two- and three-parameter ML functions has been computed by Garrappa [9]. He presented a method for the efficient computation of the ML function based on the numerical inversion of its Laplace transform as well. Accordingly, efficient Matlab code to evaluate the ML matrix function with two parameters has been obtained by Garrappa and Popolizio [10, 32]. In addition, Podlubny and Kacenak [25] have presented the efficient computation Matlab code of the ML function with desired accuracy. In this article, we use this code to compute the ML functions.

In general, the ML matrix function could be computed by the matrix eigenvalues and eigenvectors directly. In the current manuscript, our main goal is to convert the time-fractional diffusion equation to a system of FODEs with the initial values via finite difference MOL method. Then, we solve this system analytically by means of ML matrix function. Eventually, knowing the eigenvalues and eigenvectors of tridiagonal matrix, we compute the ML matrix function directly.

2 Preliminaries and definitions

First, we give some basic definitions and properties of the fractional calculus theory which are needed next. Then, the definition and some properties of Mittag–Leffler functions are discussed. The Kronecker product and Kronecker sum of matrices are defined, also some properties of tridiagonal matrix, such as the characteristic equation and eigenvalues of them are presented in the end of this section.

Definition 2.1

The Caputo derivative is defined as follows [24]:

$$\begin{aligned} D_{*}^{\alpha } f(x)= & {} \frac{1}{\Gamma (n-\alpha )}\int _{0}^{x} (x-t)^{n-\alpha -1} \frac{d^{n}f(t)}{dx^{n}} dt, \qquad \alpha \in (n-1,n],~ n \in \mathbb {N}, \end{aligned}$$

where $\alpha>0$ is the order of the derivative, n is the smallest integer greater than $\alpha$, and $\mathbb {N}$ denotes the set of natural numbers.

For the Caputo derivative, we have $D_{*}^{\alpha } c = 0,$ where c is a constant, and

$$\begin{aligned} D_ * ^\alpha {x^\beta } = \left\{ \begin{array}{l} 0,\,\,\,\,~~~~~~~~~~~~~~~~\quad \beta \in {\mathbb {N}_0}~~\mathrm {and}~~ \beta < \left\lceil \alpha \right\rceil , \\ \frac{{\Gamma (\beta + 1)}}{{\Gamma (\beta + 1 - \alpha )}} {x^{\beta - \alpha }},~~~~~~\beta \in {\mathbb {N}_0}~~\mathrm {and}~~\beta \ge \left\lceil \alpha \right\rceil ~~\mathrm {or}~~\beta \notin \mathbb { N}~~\mathrm {and}~~ \beta> \left\lfloor \alpha \right\rfloor , \\ \end{array} \right. \end{aligned}$$

where $\mathbb {N}_0=\{0,1,2,\cdots \}.$

Definition 2.2

For n to be the smallest integer that exceeds $\alpha$, the Caputo time-fractional derivative operator of order $\alpha>0$ is defined as [24]

$$\begin{aligned} D_ * ^\alpha u(\mathbf {x},t) = \frac{{{\partial ^\alpha }u(\mathbf {x},t)}}{{\partial {t^\alpha }}} = \left\{ \begin{array}{l} \frac{1}{{\Gamma (n - \alpha )}}\int _0^t ( t - \tau {)^{n - \alpha - 1}} \frac{{{\partial ^n}u(\mathbf {x},\tau )}}{{\partial {\tau ^n}}}d\tau ,\,\,\,\,~~~~~n-1<\alpha <n , \\ \frac{{{\partial ^n}u(\mathbf {x},t)}}{{\partial {t^n}}}, ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\quad \alpha = n \in \mathbb {N}. \\ \end{array} \right. \end{aligned}$$

2.1 Mittag–Leffler function

The one, two and three-parameter Mittag–Leffler functions which are relevant to the fractional calculus, are defined as

$$\begin{aligned} \begin{array}{l} {E_\alpha }(z) = \sum \limits _{k = 0}^\infty {\frac{{{z^k}}}{{\Gamma (\alpha k + 1)}}} ,~~~~~~~~~~\mathscr {R}(\alpha )> 0,~z \in \mathbb {C}, \\ {E_{\alpha ,\beta }}(z) = \sum \limits _{k = 0}^\infty {\frac{{{z^k}}}{{\Gamma (\alpha k + \beta )}}} , ~~~~~~~\mathscr {R}(\alpha )> 0,~\beta ,~z \in \mathbb {C}. \end{array} \end{aligned}$$

In the case, $\alpha$ and $\beta$ are real and positive, and these series converge for all values of z. Note that when $\beta =1$, $E_{\alpha ,1 }(z)=E_{\alpha }(z)$. The solutions of linear fractional differential equations are often indicated in terms of Mittag–Leffler functions because of the following property of these functions:

$$\begin{aligned} D_* ^\alpha E_{\alpha }(\lambda x^{\alpha }) = \lambda E_{\alpha }(\lambda x^{\alpha }). \end{aligned}$$

Lemma 2.1

For any real$a\ne b,$we have the following relation [24]:

$$\begin{aligned} \int _{0}^{t}\tau ^{\alpha -1}{E_{\alpha ,\alpha }}(a \tau ^{\alpha })E_{\alpha }(b (t-\tau )^{\alpha })d\tau = \frac{1}{a-b} \left( E_{\alpha }(a t^{\alpha })-E_{\alpha }(b t^{\alpha })\right) . \end{aligned}$$

Definition 2.3

Let $A\in \mathbb {R}^{m,n}$ and $B\in R^{p,q}.$ Then, the Kronecker product (or tensor product) of A and B is defined as the matrix [1]:

$$\begin{aligned} A\otimes B =\left( \begin{array}{cccc} a_{11}B &{} ... &{} a_{n1}B \\ \vdots &{} \ddots &{} \vdots \\ a_{n1}B &{} ... &{} a_{nm}B \end{array} \right) \in \mathbb {R}^{mp,nq}. \end{aligned}$$

Definition 2.4

Let $A\in \mathbb {R}^{m,m}$ and $B\in R^{n,n}.$ Then, the Kronecker sum (or tensor product) of A and B is the $mn\times mn$ matrix defined by [1]

$$\begin{aligned} A\oplus B =I_n\otimes A + B\otimes I_m. \end{aligned}$$

The following lemma assists us to compute the Mittag–Leffler matrix functions effectively in the next sections.

Lemma 2.2

For the diagonalizable matrices$A=X_A\Lambda _AX_A^{-1}\in \mathbb {R}^{m,m}$ and $B=X_B\Lambda _BX_B^{-1}\in R^{n,n}$, where$X_A$and$X_B$are matrices of eigenvectors ofAandB,  respectively, and also$\Lambda _A$and$\Lambda _B$are diagonal matrices of their eigenvalues, we have

$$\begin{aligned} A\oplus B =(X_B\otimes X_A)(\Lambda _A\oplus \Lambda _B)(X_B\otimes X_A)^{-1}. \end{aligned}$$

Proof

Using the definition of Kronecker sum for term $\Lambda _A\oplus \Lambda _B$, we can prove the lemma. $\square$

The pervious lemma can be simply generalized for r diagonalizable matrices $A_i=X_i\Lambda _i X_i^{-1}\in \mathbb {R}^{m_i,m_i},~i=1,...,r,$ as follows:

$$\begin{aligned} A_1\oplus ...\oplus A_r = (A_r\otimes ...\otimes A_1)(\Lambda _1\oplus ...\oplus \Lambda _r)(A_r\otimes ...\otimes A_1)^{-1}. \end{aligned}$$

Definition 2.5

Consider the tridiagonal matrix

$$\begin{aligned} \small T_n=\left( \begin{array}{cccccc} \alpha _1 &{} \gamma _1 &{} &{} &{} &{} \\ \beta _2 &{} \alpha _2 &{}~~~~ \gamma _2 &{} &{} &{} \\ &{} \ddots &{}~ ~\ddots &{}~~~\ddots &{} &{} \\ &{} &{} \beta _{n-1} &{} \alpha _{n-1} &{} \gamma _{n-1}\\ &{} &{} &{} \beta _{n} &{} \alpha _{n} \end{array} \right) . \end{aligned}$$

(2.1)

Denote the characteristic polynomial of $T_n$ by $p_n(\lambda )=det(\lambda I- T_n).$ The recursion for computing $p_n(\lambda )$ is [2]

$$\begin{aligned} p_0(\lambda )=1,\qquad p_1(\lambda )=\lambda -\alpha _1,\qquad p_i(\lambda )=(\lambda -\alpha _i)p_{i-1}(\lambda )-\beta _i \gamma _{i-1}p_{i-2}(\lambda ), \end{aligned}$$

where $2\le i\le n.$

For more details about the eigenvalues of tridiagonal matrix for special case, please see [20].

This paper is arranged as follows: in Sect. 3, the finite difference method for 1D fractional diffusion equation has been applied to convert this equation to a system of fractional ordinary differential equations. The eigenvalues and eigenvectors of the coefficient matrix of this system for different boundary conditions have been presented. In Sects. 4 and 5, we generalize FDM for 2D and 3D problems as well. The analytical solution of linear system of fractional ordinary differential equations has been described in Sect. 6. The property of direct methods which could solve the system of fractional ODEs obtained by MOL [6] on TFDE analytically is described in Sect. 7. Some test problems are solved with the proposed method in Sect. 8. The conclusion and future work are discussed in the final section.

3 Finite difference method for 1D diffusion equation

In this section, we decide to convert the 1D diffusion equation, with various types of boundary conditions, to the system of FODEs in the form $u ^{(\alpha )}=Au +\mathbf f,$ via central finite difference MOL method. Then, by obtaining the eigenvalues and eigenvectors of A,  we solve this system directly.

First, consider the heat equation with heat sources which models the temperature distribution in a long thin rod of length L. The time-fractional partial differential equation (PDE) for this problem with the source term f and the initial condition is

$$\begin{aligned}&U^{(\alpha )}_t= U_{xx}+f(x,t),\qquad ~~~~~ x\in (x_0,L], ~t>0,~0<\alpha \le 1,\nonumber \\&U(x,0)=U_0(x),\qquad \qquad \qquad x\in (x_0,L]. \end{aligned}$$

(3.1)

Evaluating the diffusion operator $U_{xx}$ using a central finite difference schemes around $x_i$ gives

$$\begin{aligned} {\left\{ \begin{array}{ll} U^{(\alpha )}_i= \frac{1}{h^2}\left( U_{i+1}-2U_{i}+U_{i-1}\right) +f_i+ {O(h^2)},\qquad i=1,2,...,M-1,\\ U_i(0)=U_0(x_i), \end{array}\right. } \end{aligned}$$

(3.2)

where $h=(L-x_0)/M$ and $U_i=U(x_i,t)$. This method converges with second-order accuracy in space, while $U\in C^2[x_0,L]$. Equation (3.2) could be redefined in the following system of FODEs:

$$\begin{aligned} \mathbf u ^{(\alpha )}=A\mathbf u +\mathbf f ,~~~~\qquad \mathbf u (0)=\mathbf u _0, \end{aligned}$$

(3.3)

where the initial condition $\mathbf u _0,$ the vector $\mathbf f$, and matrix A are different for some boundary conditions. We will discuss about these matrices and their properties in the next subsections.

3.1 Two-side Dirichlet boundary conditions

In the case of heat conduction equation, Dirichlet boundary conditions for the region would be to specify the temperature at the bounds of the region.

Dirichlet boundary conditions at the two boundaries ($U(x_0,t)=U(L,t)=0$) give

$$\begin{aligned} \mathbf f =[f_1,...,f_{M-1}]^T,\qquad \mathbf u _0=[U_1(0),...,U_{M-1}(0)]^T,\qquad A=\frac{1}{h^2}\mathrm {Trid}(1,-2,1). \end{aligned}$$

The eigenvalues and eigenvectors of A are [20]

$$\begin{aligned} \lambda _i= & {} -\frac{4}{h^2}\sin ^2 \left(\frac{i\pi }{2M} \right),\qquad i=1,2,...,M-1,\\ x_j^{(i)}= & {} \sqrt{\frac{2}{M}}\sin \left(\frac{ij}{M}\pi \right),\quad i=1,2,...,M-1,\quad j=1,2,...,M-1. \end{aligned}$$

The matrix A is symmetric, thus, its eigenvectors are orthonormal, and then, we have

$$\begin{aligned} A=X\Lambda X^T,\qquad ~~X_{ij}=x_j^{(i)}. \end{aligned}$$

3.2 Two-side Neumann boundary conditions

Boundary conditions of the Neumann type are specified functions of time representing the heat flow across the boundary.

Two-side Neumann boundary conditions, $U_x(x_0,t)=U_x(L,t)=0$, give

$$\begin{aligned} \mathbf f =[f_0,...,f_M]^T,\qquad \mathbf u _0=[U_0(0),...,U_{M}(0)]^T, \end{aligned}$$

and also

$$\begin{aligned} A=\frac{1}{h^2} \left( \begin{array}{cccccc} -2 &{} ~~2 &{} &{} &{} &{} \\ 1 &{} -2 &{}~~~~ 1 &{} &{} &{} \\ &{} \ddots &{}~ ~\ddots &{}~~~\ddots &{} &{} \\ &{} &{} 1 &{} -2 &{} 1\\ &{} &{} &{} 2 &{} -2 \end{array} \right) _{(M+1)\times (M+1)}, \end{aligned}$$

which its eigenvalues and eigenvectors are [20]

$$\begin{aligned}&\lambda _{i+1}=-\frac{4}{h^2}\sin ^2\big (\frac{i\pi }{2M}\big ), \qquad i=0,1,2,...,M,\\&x_{j+1}^{(i+1)}=\cos \big (\frac{ij}{M}\pi \big ),\quad i=0,1,...,M,\quad j=0,1,...,M. \end{aligned}$$

In addition, we can write

$$\begin{aligned} X^{-1}_{ij}=\frac{2}{Mc_ic_j}x_i^{(j)},~~~~i,j=1,...,M+1, \end{aligned}$$

where $c_1=c_{M+1}=2$ and $c_i=1,~i=2,3,...,M$.

3.3 Neumann–Dirichlet boundary conditions

Here, the matrix A for left-side Neumann and right-side Dirichlet or left-side Dirichlet and right-side Neumann boundary conditions is as follows:

$$\begin{aligned} A=\left( \begin{array}{cccccc} -2 &{} ~~2 &{} &{} &{} &{} \\ 1 &{} -2 &{}~~~~ 1 &{} &{} &{} \\ &{} \ddots &{}~ ~\ddots &{}~~~\ddots &{} &{} \\ &{} &{} 1 &{} -2 &{} 1\\ &{} &{} &{} 1 &{} -2 \end{array} \right) _{M\times M}\qquad \mathrm {or}\qquad \left( \begin{array}{cccccc} -2 &{} ~~1 &{} &{} &{} &{} \\ 1 &{} -2 &{}~~~~ 1 &{} &{} &{} \\ &{} \ddots &{}~ ~\ddots &{}~~~\ddots &{} &{} \\ &{} &{} 1 &{} -2 &{} 1\\ &{} &{} &{} 2 &{} -2 \end{array} \right) _{M\times M}. \end{aligned}$$

(3.4)

For each matrix, the eigenvalues are [20]

$$\begin{aligned} \lambda _{i}=-4\sin ^2\left(\frac{2i-1}{4M}~\pi \right),\qquad i=1,2,...,M. \end{aligned}$$

The eigenvectors for the left matrix of Eq. (3.4) are

$$\begin{aligned} x_{j}^{(i)}=\sin \bigg (\frac{(M-j+1)(2i-1)}{2M}~\pi \bigg ),\qquad i,~j=1,...,M, \end{aligned}$$

and the eigenvectors of the right matrix of Eq. (3.4) are

$$\begin{aligned} \bar{x}_{j}^{(1)}=x_{j}^{(M)},~~\bar{x}_{j}^{(M)}=x_{j}^{(1)},\quad \bar{x}_{j}^{(i)}=x_{j}^{(i)},\quad i=2,...,M-1,~~~~j=1,...,M. \end{aligned}$$

$X_{ij}=x_j^{(i)},~\bar{X}_{ij}=\bar{x}_j^{(i)}~,i,~j=1,...,M$, and also we have

$$\begin{aligned} X^{-1}_{ij}=\frac{1}{2c_i}x_i^{(j)},~~~\bar{X}^{-1}_{ij}=\frac{1}{2\bar{c}_i}\bar{x}_i^{(j)},~~~~i,~j=1,...,M, \end{aligned}$$

where $c_1=\bar{c}_M=2$ and $c_i=1,~i=2,3,...,M,~ \bar{c}_i=1,~i=1,2,...,M-1$.

3.4 Periodic boundary conditions

In heat conduction equation, the periodic boundary conditions mean that at the ends of the boundaries, both the temperature and the heat flux must be equal.

Therefore, we have the boundary conditions $U(x_0,t)=U(L,t)$ and $U_x(x_0,t)=U_x(L,t)$, or

$$\begin{aligned} U_0=U_M,\quad U_x|_0=U_x|_M. \end{aligned}$$

Then, from Eq. (3.2) for $i=M-1$, we can write

$$\begin{aligned} U^{(\alpha )}_{M-1}=\frac{1}{h^2}(U_{0}-2U_{M-1}+U_{M-2})+f_{M-1}. \end{aligned}$$

(3.5)

In addition, using $U_{-1}=U_0-hU_x|_0+O(h^2)$ and from Eq. (3.2) for $i=0$, we obtain

$$\begin{aligned} U^{(\alpha )}_{0}=\frac{1}{h^2}(U_{1}-U_{0}-hU_x|_M)+f_{0}+O(h^2), \end{aligned}$$

and subsequently, applying $U_x|_M=(U_M-U_{M-1})/h+O(h)$ yields

$$\begin{aligned} h^2U^{(\alpha )}_{0}=\frac{1}{h^2}(U_{1}-2U_{0}+U_{M-1})+f_{0}+O(h^2). \end{aligned}$$

(3.6)

Therefore, we have

$$\begin{aligned} \mathbf f =[f_0,...,f_{M-1}]^T,\qquad \mathbf u _0=[U_0(0),...,U_{M-1}(0)]^T, \end{aligned}$$

and matrix A, according to Eqs. (3.5) and (3.6), will be defined by

$$\begin{aligned}A=\frac{1}{h^2}\left( \begin{array}{cccccc} -2 &{} ~~1 &{}0 &{}... &{} 1 &{} \\ 1 &{} -2 &{}~~~~ 1 &{} &{} &{} \\ &{} \ddots &{}~ ~\ddots &{}~~~\ddots &{} &{} \\ &{} &{} 1 &{} -2 &{} 1\\ 1&{}0 &{} ... &{} 1 &{} -2 \end{array} \right) _{M\times M}. \end{aligned}$$

(3.7)

Defining $A=-2I+P,$ we have $\lambda (A)=-2+\lambda (P)$. The characteristic equation of matrix P is

$$\begin{aligned} \mathrm {det}(P-\lambda I)=\lambda u_{M-1}(\lambda /2)-2 u_{M-2}(\lambda /2)-2=0, \end{aligned}$$

where $u_{M}(\lambda )$ is M-order second-kind Chebyshev polynomial. Defining $\lambda =2\cos (\theta )$ yields $u_{M}(\lambda )=\sin \big ((M+1)\theta \big )/\sin (\theta ),$ so we can write

$$\begin{aligned} \mathrm {det}(P-\lambda I)=\frac{\cos (\theta )\sin (M\theta )-\sin \big ((M-1)\theta \big )}{\sin (\theta )}-1=0. \end{aligned}$$

Consequently, $\theta$ and then $\lambda (A)$ will be easily found as

$$\begin{aligned} \theta _j=\frac{2\pi }{M}j,\qquad \lambda _j(A)=-2+2\cos \left(\frac{2\pi }{M}j\right),\qquad j=1,2,...,M. \end{aligned}$$

The eigenvectors of a circulant matrix A and P are given by

$$\begin{aligned} x_j^{(i)}=\frac{1}{\sqrt{M}}\exp \left(\frac{2\pi \mathrm {i}}{M}ij\right),\quad i=1,2,...,M,\quad j=1,2,...,M, \end{aligned}$$

where $\mathrm {i}=\sqrt{-1}$. The eigenvectors are orthonormal in $\mathbb {C}^M$; therefore, we have $A=X\Lambda X^*,~X_{ij}=x_j^{(i)},$ where $X^*$ is the conjugate transpose of X.

4 Finite difference method for 2D-diffusion equation

Same as the previous section, we decide to convert the 2D diffusion equation with various types of boundary conditions, to the system of FODEs, and then, by obtaining the eigenvalues and eigenvectors of system, we solve it directly.

Consider the two-dimensional heat equation satisfying the initial condition:

$$\begin{aligned}&U^{(\alpha )}_t= U_{xx}+U_{yy}+f(x,y,t),\qquad ~~~~~ x \in (x_0,L_x],~y\in (y_0,L_y],~t>0,\\&U(x,y,0)=U_0(x,y),\qquad \qquad \qquad ~\quad x\in (x_0,L_x],~y\in (y_0,L_y].\nonumber \end{aligned}$$

(4.1)

Employing a central finite difference formula to evaluate the diffusion operators $U_{xx}$ and $U_{yy}$ yields

$$\begin{aligned} {\left\{ \begin{array}{ll} U^{(\alpha )}_{i,j}=\frac{1}{h_x^2}(U_{i-1,j}+U_{i+1,j}) +\frac{1}{h_y^2}(U_{i,j-1}+U_{i,j+1})-2(\frac{1}{h_x^2} +\frac{1}{h_y^2})U_{i,j}+f_{i,j} {+O(h_x^2)+O(h_y^2)}~,\\ U_{i,j}(0)=U_0(x_i,y_j), \end{array}\right. } \end{aligned}$$

(4.2)

where $h_x=(L_x-x_0)/M_x$ and $h_y=(L_y-y_0)/M_y$. Equation (4.2) could be redefined in the following system of FODEs:

$$\begin{aligned} \mathbf u ^{(\alpha )}=\mathbf {A}_2\mathbf u +\mathbf f _2.~~~~\qquad \end{aligned}$$

(4.3)

4.1 Dirichlet boundary conditions

Here, we have

$$\begin{aligned} \mathbf f _2=\big [f_{1,1},f_{1,2},...,f_{1,M_y-1},f_{2,1},..., f_{2,M_y-1},...,f_{M_x-1,1},...,f_{M_x-1,M_y-1}\big ]^T, \end{aligned}$$

the initial condition is

$$\begin{aligned} & \mathbf u _0=\big [U_{1,1}(0),U_{1,2}(0),...,U_{1,M_y-1}(0),\\ & \quad U_{2,1}(0),...,U_{2,M_y-1}(0),...,U_{M_x-1,1}(0),...,U_{M_x-1,M_y-1}(0)\big ]^T, \end{aligned}$$

and also

$$\begin{aligned} \small \mathbf {A}_2= \left( \begin{array}{ccccccccc} A &{} \frac{1}{h_x^2}I_y &{} &{} &{} &{} \\ \frac{1}{h_x^2}I_y &{} A &{}\frac{1}{h_x^2}I_y &{} &{} &{} \\ &{} \ddots &{}~~\ddots &{}~~\ddots &{} \\ &{} &{} &{} \frac{1}{h_x^2}I_y &{} A &{} \frac{1}{h_x^2}I_y\\ &{} &{} &{} &{} \frac{1}{h_x^2}I_y &{} A \end{array} \right) , \end{aligned}$$

(4.4)

where A is $(M_y-1)\times (M_y-1)$ tridiagonal matrix in the following form:

$$\begin{aligned} A=\mathrm {Trid}\bigg (\frac{1}{h_y^2},-2\left(\frac{1}{h_x^2}+ \frac{1}{h_y^2}\right),\frac{1}{h_y^2}\bigg ), \end{aligned}$$

and $I_y$ is identity matrix of order $(M_y-1)\times (M_y-1)$. Now, we can rewrite $\mathbf {A}_2$ as

$$\begin{aligned} \mathbf {A}_2=I_x\otimes A+\frac{1}{h_x^2}T_x\otimes I_y, \end{aligned}$$

where $T_x=\mathrm {Trid}(1,0,1)$ is $(M_x-1)\times (M_x-1)$ matrix. In addition, we can write

$$\begin{aligned} A=\frac{1}{h_y^2}T_y-2\big (\frac{1}{h_x^2}+\frac{1}{h_y^2}\big )I_y. \end{aligned}$$

Therefore, $\mathbf {A}_2$ reduces to

$$\begin{aligned} \mathbf {A}_2=I_x\otimes \mathscr {T}_y+\mathscr {T}_x\otimes I_y =\mathscr {T}_y\oplus \mathscr {T}_x, \end{aligned}$$

where

$$\begin{aligned} \mathscr {T}_p=\frac{1}{h_p^2}(T_p-2I_p)=\frac{1}{h_p^2}\mathrm {Trid}(1,-2,1),\qquad p=x,~y. \end{aligned}$$

The eigenvalues and eigenvectors of $T_p$ ($p=x$ or y) are

$$\begin{aligned}&\lambda _i(T_p)=2-4\sin ^2\left(\frac{i\pi }{2M_p}\right), \qquad i=1,2,...,M_p-1,\\&x_j^{(i)}=\sqrt{\frac{2}{M_p}}\sin \left(\frac{ij}{M_p}\pi \right), \quad i=1,2,...,M_p-1,\quad j=1,2,...,M_p-1. \end{aligned}$$

In addition, the eigenvectors of $\mathscr {T}_p$ are the same as $T_p$ and its eigenvalues are

$$\begin{aligned}&\lambda _i(\mathscr {T}_p)=\frac{1}{h_p^2}(\lambda _i(T_p)-2),\qquad i=1,2,...,M_p-1. \end{aligned}$$

Denoting the matrices of eigenvectors and eigenvalues of matrix $\mathscr {T}_p$ by $X_p$ and $\Lambda _p$ and using Lemma 2.1, we can write

$$\begin{aligned} \mathbf {A}_2=(X_x\otimes X_y)(\Lambda _y\oplus \Lambda _x)(X_x\otimes X_y)^{-1}. \end{aligned}$$

4.2 Neumann boundary conditions

Here, we have

$$\begin{aligned} \mathbf f _2=\big [f_{0,0},f_{0,1},...,f_{0,M_y}, f_{1,0},....,f_{1,M_y},...,f_{M_x,0},...,f_{M_x,M_y}\big ]^T, \end{aligned}$$

(4.5)

the initial condition is

$$\begin{aligned} & \mathbf u _0=\big [U_{0,0}(0),U_{0,1}(0),...,U_{0,M_y}(0), \\& \quad U_{1,0}(0),..., U_{1,M_y}(0),...,U_{M_x,0}(0),...,U_{M_x,M_y}(0)\big ]^T, \end{aligned}$$

and also $\mathbf {A}_2$ is similar to Eq. (4.4), but matrix A is $(M_y+1)\times (M_y+1)$ tridiagonal matrix in the following form:

$$\begin{aligned}\small {A}= \left( \begin{array}{ccccccccc} \frac{-2}{h_x^2}+\frac{-2}{h_y^2} &{} \frac{2}{h_y^2} &{} &{} &{} &{} \\ \frac{1}{h_y^2} &{} \frac{-2}{h_x^2}+\frac{-2}{h_y^2} &{}\frac{1}{h_y^2} &{} &{} &{} \\ &{} \ddots &{}~~\ddots &{}~~\ddots &{} \\ &{} &{} &{} \frac{1}{h_y^2} &{} \frac{-2}{h_x^2}+\frac{-2}{h_y^2} &{} \frac{1}{h_y^2}\\ &{} &{} &{} &{} \frac{2}{h_y^2} &{} \frac{-2}{h_x^2}+\frac{-2}{h_y^2} \end{array} \right) , \end{aligned}$$

and $I_y$ is the identity matrix of order $(M_y+1)\times (M_y+1)$. $\mathbf {A}_2$ is similar to a symmetric matrix, so has real eigenvalues. Similar to Dirichlet boundary condition, we have

$$\begin{aligned} \mathbf {A}_2=\mathscr {T}_y\oplus \mathscr {T}_x, \end{aligned}$$

but here

$$\begin{aligned} T_p= \left( \begin{array}{cccccccc} 0 &{} 2 &{} &{} &{} &{} \\ 1 &{} 0 &{}1 &{} &{} &{} \\ &{} \ddots &{}\ddots &{}\ddots &{} &{} \\ &{} &{} 1 &{} 0 &{} 1\\ &{} &{} &{} 2 &{} 0 \end{array} \right) _{(M_p+1)\times (M_p+1)},\qquad p=x,~y, \end{aligned}$$

which its eigenvalues and eigenvectors are [20]

$$\begin{aligned}&\lambda _{i+1}=2-4\sin ^2\left(\frac{i\pi }{2M_p}\right), \qquad i=0,1,2,...,M_p,\\&x_{j+1}^{(i+1)}=\cos \left(\frac{ij}{M_p}\pi \right),\quad i=0,1,...,M_p,\quad j=0,1,...,M_p. \end{aligned}$$

4.3 Periodic boundary conditions

In this case, we have

$$\begin{aligned} \mathbf f _2=\big [f_{0,0},f_{0,1},...,f_{0,M_y-1},f_{1,0},..., f_{1,M_y-1},...,f_{M_x-1,0},...,f_{M_x-1,M_y-1}\big ]^T, \end{aligned}$$

the initial condition is

$$\begin{aligned} & \mathbf u _0=\big [U_{0,0}(0),U_{0,1}(0),...,U_{0,M_y-1}(0), \\ & \quad U_{1,0}(0),..., U_{1,M_y-1}(0),...,U_{M_x-1,0}(0),...,U_{M_x-1,M_y-1}(0)\big ]^T, \end{aligned}$$

and

$$\begin{aligned}\small \mathbf {A}_2= \left( \begin{array}{ccccccccc} A &{} \frac{1}{h_x^2}I_y &{} 0 &{} \dots &{} &{}\frac{1}{h_x^2}I_y \\ \frac{1}{h_x^2}I_y &{} A &{}\frac{1}{h_x^2}I_y &{} &{} &{} \\ &{} \ddots &{}~~\ddots &{}~~\ddots &{} \\ &{} &{} &{} \frac{1}{h_x^2}I_y &{} A &{} \frac{1}{h_x^2}I_y\\ \frac{1}{h_x^2}I_y&{} 0&{} \dots &{} &{} \frac{1}{h_x^2}I_y &{} A \end{array} \right) , \end{aligned}$$

where A is $M_y\times M_y$ matrix in the following form:

$$\begin{aligned}\small {A}= \left( \begin{array}{ccccccccc} \frac{-2}{h_x^2}+\frac{-2}{h_y^2} &{} \frac{1}{h_y^2} &{}0 &{} \dots &{} &{} \frac{1}{h_y^2}\\ \frac{1}{h_y^2} &{} \frac{-2}{h_x^2}+\frac{-2}{h_y^2} &{}\frac{1}{h_y^2} &{} &{} &{} \\ &{} \ddots &{}~~\ddots &{}~~\ddots &{} \\ &{} &{} &{} \frac{1}{h_y^2} &{} \frac{-2}{h_x^2}+\frac{-2}{h_y^2} &{} \frac{1}{h_y^2}\\ \frac{1}{h_y^2}&{} &{} \dots &{} 0 &{} \frac{1}{h_y^2} &{} \frac{-2}{h_x^2}+\frac{-2}{h_y^2} \end{array} \right) , \end{aligned}$$

and $I_y$ is identity matrix of order $M_y\times M_y$. Now, we can rewrite $\mathbf {A}_2$ same as pervious, but here

$$\begin{aligned} T_p=\left( \begin{array}{cccccc} 0 &{} ~~1 &{}0 &{}... &{} 1 &{} \\ 1 &{} 0 &{}~~~~ 1 &{} &{} &{} \\ &{} \ddots &{}~ ~\ddots &{}~~~\ddots &{} &{} \\ &{} &{} 1 &{} 0 &{} 1\\ 1&{}0 &{} ... &{} 1 &{} 0 \end{array} \right) _{M_p\times M_p}. \end{aligned}$$

It should be noted that the order of matrix $\mathbf {A}_2$ is $(M_x-1)\times (M_y-1)$ for Dirichlet, $M_x\times M_y$ for periodic and $(M_x+1)\times (M_y+1)$ for Neumann boundary conditions.

5 Finite difference method for 3D diffusion equation

To complete our discussion about solving the time-fractional diffusion equation, we investigate three-dimensional problem as well.

Consider the 3D heat equation satisfying the initial condition:

$$\begin{aligned}&U_t= U_{xx}+U_{yy}+U_{zz}+f(x,y,z,t),\qquad x\in (x_0,L_x],~ y\in (y_0,L_y],~z\in (z_0,L_z],~t>0,\\&U(x,y,z,0)=U_0(x,y,z),\qquad \qquad \qquad ~~ x\in (x_0,L_x],~y\in (y_0,L_y],~z\in (z_0,L_z].\nonumber \end{aligned}$$

(5.1)

Evaluating the diffusion operators $U_{xx}$, $U_{yy}$, and $U_{zz}$ using a central finite difference gives

$$\begin{aligned} {\left\{ \begin{array}{ll} U^{(\alpha )}_{i,j,k}=\frac{1}{h_x^2}(U_{i-1,j,k}+U_{i+1,j,k}) +\frac{1}{h_y^2}(U_{i,j-1,k}+U_{i,j+1,k})\\ +\frac{1}{h_z^2}(U_{i,j,k-1}+U_{i,j,k+1})-2\big (\frac{1}{h_x^2} +\frac{1}{h_y^2}+\frac{1}{h_z^2}\big )U_{i,j,k} +f_{i,j,k} {+O(h_x^2)+O(h_y^2)+O(h_z^2)}~,\\ U_{i,j,k}(0)=U(x_i,y_j,z_k,0), \end{array}\right. } \end{aligned}$$

(5.2)

where, $h_x=(L_x-x_0)/M_x$, $h_y=(L_y-y_0)/M_y$ and $h_z=(L_z-z_0)/M_z$. Equation (5.2) could be redefined in the following system of FODEs

$$\begin{aligned} \mathbf u ^{(\alpha )}=\mathbf {A}_3\mathbf u +\mathbf f _3.~~~~\qquad \end{aligned}$$

(5.3)

$\mathbf {A}_3$ will be obtained in the following for different boundary conditions.

5.1 Dirichlet boundary conditions

Here, we have

$$\mathbf f _3=\big [f_{1,1,1},f_{1,1,2},...,f_{1,1,M_z-1}, f_{1,2,1},....,f_{1,2,M_z-1},...,f_{M_x-1,My-1,1},...,f_{M_x-1,M_y-1,M_z-1} \big ]^T,$$

the initial conditions are

$$\mathbf u _0^T=\big [U_{1,1,1},U_{1,1,2},...,U_{1,1,M_z-1}, U_{1,2,1},....,U_{1,2,M_z-1},...,U_{M_x-1,My-1,1},..., U_{M_x-1,M_y-1,M_z-1}\big ]_{t=0},$$

and also

$$\begin{aligned}\small \mathbf {A}_3= \left( \begin{array}{ccccccccc} \mathbf {A}_2 &{} \frac{1}{h_x^2}I_{yz} &{} &{} &{} &{} \\ \frac{1}{h_x^2}I_{yz} &{} \mathbf {A}_2 &{}\frac{1}{h_x^2}I_{yz} &{} &{} &{} \\ &{} \ddots &{}~~\ddots &{}~~\ddots &{} \\ &{} &{} &{} \frac{1}{h_x^2}I_{yz} &{} \mathbf {A}_2 &{} \frac{1}{h_x^2}I_{yz}\\ &{} &{} &{} &{} \frac{1}{h_x^2}I_{yz} &{} \mathbf {A}_2\\ \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned}\small \mathbf {A}_2= \left( \begin{array}{ccccccccc} {A} &{} \frac{1}{h_y^2}I_z &{} &{} &{} &{} \\ \frac{1}{h_y^2}I_z &{} {A} &{}\frac{1}{h_y^2}I_z &{} &{} &{} \\ &{} \ddots &{}~~\ddots &{}~~\ddots &{} \\ &{} &{} &{} \frac{1}{h_y^2}I_z &{} {A} &{} \frac{1}{h_y^2}I_z\\ &{} &{} &{} &{} \frac{1}{h_y^2}I_z &{} {A}\\ \end{array} \right) , \end{aligned}$$

and A is $(M_z-1)\times (M_z-1)$ tridiagonal matrix in the following form:

$$\begin{aligned} A=\mathrm {Trid}\bigg (\frac{1}{h_z^2},-\frac{2}{h_x^2}-\frac{2}{h_y^2}-\frac{2}{h_z^2},\frac{1}{h_z^2}\bigg ), \end{aligned}$$

$I_z$ is the identity matrix of order $(M_z-1)\times (M_z-1)$ and $I_{yz}$ is identity matrix of order $(M_y-1)(M_z-1)\times (M_y-1)(M_z-1)$. Now, we can rewrite $\mathbf {A}_3$ as follows:

$$\begin{aligned} \mathbf {A}_3=I_x\otimes \mathbf {A}_2+\frac{1}{h_x^2}T_x\otimes I_{yz}, \end{aligned}$$

where $T_x=\mathrm {Trid}(1,0,1)$ and the order is $(M_x-1)\times (M_x-1)$. In addition, $\mathbf {A}_2$ deduces to

$$\begin{aligned} \mathbf {A}_2=I_y\otimes A+\frac{1}{h_y^2}T_y\otimes I_z. \end{aligned}$$

Thus we obtain

$$\begin{aligned} \mathbf {A}_3 & =-2\left(\frac{1}{h_x^2}+\frac{1}{h_y^2}+\frac{1}{h_z^2}\right)I +\frac{1}{h_z^2}I_{xy}\otimes T_{z} \\ & \quad +\frac{1}{h_y^2}I_x\otimes T_y\otimes I_{z} +\frac{1}{h_x^2}T_x\otimes I_{yz} \end{aligned}$$

or

$$\begin{aligned} \mathbf {A}_3=\mathscr {T}_z\oplus \mathscr {T}_y\oplus \mathscr {T}_x, \end{aligned}$$

(5.4)

where

$$\begin{aligned} \mathscr {T}_p=\frac{1}{h_p^2}(T_p-2I_p)=\frac{1}{h_p^2}\mathrm {Trid}(1,-2,1),\qquad p=x,~y,~z. \end{aligned}$$

In addition, the matrix $\mathbf {A}_3$ using its eigenvalues and eigenvectors could be written as follows:

$$\begin{aligned} \mathbf {A}_3=(X_x\otimes X_y\otimes X_z)(\Lambda _z\oplus \Lambda _y\oplus \Lambda _x)(X_x\otimes X_y\otimes X_z)^{-1}. \end{aligned}$$

5.2 Neumann boundary conditions

Here, similar to Dirichlet condition, $\mathbf {A}_3$ has been obtained by Eq. (5.4), but $T_x,~T_y$ and $T_z$ are $(M_x+1)\times (M_x+1),~(M_y+1)\times (M_y+1)$, and $(M_z+1)\times (M_z+1)$, respectively, and are defined by

$$\begin{aligned} T_p= \left( \begin{array}{cccccccc} 0 &{} 2 &{} &{} &{} &{} \\ 1 &{} 0 &{}1 &{} &{} &{} \\ &{} &{} \ddots &{}\ddots &{}\ddots &{} &{} \\ &{} &{} &{} 1 &{} 0 &{} 1\\ &{} &{} &{} &{} 2 &{} 0\\ \end{array} \right) ,\qquad \quad p=x,~y,~z. \end{aligned}$$

(5.5)

5.3 Periodic boundary conditions

Here, similar to Dirichlet condition, $\mathbf {A}_3$ has been obtained by Eq. (5.4), but $T_x,~T_y$ and $T_z$ are $M_x\times M_x,~M_y\times M_y$ and $M_z\times M_z$, respectively, and are defined by

$$\begin{aligned} T_p= \left( \begin{array}{cccccccc} 0 &{} 1 &{} 0 &{} \dots &{} &{}1 \\ 1 &{} 0 &{}1 &{} &{} &{} \\ &{} &{} \ddots &{}\ddots &{}\ddots &{} &{} \\ &{} &{} &{} 1 &{} 0 &{} 1\\ 1 &{} 0&{} \dots &{} &{} 1 &{} 0\\ \end{array} \right) ,\qquad \quad p=x,~y,~z. \end{aligned}$$

6 Analytical solution of linear system ofFODEs

In the previous sections, we converted the time-fractional diffusion equation to the system of FODEs with the initial condition. In this section, we investigate the solution of the system of FODEs in the following form:

$$\begin{aligned} \mathbf y ^{(\alpha )}(t)-M\mathbf y (t)=\mathbf g (t),~~~~\qquad \mathbf y (0)=\mathbf y _0,\quad 0<\alpha \le 1, \end{aligned}$$

(6.1)

where M is an invertible matrix and the fractional derivative is Caputo type.

Taking the Laplace transform form, Eq. (6.1) gives [15]

$$\begin{aligned} s^{\alpha }{} \mathbf Y (s)-s^{\alpha -1}{} \mathbf y _0 -M\mathbf Y (s)=\mathbf G (s), \end{aligned}$$

(6.2)

and simplifying the result yields

$$\begin{aligned} \mathbf Y (s)=\mathbf G (s)(s^{\alpha }I-M)^{-1} +s^{\alpha -1}{} \mathbf y _0(s^{\alpha }I-M)^{-1}, \end{aligned}$$

where I is an identity matrix. The inverse Laplace transform gives the solution in the form [3, 15]:

$$\begin{aligned} \mathbf y (t)=E_{\alpha }(Mt^{\alpha })\mathbf y _0+ \int _{0}^{t}\tau ^{\alpha -1}E_{\alpha ,\alpha }(M\tau ^{\alpha })~\mathbf f (t-\tau )~ d\tau . \end{aligned}$$

(6.3)

For the homogenous system of FODEs, the solution is

$$\begin{aligned} \mathbf y (t)=E_{\alpha }(Mt^{\alpha })\mathbf y _0. \end{aligned}$$

Now, we describe the analytical solution of the Mittag–Leffler matrix functions which are obtained via FDM by applying its eigenvalues and eigenvectors of the corresponding matrix in the next section.

7 Direct method to obtain Mittag–Leffler matrix functions

There are several techniques for lifting a real function to a square matrix function such as power series, diagonalizable matrices, Jordan decomposition, Cauchy integral, and so on [12]. However, in this paper, we only focus on Diagonalizable matrices method. The eigenvalues and eigenvectors of our matrix are exactly obtained thus the diagonalizable matrices method may be a simple and efficient method to compute the Mittag–Leffler (ML) matrix functions. For the diagonalizable matrix A, the matrix function f(A) can be obtained by [12]

$$\begin{aligned} f(A)=Xf(\Lambda )X^{-1},\qquad ~~~ f(\Lambda )=diag(f(\lambda _1),...,f(\lambda _M)), \end{aligned}$$

where $\lambda _i$s are eigenvalues of A and X is the matrix of its eigenvectors.

Now, we discuss the solution of TFDEs. The ML matrix function, where A is a diagonalizable matrix, can be obtained as follows:

$$\begin{aligned} E_{\alpha ,\beta }(A)=XE_{\alpha ,\beta }(\Lambda ) X^{-1}. \end{aligned}$$

It should be noted that the values of $E_{\alpha ,\beta }(\lambda _i)$ obtained using the $mlf.m$ matlab code [25]. Subsequently, Eq. (3.3) may be computed in the following form:

$$\begin{aligned} \mathbf u (t)=XE_{\alpha }({\Lambda } t^{\alpha })X^{-1}{} \mathbf u _0+X\int _{0}^{t}\tau ^{\alpha -1} E_{\alpha ,\alpha }(\Lambda \tau ^{\alpha })X^{-1}{} \mathbf f (t-\tau )~d\tau . \end{aligned}$$

(7.1)

It should be noted that the matrices $X,~X^{-1}$ and $\Lambda$ are obtained exactly for one-, two-, and three-dimensional diffusion equations in the pervious sections as well, respectively.

Now, we discuss about the solution of Eq. (7.1), for some types of heat source term f.

• fis a separable function in the form$f(\mathbf {x},t)=h(t)g(\mathbf {x})$, then we have

$$\begin{aligned} \mathbf f (t)=h(t)\mathbf g =h(t)[g(\mathbf {x}_0),...,g(\mathbf {x}_M)]^T. \end{aligned}$$

Consequently, we can write

$$\begin{aligned} \mathbf u (t)=XE_{\alpha }(\Lambda t^{\alpha })X^{-1}{} \mathbf u _0+XS(t)X^{-1}{} \mathbf g , \end{aligned}$$

(7.2)

where S(t) is the diagonal matrix and its ith entries will be

$$\begin{aligned} s_i(t)=\int _{0}^{t}\tau ^{\alpha -1}E_{\alpha ,\alpha } ({\lambda _i} \tau ^{\alpha })h(t-\tau )~d\tau . \end{aligned}$$

For $h(t)=t^{\mu }$, the author of [7] proved that the above equation reduces to

$$\begin{aligned} s_{i}(t)=\Gamma (\mu +1)t^{\mu +\alpha }E_{\alpha ,\alpha +\mu +1} ({\lambda _i}t^{\alpha }), \end{aligned}$$

and also if h(t) is in the form:

$$\begin{aligned} h(t)=\sum _{k=1}^{p}v_kt^{\mu _k}, \end{aligned}$$

one has

$$\begin{aligned} s_{i}(t)=\sum _{k=1}^{p}v_k\Gamma (\mu _k+1)t^{\mu _k+\alpha }E_{\alpha ,\alpha +\mu _k+1} (\lambda _i t^{\alpha }). \end{aligned}$$

For the special $h(t)=E_{\alpha }(at^{\alpha }),$ we have the following function for $s_i(t)$ using Lemma 2.1 as

$$\begin{aligned} s_i(t)=\frac{1}{\lambda _i-a}\left( E_{\alpha }(\lambda _it^{\alpha })-E_{\alpha }(at^{\alpha })\right) . \end{aligned}$$

(7.3)

• f is a general form of separable functions in the form

$$\begin{aligned} f(\mathbf {x},t)=\sum _{k=0}^{m}h_k(t)g_k(\mathbf {x}), \end{aligned}$$

then Eq. (7.1) could be rewritten by

$$\begin{aligned} \mathbf u (t)=XE_{\alpha }(\Lambda t^{\alpha })X^{-1}{} \mathbf u _0+X\sum _{k=0}^{m}S_k(t)X^{-1}{} \mathbf g _k, \end{aligned}$$

(7.4)

where

$$S_k(t)=diag\left( \int _{0}^{t}\tau ^{\alpha -1}E_{\alpha ,\alpha }({\lambda _1} \tau ^{\alpha })h_k(t-\tau )~d\tau ,~...~,\int _{0}^{t}\tau ^{\alpha -1}E_{\alpha ,\alpha } ({\lambda _M} \tau ^{\alpha })h_k(t-\tau )~d\tau \right),$$

and

$$\begin{aligned} \mathbf g _k=[g_k(\mathbf {x}_0),...,g_k(\mathbf {x}_M)]^T. \end{aligned}$$

8 Test problems

Before considering the test problems, we first express the well-known fractional finite difference method (FFDM) [30] for the system of ODEs (3.3). Applying this method by time step, $\Delta t =T/N,$ reduces Eq. (3.3) to

$$\begin{aligned} (I-sA)\mathbf u _{n}=s\mathbf f _{n} + b_{n-1} \mathbf u _0 -\sum _{j=1}^{n-1}(b_{n-j}-b_{n-j-1})\mathbf u _{j},\qquad n=1,...N, \end{aligned}$$

where $\mathbf u _{j}=\mathbf u (j\Delta t ),$$b_j=(j+1)^{1-\alpha }-j^{1-\alpha }$ and $s=\Delta t^\alpha \Gamma (2-\alpha ).$ This method gives the solution of the problem in any step of time recursively. To obtain the appropriate accuracy in time variable, we set $\Delta t$ very small.

To confirm the utility of the presented method, we apply the method to five examples. In the examples with the exact solution, we report the absolute maximum error between any finite difference nodes at the final time. In addition, then, the logarithmic graph of error by increasing the number of nodes is plotted. According to these graphs, we show that if the unknown function $U\in C^2(\Omega ),$ the method converges with the second-order accurate in space as well. We implemented the proposed method using Matlab 2016 with hardware configuration: desktop; Intel Core i7 CPU (4M Cache, 2.80 GHz), 8GB of RAM.

8.1 1D problem

Consider the homogenous heat problem with the exact solution

$$\begin{aligned} U(x,t)=E_{\alpha }(-\pi ^2t^{\alpha })\sin (\pi x),\qquad x\in [0,6], \end{aligned}$$

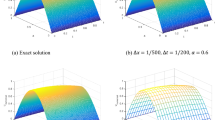
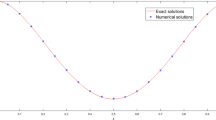
with Dirichlet and periodic boundary conditions. The numerical results for this problem are obtained (see Fig. 1) and also the maximum error corresponding to different M with present method in the final time $T=1$ is illustrated in Fig. 2. For this problem, FFDM gives the same results, while $\Delta t$ is very small ($\Delta t = 10^{-5}$). To show the superiority of the proposed method against the FFDM, Fig. 3 is prepared. This figure shows that the FFDM is more time consuming than the MOL method which is proposed in this paper.

Fig. 1

Function U(x, t) with $M=100$ and $\alpha =0.5$ in the final time $T=1$

Fig. 2

Maximum error corresponding to different M with $\alpha =0.5$ in the final time $T=1$

Fig. 3

CPU time corresponding to different M with $\alpha =0.5$ in the final time $T=1$

8.2 2D problems

• Consider the non-homogenous problem with the exact solution:

$$\begin{aligned} U(x,y,t)=E_{\alpha }(-\pi ^2t^{\alpha })\sin (\pi x)\sin (\pi y),\qquad (x,y)\in [0,1]^2, \end{aligned}$$

and heat source term $f=\pi ^2 U$ with Dirichlet boundary conditions. In this problem, the solution is obtained using Eq. (7.2), where the entries of the diagonal matrix S(t) could be achieved via Eq. (7.3) as follows:

$$\begin{aligned} s_i(t)=\frac{1}{\lambda _i+\pi ^2}\left( E_{\alpha }(\lambda _it^{\alpha }) -E_{\alpha }(-\pi ^2t^{\alpha })\right) . \end{aligned}$$

The numerical results for this problem are obtained and displayed in Fig. 4, and also the maximum error corresponding to different M with present method in the final time $T=1$ is illustrated in Fig. 5.

Fig. 4

Function U(x, y, t) with $M=10000$ and $\alpha =0.5$ in times $t=0.25,~0.5,~0.75$ and $t=1$

Fig. 5

Maximum error corresponding to different M with $\alpha =0.5$ in the final time $T=1$

• Consider 2D homogenous heat conduction problem with the homogenous Dirichlet boundary condition on $[0,1]^2$ and the non-smooth initial condition

  $$\begin{aligned} u(x,y,0)=\delta (x)\delta (y), \end{aligned}$$

  where $\delta (.)$ denotes the Dirac delta function and defined by

  $$\begin{aligned} \delta (x)=\lim _{\sigma \rightarrow 0}\frac{1}{\sigma \sqrt{\pi }}\exp \left( -(\frac{x}{\sigma })^2\right) . \end{aligned}$$

  For solving this problem, we fix $\sigma =10^{-5}.$ Figure 6 includes numerical calculations for $\alpha = 1$ and $M = 120$.

  Fig. 6

  

  Approximation of function U(x, y, t) with $M=120$ and $\alpha =1$ in times $t=0.5,~1,~1.5$ and $t=2$

• Consider 2D non-homogenous heat conduction problem with Dirichlet boundary conditions and the exact solution

  $$\begin{aligned} & U_{\beta }(x,y,t)=(x-x^2)^\beta (y-y^2)^\beta E_\alpha (-t^\alpha ),\\ & \quad (x,y)\in [0,1]^2, \end{aligned}$$

  and heat source term:

  $$\begin{aligned} f = -U_\beta -\beta U_{\beta -2}\left( p_2(x)(y-y^2)^2+p_2(y)(x-x^2)^2\right) , \end{aligned}$$

  where $p_2(\eta )=(4\beta -2)\eta ^2-(4\beta -2)\eta +\beta -1.$

In this problem, the solution is obtained using Eq. (7.2), where the entries of the diagonal matrix S(t) could be achieved via Eq. (7.3) as follows:

$$\begin{aligned} s_i(t)=\frac{1}{\lambda _i+1}\left( E_{\alpha }(\lambda _it^{\alpha }) -E_{\alpha }(-t^{\alpha })\right) . \end{aligned}$$

The numerical results for this problem for various values of $\beta$, and the maximum error corresponding to different M with present method in the final time $T=1$ are illustrated in Figs. 7 and 8. According to these figures, we could confirm that the convergence order in space for this problem is $O(h^{\beta })$ for $0<\beta <2,~\beta \ne 1.$

Fig. 7

Maximum error corresponding to $\beta =1.2,~1.4,~1.6,~1.8$ and different M with $\alpha =0.5$ in the final time $T=1$

Fig. 8

Maximum error corresponding to $\beta =0.25,~0.5$ and different M with $\alpha =0.5$ in the final time $T=1$

8.3 3D problem

Consider the homogenous problem with the exact solution

$$\begin{aligned} U(x,y,z,t)=E_{\alpha }(-3\pi ^2t^{\alpha })\sin (\pi x)\sin (\pi y)\sin (\pi z),\qquad (x,y,z)\in [0,1]^3, \end{aligned}$$

with Dirichlet boundary conditions. The maximum error corresponding to different M via present method in the final time $T=1$ is illustrated in Fig. 9.

Fig. 9

Maximum error corresponding to different M with $\alpha =0.5$ in the final time $T=1$

9 Conclusion and future work

The method of lines for solving the one-, two-, and three-dimensional linear time-fractional diffusion equations with three well-known boundary conditions has been presented in this paper. The MOL involves discretising the diffusion equation in space dimensions (by central finite difference scheme) and then converts this equation to a system of fractional ordinary differential equations. This system has been solved analytically in terms of the one and two-parameter Mittag–Leffler matrix functions. The values of Mittag–Leffler matrix functions have been computed by the matrix eigenvalues and eigenvectors exactly. Consequently, the semi-analytical solutions of linear time-fractional diffusion equations have been presented for some diffusion source terms. In this paper, the diffusion derivative discretised using central finite difference scheme which is second-order accurate. In addition, we will apply the high-order finite difference methods in our future works.