1 Introduction

Nanotechnology has become indispensable in modern life due to the superior mechanical, electronic, optical and magnetic properties of nanomaterials [1]. In particular, it provides vital tools to desalinate and purify water, and this becomes increasingly paramount due to the current economic growth and climate change. To address the undeniable need of pure water, various methodologies such as distillation, adsorption, solar evaporation and reverse osmosis, to name a few, have been proposed to extract pure water [2]. However, most of these techniques are energetically and operationally expensive, and some of them are not capable of removing pollutants effectively [2]. Well aligned carbon nanotubes embedded inside membrane provide robust channels for water desalination and purification [3] and they exhibit the following properties: nanotubes with appropriate pore sizes constitute energy barriers at the tube’s entries so as to reject salt ions and permit water through the nanotubes [4,5,6,7]; it is possible to modify and functionalize nanotubes to selectively accept/reject ions mimicking biological channels [4, 8, 9]; carbon nanotubes also show antifouling, self-cleaning and reusable functionalities [2, 10]; water permeability inside nanotubes is remarkably high due to the frictionless/almost frictionless transport of water molecules [11, 12], and the flow rate in a carbon nanotube membrane is observed at several orders of magnitude larger than that predicted by the conventional fluid theory or continuum hydrodynamics theory [13]; least but not last, the velocity of individual molecules could reach as high as 1000 ms\(^{-1}\) inside small radii nanotubes [14]. Spinning carbon nanotubes have also been investigated to achieve better desalination effect through the centrifugal force [15]. Therefore, the combination of high water permeability and species selectivity turn them into an excellent candidate for water-ion/pollutant separation.

Several attempts have been tried to describe the flow inside nanotube [11, 12, 16], however they fail to take into account the molecular effects. For ultra-small radii nanotube, even a single file transport of molecules is observed [6, 17]. For nanotubes with much larger radius, numerous studies have shown that the flow rate is far higher than that predicted by the conventional Poiseuille flow model, even a slip boundary condition is taken into account. We comment that a number of solutions have been derived for Poiseuille flow inside both rectangular [18, 19] and cylindrical porous channels [20,21,22], but until most recently, no theory has successfully addressed such high flow rate at the nanoscale.

Here, we investigate water flow rate inside carbon nanotube of radius 20 Å. We comment that water flow inside nanotubes of extra-small radii is not in our interest. For such nanotube, Navier–Stokes (NS) equation appears to be the best approximation to depict the fluid flow inside the tube [16]. Even fluid density and viscosity are expected to be varied inside nanotube [23], Newtonian fluid is assumed here so as to minimize the unnecessary mathematical complexity and test major molecular effects. However, our numerical solution still reveals a boundary layer near the tube wall (see Fig. 7). Apart from adopting slip boundary condition [see Eq. (2c)], the molecular interaction between water and nanotube is also considered to better capture the nano effect arising at the nanotube. Such molecular interaction is modeled using the continuum approximation [24, 25], which has shown tremendous success in various problems such as particle-laden flow inside nanomaterials [26], ultra-filtration and desalination [4, 5, 27, 28], and hydrogen yield [9] and storage using nanomaterials [29]. We find that the resultant axial and radial velocity satisfies the prescribed boundary conditions and the flow rate is lifted almost sevenfold when the molecular interaction is incorporated, which may partially explain such a high nano flow.

2 Theory

In this section, we derive the basic theory for the present paper. In the first subsection, radial and axial velocities are determined, followed by the derivation of the pressure and the radial force, induced by carbon nanotube. Then, we incorporate the pressure driven by tube entry and radial force into the pressure and body acceleration terms of the Navier–Stokes equation, respectively to describe the fluid flow inside the nanotube.

Fig. 1
figure 1

Geometric setup for this problem

Full size image

2.1 Axial and radial velocities

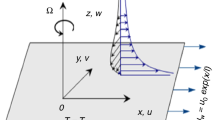
Suppose water pass through a carbon nanotube with the radial velocity u and the translation velocity v (see Fig. 1). The stationary Navier–Stokes equation and the incompressible condition read

$$\begin{aligned}&u\frac{\partial u}{\partial r}+v\frac{\partial u}{\partial z}=-\frac{1}{\rho }\frac{\partial P}{\partial r}+\frac{\mu }{\rho }\left( \nabla ^{2} u-\frac{u}{r^{2}} \right) +g_{r}, \end{aligned}$$
(1a)
$$\begin{aligned}&u\frac{\partial v}{\partial r}+v\frac{\partial v}{\partial z}=-\frac{1}{\rho }\frac{\partial P}{\partial z}+\frac{\mu }{\rho }\nabla ^{2}v, \end{aligned}$$
(1b)
$$\begin{aligned}&\frac{\partial u}{\partial r}+\frac{u}{r}+\frac{\partial v}{\partial z}=0, \end{aligned}$$
(1c)

where \(\rho \), \(\mu \), P and \(g_{r}\) denote the water density, viscosity, pressure and body acceleration in r-direction, respectively. We comment that gravitational force is ignored here and we will show later that the body force induced by the nanotube acts only in the r-direction. Linear slip boundary condition is assumed for v, and the boundary conditions for both u and v are given, respectively by

$$\begin{aligned} u(a,z)= & {} 0, \end{aligned}$$
(2a)
$$\begin{aligned} u(0,z)= & {} 0, \end{aligned}$$
(2b)
$$\begin{aligned} v(a,z)= & {} \ell \frac{\partial v}{\partial r}\mid _{r=a}, \end{aligned}$$
(2c)

where a and \(\ell \) denote the radius of the tube and the slip length, respectively. Upon assuming u is homogeneous along z and depends only on r, using Eq. (1c) gives \(v=v_{1}(r)z+v_{0}(r)\) for some functions \(v_{0}(r)\) and \(v_{1}(r)\). Assuming the pressure P is only a function of z, using \(v=v_{1}(r)z+v_{0}(r)\), Eqs. (1a, 1b) become, respectively

$$\begin{aligned} -\rho G_{r}= & {} \mu \left( \frac{du}{dr} +\frac{u}{r} \right) -\frac{\rho }{2}u^{2}, \end{aligned}$$
(3)
$$\begin{aligned} u\frac{\partial v}{\partial r}+v\frac{\partial v}{\partial z}= & {} \frac{-1}{\rho }\frac{d P}{dz}+\frac{\mu }{\rho }\left( \frac{\partial ^{2} v}{\partial r^{2}} +\frac{1}{r}\frac{\partial v}{\partial r}\right) , \end{aligned}$$
(4)

where we assume that the anti-derivative of \(g_{r}\) exists and denote \(G_{r}\). Now, we express u and v in terms of the stream function \(\psi \), gives

$$\begin{aligned} u=\frac{1}{r}\frac{\partial \psi }{\partial z}\quad \quad v=-\frac{1}{r}\frac{\partial \psi }{\partial r}. \end{aligned}$$
(5)

Since u is a function of r, from Eq. (5), \(\psi \) can be written as

$$\begin{aligned} \psi (r, z)=zf(r)+h(r), \end{aligned}$$
(6)

for some functions f(r) and h(r). Due to the symmetry of the present problem, we adopt the change of variables, i.e. \(\xi =a^{2}-r^{2}\), where \(\xi \in [0, a^{2}]\). There are two reasons that we make this transformation. Firstly, \(\xi \) appears in every solution form of laminar flow. Secondly, it turns the “radius” from the denominator into the numerator, which is much easier to deal with. Using Eq. (5), u and v in terms of the new variable \(\xi \) become, respectively

$$\begin{aligned} u(\xi )=\frac{F(\xi )}{\sqrt{a^{2}-\xi }}, \quad v(\xi ,z)=2[zF'(\xi )+H'(\xi )], \end{aligned}$$
(7)

where \(F(\xi )=f(r(\xi ))\) and \(H(\xi )=h(r(\xi ))\), and \(\xi \in [0,a^{2}]\). In addition, \('\) refers to the derivative with respect to \(\xi \). We still need to determine both \(F(\xi )\) and \(H(\xi )\) in order to obtain u and v.

Upon substituting the new form of u and v into Eqs. (3) and (4), we turn both equations into ordinary differential equations as follows

$$\begin{aligned} -\rho G_{r}(\xi )= & {} -2\mu F'-\frac{\rho }{2(a^{2}-\xi )}F^{2},\end{aligned}$$
(8)
$$\begin{aligned} \frac{1}{\rho }\frac{dP}{dz}= & {} \left\{ 8\nu [(a^{2}-\xi )F'''-F'']\right. \nonumber \\&\left. +\,4(FF''-F'^{2}) \right\} z+\left\{ 8\nu [(a^{2}-\xi )H'''-H'']+4(FH''-F'H')\right\} ,\nonumber \\= & {} c_{1}z+c_{2}, \end{aligned}$$
(9)

where, \(\nu =\mu /\rho \), and \(c_{1}\) and \(c_{2}\) define integral equations, which can be expressed, respectively

$$\begin{aligned} \frac{-c_{1}}{16}= & {} \frac{F'^{2}}{2}-\frac{d}{d\xi }\left\{ \frac{\nu }{2}(a^{2}-\xi )F''+\frac{1}{4}FF' \right\} ,\end{aligned}$$
(10)
$$\begin{aligned} \frac{-c_{2}}{4}= & {} \frac{F'H'}{2}-\frac{d}{d\xi }\left\{ \frac{\nu }{2}(a^{2}-\xi )H''+\frac{FH'}{4} \right\} , \end{aligned}$$
(11)

where \(c_{1}\) and \(c_{2}\) define the “conservation rule” for F, and (F and H), respectively. We will show later in our case that \(c_{1}=0\) and \(c_{2}\) defines the pressure drop across the nanotube divided by the fluid density [see Eq. (9) by letting \(c_{1}=0\)].

Now, we are equipped with sufficient materials to derive the analytical solution for u and v. Observing from Eq. (7), v diverges when \(z\rightarrow \infty \). To resolve this problem, we force \(F'=0\) (We comment that in general \(F'\ne 0\) if water is allowed to enter or leave from the tube side but we assume no leak in this paper). Using Eqs. (7) and (8), we obtain

$$\begin{aligned} F(\xi )=\sqrt{2(a^{2}-\xi )G_{r}(\xi )} \quad \quad \text {and} \quad \quad u(\xi )=\sqrt{2G_{r}(\xi )}, \end{aligned}$$
(12)

where \(F(\xi )\) is a constant if \(G_{r}(\xi )\) follows the form of \(1/(a^{2}-\xi )\). Here, we relax this form as \(G_{r}(\xi )\) might follow other power laws and assume that \(F'\) is still zero. Now, we have to check if u satisfies the prescribed boundary conditions. On the center of the tube, as the van der Waals forces vanish, \(G_{r}(a^{2})\rightarrow 0\) and hence Eq. (2b) is satisfied. Now, consider u near the tube wall. Since the net radial force in the vicinity of the wall is zero, we have

$$\begin{aligned} u(0)=\sqrt{2G_{r}(0)}=0. \end{aligned}$$
(13)

Therefore, the radial velocity satisfies both boundary conditions Eqs. (2a, 2b).

Given \(F'=0\) for the impermeable wall, \(v(\xi )\) reduces to \(v(\xi )=2H'(\xi )\) and we remain to determine \(H'(\xi )\), which can be solved using the integral equation, i.e. Eq. (11). Upon assuming \(F'=0\) and \(K=H'\). Integrating both sides of Eq. (11) by \(\xi \) leads to

$$\begin{aligned} \frac{\nu (a^{2}-\xi )}{2}K'(\xi )+\frac{F(\xi )}{4}K(\xi )=\frac{1}{4\rho }\frac{dP}{dz}\xi +c_{3}, \end{aligned}$$
(14)

where \(c_{3}\) is an integration constant, which can be determined using the final slip boundary condition, i.e. Eq. (2c). From Eq. (2c), we deduce

$$\begin{aligned} K'(0)=-\frac{K(0)}{2\ell a}. \end{aligned}$$
(15)

In conjunction with Eq. (14), \(c_{3}\) becomes

$$\begin{aligned} c_{3}=-\frac{a\nu }{4\ell }K(0). \end{aligned}$$
(16)

where \(K(0)=v(0)/2\) and v(0) denotes the axial velocity at the wall to be determined. Upon approximating dP / dz by the pressure difference across the tube due to both mechanical pressure and the pressure driven by the tube entry, divided by the tube length, i.e. \(\Delta P/\lambda \), where \(\lambda \) is the tube length. After some simple calculus, Eq. (14) further reduces to

$$\begin{aligned} K'(\xi )+\frac{F(\xi )}{2\nu (a^{2}-\xi )}K(\xi )=\frac{\Delta P}{2\mu \lambda (a^{2}-\xi )}\xi +L(\xi ), \end{aligned}$$
(17)

where

$$\begin{aligned} L(\xi )=-\frac{a}{2\ell (a^{2}-\xi )}K(0). \end{aligned}$$

Equation (17) is a first-order ordinary differential equation, which can be solved using the integrating factor technique. Assuming

$$\begin{aligned} I(\xi )=\exp \left\{ \int \frac{F(\xi )}{2\nu (a^{2}-\xi )} d\xi \right\} , \end{aligned}$$

we can deduce both radial and axial velocities, respectively as

$$\begin{aligned} u(\xi )= & {} \sqrt{2G_{r}(\xi )}, \nonumber \\ v(\xi )= & {} \left( \frac{2}{I(\xi )}\right) \int I(\xi ) \left\{ \frac{\Delta P}{2\mu \lambda (a^{2}-\xi )}\xi +L(\xi ) \right\} d\xi +c, \end{aligned}$$
(18)

where c is another integration constant to be determined. Suppose the tube radius is small, one can deduce that \(I(\xi )\approx 1\). In other words, v is weakly coupled with u and \(v(\xi )\) further reduces to

$$\begin{aligned} v(\xi )\approx -\frac{\Delta P}{\mu \lambda }\xi +\left( \frac{av_{wall}}{2\ell }-\frac{\Delta P a^{2}}{\mu \lambda }\right) \ln (a^{2}-\xi )+c, \end{aligned}$$
(19)

where \(v(\xi =0)=v_{wall}\) denotes the slip velocity at the wall. To avoid the singularity arising at the center, i.e. \(\xi =a^{2}\), we let the mid-term of Eq. (19) equal zero and the slip velocity is found to be

$$\begin{aligned} v_{wall}=\frac{2a\ell \Delta P}{\mu \lambda }, \end{aligned}$$
(20)

where \(v_{wall}\) depends linearly with the slip length \(\ell \). Upon using \(v(\xi =0)=v_{wall}\) again from Eq. (19), the axial velocity in r coordinate becomes

$$\begin{aligned} v(r)=-\frac{\Delta P}{\mu \lambda }(a^{2}-r^{2})+\frac{2a \ell \Delta P}{\mu \lambda }, \end{aligned}$$
(21)

which is a laminar flow equipped with the slip boundary condition and satisfies the slip boundary condition, i.e. Eq. (2c). In addition, we have successfully used \(I(\xi )\approx 1\) to linearize the NS equation and the axial velocity does not depend on the radial velocity, which makes sense when the radius of nanotube is extremely small.

2.2 Molecular forces driven by nanotube

In this subsection, we deduce the pressure \(P_{z}(z)\) and the radial acceleration \(g_{r}(r)\), driven by molecular interactions between water and nanotube. It is evident that when water molecule approaches the proximity of nanotube, it experiences a suck in force [24, 25]. According to [9, 27], the total force acting on a water molecule intruding into the nanotube, \(F^{tot}\) is given by

$$\begin{aligned} F^{tot}=F_{O-T}+F_{H_{1}-T}+F_{H_{2}-T}+F_{hydra}+F_{app}, \end{aligned}$$
(22)

where \(F_{O-T}\), \(F_{H_{1}-T}\), \(F_{H_{2}-T}\) denote the molecular force for oxygen-nanotube, the first hydrogen on water molecule-nanotube, the second hydrogen-nanotube, respectively. In addition, \(F_{hydra}\) and \(F_{app}\) denote the hydraulic force and the applied force, where the hydraulic force could be interpolated using molecular dynamics simulations. Here, we adopt the alternative approach proposed by Cox et al. [24, 25], where they use the continuum approximation to approximate such forces, and the analytical form for Eq. (22) can be found in [4]. Due to the rapid rotation of water molecules under finite temperature, Boltzmann’s statistics will also be used to obtain the ensemble force, which is given by

$$\begin{aligned} F_{z}(z):=F^{Avg}=\frac{\sum _{j}\left\{ F_{j}^{tot}\exp (-\beta V_{j}^{tot})\right\} }{\sum _{j}\exp (-\beta V_{j}^{tot})}, \end{aligned}$$
(23)

where j and \(V^{tot}\) denote the j-orientation and the total energy, which can be obtained by integrating the total force, \(F^{tot}\), respectively. On the other hand, following the account given by Chan et al. [30], upon assuming the water molecules as point masses and describing the interaction between molecules by Lennard-Jones potential, perturbation is used to approximate the radial acceleration \(g_{r}\) by

$$\begin{aligned} g_{r}=m^{-1}\int _{-\pi }^{\pi }\int _{-\infty }^{\infty }\left\{ \frac{24\epsilon }{\sigma }\left[ 2\left( \frac{\sigma }{\rho }\right) ^{13}-\left( \frac{\sigma }{\rho }\right) ^{7} \right] \right\} adzd\theta , \end{aligned}$$
(24)

where \(\rho , m\), \(\epsilon \) and \(\sigma \) denote the distance between the interacting molecules, mass of a single water molecule, the well depth and the van der Waals diameter, respectively. In addition, z and \(\theta \) denote the usual height and azimuthal coordinates for the cylindrical coordinate system. This radial acceleration acting on all water inside the nanotube, gives

$$\begin{aligned} g_{r}=24m^{-1}\epsilon \left\{ 2\sigma ^{12}I_{13}-\sigma ^{6}I_{7} \right\} , \end{aligned}$$
(25)

where \(\rho =(a^{2}+r^{2}-2ar\cos \theta +z^{2})^{1/2}\) and r is the radial coordinate. \(I_{n}\) is given by

$$\begin{aligned} I_{n}= & {} \int _{-\pi }^{\pi }\int _{-\infty }^{\infty }\frac{a}{\rho ^{n/2}}d\theta dz\\= & {} \frac{4\pi a}{(a-r)^{n-1}}\left\{ \int _{0}^{\pi /2}\cos ^{n-2}\theta d\theta \right\} F\left( \frac{n-1}{2},\frac{1}{2};1;\frac{-4ar}{(a-r)^{2}}\right) , \end{aligned}$$

where F is usual hypergeometric function. In addition, \(G_{r}(r)\) can be obtained by integrating \(g_{r}\) with respect to r.

3 Numerical results and discussion

In this section, we determine several numerical results for the present paper and make some discussion. Water experiences a suck in force when it approaches the proximity of nanotube entry. Using Eq. (23), the axial molecular force for a water molecule intruding into a carbon nanotube of radii 3.8, 4, 5, 10 and 20 Å, i.e. is given, respectively in Fig. 2, where the parameters adopted for the present paper can be obtained from [5].

Fig. 2
figure 2

Total axial molecular force for water molecule intruding into nanotube of radius a

Full size image

This axial force forms an impulse at the tube entry so that it can be incorporated into the pressure term of Eqs. (1a, 1b), where the positive and negative forces represent the repulsive and attractive forces, respectively. The sum of the pressure driven by the nanotube entry, i.e. \(F^{tot}{/}(\pi a^{2})\) and the mechanical pressure drop \(\Delta P_{mech}\) over the tube constitute the total pressure drop, \(\Delta P\) in Eq. (17). For the nanotube of radius 3.8 Å, both attractive and repulsive forces coexist in the proximity of the nanotube entry. Chan and Hill [5] show that the water molecule could get into such nanotube without applying any external force. For nanotubes of radius larger than 3.4 Å [5], water will spontaneously tunnel through the nanotube and the strength of the suck in force decreases when the tube radius increases. We will show later that such force will enhance the axial velocity of water inside the nanotube.

Once water gets into the nanotube, it will experience the radial force generated by the nanotube, which is given in Eq. (25). Numerical result of the radial force, i.e. \(mg_{r}\), where m denotes the mass of a water molecule, driven by nanotubes of radius 4 and 20 Å is given in Fig. 3 for comparison.

Fig. 3
figure 3

(Left) radial force (m\(g_{r}\), where m is the mass of a water molecule) for nanotube of radius 4 Å; (right) radial force for nanotube of radius 20 Å

Full size image

The radial force acts on all water inside the body of the nanotube and therefore it can be incorporated into the body acceleration of Eq. (1a). For nanotube of radius 4 Å, the maximum radial force occurs at center. This violates the prescribed boundary condition where \(u(r=0)=0\) [see Eqs. (2) and (5)]. However, in such a small radii nanotube, continuum assumption is broken and water molecules will feature an intriguing single-file transport [6]. On the other hand, for nanotube of radius 20 Å, the radial force is zero at nanotube center and wall vicinity, which satisfies the boundary conditions as stated in Eqs. (2a, 2b). We comment that water molecules are unable to reach the nanotube wall due to the strong repulsive forces generated by the wall of the nanotube.

To determine flow fields inside nanotubes of relatively large radii, we adopt the following parameters as given in Cox and Hill [16]: tube radius (\(a=20\) Å), tube length (\(\lambda =1\,\hbox {nm}\)), viscosity (\(\mu =10^{-3}\) Pa s), density (\(10^{3}\) kg m\(^{-3}\)), slip length (3 nm) and mechanical pressure drop across the tube \(\Delta P_{mech}=10^{5}\) Pa. The radial velocity is determined using Eq. (18), which is shown in Fig. 4.

Fig. 4
figure 4

Radial velocity for nanotube of radius 20 Å

Full size image

Maximum radial velocity occurs at \(r=16\) Å and reaches minimum at both the tube center and wall, which correlates with the radial force and satisfies the prescribed boundary conditions, i.e. Eqs. (2a, 2b). Using Eqs. (19) or (21), the numerical result for the axial velocity without the consideration of the suck in force is given in Fig. 5

Fig. 5
figure 5

Axial velocity without consideration of suck in force, where the arrows denote vector fields

Full size image

The axial velocity features the usual laminar flow with the slip boundary condition. The maximum velocity reaches 0.8 ms\(^{-1}\) at the center of the tube and the slip velocity at the boundary is 0.4 ms\(^{-1}\). Equation (21) turns out to be an excellent approximation to v as the integration factor, \(I(\xi )\) is found to be approximately equal to one. To take into account of the suck in effect, the pressure driven by the tube entry is incorporated and the axial velocity for both with and without consideration of the suck in force is given in Fig. 6 for comparison.

Fig. 6
figure 6

Axial velocity with and without consideration of suck in force

Full size image
Fig. 7
figure 7

Velocity fields inside the nanotube of length 1 nm

Full size image

Due to the suck in force occurring at the tube entry, the axial velocity is lifted and the maximum velocity reaches 5.2 ms\(^{-1}\) at the tube center, which is almost sevenfold larger than that without the suck in force. Laminar flow with the slip boundary condition still holds and the slip velocity is raised to 2.6 ms\(^{-1}\). Due to the significantly larger suck in force for nanotube with smaller radii (see Fig. 2), we expect that the axial velocity is lifted even higher for nanotubes with radius smaller than 20 Å but not too small, where the continuum assumption is violated. Now, both axial and radial velocities are considered and shown in terms of vector fields in Eq. (7). Axial velocity attains maximum at \(r=0\) and decreases with r. The radial velocity is almost zero at \(r=0\) and increases with r and then approaches zero in the vicinity of the wall. Even no boundary layer is assumed here, Fig. 7 features a distinctive boundary layer, in which water are more comfortably to be situated.

Least but not last, the flux is given by \(\mathbf {J}=\rho (\pi a^{2})^{-1}\int \mathbf {U}\cdot d\mathbf {S}\), where \(\mathbf {U}\) and \(d\mathbf {S}\) denote the total velocity and the surface element, respectively. The ratio of flux with and without the consideration of the suck in force is given by (3894.5 kg m\(^{-2}\)  s\(^{-1}\))/(600 kg m\(^{-2}\)  s \(^{-1}\)) = 6.5, which again shows an increase in flux due to the suck in force.

4 Conclusion

In conclusion, Newtonian fluid with the slip boundary condition is used to simulate the fluidic flow inside carbon nanotube with impermeable wall. Molecular effect is considered, and both the radial and axial velocities are derived analytically. While the velocity fields satisfy the prescribed boundary conditions, the axial velocity and the flux is raised almost sevenfold due to the suck in force generated at the tube entry. The current result may resolve the mystery of unexpectedly high flow rate occurring inside nanotubes.