1 Introduction

Chemical kinetics aims to describe the time evolution of chemical reactions. This is usually achieved by establishing a rate equation, which gives the rate of concentration changes in a system as a function of the concentrations [1, 2]. The concentrations can be considered continuous variables, so the rate equations are autonomous, ordinary differential equations that need to be solved to obtain the time dependence of the concentrations. In cases when very small amounts of substance are involved, an alternative approach, usually called stochastic chemical kinetics should be used to take the particulate nature of matter into account. In this approach, the time dependence of the process is characterized by probabilities through a master equation [2, 3]. Yet in the large majority of practical cases, the traditional (deterministic) approach to chemical kinetics is quite sufficient.

A key element in deterministic kinetics is solving the rate equation. The rate equation is typically an ordinary differential equation. Quite general solutions are known when the equation is linear or only involves the concentration of a single species [1, 2]. For other cases, general numerical solution methods are known [4], but analytical solutions are typically difficult to find. Yet, it is clear that analytical solutions offer major advantages: the parameter dependence is transparent. Also, when measured data are fitted to the scheme, numerical differentiation, which is typically a not very stable and computationally very demanding process, can be avoided. This is probably the reason why a fair number of recent publications devote considerable efforts to finding analytical solutions to various kinetic schemes with practical importance [5–21].

In a previous article of the present author, analytical solutions were reported for a family of two-step kinetic schemes where the second process was first order with respect to the intermediate [19]. As an extension of that previous work, the present paper reports solutions for four two-step schemes in which the second step is second order with respect to the intermediate.

2 General remarks on the solution methods

In the previous paper about two-step schemes with first order second steps, a general solution method could be found [19]. For the schemes investigated in this work, no such strategy could be implemented. However, for solving the differential equations of three of the four schemes considered here, a common initial set of transformations was useful, which will be discussed here at some length.

The schemes always involve the initial transformation of a reactant A to an intermediate B, then a decay of B. The general rate equation describing these systems can be given as follows:

$$\begin{aligned} \begin{aligned} \frac{d\hbox {[A]}}{dt}&=-f\hbox {([A])}\\ \frac{d\hbox {[B]}}{dt}&=f\hbox {([A])}-2k_2 \hbox {[B]}^{{2}} \end{aligned} \end{aligned}$$
(1)

[A] and [B] denote the concentrations of species A and B, whereas \(\hbox {[A]}_{0}\) and \(\hbox {[B]}_{0}\) will refer to the initial concentrations (i.e. those at \(t = 0\)). The general strategy used in this paper relies on first determining the time dependence of the concentration of the reactant (A) in the initial step. This is possible independently of the rest of the concentrations because the reactions are irreversible, so in effect, the rate equation of a single-stage scheme needs to be solved. The concentration of A always changes in a monotonous fashion (decreases). Because of this, it is often fruitful to seek the dependence of the concentration of B on the concentration of A first. The differential equation is as follows:

$$\begin{aligned} \frac{d\hbox {[B]}}{d\hbox {[A]}}=-1+\frac{2k_2 \hbox {[B]}^{{2}}}{f\hbox {([A])}} \end{aligned}$$
(2)

After solving this equation, the time dependence of the concentration of B can be obtained simply by substituting the known time dependence of the concentration of A. This strategy cannot be used when the first step is zeroth order with respect to [A], because the rate of concentration change for species B is independent of the concentration of [A] in this case. The main text of this paper will only state the solutions of the differential equations. The validity of these solutions can be checked by simple differentiation. However, the Supplementary Information also gives guidelines on how the equations can be solved.

2.1 Zeroth order first step

If the first reaction is zeroth order with respect to its reagent, the consecutive reactions are given by the following scheme:

$$\begin{aligned} \begin{aligned}&{\text {A}}\xrightarrow {{{\text {zeroth order, }}k_{1} }}{\text {B}} \\&{\text {2B}}\xrightarrow {{k_{2} }}{\text {C}} \end{aligned} \end{aligned}$$
(3)

The simultaneous differential equations describing the system shown in Eq. 3 are as follows:

$$\begin{aligned} \begin{aligned} \frac{d\hbox {[A]}}{dt}&=-\hbox {sgn([A])}k_1 \\ \frac{d\hbox {[B]}}{dt}&=\hbox {sgn([A])}k_1 -2k_2 \hbox {[B]}^{{2}} \end{aligned} \end{aligned}$$
(4)

The concentration of C can be given simply from mass balance, so this will not be indicated in the rate equations. The notation sgn refers to the signum function [22], similarly to the previous article of this author [19]. The multiplicator 2 appears before \(k_{2}\) in the second equation to satisfy well established kinetic conventions about second order reactions [1, 21, 23, 24]. The time dependence of the concentration of A is easily given in a zeroth order process [1, 21]:

$$\begin{aligned} \hbox {[A]}=\left\{ {{\begin{array}{ll} \hbox {[A]}_{0} -k_1 t&{}\quad \hbox {if}\quad t\le \hbox {[A]}_{0} /k_1 \\ \hbox {0} &{}\quad \hbox {if}\quad t\hbox { > [A]}_{0} /k_1 \\ \end{array} }} \right. \end{aligned}$$
(5)
Fig. 1
figure 1

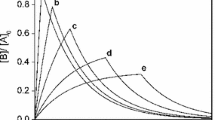
Representative scaled kinetic traces for the intermediate in the zeroth order–second order consecutive reaction (Eq. 5). The values of the shape parameter \(k_{2}\hbox {[A]}_{0}^{2}/k_{1}:\,0.1\) (a), 0.5 (b), 1 (c), 2 (d), 5 (e)

Full size image

This is the only case in this paper where the general approach described in Eq. 2 cannot be used. This is because at \(t> \hbox {[A]}_{0}/k_{1}\), [A] is invariably zero but [B] changes, so [B] cannot be thought of as a function [A]. Yet, as the rate of concentration change of B is independent of the concentration of A, this is the simplest case of all here. The second differential equation in Eq. 4 is separable without any transformations and the solution for the concentration of B is readily obtained as (see Supplementary Information):

$$\begin{aligned} \hbox {[B]}=\left\{ {{\begin{array}{l@{\quad }l} \sqrt{\frac{k_1 }{2k_2 }}\hbox {th}\left( {\sqrt{2k_1 k_2 }t+\hbox {arth}\left( {\sqrt{2k_2 /k_1 }\hbox {[B]}_{0} } \right) } \right) &{}\hbox {if}\quad t\le \hbox {[A]}_{0} /k_1 \\ \frac{\hbox {[B]([A]}_{0} /k_1 )}{1+2k_2 (t-\hbox {[A]}_{0} /k_1 \hbox {)[B]([A]}_{0} /k_1 )}&{}\hbox {if}\quad t\hbox { > [A]}_{0} /k_1 \\ \end{array}}} \right. \end{aligned}$$
(6)

The concentration of B at the critical time \(t = \hbox {[A]}_{0}/k_{1}\) is separate parameter combination in Eq. 6 and can be given based on the first part of Eq. 6:

$$\begin{aligned} \hbox {[B]([A]}_{0} /k_1 )=\sqrt{\frac{k_1 }{2k_2 }}\hbox {th}\left( {\sqrt{2k_2 /k_1 }\hbox {[A]}_{0} +\hbox {arth}\left( {\sqrt{2k_2 /k_1 }\hbox {[B]}_{0} } \right) } \right) \end{aligned}$$
(7)

Finally, the concentration of the final product formed in the second order transformation of (denoted as C) is given easily from mass balance equations (i.e. noting that the sum 2[A] \(+\) 2[B] \(+\) [C] is independent of time):

$$\begin{aligned} \hbox {[C]}=\frac{\hbox {[A]}_{0} +\hbox {[B]}_{0} -\hbox {[A]}-\hbox {[B]}}{{2}}+\hbox {[C]}_{0} \end{aligned}$$
(8)

For the most often encountered problems in chemical kinetics, the reaction usually starts purely from species A, and \(\hbox {[B]}_{0} = \hbox {[C]}_{0} = 0\). In this case, the formation and decay of B serves as a classical example of the behavior of an intermediate. Figure 1 displays a few sample kinetic curves calculated using Eq. 7. The scaling used in this figure is adopted especially for this system with an emphasis on curve shapes: the concentrations on the \(y\) axis is given in \(\hbox {[A]}_{0}\) units, whereas time on the \(x\) axis is given in \(1/(k_{2}\hbox {[A]}_{0})\) units. The whole system has three parameters (\(\hbox {[A]}_{0},\,k_{1}\) and \(k_{2}\)), but two of these are scaling parameters (\(\hbox {[A]}_{0}\) and \(k_{2}\hbox {[A]}_{0}\)) and the only parameter determining the shapes of the curves is \(k_{2}\hbox {[A]}_{0}^{2}/k_{1}\). Figure 1 shows five different curves for five different values of the shape parameter. Similar scaling will later as well.

The curves in Fig. 1 have a break point at time \(\hbox {[A]}_{0}/k_{1}\). This is similar to the case of the zeroth order–first order reaction [19], and the primary reason is that the zeroth order curves describing the time dependence of the concentration of A also has a break point here (i.e. it reaches its 0 final value).

2.2 First order first step

When the first step in the two consecutive reactions is first order with respect to A, the scheme is described as follows:

$$\begin{aligned} \begin{aligned}&{\text {A}}\xrightarrow {{k_{1} }}{\text {B}}\\&{\text {2B}}\xrightarrow {{k_{2} }}{\text {C}} \end{aligned} \end{aligned}$$
(9)

The simultaneous differential equations based on this scheme can be give as:

$$\begin{aligned} \begin{aligned} \frac{d\hbox {[A]}}{dt}&=-k_1 \hbox {[A]} \\ \frac{d\hbox {[B]}}{dt}&=k_1 \hbox {[A]}-2k_2 \hbox {[B]}^{{2}} \end{aligned} \end{aligned}$$
(10)

The first equation in this series is a well-known first order rate equation, the solution of which is available in almost any textbook on chemical kinetics [1, 21]:

$$\begin{aligned} \hbox {[A]}=\hbox {[A]}_{0} e^{-k_1 t} \end{aligned}$$
(11)

Following the general approach described earlier, Eq. 2 takes the following particular form:

$$\begin{aligned} \frac{d\hbox {[B]}}{d\hbox {[A]}}=-1+\frac{2k_2 \hbox {[B]}^{{2}}}{k_1 \hbox {[A]}} \end{aligned}$$
(12)

This is not a separable differential equation. Yet, after some well selected substitutions, it can be transformed into the modified Bessel differential equation (see Supplementary Information). The solution is given as:

$$\begin{aligned} \begin{aligned} \hbox {[B]}&=\sqrt{\frac{\hbox {[A]}}{2k_2 /k_1 }}\frac{2K_1 \left( {\sqrt{8\hbox {[A]}k_2 /k_1 }} \right) -\omega I_1 \left( {\sqrt{8\hbox {[A]}k_2 /k_1 }} \right) }{2K_0 \left( {\sqrt{8\hbox {[A]}k_2 /k_1 }} \right) +\omega I_0 \left( {\sqrt{8\hbox {[A]}k_2 /k_1 }} \right) } \\ \omega&=\frac{\sqrt{8\hbox {[A]}_{0} /(k_2 /k_1 )}K_1 \left( {\sqrt{8(k_2 /k_1 \hbox {)[A]}_{0} }} \right) -4\hbox {[B]}_{0} K_0 \left( {\sqrt{8(k_2 /k_1 \hbox {)[A]}_{0} }} \right) }{\sqrt{2\hbox {[A]}_{0} /(k_2 /k_1 )}I_1 \left( {\sqrt{8(k_2 /k_1 \hbox {)[A]}_{0} }} \right) +2\hbox {[B]}_{0} I_0 \left( {\sqrt{8(k_2 /k_1 \hbox {)[A]}_{0} }} \right) }\quad \quad \quad \end{aligned} \end{aligned}$$
(13)

In Eq. 13, \(I_{1}\) and \(I_{0}\) are modified Bessel functions of the first kind [25], whereas \(K_{1}\) and \(K_{0}\) are modified Bessel function of the second kind [26]. These elementary mathematical functions can be calculated as follows:

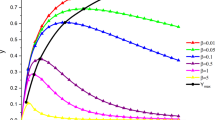
$$\begin{aligned} \begin{aligned} I_n (x)&=\left( {\frac{x}{2}} \right) ^{n}\sum _{j=0}^\infty {\frac{1}{j\hbox {!(}n+j\hbox {)!}}\left( {\frac{x^{2}}{4}} \right) ^{j}} \\ K_n (x)&=x^{n}\prod _{j=1}^n {\left( {2j-1} \right) } \int \limits _0^\infty {\frac{\hbox {cos}w}{(w^{2}+x^{2})^{n+1/2}}} dw \end{aligned} \end{aligned}$$
(14)

Figure 2 displays the concentration of [B] as a function of [A]. The initial concentration \(\hbox {[A]}_{0}\) is used as a concentration unit. The only shape parameter of this system is \(k_{2}\hbox {[A]}_{0}/k_{1}\), the curves are drawn for in Fig. 2 five different cases.

Fig. 2
figure 2

Scaled concentration of the intermediate as a function of the scaled concentration of the reagent in the first order–second order consecutive reaction (scheme in Eq. 9). The values of the shape parameter \(k_{2}\hbox {[A]}_{0}/k_{1}:\,0.05\) (a), 0.2 (b), 1 (c), 2.5 (d), 10 (e)

Full size image

After substituting the concentration of A given in Eq. 11, the solution for [B] can also be stated directly as a function of time:

$$\begin{aligned} \hbox {[B]}=\sqrt{\frac{k_1 \hbox {[A]}_{0} e^{-k_1 t}}{2k_2 }}\frac{2K_1 \left( {\sqrt{8k_2 \hbox {[A]}_{0} e^{-k_1 t}/k_1 }} \right) -\omega I_1 \left( {\sqrt{8k_2 \hbox {[A]}_{0} e^{-k_1 t}/k_1 }} \right) }{2K_0 \left( {\sqrt{8k_2 \hbox {[A]}_{0} e^{-k_1 t}/k_1 }} \right) +\omega I_0 \left( {\sqrt{8k_2 \hbox {[A]}_{0} e^{-k_1 t}/k_1 }} \right) }\quad \quad \quad \end{aligned}$$
(15)

Figure 3 shows five different examples based on this equation. On this scaled graph, the time unit is \(1/(k_{2}\hbox {[A]}_{0})\) and the concentration unit is \(\hbox {[A]}_{0}\). The shape parameter is again \(k_{2}\hbox {[A]}_{0}/k_{1}\). All the curves in Fig. 3 show the expected maximum. The concentration value at this maximum is higher and it occurs earlier as the value of the shape parameter decreases. The concentration of C can be calculated by mass balance with an equation identical to Eq. 8.

Fig. 3
figure 3

Representative scaled kinetic traces for the intermediate in the first order–second order consecutive reaction (Eq. 13). The values of the shape parameter \(k_{2}\hbox {[A]}_{0}/k_{1}:\,0.05\) (a), 0.2 (b), 1 (c), 2.5 (d), 10 (e)

Full size image

2.3 Second order first step

When the first step is a second order process, the kinetic scheme is represented as follows:

$$\begin{aligned} \begin{aligned}&2\hbox {A}\mathop {\rightarrow }^{k_1 }\hbox {B} \\&\hbox {2B}\mathop {\rightarrow }^{k_2 }\hbox {C} \end{aligned} \end{aligned}$$
(16)

The simultaneous differential equations that can be written based on this scheme for the concentrations of A and B take the following form:

$$\begin{aligned} \begin{aligned} \frac{d\hbox {[A]}}{dt}&=-2k_1 \hbox {[A]}^{{2}} \\ \frac{d\hbox {[B]}}{dt}&=k_1 \hbox {[A]}^{{2}}-2k_2 \hbox {[B]}^{{2}} \end{aligned} \end{aligned}$$
(17)

Again, the first of these differential equations, describing only the concentration change of A, is the well-known case of second order kinetics, and the solution is given in standard textbooks of chemical kinetics [1, 21]:

$$\begin{aligned} \hbox {[A]}=\frac{\hbox {[A]}_{0} }{1+2k_1 \hbox {[A]}_{0} t} \end{aligned}$$
(18)

Therefore, Eq. 2 takes the following particular form for this scheme:

$$\begin{aligned} \frac{d\hbox {[B]}}{d\hbox {[A]}}=-\frac{1}{2}+\frac{k_2 \hbox {[B]}^{{2}}}{k_1 \hbox {[A]}^{{2}}} \end{aligned}$$
(19)

After some well selected substitutions (see Supplementary Information), Eq. 19 can be transformed into a separable equation and solved:

$$\begin{aligned} \hbox {[B]}= & {} \frac{\hbox {[A]}}{(\alpha -\hbox {1)(}\alpha +1)}-\frac{\alpha \hbox {[A]}}{(\alpha -\hbox {1)(}\alpha +\hbox {1)}}\hbox {th}\left( \frac{\alpha }{2}\hbox {ln}\frac{\hbox {[A]}}{\hbox {[A]}_{0} }\right. \nonumber \\&\left. \quad +\,\hbox {arth}\frac{\hbox {[A]}_{0} -\hbox {[B]}_{0} (\alpha -1)(\alpha +1)}{\alpha \hbox {[A]}_{0} } \right) \\ \alpha= & {} \sqrt{2k_2 /k_1 +1}\nonumber \end{aligned}$$
(20)

Figure 4 shows five example traces in the form of concentration–concentration plot similar to Fig. 2. The only shape parameter of this plot is the rate constant ratio \(k_{2}/k_{1}\).

Fig. 4
figure 4

Scaled concentration of the intermediate as a function of the scaled concentration of the reagent in the second order–second order consecutive reaction (scheme in Eq. 16). The values of the shape parameter \(k_{2}/k_{1}:\,0.05\) (a), 0.2 (b), 1 (c), 2 (d), 10 (e)

Full size image

After substituting Eq. 18 into Eq. 20 and expanding the hyperbolic tangent function as the rational function of exponentials, the concentration of B can also be stated directly as a function of time:

$$\begin{aligned} \begin{aligned} \hbox {[B]}&=\frac{k_1 \hbox {[A]}_{0} }{2k_2 }\frac{(1+\alpha \hbox {)(}\sqrt{1+2k_1 \hbox {[A]}_{0} t})^{-1+\alpha }+\omega (1-\alpha \hbox {)(}\sqrt{1+2k_1 \hbox {[A]}_{0} t})^{-1-\alpha }}{(\sqrt{1+2k_1 \hbox {[A]}_{0} t})^{1+\alpha }+\omega (\sqrt{1+2k_1 \hbox {[A]}_{0} t})^{1-\alpha }} \\ \omega&=\frac{1+\alpha -(\alpha -\hbox {1)(}\alpha +\hbox {1)[B]}_{0} /\hbox {[A]}_{0} }{(\alpha -\hbox {1)(}\alpha +\hbox {1)[B]}_{0} /\hbox {[A]}_{0} +\alpha -1} \end{aligned} \end{aligned}$$
(21)

Finally, the concentration of C can be calculated by a mass conservation equation similar to

$$\begin{aligned} \hbox {[C]}=\frac{\hbox {[A]}_{0} -\hbox {[A]}}{\hbox {4}}+\frac{\hbox {[B]}_{0} -\hbox {[B]}}{{2}}+\hbox {[C]}_{0} \end{aligned}$$
(22)

Figure 5 gives five example kinetic curves calculated using Eq. 21. In this graph, \(\hbox {[A]}_{0}\) is the concentration unit, \(1/(k_{2}\hbox {[A]}_{0})\) is the time unit (scaling parameters), whereas the single shape parameter is \(k_{2}/k_{1}\).

Fig. 5
figure 5

Representative scaled kinetic traces for the intermediate in the second order–second order consecutive reaction (Eq. 21). The values of the shape parameter \(k_{2}/k_{1}:\,0.05\) (a), 0.2 (b), 1 (c), 2 (d), 10 (e)

Full size image

2.4 Mixed second order first step

In a mixed second order step, two different substances (rather than two identical ones as in the previous case) react to give a product. The scheme of a mixed second order step followed by a true second order reaction looks like this:

$$\begin{aligned} \begin{aligned}&\hbox {A}_1 +\hbox {A}_2 \mathop {\rightarrow }^{k_1 }\hbox {B} \\&\hbox {2B}\mathop {\rightarrow }^{k_2 }\hbox {C} \end{aligned} \end{aligned}$$
(23)

The rate equation is given as follows:

$$\begin{aligned}&\frac{d\hbox {[A}_1 \hbox {]}}{dt}=-k_1 \hbox {[A}_1 \hbox {][A}_{2} \hbox {]} \nonumber \\&\frac{d\hbox {[A}_{2} \hbox {]}}{dt}=-k_1 \hbox {[A}_1 \hbox {][A}_{2} \hbox {]} \\&\frac{d\hbox {[B]}}{dt}=k_1 \hbox {[A}_1 \hbox {][A}_{2} \hbox {]}-2k_2 \hbox {[B]}^{{2}}\nonumber \end{aligned}$$
(24)

Let \(\hbox {A}_{1}\) be the limiting reagent and \(\hbox {A}_{2}\) the excess reagent. This is simply a matter of choice as the notations \(\hbox {A}_{1}\) and \(\hbox {A}_{2}\) can be exchanged. Equation \([\hbox {A}_{2}] - [\hbox {A}_{1}] = [\hbox {A}_{2}]_{0} - [\hbox {A}_{1}]_{0}=\Delta \) holds at all time so that the first equation of Eq. 24 can be transformed into:

$$\begin{aligned} \frac{d\hbox {[A}_1 \hbox {]}}{dt}=-k_1 \hbox {[A}_1 \hbox {]([A}_1 \hbox {]}+\Delta ) \end{aligned}$$
(25)

If \([\hbox {A}_{2}]_{0} = [\hbox {A}_{1}]_{0}\) (so \(\Delta = 0\)), the solution is identical to the solution already derived in the previous section and given in Eq. 21. Again, the solution of Eq. 25 is found in textbooks [1, 21]:

$$\begin{aligned} \hbox {[A}_1 \hbox {]}=\frac{\Delta \hbox {[A}_1 \hbox {]}_{0} }{\hbox {[A}_{2} \hbox {]}_{0} e^{\Delta k_1 t}-\hbox {[A}_1 \hbox {]}_{0} }\quad \hbox {[A}_{2} \hbox {]}=\frac{\Delta \hbox {[A}_{2} \hbox {]}_{0} }{\hbox {[A}_{2} \hbox {]}_{0} -\hbox {[A}_1 \hbox {]}_{0} e^{-\Delta k_1 t}} \end{aligned}$$
(26)

In this system, Eq. 2 assumes the following form:

$$\begin{aligned} \frac{d\hbox {[B]}}{d\hbox {[A}_1 \hbox {]}}=-1+\frac{2k_2 \hbox {[B]}^{{2}}}{k_1 \hbox {([A}_1 \hbox {]}+\Delta \hbox {)[A}_1 \hbox {]}} \end{aligned}$$
(27)

After substitutions and some further transformations, this equation can be reduced to the Legendre differential equation (see Supplementary Information). The solution connecting the concentrations of \(\hbox {A}_{1}\) and B can be stated as follows:

$$\begin{aligned} \hbox {[B]}= & {} \frac{\Delta +2\hbox {[A}_1 \hbox {]}}{2\alpha }-\frac{\Delta \omega P_{\alpha +1} \left( {1+\frac{2\hbox {[A}_1 \hbox {]}}{\Delta }} \right) +\Delta {{\mathbf {Q}}}_{\alpha +1}^0 \left( {1+\frac{2\hbox {[A}_1 \hbox {]}}{\Delta }} \right) }{2\alpha \omega P_\alpha \left( {1+\frac{2\hbox {[A}_1 \hbox {]}}{\Delta }} \right) +2\alpha {{\mathbf {Q}}}_\alpha ^0 \left( {1+\frac{2\hbox {[A}_1 \hbox {]}}{\Delta }} \right) } \nonumber \\ \omega= & {} \frac{\Delta {{\mathbf {Q}}}_{\alpha +1}^0 (x_0 )-\Delta x_0 {{\mathbf {Q}}}_\alpha ^0 (x_0 )+2\hbox {[B]}_0 \alpha {{\mathbf {Q}}}_\alpha ^0 (x_0 )}{\Delta x_0 P_\alpha (x_0 )-\Delta P_{\alpha +1} (x_0 )-2\hbox {[B]}_0 \alpha P_\alpha (x_0 )} \\ \alpha= & {} \frac{\sqrt{8(k_2 /k_1 )+1}-1}{2}\quad x_0 =1+\frac{2\hbox {[A}_1 \hbox {]}_{0} }{\Delta }\nonumber \end{aligned}$$
(28)

In Eq. 28, \(P_{\alpha }(x)\) represents the Legendre function of the first kind [27], whereas \({{\mathbf {Q}}}_{\alpha }^{0}(x)\) is the associated Legendre function of the second kind type 3 [28]. Possible definitions of these functions include the following identities:

$$\begin{aligned}&P{ }_\alpha (x)\nonumber \\&\quad ={ }_2F_1 \left( {-\alpha ,\alpha +1,1,\frac{1-x}{2}} \right) \nonumber \\&\quad = 1+\sum _{n=1}^\infty {\frac{(-\alpha \hbox {)(}-\alpha +1)\cdots (-\alpha +n-1\hbox {)(}\alpha +1\hbox {)(}\alpha +2)\cdots (\alpha +n)}{n\hbox {!}n\hbox {!}}} \left( {\frac{1\!-\!x}{2}} \right) ^{n} \nonumber \\&{{\mathbf {Q}}}_\alpha ^0 (x) \nonumber \\&\quad =-\frac{\hbox {cos(}\alpha \pi )\Gamma (-\alpha -1/2)\Gamma (\alpha +1)}{(x-1)^{\alpha +1}2^{\alpha +1}\sqrt{\pi }}{ }_2F_1 \left( {\alpha +1,\alpha +1,2\alpha +2,\frac{2}{1-x}} \right) \end{aligned}$$
(29)

The function \(_{2}F_{1}\) in Eq. 29 is the hypergeometric function [29]. The use of this function was also necessary in the solution of the mixed second order–first order consecutive scheme [19]. The notation \(\varGamma (\hbox {x})\) refers to the gamma function, which is an extension of the factorial function to real numbers [30]. Figure 6 shows five examples of concentration–concentration traces based on Eq. 28. Unlike in the three previous cases, there are two shape parameters in this system: \([\hbox {A}_{2}]/[\hbox {A}_{1}]\) and \(k_{2}/k_{1}\).

Fig. 6
figure 6

Scaled concentration of the intermediate as a function of the scaled concentration of the limiting reagent in the mixed second order–second order consecutive reaction (scheme in Eq. 23). The values of the shape parameters \([\hbox {A}_{2}]_{0}/[\hbox {A}_{1}]_{0} = 2\) (a), 5 (b), 2 (c), 5 (d), 2 (e); \(k_{2}/k_{1} = 0.2\) (a), 1 (b), 1 (c), 5 (d), 4 (e)

Full size image

The concentration of B can also be given as the function of time. For this purpose, the following substitution needs to be made in Eq. 28:

$$\begin{aligned} 1+\frac{2\hbox {[A}_1 \hbox {]}}{\Delta }=\frac{\hbox {[A}_{2} \hbox {]}_{0} e^{\Delta k_1 t}+\hbox {[A}_1 \hbox {]}_{0} }{\hbox {[A}_{2} \hbox {]}_{0} e^{\Delta k_1 t}-\hbox {[A}_1 \hbox {]}_{0} } \end{aligned}$$
(30)

Some sample kinetic curves are shown in Fig. 7. The scaling parameters are concentration unit \([\hbox {A}_{1}]_{0}\) and time unit \(1/(k_{1}[\hbox {A}_{1}]_{0})\), whereas the shape parameters are the same as in Fig. 6: \([\hbox {A}_{2}]/[\hbox {A}_{1}]\) and \(k_{2}/k_{1}\). The usual mass balance equation can be used to obtain the concentration of C:

$$\begin{aligned} \hbox {[C]}=\frac{\hbox {[A}_1 \hbox {]}_{0} +\hbox {[B]}_{0} -\hbox {[A}_1 \hbox {]}-\hbox {[B]}}{{2}}+\hbox {[C]}_{0} \end{aligned}$$
(31)

Finally, it should be remarked that the third order–second order scheme, in analogy with the paper reporting the solutions of consecutive reactions with first order second steps [19], was also given some considerations. Unfortunately, attempts to find an analytical solution for this case have remained unsuccessful to date.

Fig. 7
figure 7

Representative scaled kinetic traces for the intermediate in the mixed second order–second order consecutive reaction (Eq. 28). The values of the shape parameters \([\hbox {A}_{2}]_{0}/[\hbox {A}_{1}]_{0} = 2\) (a), 5 (b), 2 (c), 5 (d), 2 (e); \(k_{2}/k_{1} = 0.2\) (a), 1 (b), 1 (c), 5 (d), 4 (e)

Full size image

2.5 Practical applications of the derived analytical solutions

The analytical solutions derived in this paper offer advantages compared to the numerical solutions of the same ordinary differential equations [4], which can be routinely carried by a considerable variety of scientific software packages. First, the parameter dependence of the solutions is much clearer in the analytical solutions. Scaling and shape parameters [21] are readily identified in these formulas, which is not obvious in numerical solutions. Furthermore, calculating the actual solutions for a problem is much less computationally intensive in this way. The major advantage in calculations probably lies in derivation: whenever curve fitting is attempted, the analytical solutions provide a way of obtaining analytical derivatives, which is very favorable compared to the option of highly unstable and computationally demanding numerical differentiation [21].

The kinetic schemes discussed here are not uncommon in chemistry. For example, in laser flash photolysis studies the first order formation of a reactive radical and it subsequent second-order decay is not uncommon, a recent example is the case of the chlorine, bromine and iodine molecule radicals (\(\hbox {Cl}_{2}^{-},\, \hbox {Br}_{2}^{-}\), and \(\hbox {I}_{2}^{-}\)) [31]. When radicals are generated and undergo recombination in experiments, one of the schemes studied here is likely to be useful. Two very recent experimental examples are investigations of the recombination of benzophenone ketyl free radicals [32] and dichlorocarbene radicals [33].

In addition to the direct uses, some less direct applications can be envisioned too. In chain mechanism, especially those involving radicals, second-order termination reactions are very common. The mathematical logic of the description of chain reactions [21] often makes it possible to set up two-step rate equations for the concentrations of the chain carriers, and the second step in these equations is second-order because of the second order termination. Such reaction networks are regularly encountered: rubber vulcanization kinetics [34, 35] and the autoxidation of aqueous sulfur(IV) [36, 37] are only two examples.

3 Conclusion

It is concluded that the analytical solutions of two-step consecutive reaction scheme with second order later steps can be found in a few selected cases. The solutions of the zeroth order–second order and second order–second order schemes are reasonably simple, and a common scientific calculator would be enough to carry out all necessary computations when their values are needed. The first order–second order and the mixed second order–second order schemes are a bit more complicated as the solutions use Legendre functions and modified Bessel functions. Commonly used mathematical softwares can readily handle these cases as well, and fitting experimental data to these analytical formulas should also be straightforward.