Differential model accounting for reversion for EPDM vulcanized with peroxides

Abstract

One of the main drawbacks of EPM/EPDM rubber vulcanization by peroxides is the lack of selectivity, which leads to a number of side reactions. The reaction mechanisms at the base of peroxides crosslinking are generally known and include the formation of alkyl and allyl (in the EPDM case) macro-radicals through H-abstraction from the macromolecular chains and the combination of these macro-radicals, which macroscopically is known with the term “vulcanization”. In the paper, a simple but effective mathematical model having kinetic base, to predict the vulcanization degree of rubber vulcanized with peroxides, is presented. The approach takes contemporarily into consideration, albeit within a simplified scheme, the actual reactions occurring during peroxidic curing, namely initiation, H-abstraction, combination and addition, and supersedes the simplified approach used in practice, which assumes for peroxidic curing a single first order reaction. After a suitable re-arrangement of the first order system of differential equations obtained from the actual kinetic system adopted, a single second order non-linear differential equation is obtained and numerically solved by means of a Runge–Kutta approach. Kinetic parameters to set are evaluated by means of a standard least squares procedure where target data are represented by experimental values available, i.e. normalized rheometer curves or percentage crosslink density experimentally evaluated by means of more sophisticated procedures. In order to have an insight into the reliability of the numerical approach proposed, two cases of technical interest are investigated in detail: the first is an EPDM crosslinked with two different peroxides, whereas the second is a compound with high level of unsaturation, showing reversion at medium-high vulcanization temperature ($175^\circ \text{ C}$).

1 Introduction

Peroxide curing [1, 2] has always been of interest to chemists working in the elastomer field, because of the relatively simple chemistry involved and the simple resulting network structure. The more widely used vulcanization systems based upon sulphur or sulphur compounds are very much more complex in mechanism and produce more varied crosslinks [3–7].

Terpolymerization of ethylene, propylene and a non-conjugated diene yields ethylene-propylene-diene-monomer (EPDM) rubber with a saturated polymer backbone and residual unsaturation in the side groups.

The main properties of ethylene-propylene elastomers depend on several parameters, among the others the most important are: composition, molecular weight and molecular weight distribution, the distribution of the inter- and intra-molecular composition and the length of the ethylene sequence. In addition, in ter-polymers, the type, amount and distribution of the third monomer play a crucial role on the final mechanical properties of the vulcanized rubber.

As a result, EPDM rubber has a superior resistance against oxygen, ozone, heat and irradiation when compared to natural rubber (NR), butyl rubber (BR) and styrene-butyl rubber (SBR) [8, 9].

All the aforementioned parameters may be varied within quite broad limits and the polymers thus obtained become quite specific, not only for the various applications typical of the traditional rubber industry, but also as modifiers for some plastics as well as for lubrificating oils, bitumen, etc. Furthermore, EP(D)M may be an excellent elastomer to be used for medium and elevated-temperature applications, such as electrical cables, automotive profiles, window gaskets, roof sheeting, etc. [10, 11].

As well known, ethylene-propylene elastomers can be produced with either a totally amorphous or a semi-crystalline structure, depending on the content and average length of the ethylene sequence. The propylene content in an amorphous elastomer is approximately 40–50 %wt. and the two main monomers (ethylene and propylene) are distributed throughout the polymeric chain in an alternating or chance fashion depending on what catalytic system has been employed. The pseudo-crystalline or semi-crystalline EPM elastomers have, on the other hand, a propylene content of less than 35 %wt. They are elastomers with an elevated “green strength” mainly determined by the length of the ethylenic sequence, which can be set beforehand through the appropriate choice of catalytic system and special synthesis conditions.

This ideal behavior appears to be dependent on the following structural and molecular parameters: (1) statistical monomer distribution in macro-molecular chains; (2) molecular weight distribution MWD; (3) molecular ratio C2/C3; (4) the amount and type of the third monomer.

The introduction of the third monomer does not change the backbone, the double bond enables sulfur vulcanization (80 % of EPDM applications) and enhances the peroxide curing efficiency (15 %) [12–16]. Indeed, the third monomer introduces the allylic hydrogen, which has, see Fig. 1, a lower abstraction energy [17].

Fig. 1

Energy required in order to extract hydrogen atom from the backbone of the macromolecules at 0 K. At $25^\circ \text{ C}$ add 1 Kcal [17]

At present, a huge amount of both experimental investigations and numerical models on EPDM cured with peroxides is available in the technical literature. These notwithstanding, the determination of the exact chemistry of vulcanization as well as the identification of the partial reactions occurring during curing are still an open issue.

Recently, several experimental studies have been performed to obtain further insight in the chemical mechanisms. First, a study on peroxide crosslinking of low-molecular-weight model compounds for EPDM was performed [18]. The use of gas chromatography (GC) allowed the separation of a wide variety of “cross-linked” products.

The precise structure of the various products could be obtained either by an interpretation of the mass spectrometry data or by means of a solid state $^{13}\text{ C}$ nuclear magnetic resonance (NMR) study, as done in [19], where it is shown that an increase in sensitivity is achieved.

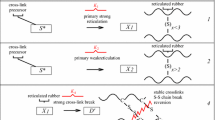
The basic chemistry in the generally accepted mechanism of peroxide cure of EPDM has been reviewed by van Duin and co-workers in [13–16, 18, 19], and may be summarized by means of the following partial reactions occurring in series and parallel:

$$\begin{aligned} {\begin{array}{l@{\qquad }l} \frac{1}{2}\text{ ROOR}\rightarrow \text{ RO}{\bullet } \rightarrow \text{ R}^{\prime }{\bullet }&\text{ initiation} \\ \text{ EP(D)M-H}+\text{ RO}{\bullet } \text{/R}^{\prime }{\bullet } \rightarrow \text{ EP(D)M}{\bullet } +\text{ ROH/R}^{\prime }\text{ H}&{\text{ H-abstraction}} \\ {\text{2EP(D)M}{\bullet } \rightarrow \text{ EP(D)M-EP(D)M}}&{\text{ combination}} \\ \text{ EP(D)M}{\bullet } +\text{ EP(D)M}\rightarrow \text{ EP(D)M}-\text{ EP(D)M}{\bullet } \rightarrow&\\ \text{ EP(D)M}-\text{ EP(D)M}-\text{ H}&{\text{ addition}} \\ \end{array} } \end{aligned}$$

(1)

The chain of free-radical reactions is initiated by thermal decomposition of the peroxide, yielding primary alkoxy ($\text{ RO}{\bullet }$) or secondary alkyl radicals ($\text{ R}{\bullet }$). Subsequent abstraction of H-atoms from the EPDM polymer results in the formation of EPDM macro-radicals ($\text{ EPDM}{\bullet }$). Calculations based on kinetic data for H-abstraction indicate that H-abstraction mainly occurs along the saturated EPM polymer backbone [20], whereas several electron paramagnetic resonance (EPR) spectroscopy studies have shown the selective formation of allyl radicals derived from the diene monomer.

Considering the energy required for the abstraction of the H-atoms, see Fig. 1, within the formation of the back-bone, the allyl radicals are more probable than the others, because of the lowest energy required by the abstraction of the H-atoms [17].

The actual cross-linking proceeds through two pathways, which have been shown to be additive [21]. Two EPDM macro-radicals either combine or, alternatively, a macro-radical adds to an EPDM unsaturation. Visible spectroscopy has confirmed the conversion of the EPDM unsaturation upon peroxide cure [13–16, 18–25]. It is noted that in practical EPDM/peroxide compounds, usually co-agents, such as triallyl (iso)cyanurate, trimethylolpropane trimethacrylate or m-phenylenebis(maleimide), are included to increase the peroxide curing efficiency [15], which obviously affects the mechanism of peroxide cure.

In the paper, a simple but effective mathematical model having kinetic base, to predict the vulcanization degree of rubber vulcanized with peroxides is presented.

The approach schematically summarized in (1) takes contemporarily into consideration four main reactions occurring during peroxidic curing, i.e. initiation, H-abstraction, combination and addition, overcoming the simplified approach which assumes for peroxidic curing a single first order reaction. After a suitable re-arrangement of the first order system of differential equations obtained from the actual kinetic system adopted, a single second order non-linear differential equation is obtained and numerically solved by means of a Runge–Kutta approach [26]. Kinetic parameters to set are evaluated by means of a standard least squares procedure where target data are represented by experimental values available, i.e. normalized rheometer curves or percentage crosslink density experimentally evaluated by means of more sophisticated procedures.

Two cases of technical interest are critically discussed, the first relying into an EPDM crosslinked with di-cumyl peroxide, the second into a compound with high level of unsaturation exhibiting reversion at relatively high temperatures ($175^\circ \text{ C}$) near the end of the vulcanization process. A quite promising agreement is experienced, even in presence of reversion.

2 The kinetic mathematical model proposed

The mechanism of EPM/EPDM peroxide curing and the structures formed are still lacking, mainly due to the complexity of the system (large number of structures formed at low concentrations) combined with the difficulties to determine the cross-linked polymer networks.

The complex set of the reactions that characterize peroxide cross-linking involves homolytic cleavage of peroxide, oxy and alkyl radicals, hydrogen abstraction, radical coupling (cross-link formation), polymer scission and radical transfer. In the case of EPDM, the amount and type of the third-monomer, are also important parameters to consider, but they can be safely disregarded in a first approximation of the phenomenon for those EPDMs having lower concentrations of the third-monomer. Therefore, our curing scheme considers the different activity of alkyl and oxy radicals in the homolytic cleavage of peroxide and the secondary reactions as oxygenation and acid-catalyzed decomposition of the peroxide. In this framework, we have adopted for EPM/EPDM the kinetic scheme constituted by the chemical reactions summarized in Eq. (1) and already adopted by other authors, see e.g. [21, 25].

In order to deduce mathematical differential relations among chemical quantities involved in the reticulation process (1), the chemical reactions appearing in (1) are simplified schematically as follows:

$$\begin{aligned} \begin{array}{l} I\mathop \rightarrow \limits ^{k_1 } 2R \\ R+P\mathop \rightarrow \limits ^{k_2 } P^{*} \\ 2P^{*}\mathop \rightarrow \limits ^{k_3 } P_r^*\\ P^{*}\mathop \rightarrow \limits ^{k_4 } P_i^*\\ \end{array} \end{aligned}$$

(2)

In Eq. (2), $I$ is the peroxide, $R$ the primary alkoxy ($\text{ RO}{\bullet }$) or secondary alkyl radicals ($\text{ R}{\bullet }),\,P$ the uncured polymer, $P^{*}$ is the EPDM macro-radical, $P_r^*$ and $P_i^*$ the matured cross-linked polymers, and $K_{1,\ldots ,4}$ are kinetic reaction constants. Here it is worth emphasizing that $K_{1,\ldots ,4}$ are temperature dependent quantities, hence they rigorously should be indicated as $K_{1,\ldots ,4} (T)$, where $T$ is the absolute temperature. In what follows, for the sake of simplicity, the temperature dependence will be left out.

By means of the so called xyz method, independent variables may be established. From stoichiometry of the reaction, it can be argued that:

$$\begin{aligned} \begin{array}{l} I=I_0 -x \\ R=2x-y \\ P=P_0 -y \\ P^{*}=y-2z-q \\ P_r^*=z \\ P_i^*=q \\ \end{array} \end{aligned}$$

(3)

Obviously, from (3) it can be also deduced that independent variables are $I\left( t \right),\,R\left( t \right), P_r^*\left( t \right)$ and $P_i^*\left( t \right)$. Indeed, from (3) it turns out that:

$$\begin{aligned} \begin{array}{l} x=I-I_0 \\ y=2(I-I_0 )-R \\ P=P_0 +R-2\left( {I-I_0 } \right) \\ P^{*}=2(I-I_0 )-R-2P_r^*-P_i^*\\ z=P_r^*\\ q=P_i^*\\ \end{array} \end{aligned}$$

(4)

The aim is to provide an analytical expression for vulcanized rubber, i.e. concentration of $P^{*}$ with respect to time.

From (2) and (3) and well established kinetic rules, the following set of differential equations may be written:

$$\begin{aligned} \begin{array}{l} (\text{ a})\;\frac{dI}{dt}=-K_1 I\\ (\text{ b})\;\frac{dR}{dt}=2K_1 I-K_2 RP\\ (\text{ c})\;\frac{dP}{dt}=-K_2 RP\\ (\text{ d})\;\frac{dP^{*}}{dt}=K_2 RP-K_3 \left( {P^{*}} \right)^{2}-K_4 P^{*}\\ (\text{ e})\;\frac{dP_r^*}{dt}=K_3 \left( {P^{*}} \right)^{2}\\ (\text{ f})\;\frac{dP_i^*}{dt}=K_4 P^{*} \\ \end{array} \end{aligned}$$

(5)

First order differential equations (a), (b) and (c) in (5) constitute a system of first order differential equations in three variables, which may be solved by means of an ad-hoc strategy summarized in what follows. In particular, equation (a) may be solved immediately by separation of variables, allowing to determine the concentration of peroxide with respect to time:

$$\begin{aligned} I=I_0 e^{-K_1 \left( {t-t_0 } \right)} \end{aligned}$$

(6)

From (6) and performing the difference between equations (b) and (c) in (5) we obtain:

$$\begin{aligned} \frac{dR}{dt}-\frac{dP}{dt}=2K_1 I=2K_1 I_0 e^{-K_1 \left( {t-t_0 } \right)} \end{aligned}$$

(7)

Differentiating Eq. (5)(c), it turns out that:

$$\begin{aligned} \frac{d^{2}P}{dt^{2}}=-K_2 R\frac{dP}{dt}-K_2 P\frac{dR}{dt} \end{aligned}$$

(8)

From (7), remembering from (5) that $R=-\frac{1}{K_2 P}\frac{dP}{dt}$, the second order differential Eq. (8) may be re-written exclusively in terms of $P$ as follows:

$$\begin{aligned} \frac{d^{2}P}{dt^{2}}-\frac{1}{P}\left( {\frac{dP}{dt}} \right)^{2}+K_2 P\frac{dP}{dt}+2K_1 K_2 I_0 Pe^{-K_1 \left( {t-t_o } \right)}=0 \end{aligned}$$

(9)

Equation (9) is a non-linear and non-homogeneous second order differential equation in the sole variable $P$. The determination of a closed form solution for (9) is not an easy task, however its numerical solution by means of a standard Runge–Kutta algorithm [26] is very straightforward and allows a quite fast evaluation of the polymer concentration $P(t)$. The knowledge of $P(t)$ allows to determine $R(t)$ and, from Eq. (5)(d), $P^{*}$ as:

$$\begin{aligned} \frac{dP^{*}}{dt}=K_2 R(t)P(t)-K_3 \left( {P^{*}} \right)^{2}-K_4 P^{*} \end{aligned}$$

(10)

Equation (10) is a first order non linear differential equation, again solved using a Runge–Kutta numerical approach.

3 Numerical applications

In order to assess the capabilities of the differential equation model proposed in reproducing the experimental vulcanization process of EPDM cured with peroxides, two different rubber typologies experimentally tested either by the authors [27] or available in the technical literature [19, 25] are here re-considered as reference data.

Attention is focused exclusively on the capabilities of the numerical approach to fit experimental evidences. The first example relies into an EPDM blend with low unsaturation level and vulcanized either with Perkadox BC-FF or with Perkadox 14S-FL, both at two different temperatures, namely $180$ and $200^\circ \text{ C}$. The second EPDM considered has been experimentally tested in both [19] and [25], and is characterized by a high ENB content (9 %), so resulting extremely unsaturated. A marked reversion on the crosslinking density was noted by means of 13-C NMR by van Duin and co-workers [19, 24] after long vulcanization at $175^\circ \text{ C}$. It is therefore an example particularly indicated to test the capability of the numerical model in reproducing rubber curing behavior even in the reversion branch.

3.1 Mix without reversion

The blend under consideration has the composition schematically reported in Table 1. Experimental results, hereafter reported with the sole aim of testing the capabilities of the numerical model proposed, belong to a wider experimental program still running and promoted by the authors in cooperation with Mixer Spa [27] to analyze the effectiveness of peroxidic curing.

Table 1 First experimental data set analyzed, EPDM type I, composition in phr

Rheometer data were obtained in an oscillating disc curometer at two different temperatures, respectively equal to $180$ and $200^\circ \text{ C}$. A wider range of temperatures has been experimentally investigated by the authors, from $120^\circ \text{ C}$ up to $220^\circ \text{ C}$, but the presentation of all the results is postponed for the sake of conciseness. Two different peroxides produced by Akzo, with commercial names Perkadox BC-FF and Perkadox 14S-FL, were tested to vulcanize the EPDM under consideration. Perkadox BC-FF is dycumil peroxide whereas Perkadox 14S-FL is a di(tert-butylperoxyisopropyl) benzene. They exhibit a half time equal to 1 min at $138$ and $146^\circ \text{ C}$, respectively. The peroxides are therefore quite similar; nonetheless, some perceivable differences in the experimental rheometer curves of the EPDM under consideration are visible. In both cases, experimental results, as expected, do not exhibit perceivable reversion. Experimental rheometer curves are comparatively represented for both peroxides in Fig. 2a, b at $180$ and $200^\circ \text{ C}$ respectively.

Fig. 2

EPDM type I vulcanized with two different peroxides, experimental data. a $180^\circ \text{ C}$. b $200^\circ \text{ C}$

To perform a numerical optimization of the kinetic model proposed, experimental cure values are normalized dividing each point of the curve by the maximum torque values, so that experimental data are always within the range 0–1.

A comparison between present numerical curve and experimental data is provided in Figs. 3 and 4 for EPDM vulcanized with Perkadox BC-FF at $180$ and $200^\circ \text{ C}$ respectively. The resultant kinetic constants found numerically are summarized in Table 2.

Fig. 3

EPDM type I vulcanized with Perkadox BC-FF, $180^\circ \text{ C}$. Comparison between experimental data and the numerical system based on the second order non linear differential equation. a Full normalized curve. b Difference between numerical model and experimental normalized torque at successive iterations

Fig. 4

EPDM type I vulcanized with Perkadox BC-FF, $200^\circ \text{ C}$. Comparison between experimental data and the numerical system based on the second order non linear differential equation. a Full normalized curve. b Difference between numerical model and experimental normalized torque at successive iterations

Table 2 Numerical results obtained after least squares optimization for kinetic constants $K_1 \quad K_2$

Numerical curves are obtained using a non-linear least squares procedure, for which the convergence performance is evaluated in Figs. 3b, 4b. In particular, in the figures, the absolute difference between normalized experimental torque and numerical predictions is represented, at successive iterations and at increasing instants between the initial and final time of experimentation. Obviously, as expected, passing from the initial iteration to the final, such difference decreases drastically, meaning that the least squares routine is achieving convergence. As it is possible to notice, the gap between numerical models and experimental data tends to zero for almost all the instants inspected, exception made for the initial simulation range, near scorch point. Here the experimental curve exhibits a sudden increase in the first derivate, meaning that the initiation of vulcanization is prone to occur. In any case, this stage is of little interest for the models proposed, which are designed for a reliable prediction of final reticulation level. In general, the agreement with experimental response seems rather promising, with an almost perfect superposition of the numerical curves with experimental data.

Simulations are replicated for the second set of data available in presence of Perkadox 14S-FL peroxide, and the results are summarized in Figs. 5 and 6 for curing temperatures equal to $180$ and $200^\circ \text{ C}$ respectively. The same considerations done for the previous set of numerical simulations may be repeated here, with an almost perfect superposition of experimental and numerical curves for the majority of the time intervals inspected. The convergence map of the least squares algorithm (see Figs. 5b and 6b) shows that after around 50 iterations the best fitting is always achieved, with errors in practice vanishing. The numerical values of the four kinetic constants defining completely the reaction kinetic are summarized, as done for the previous peroxide, in Table 2.

Fig. 5

EPDM type I vulcanized with Perkadox 14S-FL, $180^\circ \text{ C}$. Comparison between experimental data and the numerical system based on the second order non linear differential equation. a Full normalized curve. b Difference between numerical model and experimental normalized torque at successive iterations

Fig. 6

EPDM type I vulcanized with Perkadox 14S-FL, $200^\circ \text{ C}$. Comparison between experimental data and the numerical system based on the second order non linear differential equation. a Full normalized curve. b Difference between numerical model and experimental normalized torque at successive iterations

Considering the numerical values obtained for the first two constants $K_1$ and $K_2$, reported in Table 2 (the other constants are almost zero, indicating that no reversion is experienced) at two distinct temperatures, it appears interesting to plot the straight lines passing from such values in the Arrhenius plane. In such space, the horizontal axis is represented by the inverse of the absolute temperature, $1/T$, whereas the vertical axis is $\log \left( {K_i } \right)$, where $K_i$ is the i-th kinetic constant. It is, indeed, commonly accepted that the variability of a single kinetic constant follows the so called Arrhenius law, which may be written as $K_i \left( T \right)=K_{i0} e^{\frac{E_{ai} }{R_g T}}$, where $K_{i0}$ is the value of the i-th kinetic constant at an infinite temperature, $E_{ai}$ is a constant typical of the reaction and $R_g$ is the universal gas constant. In a $1/T-\log \left( {K_i } \right)$ Cartesian plane, the Arrhenius law is thus represented by a straight line, intercepting vertical axis at $\log \left( {K_{i0} } \right)$. Since experimental data are available at two distinct temperatures, and accepting that each single constant follows an Arrhenius law, it is possible to sketch $K_i \left( T \right)$ lines in the $1/T-\log \left( {K_i } \right)$ plane, for both peroxides under consideration. Such representation is particularly useful from a practical point of view, because it allows a direct evaluation of the kinetic constants describing the velocity of the partial reactions at any vulcanization temperature. The straight lines numerically deduced are depicted in Figs. 7 and 8 for Perkadox BC-FF and Perkadox 14S-FL respectively. Subfigures–a refer to a wide temperature range, whereas in subfigures–b a detail near $200^\circ \text{ C}$ is sketched. Numerical data of Table 2, utilized to plot the straight lines, are also indicated for the sake of clearness. In order to evaluate if the numerical approach proposed is in agreement with simplified procedures commonly used in practice, it is also possible to compare numerical results with commercial data available for both peroxides under consideration. In particular, Akzo Nobel furnishes in tabular form values of the kinetic constants [28] of both Perkadox BC-FF and Perkadox 14S-FL at three different temperatures, corresponding to a half-time life equal to 0.1, 1 and 10 h respectively. It is implicitly assumed that the reaction describing peroxide decomposition is of first order and that the single kinetic constant associated to such a reaction follows and Arrhenius law. It is very straightforward the deduction of the numerical values of the constants at the three temperatures considered, from the experimental knowledge of the half time life $t_{1/2}$, being simply $K_i \ln 2=t_{1/2}$.

Fig. 7

EPDM type I vulcanized with Perkadox BC-FF. Linear regression interpolation of the kinetic constants $K_1$ and $K_2$ provided by the single differential equation model, the resultant linear regression obtained as $K_1 +K_2$ and comparison with commercial data provided by Akzo Nobel for the peroxide under consideration. a Large range of temperatures. b Detail near $200^\circ \text{ C}$

Fig. 8

EPDM type I vulcanized with Perkadox 14S-FL. Linear regression interpolation of the kinetic constants $K_1$ and $K_2$ provided by the single differential equation model, the resultant linear regression obtained as $K_1 +K_2$ and comparison with commercial data provided by Akzo Nobel for the peroxide under consideration. a Large range of temperatures. b Detail near $200^\circ \text{ C}$

Since in our numerical model, first and second reactions occur in series, and the first reaction produces $2R$ radicals, the comparison with the simplified practical approach above discussed, may be attempted considering the weighted average between constants $K_1$ and $K_2$, i.e. plotting the straight line 1/3*($2\text{ log}K_1 +\text{ log}K_2$), again deduced from present numerical results and represented with a dash-dot line in Figs. 7 and 8 for Perkadox BC-FF and Perkadox 14S-FL respectively. In the same figures, data deduced from commercial catalogues provided by Akzo Nobel [28] are represented with circles. As it is possible to notice, the agreement is almost perfect, meaning that the predictivity of the numerical procedure here presented is very promising.

3.2 Mix with reversion

Orza et al. [19] and Orza [24] analyzed experimentally an EPDM with a high ENB content, i.e. very unsaturated, and they evaluated experimentally the crosslink density achieved during a vulcanization at controlled temperature equal to $175^\circ \text{ C}$.

The EPDM considered in [19, 24] has the composition roughly reported in Table 3. As it is possible to notice, the amount of the third monomer is quite high, namely 9 % ENB-EPDM at 230 mmol/kg. It is therefore expected a visible reversion at the end of the vulcanization process.

Table 3 Second experimental data set analyzed, EPDM type II, composition in phr

The experimental crosslink density at time zero had a substantial experimental error because the experimentation was performed for the non-crosslinked rubber at $90^\circ \text{ C}$, a temperature which is not adequate for an accurate estimation of the entanglement density. As a consequence, it was simply assumed equal to zero according to intuition. The experimental evolution of the chemical crosslink density as a function of time is sketched in Fig. 9 in semi-logarithmic scale (see [7] for an explanation of the reasons at the base of this choice) and the reader is referred to Orza et al. [19] and Orza [24] for details.

Fig. 9

EPDM type II experimental crosslinking density (figure elaborated from [19] and transferred in semi-logarithmic scale to show reversion, see also [7])

The time dependence of the crosslink density was experimentally derived by means of a so-called 1H NMR T2 relaxation. The curve shows that the network formation follows a concave curve and is completed after approximately 10 min at $175^\circ \text{ C}$, which is consistent with the half life time of 1 min of the peroxide used at $175^\circ \text{ C}$. Due the unsaturation level, reversion is experienced after around 12 min. At 19 min the % drop of the crosslink density curve is around 7 %.

In Fig. 10a, a comparison between the experimental normalized curve representing the ter-polymer crosslink density and the numerical curve provided by the kinetic curing model is depicted. Figure 10b shows the convergence of the least squares routine on experimental data at successive iterations, in analogy to what done in the previous case. Finally, in Table 2, the values of the three kinetic constants corresponding to the converged least squares solution are reported.

Fig. 10

EPDM type II with high unsaturation percentage, $175^\circ \text{ C}$. Comparison between experimental data and the numerical system based on the second order non linear differential equation. a Full normalized curve. b Difference between numerical model and experimental normalized torque at successive iterations

As it is possible to notice, in this case constant $K_4$ is much higher with respect to the previous two sets of examples (Type I EPDM), meaning that a visible reversion is present at the end of the vulcanization process.

The agreement with experimental data, see Fig. 10, is quite satisfactory also in this case. However, while for Type I EPDM, numerical and experimental data were almost always superimposable, in this case a small deviation from experimental data may be observed, especially near the initiation of the reversion process, which is found a little bit earlier in the numerical model (around 8.5 min). Such a discrepancy may be easily explained, since it is connected to the complex reactions occurring in parallel during reversion, for the presence of a high unsaturation level as well and the presence of many coadiuvants, with chemical effect hardily predictable. All these physical phenomena, sometimes still unknown in detail, are not taken into account in the simplified chemical scheme at the base of the differential equations simplified model reported in (1)–(3).

4 Conclusions

A simple numerical model for a detailed kinetic interpretation of EPDM vulcanization by means of peroxides has been discussed. The model moves its steps within the generally accepted partial reactions occurring in practice, Eq. (1), and allows the estimation of the vulcanized polymer concentration as a function of curing time, at a fixed external vulcanization temperature.

It is shown how a detailed analysis of the reactions occurring during peroxide curing may be described properly by means of the knowledge of four different kinetic constants, each one representing a single reaction within the chemical basic scheme adopted.

The first order differential equations system deduced from (1) is suitably manipulated and a single non-homogeneous and non-linear second order differential equation is deduced, allowing a direct numerical estimation of cured polymer concentration. The equation is numerically solved by means of a consolidated explicit approach and the kinetic constants at the base of the vulcanization process are estimated simply by means of a non-linear least squares data fitting. Experimental data are represented either by scaled rheometer curves at fixed temperatures or by scaled crosslink density evaluated experimentally through more sophisticated approaches.

The cases of EPDM with both low and high unsaturation level may be reproduced with promising accuracy. The second case refers to a rubber material exhibiting reversion at the end of the vulcanization process, i.e. a decrease of the crosslink density for vulcanization times exceeding the optimal point.

Two cases of technical interest are analyzed in detail to evaluate the capabilities of the numerical approach proposed, the first relying on a standard EPDM without reversion, the second on a rubber compound with high unsaturation level, showing marked reversion when vulcanized over the optimal curing time. In both cases, the numerical response fits well experimental evidences, meaning that the approach proposed may represent a valuable tool for all practitioners interested in both (1) a fast evaluation of reaction kinetic constants and (2) a prediction of the final mechanical properties of vulcanized rubber without the need of performing expensive experimental campaigns.