1 Introduction

The final goal of the kinetics of a chemical reaction is finding the temporal dependence of the concentration of its reagents [1–3]. Usually, upon formulating the mathematical model of a specific chemical reaction, solutions of the corresponding nonlinear differential equations are found by numerical methods [4–8]. Therefore, rather interesting and unexpected is the fact that sometimes, despite of its complexity, it is possible to solve a system of nonlinear equations by analytical methods [9–11].

To this end, of extreme importance are two aspects: transition to the dimensionless form of evolutionary equations and the symmetry of the problem under consideration. The presence of these two aspects allows as essential reduction of the number of the effective parameters of the model and to present the solution in an analytical form. This type of solution, contrary to numerical, allows presenting the time-dependence of the concentrations on the parameters, often employing special mathematical functions, though.

Usually, the maximum allowed by analytical methods goes not further than merely constructing the phase portrait of a system. For this purpose, an essential bonus is the use of the corresponding conservation laws [12]. Investigation of the chemical reaction model allowing analytical solutions of the corresponding evolutionary equations, has a double purpose: on the one hand, to obtain the temporary dependence of reagent concentrations in an analytical form and, on the other hand, to assist the mathematical theory in finding the criterion of integrability.

In order to concretize the reasons that allow obtaining a solution in analytical form, it is desirable to examine a concrete example of a chemical reaction whose mathematical model would be pithy enough and at the same time allowing to find the corresponding solutions in an analytical form.

2 The mathematical model of a chemical reaction

As an example of the mathematical model of a chemical reaction, which allows an analytical solution, let us consider the reaction of the formation of the ester ethylene glycol [13] and acetic acid [14]. The initial substances are disodium salt of ethylene glycol \(\mathrm{NaOCH }^{}_2\mathrm{CH }^{}_2\mathrm{ONa }\) and an acetic acid derivative, the so-called acetyl chloride \(\mathrm{CH }^{}_3\mathrm{COCl }\) [15, 16]:

$$\begin{aligned}&\begin{array}{cccc} \mathrm{H^{}_3C-C-Cl } &{} +\quad \mathrm{NaO-CH^{}_2CH^{}_2-ONa } &{} \mathrm{+\quad Cl-C-CH^{}_3 } &{} \longrightarrow \\ \;\;\,|| &{}&{} \;\;\;|| \\ \mathrm{\;\;\;O } &{} &{} \mathrm{\;\;\;O } &{} \end{array}\\&\quad \quad \begin{array}{ccccc} \longrightarrow &{} \mathrm{\;H^{}_3C-C-O\,- }&{} \mathrm{CH^{}_2CH^{}_2 }&{} \mathrm{\!-\,O-C-CH^{}_3 } &{} + \quad \mathrm{2NaCl } \\ &{} \;\,|| &{} &{} \!\!\!\!|| &{} \\ &{} \mathrm{\;\; O } &{} &{} \mathrm{\!\!\!\!O } &{} \end{array}\nonumber \end{aligned}$$
(1)

This reaction proceeds in two stages: first, one molecule of acetyl chloride react with the salt and then the other one. Upon denoting the initial substances as X and Y, the mechanism of the reaction may be put as follows:

$$\begin{aligned} \mathrm{X + Y }&\stackrel{k}{\longrightarrow }&\mathrm{XY },\nonumber \\ \mathrm{XY + Y }&\stackrel{k}{\longrightarrow }&\mathrm{XY^{}_2 }, \end{aligned}$$
(2)

where \(\mathrm{XY^{}_2 }\) is the reaction product—a complete ester, and \(\mathrm{XY }\) is intermediate substance containing only one ester group \(\mathrm{-O-CO- }\). Since in each case interreaction occurs among the same atoms, the velocity constants \(k\) in both stages are the same. As we shall see below, this notion is of decisive importance for the analytical kinetic equations of this reaction.

Let \(\left[ \mathrm{X }\right] =[\mathrm{X }](t),\,[\mathrm{Y }]=[\mathrm{Y }](t),\,[\mathrm{XY }]=[\mathrm{XY }](t)\) and \([\mathrm{XY^{}_2 }]=[\mathrm{XY^{}_2 }](t)\) be the concentrations of the respective substances at an arbitrary moment of time \(t\). Then a system of kinetic equations for this reaction are

$$\begin{aligned} \frac{d\,[\mathrm{X }]}{dt}&= -k[\mathrm{X }][\mathrm{Y }],\nonumber \\ \frac{d\,[\mathrm{Y }]}{dt}&= -k[\mathrm{X }][\mathrm{Y }]-k[\mathrm{XY }][\mathrm{Y }],\nonumber \\ \frac{d\,[\mathrm{XY }]}{dt}&= -k[\mathrm{X }][\mathrm{Y }]-k[\mathrm{XY }][\mathrm{Y }],\nonumber \\ \frac{d\,[\mathrm{XY^{}_2 }]}{dt}&= k[\mathrm{XY }][\mathrm{Y }]. \end{aligned}$$
(3)

Let us select the initial conditions so as the quantities of the substances would correspond to the reaction equation in the absence of products at the initial moment of time:

$$\begin{aligned}{}[\mathrm{X }](0)=[\mathrm{X }]^{}_{0}, \quad [\mathrm{Y }](0)=[\mathrm{Y }]^{}_{0}, \quad [\mathrm{XY }](0)=[\mathrm{XY^{}_2 }](0)=0\,. \end{aligned}$$
(4)

To meet this condition, the initial ratio of concentrations \([\mathrm{Y }]^{}_{0}/[\mathrm{X }]^{}_{0}\) should be not an arbitrary but quite a definite number:

$$\begin{aligned} r=\frac{[\mathrm{Y }]^{}_{0}}{[\mathrm{X }]^{}_{0}}\,. \end{aligned}$$
(5)

Let us pass on to the dimensionless from of the kinetic equations (3) and initial conditions (4). For this purpose, we will perform the following replacement of functions and of the variable:

$$\begin{aligned} x\equiv \dfrac{[\mathrm{X }]}{\,[\mathrm{X }]^{}_{0}}; \quad y\equiv \dfrac{[\mathrm{Y }]}{\,[\mathrm{X }]^{}_{0}}; \quad z\equiv \dfrac{[\mathrm{XY }]}{\,[\mathrm{X }]^{}_{0}}; \quad w\equiv \dfrac{[\mathrm{XY^{}_2 }]}{\,[\mathrm{X }]^{}_{0}}; \quad \tau \equiv kY^{}_{0}t\,. \end{aligned}$$
(6)

In these variables, the system of kinetic equations takes the following form:

$$\begin{aligned} x^{\prime }&= -xy,\nonumber \\ ry^{\prime }&= -xy-zy,\nonumber \\ z^{\prime }&= xy-zy,\nonumber \\ w^{\prime }&= zy, \end{aligned}$$
(7)

where, in this case, \(^{\prime }\) denotes the derivative according to the dimensionless time \(\tau \) and the initial conditions (4) are noted as follows:

$$\begin{aligned} x(0)=1\,, \quad y(0)=2\,, \quad z(0)=w(0)=0\,. \end{aligned}$$
(8)

The totality of the kinetic equations (7) and initial conditions (8) comprises the mathematical model of the chemical reaction (1).

3 The analytical solution

As a rule, the analysis of mathematical model of this kind is made by numerical methods [17–20]. The peculiarity of the present mathematical model is that it allows a solution in the analytical form. Let us divide the third equation in the system (7) by the first one. We will obtain a differential equation writing the deference of the dimensionless concentrations of \(z\) and \(x\):

$$\begin{aligned} \dfrac{dz}{dx}=\dfrac{z}{x}-1\,. \end{aligned}$$
(9)

Employing the initial conditions (8), we will find that for the dependence \(z=z(x)\):

$$\begin{aligned} z(1)=0. \end{aligned}$$
(10)

Equation (9) with the initial condition (10) has the only one solution:

$$\begin{aligned} z=-x\ln x. \end{aligned}$$
(11)

Thus, we obtain the dependence of the relative concentration \([\mathrm{XY }]\) on the concentration of the substance \([\mathrm{X }]\).

By dividing the second equation in the system (7) by the first equation and employing the initial condition (8), we will obtain a differential equation which relates the interdependence of the dimensionless concentrations of \(y\) and \(x\):

$$\begin{aligned} r\dfrac{dy}{dx}=1+\dfrac{z}{x}, \quad y(1)=1\,. \end{aligned}$$
(12)

Upon substituting into this equation the already known dependence \(z=z(x)\) (11), we will obtain:

$$\begin{aligned} r\dfrac{dy}{dx}=1-\ln x, \quad y(1)=1\,. \end{aligned}$$
(13)

The function

$$\begin{aligned} y=1-\dfrac{2}{r}+\dfrac{x}{r}\left( 2-\ln x\right) \,, \end{aligned}$$
(14)

is the solution of this equation with the indicated initial condition.

Finally, upon dividing in the system (7) the fourth equation by the first one and employing the dependence \(z=z(x)\) (11), we will obtain the equation for the relative dimensionless concentrations \(w\) and \(x\) which corresponds to the substances \([\mathrm{XY^{}_{2} }]\) and \([\mathrm{X }]\):

$$\begin{aligned} \dfrac{dw}{dx}=-\dfrac{z}{x}=\ln x\,, \end{aligned}$$
(15)

and from the initial conditions (8) we will obtain the initial conditions for the function \(w(x)\):

$$\begin{aligned} w(1)=0\,. \end{aligned}$$
(16)

The function

$$\begin{aligned} w=1+x(\ln x-1)\,, \end{aligned}$$
(17)

is the solution of Eq. (15) with the initial condition (16).

Thus, we have the dependence of all dimensionless concentrations as regards the concentration of the \([\mathrm{X }]\).

To determine the interrelation of substance concentrations on the dimensionless time, we should substitute the dependence \(y(x)\) (14) into the first equation of the system (7) and to solve the obtained equation:

$$\begin{aligned} x^{\prime }\left( \tau \right) =-x\left[ 1-\dfrac{2}{r}+\dfrac{x}{r}(2-\ln x)\right] , \quad x(0)=1\,. \end{aligned}$$
(18)

Unfortunately, the solution of this equation for an arbitrary \(r\) is unknown. However, in case the correlation of the initial concentrations \([\mathrm{Y }]^{}_{0}\) and \([\mathrm{X }]^{}_{0}\) satisfies the condition (5), the solution is known and is expressed via the special function \(Ei(z)\):

$$\begin{aligned} \tau = \dfrac{2}{e^{2}}\left[ Ei(2-\ln x)-Ei(2)\right] \,, \end{aligned}$$
(19)

here \(e\) is the base of the natural logarithms and the second exponential integral function is defined by:

$$\begin{aligned} Ei(z)=-\int \limits _{-z}^{\infty }\dfrac{e^{-t}}{t}dt, \quad z>0\,, \end{aligned}$$
(20)

where the principal value of the integral is taken.

Thus, the sum total of the solutions (11), (14), (17) and (19) is an analytical solution of the kinetic equations (7) in the parametric form. Upon performing transformations inverse to the transformations (6) we will obtain the solution for the initial dimensional concentrations:

$$\begin{aligned} t&= \dfrac{2}{e^2} \left[ Ei\left( 2-\ln \dfrac{[\mathrm{X }]}{\;[\mathrm{X }]^{}_{0}}\right) -Ei(2)\right] \dfrac{1}{k[\mathrm{Y }]^{}_{0}},\nonumber \\ \left[ \mathrm{Y }\right]&= \left[ \mathrm{X }\right] \left( 2-\ln \dfrac{[\mathrm{X }]}{\;[\mathrm{X }]^{}_{0}}\right) ,\nonumber \\ \left[ \mathrm{XY }\right]&= -\left[ \mathrm{X }\right] \ln \dfrac{[\mathrm{X }]}{\;[\mathrm{X }]^{}_{0}},\nonumber \\ \left[ \mathrm{XY }^{}_{2}\right]&= \left[ \mathrm{X }\right] ^{}_{0}+[\mathrm{X }]\left( \ln \dfrac{[\mathrm{X }]}{\;[\mathrm{X }]^{}_{0}}-1 \right) . \end{aligned}$$
(21)

The graphical representation of the solutions (21) is shown in Fig. 1. At this point, the main task of any kinetic system of equations is fulfilled: we have obtained the time-dependent concentrations. The analytical form of the solution is a peculiarity of this mathematical model.

Fig. 1
figure 1

Dependence of the concentrations of components X, Y, XY and \(\mathrm{XY }^{}_{2}\) on time. The initial concentrations are determined by conditions (4)

Full size image

4 The phase portrait

The possibility to resolve a mathematical model of a chemical reaction in the analytical form is rather an enjoyable exception than a rule. There is, however, a special method to simplify the system: instead of considering the concentrations as the functions of time, it is possible to exclude time and to find the interdependence of the concentrations. In physical chemistry, this approach is called compiling the phase portrait of a system.

Let us go back to the initial mathematical model of the reaction in the dimensionless form (7) with the initial conditions (8). By dividing the third equation by the first one and employing the initial conditions, we will get the solution (11) expressing the dependence of the dimensionless concentration of the substance \(z\) on \(x\):

$$\begin{aligned} z=-x\ln x\,. \end{aligned}$$
(22)

The concentrations of the rest of the substances may be found by employing the mass conservation law: at any time moment, the sum total concentrations of substances containing \(\mathrm{X }\) fragments is equal to the initial concentration \([\mathrm{X }]^{}_0\), i.e. in our case to 1. For the dimensionless concentrations we have:

$$\begin{aligned} x+z+w=x(0)=1\,, \end{aligned}$$
(23)

hence

$$\begin{aligned} w=1+x\ln x-x\,. \end{aligned}$$
(24)

In an analogous way, the law of the conservation of the substance \(\mathrm{Y }\) fragments is expressed:

$$\begin{aligned} y+z+2w=y(0)=2\,, \end{aligned}$$
(25)

hence

$$\begin{aligned} y=2x-x\ln x\,. \end{aligned}$$
(26)

The obtained expression coincides with the earlier obtained dependence (14) for \(r=2\).

The transformations opposite to the transformations (6) will give us the last three equations of the system (21) for the initial concentrations of substances. The employed mathematical method does not allow obtaining the time dependence of the reacting substances; however, the phase portrait of the system is presented in its full. Thus, we will obtain an exhaustive description of the initial two-stage reaction. In this section, we have used the mass conservation law and obtained a “chemical” proof of the expressions (21). Let us present the obtained functional relations as a graph of the dependence of the concentration of all substances of the concentration of the substance \(\mathrm{X }\) (Fig. 2): In Fig. 2, the direction of the axis \(X\) was selected so as the left side of the graph would correspond to the starting point of the reaction.

Fig. 2
figure 2

Phase portrait of the two-stage reaction \(\mathrm{X }+2\mathrm{Y }=\mathrm{XY }^{}_2\)

Full size image

5 The half-life

The obtained solutions of the kinetic equations of the chemical reaction and its phase portrait allow a detailed following of concentration changes of all involved chemical substances.

The most important time-related feature of a substance involved in a chemical reaction is its half-life period, i.e. the time during which the concentration of the initial products diminishes by half, whereas the concentration of the intermediate or final products reaches the values equal to their half maximum.

Let us characterize the dynamics of concentration change of all involved substances:

\([\mathbf X ]\)) upon substituting in the solutions of the kinetic equations (21) the value \([\mathrm{X }]/[\mathrm{X }]^{}_{0}=0.5\), we obtain that the time of the substance concentration is:

$$\begin{aligned} t^{}_{0.5\mathrm{X }}=\frac{2}{e^2}\left[ Ei(2+\ln 2)-Ei(2)\right] \dfrac{1}{k[\mathrm{Y }]^{}_{0}}\approx 0.844 \dfrac{1}{k[\mathrm{Y }]^{}_{0}}\,, \end{aligned}$$
(27)

where multiplier \(1/k[\mathrm{Y }]^{}_{0}\) in this chemical reaction could be considered as a natural unit of time. The concentrations of the other components of the reaction are, respectively:

$$\begin{aligned}{}[\mathrm{Y }](t^{}_{0.5\mathrm{X }})&= \dfrac{2+\ln 2}{2}[\mathrm{X }]^{}_{0}\approx 1.35[\mathrm{X }]^{}_{0}\approx 0.673[\mathrm{Y }]^{}_{0},\nonumber \\ \left[ \mathrm{XY }\right] (t^{}_{0.5\mathrm{X }})&= \dfrac{\ln 2}{2}[\mathrm{X }]^{}_{0}\approx 0.347[\mathrm{X }]^{}_{0},\nonumber \\ \left[ \mathrm{XY ^{}_{2}}\right] (t^{}_{0.5\mathrm{X }})&= \dfrac{1-\ln 2}{2}[\mathrm{X }]^{}_{0}\approx 0.153[\mathrm{X }]^{}_{0}. \end{aligned}$$
(28)

The obtained correlations give us the quantitative characteristic of the chemical reaction velocity. After the time \(t^{}_{0.5\mathrm{X }}\) (27) following the beginning of the reaction, the ratios of the concentrations are \([\mathrm{X }]:[\mathrm{Y }]:[\mathrm{XY }]:[\mathrm{XY ^{}_{2}}]=0.5:1.35:0.347:0.153\), implying that at the time \(t^{}_{0.5\mathrm{X }}\) the smallest quantity for the formation is of the final product \([\mathrm{XY ^{}_{2}}]\).

\([\mathbf Y ]\)) upon substituting the value \([\mathrm{Y }]/[\mathrm{Y }]^{}_{0}=0.5\) into the solutions of the kinetic equations (21), we see that the half-life time of the substance concentration \([\mathrm{Y }]\) is determined by the solution of the transcendental equation:

$$\begin{aligned} x\left( 2-\ln x\right) =1\,. \end{aligned}$$
(29)

This equation has two solutions:

$$\begin{aligned} x^{}_{1}&= -W^{-1}(-e^{-2})\approx 0.3178, \nonumber \\ x^{}_{2}&= -W^{-1}_{\,-1}(-e^{-2})\approx 6.3054, \end{aligned}$$
(30)

where function \(W(z)\) is determined as principal solution of the equation \(z=we^w\) and function \(W^{}_{k}(z)\) gives \(k\)th solution. Since by definition \(x\equiv [\mathrm{X }]/[\mathrm{X }]^{}_{0}\), the second solution should be rejected as devoid of chemical sense.

The \(x^{}_{1}\) value allows finding the half-life period of the substance \(\mathrm{Y }\):

$$\begin{aligned} t^{}_{0.5\mathrm{Y }}=\frac{2}{e^{2}}\left[ Ei(2-\ln x^{}_{1})-Ei(2)\right] \dfrac{1}{k[\mathrm{Y }]^{}_{0}}\approx 1.626\dfrac{1}{k[\mathrm{Y }]^{}_{0}}\,, \end{aligned}$$
(31)

the concentrations of the other components of the reaction being as follows:

$$\begin{aligned}{}[\mathrm{Y }](t^{}_{0.5\mathrm{Y }})&= -W^{-1}(-e^{-2})[\mathrm{X }]^{}_{0} \approx 0.3178[\mathrm{X }]^{}_{0},\nonumber \\ \left[ \mathrm{XY }\right] (t^{}_{0.5\mathrm{Y }})&= -x^{}_{1}\ln x^{}_{1}\cdot [\mathrm{X }]^{}_{0}\approx 0.364[\mathrm{X }]^{}_{0},\nonumber \\ \left[ \mathrm{XY ^{}_{2}}\right] (t^{}_{0.5\mathrm{Y }})&= [1+x^{}_{1}(\ln x^{}_{1}-1)][\mathrm{X }]^{}_{0}\approx 0.318[\mathrm{X }]^{}_{0}. \end{aligned}$$
(32)

The concentration ratio after the time \(t^{}_{0.5\mathrm{Y }}\) following the beginning of the reaction is \([\mathrm{X }]:[\mathrm{Y }]:[\mathrm{XY }]:[\mathrm{XY ^{}_{2}}]=0.318:0.5:0.364:0.318\), indicating that after \(t^{}_{0.5\mathrm{Y }}\) (31) the concentrations of the substances \(\mathrm{X }, \mathrm{XY }\) and \(\mathrm{XY ^{}_{2}}\) comprise about one third of their maximum values.

\([\mathbf{XY }]\)) As shown from the temporal dependence of concentrations in Fig. 1 and the phase portrait in Fig. 2, changes of the substance concentration \([\mathrm{XY }]\) is not monotonous. If initially \([\mathrm{XY }](0)=0\), the concentration rather rapidly reaches its maximum value and gradually decreases. The obtained solutions allow finding the maximum concentration of the intermediate substance \([\mathrm{XY }]\). The maximum value of the function \(z=-x\ln x\) is reached at \(x=1/e\) and equals \(1/e \approx 0.368\), but not 1 as implied by the scheme of the consecutive reaction \(\mathrm{X+Y+Y }\). This means that the substance \(\mathrm{XY }\), immediately after it has been produced, begins turning into the final product \(\mathrm{XY ^{}_{2}}\). As to the dimensional concentrations, at the moment the substance \(\mathrm{X }\) concentration decreases \(e\) times,

$$\begin{aligned}{}[\mathrm{X }]=\dfrac{[\mathrm{X }]^{}_{0}}{e}\approx 0.368[\mathrm{X }]^{}_{0}\,, \end{aligned}$$
(33)

the substance \([\mathrm{XY }]\) concentration reaches its maximum value:

$$\begin{aligned}{}[\mathrm{XY }]=\dfrac{[\mathrm{X }]^{}_{0}}{e}\approx 0.368[\mathrm{X }]^{}_{0}\,, \end{aligned}$$
(34)

As follows from Eq. (21), this occurs at the time moment and the concentration of the substances equals:

$$\begin{aligned} t^{}_{m}=\frac{1}{e^{2}}[ Ei(3)-Ei(2)] \dfrac{1}{k[\mathrm{Y }]^{}_{0}}\approx 0.674\dfrac{1}{k[\mathrm{Y }]^{}_{0}}\,, \end{aligned}$$
(35)

and the concentration of the substances equals:

$$\begin{aligned}{}[\mathrm{Y }]&= 3[\mathrm{X }]=\dfrac{3X^{}_{0}}{e}\approx 1.104[\mathrm{X }]^{}_{0}\approx 0.552[\mathrm{Y }]^{}_{0},\nonumber \\&[\mathrm{XY ^{}_{2}}]=\left( 1-\dfrac{2}{e}\right) [\mathrm{X }]^{}_{0}\approx 0.264[\mathrm{X }]^{}_{0}. \end{aligned}$$
(36)

Thus, the time \(t^{}_{m}\) (29), alongside the half-life period of the substances \(\mathrm{X }\) and \(\mathrm{Y }\) (27), (31), may be considered as characteristic time-scale of a chemical reaction under consideration.

The substance \(\mathrm{XY }\) half-life period is found from the equation:

$$\begin{aligned} t^{}_{0.5\mathrm{XY }}=\dfrac{2}{e^2}[Ei(2-\ln x)-Ei(2)] \dfrac{1}{k[\mathrm{Y }]^{}_{0}}\,, \end{aligned}$$
(37)

here \(x\) is the solution of the equation which follows from the condition \(z(x)=\frac{1}{2}z^{}_{max} =\frac{1}{2e}\):

$$\begin{aligned} -x\ln x=\dfrac{1}{2}\,. \end{aligned}$$
(38)

Equation (38) has two solutions:

$$\begin{aligned} x^{}_{1}&= -\dfrac{1}{2e}W^{-1}_{\,-1}\left( -\dfrac{1}{2e}\right) \approx 0.7930,\nonumber \\ x^{}_{2}&= -\dfrac{1}{2e}W^{-1}\left( -\dfrac{1}{2e}\right) \approx 0.0687. \end{aligned}$$
(39)

As follows from Fig. 1, both of them are chemically meaningful because the substance \(\mathrm{XY }\) reaches its half-life value twice—before and after attaining its maximum value. Correspondingly,

$$\begin{aligned} t^{(1)}_{0.5\mathrm{XY }}&= \dfrac{2}{e^2}[Ei(2-\ln x^{}_{1})-Ei(2)]\dfrac{1}{k[\mathrm{Y }]^{}_{0}}\approx 0.2465 \dfrac{1}{k[\mathrm{Y }]^{}_{0}},\nonumber \\ t^{(2)}_{0.5\mathrm{XY }}&= \dfrac{2}{e^2}[Ei(2-\ln x^{}_{2})-Ei(2)]\dfrac{1}{k[\mathrm{Y }]^{}_{0}}\approx 7.256\; \dfrac{1}{k[\mathrm{Y }]^{}_{0}}. \end{aligned}$$
(40)

\([\mathbf{XY }{}_\mathbf{2}]\)) What is the maximum quantity of the final product of the reaction? As follows from the expression (24), for \(x\rightarrow 0,\,w(x)\rightarrow 1\). This means that the quantity of the final product equals the content of the initial substance \(\mathrm{X }^{}_{0}\). Unfortunately, this takes an unlimited quantity of time.

The half-life period of the substance \(\mathrm{XY }^{}_{2}\) is determined from the condition \(w(x) =\frac{1}{2}\):

$$\begin{aligned} 1+x\ln x-x=\dfrac{1}{2}\,. \end{aligned}$$
(41)

Equation (41) has two solutions:

$$\begin{aligned} x^{}_{1}&= -\dfrac{1}{2}W\left( -\dfrac{1}{2e}\right) \approx 0.1867,\nonumber \\ x^{}_{2}&= -\dfrac{1}{2}W^{-1}_{\,-1}\left( -\dfrac{1}{2e}\right) \approx 2.156, \end{aligned}$$
(42)

from which the second root \(x^{}_2\), like in the expression (30), should be rejected for chemical reasons. The substitution \(x^{}_1\) into (21) gives the half-life period of the substance \(\mathrm{XY }^{}_{2}\):

$$\begin{aligned} t^{}_{0.5\mathrm{XY ^{}_2}}=\dfrac{2}{e^2}[Ei(2-\ln x^{}_{1})-Ei(2)]\dfrac{1}{k[\mathrm{Y }]^{}_{0}}\approx 2.9155 \dfrac{1}{k[\mathrm{Y }]^{}_{0}}\,. \end{aligned}$$
(43)

6 Conclusions and discussion

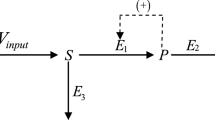
Let us summarize our knowledge of this reaction. In the previous section, we have presented a detailed description of the concentration kinetics of each of its components. By arranging the half-life periods of each component in the chronological order we shall obtain a visual temporal diagram of the reaction (see Fig. 3).

Fig. 3
figure 3

The temporal diagram of the reaction in time units \(1/k[\mathrm{Y }]^{}_{0}\). Lines indicate the half-life or maximum periods of a correspondent component

Full size image

The temporal diagram in Fig. 3 shows a unique presentation of this chemical reaction: any other chemical reaction will have another type of diagram. If we mark on the diagram a quarter-life period \(\frac{1}{2}t^{}_{0.5}\) and three quarters of the life period \(\frac{3}{2}t^{}_{0.5}\) of the main substance \([\mathrm{XY ^{}_{2}}]\), this will give us a visual representation of the whole reaction. In my opinion, it would be extremely useful in a real technological process.

The phase portrait of a chemical is possible to obtain by numerical methods, but the temporal dependence of substance concentrations, expressed trough specific functions, depends on analytical solvability of the mathematical model. The decisive circumstances that allowed obtaining the analytical solutions (21) were the equality of the reaction rates (2) and the ratio of initial concentrations (5). Indeed, if we suppose that the reactions (2) proceed at different rates \(k^{}_{1}\) and \(k^{}_{2}\,(k\equiv k^{}_{1}/k^{}_{2})\), then it is possible to show that as the mathematical model of such a reaction we may take the system:

$$\begin{aligned} {\left\{ \begin{array}{ll} \,x^{\prime }\!\!&{}=-xy\,, \\ ry^{\prime }&{}=-xy-kzy\,, \\ \,z^{\prime }\!\!&{}=xy-kzy\,, \\ \,w \!\!\!\!\!&{}= kzy\,, \end{array}\right. } \end{aligned}$$
(44)

with the initial conditions:

$$\begin{aligned} x(0)=1\,,\quad y(0)=2\,. \end{aligned}$$
(45)

In this case, the phase portrait of the system, analogous to the one shown in Fig. 2, is possible to obtain, whereas to obtain the temporal dependence of the chemical reaction in the analytical form of the type (21) is, unfortunately, impossible. Moreover, even the Eq. (18), for \(r\ne 2\), it cannot be integrated in analytical form.

But is the solution of kinetic equation in the analytical form so important? Indeed, nowadays when the numerical methods of solving differential equations have been developed (see e.g. [19, 20]), attempts to solve a system of nonlinear equations in an analytical form, even among mathematicians, are sometimes regarded as anachronism. However, we should bear in mind that the entire spheres of not only of mathematics, but also of natural sciences in general, would be lost in the absence of serious attempts to solve the corresponding mathematical model in the analytical form [21–23]. Without going into details [9], it is worth noting here that the integrability is related to the symmetry of a model, and the latter reflects the balance of various factors influencing its dynamics. As soon as this balance is reached, different parts of the model begin correlating with each other and thus reflect its internal harmony, so it becomes possible to obtain an analytical solution. To confirm the above statement, let us consider the system (43). The initial system contains four independent parameters - the velocity of reactions \(k^{}_{1}\) and \(k^{}_{2}\) and the initial concentrations \([\mathrm{X }]^{}_{0}\) and \([\mathrm{Y }]^{}_{0}\). In the system (44), in the dimensionless form, the number of the independent parameters is less by half: the ratio of velocities \(k\equiv k^{}_{2}/k^{}_{1}\) and the ratio of the initial concentrations \(r=[\mathrm{Y }]^{}_{0}/[\mathrm{X }]^{}_{0}\). Independently of the form of the solution of such a system, it depends not on the parameters \(k^{}_{1},\,k^{}_{2},\,[\mathrm{X }]^{}_{0},\,[\mathrm{Y }]^{}_{0}\) themselves, but on their ratios \(k\) and \(r\) only. The decreasing number of the independent parameters of the model is a peculiar feature of the method of dimensionless values.

Therefore, passing to the dimensionless form of the mathematical model, non-linear in particular, is highly desirable and efficient.

Actually, the dependence of the concentration of the reagents on the concentration of the initial substance \(X\) has already been obtained in the formulas (14), (11) and (17). To show that the temporal dependence, we shall obtain in other way. The first step is the dependence \(z(x)\), the same as above.

To conclude, let us note that the mathematical model analyzed in the present paper is applicable to any two-stage reaction of the form (2). Also, while reflecting on the interrelation of the chemistry and mathematics, we should agree that successful application of mathematical methods in chemistry gives beautiful and nontrivial result and contributes to enrichment of both sciences.