1 Introduction

In the field of low temperature physics, the quartz tuning forks (QTFs) have proven to be a vital experimental tool used in the study of quantum liquids and solids, quantum turbulence, etc. [1,2,3,4,5,6,7,8,9,10]. Due to their obvious advantages (low cost, simplicity of measurement, extremely fine displacement), these resonators are widely used in scanning probe techniques like AFM, STM, etc. [11,12,13] as well. In a latter case, the measurements are carried out in vacuum at low temperatures and in high magnetic fields. Therefore, it is important to know the influence of such conditions, namely high magnetic fields, on the resonant characteristics of the quartz tuning forks.

Our previous works showed that a tuning fork constant \(\alpha _\mathrm {f}\) does not depend on the applied magnetic field [14], and that quartz tuning forks, in principle, have potential to be used as thermometers in millikelvin temperature regime and high magnetic fields [15]. In the following, we show that a quartz tuning fork being exposed to high magnetic fields exhibit the property of a parametric resonator, i.e., such quartz tuning fork can be excited parametrically.

Fig. 1
figure 1

The three specimens of quartz tuning forks placed inside their copper holders with additional superconducting coils for the modulation of magnetic field. All of them are mounted on the experimental plate of cold finger of the cryogen-free dilution refrigerator Triton 200 (Color figure online)

Full size image

2 Idea of an Experiment

The recently observed temperature dependence of the quartz tuning forks resonance frequencies in zero magnetic field has been interpreted using a phenomenological model based on the presence of the van der Waals interactions, which emerges on cooling and increases the stiffness of the potential energy [15, 16]

$$\begin{aligned} V_{\mathrm {pot}} \approx \left( k + \frac{Q^2}{\alpha (T)}\right) x^2, \end{aligned}$$
(1)

where the first term is related to the potential energy associated with elastic deformation of the lattice with k being the spring constant. The second term expresses the contribution of the van der Waals interaction with \(\alpha (T)\) being the polarizability, Q is the electric charge and x is the deflection of the ions from equilibrium position. This interpretation is based on the fact that in piezo-materials there are the oscillating induced electric dipoles \(\mathbf {p}=Q \mathbf {d} = \alpha (T) \mathbf {E}_{\mathrm {loc}}\) (where \(\mathbf {d}\) is the distance between the charges that is proportional to deflection of the ions from equilibrium position \(\mathbf {x}\)), and each of them experiences a local electric field of the intensity \(\mathbf {E}_{\mathrm {loc}}\) produced by other electric dipoles including an initial voltage pulse (and other electric fields).

Once a quartz tuning fork oscillates in a high magnetic field \(\mathbf {B}\) with velocity \(\mathbf {v}\), so do its metal electrodes. As a consequence of the fork’s oscillating motion, the Lorentz force \(\mathbf {F}_\mathrm {L} = q(\mathbf {v}\times \mathbf {B})\) acts on free electric charges q in the metal electrodes and redistributes them. We presume in our experiment that \(\mathbf {B}\bot \mathbf {v}\). An amount of the electric charge q in metal electrodes varies with time and depends on the voltage across tuning fork as \(q(t) = q_0 + C_\mathrm {P} V_0 \sin (\omega t)\), where \(q_0\) is the free charge in fork’s electrodes, \(C_\mathrm {P}\) is the fork capacitance (the capacitance of electrodes) and \(V_0\) is the voltage amplitude. Simultaneously, the fork velocity \(\mathbf {v}\) is a harmonic function of the time (\(v=v_0 \sin (\omega t +\varphi ))\), where \(\varphi \) is the phase between velocity v and voltage V(t) [17].

Substituting all above-mentioned expressions for q(t) and fork velocity v(t) including the relation between fork’s velocity v and fork’s current \(I_\mathrm {F}\) as \(v_0 = I_\mathrm {F0}/ \alpha _\mathrm {f}\) (where \(\alpha _\mathrm {f}\) is the fork constant [2]) to \(\mathbf {F}_\mathrm {L} = q(\mathbf {v}\times \mathbf {B})\), one gets a resulting expression for the Lorentz force amplitude in form [15, 20]

$$\begin{aligned} F_{\mathrm {L}}(t) = \frac{q_0 I_\mathrm {F0}B}{\alpha _\mathrm {f}} \sin (\omega t + \varphi ) + \frac{C_\mathrm {P} V_0 I_\mathrm {F0}B}{2\alpha _\mathrm {f}}\left[ \cos \varphi -\cos (2\omega t + \varphi )\right] . \end{aligned}$$
(2)

Resulting expression for \(F_\mathrm {L}\) (and for potential energy \(V_\mathrm {pot}\)) has three components: one is constant, one oscillating at the fork’s fundamental frequency and the third one oscillating at twice of the fork’s resonance frequency. Thus, the time-dependent Lorentz force \(\mathbf {F}_\mathrm {L}(t)\) generates an additional, induced voltage on the fork’s electrodes and a corresponding induced electric field \(\mathbf {E}_\mathrm {ind}\) simultaneously modifies the intensity of the local electric field \(\mathbf {E}_\mathrm {loc}\). Neglecting the first term in Eg. (2) because of its smallness, the potential energy of the system of dipoles can be expressed as

$$\begin{aligned} V_\mathrm {pot} \approx \left( k + \frac{Q^2}{\alpha (T)}+ a B \left[ \cos \varphi -\cos (2\omega t + \varphi )\right] \right) x^2, \end{aligned}$$
(3)

where B is the magnetic field magnitude and a is the proportionality constant. We also assume that \(V_0 \sim E_\mathrm {loc} \approx E_\mathrm {eff}x\) (see Eq. (2)), where \(E_\mathrm {eff}\) is the effective magnitude of the electric field intensity and x is the above-mentioned deflection. While the first three terms characterize the temperature and magnetic field dependencies of the tuning fork resonance frequency, the last term allows to excite the tuning fork parametrically using an alternating magnetic field.

3 Experimental Details

The measurements have been performed using a standard commercially available 32 kHz quartz tuning fork. Due to the high magnetic field applied, the original metal encapsulation had to be removed and magnetic leads replaced by a twisted copper wire pair. The dimensions of bare quartz tuning fork are as follows: the thickness of SiO\(_2\) wafer \(T=235\) \(\mu \)m and the fork’s prong width \(W = 400\) \(\mu \)m and length \(L = 3150\) \(\mu \)m. After this modification, the tuning fork was attached and thermally anchored to a special copper holder. As a next step, a small superconducting AC coil was slid onto the holder. The coil has 60 turns wound from a monofilamentary NbTi wire of 150 \(\mu \)m diameter. The corresponding coil holder was made of epoxy Stycast 1266. The whole setup was then mounted on the cold finger of a cryogen-free dilution refrigerator Triton 200 by Oxford Instruments (see Fig. 1). This apparatus is capable to cool down samples to 10 mK temperature in magnetic fields up to 8 Tesla. The orientation of the tuning fork’s prong was chosen to be parallel to the applied magnetic field.

Fig. 2
figure 2

A scheme of the measurement setup; here the following abbreviations are used: QTF—Quartz tuning fork, SM—superconducting magnet, AC coil—small superconducting coil used for the modulation of magnetic field

Full size image

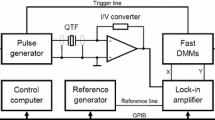
With aim to observe the parametric resonance of the quartz tuning fork, we have modified the pulse-demodulation technique introduced previously [18]. A scheme of the experimental setup is presented in Fig. 2. The most important modification is that the quartz tuning fork is not directly driven anymore. Instead, the first programmable function generator is responsible for the tiny variation of the static magnetic field with the help of a small superconducting AC coil mounted on the copper holder of the quartz resonator. Initially, a sequence of pulses at modulation (excitation) frequency \(f_\mathrm {exc} \sim 2 \;\! f_0\) is applied, where \(f_0\) is the tuning fork’s resonant frequency. In order to minimize the losses in the detection circuit, the corresponding alternating piezoelectric current is amplified and converted to the voltage by a custom-made current-to-voltage (I/U) converter [17, 19]. Subsequently, the I/U converter output voltage is measured by a lock-in amplifier SR830. The reference signal for the lock-in amplifier is provided by the second function generator and its frequency \(f_\mathrm {ref}\) is slightly lower than the tuning fork’s resonant frequency \(f_0\). The resulting signal processed by the lock-in amplifier oscillates at a frequency determined by a frequency difference \(f_0 - f_\mathrm {ref}\) and has two (in-phase and quadrature) components mutually shifted in phase by \(\pi /2\). Then, both signal components are measured by two fast digital multimeters triggered by the end of the initial pulse sequence. The high static magnetic field (up to 8 Tesla) is generated by a superconducting 8 Tesla magnet powered by a DC power supply IPS 120-10 by Oxford Instruments. The whole experimental setup is controlled via GPIB bus by a LabView software running on a control PC.

4 Results and Discussion

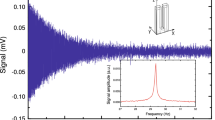
Once the high static magnetic field was applied (we present results obtained in a field of 1.5 Tesla), we started to search for the parametric resonance of the 32 kHz quartz tuning fork. To excite the parametric resonance of the tuning fork, we used the modified pulse-demodulation technique as described above. We applied a short voltage pulse to the AC coil at twice of fork’s resonance frequency (\(f_\mathrm {exc}\) = 65408 Hz) to generate a small alternating magnetic field, thus modifying the fork potential energy (see Eq. (3)). This “time perturbation” of the potential energy forced the tuning fork to oscillate at its fundamental frequency. The corresponding signal example of the tuning fork’s free decay oscillations measured in the magnetic field of 1.5 Tesla is presented in Fig. 3. We note that measured frequency of the free decay signal is the difference between the fork’s resonance frequency \(f_0\) and frequency of the reference signal \(f_\mathrm {ref}\). As the reference frequency \(f_\mathrm {ref}\) equals to 32 670 Hz, and frequency of the measured free decay signal, taken from FFT spectrum is \(\sim 34\) Hz (see Fig. 4–right), the resonant frequency of the quartz tuning fork is \(f_0 = 32704.09\) Hz, i.e., the frequency of the parametric excitation \(f_\mathrm {exc}\) is twice of the tuning fork’s resonant frequency.

Fig. 3
figure 3

Example of the free decay signal of the 32 kHz quartz tuning fork excited parametrically using a small alternating magnetic field excited by AC coil in the magnetic field of 1.5 Tesla (left) and corresponding FFT spectrum (right). The applied setting were as follows: the modulation frequency \(f_\mathrm {exc} = 65408\) Hz, the length of pulse \(N = 3000\) periods and the reference frequency \(f_\mathrm {ref} = 32670\) Hz (Color figure online)

Full size image
Fig. 4
figure 4

FFT spectrum of the signals of parametric resonance of 32 kHz quartz tuning fork measured in the magnetic field of 1.5 Tesla in vacuum at temperature \(\sim 20\) mK. The following settings were used: amplitude of voltage excitation \(u_\mathrm {exc} = 2\) V\(_\mathrm {rms}\), number of periods at given pulse frequency \(N = 3000\) and reference frequency \(f_\mathrm {ref} = 32 670\) Hz. The corresponding resonant frequency of the quartz tuning fork at this field is \(f_0 = 32704.09\) Hz (Color figure online)

Full size image
Fig. 5
figure 5

The same 32 kHz quartz tuning fork measured in zero magnetic field in vacuum at temperature \(\sim 20\) mK. The following settings were used: amplitude of voltage excitation \(u_\mathrm {exc} = 2\) V\(_\mathrm {rms}\), number of periods at given modulation frequency \(N = 65000\) and reference frequency \(f_\mathrm {ref} = 32 670\) Hz. Notice that the scale on the averaged FFT noise spectra is more than \(100\times \) smaller than in the previous figure (Color figure online)

Full size image

With aim to support “the proof of concept,” i.e., to confirm the presence of the parametric excitation of the tuning fork in high magnetic field, we performed two additional experiments. Firstly, we checked the resonant character of the tuning fork’s parametric oscillations. During these measurements, we varied the modulation frequency of the AC magnetic field \(f_\mathrm {exc}\) (i.e., pulse frequency) in the frequency range of \(2f_0 \pm 100\) Hz. For particular modulation frequency \(f_\mathrm {exc}\), the pulse with \(N = 3000\) periods was applied and the response of the quartz tuning fork was stored. We repeated these measurements for particular excitation frequency 5 times; the corresponding FFT spectra for all demodulated signals were determined and stored, and subsequently we calculated the averaged FFT spectrum. Figure 4 shows the results. As one can see, there is a range of excitation frequencies \(f_\mathrm {exc}\), where the tuning fork can be excited parametrically. The maximal response of the tuning fork on parametric excitation can be found at a frequency corresponding to twice of its fundamental resonance frequency, i.e., \(f_\mathrm {exc}= 65 408\) Hz = \(2\times f_0\). We assume that the width of frequency range of the excitation pulses capable to excite the tuning fork parametrically is related to its Q-value. However, more work has to be done to elucidate this question.

In order to justify a need of static magnetic field to excite the tuning fork parametrically (see Eq. 3), we performed a set of measurements in zero magnetic field. Results are presented in Fig. 5. Despite the application of the longer modulation pulse (65000 vs 3000 periods), there is no obvious signal of parametric resonance present. The only signal one can see is a tiny noise signal at a frequency corresponding to the resonant frequency of the tuning fork, as this fork acts as a narrow-band frequency filter. This noise signal is more than two order of magnitude lower that the signal presented in Fig. 4. This experimental fact proves that the presence of the high static magnetic field is crucial in order to excite the quartz tuning fork parametrically.

5 Conclusions

In conclusion, we showed that a quartz tuning fork exposed to a high static magnetic field can be excited parametrically. This phenomenon seems to originate as a consequence of the presence of the free electric charges in the tuning fork’s metal electrodes. These electric charges being exposed to static and alternating magnetic fields, due to the acting Lorentz force, modify the potential energy of the tuning fork itself creating a time-dependent term oscillating at twice of the fork’s resonance frequency, thus giving a possibility of parametric excitation. Zero magnetic field does not give any possibility to excite the quartz tuning fork parametrically. The successful observation of parametric resonance opens the possibility to use the quartz tuning fork as a parametric oscillator and/or amplifier.