Ab Initio Study of the Electronic Structure, Elastic Properties, Magnetic Feature and Thermodynamic Properties of the Ba₂NiMoO₆ Material

Abstract

We report first-principles calculations of the elastic properties, electronic structure and magnetic behavior performed over the Ba₂NiMoO₆ double perovskite. Calculations are carried out through the full-potential linear augmented plane-wave method within the framework of the Density Functional Theory (DFT) with exchange and correlation effects in the Generalized Gradient and Local Density Approximations, including spin polarization. The elastic properties calculated are bulk modulus (B), the elastic constants (C₁₁, C₁₂ and C₄₄), the Zener anisotropy factor (A), the isotropic shear modulus (G), the Young modulus (Y) and the Poisson ratio (υ). Structural parameters, total energies and cohesive properties of the perovskite are studied by means of minimization of internal parameters with the Murnaghan equation, where the structural parameters are in good agreement with experimental data. Furthermore, we have explored different antiferromagnetic configurations in order to describe the magnetic ground state of this compound. The pressure and temperature dependence of specific heat, thermal expansion coefficient, Debye temperature and Grüneisen parameter were calculated by DFT from the state equation using the quasi-harmonic model of Debye. A specific heat behavior C_V ≈ C_P was found at temperatures below T = 400 K, with Dulong–Petit limit values, which is higher than those, reported for simple perovskites.

1 Introduction

Perovskite-like ceramics are a family of natural and synthetic materials that are characterized by having a crystalline arrangement very similar to the structure of CaTiO₃. The formula that ideally describes these materials is ABX₃, wherein A and B atoms are metal cations (positively charged ions), whereas X atoms are nonmetallic anions (negatively charged ions, usually oxygen). An A cation (the one with the highest ionic radius of the two kinds of metals) is usually located in the center of the ideally cubic structure. The eight vertices are occupied by the cations B, in octahedral coordination with the anions X, which are located in the middle points of the edges of the cubes that make up the volumetric structure [1].

Perovskites evidence numerous physical properties, which are particularly sensible to inhomogeneities like distortions from their ideal cubic structure, vacancies and chemical substitutions [2]. One of these anomalies, which raise the complex perovskite with A₂BB′O₆ formula, results from the ordering of B and B′ cations on the octahedral site of the primitive perovskite unit cell. The importance of complex perovskites lies in the possibility of creating new magnetic materials A₂BB′O₆, with B and B′ constituted by magnetic 3d cations.

These materials have been extensively studied due their exotic magnetic properties, which suggest the applications of these perovskite ceramics in the design and technology of magnetic devices for applications in the spintronics area as read–write heads of hard disks for storing high capacity of information in magnetic media [3], spin valves for RAM memories [4], devices for polarization of electron currents [5], permanent magnets [6], magnetic sensors [7] and systems of magnetic nanoparticles [8], among others.

First-principles calculations based on Density Functional Theory (DFT) have been demonstrated to provide a safe and very accurate method to predict some properties of perovskite materials, such as the crystal structure, electrical transport type for the spin polarization channels up and down to the valence electrons around the Fermi level (conductor, semiconductor, insulator, half-metallic), contribution of different electronic orbitals to magnetic and electrical transport properties and ferroelectric character [9]. Recently, experimental results of the structural, electrical and magnetic behavior of the Ba₂NiMoO₆ double perovskite were reported [10]. The authors claim that this material crystallizes in one structure, belonging to the cubic Fm$\bar{3}$m (#225) space group. By neutron diffraction experiments, they determined the occurrence of a magnetic behavior that can be described as a stacking of ferromagnetic layers of Mn moments perpendicularly orientated to the [111] direction, which are antiferromagnetically coupled between layers.

With the aim to theoretically study the structural characteristics and infer magnetic and transport properties of the Ba₂NiMoO₆ complex perovskite, in this paper a study of the crystallographic parameters, density of states and elastic properties is presented. Thermodynamic properties are relevant in order to establish eventual technological applications. In addition to the structural, elastic and calculations of electronic and band structures calculations, in this report we present theoretical studies of the pressure and temperature dependence of the specific heat, the thermal expansion, the temperature of Debye and the Grüneisen coefficient. The calculations of the elastic and thermodynamic properties were made by applying the quasi-harmonic Debye model [11].

2 Theoretical Setup

2.1 Calculation Details

The structural optimization and the elastic properties calculations were performed by using the self-consistent full-potential linearized augmented plane-wave (FP-LAPW) method, implemented in the Wien2k code [12], in the framework of the DFT [13]. The exchange–correlation function has been described using the Local Density Approximation (LDA) and the Generalized Gradient Approximation with the Perdew–Burke–Ernzerhof formalism (GGA-PBE) [14]. The muffin-tin radii used were 2.4, 1.8, 1.7 and 1.6 bohr for the Ba, Ni, Mo and O atom, respectively. The cutoff parameter for the plane wave was set to R_MT × K_max = 7.0, where K_max is the maximum modulus for the reciprocal lattice vector, and G_max = 12.0. The reciprocal space was sampled with a mesh of 1500 k-points in the first Brillouin zone (equivalent to 56 k-points in the irreducible Brillouin zone). The convergence criterion for the self-consistent calculation was 10⁻⁵ Ry for the total energies and 1.0 mRy/u.a for the internal forces. Spin polarization was included in the calculations. These kinds of variables assure excellent convergence for total energy. The elastic constants here reported for the Ba₂NiMoO₆ were calculated using the Wien2k Cubic-elastic package [15], considering the second-order derivative of a polynomial fit of the total energy [E = E(δ)] versus strains (δ) at zero strain (δ = 0). On the other hand, in order to explore different antiferromagnetic configurations between Ni atoms, we have used a 2 × 2×2 supercell of Ba₂NiMoO₆ (320 atoms), where antiferromagnetism along the planes [001], [110] and [111] has been considered. All calculations were performed using the Quantum Espresso code [16] where the self-consistent Kohn–Sham equations were solved using pseudopotentials and plane-wave method and the exchange–correlation part was described by GGA-PBE scheme [14]. All atoms were described using Projector Augmented-Wave (PAW) pseudopotentials data set; a 50 Ry and 500 Ry cutoff was used for the wave function and electron spin density, respectively. Furthermore, for calculations of spin polarization, the Brillouin zone was sampled using a grid of 4 × 4×4 k-points with Marzari–Vanderbilt [17] occupational smearing width of 0.002 Ry. In summary, the processes of minimization of the energy with respect to the volume of the crystallographic cell and its respective adjustment with the equation of state, as well as the calculations of the elastic properties of the material, were carried out by means of the use of the Wien2k code, while that the calculations of density of states and the introduction of the exchange and correlation potential were made through the application of the Quantum Espresso code. The Wien2k and Quantum Espresso apply different methodologies. The Wien2k was used because it contains the necessary tools to study the elastic, thermodynamic and structural properties. It is a linearized method in which the crystalline symmetries are used so that the calculations are not computationally expensive as a result of the FP-LAPW method, which reconstructs the potential throughout the space of the solid. However, when there are differences between atoms, which are crystallographically similar but magnetically different, it is necessary to use supercells and the method on which the Wien2k is based makes the calculation computationally expensive. In those cases, other methods such as flat waves and pseudopotentials (of the Quantum Espresso type) are used, which is faster because the potential is parameterized in the pseudopotential. That is why in this work the Quantum Espresso is used to explore different magnetic configurations like the ones described below. This methodology is widely used because both codes describe well the physical and chemical properties of the materials, as has been found in a broad study on the efficiency and concordance between different methods based on the Density Functional Theory [18].

2.2 Quasi-Harmonic Approximation of the Debye Model

The vibrational density of states g(w) of a crystal can be used to determine some of its thermodynamic properties, because this function provides the number of normal modes of vibration in an infinitesimal range of frequencies between w and w + dw. This concept is applied in the Debye model, considering that the crystal can be modeled as a continuous medium so with normal vibrations like elastic stationary waves. Thus, through the density of states, the wave number can be calculated in that infinitesimal frequency range. In the Debye model, a harmonic consideration of the potential energy is made to evaluate the force constants, whereby the temperature of Debye (Θ_D) is constant and must be obtained from the elastic constants. Meanwhile, this harmonic model lacks the thermal expansion, which is one of the most important experimental properties that can be measured in the crystals. Since the temperature only has influence on the Helmholtz’s function through the vibrational term, and this in turn depends on the elastic constants, in principle there would be no relation between the temperature and the geometry of the system. For this reason, it is necessary to introduce into the model the interdependence between temperature and volume. This circumstance suggests the application of the quasi-harmonic approximation, in which harmonic vibrations are assumed in positions that are no equilibrium. In this way, the vibration frequencies become dependent on the volume and can be evaluated from the second derivatives of the potential energy surface at those off-balance positions. We must note that under static conditions, the second derivatives produce vibration frequencies that occur around a minimum. On the other hand, in the presence of generalized forces such as pressure, the equilibrium geometry is displaced in such a way that the external forces tend to override the gradient of the static potential energy surface. Thus, the quasi-harmonic model of Debye has harmonic behavior, but introduces anharmonic effects through the dependence of the frequencies in the configuration. It is then possible to predict the thermal expansion of the crystal by the dependence of volume and temperature on equilibrium.

From the above, it can be established that a non-static equilibrium configuration can be achieved through external links. Because the stringent treatment of these bonds is quite complex, the way to simplify it is by resorting to thermodynamic equilibrium conditions. Then, assuming that the system is at a given temperature and pressure, the system can be thermodynamically described by the non-equilibrium Gibbs function, which, in its general form, can be written as

$$ G^{*} \left( {T,P,\vec{a}} \right) = E_{e} \left( {\vec{a}} \right) + PV\left( {\vec{a}} \right) + A_{\text{vib}} \left[ {T,w_{j} \left( {\vec{a}} \right)} \right], $$

(1)

which is a function of temperature T, pressure P and the lattice parameters $\vec{a}$. In Eq. (1), E_e is the total energy of the crystal and A_vib represents the vibrational Helmholtz free energy. The equilibrium situation of the system corresponds to the lowest Gibbs energy at a given set of temperature and pressure. The dependence of the E_e on the lattice parameters $\vec{a}$ is explicit, while A_vib depends implicitly on $\vec{a}$ through the vibration frequencies of the solid. The equilibrium configuration of the system will be the minimum of this Gibbs function that depends on T and P. Since the volume is also dependent on $\vec{a}$, this gives the desired interdependence between temperature and volume. Once the system equilibrates, the external bonds are eliminated, because their strength cancels terms associated with the first derivatives of E_e at each point of the potential energy, as this is an equilibrium point. Under certain conditions of T and P, the equilibrium configuration of the system corresponds to the lowest Gibbs energy. Within this scheme, it is possible to consider the geometries of quasi-harmonic crystalline equilibrium and all the thermodynamic properties of the crystal as functions of temperature and pressure. The difference between this model and the Debye model is that A_vib depends on the geometry through Θ_D, which in turn can be calculated from the elastic constants of the crystal, and these are the second derivatives of energy with respect to displacements of the lattice parameters.

A good simplification of the problem to obtain the Θ_D can be made by the isotropic solid approximation, but it is necessary to further reduce the number of properties required for the Θ_D of the system in any configuration. One way to do this is by assuming that the solid acts as a fluid, which does not exhibit resistance to shear deformations (C₄₄ = 0). For this reason, transverse elastic waves are no taken into account. For the purposes of the approximation, the average speed for the longitudinal velocity of the solid calculated as done in a fluid is considered. Thus, the expression $\bar{c} = c_{l} = \sqrt {c_{11} /\rho }$ is obtained, which is associated with the static compression module of the crystal through $B_{\text{static}} = V\left( {\frac{{\partial^{2} E_{e} }}{{\partial V^{2} }}} \right) = \left( {\lambda + 2\mu /3} \right)$, which takes the λ value as in a fluid, with μ the chemical potential. This gives the average speed $\bar{c} \approx \sqrt {B_{\text{static}} /\rho }$, which in turn gives rise to the Debye temperature

$$ \varTheta_{\text{D}} = \frac{{h\bar{c}}}{{k_{\text{B}} }}\left( {\frac{{3n_{r} }}{{4\pi V_{r} }}} \right)^{{\frac{1}{3}}} \approx \frac{h}{{k_{\text{B}} }}\left( {\frac{{3n_{r} }}{{4\pi V_{r} }}} \right)^{{\frac{1}{3}}} \sqrt {B_{\text{static}} /\rho } , $$

(2)

where ρ = M_r/V_r, with M_r the molecular mass and $\hbar = \frac{h}{2\pi }$. Then, the Debye temperature in the isotropic fluid model can be written as [17]

$$ \varTheta_{\text{D}} = \frac{\hbar }{{k_{\text{B}} }}\left( {6\pi^{2} n_{r} V_{r}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} } \right)^{{\frac{1}{3}}} \sqrt {B_{\text{static}} /M_{\text{r}} } . $$

(3)

A second approach to reduce the elastic constants is to consider the value of the Poisson ratio, which is defined as the ratio between the transverse deformation and the longitudinal deformation for an isotropic crystal under axial tension. This coefficient that can be written as $\nu = \lambda /2\left( {\lambda + \mu } \right)$ usually has a value between 0.2 and 0.5, and it is characteristic of each material [19]. Thus, it is possible to determine a parameter that can be chosen between λ, γ and B_static. Through an appropriate choice of the parameter B_static, the average velocity can be expressed in the form

$$ \bar{c} = \sqrt {\frac{{B_{\text{static}} }}{\rho }f\left( \nu \right)} , $$

(4)

where

$$ f(\nu ) = \left\{ {3\left[ {2\left( {\frac{{2\left( {1 + \nu } \right)}}{{3\left( {1 - 2\nu } \right)}}} \right)^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} + \left( {\frac{1 + \nu }{{3\left( {1 - \nu } \right)}}} \right)^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} } \right]^{ - 1} } \right\}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} . $$

(5)

Then Eq. (3) changes and the temperature of Debye becomes

$$ \varTheta_{\text{D}} = 0.85995\frac{\hbar }{{k_{\text{B}} }}\left( {6\pi^{2} n_{r} V_{r}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} } \right)^{{\frac{1}{3}}} \sqrt {B_{\text{static}} /M_{r} } . $$

(6)

This expression is analogous to the fluid model, except for the function f(ν), where the bulk modulus and the Poisson coefficient are still present. We have considered the ions in centrosymmetric positions, whereby the potential energy surface could be described as a sum of the potential for central interaction. Thus, it is possible to apply the Cauchy relation, for which ν = 1/4 [20], with function f(ν) = 0.85995.

With this approach, in the Gibbs function of Eq. (1), $A_{\text{vib}} \left[ {T,w_{j} \left( {\vec{a}} \right)} \right] = A_{\text{vib}} \left[ {T,\varTheta_{D} \left( {V\left( {\vec{a}} \right)} \right)} \right].$

So the dependencies of the internal parameters $\vec{a}$ are contained in E_e and V, so that in obtaining the internal parameters $\vec{a}$ that minimize E_e in a certain V, the Gibbs function will also be minimal in that volume. Therefore, assuming that the minimum energies with respect to internal parameters at different volumes are known, i.e., E_e(V) is known, the Gibbs non-equilibrium function is then

$$ G^{*} \left( {T,P,V} \right) = E_{e} \left( V \right) + PV + A_{\text{vib}} \left[ {T,\varTheta_{D} \left( V \right)} \right]. $$

(7)

As can be seen, internal parameters are a function of volume, but this is a function of temperature and pressure, a[V(T, P)]. That is, the internal parameters change with the temperature in an isotropic form, such that an increase in T equals a decrease in P. This isotropic approximation is quite reasonable, although it has not been considered that the vibrational frequencies depend on all coordinates. With the above approximations, Eq. (7) allows to obtain the Gibbs function of the crystal as a function of T, P and V. This function must be minimum with respect to any geometric parameter, and in particular with respect to the volume. Thus, by minimizing this function for values other than T and P, the system state equation is obtained and, from this, any thermodynamic property can be determined.

The bulk module is related to the electronic energy by means $B_{\text{static}} \left( {V_{r} } \right) = V_{r} \left( {\frac{{\partial^{2} E_{e} \left( {V_{r} } \right)}}{{\partial V_{r}^{2} }}} \right)$, which allows to rewrite the temperature of Debye as well

$$ \varTheta_{\text{D}} = 0.85995\frac{\hbar }{{k_{\text{B}} }}\left( {6\pi^{2} n_{r} V_{r}^{1/2} } \right)^{{\frac{1}{3}}} \sqrt {{{\left( {\frac{{\partial^{2} E_{e} \left( {V_{r} } \right)}}{{\partial V_{r}^{2} }}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{\partial^{2} E_{e} \left( {V_{r} } \right)}}{{\partial V_{r}^{2} }}} \right)} {M_{r} }}} \right. \kern-0pt} {M_{r} }}} . $$

(8)

Then, Θ_D(V_r) can be obtained through the second derivative of the curve E_e(V_r). In order to determine the vibration function of Helmholtz at different temperatures and volumes, it can be inferred that [21]

$$ \bar{A}_{\text{vib}} \left( {T,V_{r} } \right) = \bar{U}_{\text{vib}} - TS_{\text{vib}} = \frac{9}{8}n_{r} k_{\text{B}} \varTheta_{\text{D}} \left( {V_{r} } \right) + 3n_{r} k_{\text{B}} T{\text{Ln}}\left( {1 - e^{{ - \varTheta_{\text{D}} \left( {V_{r} } \right)/T}} } \right) - n_{r} k_{\text{B}} TD\left[ {\varTheta_{\text{D}} \left( {V_{r} } \right)/T} \right]. $$

(9)

To determine the equilibrium situation of the system it is necessary to minimize the Gibbs non-equilibrium function $\bar{G}^{*} \left( {T,P,V_{r} } \right) = E_{e} \left( {V_{r} } \right) + PV_{r} + \bar{A}_{\text{vib}} \left( {T,V_{r} } \right)$ with respect to V_r. The asterisk symbolizes that the function is being evaluated in non-equilibrium states, so that the function has three variables, not two as in equilibrium thermodynamics.

Through the above-described model, it is clear that the thermodynamic properties can be obtained from the state equation. First, the Gibbs equilibrium function is obtained by minimizing Eq. (19) for given values of P and T. Also, an evaluation of the second derivative of the Gibbs function allows checking that it is positive for all points and the stationary point is minimum. Thus, from the second derivative it is possible to obtain the isothermal volume modulus of the system,

$$ B_{T} = - V_{r} \left( {\frac{\partial P}{{\partial V_{r} }}} \right)_{T} = - V_{r} \left( {\frac{{\partial^{2} G^{*} }}{{\partial V_{r}^{2} }}} \right)_{T,P} . $$

(10)

Deriving Eq. (10) with respect to the pressure, we obtain

$$ B_{T}^{\prime } = \left( {\frac{{\partial B_{T} }}{\partial P}} \right)_{T} = \left( {\frac{{\partial B_{T} }}{{\partial V_{r} }}} \right)_{T} \left( {\frac{{\partial V_{r} }}{\partial P}} \right)_{T} . $$

(11)

The heat capacity at constant volume can be obtained as

$$ \bar{C}_{v} = 3n_{r} R \left( {4D\left[ {\varTheta_{\text{D}} /T} \right] - \frac{{3\varTheta_{\text{D}} /T}}{{e^{{\varTheta_{\text{D}} /T}} - 1}}} \right). $$

(12)

The Grüneisen parameter, which depends explicitly on the volume and implicitly on T and P, is defined as

$$ \gamma = - \frac{{{\text{d}}\,{\text{Ln}}\left[ {\varTheta_{D} \left( {V_{r} } \right)} \right]}}{{{\text{d}}\,{\text{Ln}}\left( {V_{r} } \right)}}. $$

(13)

On the other hand, it is more accurate to evaluate the parameter of Grüneisen from the equation of state of Mie-Grüneisen, because that is a more general equation than the Debye model, since it ensures that all vibrational frequencies change in the same way in the volume of the crystal.

$$ P - P_{\text{static}} = \gamma \frac{{\bar{U}_{\text{vib}} }}{{V_{r} }}, $$

(14)

where

$$ P = - \left( {\frac{{\partial \bar{A}}}{{\partial V_{r} }}} \right)_{T} , $$

(15)

and $P_{\text{static}} = - \frac{{{\text{d}}E_{e} \left( {V_{r} } \right)}}{{{\text{d}}V_{r} }}$ is the pressure that the crystal volume V_r would have on the static model, and therefore represents the thermal vibrational contribution to the pressure.

The coefficient of thermal expansion at constant pressure can be found through the expression

$$ \alpha = \frac{1}{{V_{r} }}\left( {\frac{{\partial V_{r} }}{\partial T}} \right)_{P} = \frac{1}{{B_{T} }}\left( {\frac{\partial P}{\partial T}} \right)_{{V_{r} }} $$

(16)

α can be derived from State Equation-V_r(T, P), but it is preferable to get α from γ because the quasi-harmonic Debye model necessarily satisfies the Mie-Grüneisen equation. Thus, deriving both members of the Eq. (15) with respect to temperature at constant volume, we obtain

$$ \left( {\frac{\partial P}{\partial T}} \right)_{{V_{r} }} = \gamma \frac{{\bar{C}_{v} }}{{V_{r} }}, $$

(17)

thus

$$ \alpha = \gamma \frac{{\bar{C}_{v} }}{{B_{T} V_{r} }}. $$

(18)

The isobaric heat capacity is given by

$$ \bar{C}_{p} = \bar{C}_{v} + TV_{r} \alpha^{2} B_{T} = \bar{C}_{v} \left( {1 + \alpha \gamma T} \right), $$

(19)

and, from the adiabatic bulk modulus

$$ B_{S} = B_{T} \frac{{\bar{C}_{p} }}{{\bar{C}_{v} }} = B_{T} \left( {1 + \alpha \gamma T} \right), $$

(20)

because $B_{S} = - V_{r} \left( {\frac{\partial P}{{\partial V_{r} }}} \right)_{S}$.

3 Results and Discussion

3.1 Structural Properties

From the Structure Prediction Diagnostic Software SPuDs [22], specially designed for perovskite-like materials, it is possible to predict the crystal parameters for the Fm$\bar{3}$m (#225) space group. The obtained Wyckoff positions in the structure are shown in Table 1.

Table 1 Atomic positions for the Ba₂NiMoO₆ double perovskite in the Fm$\bar{3}$m (#225) space group as predicted by SPuDS [21]

Then, by using the PowderCell (PCW) code [23], the respective diffraction pattern can be theoretically generated as presented in Fig. 1.

Fig. 1

XRD simulated pattern for the Ba₂NiMoO₆ complex perovskite obtained from the theoretical cell parameters (Color figure online)

This perovskite can be indexed in the A₂BB′O₆ cubic structure with the cell edge a = 2a_p, where a_p represents the cell lattice of the cubic perovskite. The presence of the superstructure reflection lines (311), (331), (511) and (531) in the XRD pattern of the A₂BB′O₆ double perovskite is the signature of B, B′ cationic ordering. In a substitutional solid solution BB′, there is a random arrangement of B and B′ on equivalent lattice positions in the crystal structure. It upon stable heat treatment, the random solid solution rearranges into a structure in which B and B′ occupy the same set of positions, but in a regular way, such a structure is described as superstructure. Figure 2 shows the expected structure for the Ba₂NiMoO₆ double perovskite constructed from the simulation data.

Fig. 2

Crystal structure of the Ba₂NiMoO₆ material for the Fm$\bar{3}$m (#125) space group. In the figure, the small red spheres identify the positions of the oxygens in the structure (Color figure online)

In the superstructure, the position occupied by B and B′ is no longer equivalent and this feature is exhibited in the XRD pattern of the material by the presence of superstructure reflection lines [24]. For a double cubic perovskite of the formula A₂BB′O₆, the intensity of XRD reflections, in particular the (111) superstructure plane, is proportional to the difference in the scattering power of the B and B′ atoms when all the atoms are situated in the ideal position [25, 26]. A disordered arrangement of B and B′ should result in zero intensity. In the Ba₂NiMoO₆, the Ni⁴⁺ and Mo⁴⁺ cation ordering of the B and B′ positions must be clearly distinguished by the presence of the significant intensity of (311), (331), (511) and (531) superstructural reflection lines. The lattice constant of the Ba₂NiMoO₆, calculated from the simulation, is a = 7.9159 Å.

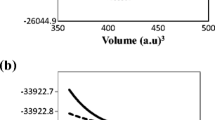
From the crystallographic information described above, a set of calculation of the total energy versus volume were performed and fitted with the Murnaghan’s equation state [27] in order to obtain the equilibrium lattice parameter (a₀) from the ab initio calculation, see Fig. 3.

Fig. 3

Total energy as a function of volume for Ba₂NiMoO₆ considering the Fm–3 m space group. Points represent the minimization calculations, and the line corresponds to the adjustment with Murnaghan’s equation of state (Color figure online)

The a₀ obtained was 7.9488 Å, which is 0.4% offset from the value predicted by the SPuDS and 0.8% overestimates the experimental value [10]. On the other hand, when the LDA approximation is used the a₀ value is 7.8965 Å, which turns out to be 0.3% different from the SPuDs prediction and underestimates the experimental value in 1.5% [10]. In Table 2, we report the atomic positions optimized using different theoretical procedures and the experimental values [10], where the values obtained with GGA–PBE are in total agreement with experimental values. For the rest of the present work, we will consider this value of the lattice parameter.

Table 2 Ba₂NiMoO₆ unit cell internal coordinates (Wyckoff positions) obtained from the ab initio calculations, SPuDs and experimental data, which are included for comparison [9]

3.2 Elastic Properties

The elastic constants for this compound have not been previously reported in the literature; knowledge of these properties is important since they might be correlated with the equation of state (EOS) and thermo-physical properties such as the specific heat, thermal expansion, Debye temperature, melting point, etc. Also, from the elastic constants, valuable information about the binding and mechanical stability of the solid can be obtained.

By considering the generalized Hook’s law: σ_ij = c_ij ε_j, we calculated the elastic constants for the Ba₂NiMoO₆ compound in the cubic structure. There are three independent elastic constants for the cubic structure, called C₁₁, C₁₂, C₄₄. The requirement of mechanical stability of the crystalline systems for any homogeneous lattice deformation places restrictions for the elastic constants [28]. The necessary conditions for mechanical stability in the cubic crystal are: C₁₁ > 0 and C₁₁− C₁₂ > 0. The calculated zero-temperature elastic constants are shown in Table 3. The values of Table 3 satisfy the criteria for mechanical stability of Ba₂NiMoO₆, suggesting that its bulk form is experimentally accessible. There are no experimental values to compare with the present calculations.

Table 3 Calculated elastic constants (in GPa) for the polycrystalline elastic moduli in the Ba₂NiMoO₆

From the elastic constants of single crystals we calculate the elastic moduli, which are of more interest for the development of technological materials [28]. The Reuss (R), Voigt (V), and Hill (H) polycrystalline average values of the Young modulus (E), the shear modulus (G) and the Poisson ratio (ν) for the cubic Ba₂NiMoO₆ calculated by means of the expressions given in Ref. [16] are given in Table 3. As indicated in Table 3, A is the Zener’s anisotropy factor A = 2C₄₄/(C₁₁ − C₁₂). Since a departure from unity of this factor is a measure of anisotropy, the results in Table 3 indicate that the Ba₂NiMoO₆ compound is less anisotropic than pure Ni. Materials with high B and G are likely to be hard materials. The Young modulus on the other side determines the stiffness of the material. From the results shown in Table 3, we note that the elastic moduli of the Ba₂NiMoO₆ compound are close but lower than those of pure Ni. The present results predict that the stiffness and hardness of the compound are big than pure Ni. The brittle/ductile behavior can be predicted through the ratio of B/G as an index of the plastic characteristic of materials [29,30,31].

The critical threshold value for differentiating the physical properties of materials is about 1.75. If the B/G ratio is larger than that, the polycrystalline sample is predicted to behave like a ductile material; otherwise, it would act as a brittle material. The present value of B/G is 1.6 for the Ba₂NiMoO₆ compound, indicating that this compound will behave as a brittle material. The Poisson’s ratio provides more information about the characteristics of the bonding forces than any of the other elastic constants. The calculated Poisson’s ratio for the studied Ba₂NiMoO₆ compound is ~ 0.3, which falls within the expected range for materials of double perovskite type [32].

3.3 Electronic Structure and Magnetic Properties

In order to find the magnetic ground state of the complex perovskite Ba₂NiMoO₆, we have considered the ferromagnetic coupling (FM) between Ni atoms, and different antiferromagnetic (AF) configurations coupling between the Ni atoms. For the AF cases, we have used a 2 × 2×2 supercell of Ba₂NiMoO₆, with the purpose to explore different AF configurations, such as [001], [110] and [111], as showed in Fig. 4. In the ferromagnetic case of Fig. 4a, all the spins due to the magnetic moments of the Ni are oriented in the direction of application of an external magnetic field (up). In the antiferromagnetic case, there are three types of configuration: Fig. 4b, the alignment of the spins is parallel to the applied field (up) in a plane with direction [001] and antiparallel (down) in the next plane, interspersed successively; Fig. 4c presents the same distribution as in Fig. 4b but in the direction [110]; finally, in Fig. 4d, antiferromagnetism occurs in the direction [111]

Fig. 4

Different magnetic configurations considered: a FM, b AF [001], c AF [110] and d AF [111]. The colors of the spheres are previously defined in Fig. 2 (Color figure online)

In Table 4, we report the difference of energy (ΔE) respect to AF [111] case, the total magnetic moment (M_T) and the magnetic moment of the Ni atom (m_Ni), where the magnetic ground state of the Ba₂NiMoO₆ is AF [111], i.e., the antiferromagnetic coupling between Ni atoms is across the propagation vector (1/2, 1/2, 1/2). These results are in agreement with experimental studies, where using X-Ray and neutron powder diffraction patterns collected at 2 K [10].

Table 4 Value of the difference of energy (ΔE in meV) respect to AF [111] configuration, total magnetic moment (M_T in μ_B/f.u.) and magnetic moment of Ni atoms (m_Ni in μ_B)

Figure 5 shows the total density of state (DOS) and the projected density of state per atom (PDOS) of the Ba₂NiMoO₆ for AF [111] case. In this figure, the positive part in the vertical axis of the density of states represents the contributions due to the electrons with spin-up orientation (up arrow) and the negative part is associated to the contributions from the electrons with spin down (down arrow). In Fig. 5a, the total DOS is presented, and partial contributions of Ni, Ba, Mo and O are exemplified in Figs. 5b–e. The low- and high-spin configurations (e.g., and t_2g orbitals) are denoted in Fig. 5b as (↑) and (↓), respectively.

Fig. 5

a Total DOS and PDOS for the atoms, b Ni, c Ba, d Mo and e O of the compound Ba₂NiMoO₆ belong to the magnetic ground state configuration AF [111]. In (b), the arrows indicate high-spin configuration (up) and low-spin configuration (down) (Color figure online)

From the figure, it is possible to establish the occurrence of hybridization due to the p-Ni orbitals and some d-Mo [d(z²) and d(x² − y²)] in the range of energy − 8.0 and − 5.0 eV, whereas in the range − 2.5 eV and E_f exist a hybridization between the orbitals p-Ba, p-Mo and s–O, which are responsible by the conductor behavior in this material. For energies higher than E_f, conduction band, we found a remarkable hybridization between the orbital d-Ni and p-O, where both t_2g and, e.g., orbitals of the Ni atoms are occupied; this is characterized of an octahedral high-spin configuration.

The magnetic moment of the Ni atoms (m_Ni) come from, mainly, polarization of the d-Ni orbital, where the absolute value of (|m_Ni|) is 1.61 μ_B, due to unequal distribution in the PDOS-up and PDOS-down of the 3d-Ni orbitals. In Fig. 6, we show the electron spin density for the crystallographic plane [200], where is possible see the antiferromagnetic coupling between the Ni atoms for the AF [111] case. In the figure, the positive electronic density represents the spin-up orientation and the negative density corresponds to the spin-down polarization.

Fig. 6

Electron spin density for the crystallographic plane [200] of the compound Ba₂NiMoO₆ for the magnetic ground state AF [111] (Color figure online)

The value of |m_Ni| obtained from the ab initio calculations is lower than proposed experimentally [10] based on the spin only moment of isolated Ni²⁺ ion, but is similar that |m_Ni| found in the NiO compound, 1.7 μ_B [33], where Ni atoms are located in an octahedral site surrounded by oxygen atoms, similar to the Ni atoms of the Ba₂NiMoO₆ compound; furthermore, the magnetic ground state of the NiO is antiferromagnetic with the same propagation vector found in the present work.

3.4 Thermodynamic Properties

The effects of temperature and pressure on the thermodynamic properties of the Ba₂NiMoO₆ material from the state equation, under the considerations of the quasi-harmonic approximation of the Debye model described in Sect. 3.2, were analyzed as presented below. Figure 8 shows the results of specific heat at constant volume, C_V (a), and at constant pressures, C_P (b), as functions of temperature. As can be seen in the figures, the temperature was varied between 0 and 1500 K for eight applied pressure values, from 0 to 25 GPa. It is observed in Fig. 7 that below T = 400 K, for all applied pressure values, C_V≈ C_P. This result occurs because α²B_TV_r is a very small number in Eq. (19).

Fig. 7

Specific heat C_v (a) and C_p (b) calculated through the quasi-harmonic Debye model for the Ba₂NiMoO₆ material from the Murnaghan state equation (Color figure online)

Figure 7a shows more clearly than in Fig. 7b the trend of specific heat toward the Dulong–Petit limit, which is the specific heat value independent of temperature. From this limit value of Dulong–Petit, as the temperature increases, each of the atoms in the material absorbs the same amount of energy proportional to this temperature increase. In the case of C_V, this value corresponds to 233.09 J/mol K for all applied pressure values, while for C_P this limit is between 247,67 and 230.98 J/mol K for pressures between 10 and 25 GPa. These values of the Dulong–Petit specific heat limit are high, since they practically duplicate other results reported for simple perovskites [34]. At high temperatures (T > 600 K), a specific heat divergence is observed, which can be due to that for very high temperatures the model is not reliable. At very low temperatures, it should be possible to determine a behavior dominated by the purely electronic response, while at medium and high temperatures the predominance of the phononic response should be expected. However, it is important to note that only the p-Ba orbitals for both up and down spin polarizations in the density of states are enough close to the Fermi level, giving rise to a reasonable electronic contribution to specific heat. Then, when the material is heated, contributions to specific heat are mostly due to the movement of the atoms and ions around their equilibrium positions as a result of the absorption of heat. In the real Ba₂NiMoO₆, this result may vary because this material is polycrystalline and the specific heat depends on the porosity, since the thermal energy needed to increase the temperature of the material is lower in the less porous materials and higher in the denser ones.

In Fig. 8, results of calculations of the Debye temperature (a), thermal expansion (b) coefficient and Grüneisen coefficient (c) as functions of temperature are presented. We have calculated the dependence of Θ_D(T) (as a function of temperature), plotting isobar curves as shown in Fig. 8a. These results show that the Debye temperature is increased substantially with increasing pressure, from 520.42 K for P = 0 GPa to 672.45 K for P  = 25 GPa (at T  = 0 K). This occurs because as the pressure increases, all the velocities of the elastic waves increase gradually and their increase directly affects the temperature of Debye. Likewise, a mild nonlinear decreasing behavior of Θ_D(T) can be observed with increasing temperature for applied pressures. This decrease in temperature of Debye as a function of temperature is characteristic of perovskite-type materials [35]. Interpreting the Debye temperature as the highest temperature that can be achieved as a result of a single normal vibration, it can be argued that the effect of pressure is the increase of cation–anion vibration frequencies, while the effect of temperature is the expansive distortion of the structure, increasing the wavelength of the vibrations, decreasing the frequency and, consequently, the temperature of Debye.

Fig. 8

Debye temperature (a), thermal expansion coefficient (b) and Grüneisen coefficient (c) for the Ba₂NiMoO₆ calculated by the application of the quasi-harmonic Debye model (Color figure online)

Figure 8 shows the dependence of thermal expansion coefficient, α, with temperature and pressure. It can be established from the figure that α(T) decreases drastically with increasing pressure. On the other hand, it can be seen that at low temperatures (between 0 and 300 K) α(T) grows rapidly with temperature, and above 300 K it grows smoothly, following an approximately linear behavior. In spite of considering that the Ba₂NiMoO₆ has a cubic structure, its character of perovskite type confers an anisometric structure to it, and, therefore, very great differences of the thermal expansion must be presented along the different crystallographic directions.

This behavior can be associated to the structural distortions to which the perovskite-type materials are sensitive, because both temperature and pressure can give rise to inclinations and/or rotations of the Ni-O₆ and Mo-O₆ octahedrons, elongation of the structure in certain crystallographic directions and eventual contractions in other directions. Thus, the type of response in α(T) is associated with the type of distortion or transition that is occurring because of the application of temperature and pressure to the material. This circumstance could slightly divert any experimental results with respect to the theoretical result of Fig. 8. On the other hand, the relatively low value of α(T) is characteristic of ceramic materials [36].

One aspect, which is not considered in the calculations that we have carried out, is that as the temperature increases, structural phase transitions can occur and the material could no longer have a cubic structure. Finally, the Grüneisen parameter, shown in Fig. 8c, shows a gradual decrease with the increase in applied pressure (for example, from 2.25 for P = 0 GPa to 1.97 for P = 25 GPa, at T = 0 K). This behavior is observed for all the temperatures considered in the calculations. On the other hand, the Grüneisen coefficient presents a smooth and nonlinear increase with the increase in temperature. These characteristics observed in the Grüneisen parameter as a function of pressure and temperature are related to the alteration in the vibration frequency of a crystalline lattice, according to the discussion presented above in relation to the coefficient of thermal expansion [37].

4 Conclusions

DFT calculations of structural parameters for the Ba₂NiMoO₆ perovskite were performed by considering the Fm$\bar{3}$m (#225) space group. The theoretical lattice parameter for the cubic perovskite structure, calculated both within the GGA and LDA approximations, differs around 0.4% from the value predicted by the SPuDs software and the experimental value 0.8%. The calculated zero-temperature elastic constants satisfy the criteria for mechanical stability, indicating that the bulk form of this phase is experimentally accessible. From the calculated polycrystalline average values of the Young modulus, shear modulus, the Poisson ratio and the Zener’s anisotropic factor for the cubic Ba₂NiMoO₆, it is predicted that the stiffness and hardness of the compound are big than of pure Ni. Moreover, the compound is expected to be anisotropic and brittle. Respect to the magnetic properties, we have found that the magnetic ground state of the cubic Ba₂NiMoO₆ compound is antiferromagnetic across the propagation vector (1/2, 1/2, 1/2) being in total agreement with experimental prediction previously reported; furthermore, the magnetic moment of the Ni cations and the antiferromagnetic configuration is similar to the cubic compound NiO. The calculations of the thermodynamic properties from the state equation, by means of the quasi-harmonic approximation of the Debye model, show that the effects of the interatomic vibrations give rise to a specific heat that decreases with the applied pressure and evidences a Dulong–Petit limit relatively high (233.09 J/mol K), compared to other results reported for simple perovskite-type materials. Likewise, we conclude that C_V ≈ C_P, mainly due to the low value of the coefficient of thermal expansion. The Debye temperature shows an increasing dependence on the pressure and decreasing with the temperature. By contrast, both the coefficient of thermal expansion and the Grüneisen parameter decrease with the pressure and increase slightly as a function of temperature. In general, except for the high specific heat value of Dulong–Petit, the behavior observed in the thermodynamic properties is characteristic of the perovskite-like ceramic materials. We emphasize that the thermodynamic properties depend fundamentally on the value of the parameter Grüneisen. Since the γ is derived from a third derivative of the E_e function, it is very sensitive both to the numerical errors in the derivation and to the smoothness of the E_e(V_r) curves. For this reason, it would be highly advisable to obtain experimental results of the thermodynamic properties in order to more objectively establish the microscopic mechanisms that originate them.