Exact SDP reformulations of adjustable robust linear programs with box uncertainties under separable quadratic decision rules via SOS representations of non-negativity

Abstract

In this paper we show that two-stage adjustable robust linear programs with affinely adjustable data in the face of box data uncertainties under separable quadratic decision rules admit exact semi-definite program (SDP) reformulations in the sense that they share the same optimal values and admit a one-to-one correspondence between the optimal solutions. This result allows adjustable robust solutions of these robust linear programs to be found by simply numerically solving their SDP reformulations. We achieve this result by first proving a special sum-of-squares representation of non-negativity of a separable non-convex quadratic function over box constraints. Our reformulation scheme is illustrated via numerical experiments by applying it to an inventory-production management problem with the demand uncertainty. They demonstrate that our separable quadratic decision rule method to two-stage decision-making performs better than the single-stage approach and is capable of solving the inventory production problem with a greater degree of uncertainty in the demand.

1 Introduction

Real-world optimization models of technical decision-making involve input data that are often noisy or uncertain due to prediction or measurement errors. The conventional (single-stage) robust optimization models for static decision-making contain only “here-and-now” decision variables for which we have to determine their values now and cannot wait until we have more or full information [3, 6].

Many dynamic decision-making models, where the decision-maker is able to adjust her strategy to information revealed over time (in stages), are difficult multi-stage robust optimization problems [4, 10]. They not only contain “here-and-now” (first-stage) decisions, but also “wait-and-see” (later-stage) decisions. The values of “wait-and-see” variables can be fixed after some of the uncertain parameters have revealed their values. Consider, for instance, a multi-stage inventory system affected by uncertain demand. The replenishment orders are made one at a time and the weekly replenishment order is made when we already know the actual demands in the preceding weeks.

Adjustable robust optimization (ARO), pioneered by Ben-Tal and his collaborators in the late 1990’s [5], is increasingly becoming an important deterministic methodology to handle multi-stage optimization problems involving both “here-and-now” and “wait-and-see” decision variables [11, 23]. It offers less conservative decisions than the classical static (single-stage) robust optimization [3, 14, 15, 19] as some of the decisions can be adjusted at later stages. However, even two-stage robust optimization problems with adjustable variables are in general computationally intractable unless they are limited to satisfy some special rules, called “decision rules” [3, 4, 25].

A great deal of attention has recently been focused on studying two-stage adjustable robust linear programs with linear (or affine) decision rules by transforming them into single-stage problems as they lead, in many cases, to computationally tractable reformulations [4, 9, 25]. On the other hand, the transformations of these two-stage linear programs with quadratic decision rules to single-stage robust problems result in numerically intractable non-convex quadratic optimization problems unless the decision rules or uncertainty sets are restricted to certain class of rules or sets respectively.

Some progress has recently been made in transforming an adjustable robust linear program with general quadratic decision rules [22, 24] into equivalent semi-definite programs in the case of an ellipsoid uncertainty set. An equivalent second-order cone program reformulation has also been established in [22] for such a program under a separable quadratic decision rule. These results were achieved by employing a numerically tractable linear matrix inequality representation of a non-negative non-convex quadratic function over an ellipsoid, known as S-lemma [3, 21].

Unfortunately, no numerically tractable representation exists for a general non-negative non-convex quadratic function over boxes because a non-convex quadratic optimization problem over box constraints is a fundamental NP-hard global optimization problem [13]. Consequently, an adjustable robust linear program with box uncertainty sets under a general quadratic decision rule remains a hard problem to study, theoretically and computationally. In this paper, by restricting the quadratic decision rule to a separable quadratic rule, we examine an affinely adjustable two-stage robust linear program under the box uncertainty set and make the following contributions.

• (i) Firstly, we establish a special sum-of-squares (SOS) representation and semi-definite representation conditions for the non-negativity of a separable non-convex quadratic function over box constraints. We do this by exploiting the separability and employing a surjective transformation from an interval to the real line. We also show that this SOS representation condition is equivalent to the existence of a solution to a system of semi-definite linear inequalities which can easily be verified numerically by solving a semi-definite linear program.

• (ii) By employing the SOS representation conditions, we then show that an affinely adjustable robust linear program (AARLP) in the face of box data uncertainty under a separable quadratic decision rule (QDR) is numerically tractable by presenting an exact semi-definite program reformulation in the sense that they share the same optimal values. This result shows how adjustable robust solutions of uncertain linear programs can readily be found by solving their SDP reformulations. Our approach in this paper differs from the exact second order cone program reformulation, established recently in [22] for the AARLPs with the separable QDR in the face of ellipsoidal data uncertainty, where S-lemma [22] and the Schur’s complement played important roles.

• (iii) Finally, we illustrate our reformulation approach by applying it to an inventory-production management problem with demand uncertainty. Numerical experiments demonstrate that our QDR approach to two-stage decision-making performs better than the single-stage approach and is capable of solving the inventory production problem with a greater degree of uncertainty in the demand.

The outline of the paper is as follows. Section 2 provides sum-of-squares and semi-definite representations of non-negativity of separable quadratic functions over box constraints. Section 3 presents an exact semi-definite program reformulation of an affinely adjustable robust linear program with a quadratic decision rule. Section 4 illustrates the quadratic decision rule approach by applying it to an inventory-production management problem with the demand uncertainty. Section 5 concludes with a brief discussion on further research.

2 Numerically tractable SOS representations

Consider the following uncertain linear program with adjustable variables

$$\begin{aligned}&\inf _{x, y(\cdot )}\{ c^Tx + \varphi ^Ty(z)\mid A(z)x+B y(z) \le d(z)\}, \end{aligned}$$

(U)

where $c\in {\mathbb {R}}^n$ and $\varphi :=(\varphi _1,\ldots ,\varphi _s)\in {\mathbb {R}}^s$ are fixed, $x\in {\mathbb {R}}^n$ is the first-stage decision variable, $y(\cdot )$ is the second-stage decision. It is represented as an adjustable decision variable that depends on the uncertain parameter z which lies in a box uncertainty set, ${\mathcal {U}}_\mathrm{box}:=\prod _{j=1}^q [\beta _j,\gamma _j]$ with $\beta _j ,\gamma _j \in {\mathbb {R}}$ and $\beta _j \le \gamma _j$, $j=1,\ldots ,q$, $A:{\mathbb {R}}^q\rightarrow {\mathbb {R}}^{p\times n}$ and $d:{\mathbb {R}}^q\rightarrow {\mathbb {R}}^p$ are affine maps given, respectively, by

$$\begin{aligned} A(z):=A^0+ \sum _{j=1}^{q}z_j A^j,\; d(z):=d_0 + \sum _{j=1}^{q}z_j d_j,\; z:=(z_1,\ldots ,z_q), \end{aligned}$$

(2.1)

for given matrices $A^j \in {\mathbb {R}}^{p \times n}$ and $d_j \in {\mathbb {R}}^{p}, j=0,1,\ldots ,q$. The matrix $B \in {\mathbb {R}}^{p \times s}$ is a fixed recourse matrix; that is, B is independent of the uncertain variable z. Two-stage adjustable linear programming models of the form (U) under these assumptions commonly appear in real-world decision-making problems [4, 23] such as the inventory production problems examined in Sect. 4.

The robust counterpart of the two-stage adjustable linear programs (i.e. robust programs) with affine decision rules can be transformed into computationally tractable single-stage problems in many cases, including box uncertainty sets [4, 9, 24, 25]. In the case of an ellipsoidal uncertainty set, making use of the well-known semi-definite representation of non-negative quadratic function over a single quadratic constraint [3, 21], the authors in [22] reformulated an adjustable robust linear program under quadratic decision rules into a numerically tractable semi-definite program. In particular, for such a problem with a separable quadratic decision rule, an equivalent second-order cone program has also been given in [22]. Unfortunately, no numerically tractable representation exists for a general non-negative non-convex quadratic function over boxes because a non-convex quadratic optimization problem over box constraints is, in general, a fundamental NP-hard global optimization problem [13].

In this section we present a sum-of squares (SOS) representation as well as a semi-definite representation of the non-negativity of a separable non-convex quadratic function over box constraints. This representation plays a key role in transforming an adjustable robust problem into a numerically tractable optimization problem in the next section. The role of SOS representations in solving hard polynomial optimization problems can be found in [2, 7, 8].

Recall that the symbol $I_m\in {\mathbb {R}}^{m\times m}$ stands for the $(m\times m)$ identity matrix. $0_m\in {\mathbb {R}}^m$ denotes the m-dimensional (column) vector of all zeros. Let ${\mathbb {S}}^m$ be the space of all symmetric $(m\times m)$ matrices. A matrix $A\in {\mathbb {R}}^{m\times n}$ can be denoted as $A:=(a_1,\ldots ,a_m)^T$ for its rows $a_i\in {\mathbb {R}}^n, i=1,\ldots ,m$ or as $A:=(a_1,\ldots ,a_n)$ for its columns $a_j\in {\mathbb {R}}^m, j=1,\ldots ,n.$ A matrix $A\in {\mathbb {S}}^m$ is said to be positive semidefinite, denoted by $A\succeq 0$, whenever $x^T Ax\ge 0$ for all $x\in {\mathbb {R}}^m.$ If $x^T Ax> 0$ for all $x\in {\mathbb {R}}^m{\setminus }\{0_m\}$, then A is called positive definite, denoted by $A\succ 0$. The matrix $M = \mathrm{diag}(v)\in {\mathbb {R}}^{m\times m}$ is a diagonal matrix whose elements are given by the vector $v\in {\mathbb {R}}^m$.

Theorem 2.1

(Semi-definite and SOS Representations) Let $\alpha \in {\mathbb {R}},$ $u:=(u_1,\ldots ,u_q)\in {\mathbb {R}}^q$ and $W:=\mathrm{diag}(w_1,\ldots ,w_q)$ be a diagonal matrix, where $w_j \in {\mathbb {R}}$, $j=1,\ldots ,q$. Then, the following statements are equivalent:

• (a) The following implication holds:

  $$\begin{aligned} z:=(z_1,\ldots ,z_q) \in \prod _{j=1}^{q} [\beta _j,\gamma _j] \ \Longrightarrow \alpha +u^Tz + z^T Wz \ge 0, \end{aligned}$$

  where $\beta _{j},\gamma _j \in {\mathbb {R}}$ with $\beta _j \le \gamma _j$, $j=1,\ldots ,q$.

• (b) There exist $\alpha _j \in {\mathbb {R}}$, $j=1,\ldots ,q$, such that $\sum _{j=1}^q \alpha _j \le \alpha$ and

  $$\begin{aligned} \alpha _jh^1_j+u_jh^2_j + w_jh^3_j \in \Sigma _4^2[z_j], \ j=1,\ldots ,q,\end{aligned}$$

  where $\Sigma _4^2[z_j]$ denotes the set consisting of all the sum of squares polynomials with variable $z_j$ and degree at most 4, $h^1_j(z_j):=(1+z_j^2)^2, h^2_j(z_j):=(\beta _j+\gamma _jz_j^2)(1+z_j^2)$ and $h^3_j(z_j):=(\beta _j+\gamma _jz_j^2)^2$ for $z_j\in {\mathbb {R}}$.

• (c) There exist $\alpha _j \in {\mathbb {R}}$, $j=1,\ldots ,q$ and

  $$\begin{aligned} X^j:=\begin{pmatrix} X^j_{11} &{}\quad X^j_{12} &{}\quad X^j_{13} \\ X^j_{12} &{}\quad X^j_{22} &{}\quad X^j_{23} \\ X^j_{13} &{}\quad X^j_{23} &{}\quad X^j_{33} \\ \end{pmatrix} \succeq 0, \ j=1,\ldots ,q \end{aligned}$$

  such that $\sum _{j=1}^q \alpha _j \le \alpha$ and

  $$\begin{aligned} \left\{ \begin{array}{l} X^j_{11}= \alpha _j + u_j \beta _j + w_j \beta _j^2, \\ X^j_{12}=0, \\ 2X^j_{13} + X^j_{22} = 2 \alpha _j+u_j(\beta _j+\gamma _j)+2w_j \beta _j\gamma _j,\\ X^j_{23}=0, \\ X^j_{33}= \alpha _j + u_j \gamma _j + w_j \gamma _j^2. \end{array} \right. \end{aligned}$$

Proof

$[\mathrm{(a)} \Leftrightarrow \mathrm{(b)}]$ We first note that (a) is equivalent to

$$\begin{aligned} 0 \le \min \{\alpha + u^Tz + \sum _{j=1}^qw_jz_j^2\mid z \in \prod _{j=1}^{q} [\beta _j,\gamma _j]\}= \alpha + \sum _{j=1}^q \min \{u_jz_j + w_jz_j^2\mid z_j \in [\beta _j,\gamma _j]\}. \end{aligned}$$

Then, (a) is further equivalent to the fact that there exist $\alpha _j \in {\mathbb {R}}$, $j=1,\ldots ,q$, such that

$$\begin{aligned} \min \{u_jz_j + w_jz_j^2\mid z_j \in [\beta _j,\gamma _j]\} \ge -\alpha _j, j=1,\ldots , q \text{ and } \sum _{j=1}^q \alpha _j \le \alpha . \end{aligned}$$

For each $j\in \{1,\ldots ,q\}$, defining

$$\begin{aligned} f_j(z_j):=\alpha _j + u_jz_j + w_jz_j^2, \end{aligned}$$

we arrive at the assertion that (a) is equivalent to $f_j(z_j) \ge 0$ for all $z_j \in [\beta _j,\gamma _j], j=1,\ldots ,q$ and $\sum _{j=1}^q \alpha _j \le \alpha$. Now, let

$$\begin{aligned} g_j(z_j):=(1+z_j^2)^2f_j\left( \frac{\beta _j+\gamma _jz_j^2}{1+z_j^2}\right) =\alpha _j(1+z_j^2)^2+u_j(\beta _j+\gamma _jz_j^2)(1+z_j^2) + w_j(\beta _j+\gamma _jz_j^2)^2. \end{aligned}$$

We see that each $g_j$ is a real polynomial on ${\mathbb {R}}$ with degree at most 4. Since $\beta _j\le \gamma _j$, we have the following two cases:

Case 1 Let $\beta _j<\gamma _j$. As $z_j \mapsto \frac{\beta _j+\gamma _jz_j^2}{1+z_j^2}$ is a surjective map from ${\mathbb {R}}$ to $[\beta _j, \gamma _j)$, we obtain that

$$\begin{aligned} f_j(z_j) \ge 0 \ \forall z_j \in [\beta _j,\gamma _j]\Leftrightarrow & {} f_j(z_j) \ge 0 \ \forall z_j \in [\beta _j,\gamma _j) \\\Leftrightarrow & {} g_j(z_j) \ge 0 \ \forall \ z_j \in {\mathbb {R}}. \end{aligned}$$

where the first equivalence follows by the continuity of $f_j$.

Case 2 Let $\beta _j=\gamma _j$. We can verify directly that

$$\begin{aligned} f_j(z_j) \ge 0 \ \forall z_j \in [\beta _j,\gamma _j]\Leftrightarrow & {} g_j(z_j) \ge 0 \ \forall \ z_j \in {\mathbb {R}}. \end{aligned}$$

Note that a one-variable polynomial is nonnegative if and only if it is a sums-of-squares polynomial [17, Theorem 2.5]. Then, $g_j \in \Sigma _4^2[z_j],$ and so we arrive at the conclusion that

$$\begin{aligned} \alpha _jh^1_j+u_jh^2_j + w_jh^3_j \in \Sigma _4^2[z_j],\ j=1,\ldots ,q, \end{aligned}$$

where $h^1_j(z_j):=(1+z_j^2)^2, h^2_j(z_j):=(\beta _j+\gamma _jz_j^2)(1+z_j^2)$ and $h^3_j(z_j):=(\beta _j+\gamma _jz_j^2)^2$ for $z_j\in {\mathbb {R}}$.

$[\mathrm{(b)} \Leftrightarrow \mathrm{(c)}]$ To see the equivalence of (b) and (c), note that each $g_j$ is a sums-of-squares one variable polynomial if and only if there exists $X^j:=(X^j_{kl})_{1 \le k,l \le 3} \in {\mathbb {S}}^3$ such that $X^j \succeq 0$ and

$$\begin{aligned} \alpha _j(1+z_j^2)^2+u_j(\beta _j+\gamma _jz_j^2)(1+z_j^2) + w_j(\beta _j+\gamma _jz_j^2)^2 = \begin{pmatrix} 1 \\ z_j \\ z_j^2 \end{pmatrix}^T \begin{pmatrix} X^j_{11} &{}\quad X^j_{12} &{}\quad X^j_{13} \\ X^j_{12} &{}\quad X^j_{22} &{}\quad X^j_{23} \\ X^j_{13} &{}\quad X^j_{23} &{}\quad X^j_{33} \\ \end{pmatrix}\begin{pmatrix} 1 \\ z_j \\ z_j^2 \end{pmatrix}. \end{aligned}$$

for all $z_j\in {\mathbb {R}}$ (for example, see [17, Proposition 2.1]). Thus, we have

$$\begin{aligned} \left\{ \begin{array}{l} X^j_{11}= \alpha _j + u_j \beta _j + w_j \beta _j^2, \\ X^j_{12}=0, \\ 2X^j_{13} + X^j_{22} = 2 \alpha _j+u_j(\beta _j+\gamma _j)+2w_j \beta _j\gamma _j,\\ X^j_{23}=0, \\ X^j_{33}= \alpha _j + u_j \gamma _j + w_j \gamma _j^2. \end{array} \right. \end{aligned}$$

Consequently, the equivalence of (b) and (c) holds, and the proof is complete. $\square$

3 Separable QDRs and box uncertainties

In this section, we begin with the formulation of the robust counterpart of the affinely adjustable robust linear program (U) with fixed recourse under the box uncertainty set. We assume that the adjustable variable $y(\cdot )$ admits a separable quadratic decision rule of the form:

$$\begin{aligned} y(z):=y_0+Pz+\left( \begin{array}{c} z^TQ_1z \\ \vdots \\ z^TQ_sz \end{array} \right) , \end{aligned}$$

(3.1)

where $y_0\in {\mathbb {R}}^s$, $P \in {\mathbb {R}}^{s \times q}$ and $Q_r \in {\mathbb {S}}^{q}, r=1,\ldots ,s,$ are (non-adjustable) variables. Moreover, $Q_r, r=1,\ldots ,s$ are assumed to be diagonal matrices given by $Q_r:=\mathrm{diag}(\xi _r^1,\ldots ,\xi _r^q)$ with $\xi ^j_r\in {\mathbb {R}}, j=1,\ldots ,q$.

Let us consider the robust counterpart of (U) as

$$\begin{aligned} \inf _{\begin{array}{c} x \in {\mathbb {R}}^n, y_0\in {\mathbb {R}}^s,\\ P \in {\mathbb {R}}^{s\times q}, Q_r\in {\mathbb {S}}^q \end{array}}\Big \{ c^Tx +&{\max _{z\in {\mathcal {U}}_{\mathrm{box}}}{\varphi ^Ty(z)}} \mid \\&A(z)x+B y(z) \le d(z),\\ {}&y(z)=y_0+Pz+\left( \begin{array}{c} z^TQ_1z \\ \vdots \\ z^TQ_sz \end{array} \right) ,\;\forall z\in {\mathcal {U}}_{\mathrm{box}},\\ {}&Q_r:=\mathrm{diag}(\xi _r^1,\ldots ,\xi _r^q), \xi ^j_r\in {\mathbb {R}}, j=1,\ldots ,q, r=1,\ldots ,s\Big \}. \end{aligned}$$

(P)

Denote $B:=(b_1,\ldots ,b_p)^T$ for its rows $b_i:=(b_{i1},\ldots ,b_{is})\in {\mathbb {R}}^s, i=1,\ldots ,p.$ Denoting by $a^j_i\in {\mathbb {R}}^n, i=1,\ldots ,p$ the rows of $A^j$ for $j=0,1,\ldots ,q$, i.e, $A^j:=(a^j_1,\ldots ,a^j_p)^T, j=0,1,\ldots ,q,$ we let $W_i:=(a^1_i,\ldots ,a^q_i), i=1,\ldots ,p$. Then, A(z) becomes

$$\begin{aligned} A(z) = \begin{pmatrix} (a_1^0 + W_1z)^T \\ \vdots \\ (a_p^0 + W_pz)^T \end{pmatrix}. \end{aligned}$$

(3.2)

Similarly, denoting $d_j:=(d_{j1},\ldots ,d_{jp}), j=0,1,\ldots ,q$, we let $v_i:=(d_{1i},\ldots , d_{qi}), i=1,\ldots ,p$. Then d(z) is given by

$$\begin{aligned} d(z) = \begin{pmatrix} d_{01} + v_1^Tz \\ \vdots \\ d_{0p} + v_p^Tz \end{pmatrix}. \end{aligned}$$

(3.3)

We associate with (P) the following semidefinite programming (SDP) problem:

$$\begin{aligned}&\inf _{\begin{array}{c} x \in {\mathbb {R}}^n, \tau \in {\mathbb {R}}, y_0\in {\mathbb {R}}^s,\\ \alpha ^{i,j} \in {\mathbb {R}}, X^{i,j} \in {\mathbb {S}}^3, \\ \sigma ^j\in {\mathbb {R}}, Y^j\in {\mathbb {S}}^3 \end{array}}\Big \{ c^Tx + \tau \,\mid \, \displaystyle X^{i,j}:=\begin{pmatrix} X^{i,j}_{11} &{}\quad X^{i,j}_{12} &{}\quad X^{i,j}_{13} \\ X^{i,j}_{12} &{}\quad X^{i,j}_{22} &{}\quad X^{i,j}_{23} \\ X^{i,j}_{13} &{}\quad X^{i,j}_{23} &{}\quad X^{i,j}_{33} \\ \end{pmatrix} \succeq 0, \ i=1,\ldots ,p, \, j=1,\ldots ,q,\\&\quad X^{i,j}_{11}=\alpha ^{i,j} - (W_i^Tx+ P^Tb_i-v_i)_j \beta _j - \sum _{r=1}^sb_{ir}\xi _r^{j} \beta _j^2,\\&\quad 2X^{i,j}_{13} + X^{i,j}_{22} = 2 \alpha ^{i,j}- (W_i^Tx+ P^Tb_i-v_i)_j(\beta _j+\gamma _j)- 2\sum _{r=1}^sb_{ir}\xi _r^{j} \beta _j\gamma _j,\\&\quad X^{i,j}_{33}= \alpha ^{i,j} - (W_i^Tx+ P^Tb_i-v_i)_j \gamma _j - \sum _{r=1}^sb_{ir}\xi _r^{j} \gamma _j^2,\\&\quad X^{i,j}_{12}=0,\;X^{i,j}_{23}=0,\;\sum _{j=1}^q \alpha ^{i,j} \le -(a^0_i)^Tx -b_i^Ty_0+d_{0i},\\&\quad \displaystyle Y^j:=\begin{pmatrix} Y^j_{11} &{}\quad Y^j_{12} &{}\quad Y^j_{13} \\ Y^j_{12} &{}\quad Y^j_{22} &{}\quad Y^j_{23} \\ Y^j_{13} &{}\quad Y^j_{23} &{}\quad Y^j_{33} \\ \end{pmatrix} \succeq 0, \, j=1,\ldots ,q,\\&\quad Y^j_{11}=\sigma ^j - (P^Tt)_j \beta _j - {\sum _{r=1}^s\varphi _r\xi _r^{j} \beta _j^2},\\&\quad 2Y^j_{13} + Y^j_{22} = 2 \sigma ^j- {(P^T\varphi )_j}(\beta _j+\gamma _j)- {2\sum _{r=1}^s\varphi _r\xi _r^{j} \beta _j\gamma _j},\\&\quad Y^j_{33}= \sigma ^j - {(P^T\varphi )_j} \gamma _j - {\sum _{r=1}^st_r\xi _r^{j} \gamma _j^2,} \\&\quad Y^j_{12}=0,\;Y^j_{23}=0,\;\sum _{j=1}^q \sigma ^j \le \tau -{ \varphi ^Ty_0} \Big \}, \end{aligned}$$

(SDP)

where $W_i$ and P are given in (3.2) and (3.1) respectively, and $v_i$ is defined as in (3.3).

Theorem 3.1

(Exact SDP Reformulation) Consider the adjustable robust linear program with the separable quadratic decision rule under the box data uncertainty (P) and the semidefinite programming problem (SDP). Then,

$$\begin{aligned} \inf (P)=\inf (SDP). \end{aligned}$$

Moreover, $(x^*,y_0^*,P^*,Q_1^*,\dots ,Q_s^*)$, where $Q_r^*:=\mathrm{diag}({\xi _r^1}^*,\dots ,{\xi _r^q}^*)$ with ${\xi _r^j}^*\in {\mathbb {R}}$, $j=1,\dots ,q$, $r=1,\ldots ,s$, is an optimal solution of problem (P) if and only if there exist $\tau \in {\mathbb {R}},$ $\alpha ^{i,j}\in {\mathbb {R}},X^{i,j}\in {\mathbb {S}}^3,\sigma ^j\in {\mathbb {R}},Y^j\in {\mathbb {S}}^3,i=1,\dots ,p, j=1,\dots ,q$ such that $(x^*,y_0^*,P^*,Q_1^*,\dots ,Q_s^*, {\tau ,} \alpha ^{1,1},\dots ,\alpha ^{p,q},$ $X^{1,1},\dots ,X^{p,q},\sigma ^1,\dots ,\sigma ^q,Y^1,\dots ,Y^q)$ is an optimal solution of problem (SDP).

Proof

Observe first that (P) is equivalent to the adjustable robust linear program

$$\begin{aligned}&\inf _{\begin{array}{c} x \in {\mathbb {R}}^n, \tau \in {\mathbb {R}}, y_0\in {\mathbb {R}}^s,\\ P \in {\mathbb {R}}^{s\times q}, Q_r\in {\mathbb {S}}^q \end{array}}\Big \{ c^Tx + \tau \mid \, A(z)x+B y(z) \le d(z),\nonumber \\&\qquad {\varphi ^Ty(z)}{\le \tau ,}\nonumber \\&\qquad y(z)=y_0+Pz+\left( \begin{array}{c} z^TQ_1z \\ \vdots \\ z^TQ_sz \end{array} \right) ,\;\forall z\in {\mathcal {U}}_{\mathrm{box}},\nonumber \\ {}&\quad Q_r:=\mathrm{diag}(\xi _r^1,\ldots ,\xi _r^q), \, \xi ^j_r\in {\mathbb {R}}, j=1,\ldots ,q, r=1,\ldots ,s{ \Big \},} \end{aligned}$$

(3.4)

where $\tau$ is an introduced auxiliary (here-and-now) decision variable which does not alter the optimal value. It is therefore sufficient to show that the feasible regions of (3.4) and (SDP) are equivalent. Problem (3.4) can be written in a standard form:

$$\begin{aligned}&\inf _{\begin{array}{c} {\tilde{x}} \in {\mathbb {R}}^{n+1}, y_0\in {\mathbb {R}}^s, \\ P \in {\mathbb {R}}^{s\times q}, Q_r\in {\mathbb {S}}^q \end{array}}\Big \{ {\tilde{c}}^T{\tilde{x}} \mid \, {\tilde{A}}(z){\tilde{x}}+{\tilde{B}} y(z) \le {\tilde{d}}(z),\nonumber \\&\quad y(z)=y_0+Pz+\left( \begin{array}{c} z^TQ_1z \\ \vdots \\ z^TQ_sz \end{array} \right) ,\;\forall z\in {\mathcal {U}}_{\mathrm{box}},\nonumber \\&\quad Q_r:=\mathrm{diag}(\xi _r^1,\ldots ,\xi _r^q), \, \xi ^j_r\in {\mathbb {R}}, j=1,\ldots ,q, r=1,\ldots ,s{ \Big \},} \end{aligned}$$

(3.5)

where

$$\begin{aligned} {\tilde{c}} = \begin{pmatrix} c \\ 1 \end{pmatrix}\in {\mathbb {R}}^{n+1}, \, {\tilde{x}} = \begin{pmatrix} x \\ \tau \end{pmatrix}\in {\mathbb {R}}^{n+1}, \, { {\tilde{A}}(z) = \begin{pmatrix} A(z) &{} 0_p \\ 0_n^T &{} -1 \end{pmatrix}}\in {\mathbb {R}}^{(p+1)\times (n+1)},\nonumber \\ {\tilde{B}} = \begin{pmatrix} B \\ {\varphi ^T} \end{pmatrix}\in {\mathbb {R}}^{(p+1)\times s}, \, {\tilde{d}}(z) = \begin{pmatrix} d(z) \\ 0\end{pmatrix}\in {\mathbb {R}}^{p+1}. \end{aligned}$$

(3.6)

Note that problem (3.5) has $p+1$ robust inequality constraints. We handle these in two cases.

Case 1 Let $i = 1,\dots ,p$. By (3.2), (3.3) and (3.6), the $i{\mathrm{th}}$ inequality constraint of (3.5) is of the form

$$\begin{aligned} (a^0_i + W_iz)^Tx+b_i^T\left( y_0+Pz+ \left( \begin{array}{c} z^TQ_1z \\ \vdots \\ z^TQ_sz \end{array} \right) \right) \le d_{0i}+v_i^Tz, \; \forall z \in { {\mathcal {U}}_{\mathrm{box}}.} \end{aligned}$$

(3.7)

As each $Q_r$ is a $(q \times q)$ diagonal matrix with $Q_r=\mathrm{diag}(\xi _r^{1},\ldots ,\xi _r^{q}), r=1,\ldots ,s$, it follows that

$$\begin{aligned} \sum _{r=1}^sb_{ir}Q_r=\mathrm{diag}\Big (\sum _{r=1}^sb_{ir}\xi _r^{1},\ldots ,\sum _{r=1}^sb_{ir}\xi _r^{q}\Big ) \end{aligned}$$

is also a $(q \times q)$ diagonal matrix.

Note that (3.7) amounts to

$$\begin{aligned} -\left( (a^0_i)^Tx + b_i^Ty_0-d_{0i}+(W^T_ix+ P^Tb_i-v_i)^Tz+ z^T\Big (\sum _{r=1}^sb_{ir}Q_r\Big )z\right) \ge 0, \; \forall z \in {\mathcal {U}}_{\mathrm{box}}. \end{aligned}$$

Applying Theorem 2.1 with $\alpha :=-((a^0_i)^Tx + b_i^Ty_0-d_{0i})$, $u:=-(W^T_ix+ P^Tb_i-v_i)$ and $W:=-\sum _{r=1}^s b_{ir} Q_r$, we find $\alpha ^{i,j} \in {\mathbb {R}}$, $j=1,\ldots ,q$ and

$$\begin{aligned} X^{i,j}=\begin{pmatrix} X^{i,j}_{11} &{}\quad X^{i,j}_{12} &{}\quad X^{i,j}_{13} \\ X^{i,j}_{12} &{}\quad X^{i,j}_{22} &{}\quad X^{i,j}_{23} \\ X^{i,j}_{13} &{}\quad X^{i,j}_{23} &{}\quad X^{i,j}_{33} \\ \end{pmatrix} \succeq 0, { j=1,\ldots ,q,} \end{aligned}$$

such that $\sum _{j=1}^q \alpha ^{i,j} \le -((a^0_i)^Tx + b_i^Ty_0-d_{0i})$ and

$$\begin{aligned} \left\{ \begin{array}{l} X^{i,j}_{11}=\alpha ^{i,j} - (W_i^Tx+ P^Tb_i-v_i)_j \beta _j - \sum _{r=1}^sb_{ir}\xi _r^{j} \beta _j^2, \\ X^{i,j}_{12}=0, \\ 2X^{i,j}_{13} + X^{i,j}_{22} = 2 \alpha ^{i,j}- (W_i^Tx+ P^Tb_i-v_i)_j(\beta _j+\gamma _j)- 2\sum _{r=1}^sb_{ir}\xi _r^{j} \beta _j\gamma _j,\\ X^{i,j}_{23}=0, \\ X^{i,j}_{33}= \alpha ^{i,j} - (W_i^Tx+ P^Tb_i-v_i)_j \gamma _j - \sum _{r=1}^sb_{ir}\xi _r^{j} \gamma _j^2. \end{array} \right. \end{aligned}$$

(3.8)

Case 2 Let $i = p+1$. By (3.6) the $(p+1)^{\mathrm{th}}$ inequality constraint of (3.5) is

$$\begin{aligned} -\tau + {\varphi ^T}\left( y_0+Pz+\left( \begin{array}{c} z^TQ_1z \\ \vdots \\ z^TQ_sz \end{array}\right) \right) \le 0,\;\forall z\in {{\mathcal {U}}_{\mathrm{box}}.} \end{aligned}$$

(3.9)

In the same manner as Case 1, we apply Theorem 2.1 to (3.9) with $\alpha := \tau - {\varphi ^Ty_0}$, $u := {-P^T\varphi }$ and $W := -\sum _{r=1}^{s}{\varphi _rQ_r}$, we see that (3.9) is equivalent to the assertion that there exist $\sigma ^j\in {\mathbb {R}}, j=1,\dots ,q$ and

$$\begin{aligned} Y^j = \begin{pmatrix} Y^j_{11} &{}\quad Y^j_{12} &{}\quad Y^j_{13} \\ Y^j_{12} &{}\quad Y^j_{22} &{}\quad Y^j_{23} \\ Y^j_{13} &{}\quad Y^j_{23} &{}\quad \quad Y^j_{33} \\ \end{pmatrix} \succeq 0, \, j=1,\ldots ,q \end{aligned}$$

such that $\sum _{j=1}^{q}{\sigma ^j}\le \tau - {\varphi ^Ty_0}$ and

$$\begin{aligned} \left\{ \begin{array}{l} Y^j_{11}=\sigma ^j - {(P^T\varphi )}_j \beta _j - {\sum _{r=1}^s\varphi _r\xi _r^{j} \beta _j^2}, \\ Y^j_{12}=0, \\ 2Y^j_{13} + Y^j_{22} = 2 \sigma ^j- {(P^T\varphi )_j}(\beta _j+\gamma _j)- 2{\sum _{r=1}^s\varphi _r\xi _r^{j} \beta _j\gamma _j},\\ Y^j_{23}=0, \\ Y^j_{33}= \sigma ^j - {(P^T\varphi )_j} \gamma _j - {\sum _{r=1}^s\varphi _r\xi _r^{j} \gamma _j^2}. \end{array} \right. \end{aligned}$$

Now, let $(x,y_0,P,Q_1,\ldots ,Q_s)$ be a feasible point of problem (P). Taking Case 1 and Case 2 into account, we assert that the feasibility of $(x,y_0,P,Q_1,\ldots ,Q_s)$ is equivalent to the assertion that $(x,y_0,P,Q_1,\dots ,Q_s,\tau ,\alpha ^{1,1},\dots ,\alpha ^{p,q},$ $X^{1,1},\dots ,X^{p,q},$ $\sigma ^1,\dots ,\sigma ^q,Y^1,\dots ,Y^q)$ is a feasible point of problem (SDP), which completes the proof. $\square$

Remark 3.2

As an easy consequence of Theorem 3.1 we see that the following adjustable robust linear program

$$\begin{aligned}&\inf _{\begin{array}{c} x \in {\mathbb {R}}^n, y_0\in {\mathbb {R}}^s,\\ P \in {\mathbb {R}}^{s\times q}, Q_r\in {\mathbb {S}}^q \end{array}}\Big \{ c^Tx \mid A(z)x+B y(z) \le d(z),\\&\quad y(z)=y_0+Pz+\left( \begin{array}{c} z^TQ_1z \\ \vdots \\ z^TQ_sz \end{array} \right) ,\;\forall z\in {\mathcal {U}}_{\mathrm{box}}\\&\quad Q_r:=\mathrm{diag}(\xi _r^1,\ldots ,\xi _r^q), \xi ^j_r\in {\mathbb {R}}, j=1,\ldots ,q, r=1,\ldots ,s { \Big \}} \end{aligned}$$

admits the following exact SDP reformulation:

$$\begin{aligned}&\inf _{\begin{array}{c} x \in {\mathbb {R}}^n, y_0\in {\mathbb {R}}^s,\\ \alpha ^{i,j} \in {\mathbb {R}}, X^{i,j} \in {\mathbb {S}}^3 \end{array}}\Big \{ c^Tx \,\mid \, \displaystyle X^{i,j}:=\begin{pmatrix} X^{i,j}_{11} &{}\quad X^{i,j}_{12} &{}\quad X^{i,j}_{13} \\ X^{i,j}_{12} &{}\quad X^{i,j}_{22} &{}\quad X^{i,j}_{23} \\ X^{i,j}_{13} &{}\quad X^{i,j}_{23} &{}\quad X^{i,j}_{33} \\ \end{pmatrix} \succeq 0, \ i=1,\ldots ,p, \, j=1,\ldots ,q,\\&\quad X^{i,j}_{11}=\alpha ^{i,j} - (W_i^Tx+ P^Tb_i-v_i)_j \beta _j - \sum _{r=1}^sb_{ir}\xi _r^{j} \beta _j^2, \\&\quad 2X^{i,j}_{13} + X^{i,j}_{22} = 2 \alpha ^{i,j}- (W_i^Tx+ P^Tb_i-v_i)_j(\beta _j+\gamma _j)- 2\sum _{r=1}^sb_{ir}\xi _r^{j} \beta _j\gamma _j,\\&\quad X^{i,j}_{33}= \alpha ^{i,j} - (W_i^Tx+ P^Tb_i-v_i)_j \gamma _j - \sum _{r=1}^sb_{ir}\xi _r^{j} \gamma _j^2,\\&\quad X^{i,j}_{12}=0,\;X^{i,j}_{23}=0,\;\sum _{j=1}^q \alpha ^{i,j} \le -(a^0_i)^Tx -b_i^Ty_0+d_{0i} { \Big \}.} \end{aligned}$$

This can be seen by setting $\varphi :=0_s$ in (P).

Single-Stage Robust Linear Programs Let us consider a particular case of problem (P) where $\varphi : = 0_s$ and $B:=0_{p\times s}$. In this case, we arrive at the (single-stage) robust linear program:

$$\begin{aligned} \inf _{\begin{array}{c} x \in {\mathbb {R}}^n \end{array}}\Big \{ c^Tx \mid A(z)x \le d(z), \;\forall z\in {\mathcal {U}}_{\mathrm{box}}\Big \}, \end{aligned}$$

(LP)

where A(z) and d(z) are given as in (2.1). The corresponding problem (SDP) results in the following form:

$$\begin{aligned}&\inf _{\begin{array}{c} x \in {\mathbb {R}}^n, \alpha ^{i,j} \in {\mathbb {R}},\\ X^{i,j} \in {\mathbb {S}}^3 \end{array}}\Big \{ c^Tx \,\mid \, \displaystyle X^{i,j}:=\begin{pmatrix} X^{i,j}_{11} &{}\quad X^{i,j}_{12} &{}\quad X^{i,j}_{13} \\ X^{i,j}_{12} &{}\quad X^{i,j}_{22} &{}\quad X^{i,j}_{23} \\ X^{i,j}_{13} &{}\quad X^{i,j}_{23} &{}\quad X^{i,j}_{33} \\ \end{pmatrix} \succeq 0, \ i=1,\ldots ,p, \, j=1,\ldots ,q,\\&\quad X^{i,j}_{11}=\alpha ^{i,j} - (W_i^Tx-v_i)_j \beta _j,\\&\quad 2X^{i,j}_{13} + X^{i,j}_{22} = 2 \alpha ^{i,j}- (W_i^Tx-v_i)_j(\beta _j+\gamma _j),\\&\quad X^{i,j}_{33}= \alpha ^{i,j} - (W_i^Tx-v_i)_j \gamma _j,\\&\quad X^{i,j}_{12}=0,\;X^{i,j}_{23}=0,\sum _{j=1}^q \alpha ^{i,j} \le -(a^0_i)^Tx+d_{0i}\Big \}. \end{aligned}$$

(SDPL)

As we see in the following corollary, our SDP reformulation and the well-known LP reformulation [3] for the problem (LP) share the same value.

Corollary 3.3

(Exact LP Reformulation) For the problem (LP), it holds that

$$\begin{aligned} \inf (LP)=\inf (SDPL)=\inf (LDP), \end{aligned}$$

where (LDP) is the following linear program

$$\begin{aligned} \inf _{\begin{array}{c} x \in {\mathbb {R}}^n, \alpha ^{i,j} \in {\mathbb {R}} \end{array}} \Big \{ c^Tx \,\mid \,&(a^0_i)^Tx -d_{0i}+\sum _{j=1}^q\frac{\gamma _j+\beta _j}{2}(W^T_ix-v_i)_j+\sum _{j=1}^q\frac{\gamma _j-\beta _j}{2}\alpha ^{i,j}\le 0, i=1,\ldots ,p,\\&-\alpha ^{i,j}\le (W^T_ix-v_i)_j \le \alpha ^{i,j}, j=1,\ldots ,q,\;i=1,\ldots ,p\Big \}. \end{aligned}$$

(LDP)

Moreover, $x^*$ is an optimal solution of problem (LP) if and only if there exist $\alpha ^{i,j} \in {\mathbb {R}}, X^{i,j} \in {\mathbb {S}}^3$, $i=1,\ldots ,p$, $j=1,\ldots ,q$ such that $(x^*, \alpha ^{1,1},\ldots ,\alpha ^{p,q},X^{1,1},\ldots ,X^{p,q})$ is an optimal solution of problem (SDPL) or if and only if there exist $\alpha ^{i,j} \in {\mathbb {R}}$, $i=1,\ldots ,p$, $j=1,\ldots ,q$ such that $(x^*,\alpha ^{1,1},\ldots ,\alpha ^{p,q})$ is an optimal solution of problem (LDP).

Proof

By Theorem 3.1, we first obtain the equality that $\inf (LP)=\inf (SDPL).$ The equality $\inf (LP)=\inf (LDP)$ can be derived from a more general result in [3]. Here, we give a short proof for the purpose of self-containment and completeness. Let x be a feasible point of problem (LP). Then x is a solution to the following inequalities

$$\begin{aligned} (a^0_i + W_iz)^Tx \le d_{0i}+v_i^Tz, \; \forall z \in {\mathcal {U}}_{\mathrm{box}}, \ i=1,\ldots ,p,\end{aligned}$$

(3.10)

where $a^j_i\in {\mathbb {R}}^n, i=1,\ldots ,p$ are the rows of $A^j$ for $j=0,1,\ldots ,q$, i.e, $A^j:=(a^j_1,\ldots ,a^j_p)^T, j=0,1,\ldots ,q,$, $W_i:=(a^1_i,\ldots ,a^q_i), i=1,\ldots ,p$, $d_j:=(d_{j1},\ldots ,d_{jp}), j=0,1,\ldots ,q$, and $v_i:=(d_{1i},\ldots , d_{qi}), i=1,\ldots ,p$ are denoted as per (3.2) and (3.3). Note that (3.10) can be written as

$$\begin{aligned}(a^0_i)^Tx -d_{0i}+\sum _{j=1}^qz_j(W^T_ix-v_i)_j\le 0, \; \forall z_j\in [\beta _j, \gamma _j], j=1,\ldots ,q, \ i=1,\ldots ,p,\end{aligned}$$

and so

$$\begin{aligned} (a^0_i)^Tx -d_{0i}+\max _{\beta _j\le z_j\le \gamma _j, j=1,\ldots ,q}\Big (\sum _{j=1}^qz_j(W^T_ix-v_i)_j\Big )\le 0, \; \ i=1,\ldots ,p.\end{aligned}$$

(3.11)

Letting $\tilde{z}_j:=z_j-\frac{\gamma _j+\beta _j}{2}, j=1,\ldots ,q,$ we see that (3.11) is equivalent to the following ones:

$$\begin{aligned}&(a^0_i)^Tx -d_{0i}+\sum _{j=1}^q\frac{\gamma _j+\beta _j}{2}(W^T_ix-v_i)_j+\max _{|\tilde{z}_j|\le \frac{\gamma _j-\beta _j}{2}, j=1,\ldots ,q}\Big (\sum _{j=1}^q{{\tilde{z}}}_j(W^T_ix-v_i)_j\Big )\le 0, \nonumber \\ {}&\quad i=1,\ldots ,p.\end{aligned}$$

(3.12)

Moreover, it is easy to see that

$$\begin{aligned} \max _{|{{\tilde{z}}}_j|\le \frac{\gamma _j-\beta _j}{2}, j=1,\ldots ,q}\Big (\sum _{j=1}^q\tilde{z}_j(W^T_ix-v_i)_j\Big )=\sum _{j=1}^q\frac{\gamma _j-\beta _j}{2}|(W^T_ix-v_i)_j|, i=1,\ldots ,p, \end{aligned}$$

and so, (3.12) amounts to the assertion that there exist $\alpha ^{i,j} \in {\mathbb {R}}$, $i=1,\ldots ,p$, $j=1,\ldots ,q$ (cf. [3, Page 19] for a similar linear inequality representation) such that

$$\begin{aligned}&(a^0_i)^Tx -d_{0i}+\sum _{j=1}^q\frac{\gamma _j+\beta _j}{2}(W^T_ix-v_i)_j+\sum _{j=1}^q\frac{\gamma _j-\beta _j}{2}\alpha ^{i,j}\le 0, \\ {}&-\alpha ^{i,j}\le (W^T_ix-v_i)_j \le \alpha ^{i,j}, j=1,\ldots ,q, i=1,\ldots ,p.\end{aligned}$$

This shows that $(x,\alpha ^{1,1},\ldots ,\alpha ^{p,q})$ is a feasible point of problem (LDP), which completes the proof. $\square$

The following example illustrates how to obtain adjustable robust solutions and the corresponding values of a two-stage robust linear program in the face of box data uncertainty using our results of this section.

Example 3.4

(Adjustable Robust Solutions) Consider an adjustable uncertain problem of the form:

$$\begin{aligned} \inf _{x\in {\mathbb {R}}^2, y(\cdot )}{}\Big \{x_1 + 2x_2 \;\mid \;&-3x_1-x_2+z_1x_1+z_2x_2+e_1^Ty(z)+z_2-2\le 0, -x_2+z_1\le 0, \\ {}&-x_1-z_1+z_2\le 0, -x_2+2e_2^Ty(z)+z_1-z_2\le 0 \Big \}, \end{aligned}$$

(EU)

where $e_1, e_2\in {\mathbb {R}}^2,$ are fixed recourse parameters, $x:=(x_1,x_2)$ is the first-stage here-and-now decision, $y(\cdot )$ is the second-stage wait-and-see decision, which is an adjustable decision variable depending on uncertain $z:=(z_1,z_2)\in [-1,1]\times [0,2].$ Here, we consider a separable quadratic decision rule $y(\cdot )$ given by

$$\begin{aligned} y(z):=y_0 +Pz+\left( \begin{array}{c} z^TQ_1z \\ z^TQ_2z \end{array} \right) , \end{aligned}$$

where $y_0\in {\mathbb {R}}^2$, $P\in {\mathbb {R}}^{2\times 2}$ and $Q_r:=\mathrm{diag}(\xi _r^1,\xi _r^2)$ with $\xi _r^j\in {\mathbb {R}}, r=1,2, j=1,2$ are (static) variables.

The adjustable robust counterpart of (EU) is given by:

$$\begin{aligned} \inf _{\begin{array}{c} x \in {\mathbb {R}}^2, y_0\in {\mathbb {R}}^2,\\ P \in {\mathbb {R}}^{2\times 2}, Q_r \in {\mathbb {S}}^2 \end{array} }\Big \{&x_1 +2x_2 \;\mid \; -3x_1-x_2+z_1x_1+z_2x_2+e_1^Ty(z)+z_2-2\le 0, -x_2+z_1\le 0, \\ {}&-x_1-z_1+z_2\le 0, -x_2+2e_2^Ty(z)+z_1-z_2\le 0, \\ {}&{ y(z):=y_0 +Pz+\left( \begin{array}{c} z^TQ_1z \\ z^TQ_2z \end{array} \right) }, \forall z:=(z_1,z_2)\in [-1,1]\times [0,2],\\ {}&Q_r:=\mathrm{diag}(\xi _r^1,{ \xi _r^2) ,} \, \xi _r^j\in {\mathbb {R}}, \, r=1,2, j=1,2 \Big \}. \end{aligned}$$

(ER)

(i)  Let $e_1:=(1,0), e_2:=(0,1).$ In this setting, we can verify directly that the problem (ER) admits optimal solutions (for example, $({{\bar{x}}},{{\bar{y}}}_0,{{\bar{P}}},{{\bar{Q}}}_1,{{\bar{Q}}}_2)$ with ${{\bar{x}}}:=(3,1), {{\bar{y}}}_0:=0_2, {{\bar{P}}}:=0_{2\times 2}, \bar{Q}_1:={{\bar{Q}}}_2:=0_{2\times 2}$), and its optimal value is $\min (ER)=5$.

Let us now employ Theorem 3.1 to verify the optimal value or find an optimal solution of problem (ER). To do this, let $\beta _1:=-1, \beta _2:=0, \gamma _1:=1, \gamma _2:=2,$

$$\begin{aligned} A^0:= \left( \begin{array}{cc} -3 &{}\quad -\,1 \\ 0&{}\quad -\,1 \\ -\,1&{}\quad 0 \\ 0 &{}\quad -\,1 \\ \end{array} \right) ,\quad A^1:= \left( \begin{array}{cc} 1 &{}\quad 0 \\ 0&{}\quad 0 \\ 0&{}\quad 0 \\ 0 &{}\quad 0 \\ \end{array} \right) ,\quad A^2:= \left( \begin{array}{cc} 0 &{} 1 \\ 0&{} 0 \\ 0&{} 0 \\ 0 &{} 0 \\ \end{array} \right) , \quad B:= \left( \begin{array}{cc} 1&{}\quad 0 \\ 0&{}\quad 0 \\ 0&{}\quad 0 \\ 0 &{}\quad 2 \\ \end{array} \right) \end{aligned}$$

and $d_0:=(2,0,0,0), d_1:=(0,-1,1,-1), d_2=(-1,0,-1,1).$ The problem (ER) becomes the following one:

$$\begin{aligned} \inf _{\begin{array}{c} x \in {\mathbb {R}}^2, y_0\in {\mathbb {R}}^2,\\ P \in {\mathbb {R}}^{2\times 2}, Q_r \in {\mathbb {S}}^2 \end{array}}\Big \{x_1 +2x_2 \;\mid \;&A(z)x+By(z)\le d(z), \\ {}&y(u)=y_0 +Pu+\left( \begin{array}{c} z^TQ_1z \\ z^TQ_2z \end{array} \right) ,\forall z\in {\mathcal {U}}_{\mathrm{box}}:=\prod _{j=1}^2 [\beta _j,\gamma _j],\\ {}&Q_r:=\mathrm{diag}(\xi _r^1,\xi _r^2), , \xi _r^j\in {\mathbb {R}}, r=1,2, j=1,2 \Big \},\end{aligned}$$

(EP)

where $A(z):=A^0+\sum _{j=1}^2z_jA^j$ and $d(z):=d_0+\sum _{j=1}^2z_jd_j$ for $z:=(z_1,z_2)\in {\mathcal {U}}_{\mathrm{box}}.$

Clearly, the problem (EP) is in the form of problem (P), and so its corresponding SDP relaxation program is given by

$$\begin{aligned}&\inf _{\begin{array}{c} x \in {\mathbb {R}}^2, y_0\in {\mathbb {R}}^2,\\ \alpha ^{i,j} \in {\mathbb {R}}, X^{i,j} \in {\mathbb {S}}^3 \end{array}}\Big \{ x_1 + 2x_2\mid \displaystyle X^{i,j}:=\begin{pmatrix} X^{i,j}_{11} &{}\quad X^{i,j}_{12} &{}\quad X^{i,j}_{13} \\ X^{i,j}_{12} &{}\quad X^{i,j}_{22} &{}\quad X^{i,j}_{23} \\ X^{i,j}_{13} &{}\quad X^{i,j}_{23} &{}\quad X^{i,j}_{33} \\ \end{pmatrix} \succeq 0, \ i=1,2,3,4, \, j=1,2,\\&\quad X^{i,j}_{11}=\alpha ^{i,j} - (W_i^Tx+ P^Tb_i-v_i)_j \beta _j - \sum _{r=1}^2b_{ir}\xi _r^{j} \beta _j^2,\\&\quad 2X^{i,j}_{13} + X^{i,j}_{22} = 2 \alpha ^{i,j}- (W_i^Tx+ P^Tb_i-v_i)_j(\beta _j+\gamma _j)- 2\sum _{r=1}^2b_{ir}\xi _r^{j} \beta _j\gamma _j,\\&\quad X^{i,j}_{33}= \alpha ^{i,j} - (W_i^Tx+P^Tb_i-v_i)_j \gamma _j - \sum _{r=1}^2b_{ir}\xi _r^{j} \gamma _j^2, \\&\quad X^{i,j}_{12}=0,\; X^{i,j}_{23}=0,\;\sum _{j=1}^2 \alpha ^{i,j} \le -(a^0_i)^Tx - b_i^Ty_0+d_{0i}\Big \}, \end{aligned}$$

(SDP)

where $W_1=I_2, W_2=W_3=W_4=0_{2\times 2},$ $a^0_1=(-3,-1), a^0_2=(0,-1), a^0_3=(-1,0), a^0_4=(0,-1),$ $b_1=(b_{11},b_{12})=(1,0), b_2=(b_{21},b_{22})=b_3=(b_{31},b_{32})=(0,0), b_4=(b_{41},b_{42})=(0,2),$ $v_1=(0,-1), v_2=(-1,0), v_3=(1,-1), v_4=(-1,1)$ and $d_{01}=2, d_{02}= d_{03}= d_{04}=0.$

Using the Matlab toolbox CVX [12], we solve the SDP problem (SDP). The solver returns the optimal value of problem (ER) as $+5=\min (ER)$. Moreover, on account of Theorem 3.1, the output gives a corresponding optimal solution of problem (ER) as $(x^*,y^*_0,P^*,Q^*_1,Q^*_2)$, where $x^*=(3.0000, 1.0000), y^*_0=(-62.1975, -21.1526),$ $P^*:= \left( \begin{array}{cc} 57.7064 &{} -0.5000 \\ 10.3729 &{} 6.6865\\ \end{array}\right) ,Q_1^*:= \left( \begin{array}{cc} -36.7992 &{} 0.0000 \\ 0.0000&{} -6.1865\\ \end{array}\right)$ and $Q_2^*:= \left( \begin{array}{cc} -3.0932 &{} 0.0000 \\ 0.0000&{} -3.0932\\ \end{array}\right) .$

(ii)  Let $e_1:=0_2, e_2:=0_2.$ In this case, the two-stage robust problem (EP) reduces to the following (single-state) robust linear program:

$$\begin{aligned} \inf _{\begin{array}{c} x \in {\mathbb {R}}^2 \end{array}}\big \{x_1 +2x_2 \;\mid \; A(z)x\le d(z) \big \},\end{aligned}$$

(LP)

where $A(z):=A^0+\sum _{j=1}^2z_jA^j$ and $d(z):=d_0+\sum _{j=1}^2z_jd_j$ for $z:=(z_1,z_2)\in {\mathcal {U}}_\mathrm{box}.$ Similarly as above, we can verify directly that the problem (LP) admits optimal solutions (for example, $\bar{x}:=(3,1)$) and its optimal value is $\min (LP)=5$.

Let us now employ Corollary 3.3 to verify the optimal value or find an optimal solution of problem (LP). Since the problem (LP) is the form of (LP), the corresponding LP reformulation of problem (LP) is given by

$$\begin{aligned}&\inf _{\begin{array}{c} x \in {\mathbb {R}}^2, \alpha ^{i,j} \in {\mathbb {R}} \end{array}}\Big \{ x_1 + 2x_2 \mid (a^0_i)^Tx -d_{0i}+\sum _{j=1}^2\frac{\gamma _j +\beta _j}{2}(W^T_ix-v_i)_j+\sum _{j=1}^2\frac{\gamma _j-\beta _j}{2}\alpha ^{i,j} \\&\quad \le 0, \ i=1,2,3,4, \\&\quad \quad -\alpha ^{i,j}\le (W^T_ix-v_i)_j \le \alpha ^{i,j}, j=1,2,\;i=1,2,3,4 \Big \}. \end{aligned}$$

(LDP)

Using the Matlab toolbox CVX again, we solve the LP problem (LDP). The solver returns the optimal value of problem (LP) as $+5=\min (LP)$. Moreover, on account of Corollary 3.3, the output gives a corresponding optimal solution of problem (LP) as $x^*:=(3.0000, 1.0000).$

4 Applications: inventory-production management

The following nominal model of an inventory-production management problem is adapted from [4]. Consider a single product inventory system, comprised of a warehouse and I factories. Also consider a planning horizon comprised of T time periods. We define:

• $d_t$: the demand for the product at the end of period t.

• $v_t$: the amount of product in the warehouse at the end of period t. $v_0$ is given as the initial amount of product in the warehouse.

• $p_i^t$: the amount of product to be produced in factory i during period t.

• $P_i^t$: the maximal production capacity of factory i during period t.

• $\kappa _i$: the maximal cumulative production capacity of factory i over the planning horizon.

• $c_i^t$: the cost of producing one unit of product in factory i during period t.

• $V_\text {min}$: the minimal allowed level of inventory in the warehouse at all times.

• $V_\text {max}$: the maximal allowed level of inventory in the warehouse at all times.

The problem is to satisfy the demand at all time periods whilst minimising the total cost. Eliminating variables $v_t$ as in [4], we arrive at the following linear program:

$$\begin{aligned}&(IP) \min _{p_i^t\in {\mathbb {R}}} \sum _{t=1}^{T}{\sum _{i=1}^{I}{c_i^t\, p_i^t}} \\&\quad \text {subject to}\, 0 \le p_i^t \le P_i^t, \quad i=1,\dots ,I \quad { t=1,\dots ,T,} \\&\quad \sum _{t=1}^{T}{p_i^t}\le \kappa _i, \quad { i=1,\dots ,I,} \\&\quad V_{\text {min}}\,\le v_0 + \sum _{s=1}^{t}{\sum _{i=1}^{I}{p_i^s}} - \sum _{s=1}^{t}{d_s} \le V_{\text {max}}, \quad { t=1,\dots ,T.} \end{aligned}$$

Affinely Adjustable Robust Optimisation Model with Separable QDRs In practice, the demand at period t is not revealed until the period is concluded. In this respect, $d_t$, $t=1,\dots ,T$ are regarded as uncertain parameters, lying within a box around a chosen nominal value $d_t^*$:

$$\begin{aligned} d_t\in \left[ (1-\delta )d_t^*,\,(1+\delta )d_t^*\right] ,\quad { \delta \in [0,1].} \end{aligned}$$

We therefore allow our optimisation variables $p_i^t$ to become wait-and-see variables depending on the uncertain demand. Assuming that the decision on supplies $p_i^t$ is to be made at the beginning of period t, we allow the decision $p_i^t$ to be based on the demands up to (but not including) time t. That is, defining our information basis [4] as

$$\begin{aligned} {\mathcal {I}}_t = \{1,\dots ,t-1\} \end{aligned}$$

and defining¹$d_{{\mathcal {I}}_t} = \begin{bmatrix} d_1&\dots&d_{t-1} \end{bmatrix}^\top$, we have

$$\begin{aligned} p_i^t: {\mathbb {R}}^{t-1}\rightarrow {\mathbb {R}},\quad p_i^t = p_i^t(d_{{\mathcal {I}}_t}) \end{aligned}$$

and so (IP) can be written as an adjustable robust linear program

$$\begin{aligned}&(IP-ARO) \min _{p_i^t:{\mathbb {R}}^{t-1}\rightarrow {\mathbb {R}}} \max _{d\in {\mathcal {D}}}{\left\{ \sum _{t=1}^{T}{\sum _{i=1}^{I}{c_i^t\, p_i^t (d_{{\mathcal {I}}_t})}}\right\} } \\&\quad \text {subject to}\, 0 \le p_i^t(d_{{\mathcal {I}}_t}) \le P_i^t, \quad i=1,\dots ,I \quad t=1,\dots ,T, \quad {\forall d\in {\mathcal {D}},}\\&\quad \sum _{t=1}^{T}{p_i^t(d_{{\mathcal {I}}_t})}\le \kappa _i, \quad i=1,\dots ,I, \quad {\forall d\in {\mathcal {D}},}\\&\quad V_{\text {min}}\,\le v_0 + \sum _{s=1}^{t}{\sum _{i=1}^{I}{p_i^s(d_{{\mathcal {I}}_s})}} - \sum _{s=1}^{t}{d_s} \le V_{\text {max}}, \quad t=1,\dots ,T, \quad {\forall d\in {\mathcal {D}},} \end{aligned}$$

where ${\mathcal {D}} = \displaystyle \prod _{t=1}^{T}{[(1-\delta )d_t^*, (1+\delta )d_t^*]}$.

We wish to solve $(IP-ARO)$ via a separable QDR of the form

$$\begin{aligned} p_i^t(d_{{\mathcal {I}}_t}) = p_i^t(d) = y_i^t + { (w_i^t)^\top d + d^\top Q_i^t d,} \end{aligned}$$

where $w_i^t\in {\mathbb {R}}^T, (w_i^t)_j = 0$ for $j \ge t$, and $Q_i^t\in {\mathbb {R}}^{T\times T}, Q_i^t = \text {diag }\left( \xi _{i1}^t, \, \xi _{i2}^t, \, \dots \, , \xi _{i(t-1)}^t, \, 0,\right.$   $\left. \dots \, , 0\right)$ (in order to maintain dependency on only $d_1,\dots ,d_{t-1}$) . Problem $(IP-ARO)$ can then be written in the form

$$\begin{aligned}&(IP-QDR) \min _{\begin{array}{c} y_i^t\in {\mathbb {R}},\, w_i^t\in {\mathbb {R}}^T \\ Q_i^t\in {\mathbb {R}}^{T\times T},\, F \end{array}} F \\&\quad \text {subject to } aF + B\left( \begin{bmatrix} y_1^1 \\ \vdots \\ y_I^T \end{bmatrix} + \begin{bmatrix} (w_1^1)^\top \\ \vdots \\ (w_I^T)^\top \end{bmatrix}d + \begin{bmatrix} d^\top Q_1^1 d \\ \vdots \\ d^\top Q_I^T d\end{bmatrix} \right) \le g_0 + Gd,\quad { \forall d\in {\mathcal {D}},} \end{aligned}$$

where F is introduced as an auxiliary (here-and-now) variable as in Theorem 3.1, $a\in {\mathbb {R}}^{2IT+2T+I+1}$ is fixed, $B\in {\mathbb {R}}^{(2IT+2T+I+1)\times IT}$ is fixed recourse, $g_0\in {\mathbb {R}}^{2IT+2T+I+1}$, $G\in {\mathbb {R}}^{(2IT+2T+I+1)\times T}$, and $w_i^t$ and $Q_i^t$ are constrained as above. For details see Appendix.

We can now apply Theorem 3.1 to $(IP-QDR)$ and obtain its solution by solving an SDP (see Appendix for the formulation). Note that $(IP-QDR)$ cannot be solved by a standard LP as in [4] since we now have quadratic terms in d.

Data Sets We use the same dataset as in the illustrative example in [4], as well as two other values of I (with appropriate generalisations). We will solve $(IP-QDR)$, and compare the realised cost to that generated by both the single-stage robust optimisation formulation (as in Corollary 3.3), the adjustable ADR cost (as in [4]), and the ideal solution to (IP).

For I factories, $I=3, 5, 10$, producing a seasonal product over a period 48 weeks, let decisions be made fortnightly (that is, $T=24$). Suppose the nominal demand is seasonal, taking the form

$$\begin{aligned} d_t^* = 1000\left( 1+\frac{1}{2}\sin \left( \frac{\pi (t-1)}{12}\right) \right) ,\quad t=1,\dots ,24 \end{aligned}$$

and likewise, production costs (see Fig. 1) are of the form

$$\begin{aligned}&c_i^t = \alpha _i\left( 1+\frac{1}{2}\sin \left( \frac{\pi (t-1)}{12}\right) \right) ,\quad t=1,\dots , { 24,} \\&\alpha _i = 1 + \frac{i-1}{I-1}, \ i=1,\dots ,{I}. \end{aligned}$$

Also let the maximal production capacity of each factory at each period be $P_i^t = 567$ units, and the cumulative production capacity of each factory be $\kappa _i = 13{,}600$. Finally, the inventory at the warehouse must be between 500 and 2000 units (inclusive) at all times.

Fig. 1

Production costs: $I=3$

Fig. 2

A sample demand trajectory (red) and the nominal demand trajectory (solid), enclosed within a “demand tube” (dashed): nominal demand $\pm \, 20\%$ ($\delta = 0.2$)

Experimental Results We consider three policies to compute a solution to the problem: the QDR policy (outlined above); an affine decision rule (ADR) policy, solved as a conic program via the reformulations obtained in [4]; and the single-stage solution, that is, $p_i^t(d) = p_i^t$ constant. There are 4 experiments performed, for uncertainty set ${\mathcal {D}} = \prod _{i=1}^{T}{[(1-\delta )d_t^*, (1+\delta )d_t^*]}$ and different uncertainty levels $\delta = 10\%,\, 7.5\%,\, 5\%,\, 2.5\%$. For each $\delta$ we generate 500 instances of our uncertain demand (500 simulated demand trajectories, see Fig. 2) and use these to compute the average costs for each policy, as well as the average price of robustness (in comparison to the ideal solution); that is, for each simulated demand trajectory we calculate the price of robustness as

$$\begin{aligned} { \frac{c_1 - c_2}{c_2},} \end{aligned}$$

where $c_1$ is the realised cost for the policy, and $c_2$ is the ideal cost.

All our programs were solved using the MOSEK toolbox (see, e.g. [20]), handled through the YALMIP interface [18]. All computations were performed on a machine equipped with 2.6GHz Intel(R) Core(TM) i7-9750H, 32GB of DDR4 RAM, and MATLAB R2019b.

Numerical Results

Table 1 presents average policy costs and performances across different uncertainty levels and number of factories. Columns are interpreted as follows: Policy Mean, the average cost over all 500 simulations, per policy, per instance; P.O.R., the average price of robustness over all 500 simulations. The Ideal Mean, listed in the 6th column, is the lowest possible achievable cost.

Table 1 Average policy costs and performances across different uncertainty levels and number of factories

As expected, the higher the level of uncertainty ($\delta$), the higher the price of robustness, across all policies. However, it is clear that our adjustable QDR policy well outperforms the classic static approach, since the static problem is not even feasible for $\delta$ greater than 2.5%. It is also consistently better than the adjustable ADR policy, which is to be expected (since the QDR is a generalisation of the ADR). Further, the price of robustness for our QDR policy is reasonably low relative to the uncertainty itself: beginning at approximately 3% for uncertainty 2.5%, and moving to approximately 10% for uncertainty 10%. The price of robustness tends to decrease as more factories are added to the network; this is in line with the decrease in overall cost. It seems also that the ADR approaches the performance of the QDR as I increases, suggesting that a QDR approach is preferred (when also considering computational effort) for smaller, more reasonable sized networks.

In Table 2 we present the problem sizes and computational times required for the different instances. Note that $\delta$ has no effect on problem size or computational time. The time reported (in seconds) is the average over all (four) problems solved for each instance, per policy.

Table 2 Problem instance sizes and the average time required to solve one such instance, for each policy

As demonstrated in Table 2, whilst the problem sizes grow linearly in I (this can be directly verified from the formulations also), they are non-trivial. This is particularly the case for the QDR, whose reformulation is considerably larger due to matrix variables and semidefinite constraints, and takes several minutes to solve. In comparison to the ideal solution, in which all demands are known exactly before making any decisions, the problem sizes and computational times for all robust methods are considerably larger, which is a by-product of robustness.

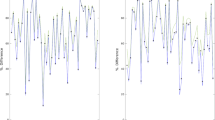
Figures 3, 4 and 5 below show the individual results, for $\delta =2.5\%$, over every (fifth) simulation, for each of the problem instances. We see, in fact, that the relationships from Table 2 do not just hold on average, but also consistently across every simulation; i.e. the QDR outperforms the ADR on every individual simulation.

Fig. 3

Price of robustness for all policies, for each of the 500 simulated demand trajectories, for uncertainty level $\delta = 2.5\%$ and $I=3$

Fig. 4

Price of robustness for all policies, for each of the 500 simulated demand trajectories, for uncertainty level $\delta = 2.5\%$ and $I=5$

Fig. 5

Price of robustness for all policies, for each of the 500 simulated demand trajectories, for uncertainty level $\delta = 2.5\%$ and $I=10$

Remark 4.1

We note that there are several means to deal with the multi-stage setting of the problem. In our approach, we have used a reduction to a two-stage problem by stacking each of our time-dependent adjustable decisions into a single vector, which is solved for simultaneously. An alternative method, as used in [4] would be to solve the problem by some iterative algorithm (for example, a rolling horizon approach), where decisions are made in stages, each incorporating the revealed information and optimal solution of the previous time step. This approach can result in better optimal solutions (compare, e.g. Table 1 for $I=3$ with [4, Table 1]), but takes considerably longer to solve, as a problem instance must be solved at each time step.

We also note that similar numerical experiments on inventory-production management were performed in [1] where only a single factory was considered in comparison to our multi-factory model. It is therefore difficult to draw comparisons of the performance of our QDR method against the piecewise linear functions method SDP-RC presented in [1]. However, in comparison to the AARC method (the same as what we have labelled the ADR method), our QDR and the SDP-RC have similar performances and are both solved by an SDP. Moreover, our method is capable of solving problems with $T\ge 24$ and $I=10$, whilst the SDP-RC solves problems with $T=10$ and $I=1$.

5 Conclusion and further work

In this paper by establishing a sum-of-squares representation for the non-negativity of a separable non-convex quadratic function over box constraints, we were able to prove that an adjustable robust linear program with a separable quadratic decision rule admits an equivalent semi-definite program reformulation. Our result also showed how an adjustable robust solution to such a program can be found by simply solving an equivalent semidefinite program. We illustrated our reformulation scheme via numerical experiments by applying it to an inventory-production management problem with the demand uncertainty. They showed that our QDR approach to two-stage decision-making performs better than the single-stage approach and is capable of solving the inventory production problem with a greater degree of uncertainty in the demand.

Our approach may be extended to study adjustable robust linear programs over box data uncertainty sets under a more general separable polynomial decision rule and will be investigated in a further study together with applications to two-stage decision-making problems, such us the lot-sizing problems with demand uncertainty.

Appendix: Exact reformulations for the inventory production problem

Standard Formulation In order to transform the problem (IP) into a standard matrix form, we further define:

$$\begin{aligned} p^t = \begin{bmatrix} p_1^t \\ \vdots \\ p_I^t \end{bmatrix},\quad p = \begin{bmatrix} p^1 \\ \vdots \\ p^T\end{bmatrix},\quad c^t = \begin{bmatrix} c_1^t \\ \vdots \\ c_I^t \end{bmatrix},\quad c = \begin{bmatrix} c^1 \\ \vdots \\ c^T \end{bmatrix}, \quad P^t = \begin{bmatrix} P_1^t \\ \vdots \\ P_I^t \end{bmatrix}, \quad P = \begin{bmatrix} P^1 \\ \vdots \\ P^T\end{bmatrix}, \quad { \kappa = \begin{bmatrix} \kappa _1 \\ \vdots \\ \kappa _I \end{bmatrix}.} \end{aligned}$$

After also introducing the auxiliary (here-and-now) variable F as per the methodology in the proof of Theorem 3.1, (IP) is equivalently rewritten as

$$\begin{aligned}&(IP) \min _{p,\,F} F \\&\quad \text {subject to } -F + c^\top p \le { 0,} \\&\quad -p \le { 0_{IT},} \\&\quad p {\le P,} \\&\quad \left( {\mathbf {1}}_T^\top \otimes \text {Id }_I\right) p \le {\kappa ,} \\&\quad \begin{bmatrix} {\mathbf {1}}_{It} \\ {0_{I(T-t)}}\end{bmatrix}^\top p \le V_{\text {max }} - v_0 + \begin{bmatrix} {\mathbf {1}}_t \\ {0_{T-t}} \end{bmatrix}^\top d,\quad t = 1,\dots ,{T,} \\&\quad -\begin{bmatrix} {\mathbf {1}}_{It} \\ { 0_{I(T-t)}}\end{bmatrix}^\top p \le -V_{\text {min }} + v_0 - \begin{bmatrix} {\mathbf {1}}_t \\ { 0_{T-t}} \end{bmatrix}^\top d,\quad t = 1,\dots ,{ T,} \end{aligned}$$

or in a standard form,

$$\begin{aligned}&(IP) \min _{p,\, F} F\\&\quad \text {subject to } aF + Bp \le g_0 + { Gd,} \end{aligned}$$

where

$$\begin{aligned} a&= \begin{bmatrix} -1 \\ { 0_{2IT + 2T + I}}\end{bmatrix}\in {\mathbb {R}}^{2IT + 2T + I + 1},&B = \begin{bmatrix} c^\top \\ -\text {Id }_{IT} \\ \text {Id }_{IT} \\ {\mathbf {1}}_T^\top \otimes \text {Id }_I \\ ({\mathbf {1}}_{T\times T})_{\nabla }\otimes {\mathbf {1}}_I^\top \\ -({\mathbf {1}}_{T\times T})_{\nabla }\otimes {\mathbf {1}}_I^\top \end{bmatrix}\in {\mathbb {R}}^{(2IT + 2T + I + 1)\times T}{,} \\ g_0&= \begin{bmatrix} { 0_{IT + 1}} \\ P \\ \kappa \\ {\mathbf {1}}_T(V_{\text {max }}-v_0) \\ -{\mathbf {1}}_T(V_{\text {min }}-v_0)\end{bmatrix}\in {\mathbb {R}}^{2IT + 2T + I 1},&G = \begin{bmatrix} { 0_{(2IT + I + 1)\times T}} \\ ({\mathbf {1}}_{T\times T})_\nabla \\ -({\mathbf {1}}_{T\times T})_\nabla \end{bmatrix}\in {\mathbb {R}}^{(2IT + 2T + I + 1)\times T}{,} \end{aligned}$$

where $\text {Id }_n$ is the $n\times n$ identity matrix, $\otimes$ refers to the Kronecker product, and $M_\nabla$ is the lower triangular part of matrix M.

Recall we wish to solve $(IP-ARO)$ via a separable QDR of the form

$$\begin{aligned} p_i^t(d_{{\mathcal {I}}_t}) = p_i^t(d) = y_i^t + (w_i^t)^\top d + { d^\top Q_i^t d,} \end{aligned}$$

where $w_i^t\in {\mathbb {R}}^T, (w_i^t)_j = 0$ for $j \ge t$, and $Q_i^t\in {\mathbb {R}}^{T\times T}, Q_i^t = \text {diag }( \xi _{i1}^t, \, \xi _{i2}^t, \, \dots \, , \xi _{i(t-1)}^t,$ $\, 0, \, \dots \, , 0 )$. Let

$$\begin{aligned} y^t = \begin{bmatrix} y_1^t \\ \vdots \\ y_I^t\end{bmatrix},\quad y = \begin{bmatrix} y^1 \\ \vdots \\ y^T \end{bmatrix}, \quad W^t = \begin{bmatrix} (w_1^t)^\top \\ \vdots \\ (w_I^t)\top \end{bmatrix},\quad {W = \begin{bmatrix} W^1 \\ \vdots \\ W^T \end{bmatrix}.} \end{aligned}$$

Then $(IP-QDR)$ can be written as

$$\begin{aligned}&(IP-QDR) \min _{\begin{array}{c} y\in {\mathbb {R}}^{IT},\, W\in {\mathbb {R}}^{IT\times T} \\ Q_r\in {\mathbb {R}}^{T\times T},\, F\in {\mathbb {R}} \end{array}} F \\&\quad \text {subject to } aF + B\left( y + Wd + \begin{bmatrix} d^\top Q_1 d \\ \vdots \\ d^\top Q_{IT} d\end{bmatrix} \right) \le g_0 + Gd,\quad \forall { d\in {\mathcal {D}},} \end{aligned}$$

where $W_{ij} = 0$ for $j\ge \lceil \frac{i}{I}\rceil$, $Q_{r} = Q_i^t$ for $r = I(t-1)+i$ and $Q_r = \text {diag }(\xi _r^{(1)},\dots ,\xi _r^{(t-1)},0,\dots ,0)$. The problem is now in a standard form. Notice that the coefficient matrix of the here-and-now variable F is also fixed, and has no affine dependence on the uncertainty d.

Exact SDP Reformulation Applying Theorem 3.1 to $(IP-QDR)$ we find that the exact SDP reformulation is

$$\begin{aligned}&(IP-SDP) \\&\quad \min _{\begin{array}{c} F\in {\mathbb {R}},\,\lambda _t^i\in {\mathbb {R}}, \\ y\in {\mathbb {R}}^{IT},\, W\in {\mathbb {R}}^{IT\times T} \\ Q_r\in {\mathbb {R}}^{T\times T},\, M^{i,t}\in {\mathbb {S}}^{3\times 3} \end{array}} F \\&\quad \text {subject to } M^{i,t} = \begin{bmatrix} M^{i,t}_{1,1} &{}\quad M^{i,t}_{1,2} &{}\quad M^{i,t}_{1,3} \\ M^{i,t}_{1,2} &{}\quad M^{i,t}_{2,2} &{}\quad M^{i,t}_{2,3} \\ M^{i,t}_{1,3} &{}\quad M^{i,t}_{2,3} &{}\quad M^{i,t}_{3,3} \end{bmatrix} \succeq 0,\\&\quad M^{i,t}_{1,1} = \lambda _t^i - (1-\delta )\left( W^\top b_i - g_i\right) _t d_t^* - { \sum _{r=1}^{IT}{(b_i)_r \xi _r^{(t)}\left( (1-\delta )d_t^*\right) ^2},} \\&\quad { M^{i,t}_{1,2} = 0,} \\&\quad 2M^{i,t}_{1,3} + M^{i,t}_{2,2}= 2\lambda _t^i - 2d_t^*\left( W^\top b_i - g_i\right) _t - 2\sum _{r=1}^{IT}{(b_i)_r \xi _r^{(t)}(1-\delta )(1+\delta ){d_t^*}^2}{,} \\&\quad { M^{i,t}_{2,3} = 0,} \\&M^{i,t}_{3,3} = \lambda _t^i - (1+\delta )\left( W^\top b_i - g_i\right) _td_t^* - \sum _{r=1}^{IT}{(b_i)_r\xi _r^{(t)}\left( (1+\delta )d_t^*\right) ^2}{,} \\&\quad \sum _{t=1}^{T}{\lambda _t^i} \le - \left( a_i F + b_i^\top y - (g_0)_i\right) {,} \\&\quad \text {for } i = 1,\dots ,m\quad { t = 1,\dots ,T.} \end{aligned}$$