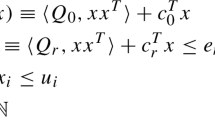An interval branch and bound method for global Robust optimization

Abstract

In this paper, we design a Branch and Bound algorithm based on interval arithmetic to address nonconvex robust optimization problems. This algorithm provides the exact global solution of such difficult problems arising in many real life applications. A code was developed in MatLab and was used to solve some robust nonconvex problems with few variables. This first numerical study shows the interest of this approach providing the global solution of such difficult robust nonconvex optimization problems.

1 Introduction

Robust optimization studies optimization problems in which uncertainty involving the objective function or the feasible set is not negligible. See [7, 8] for recent references containing an updated review of models, algorithmic tools and fields of applications.

While most papers in the literature on robust optimization address the fully convex case, [1, 2], some efforts have been made to cope with the more realistic situations in which nonconvexities appear. For instance, [22] addresses nonconvex problems, for which a first-order approximate robust model is proposed, and thus applicable when a good approximation of the uncertain parameters are known. Robust local-search procedures for problems in which the objective may be evaluated via simulations are described in [5, 6].

In this paper, we develop a new algorithm based on a Branch and Bound scheme to provide the global solution of a broad class of robust nonconvex problems. Some properties are first studied, and the algorithm is then provided, describing how lower and upper bounds are obtained to make the procedure converge. Examples validate our approach by solving difficult robust nonlinear and nonconvex optimization problems.

2 Problem statement

Given a function $f:I\!\! R^n\longrightarrow I\!\! R$ and also a box $\tilde{X}\subseteq I\!\! R^n$, consider the nominal problem of optimizing f over $\tilde{X}$ as

$$\begin{aligned} \min _{x \in \tilde{X}} f(x) \end{aligned}$$

(1)

The robust counterpart of (1) is obtained when each solution $x \in \tilde{X}$ is perturbed by a vector $y \in \tilde{Y}$ (a box in $I\!\! R^n$) and a worst-case analysis is performed. This leads us to the following optimization problem:

$$\begin{aligned} \min _{x \in \tilde{X}} \max _{y \in \tilde{Y}} f(x+y) \end{aligned}$$

(2)

The set $\tilde{Y}$ of perturbations, called the uncertainty set, is assumed here to be a box in $I\!\! R^n$ (compare e.g. with [5, 6], in which a Euclidean ball is used as uncertainty set), and f is assumed to be continuous on $\tilde{X}+\tilde{Y}.$

Defining $z\!: \tilde{X} \longrightarrow I\!\! R$ as

$$\begin{aligned} z(x) = \max _{y \in \tilde{Y}} f(x+y), \end{aligned}$$

(3)

we rewrite our problem as:

$$\begin{aligned} \min _{x \in \tilde{X}} z(x) \end{aligned}$$

(4)

The interpretation of Problem (4) is natural: one wants to optimize the nominal function f,  but taking into account that, once a solution $x \in \tilde{X}$ is chosen, the solution actually implemented will be of the form $x+y$ for some errors $y\in \tilde{Y}.$ This may have a non-negligible impact on the optimal decision either when the nominal function f varies very rapidly around x or when the uncertainty set $\tilde{Y}$ is large. The reader is referred to e.g. [5, 6] for real-world applications.

We illustrate the approach in Example 1.

Example 1

Let $x\in [-0.2,3]$, f and z are:

$$\begin{aligned}&\qquad \qquad f(x)=((x-2)^6+0.2)\times (\log (1+x^2))\\&z(x) = \max _{y \in \tilde{Y}=[-0.1,0.1]} (((x+y)-2)^6+0.2)\times (\log (1+(x+y)^2)) \end{aligned}$$

The global solution of f in $[-0.2,3]$ without uncertainty, i.e. $\tilde{Y}=[0,0]$ is 0, providing a value of 0. However, if we consider a non-degenerate uncertainty interval $\tilde{Y}$, we may obtain a different optimal solution for the perturbed problem. Indeed, taking $\tilde{Y}=[-0.1,0.1]$, the global solution is around 1.52 with an optimal value around 0.26. Both functions f and z for this case are plotted in Fig. 1.

Fig. 1

Functions f and z. Global minimum and robust global minimum

When f is convex, local search techniques are sufficient to address Problem (4). Indeed, one has the following result:

Proposition 1

If f is convex on $\tilde{X}+\tilde{Y},$ then z is convex on $\tilde{X},$ and thus any local minimum of Problem (4) is a global one.

Proof

For all $\alpha \in [0,1]$ and for all $(u,v)\in \tilde{X}$, one has:

$$\begin{aligned} z(\alpha u+(1-\alpha )v)= & {} \max _{y\in \tilde{Y}} f(\alpha u+(1-\alpha )v+y)\\= & {} \max _{y\in \tilde{Y}} f(\alpha u+(1-\alpha )v+\alpha y+(1-\alpha ) y)\\= & {} \max _{y\in \tilde{Y}} f(\alpha (u+y)+(1-\alpha ) (v+y))\\\le & {} \max _{y\in \tilde{Y}} \alpha f(u+y)+(1-\alpha )f(v+y)\\\le & {} \alpha \max _{y\in \tilde{Y}} f(u+y)+ (1-\alpha ) \max _{y\in \tilde{Y}} f(v+y) = \alpha z(u)+(1-\alpha ) z(v). \end{aligned}$$

Hence, z is convex on $\tilde{X}$ and it is quite straightforward because z is a $\max$ function which is a convex function. $\square$

When f is not convex, solving the non-convex optimization Problem (4) is challenging, since we want to optimize an objective function z whose evaluation calls for solving a global optimization problem, as given by (3). [3] proposes a simulated annealing algorithm, [6] uses a local-search, and [12, 13] give global optimization approaches valid for polynomial functions f. Our aim is to design a Branch and Bound algorithm that converges to an optimal solution for arbitrary differentiable functions f. In the next section, some properties on Problem (4) are derived. These properties will be necessary to provide routines for the computations of the bounds and also for the design of the monotonicity tests required by our methodology.

3 Properties

Here, we are interested in the nonconvex case, for which global optimization tools are needed. In particular, a spatial branch and bound algorithm is proposed to find a global solution of Problem (4). The algorithm is based on Interval Arithmetic, [9, 10, 15,16,17, 19].

We assume in what follows that an inclusion function F is available for f; i.e. $[\min _{x\in X}f(x),\max _{x\in X}f(x)]\subseteq F(X):=[\underline{F(X)},\overline{F(X)}]$, for all box X. For any box $I \subset \tilde{X}+\tilde{Y},$ let $\overline{F(I)}$ (respectively $\underline{F(I)}$) denote the upper bound (respectively the lower bound) of the interval F(I).

Lower and upper bounds of $\min _{x \in X} z(x)$ are easily obtained from the inclusion function F,  as shown in the following two propositions.

Proposition 2

Given the box $X \subset \tilde{X},$ one has

$$\begin{aligned} \min _{x \in X} z(x) \ge \underline{F(X+y^*)} \qquad \forall y^* \in \tilde{Y}. \end{aligned}$$

(5)

Proof

One has: $\min _{x \in X} z(x)=\min _{x \in X} \max _{y \in \tilde{Y}} f(x+y)\ge \min _{x \in X} f(x+y^*)$, for all $y^*\in \tilde{Y}$, and then the result follows using the properties of interval inclusion functions $\min _{x \in X} f(x+y^*)\ge \underline{F(X+y^*)}$, for all $y^*\in \tilde{Y}$. $\square$

Proposition 3

Given the box $X \subset \tilde{X},$ suppose $Y^1,\ldots ,Y^k \subset \tilde{Y}$ are boxes known to satisfy

$$\begin{aligned} z(x) = \max _{y \in \bigcup _{j=1}^k Y^j} f(x+y) \qquad \forall x \in X. \end{aligned}$$

Then

$$\begin{aligned} \min _{x \in X} z(x) \le \max _{1\le j \le k} \overline{F(x^*+Y^j)} \qquad \forall x^*\in X \end{aligned}$$

Proof

For $x^* \in X$ given, one has

$$\begin{aligned} \min _{x \in X} z(x)\le & {} z(x^*) \\= & {} \max _{y \in \bigcup _{j=1}^k Y^j} f(x^*+y) \\\in & {} \bigcup _{1 \le j \le k} F(x^*+Y^j). \end{aligned}$$

Hence,

$$\begin{aligned} \min _{x \in X} z(x) \le \max _{1 \le j \le k} \overline{F(x^*+Y^j)}. \end{aligned}$$

$\square$

Proposition 4

Given boxes $X \subset \tilde{X},$ $Y \subset \tilde{Y},$ if $\overline{F(X+Y)} < \underline{F(X + y_0)}$ for some $y_0 \in \tilde{Y}\setminus Y$, then

$$\begin{aligned} f(x+y) < z(x) \qquad \forall (x,y) \in X\times Y. \end{aligned}$$

In other words, the box Y is useless in order to compute z at points in the box X,  and can thus be eliminated from the list of boxes to be inspected.

Proof

First one has, $f(x+y)\le \overline{F(X+Y)}, \forall (x,y) \in X\times Y$. By using the assumption of the proposition, $\overline{F(X+Y)} < \underline{F(X + y_0)}, \forall y_0\in Y$ one obtains:

$$\begin{aligned} f(x+y)\le \overline{F(X+Y)} < \underline{F(X + y_0)}, \forall (x,y,y_0)\in X\times Y^2. \end{aligned}$$

By using Proposition 2, on has $\underline{F(X + y_0)}\le \min _{x \in X} z(x), \forall y_0\in Y$, and the result follows.$\square$

Proposition 5

Let f be differentiable in $\tilde{X}+\tilde{Y},$ and let $F'_j$ denote an inclusion function for its partial derivative with respect to the j-th coordinate; i.e., $\frac{\partial f}{\partial x_j}(x)\in F'_j(X)$, for all box X and $x\in X$. Given boxes $X \subset \tilde{X},$ $Y \subset \tilde{Y}$, suppose $x^* \in X$ and $y^* \in Y$ exist such that $x^*$ is an optimal solution to Problem (4) and $z(x^*) = f(x^* + y^*).$ If $\overline{F'_j(X+Y) }< 0$, then one has

$$\begin{aligned}&\underline{Y} = \underline{\tilde{Y}} \end{aligned}$$

(6)

$$\begin{aligned}&\underline{X} = \underline{\tilde{X}} \end{aligned}$$

(7)

Proof

We have by assumption that $f'_j(x^*+y^*) < 0,$ and then, the function $t \, \longmapsto f(x^*+y^* + t e_j)$ is decreasing in a neighborhood of 0,  where $e_j$ denotes the vector with 1 in its j-th coordinate and zero elsewhere. This implies that $f(x^*+y^* - t e_j) > f(x^* + y^*) = z(x^*)$ for some t close to 0. Hence, no such $t>0$ makes $y^* -t e_j \in \tilde{Y},$ which implies condition (6), and no such $t>0$ makes $x^*-te_j \in \tilde{X},$ which implies condition (7).$\square$

In the same way one obtains the counterpart for $\underline{F'_j(X+Y)}$ as follows:

Proposition 6

Let f be differentiable in $\tilde{X}+\tilde{Y},$ and let $F'_j$ denote an inclusion function for its partial derivative with respect to the j-th coordinate. Given boxes $X \subset \tilde{X},$ $Y\subset \tilde{Y}$. Suppose $x^* \in X$ and $y^* \in Y$ exist such that $x^*$ is an optimal solution to Problem (4) and $z(x^*) = f(x^* + y^*).$ If $\underline{F'_j(X+Y)} > 0,$ then one has

$$\begin{aligned}&\overline{Y} = \overline{\tilde{Y}} \end{aligned}$$

(8)

$$\begin{aligned}&\overline{X} = \overline{\tilde{X}} \end{aligned}$$

(9)

Propositions 5 and 6 are keys for the following test: Given the pair (X, Y),  if $\overline{F_j'(X+Y)} <0$, then the pair $(X,Y) = (\prod _{k=1}^n X_k ,\prod _{k=1}^n Y_k)$ can be replaced in the list by the degenerate pair $(\prod _{k=1}^n X^*_k ,\prod _{k=1}^n Y^*_k),$ with

$$\begin{aligned} \begin{array}{ll} X^*_k = \left\{ \begin{array}{ll} X_k, &{} \text {if }k \ne j\\ \overline{\tilde{X_j}}, &{} \text {if }k = j \end{array} \right. &{} Y^*_k = \left\{ \begin{array}{ll} Y_k, &{} \text {if }k \ne j \\ \overline{\tilde{Y_j}}, &{} \text {if }k = j \end{array} \right. \end{array} \end{aligned}$$

if $\overline{\tilde{X_j}} = \overline{X_j}$ and if $\overline{\tilde{Y_j}} = \overline{Y_j}$, and otherwise the pair (X, Y) can be eliminated from further consideration, since it is then known that either Y is useless to evaluate z at points in $x \in X,$ or points in X cannot be optimal for Problem (4). Similarly, if $\underline{F_j'(X+Y)} >0,$ then the j-th component of (X, Y) can be replaced by the degenerate interval consisting of the lower bounds, or eliminated.

When a box X is small enough, it can be replaced by its midpoint, since z cannot vary too much inside X. This is formalized in Proposition 7.

Proposition 7

Given the box $X= \prod _{j=1}^n X_j \subset \tilde{X},$ suppose $Y^1,\ldots ,Y^k \subset \tilde{Y}$ are boxes known to satisfy

$$\begin{aligned} z(x) = \max _{y \in \bigcup _{j=1}^k Y^j} f(x+y) \qquad \forall x \in X. \end{aligned}$$

Let $x_m$ denote the midpoint of X and, for $i=1,2,\ldots , k,$ let $y_m^i$ denote the midpoint of the box $Y^i.$ Suppose f be differentiable in $\tilde{X}+\tilde{Y},$ and let $F'_j$ denote an inclusion function for its partial derivative with respect to the j-th coordinate. For $i = 1,\ldots , k,$ define $\varepsilon ^i$ as

$$\begin{aligned} \varepsilon ^i = \max \left\{ \sum _{j=1}^n \overline{|F'_j(X+y_m^i)|}\times \overline{|(x_{m})_j - X_j|}, \sum _{j=1}^n \overline{|F'_j(x_m+Y^i)|}\times \overline{|(y_{m}^i)_j - Y_j^i|} \right\} . \end{aligned}$$

Then

$$\begin{aligned} \left| \max _{1 \le i \le k} f(x_m +y_m^i) - \min _{x \in X } z(x)\right| \le \max _{1 \le i \le k} \varepsilon ^i. \end{aligned}$$

(10)

Proof

Let $x^* \in \arg \min _{x \in X} z(x),$ and let $i^* \in \{1,2,\ldots ,k\}$ be such that

$$\begin{aligned} \max _{1 \le i \le k} f(x_m + y_m^i) = f(x_m + y_m^{i^*}). \end{aligned}$$

One has

$$\begin{aligned} \max _{1 \le i \le k} f(x_m + y_m^i) - \min _{x \in X} z(x)= & {} \max _{1 \le i \le k} f(x_m + y_m^i) - z(x^*)\\\le & {} f(x_m + y_m^{i^*}) - f(x^*+y_m^{i^*}) \\= & {} \sum _{j=1}^n f'_j(\xi +y_m^{i^*}) ((x_m)_j -x^*_j) \end{aligned}$$

for some $\xi$ in the segment with endpoints $x_m,x^* \in X.$ Hence,

$$\begin{aligned} \max _{1 \le i \le k} f(x_m + y_m^i) - \min _{x \in X} z(x)\le & {} \sum _{j=1}^n \overline{|F'_j(X+y_m^{i^*})|}\times \overline{|(x_m)_j -x^*_j|} \le \varepsilon ^{i^*} \\\le & {} \max _{1 \le i \le k} \varepsilon ^i. \end{aligned}$$

Now, let $i^* \in \{1,\ldots ,k\}$ and let $y^* \in Y^{i^*}$ be such that $z(x_m) = f(x_m+y^*).$

$$\begin{aligned} \min _{x \in X} z(x) - \max _{1 \le i \le k} f(x_m + y_{m}^i)\le & {} z(x_m) - \max _{1 \le i \le k} f(x_m + y_{m}^i) \\\le & {} f(x_m + y^*) - f(x_m+ y_m^{i^*}) \\= & {} \sum _{j=1}^n f'_j(x_m+\xi ) (y^*_j - (y_m^{i^*})_j) \end{aligned}$$

for some $\xi$ in the segment with endpoints $y^*, y_m^{i^*} \in X.$ Hence,

$$\begin{aligned} \left| \max _{1 \le i \le k} f(x_m + y_m^i) - \min _{x \in X} z(x) \right|\le & {} \sum _{j=1}^n \overline{|F'_j(x_m+Y^{i^*})|}\times \overline{|Y^{i^*}_j -(y_m^{i^*})_j|} \le \varepsilon ^{i^*} \\\le & {} \max _{1 \le i \le k} \varepsilon ^i. \end{aligned}$$

$\square$

Corollary 1

Given the box $X= \prod _{j=1}^n X_j \subset \tilde{X},$ suppose $Y^1,\ldots ,Y^k \subset \tilde{Y}$ are boxes known to satisfy

$$\begin{aligned} z(x) = \max _{y \in \bigcup _{j=1}^k Y^j} f(x+y) \qquad \forall x \in X. \end{aligned}$$

Let $x_m$ denote the midpoint of X and, for $i=1,2,\ldots , k,$ let $y_m^i$ denote the midpoint of the box $Y^i.$ Suppose f be differentiable in $\tilde{X}+\tilde{Y}$, we obtain:

$$\begin{aligned} \left| \max _{1 \le i \le k} f(x_m +y_m^i) - \min _{x \in X } z(x)\right| \le \frac{n}{2}L\times W, \end{aligned}$$

(11)

where $L=\max _{i,j} \overline{|F'_j(X+Y^i)|}$ and $W=\max \{w(X),w(Y^1),\ldots , w(Y^k)\}$; we use the notation $w([a,b])=b-a$ and $w(X)=\max _{1\le i\le n} w(X_i)$.

Proof

From Proposition 7, one has:

$$\begin{aligned} \left| \max _{1 \le i \le k} f(x_m +y_m^i) - \min _{x \in X } z(x)\right| \le \max _{1 \le i \le k} \varepsilon ^i, \end{aligned}$$

with

$$\begin{aligned} \varepsilon ^i = \max \left\{ \sum _{j=1}^n \overline{|F'_j(X+y_m^i)|}\times \overline{|(x_{m})_j - X_j|}, \sum _{j=1}^n \overline{|F'_j(x_m+Y^i)|}\times \overline{|(y_{m}^i)_j - Y_j^i|} \right\} . \end{aligned}$$

In what follows, index i is in $\{1,\ldots ,k\}$ and index j is in $\{1,\ldots ,n\}$.

Hence, remark that we have: $|(x_{m})_j - X_j|=\frac{w(X_j)}{2}\le \frac{w(X)}{2}\le \frac{W}{2}$ and in a similar way, $|(y_{m}^i)_j - Y^i_j|=\frac{w(Y^i_j)}{2}\le \frac{w(X)}{2} \le \frac{W}{2}$.

Moreover, one has $|F'_j(x_m+Y^i)|\le |F'_j(X+Y^i)|\le L$ and $|F'_j(X+y^i_m)|\le |F'_j(X+Y^i)|\le L$.

Therefore, one obtains:

$$\begin{aligned} \sum _{j=1}^n \overline{|F'_j(X+y_m^i)|}\times \overline{|(x_{m})_j - X_j|}\le nL\times \frac{W}{2}, \ \forall i\in \{1,\ldots ,k\} \end{aligned}$$

and

$$\begin{aligned} \sum _{j=1}^n \overline{|F'_j(x_m+Y^i)|}\times \overline{|(y_{m}^i)_j - Y_j^i|}\le nL\times \frac{W}{2}, \ \forall i\in \{1,\ldots ,k\} \end{aligned}$$

Hence, $\epsilon ^i\le nL\times \frac{W}{2}, \forall i\in \{1,\ldots ,k\}$ and thus the result follows.$\square$

Thus, in order to find the robust global minimum with an accuracy $\epsilon$, by using a Branch and Bound algorithm which will split boxes into sufficiently small ones X and $Y^i (\forall i)$ such that $W\le \frac{2\epsilon }{nL}$ and by using Corollary 1 (with f differentiable), we have:

$$\begin{aligned} \left| \max _{1 \le i \le k} f(x_m +y_m^i) - \min _{x \in X } z(x)\right| \le \frac{n}{2}L\times W\le \epsilon . \end{aligned}$$

(12)

Therefore, we have two possibilities:

• if $\max _{1 \le i \le k} f(x_m +y_m^i)>\tilde{f}$ (where $\tilde{f}$ is the best current upper bound of the robust global minimum known at this iteration of the Branch and Bound algorithm) then X and $Y^i (\forall i)$ is deleted,

• if $\max _{1 \le i \le k} f(x_m +y_m^i)\le \tilde{f}$ then $\tilde{f}$ changes and $X, Y^i (\forall i)$, or just $x_m, y_m^i(\forall i)$ are stored in a list of solutions.

Hence, if f is differentiable using Corollary 1, we show that a Branch and Bound algorithm will converge in a finite number of iterations to a robust global minimum with an accuracy $\epsilon$. Note that, this result of convergence can be extended when f is only Lipschitz.

4 A branch-and-bound algorithm for Robust optimization

Our deterministic robust global optimization algorithm is described in Algorithm 1. The main idea of this branch-and-bound code is to search the solution by bisecting the initial boxes $\tilde{X}$ and $\tilde{Y}$, and by managing a list whose the elements are: a box X, a list of boxes $Y^i$ and a list of points inside $\cup _i Y^i$. Hence, from the above properties, a Robust Interval Branch and Bound algorithm is provided. However, even if this algorithm is based on a standard interval branch-and-bound code, it differs in some points inside the main loop:

• An element of the list is constituted by: (i) a box X, which is an interval vector; (ii) a list of boxes $Y^i$; (iii) a list of points inside $\cup _i Y^i$; (iv) a lower bound of f over $X\times \left( \cup _i Y^i\right)$.

• The element Z of the list with the lowest lower bound is considered first.

• Bisection following a component of x: in Z, the box X is bisected by the middle of its largest edge. In both cases the same two lists of $Y^i$ and of points inside $\cup _i Y^i$ have to be kept.

• Bisection following a component of y: in Z, the largest box of boxes $Y^i$ (belonging to the list) is selected. If the length of its largest edge is large enough with respect to the width of X,  then such a box $Y^i$ is bisected by its largest edge. The midpoint of the two sub-boxes of $Y^i$ are inserted in the list of points inside $\cup _i Y^i$.

• Monotonicity test on y: For all sub-boxes $Y^i$ in the list associated to box X, check if in one direction on y, f(x, y) is monotone over the whole box X. If this is the case, remove $Y^i$ from the list corresponding to box X or reduce $Y^i$ to the side of the initial box ${\tilde{Y}}$. Moreover, if no sub-boxe $Y^i$ remains in the list, eliminate the box X of the main list. If the list of $Y^i$ has changed, then update the list of points associated to box X by inserting the new points generated as the mid-points of each new $Y^i$ and by discarding points belonging to removed boxes.

• Monotonicity test on the component of x: check the monotonicity if all the sub-boxes in the list of $Y^i$ are points.

• Lower and upper bound calculations: the computations of lower and upper bounds follow from Propositions 2 and 3 in Sect. 3.

Note that in Algorithm 1 the termination criterion is not directly provided by Proposition 7, but directly by using the differences between the upper and lower bounds (see line 5 of Algorithm 1). Note also that if the interval Taylor inclusion function at the first order (see [19]) is chosen, this provides a more accurate stopping criterion than using Proposition 7.

Concerning the convergence of Algorithm 1, note that during the iterations a box $X\subseteq \tilde{X}$ will be split into smaller sub-boxes: $X^i\subset X$ (see line 16 of Algorithm  1) and so, if we compute the lower bounds on the same point y, we have: $\underline{F(X+y)}\ge \underline{F(X^i+y)}, \forall i.$ This result comes from Proposition 2 and it is due to the isotonicity property¹ of interval arithmetic based inclusion functions, [9, 10, 16]. Hence, keeping the same points $y^j\in \tilde{Y}$ during the iterations of Algorithm 1, we obtain:

$$\begin{aligned} \max _j\underline{F(X+y^j)}\ge \max _j\underline{F(X^i+y^j)}, \forall i. \end{aligned}$$

Remark 1

During the iterations of Algorithm 1, by taking care to keep the same points $y^j\in \tilde{Y}$ (see list of points Z.lY in 1) and to delete points when they are not used to provide better lower bounds (see lines 11 and 32 of Algorithm 1), the lowest lower bound remaining in the list $\mathcal {L}$ will increase.

Moreover, the upper bound of the robust global minimum, denoted by $\tilde{f}$ in Algorithm 1, can only decrease during the iterations of Algorithm 1 (see line 41). This is also due to the isotonocity property of interval arithmetic based inclusion functions and derived from Proposition 3. Hence, during the iterations of Algorithm 1 the lowest lower bound will increase and the incumbent $\tilde{f}$ will decrease until a given tolerance $\epsilon$ is reached (see line 5). Note that if f is differentiable and if $\tilde{X}$ and $\tilde{Y}$ are split into sufficiently small sub-boxes, using Proposition 7 and Corollary 1 the branching can be stopped.

5 Some numerical examples

In order to illustrate and to validate Algorithm 1, which we have implemented in MatLab version R2017b using IntLab version 10 [20], we solved the following robust optimization problems on a MacBookPro laptop with 2.8GHz and 16GB. We choose the interval Taylor inclusion function at the first order (see [19]) to compute lower and upper bounds in Algorithm 1; the enclosure of the gradient is computed by using interval automatic differentiation implemented in IntLab. In Tables 1, 2, 3, the performance of Algorithm 1 is reported by considering as stopping criterion a gap $\epsilon$ equals to $10^{-3}$ or $10^{-10}$. In these three tables, the columns f, $\epsilon _Y$, $\epsilon$, # Its, Time(s), $f(x^*+y^*)$, $x^*$ and $f(x^*)$ are respectively the name of the function, the value of the uncertainty that defines $\tilde{Y}$, the accuracy for the stopping criterion at line 45 of Algorithm 1, the number of iterations, the CPU time in seconds, the maximal value of the function at a point around the robust global optimizer but in $x^*+\tilde{Y}$, a robust global optimizer, the value of the function at $x^*$. Note that all results are rounded to 4 decimal places.

The first instance we consider, is a generalization, to the $n-$dimensional case, of Example 1:

$$\begin{aligned} g_n(x) = \sum _{i=1}^n\left( (x_i)-2)^6+0.2\right) \log \left( 1+x_i^2\right) . \end{aligned}$$

The results are presented at the top of Table 1. For this function, the searched domain is $\tilde{X} = [-10,10]^n,$ and the uncertainty set is $\tilde{Y} = [-\epsilon _Y, \epsilon _Y]^n$ where $\epsilon _Y$ is defined in the second column of Table 1. This yields the following robust optimization problem:

$$\begin{aligned} \min _{x \in \tilde{X}} \max _{y \in \tilde{Y}} g_n(x+y)=\sum _{i=1}^n\left( (x_i+y_i)-2)^6+0.2\right) \log \left( 1+(x_i+y_i)^2\right) . \end{aligned}$$

(13)

The global minimizer of $g_n$ without uncertainty is $(0,\ldots ,0)$ providing an optimal value of 0. However, by considering the uncertainty set $\tilde{Y}=[-0.1, 0.1]^n$ in Problem (13), the robust global optimum is found to be around $(1.52, \ldots , 1.52)$ yielding an optimal value of $g_n$ around $n\times 0.25$ which corresponds to another local optimum analogous to Fig. 1. In Table 1, remark that for this function $g_n$, if $\epsilon _Y$ becomes 0.5 the solution changes slightly but the number of iterations and the CPU time increases quite strongly; it is also the case when the required accuracy (stopping criterion) changes from $10^{-3}$ to $10^{-10}$.

The remainder of Table 1 presents numerical results for functions coming from the global optimization literature, they are provided in [21] and are recalled below:

• Three Hump Camel Function: $f_1(x) = 2x_1^2-1.05x_1^4+\frac{x_1^6}{6}+x_1x_2+x_2^2$, where $x\in [-5,5]\times [-5,5]$. It has a global minimum $f(x^*)=0$ at $x^*=(0,0)$.

• Easom Function: $f_2(x) = -\cos (x_1)\cos (x_2)\exp (-(x_1-\pi )^2-(x_2-\pi )^2)$, where $x\in [-100,100]\times [-100,100]$. It has a global minimum $f(x^*)=-1$ at $x^*=(\pi ,\pi )$.

• Banana Rosenbrook Function: $f_3(x) = 100(x_2-x_1^2)^2+(x_1-1)^2$, where $x\in [-5,10]\times [-5,10]$. It has a global minimum $f(x^*)=0$ at $x^*=(1,1)$.

• Six Hump Camel Function: $f_4(x) = \left( 4-2.1x_1^2+\frac{x_1^4}{3}\right) x_1^2 + x_1x_2 + (-4+4x_2^2) x_2^2$, where $x\in [-3,3]\times [-2,2]$. It has two global minima $f(x^*)=-1.0316$ at $x^*=(0.898,-0.7126)$ and $(-0.898,0.7126)$.

• Dixon-Price Function: $f_5(x) = (x_1-1)^2 + 2(2x_2^2-x_1)^2$, where $x\in [-10,10]\times [-10,10]$. It has a global minimum $f(x^*)=0$ at $x^*=(1,\frac{\sqrt{2}}{2})$.

• Beale Function: $f_6(x) = (1.5 - x_1 + x_1x_2)^2 + (2.25 - x_1 + x_1x_2^2)^2 + (2.625 - x_1 + x_1x_2^3)^2$, where $x\in [-4.5,4.5]\times [-4.5,4.5]$. It has a global minimum $f(x^*)=0$ at $x^*=(3,0.5)$.

For these 6 functions, we change the uncertainty $\epsilon _Y$ to show the changes between an initial global solution and a new robust one. We remark that for the first two functions $f_1$ and $f_2$, the robust global solution remains close to the global one even if $\epsilon _Y$ is quite high (0.1 or 0.5). Contrarily, for the last four functions $f_3$ to $f_6$, the robust global solution switches to another point which is a new robust global minimum corresponding to a local minimum; it is emphasized in bold in Table 1. Note that obviously when $\epsilon _Y$ increases the values of $f(x^*+y^*)$ and $f(x^*)$ increase also. However, we remark that there is no link between the number of iterations and the fact that $\epsilon _Y$ increases.

Table 1 Numerical results for 8 classical functions

From these results, note that, as expected, the stopping criterion $\epsilon =10^{-3}$ is attained earlier than for $\epsilon =10^{-10}$. However, a high precision ($\epsilon =10^{-10}$) can be reached in a quite reasonable time. This seems to be due to the use of interval Taylor inclusion function to compute the lower and upper bounds.

A last example coming from the literature about robust optimization [3, 6, 13] is addressed:

$$\begin{aligned} f_B(x)= & {} x_1(6.2+x_1(-4.7+x_1(-6.4+x_1(21.2+x_1(-12.2+2x_1)))))\\&+ x_2(-10+x_2(56.9+x_2(-74.8+x_2(43.3+x_2(-11+x_2)))))\\&+ x_1x_2(-4.1-0.1x_2x_1+0.4x_2+0.4x_1) \end{aligned}$$

For this test function, the global optimizer of $f_B$ in $\tilde{X}$ is $x^*=(2.8152\ldots , 4.0090\ldots )$ with $f_B(x^*)=-20.8289\ldots$, see [3, 6, 13].

For this function, two search domains are taken into account $[-0.1,3]\times [0,4]$ and $[-1,5]^2$ yielding respectively Tables 2 and 3.

Nevertheless, Algorithm 1 cannot solve directly this problem; this is mainly due to the fact that the expression of $f_B$ owns a lot of occurrences of the variables $x_1$ and $x_2$. Thus, even if a Horner scheme is taken into account, the bounds computed using interval arithmetic are not efficient enough. In order to improve the efficiency of Algorithm 1, we introduce an accelerating routine based on a convexity test which is derived from Proposition 1. This convexity test routine is described as follows:

• 1. A convexity test of $f_B$ over an element Z of the list $\mathcal {L}$ is done at line 7of Algorithm 1(when the box Z.X is small enough, herein less than 0.01):

  • Compute H an enclosure of the Hessian matrix of $f_B$ over Z.X (here a formal expression is provided but interval automatic differentiation implemented in IntLab could be used).

  • If $\underline{(Z.X)^T.H.(Z.X)}>0$ then $f_B$ is strictly convex on Z.X.

  • For all $k\in \{1,\ldots ,n_Y\}$, compute $H_k$ an enclosure of the Hessian matrix of $f_B$ over $Z.X+Z.Y(k)$.

  • If $\underline{(Z.X+Z.Y(k))^T.H_k.(Z.X+Z.Y(k))}> 0$ for all $k\in \{1,\ldots ,n_Y\}$, then $f_B$ is strictly convex on all $Z.X+Z.Y(k)$

• 2. If $f_B$ is strictly convex on Z (i.e., $f_B$ strictly convex on Z.X and all $Z.X+Z.Y(k)$), then:

  • Solve using a local solver $x^*:=\arg \min _{x\in Z.X} f_B(x)$.

  • $v^*:=\arg \max _{v\in \cup _{k} V_k} f_B(x^*+v)$, where $V_k$ is the set of the 4 vertices of the box Z.Y(k), for all $k\in \{1,\ldots ,n_Y\}$.

  • $lb:=\min _{x\in Z.X} f_B(x+v^*).$

  • $ub:=f_B(x^*+v^*).$

In Step 2. of this routine, the minima are directly computed using a local solver (active-set algorithm of the MatLab fmincon subroutine). Because $f_B$ is proved to be strictly convex on Z.X, the local minima are the global ones. For the maximization of $f_B(x^*+v)$, because $f_B$ is stricly convex on $Z.X+Z.Y(k)$, the global maximum is a vertex of the box $Z.X+Z.Y(k)$. Note that from Propositions 2 and 3 and because $f_B$ is proved to be convex on Z, we have:

$$\begin{aligned} lb\le f(x+y)\le ub, \forall x\in Z.X \text { and } \forall y\in \cup _k Z.Y(k), \text { for all } k\in \{1,\ldots ,n_Y\}. \end{aligned}$$

If $lb=ub$, this implies that $x^*$ is the robust global solution of $f_B$ over Z and then the research is terminated for Z, else efficient lower and upper bounds of $f_B$ over Z are provided and used in lines 37 and 39 of Algorithm 1.

In order to make numerically reliable the bounds provided by this convexity test, Theorem 1 in [14] is used. Hence, Step 2 of the convexity test has to be modified as follows:

• Solve using a local solver $x^*:=\arg \min _{x\in Z.X} f_B(x)$.

  • For all $i\in \{1,\ldots n\}$, if $\underline{x_i^*}<\underline{Z.X_i}$ then $\underline{x_i^*}:=\underline{Z.X_i}$ and if $\overline{x_i^*}>\overline{Z.X_i}$ then $\overline{x_i^*}:=\overline{Z.X_i}$; note that it can occur because in MatLab the fmincon routine solves optimization problems with a tolerance about $10^{-6}$ on the constraints.

• $v^*:=\arg \max _{v\in \cup _{k} V_k} f_B(x^*+v)$, (no change)

• $xb:=\arg \min _{x\in Z.X} f_B(x+v^*)$

  • For all $i\in \{1,\ldots n\}$, if $\underline{xb_i}<\underline{Z.X_i}$ then $\underline{xb_i}:=\underline{Z.X_i}$ and if $\overline{xb_i}>\overline{Z.X_i}$ then $\overline{xb_i}:=\overline{Z.X_i}$

  • $G:=F_B^{\prime }(xb+v^*)$, where $F^\prime _B$ is the inclusion function of the first derivative of $f_B$. Note that to be reliable all the computations have to be done using rounded interval arithmetic, [16].

  • For all $i\in \{1,\ldots n\}$, if $\underline{G_i}>0$ then $z_i:=\underline{Z.X_i^*}$ and if $\overline{G_i}<0$ then $z_i:=\overline{Z.X_i^*}$. Moreover, if $0\in G$ then $z_i:=Z.X_i$.

  • $lb:=\underline{F_B(xb+v^*)+(z-xb)^T.G}$, see Theorem 1 in [14].

• $ub:=\overline{F_B(x^*+v^*)}.$

This reliable routine has been inserted after line 7 of Algorithm 1, and this makes it possible to solve the robust nonconvex Problem (2) with $f_B$ over $\tilde{X}$. The results are provided in Table 2 for $\tilde{X}=[-0.5,3]\times [0,4]$ and Table 3 for $\tilde{X}\in [-1,5]^2$. Note that another value in the column # Cvx is added corresponding to the number of times the convexity routine is used. Let us remark that there is no real differences between the efficiencies of Algorithm 1 if the required accuracy is $10^{-3}$ or $10^{-10}$ when the solution is searched in $[-0.5,3]\times [0,4]$ but it has a big impact for the CPU time if the searched domain is enlarged to $\tilde{X}=[-1,5]^2$ see Table 3; note that for two instances the asked accuracy has been changed from $10^{-10}$ to $10^{-6}$ in order to obtain a solution within a reasonable amount of time. It seems to be due to the fact that, for $\tilde{X}=[-0.5,3]\times [0,4]$, $x_2^*=4$ is the upper bound of the searched domain. In both cases, for $\epsilon _Y=0.5$ the robust solution switches to another local minimum of $f_B$ as it was noticed in the literature [3, 6, 13].

Table 2 Numerical results for Bertsimas function $f_B$ for $x\in \tilde{X}=[-0.5,3]\times [0,4]$

Table 3 Numerical results for Bertsimas function $f_B$ for $x\in \tilde{X}=[-1,5]\times [-1,5]$

Remark 2

The results presented in Table 1 are reliable numerically and by using Theorem 1 in [14], the results presented in Tables 2 and 3 are also reliable. Indeed, Algorithm 1 is reliable because it is mainly based on interval computations. Thus, Algorithm 1 is a rigorous robust global optimization code as it is defined in [10] by Kearfott.

In this paper, we address only problems with 1 or 2 variables; this yields problems with 2 or 4 variables by introducing new variables $y_i$. For our new Algorithm 1 which is implemented in MatLab using IntLab library [20], it is difficult to solve problems with more than 2 variables in a reasonable amount of time (less than 1h). Indeed, in [18], Pál and Csendes compare a classical interval global optimization Branch-and-Bound algorithm implemented by using MatLab-IntLab versus a C-code which uses C-XSC library (for interval arithmetic), see [11]. Pál and Csendes shows that due to the MatLab interpreter their IntLab-based code is on average 700 times slower than their C-code (more precisely between 165 and 2106 times slower depending on the instances), see [18]. Thus, we think that we could obtain closely the same ratio comparing our implementation in MatLab-IntLab of Algorithm 1 to another one based on a compiled language (e.g., C or Fortran). Hence, all the results, provided in this paper, could be solved in less than 10s (compared to close 1h for the slowest). Therefore, with a compiled code, we hope that problems with 3 or 4 variables could be addressed in a reasonable amount of time.

6 Conclusion

In this paper, we propose a deterministic global optimization algorithm to solve robust nonconvex optimization problems. This algorithm is derived from some properties previously established. A code was developed in MatLab and is validated on some numerical examples proving thereby the intrinsic interest and efficiency of our Robust Interval Branch-and-Bound Optimization Algorithm. A convexity routine is implemented and added to this Algorithm to tackle the Bertsimas et al. robust nonconvex problem. Preliminary numerical experiments demonstrate that our approach is promising.