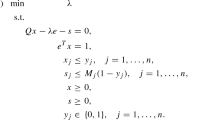A vector linear programming approach for certain global optimization problems

Abstract

Global optimization problems with a quasi-concave objective function and linear constraints are studied. We point out that various other classes of global optimization problems can be expressed in this way. We present two algorithms, which can be seen as slight modifications of Benson-type algorithms for multiple objective linear programs (MOLP). The modification of the MOLP algorithms results in a more efficient treatment of the studied optimization problems. This paper generalizes results of Schulz and Mittal (Math Program 141(1–2):103–120, 2013) on quasi-concave problems and Shao and Ehrgott (Optimization 65(2):415–431, 2016) on multiplicative linear programs. Furthermore, it improves results of Löhne and Wagner (J Glob Optim 69(2):369–385, 2017) on minimizing the difference $f=g-h$ of two convex functions g, h where either g or h is polyhedral. Numerical examples are given and the results are compared with the global optimization software BARON.

1 Introduction

The object of study is a global optimization problem with a quasi-concave objective function $f :\mathbb {R}^q \rightarrow \bar{\mathbb {R}}$ and linear constraints of the form

$$\begin{aligned} \min f(Px) \quad \text {s.t.} \quad Ax \ge b\text {,} \end{aligned}$$

(QCP)

where $P \in \mathbb {R}^{q \times n}$, $A \in \mathbb {R}^{m \times n}$ and $b \in \mathbb {R}^m$. The symbol $\bar{\mathbb {R}}:=\mathbb {R}\cup \{\,\pm \infty \,\}$ denotes the set of extended reals. The following four examples show classes of global optimization problems which are covered by (QCP).

Example 1

(DC programming - “convex component” being polyhedral) Consider

$$\begin{aligned} \min _{x \in {{\mathrm{dom\,}}}g} [g(x) - h(x)] \end{aligned}$$

(1)

where $g: \mathbb {R}^n \rightarrow \mathbb {R}\cup \{+\infty \}$ is polyhedral convex and $h: \mathbb {R}^n \rightarrow \mathbb {R}\cup \{+\infty \}$ is convex. The reformulation

$$\begin{aligned} \min _{x,\, r} \left[ r - h(x)\right] \quad \text {s.t.}\quad (x,r) \in {{\mathrm{epi\,}}}g \end{aligned}$$

has a concave objective function. As $g$ is polyhedral, the constraints are linear. See, e.g. [12] for more details.

Example 2

(DC programming - “concave component” being polyhedral) Consider the DC program (1) but, in contrast to Example 1, let g be convex and h be polyhedral convex and proper. As shown in [12], the Toland–Singer dual problem

$$\begin{aligned} \min _{y \in {{\mathrm{dom\,}}}h^*} [h^*(y) - g^*(y)] \end{aligned}$$

(2)

can be utilized to solve (1), where $g^*: \mathbb {R}^n \rightarrow \mathbb {R}\cup \{+\infty \}$ and $h^*: \mathbb {R}^n \rightarrow \mathbb {R}\cup \{+\infty \}$ are the conjugates of g and h, respectively. Since $h^*$ is polyhedral convex and $g^*$ is convex, we can proceed as in Example 1 to obtain a reformulation as (QCP).

Example 3

(Minimizing a convex function over the boundary of a polytope) Let $g: \mathbb {R}^q \rightarrow \mathbb {R}\cup \{+\infty \}$ be convex and let

$$\begin{aligned} Q = \left\{ x \in \mathbb {R}^q \,\big |\,\exists u \in \mathbb {R}^k:A x + B u \ge b\right\} \end{aligned}$$

be a polytope. We consider the problem

$$\begin{aligned} \min g(x) \quad \text {s.t.} \quad x \in {{\mathrm{bd\,}}}Q\text {,} \end{aligned}$$

(3)

where ${{\mathrm{bd\,}}}Q$ denotes the boundary of Q.

We assume $0 \in {{\mathrm{int\,}}}Q$ and that g is Lipschitz over Q. For some real parameter $c > 0$ we define $h_c: \mathbb {R}^q \rightarrow \mathbb {R}\cup \{+\infty \}$ by its epigraph:

$$\begin{aligned} {{\mathrm{epi\,}}}h_c = \left\{ (x,r) \in \mathbb {R}^q \times \mathbb {R}\,\big |\, \exists u \in \mathbb {R}^k:A x + B u - \frac{1}{c}\, b\, r \ge 0,\; r \ge 0\right\} \text {.} \end{aligned}$$

Because ${{\mathrm{epi\,}}}h_c$ is equal to the cone generated by the set $Q \times \{c\}$, the negative of the polyhedral convex function $h(x) = h_c(x) - c$ penalizes points belonging to the interior of Q. Thus, for c chosen sufficiently large, (3) can be replaced by the equivalent problem

$$\begin{aligned} \min g(x) - (h_c(x) - c) \quad \text {s.t.} \quad x \in Q\text {.} \end{aligned}$$

(4)

Problem (4) is a DC program as considered and transformed into (QCP) in Example 2. Note that g needs to be modified by setting $g(x) = \infty$ for $x \not \in Q$. For more details see Sect. 7.4 below.

Example 4

(Linear multiplicative programming [18]) A special instance of (QCP) is to minimize the product of affine functions under linear constraints:

$$\begin{aligned} \min \prod _{i=1}^q (c_i^{\intercal } x + d_i) \quad \text { s.t. } \quad A x \ge b\text {.} \end{aligned}$$

(5)

Here, we assume $c_i^\intercal x + d_i > 0$ for feasible x. Various applications of this problem class can be found in the literature, see e.g. [18].

Our approach to solve (QCP) can be summarized as follows: We show that solving (QCP) is equivalent to solve

$$\begin{aligned} \min _{y\in {{\mathrm{vert\,}}}\mathcal {P}} f(y)\text {,} \end{aligned}$$

where ${{\mathrm{vert\,}}}\cdot$ denotes the vertex set of a polyhedron, and

$$\begin{aligned} \mathcal {P}= \left\{ \, y \in \mathbb {R}^q \big |\, y - P x \in C,\; Ax \ge b\,\right\} \end{aligned}$$

denotes the upper image of the vector linear program

$$\begin{aligned} \min \nolimits _C Px \quad \text { s.t. } \quad Ax \ge b \text {.} \end{aligned}$$

(VLP)

Here, C is some polyhedral convex pointed cone with respect to which f is monotone, that is $y-x \in C$ implies $f(x) \le f(y)$. A vector linear program describes the minimization of the linear function Px under the constraints $Ax \ge b$ with respect to the partial ordering induced by C. For further information and applications compare, for example, [7]. Algorithms designed for solving vector linear programs, in particular Benson-type algorithms [7], also compute the set ${{\mathrm{vert\,}}}\mathcal {P}$. Thus, those algorithms could be utilized directly to solve (QCP). However, computing all the vertices of $\mathcal P$ may be too expensive in practice. Therefore we alter the algorithms for solving (VLP) slightly by introducing certain bounding techniques, which are introduced in [18] for the special case of linear multiplicative programming (5). These bounding techniques usually lead to a decline in the number of vertices of $\mathcal {P}$ that need to be computed.

An overview over various solution techniques for global optimization problems can be found in [9, 10]. Quasi-concave minimization problems have been investigated, for instance, in [15, 20]. The idea to solve a (scalar) global optimization problem via a multiple objective linear program (MOLP) (which we understand to be a vector linear program with the special cone $C=\mathbb {R}^q_+$) is not new in the literature. Fülöp [6] shows that a linear bilevel programming problem can be solved by optimizing a linear function over the Pareto set of a MOLP. Mittal and Schulz [16] minimize a quasi-concave objective function under linear constraints via a corresponding MOLP. Shao and Ehrgott [18] investigate the special case of multiplicative linear programs using this idea. Löhne and Wagner [12] solve DC optimization problems with one polyhedral component (compare Examples 1 and 2) by utilizing a MOLP solver.

The article is organized as follows. In Sect. 2 we introduce some concepts and notation. The problem formulation and corresponding concepts and results are given in Sect. 3. Section 4 is devoted to a first algorithm, which we call the primal algorithm as it is a modification of (the primal version of) Benson’s algorithm [1, 7] for vector linear programs. Section 5 deals with the dual algorithm, which is a modification of the dual variant of Benson’s algorithm for VLP [3, 7]. We also recall some facts about geometric duality for vector linear programs [8]. In Sect. 6, our methods are extended to the case of non-solid cones, which requires a problem reformulation in order to be able to use these methods for VLPs. The last section provides numerical examples.

2 Preliminaries

A polyhedral convex set or convex polyhedron is defined to be the solution set of a system of finitely many affine inequalities. Since all polyhedral sets in this article are convex, we will say polyhedral set or polyhedron for short. If a polyhedron is given as in the latter definition, we speak about an H-representation of the polyhedron. The well-known Minkowski–Weyl theorem states that every nonempty polyhedron $K \subseteq \mathbb {R}^q$ can be represented as a generalized convex hull of finitely many points $\{\,v^1,\dots ,v^r\,\} \subseteq \mathbb {R}^q$, $r \ge 1$ and finitely many directions $\{\,d^1,\dots ,d^s\,\}\subseteq \mathbb {R}^q$, $s \ge 0$, that is,

$$\begin{aligned} K = \left\{ \sum _{i=1}^r \lambda _i v^i + \sum _{j=1}^s \mu _j d^j \,\big |\,\lambda _i \ge 0\; (i=1,\dots ,r),\; \mu _j \ge 0\; (j=1,\dots ,s),\; \sum _{i=1}^r \lambda _i = 1\right\} \text {.} \end{aligned}$$

The pair $(K_\mathrm{poi},K_\mathrm{dir})$ consisting of the two sets $K_\mathrm{poi}:=\{\,v^1,\dots ,v^r\,\}$ and $K_\mathrm{dir}:=\{\,d^1,\dots ,d^r\,\}$ is called V-representation of K. We also write

$$\begin{aligned} K={{\mathrm{conv\,}}}K_\mathrm{poi}+ {{\mathrm{cone\,}}}K_\mathrm{dir}\text {,} \end{aligned}$$

where ${{\mathrm{conv\,}}}\cdot$ denotes the convex, and ${{\mathrm{cone\,}}}\cdot$ the conical hull of a set. We assume that $K_\mathrm{poi}$ is nonempty and define ${{\mathrm{cone\,}}}\emptyset :=\{0\}$ as $K_\mathrm{dir}$ is allowed to be empty.

A polyhedron K can be expressed as

$$\begin{aligned} K = \left\{ x \in \mathbb {R}^q \,\big |\, \exists u \in \mathbb {R}^k:A x + B u \ge b\right\} \text {,} \end{aligned}$$

where $A \in \mathbb {R}^{m\times q}$, $B \in \mathbb {R}^{m \times k}$ and $b \in \mathbb {R}^m$. This type of representation is referred to as projection- or P-representation, as K is the projection of the polyhedron $Q = \left\{ (x,u) \in \mathbb {R}^q \times \mathbb {R}^k \,\big |\, A x + B u \ge b \right\}$ onto $\mathbb {R}^q$.

A multiple objective linear program (MOLP) is an optimization problem of the form

$$\begin{aligned} \min Px \quad \text { s.t. } \quad Ax \ge b\text {,} \end{aligned}$$

(MOLP)

where $P \in \mathbb {R}^{q\times n}$, $A \in \mathbb {R}^{m\times n}$ and $b \in \mathbb {R}^m$. Typically we have at least two linear objective functions, i.e. $q\ge 2$. The operator $\min \cdot$ in (MOLP) is to be understood with respect to the component-wise partial ordering in $\mathbb {R}^q$: $y \le z$ if and only if $z-y \in \mathbb {R}^q_+ :=\{ \, w \in \mathbb {R}^q \mid w_1\ge 0,\dots , w_q \ge 0\,\}$. If the cone $\mathbb {R}^q_+$ is replaced by a general polyhedral convex pointed cone $C \subseteq \mathbb {R}^q$, we obtain a vector linear program (VLP):

$$\begin{aligned} \min \nolimits _C Px \quad \text {s.t.} \quad Ax \ge b \text {.} \end{aligned}$$

(VLP)

For a polyhedral convex pointed cone $C \subseteq \mathbb {R}^q$ there exist matrices $Y \in \mathbb {R}^{q \times o}$ and $Z \in \mathbb {R}^{q \times p}$, $o,p \in \mathbb {N}$, such that

$$\begin{aligned} C=\left\{ \, Y \lambda \,\big |\, \lambda \in \mathbb {R}^o_+ \,\right\} =\left\{ \, y \in \mathbb {R}^q \,\big |\, Z^\intercal y \ge 0 \,\right\} \text {.} \end{aligned}$$

(6)

The equivalence $x \le _C y \iff Z^\intercal x \le Z^\intercal y$ follows. Elements of $S:=\left\{ \, x \in \mathbb {R}^n \mid Ax \ge b \,\right\}$ are called feasible points. Elements of $0^+ S :=\left\{ \, x \in \mathbb {R}^n \mid Ax \ge 0\,\right\}$, the recession cone of S, are feasible directions. By $P[S]:=\left\{ Px\,\big |\, x\in S\right\}$ we denote the image of $S$ under $P$. The polyhedron $\mathcal {P}:=P[S]+C$ is known as upper image of (VLP).

We call a point $y \in \mathbb {R}^q$ a minimal point of the polyhedron $P \subseteq \mathbb {R}^q$ if there is no $z \in P$ with $z \le _C y$ and $z \ne y$. The set of minimal points of P is denoted by ${{\mathrm{Min}}}_C P$. A vector $x \in S$ is called minimizer of (VLP) if $Px \in {{\mathrm{Min}}}_C P[S]$. A feasible direction $x \in 0^+S$ is called minimizer of (VLP) if $Px \in {{\mathrm{Min}}}_C P[0^+ S]{\setminus }\{\,0\,\}$. Let $S_\mathrm{poi}\subseteq S$ and $S_\mathrm{dir}\subseteq 0^+ S$ with $P[S_\mathrm{dir}]\cap \{\,0\,\}=\emptyset$, be finite sets. We call $(S_\mathrm{poi},S_\mathrm{dir})$ a finite infimizer of (VLP) if

$$\begin{aligned} {{\mathrm{conv\,}}}P[S_\mathrm{poi}]+{{\mathrm{cone\,}}}P[S_\mathrm{dir}]+C = \mathcal {P}\text {.} \end{aligned}$$

A finite infimizer consisting of minimizers only is called a solution of (VLP), see [7, 11].

Finally we recall two types of scalarizations for (VLP). For a $w \in \mathbb {R}^q$, the weighted sum scalarization is

The corresponding dual problem is

Another relevant scalarization is the translative scalarization (or scalarization by a reference variable) for some $t \in \mathbb {R}^q$:

Note that the second inequality is equivalent to $Px \le _C t+z \cdot c$. The purpose of this scalarization method is depicted in Proposition 7. The corresponding dual problem of ($\hbox {P}_{2}(t)$) (in a slightly modified form, see [7] for details) is

A function $f :\mathbb {R}^q \rightarrow \bar{\mathbb {R}}$ is said to be quasi-concave if its super level sets $U_r :=\{\, x \in \mathbb {R}^q \mid f(x) \ge r\,\}$ are convex for every $r \in \mathbb {R}$. Equivalently [2, Section 3.4], f is quasi-concave if and only if

$$\begin{aligned} \forall \lambda \in (0,1),\; \forall x,y \in \mathbb {R}^q:\; f(\lambda x + (1-\lambda )y) \ge \min \{ \, f(x),f(y)\,\}\text {.} \end{aligned}$$

Let $C \subseteq \mathbb {R}^q$ be a pointed (i.e. $C \cap (-C) = \{\,0\,\}$) convex cone. As usual, we write $x \le _{C} y$ if $y-x \in C$. A function $g :\mathbb {R}^q \rightarrow \bar{\mathbb {R}}$ is said to be C-monotone on a set $D\subseteq \mathbb {R}^q$ if for all $x,y \in D$, $x \le _{C} y$ implies $g(x) \le g(y)$.

A function $f :\mathbb {R}^q \rightarrow \bar{\mathbb {R}}$ is called polyhedral convex (polyhedral) if its epigraph ${{\mathrm{epi\,}}}f :=\left\{ (x,r) \in \mathbb {R}^n \times \mathbb {R}\; | \; f(x) \le r \right\}$ is a polyhedral convex set. The domain of f is defined as ${{\mathrm{dom\,}}}f :=\left\{ x \in \mathbb {R}^n \; | \; f(x) < + \infty \right\}$.

The conjugate $f^* :\mathbb {R}^q \rightarrow \mathbb {R}\cup \left\{ + \infty \right\}$ of f with ${{\mathrm{dom\,}}}f \ne \varnothing$ is defined as

$$\begin{aligned} f^*(x^*)=\sup _{x \in {{\mathrm{dom\,}}}f} \left\{ x^\intercal x^* -f(x) \right\} \, . \end{aligned}$$

3 Problem formulation

The optimization problem we intend to solve is

$$\begin{aligned} \min f(Px) \quad \text {s.t.} \quad Ax \ge b \text {,} \end{aligned}$$

(QCP)

where $f :\mathbb {R}^q \rightarrow \bar{\mathbb {R}}$ is a quasi-concave function, $P \in \mathbb {R}^{q \times n}$, $A \in \mathbb {R}^{m \times n}$ are matrices and $b \in \mathbb {R}^m$ is a vector. In typical applications one has $q \ll n$. A low rank of non-linearity (see e.g. [20]) is indicated by the projection of the n-dimensional feasible polyhedron $S:=\{x \in \mathbb {R}^n | \; Ax \ge b\}$ onto the “low”-dimensional polyhedron $P[S]\subseteq \mathbb {R}^q$. In other words, the problem is non-linear with respect to only $q$ instead of $n$ variables. The problem can be solved if q is not “too large” (say up to $q=20$). The low rank property can arise from modeling techniques, e.g. by introducing slack variables, or by auxiliary variables which are inserted in order to transform polyhedral convex terms (such as finite maximum or absolute value) into linear constraints, see e.g. [12] for an example from location analysis.

We assume that $C\subseteq \mathbb {R}^q$ is a polyhedral convex pointed cone such that:

Note that assumption (M) is always satisfied for the cone $C=\{0\}$. There are three reasons for a larger (with respect to set inclusion) cone C. First, if one is able to find a cone with ${{\mathrm{int\,}}}C \ne \emptyset$, a direct application of modified VLP algorithms is possible, while in the case of ${{\mathrm{int\,}}}C = \emptyset$ a reformulation of the problem is necessary, which is discussed in Sect. 6. Secondly, a larger cone C tends to reduce the number of iteration steps required. Third, a larger cone C can be necessary to satisfy the boundedness assumption (B).

A further assumption is made in the algorithms following subsequently: We assume that an H-representation of an initial outer approximation $\mathcal {O}$ is available as input. In order to ensure that $\mathcal {O}$ possesses a vertex, we additionally require $\mathcal {O}$ to be $C$-bounded. Thus, the assumption reads as follows:

An initial approximation according to (O) can be computed whenever assumption (B) holds. Appropriate techniques for constructing $\mathcal {O}$ can be found in, e.g., [7].

We next show existence of an optimal solution of (QCP) and its attainment in a vertex of $\mathcal {P}$.

Proposition 5

Let the assumptions (M) and (B) be satisfied. Let $\mathcal {O}$ denote a polyhedron according to (O). Then

$$\begin{aligned} \min _{y \in {{\mathrm{vert\,}}}\mathcal {O}} f(y) \le \inf _{x \in S} f(Px)\text {.} \end{aligned}$$

Proof

As $C$ is supposed to be pointed, ${{\mathrm{vert\,}}}\mathcal {O}\ne \emptyset$ follows from ${{\mathrm{0^+\!}}}\mathcal {O}= C$. Let ${{\mathrm{vert\,}}}\mathcal {O}= \{y^1,\ldots ,y^k\}$. For any $x\in S$ there exist $\lambda _j\in \left[ 0,1\right]$, $j=1,\ldots ,k$; and a direction $c\in C$ such that

$$\begin{aligned} Px = \sum _{j=1}^k\lambda _jy^j + c\text {.} \end{aligned}$$

From (M) follows $f(Px)\geqslant f(Px - c)\geqslant f\left( \sum _{j=1}^k\lambda _j y^j\right)$. As $f$ is supposed to be quasi-concave, this leads to

$$\begin{aligned} f(Px)\geqslant \min _{j=1,\ldots ,k}f(y^j)\text {,} \end{aligned}$$

which proves the claim. $\square$

Note that in the preceding proof we need $C$-monotonicity of $f$ on the set $\mathcal {O}\cap \left( P[S]-C\right)$ only. If we are given an objective function $f^\prime$ and an outer approximation $\mathcal {O}$ according to (O) such that $f^\prime$ is $C$-monotone on $\mathcal {O}\cap \left( P[S]-C\right)$, we can transform $f^\prime$ in the following way in order to obtain a quasi-concave function $f$ that complies with (M):

$$\begin{aligned} f(y):={\left\{ \begin{array}{ll} f^\prime (y)&{} \text {if }y\in \mathcal {O},\\ -\infty &{}\text {otherwise.} \end{array}\right. } \end{aligned}$$

Corollary 6

Let the assumptions (M) and (B) be satisfied. Then (QCP) has an optimal solution $x^* \in S$ such that

$$\begin{aligned} f(Px^*) = \min _{y \in {{\mathrm{vert\,}}}\mathcal {P}} f(y)\text {.} \end{aligned}$$

Proof

By applying Proposition 5 to the set $\mathcal {O}= \mathcal {P}$, we know that $\min _{y \in {{\mathrm{vert\,}}}\mathcal {P}} f(y)$ is a lower bound for the optimal value of (QCP). There are only finitely many vertices y of $\mathcal {P}$, each of which can be expressed as $y = Px$ for some $x \in S$. Thus, the lower bound is attained by some $x^* \in S$ and $x^*$ is an optimal solution for (QCP). $\square$

4 Primal algorithm for QCP

We begin this section by recalling some facts about Benson’s algorithm for vector linear programs following the exposition of [7]. A modified variant of the algorithm is then developed (the results of [18] are generalized) to solve the quasi-concave scalar optimization problem (QCP).

4.1 Primal Benson-type algorithm for VLP

Benson’s algorithm can briefly be described as a procedure computing a shrinking sequence of outer approximating polyhedra $\mathcal {O}_j = \{ y \in \mathbb {R}^q \mid B^j y \ge c^j\}$ for $\mathcal {P}$, that is,

$$\begin{aligned} \mathcal {O}_0 \supsetneq \mathcal {O}_1 \supsetneq \dots \supsetneq \mathcal {O}_j \supsetneq \dots \supsetneq \mathcal {O}_k = \mathcal {P}\text {.} \end{aligned}$$

The procedure is started with $\mathcal {O}_0 :=\mathcal {O}$ from assumption (O). By solving the linear program ($\hbox {P}_{2}(t)$) parametrized by an arbitrary vertex t of the current outer approximation $\mathcal {O}_j$, we obtain a boundary point v of $\mathcal {P}$. An optimal solution of the dual problem ($\hbox {D}_{2}(t)$) yields a half-space $\mathcal {H}_j$ supporting $\mathcal {P}$ in v, that is, $\mathcal {H}_j \supseteq \mathcal {P}$ and $v \in \mathcal {P}\cap -\mathcal {H}_j$. The refinement of outer approximations is based on setting

$$\begin{aligned} \mathcal {O}_{j+1} :=\mathcal {O}_j \cap \mathcal {H}_j\text {.} \end{aligned}$$

(7)

The algorithm terminates when all vertices of $\mathcal {O}_j$ belong to $\mathcal {P}$. Benson’s algorithm can be seen as a cutting plane method. The algorithm as presented in [7] requires the cone C to be solid, i.e. ${{\mathrm{int\,}}}C \ne \emptyset$. The following proposition summarizes the role of scalarizations for the algorithm.

Proposition 7

([7, Proposition 4.2]) Let $S\ne \emptyset$ and let assumption (B) be satisfied. Furthermore, assume $C$ to be solid and let $c \in {{\mathrm{int\,}}}C$. Let an H-representation of $C$ be given by $C = \{ y \in \mathbb {R}^q \mid Z^{\intercal } y \ge 0\}$. Then, for every $t \in \mathbb {R}^q$, there exist optimal solutions $(\bar{x},\bar{z})$ to ($\hbox {P}_{2}(t)$) and $(\bar{u},\bar{w})$ to ($\hbox {D}_{2}(t)$). Each solution $(\bar{u},\bar{w})$ to ($\hbox {D}_{2}(t)$) defines a half-space $\mathcal {H}:=\left\{ y \in \mathbb {R}^q \big |\, \bar{w}^\intercal y \ge b^\intercal \bar{u} \right\} \supseteq \mathcal {P}$ such that $s:=t+c\cdot \bar{z} \in \mathcal {P}\cap -\mathcal {H}$. Furthermore, one has

$$\begin{aligned} t \notin \mathcal {P}\iff \bar{z}>0\text {.} \end{aligned}$$

Assumption (O) ensures that an H-representation of the initial outer polyhedral approximation $\mathcal {O}=\mathcal {O}_0$ of $\mathcal {P}$ is given and by (7) we obtain iteratively H-representations of all subsequent outer approximations $\mathcal {O}_j$. It is necessary to compute (or to update) a V-representation of $\mathcal {O}_j$. This step is called vertex enumeration. Algorithm 1 is a simplified and slightly improved version of the primal Benson algorithm as formulated in [7]. In contrast to [7, Algorithm 1] we do not store the “pre-image information”, i.e. x and (u, w). Moreover, for simplicity, we store the H-representation of $\mathcal {O}$ directly instead of using duality theory. We enhance [7, Algorithm 1] as we do not re-initialize the set T, and thus avoid solving the same linear program twice. The operation $\texttt {solve}(\cdot )$ returns optimal solutions of a given pair of dual linear programs.

Theorem 8

[see [7, Theorem 4.5]] Let $S\ne \emptyset$, denote by C a polyhedral convex solid pointed cone as defined in (6) which satisfies assumption (B). Then Algorithm 1 is correct and finite.

4.2 Modified primal Benson-type algorithm for QCP

We already know that an optimal solution of (QCP) can be found if in Algorithm 1 the vector x with the smallest value f(Px) is stored. Algorithm 2 is just a modification and simplification of Algorithm 1, which also yields an optimal solution of (QCP). In general, Algorithm 2 requires less iteration steps.

Theorem 9

Let $S\ne \emptyset$, $f:\mathbb {R}^q\rightarrow \mathbb {R}$ quasi-concave. Let C be a polyhedral convex solid pointed cone according to (6) which satisfies assumptions (M) and (B). Then Algorithm 2 is correct and finite.

Proof

The main difference between Algorithms 1 and 2 is that Algorithm 2 terminates after z equals zero for the first time. Since Algorithm 1 is finite and as it terminates only if the case $z=0$ occurred at least once, Algorithm 2 must be finite, too. Thus, it remains to show that x is an optimal solution of (QCP). By Proposition 5 and taking into account that $\mathcal {O}_\mathrm{poi}= {{\mathrm{vert\,}}}\mathcal {O}$, we have

$$\begin{aligned} f(t) = \min \{\, f(y) \mid y \in \mathcal {O}_\mathrm{poi}\,\} \le \inf \{\, f(P v) \mid v \in S\,\}\text {.} \end{aligned}$$

(8)

At termination, $z=0$ in ($\hbox {P}_{2}(t)$) implies $Px \le _C t$. Assume that $Px \ne t$. Then there is some $c \in C{\setminus }\{0\}$ such that $t-c = Px \in \mathcal {P}\subseteq \mathcal {O}$. We also have $t+c \in \mathcal {O}$. This contradicts the fact that t is a vertex of $\mathcal {O}$. Hence $t=Px$. We obtain $f(Px) = f(t)$, where x is feasible for (QCP). Together with (8) we conclude that x solves (QCP). $\square$

Example 10

The following problem is a slight modification of the problem stated and solved in [10, p. 256] using polyhedral annexation methods:

$$\begin{aligned} \min \phantom {platz}&g(x)=- |x_1 |^{\frac{3}{2}} - \frac{1}{10}\left( x_1-0.5x_2+0.3x_3+x4-4.5 \right) ^{2}\\ \text {s.t.} \phantom {platz}&\begin{bmatrix} 1.2&\quad 1.4&\quad 0.4&\quad 0.8 \\ -\,0.7&\quad 0.8&\quad 0.8&\quad 0.0 \\ 0.0&\quad 1.2&\quad 0.0&\quad 0.4 \\ 2.8&\quad -\,2.1&\quad 0.5&\quad 0.0 \\ 0.4&\quad 2.1&\quad -\,1.5&\quad -\,0.2 \\ -\,0.6&\quad -\,1.3&\quad 2.4&\quad 0.5 \end{bmatrix} x\le \begin{bmatrix} 6.8 \\ 0.8 \\ 2.1 \\ 1.2 \\ 1.4\\ 0.8 \end{bmatrix},\quad x \ge 0\text {.}\\ \end{aligned}$$

We have $y=Px$ for the matrix

$$\begin{aligned} P= \begin{bmatrix} 1&\quad 0&\quad 0&\quad 0 \\ 1&\quad -\,0.5&\quad 0.3&\quad 1 \\ \end{bmatrix} \end{aligned}$$

and the objective function turns into

$$\begin{aligned} f(y)=-|y_1 |^{\frac{3}{2}}-\frac{1}{10}\left( y_2-4.5 \right) ^{2} \end{aligned}$$

with $g(x)=f(Px)$. The feasible region and some level sets of the projected problem are depicted in Fig. 1. The iteration steps of Algorithm 2 are shown in Fig. 2. We obtain the optimal value $-\,2.494$ attained at (1.084, 0.804).

Fig. 1

P[S] and level sets of f for Example 10. The cone C generated by $(-\,1,0)^\intercal$ and $(0,1)^\intercal$ is indicated by the dashed lines. It apparently reflects the objective’s monotonicity within the feasible region

Fig. 2

Iteration steps for Example 10. The white circle shows the current point t, whereas the gray dots indicate the boundary points s calculated by ($\hbox {P}_{2}(t)$). Note that we avoid two additional iteration steps in comparison to Algorithm 1 since there are two remaining vertices of the outer approximation, which do not need to be processed

5 Dual algorithm for QCP

In this section we propose a dual algorithm for the quasi-concave problem (QCP), which is related to the dual variant of Benson’s algorithm for vector linear programs, introduced in [3]. In [18], Shao and Ehrgott introduced a similar algorithm for linear multiplicative programs, which is a special case of our setting. Here, we propose a modification of Shao and Ehrgott’s algorithm, which turns out to yield better numerical results.

We start by recalling several facts about duality theory for vector linear programs. Afterwards we recapitulate the dual variant of Benson’s algorithm for vector linear programs, which we present in a simplified form. The final subsection deals with the dual algorithm for quasi-concave programs.

5.1 Geometric duality for VLP

The dual problem associated with (VLP), introduced in [8] (see also [3, 11]), is

with objective function $D^* :\mathbb {R}^m \times \mathbb {R}^q \rightarrow \mathbb {R}^q$ defined by

$$\begin{aligned} D^*(u,w)=\left( w_1,\ldots ,w_{q-1},b^\intercal u \right) ^\intercal \text {,} \end{aligned}$$

feasible set

$$\begin{aligned} T:=\left\{ \, (u,w) \in \mathbb {R}^m \times \mathbb {R}^q \big |\, u \ge 0 ,\; A^{\intercal } u=P^{\intercal }w, \; c^\intercal w=1, \; Y^{\intercal } w \ge 0 \,\right\} \end{aligned}$$

and ordering cone

$$\begin{aligned} K:=\mathbb {R}_+ \cdot (0,\ldots ,0,1)^\intercal \text {.} \end{aligned}$$

Throughout, we assume that

$$\begin{aligned} c \in \text {int }C \quad \text {and} \quad c_q=1\text {.} \end{aligned}$$

(9)

Observe that this assumption does not constitute a restriction: As ${{\mathrm{int\,}}}C \ne \emptyset$, it is always possible to chose $c \in {{\mathrm{int\,}}}C$ such that either $c_q=1$ or $c_q=-1$. In the latter case, an equivalent problem where C, P and c are replaced by $-C$, $-P$ and $-c$, respectively, can be considered.

Similar to the upper image $\mathcal {P}$ for (VLP), the lower image for (VLP$^*$) is defined as

$$\begin{aligned} \mathcal {D}^*:=D[T]-K\text {.} \end{aligned}$$

To express the duality relations, we make use of the following bi-affine coupling function:

$$\begin{aligned} \varphi :\mathbb {R}^q \times \mathbb {R}^q \rightarrow \mathbb {R},\quad \varphi (y,y^*):=\sum _{i=1}^{q-1} y_iy_i^* +y_q \left( 1- \sum _{i=1}^{q-1}c_i y_i^* \right) -y_q^*\text {.} \end{aligned}$$

(10)

Theorem 11

(weak duality [8, 11]) One has

$$\begin{aligned} \left[ \,y \in \mathcal {P}\wedge y^* \in \mathcal {D}^*\,\right] \implies \varphi (y,y^*)\ge 0\text {.} \end{aligned}$$

Theorem 12

(strong duality [8, 11]) Let S and T be nonempty. Then

$$\begin{aligned} \left[ \,\forall y^* \in \mathcal {D}^* :\varphi (y,y^*)\ge 0\,\right]&\implies y \in \mathcal {P}\\ \left[ \,\forall y \in \mathcal {P}:\varphi (y,y^*)\ge 0\,\right]&\implies y^* \in \mathcal {D}^*\text {.} \end{aligned}$$

Using the coupling function $\varphi$ we define half-space-valued functions

$$\begin{aligned} \mathcal {H}^*&:\mathbb {R}^q \rightrightarrows \mathbb {R}^q&\mathcal {H}^*(y)&:=\left\{ y^* \in \mathbb {R}^q \big |\, \varphi (y,y^*) \ge 0 \right\} \\ \mathcal {H}&:\mathbb {R}^q \rightrightarrows \mathbb {R}^q&\mathcal {H}(y^*)&:=\left\{ y \in \mathbb {R}^q \big |\, \varphi (y,y^*)\ge 0 \right\} \end{aligned}$$

and a duality mapping

$$\begin{aligned} \Psi :2^{\mathbb {R}^q} \rightarrow 2^{\mathbb {R}^q}, \quad \Psi (F^*):=\bigcap _{y^* \in F^*} -\mathcal {H}(y^*) \cap \mathcal {P}\text {.} \end{aligned}$$

A proper face $F^*$ of the lower image $\mathcal {D}^*$ is called vertical if $F^*=F^*-K$. Non-vertical proper faces of $\mathcal {D}^*$ are also called K-maximal as they consist of K-maximal points only.

Theorem 13

(Geometric Duality [8]) $\Psi$ is an inclusion reversing one-to-one map (i.e. $F_1^* \subseteq F_2^* \iff \Psi (F_1^*) \supseteq \Psi (F_2^*)$) between the set of all non-vertical proper faces $F^*$ of $\mathcal {D}^*$ and the set of all proper faces F of $\mathcal {P}$. The inverse map is given by

$$\begin{aligned} \Psi ^{-1} :2^{\mathbb {R}^q} \rightarrow 2^{\mathbb {R}^q}, \quad \Psi ^*(F):=\bigcap _{y \in F}-\mathcal {H}^*(y) \cap \mathcal {D}^* \text {.} \end{aligned}$$

For non-vertical proper faces $F^*$ of $\mathcal {D}^*$ one has

$$\begin{aligned} \dim F^* + \dim \Psi (F^*) = q-1\text {.} \end{aligned}$$

In particular, vertices of $\mathcal {D}^*$ correspond to facets of $\mathcal {P}$ and vertices of $\mathcal {P}$ correspond to non-vertical facets of $\mathcal {D}^*$. There is also a correspondence between the vertical facets of $\mathcal {D}^*$ and extremal directions of $\mathcal {P}$, see [11, Section 4.6].

5.2 Dual variant of Benson’s algorithm for VLP

The dual variant of Benson’s algorithm constructs the lower image $\mathcal {D}^*$ by a shrinking sequence of polyhedral outer approximations

$$\begin{aligned} \mathcal {O}_0^* \supsetneq \mathcal {O}_1^* \supsetneq \dots \supsetneq \mathcal {O}^*_j \supsetneq \dots \supsetneq \mathcal {O}_k^* = \mathcal {D}^*\text {.} \end{aligned}$$

This refinement procedure is analogous to the one described in the primal case. An arbitrary vertex of $\mathcal {O}^*_j$ is either identified as element of $\mathcal {D}^*$ or is cut off by intersecting $\mathcal {O}^*_j$ with a suitable half-space $\mathcal {H}^*_j$ obtained from the solution of a scalar problem. This results in the improved outer approximation $\mathcal {O}^*_{j+1}:=\mathcal {O}^*_j \cap \mathcal {H}^*_j$.

In order to give a counterpart to Proposition 7, let $t^*$ be a vertex of $\mathcal {O}_j^*$. By

$$\begin{aligned} C^+ :=\left\{ y^*\in \mathbb {R}^q\,\big |\,y\in C \Longrightarrow y^\intercal y^*\geqslant 0\right\} \end{aligned}$$

we denote the positive dual of $C$. We set

$$\begin{aligned}&\omega (t^*):=\left( t^*_1,\ldots ,t^*_{q-1},1-\sum _{i=1}^{q-1} c_i t^*_i\right) ^\intercal&\text {and}&\Delta :=\left\{ \, y^* \in \mathbb {R}^q \big |\, \omega (y^*) \in C^+ \,\right\} \text {.} \end{aligned}$$

Proposition 14

([7, Proposition 4.6]) Let $S \ne \emptyset$, and let C as in (6) be a solid, polyhedral convex pointed cone with $c \in {{\mathrm{int\,}}}C$ and $c_q = 1$ that satisfies assumption (B). Consider $t^* \in \Delta$. For $w:=\omega (t^*)$, there exists an optimal solution x to ($\hbox {P}_{1}(w)$). Each solution x to ($\hbox {P}_{1}(w)$) defines a half-space $\mathcal {H}^*(P x):=\left\{ y^* \in \mathbb {R}^q \, |\, \varphi \left( P x,y^* \right) \ge 0 \right\} \supseteq \mathcal {D}^*$ such that $s^*:=\left( t_1^*,\ldots ,t_{q-1}^*,w^\intercal Px \right) ^\intercal \in -\mathcal {H}^* \cap \mathcal {D}^*$. Furthermore, one has $P x \in {{\mathrm{bd\,}}}\mathcal {P}$, and

$$\begin{aligned} t^* \notin \mathcal {D}^* \iff w^\intercal Px < t_q^*\text {.} \end{aligned}$$

Algorithm 3 is a simplified and slightly modified version of the dual variant of Benson’s algorithm, compare [7, Algorithm 2]. Note that all outer polyhedral approximations $\mathcal {O}^*$ are contained in the set $\Delta$, compare line 2 of Algorithm 3. As the recession cone of the sets $\mathcal {O}_j^*$ is always $-K$, their V-representations are already specified by a finite set of points (rather than both points and directions). Because of the modifications of the algorithm in comparison to [7], we sketch the proof of the following theorem.

Theorem 15

(compare [7, Theorem 4.9]) Let $S\ne \emptyset$, let C according to (6) be a polyhedral convex solid pointed cone with $c \in {{\mathrm{int\,}}}C$ and $c_q=1$ such that assumption (B) is satisfied. Then Algorithm 3 is correct and finite.

Proof

Since $c \in {{\mathrm{int\,}}}C$ and w computed in line 4 belongs to $C^+ {\setminus } \{0\}$, we obtain that $c^\intercal w$ in line 5 is not zero. The linear program in line 9 always has a solution since $t^* \in \Delta$, which holds as the initial set $\mathcal {O}^*$ equals $\Delta$ by line 2. The last component of the normal vector of the half-space $\{y^* \in \mathbb {R}^q\mid \varphi (Px,y^*) \ge 0\}$ in line 11 is $-1$, see (10). Thus, after the first cut in line 11 was made, $\mathcal {O}^*$ has a vertex. It follows that $\mathcal {O}^*_\mathrm{poi}$ is always nonempty. At termination, we have $\mathcal {O}^*_\mathrm{poi}\subseteq T^*$. Since $T^* \subseteq \mathcal {D}^*$ and $\mathcal {O}^*\supseteq \mathcal {D}^*$, we obtain $\mathcal {O}^* = \mathcal {D}^*$.

To prove that the algorithm is finite, observe that $F^* :=-\mathcal {H}^* \cap \mathcal {D}^*$ in Proposition 14 is a face of $\mathcal {D}^*$ which belongs to the boundary of $\mathcal {O}^*$ after the cut in line 11. A vertex $t^*$ of $\mathcal {O}^* \supseteq \mathcal {D}^*$ chosen in a subsequent iteration either belongs to $\mathcal {D}^*$ or cannot belong to the relative interior of $F^*$. In the first case $t^*$ is a vertex of $\mathcal {D}^*$ and is stored in $T^*$. In the second case, another face of $\mathcal {D^*}$ corresponds to the cut. Since $\mathcal {D}^*$ has only finitely many faces, the algorithm is finite. $\square$

5.3 Modified dual variant of Benson’s algorithm to solve QCP

Now the ideas from Sect. 4 are applied to modify the dual variant of Bensons’s algorithm in order to get a more efficient algorithm for (QCP). The main difference in comparison to the primal case is that a shrinking sequence of outer polyhedral approximations $\mathcal {O}_j$ for $\mathcal {P}$ is not part of Algorithm 3, but values of f at vertices of $\mathcal {O}_j$ are required in order to be able to use the ideas of Sect. 4.2. Accepting the computational cost of an extra vertex enumeration step per iteration allows us to calculate the required sequence of outer polyhedral approximations $\mathcal {O}_j$ of $\mathcal {P}$.

Shao and Ehrgott [18] developed a similar algorithm for the special case of multiplicative linear programs, also see Sect. 7.

The main idea of Algorithm 4 can be explained as follows: In the loop we compute both, shrinking sequences of outer approximations $\mathcal {O}_j$ of $\mathcal {P}$ and $\mathcal {O}^*_j$ of $\mathcal {D}^*$. First, in the manner of Algorithm 2, a vertex t of $\mathcal {O}$ with minimal value f(t) is selected. Thereafter, a vertex $t^*$ of $\mathcal {O}^*$ which has not yet been identified as a member of $\mathcal {D}^*$ is selected such that $\varphi (t,\cdot )$ is minimal. The difference to Algorithm 3 is that $t^*$ is selected in this special way. If $\varphi (t,t^*) \ge 0$ for a vertex t of $\mathcal {O}$ with f being minimal and for all vertices $t^*$ of $\mathcal {O}^*$, then $x \in S$ with $t=Px$ is an optimal solution for (QCP). Thus, the selection rule for t and $t^*$ can be motivated as the choice corresponding to the strongest violation of this optimality condition.

Theorem 16

Let $S \ne \emptyset$, $f :\mathbb {R}^q \rightarrow \bar{\mathbb {R}}$ quasi-concave, and let $C= \left\{ y \in \mathbb {R}^q \,\big |\, Z^{\intercal }y \ge 0 \right\}$ be a polyhedral convex solid pointed cone which satisfies assumptions (M) and (B). Then Algorithm 4 is correct and finite.

Proof

Note that Algorithms 4 coincides with Algorithm 3 up to the following changes:

• (a) the additional lines 16–18 to compute the outer approximations $\mathcal {O}$ of $\mathcal {P}$,

• (b) a different stopping condition for the loop in line 19,

• (c) a specific rule to select some $t^*$ from the set $\mathcal {O}^*_\mathrm{poi}{\setminus } T^*$ in line 20,

• (d) the computation of the result x in line 22.

Therefore, the result follows from Theorem 15 by taking into account the following facts:

• (a) The new lines 16–18 are well defined, in particular, by assumption (O), the set $\mathcal {O}$ has a vertex.

• (b) We show that the condition

  $$\begin{aligned} \min \left\{ \varphi (t,y^*) \mid y^* \in \mathcal {O}^*_\mathrm{poi}\right\} < 0 \end{aligned}$$

  (11)

  in Algorithm 4, line 19 implies the corresponding condition

  $$\begin{aligned} \mathcal {O}^*_\mathrm{poi}{\setminus } T^* \ne \emptyset \end{aligned}$$

  (12)

  in Algorithm 3, line 16. Assume that (11) is satisfied but (12) is violated, i.e., $\mathcal {O}^*_\mathrm{poi}\subseteq T^*$. Since $T^* \subseteq \mathcal {D}^*$ and $\mathcal {O}^*\supseteq \mathcal {D}^*$, we obtain $\mathcal {O}^* = \mathcal {D}^*$. By construction, we have

  $$\begin{aligned} \mathcal {O}\subseteq \{y \in \mathbb {R}^q\mid \forall t^* \in T^*:\; \omega (t^*)^\intercal y \ge t^*_q\} \subseteq \{y \in \mathbb {R}^q\mid \forall t^* \in \text {vert}\,\mathcal {D}^*:\;\varphi (y,t^*)\ge 0\} = \mathcal {P}\text {,} \end{aligned}$$

  where the last equation follows from geometric duality, see Theorem 13. On the other hand, we have $\mathcal {O}\supseteq \mathcal {P}$, whence $t \in \mathcal {O}= \mathcal {P}$. Weak duality (Theorem 11) implies that $\varphi (t,t^*)\ge 0$ for all $t^* \in \mathcal {O}^*_\mathrm{poi}$, which contradicts (11). This proves that (11) implies (12). Hence, from the finiteness of Algorithm 3 finiteness of Algorithm 4 follows.

• (c) As shown in (b), the specific choice of $t^*$ in line 20 is well-defined.

• (d) At termination, we have $\varphi (t,y^*) \ge 0$ for all $y^* \in \mathcal {O}^*_\mathrm{poi}$. As $\mathcal {O}^* = {{\mathrm{conv\,}}}\mathcal {O}^*_\mathrm{poi}-K$, the inequality also holds for all $y^* \in \mathcal {D}^* \subseteq \mathcal {O}^*$. Theorem 12 implies $t \in \mathcal {P}$. Since $t \in \mathcal {P}$ is a vertex of $\mathcal {O}$ and $\mathcal {O}\supseteq \mathcal {P}$, t is also a vertex of $\mathcal {P}$. Taking into account that $\mathcal {P}= P[S] + C$, we conclude that there exists $x \in S$ with $t =Px$. Since t in line 18 was chosen from $\mathcal {O}_\mathrm{poi}$ such that f(t) is minimal, Proposition 5 yields that x is an optimal solution of (QCP). $\square$

Fig. 3

Visualization of the initialization and the first two iteration steps of Algorithm 4 by Example 17. The shrinking sequence $\mathcal {O}^*_j$ of outer approximations of $\mathcal {D}^*$ corresponds to the expanding sequence $\mathcal {I}_j :=\{ y \in \mathbb {R}^q \mid \forall y^* \in \mathcal {O}^*_j:\; \varphi (y,y^*)\ge 0\}$ of inner approximations of $\mathcal {P}$ by geometric duality. Likewise, there is an expanding sequence $\mathcal {I}_j^* :=\{ y^* \in \mathbb {R}^q \mid \forall y \in \mathcal {O}_j:\; \varphi (y,y^*)\ge 0\}$ of inner approximations of $\mathcal {D}^*$ corresponding to the shrinking sequence of outer approximations $\mathcal {O}_j$ of $\mathcal {P}$. The white circle indicates the vertex of $\mathcal {O}_j$ chosen as t in line 18. The black dots label the corresponding points $t^*$, see line 20. Again, the gray dots indicate the calculated boundary points. The calculations are based on the choice of $c=(-0.25 , 1)^\intercal$ as inner point of C. Notice that even though we have $\mathcal {D}^*=\mathcal {O}^*_2$, the algorithm does not terminate after two iterations because t is not an element of $\mathcal {P}$. Another two iteration steps are required to identify the problems solution $(1.084,0.804)^\intercal$

Example 17

Consider the problem stated in Example 10. The first steps of Algorithm 4 are shown in Fig. 3.

6 Extension to the case of non-solid cones

The algorithms developed in Sects. 4 and 5 are based on the assumption that the cone C has a nonempty interior. Some $c \in {{\mathrm{int\,}}}C$ is required in Proposition 7 and for the duality results in Sect. 5.1.

As shown in [13], any vector linear program

$$\begin{aligned} \min \nolimits _C \;Px \quad \text {s.t.} \quad Ax \ge b \text {,} \end{aligned}$$

(VLP)

for $C=\{y \in \mathbb {R}^q \mid Z^{\intercal } y \ge 0\}$, can be reformulated as a vector linear program

We use $e$ to denote the vector whose entries are all equal to one of appropriate dimension. Observe that the ordering cone used in (VLP’) is the non-negative orthant $\mathbb {R}^{q+1}_+$. The relationship between the upper images $\mathcal {P}$ of (VLP) and $\mathcal {M}$ of (VLP’) can be described as follows. Consider the hyperplane $H:=\{y \in \mathbb {R}^{q+1} \mid e^{\intercal } y = 0\}$ and let $\pi : \mathbb {R}^{q+1} \rightarrow \mathbb {R}^q$ be the projection defined by $\pi (y_1,\dots ,y_q,y_{q+1}) :=(y_1,\dots ,y_q)$ (i.e. cancellation of the last component). Then

$$\begin{aligned} \mathcal {P}= \pi (\mathcal {M} \cap H)\text {.} \end{aligned}$$

The next result shows that assumption (B) is not satisfied for (VLP’) in most cases.

Proposition 18

Let $C\ne \{0\}$. If Problem (VLP’) is feasible, then it is unbounded.

Proof

Since $C \ne \{0\}$, there is a nonzero vector $c \in C$. Consider the vector

$$\begin{aligned} \bar{c}:=\begin{pmatrix} c \\ -e^\intercal c \end{pmatrix} \in \mathbb {R}^{q+1}\text {.} \end{aligned}$$

Let $\bar{z}$ be an arbitrary point in the upper image

$$\begin{aligned} \mathcal {M} = \left\{ \begin{pmatrix}z \\ \zeta \end{pmatrix} \big |\, \exists y \in \mathcal {P}:z \ge y,\; \zeta \ge -e^\intercal y \right\} \end{aligned}$$

of (VLP’) and $\lambda \ge 0$. Then $\bar{z} + \lambda \bar{c} \in \mathcal {M}$, i.e., $\bar{c}$ is a direction of $\mathcal {M}$. But obviously $\bar{c}$ does not belong to $\mathbb {R}^{q+1}_+$. Thus, (VLP’) is unbounded. $\square$

This problem can be solved by enlarging the ordering cone $\mathbb {R}^{q+1}_+$ appropriately. Let $Y \in \mathbb {R}^{q\times o}$ denote a matrix whose columns are generators of the cone C, that is, $C=\{ Y \mu \mid \mu \ge 0 \}$. Set

$$\begin{aligned} R :=\left\{ \left( I ,\begin{matrix} Y\\ -e^\intercal Y \end{matrix} \right) \begin{pmatrix}\lambda \\ \mu \end{pmatrix} \; \vert \; \lambda \in \mathbb {R}^{q+1}_+ ,\, \mu \in \mathbb {R}^{o}_+ \right\} \end{aligned}$$

and consider the problem

Problems (VLP) and (VLP”) are related in the following sense.

Proposition 19

Let $\mathcal {P}$ be the upper image of (VLP) and let $\mathcal {M}$ be the upper image of (VLP”). Then

$$\begin{aligned} \mathcal {P}= \pi (\mathcal {M} \cap H)\text {.} \end{aligned}$$

Proof

From the problem definitions we have

$$\begin{aligned} \mathcal {M}&= \left\{ \begin{pmatrix} z \\ \zeta \end{pmatrix} \big |\; \exists x \in S:\begin{pmatrix} z \\ \zeta \end{pmatrix} \ge _R \begin{pmatrix} Px \\ -e^\intercal Px \end{pmatrix} \right\} \\&= \left\{ \begin{pmatrix} z \\ \zeta \end{pmatrix} \big |\; \exists x \in S,\; \exists \mu \in \mathbb {R}^{o}_+:\begin{pmatrix} z \\ \zeta \end{pmatrix} - \begin{pmatrix} Px \\ -e^\intercal Px \end{pmatrix} \ge \begin{pmatrix} Y \\ -e^\intercal Y \end{pmatrix} \mu \right\} \text {.} \end{aligned}$$

Thus, we have

$$\begin{aligned} \mathcal {M} \cap H&= \left\{ \begin{pmatrix} z \\ -e^\intercal z \end{pmatrix} \big |\; \exists x \in S,\; \exists \mu \in \mathbb {R}^{o}_+:\begin{pmatrix} z- Px \\ -e^\intercal (z-Px) \end{pmatrix} \ge \begin{pmatrix} Y \mu \\ -e^\intercal Y \mu \end{pmatrix} \right\} \\&= \left\{ \begin{pmatrix} z \\ -e^\intercal z \end{pmatrix} \big |\; \exists x \in S,\; \exists \mu \in \mathbb {R}^{o}_+:z- Px = Y \mu \right\} \text {,} \end{aligned}$$

which implies the claim. $\square$

Let Problem (QCP) as defined in Sect. 3, in particular, let a quasi-concave function $f:\mathbb {R}^q \rightarrow \bar{\mathbb {R}}$, be given and let $C \subseteq \mathbb {R}^q$ be a polyhedral convex pointed cone such that the assumptions (M) and (B) are satisfied. We define

$$\begin{aligned} \bar{f} :\mathbb {R}^{q+1} \rightarrow \mathbb {R},\quad \bar{f} \left( \begin{pmatrix} y\\ \eta \end{pmatrix} \right) :={\left\{ \begin{array}{ll} f(y)&{} \text {if } e^\intercal y +\eta \geqslant 0\text {,}\\ -\infty &{}\text {otherwise.} \end{array}\right. } \end{aligned}$$

As f is quasi-concave on $\mathbb {R}^q$, $\bar{f}$ is quasi-concave on $\mathbb {R}^{q+1}$. Further, we define

$$\begin{aligned} \bar{P}:=\begin{pmatrix} P\\ -e^\intercal P \end{pmatrix}\text {.} \end{aligned}$$

The following quasi-concave problem is a reformulation of (QCP) with the same optimal solution:

The associated vector linear program is (VLP”).

Proposition 20

Let (M) be satisfied for (QCP) and cone $C$. Then assumption (M) does also hold for (QCP’) with respect to the cone $R$, i.e. $\bar{f}$ is $R$-monotone on the set $\bar{P}[S] - R$.

Proof

Consider $z^1\in \bar{P}[S]-R$, i.e.

$$\begin{aligned} z^1 = \begin{pmatrix} y - c^1\\ -e^\intercal (y -c^1) \end{pmatrix} - \sigma ^1 \end{aligned}$$

for $y\in P[S]$ and some $\sigma ^1\in \mathbb {R}^{q+1}_+, c^1\in C$. Furthermore, let $z^2\in \mathbb {R}^{q+1}$ with $z^2\leqslant _R z^1$, meaning

$$\begin{aligned} z^2&= z^1 - \begin{pmatrix} c^2\\ -e^\intercal c^2 \end{pmatrix} -\sigma ^2\\&= \begin{pmatrix} y - c^1 - c^2\\ -e^\intercal \left( y - c^1 - c^2\right) \end{pmatrix} -\left( \sigma ^1 + \sigma ^2\right) \end{aligned}$$

for some $\sigma ^2\in \mathbb {R}^{q+1}_+,c^2\in C$, be given. Then

$$\begin{aligned} \bar{f}(z^2) = {\left\{ \begin{array}{ll} f(y - c^1 - c^2) &{} \text {if }\sigma ^1 = \sigma ^2 = 0\\ -\infty &{}\text {otherwise} \end{array}\right. } \end{aligned}$$

holds. In the case $\sigma ^j = 0$ for $j=1,2$, due to condition (M) for (QCP), we get

$$\begin{aligned} \bar{f}(z^2)=f(y - c^1 - c^2) \leqslant f(y - c^1) = \bar{f}(z^1)\text {,} \end{aligned}$$

which proves the claim. $\square$

Proposition 21

Let (B) be satisfied for Problem (QCP) with cone $C$. Then (B) does also hold for (QCP’), i.e. $\bar{P}[S]$ is bounded with respect to $R$.

Proof

Let P[S] be C-bounded, i.e. it holds $0^+P[S] \subseteq C$. The claimed statement immediately follows from

$$\begin{aligned} 0^+\bar{P}[S] = \begin{pmatrix} 0^+P[S] \\ -e^\intercal \left( 0^+P[S] \right) \end{pmatrix} \subseteq \begin{pmatrix} C \\ -e^\intercal C \end{pmatrix} \subseteq R \, . \end{aligned}$$

$\square$

Let us summarize the results.

Corollary 22

The assumption ${{\mathrm{int\,}}}C \ne \emptyset$ can be dropped, when Algorithm 2 or Algorithm 4 is applied to the reformulated quasi-concave problem (QCP’).

For illustration reasons we close this section with an example.

Example 23

Consider the concave problem

$$\begin{aligned} \min \; y_1 -y_2^2 \quad \text {s.t.}\quad x\in S , \; y=Px \text {.} \end{aligned}$$

for a matrix $P \in \mathbb {R}^{2 \times n}$. Without any information about the structure of P[S] and due to the quadratic impact of $y_2$, the largest polyhedral monotonicity cone usable is $C=(1, 0)^\intercal \cdot \mathbb {R}_+$. This cone is obviously non-solid in $\mathbb {R}^2$. To illustrate the method discussed above we consider the problem

$$\begin{aligned} \min \; y_1 -y_2^2 \quad \text {s.t.}\quad -e \le x,\; x_1\le 1,\; x_3 \le 1, \; y=Px\text {,} \end{aligned}$$

where we set

$$\begin{aligned} P=\begin{pmatrix} 1 &{}\quad 1 &{}\quad -1 \\ 1 &{}\quad 0 &{}\quad 1\end{pmatrix}\text {.} \end{aligned}$$

The upper images $\mathcal {P}$ of (VLP) and $\mathcal {M}$ of (VLP”) are depicted in Fig. 4. Obviously both $(1,-1,1)^\intercal$ and $(-1,-1,-1)^\intercal$ solve the given problem with optimal value $-5$. Notice the solid recession cone of $\mathcal {M}$.

Fig. 4

Image P[S] and upper image $\mathcal {P}$ of (VLP) and upper image $\mathcal {M}$ of (VLP”) for Example 23. Notice the facet in $\mathcal {M}$ corresponding to $\mathcal {P}$

7 Numerical results

The present section contains various numerical examples. The package bensolve tools [14] for Gnu Octave / Matlab contains an implementation of the algorithms developed in this article. The test problems in this section are solved using bensolve tools with Gnu Octave on a computer with Intel$^{\textregistered }$ Core™ i7-6700HQ CPU with 2.6 GHz. For bensolve tools we use the default tolerance for numerical inaccuracies of $10^{-7}$. We compare these results to the running times achieved with BARON [19], the general purpose solver for mixed-integer nonlinear optimization problems. The convergence tolerance of BARON is also set to $10^{-7}$.

7.1 Linear multiplicative programs

Shao and Ehrgott [18] treat the problem class of linear multiplicative programs. For $c_i,l,u\in \mathbb {R}^n, b \in \mathbb {R}^m, d_i \in \mathbb {R}$ and $A \in \mathbb {R}^{m \times n}$, they consider the problem

The parameters $c_i,d_i$ of the objective function and the constraint set in (LMP) is chosen in such a way that $c_i^\intercal x +d_i >0$ holds for all feasible points. In the following example we generate random instances in the same way as Shao and Ehrgott [18].

Example 24

Let A consist of equally distributed random real numbers out of the interval [0, 10]. The vectors $c_i$ and b are generated in the same way. The variable bounds are set to $l_j=0$ and $u_j=100$. For the sake of simplicity, we set $d_i=0$. We can now transform (LMP) to an equivalent problem of type (QCP):

$$\begin{aligned} \min f(Px) \quad \text {s.t.}\quad \left\{ \begin{aligned} b&\le Ax\text {,}\\ l&\le x \le u\text {,} \end{aligned} \right. \end{aligned}$$

where the rows of P consist of $c_i^\intercal$ from (LMP) and the objective $f$ is defined as

$$\begin{aligned} f(y) = {\left\{ \begin{array}{ll} \prod \limits _{i=1}^q y_i&{} \text {if }y \in \mathbb {R}^q_+,\\ -\infty &{} \text {else.} \end{array}\right. } \end{aligned}$$

Then $f$ is a quasi-concave function being $\mathbb {R}^q_+$-monotone on the whole space $\mathbb {R}^q$.

The dual algorithm introduced in [18] is similar to ours, but a different vertex selection rule is used: While in line 20 of Algorithm 4 we determine a vertex $t^*$ of $\mathcal {O}^*{\setminus } T^*$ such that $\varphi (t,t^*)$ is minimal, in [18, Algorithm 3.17, step (k1)] an arbitrary vertex $t^*$ of $\mathcal {O}^*$ with $\varphi (t,t^*)<0$ is chosen. In order to compare the different vertex selection rules, we also implement Algorithm 4 with the vertex selection rule from [18]. This modification is denoted by Algorithm 4*. In Table 1 we compare the running times of Algorithms 2, 4 and 4* to the times BARON needs to solve the problem instances of Example 24. For reference, we also include the average running times for this problem class as reported in [18], where a personal computer with 2.5 GHz CPU and 4 GB RAM is used for the computations.

Table 1 Average running time in seconds and number of iterations in parentheses for ten randomly generated instances of Example 24 of Algorithm 2 and Algorithm 4. Algorithm 4* is a modified version of Algorithm 4 utilizing Shao and Ehrgott’s vertex selection rule. The two columns primal and dual contain the average running times of the respective algorithm taken from [18]. The fourth column lists the average running times achieved by global optimization solver BARON. A ‘–’ indicates that at least one test instance of the respective size was not solved within 600 seconds

The dual vertex $t^*$ chosen in Algorithm 4, line 20 may generate a half-space in the following iteration step which contains the currently selected primal vertex $t$ (line 18). In this case the algorithm fails to cut off the vertex $t$ in line 11, and thus fails to improve the current lower bound. We call occurences of this case a failed cut. In Table 2 we compare the number of such failed cuts generated by Algorithm 4 and the modification of this algorithm with the vertex selection rule of [18] (Algorithm 4*).

Table 2 Average number of failed cuts for Algorithm 4 and Algorithm 4$^*$ for Example 24. The data was generated by averaging the results of 10 different instances with 100 constraints and 60 variables for each value of q

7.2 Concave quadratic programs

Let $M\in \mathbb {R}^{n \times n}$ be a positive semi-definite symmetric matrix with $M = P^\intercal P$ for some matrix $P\in \mathbb {R}^{q\times n}$. The problem

where $S\subseteq \mathbb {R}^n$ is a polytope, is a concave quadratic optimization problem. Problem (CQP) can be transformed to (QCP) by using the concave objective function $f:\mathbb {R}^q\rightarrow \mathbb {R}$ defined by $f(y)= -y^\intercal y$. We obtain

$$\begin{aligned} -x^\intercal Mx = f(Px)\text {.} \end{aligned}$$

Monotonicity holds for the trivial cone $C= \{\,0\,\}$. Hence, Algorithms 2 and 4 can be applied to solve (CQP) using the techniques discussed in Sect. 6.

Example 25

([12, Example 23]) For $q,n \in \mathbb {N}$, let $P \in \mathbb {R}^{q \times n}$ be defined as

$$\begin{aligned} P_{ij}=\left\lfloor q \cdot \sin \left( \left( j-1 \right) \cdot q +i \right) \right\rfloor \text {,} \end{aligned}$$

where $\lfloor x\rfloor :=\max \{z \in \mathbb {Z}\mid z \le x\}$. Then $M :=P^\intercal P$ is a positive semi-definite symmetric matrix. We solve (QCP) with $f(y)=y^\intercal y$, matrix $P$ as defined above and feasible region $S=\left\{ x \in \mathbb {R}^n \,\big |\, -e \le x \le e \right\}$. We compare our results to the ones achieved by the non-convex problem solver BARON , see [17], and to the results of the approach taken in [12]. The numerical results are listed in Table 3.

Table 3 Numerical results for the concave quadratic program of Example 25. Running times are given in seconds. Again, no number given in the column corresponding to BARON indicates the exceeding of 600 s given. The last column contains results of [12] obtained by a DC-programming reformulation and using an unmodified MOLP solver

7.3 DC-programs

Recall the problem class of DC-programs with one polyhedral component introduced in Examples 1 and 2 in the introduction, which were shown to be special cases of (QCP).

Example 26

We want to solve the following problem from [5] and discussed in [12]:

$$\begin{aligned} \min _{x \in S} g(x)-h(x) \text {,} \end{aligned}$$

(13)

where

$$\begin{aligned}&g(x)=|x_1 -1 |+200 \sum _{i=2}^q \max \left\{ 0, |x_{i-1} |-x_i \right\}&\text {and}&h(x)=100 \sum _{i=2}^q \left( |x_{i-1} |-x_i \right) \text {.} \end{aligned}$$

The feasible region is $S=\left\{ x \in \mathbb {R}^q \,\big |\, -10 \cdot e \le x \le 10 \cdot e \right\}$. Both of the given functions are polyhedral. Hence, by following the procedure in the introducing section (Examples 1 and 2) we obtain the two equivalent problems

$$\begin{aligned} \min r -h(x) \quad \text {s.t. }(x,r) \in {{\mathrm{epi\,}}}\hat{g} \end{aligned}$$

and

$$\begin{aligned} \min r^* -\hat{g}^*(x^*) \quad \text {s.t. } (x^*,r^*) \in {{\mathrm{epi\,}}}h^*, \end{aligned}$$

where we set

$$\begin{aligned} \hat{g}(x) :={\left\{ \begin{array}{ll} g(x)&{} \text {if }x \in S,\\ +\infty &{} \text {else.} \end{array}\right. } \end{aligned}$$

We can now solve our initial problem by solving one of the two problems above. They both have a polyhedral feasible region and concave objective functions. The objectives of both problems are monotone with respect to the cone $C = \left\{ (0,\ldots ,0,t)^\intercal \in \mathbb {R}^{q + 1}\,\big |\,t\ge 0\right\}$. As ${{\mathrm{int\,}}}C = \emptyset$, this problem is solved by using the extension discussed in Sect. 6. The optimal value of (13) is $0$, and a solution is given by $e\in \mathbb {R}^q$. In Table 4 we list numerical results for Algorithm 2 compared to the ones obtained in [12] and [5]. BARON solves any instance of this problem in 0.01 s. This is probably due to the simple structure of the solution.

Table 4 Running time in seconds for Example 26. The first two columns are results of [4] obtained by the DC extended cutting angle method (DCECAM) and the DC prismatic algorithm (DCPA). It should be pointed out that these two methods do not require one of the two objective functions to be polyhedral. Thus, they are capable of solving more general problems than we do in this article. The next two columns, DC and DC$^*$, are results of [12] obtained by using an unmodified MOLP solver. The last two columns, QCP and QCP$^*$, are results obtained by the extension of Algorithm 2 using the cone $\mathbb {R}_+ \cdot \left( 0,\ldots ,0,1 \right) ^\intercal$. DC and QCP are based on the primal approach in Example 1. DC$^*$ and QCP$^*$ are based on the dual approach outlined in Example 2

7.4 Minimizing a convex function over the boundary of a polytope

Example 3 in the introduction motivates the class (QCP) by the problem to minimize a Lipschitz continuous convex function g over the boundary of a polytope Q. To this end, the optimization problem (3) is reformulated as the DC optimization problem (4), which depends on a sufficiently large constant $c>0$. Let $L>0$ be the Lipschitz constant of g as a function defined on Q, that is,

$$\begin{aligned} \forall x,y \in Q:g(x)-g(y) \le L ||x-y||\text {,} \end{aligned}$$

(14)

where $||\cdot ||$ denotes the Euclidean norm. The next statement provides a proper choice of the parameter c in dependence of L.

Proposition 27

Let $Q=\left\{ x \in \mathbb {R}^q \,\big |\, \exists u \in \mathbb {R}^k:A x + B u \ge b\right\}$ be a polytope with $0 \in {{\mathrm{int\,}}}Q$ and let $g:\mathbb {R}^q \rightarrow \mathbb {R}\cup \{\,+\infty \,\}$ be a convex function such that (14) holds. Let $R\in \mathbb {R}$ with

$$\begin{aligned} R \ge \max \left\{ ||x||\,\big |\, x \in Q\right\} \text {.} \end{aligned}$$

When the parameter c in Problem (4) is chosen such that $c > L R$, then (3) and (4) have the same set of optimal solutions and the same optimal value.

Proof

First note that the objective functions of (3) and (4) coincide on the boundary of Q. Hence, it suffices to show that every optimal solution of (4) belongs to the boundary of Q. Assume that an optimal solution $x^*$ of (4) belongs to the interior of Q. We start with the case where $x^* \ne 0$. There exists $\mu > 1$ such that $\mu x^* \in Q$ and we have

$$\begin{aligned} g(\mu x^*) - (h_c(\mu x^*) - c) \ge g(x^*) - (h_c(x^*)-c)\text {.} \end{aligned}$$

Thus

$$\begin{aligned} L (\mu -1) ||x^* ||\ge g(\mu x^*) - g(x^*) \ge h_c(\mu x^*) - h_c(x^*) \ge \frac{c}{R} (\mu -1) ||x^* ||\text {,} \end{aligned}$$

where the latter inequality follows from the fact that the epigraph of $h_c$ is the cone generated by the set $Q \times \{c\}$. Hence $L R \ge c$, which contradicts the assumption $LR < c$. The case $x^*=0$ can be shown likewise by replacing $\mu x^*$ by some arbitrary $x \in Q {\setminus } \{0\}$. $\square$

Example 28

Let q, m be positive integers with $q\le m$ and let $P \in \mathbb {R}^{q \times m}$ be the matrix described in Example 25. Furthermore let $S=\left\{ u \in \mathbb {R}^m \, | \, -e \le u \le e \right\}$. We intend to solve the problem

$$\begin{aligned} \min _{x \in {{\mathrm{bd\,}}}P[S]} x^\intercal x\text {.} \end{aligned}$$

(15)

Note that the polyhedron $Q:=P[S]$ is given by a P-representation

$$\begin{aligned} Q=\left\{ x \in \mathbb {R}^p \,\vert \, \exists u \in \mathbb {R}^m:u \in S , x=Pu \right\} \text {.} \end{aligned}$$

Following the procedure described in Example 3 we obtain a DC optimization problem as considered in Example 2. We set

$$\begin{aligned} g(x)= {\left\{ \begin{array}{ll} x^\intercal x&{} \text {if }x \in Q, \\ \infty &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

Thus, the conjugate in (2) is obtained by solving the quadratic convex program

$$\begin{aligned} -g^*(y) = \min _{x \in Q} \{\,x^\intercal x - y^\intercal x\,\}\text {.} \end{aligned}$$

(16)

The definition of the polyhedral convex function $h$ in Example 3 requires the parameter $c$ being sufficiently large. Let r be the vector of row sums of absolute values in P. We choose $c$, according to Proposition 27 with $R = ||r||$ and Lipschitz-constant $L = 2||r||$ of $g$, as $c:=2 ||r ||^2+1$. A representation of $h^*$, as needed in (2), is obtained as described in [12, Proposition 6].

Numerical results of Algorithm 2 applied to this problem are listed in Table 5. Problem (15) cannot be solved by BARON in the way described above, as BARON requires explicitly expressed algebraic functions, see [17].

Table 5 Running time in seconds for Example 28 using Algorithm 2 and Octaves’s sqp solver for solving (16)

8 Conclusion

The contribution of this article can be summarized as follows:

We generalize the approach of Mittal and Schulz [16] with respect to the following three aspects: First, the objective function is not supposed to have a certain scaling property at the price of loosing polynomial running time. Secondly, our approach is based on Benson-type algorithms for MOLPs instead of using grid-based scalarization parameters. Thirdly, we allow polyhedral ordering cones C which are more general than $\mathbb {R}^q_+$ in order to weaken the monotonicity assumption to the objective function. In particular, in Sect. 6 we even allow the cone $C=\{0\}$, which means that no monotonicity assumption is required. We present a technique that allows to treat the case of ${{\mathrm{int\,}}}C = \emptyset$ even though the VLP solver requires an ordering cone C with nonempty interior.

The results of Shao and Ehrgott [18] for multiplicative linear programs (compare Example 4) are generalized to the class (QCP). Moreover, we suggest an improvement of the dual algorithm introduced in [18], which consists of a vertex selection rule based on the strongest violation of an optimality condition.

The results of [12], where a MOLP solver without any modification was used to solve the problem classes of Examples 1 and 2 are generalized and improved, since the approach we introduced requires less iteration steps, in general. Numerical examples show that our approach via (a modified) VLP solver is competitive with the global optimization software BARON [17].