1 Problem formulations and solution concepts

Let k, n, p be positive integers and let two matrices \(G \in \mathbb {R}^{k \times n},\;H\in \mathbb {R}^{k \times p}\) and a vector \(h \in \mathbb {R}^k\) be given. We consider the problem of polyhedral projection, that is,

$$\begin{aligned} \text {Compute } Y = {\left\{ y \in \mathbb {R}^p |\;\exists x \in \mathbb {R}^n: G x + H y \ge h \right\} }. \end{aligned}$$
(PP)

A point \((x,y) \in \mathbb {R}^n \times \mathbb {R}^p\) is said to be feasible for (PP) if it satisfies \(G x + H y \ge h\). A direction \((x,y) \in \mathbb {R}^n \times (\mathbb {R}^p\!\setminus \!\{0\})\) is said to be feasible for (PP) if it satisfies \(G x + H y \ge 0\). A pair \((X^\mathrm{poi},X^\mathrm{dir})\) is said to be feasible for (PP) if \(X^\mathrm{poi}\) is a nonempty set of feasible points and \(X^\mathrm{dir}\) is a set of feasible directions.

We use proj\(:\mathbb {R}^{n+p}\rightarrow \mathbb {R}^{p}\) to denote the projection of a set \(X \subseteq \mathbb {R}^{n+p}\) onto its last p components. For a nonempty set \(B\subseteq \mathbb {R}^p,\;\mathrm{conv \,}B\) is the convex hull, and \(\mathrm{cone\,}B:={\left\{ \lambda x |\;\; \lambda \ge 0,\; x \in \mathrm{conv \,}B \right\} }\) is the convex cone generated by this set. We set \(\mathrm{cone\,}\emptyset := {\left\{ 0 \right\} }\).

Definition 1

A pair \((X^\mathrm{poi},X^\mathrm{dir})\) is called a solution to (PP) if it is feasible, \(X^\mathrm{poi}\) and \(X^\mathrm{dir}\) are finite sets, and

$$\begin{aligned} Y = \mathrm{conv \,}\hbox {proj} X^\mathrm{poi}+ \mathrm{cone\,}\hbox {proj} X^\mathrm{dir}. \end{aligned}$$
(1)

For positive integers n, m, q, r, let \(A \in \mathbb {R}^{m\times n},\;P \in \mathbb {R}^{q \times n},\;Z \in \mathbb {R}^{q \times r}\) and \(b \in \mathbb {R}^m\) be given. Consider the vector linear program

$$\begin{aligned} \text {minimize } Px \text { s.t. } A x \ge b, \end{aligned}$$
(VLP)

where minimization is understood with respect to the ordering cone

$$\begin{aligned} C:={\left\{ y \in \mathbb {R}^q |\;Z^T y \ge 0 \right\} }. \end{aligned}$$

This means that we use the ordering

$$\begin{aligned} w \le _C y \quad :\Leftrightarrow \quad y-w \in C \quad \Leftrightarrow \quad Z^T w \le Z^T y. \end{aligned}$$
(2)

We assume \( \ker Z^T := {\left\{ y \in \mathbb {R}^q |\;Z^T y = 0 \right\} } = {\left\{ 0 \right\} }\), which implies that the ordering cone C is pointed. Thus, (2) defines a partial ordering. If Z is the \(q\times q\) unit matrix, (VLP) reduces to a multiple objective linear program. This special class of (VLP) is denoted by (MOLP).

A point \(x \in \mathbb {R}^n\) is called feasible for (VLP) if it satisfies the constraint \(A x \ge b\). A direction \(x \in \mathbb {R}^n \!\setminus \!\{0\}\) is called feasible for (VLP) if \(A x \ge 0\). The feasible set of (VLP) is denoted by

$$\begin{aligned} S:={\left\{ x \in \mathbb {R}^n |\;A x \ge b \right\} }. \end{aligned}$$

A pair \((S^\mathrm{poi}, S^\mathrm{dir})\) is called feasible for (VLP) if \(S^\mathrm{poi}\) is a nonempty set of feasible points and \(S^\mathrm{dir}\) is a set of feasible directions. The recession cone of S is the set \(0^+S = {\left\{ x \in \mathbb {R}^n |\;A x \ge 0 \right\} }\). This means that \(0^+S\!\setminus \!\{0\}\) represents the set of feasible directions. We refer to a homogeneous problem (associated to (VLP)) if the feasible set S is replaced by \(0^+S\).

For a set \(X \subseteq \mathbb {R}^n\), we write \(P[X]:={\left\{ P x |\;x \in X \right\} }\). The set

$$\begin{aligned} \mathcal {P}:=P[S]+C = {\left\{ y \in \mathbb {R}^q |\; \exists x \in \mathbb {R}^n, Z^T y \ge Z^T P x,\; Ax \ge b \right\} } \end{aligned}$$

is called the upper image of (VLP).

Definition 2

A point \(x \in S\) is said to be a minimizer for (VLP) if there is no \(v \in S\) such that \(P v \le _C P x,\;P v \ne P x\), that is,

$$\begin{aligned} x \in S,\quad P x \not \in P[S] + C\!\setminus \!\{0\}. \end{aligned}$$

A direction \(x \in \mathbb {R}^n \!\setminus \!\{0\}\) of S is called a minimizer for (VLP) if the point x is a minimizer for the homogeneous problem. This can be expressed equivalently as

$$\begin{aligned} x \in (0^+ S) \!\setminus \!\{0\},\quad P x \not \in P[0^+ S] + C\!\setminus \!\{0\}. \end{aligned}$$

If \((S^\mathrm{poi}, S^\mathrm{dir})\) is feasible for (VLP) and the sets \(S^\mathrm{poi},\;S^\mathrm{dir}\) are finite; and if

$$\begin{aligned} \mathrm{conv \,}P[S^\mathrm{poi}] + \mathrm{cone\,}P[S^\mathrm{dir}] + C = \mathcal {P}, \end{aligned}$$
(3)

then \((S^\mathrm{poi}, S^\mathrm{dir})\) is called a finite infimizer for (VLP).

A finite infimizer \((S^\mathrm{poi}, S^\mathrm{dir})\) is called a solution to (VLP) if its two components consist of minimizers only.

This solution concept for (VLP) has been introduced in Löhne (2011). It can be motivated theoretically by a combination of minimality and infimum attainment established in Heyde and Löhne (2011). Its relevance for applications has been already discussed indirectly in earlier papers, see e.g. Dauer (1987), Dauer and Liu (1990), Benson (1998), Ehrgott et al. (2012). The solver Bensolve (see Löhne and Weißing 2015, 2016) uses this concept.

2 Equivalence between (PP), (MOLP) and (VLP)

As a first result, we show that a solution of (PP) can be easily obtained from a solution of the following multiple objective linear program

$$\begin{aligned} \min \left( \begin{array}{c} y \\ -e^T y \end{array}\right) \text { s.t. } G x + H y \ge h, \end{aligned}$$
(4)

where \(e := (1,\dots ,1)^T\). Both problems (PP) and (4) have the same feasible set but (4) has one additional objective space dimension.

Theorem 3

Let a polyhedral projection problem (PP) be given. If (PP) is feasible, then a solution \((S^\mathrm{poi},S^\mathrm{dir})\) (compare Definition 2) of the associated multiple objective linear program (4) exists. Every solution \((S^\mathrm{poi},S^\mathrm{dir})\) of (4) is also a solution of (PP) (Definition 1).

Proof

Since (PP) is feasible, the projected polyhedron Y is nonempty. Thus it has a finite representation. This implies that a solution \(\mathcal {X}=(X^\mathrm{poi},X^\mathrm{dir})\) of (PP) exists. We show that \(\mathcal {X}\) is also a solution of the associated multiple objective linear program (4). \(\mathcal {X}\) is feasible for (4) and its two components are finite sets. By (1), we have

$$\begin{aligned} P[S] = {\left\{ \left( \begin{array}{c}y\\ -e^T y\end{array}\right) \bigg |\; y \in Y \right\} } = \mathrm{conv \,}P[X^\mathrm{poi}] + \mathrm{cone\,}P[S^\mathrm{dir}] \end{aligned}$$

which implies (3) for \(C=\mathbb {R}^{p+1}_+\), i.e., \(\mathcal {X}\) is a finite infimizer. We have

$$\begin{aligned} P[S] \subseteq {\left\{ y \in \mathbb {R}^{p+1} |\;e^T y = 0 \right\} }, \end{aligned}$$

which implies that all points and directions of S are minimizers. Thus \(\mathcal {X}\) consists of minimizers only. We conclude that a solution of (4) exists.

Let \(\mathcal {S}=(S^\mathrm{poi},S^\mathrm{dir})\) be an arbitrary solution of (4). By (3) we have

$$\begin{aligned} \mathrm{conv \,}P[S^\mathrm{poi}] + \mathrm{cone\,}P[S^\mathrm{dir}] + \mathbb {R}^{p+1} _+= P[S] + \mathbb {R}^{p+1}_+, \end{aligned}$$
(5)

where \(\mathbb {R}^{p+1} _+\) denotes the nonnegative orthant. We show that

$$\begin{aligned} \mathrm{conv \,}P[S^\mathrm{poi}] + \mathrm{cone\,}P[S^\mathrm{dir}] = P[S] \end{aligned}$$
(6)

holds. The inclusion \(\subseteq \) is obvious by feasibility. Let \(y \in P[S]\), then \(e^T y = 0\). By (5), \(y \in B + \mathbb {R}^{p+1}_+\) for \(B:=\mathrm{conv \,}P[S^\mathrm{poi}] + \mathrm{cone\,}P[S^\mathrm{dir}]\). There is \(v \in B\) and \(c \in \mathbb {R}^{p+1}_+\) such that \(y = v + c\). Assuming that \(c \in \mathbb {R}^{p+1}_+\!\setminus \!\{0\}\) we obtain \(e^T c > 0\). But \(B \subseteq P[S]\) and hence the contradiction \(0 = e^T y = e^T v + e^T c > 0\). Thus (6) holds. Omitting the last components of the vectors occurring in (6), we obtain (1), which completes the proof. \(\square \)

Of course, (MOLP) is a special case of (VLP). In order to obtain equivalence between (VLP), (MOLP) and (PP), it remains to show that a solution of (VLP) can be obtained from a solution of (PP). We assign to a given (VLP) the polyhedral projection problem

$$\begin{aligned} \text {compute } \mathcal {P}= {\left\{ y \in \mathbb {R}^p |\;\exists x \in \mathbb {R}^n :\, Z^T y \ge Z^T Px,\; A x \ge b \right\} }. \end{aligned}$$
(7)

Obviously, (VLP) is feasible if and only if (7) is feasible. The next result states that a solution of (VLP), whenever it exists, can be obtained from a solution of the associated polyhedral projection problem (7). This result is prepared by the following proposition. The main idea is that non-minimal points and directions can be omitted in a certain representation of a nonempty closed convex set.

Proposition 4

Let a nonempty compact set \(V \subseteq \mathbb {R}^q\) of points and a compact set \(R \subseteq \mathbb {R}^q\setminus {\left\{ 0 \right\} }\) of directions be given and define \(\mathcal {P}:= \mathrm{conv \,}V + \mathrm{cone\,}R\). Furthermore, let \(C \subseteq \mathbb {R}^q\) be a nonempty closed convex cone. If \(\mathcal {P}+ C \subseteq \mathcal {P}\) and

$$\begin{aligned} L \cap C = {\left\{ 0 \right\} }, \end{aligned}$$
(8)

where \(L:=0^+\mathcal {P}\cap -0^+\mathcal {P}\) is the lineality space of \(\mathcal {P}\), then

$$\begin{aligned} \mathcal {P}= \mathrm{conv \,}\bigl ( V\setminus (\mathcal {P}+C\setminus {\left\{ 0 \right\} }) \bigr ) + \mathrm{cone\,}\bigl ( R\setminus (0^+\mathcal {P}+C\setminus {\left\{ 0 \right\} }) \bigr ) + C. \end{aligned}$$

Proof

The inclusion \(\supseteq \) is obvious. To show the reverse inclusion, let U be a linear subspace complementary to L. Since V and R are compact, and \(V \ne \emptyset ,\;\mathcal {P}\) is a nonempty closed convex set. Then the set \({{\mathrm{ext}}}(\mathcal {P}\cap U)\) of extreme points of \(\mathcal {P}\cap U\) is nonempty, see e.g. Grünbaum (2003, Sect.2.4). An element \(v \in {{\mathrm{ext}}}(\mathcal {P}\cap U)\) admits the representation

$$\begin{aligned} v = \sum _{j\in J}\lambda _j v^j + \sum _{i\in I}\mu _i r^i, \end{aligned}$$

with finite index sets J and \(I,\;v^j \in V,\;\lambda _j\ge 0\) for \(j\in J,\;\sum _{j\in J} \lambda _j = 1\), and \(r^i \in R,\;\mu _i \ge 0\) for \(i\in I\). Every \(v^j\) and \(r^i\) may be decomposed by means of \(v^j = v^j_ U + v^j_ L\) and \(r^i = r^i_ U + r^i_ L\) with \(v^j_ U,r^i_ U\in U\) and \(v^j_ L,r^i_ L\in L\). Therefore,

$$\begin{aligned} v = \sum _{j \in J}\lambda _j v^j_ U +\sum _{i \in I}\mu _i r^i_ U +\underbrace{ \sum _{j \in J}\lambda _j v^j_ L + \sum _{i \in I}\mu _i r^i_ L }_{{}\in L}. \end{aligned}$$

Because \(v\in U\), the last two sums vanish. In the resulting representation

$$\begin{aligned} v = \sum _{j \in J}\lambda _j v^j_ U + \underbrace{\sum _{i \in I}\mu _i r^i_ U}_{{}=0} \end{aligned}$$

the second sum equals to zero because v is an extremal point. For the same reason, \(v^j_ U = v\) for every j with \(\lambda _j>0\) follows. Hence, \(v^j = v + v^j_ L\).

Assume that \(v^j \in \mathcal {P}+ C\setminus {\left\{ 0 \right\} }\). There exist \(y\in \mathcal {P}\) and \(c\in C\setminus {\left\{ 0 \right\} }\) such that \(v^j = y + c\). With decompositions \(y=y_ L + y_ U\) and \(c=c_ L + c_ U\), where \(c_ U \ne 0\) (because of condition (8) and \(c\ne 0\)), this leads to

$$\begin{aligned} v + v^j_ L = v_j = y_ U + y_ L + c_ U + c_ L, \end{aligned}$$

whence

$$\begin{aligned} v = y_ U + c_ U + \underbrace{y_ L + c_ L - v^j_ L}_{{}=0}. \end{aligned}$$

Again, the last part being zero results from v being an element of U. Let \(\mu \in (0,1)\) be given. As a linear combination of elements of \(U,\;y_ U + \frac{1}{\mu } c_ U\) belongs to U. On the other hand,

$$\begin{aligned} y_ U + \frac{1}{\mu } c_ U = \underbrace{y+\frac{1}{\mu } c}_{{}\in \mathcal {P}} \underbrace{-y_ L -\frac{1}{\mu } c_ L}_{{}\in L} \in \mathcal {P}. \end{aligned}$$

Hence, \(y_ U+\frac{1}{\mu } c_ U \in \mathcal {P}\cap U\). By adding a meaningful zero, a representation of v,

$$\begin{aligned} v&= y_ U + c_ U\\&= \mu \left( y_ U + \frac{1}{\mu }c_ U \right) + (1-\mu )y_ U, \end{aligned}$$

as a convex combination of different points of \(\mathcal {P}\cap U\) is found, which contradicts v being an extremal point. Thus, \(v^j \notin \mathcal {P}+ C\setminus {\left\{ 0 \right\} }\); and altogether

$$\begin{aligned} {{\mathrm{ext}}}(\mathcal {P}\cap U) \subseteq V\setminus (\mathcal {P}+C\setminus {\left\{ 0 \right\} }) + L. \end{aligned}$$
(9)

Now an extremal direction \(r\in 0^+{\left( \mathcal {P}\cap U\right) }\) is considered. Since V and R are compact, \(\mathcal {P}= \mathrm{conv \,}V + \mathrm{cone\,}R\) implies \(0^+\mathcal {P}= \mathrm{cone\,}R\) (see e.g. Rockafellar (1972, Corollary 9.1.1)). Thus, a representation

$$\begin{aligned} r = \sum _{j \in J}\mu _j r^j_ U + \underbrace{\sum _{j \in J}\mu _j r^j_ L}_{{}=0} \end{aligned}$$

by \(r^j = r^j_U + r^j_L \in R\) can be obtained. From extremality of r it follows that all \(r^j_U\ne 0\) with \(\mu _j > 0\) coincide with r up to positive scaling. Such an j is taken and, without loss of generality, one may assume \(\mu _j=1\), i.e.:

$$\begin{aligned} r^j = r+r^j_L. \end{aligned}$$

We show that

$$\begin{aligned} r^j \in \left( R\setminus \left( 0^+\mathcal {P}+C\setminus {\left\{ 0 \right\} }\right) \right) \cup (C+L). \end{aligned}$$
(10)

Indeed, let \(r^j\in 0^+\mathcal {P}+C\setminus {\left\{ 0 \right\} }\), that is, \(r^j = y^h + c\) for \(y^h \in 0^+\mathcal {P}\) and \(c\in C\setminus {\left\{ 0 \right\} }\). We need to show that \(r^j \in C+L\) follows. If \(y^h\in L\), this is obvious. Thus, let \(y^h\not \in L\). Consider the decompositions \(y^h = y^h_U +y^h_L\) and \(c = c_U+c_L\) with \(y^h_U,c_U\in U,\;y^h_L,c_L\in L,\;y^h_U\ne 0\) and, by (8), \(c_U \ne 0\). We obtain

$$\begin{aligned} r+r^j_L = r^j = y^h_U+y^h_L + c_U + c_L. \end{aligned}$$

Since \(r \in U\),

$$\begin{aligned} r = y^h_U + c_U + y^h_L+c_L-r^j_L= y^h_U + c_U. \end{aligned}$$

From \(L\subseteq 0^+\mathcal {P}\) the inclusion \(0^+\mathcal {P}+L\subseteq 0^+\mathcal {P}\) and subsequently \(y^h_U \in 0^+\mathcal {P}- {\left\{ y^h_L \right\} }\subseteq 0^+\mathcal {P}\) is deduced. Moreover, \(c_U\in C+L \subseteq C + 0^+\mathcal {P}\subseteq 0^+\mathcal {P}\). Noted that \(0^+(\mathcal {P}\cap U) = 0^+\mathcal {P}\cap U\), both directions \(y^h_u\) and \(c_U\) are in \(0^+(\mathcal {P}\cap U)\). Therefore the representation of \(r = y^h_U + c_U\) as conic combination of elements of \(0^+(\mathcal {P}\cap U)\), in which r was supposed to be extremal, proves equality of \(r,y^h_U\) and \(c_U\) up to positive scaling. This implies \(r\in C+L\) and \(r^j \in C+L\).

From (10) we deduce

$$\begin{aligned} r^j \in \mathrm{cone\,}\left( R\setminus \left( 0^+\mathcal {P}+C\setminus {\left\{ 0 \right\} }\right) \right) +C + L \end{aligned}$$

and hence

$$\begin{aligned} 0^+(\mathcal {P}\cap U)\subseteq \mathrm{cone\,}\left( R\setminus (0^+\mathcal {P}+ C\setminus {\left\{ 0 \right\} }) \right) + C + L. \end{aligned}$$
(11)

Any lineality direction \(l\in L\) can be represented by a conic combination of elements of \(R:\;l = \sum _{j\in J} \mu _j l^j\). For any \(l^k\) with \(\mu _k >0\) this results in

$$\begin{aligned} l^k = \frac{1}{\mu _k}\left( l - \sum _{j \in J\setminus {\left\{ k \right\} }}\mu _j l^j\right) \in - 0^+\mathcal {P}\end{aligned}$$

and therefore in \(l^k \in L\). If such an \(l^k\) is an element of \( 0^+\mathcal {P}+C\), then there exist \(r\in 0^+\mathcal {P}\) and \(c\in C\) with \(l^k = r + c\). This implies

$$\begin{aligned} c = \underbrace{l^k-r}_{{}\in - 0^+\mathcal {P}} \in L, \end{aligned}$$

and by (8), \(c=0\) follows. Therefore, \(l^k\in R\setminus (0^+\mathcal {P}+C\setminus {\left\{ 0 \right\} })\), resulting in

$$\begin{aligned} L\subseteq \mathrm{cone\,}\left( R\setminus (0^+\mathcal {P}+C\setminus {\left\{ 0 \right\} }) \right) . \end{aligned}$$
(12)

Combining the results (12) and (11) yields

$$\begin{aligned} L + 0^+ (\mathcal {P}\cap U)&\subseteq L + \mathrm{cone\,}\left( R\setminus (0^+\mathcal {P}+ C\setminus {\left\{ 0 \right\} }) \right) + C + L\\&\subseteq \mathrm{cone\,}\left( R\setminus (0^+\mathcal {P}+ C\setminus {\left\{ 0 \right\} }) \right) + C. \end{aligned}$$

Using (9) and the decomposition \(\mathcal {P}= L + \left[ \mathcal {P}\cap U\right] \), we obtain

$$\begin{aligned} \mathcal {P}&= L + (\mathcal {P}\cap U)\\&= L + \left( \mathrm{conv \,}{{\mathrm{ext}}}(\mathcal {P}\cap U) + 0^+(\mathcal {P}\cap U) \right) \\&\subseteq \mathrm{conv \,}\left( V\setminus (\mathcal {P}+C\setminus {\left\{ 0 \right\} }) \right) +\mathrm{cone\,}\left( R\setminus (0^+\mathcal {P}+C\setminus {\left\{ 0 \right\} }) \right) + C, \end{aligned}$$

which proves the claim. \(\square \)

Theorem 5

Let a vector linear program (VLP) be given. If (VLP) is feasible, a solution of the associated polyhedral projection problem (7) according to Definition 1 exists. Let \(\mathcal {X}=(X^\mathrm{poi},X^\mathrm{dir})\) be a solution of (7). Assume that (8) is satisfied and set

$$\begin{aligned} S^\mathrm{poi}:= & {} {\left\{ x \in \mathbb {R}^n |\;(x,y) \in X^\mathrm{poi},\; y \not \in \mathcal {P}+ C\!\setminus \!\{0\} \right\} },\\ S^\mathrm{dir}:= & {} {\left\{ x \in \mathbb {R}^n |\;(x,y) \in X^\mathrm{dir},\; y \not \in 0^+ \mathcal {P}+ C\!\setminus \!\{0\} \right\} }. \end{aligned}$$

Then \((S^\mathrm{poi},S^\mathrm{dir})\) is a solution of (VLP) in the sense of Definition 2. Otherwise, if (8) is violated, (VLP) has no solution.

Proof

The existence of a solution of the polyhedral projection problem (7) is evident, because a polyhedron has a finite representation. Consider a solution \((X^\mathrm{poi},X^\mathrm{dir})\) of (7). From Proposition 4, we obtain

$$\begin{aligned} \mathcal {P}= \mathrm{conv \,}P[S^\mathrm{poi}] + \mathrm{cone\,}P[S^\mathrm{dir}] + C. \end{aligned}$$

Hence, \((S^\mathrm{poi},S^\mathrm{dir})\) is a finite infimizer for (VLP). It is evident that \(S^\mathrm{poi}\) and \(S^\mathrm{dir}\) consist of minimizers only.

Assume now that (8) is violated. Take \(y \in L\cap C\!\setminus \!\{0\}\), then for any \(x\in S,\;Px = Px - y + y\), where \(Px-y \in \mathcal {P}\) and \(y \in C\!\setminus \!\{0\}\). Thus, x is not a minimizer.

The following statement is an immediate consequence of Theorem 5.

Corollary 6

A solution for (VLP) exists if and only if (VLP) is feasible and (8) is satisfied.

In the remainder of this paper we show how a solution of (VLP) can be obtained from an irredundant solution of the associated projection problem (PP). A solution \((X^\mathrm{poi}, X^\mathrm{dir})\) of (PP) is called irredundant if there is no solution \((V^\mathrm{poi},V^\mathrm{dir})\) of (PP) satisfying

$$\begin{aligned} V^\mathrm{poi}\subseteq X^\mathrm{poi},\quad V^\mathrm{dir}\subseteq X^\mathrm{dir}, \quad (V^\mathrm{poi},V^\mathrm{dir}) \ne (X^\mathrm{poi},X^\mathrm{dir}). \end{aligned}$$

The computation of an irredundant solution of (PP) from an arbitrary solution of (PP) does not depend on the dimension n. It can be realized, for instance, by vertex enumeration in \(\mathbb {R}^p\).

Theorem 7

Let a vector linear program (VLP) be given. If (VLP) is feasible, an irredundant solution of the associated polyhedral projection problem (7) exists. Let \(\mathcal {X}=(X^\mathrm{poi},X^\mathrm{dir})\) be an irredundant solution of (7). Assume that (8) is satisfied and set

$$\begin{aligned} S^\mathrm{poi}:= & {} {\left\{ x \in \mathbb {R}^n |\;(x,y) \in X^\mathrm{poi} \right\} },\\ S^\mathrm{dir}:= & {} {\left\{ x \in \mathbb {R}^n |\;(x,y) \in X^\mathrm{dir},\; y \not \in L + C\!\setminus \!\{0\} \right\} }. \end{aligned}$$

Then \((S^\mathrm{poi},S^\mathrm{dir})\) is a solution of (VLP). Otherwise, if (8) is violated, (VLP) has no solution.

Proof

By Theorem 5, it remains to show that \((S^\mathrm{poi},S^\mathrm{dir})\) consists of minimizers only. Assume that x for \((x,y)\in X^\mathrm{poi}\) is not a minimizer. There exists \(z \in \mathcal {P}\) and \(c \in C\!\setminus \!\{0\}\) such that \(y = z + c\). Let us denote the elements of \(X^\mathrm{poi}\) as

$$\begin{aligned} X^\mathrm{poi}= {\left\{ (x^1,y^1), \dots , (x^{\alpha -1}, y^{\alpha -1}),(x, y) \right\} }. \end{aligned}$$

The point z can be represented by \(X^\mathrm{poi}\) and \(d \in 0^+\mathcal {P}\), which yields

$$\begin{aligned} y - c = z = \sum _{i=1}^{\alpha -1} \lambda _i y^i + \lambda y +d,\qquad \lambda _1,\dots ,\lambda _{\alpha -1},\lambda \ge 0,\quad \sum _{i=1}^{\alpha -1} \lambda _i + \lambda = 1. \end{aligned}$$

We set \(v := \sum _{i=1}^{\alpha -1} \lambda _i y^i \in \mathcal {P}\) and consider two cases: (i) For \(\lambda = 1\), we have \(v=0\) and hence \(c = -d\), a contradiction to (8). (ii) For \(\lambda < 1\), we obtain

$$\begin{aligned} y&= \sum _{i=1}^{\alpha -1} \frac{\lambda _i}{1-\lambda } y^i + \frac{1}{1-\lambda } (c+d) \in \mathrm{conv \,}{\left\{ y^1,\dots , y^{\alpha - 1} \right\} } + \mathrm{cone\,}\hbox {proj} X^\mathrm{dir}\\&= \mathrm{conv \,}\left( ( \hbox {proj} X^\mathrm{poi}) \setminus {\left\{ y \right\} } \right) + \mathrm{cone\,}\hbox {proj} X^\mathrm{dir}. \end{aligned}$$

This contradicts the assumption that the solution \((X^\mathrm{poi},X^\mathrm{dir})\) is irredundant.

Assume now that \((x,y)\in X^\mathrm{dir}\) with \(y \not \in L+C\!\setminus \!\{0\}\) is not a minimizer. There exists \(z \in 0^+\mathcal {P}\) and \(c \in C\!\setminus \!\{0\}\) such that \(y = z + c\). Let us denote the elements of \(X^\mathrm{dir}\) by

$$\begin{aligned} X^\mathrm{dir}= {\left\{ (x^1, y^1) , \dots , (x^{\beta -1}, y^{\beta -1}), (x , y) \right\} }. \end{aligned}$$

The direction z can be represented by \(X^\mathrm{dir}\), which yields

$$\begin{aligned} y - c = z = \sum _{i=1}^{\beta -1} \lambda _i y^i + \lambda y, \qquad \lambda _1,\dots ,\lambda _{\beta -1},\lambda \ge 0. \end{aligned}$$

We set \(v := \sum _{i=1}^{\beta -1} \lambda _i y^i \in 0^+\mathcal {P}\) and distinguish two cases: (i) Let \(\lambda \ge 1\). Then \((1-\lambda ) y - v \in -0^+\mathcal {P}\cap C\!\setminus \!\{0\}\). This contradicts (8) since \(C \subseteq 0^+\mathcal {P}\). (ii) Let \(\lambda < 1\). Then

$$\begin{aligned} y = w + d \quad \text { for } \quad \gamma _i := \frac{\lambda _i}{1-\lambda } \ge 0, \quad w := \sum _{i=1}^{\beta -1} \gamma _i y^i \quad \text { and }\quad d:=\frac{1}{1-\lambda } c \in C\!\setminus \!\{0\}. \end{aligned}$$

We have \(w \not \in -0^+\mathcal {P}\) since otherwise \(y \in L + C\!\setminus \!\{0\}\) would follow. For d there is a representation

$$\begin{aligned} d = \sum _{i=1}^{\beta -1} \mu _i y^i + \mu y \qquad \mu _1,\dots ,\mu _{\beta -1},\mu \ge 0. \end{aligned}$$

The condition \(\mu \ge 1\) would imply \( w = (1-\mu ) y - d \in -0^+\mathcal {P}\). Thus we have \(\mu < 1\) and hence

$$\begin{aligned} y = \sum _{i=1}^{\beta -1} \frac{\gamma _i + \mu _i}{1-\mu } y^i \in \mathrm{cone\,}{\left\{ y^1,\dots , y^{\beta - 1} \right\} } = \mathrm{cone\,}\left( ( \hbox {proj} X^\mathrm{dir}) \setminus {\left\{ y \right\} } \right) . \end{aligned}$$

This contradicts the assumption that the solution \((X^\mathrm{poi},X^\mathrm{dir})\) is irredundant. \(\square \)

3 Examples and remarks

It is well known that (VLP) can be solved by considering the multiple objective linear program

$$\begin{aligned} \text {minimize } Z^TPx \text { s.t. } A x \ge b, \end{aligned}$$
(13)

compare, c.f., Sawaragi et al. (1985). The r columns of the matrix \(Z\in \mathbb {R}^{q\times r}\) correspond to the defining inequalities of C (or equivalently, to the generating vectors of the dual cone). The objective space dimension r of (13) can be much larger than the objective space dimension q of the initial vector linear program, see e.g. Roux and Zastawniak (2015) for a sample application and Löhne and Rudloff (2015) for the number of inequalities required to describe the ordering cone there. In contrast to (13), with our approach, the objective space dimension is increased only by one.

In the following toy-example with \(q=2\) we illustrate the procedure.

Example 8

Let us consider the following instance of (VLP):

$$\begin{aligned} \text {minimize}\; \left( \begin{array}{cc} 1 &{} -1\\ 1 &{} 1 \end{array}\right) x\quad \text {s.t.}\;\;x\in S, \end{aligned}$$
(14)

where the feasible set S is defined by

$$\begin{aligned} S:=\left\{ x\in \mathbb {R}^n \bigg | \left( \begin{array}{cc} 1&{}0\\ 1&{}-1\\ 1&{}1\\ \end{array}\right) x \ge \left( \begin{array}{c} 0\\ -1\\ -1\\ \end{array}\right) \right\} . \end{aligned}$$
(15)

Minimization is understood with respect to the partial ordering generated by the ordering cone

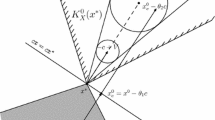
$$\begin{aligned} C:=\biggl \{ y\in \mathbb {R}^q\,\bigg |\, \underbrace{\left( \begin{array}{cc} -1 &{} 2\\ 2 &{} 1 \end{array}\right) }_{=:Z^T} y\geqslant 0 \biggr \} . \end{aligned}$$

The solution concept for the vector linear program (14) demands the computation of a representation of the upper image \(\mathcal {P}=P[S]+C\), which is depicted in Fig. 1. First, we express \(\mathcal {P}\) as an instance of (PP). This step pushes the ordering cone into the constraint set, compare (7):

$$\begin{aligned} \text {Compute}\;\mathcal {P}= {\left\{ y\in \mathbb {R}^q|\,\exists \, x\in S, Z^Ty\le Z^TPx \right\} }, \end{aligned}$$
(16)

Now we formulate the corresponding instance of (MOLP), with one additional image space dimension, compare (4):

$$\begin{aligned} \text {minimize}\,\underbrace{ \left( \begin{array}{cccc} 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1\\ 0 &{} 0 &{} -1 &{} -1 \end{array}\right) }_{=:{\hat{P}}} \left( \begin{array}{c} x\\ y\\ \end{array}\right) \quad \text {s.t.}\; \left( \begin{array}{c} x\\ y\\ \end{array}\right) \in {\hat{S}}, \end{aligned}$$
(17)

where the feasible set \({\hat{S}}\) is the same as in (16), i.e.

$$\begin{aligned} {\hat{S}} :={\left\{ \left( \begin{array}{c} x\\ y\\ \end{array}\right) \in \mathbb {R}^{n+q}\bigg | \left( \begin{array}{cc} 1 &{} 0\\ 1 &{} -1\\ 1 &{} 1\\ -1&{} -3\\ -3 &{} 1 \end{array}\right) x + \left( \begin{array}{cc} 0 &{} 0\\ 0 &{} 0\\ 0 &{} 0\\ -1 &{} 2\\ 2 &{} 1 \end{array}\right) y \geqslant \left( \begin{array}{c} 0\\ -1\\ -1\\ 0\\ 0\\ \end{array}\right) \right\} }. \end{aligned}$$
Fig. 1
figure 1

The feasible set S and the upper image \(P[S]+C\) of Example 8. A solution is given by the feasible points \(x^1\), \(x^2\) and the feasible direction \(x^3\). Their respective image-vectors \(y^1\), \(y^2\) and \(y^3\) generate the upper image. It can be seen that \(x^4\) is not part of a solution, as the image-vector \(y^4\) belongs to the ordering cone C and is therefore not a minimal direction

Full size image

Now we consider a solution \(({\hat{S}}^\mathrm{poi},{\hat{S}}^\mathrm{dir})\) to (17), which consists of \({\hat{S}}^\mathrm{poi}:={\left\{ {\hat{y}}^1,{\hat{y}}^2 \right\} }\) with feasible points

$$\begin{aligned} {\hat{y}}^1 = \left( \begin{array}{c} x^1\\ y^1 \end{array}\right) = \left( \begin{array}{c} 0\\ 1 \\ -1\\ 1 \end{array}\right) ,\qquad {\hat{y}}^2 = \left( \begin{array}{c} x^2\\ y^2\\ \end{array}\right) = \left( \begin{array}{c} 0\\ -1\\ 1\\ -1\\ \end{array}\right) ; \end{aligned}$$

and \({\hat{S}}^\mathrm{dir}:={\left\{ {\hat{y}}^3,{\hat{y}}^4 \right\} }\) with the feasible directions

$$\begin{aligned} {\hat{y}}^3 = \left( \begin{array}{c} x^3\\ y^3\\ \end{array}\right) = \left( \begin{array}{c} 1\\ -1\\ 2\\ 0\\ \end{array}\right) ,\quad {\hat{y}}^4 = \left( \begin{array}{c} x^4\\ y^4\\ \end{array}\right) = \left( \begin{array}{c} 0\\ 0\\ -1\\ 2\\ \end{array}\right) . \end{aligned}$$

This means \({\hat{y}}^i\) is \(\mathbb {R}^3_+\)-minimal for \(i=1,\ldots ,4\) and

$$\begin{aligned} {\hat{P}}[{\hat{S}}]+\mathbb {R}^3_+ = \mathrm{conv \,}{\hat{P}}[{\hat{S}}^\mathrm{poi}]+\mathrm{cone\,}{\hat{P}}[{\hat{S}}^\mathrm{dir}]+\mathbb {R}^3_+. \end{aligned}$$

From Theorem 3 we deduce that \(({\hat{S}}^\mathrm{poi},{\hat{S}}^\mathrm{dir})\) is also a solution for the polyhedral projection problem (16). This solution is irredundant, so the x-components of the points \({\hat{y}}^1,{\hat{y}}^2\), that is \(x^1\) and \(x^2\), are the points of a solution to the original vector linear program (14) by Theorem 7. It remains to sort out those directions whose y-part belongs to the ordering cone C (compare Theorem 7): This is the case for the direction \({\hat{y}}^4\), as \(Z^Ty^4= (5,0)^T \geqslant 0 \). Thus the solution for (14) consists of the feasible points \(x^1,x^2\) and the feasible direction \(x^3\) (also compare Fig. 1):

$$\begin{aligned} S^\mathrm{poi}={\left\{ \left( \begin{array}{c} 0\\ 1 \end{array}\right) , \left( \begin{array}{c} 0\\ -1 \end{array}\right) \right\} }\qquad S^\mathrm{dir}={\left\{ \left( \begin{array}{c} 1\\ -1 \end{array}\right) \right\} }. \end{aligned}$$

It generates the upper image of (14) (Fig. 1) by means of

$$\begin{aligned} \mathcal {P}= \mathrm{conv \,}P[S^\mathrm{poi}]+\mathrm{cone\,}P[S^\mathrm{dir}]+C. \end{aligned}$$

Finally, let us demonstrate how \(\mathcal {P}\) can be obtained directly from \({\hat{\mathcal {P}}}\). We start with an irredundant representation

$$\begin{aligned} {\hat{\mathcal {P}}} = \mathrm{conv \,}{\left\{ \bar{y}^1, \bar{y}^2 \right\} } + \mathrm{cone\,}{\left\{ \bar{y}^3, \bar{y}^4, \bar{y}^5 \right\} }, \end{aligned}$$

where

$$\begin{aligned} {\bar{y}^1=\left( \begin{array}{c} -1\\ 1\\ 0 \end{array}\right) },\;{\bar{y}^2=\left( \begin{array}{c} 1\\ -1\\ 0 \end{array}\right) },\; {\bar{y}^3=\left( \begin{array}{c} 2\\ 0\\ -2 \end{array}\right) },\;{\bar{y}^4=\left( \begin{array}{c} -1\\ 2\\ -1 \end{array}\right) },\; {\bar{y}^5=\left( \begin{array}{c} 0\\ 0\\ 1 \end{array}\right) }. \end{aligned}$$

We rule out those \(\bar{y}^i\) where the condition \(e^T \bar{y}^i = 0\) is violated, whence \(\bar{y}^5\) is cancelled. Then we delete the last component of each vector and obtain

$$\begin{aligned} \mathcal {P}= \mathrm{conv \,}{\left\{ y^1, y^2 \right\} } + \mathrm{cone\,}{\left\{ y^3,y^4 \right\} } \end{aligned}$$

with

$$\begin{aligned} y^1=\left( \begin{array}{c} -1\\ 1 \end{array}\right) ,\; y^2=\left( \begin{array}{c} 1\\ -1 \end{array}\right) ,\; y^3=\left( \begin{array}{c} 2\\ 0 \end{array}\right) ,\; y^4=\left( \begin{array}{c} -1\\ 2 \end{array}\right) . \end{aligned}$$

In the preceeding example one needs one additional objective, whereas the “classical” approach (13) does not require any additional objective. Note that every step of the procedure presented here is independent of the actual values of \(q\geqslant 2\) and \(r\geqslant q\). In the following example we consider the case \(r > q+1\). This leads to an advantage in comparison to the classical method (13). The cone \(C \subseteq \mathbb {R}^3\) of the vector linear program (18) has 6 extreme directions and a solution is obtained from a solution of a corresponding multiple objective linear program (19) with only 4 objectives. Note that in the classical approach, see (13), 6 objectives are required.

Example 9

Consider the vector linear program

$$\begin{aligned} \text {minimize } Px \text { s.t. } B x \ge a, \; x \ge 0 \end{aligned}$$
(18)

with ordering cone \(C = {\left\{ y \in \mathbb {R}^3 |\;Z^T y \ge 0 \right\} }\) and data

$$\begin{aligned} P=\left( \begin{array}{ccc} 1&{} 0&{}-1\\ 1&{} 1&{} 0\\ 0&{} 1&{} 1\\ \end{array}\right) \!,\, B = \left( \begin{array}{ccc} 1&{} 1&{} 1\\ 1&{} 2&{} 2\\ 2&{} 2&{} 1\\ 2&{} 1&{} 2\\ \end{array}\right) \!,\, a = \left( \begin{array}{c} 3\\ 4\\ 4\\ 4\\ \end{array}\right) \!,\, Z = \left( \begin{array}{cccccc} 4&{} 2&{} 4&{} 1&{} 0&{} 0\\ 2&{} 4&{} 0&{} 0&{} 1&{} 4\\ 2&{} 2&{} 2&{} 2&{} 2&{} 2\\ \end{array}\right) \!. \end{aligned}$$

We assign to (18) the multiple objective linear program

$$\begin{aligned} \min \hat{P} \left( \begin{array}{c} x\\ y \end{array}\right) \text { s.t. } \hat{B} \left( \begin{array}{c} x\\ y \end{array}\right) \ge \hat{a}, \; x \ge 0 \end{aligned}$$
(19)

with objective function

$$\begin{aligned} \hat{P} \left( \begin{array}{c} x\\ y \end{array}\right) = \left( \begin{array}{c} y\\ -e^T y \end{array}\right) \end{aligned}$$

and constraints \(B x \ge a,\;Z^T y \ge Z^T P x,\;x \ge 0\). Thus, the data of (19) are

$$\begin{aligned} \hat{P} = \left( \begin{array}{cccccc} 0&{} 0&{} 0&{} 1&{} 0&{} 0\\ 0&{} 0&{} 0&{} 0&{} 1&{} 0\\ 0&{} 0&{} 0&{} 0&{} 0&{} 1\\ 0&{} 0&{} 0&{}-1&{}-1&{}-1\\ \end{array}\right) \!,\, \hat{B} = \left( \begin{array}{cccccc} 1&{} 1&{} 1&{} 0&{} 0&{} 0\\ 1&{} 2&{} 2&{} 0&{} 0&{} 0\\ 2&{} 2&{} 1&{} 0&{} 0&{} 0\\ 2&{} 1&{} 2&{} 0&{} 0&{} 0\\ -6&{}-4&{} 2&{} 4&{} 2&{} 2\\ -6&{}-6&{} 0&{} 2&{} 4&{} 2\\ -4&{}-2&{} 2&{} 4&{} 0&{} 2\\ -1&{}-2&{}-1&{} 1&{} 0&{} 2\\ -1&{}-3&{}-2&{} 0&{} 1&{} 2\\ -4&{}-6&{}-2&{} 0&{} 4&{} 2\\ \end{array}\right) \!,\, \hat{a} = \left( \begin{array}{c} 3\\ 4\\ 4\\ 4\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{array}\right) \!. \end{aligned}$$

A solution to (19) consists of \(\hat{S}^\mathrm{poi}= {\left\{ \hat{y}^1, \hat{y}^2, \hat{y}^3 \right\} }\) with

$$\begin{aligned} \hat{y}^1 = \left( \begin{array}{c} x^1\\ y^1 \end{array}\right) = \left( \begin{array}{c} 2\\ 0\\ 1\\ 1\\ 2\\ 1\\ \end{array}\right) ,\, \hat{y}^2 = \left( \begin{array}{c} x^2\\ y^2 \end{array}\right) = \left( \begin{array}{c} 1\\ 0\\ 2\\ -1\\ 1\\ 2\\ \end{array}\right) ,\, \hat{y}^3 = \left( \begin{array}{c} x^3\\ y^3 \end{array}\right) = \left( \begin{array}{c} 0\\ 0\\ 4\\ -4\\ 0\\ 4\\ \end{array}\right) \end{aligned}$$

and \(\hat{S}^\mathrm{dir}= {\left\{ \hat{y}^4,\dots ,\hat{y}^8 \right\} }\), (again \(\hat{y}^i = (x^i,y^i)^T\)) with

$$\begin{aligned} \hat{y}^4= \left( \begin{array}{c} 0\\ 0\\ 0\\ 0\\ -1\\ 2\\ \end{array}\right) \!,\; \hat{y}^5= \left( \begin{array}{c} 0\\ 0\\ 0\\ 2\\ 2\\ -1\\ \end{array}\right) \!,\; \hat{y}^6= \left( \begin{array}{c} 0\\ 0\\ 1\\ -1\\ 0\\ 1\\ \end{array}\right) \!,\; \hat{y}^7= \left( \begin{array}{c} 0\\ 0\\ 0\\ 1\\ 0\\ 0\\ \end{array}\right) \!,\; \hat{y}^8= \left( \begin{array}{c} 0\\ 0\\ 0\\ 0\\ 1\\ 0\\ \end{array}\right) \!. \end{aligned}$$

One can easily check that \(y^4, y^5, y^7, y^8 \in C\) and \(y^6 \not \in C\). Thus, a solution to the VLP (18) consists of \(S^\mathrm{poi}= {\left\{ x^1, x^2, x^3 \right\} }\) and \(S^\mathrm{dir}= {\left\{ x^6 \right\} }\), that is,

$$\begin{aligned} S^\mathrm{poi}= {\left\{ \left( \begin{array}{c} 2\\ 0\\ 1\\ \end{array}\right) \left( \begin{array}{c} 0\\ 0\\ 4\\ \end{array}\right) \left( \begin{array}{c} 1\\ 0\\ 2\\ \end{array}\right) \right\} },\quad S^\mathrm{dir}= {\left\{ \left( \begin{array}{c} 0\\ 0\\ 1\\ \end{array}\right) \right\} } \end{aligned}$$

The upper image \({\hat{\mathcal {P}}}\) of the MOLP (19) is given by its vertices

$$\begin{aligned} \bar{y}^1 = \left( \begin{array}{c} 1\\ 2\\ 1\\ -4\\ \end{array}\right) \!,\, \bar{y}^2 = \left( \begin{array}{c} -1\\ 1\\ 2\\ -2\\ \end{array}\right) \!,\, \bar{y}^3 = \left( \begin{array}{c} -4\\ 0\\ 4\\ 0\\ \end{array}\right) \end{aligned}$$

and its extreme directions

$$\begin{aligned} \bar{y}^4 = \left( \begin{array}{c} 0\\ -1\\ 2\\ -1\\ \end{array}\right) \!,\, \bar{y}^5 = \left( \begin{array}{c} 2\\ 2\\ -1\\ -3\\ \end{array}\right) \!,\, \bar{y}^6 = \left( \begin{array}{c} -1\\ 0\\ 1\\ 0\\ \end{array}\right) ,\\ \bar{y}^7 = \left( \begin{array}{c} 1\\ 0\\ 0\\ -1\\ \end{array}\right) \!,\, \bar{y}^8 = \left( \begin{array}{c} 0\\ 1\\ 0\\ -1\\ \end{array}\right) \!,\, \bar{y}^9 = \left( \begin{array}{c} 0\\ 0\\ 0\\ 1\\ \end{array}\right) . \end{aligned}$$

We sort out \(\bar{y}^9\), as \(e^T \bar{y}^9 \ne 0\), and we delete the last component of each vector \(\bar{y}^1, \dots , \bar{y}^8\). As a result we obtain the vertices

$$\begin{aligned} y^1 = \left( \begin{array}{c} 1\\ 2\\ 1\\ \end{array}\right) \!,\, y^2 = \left( \begin{array}{c} -1\\ 1\\ 2\\ \end{array}\right) \!,\, y^3 = \left( \begin{array}{c} -4\\ 0\\ 4\\ \end{array}\right) \end{aligned}$$

and the extreme directions

of the upper image \(\mathcal {P}\) of the VLP (18).

In the next example we have used the VLP solver bensolve (see Löhne and Weißing 2015, 2016) in order to compute the image of a linear map over a polytope, which can be expressed as a polyhedral projection problem. The solver is not able to handle ordering cones \(C={\left\{ 0 \right\} }\). Therefore a transformation into (MOLP) with one additional objective space dimension is required.

Example 10

Let W be the 729-dimensional unit hypercube and let P be the \(3\times 729\) matrix whose columns are the \(9^3=729\) different ordered arrangements of 3 numbers out of the set \({\left\{ -4,-3,-2,-1,0,1,2,3,4 \right\} }\). The aim is to compute the polytope \(P[W]:={\left\{ Pw|\;w \in W \right\} }\). To this end, we consider the multiple objective linear program

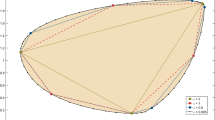
$$\begin{aligned} \text {minimize } \left( \begin{array}{c}Px \\ -e^TPx\end{array}\right) \text { s.t. } x \in W, \end{aligned}$$

having 4 objectives, 729 variables, and 729 double-sided constraints. The upper image intersected with the hyperplane \({\left\{ y \in \mathbb {R}^4 |\;e^T y = 0 \right\} }\) is the set P[W], see Fig. 2.

Fig. 2
figure 2

The polytope P[W] of Example 10 computed by Bensolve (see Löhne and Weißing 2015, 2016) via MOLP reformulation. The resulting polytope has 43, 680 vertices and 26, 186 facets. The upper image \(\mathcal {P}\subseteq \mathbb {R}^4\) of the corresponding MOLP has 43, 680 vertices and 26, 187 facets. The displayed polytope is one of these facets, the only one that is bounded

Full size image

We close this article by enumerating some related results which can be found in the literature. It is known Jones et al. (2008) that the parametric linear program

is equivalent to the problem to project a polyhedral convex set onto a subspace. For every parameter vector y we can consider the dual parametric linear program

which is closely related to an equivalent characterization of a vector linear program (or multiple objective linear program) by the family of all weighted sum scalarizations, see e.g. Focke (1973).

Fülöp’s seminal paper Fülöp (1993) has to be mentioned because a problem similar to (4) was used there to show that linear bilevel programming is equivalent to optimizing a linear objective function over the solution of a multiple objective linear program.

The book Lotov et al. (2004) provides interesting links between multiple objective linear programming and computation of convex polyhedra.