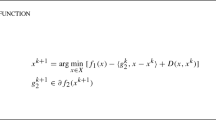1 Introduction

Consider the problem:

$$\begin{aligned} \min _{x \in \mathbb {R}^n}f(x) \end{aligned}$$
(1)

where we assume that \(f: \mathbb {R}^n \mapsto \mathbb {R}\) is a DC function, according to the following

Definition 1

A function \(f:\mathbb {R}^n \rightarrow \mathbb {R}\) is a DC function if there exist convex functions \(f_1,~f_2:\mathbb {R}^n \rightarrow \mathbb {R}\) such that:

$$\begin{aligned} f(x)=f_1(x)-f_2(x). \end{aligned}$$

Here \(f_1-f_2\) is called a DC decomposition of f, while \(f_1\) and \(f_2\) are called DC components of f. A function f is locally DC if for any \(x_0 \in \mathbb {R}^n\), there exist \(\epsilon >0\) such that f is DC on the ball \(B(x_0,\epsilon )\). It is well known that every locally DC function is DC.

Problem (1) is known as a DC program and some typical problems which can be modeled in such form are the bridge location problem, the design centering problem, the packing problem [1], the production-transportation planning [18], the location planning problem [23], cluster analysis [5, 22], clusterwise linear regression analysis [7] and supervised data classification [2]. To date, DC programming has been mostly considered as a part of global optimization. Several algorithms are available to solve this problem globally [19, 27].

Nonsmooth DC programming is an important subclass of DC programming problems. Several algorithms have been developed to solve such problems. An algorithm based on quasidifferentials of DC functions and discrete gradients is developed in [3]. A codifferential method is introduced in [6] and a proximal linearized algorithm is proposed in [24]. The paper [21] introduces a proximal bundle method that utilizes nonconvex cutting planes. A gradient splitting method introduced in [14] can be modified for minimizing DC functions. General references on bundle methods are [4, 17], while possible variants are [8, 12, 15].

In this paper, we develop a proximal bundle method for the numerical minimization of nonsmooth DC functions by iteratively building two separate piecewise-affine approximations of the component functions. Combining these two convex piecewise-affine approximations we generate a DC piecewise-affine model, which can also be seen as the pointwise maximum of several concave piecewise-affine functions. Such a nonconvex model is then tackled by means of two auxiliary quadratic programs, that have different local approximation properties.

The rest of the paper is organized as follows. Section 2 presents some definitions and preliminary results on DC functions and DC programs. A cutting plane model for DC functions is introduced in Sect. 3. The description of the proposed method is given in Sect. 4. Termination properties of the algorithm, as well as some results on its convergence are discussed in Sect. 5. Computational results are reported in Sect. 6, and Sect. 7 contains some concluding remarks.

2 Some preliminary results

In the following we focus only on a few theoretical results regarding some relevant stationarity conditions that will be useful for later developments. We refer the reader to [1, 16, 25, 26], and the references therein, for a thorough analysis of DC optimality conditions.

Definition 2

A point \(x^*\) is called a local minimizer of the problem (1) if \(f_1(x^*)-f_2(x^*)\) is finite and there exists a neighborhood \(\mathcal {N}\) of \(x^*\) such that

$$\begin{aligned} f_1(x^*)-f_2(x^*)\le f_1(x)-f_2(x),~~\forall x\in \mathcal {N}. \end{aligned}$$
(2)

In general, nonsmooth DC functions are not regular, and the Clarke subdifferential calculus exists for such functions in the form of inclusions. Such a calculus cannot be used to compute subgradients of the DC function since

$$\begin{aligned} \partial _{cl} f(x) \subseteq \partial f_1(x) - \partial f_2(x), \end{aligned}$$
(3)

where the symbol \(\partial _{cl} f(\cdot )\) denotes Clarke’s subdifferential.

Nonsmooth DC functions are quasidifferentiable. Depending on generalized subgradients used to approximate nonsmooth DC functions, different stationary points can be defined for them. A point \(x^*\) is called \(\inf \)-stationary for problem (1) if

$$\begin{aligned} \emptyset \ne \partial f_2(x^*) \subseteq \partial f_1(x^*). \end{aligned}$$
(4)

A point \(x^*\) is called Clarke stationary for problem (1) if

$$\begin{aligned} 0 \in \partial _{cl} f(x^*). \end{aligned}$$
(5)

Finally, a point \(x^*\) is called a critical point of the function f if

$$\begin{aligned} \partial f_2(x^*)\cap \partial f_1(x^*) \ne \emptyset . \end{aligned}$$
(6)

It is interesting to analyze the relationships between different stationary points. Consider the special case where the function \(f_1\) is nonsmooth convex and the function \(f_2\) is smooth convex.

Proposition 1

The generalized subdifferential of the DC function f, obtained as the difference between a nonsmooth convex function \(f_1\) and a smooth convex function \(f_2\), can be computed as

$$\begin{aligned} \partial _{cl} f(x) = \partial f_1(x)- \nabla f_2(x). \end{aligned}$$

Proof

Let \(D(x) = \partial f_1(x)- \nabla f_2(x)\). The inclusion \(\partial _{cl} f(x) \subseteq D(x)\) follows from the calculus for generalized subdifferentials. Therefore we prove only the opposite inclusion. As convex functions \(f_1\) and \(f_2\) are directionally differentiable, then f is also directionally differentiable and

$$\begin{aligned} f'(x,d) = f_1^\prime (x,d) - f_2^\prime (x,d), ~d \in \mathbb {R}^n. \end{aligned}$$

It is known that

$$\begin{aligned} f_1^\prime (x,d)= \max _{\xi \in \partial f_1(x)} \xi ^\top d, \,\,\,\,\, f_2^\prime (x,d) = \nabla f_2(x)^\top d. \end{aligned}$$

Then

$$\begin{aligned} f^\prime (x,d) = f_1^\prime (x,d) - f_2^\prime (x,d) = \max _{\xi \in \partial f_1(x)} (\xi -\nabla f_2(x))^\top d \end{aligned}$$
(7)

for all \(d \in \mathbb {R}^n\). This means that \(f^\prime (x,d) \ge u^\top d\) for all \(d \in \mathbb {R}^n\) and \(u \in D(x)\), which in turn, due to the convexity and compactness of the set D(x), implies that \(D(x) \subseteq \partial _{cl} f(x)\).\(\square \)

Now assume that \(f_1\) is smooth and \(f_2\) is any convex nonsmooth function.

Proposition 2

The generalized subdifferential of the DC function f, obtained as the difference between a smooth convex function \(f_1\) and a nonsmooth convex function \(f_2\), can be computed as

$$\begin{aligned} \partial _{cl} f(x) = \nabla f_1(x)- \partial f_2(x). \end{aligned}$$

Proof

The proof follows from Proposition 1 and from the fact if f is a DC function, then \(-f\) is also DC. \(\square \)

Proposition 3

Let \(S_{inf}\) be a set of inf-stationary points, \(S_{cl}\) a set of Clarke stationary points and \(S_{cr}\) a set of critical points of the function f. Then

  1. (1)

    \(S_{inf} \subseteq S_{cl} \subseteq S_{cr}\);

  2. (2)

    if the function \(f_1\) is continuously differentiable in \(\mathbb {R}^n\) then \(S_{cl}=S_{cr}\);

  3. (3)

    if the function \(f_2\) is continuously differentiable in \(\mathbb {R}^n\) then \(S_{inf}=S_{cl}=S_{cr}\).

Proof

  1. (1)

    First we show that \(S_{inf} \subseteq S_{cl}\). Take any \(x \in S_{inf}\). Let \(f^0(x,d)\) be a generalized directional derivative of the function f at the point x in a direction \(d \in \mathbb {R}^n\) [4]:

    $$\begin{aligned} f^0(x,d)= \limsup _{y \rightarrow x, \alpha \downarrow 0} \frac{f(y+\alpha d) - f(y)}{\alpha }. \end{aligned}$$

    Since both functions \(f_1\) and \(f_2\) are directionally differentiable, taking into account inf-stationarity of the point x, we get

    $$\begin{aligned} f^0(x,d) \ge f'(x,d) = f_1'(x,d) - f_2'(x,d) \ge 0 \end{aligned}$$

    for all \(d \in \mathbb {R}^n\). This implies that \(0 \in \partial _{cl} f(x)\), hence that \(x \in S_{cl}\). The inclusion \(S_{cl} \subseteq S_{cr}\) is obvious since according to (3) for any \(x \in S_{cl}\) one gets \(0 \in \partial f_1(x) - \partial f_2(x)\) and therefore \(\partial f_1(x) \cap \partial f_2(x) \ne \emptyset \).

  2. (2)

    Now assume that the function \(f_1\) is continuously differentiable in \(\mathbb {R}^n\), then \(\nabla f_1(x) \in \partial f_2(x)\) for any \(x \in S_{cr}\). In this case Proposition 2 implies that \(0 \in \partial _{cl} f(x)\) that is \(x \in S_{cl}\).

  3. (3)

    Finally, if the function \(f_2\) is continuously differentiable in \(\mathbb {R}^n\), then \(\nabla f_2(x) \in \partial f_1(x)\) for any \(x \in S_{cr}\). In this case, according to Proposition 1, \(0 \in \partial _{cl} f(x)\). Therefore \(x \in S_{inf}\) and \(x \in S_{cl}\).

\(\square \)

In the next sections we will introduce a method requiring no differentiability assumptions of both \(f_1\) and \(f_2\), for which we will prove finite termination at a point approximately satisfying the criticality condition (6).

3 The model function

Our approach is based on some ideas coming from the classic cutting plane method for minimizing convex functions. In particular we assume that, within an iterative procedure, a certain set of couples \((x_j, g_j^{(2)})\), \(j=1, \ldots , k\), with \(x_j \in \mathbb {R}^n\) and \(g_j^{(2)} \in \partial f_2(x_j)\) are given. We single out the point \(x_k\) from the set of points \(x_j\), \(j=1, \ldots , k\), and calculate \(g_k^{(1)} \in \partial f_1(x_k)\). Convexity of \(f_2\) implies that the following inequalities hold for any \(x \in \mathbb {R}^n\):

$$\begin{aligned} f_2(x) \ge f_2(x_j)+ g_j^{(2)\top }(x-x_j), \,\,\, j=1,\ldots , k, \end{aligned}$$
(8)

which, by introducing the change of variables \(d \triangleq x-x_k\), can be rewritten in the form:

$$\begin{aligned} f_2(x_k+d) \ge f_2(x_k)+ g_j^{(2)\top }d -\alpha _j^{(2)}, \,\,\, j=1,\ldots , k, \end{aligned}$$
(9)

where \(\alpha _j^{(2)}\), \( j=1,\ldots , k\), is the linearization error associated to the jth first order expansion of \(f_2\) rooted at \(x_j\) and is defined as

$$\begin{aligned} \alpha _j^{(2)}= f_2(x_k)- \left( f_2(x_j)+ g_j^{(2)\top }(x_k-x_j)\right) . \end{aligned}$$
(10)

It follows from the definition of the \(\varepsilon \)-subdifferential \(\partial _{\varepsilon }f_i(\cdot )\) of the convex function \(f_i(\cdot )\), with \(i=1,2\) and \(\varepsilon \ge 0\), that \(g_j^{(2)} \in \partial _{\alpha _j^{(2)}}f_2(x_k)\). Similarly, for any given \(x \in \mathbb {R}^n\) and \(g^{(1)} \in \partial f_1(x)\), it holds that \(g^{(1)} \in \partial _{\alpha } f_1(x_k)\), with \(\alpha \triangleq f_1(x_k)-f_1(x)-g^{(1)\top }(x_k-x) \).

We observe that the following inequality

$$\begin{aligned} f_2(x_k+d) \ge f_2(x_k) +\displaystyle \max _{j=1,\ldots ,k} \left\{ g_j^{(2)\top }d- \alpha _j^{(2)}\right\} \end{aligned}$$
(11)

follows from (9), and thus we obtain:

$$\begin{aligned} f(x_k+d)=f_1(x_k+d)-f_2(x_k+d) \le f_1(x_k+d) - \left( f_2(x_k) + \displaystyle \max _{j=1,\ldots ,k} \left\{ g_j^{(2)\top }d- \alpha _j^{(2)}\right\} \right) . \end{aligned}$$
(12)

The right-hand side of (12) is still DC, with \(f_2(x_k+d) \) being replaced by its lower approximation provided by the convex cutting plane function

$$\begin{aligned} f_2(x_k)+\ell _2^{(k)}(d), \end{aligned}$$

with

$$\begin{aligned} \ell _2^{(k)}(d) \triangleq \displaystyle \max _{j=1,\ldots ,k} \left\{ g_j^{(2)\top }d- \alpha _j^{(2)}\right\} . \end{aligned}$$
(13)

Now we define a concave model \(h_k(d)\) for the difference function \(f(x_k+d)-f(x_k)\). We first note that from (12) it follows

$$\begin{aligned} f(x_k+d)-f(x_k)= & {} f_1(x_k+d)-f_2(x_k+d)-f_1(x_k)+f_2(x_k) \nonumber \\\le & {} f_1(x_k+d) - \left( f_2(x_k)+\ell _2^{(k)}(d)\right) -f_1(x_k)+f_2(x_k)\nonumber \\= & {} f_1(x_k+d) - f_1(x_k) - \ell _2^{(k)}(d). \end{aligned}$$
(14)

Next, by substituting \(f_1(x_k+d)\) with the affine approximation \(f_1(x_k)+ g_k^{(1)\top }d\) in (14), we have:

$$\begin{aligned} h_k(d) \triangleq g_k^{(1)\top }d - \ell _2^{(k)}(d)= \displaystyle \min _{j=1,\ldots ,k} \left\{ (g_k^{(1)}-g_j^{(2)})^\top d+ \alpha _j^{(2)}\right\} . \end{aligned}$$
(15)

We observe that \(h_k(\cdot )\) interpolates the difference function at \(d=0\), since \(\alpha _j^{(2)} \ge 0\) for every \(j=1,\ldots ,k\), with, in particular, \(\alpha _k^{(2)} =0\).

The rationale of our approach is the following. Suppose any direction \(\bar{d}\) is calculated such that \(h_k(\bar{d}) <0\). If for a given \(m \in (0,1)\) it is

$$\begin{aligned} f(x_k+\bar{d}) -f(x_k) < m h_k(\bar{d}), \end{aligned}$$

then a decrease has been achieved and a new iterate can be generated by setting \(x_{k+1}= x_k + \bar{d}\). Suppose, on the contrary, that

$$\begin{aligned} f(x_k+\bar{d}) - f(x_k) \ge mh_k(\bar{d}), \end{aligned}$$

and consider any \(g^{(1)}_+ \in \partial f_1(x_k+\bar{d})\). Convexity of \(f_1\) implies

$$\begin{aligned} f_1(x_k) \ge f_1(x_k+\bar{d})- g^{(1)\top }_+\bar{d}, \end{aligned}$$

which, taking into account (11) and (13), leads to

$$\begin{aligned} g^{(1)\top }_+\bar{d} - \ell _2^{(k)}(\bar{d})\ge & {} f_1(x_k+\bar{d})-f_1(x_k) - \ell _2^{(k)}(\bar{d}) \nonumber \\\ge & {} f_1(x_k+\bar{d})-f_1(x_k) -(f_2(x_k+\bar{d})-f_2(x_k)) \nonumber \\= & {} f(x_k+\bar{d})-f(x_k) \nonumber \\\ge & {} m h_k(\bar{d}). \end{aligned}$$
(16)

The latter formula is of relevant importance as it will be used in the sequel in order to get better and better models of the objective function whenever descent is not achieved. In fact, suppose that the condition

$$\begin{aligned} f(x_k+\bar{d}) - f(x_k) \ge mh_k(\bar{d}) \end{aligned}$$
(17)

is satisfied with \(x_k+\bar{d}\) very close to \(x_k\), so that \(g^{(1)}_+\) can be considered to approximately belong to \(\partial f_1(x_k)\). More precisely, let

$$\begin{aligned} 0 \le \alpha _+^{(1)} \triangleq f_1(x_k) - f_1(x_k+\bar{d})+ g^{(1)\top }_+\bar{d}, \end{aligned}$$
(18)

and, for some given \(\varepsilon >0\), assume that

$$\begin{aligned} \alpha _+^{(1)} \in [0,\varepsilon ] \end{aligned}$$
(19)

and

$$\begin{aligned} g^{(1)}_+ \in \partial _{\alpha _+^{(1)}} f_1(x_k). \end{aligned}$$
(20)

Then, a better model \(H_k(\cdot )\) than \(h_k(\cdot )\) at \(\bar{d}\), can be obtained by letting

$$\begin{aligned} H_k(d) \triangleq \max \left\{ g_k^{(1)\top }d - \ell _2^{(k)}(d), \,\, g^{(1)\top }_+d - \alpha _+^{(1)} - \ell _2^{(k)}(d) \right\} . \end{aligned}$$
(21)

Indeed, noting that (18) is equivalent to

$$\begin{aligned} g^{(1)\top }_+\bar{d} - \alpha _+^{(1)} = f_1(x_k+\bar{d})-f_1(x_k), \end{aligned}$$
(22)

and taking into account (21), (22), (11), (17), and \(h_k(\bar{d}) <0\), we obtain

$$\begin{aligned} H_k(\bar{d})\ge & {} g^{(1)\top }_+\bar{d} -\alpha _+^{(1)} - \ell _2^{(k)}(\bar{d}) \nonumber \\= & {} f_1(x_k+\bar{d})-f_1(x_k)- \ell _2^{(k)}(\bar{d}) \nonumber \\\ge & {} f_1(x_k+\bar{d})-f_1(x_k)- (f_2(x_k+\bar{d})-f_2(x_k)) \nonumber \\= & {} f(x_k+\bar{d})-f(x_k) \nonumber \\\ge & {} m h_k(\bar{d})\nonumber \\> & {} h_k(\bar{d}). \end{aligned}$$
(23)

Hence, at the point \(\bar{d}\), if a large gap between \(h_k(\bar{d})\) and \(f(x_k+\bar{d})-f(x_k)\) occurs, then \(H_k(\bar{d})\) is significantly higher than \(h_k(\bar{d})\).

More in general, given any set \(\{ g^{(1)}_1,\ldots , g^{(1)}_s \}\) of \(\alpha _i^{(1)}\)-subgradients of \(f_1\) at \(x_k\), with \(\alpha _i^{(1)} \le \varepsilon \), \(i=1\ldots ,s\), we redefine the nonconvex model \(H_k(\cdot )\) as the following maximum of finitely many concave piecewise-affine functions

$$\begin{aligned} H_k(d) \triangleq \max _{i=1,\ldots ,s} \left\{ g_i^{(1)\top }d - \alpha _i^{(1)} - \ell _2^{(k)}(d) \right\} . \end{aligned}$$
(24)

Next, we examine some differential properties of the model function \(H_k\). Note that, taking into account definitions (13) and (24), function \(H_k(d)\) may be rewritten in the form

$$\begin{aligned} H_k(d)= \max _{i \in I}h_k^{(i)}(d), \end{aligned}$$
(25)

where \(I \triangleq \{1,\ldots , s\}\) and \(h_k^{(i)}(d)\), \(i \in I\), is a concave piecewise-affine function defined as

$$\begin{aligned} h_k^{(i)}(d) \triangleq \min _{j\in J} \left\{ (g_i^{(1)}-g_j^{(2)})^\top d -\alpha _i^{(1)} +\alpha _j^{(2)}\right\} \end{aligned}$$
(26)

with \(J \triangleq \{1,\ldots ,k\}\). Thus, the function \(H_k(d)\) is of the maxmin type, it is directionally differentiable, and its directional derivative \(H^\prime _k(d;\xi )\) along any direction \(\xi \in \mathbb {R}^n\) depends on the directional derivatives of the functions \(h_k^{(i)}(d)\), \(i \in I\) as follows:

$$\begin{aligned} H^\prime _k(d;\xi )=\max _{i \in I(d)} h_k^{(i)\prime }(d;\xi ), \end{aligned}$$

where

$$\begin{aligned} I(d) \triangleq \{i \in I|H_k(d)=h_k^{(i)}(d) \}, \end{aligned}$$

and

$$\begin{aligned} h_k^{(i)\prime }(d;\xi ) = \min _{j\in J(d)} \{(g_i^{(1)}-g_j^{(2)})^\top \xi \} \end{aligned}$$

with

$$\begin{aligned} J(d) \triangleq \{j \in J| g_j^{(2)\top } d -\alpha _j^{(2)} = \ell _2^{(k)} (d)\}. \end{aligned}$$

For an in-depth analysis of the differential properties of functions of the maxmin type we refer the reader to the historical paper [9].

In the following remark an approximate criticality condition for \(x_k\) is highlighted as a result of the minimization of \(H_k(d)\).

Remark 1

Assume that \(d=0\) is a minimizer for \(H_k(d)\). This implies that \(H^\prime (0;\xi )\ge 0\), for every \(\xi \in \mathbb {R}^n\), which, in turn, is equivalent to infeasibility of the following inequality:

$$\begin{aligned} \max _{i\in I(0)} \min _{j\in J(0)}\left\{ (g_i^{(1)}-g_j^{(2)})^\top \xi \right\} <0. \end{aligned}$$
(27)

Now observe that I(0) and J(0) contain each at least one index assigned to a subgradient of \(f_1(x_k)\) and of \(f_2(x_k)\), respectively. Hence, defining the following system \(\mathcal{{S}}_j\) of |I(0)| linear inequalities

$$\begin{aligned} (g_i^{(1)}-g_j^{(2)})^\top \xi <0 \,\,\,\, i\in I(0), \end{aligned}$$

for each index \(j \in J(0)\), we have that infeasibility of (27) implies infeasibility of all systems \(\mathcal{{S}}_j\), \(j \in J(0)\). By Gordan’s theorem the latter is equivalent to

$$\begin{aligned} g_j^{(2)} \in \mathrm{conv}\{g_i^{(1)}, \, i\in I(0) \},\,\,\,j \in J(0), \end{aligned}$$

and, consequently,

$$\begin{aligned} \mathrm{conv}\{g_j^{(2)},\,j \in J(0)\} \subseteq \mathrm{conv}\{g_i^{(1)}, \, i \in I(0) \}, \end{aligned}$$

which can be interpreted as an approximation of the criticality condition (6) at the point \(x_k\).

4 The algorithm

The approximate criticality condition presented in Remark 1, along with the properties of \(H_k(\cdot )\) summarized in (23), would suggest to develop a method for solving problem (1) which is based on iterative minimizations of \(H_k(d)\). The model function \(H_k(d)\) is, as previously mentioned, of the maxmin type and can also be seen as the pointwise maximum of a (finite) number of concave functions. Although there exist several algorithms dealing with minimization of such a family of functions, the idea of direct minimization, at each iteration k, of \(H_k(d)\) does not seem viable in terms of computational effort. Thus, borrowing some ideas from the approach proposed in [13] for the minimization of piecewise-concave functions, we introduce an iterative algorithm that does not require the direct minimization of the model function \(H_k(d)\). In particular, at each iteration of the algorithm, a displacement vector \(d_k\) is calculated, such that \(H_k(d_k) <0\), along which a line search for function f is performed. The calculation of the search direction \(d_k\) is made on the basis of the solution of an auxiliary quadratic program that locally approximates \(H_k(d)\), hence next referred to as the local program. In fact, we note that \(\partial h_k^{(i)}(0)\), the subdifferential of \(h_k^{(i)}(d) \) at \(d=0\), has the following expression

$$\begin{aligned} \partial h_k^{(i)}(0) = \mathrm{conv}\{(g_i^{(1)}-g_j^{(2)})|j \in J(0)\}, \end{aligned}$$

where \(J(0) = \{j \in J \mid \alpha _j^{(2)}=0\}\). Hence, any subgradient \(u_i\), \(u_i \in \partial h_k^{(i)}(0)\), can be calculated by selecting any index \( j_i \in J(0)\) and setting

$$\begin{aligned} u_i=g_i^{(1)}-g_{j_i}^{(2)}. \end{aligned}$$

We observe that in case the set J(0) is a singleton, that is \(j_i=j\), \(i \in I\), the function \(H_k(d)\) has the form

$$\begin{aligned} H_k(d)= \displaystyle \max _{i \in I}\{(g_i^{(1)}-g_j^{(2)})^\top d- \alpha _i^{(1)}\}, \end{aligned}$$

which is convex piecewise-affine. To make its minimization well-posed we add to \(H_k(d)\) the strictly convex term \(\frac{1}{2}\Vert d\Vert ^2\), thus coming out with the minimization of the maximum of finitely many strictly convex functions of d. Such a problem can be equivalently formulated as the following auxiliary local problem QP(I)

figure a

Denoting by \((\bar{d},\bar{v})\) the unique optimal solution of (QP(I)), a standard duality argument ensures that

$$\begin{aligned} \bar{d}= & {} - \displaystyle \sum _{i \in I}\bar{\lambda }_i u_i, \end{aligned}$$
(28)
$$\begin{aligned} \bar{v}= & {} - \left\| \displaystyle \sum _{i \in I}\bar{\lambda }_i u_i\right\| ^2 -\displaystyle \sum _{i \in I}\bar{\lambda }_i \alpha _i^{(1)} \end{aligned}$$
(29)

where \(\bar{\lambda }_i \ge 0\), \(i \in I\), with \( \sum _{i \in I}\bar{\lambda }_i=1\), are the optimal variables of the dual of QP(I). Although, in principle, the set J(0) may contain multiple indices (i.e., multiple affine pieces of \(f_2\) may be active at \(x_k\)), next we will adopt the strategy of forcing J(0) to be a singleton.

We focus now on the properties of the solution returned by QP(I). We observe that when \(|\bar{v}|\) is small, by taking into account equation (29), the condition (6) for the point \(x_k\) to be critical is approximately satisfied. On the contrary, when \(|\bar{v}|\) is large, since

$$\begin{aligned} 0\ge \bar{v}= \displaystyle \max _{i \in I} \{ u_i^\top \bar{d}-\alpha _i^{(1)}\} \ge \displaystyle \max _{i \in I} h_k^{(i)}(\bar{d})= H_k(\bar{d}) \end{aligned}$$
(30)

we observe that a “good agreement” between the predicted reductions \(\bar{v}\) and \(H_k(\bar{d})\), denotes that the local program is still a good approximation of \(H_k\) at \(\bar{d}\), hence \(\bar{d}\) can be considered as a possible descent direction for function f. In case a “poor agreement” between \(\bar{v}\) and \(H_k(\bar{d})\) is detected, we propose to refine calculation of the search direction, by constructing a more accurate model of function \(H_k\) at \(\bar{d}\), i.e., away from \(d=0\). In particular, we calculate, for every \(i \in I\), the index \(\bar{\jmath }_i \in J\) such that

$$\begin{aligned} h_k^{(i)}(\bar{d})=(g_i^{(1)}-g_{\bar{\jmath }_i}^{(2)})^\top \bar{d} - \alpha _{i}^{(1)} + \alpha _{\bar{\jmath }_i}^{(2)} \end{aligned}$$

and we introduce the following auxiliary away problem \({{ QP}{(I,\bar{J})}}\)

figure b

again a (strictly) convex quadratic program, where \(\bar{u}_i \triangleq g_i^{(1)}-g_{\bar{\jmath }_i}^{(2)}\) and \(\bar{J}\) is the set of indices \(\bar{\jmath }_i\), \(i \in I\). It is worth noting that while problem \({ QP{(I,\bar{J})}}\) embeds the function

$$\begin{aligned} \displaystyle \max _{i \in I} \, \{\bar{u}_i^\top d - \alpha _{i}^{(1)} + \alpha _{\bar{\jmath }_i}^{(2)}\} \end{aligned}$$
(31)

which interpolates the maxmin model \(H_k\) at \(\bar{d}\), the problem QP(I) uses the function

$$\begin{aligned} \max _{i \in I} \, \{u_i^\top d -\alpha _{i}^{(1)}\}, \end{aligned}$$
(32)

which, in turn, interpolates \(H_k\) at \(d=0\). Function (31) resembles \(H_k\) around \(\bar{d}\), but it can be a poor representation for small values in norm of d, as it does not even interpolate \(H_k\) (and f) at \(d=0\), provided \( \alpha _{\bar{\jmath }_i}^{(2)}>0\) for at least one index \(i \in I\). As a consequence, denoting by \((\hat{d},\hat{v})\) the (unique) optimal solution of \(QP{(I,\bar{J})}\), we will adopt \(\hat{d}\) as an alternative search direction in case the predicted reduction \(H_k(\hat{d})\) is strictly lower than \(H_k(\bar{d})\).

We are now ready to describe our DC Piecewise-Concave algorithm (DCPCA). A compact description of DCPCA is first given in Scheme 1, where its essential steps are highlighted. The comments therein refer to the actual steps of DCPCA, which is fully detailed in Algorithm 1.

figure c

DCPCA takes as an input any starting point \(x_0 \in \mathbb {R}^n\), and returns an approximate critical point \(x^*\). We assume that the set

$$\begin{aligned} S_0 \triangleq \{x \in \mathbb {R}^n | f(x) \le f(x_0) \} \end{aligned}$$

is bounded. The following parameters are to be set: the optimality parameter \(\theta >0\), the subgradient threshold \(\eta >0\), the linearization-error threshold \(\varepsilon > 0\), the approximate line-search parameter \(m \in (0,1)\), the step-size reduction parameter \(\sigma \in (0,1)\), the agreement rate \(\rho \in (0,1)\).

figure d

Some explanatory comments about the structure of the algorithm are in order. Given the current iterate \(x_k\), DCPCA first determines the main search-direction \(\bar{d}\) and the main predicted-reduction \(\bar{v}\) by solving QP(I). Next, the condition \(\bar{v} < \rho H_k(\bar{d})\) checked at step 7 is meant to detect if a “good agreement” holds between \(\bar{v}\) and the strong predicted reduction \(H_k(\bar{d})\) provided by the model at \(\bar{d}\). Then, in case of “poor agreement” between \(\bar{v}\) and \(H_k(\bar{d})\), DCPCA generates an alternative search-direction \(\hat{d}\) by solving \({ QP{(I,\bar{J})}}\), and selects the search direction \(d_k\) at steps 11–15 as the most promising one between \(\bar{d}\) and \(\hat{d}\). Independent of the selected search-direction, an Armijo-type line-search is executed adopting the strong predicted-reduction yielded by the nonconvex model at \(d_k\), i.e., \(H_k(d_k)\). As soon as the line-search is successful (a sufficient decrease is achieved at step 18), a serious step is made, namely, the current estimate of the minimum is updated and a new iteration takes place. It is worth noting that the failure of the line-search, at a point that is very close to the current iterate, does not immediately imply a null-step execution (i.e., information enrichment of \(\mathcal{B}_1\) about the subdifferential of \(f_1\) at \(x_k\)) at steps 35–39. In fact, the role of the preliminary steps 29–34 is to prevent the algorithm from certifying the line-search failure, until the main search-direction has been checked for sufficient descent with respect to the main predicted-reduction. We note that, whenever \(g_+^{(1)}\) is inserted into \(\mathcal{B}_1\) at step 36, then \(t\Vert d_k\Vert \le \eta \) implies that \(g_+^{(1)} \in \partial _{\varepsilon _1}f_1(x_k)\) for \(\varepsilon _1 \le 2\eta L_1\), where \(L_1\) is the Lipschitz constant of \(f_1\) on the set

$$\begin{aligned} S_0 (\eta ) \triangleq \left\{ x \in \mathbb {R}^n : \mathrm{dist}(x, S_0)\le \eta \right\} . \end{aligned}$$

Finally, the following remark aims at clarifying the role of the stopping condition in terms of an approximate stationarity condition for problem (1).

Remark 2

The stopping condition \(\bar{v} \ge -\theta \), checked at step 5 of DCPCA, is an approximate \(\theta \)-criticality condition for \(x^*\). Indeed, taking into account (29), the stopping condition ensures that

$$\begin{aligned} \left\| \sum _{i \in I} \lambda _i^* g_i^{(1)} - \sum _{i \in I} \lambda _i^* g_{j_i}^{(2)}\right\| \le \sqrt{\theta } \,\,\,\,\, \mathrm {and} \,\,\,\,\, \left\| \sum _{i \in I} \lambda _i^* \alpha _i^{(1)} \right\| \le \sqrt{\theta }, \end{aligned}$$

which in turn implies that there exist \(g_*^{(1)} \in \partial _{\theta } f_1(x^*)\) and \(g_*^{(2)} \in \partial f_2(x^*)\) such that

$$\begin{aligned} \Vert g_*^{(1)}-g_*^{(2)}\Vert ^2 \le \theta , \end{aligned}$$

namely, that

$$\begin{aligned} \mathrm{dist}\left( \partial _{\theta } f_1(x^*), \partial f_2(x^*)\right) \le \theta , \end{aligned}$$

an approximate \(\theta \)-criticality condition for \(x^*\), see (6).

5 Termination properties

Before introducing the main theorem about convergence of Algorithm 1, in the following lemma we give a bound on the size of the search-directions.

Lemma 1

Let \(L_1\) and \(L_2\) be the Lipschitz constants of \(f_1\) and \(f_2\), respectively, on the set \(S_0 (\eta )\). Then the following bound holds

$$\begin{aligned} \Vert d_k\Vert \le 2L \end{aligned}$$
(33)

where \(L \triangleq \max \{L_1,L_2\}\).

Proof

Assume first that \(d_k = \bar{d}\), then the result follows by taking into account (28). Next, assuming that \(d_k = \hat{d}\), the result follows by observing that \(H_k(\hat{d})<H_k(\bar{d}) <0\) (see steps 11 and 12, and, consequently, that \(\hat{d}\) belongs to the set \(\hat{S}\) where the objective function of problem \({{ QP}{(I,\bar{J})}}\) is negative. Then, the property follows by noting that \(\hat{S} \subset S'\), with

$$\begin{aligned} S' = \{d| \bar{u}'^{\top } d+\frac{1}{2}\Vert d\Vert ^2 \le 0\} \end{aligned}$$

where \(\bar{u}'= g_i^{(1)}-g_{\bar{\jmath }_i}^{(2)}\) for the index i with corresponding \( \alpha _{i}^{(1)}=0\), independently of the choice of the index \({\bar{\jmath }_i}\). \(\square \)

Next we present the convergence results. We start by proving finiteness of the null-step sequence.

Lemma 2

At any given iterate \(x_k \in S_0\), the sequence of null-step execution made by Algorithm 1 terminates after finitely many iterations either fulfilling the sufficient decrease condition at step 18 or satisfying the stopping condition at step 5.

Proof

We need to show that the algorithm cannot loop infinitely many times between 38 and step 4. Observe, indeed, that a null step is made, with consequent enrichment of bundle \(\mathcal{B}_1\) and return to step 4, only when the main search-direction \(d_k=\bar{d}\) reveals itself unsuccessful with respect to the main predicted-reduction \(v_k = \bar{v}\), see step 35. Now suppose, for a contradiction, that an infinite sequence of null steps occurs, and, to simplify the notation, let \(\{\bar{v}_h \}\), \(\{\bar{d}_h \}\), \(\{\bar{z}_h \}\) and \(\{t_h\}\) be the corresponding sequences of values of \(\bar{v} \), \(\bar{d}\), \(\bar{z}\) and of the step-size t, respectively, where

$$\begin{aligned} \bar{z}_h = \bar{v}_h + \frac{1}{2} \Vert \bar{d}_h\Vert ^2. \end{aligned}$$

Indexing by \(h+1\) the bundle element \(\{(g^{(1)}_+,\alpha ^{(1)}_+)\}\) inserted into \(\mathcal{B}_1\) at the hth null-step iteration, we observe that from condition

$$\begin{aligned} f(x_k+t_h\bar{d_h}) - f(x_k) > m t_h \bar{v}_h, \end{aligned}$$
(34)

taking into account (22) and applying the subgradient inequality (9) to \(f_2\), it follows that

$$\begin{aligned} \left( g^{(1)}_{h+1}-g^{(2)}_{j}\right) ^\top \bar{d_h} > m \bar{v}_h + \frac{1}{t_h} \alpha _{h+1}^{(1)}, \,\,\,\, j \in J(0), \end{aligned}$$
(35)

which in turn implies that

$$\begin{aligned} \left( g^{(1)}_{h+1}-g^{(2)}_{j}\right) ^\top \bar{d_h} - \alpha _{h+1}^{(1)} > m \bar{v}_h + \left( \frac{1}{t_h} - 1\right) \alpha _{h+1}^{(1)} \ge m \bar{v}_h, \,\,\,\, j \in J(0) \end{aligned}$$
(36)

since \(t_h \le 1\). From (36) it follows that, once the element \(\{(g^{(1)}_{h+1},\alpha ^{(1)}_{h+1})\}\) is inserted into \(\mathcal{B}_1\), a cut is introduced in the feasible region of problem QP(I) and, consequently, the sequence \(\{\bar{z}_h \}\) is monotonically increasing and convergent, being negative, to a limit \(\tilde{z} \le 0\). Moreover, see (33), the sequence \(\{\bar{d}_h\}\) admits a convergent subsequence, corresponding to a certain set of indices \( \mathcal {H}\), and let \(\tilde{d}\) be its limit point. Hence, the corresponding subsequence \(\{\bar{v}_h\}_{h \in \mathcal{H}}\) is convergent as well to a limit \(\tilde{v} \le 0\). Consider now two successive indices \(p, q \in \mathcal {H}\). From (36) and the definition of problem QP(I) we have, for \(j \in J(0)\), that

$$\begin{aligned} \left( g^{(1)}_{p+1}-g^{(2)}_{j}\right) ^\top \bar{d_p} - \alpha _{p+1}^{(1)} > m \bar{v}_p, \end{aligned}$$

and

$$\begin{aligned} \left( g^{(1)}_{p+1}-g^{(2)}_{j}\right) ^\top \bar{d_q} - \alpha _{p+1}^{(1)} \le \bar{v}_q. \end{aligned}$$

They in turn imply that

$$\begin{aligned} \bar{v}_q -m\bar{v}_p > \left( g^{(1)}_{p+1}-g^{(2)}_{j}\right) ^\top ( \bar{d_q} - \bar{d_p}) \end{aligned}$$

which, passing to the limit, would imply

$$\begin{aligned} (1-m)\tilde{v} \ge 0, \end{aligned}$$

a contradiction, since in an infinite sequence of null steps the stopping condition can never be satisfied. \(\square \)

Now we can prove finite termination of the algorithm

Theorem 1

For any starting point \(x_0 \in \mathbb {R}^n\), Algorithm 1 terminates after finitely many iterations at a point \(x^*\) satisfying the stopping criterion at step 5.

Proof

Suppose for a contradiction that the stopping criterion at step 5 is never fulfilled. Lemma 2 ensures that, in such a case, an infinite sequence of serious steps can only occur, with the algorithm looping infinitely many times between step 25 and step 4.

Observe now that whenever the main search-direction \(d_k=\bar{d}\) is adopted (see steps 8, 14, or 30), it follows from (30) that \(v_k=H_k(\bar{d}) \le \bar{v}\) (see steps 17 and 31). On the other hand, whenever the alternative search-direction \(d_k=\hat{d}\) is adopted (see steps 11 and 12), it holds \(v_k=H_k(\hat{d}) < H_k(\bar{d})\le \bar{v}\) (see step 17). Summing up, every time a serious step is entered at step 19, taking into account the failed stopping test at step 5, it is

$$\begin{aligned} v_k \le \bar{v} \le -\theta < 0. \end{aligned}$$
(37)

Furthermore, it also holds that either \(t=1\) or \(t\Vert d_k\Vert > \sigma \eta \). As a consequence, the fulfillment of the sufficient decrease condition at step 18 implies that either

$$\begin{aligned} f(x_k+td_k) - f(x_k) < - m \theta , \end{aligned}$$
(38)

in case \(t=1\), or

$$\begin{aligned} f(x_k+td_k) - f(x_k) < -\frac{m \sigma \eta \theta }{2L}, \end{aligned}$$
(39)

in case \(t\Vert d_k\Vert > \sigma \eta \), since Lemma 1 implies that \(-t < -\frac{\sigma \eta }{\Vert d_k\Vert } \le -\frac{\sigma \eta }{2L}\). Hence, inequalities (38) and (39) imply that the decrease in the objective function value is bounded away from zero every time a serious step is made. This contradicts the fact that an infinite number of descent steps occurs, under the assumption that \(S_0\) is bounded. \(\square \)

6 Numerical results

In order to evaluate the practical behavior of the proposed approach, in the following we report on the computational performance of DCPCA applied to the solution of a set of 46 academic test problems, presented in [21], that belong to 10 different instance classes, with size ranging from \(n = 2\) to \(n=50000\). The 10 instance classes all refer to nonsmooth DC problems, at least one DC component being always nonsmooth. Moreover, a starting point is given as a feature of each instance. A summary of some relevant information regarding the test set is provided in Table 1, where for each instance we report

  • id, an instance identifier,

  • n, the number of variables,

  • \(f^*\), the known best value of the objective function,

  • \(f(x_0)\), the objective function value at the starting point.

Table 1 Summary of test instances
Full size table

Algorithm DCPCA has been implemented in Java, and the tests have been executed on a 3.50 GHz Intel Core i7 computer. The QP solver of IBM ILOG CPLEX 12.6 [20] has been used to solve the quadratic subprograms. The following set of parameters has been adopted: \(\theta = 10^{-6}\), \(\eta =0.7\), \(m=10^{-4}\), \(\rho = 0.95\), and \(\varepsilon =0.95\). Furthermore, the setting of the step-size reduction parameter \(\sigma \) depends on the instance size as follows: \(\sigma = 0.05\) if \(n < 10\), and \(\sigma = 0.6\) if \(\sigma \ge 10\).

We have compared the computational behavior of DCPCA against NCVX, a state-of-the-art general-purpose solver for nonconvex nonsmooth optimization introduced in [12], and against PBDC, a proximal bundle method for nonsmooth DC programs introduced in [21] where its practical efficiency has been thoroughly verified. We remark that PBDC terminates as soon as the distance between the convex hulls of subgradients of \(f_1\) and \(f_2\), in a neighborhood of the current iterate, is below a given threshold, while the stopping criterion of NCVX is based on the distance from zero of the Goldstein \(\epsilon \)-subdifferential of f at the current point, as it does not exploit at all the DC structure of f. Since the stopping criteria and the related tolerance parameters are significantly different between the adopted algorithms, the rationale of the tolerance tuning of each algorithm has been to guarantee similar level of precision for as many instances as possible across the three algorithms. We have adopted a double-precision Fortran 95 implementation of PBDC, and a Java implementation of NCVX, running the experiments on the same machine.

A summary of the computational behavior of the three solvers is presented in Table 2 where, for each instance and each solver, we report an appropriate subset of the following results:

  • \(f(x^*)\), the objective function value returned by the algorithm upon termination,

  • \(N_f\), the number of the objective function evaluations,

  • cpu, the CPU execution time measured in seconds,

  • \(N_{g_1}\), the number of subgradient evaluations for \(f_1\),

  • \(N_{g_2}\), the number of subgradient evaluations for \(f_2\),

  • \(N_{g}\), the number of subgradient evaluations for f.

The results show the good performance of DCPCA, both in terms of effectiveness, as it attains the known best value of the objective function for 45 out of 46 instances, and in terms of efficiency, since very good precision is attained for almost all cases, and the number of function evaluations is always kept to reasonably low levels, along with the corresponding computational time.

Focusing on the comparison against PBDC, we report only the number of function evaluations and the number of subgradient evaluations for \(f_1\) and \(f_2\), being the cpu execution times not comparable due to the different implementation languages adopted. We observe a slight advantage of DCPCA over PBDC in terms of effectiveness, as PBDC attains the known best value of the objective function for 43 out of 46 instances, while DCPCA and PBDC have comparable performance in terms of the number of function evaluations, with the former seemingly more suitable for large-scale instances. A sharper difference in favor of DCPCA can be observed considering the total number of subgradient evaluations, since the simpler structure of DCPCA allows to achieve remarkable performance even for large-scale instances by using fewer subgradients and, hence, by solving quadratic subproblems of smaller size.

Focusing, finally, on the comparison against NCVX, we observe that although DCPCA seems to have lower efficiency than NCVX in terms of the number of function evaluations, still DCPCA has a clear advantage in terms of effectiveness, as NCVX can find the known best value of the objective function for only 38 out of 46 instances. Making a fair comparison in terms of the number of subgradient evaluations is not straightforward, nevertheless we observe that for large instances DCPCA performs better than NCVX even comparing \(N_g\) with the sum of \(N_{g_1}+N_{g_2}\). A similar trend can also be seen analyzing the cpu execution times. In summary, the simpler structure of the bundle management phase, coupled with the line-search approach, makes DCPCA more suited than NCVX to deal even with large-scale instances, although at the expenses of a possibly larger number of function evaluations for small-scale instances.

Table 2 Computational results with DCPCA, PBDC, and NCVX
Full size table

7 Conclusions

We have introduced a proximal bundle method for the unconstrained minimization of a nonsmooth DC function. The main novelty of the approach is represented by the model adopted to approximate the function reduction, which is of the piecewise concave type, pieces being piecewise-affine, hence it is nonconvex. In particular, the model is built by using two separate piecewise-affine approximations of the DC components, which combine themselves into a DC piecewise-affine model. Rather than directly tackling the minimization of the nonconvex model, we resort to an auxiliary convex quadratic program, whose solution returns a descent search-direction, or certifies stationarity. Furthermore, in order to cope with possible poor approximation properties of the former model, at points that are far from the current estimate of the minimizer, we have introduced another auxiliary convex quadratic program, with improved approximation properties far from the current iterate, that can possibly provide an alternative more promising search-direction. Such two search-directions are then explored via a line-search approach aiming at finding a sufficient descent or a model improvement. We have proved finite termination of the method at points that satisfy an approximate criticality condition, and have tested the approach on a set of academic instances, with sizes ranging from extra-small to extra-large, obtaining rather encouraging performance in terms of effectiveness and efficiency. Future work would be focused on the possibility of adopting appropriate aggregation schemes to keep the bundle size limited.