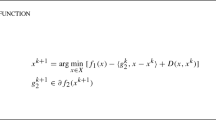Enhanced proximal DC algorithms with extrapolation for a class of structured nonsmooth DC minimization

Abstract

In this paper we consider a class of structured nonsmooth difference-of-convex (DC) minimization in which the first convex component is the sum of a smooth and nonsmooth functions while the second convex component is the supremum of possibly infinitely many convex smooth functions. We first propose an inexact enhanced DC algorithm for solving this problem in which the second convex component is the supremum of finitely many convex smooth functions, and show that every accumulation point of the generated sequence is an $(\alpha ,\eta )$-D-stationary point of the problem, which is generally stronger than an ordinary D-stationary point. In addition, inspired by the recent work (Pang et al. in Math Oper Res 42(1):95–118, 2017; Wen et al. in Comput Optim Appl 69(2):297–324, 2018), we propose two proximal DC algorithms with extrapolation for solving this problem. We show that every accumulation point of the solution sequence generated by them is an $(\alpha ,\eta )$-D-stationary point of the problem, and establish the convergence of the entire sequence under some suitable assumption. We also introduce a concept of approximate $(\alpha ,\eta )$-D-stationary point and derive iteration complexity of the proposed algorithms for finding an approximate $(\alpha ,\eta )$-D-stationary point. In contrast with the DC algorithm (Pang et al. 2017), our proximal DC algorithms have much simpler subproblems and also incorporate the extrapolation for possible acceleration. Moreover, one of our proximal DC algorithms is potentially applicable to the DC problem in which the second convex component is the supremum of infinitely many convex smooth functions. In addition, our algorithms have stronger convergence results than the proximal DC algorithm in Wen et al. (2018).

1 Introduction

Difference-of-convex (DC) minimization, which refers to the problem of minimizing the difference of two convex functions, forms a large class of nonconvex optimization problems and has been studied extensively for decades in the literature of mathematical programming. In this paper we consider a class of DC minimization in the form of

$$\begin{aligned} \min _{x\in {\mathbb {R}}^n} F(x) := f(x) - g(x), \end{aligned}$$

(1.1)

where

$$\begin{aligned} f(x) := f_s(x) + f_n(x), \qquad g(x) := \max _{y\in \mathcal {Y}} \psi (x,y). \end{aligned}$$

(1.2)

Throughout this paper we make the following assumptions for problem (1.1).

Assumption 1

• (a) $f_n$ is a proper closed convex function with a nonempty domain denoted by $\mathrm {dom}(f_n)$.

• (b) $f_s$ is convex and continuously differentiable on ${\mathbb {R}}^n$, and its gradient $\nabla f_s$ is Lipschitz continuous with Lipschitz constant $L>0$.

• (c) $\mathcal {Y}$ is a compact set in ${\mathbb {R}}^m$. For any $y\in \mathcal {Y}$, $\psi (\cdot ,y)$ is convex and continuously differentiable on an open convex set $\Omega$ containing $\mathrm {dom}(f_n)$. Moreover, as a function of (x, y), $\psi$ is continuous on $\Omega \times \mathcal {Y}$.

• (d) The optimal value of (1.1), denoted as $F^{*}$, is finite.

It is not hard to observe that both f and g are convex but possibly nonsmooth. In addition, g is finite and continuous on $\Omega$, and $F:{\mathbb {R}}^n\rightarrow (-\infty ,\infty ]$ is lower-semicontinuous with $\mathrm {dom}(F) = \mathrm {dom}(f) = \mathrm {dom}(f_n)$. Applications of DC problem (1.1) can be found in sparse recovery [9, 11], digital communication system [1, 13], assignment allocation [17] and low-rank matrix optimization [11].

The classical difference-of-convex algorithm (DCA) is broadly used in DC programming (e.g., see [8,9,10, 14]) and can be applied to problem (1.1). Given an iterate $x^k$, DCA generates the next one by solving the convex optimization problem

$$\begin{aligned} x^{k+1} \in \mathop {{{\mathrm{Argmin}}}}\limits _{x\in {\mathbb {R}}^n} f(x) - \langle v^k, x \rangle \end{aligned}$$

for some $v^k\in \partial g(x^k)$. By exploiting the structure of f, the proximal DCA (PDCA) has recently been proposed for solving a class of DC programming (e.g., see [9]). It can be suitably applied to (1.1) for which the new iterate is obtained by solving the proximal subproblem

$$\begin{aligned} x^{k+1} = \mathop {{\text {argmin}}}\limits _{x\in {\mathbb {R}}^n} f_n(x) + \langle \nabla f_s(x^k) - v^k, x \rangle + \frac{L}{2}\Vert x - x^k\Vert ^2 \end{aligned}$$

(1.3)

for some $v^k\in \partial g(x^k)$, where $L>0$ is the Lipschitz constant of $\nabla f_s$. For possibly accelerating PDCA, Wen et al. [19] recently proposed a proximal DCA with extrapolation (PDCAe) that is also applicable to solve (1.1). In particular, an extrapolation point $z^k = x^k + \beta _k(x^k - x^{k-1})$ is first constructed for some $\beta _k\in [0,1)$, and the next iterate is then computed by

$$\begin{aligned} x^{k+1} = \mathop {{\text {argmin}}}\limits _{x\in {\mathbb {R}}^n} f_n(x) + \langle \nabla f_s(z^k) - v^k, x \rangle + \frac{L}{2}\Vert x - z^k\Vert ^2 \end{aligned}$$

(1.4)

for some $v^k\in \partial g(x^k)$. It has been shown that every accumulation point $x^\infty$ of the sequence $\{x^k\}$ generated by DCA, PDCA and PDCAe is a critical point of problem (1.1), that is, $\partial f(x^\infty ) \cap \partial g(x^\infty ) \ne \emptyset$.

By exploring the structure of g, Pang et al. [13] recently proposed a novel enhanced DCA (EDCA) for solving problem (1.1) with $\mathcal {Y}$ being a finite set. For the sake of convenience, assume $\mathcal {Y}=\{1,\ldots , I\}$ and $\psi (x,i)=\psi _i(x)$ for every $i\in \mathcal {Y}$. Given the iterate $x^k$, EDCA first solves the following convex optimization problems

$$\begin{aligned} x^{k,i} = \mathop {{\text {argmin}}}\limits _{x\in {\mathbb {R}}^n} f(x) - \langle \nabla \psi _i(x^k),x \rangle + \frac{1}{2}\Vert x - x^k\Vert ^2 \end{aligned}$$

(1.5)

for each $i\in \mathcal {A}(x^k,{\tilde{\eta }})$, where $\mathcal {A}(x^k,{\tilde{\eta }}) = \{i\in \mathcal {Y}: \psi _i(x^k) \ge g(x^k) - {\tilde{\eta }}\}$ for some ${\tilde{\eta }}>0$. It then generates the next iterate by letting $x^{k+1} = x^{k,{\hat{i}}}$ with ${\hat{i}}$ given by

$$\begin{aligned} {\hat{i}} \in \mathop {{{\mathrm{Argmin}}}}\limits _{i\in \mathcal {A}(x^k,{\tilde{\eta }})} F(x^{k,i}) + \frac{1}{2}\Vert x^{k,i} - x^k\Vert ^2. \end{aligned}$$

(1.6)

It is shown in [13] that any accumulation point $x^\infty$ of the sequence $\{x^k\}$ generated by EDCA is a directional-stationary (D-stationary) point of problem (1.1), that is, $\partial g(x^\infty ) \subseteq \partial f(x^\infty )$, which is stronger than the aforementioned critical point.

Although EDCA generally enjoys stronger convergence than DCA, PDCA and PDCAe, its convergence proof requires an exact solution of its subproblems (1.5). Since these subproblems are generally not simple and their exact solution typically requires an iterative scheme, it would be desirable to have a version of EDCA that would alleviate this requirement. Motivated by this, we propose an inexact EDCA, referred to as iEDCA, for solving problem (1.1) with $\mathcal {Y}$ being a finite set, whose subproblems are solved only inexactly. In particular, given an iterate $x^k$, iEDCA first finds an approximate solution $x^{k,i}$ of subproblem (1.5) such that

$$\begin{aligned} \text{ dist }(0,\partial f(x^{k,i}) - \nabla \psi _i(x^k) + x^{k,i} - x^k) \le \delta _k \end{aligned}$$

(1.7)

for each $i\in \mathcal {A}(x^k,{\tilde{\eta }})$ and some $\delta _k\ge 0$. It then generates the next iterate by letting $x^{k+1} = x^{k,{\hat{i}}}$ with ${\hat{i}}$ given by (1.6). Given that $x^{k,i}$ satisfying (1.7) can be found, iEDCA is practically implementable. We show that if $\sum _{k=0}^\infty \delta _k^2 < \infty$, any accumulation point of the sequence generated by iEDCA is an $(\alpha ,\eta )$-D-stationary point¹ of problem (1.1) (see Sect. 2 for the definition) for some $\alpha >0$ and $\eta \ge 0$, which is generally stronger than an ordinary D-stationary point. Also, notice that iEDCA reduces to EDCA if $\delta _k\equiv 0$. As a byproduct, we thus improve the convergence results in [13] on EDCA.

Though iEDCA generally enjoys stronger convergence than PDCA and PDCAe, its subproblems (1.5) are, however, generally complicated, which require some iterative method for finding an approximate solution and render the entire algorithm a doubly iterative method. On the other hand, the subproblems (1.3) and (1.4) of PDCA and PDCAe are much simpler, which only require evaluating the proximal operator associated with $f_n$.² Motivated by this, we propose an enhanced PDCA algorithm, referred to as $\mathrm{EPDCA}_1$, for solving problem (1.1) with $\mathcal {Y}$ being a finite set, which inherits the advantages of EDCA and PDCAe. In particular, its subproblems are analogous to those of PDCAe with extrapolation incorporated for possible acceleration. Moreover, any accumulation point of the sequence generated by the proposed algorithm is an $(\alpha ,\eta )$-D-stationary point of problem (1.1). We also show that its entire sequence is convergent under some suitable assumption. We shall mention that the framework of $\mathrm{EPDCA}_1$ includes EDCA as a special case. Therefore, as a byproduct we also provide some sufficient conditions on the convergence of the entire sequence generated by EDCA.

It shall be mentioned that EDCA, iEDCA and $\mathrm{EPDCA}_1$ are only applicable to problem (1.1) with $\mathcal {Y}$ being a finite set. As remarked in [13], it has remained open to design an algorithm converging (subsequentially) to a D-stationary point of problem (1.1) for which $\mathcal {Y}$ is an infinite compact set. In this paper we make an attempt to answer this question. In particular, we propose another enhanced PDCA, referred to as $\mathrm{EPDCA}_2$, for solving problem (1.1) with $\mathcal {Y}$ being a (possibly infinite) compact set. Similar to $\mathrm{EPDCA}_1$, the extrapolation scheme is incorporated in this algorithm for possible acceleration. It is also shown that any accumulation point of the sequence generated by $\mathrm{EPDCA}_2$ is an $(\alpha ,\eta )$-D-stationary point of problem (1.1). The key difference between this algorithm and $\mathrm{EPDCA}_1$ and EDCA is that it contains a single minimization subproblem at each iteration. Even for the case where $\mathcal {Y}$ is a finite set, $\mathrm{EPDCA}_2$ also distinguishes from $\mathrm{EPDCA}_1$ and EDCA. Albeit nonconvex in general, we show that this subproblem can be efficiently solved for some instances of (1.1).

Though EDCA, iEDCA, $\mathrm{EPDCA}_1$ and $\mathrm{EPDCA}_2$ converge subsequentially to an $(\alpha ,\eta )$-D-stationary point of problem (1.1) in long run, in practical computation one has to terminate the methods at some approximate $(\alpha ,\eta )$-D-stationary point. We introduce the concept of an approximate $(\alpha ,\eta )$-D-stationary point and study some properties of it. We also derive the iteration complexity of $\mathrm{EPDCA}_1$ and $\mathrm{EPDCA}_2$ for computing an approximate $(\alpha ,\eta )$-D-stationary point of problem (1.1).

The rest of this paper is organized as follows. In Sect. 2, we introduce the concepts of $(\alpha ,\eta )$-D-stationary point and approximate $(\alpha ,\eta )$-D-stationary point, and study some of their properties. In Sects. 3 and 4, we respectively propose an inexact enhanced DCA and an enhanced PDCA with extrapolation for solving problem (1.1) with g given by a finite supremum and study the convergence of the methods. In Sect. 5, we propose another enhanced PDCA with extrapolation that is potentially applicable to problem (1.1) with g given by an infinite supremum and establish its convergence. Finally, in Sect. 6 we present some concluding remarks.

1.1 Notation

Let ${\mathbb {R}}^n$ denote the n-dimensional Euclidean space, $\langle \cdot ,\cdot \rangle$ denote the standard inner product, and $\Vert \cdot \Vert$ denote the Euclidean norm. Given a function $h:{\mathbb {R}}^n\rightarrow (-\infty ,\infty ]$, we use $\mathrm {dom}(h)$ to denote the domain of h, that is, $\mathrm {dom}(h) = \{x\in {\mathbb {R}}^n: h(x)<\infty \}$. The directional derivative of h at a point $x \in \mathrm {dom}(h)$ along a direction $d\in {\mathbb {R}}^n$ is defined as

$$\begin{aligned} h'(x; d)=\lim \limits _{\tau \downarrow 0}\frac{h(x+\tau d)-h(x)}{\tau }. \end{aligned}$$

Suppose h is additionally convex. We use $\partial h$ to denote the subdifferential of h (e.g., see [15]). The proximal operator of h, denoted as $\mathrm {prox}_h$, is a mapping from ${\mathbb {R}}^n$ to ${\mathbb {R}}^n$ defined as

$$\begin{aligned} \mathrm {prox}_h(z) = \mathop {{\text {argmin}}}\limits _{x\in {\mathbb {R}}^n} \frac{1}{2}\Vert x - z\Vert ^2 + h(x). \end{aligned}$$

(1.8)

Given any $x\in {\mathbb {R}}^n$, we define the level set $\mathcal {L}(x):=\{z\in {\mathbb {R}}^n: F(z)\le F(x)\}$. For the function g given in (1.2) and any scalar $\eta \ge 0$, we define

$$\begin{aligned} \mathcal {A}(x):=\{y\in \mathcal {Y}: \psi (x,y) = g(x)\}, \quad \quad \mathcal {A}(x,\eta ):=\{y\in \mathcal {Y}: \psi (x,y) \ge g(x) - \eta \}. \end{aligned}$$

(1.9)

Clearly, $\mathcal {A}(x)$ is the associated active indices in defining g(x). Moreover, $\mathcal {A}(x,0) = \mathcal {A}(x)$ and $\mathcal {A}(x)\subseteq \mathcal {A}(x,\eta )\subseteq \mathcal {Y}$ for any $\eta \ge 0$.

Before ending this section, we briefly introduce some concepts of stationarity for problem (1.1). We refer the interested readers to [13] for the detailed discussion. Given $x\in \mathrm {dom}(F)$, x is said to be a critical point of problem (1.1) if $0 \in \partial f(x) - \partial g(x)$, or equivalently, $\partial f(x) \cap \partial g(x) \ne \emptyset$. In addition, x is called a directional-stationary (D-stationary) point of (1.1) if $F^\prime (x;d)\ge 0$ for all $d\in {\mathbb {R}}^n$. It is known that x is a D-stationary point of (1.1) if and only if $\partial g(x) \subseteq \partial f(x)$. It is also known that any local minimizer of problem (1.1) must be a critical point and also a D-stationary point of (1.1). In addition, a D-stationary point of (1.1) must be a critical point of (1.1), but the converse generally does not hold.

2 Preliminaries

In this section we introduce the concepts of $(\alpha ,\eta )$-D-stationary point and approximate $(\alpha ,\eta )$-D-stationary point of (1.1), and study some of their properties. To proceed, we start with a characterization of D-stationary point of (1.1).

Proposition 1

Let $\alpha >0$ be given. Then ${\bar{x}}$ is a D-stationary point of (1.1) if and only if

$$\begin{aligned} {\bar{x}}=\mathop {{\mathrm{argmin}}}\limits _{x\in {\mathbb {R}}^n} \ f(x) - \langle \nabla _x\psi ({\bar{x}},y), x-{\bar{x}} \rangle +\frac{1}{2\alpha } \Vert x-{\bar{x}}\Vert ^2, \quad \forall y\in \mathcal {A}({\bar{x}}), \end{aligned}$$

(2.1)

or equivalently,

$$\begin{aligned} {\bar{x}} = \mathrm {prox}_{\alpha f}\left( {\bar{x}} + \alpha \nabla _x\psi ({\bar{x}},y)\right) , \quad \forall y\in \mathcal {A}({\bar{x}}). \end{aligned}$$

(2.2)

Proof

By Danskin’s theorem (e.g., see [3, Theorem B.25]), one has

$$\begin{aligned} g^\prime (x;d) = \max _{y\in \mathcal {A}(x)} \langle \nabla _x\psi (x,y), d\rangle . \end{aligned}$$

(2.3)

Since the objective of problem (2.1) is convex, it follows that (2.1) holds if and only if $f^\prime ({\bar{x}};d)\ge \langle \nabla _x\psi ({\bar{x}},y),d\rangle$ for any $d\in {\mathbb {R}}^n$ and $y\in \mathcal {A}({\bar{x}})$. Due to (2.3), the latter holds if and only if $f^\prime ({\bar{x}};d)\ge g^\prime ({\bar{x}};d)$ for any $d\in {\mathbb {R}}^n$, which is equivalent to $F^\prime ({\bar{x}};d)\ge 0$ for any $d\in {\mathbb {R}}^n$, that is, ${\bar{x}}$ is a D-stationary point of (1.1). It follows from these and (1.8) that the conclusion holds. $\square$

From Proposition 1, we see that ${\bar{x}}$ is a D-stationary point of (1.1) if and only if

$$\begin{aligned} F({\bar{x}})\le & {} f(x) - \psi ({\bar{x}},y) - \langle \nabla _x\psi ({\bar{x}},y), x-{\bar{x}} \rangle \\&+\frac{1}{2\alpha } \Vert x-{\bar{x}}\Vert ^2, \quad \forall x\in {\mathbb {R}}^n,\;\forall y\in \mathcal {A}({\bar{x}}). \end{aligned}$$

We next introduce the concept of $(\alpha ,\eta )$-D-stationary point of (1.1) by strengthening this inequality.

Definition 1

($(\alpha ,\eta )$-D-stationary point of (1.1)) Given any $\eta \ge 0$ and $\alpha >0$, we say that ${\bar{x}}$ is an $(\alpha ,\eta )$-D-stationary point of problem (1.1) if it satisfies that

$$\begin{aligned} F({\bar{x}})\le & {} f(x) - \psi ({\bar{x}},y) - \langle \nabla _x\psi ({\bar{x}},y),x - {\bar{x}}\rangle \nonumber \\&+ \frac{1}{2\alpha }\Vert x - {\bar{x}}\Vert ^2,\forall x\in {\mathbb {R}}^n,\; \forall y\in \mathcal {A}({\bar{x}},\eta ). \end{aligned}$$

(2.4)

One can observe from (2.4) that an $(\alpha ,\eta )$-D-stationary point of (1.1) is also an $(\bar{\alpha },\bar{\eta })$-D-stationary point of (1.1) for any $\bar{\eta }\in [0,\eta ]$ and $\bar{\alpha }\in (0,\alpha ]$. We next study some further properties of $(\alpha ,\eta )$-D-stationary points.

Proposition 2

Let $x^*$ be a global minimizer of problem (1.1). Then, $x^*$ is an $(\alpha ,\eta )$-D-stationary of problem (1.1) for any $\alpha >0$ and $\eta \ge 0$,

Proof

Since $x^*$ is a global minimizer of (1.1), we have that for any $\alpha >0$, $x\in {\mathbb {R}}^n$ and $y\in \mathcal {Y}$,

$$\begin{aligned} F(x^*)&\le F(x) = f(x) - g(x) \le f(x) - \psi (x,y) \end{aligned}$$

(2.5)

$$\begin{aligned}&\le f(x) - \psi (x^*,y) - \langle \nabla _x\psi (x^*,y), x - x^*\rangle \end{aligned}$$

(2.6)

$$\begin{aligned}&\le f(x) - \psi (x^*,y) - \langle \nabla _x\psi (x^*,y), x - x^*\rangle + \frac{1}{2\alpha }\Vert x - x^*\Vert ^2, \end{aligned}$$

(2.7)

where (2.5) is due to (1.2) and (2.6) follows from the convexity of $\psi (\cdot ,y)$. By (1.9), one has $\mathcal {A}(x,\eta )\subseteq \mathcal {Y}$ for any $\eta \ge 0$. Using this and (2.7), we obtain that for any $\alpha >0$ and $\eta \ge 0$,

$$\begin{aligned} F(x^*)\le & {} f(x) - \psi (x^*,y) - \langle \nabla _x\psi (x^*,y), x -x^*\rangle \\&+ \frac{1}{2\alpha }\Vert x - x^*\Vert ^2, \quad \forall x\in {\mathbb {R}}^n,\;\forall y\in \mathcal {A}(x^*,\eta ). \end{aligned}$$

This together with Definition 1 implies that $x^*$ is an $(\alpha ,\eta )$-D-stationary point of (1.1) for any $\eta \ge 0$ and $\alpha >0$. $\square$

Proposition 3

Suppose that ${\bar{x}}$ is an $(\alpha ,\eta )$-D-stationary point of problem (1.1) for some $\eta \ge 0$ and $\alpha >0$. Then, it holds that

$$\begin{aligned} \Vert {\bar{x}} - \mathrm {prox}_{\alpha f}\left( {\bar{x}} + \alpha \nabla _x\psi ({\bar{x}},y)\right) \Vert \le \sqrt{2\alpha (g({\bar{x}}) - \psi ({\bar{x}},y))}, \quad \forall y\in \mathcal {A}({\bar{x}},\eta ). \end{aligned}$$

(2.8)

Consequently, we have

$$\begin{aligned} \Vert {\bar{x}} - \mathrm {prox}_{\alpha f}\left( {\bar{x}} + \alpha \nabla _x\psi ({\bar{x}},y)\right) \Vert \quad \left\{ \begin{array}{ll} =0, &{} \; \mathrm {if}\; y\in \mathcal {A}({\bar{x}}); \\ \le \sqrt{2\alpha \eta }, &{} \; \mathrm {if}\; y\in \mathcal {A}({\bar{x}},\eta )\setminus \mathcal {A}({\bar{x}}). \end{array} \right. \end{aligned}$$

(2.9)

Furthermore, ${\bar{x}}$ is a D-stationary point of problem (1.1).

Proof

Let $y\in \mathcal {A}({\bar{x}},\eta )$ be arbitrarily chosen, and let $x^+ = \mathrm {prox}_{\alpha f}({\bar{x}} + \alpha \nabla _x\psi ({\bar{x}},y))$. It then follows from (1.8) that

$$\begin{aligned} x^+ = \mathop {{\text {argmin}}}\limits _{x\in {\mathbb {R}}^n} f(x) - \langle \nabla _x\psi ({\bar{x}},y), x - {\bar{x}} \rangle + \frac{1}{2\alpha }\Vert x - {\bar{x}}\Vert ^2. \end{aligned}$$

(2.10)

Its first-order optimality condition yields

$$\begin{aligned} \nabla _x \psi ({\bar{x}},y) = \frac{1}{\alpha }(x^{+} - {\bar{x}}) + v \end{aligned}$$

(2.11)

for some $v\in \partial f(x^+)$. Hence, we have

$$\begin{aligned}&f(x^+) - \langle \nabla _x\psi ({\bar{x}},y), x^+ - {\bar{x}} \rangle + \frac{1}{2\alpha }\Vert x^+ - {\bar{x}}\Vert ^2 \nonumber \\&\quad = f(x^{+}) + \langle v, {\bar{x}} - x^{+} \rangle - \frac{1}{2\alpha }\Vert x^+ - {\bar{x}}\Vert ^2 \nonumber \\&\quad \le f({\bar{x}}) - \frac{1}{2\alpha }\Vert x^+ - {\bar{x}}\Vert ^2 \end{aligned}$$

(2.12)

where the equality is due to (2.11) and the inequality uses the convexity of f. Since ${\bar{x}}$ is an $(\alpha ,\eta )$-D-stationary point of (1.1), it follows from (2.4) with $x = x^+$ that

$$\begin{aligned} f({\bar{x}}) - g({\bar{x}}) \le f(x^{+}) - \psi ({\bar{x}},y) - \langle \nabla _x\psi ({\bar{x}},y), x^+ - {\bar{x}} \rangle + \frac{1}{2\alpha }\Vert x^+ - {\bar{x}}\Vert ^2. \end{aligned}$$

Summing up the above two inequalities yields $\Vert x^+ - {\bar{x}}\Vert \le \sqrt{2\alpha (g({\bar{x}}) - \psi ({\bar{x}},y))}$. This together with the definition of $x^+$ leads to (2.8). In addition, by (1.9), one can see that $\psi ({\bar{x}},y)=g({\bar{x}})$ for every $y\in \mathcal {A}({\bar{x}})$ and $\psi ({\bar{x}},y) \ge g({\bar{x}}) - \eta$ for all $y\in \mathcal {A}({\bar{x}},\eta )\setminus \mathcal {A}({\bar{x}})$. These and (2.8) yield (2.9). Finally, in view of (2.9) and Proposition 1, we have that ${\bar{x}}$ is a D-stationary point of (1.1). $\square$

From Propositions 2 and 3, one can see that an $(\alpha ,\eta )$-D-stationary point is generally stronger than an ordinary D-stationary point. Therefore, it is of interest to develop algorithms converging (subsequentially) to an $(\alpha ,\eta )$-D-stationary point of (1.1) rather than just an ordinary D-stationary point. In the subsequent sections, we will propose such algorithms for (1.1). Though our proposed algorithms converge (subsequentially) to an $(\alpha ,\eta )$-D-stationary point of (1.1), in practical computation one has to terminate them at some approximate $(\alpha ,\eta )$-D-stationary point. We next introduce the concept of approximate $(\alpha ,\eta )$-D-stationary point and study some properties of it.

Definition 2

($\epsilon$-approximate $(\alpha ,\eta )$-D-stationary point of (1.1)) Given any $\epsilon ,\eta \ge 0$, $\alpha >0$, we say that ${\bar{x}}$ is an $\epsilon$-approximate $(\alpha ,\eta )$-D-stationary point of problem (1.1) if it satisfies that

$$\begin{aligned} F({\bar{x}})\le & {} f(x) - \psi ({\bar{x}},y) - \langle \nabla _x\psi ({\bar{x}},y), x - {\bar{x}} \rangle \nonumber \\&+ \frac{1}{2\alpha }\Vert x - {\bar{x}}\Vert ^2 + \epsilon , \quad \forall x\in {\mathbb {R}}^n,\;\forall y\in \mathcal {A}({\bar{x}},\eta ). \end{aligned}$$

(2.13)

Proposition 4

Suppose that ${\bar{x}}$ is an $\epsilon$-approximate $(\alpha ,\eta )$-D-stationary point of (1.1) for some $\epsilon \ge 0$, $\alpha >0$ and $\eta \ge 0$. Then, it holds that

$$\begin{aligned} \Vert {\bar{x}} - \mathrm {prox}_{\alpha f}\left( {\bar{x}} + \alpha \nabla _x\psi ({\bar{x}},y)\right) \Vert \le \sqrt{2\alpha (g({\bar{x}}) - \psi ({\bar{x}},y) + \epsilon )}, \quad \forall y\in \mathcal {A}({\bar{x}},\eta ). \end{aligned}$$

(2.14)

Consequently, we have

$$\begin{aligned} \Vert {\bar{x}} - \mathrm {prox}_{\alpha f}\left( {\bar{x}} + \alpha \nabla _x\psi ({\bar{x}},y)\right) \Vert \le \left\{ \begin{array}{ll} \sqrt{2\alpha \epsilon }, &{} \; \mathrm {if}\; y\in \mathcal {A}({\bar{x}}); \\ \sqrt{2\alpha (\eta +\epsilon )}, &{} \; \mathrm {if}\; y\in \mathcal {A}({\bar{x}},\eta )\setminus \mathcal {A}({\bar{x}}). \end{array} \right. \end{aligned}$$

(2.15)

Proof

Let $y\in \mathcal {A}({\bar{x}},\eta )$ be arbitrarily chosen, and let $x^+ = \mathrm {prox}_{\alpha f}({\bar{x}} + \alpha \nabla _x\psi ({\bar{x}},y))$. It then follows from the same arguments as those in the proof of Proposition 3 that (2.12) holds. Since ${\bar{x}}$ is an $\epsilon$-approximate $(\alpha ,\eta )$-D-stationary point of (1.1), it follows from (2.13) with $x=x^+$ that

$$\begin{aligned} f({\bar{x}}) - g({\bar{x}}) \le f(x^{+}) - \psi ({\bar{x}},y) - \langle \nabla _x\psi ({\bar{x}},y), x^+ - {\bar{x}} \rangle + \frac{1}{2\alpha }\Vert x^+ - {\bar{x}}\Vert ^2 +\epsilon . \end{aligned}$$

Summing up the above inequality and (2.12) yields $\Vert x^+ - {\bar{x}}\Vert \le \sqrt{2\alpha (g({\bar{x}}) - \psi ({\bar{x}},y) + \epsilon )}$. Using this and the same arguments as those in the proof of Proposition 3, we can conclude that (2.14) and (2.15) hold. $\square$

Before ending this section, we establish a lemma that will be used subsequently.

Lemma 1

Suppose that Assumption 1 is satisfied, and let ${\bar{x}}\in \Omega$ and $\eta >0$ be arbitrarily given. Then, for any $\bar{\eta }\in [0,\eta )$, there exists a scalar $\gamma >0$ such that $\mathcal {A}({\bar{x}},\bar{\eta })\subseteq \mathcal {A}(x,\eta )$ whenever $\Vert x - {\bar{x}}\Vert \le \gamma$.

Proof

Suppose for contradiction that the statement is not true. Then there must exist an $\bar{\eta }\in [0,\eta )$ and a sequence $\{(x^t,y^t)\}_{t\ge 0}$ such that $\lim _{t\rightarrow \infty }x^t = {\bar{x}}$, $y^t\in \mathcal {A}({\bar{x}},\bar{\eta })$ but $y^t\notin \mathcal {A}(x^t,\eta )$ for all t. By Assumption 1 (c) and (1.9), one can observe that $\mathcal {A}({\bar{x}},\bar{\eta })$ is compact. Hence, by passing to a subsequence if necessary, we assume for convenience that $\lim _{t\rightarrow \infty }y^t = {\bar{y}}$ for some ${\bar{y}}\in \mathcal {A}({\bar{x}},\bar{\eta })$, which implies $\psi ({\bar{x}},{\bar{y}}) \ge g({\bar{x}}) - \bar{\eta }$. On the other hand, by $y^t\notin \mathcal {A}(x^t,\eta )$ and (1.9), one has $\psi (x^t,y^t) < g(x^t) - \eta$. Passing to the limit and using the continuity of $\psi$ and g, it follows that $\psi ({\bar{x}},{\bar{y}}) \le g({\bar{x}}) - \eta$, which contradicts $\psi ({\bar{x}},{\bar{y}}) \ge g({\bar{x}}) - \bar{\eta }$ due to $\eta >\bar{\eta }$. The proof is then completed. $\square$

3 An inexact enhanced DCA for DC problem with finite supremum

In this section we consider problem (1.1) in which g is defined as the supremum of a finite number of smooth convex functions, namely, the associated $\mathcal {Y}$ in (1.2) is a finite set. For the sake of convenience, throughout this section we assume that

$$\begin{aligned} \mathcal {Y}= \{1,\ldots , I\}, \quad \quad \psi (x,i)=\psi _i(x), \ \forall i\in \mathcal {Y}. \end{aligned}$$

(3.1)

It follows from (1.2) that for such $\mathcal {Y}$ and $\psi (\cdot ,\cdot )$, g can be rewritten as

$$\begin{aligned} g(x)=\max _{1 \le i\le I} \psi _i(x), \quad \forall x\in {\mathbb {R}}^n. \end{aligned}$$

(3.2)

Recently, Pang et al. [13] proposed a novel enhanced DCA (EDCA) for solving problem (1.1) with g given in (3.2). They showed that any accumulation point of the sequence generated by EDCA is a D-stationary point of problem (1.1). As mentioned in Sect. 1, EDCA is, however, generally not implementable because it requires the exact solution of its subproblems. In this section, we propose an inexact EDCA (iEDCA), which only requires a suitable approximate solution of its subproblems. Moreover, we show that any accumulation point of the sequence generated by the proposed algorithm is an $(\alpha ,\eta )$-D-stationary point of problem (1.1) for some $\alpha >0$ and $\eta \ge 0$.

The details of iEDCA are presented as follows.

Algorithm 1

(The inexact enhanced DCA (iEDCA))

• 0. Input $x^0\in \mathrm{dom}(F)$, ${\tilde{\eta }}>0$ and a sequence $\{\delta _k\}\subset {\mathbb {R}}_+$ such that $B:=\sum _{k=0}^\infty \delta _k^2 < \infty$. Set $k\leftarrow 0$.

• 1. For each index $i\in \mathcal {A}(x^k,{\tilde{\eta }})$, find an approximate solution ${\hat{x}}^{k,i}$ of the problem

  $$\begin{aligned} \min _{x\in {\mathbb {R}}^n} \left\{ Q_{k,i}(x):= f(x) - \psi _i(x^k) - \langle \nabla \psi _i(x^k),x - x^k\rangle + \frac{1}{2}\Vert x - x^k\Vert ^2\right\} \end{aligned}$$

  (3.3)

  such that

  $$\begin{aligned} \mathrm{dist}\left( 0, \partial Q_{k,i}({\hat{x}}^{k,i})\right) \le \delta _k. \end{aligned}$$

  (3.4)

• 2. Let ${\hat{i}} \in \mathop {{{\mathrm{Argmin}}}}\nolimits _{i\in \mathcal {A}(x^k,{\tilde{\eta }})} \left\{ F({\hat{x}}^{k,i}) + \frac{1}{2}\Vert {\hat{x}}^{k,i} - x^k\Vert ^2 \right\}$ and set $x^{k+1} = {\hat{x}}^{k,{\hat{i}}}$.

• 3. Set $k\leftarrow k + 1$ and go to Step 1.

End.

Remark 1

The above approximate solution ${\hat{x}}^{k,i}$ of (3.3) can be found by some iterative methods such as proximal gradient method. In addition, Algorithm 1 reduces to EDCA if $\delta _k\equiv 0$.

In what follows, we conduct convergence analysis for Algorithm 1.

Theorem 1

Suppose that the function g is in the form of (3.2) and $x^0$ is a point such that the level set $\{x\in {\mathbb {R}}^n: F(x) \le F(x^0) + B/2\}$ is bounded. Let $\{x^k\}$ be the sequence generated by Algorithm 1. Then the following statements hold.

• (i) The sequence $\{x^k\}$ is bounded.

• (ii) $\lim _{k\rightarrow \infty }\Vert x^k - x^{k-1}\Vert = 0$.

• (iii) $\lim _{k\rightarrow \infty } F(x^k)$ exists and $\lim _{k\rightarrow \infty }F(x^k) = F(x^\infty )$ for any accumulation point $x^\infty$ of $\{x^k\}$.

• (iv) Any accumulation point of $\{x^k\}$ is an $(\alpha ,\eta )$-D-stationary point of (1.1) for any $\alpha \in (0,1]$ and $\eta \in [0,{\tilde{\eta }})$.

Proof

(i) For any $k\ge 0$ and $i\in \mathcal {A}(x^k,{\tilde{\eta }})$, it follows from (3.4) that there exists some $s\in \partial Q_{k,i}({\hat{x}}^{k,i})$ such that $\Vert s\Vert \le \delta _k$. Moreover, one can observe that $Q_{k,i}(x)$ is strongly convex with modulus 1. Hence, we have

$$\begin{aligned} Q_{k,i}(x) \ge Q_{k,i}(\hat{x}^{k,i}) + s^T(x - \hat{x}^{k,i}) + \frac{1}{2}\Vert x - \hat{x}^{k,i}\Vert ^2, \quad \forall x\in {\mathbb {R}}^n, \end{aligned}$$

which leads to

$$\begin{aligned} Q_{k,i}(x)\ge & {} \min _z \left\{ Q_{k,i}(\hat{x}^{k,i}) + s^T(z - \hat{x}^{k,i}) + \frac{1}{2}\Vert z - \hat{x}^{k,i}\Vert ^2\right\} \\= & {} Q_{k,i}(\hat{x}^{k,i}) - \frac{\Vert s\Vert ^2}{2}, \quad \forall x\in {\mathbb {R}}^n. \end{aligned}$$

This together with $\Vert s\Vert \le \delta _k$ implies that

$$\begin{aligned} Q_{k,i}(\hat{x}^{k,i}) \le Q_{k,i}(x) + \frac{\delta _k^2}{2}, \quad \forall x\in {\mathbb {R}}^n. \end{aligned}$$

(3.5)

By (3.2), (3.3), the convexity of $\psi _i(x)$, and Step 2 of Algorithm 1, we obtain that

$$\begin{aligned} Q_{k,i}(\hat{x}^{k,i})&= f(\hat{x}^{k,i}) - \psi _i(x^k) - \langle \nabla \psi _i(x^k), \hat{x}^{k,i} - x^k \rangle + \frac{1}{2}\Vert \hat{x}^{k,i} - x^k\Vert ^2 \end{aligned}$$

(3.6)

$$\begin{aligned}&\ge f(\hat{x}^{k,i}) - \psi _i(\hat{x}^{k,i}) + \frac{1}{2}\Vert \hat{x}^{k,i} - x^k\Vert ^2 \end{aligned}$$

(3.7)

$$\begin{aligned}&\ge f(\hat{x}^{k,i}) - g(\hat{x}^{k,i}) + \frac{1}{2}\Vert \hat{x}^{k,i} - x^k\Vert ^2 \end{aligned}$$

(3.8)

$$\begin{aligned}&= F(\hat{x}^{k,i}) + \frac{1}{2}\Vert \hat{x}^{k,i} - x^k\Vert ^2 \ \ge \ F(x^{k+1}) + \frac{1}{2}\Vert x^{k+1} - x^k\Vert ^2, \end{aligned}$$

(3.9)

where (3.7) follows from the convexity of $\psi _i(x)$, (3.8) is due to (3.2), and (3.9) is by Step 2 of Algorithm 1. It then follows from (3.5) and (3.9) that for any $k\ge 0$ and $i\in \mathcal {A}(x^k,{\tilde{\eta }})$,

$$\begin{aligned} F(x^{k+1}) + \frac{1}{2}\Vert x^{k+1} - x^k\Vert ^2 \le Q_{k,i}(x) + \frac{\delta _k^2}{2}, \quad \forall x\in {\mathbb {R}}^n. \end{aligned}$$

(3.10)

By letting $i\in \mathcal {A}(x^k)$ and $x = x^k$ in (3.10), we obtain that

$$\begin{aligned} F(x^{k+1})\le & {} F(x^{k+1}) + \frac{1}{2}\Vert x^{k+1} - x^k\Vert ^2 \le Q_{k,i}(x^k) + \frac{\delta _k^2}{2} = f(x^k) - \psi _i(x^k) + \frac{\delta _k^2}{2} \nonumber \\= & {} F(x^k) + \frac{\delta _k^2}{2}, \end{aligned}$$

(3.11)

where the last equality follows from $i\in \mathcal {A}(x^k)$ and (1.9). Hence, for any $k\ge 0$, we have

$$\begin{aligned} F(x^k) \le F(x^0) + \frac{1}{2}\sum _{i=0}^{k-1}\delta _i^2 \le F(x^0) + \frac{B}{2}, \end{aligned}$$

which together with the boundedness of the level set $\left\{ x\in {\mathbb {R}}^n: F(x) \le F(x^0) + B/2\right\}$ implies that statement (i) holds.

(ii) It follows from (3.11) that for any $k\ge 0$,

$$\begin{aligned} \Vert x^{k+1} - x^k\Vert ^2 \le 2F(x^k) - 2F(x^{k+1}) + \delta _k^2. \end{aligned}$$

Hence, we obtain that for any $j\ge 0$,

$$\begin{aligned} \sum _{k=0}^j\Vert x^{k+1} - x^k\Vert ^2 \le 2F(x^0) -2 F(x^{j+1}) + \sum _{k=0}^j\delta _k^2 \le 2F(x^0) - 2F^* + B < \infty , \end{aligned}$$

which implies that statement (ii) holds.

(iii) We first show that $\lim _{k\rightarrow \infty }F(x^k)$ exists. For all $i\ge 0$, let $\Delta _i = F(x^{i+1}) - F(x^i)$, $\Delta _i^+ = \max (\Delta _i,0)$, $\Delta _i^- = \max (-\Delta _i,0)$. It is clear that $\Delta _i = \Delta _i^+ - \Delta _i^-$ for all $i\ge 0$. In addition, by (3.11), one can see that $\Delta _i^+ \le \delta _i^2/2$ for every $i\ge 0$, which along with the fact that $\sum _{i=0}^\infty \delta _i^2 < \infty$ implies that $\sum _{i=0}^\infty \Delta _i^+ < \infty$. By this and $\Delta _i^+ \ge 0$ for all $i\ge 0$, we have that $\{\sum _{i=0}^k\Delta _i^+\}$ converges as $k\rightarrow \infty$. Also, by $\Delta _i = F(x^{i+1}) - F(x^i)$ and $\Delta _i = \Delta _i^+ - \Delta _i^-$ for all $i\ge 0$, we obtain that

$$\begin{aligned} \sum _{i=0}^k \Delta _i^- \!= \!\sum _{i=0}^k \Delta _i^+ \!-\! \sum _{i=0}^k \Delta _i = \sum _{i=0}^k \Delta _i^+ + F(x^0) - F(x^{k+1}) \!\le \! \sum _{i=0}^k \Delta _i^+ + F(x^0) - F^*, \end{aligned}$$

which along with $\sum _{i=0}^\infty \Delta _i^+ < \infty$ implies that $\sum _{i=0}^\infty \Delta _i^- < \infty$. By this and $\Delta _i^- \ge 0$ for all $i\ge 0$, we have that $\{\sum _{i=0}^k\Delta _i^-\}$ converges as $k\rightarrow \infty$. Notice that

$$\begin{aligned} F(x^{k+1}) = F(x^0) + \sum _{i=0}^k\Delta _i = F(x^0) + \sum _{i=0}^k\Delta _i^+ - \sum _{i=0}^k\Delta _i^-, \end{aligned}$$

which together with the convergence of $\{\sum _{i=0}^k\Delta _i^+\}$ and $\{\sum _{i=0}^k\Delta _i^-\}$ implies that $\lim _{k\rightarrow \infty }F(x^k)$ exists.

Let $\zeta := \lim _{k\rightarrow \infty }F(x^k)$, and let $x^\infty$ be any accumulation point of $\{x^k\}$, whose existence is ensured by statement (i). We next show that $F(x^\infty ) = \zeta$. By (3.3) and (3.10), we have that for any $k\ge 0$ and $i\in \mathcal {A}(x^k,{\tilde{\eta }})$,

$$\begin{aligned} F(x^{k+1})\le & {} Q_{k,i}(x) + \frac{\delta _k^2}{2}\nonumber \\= & {} f(x) - \psi _i(x^k) - \langle \nabla \psi _i(x^k), x - x^k\rangle \nonumber \\&+ \frac{1}{2}\Vert x - x^k\Vert ^2 + \frac{\delta _k^2}{2}, \quad \forall x\in {\mathbb {R}}^n. \end{aligned}$$

(3.12)

Since $x^\infty$ is an accumulation point of $\{x^k\}$, there exists a subsequence $\mathcal {K}$ such that $\lim _{{\mathcal K}\ni k \rightarrow \infty }x^k = x^\infty$. Let $\eta \in [0,{\tilde{\eta }})$ be arbitrarily chosen. It then follows from Lemma 1 that $\mathcal {A}(x^\infty ,\eta )\subseteq \mathcal {A}(x^k,{\tilde{\eta }})$ for sufficiently large $k\in \mathcal {K}$. This together with (3.12) yields that for all $k\in \mathcal {K}$ sufficiently large,

$$\begin{aligned} F(x^{k+1})\le & {} f(x) - \psi _i(x^k) - \langle \nabla \psi _i(x^k), x - x^k\rangle \nonumber \\&+ \frac{1}{2}\Vert x - x^k\Vert ^2 + \frac{\delta _k^2}{2}, \quad \forall x\in {\mathbb {R}}^n, \ \forall i\in \mathcal {A}(x^\infty ,\eta ). \end{aligned}$$

(3.13)

Notice that $\lim _{k\rightarrow \infty } \delta _k = 0$ due to $\sum _{k=0}^\infty \delta _k^2 < \infty$. Also, recall that $\zeta = \lim _{k\rightarrow \infty }F(x^k)$ and that $\psi _i$ and $\nabla \psi _i$ are continuous on the open set $\Omega$ containing $\mathrm {dom}(f)$. Using these and taking limit of both sides of (3.13) as $\mathcal {K}\ni k\rightarrow \infty$, we have

$$\begin{aligned} \zeta \le f(x) - \psi _i(x^\infty ) - \langle \nabla \psi _i(x^\infty ), x - x^\infty \rangle + \frac{1}{2}\Vert x - x^\infty \Vert ^2, \quad \forall x\in {\mathbb {R}}^n, \ \forall i\in \mathcal {A}(x^\infty ,\eta ). \end{aligned}$$

(3.14)

By letting $x = x^\infty$ and $i\in \mathcal {A}(x^\infty )$ in (3.14) and using (1.9), we have $\zeta \le F(x^\infty )$. On the other hand, by $\lim _{{\mathcal K}\ni k \rightarrow \infty }x^k = x^\infty$, $\zeta = \lim _{k\rightarrow \infty }F(x^k)$ and the lower-semicontinuity of F, one has $F(x^\infty ) \le \zeta$. Hence, $\lim _{k\rightarrow \infty }F(x^k) = \zeta = F(x^\infty )$.

(iv) By $\zeta = F(x^\infty )$, one can rewrite (3.14) as

$$\begin{aligned} F(x^\infty )\le & {} f(x) - \psi _i(x^\infty ) - \langle \psi _i(x^\infty ), x - x^\infty \rangle \\&+ \frac{1}{2}\Vert x - x^\infty \Vert ^2, \quad \forall x\in {\mathbb {R}}^n, \ \forall i\in \mathcal {A}(x^\infty ,\eta ). \end{aligned}$$

It then follows from the arbitrarity of $\eta \in [0,{\tilde{\eta }})$ and Definition 1 that $x^\infty$ is an $(\alpha ,\eta )$-D-stationary point of (1.1) for any $\alpha \in (0,1]$ and $\eta \in [0,{\tilde{\eta }})$. $\square$

Remark 2

Since Algorithm 1 includes EDCA as a special case, Theorem 1 also holds for EDCA. Consequently, it provides some new results for EDCA, particularly, the ones in statements (iii) and (iv).

4 An enhanced proximal DCA with extrapolation for DC problem with finite supremum

Though iEDCA generally enjoys stronger convergence than PDCA and PDCAe, its subproblems (1.5) are, however, generally complicated, which require some iterative method for finding an approximate solution and render the entire algorithm a doubly iterative method. On the other hand, the subproblems (1.3) and (1.4) of PDCA and PDCAe are much simpler, which only require evaluating the proximal operator associated with $f_n$. Motivated by this, in this section we propose an enhanced PDCA algorithm, referred to as $\mathrm{EPDCA}_1$, for solving problem (1.1) with g given in (3.2), which inherits the advantages of iEDCA and PDCAe. In particular, its subproblems are analogous to those of PDCAe with extrapolation incorporated for possible acceleration. Moreover, any accumulation point of the sequence generated by the proposed algorithm is an $(\alpha ,\eta )$-D-stationary point of problem (1.1).

The details of $\mathrm{EPDCA}_1$ are presented as follows.

Algorithm 2

(The first enhanced PDCA with extrapolation ($\mathrm{EPDCA}_1$))

• 0. Input $x^0\in \mathrm{dom}(F)$, ${\tilde{\eta }},c>0$ and $\{\beta _t\}_{t\ge 0}\subseteq [0,\sqrt{c/L})$ with $\sup _t\beta _t<\sqrt{c/L}$. Set $x^{-1} = x^0$, $k\leftarrow 0$.

• 1. Set $z^k = x^k + \beta _k(x^k - x^{k-1})$.

• 2. For each index $i\in \mathcal {A}(x^k,{\tilde{\eta }})$, compute $\hat{x}^{k,i}$ as

  $$\begin{aligned} \hat{x}^{k,i} = \mathop {{\text {argmin}}}_{x\in {\mathbb {R}}^n} \left\{ \ell _{k,i}(x) + \frac{c}{2}\Vert x - x^k\Vert ^2 + \frac{L}{2}\Vert x - z^k\Vert ^2\right\} , \end{aligned}$$

  (4.1)

  where

  $$\begin{aligned} \ell _{k,i}(x) = f_n(x) + f_s(z^k) + \langle \nabla f_s(z^k), x - z^k\rangle - \psi _i(x^k) - \langle \nabla \psi _i(x^k), x - x^k\rangle . \end{aligned}$$

• 3. Let $\hat{i} \in \mathop {{{\mathrm{Argmin}}}}\nolimits _{i\in \mathcal {A}(x^k,{\tilde{\eta }})}\left\{ F(\hat{x}^{k,i}) + \frac{c}{2}\Vert \hat{x}^{k,i} - x^k\Vert ^2\right\}$. Set $x^{k+1} = \hat{x}^{k,\hat{i}}$.

• 4. Set $k\leftarrow k+1$ and go to Step 1.

End.

Before studying its convergence, we make some remarks on Algorithm 2.

Remark 3

• (a) Algorithm 2 is motivated by PDCAe [19]. However, it differs substantially from PDCAe in two aspects. Firstly, Algorithm 2 solves possibly multiple convex subproblems every iteration while PDCAe only solves one convex subproblem. Secondly, compared to the subproblem (1.4) of PDCAe, the subproblem (4.1) of Algorithm 2 has an additional proximal term $c\Vert x - x^k\Vert ^2/2$. These two new features are crucial for establishing (subsequential) convergence to an $(\alpha ,\eta )$-D-stationary point of Algorithm 2.

• (b) EDCA can be viewed as a special case of Algorithm 2. Indeed, Algorithm 2 reduces to EDCA by choosing $\beta _t\equiv 0$, $f_s \equiv 0$, $f_n = f$, $L = 0$ and $c = 1$, assuming $1/0=\infty$. An immediate consequence of this remark is that any convergence result of Algorithm 2 also holds for EDCA.

• (c) The subproblem (4.1) is equivalent to

  $$\begin{aligned} \hat{x}^{k,i} = \mathrm{prox}_{\frac{1}{L+c}f_n}\left( \frac{cx^k + Lz^k - \nabla f_s(z^k) + \nabla \psi _i(x^k)}{L+c}\right) . \end{aligned}$$

  Consequently, it has a closed-form solution when the proximal operator of $f_n$ admits a simple calculation (e.g., see Tables 10.2 and 10.3 in [6] for a list of such functions).

• (d) The parameters c and $\{\beta _t\}_{t\ge 0}$ can be chosen by the restarting scheme [12]. In particular, one can set $c = \tau ^2 L$ for some $\tau \in [0,1]$, and $\beta _t = \tau (\theta _{t-1}-1)/\theta _t$, where

  $$\begin{aligned} \theta _{-1} = \theta _0 = 1, \ \theta _{t+1} = \frac{1 + \sqrt{1 + 4\theta _t^2}}{2}, \end{aligned}$$

  and reset $\theta _{t-1} = \theta _t = 1$ when $t = T, 2T, 3T, \ldots$ for some positive integer T. It is not hard to verify that such c and $\{\beta _t\}_{t\ge 0}$ satisfy $\{\beta _t\}_{t\ge 0}\subseteq [0,\sqrt{c/L})$ and $\sup _t\beta _t<\sqrt{c/L}$ as desired.

In the rest of this section we will study the convergence properties of Algorithm 2. In particular, we first show that any accumulation point of the sequence $\{x^k\}$ generated by Algorithm 2 is an $(\alpha ,\eta )$-D-stationary point of problem (1.1) for some $\alpha >0$ and $\eta \ge 0$. Secondly, we establish convergence of the entire sequence $\{x^k\}$ under the so-called Kurdyka–Łojasiewicz (KL) condition. Finally, we derive the iteration complexity of Algorithm 2 for computing an approximate $(\alpha ,\eta )$-D-stationary point. Since EDCA can be viewed as a special case of Algorithm 2, all these theoretical results also hold for EDCA.

4.1 Subsequential convergence to an $(\alpha ,\eta )$-D-stationary point

In this subsection we show that any accumulation point of the sequence $\{x^k\}$ generated by Algorithm 2 is an $(\alpha ,\eta )$-D-stationary point of problem (1.1) for some $\alpha >0$ and $\eta \ge 0$.

Theorem 2

Suppose that Assumption 1 holds, the function g is in the form of (3.2), and $x^0$ is a point such that $\mathcal {L}(x^0)$ is bounded. Let $\{x^k\}$ be the sequence generated by Algorithm 2. Then the following statements hold.

• (i) The sequence $\{x^k\}$ is bounded.

• (ii) $\lim _{k\rightarrow \infty } \Vert x^k - x^{k-1}\Vert = 0$.

• (iii) $\lim _{k\rightarrow \infty }F(x^k)$ exists and $\lim _{k\rightarrow \infty }F(x^k)=F(x^\infty )$ for any accumulation point $x^\infty$ of $\{x^k\}$.

• (iv) Any accumulation point of $\{x^k\}$ is an $(\alpha ,\eta )$-D-stationary point of (1.1) for any $\alpha \in (0,(L+c)^{-1}]$ and $\eta \in [0,{\tilde{\eta }})$.

Proof

(i) By (4.1), the convexity of $f_s$ and $\psi$, the Lipschitz continuity of $\nabla f_s$, and Step 3 of Algorithm 2, we have that for all $k\ge 0$ and $i\in \mathcal {A}(x^k,\tilde{\eta })$,

$$\begin{aligned}&f_s(x^k) + f_n(x^k) - \psi _i(x^k) \ge f_s(z^k) + \langle \nabla f_s(z^k), x^k - z^k\rangle + f_n(x^k) - \psi _i(x^k)\end{aligned}$$

(4.2)

$$\begin{aligned}&\quad \ge f_s(z^k) + f_n(\hat{x}^{k,i}) + \langle \nabla f_s(z^k), \hat{x}^{k,i} - z^k\rangle - \langle \nabla \psi _i(x^k), \hat{x}^{k,i} - x^k \rangle \nonumber \\&\qquad + \frac{L}{2}\Vert \hat{x}^{k,i} - z^k\Vert ^2 - \frac{L}{2}\Vert x^k - z^k\Vert ^2 + \frac{c}{2}\Vert x^k - \hat{x}^{k,i}\Vert ^2 - \psi _i(x^k) \end{aligned}$$

(4.3)

$$\begin{aligned}&\quad \ge f_s(\hat{x}^{k,i}) + f_n(\hat{x}^{k,i}) - \psi _i(x^k) - \langle \nabla \psi _i(x^k), \hat{x}^{k,i} - x^k\rangle \nonumber \\&\qquad - \frac{L}{2}\Vert x^k - z^k\Vert ^2 + \frac{c}{2}\Vert x^k - \hat{x}^{k,i}\Vert ^2 \end{aligned}$$

(4.4)

$$\begin{aligned}&\quad \ge f_s(\hat{x}^{k,i}) + f_n(\hat{x}^{k,i}) - \psi _i(\hat{x}^{k,i}) - \frac{L}{2}\Vert x^k - z^k\Vert ^2 + \frac{c}{2}\Vert x^k - \hat{x}^{k,i}\Vert ^2 \end{aligned}$$

(4.5)

$$\begin{aligned}&\quad \ge f_s(\hat{x}^{k,i}) + f_n(\hat{x}^{k,i}) - \max _{i\in \mathcal {Y}}\psi _i(\hat{x}^{k,i}) - \frac{L}{2}\Vert x^k - z^k\Vert ^2 + \frac{c}{2}\Vert x^k - \hat{x}^{k,i}\Vert ^2 \nonumber \\&\quad = F(\hat{x}^{k,i}) - \frac{L}{2}\Vert x^k - z^k\Vert ^2 + \frac{c}{2}\Vert x^k - \hat{x}^{k,i}\Vert ^2 \nonumber \\&\quad \ge F(x^{k+1}) - \frac{L}{2}\Vert x^k - z^k\Vert ^2 + \frac{c}{2}\Vert x^k - x^{k+1}\Vert ^2, \end{aligned}$$

(4.6)

where (4.2) and (4.5) are respectively due to the convexity of $f_s$ and $\psi$, (4.3) follows from (4.1), (4.4) is by the Lipschitz continuity of $\nabla f_s$ and (4.6) is due to Step 3 of Algorithm 2. Notice that $\mathcal {A}(x^k) \subseteq \mathcal {A}(x^k,\tilde{\eta })$. It follows from (4.6) that for any $i\in \mathcal {A}(x^k)$, we have

$$\begin{aligned} F(x^k) = f_s(x^k) + f_n(x^k) - \psi _i(x^k) \ge F(x^{k+1}) - \frac{L}{2}\Vert x^k - z^k\Vert ^2 + \frac{c}{2}\Vert x^k - x^{k+1}\Vert ^2. \end{aligned}$$

This, together with $\bar{\beta } :=\sup _t\beta _t < \sqrt{c/L}$ and $z^k = x^k + \beta _k(x^k - x^{k-1})$, gives us

$$\begin{aligned} F(x^{k+1}) + \frac{c}{2}\Vert x^{k+1} - x^k\Vert ^2&\le F(x^k) + \frac{L}{2}\Vert x^k - z^k\Vert ^2 \nonumber \\&\le F(x^k) + \frac{L\bar{\beta }^2}{2}\Vert x^k - x^{k-1}\Vert ^2\nonumber \\&\le F(x^k) + \frac{c}{2}\Vert x^k - x^{k-1}\Vert ^2. \end{aligned}$$

(4.7)

Hence, $\left\{ F(x^{k}) + \frac{c}{2}\Vert x^{k} - x^{k-1}\Vert ^2\right\}$ is non-increasing. It then follows that for any $k\ge 0$,

$$\begin{aligned} F(x^k) \le F(x^k) + \frac{c}{2}\Vert x^k - x^{k-1}\Vert ^2 \le F(x^0) + \frac{c}{2}\Vert x^0 - x^{-1}\Vert ^2 = F(x^0), \end{aligned}$$

which along with the boundedness of $\mathcal {L}(x^0)$ implies that $\{x^k\}$ is bounded.

(ii) It follows from (4.7) that for all $k\ge 0$,

$$\begin{aligned} \frac{c - L\bar{\beta }^2}{2}\Vert x^{k+1} - x^k\Vert ^2\le & {} \left( F(x^k) + \frac{L\bar{\beta }^2}{2}\Vert x^k - x^{k-1}\Vert ^2\right) \\&-\left( F(x^{k+1})+\frac{L\bar{\beta }^2}{2}\Vert x^{k+1} - x^k\Vert ^2\right) , \end{aligned}$$

which together with $x^{-1} = x^0$ yields that for any integer $j\ge 0$,

$$\begin{aligned} \frac{c - L\bar{\beta }^2}{2}\cdot \sum _{k=0}^j\Vert x^k - x^{k-1}\Vert ^2 \le F(x^0) - F(x^{j}) \le F(x^0) - F^*, \end{aligned}$$

(4.8)

By this and $\bar{\beta }<\sqrt{c/L}$, one can see that $\lim _{k\rightarrow \infty } \Vert x^k - x^{k-1}\Vert = 0$.

(iii) Recall that $\{F(x^{k}) + \frac{c}{2}\Vert x^{k} - x^{k-1}\Vert ^2\}$ is non-increasing and bounded below. Hence, $\lim _{k\rightarrow \infty } \{F(x^k) + \frac{c}{2}\Vert x^k - x^{k-1}\Vert ^2\}$ exists. This, together with statement (ii), implies that $\lim _{k\rightarrow \infty }F(x^k)$ exists.

Let $x^\infty$ be any accumulation point of $\{x^k\}$, whose existence is guaranteed by statement (i). We next show that $F(x^\infty )=\lim _{k\rightarrow \infty }F(x^k)$. By (4.1), (4.3) and (4.6), we have that for all $i\in \mathcal {A}(x^k,\tilde{\eta })$,

$$\begin{aligned}&F(x^{k+1}) \le F(x^{k+1}) + \frac{c}{2}\Vert x^k - x^{k+1}\Vert ^2 \nonumber \\&\quad \le f_s(z^k) + f_n(\hat{x}^{k,i}) + \langle \nabla f_s(z^k), \hat{x}^{k,i}- z^k\rangle - \langle \nabla \psi _i(x^k), \hat{x}^{k,i} - x^k \rangle \nonumber \\&\qquad + \frac{L}{2}\Vert \hat{x}^{k,i} - z^k\Vert ^2 + \frac{c}{2}\Vert x^k - \hat{x}^{k,i}\Vert ^2 - \psi _i(x^k) \end{aligned}$$

(4.9)

$$\begin{aligned}&\quad \le f_s(z^k) + f_n(x) + \langle \nabla f_s(z^k), x - z^k\rangle - \langle \nabla \psi _i(x^k), x - x^k \rangle + \frac{L}{2}\Vert x - z^k\Vert ^2 \nonumber \\&\qquad + \frac{c}{2}\Vert x^k - x\Vert ^2 - \psi _i(x^k), \quad \forall x\in {\mathbb {R}}^n, \end{aligned}$$

(4.10)

where (4.9) follows from (4.3) and (4.6), and (4.10) is due to (4.1). Since $x^\infty$ is an accumulation point of $\{x^k\}$, there exists a subsequence ${\mathcal K}$ such that $\lim _{{\mathcal K}\ni k \rightarrow \infty }x^k = x^\infty$. By this, $z^k = x^k + \beta _k(x^k - x^{k-1})$, $\beta _k\in [0,\sqrt{c/L})$ and statement (ii), one has $\lim _{{\mathcal K}\ni k \rightarrow \infty }x^{k+1} = x^\infty$ and $\lim _{{\mathcal K}\ni k \rightarrow \infty } z^k = x^\infty$. Let $\eta \in [0,{\tilde{\eta }})$ be arbitrarily chosen. It then follows from Lemma 1 that $\mathcal {A}(x^\infty ,\eta )\subseteq \mathcal {A}(x^k,{\tilde{\eta }})$ for sufficiently large $k\in \mathcal {K}$. This together with (4.10) yields that for all $k\in \mathcal {K}$ sufficiently large,

$$\begin{aligned} F(x^{k+1})&\le f_s(z^k) + f_n(x) + \langle \nabla f_s(z^k), x - z^k\rangle \nonumber \\&\quad - \langle \nabla \psi _i(x^k), x - x^k \rangle + \frac{L}{2}\Vert x - z^k\Vert ^2 \nonumber \\&\quad + \frac{c}{2}\Vert x^k - x\Vert ^2 - \psi _i(x^k), \quad \forall x\in {\mathbb {R}}^n, \; \forall i\in \mathcal {A}(x^\infty ,\eta ). \end{aligned}$$

(4.11)

Notice from Assumption 1 that $f_s$, $\nabla f_s$, $\psi _i$ and $\nabla \psi _i$ are continuous on the open set $\Omega$ containing $\mathrm {dom}(f_n)$. Using this and taking limit of both sides of (4.11) as $\mathcal {K}\ni k \rightarrow \infty$, we obtain

$$\begin{aligned} \zeta&\le f_s(x^\infty ) + f_n(x) + \langle \nabla f_s(x^\infty ) - \nabla \psi _i(x^\infty ), x - x^\infty \rangle \nonumber \\&\quad + \frac{L+c}{2}\Vert x - x^\infty \Vert ^2 - \psi _i(x^\infty ) \nonumber \\&\le f(x) - \psi _i(x^\infty ) - \langle \nabla \psi _i(x^\infty ), x - x^\infty \rangle \nonumber \\&\quad + \frac{L+c}{2}\Vert x - x^\infty \Vert ^2, \quad \forall x\in {\mathbb {R}}^n, \;\forall i\in \mathcal {A}(x^\infty ,\eta ), \end{aligned}$$

(4.12)

where $\zeta :=\lim _{k\rightarrow \infty } F(x^k)$ and (4.12) follows from the convexity of $f_s$ and the relation $f = f_s + f_n$. Letting $x=x^\infty$ in (4.12), we have $\zeta \le f(x^\infty ) - \psi _i(x^\infty ), \ \forall i\in \mathcal {A}(x^\infty )$, which along with (1.9) yields $\zeta \le F(x^\infty )$. On the other hand, by $\lim _{{\mathcal K}\ni k \rightarrow \infty }x^k = x^\infty$, $\zeta =\lim _{k\rightarrow \infty } F(x^k)$ and the lower-semicontinuity of F, one has $F(x^\infty )\le \zeta$. Hence, $\lim _{k\rightarrow \infty } F(x^k)=\zeta =F(x^\infty )$.

(iv) By $\zeta =F(x^\infty )$, one can rewrite (4.12) as

$$\begin{aligned} F(x^\infty )\le & {} f(x) - \psi _i(x^\infty ) - \langle \nabla \psi _i(x^\infty ), x - x^\infty \rangle \\&+ \frac{L+c}{2}\Vert x - x^\infty \Vert ^2, \quad \forall x\in {\mathbb {R}}^n, \; \forall i\in \mathcal {A}(x^\infty ,\eta ). \end{aligned}$$

It then follows from the arbitrarity of $\eta \in [0,{\tilde{\eta }})$ and Definition 1 that $x^\infty$ is an $(\alpha ,\eta )$-D-stationary point of (1.1) for any $\alpha \in (0,(L+c)^{-1}]$ and $\eta \in [0,{\tilde{\eta }})$. $\square$

4.2 Convergence of the entire sequence

In this subsection we study the convergence of the entire sequence $\{x^k\}$ generated by Algorithm 2 based on the following concept of Kurdyka–Łojasiewicz (KL) property.

Definition 3

(KL property) A lower-semicontinuous function h is said to be a KL function if for any $\tilde{x}\in \mathrm {dom}(\partial h),$³ there exists a scalar $\kappa \in (0,\infty ]$, a neighborhood $\mathcal{U}$ of $\tilde{x}$ and a continuous concave function $\varphi :[0,\kappa )\rightarrow {\mathbb {R}}_{+}$ such that:

• (i) $\varphi$ is continuously differentiable on $(0,\kappa )$ with $\varphi ^\prime >0$;

• (ii) For any $x\in \mathcal{U}$ with $h(\tilde{x})< h(x) < h(\tilde{x}) + \kappa$, it holds that

  $$\begin{aligned} \varphi ^\prime (h(x) - h(\tilde{x}))\cdot \mathrm {dist}(0,\partial h(x)) \ge 1. \end{aligned}$$

It is known that the KL property holds for a wide range of functions in applications. For example, any proper closed semialgebraic function is a KL function. Moreover, with the aid of the KL property, the convergence of the entire sequence can be established for various iterative algorithms (see, for example, [2] for more discussion).

To establish the convergence of $\{x^k\}$, inspired by [19] we introduce the following auxiliary function $H:{\mathbb {R}}^n\times {\mathbb {R}}^n\rightarrow (-\infty ,+\infty ]$:

$$\begin{aligned} H(x,y) := F(x) + \frac{c}{2}\Vert x - y\Vert ^2 = f_s(x) + f_n(x) - g(x) + \frac{c}{2}\Vert x - y\Vert ^2. \end{aligned}$$

(4.13)

We first prove the following lemma that will be used subsequently.

Lemma 2

Let $\{x^k\}$ be the sequence generated by Algorithm 2. Suppose that H is a KL function and the premise of Theorem 2 holds. If there exist a scalar $\nu _0>0$ and K such that

$$\begin{aligned} \mathrm {dist}\left( (0,0),\partial H(x^{k}, x^{k-1})\right) \le \nu _0\left( \Vert x^k - x^{k-1}\Vert + \Vert x^{k-1} - x^{k-2}\Vert \right) \quad \forall k\ge K, \end{aligned}$$

(4.14)

then the entire sequence $\{x^k\}$ converges.

Proof

Let $\Gamma$ denote the set of accumulation points of $\{x^k\}$, and let $w^k = (x^k,x^{k-1})$ for all $k\ge 0$. By Theorem 2 (i) and the definition of $\Gamma$, one can easily see that $\Gamma$ is a compact set. In view of (4.7) and (4.13), $\bar{\beta } =\sup _t\beta _t < \sqrt{c/L}$ and $w^k = (x^k,x^{k-1})$, one has

$$\begin{aligned} H(w^{k+1}) + \nu _1\Vert x^k - x^{k-1}\Vert ^2 \le H(w^k),\quad \forall k\ge 0, \end{aligned}$$

(4.15)

where $\nu _1= (c-L\bar{\beta }^2)/2>0$. Hence, $\{H(w^k)\}$ is non-increasing. In addition, one can observe from (4.13) and Theorem 2 (ii) and (iii) that $\lim _{k\rightarrow \infty }H(w^k) = \zeta$, where $\zeta =\lim _{k\rightarrow \infty } F(x^k)$. Also, recall from Theorem 2 (ii) that $\lim _{k\rightarrow \infty }\Vert x^k - x^{k-1}\Vert = 0$. In view of this, it is not hard to show that the set of accumulation points of $\{w^k\}$, denoted as $\bar{\Gamma }$, is given by $\bar{\Gamma } = \{(x,x):x\in \Gamma \}$ and is compact. This together with Theorem 2 (iii) implies that $H(w) = \zeta$ for any $w\in \bar{\Gamma }$.

Recall from above that $\{H(w^k)\}$ is non-increasing and $\lim _{k\rightarrow \infty }H(w^k) = \zeta$. Therefore, one of the following two cases must occur:

Case (a): there exists some $K_1>0$ such that $H(w^k) = \zeta$ for all $k\ge K_1$.

Case (b): $H(w^k)>\zeta$ for all $k\ge 0$.

To prove that the entire sequence $\{x^k\}$ converges, it suffices to show that $\sum _{k=0}^\infty \Vert x^k - x^{k-1}\Vert < \infty$. We next prove this by considering the above two cases separately.

Suppose that Case (a) holds. By (4.15), we have $\Vert x^k - x^{k-1}\Vert = 0$ for all $k\ge K_1$. Then it is clear that $\sum _{k=0}^\infty \Vert x^k - x^{k-1}\Vert < \infty$.

Suppose that Case (b) holds. Recall that $\bar{\Gamma }$ is a compact set, H is constant on $\bar{\Gamma }$ and H is a KL function. It follows from these and [4, Lemma 6] that H satisfies the so-called uniformized KL property. That is, there exist some scalars $\delta >0$, $\kappa >0$ and a function $\varphi$ that is continuous concave nonnegative in $[0,\kappa )$ and continuously differentiable on $(0,\kappa )$ with $\varphi ^\prime >0$ such that

$$\begin{aligned} \varphi ^\prime (H(w) - \zeta )\cdot \mathrm {dist}(0,\partial H(w))\ge 1 \end{aligned}$$

(4.16)

for all w satisfying

$$\begin{aligned} \mathrm {dist}(w,\bar{\Gamma })<\delta , \; \zeta<H(w)<\zeta +\kappa . \end{aligned}$$

(4.17)

Since $\bar{\Gamma }$ is the set of accumulation points of $\{w^k\}$ and $\bar{\Gamma }$ is compact, it is not hard to see that $\lim _{k\rightarrow \infty } \mathrm {dist}(w^k,\bar{\Gamma })=0$. Also, notice that $\lim _{k\rightarrow \infty }H(w^k) = \zeta$ and $H(w^k)>\zeta$ for all $k\ge 0$. Hence, there exists $K_2$ such that $w^k$ satisfies (4.17) for all $k\ge K_2$, which implies that (4.16) holds at $w^k$ for all $k\ge K_2$. In addition, by the concavity of $\varphi$ and (4.15), we have that for any $k\ge 0$,

$$\begin{aligned} \varphi (H(w^k) - \zeta ) - \varphi (H(w^{k+1}) - \zeta )\ge & {} \varphi ^\prime (H(w^k) - \zeta )[H(w^k) - H(w^{k+1})] \\\ge & {} \nu _1\varphi ^\prime (H(w^k) - \zeta )\Vert x^k - x^{k-1}\Vert ^2, \end{aligned}$$

where the first inequality follows from the concavity of $\varphi$ and the second one is due to (4.15). This, together with the KL inequality (4.16), leads to

$$\begin{aligned} 1\le & {} \varphi ^\prime (H(w^k) - \zeta )\cdot \mathrm {dist}(0,\partial H(w^k)) \\\le & {} \frac{\varphi (H(w^k) - \zeta ) - \varphi (H(w^{k+1}) - \zeta )}{\nu _1\Vert x^k - x^{k-1}\Vert ^2}\cdot \mathrm {dist}(0,\partial H(w^k)), \end{aligned}$$

for any $k\ge K_2$ such that $\Vert x^k - x^{k-1}\Vert \ne 0$. By this relation and (4.14), one has that for any $k\ge K_0:=\max \{K,K_2\}$ such that $\Vert x^k - x^{k-1}\Vert \ne 0$,

$$\begin{aligned} \begin{aligned} \Vert x^{k} - x^{k-1}\Vert ^2&\le \frac{\nu _0}{\nu _1}\left( \varphi (H(w^k) - \zeta ) - \varphi (H(w^{k+1}) - \zeta )\right) \\&\quad \times \left( \Vert x^k - x^{k-1}\Vert + \Vert x^{k-1} - x^{k-2}\Vert \right) \\&\le \frac{1}{4}\left[ \frac{2\nu _0}{\nu _1}\left( \varphi (H(w^k) - \zeta ) - \varphi (H(w^{k+1}) - \zeta )\right) + \frac{1}{2}\Vert x^k - x^{k-1}\Vert \right. \\&\left. \quad + \frac{1}{2}\Vert x^{k-1} - x^{k-2}\Vert \right] ^2, \end{aligned} \end{aligned}$$

where the second inequality follows from the fact that $ab\le (a+b)^2/4$ for any a and b. Taking the square root of both sides of this relation and rearranging the term $\Vert x^{k} - x^{k-1}\Vert$, we obtain that for any $k\ge K_0$ such that $\Vert x^k - x^{k-1}\Vert \ne 0$,

$$\begin{aligned} \Vert x^{k} - x^{k-1}\Vert\le & {} \frac{2\nu _0}{\nu _1}\left( \varphi (H(w^k) - \zeta ) - \varphi (H(w^{k+1}) - \zeta )\right) \nonumber \\&+ \frac{1}{2}\Vert x^{k-1} - x^{k-2}\Vert - \frac{1}{2}\Vert x^{k} - x^{k-1}\Vert . \end{aligned}$$

(4.18)

Recall that $\varphi ^\prime >0$ on $(0,\kappa )$. This together with $\{H(w^k)\}$ non-increasing and $\zeta<H(w^k)<\zeta +\kappa$ for all $k\ge K_0$ yields that $\varphi (H(w^k) - \zeta ) - \varphi (H(w^{k+1}) - \zeta )\ge 0$ for all $k\ge K_0$, which further implies that (4.18) also holds for any $k\ge K_0$ such that $\Vert x^k - x^{k-1}\Vert = 0$. Hence, (4.18) holds for all $k\ge K_0$. Notice that $\varphi$ is nonnegative in $[0,\kappa )$ and $\zeta<H(w^k)<\zeta +\kappa$ for all $k \ge K_0$. It follows that $\varphi (H(w^k) - \zeta )\ge 0$ for all $k\ge K_0$. Summing up the inequality (4.18) from $k=K_0$ to $\infty$ yields

$$\begin{aligned} \sum _{k=K_0}^{\infty }\Vert x^{k} - x^{k-1}\Vert \le \frac{2c}{c_1}\cdot \varphi (H(w^{K_0}) - \zeta ) + \frac{1}{2}\Vert x^{K_0-1} - x^{K_0 - 2}\Vert , \end{aligned}$$

which implies that $\sum _{k=0}^\infty \Vert x^{k} - x^{k-1}\Vert <\infty$ also holds for Case (b). The proof is then completed. $\square$

Equipped with Lemma 2, we are now ready to establish the convergence of the entire sequence $\{x^k\}$ generated by Algorithm 2.

Theorem 3

Let $\{x^k\}$ be the sequence generated by Algorithm 2 and $\Gamma$ the set of accumulation points of $\{x^k\}$. Suppose that the premise of Theorem 2 holds. Then the entire sequence $\{x^k\}$ converges to an $(\alpha ,\eta )$-D-stationary point of (1.1) for any $\alpha \in (0,(L+c)^{-1}]$ and $\eta \in [0,{\tilde{\eta }})$ if one of the following additional conditions holds:

• (i) One of the elements of $\Gamma$ is isolated.

• (ii) The function H defined in (4.13) is a KL function and $\nabla \psi _i(x)$ is locally Lipschitz continuous for all $i\in \mathcal {Y}$. Moreover, for each $x\in \Gamma$, $\mathcal {A}(x)$ is a singleton and satisfies

  $$\begin{aligned} g(x) - \max _{i\in \mathcal {A}^\circ (x)} \psi _i(x) > 2\tilde{\eta }, \end{aligned}$$

  (4.19)

  where $\mathcal {A}^\circ (x) = \mathcal {Y}\setminus \mathcal {A}(x)$.

Proof

In view of Theorem 2, it suffices to show that the entire sequence $\{x^k\}$ converges.

We know from Theorem 2 that $\lim _{k\rightarrow \infty }\Vert x^k - x^{k-1}\Vert = 0$. Suppose that one of the elements of $\Gamma$ is isolated. By this, $\lim _{k\rightarrow \infty }\Vert x^k - x^{k-1}\Vert = 0$, and a similar argument as in [7, Proposition 8.3.10], one can show that $\{x^k\}$ is convergent.

Suppose that the condition (ii) in the statement of Theorem 3 holds. In view of Lemma 2, it suffices to show that (4.14) holds for some $\nu _0$ and K. Let ${\bar{x}}\in \Gamma$ be arbitrarily chosen. Due to our assumption that $\mathcal {A}({\bar{x}})$ is a singleton, $\mathcal {A}({\bar{x}}) = \{\tilde{i}\}$ for some $\tilde{i}\in \mathcal {Y}$. Since $\psi _i$ is continuous for each $i\in \mathcal {Y}$ and $\mathcal {Y}$ is a finite set, there exists $\delta >0$ such that $|\psi _i(x) - \psi _i({\bar{x}})|\le \tilde{\eta }/2$ for all $i\in \mathcal {Y}$ whenever $\Vert x - {\bar{x}}\Vert \le 2\delta$. This, together with (4.19) and $\mathcal {A}({\bar{x}}) = \{\tilde{i}\}$, implies that

$$\begin{aligned} \mathcal {A}(x) = \{\tilde{i}\}, \quad g(x) - \max _{i\in \mathcal {A}^\circ (x)}\psi _i(x)>\tilde{\eta }, \quad \text{ whenever }\ \ \Vert x - {\bar{x}}\Vert \le 2\delta . \end{aligned}$$

(4.20)

Recall from Theorem 2 that $\{x^k\}$ is bounded and $\lim _{k\rightarrow \infty }\Vert x^k - x^{k-1}\Vert = 0$. It follows from this and [7, Theorem 8.3.9] that $\Gamma$ is compact and connected. By this, (4.20) and a standard argument based on the Heine-Borel theorem, one can conclude that there exists $\bar{\delta }>0$ such that

$$\begin{aligned} \mathcal {A}(x) = \{\tilde{i}\}, \quad g(x) - \max _{i\in \mathcal {A}^\circ (x)}\psi _i(x)>\tilde{\eta }, \quad \text{ whenever }\ \ \mathrm {dist}(x,\Gamma )\le 2\bar{\delta }. \end{aligned}$$

(4.21)

It then follows that $g(x)=\psi _{\tilde{i}}(x)$ for all x satisfying $\mathrm {dist}(x,\Gamma )\le 2\bar{\delta }$. By this, (4.21), the compactness of $\Gamma$, and the assumption that $\psi _{\tilde{i}}$ is continuously differentiable and $\nabla \psi _{\tilde{i}}$ is locally Lipschitz continuous, we see that g is continuously differentiable and $\nabla g$ is Lipschitz continuous on $\mathcal {N}:=\{x:\mathrm {dist}(x,\Gamma )\le \bar{\delta }\}$. Recall from the proof of Lemma 2 that $\lim _{k\rightarrow \infty }\mathrm {dist}(x^k,\Gamma )=0$, which implies that there exists some K such that $x^k\in \mathcal {N}$ for all $k\ge K$. Hence, $\mathcal {A}(x^k) = \{\tilde{i}\}$, g is continuously differentiable at $x^k$ and $g(x^k) - \max _{i\in \mathcal {A}^\circ (x^k)}\psi _i(x^k)>\tilde{\eta }$ for all $k\ge K$. It follows that $\mathcal {A}(x^k,\tilde{\eta }) = \mathcal {A}(x^k)$ for all $k\ge K$. By this and the updating scheme (4.1), one has that for all $k\ge K$, $x^{k+1} = \hat{x}^{k,\tilde{i}}$ and moreover,

$$\begin{aligned} 0\in \partial f_n(x^{k+1}) + \nabla f_s(z^k) - \nabla \psi _{\tilde{i}}(x^k) + c(x^{k+1} - x^k) + L(x^{k+1} - z^k). \end{aligned}$$

(4.22)

Since $\mathcal {A}(x^k)=\{\tilde{i}\}$ for all $k\ge K$, one has that $\nabla \psi _{\tilde{i}}(x^k) = \nabla g(x^k)$ for all $k\ge K$. In view of this and (4.22), we have

$$\begin{aligned} -\nabla f_s(z^k) +\nabla g(x^k) - c(x^{k+1} - x^k) - L(x^{k+1} - z^k) \in \partial f_n(x^{k+1}), \quad \forall k\ge K. \end{aligned}$$

(4.23)

In addition, since g is continuously differentiable at $x^k$ for all $k\ge K$, it follows from [16, Exercise 8.8(c)] that for all $k\ge K$,

$$\begin{aligned} \partial H(x^{k+1},x^k)= & {} \left\{ v^{k+1} + \nabla f_s(x^{k+1})- \nabla g(x^{k+1}) + c(x^{k+1} - x^k): v^{k+1}\in \partial f_n(x^{k+1})\right\} \\&\times \{c(x^k - x^{k+1})\}. \end{aligned}$$

Combining this with (4.23), we obtain that for all $k\ge K$.

$$\begin{aligned} \mathrm {dist}((0,0),\partial H(x^{k+1},x^k))&\le \Vert -\nabla f_s(z^k) +\nabla g(x^k) - L(x^{k+1} - z^k)\\&\quad + \nabla f_s(x^{k+1})- \nabla g(x^{k+1})\Vert \\&\quad + c\Vert x^k - x^{k+1}\Vert . \end{aligned}$$

By this and the Lipschitz continuity of $\nabla f_s$ and $\nabla g$ on $\mathcal {N}$, we obtain that

$$\begin{aligned} \mathrm {dist}((0,0),\partial H(x^{k+1},x^k)) \le \nu \left( \Vert x^{k+1} - x^k\Vert + \Vert x^{k+1} - z^k\Vert \right) , \quad \forall k\ge K \end{aligned}$$

for some $\nu >0$. This together with $z^k=x^k+\beta _k(x^k - x^{k-1})$ and $\beta _k\in [0,\sqrt{c/L})$ implies that there exists $\nu _0>0$ such that

$$\begin{aligned} \mathrm {dist}((0,0),\partial H(x^{k+1},x^k)) \le \nu _0\left( \Vert x^{k+1} - x^k\Vert + \Vert x^k - x^{k-1}\Vert \right) , \quad \forall k\ge K \end{aligned}$$

and hence (4.14) holds as desired. The proof is then completed. $\square$

Recall that EDCA is a special case of Algorithm 2. As a consequence of Theorem 3, the sequence generated by EDCA also converges under the same assumption.

Corollary 1

Let $\{x^k\}$ be the sequence generated by EDCA. Suppose that the premise of Theorem 3 holds except that F instead of H is a KL function. Then the entire sequence $\{x^k\}$ converges to an $(\alpha ,\eta )$-D-stationary point of (1.1) for any $\alpha \in (0,1]$ and $\eta \in [0,{\tilde{\eta }})$.

4.3 Iteration complexity for computing an approximate $(\alpha ,\eta )$-D-stationary point

In this subsection we study the iteration complexity of Algorithm 2 for computing an $\epsilon$-approximate $((2L+c)^{-1},{\tilde{\eta }})$-D-stationary point of problem (1.1).

Theorem 4

Let $\epsilon >0$ be arbitrarily given, $\bar{\beta } =\sup _t\beta _t$, and $\{x^k\}$ generated by Algorithm 2. Suppose that the premise of Theorem 2 holds and F is Lipschitz continuous on $\mathcal {L}(x^0)$ with Lipschitz constant $L_0$. Then the following statements hold.

• (i) If $(x^{k-1}, x^k, x^{k+1})$ satisfies

  $$\begin{aligned} \Vert x^{k+1} - x^k\Vert + \Vert x^k - x^{k-1}\Vert \le \min \left\{ 1,\frac{\epsilon }{L\bar{\beta }^2}, \frac{\epsilon }{L_0}\right\} \end{aligned}$$

  (4.24)

  for some $k \ge 0$, then $x^k$ is an $\epsilon$-approximate $((2L+c)^{-1},{\tilde{\eta }})$-D-stationary point of (1.1).

• (ii) The number of iterations of Algorithm 2 for computing an $\epsilon$-approximate $((2L+c)^{-1},{\tilde{\eta }})$-D-stationary point of (1.1) is no more than

  $$\begin{aligned} \bar{K} =\left\lceil \frac{8(F(x^0) - F^{*})}{c - L\bar{\beta }^2}\cdot \max \left\{ 1,\frac{L^2\bar{\beta }^4}{\epsilon ^2}, \frac{L_0^2}{\epsilon ^2}\right\} \right\rceil +1. \end{aligned}$$

  (4.25)

Proof

(i) Suppose that $(x^{k-1}, x^k, x^{k+1})$ satisfies (4.24) for some $k\ge 0$. It follows from (4.10) that for any $x\in {\mathbb {R}}^n$ and $i\in \mathcal {A}(x^k,{\tilde{\eta }})$,

$$\begin{aligned} F(x^{k+1})&\le f_s(z^k) + f_n(x) + \langle \nabla f_s(z^k), x - z^k\rangle - \langle \nabla \psi _i(x^k), x - x^k\rangle \nonumber \\&\quad + \frac{L}{2}\Vert x - z^k\Vert ^2 + \frac{c}{2}\Vert x^k - x\Vert ^2 - \psi _i(x^k) \nonumber \\&\le f(x) - \psi _i(x^k) - \langle \nabla \psi _i(x^k), x - x^k\rangle + \frac{L}{2}\Vert x - z^k\Vert ^2 + \frac{c}{2}\Vert x^k - x\Vert ^2 \nonumber \\&\le f(x) - \psi _i(x^k) - \langle \nabla \psi _i(x^k), x - x^k\rangle \nonumber \\&\quad + \frac{2L+c}{2}\Vert x - x^k\Vert ^2 + L\beta _k^2\Vert x^k - x^{k-1}\Vert ^2, \end{aligned}$$

(4.26)

where the second inequality follows from the convexity of $f_s$ and the third one is due to $z^k=x^k+\beta _k(x^k - x^{k-1})$ and $\Vert a + b\Vert ^2 \le 2(\Vert a\Vert ^2 + \Vert b\Vert ^2)$ for any a and b. Recall from the proof of Theorem 2 that $x^k, x^{k+1} \in \mathcal {L}(x^0)$. Since F is Lipschitz continuous on $\mathcal {L}(x^0)$ with Lipschitz constant $L_0$, we have

$$\begin{aligned} F(x^k) - F(x^{k+1}) \le L_0\Vert x^{k+1} - x^k\Vert . \end{aligned}$$

By this and (4.26), one has that for any $x\in {\mathbb {R}}^n$ and $i\in \mathcal {A}(x^k,{\tilde{\eta }})$,

$$\begin{aligned} F(x^{k})&\le f(x) - \psi _i(x^k) - \langle \nabla \psi _i(x^k), x - x^k\rangle + \frac{2L+c}{2}\Vert x - x^k\Vert ^2 \nonumber \\&\quad + L\beta _k^2\Vert x^k - x^{k-1}\Vert ^2 + L_0\Vert x^{k+1} - x^k\Vert . \end{aligned}$$

(4.27)

Since $(x^{k-1},x^k,x^{k+1})$ satisfies (4.24), it follows that $\Vert x^k - x^{k-1}\Vert \le 1$ and thus

$$\begin{aligned} \Vert x^{k+1} - x^k\Vert + \Vert x^k - x^{k-1}\Vert ^2 \le \frac{\epsilon }{\max \{L\bar{\beta }^2,L_0\}}. \end{aligned}$$

This together with $\bar{\beta } = \sup _t\beta _t$ yields

$$\begin{aligned}&L\beta _k^2\Vert x^k - x^{k-1}\Vert ^2 + L_0\Vert x^{k+1} - x^k\Vert \\&\quad \le \max \{L\bar{\beta }^2,L_0\}\left( \Vert x^{k} - x^{k-1}\Vert ^2 + \Vert x^{k+1} - x^k\Vert \right) \le \epsilon . \end{aligned}$$

In view of this and (4.27), one has that

$$\begin{aligned} F(x^{k})\le & {} f(x) - \psi _i(x^k) - \langle \nabla \psi _i(x^k), x - x^k\rangle \\&+ \frac{2L+c}{2}\Vert x - x^k\Vert ^2 + \epsilon , \quad \forall x\in {\mathbb {R}}^n, \ \forall i\in \mathcal {A}(x^k,{\tilde{\eta }}). \end{aligned}$$

Hence, it follows from Definition 2 that $x^k$ is an $\epsilon$-approximate $((2L+c)^{-1},{\tilde{\eta }})$-D-stationary point of (1.1).

(ii) In view of statement (i), it suffices to show that a triplet $(x^{k-1},x^{k},x^{k+1})$ satisfying (4.24) can be found by Algorithm 2 in at most $\bar{K}$ iterations, where $\bar{K}$ is given in (4.25). By (4.8), one has that for all $K>0$,

$$\begin{aligned} \sum _{i=1}^K\Vert x^{i+1} - x^i\Vert ^2\le & {} \frac{2}{c - L\bar{\beta }^2}(F(x^0)-F^{*}),\quad \\ \sum _{i=1}^K\Vert x^i - x^{i-1}\Vert ^2\le & {} \frac{2}{c - L\bar{\beta }^2}(F(x^0)-F^{*}). \end{aligned}$$

Summing up these two inequalities yields

$$\begin{aligned} \sum _{i=1}^K\Vert x^{i+1} - x^i\Vert ^2 + \Vert x^i - x^{i-1}\Vert ^2 \le \frac{4}{c - L\bar{\beta }^2}(F(x^0) -F^{*}). \end{aligned}$$

It thus follows that there exists some $\hat{k}\le K$ such that

$$\begin{aligned} \Vert x^{\hat{k}+1} - x^{\hat{k}}\Vert ^2 + \Vert x^{\hat{k}} - x^{\hat{k}-1}\Vert ^2 \le \frac{4}{(c - L\bar{\beta }^2)K}(F(x^0) - F^{*}). \end{aligned}$$

By this and $\Vert a + b\Vert ^2 \le 2(\Vert a\Vert ^2 + \Vert b\Vert ^2)$, one has

$$\begin{aligned} \Vert x^{\hat{k}+1} - x^{\hat{k}}\Vert + \Vert x^{\hat{k}} - x^{\hat{k}-1}\Vert \le \frac{2\sqrt{2}}{\sqrt{c - L\bar{\beta }^2}\sqrt{K}}\cdot \sqrt{F(x^0) - F^{*}}. \end{aligned}$$

Letting $K = \bar{K}-1$, we can see that there exists $\hat{k}\le \bar{K}-1$ such that $(x^{\hat{k}-1}, x^{\hat{k}}, x^{\hat{k}+1})$ satisfies (4.24). Hence, an $x^k$ satisfying (4.24) can be found by Algorithm 2 in no more than $\bar{K}$ iterations. $\square$

Remark 4

In general, it is not easy to check an $\epsilon$-approximate $(\alpha ,\eta )$-D-stationary point according to Definition 2. One can see from Theorem 4 that (4.24) can be used as a practical termination criterion for Algorithm 2 for generating an $\epsilon$-approximate $((2L+c)^{-1},{\tilde{\eta }})$-D-stationary point of (1.1).

By similar arguments as those in the proof of Proposition 4, one can establish the following iteration complexity of EDCA for computing an approximate $(\alpha ,\eta )$-D-stationary point, whose derivation is omitted.

Theorem 5

Let $\epsilon >0$ be arbitrarily given and $\{x^k\}$ generated by EDCA. Suppose that the premise of Theorem 2 holds and F is Lipschitz continuous on $\mathcal {L}(x^0)$ with Lipschitz constant $L_0$. Then the following statements hold.

• (i) If $(x^k, x^{k+1})$ satisfies $\Vert x^{k+1} - x^k\Vert \le \epsilon /L_0$ for some $k \ge 0$, then $x^k$ is an $\epsilon$-approximate $(1,{\tilde{\eta }})$-D-stationary point of (1.1).

• (ii) The number of iterations of EDCA for computing an $\epsilon$-approximate $(1,{\tilde{\eta }})$-D-stationary point of (1.1) is no more than

  $$\begin{aligned} \left\lceil \frac{2L_0^2(F(x^0) - F^{*})}{\epsilon ^2} \right\rceil +1. \end{aligned}$$

5 An enhanced proximal DCA with extrapolation for DC problem with possibly infinite supremum

In Sects. 3 and 4 we have considered computing an $(\alpha ,\eta )$-D-stationary point of problem (1.1) in which g is defined as the supremum of a finite number of smooth convex functions, namely, the associated $\mathcal {Y}$ in defining g is a finite set. In this section we are interested in finding an $(\alpha ,\eta )$-D-stationary point of (1.1) for which the associated $\mathcal {Y}$ in defining g is possibly an infinite set. To this aim, we assume throughout this section that $\mathcal {Y}$ in (1.2) is a (possibly infinite) compact set.

As discussed in Sect. 4, Algorithm 2 can be applied to find an $(\alpha ,\eta )$-D-stationary point of (1.1) with a finite set $\mathcal {Y}$. We now check whether it can be directly applied to (1.1) with an infinite set $\mathcal {Y}$. For the latter problem, it looks natural to simply replace Steps 2 and 3 of Algorithm 2 by the following two steps, respectively:

• 1. For each $y\in \mathcal {A}(x^k,{\tilde{\eta }})$, compute $\hat{x}^k(y)$ as

  $$\begin{aligned} \hat{x}^k(y) = \mathop {{\text {argmin}}}_{x\in {\mathbb {R}}^n} \left\{ \ell _k(x,y) + \frac{c}{2}\Vert x - x^k\Vert ^2 + \frac{L}{2}\Vert x - z^k\Vert ^2 \right\} , \end{aligned}$$

  where

  $$\begin{aligned} \ell _k(x,y) = f_n(x) + f_s(z^k) + \langle \nabla f_s(z^k), x - z^k \rangle - \psi (x^k,y) - \langle \nabla _x\psi (x^k,y), x - x^k\rangle . \end{aligned}$$

  (5.1)

• 2. Let $\hat{y}\in \mathop {{{\mathrm{Argmin}}}}\nolimits _{y\in \mathcal {A}(x^k,{\tilde{\eta }})}\{F(\hat{x}^k(y)) + \frac{c}{2}\Vert \hat{x}^k(y) - x^k\Vert ^2\}$. Set $x^{k+1} = \hat{x}^k(\hat{y})$.

When $\mathcal {Y}$ is an infinite set, it is generally hard to find $\hat{y}$ and $x^{k+1}$. For example, computing $\hat{y}$ involves the DC function F, which appears to be impossible when $\mathcal {Y}$ is an infinite set. Therefore, such a direct application of Algorithm 2 is generally not implementable.

Due to the above difficulty of Algorithm 2, we propose an alternative algorithm, which is a modification of Algorithm 2 but potentially applicable to problem (1.1) with g being the supremum of infinitely many convex functions.

Algorithm 3

(The second enhanced PDCA with extrapolation ($\mathrm{EPDCA}_2$))

• 0. Input $x^0\in \mathrm {dom}(F)$, $c,{\tilde{\eta }}>0$, and $\{\beta _t\}_{t\ge 0}\subseteq [0,\sqrt{c/L})$ with $\sup _t\beta _t<\sqrt{c/L}$. Set $x^{-1} = x^0$ and $k\leftarrow 0$.

• 1. Set $z^k = x^k + \beta _k(x^k - x^{k-1})$.

• 2. Update $x^{k+1}$ as follows:

  $$\begin{aligned} x^{k+1} \in \mathop {{{\mathrm{Argmin}}}}\limits _{x\in {\mathbb {R}}^n} \left\{ \min _{y\in \mathcal {A}(x^k,{\tilde{\eta }})} \ell _k(x,y) + \frac{c}{2}\Vert x - x^k\Vert ^2 + \frac{L}{2}\Vert x - z^k\Vert ^2 \right\} , \end{aligned}$$

  (5.2)

  where $\ell _k(x,y)$ is given in (5.1).

• 3. Set $k\leftarrow k+1$ and go to Step 1.

End.

The parameters $\{\beta _t\}_{t\ge 0}$, c, and ${\tilde{\eta }}$ in Algorithm 3 can be set identically to those in Algorithm 2. The key difference between Algorithms 2 and 3 is that at each iteration Algorithm 3 solves a single optimization problem while Algorithm 2 solves two optimization problems with different objective. In the rest of this section we first study the convergence of Algorithm 3 and then discuss how to solve subproblem (5.2).

5.1 Convergence results

Theorem 6

Suppose that Assumption 1 holds, and $x^0$ is a point such that $\mathcal {L}(x^0)$ is bounded. Let $\{x^k\}$ be the sequence generated by Algorithm 3. Then the following statements hold.

• (i) The sequence $\{x^k\}$ is bounded.

• (ii) $\lim _{k\rightarrow \infty } \Vert x^k - x^{k-1}\Vert = 0$.

• (iii) $\lim _{k\rightarrow \infty }F(x^k)$ exists and $\lim _{k\rightarrow \infty }F(x^k)=F(x^\infty )$ for any accumulation point $x^\infty$ of $\{x^k\}$.

• (iv) Any accumulation point of $\{x^k\}$ is an $(\alpha ,\eta )$-D-stationary point of (1.1) for any $\alpha \in (0,(L+c)^{-1}]$ and $\eta \in [0,{\tilde{\eta }})$.

Proof

By (5.2), the convexity of $f_s$ and $\psi (\cdot ,y)$ and the Lipschitz continuity of $\nabla f_s$, we have that for any ${\tilde{y}}\in \mathcal {A}(x^k,{\tilde{\eta }})$,

$$\begin{aligned}&f_n(x^k) + f_s(x^k) - \psi (x^k,{\tilde{y}}) \nonumber \\&\quad \ge \min _{y\in \mathcal {A}(x^k,{\tilde{\eta }})} f_n(x^k) + f_s(x^k) - \psi (x^k,y) \nonumber \\&\quad \ge \min _{y\in \mathcal {A}(x^k,{\tilde{\eta }})} f_s(z^k) + \langle \nabla f_s(z^k), x^k - z^k \rangle + f_n(x^k) - \psi (x^k,y) \nonumber \\&\quad \ge \min _{y\in \mathcal {A}(x^k,{\tilde{\eta }})} \left\{ \begin{array}{ll} &{} f_s(z^k) + \langle \nabla f_s(z^k), x^{k+1} - z^k \rangle + f_n(x^{k+1}) + \frac{c}{2}\Vert x^{k+1} - x^k\Vert ^2 \\ &{} \quad - \psi (x^k,y) - \langle \nabla _x\psi (x^k,y), x^{k+1} - x^k \rangle \\ &{}\quad + \frac{L}{2}\Vert x^{k+1}- z^k\Vert ^2 - \frac{L}{2}\Vert x^k - z^k\Vert ^2 \end{array}\right\} \end{aligned}$$

(5.3)

$$\begin{aligned}&\quad \ge \min _{y\in \mathcal {A}(x^k,{\tilde{\eta }})} f_s(x^{k+1}) \!+ \!f_n(x^{k+1}) \!-\! \psi (x^{k+1}, y) \!-\! \frac{L}{2}\Vert x^k \!-\! z^k\Vert ^2 + \frac{c}{2}\Vert x^{k+1} - x^k\Vert ^2 \nonumber \\&\quad \ge F(x^{k+1}) - \frac{L}{2}\Vert x^k - z^k\Vert ^2 + \frac{c}{2}\Vert x^k - x^{k+1}\Vert ^2, \end{aligned}$$

(5.4)

where the second inequality is by the convexity of $f_s$, the third one is due to (5.2), the fourth one is by Lipschitz continuity of $\nabla f_s$ and convexity of $\psi (\cdot ,y)$, and the last one is by the definition of F. It then follows from (5.4) that for every ${\tilde{y}}\in \mathcal {A}(x^k)$,

$$\begin{aligned} F(x^{k+1}) + \frac{c}{2}\Vert x^{k+1} - x^k\Vert ^2\le & {} f(x^k) - \psi (x^k,{\tilde{y}}) + \frac{L}{2}\Vert x^k - z^k\Vert ^2 \\= & {} F(x^k) + \frac{L}{2}\Vert x^k - z^k\Vert ^2. \end{aligned}$$

This, together with the definition of $z^k$ and $\bar{\beta } = \sup _t\beta _t$, gives us

$$\begin{aligned} F(x^{k+1}) + \frac{c}{2}\Vert x^{k+1} - x^k\Vert ^2 \le F(x^k) + \frac{L\bar{\beta }^2}{2}\Vert x^k - x^{k-1}\Vert ^2. \end{aligned}$$

By this, $\bar{\beta }\in [0,\sqrt{c/L})$ and the same arguments as those in the proof of Theorem 2, one can have that (i) and (ii) hold, and moreover

$$\begin{aligned} \zeta := \lim _{k\rightarrow \infty } F(x^k) = \lim _{k\rightarrow \infty } F(x^k) + \frac{c}{2}\Vert x^k - x^{k-1}\Vert ^2 \end{aligned}$$

(5.5)

exists. It follows from (5.3), (5.4) and the convexity of $f_s$ that

$$\begin{aligned}&F(x^{k+1}) \le F(x^{k+1}) + \frac{c}{2}\Vert x^{k+1} - x^k\Vert ^2 \nonumber \\&\quad \le \min _{y\in \mathcal {A}(x^k,{\tilde{\eta }})} \left\{ \begin{array}{ll} &{}\quad f_s(z^k) + \langle \nabla f_s(z^k), x^{k+1} - z^k \rangle + f_n(x^{k+1}) - \psi (x^k,y) \\ &{} \qquad - \langle \nabla _x\psi (x^k,y), x^{k+1} - x^k \rangle + \frac{c}{2}\Vert x^{k+1} - x^k\Vert ^2 + \frac{L}{2}\Vert x^{k+1} - z^k\Vert ^2 \end{array}\right\} \nonumber \\&\quad \le \min _{y\in \mathcal {A}(x^k,{\tilde{\eta }})} \left\{ \begin{array}{ll} &{} \quad f_s(z^k) + \langle \nabla f_s(z^k), x - z^k \rangle + f_n(x) - \psi (x^k,y) \\ &{} \qquad - \langle \nabla _x\psi (x^k,y), x - x^k \rangle + \frac{c}{2}\Vert x - x^k\Vert ^2 + \frac{L}{2}\Vert x - z^k\Vert ^2 \end{array}\right\} , \quad \forall x\in {\mathbb {R}}^n \nonumber \\&\quad \le f_s(x) + f_n(x) - \psi (x^k,y) - \langle \nabla _x\psi (x^k,y), x - x^k \rangle \nonumber \\&\qquad +\, \frac{c}{2}\Vert x - x^k\Vert ^2 + \frac{L}{2}\Vert x - z^k\Vert ^2, \quad \forall x\in {\mathbb {R}}^n,\; \forall y\in \mathcal {A}(x^k,{\tilde{\eta }}), \end{aligned}$$

(5.6)

where the second inequality follows from (5.3) and (5.4), and the third one is due to (5.2) and last one is by the convexity of $f_s$. Let $x^\infty$ be any accumulation point and $\{x^k\}_{k\in \mathcal {K}}$ be a subsequence converging to $x^{\infty }$. By $\Vert x^{k+1}-x^k\Vert \rightarrow 0$, $z^k = x^k + \beta _k(x^k - x^{k-1})$ and $\beta _k\in [0,\sqrt{c/L})$, one has $\lim _{{\mathcal K}\ni k \rightarrow \infty }x^{k+1} = x^\infty$ and $\lim _{{\mathcal K}\ni k \rightarrow \infty } z^k = x^\infty$. Let $\eta \in [0,{\tilde{\eta }})$ be arbitrarily chosen. It then follows from Lemma 1 that $\mathcal {A}(x^\infty ,\eta )\subseteq \mathcal {A}(x^k,{\tilde{\eta }})$ for sufficiently large $k\in \mathcal {K}$. This together with (5.6) yields that for all $k\in \mathcal {K}$ sufficiently large, we have

$$\begin{aligned} F(x^{k+1})\le & {} f(x) - \psi (x^k,y) - \langle \nabla _x\psi (x^k,y), x - x^k \rangle + \frac{c}{2}\Vert x - x^k\Vert ^2\\&+ \frac{L}{2}\Vert x - z^k\Vert ^2, \quad \forall x\in {\mathbb {R}}^n, \; \forall y\in \mathcal {A}(x^\infty ,\eta ). \end{aligned}$$

Taking the limit on both sides as $\mathcal {K}\ni k \rightarrow \infty$, and using (5.5) as well as the continuity of $\psi$ and $\nabla _x\psi$ on the open set $\Omega$ containing $\mathrm {dom}(f_n)$, we obtain

$$\begin{aligned} \zeta\le & {} f(x) - \psi (x^\infty ,y) - \langle \nabla _x \psi (x^\infty ,y), x - x^\infty \rangle \nonumber \\&+ \frac{L+c}{2}\Vert x - x^\infty \Vert ^2, \quad \forall x\in {\mathbb {R}}^n, \;\forall y\in \mathcal {A}(x^\infty ,\eta ). \end{aligned}$$

(5.7)

By (5.5), $\lim _{{\mathcal K}\ni k \rightarrow \infty }x^k = x^\infty$ and the lower-semicontinuity of F, one has $F(x^\infty )\le \zeta$. Letting $x=x^\infty$ and $y\in \mathcal {A}(x^\infty )$ in (5.7) and using the definition of $\mathcal {A}(x^\infty )$, we have $\zeta \le F(x^\infty )$. It thus follows that $F(x^\infty ) = \zeta$, which together with (5.7) yields

$$\begin{aligned} F(x^\infty )\le & {} f(x) - \psi (x^\infty ,y) - \langle \nabla _x \psi (x^\infty ,y), x - x^\infty \rangle \\&+ \frac{L+c}{2}\Vert x - x^\infty \Vert ^2, \quad \forall x\in {\mathbb {R}}^n, \;\forall y\in \mathcal {A}(x^\infty ,\eta ). \end{aligned}$$

By this, Definition 1, and the arbitrarity of $\eta \in [0,{\tilde{\eta }})$, we conclude that $x^\infty$ is an $(\alpha ,\eta )$-D-stationary point of (1.1) for any $\alpha \in (0,(L+c)^{-1}]$ and $\eta \in [0,{\tilde{\eta }})$. $\square$

We next study the iteration complexity of Algorithm 3 for computing an approximate $(\alpha ,\eta )$-D-stationary point of (1.1).

Theorem 7

Let $\epsilon >0$ be arbitrarily given, $\bar{\beta } =\sup _t\beta _t$, and $L_0$ the Lipschitz constant of F on $\mathcal {L}(x^0)$. Let $\{x^k\}$ be generated by Algorithm 3. Suppose that the premise of Theorem 6 holds. Then the following statements hold.

• (i) If $(x^{k-1}, x^k, x^{k+1})$ satisfies

  $$\begin{aligned} \Vert x^{k+1} - x^k\Vert + \Vert x^k - x^{k-1}\Vert \le \min \left\{ 1,\frac{\epsilon }{L\bar{\beta }^2}, \frac{\epsilon }{L_0}\right\} \end{aligned}$$

  for some $k \ge 0$, then $x^k$ is an $\epsilon$-approximate $((2L+c)^{-1},{\tilde{\eta }})$-D-stationary point of (1.1).

• (ii) The number of iterations of Algorithm 3 for computing an $\epsilon$-approximate $((2L+c)^{-1},{\tilde{\eta }})$-D-stationary point of (1.1) is no more than

  $$\begin{aligned} \bar{K} =\left\lceil \frac{8(F(x^0) - F^{*})}{c - L\bar{\beta }^2}\cdot \max \left\{ 1,\frac{L^2\bar{\beta }^4}{\epsilon ^2}, \frac{L_0^2}{\epsilon ^2}\right\} \right\rceil +1. \end{aligned}$$

Proof

It follows from (5.6), $f=f_s+f_n$ and $z^k=x^k+\beta _k(x^k - x^{k-1})$ that

$$\begin{aligned} F(x^{k+1})\le & {} f(x) - \psi (x^k,y) - \langle \nabla _x(x^k,y), x - x^k\rangle \\&+ \frac{2L+c}{2}\Vert x - x^k\Vert ^2 + L\beta _k^2\Vert x^k - x^{k-1}\Vert ^2, \quad \forall y\in \mathcal {A}(x^k,{\tilde{\eta }}). \end{aligned}$$

The rest of the proof follows from this and the same arguments as those in the proof of Theorem 4. $\square$

Remark 5

In view of Theorems 6 and 7, we see that Algorithm 3 shares similar theoretical results with Algorithm 2. However, it is not clear whether the convergence of the entire sequence generated by Algorithm 3 can be established. We shall leave this to our future study.

5.2 Solving the subproblem (5.2)

Though subproblem (5.2) is nonconvex in general, we show in this subsection that it can be efficiently solved for some classes of $\mathcal {Y}$.

5.2.1 $\mathcal {Y}$ is a finite set

Suppose that $\mathcal {Y}$ is a finite set. For the sake of convenience, assume that $\mathcal {Y}= \{1,2,\ldots ,I\}$. The subproblem (5.2) for such $\mathcal {Y}$ can be solved as follows.

• 2a. For each index $i\in \mathcal {A}(x^k,{\tilde{\eta }})$, compute $\hat{x}^{k,i}$ as

  $$\begin{aligned} \hat{x}^{k,i} = \mathop {{\text {argmin}}}_{x\in {\mathbb {R}}^n} \left\{ \ell _{k,i}(x) + \frac{c}{2}\Vert x - x^k\Vert ^2 + \frac{L}{2}\Vert x - z^k\Vert ^2\right\} , \end{aligned}$$

  where

  $$\begin{aligned} \ell _{k,i}(x) = f_n(x) + f_s(z^k) + \langle \nabla f_s(z^k), x - z^k\rangle - \psi _i(x^k) - \langle \nabla \psi _i(x^k), x - x^k\rangle . \end{aligned}$$

• 2b. Let $\hat{i} \in \mathop {{{\mathrm{Argmin}}}}\nolimits _{i\in \mathcal {A}(x^k,{\tilde{\eta }})}\left\{ \ell _{k,i}(\hat{x}^{k,i}) + \frac{c}{2}\Vert \hat{x}^{k,i} - x^k\Vert ^2 + \frac{L}{2}\Vert \hat{x}^{k,i} - z^k\Vert ^2\right\}$. Set $x^{k+1} = \hat{x}^{k,\hat{i}}$.

It thus follows that Step 2 of Algorithm 3 can be replaced by the above Steps 2a and 2b. Upon such a replacement, one can observe that similar to Algorithm 2, each iteration of Algorithm 3 also solves possibly multiple convex subproblems and then executes a selection procedure. The selection of $\hat{i}$ for Algorithm 3 is, however, different from the one in Algorithm 2. In particular, Algorithm 2 needs to evaluate $g(\hat{x}^{k,i})$ for all $i\in \mathcal {A}(x^k,{\tilde{\eta }})$, but Algorithm 3 does not. Given that evaluation of g(x) requires computing $\psi _j(x)$ for each $j\in \mathcal {Y}$, the computational cost of Algorithm 3 per iteration is generally cheaper than that of Algoithm 2 when $\mathcal {Y}$ is a finite set.

5.2.2 $\psi (x,y)$ is linear of y and $f_n=0$

Suppose that $f_n=0$ and $\psi (x,y)$ is a linear function of y. That is, f is continuously differentiable in ${\mathbb {R}}^n$ and $\psi (x,y) = \langle \phi (x),y\rangle$ for some $\phi (x) = \left( \phi _1(x),\phi _2(x),\ldots ,\phi _m(x)\right) ^T$. Moreover, we assume that for all $i=1,\ldots ,m$, $\phi _i$ is continuously differentiable in ${\mathbb {R}}^n$. It thus follows from (1.2) that g can be written as

$$\begin{aligned} g(x) = \max _{y\in \mathcal {Y}} \langle \phi (x),y\rangle . \end{aligned}$$

(5.8)

We denote by $\nabla \phi (x) \in {\mathbb {R}}^{n\times m}$ the gradient of $\phi$ at x. Under these assumptions, we can show that subproblem (5.2) is equivalent to a convex maximization problem.

Proposition 5

Consider the subproblem (5.2). Suppose that g is of the form (5.8) and $f_n = 0$. Let

$$\begin{aligned} Q= & {} \frac{1}{L+c}\nabla \phi (x^k)^T\nabla \phi (x^k), \quad \\ q= & {} \phi (x^k) - \frac{1}{L+c}\nabla \phi (x^k)^T\left( \nabla f(x^k) - L(z^k - x^k)\right) . \end{aligned}$$

Then a solution $x^{k+1}$ of (5.2) can be computed by first solving the convex maximization problem

$$\begin{aligned} \begin{aligned} y^{k+1} \in \mathop {{{\mathrm{Argmax}}}}\limits _{y\in \mathcal {Y}}&\ \frac{1}{2}y^TQy + \langle q, y \rangle \\ \mathrm{s.t.}&\ \langle \phi (x^k), y \rangle \ge g(x^k) - {\tilde{\eta }}, \end{aligned} \end{aligned}$$

(5.9)

and then setting

$$\begin{aligned} x^{k+1} = \frac{1}{L+c}\left( \nabla \phi (x^k)y^{k+1} - \nabla f(z^k) + Lz^k + cx^k\right) . \end{aligned}$$

(5.10)

Proof

Since $f_n=0$, the subproblem (5.2) can be simplified as

$$\begin{aligned} x^{k+1} \in \mathop {{{\mathrm{Argmin}}}}\limits _{x}\left\{ \min _{y\in \mathcal {A}(x^k,{\tilde{\eta }})} \left\langle u - \nabla \phi (x^k)y, x \right\rangle + \frac{L+c}{2}\Vert x\Vert ^2 - \langle v , y \rangle \right\} , \end{aligned}$$

(5.11)

where

$$\begin{aligned} u = \nabla f(z^k) - Lz^k - cx^k, \quad v = \phi (x^k) - \nabla \phi (x^k)^Tx^k. \end{aligned}$$

Upon interchanging x and y in (5.11), one can calculate $x^{k+1}$ by the following two steps:

$$\begin{aligned} \left\{ \begin{aligned} y^{k+1}&\in \mathop {{{\mathrm{Argmin}}}}\limits _{y\in \mathcal {A}(x^k,{\tilde{\eta }})} \left\{ \min _x \;\left\langle u - \nabla \phi (x^k)y, x \right\rangle + \frac{L+c}{2}\Vert x\Vert ^2 - \langle v, y \rangle \right\} , \\ x^{k+1}&= \mathop {{\text {argmin}}}_x \left\{ \left\langle u - \nabla \phi (x^k)y^{k+1}, x \right\rangle + \frac{L+c}{2}\Vert x\Vert ^2 \right\} . \end{aligned} \right. \end{aligned}$$

Notice that in the above two steps, the minimization with respect to x can be solved explicitly. Thus, the above two steps can be simplified as

$$\begin{aligned} \left\{ \! \begin{aligned} y^{k+1}&\in \mathop {{{\mathrm{Argmin}}}}\limits _{y\in \mathcal {A}(x^k,{\tilde{\eta }})}\left\{ -\frac{1}{2(L\!+\!c)}y^T\nabla \phi (x^k)^T\nabla \phi (x^k)y \!-\! \left\langle v - \frac{1}{L+c}\nabla \phi (x^k)^Tu, y \right\rangle \right\} , \\ x^{k+1}&= \frac{1}{L+c}\left( \nabla \phi (x^k)y^{k+1} - u\right) . \end{aligned} \right. \end{aligned}$$

This, together with $\mathcal {A}(x^k,{\tilde{\eta }}) = \{ y\in \mathcal {Y}\mid \langle \phi (x^k), y \rangle \ge g(x^k) - {\tilde{\eta }}\}$, leads to (5.9) and (5.10). $\square$

In view of Proposition 5, subproblem (5.2) is reduced to (5.9). We next discuss two cases of $\mathcal {Y}$ for which (5.9) can be solved efficiently.

$\mathcal {Y}$is a polyhedral set. Since the objective function of (5.9) is convex, its global optimal value must be attained at some extreme point of the feasible set. Note that the feasible set of (5.9) is the intersection of $H_k := \{y\in {\mathbb {R}}^m: \langle \phi (x^k),y\rangle \ge g(x^k) - {\tilde{\eta }}\}$ with a polyhedral set $\mathcal {Y}$. Suppose that $\mathcal {Y}$ has polynomial number of one-dimensional faces. It is not hard to observe that for such $\mathcal {Y}$, $H_k\cap \mathcal {Y}$ has polynomial number of vertices and thus (5.9) is solvable in polynomial time. For example, if $\mathcal {Y}$ is a simplex, i.e., $\mathcal {Y}= \{y\in {\mathbb {R}}^m: \sum _{i=1}^my_i = 1, y\ge 0\}$, then $H_k\cap \mathcal {Y}$ has at most $O(m^2)$ number of extreme points.

$\mathcal {Y}$is an ellipsoid. Suppose that $\mathcal {Y}= \{y\in {\mathbb {R}}^m : (y - {\bar{y}})^TW(y - {\bar{y}}) \le 1\}$ for some positive definite matrix W and ${\bar{y}}\in {\mathbb {R}}^m$. To solve (5.9) with such $\mathcal {Y}$, we first transform it to a maximization problem with ball constraints. Specifically, letting ${\tilde{y}} = W^{1/2}(y - {\bar{y}})$, problem (5.9) is equivalent to

$$\begin{aligned} \max \limits _y\left\{ \frac{1}{2}{\tilde{y}}^T{\tilde{Q}}{\tilde{y}} + \langle {\tilde{q}}, {\tilde{y}} \rangle : \langle a,{\tilde{y}} \rangle \ge b, \ \Vert {\tilde{y}}\Vert \le 1\right\} , \end{aligned}$$

(5.12)

where

$$\begin{aligned} {\tilde{Q}}= & {} W^{-\frac{1}{2}}QW^{-\frac{1}{2}}, \quad {\tilde{q}} = W^{-\frac{1}{2}}(Q{\bar{y}} + q), \\ a= & {} W^{-\frac{1}{2}}\phi (x^k),\!\qquad b = g(x^k) - {\tilde{\eta }}- \langle \phi (x^k),{\bar{y}} \rangle . \end{aligned}$$

Notice that (5.12) is an extended trust region subproblem with only one affine inequality constraint, whose solution can be found by solving the following semidefinite programming relaxation problem (see, for example, [5, 18]):

$$\begin{aligned} \begin{aligned} \max \limits _{{{\tilde{Y}}}, {\tilde{y}}}&\quad \frac{1}{2}\text{ tr }({\tilde{Q}} {\tilde{Y}}) + \langle {\tilde{q}},{\tilde{y}}\rangle \\ \text{ s.t. }&\quad \Vert b{\tilde{y}} - {\tilde{Y}}a\Vert \le b - a^T{\tilde{y}}, \\&\quad \text{ tr }({\tilde{Y}})\le 1,\ {\tilde{Y}}\succeq {\tilde{y}}{\tilde{y}}^T. \end{aligned} \end{aligned}$$

(5.13)

Suppose that $({{\tilde{Y}}}^*, {\tilde{y}}^*)$ is an optimal solution of (5.13). Then ${\tilde{y}}^*$ is an optimal solution of (5.12). It thus follows that $y^{k+1} = {\bar{y}} + W^{-1/2}{\tilde{y}}^*$ is an optimal solution of (5.9).

6 Concluding remarks

In this paper we considered a class of structured nonsmooth DC minimization in which the first convex component is the sum of a smooth and nonsmooth functions while the second convex component is the supremum of possibly infinitely many convex smooth functions. In particular, we first proposed an inexact enhanced DC algorithm for solving this problem in which the second convex component is the supremum of finitely many convex smooth functions, and showed that every accumulation point of the generated sequence is an $(\alpha ,\eta )$-D-stationary point of the problem, which is generally stronger than an ordinary D-stationary point. In addition, we proposed two proximal DC algorithms with extrapolation for solving this problem, and showed that every accumulation point of the solution sequence generated by them is an $(\alpha ,\eta )$-D-stationary point of the problem. The convergence of the entire sequence was established under some suitable assumption. We also introduced a concept of approximate $(\alpha ,\eta )$-D-stationary point and derived iteration complexity of the proposed proximal DC algorithms for finding an approximate $(\alpha ,\eta )$-D-stationary point. In contrast with the DC algorithm [13], our proximal DC algorithms have much simpler subproblems and also incorporate the extrapolation for possible acceleration. Moreover, one of our algorithms is potentially applicable to the DC problem in which the second convex component is the supremum of infinitely many convex smooth functions. In addition, our algorithms have stronger convergence results than the proximal DC algorithm in [19].

From computational point of view, our algorithm for the DC problem in which the second convex component in the objective is the supremum of infinitely many convex smooth functions is only applicable to some special classes of problems. It is worthy of a further research in developing efficient algorithms for solving D-stationary points of this type of DC problems. In addition, our proximal DC algorithms use the global Lipschitz constant of the gradient of the smooth function in the objective. We believe it can be replaced by some suitable quantity obtained by a line search technique that can improve the efficiency of the algorithms. The numerical implementation of our algorithms and its comparison with other competitive methods are left as future research.