1 Introduction

Let H be a Hilbert space with the inner product \(\langle .,.\rangle \) and \(C \subseteq H\) be a nonempty closed and convex set in H.

In this article, we are concerned with the classical variational inequality, which is to find a point \(x^*\in C\) such that

$$\begin{aligned} \langle f(x^*),x-x^*\rangle \ge 0,\quad \forall x\in C, \end{aligned}$$
(1)

where \(f : H \rightarrow H\) is a mapping. This problem captures various applications arising in many areas, such as partial differential equations, optimal control, optimization, mathematical programming and some other nonlinear problems (see, for example, [1] and references therein).

It is well-known that if f is L-Lipschitz continuous and \(\eta \)-strongly monotone on C, i.e.

$$\begin{aligned} \Vert f(x)-f(y)\Vert \le L\Vert x-y\Vert ,\quad \forall x,y \in C, \end{aligned}$$

and

$$\begin{aligned} \langle f(x)-f(y),x-y\rangle \ge \eta \Vert x-y\Vert ^2, \quad \forall x,y \in C, \end{aligned}$$

where \(L>0\) and \(\eta >0\) are the Lipschitz and strong monotonicity constants, respectively, then the variational inequality (1) has a unique solution. Recently, Zhou et al. [2] weakened the Lipschitz continuity to the hemicontinuity. However, if f is simply L-Lipschitz continuous and monotone on C, i.e.

$$\begin{aligned} \langle f(x)-f(y),x-y\rangle \ge 0, \quad \forall x,y \in C, \end{aligned}$$

but not \(\eta \)-strongly monotone, then the variational inequality (1) may fail to have a solution. We refer the readers to [2] for counterexamples.

Some authors have proposed and analyzed several iterative methods for solving the variational inequality (1). The simplest one is the following projection method, which can be seen an extension of the projected gradient method for optimization problems:

$$\begin{aligned} x^{k+1}=P_C(x^k-\tau f(x^k)) \end{aligned}$$
(2)

for each \(k\ge 1\), where \(\tau \in (0,\frac{2\eta }{L^2})\) and \(P_C\) denotes the Euclidean least distance projection onto C. The projection method converges provided that the mapping f is \(L-\hbox {Lipschitz}\) continuous and \(\eta \)-strongly monotone. By using a counterexample, Yao et al. (see [3]) proved that the projected gradient method may diverge if the strong monotonicity assumption is relaxed to plain monotonicity.

To avoid the hypotheses of the strong monotonicity, Korpelevich [4] proposed the extragradient method:

$$\begin{aligned} \left\{ \begin{aligned}&y^k=P_C(x^k-\tau f(x^k)),\\&x^{k+1}=P_C(x^k-\tau f(y^k)) \end{aligned} \right. \end{aligned}$$
(3)

for each \(k\ge 1\), which converges if f is Lipschitz continuous and monotone.

In fact, in the extragradient method, one needs to calculate two projections onto C in each iteration. Note that the projection onto a closed convex set C is related to a minimum distance problem. If C is a general closed and convex set, this might require a prohibitive amount of computation time.

To our knowledge, there are two kinds of methods to overcome this difficulty. The first one is the subgradient extragradient method developed by Censor et al. [5, 6]:

$$\begin{aligned} \left\{ \begin{aligned}&y^k=P_C(x^k-\tau f(x^k)),\\&T_k:=\{w\in H\,|\, \langle x^k-\tau f(x^k)-y^k,w-y^k\rangle \le 0\},\\&x^{k+1}=P_{T_k}(x^k-\tau f(y^k)) \end{aligned} \right. \end{aligned}$$
(4)

for each \(k\ge 1\). This method replaces the second projection onto C of the extragradient method by a projection onto a specific constructible subgradient half-space \(T_k\). The second one is the projection and contraction method studied by some authors [7,8,9,10]:

$$\begin{aligned} \left\{ \begin{aligned}&y^k=P_C(x^k-\tau f(x^k)),\\&d(x^k,y^k)=(x^k-y^k)-\tau (f(x^k)-f(y^k)),\\&x^{k+1}=x^k-\gamma \beta _k d(x^k,y^k) \end{aligned} \right. \end{aligned}$$
(5)

for each \(k\ge 1\), where \(\gamma \in (0,2),\)

$$\begin{aligned} \beta _k:=\frac{\varphi (x^k,y^k)}{\Vert d(x^k,y^k)\Vert ^2}, \quad \varphi (x^k,y^k):=\langle x^k-y^k,d(x^k,y^k)\rangle . \end{aligned}$$

The projection and contraction method needs only one projection onto C in each iteration and has an advantage in computing over the extragradient and subgradient extragradient methods (see [9]).

The inertial type algorithms originate from the heavy ball method (an implicit discretization) of the two order time dynamical system [11, 12], the main features of which is that the next iterate is defined by making use of the previous two iterates. Recently, there are growing interests in studying inertial type algorithms. Some latest references are inertial forward-backward splitting methods for certain separable nonconvex optimization problems [13], strongly convex problems [14, 15] and inertial dynamics methods [16, 17].

For finding the zeros of a maximally monotone operator, Bot and Csetnek [18] proposed the so-called inertial hybrid proximal-extragradient algorithm, which combines inertial type algorithms and hybrid proximal-extragradient algorithms (see, e.g. [19, 21]) and includes the following algorithm as a special case (see, e.g. [22]):

$$\begin{aligned} x^{k+1}=P_C\left( x^k-c_kf(x^k)+\alpha _k(x^k-x^{k-1})\right) . \end{aligned}$$
(6)

It is obvious that the algorithm (6) can be seen as the projection algorithm (2) with inertial effects and also can be seen as a bounded perturbation of the projection algorithm (2) (see, e.g. [20]). The authors showed that the algorithm (6) converges weakly to a solution of the variational inequality (1) provided that \((\alpha _k)\) is nondecreasing with \(\alpha _1 = 0\), \(0\le \alpha _k\le \alpha \), and \(0<\underline{c}\le c_k\le 2\gamma \sigma ^2\), for \(\alpha ,\sigma \ge 0\) such that \(\alpha (5+4\sigma ^2)+\sigma ^2<1\).

Very recently, Dong et al. [22] introduced the following algorithm:

$$\begin{aligned} \left\{ \begin{aligned}&w^k=x^k+\alpha _k(x^k-x^{k-1}),\\&y^k=P_C(w^k-\tau f(w^k)),\\&x^{k+1}=(1-\lambda _k)w^k+\lambda _kP_C(w^k-\tau f(y^k)) \end{aligned} \right. \end{aligned}$$
(7)

for each \(k\ge 1\), where \(\{\alpha _k\}\) is nondecreasing with \(\alpha _1=0\) and \(0\le \alpha _k\le \alpha <1\) for each \(k\ge 1\) and \(\lambda ,\sigma ,\delta >0\) are such that

$$\begin{aligned} \delta >\frac{\alpha [(1+\tau L)^2\alpha (1+\alpha )+(1-\tau ^2L^2)\alpha \sigma +\sigma (1+\tau L)^2]}{1-\tau ^2L^2} \end{aligned}$$

and

$$\begin{aligned} 0<\lambda \le \lambda _k\le \frac{\delta (1-\tau ^2L^2)-\alpha [(1+\tau L)^2\alpha (1+\alpha )+(1-\tau ^2L^2)\alpha \sigma +\sigma (1+\tau L)^2]}{\delta [(1+\tau L)^2\alpha (1+\alpha )+(1-\tau ^2L^2)\alpha \sigma +\sigma (1+\tau L)^2]}, \end{aligned}$$

where L is the Lipschitz constant of f.

In this paper, we study an inertial projection and contraction algorithm and analyze its convergence in a Hilbert space H. We also present a modified inertial projection and contraction algorithm for approximating a common element of the set of solutions of a variational inequality and the set of fixed points of a nonexpansive mapping in H. Finally, we give numerical examples are presented to illustrate the efficiency and advantage of the inertial projection and contraction algorithm.

2 Preliminaries

In the sequel, we use the notations:

  1. (1)

      \(\rightharpoonup \) for weak convergence and \(\rightarrow \) for strong convergence;

  2. (2)

      \(\omega _w(x^k) = \{x : \exists x^{k_j}\rightharpoonup x\}\) denotes the weak \(\omega \)-limit set of \(\{x^k\}\).

We need some results and tools in a real Hilbert space H which are listed as lemmas below.

Recall that, in a Hilbert space H,

$$\begin{aligned} \Vert \lambda x+(1-\lambda )y\Vert ^2=\lambda \Vert x\Vert ^2+(1-\lambda )\Vert y\Vert ^2-\lambda (1-\lambda )\Vert x-y\Vert ^2 \end{aligned}$$
(8)

for all \(x, y\in H\) and \(\lambda \in {\mathbb {R}}\) (see Corollary 2.14 in [23]).

Definition 2.1

Let \(B : H\rightrightarrows 2^H\) be a point-to-set operator defined on a real Hilbert space H. B is called a maximal monotone operator if B is monotone, i.e.,

$$\begin{aligned} \langle u-v,x-y\rangle \ge 0 \end{aligned}$$

for all \(u\in B(x)\) and \(v\in B(y)\) and the graph G(B) of B,

$$\begin{aligned} G(B):=\{(x,u)\in H\times H : u\in B(x)\}, \end{aligned}$$

is not properly contained in the graph of any other monotone operator.

It is clear that a monotone mapping B is maximal if and only if, for any \((x, u) \in H \times H\), if \(\langle u-v,x-y\rangle \ge 0\) for all \((v, y) \in G(B)\), then it follows that \( u\in B(x)\).

Lemma 2.1

(Goebel and Kirk [24]) Let C be a closed convex subset of a real Hilbert space H and \(T : C \rightarrow C\) be a nonexpansive mapping such that \(Fix(T)\ne \emptyset \). If a sequence \(\{x^k\}\) in C is such that \(x^k\rightharpoonup z\) and \(x^k - T x^k \rightarrow 0\), then \(z = T z\).

Lemma 2.2

Let K be a closed convex subset of real Hilbert space H and \(P_K\) be the (metric or nearest point) projection from H onto K (i.e., for \(x\in H\), \(P_Kx\) is the only point in K such that \(\Vert x-P_Kx\Vert =\inf \{\Vert x-z\Vert : z \in K\}\)). Then, for any \(x \in H\) and \(z\in K\), \(z=P_Kx\) if and only if there holds the relation:

$$\begin{aligned} \langle x-z,y-z\rangle \le 0 \end{aligned}$$

for all \(y\in K\).

Lemma 2.3

(see [11]) Let \(\{\varphi _k\}\), \(\{\delta _k\}\) and \(\{\alpha _k\}\) be the sequences in \([0, +\infty )\) such that, for each \(k\ge 1\),

$$\begin{aligned} \varphi _{k+1}\le \varphi _{k}+\alpha _k(\varphi _{k}-\varphi _{k-1})+\delta _k,\quad \sum _{k=1}^{\infty }\delta _k<+\infty \end{aligned}$$

and there exists a real number \(\alpha \) with \( 0\le \alpha _k\le \alpha <1\) for all \(k\ge 1\). Then the following hold:

  1. (i)

    \(\sum _{k=1}^{\infty }[\varphi _k-\varphi _{k-1}]_+<+\infty \), where \([t]_+= \max \{t,0\};\)

  2. (ii)

    there exists \(\varphi ^*\in [0, +\infty )\) such that \(\lim _{k\rightarrow +\infty }\varphi _k=\varphi ^*.\)

Lemma 2.4

(see [23], Lemma 2.39) Let C be a nonempty set of H and \(\{x^k\}\) be a sequence in \({\mathcal {H}}\) such that the following two conditions hold:

  1. (i)

    for all \(x\in C\), \(\lim _{k\rightarrow \infty }\Vert x^k-x\Vert \) exists;

  2. (ii)

    every sequential weak cluster point of \(\{x^k\}\) is in C.

Then the sequence \(\{x^k\}\) converges weakly to a point in C.

3 The inertial projection and contraction algorithm

In this section, we present the inertial projection and contraction algorithm and analyze its convergence.

For a mapping \(f : H\rightarrow H\), we introduce the following algorithm:

Algorithm 3.1

Choose initial guesses \(x_0,x_1\in H\) arbitrarily. Calculate the \((k+1)th\) iterate \(x^{k+1}\) via the formula:

$$\begin{aligned} \left\{ \begin{aligned}&w^k=x^k+\alpha _k(x^k-x^{k-1}),\\&y^k=P_C(w^k-\tau f(w^k)),\\&d(w^k,y^k)=(w^k-y^k)-\tau (f(w^k)-f(y^k)),\\&x^{k+1}=w^k-\gamma \beta _k d(w^k,y^k) \end{aligned} \right. \end{aligned}$$
(9)

for each \(k\ge 1\), where \(\gamma \in (0,2)\), \(\tau >0\) and

$$\begin{aligned} \beta _k:= \left\{ \begin{array}{ll} {\varphi (w^k,y^k)}/{\Vert d(w^k,y^k)\Vert ^2},&{}\quad \hbox {if}\,\,d(w^k,y^k)\ne 0 \\ 0&{}\quad \hbox {if}\,\,d(w^k,y^k)=0, \\ \end{array} \right. \end{aligned}$$
(10)

where

$$\begin{aligned} \varphi (w^k,y^k):=\langle w^k-y^k,d(w^k,y^k)\rangle , \end{aligned}$$

and \(\{\alpha _k\}\) is nondecreasing with \(\alpha _1=0,\) \(0\le \alpha _k\le \alpha <1,\) and \(\sigma ,\delta >0\) are such that

$$\begin{aligned} \delta >\frac{\alpha ^2(1+\alpha )+\alpha \sigma }{1-\alpha ^2},\quad 0<\gamma \le \frac{2\left[ \delta -\alpha ((1+\alpha )+\alpha \delta +\sigma )\right] }{\delta [1+\alpha (1+\alpha )+\alpha \delta +\sigma ]}. \end{aligned}$$
(11)

If \(y^k=w^k\) or \(d(w^k,y^k)=0\) then \(x^{k+1}\) is a solution of the variational inequality (1) (see Lemma 3.1 below) and the iterative process stops; otherwise, we set \(k:=k + 1\) and go on to (9) to evaluate the next iterate \(x^{k+2}\).

To discuss the convergence of the algorithm (9), we assume the following conditions.

Condition 3.1

The solution set of (1), denoted by SOL(C, f), is nonempty.

Condition 3.2

The mapping f is monotone on H.

Condition 3.3

The mapping f is Lipschitz continuous on H with the Lipschitz constant \(L>0\).

Lemma 3.1

Assume \(0<\tau < 1/L.\) If \(y^k=w^k\) or \(d(w^k,y^k)=0\) in (9), then \(x^{k+1}\in SOL(C,f).\)

Proof

From conditions 3.2 and 3.3, it follows

$$\begin{aligned} \begin{aligned} \Vert d(w^k,y^k)\Vert&=\Vert (w^k-y^k)-\tau (f(w^k)-f(y^k))\Vert \\&\ge \Vert w^k-y^k\Vert -\tau \Vert f(w^k)-f(y^k)\Vert \\&\ge (1-\tau L)\Vert w^k-y^k\Vert . \end{aligned} \end{aligned}$$

Similarly, we can show

$$\begin{aligned} \Vert d(w^k,y^k)\Vert \le (1+\tau L)\Vert w^k-y^k\Vert . \end{aligned}$$

So, \(d(w^k,y^k)=0\) if and only if \(y^k=w^k\). From (9), we have

$$\begin{aligned} y^k=P_C(y^k-\tau f(y^k)+d(w^k,y^k)). \end{aligned}$$

When \(d(w^k,y^k)=0\), by (9) and in (10), one has \(x^{k+1}=y^k\) and

$$\begin{aligned} y^k=P_C(y^k-\tau f(y^k)). \end{aligned}$$

which with Lemma 2.2 yields \(x^{k+1}\in SOL(C,f)\). This completes the proof. \(\square \)

Remark 3.1

From Lemma 3.1, we see that if the algorithm (9) terminates in a finite (say k) step of iterations, then \(x^k\) is a solution of the variational inequality (1). So in the rest of this section, we assume that the algorithm (9) does not terminate in any finite iterations, and hence generates an infinite sequence

The following lemma is crucial for the proof of our convergence theorem.

Lemma 3.2

Let \(\{x^k\}\) be the sequence generated by (9) and let \(0<\tau < 1/L.\) Assume \(d(w^k,y^k)\ne 0.\) If \(u \in SOL(C,f )\), then, under Conditions 3.1, 3.2 and 3.3, we have the following:

  1. (i)
    $$\begin{aligned} \Vert x^{k+1}-u\Vert ^2\le \,\Vert w^k-u\Vert ^2-\frac{2-\gamma }{\gamma }\Vert x^{k+1}-w^k\Vert ^2; \end{aligned}$$
    (12)
  2. (ii)
    $$\begin{aligned} \Vert w^k-y^{k}\Vert ^2\le \frac{1+\tau ^2L^2}{[(1-\tau L)\gamma ]^2}\Vert x^{k+1}-w^k\Vert ^2. \end{aligned}$$
    (13)

Proof

(i) From the Cauchy-Schwarz inequality and Condition 3.3, it follows

$$\begin{aligned} \begin{aligned} \varphi (w^k,y^k)&=\langle w^k-y^k,d(w^k,y^k)\rangle \\&=\langle w^k-y^k,(w^k-y^k)-\tau (f(w^k)-f(y^k))\rangle \\&=\Vert w^k-y^k\Vert ^2-\tau \langle w^k-y^k, f(w^k)-f(y^k)\rangle \\&\ge \Vert w^k-y^k\Vert ^2-\tau \Vert w^k-y^k\Vert \Vert f(w^k)-f(y^k)\Vert \\&\ge (1-\tau L)\Vert w^k-y^k\Vert ^2. \end{aligned} \end{aligned}$$
(14)

Using Condition 3.2, we have

$$\begin{aligned} \begin{aligned} \Vert d(w^k,y^k)\Vert ^2&=\Vert (w^k-y^k)-\tau (f(w^k)-f(y^k))\Vert ^2\\&=\Vert w^k-y^k\Vert ^2+\tau ^2\Vert f(w^k)-f(y^k)\Vert ^2-2\tau \langle w^k-y^k,f(w^k)-f(y^k)\rangle \\&\le \Vert w^k-y^k\Vert ^2+\tau ^2\Vert f(w^k)-f(y^k)\Vert ^2\\&\le (1+\tau ^2L^2)\Vert w^k-y^k\Vert ^2. \end{aligned} \end{aligned}$$
(15)

Combining (14) and (15), we obtain

$$\begin{aligned} \beta _k=\frac{\varphi (w^k,y^k)}{\Vert d(w^k,y^k)\Vert ^2}\ge \frac{1-\tau L}{1+\tau ^2L^2}. \end{aligned}$$
(16)

\(\square \)

By the definition of \(x^{k+1}\), we have

$$\begin{aligned} \begin{aligned} \Vert x^{k+1}-u\Vert ^2&=\Vert (w^{k}-u)-\gamma \beta _k d(w^k, y^k)\Vert ^2\\&=\Vert w^{k}-u\Vert ^2-2\gamma \beta _k\langle w^{k}-u,d(w^k, y^k)\rangle +\gamma ^2\beta _k^2\Vert d(w^k, y^k)\Vert ^2. \end{aligned} \end{aligned}$$
(17)

It follows that

$$\begin{aligned} \langle w^{k}-u,d(w^k, y^k)\rangle = \langle w^{k}-y^k,d(w^k, y^k)\rangle +\langle y^{k}-u,d(w^k, y^k)\rangle . \end{aligned}$$
(18)

By the definition of \(y^k\) and Lemma 2.2, we have

$$\begin{aligned} \langle y^{k}-u,w^k-y^k-\tau f(w^k)\rangle \ge 0. \end{aligned}$$
(19)

From Condition 3.2, it follows that

$$\begin{aligned} \langle y^{k}-u,\tau f(y^k)-\tau f(u)\rangle \ge 0. \end{aligned}$$
(20)

Since \(u \in SOL(C,f )\) and \(y^k\in C,\) it follows from (1) that

$$\begin{aligned} \langle y^{k}-u,\tau f(u)\rangle \ge 0. \end{aligned}$$
(21)

Adding up (19)–(21), we have

$$\begin{aligned} \langle y^{k}-u,d(w^k, y^k)\rangle = \langle y^{k}-u,w^k-y^k-\tau (f(w^k)-f(y^k))\rangle \ge 0. \end{aligned}$$
(22)

Combining (18) and (22), we obtain

$$\begin{aligned} \langle w^{k}-u,d(w^k, y^k)\rangle \ge \langle w^{k}-y^k,d(w^k, y^k)\rangle =\varphi (w^k,y^k). \end{aligned}$$
(23)

Substituting (23) into (17) and using \(\beta _k=\frac{\varphi (w^k,y^k)}{\Vert d(w^k,y^k)\Vert ^2}\), we have

$$\begin{aligned} \begin{aligned} \Vert x^{k+1}-u\Vert ^2&\le \Vert w^{k}-u\Vert ^2-2\gamma \beta _k\varphi (w^k,y^k)+\gamma ^2\beta _k^2\Vert d(w^k, y^k)\Vert ^2\\&=\Vert w^{k}-u\Vert ^2-\gamma (2-\gamma )\beta _k\varphi (w^k,y^k). \end{aligned} \end{aligned}$$
(24)

Again, using the definition of \(x^{k+1}\), we have

$$\begin{aligned} \beta _k\varphi (w^k,y^k)=\Vert \beta _kd(w^k,y^k)\Vert ^2=\frac{1}{\gamma ^2}\Vert x^{k+1}-w^k\Vert ^2. \end{aligned}$$
(25)

Combining (24) and (25), we obtain (12).

(ii) From (25) and (16), it follows that

$$\begin{aligned} \varphi (w^k,y^k)=\frac{1}{\beta _k\gamma ^2}\Vert x^{k+1}-w^k\Vert ^2\le \frac{1+\tau ^2L^2}{(1-\tau L)\gamma ^2}\Vert x^{k+1}-w^k\Vert ^2, \end{aligned}$$

which with (14) yields

$$\begin{aligned} \Vert w^k-y^k\Vert ^2\le \frac{1}{1-\tau L}\varphi (w^k,y^k)\le \frac{1+\tau ^2L^2}{[(1-\tau L)\gamma ]^2}\Vert x^{k+1}-w^k\Vert ^2. \end{aligned}$$

This completes the proof. \(\square \)

Theorem 3.1

Assume that Conditions 3.1, 3.2 and 3.3 hold and let \(0<\tau < \frac{1}{L}.\) Then the sequence \(\{x^k\}\) generated by (9) converges weakly to a solution of the variational inequality (1).

Proof

Fix \(u \in SOL(C,f )\). Applying (8), we have

$$\begin{aligned} \begin{aligned} \Vert w^k-u\Vert ^2&=\Vert (1+\alpha _k)(x^k-u)-\alpha _n(x^{k-1}-u)\Vert ^2\\&=(1+\alpha _k)\Vert x^k-u\Vert ^2-\alpha _k\Vert x^{k-1}-u\Vert ^2+\alpha _k(1+\alpha _k)\Vert x^k-x^{k-1}\Vert ^2. \end{aligned} \end{aligned}$$
(26)

Hence, from (12), it follows that

$$\begin{aligned} \begin{aligned} \Vert x^{k+1}-u\Vert ^2&-(1+\alpha _k)\Vert x^k-u\Vert ^2+\alpha _k\Vert x^{k-1}-u\Vert ^2\\&\le \,-\frac{2-\gamma }{\gamma }\Vert x^{k+1}-w^k\Vert ^2+\alpha _k(1+\alpha _k)\Vert x^k-x^{k-1}\Vert ^2. \end{aligned} \end{aligned}$$
(27)

We also obtain

$$\begin{aligned} \begin{aligned} \Vert x^{k+1}-w^k\Vert ^2&=\Vert (x^{k+1}-x^k)-\alpha _k(x^k-x^{k-1})\Vert ^2\\&=\Vert x^{k+1}-x^k\Vert ^2+\alpha _k^2\Vert x^k-x^{k-1}\Vert ^2-2\alpha _k\langle x^{k+1}-x^k, x^k-x^{k-1}\rangle \\&\ge \Vert x^{k+1}-x^k\Vert ^2+\alpha _k^2\Vert x^k-x^{k-1}\Vert ^2\\&\quad +\alpha _k\Big (-\rho _k\Vert x^{k+1}-x^k\Vert ^2-\frac{1}{\rho _k}\Vert x^k-x^{k-1}\Vert ^2\Big ),\\ \end{aligned} \end{aligned}$$
(28)

where \(\rho _k:=\frac{2}{2\alpha _k+\delta \gamma }.\) Combining (27) and (28), we have

$$\begin{aligned} \begin{aligned} \Vert x^{k+1}-u\Vert ^2&-(1+\alpha _k)\Vert x^k-u\Vert ^2+\alpha _k\Vert x^{k-1}-u\Vert ^2\\&\le \frac{(2-\gamma )(\alpha _k\rho _k-1)}{\gamma }\Vert x^{k+1}-x^k\Vert ^2+\lambda _k\Vert x^k-x^{k-1}\Vert ^2, \end{aligned} \end{aligned}$$
(29)

where

$$\begin{aligned} \lambda _k:=\alpha _k(1+\alpha _k)+\alpha _k\frac{(2-\gamma )(1-\alpha _k\rho _k)}{\rho _k\gamma }\ge 0 \end{aligned}$$
(30)

since \(\alpha _k\rho _k<1\) and \(\gamma \in (0,2).\) Again, taking into account the choice of \(\rho _k\), we have

$$\begin{aligned} \delta =\frac{2(1-\alpha _k\rho _k)}{\rho _k\gamma } \end{aligned}$$

and, from (30), it follows that

$$\begin{aligned} \lambda _k=\alpha _k(1+\alpha _k)+\alpha _k(1-\frac{\gamma }{2})\delta \le \alpha (1+\alpha )+\alpha \delta . \end{aligned}$$
(31)

This completes the proof. \(\square \)

In the following, we apply some techniques from [12, 25] adapted to our problems. Define the sequences \(\{\varphi _k\}\) and \(\{\xi _k\}\) by

$$\begin{aligned} \varphi _k:=\Vert x^k-u\Vert ^2,\quad \xi _k:=\varphi _k-\alpha _k\varphi _{k-1}+\lambda _k\Vert x^k-x^{k-1}\Vert ^2 \end{aligned}$$

for all \(k\ge 1\), respectively. Using the monotonicity of \(\{\alpha _k\}\) and the fact that \(\varphi _k \ge 0\) for all \(k \in {\mathbb {N}},\) we have

$$\begin{aligned} \xi _{k+1}-\xi _k\le \varphi _{k+1}-(1+\alpha _k)\varphi _{k}+\alpha _k\varphi _{k-1}+\lambda _{k+1}\Vert x^{k+1}-x^{k}\Vert ^2 -\lambda _k\Vert x^k-x^{k-1}\Vert ^2. \end{aligned}$$

Employing (29), we have

$$\begin{aligned} \xi _{k+1}-\xi _k\le \left( \frac{(2-\gamma )(\alpha _k\rho _k-1)}{\gamma }+\lambda _{k+1}\right) \Vert x^{k+1}-x^k\Vert ^2. \end{aligned}$$
(32)

Now, we claim that

$$\begin{aligned} \frac{(2-\gamma )(\alpha _k\rho _k-1)}{\gamma }+\lambda _{k+1}\le -\sigma . \end{aligned}$$
(33)

Indeed, by the choice of \(\rho _k\), we have

$$\begin{aligned} \begin{aligned}&\frac{(2-\gamma )(\alpha _k\rho _k-1)}{\gamma }+\lambda _{k+1}\le -\sigma \\&\quad \Longleftrightarrow \,\, \gamma (\lambda _{k+1}+\sigma )+(2-\gamma )(\alpha _k\rho _k-1)\le 0\\&\quad \Longleftrightarrow \,\, \gamma (\lambda _{k+1}+\sigma )-\frac{\delta \gamma (2-\gamma )}{2\alpha _k+\delta \gamma }\le 0\\&\quad \Longleftrightarrow \,\, (2\alpha _k+\delta \gamma )(\lambda _{k+1}+\sigma )+{\delta \gamma }\le 2\delta .\\ \end{aligned} \end{aligned}$$

By using (30), we have

$$\begin{aligned} (2\alpha _k+\delta \gamma )(\lambda _{k+1}+\sigma )+{\delta \gamma }\le (2\alpha +\delta \gamma )(\alpha (1+\alpha )+\alpha \delta +\sigma )+{\delta \gamma }\le 2\delta , \end{aligned}$$

where the last inequality follows by using the upper bound for \(\gamma \) in (11). Hence the claim in (33) is true.

Thus it follows from (32) and (33) that

$$\begin{aligned} \xi _{k+1}-\xi _k\le -\sigma \Vert x^{k+1}-x^k\Vert ^2. \end{aligned}$$
(34)

The sequence \(\{\mu _k\}\) is nonincreasing and the bound for \(\{\alpha _k\}\) delivers

$$\begin{aligned} -\alpha \varphi _{k-1}\le \varphi _k-\alpha \varphi _{k-1}\le \xi _k\le \xi _1. \end{aligned}$$
(35)

It follows that

$$\begin{aligned} \varphi _k\le \alpha ^k\varphi _0+\xi _1\sum _{n=0}^{k-1}\alpha ^n\le \alpha ^k\varphi _0+\frac{\xi _1}{1-\alpha }, \end{aligned}$$

where we notice that \(\xi _1=\varphi _1\ge 0\) (due to the relation \(\alpha _1=0\)). Combining (34) and (35), we have

$$\begin{aligned} \begin{aligned} \sigma \sum _{n=1}^k\Vert x^{n+1}-x^n\Vert ^2&\le \xi _1-\xi _{k+1}\le \xi _1+\alpha \varphi _k\\&\le \alpha ^{k+1}\varphi _0+\frac{\xi _1}{1-\alpha } \le \varphi _0+\frac{\xi _1}{1-\alpha }, \end{aligned} \end{aligned}$$

which shows that

$$\begin{aligned} \sum _{k\in {\mathbb {N}}}\Vert x^{k+1}-x^k\Vert ^2<+\infty . \end{aligned}$$
(36)

Thus we have \(\lim _{k\rightarrow \infty }\Vert x^{k+1}-x^k\Vert =0.\) By (9), we have

$$\begin{aligned} \Vert x^{k+1}-w^k\Vert \le \Vert x^{k+1}-x^k\Vert +\alpha _k\Vert x^k-x^{k-1}\Vert \le \Vert x^{k+1}-x^k\Vert +\alpha \Vert x^k-x^{k-1}\Vert . \end{aligned}$$
(37)

So, we have \(\lim _{k\rightarrow \infty }\Vert x^{k+1}-w^k\Vert =0.\) From (13), it follows that

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert y^{k}-w^k\Vert =0. \end{aligned}$$

Next, we prove this by using the result of Opial given in Lemma 2.4. For arbitrary \(u\in SOL(C,f),\) by (29), (31), (36) and Lemma 2.3, we derive that \(\lim _{k\rightarrow \infty }\Vert x^{k}-u\Vert \) exists (we take into consideration also that, in (29), \(\alpha _k\rho _k<1\)). Hence \(\{x^k\}\) is bounded.

Now, we only need to show \(\omega _w(x^k)\subseteq SOL(C,f).\) Due to the boundedness of \(\{x^k\}\), it has at least one weak accumulation point. Let \({\hat{x}}\in \omega _w(x^k)\). Then there exists a subsequence \(\{x^{k_i}\}\) of \(\{x^k\}\) which converges weakly to \({\hat{x}}\). Also, it follows that \(\{w^{k_i}\}\) and \(\{y^{k_i}\}\) converge weakly to \({\hat{x}}.\)

Finally, we show that \({\hat{x}}\) is a solution of the variational inequality (1). Let

$$\begin{aligned} Av= \left\{ \begin{aligned}&f(v)+N_C(v),&v\in C,\\&\emptyset ,&v\notin C, \end{aligned} \right. \end{aligned}$$
(38)

where \(N_C(v)\) is the normal cone of C at \(v\in C\), i.e.,

$$\begin{aligned} N_C(v):=\{d\in H\,|\,\langle d,y-v\rangle \le 0,\forall y \in C\}. \end{aligned}$$

It is known that A is a maximal monotone operator and \(A^{-1}(0) = SOL(C,f)\). If \((v,w) \in G(A)\), then we have \(w-f(v) \in N_C(v)\) since \(w\in A(v) = f(v) + N_C(v)\). Thus it follows that

$$\begin{aligned} \langle w-f(v),v-y\rangle \ge 0 \end{aligned}$$

for all \(y\in C\). Since \(y^{k_i}\in C\), we have

$$\begin{aligned} \langle w-f(v),v-y^{k_i}\rangle \ge 0. \end{aligned}$$

On the other hand, by the definition of \(y^k\) and Lemma 2.2, it follows that

$$\begin{aligned} \langle w^k-\tau f(w^k)-y^k, y^{k}-v\rangle \ge 0 \end{aligned}$$

and, consequently,

$$\begin{aligned} \left\langle \frac{y^k-w^k}{\tau }+f(w^k),v-y^k\right\rangle \ge 0. \end{aligned}$$

Hence we have

$$\begin{aligned} \begin{aligned} \langle w,v-y^{k_i}\rangle&\ge \langle f(v),v-y^{k_i}\rangle \\&\ge \langle f(v),v-y^{k_i}\rangle -\Big \langle \frac{y^{k_i}-w^{k_i}}{\tau }+ f(w^{k_i}),v-y^{k_i}\Big \rangle \\&=\langle f(v)-f(y^{k_i}),v-y^{k_i}\rangle +\langle f(y^{k_i})-f(w^{k_i}),v-y^{k_i}\rangle \\&\quad \, -\Big \langle \frac{y^{k_i}-w^{k_i}}{\tau },v-y^{k_i}\Big \rangle \\&\ge \langle f(y^{k_i})-f(w^{k_i}),v-y^{k_i}\rangle -\Big \langle \frac{y^{k_i}-w^{k_i}}{\tau },v-y^{k_i}\Big \rangle ,\\ \end{aligned} \end{aligned}$$

which implies

$$\begin{aligned} \langle w,v-y^{k_i}\rangle \ge \langle f(y^{k_i})-f(w^{k_i}),v-y^{k_i}\rangle -\Big \langle \frac{y^{k_i}-w^{k_i}}{\tau },v-y^{k_i}\Big \rangle . \end{aligned}$$

Taking the limit as \(i\rightarrow \infty \) in the above inequality, we obtain

$$\begin{aligned} \langle w,v-{\hat{x}}\rangle \ge 0. \end{aligned}$$

Since A is a maximal monotone operator, it follows that \({\hat{x}}\in A^{-1}(0) = SOL(C,f)\). This completes the proof.\(\square \)

Remark 3.2

(1) \(\gamma \in (0,2)\) is a relaxation factor of Algorithm 3.1 and the projection and contraction algorithm (5). Cai et. al. [10] explained why taking a suitable relaxation factor \(\gamma \in [1, 2)\) can achieve the faster convergence in the proof of main results of the projection and contraction algorithm (5). However, we do not obtain a suitable relaxation factor \(\gamma \) in the proof of Algorithm 3.1.

(2) Moudafi [26] proposed an open problem on investigating, theoretically as well as numerically, which are the best choices for the inertial parameter \(\alpha _k\) in order to accelerate the convergence. Since the open problem was proposed, there has been little progress, except for some special problems. Beck and Teboulle [27] introduced the well-known FISTA to solve the linear inverse problems, which is an inertial version of the ISTA. They proved that the FISTA has global rate \(O(1/k^2)\) of convergence, while the global rate of convergence of the ISTA is O(1 / k). The inertial parameter \(\alpha _k\) in the FISTA is chosen as follows:

$$\begin{aligned} \alpha _{k}=\frac{t_{k}-1}{t_{k+1}}, \end{aligned}$$

where \(t_1=1\), and

$$\begin{aligned} t_{k+1}=\frac{1+\sqrt{1+4t_{k}^2}}{2},\quad \forall k\ge 1. \end{aligned}$$

Chambolle and Dossal [28] took \(t_k\) as follows:

$$\begin{aligned} t_k=\frac{k+a-1}{a}, \quad \forall k\ge 1, \end{aligned}$$
(39)

where \(a>2\) and showed that the FISTA has better property, i.e., the convergence of the iterative sequence when \(t_k\) is taken as in (39).

4 The modified projection and contraction algorithm and its convergence analysis

Let \(S:H\rightarrow H\) be a nonexpansive mapping and denote by Fix(S) its fixed point set, i.e.,

$$\begin{aligned} Fix(S)=\{x\in H\,:\, S(x)=x\}. \end{aligned}$$

Next, we present a modified projection and contraction algorithm to find a common element of the set of solutions of the variational inequality and the set of fixed points of the nonexpansive mapping S as follows:

Algorithm 4.1

Choose initial guesses \(x_0,x_1\in H\) arbitrarily. Calculate the \((k+1)th\) iterate \(x^{k+1}\) via the formula:

$$\begin{aligned} \left\{ \begin{aligned}&w^k=x^k+\alpha _k(x^k-x^{k-1}),\\&y^k=P_C(w^k-\tau f(w^k)),\\&d(w^k,y^k)=(w^k-y^k)-\tau (f(w^k)-f(y^k)),\\&x^{k+1}=(1-\mu _k)w^k+\mu _kS(w^k-\gamma \beta _k d(w^k,y^k)) \end{aligned} \right. \end{aligned}$$
(40)

for each \(n\ge 1\), where \(\gamma \in (0,2),\) \(\tau >0\) and

$$\begin{aligned} \beta _k:= \left\{ \begin{array}{ll} {\varphi (w^k,y^k)}/{\Vert d(w^k,y^k)\Vert ^2},&{}\quad \hbox {if}\,\,d(w^k,y^k)\ne 0 \\ 0&{}\quad \hbox {if}\,\,d(w^k,y^k)=0, \\ \end{array} \right. \end{aligned}$$
(41)

where

$$\begin{aligned} \varphi (w^k,y^k):=\langle w^k-y^k,d(w^k,y^k)\rangle , \end{aligned}$$

and \(\{\alpha _k\}\) is nondecreasing with \(\alpha _1=0,\) \(0\le \alpha _k\le \alpha <1,\) and \(\sigma ,\delta >0\) are such that

$$\begin{aligned} \delta >\frac{\alpha ^2(1+\alpha )+\alpha \sigma }{1-\alpha ^2},\quad 0<\underline{\mu }\le \mu _k\le \frac{\left[ \delta -\alpha ((1+\alpha )+\alpha \delta +\sigma )\right] }{\delta [1+\alpha (1+\alpha )+\alpha \delta +\sigma ]}=\bar{\mu }. \end{aligned}$$

Now, we assume the following condition:

Condition 4.1

\(Fix(S)\cap SOL(C,f)\ne \emptyset \).

Set \(t^k:=w^k-\gamma \beta _k d(w^k,y^k)\) for each \(k\ge 1\). Then we have

$$\begin{aligned} x^{k+1}=(1-\mu _k)w^k+\mu _kS(t^k). \end{aligned}$$
(42)

Remark 4.1

From Lemma 3.1, if \(d(w^k,y^k)=0\) in (40), then \(y^k=w^k.\) Using the definition of \(t^k\) and (41), we have \(w^k=t^k\) when \(d(w^k,y^k)=0\).

Following along the lines of Lemma 3.2, we get the following Lemma:

Lemma 4.1

Let \(\{x^k\}\) be the sequence generated by (40) and let \(0<\tau < 1/L.\) Assume \(d(w^k,y^k)\ne 0.\) If \(u \in SOL(C,f )\), then, under Conditions 3.2, 3.3 and 4.1, we have the following:

  1. (i)

     

    $$\begin{aligned} \Vert t^{k}-u\Vert ^2\le \Vert w^k-u\Vert ^2-\frac{2-\gamma }{\gamma }\Vert w^k-t^k\Vert ^2; \end{aligned}$$
    (43)
  2. (ii)

     

    $$\begin{aligned} \Vert w^k-y^{k}\Vert ^2\le \frac{1+\tau ^2L^2}{[(1-\tau L)\gamma ]^2}\Vert w^k-t^k\Vert ^2. \end{aligned}$$
    (44)

Remark 4.2

From Remark 4.1, (43) and (44) in Lemma 4.1 still holds when \(d(w^k,y^k)=0.\)

Theorem 4.1

Assume that Conditions 3.2, 3.3 and 4.1 hold. Let \(0<\tau < \frac{1}{L}\) and \(\{\alpha _k\}\subset [c,d]\) for some \(c,d\in (0,1).\) Then the sequence \(\{x^k\}\) generated by (40) converges weakly to the same solution \(u^* \in Fix(S)\cap SOL(C,f )\).

Proof

By (28), we have

$$\begin{aligned} \begin{aligned} \Vert x^{k+1}-w^k\Vert ^2&\ge \Vert x^{k+1}-x^k\Vert ^2+\alpha _k^2\Vert x^k-x^{k-1}\Vert ^2\\&\quad +\alpha _k\Big (-\rho _k\Vert x^{k+1}-x^k\Vert ^2-\frac{1}{\rho _k}\Vert x^k-x^{k-1}\Vert ^2\Big ), \end{aligned} \end{aligned}$$
(45)

where we denote \(\rho _k=\frac{1}{\alpha _k+\delta \mu _k}.\) Let \(u\in Fix(S)\cap SOL(C,f ).\) From (26), it follows that

$$\begin{aligned} \Vert w^k-u\Vert ^2\le (1+\alpha _k)\Vert x^k-u\Vert ^2-\alpha _k\Vert x^{k-1}-u\Vert ^2+\alpha _k(1+\alpha _k)\Vert x^k-x^{k-1}\Vert ^2. \end{aligned}$$
(46)

Using (8), (42), Lemma 4.1(i) and Remark 4.2, we have

$$\begin{aligned} \begin{aligned} \Vert x^{k+1}-u\Vert ^2&=\Vert (1-\mu _k)(w^k-u)+\mu _k(S(t^k)-u)\Vert ^2\\&=(1-\mu _k)\Vert w^k-u\Vert ^2+\mu _k\Vert S(t^k)-u\Vert ^2-\mu _k(1-\mu _k)\Vert w^k- S(t^k)\Vert ^2\\&\le (1-\mu _k)\Vert w^k-u\Vert ^2+\mu _k\Vert t^k-u\Vert ^2-\frac{(1-\mu _k)}{\mu _k}\Vert x^{k+1}- w^k\Vert ^2\\&\le \Vert w^k-u\Vert ^2-(1-\mu _k)\frac{2-\gamma }{\gamma }\Vert w^k-t^{k}\Vert ^2-\frac{(1-\mu _k)}{\mu _k}\Vert x^{k+1}- w^k\Vert ^2\\&\le \Vert w^k-u\Vert ^2-\frac{(1-\mu _k)}{\mu _k}\Vert x^{k+1}- w^k\Vert ^2.\\ \end{aligned} \end{aligned}$$
(47)

Combining (45), (46) and (47), we obtain

$$\begin{aligned} \begin{aligned} \Vert x^{k+1}-u\Vert ^2&-(1+\alpha _k)\Vert x^k-u\Vert ^2+\alpha _k\Vert x^{k-1}-u\Vert ^2\\&\le \frac{(1-\mu _k)(\alpha _k\rho _k-1)}{1-\mu _k}\Vert x^{k+1}-x^k\Vert ^2+\lambda _k\Vert x^k-x^{k-1}\Vert ^2, \end{aligned} \end{aligned}$$
(48)

where

$$\begin{aligned} \lambda _k:=\alpha _k(1+\alpha _k)+\alpha _k\frac{(1-\mu _k)(1-\alpha _k\rho _k)}{\mu _k\rho _k}\ge 0 \end{aligned}$$
(49)

since \(\alpha _k\rho _k<1\) and \(\mu _k\in (0,1).\) Again, taking into account the choice of \(\rho _k\), we have

$$\begin{aligned} \delta =\frac{(1-\alpha _k\rho _k)}{\rho _k\mu _k} \end{aligned}$$

and, from (49), it follows that

$$\begin{aligned} \lambda _k=\alpha _k(1+\alpha _k)+\alpha _k(1-\mu _k)\delta \le \alpha (1+\alpha )+\alpha \delta . \end{aligned}$$
(50)

Following along the lines of Theorem 3.1, we obtain

$$\begin{aligned} \sum _{k=1}^{\infty }\Vert x^{k+1}-x^k\Vert ^2<+\infty . \end{aligned}$$

Thus we have \(\lim _{k\rightarrow \infty }\Vert x^{k+1}-x^k\Vert =0.\) From (48), (50), \(\alpha _k\rho _k<1\) and Lemma 2.3, we can show that \(\lim _{k\rightarrow \infty }\Vert x^{k}-u\Vert \) exists for arbitrary \(u\in Fix(S)\cap SOL(C,f).\) Hence \(\{x^k\}\) is bounded. By (37), we have \(\sum _{k=1}^{\infty }\Vert x^{k+1}-w^k\Vert ^2<+\infty \) and so

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert x^{k+1}-w^k\Vert =0. \end{aligned}$$
(51)

By (47), we have \(\sum _{k=1}^{\infty }\Vert t^k-w^k\Vert ^2<+\infty \) and so

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert t^k-w^k\Vert =0. \end{aligned}$$
(52)

Using (44), we have

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert w^k-y^k\Vert =0. \end{aligned}$$

Since \(\{x^k\}\) is bounded, it has a subsequence \(\{x^{k_i}\}\) which converges weakly to a point \({\hat{x}}\). By (51)–(52), the subsequences \(\{w^{k_i}\}\) and \(\{t^{k_i}\}\) also converge weakly to \({\hat{x}}\).

Now, we show that \({\hat{x}} \in Fix(S) \cap SOL(C, f)\). Define the operator A as in (38). By using arguments similar to those used in the proof of Theorem 3.1, we can show that

$$\begin{aligned} {\hat{x}}\in A^{-1}(0) = \mathrm{SOL}(C,f). \end{aligned}$$

It is now left to show that \({\hat{x}} \in Fix(S)\). To this end, it follows from (42) that

$$\begin{aligned} \Vert w^k- S(t^k)\Vert =\frac{1}{\mu _k}\Vert x^{k+1}-w^k\Vert \le \frac{1}{\underline{\mu }}\Vert x^{k+1}-w^k\Vert , \end{aligned}$$

which with (51) implies that

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert w^k-S(t^k)\Vert =0. \end{aligned}$$

Using (52), we obtain

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert t^k-S(t^k)\Vert =0. \end{aligned}$$

By Lemma 2.1, we obtain \({\hat{x}}\in Fix(S).\) Now, again, by using similar arguments to those used in the proof of Theorem 3.1, we can show that the sequence \(\{x^k\}\) converge weakly to \({\hat{x}}\in Fix(S)\cap SOL(C, f)\). This completes the proof.\(\square \)

Remark 4.3

Note that we need to restrict \(\gamma \) in the the algorithm (9) for the variational inequality, however, we only need to make restriction on \(\{\mu _k\}\) in the algorithm (40).

5 Numerical experiments

In order to evaluate the performance of the proposed algorithm, we present numerical experiments relative to the variational inequality. In this section, we provide an example to compare the inertial projection and contraction algorithm with the projection and contraction algorithm, the inertial extragradient algorithm and the extragradient algorithm.

Example 5.1

Let \(f:{\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2\) be defined by

$$\begin{aligned} f(x,y)=(2x+2y+\sin (x),-2x+2y+\sin (y)),\quad \forall x,y \in {\mathbb {R}}. \end{aligned}$$

Claim that f is Lipschitz continuous and strongly monotone. Therefore the variational inequality (1) has a unique solution and (0, 0) is its solution.

Firstly, we show that f is Lipschitz continuous. Take arbitrarily \(z_1=(x_1,y_1)\in {\mathbb {R}}^2,\) \(z_2=(x_2,y_2)\in {\mathbb {R}}^2\). Then

$$\begin{aligned} \begin{aligned} |(2x_1+2y_1+\sin (x_1))&-(2x_2+2y_2+\sin (x_2))|\\&\le 2|x_1-x_2|+2|y_1-y_2|+|\sin (x_1)-\sin (x_2)|\\&\le 3|x_1-x_2|+2|y_1-y_2|, \end{aligned} \end{aligned}$$
(53)

where the last inequality comes from

$$\begin{aligned} |\sin (x)-\sin (y)|\le |x-y|, \end{aligned}$$
(54)

for any \(x,y\in {\mathbb {R}}.\) Similarly, we have

$$\begin{aligned} |(-2x_1+2y_1+\sin (y_1))-(-2x_2+2y_2+\sin (y_2))|\le 2|x_1-x_2|+3|y_1-y_2|. \end{aligned}$$
(55)

Combining (53) and (55), we obtain that

$$\begin{aligned} \begin{aligned} \Vert f(z_1)-f(z_2)\Vert ^2&=\left[ (2x_1+2y_1+\sin (x_1))-(2x_2+2y_2+\sin (x_2))\right] ^2\\&\quad +\left[ (-2x_1+2y_1+\sin (y_1))-(-2x_2+2y_2+\sin (y_2))\right] ^2\\&\le 26[(x_1-x_2)^2+(y_1-y_2)^2]=26\Vert z_1-z_2\Vert ^2, \end{aligned} \end{aligned}$$
(56)

where the inequality comes from the relation \((a+b)^2\le 2(a^2+b^2)\) for any \(a,b\in {\mathbb {R}}\). From (56), we get that f is Lipschitz continuous with \(L=\sqrt{26}\).

Next we verify that f is strongly monotone. It is easy to get

$$\begin{aligned} \begin{aligned} \langle f(z_1)-f(z_2),z_1-z_2\rangle&=\left[ (2x_1+2y_1+\sin (x_1))-(2x_2+2y_2+\sin (x_2))\right] (x_1-x_2)\\&\quad + [(-2x_1+2y_1+\sin (y_1))-(-2x_2+2y_2+\sin (y_2))](y_1{-}y_2)\\&=2(x_1-x_2)^2+(\sin (x_1)-\sin (x_2))(x_1-x_2)\\&\quad +2(y_1-y_2)^2+(\sin (y_1)-\sin (y_2))(y_1-y_2)\\&\ge \Vert z_1-z_2\Vert ^2, \end{aligned} \end{aligned}$$

where the inequality follows from (54). Hence, f is \(1-\)strongly monotone.

Let \(C=\{x\in {\mathbb {R}}^2\,|\,e_0\le x\le 10e_1\}\), where \(e_0=(-10,-10)\) and \(e_1=(10,10)\). Take the initial point \(x_0=(1,10)\in {\mathbb {R}}^2\) and \(\tau =1/(2L)\). Since (0, 0) is the unique solution of the variational inequality (1), denote by \(\Vert x^k\Vert \le 10^{-8}\) the stopping criterion.

Fig. 1
figure 1

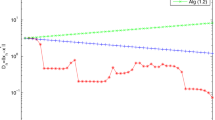
Comparison of the number of iterations of the inertial projection and contraction algorithm (iPCA) with the projection and contraction algorithm (PCA), the inertial extragradient algorithm (iEgA) and the extragradient algorithm (EgA) for Example 5.1

Full size image
Fig. 2
figure 2

Comparison of the number of iterations of the inertial projection and contraction algorithm (iPCA) with the projection and contraction algorithm (PCA), the inertial extragradient algorithm (iEgA) and the extragradient algorithm (EgA) for Example 5.2

Full size image

Example 5.2

Let \(f: {\mathbb {R}}^n \rightarrow {\mathbb {R}}^n\) defined by \(f(x)=Ax+b\), where \(A=Z^TZ\), \(Z=(z_{ij})_{n\times n}\) and \(b=(b_i)\in {\mathbb {R}}^n\) where \(z_{ij}\in [1,100]\) and \(b_i\in [-100,0]\) are generated randomly.

It is easy to verify that f is \(L-\)Lipschitz continuous and \(\eta -\)strongly monotone with \(L=\max (eig(A))\) and \(\eta =\min (eig(A))\). Take arbitrarily \(x_1,x_2\in {\mathbb {R}}^n.\) Firstly, we have

$$\begin{aligned} \Vert f(x_1)-f(x_2)\Vert =\Vert Ax_1-Ax_2\Vert \le \max (eig(A))\Vert x_1-x_2\Vert . \end{aligned}$$

On the other hand,

$$\begin{aligned} \begin{aligned} \langle f(x_1)-f(x_2),x_1-x_2\rangle&=\langle Ax_1-Ax_2,x_1-x_2\rangle =\langle A(x_1-x_2),x_1-x_2\rangle \\&= (x_1-x_2)^TA(x_1-x_2)\ge \min (eig(A))\Vert x_1-x_2\Vert ^2.\\ \end{aligned} \end{aligned}$$

where the third equality comes from the symmetry of the matrix A and the inequality follows from the symmetry and the positive definiteness of the matrix A. Note that the matrix Z is randomly generated, so it is full rank. Therefore, the matrix A is positive definite.

Let \(C:=\{x\in {\mathbb {R}}^n\,|\, \Vert x-d\Vert \le r\}\), where the center \(d\in {\mathbb {R}}^n\) and radius r are randomly chosen. Take the initial point \(x_0=(c_i)\in {\mathbb {R}}^n\), where \(c_i\in [0,1]\) is generated randomly. Set \(n=100\) and \(\tau =1/(1.05L)\). Although the variational inequality (1) has an unique solution, it is difficult to get the exact solution. So, denote by \(D_k =\Vert x^{k+1}-x^k\Vert \le 10^{-5}\) the stopping criterion.

Take \(\gamma =1.5\) in the inertial projection and contraction algorithm, and the projection and contraction algorithm. Take \(\alpha _k=0.4\) in the inertial projection and contraction algorithm and the inertial extragradient algorithm. Choose \(\lambda _k=0.6\) in the inertial extragradient algorithm.

The Figs. 1 and 2 illustrate that the inertial projection and contraction algorithm is more efficient in comparison with existing algorithms such as the the projection and contraction algorithm, the inertial extragradient algorithm and the extragradient algorithm.

6 Conclusions

In this paper, we introduce a new inertial projection and contraction algorithm by incorporating the inertial terms in the projection and contraction algorithm, which does not need the summability condition for the sequence. The convergence result is presented under some assumptions and several numerical results confirm the effectiveness of proposed algorithm.