A Special Family of Stacked Central Configurations: Lagrange Plus Euler in One

Abstract

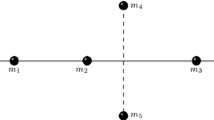
We show the existence of a family of stacked central configurations in the planar five-body problem with a special property. Three bodies $m_1$, $m_2$ and $m_3$, ordered from left to right, are collinear and form an Euler central configuration, and the other two bodies $m_4$ and $m_5$, together with $m_2$ are at the vertices of an equilateral triangle and form a Lagrange central configuration.

1 Introduction and Main Result

Central configurations play an interesting role in celestial mechanics [18]. For instance, they allow to obtain explicit solutions of the n-body problem where the initial shape of the configuration is preserved along the orbit up to rescaling and rotations.

Recently, there has been a growing interest in stacked central configuration, that is, central configurations such that a proper subset of the n bodies also form a central configuration. This concept was first introduced by Hampton in a seminal paper [9] by providing a family of central configurations in the planar five-body problem where if two masses are removed, the remaining three are at the vertices of an equilateral triangle. After that, several papers have shown the existence of other stacked central configurations in the planar five-body problem, see [3, 5, 7, 11, 12]. Besides planar configurations, stacked central configuration have also been found in the spatial case, see [10, 14, 15, 19] or in the general n-body problem, see [6, 20, 21]. Even in limit problems, as the coorbital satellite problem, see [1, 17].

At this point, a natural question rise: Given a central configuration of the n-body problem, how many different subsets of bodies, A, do exist with cardinality $|A|=k$, $k=1,\ldots , n-3$, such that the $n-k$ bodies form a central configuration of the $(n-k)$-body problem?

Using the notation, (n, k)-stacked central configuration, introduced by Fernandes and Mello in [6], where n is the number of bodies of the original central configuration and $k=1,\ldots , n-3$ is the number of the removed bodies, previous question can be stated as following: What is the number of (n, k)-stacked central configurations, for all $k=1,\ldots , n-3$?

In the non-collinearn-body problem the answer to the case of (n, 1)-stacked central configuration was given by Fernandes and Mello [6]. They proved that there exists only one. That is, the configuration where $n-1$ bodies form a co-spherical central configuration with one body, of arbitrary mass, that can be removed located at the center of the sphere.

Central configurations consisting in two nested or twisted regular polygons are exemples of two (2n, n)-stacked planar central configurations, that is, examples where two different subsets of n bodies can be removed, see [2, 13, 16]. Although, in these stacked central configurations, we have two different subsets of n bodies two choose, the central configurations obtained once the bodies are removed are similar. Because of this we are interested in counting the number of stacked central configurations that are not similar after the k bodies are removed. So, we will count the number of (n, k)-stacked central configurations, for all $k=1,\ldots , n-3$ up to similarity.

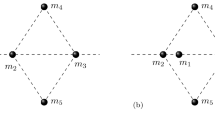
In the non-collinear planar five-body problem a configuration that, after removing two masses in three different ways, such that in each one the remaining three masses are in a collinear configuration is not geometrically realizable, unless the planar five-body configuration has four collinear masses. It that case the perpendicular bisector theorem says that such a configuration cannot be a central configuration of the five-body problem. So, it is impossible to obtain, in the non-collinear planar five-body problem, three (5, 2)-stacked central configurations where the remaining three masses form an Euler central configuration of the three-body problem. On the other hand, a planar five-body configuration that includes an equilateral triangle also can include, in three different ways, two collinear configurations after removing two masses. That is, when the two non-triangular masses are on the sides of the triangle, see Fig. 1a, when only one non-triangular mass is on one side, see Fig. 1b, and finally when the two non-triangular masses are not on any side of the triangle, see Fig. 1c. As before, the perpendicular bisector theorem says that any of these configurations cannot be a central configuration of the five-body problem. Then, in the non-collinear planar five-body problem, the number of (5, 2)-stacked central configurations up to similarity is at most two. Moreover, only the five-body central configuration given by a square, with four equal masses at its vertices, and one body located at its center, with arbitrary mass, admits a (5, 1)-stacked central configurations. The one given by the square itself, that is, a 4-gon central configuration, obtained when the central body is removed. That five-body central configuration also admits one (5, 2)-stacked central configurations, an Euler central configuration of the three-body problem, obtained when two bodies located at opposite vertices of the square are removed. In that case is impossible remove any other two masses and obtain an equilateral triangle, that is, a Lagrange central configuration of the three-body problem. Thus, we have the following result.

Fig. 1

Three different configurations in the five-body problem where after removing two bodies, one equilateral triangular configuration and two collinear configurations are obtained. All three are discarded by the perpendicular bisector theorem to be central configurations in the five-body problem

Theorem 1

In the non-collinear planar five-body problem, the number of (5, k)-stacked central configuration, for all $k=1,2$ up to similarity is at most two.

In this paper we prove the existence of a family in the planar five-body problem with two (5, 2)-stacked central configurations. In our family bodies $m_1$, $m_2$ and $m_3$, ordered from the left to the right, are collinear and form an Euler central configuration, and bodies $m_2$, $m_4$ and $m_5$ are located at the vertices of an equilateral triangle and form a Lagrange central configuration. Due to the shape obtained after removing the two different subsets of two bodies, we have called the five-body stacked central configuration Lagrange plus Euler in one. As far as we know, this is the first time that this kind of enbeded central configurations are shown in the plane. For a similar phenomena in the spatial case see [4].

Our main result is the following theorem.

Theorem 2

Consider the following configuration of the five-body problem: Three collinear masses $m_1$, $m_2$, $m_3$, ordered from left to right, and the two remaining masses, $m_4$, $m_5$ placed symmetrically with respect to the collinear configuration. Assume that $m_2$ and $m_4=m_5=1$ lie at the vertices of an equilateral triangle whose sides have length equal to one, and so, form a Lagrange central configuration of the three-body problem. Then there exist positive masses $m_1$, $m_2$, $m_3$ such that the five bodies form a central configuration of five-body problem and the three collinear masses also form an Euler central configuration of three-body problem.

2 Statement of the Problem

The planar n-body problem consists in the study of a system of n bodies in the plane with mass and position given by $m_i$ and $\mathbf q _i \in \mathbb {R}^2$, respectively, subject to their mutual Newtonian gravitational interaction. Then the equations of motion in a suitable units are

$$\begin{aligned} \ddot{q}_i = \sum _{{\mathop {j\ne i}\limits ^{j=1}}}^n m_j \frac{\mathbf{q}_j-\mathbf{q}_i}{r_{ij}^3} = \frac{\partial U}{\partial \mathbf{q}_i},\quad 1\le i \le n \end{aligned}$$

(1)

where

$$\begin{aligned} U = \sum _{1\le i <j \le n} \frac{m_im_j}{r_{ij}} \end{aligned}$$

is the potential function and $r_{ij}=\left| \mathbf q _i -\mathbf q _j \right|$ is the Euclidean distance between the ith and the jth bodies. Without loss of generality we may assume that the center of mass is fixed at the origin, $\sum _{i=1}^n m_i\mathbf q _i=0.$

A planar central configuration of the n-body problem $\mathbf q =(\mathbf q _1,\ldots , \mathbf q _n)\in {\mathbb R}^{2n}$ is a configuration such that the acceleration vector of every body is proportional (common scalar) to its position vector with respect to the center of mass. Then, by (1) a central configuration have to satisfies the equations

$$\begin{aligned} \frac{\partial U}{\partial \mathbf q _i} = \lambda m_i\mathbf q _i, \quad i=1,\ldots , n, \end{aligned}$$

for some constant $\lambda$, equal for all bodies.

In terms of the mutual distances $r_{ij}$, the equations for central configurations, named Laura/Andoyer/Dziobek Equations [8], are given by

$$\begin{aligned} f_{ij}= \sum _{{\mathop {k\ne i,j}\limits ^{k=1}}}^5 m_k (R_{ik}-R_{jk})\varDelta _{ijk}=0, \end{aligned}$$

(2)

for $1\le i < j \le n$. Here, $R_{ij}=1/r_{ij}^3$ and $\varDelta _{ijk}=(\mathbf q _i -\mathbf q _j)\wedge (\mathbf q _i-\mathbf q _k)$. Thus, $\varDelta _{ijk}$ gives twice the signed area of the triangle with vertices $\mathbf q _i$, $\mathbf q _j$ and $\mathbf q _k$. We emphasize that in the planar five-body problem this system consists of ten equations.

Consider the following particular configuration of the planar five-body problem. Three bodies $m_1$, $m_2$, $m_3$, ordered from left to right, are in collinear configuration, and two bodies, $m_4=m_5=1$ placed symmetrically, with respect to the line containing the first three bodies. We also assume that $m_2$, $m_4$ and $m_5$ are at the vertices of an equilateral triangle and so, form a Lagrange central configuration of the three-body problem, see Fig 2. Due to the impossed simmetry we have that $r_{14}=r_{15}$, $r_{24}=r_{25}=r_{45}$ and $r_{34}=r_{35}$, then system of ten equations (2) reduces to the following three equations, since $f_{12}=f_{13}=f_{23}=f_{45}=0$, $f_{14}=-f_{15}$, $f_{24}=-f_{25}$, $f_{34}=-f_{35}$.

$$\begin{aligned} f_{14}= & {} m_2(R_{12}-R_{24})\varDelta _{142} + m_3(R_{13}-R_{34})\varDelta _{143}+(R_{14}-R_{45})\varDelta _{145} =0, \nonumber \\ f_{24}= & {} m_1(R_{12}-R_{14})\varDelta _{241} + m_3(R_{23}-R_{34})\varDelta _{243} =0, \nonumber \\ f_{34}= & {} m_1(R_{13}-R_{14})\varDelta _{341} + m_2(R_{23}-R_{24})\varDelta _{342}+ (R_{34}-R_{45})\varDelta _{345} =0. \end{aligned}$$

(3)

Solving system (3), we obtain the following expressions for $m_1$, $m_2$ and $m_3$ in terms of the mutual distances.

$$\begin{aligned} m_1= & {} -\frac{(R_{23}-R_{34})\varDelta _{243}}{(R_{12}-R_{14})\varDelta _{241}}m_3, \end{aligned}$$

(4)

$$\begin{aligned} m_2= & {} -\frac{(R_{13}-R_{34})(R_{12}-R_{14})(R_{34}-R_{45})\varDelta _{143}\varDelta _{241}\varDelta _{345}+(R_{14}-R_{45})(R_{23}-R_{34})(R_{13}-R_{14})\varDelta _{145}\varDelta _{243}\varDelta _{341}}{(R_{12}-R_{45})\varDelta _{142}(R_{23}-R_{34})\varDelta _{243}(R_{13}-R_{14})\varDelta _{341}+(R_{13}-R_{34})\varDelta _{143}(R_{12}-R_{14})\varDelta _{241}(R_{23}-R_{45})\varDelta _{342}}, \nonumber \\ \end{aligned}$$

(5)

$$\begin{aligned} m_3= & {} \frac{(R_{12}-R_{14})\varDelta _{241}\left( (R_{12}-R_{45})\varDelta _{142}(R_{34}-R_{45})\varDelta _{345}-(R_{14}-R_{45})\varDelta _{145}(R_{23}-R_{45})\varDelta _{342}\right) }{(R_{12}-R_{45})\varDelta _{142}(R_{23}-R_{34})\varDelta _{243}(R_{13}-R_{14})\varDelta _{341}+(R_{13}-R_{34})\varDelta _{143}(R_{12}-R_{14})\varDelta _{241}(R_{23}-R_{45})\varDelta _{342}}.\nonumber \\ \end{aligned}$$

(6)

Fig. 2

Euler plus Lagrange stacked central configuration in the planar five-body problem

By a suitable scaling we may assume that $r_{24}=r_{25}=r_{45}=1$. Let $r_{12}=a>0$, $r_{23}=b>0$, then, according to Fig. 2, our configuration must satisfy the following relations

$$\begin{aligned}&r_{13}=a+b, \quad r_{34}=\sqrt{b^{2}-\sqrt{3}b+1 }, \quad r_{14}=\sqrt{a^{2}+\sqrt{3}a+1},\nonumber \\&\varDelta _{142}=-\frac{a}{2},\quad \varDelta _{143}=-\frac{(a+b)}{2}, \quad \varDelta _{145}=-\left( a+\frac{\sqrt{3}}{2}\right) ,\nonumber \\&\varDelta _{243}=-\frac{b}{2},\quad \varDelta _{245}=-\frac{\sqrt{3}}{2}, \quad \varDelta _{341}=\frac{(a+b)}{2}, \nonumber \\&\varDelta _{342}=\frac{b}{2},\quad \varDelta _{345}=b-\frac{\sqrt{3}}{2}, \quad \varDelta _{241}=\frac{a}{2}. \end{aligned}$$

(7)

Let $\mathscr {M}$ be the region in the (a, b)-plane such that the masses $m_i$, $i=1,2,3$, given in (4)–(6) are positive and let $\partial \mathscr {M}$ be its boundary, that is, points in the (a, b)-plane with at least one $m_i$, $i=1,2,3$, equal to zero and where the non-zero masses are positives. Figure  3 gives a numerical evidence that the set $\mathscr {M}$ is non-empty, as in [12].

Let E(a, b) be the called Euler quintic polynomial

$$\begin{aligned} \begin{array}{ll} E(a,b)&{}=-\left( m_{2}+m_{3}\right) -\left( 2m_{2}+3m_{3}\right) \alpha -\left( m_{2}+3m_{3}\right) \alpha ^{2}+\left( 3m_{1}+m_{2}\right) \alpha ^{3} \\ &{} \quad ~+~\left( 2m_{2}+3m_{1}\right) \alpha ^{4}+\left( m_{1}+m_{2}\right) \alpha ^{5}, \end{array} \end{aligned}$$

(8)

where $\displaystyle {\alpha =b/a}$.

Then $E(a,b)=0$ is the equation that the three collinear masses $m_1$, $m_2$ and $m_3$ have to satisfy in order to form an Euler central configuration. Our goal is to prove that $\left\{ E(a,b)=0 \right\} \cap \mathscr {M} \ne \varnothing$. Again, Fig. 3 give a numerical evidence that the intersection is not empty.

Fig. 3

Positive mass region $\mathscr {M}$ with $E=0$ in the (a, b)-plane

3 Proof of the Theorem 2

First we will show that $E(a,b)=0$ intersects $\partial \mathscr {M}$ at $m_1=0$, that is, there exists at least one point $(a_0,b_0)\in \partial \mathscr {M}$ such that $E(a_0,b_0)=0$ with $m_1(a_0,b_0)=0$ and $m_i(a_0,b_0)>0$, $i=2,3$.

Let L be the line segment given by $(a,b)\in (0,\frac{1}{3}) \times \{\frac{\sqrt{3}}{3}\}$. Claim: $L\subset \partial \mathscr {M}$ and for all $a \in L,$$m_1$ is zero and $m_2, m_3$ are positive.

From Eq. (4), $m_1=0$ either $m_3=0$ or $r_{23}=r_{34}$, or equivalently, $b=(b^2-\sqrt{3}b+1)^{1/2}$. Then, in the (a, b)-plane, when $m_3\ne 0$ the boundary $m_1=0$ of $\mathscr {M}$ is given by the straight line $b=\frac{\sqrt{3}}{3}$. On the other hand, $m_1>0$ when $m_3>0$ and $b<\frac{\sqrt{3}}{3}$.

From Eq. (5), when $r_{23}=r_{34}$ we have that $m_2=1$. To conclude the claim we have to show that $m_3>0$ for all $a \in L$. From Eq. (6), when $r_{23}=r_{34}$ we obtain the following expression for $m_3$ in terms of a.

$$\begin{aligned} m_3(a,b=\sqrt{3}/3)=-\frac{\left( 3a+\sqrt{3}\right) ^{2} N(a)}{27a^{3}\left( \sqrt{3}a^{2}+3a+\sqrt{3} \right) \left( a^{2}+\sqrt{3}a+1 \right) ^{\frac{3}{2}} }, \end{aligned}$$

where

$$\begin{aligned} N(a)=-2a^3-\sqrt{3}a^2+\left( 3a^5+4\sqrt{3}a^4+6a^3-a^2+\sqrt{3}a^2-\sqrt{3}a-1\right) \sqrt{a^2+a\sqrt{3}+1}. \end{aligned}$$

(9)

It is not hard to check that $\lim _{a\rightarrow 0^+} m_3(a,b=\sqrt{3}/3) =+\infty$, as well as $N(1/3)=-\frac{2}{27}-\frac{\sqrt{3}}{9}- \frac{71+14\sqrt{3}}{81} \sqrt{\frac{10}{9}+\frac{\sqrt{3}}{3}}<0,$ so, $m_3(1/3,b=\sqrt{3}/3)>0$. Finally, we are going to show that $m_3(a,b=\sqrt{3}/3)$ is never zero in L, or equivalently, N(a) does not vanish. Expression (9) can be written as a polynomial of degree 12, P(a), such that, the zeros of N(a) are a subset of the zeros of P(a).

$$\begin{aligned} P(a)=&9a^{12}+33\sqrt{3}a^{11}+165a^{10}+(162\sqrt{3}-6)a^{9}+(306-20\sqrt{3})a^{8}\\&+~(126\sqrt{3}-90)a^{7}+(96-78\sqrt{3})a^{6}+(14\sqrt{3}-126)a^{5}\\&+~(12-42\sqrt{3})a^{4}+(9\sqrt{3}-24)a^{3}+(12-2\sqrt{3})a^{2}+3\sqrt{3}a+1. \end{aligned}$$

We apply Sturm’s Theorem to conclude that P(a) has no real roots in the interval $(0,\frac{1}{3})$. Let $R_1(a)$ be the remainder obtained by dividing P(a) by $P'(a)$ and $T_1(a)=-R_1(a)$. Let $R_2(a)$ be the remainder obtained by dividing $P'(a)$ by $T_1(a)$ and $T_2(a)=-R_2(a)$. In general, let $R_k(a)$ be the remainder obtained by dividing $T_{k-2}(a)$ by $T_{k-1}(a)$ where $T_k(a)=-R_k (a)$. Next we evaluate the $T_k (a)$, $k=1,\ldots , 11$ at points $a=0$ and $a=\frac{1}{3}$, obtaining Table 1.

From the data in Table 1, we see that for $a=0$ and $a=\frac{1}{3}$ there are 6 changes of sign. Thus, the claim is complete. Notice that the omitted values in the Table 1 are due to how long are the integers involved into.

Table 1 Values of the P(a), $P'(a)$ and the Sturm’s sequence $T_k$ at $a=0$ and $a=\frac{1}{3}$

The Euler quintic equation (8) restricted to L is given by

$$\begin{aligned} E(a,\sqrt{3}/3)&=-\left( 1+m_{3}\right) -\left( 2+3m_{3}\right) \left( \frac{1}{\sqrt{3}a}\right) \\&\quad -\left( 1+3m_{3}\right) \left( \frac{1}{\sqrt{3}a}\right) ^{2}+ \left( \frac{1}{\sqrt{3}a}\right) ^{3} +2 \left( \frac{1}{\sqrt{3}a}\right) ^{4}+\left( \frac{1}{\sqrt{3}a}\right) ^{5}. \end{aligned}$$

An straightforward computation shows that $\lim _{a\rightarrow 0^+}E(a,\sqrt{3}/3) =+\infty$ and $E(1/3,\sqrt{3}/3)<0$. Then using a Bolzano argument there exist $a_0 \in L$ such that $E(a_0,\sqrt{3}/3)=0$.

To complete the proof we have to show that E(a, b) intersects $\mathscr {M}$, as well. By continuity, it is also a consequence of the change of sign of E(a, b) restricted to $\partial \mathscr {M}$ when $m_1=0$.

Numerically, we observe that Theorem 2 is valid for any fixed value of $a \in (0.043964649299756,0.162031454283589)$ and that fixes mass $m_3$ inside the triangle.

An example of stacked central configurations in the planar five-body problem, belonging to the Lagrange plus Euler family is given by $m_1=0.117224179225200$, $m_2=0.890322344850114$, $m_3=38.7407741323209$ and $m_4=m_5=1$. In that case $a=\frac{1}{8}$ and $b=0.569110604510880$.