Classification of $(n+1, 1)$-Stacked Central Configurations in $R^3$

Abstract

We classify the extensions of n-body central configurations to $(n+1)$-body central configurations in $R^3$, in both the collinear case and the non-collinear case. We completely solve the two open questions posed by Hampton (Nonlinearity 18: 2299-2304, 2005). This classification is related with study on co-circular and co-spherical central configurations. We also obtain a general property of co-circular central configurations.

1 Introduction

The classical n-body problems study the motion of n point bodies with positive masses $m_1,\ldots , m_n$, interacting under the Newton’s law of gravitation. Let ${\mathbf {q}}_i$ be the position of the ith point body, $r_{ij}=|{\mathbf {q}}_i-{\mathbf {q}}_j|$, and let U be the force function $\sum _{j\ne i}\frac{m_im_j}{r_{ij}}$. A configuration, denoted by $({\mathbf {q}}_1,\ldots , {\mathbf {q}}_n)$, is called a central configuration if it satisfies the equations

$$\begin{aligned} \nabla _i U = -\lambda m_i({\mathbf {q}}_i-c), \ i=1,\ldots , n, \end{aligned}$$

where $\nabla _i$ denotes the vector of partial derivatives with respect to the components of ${\mathbf {q}}_i$ and $c=\frac{\sum _{ i=1}^n m_i{\mathbf {q}}_i }{\sum _{ i=1}m_i}$ is the center of mass of the configuration. The quantity $\lambda$ in the above equation is called the multiplier of the central configuration. The total masses $\sum m_i$ are denoted by m.

Central configurations naturally arise in the study of the self-similar solutions, and they are involved in the classification of the topology of integral manifolds (Smale 1970). In the collection of important open problems in celestial mechanics compiled by Albouy et al. (2012), half of the list is on central configurations. Readers are referred to Albouy (2003), Albouy et al. (2012), Albouy and Kaloshin (2012), Llibre et al. (2015), Saari (1980) for introductions, recent advance and open questions.

The $(n+k)$-body central configurations extended from n-body central configurations by adding k bodies are called stacked central configurations. They were introduced by Hampton in 2005 (Hampton 2005b). Following Fernandes and Mello (2013a), such central configuration is called $(n+k, k)$-stacked. For instance, the Lagrangian equilateral triangle central configuration is (3, 1)-stacked since any two-body subconfiguration of it is central. It is also well known that a pyramidal central configuration can be obtained by adding one mass to a co-circular central configuration (Albouy 2003; Fayçal 1996; Ouyang et al. 2004). Many other examples of stacked central configurations were constructed, see (Corbera et al. 2014; Hampton and Santoprete 2007; Oliveira and Cabral 2012). Hampton also raises two questions regarding stacked central configuration (Hampton 2005b):

• (1) In addition to symmetric collinear configurations¹, the square or a regular tetrahedron with a mass at its center and the square pyramidal configuration are there any five-body central configurations with a subset forming a four-body central configuration?

• (2) Are there any five-body non-collinear central configurations all of whose four-body subsets form a central configuration?

There are some works devoted to these two questions. Assuming that a five-body central configuration is coplanar and non-collinear, in 2013, Fernandes and Mello (2013a, 2018) and Alvarez-Ramírez et al. (2013) announced independently that such configuration must be a square with equal masses and one mass at the center of the square. However, the two questions remain open.

In this work, we classify the $(n+1, 1)$-stacked central configurations of in $R^3$, planar central configurations and spatial ones included. With this classification, we solve the two open questions completely. We also find one general property of co-circular central configurations. It plays a crucial role in our study of the $(n+1, 1)$-stacked central configurations when the n-body subcentral configuration is co-circular.

There are two cases. Firstly, the extended $(n+1)$-body central configuration is collinear. In this case, we show that extensions happen only for $n= 2$. So the question of collinear extensions has already been answered by Euler (1767). Secondly, the extended $(n+1)$-body central configuration is non-collinear. In this case, it has been proved by Fernandes and Mello (2013b) that it is necessary that the n-body central configuration lies on a common circle or sphere. Our approach is different from theirs. Our results contain not only the necessary conditions, but sufficient conditions as well. Thus, we can classify all the extensions.

Let r be the radius of the circle (sphere) and $r_0=(\frac{ m}{ \lambda })^{\frac{1}{3}}$, the cube root of the ratio of total mass m and the multiplier $\lambda$ of the n-body configuration. We show that a co-circular (co-spherical) n-body central configuration can extend to an $(n+1, 1)$-stacked central configuration only in the following two cases: (1) Its center of mass equals its geometric center; (2) $r_0\ge r$ for the co-circular central configurations, and $r_0=r$ for the co-spherical ones.

Thus, the measurement of r and $r_0$ of the co-circular and co-spherical central configurations is important. We obtain one general result on the comparison between $r_0$ and the sides and diagonals for the co-circular central configurations. Then, we prove that $r_0>r$ holds for all four-, five-, and six-body co-circular central configurations. Together with the works of Hampton (2005a) and Cors and Roberts (2012) on the co-circular four-body problem, we find all (5, 1)-stacked central configurations. And we answer Hampton’s two questions completely.

The paper is organized as follows: In Sect. 2, we state the main results. In Sect. 3, we prove the main results. In Sect. 4, we discuss the extensions of two-, three-, four-, and five-body central configurations. In Sect. 5, we find several examples of co-spherical central configurations whose center of mass equals the geometric center.

2 Main Results

We are interested in the $(n+1,1)$-stacked central configurations, i.e., $(n+1)$-body central configurations extended from n-body central configurations by adding one mass. If there is no confusion raised, the n masses are $m_1,\ldots , m_n$ and the corresponding configuration is ${\mathbf {q}}=({\mathbf {q}}_1,\ldots , {\mathbf {q}}_n)$. We denote by $m_0$ the added mass and by ${\mathbf {q}}_0$ its position. We denote by ${\bar{{\mathbf {q}}}}= ({\mathbf {q}}_0, {\mathbf {q}}_1,\ldots , {\mathbf {q}}_n)$ the extended configuration. We will also call the original n-body configuration ${\mathbf {q}}$ the subconfiguration. We use $r_{ij}$ to denote the distance between any two of the $n+1$ particles, i.e., $r_{ij}= |{\mathbf {q}}_i-{\mathbf {q}}_j|$, $0\le i<j\le n$. We denote by m the sum of the n masses, and by ${{\bar{m}}}$ the sum of the $n+1$ masses, i.e.,

$$\begin{aligned} m=\sum _{i=1}^{n}m_i, \ {\bar{m}}=\sum _{i=0}^{n}m_i=m_0 +m. \end{aligned}$$

We denote by c the center of mass of the n-body subconfiguration and ${\bar{c}}$ the center of mass of the $(n+1)$-body configuration, i.e.,

$$\begin{aligned} c=\frac{\sum _{i=1}^{n} m_i {\mathbf {q}}_i }{m}, \ {\bar{c}}=\frac{\sum _{i=0}^{n} m_i {\mathbf {q}}_i }{{\bar{m}}}= \frac{m c+m_0{\mathbf {q}}_0}{m+m_0}. \end{aligned}$$

Denote by U, I and ${\bar{U}}, {\bar{I}}$ the force function and the momentum of inertia of the sub-n-body system and the $(n+1)$-body system, respectively, i.e.,

$$\begin{aligned}&U=\sum _{1 \le i< j \le n} \frac{m_im_j}{r_{ij}}, \ \ I=\sum _{1 \le i< j \le n} \frac{m_im_j}{m}|{\mathbf {q}}_i-{\mathbf {q}}_j|^2=\sum _{i=1} ^n m_i|{\mathbf {q}}_i-c|^2;\\&{\bar{U}}=\sum _{0 \le i< j \le n} \frac{m_im_j}{r_{ij}} =U + \sum _{i=1}^n \frac{m_0m_i}{r_{i0}}, \\&{\bar{I}} =\sum _{0 \le i< j \le n} \frac{m_im_j}{{\bar{m}}}|{\mathbf {q}}_i-{\mathbf {q}}_j|^2=\sum _{i=0} ^n m_i|{\mathbf {q}}_i-{\bar{c}}|^2. \end{aligned}$$

If the central configuration ${\bar{{\mathbf {q}}}}$ is $(n+1, 1)$-stacked, then the configurations ${\bar{{\mathbf {q}}}}$ and ${\mathbf {q}}$ satisfy the following two systems simultaneously:

$$\begin{aligned} \nabla U({\mathbf {q}}) + \lambda /2 \nabla I({\mathbf {q}}) =0, \ \nabla {\bar{U}}({\bar{{\mathbf {q}}}}) + {\bar{\lambda }}/2 \nabla {\bar{I}}( {\bar{{\mathbf {q}}}})=0, \end{aligned}$$

(1)

where $\lambda = U / I$ and ${\bar{\lambda }} ={\bar{U}} / {\bar{I}}$.

2.1 Classification of $(n+1, 1)$-Stacked Central Configurations in $R^3$

We separate our discussions into the collinear case and the non-collinear case.

Theorem 1

There exist no collinear $(n+1, 1)$-stacked central configurations for $n\ge 3$.

This reduces study of collinear extensions to study of the well-known three-body collinear central configurations, which has been considered by Euler (1767), see Sect. 4.1.

In what follows, we mainly discuss the non-collinear case. In this case, Fernandes and Mello (2013b) have shown that the n-body subconfiguration must lie on a common circle or sphere and the added mass is at the geometric center. Their proof employed the Laura–Andoyer equations. Our approach is different from theirs, see Sect. 3. Our results contain more details, which enables us to provide a complete classification of the non-collinear extensions. We divide our discussion into two cases: adding one mass $m_0$ at the center of mass of ${\mathbf {q}}$, i.e., ${\mathbf {q}}_0=c$, or adding one mass $m_0$ not at the center of mass of ${\mathbf {q}}$, i.e., ${\mathbf {q}}_0\ne c$.

Theorem 2

Let ${\mathbf {q}}=({\mathbf {q}}_1,\ldots , {\mathbf {q}}_n)$ be a central configuration with center of mass c. Consider the $(n+1)$-body configuration by adding $m_0$ at c, i.e., ${\bar{{\mathbf {q}}}}=(c, {\mathbf {q}}_1,\ldots , {\mathbf {q}}_n)$. Then, ${\bar{{\mathbf {q}}}}$ is an $(n+1, 1)$-stacked central configuration if and only if $|{\mathbf {q}}_1-c|=|{\mathbf {q}}_2-c|=\cdots =|{\mathbf {q}}_n-c|.$

Theorem 3

Let ${\mathbf {q}}=({\mathbf {q}}_1,\ldots , {\mathbf {q}}_n)$ be a central configuration with center of mass c, total mass m, and multiplier $\lambda$. Consider one $(n+1)$-body configuration by adding $m_0$ not at c, i.e., ${\bar{{\mathbf {q}}}}=({\mathbf {q}}_0, {\mathbf {q}}_1,\ldots , {\mathbf {q}}_n)$, ${\mathbf {q}}_0\ne c$. Then ${\bar{{\mathbf {q}}}}$ is an $(n+1, 1)$-stacked central configuration if and only if $\frac{1}{|{\mathbf {q}}_i-{\mathbf {q}}_0|^3}= \frac{ \lambda }{ m}$, $i=1,\ldots , n$.

Corollary 4

Suppose that the ${\bar{{\mathbf {q}}}}$ is an $(n+1, 1)$-stacked non-collinear central configuration for the masses $(m_0, m_1,\ldots , m_n)$. Then, ${\bar{{\mathbf {q}}}}$ is also an $(n+1, 1)$-stacked non-collinear central configuration for the masses $(m'_0, m_1, \ldots , m_n)$, where $m'_0$ is an arbitrary mass.

We answer the second question of Hampton (2005b), see Sect. 1.

Theorem 5

In $R^3$, there are only three types of $(n+1)$-body central configurations all of whose n-body subsets form a central configuration, namely the three-body Eulerian collinear central configurations, the Lagrangian equilateral triangle central configurations and the regular tetrahedron central configurations.

Thus, whether the added mass is at the center of mass of ${\mathbf {q}}$ or not, there exists one point a such that $|a-{\mathbf {q}}_1|=\cdots =|a-{\mathbf {q}}_n|$. Restricted to central configurations in $R^3$, the subconfiguration ${\mathbf {q}}$ must lies on a common circle or sphere. These central configurations are called co-circular central configurations, in the planar case and co-spherical central configurations, in the spatial case. To make it precise, we use the terminology “co-spherical configuration” to indicate that the configuration is not planar. Denote by r the radius of the related circle (sphere). Denote by $r_0$ the cube root of the ratio of total mass and the multiplier of the subcentral configuration, i.e.,

$$\begin{aligned} r_0= \left( \frac{ m}{ \lambda }\right) ^{\frac{1}{3}}= \left( \frac{ m I}{ U}\right) ^{\frac{1}{3}} = \left( \frac{ \sum _{1 \le i< j \le n} m_im_j r_{ij}^2 }{ \sum _{1 \le i< j \le n} m_im_j /r_{ij} }\right) ^{\frac{1}{3}}. \end{aligned}$$

An $(n+1)$-body spatial central configuration of which n points lie in an affine plane is called a pyramidal central configuration.

The classification of $(n+1, 1)$-stacked central configurations in $R^3$ is a direct corollary of Theorems 2 and 3. We state the results separately for the planar case and the spatial case.

Proposition 6

Let ${\mathbf {q}}=({\mathbf {q}}_1,\ldots , {\mathbf {q}}_n)$ be a co-circular central configuration with center of mass c, total mass m, and multiplier $\lambda$. Let r be the radius of the circle, and $r_0=(\frac{ m}{ \lambda })^{\frac{1}{3}}$. Then, ${\mathbf {q}}$ can be extended to an $(n+1, 1)$-stacked planar central configuration ${\bar{{\mathbf {q}}}}=({\mathbf {q}}_0, {\mathbf {q}}_1,\ldots , {\mathbf {q}}_n)$ only in the following two cases:

• I: c is the geometric center of ${\mathbf {q}}$, and ${\mathbf {q}}_0=c$.

• II: $r=r_0$, and ${\mathbf {q}}_0$ is at the geometric center of ${\mathbf {q}}$.

Proposition 7

Let ${\mathbf {q}}=({\mathbf {q}}_1,\ldots , {\mathbf {q}}_n)$ be a co-circular (resp. co-spherical) central configuration with center of mass c, total mass m, and multiplier $\lambda$. Let r be the radius of the circle (resp. sphere), and $r_0=(\frac{ m}{ \lambda })^{\frac{1}{3}}$. Then, ${\mathbf {q}}$ can be extended to an $(n+1, 1)$-stacked spatial central configuration ${\bar{{\mathbf {q}}}}=({\mathbf {q}}_0, {\mathbf {q}}_1,\ldots , {\mathbf {q}}_n)$ only in the following three cases:

• I: ${\mathbf {q}}$ is co-circular, $r<r_0$, and ${\mathbf {q}}_0$ is on the orthogonal axis passing through the center of the circle such that $r_{10}=r_0$;

• II: ${\mathbf {q}}$ is co-spherical, c is the geometric center of ${\mathbf {q}}$, and ${\mathbf {q}}_0=c$.

• III: ${\mathbf {q}}$ is co-spherical, $r=r_0$, and ${\mathbf {q}}_0$ is at the geometric center of ${\mathbf {q}}$.

Remark 8

Chenciner (2004) asked: Is the regular n-gon with equal masses the unique co-circular central configuration that the center of mass equals the geometric center? This question is listed as Problem 12 in a collection of open problems in celestial mechanics compiled by Albouy et al. (2012). We may ask one equivalent question: If an n-body co-circular central configuration can extend to a coplanar central configuration by adding one mass $m_0$ at the mass center, does the n-body central configuration have to be the regular n-gon with equal masses? Until now, the question has only been answered affirmatively for $n=4$, by Hampton in 2003 Hampton (2005a).

Another corollary of Theorems 2 and 3 is as follows.

Corollary 9

In case II of Proposition 6 and case I and III of Proposition 7, let ${\bar{m}}$ (resp. $\bar{\lambda }$) be the total mass (resp. the multiplier) of the $(n+1, 1)$-stacked central configuration. Let ${\bar{r}}_0= ({\bar{m}} / {\bar{\lambda }})^{\frac{1}{3}}$. Then, ${\bar{r}}_0$ does not depend on the value of $m_0$, and ${\bar{r}}_0=r_0$.

Remark 10

Fernandes–Mello announced that if ${\bar{{\mathbf {q}}}}=({\mathbf {q}}_0, {\mathbf {q}}_1,\ldots , {\mathbf {q}}_n)$ is an $(n+1, 1)$-stacked planar central configuration, then the center of mass c of the co-circular configuration ${\mathbf {q}}=({\mathbf {q}}_1, \ldots , {\mathbf {q}}_n)$ must coincide with the geometric center [Lemma 2.3 of Fernandes and Mello (2015)]. That is, case II of Proposition 6, does not exist. This statement is not accurate. The well-known Lagrangian equilateral triangle central configuration is a counterexample, see Remark 16 and Sect. 4.1. The flaw in their proof is similar to the one described in Remark 21.

2.2 The Value $r_0$ of Co-circular Central Configurations

According to Propositions 6 and  7, the measurement of the radius r and $r_0=( m / \lambda )^{\frac{1}{3}}$ of the co-circular and co-spherical central configurations is crucial for the classification of $(n+1, 1)$-stacked central configurations. We obtain a general result for the co-circular case, with which, we could prove that $r_0> r$ holds for all four-, five-, and six-body co-circular central configurations.

Some notations for the co-circular configurations: Edges are line segments connecting two different vertices of a polygon. For a co-circular configuration whose vertices are ordered counterclockwise as $({\mathbf {q}}_1,\ldots , {\mathbf {q}}_n)$, the edges $\overline{{\mathbf {q}}_i{\mathbf {q}}_j}$ are called exterior sides if $|i-j|=1$ or $n-1$, and diagonals otherwise. An edge and a vertex on that edge are called incident.

Theorem 11

Assume that $n\ge 4$. For any n-body co-circular central configuration, all the exterior sides are less than $r_0$. At each vertex, there is at least one incident diagonal larger than $r_0$.

Remark 12

For $n=2, 3$, there is no diagonal. It is easy to see that $r_0=r_{12}$ for both of the two cases. For $n\ge 4$, there are at least n/2 (n even) or $(n+1)/2$ (n odd) diagonals greater than $r_0$. For $n=4,5$, these results have been proved for a larger set of central configurations, namely the four- and five-body planar convex central configurations, by MacMillan and Bartky (1932) and Chen and Hsiao (2018), respectively. Generally, for large n, there would be many diagonals smaller than $r_0$, see the examples in Sect. 5.1.

Corollary 13

Co-circular central configurations cannot lie entirely in a semi-circle.

Remark 14

As suggested by Cors and Roberts (2012), this fact also follows nicely from the perpendicular bisector theoremMoeckel (1990).

Proposition 15

For all four-, five-, and six-body co-circular central configurations, the radius of the circle containing the bodies is smaller than $r_0$.

Remark 16

The two ends of a segment can be placed on a circle with radius equal or greater than half of the segment. Thus, for $n=2$, we have $r_0/2\le r<\infty$. For $n=3$, we have $r_0=\sqrt{3}r$.

2.3 Applications to $(n+1, 1)$-Stacked Central Configurations for $n\le 6$ and to Pyramidal Central Configurations

We find all the (5, 1)-stacked central configurations, with which we answers Hampton’s first question (Hampton 2005b), see Sect. 1.

Theorem 17

There are only three types of (5, 1)-stacked central configurations:

• the square with equal masses and an arbitrary mass $m_0$ at the center;

• any four-body co-circular central configuration and an arbitrary mass $m_0$ on the orthogonal axis passing through the center of the circle. The height of $m_0$ is $h= \sqrt{ r_0^2 -r^2}$;

• the regular tetrahedron with equal masses and an arbitrary mass $m_0$ at the center.

For (n, 1)-stacked central configurations with $n= 6, 7$, we have some partial results.

Proposition 18

Let ${\mathbf {q}}$ be a five-body (resp. six-body) co-circular central configuration with center of mass c, $r_0=(\frac{ m}{ \lambda })^{\frac{1}{3}}$ and radius of the circle r. Consider one six-body (resp. seven-body) configuration by adding $m_0$ at ${\mathbf {q}}_0$ to ${\mathbf {q}}$. Then, ${\bar{{\mathbf {q}}}}$ is a (6, 1)-stacked (resp. (7, 1)-stacked) central configuration only in the following two cases:

• To planar: c is the geometric center of ${\mathbf {q}}$, and ${\mathbf {q}}_0=c$.

• To pyramidal: The point ${\mathbf {q}}_0$ is on the orthogonal axis passing through the center of the circle such that $r_{10}=r_0$;

Our classification of the stacked central configurations also enables us to give a complete characterization of the pyramidal central configurations.

Proposition 19

Let ${\bar{{\mathbf {q}}}}=({\mathbf {q}}_0, {\mathbf {q}}_1,\ldots , {\mathbf {q}}_n)$ be an $(n+1)$-body pyramidal configuration with masses $m_0, m_1,\ldots , m_n$, where ${\mathbf {q}}_0$ is the top vertex which is off the affine plane containing $m_1,\ldots , m_n$. Then, the pyramidal configuration is central if and only if the following conditions are satisfied:

• The subconfiguration ${\mathbf {q}}=({\mathbf {q}}_1,\ldots , {\mathbf {q}}_n)$ is central and co-circular;

• $r<r_0$, where $r, r_0$ are values associated with the n-body co-circular central configuration ${\mathbf {q}}$;

• The top vertex ${\mathbf {q}}_0$ is on the orthogonal axis passing through the center of the circle. The height of ${\mathbf {q}}_0$ is $h= \sqrt{ r_0^2 -r^2}$.

The top mass $m_0$ is arbitrary.

Remark 20

When studying five-body pyramidal configurations, Fayçal (1996) showed that the base must be co-circular and that the top mass is arbitrary. She also gave a formula for the distance between the top vertex and the base vertices. Ouyang et al. (2004) generalized Fayçal’s result to n-body pyramidal configurations. Their characterization is almost the same as ours. They did not compare explicitly the two values r and $r_0$. Albouy (2003) obtained a general proposition on central configurations in $R^N$. Restricted in $R^3$, it immediately implies the base of any pyramidal central configuration is central and co-circular.

The $(n+1, 1)$-stacked central configurations are also related with perverse solutions introduced by Chenciner (2004). A solution ${\mathbf {q}}(t)={\mathbf {q}}_1(t),\ldots , {\mathbf {q}}_n(t)$ of the n-body problem with masses $m_1, m_2,\ldots , m_n$ is called a perverse solution if there exists another system of masses, $m'_1, m'_2,$ $\ldots , m'_n$, for which ${\mathbf {q}}(t)$ is still a solution. Note that any $(n+1, 1)$-stacked non-collinear central configuration obtained by adding one mass at the center of mass of the n-body configuration, i.e., in case I of Proposition 6 and case I of Proposition 7,, would provide perverse solutions, namely the relative equilibrium and the total collision solution for the planar case, and the total collision solution for the spatial case, see also Sect. 5.2.

3 Proofs of the Main Results

We first simplify the central configuration Eq. (1).

Note that there is a simple but important fact: The three points $c, {\bar{c}},$ and ${\mathbf {q}}_0$ are collinear. In fact, ${\bar{c}}$ can also be seen as the center of mass of the two material points $c, {\mathbf {q}}_0$ with masses $m, m_0$. Thus, ${\bar{c}}$ equals ${\mathbf {q}}_0$ if and only if c equals ${\mathbf {q}}_0$. The collinearity of the three points is also revealed in the following equalities:

$$\begin{aligned} {\bar{m}} ({\bar{c}}-{\mathbf {q}}_0 ) = m ( c-{\mathbf {q}}_0 ), \ A-{\bar{c}} = (A- c)- \frac{m_0}{{\bar{m}}} ({\mathbf {q}}_0 -c), \ \end{aligned}$$

(2)

where A is an arbitrary point.

Assume that ${\bar{{\mathbf {q}}}}=({\mathbf {q}}_0, {\mathbf {q}}_1,\ldots , {\mathbf {q}}_n)$ is an $(n+1, 1)$-stacked central configuration. The central configuration Eq. (1) can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\sum _{j\ne i, j=1}^n m_im_j \frac{{\mathbf {q}}_j-{\mathbf {q}}_i}{|{\mathbf {q}}_j-{\mathbf {q}}_i|^3}= - \lambda m_i({\mathbf {q}}_i-c), i=1,\ldots , n, \\ &{} \sum _{i=1}^n \frac{m_im_0({\mathbf {q}}_i-{\mathbf {q}}_0)}{r_{i0}^3} = - {\bar{\lambda }} m_0({\mathbf {q}}_0-{\bar{c}}), \\ &{} \sum _{j\ne i, j=1}^n m_im_j \frac{{\mathbf {q}}_j-{\mathbf {q}}_i}{|{\mathbf {q}}_j-{\mathbf {q}}_i|^3} + \frac{m_im_0({\mathbf {q}}_0-{\mathbf {q}}_i)}{r_{i0}^3} = - {\bar{\lambda }} m_i({\mathbf {q}}_i-{\bar{c}}), \ i= 1,\ldots , n, \end{array}\right. } \end{aligned}$$

(3)

where $\lambda = U / I$ and ${\bar{\lambda }} ={\bar{U}} / {\bar{I}}$.

Note that the third part of system (3) can be written as

$$\begin{aligned} \lambda m_i({\mathbf {q}}_i-c)+ \frac{m_0m_i({\mathbf {q}}_i-{\mathbf {q}}_0)}{r_{i0}^3} = {\bar{\lambda }} m_i({\mathbf {q}}_i-{\bar{c}}), \ i= 1,\ldots , n. \end{aligned}$$

(4)

Summing up all the n equations gives the second part of system (3). Furthermore, by (2), the n equations are equivalent to

$$\begin{aligned} \left( \lambda - {\bar{\lambda }} + \frac{m_0}{r_{i0}^3}\right) \left( {\mathbf {q}}_i-c\right) = \left( \frac{m_0}{r_{i0}^3} - \frac{{\bar{\lambda }} m_0}{{\bar{m}}} \right) ({\mathbf {q}}_0- c), \ \ i= 1,\ldots , n. \end{aligned}$$

(5)

Therefore, system (1) is equivalent to the following system:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\sum _{j\ne i, j=1}^n m_im_j \frac{{\mathbf {q}}_j-{\mathbf {q}}_i}{|{\mathbf {q}}_j-{\mathbf {q}}_i|^3}= - \lambda m_i({\mathbf {q}}_i-c), i=1,\ldots , n, \\ &{}( \lambda - {\bar{\lambda }} + \frac{m_0}{r_{i0}^3}) ({\mathbf {q}}_i-c)= ( \frac{m_0}{r_{i0}^3} - \frac{{\bar{\lambda }} m_0}{{\bar{m}}} ) ({\mathbf {q}}_0- c), \ i= 1,\ldots , n, \end{array}\right. } \end{aligned}$$

(6)

where $\lambda = U / I$ and ${\bar{\lambda }} ={\bar{U}} / {\bar{I}}$.

Proof of Theorem 1

Note that Eq. (5) can be written as

$$\begin{aligned} ( \lambda - {\bar{\lambda }}) ({\mathbf {q}}_i-{\mathbf {q}}_0) + \frac{m_0({\mathbf {q}}_i-{\mathbf {q}}_0)}{r_{i0}^3} +\left( \lambda - \frac{{\bar{\lambda }}}{{\bar{m}}}m \right) ( {\mathbf {q}}_0-c) =0, \ i= 1,\ldots , n. \end{aligned}$$

Assume that all the particles are on the x-axis, and use $x_i$ to denote the position of $m_i$. The equations become

$$\begin{aligned} ( \lambda - {\bar{\lambda }}) (x_i-x_0) + \frac{m_0(x_i-x_0)}{|x_i-x_0|^3} +\left( \lambda - \frac{{\bar{\lambda }}}{{\bar{m}}}m \right) ( x_0-c) =0, \ i= 1,\ldots , n. \end{aligned}$$

(7)

Let $y_i=x_i-x_0$, $\alpha =( \lambda - \frac{{\bar{\lambda }}}{{\bar{m}}}m )( x_0-c)$, and $\beta =\lambda - {\bar{\lambda }}$. Note that $\alpha$ and $\beta$ are constant with respect to $i=1,\ldots , n$. Fix the values of $\alpha$ and $\beta$. Let us consider the algebraic equation $\beta y+ \frac{m_0y}{|y|^3} +\alpha =0.$ Then, the n Eq. (7) implies that it has at least n distinct real nonzero solutions. Let us prove it is impossible for $n\ge 3$ by reduction to absurdity.

Assume that there are k particles on the left side of $m_0$ and $n-k$ particles on the right, $0\le k\le n$.

Then, the cubic equation

$$\begin{aligned} -m_0z^3 + \alpha z+\beta =0, \end{aligned}$$

(8)

has at least k distinct negative roots, and the cubic equation

$$\begin{aligned} m_0z^3 + \alpha z+\beta =0 \end{aligned}$$

(9)

has at least $n-k$ distinct positive roots.

Assume that $z_1, z_2, z_3$ are the roots of Eq. (8) and $z_4, z_5, z_6$ are the roots of Eq. (9). We are going to finish the proof by showing that the sum of the number of negative roots of Eq. (8) and the number of positive roots of Eq. (9) is not greater than 2. This is obviously true if $\alpha =0$ or $\beta =0$. So we assume that $\alpha \ne 0$ and $\beta \ne 0$.

Recall that a generic cubic equation $az^{3}+bz^{2}+cz+d=0, \ a\ne 0$ has only one real root and two conjugate imaginary roots if and only if

$$\begin{aligned} \Delta =18abcd-4b^{3}d+b^{2}c^{2}-4ac^{3}-27a^{2}d^{2} <0. \end{aligned}$$

For our two cubic equations, we have

$$\begin{aligned} \Delta _1=4m_0\alpha ^3 -27m_0^2\beta ^2, \ \Delta _2=-4m_0\alpha ^3 -27m_0^2\beta ^2. \end{aligned}$$

Obviously, at least one of $\Delta _1$ and $\Delta _2$ is negative. Without loss of generality, we assume that $\Delta _1 < 0$; then, only one of $z_1, z_2, z_3$ is real, say, $z_1$, and the other two are conjugate imaginary numbers.

By Vieta’s formulas, $z_4+z_5+z_6= 0$, which implies that at most two of the roots of Eq. (9) are positive. Thus, we assume that $z_1<0$. By Vieta’s formulas, $z_4z_5z_6=-z_1z_2z_3>0, z_4+z_5+z_6= 0$, which implies that Eq. (9) has only one positive root. In words, the sum of the number of negative roots of Eq. (8) and the number of positive roots of Eq. (9) is not greater than 2. This completes the proof. $\square$

Proof of Theorem 2

The proof of the necessary conditions: If the configuration ${\bar{{\mathbf {q}}}}$ is central, we have ${\mathbf {q}}_0=c={\bar{c}}$, so ${\mathbf {q}}_i\ne c, \ i=1,\ldots , n$. Then, the second part of system (6) implies that $\frac{1}{|{\mathbf {q}}_i-{\mathbf {q}}_0|^3}=\frac{{\bar{\lambda }} -\lambda }{m_0}$ for $i=1,\ldots , n$. So we obtain that $|{\mathbf {q}}_1-{\mathbf {q}}_0|=|{\mathbf {q}}_2-{\mathbf {q}}_0|=\cdots =|{\mathbf {q}}_n-{\mathbf {q}}_0|$, i.e., $|{\mathbf {q}}_1-c|=\cdots =|{\mathbf {q}}_n-c|$.

The proof of the sufficient conditions: The first part of system (6) obviously holds. Since ${\mathbf {q}}_0=c={\bar{c}}$ and $r_{10}=\cdots =r_{n0}$, we have

$$\begin{aligned}&{\bar{I}}= \sum _{i=0} ^n m_i|{\mathbf {q}}_i-{\bar{c}}|^2=\sum _{i=1} ^n m_i|{\mathbf {q}}_i-c|^2 =I= m r_{10}^2,\\&{\bar{\lambda }} = \frac{U + \sum _{i=1}^n \frac{m_im_0}{r_{i0}} }{{\bar{I}} } =\lambda + m_0 \frac{ m }{ I r_{10}} = \lambda + m_0 \frac{ 1 }{ r_{10}^3}, \end{aligned}$$

which implies that $\frac{1}{|{\mathbf {q}}_i-{\mathbf {q}}_0|^3}=\frac{{\bar{\lambda }} -\lambda }{m_0}$ for $i=1,\ldots , n$. Thus, the second part of system (6) holds and the proof is completed. $\square$

Proof of Theorem 3

The proof of the necessary conditions: Assume that the configuration ${\bar{{\mathbf {q}}}}$ is central. There exists some body not on the line $\overline{c {\mathbf {q}}_0}$ since the configuration $\bar{{\mathbf {q}}}$ is non-collinear. Suppose that ${\mathbf {q}}_k\notin \overline{c {\mathbf {q}}_0}$. Note that the kth equation of the second part of system (6) holds only if

$$\begin{aligned} \frac{1}{|{\mathbf {q}}_k-{\mathbf {q}}_0|^3}=\frac{{\bar{\lambda }} -\lambda }{m_0}= \frac{{\bar{\lambda }}}{{\bar{m}}}. \end{aligned}$$

Note that $|{\mathbf {q}}_k-{\mathbf {q}}_0|=|{\mathbf {q}}_j-{\mathbf {q}}_0|$ also holds if ${\mathbf {q}}_k\notin \overline{c {\mathbf {q}}_0}, {\mathbf {q}}_j\in \overline{c {\mathbf {q}}_0}$. By (4), we have

$$\begin{aligned} \lambda ({\mathbf {q}}_i-c)+ \frac{m_0({\mathbf {q}}_i-{\mathbf {q}}_0)}{r_{i0}^3} = {\bar{\lambda }} ({\mathbf {q}}_i-{\bar{c}}), \ i= k, j. \end{aligned}$$

Subtracting the two equations, we obtain

$$\begin{aligned}&\lambda ({\mathbf {q}}_k-{\mathbf {q}}_j) + \frac{m_0({\mathbf {q}}_k-{\mathbf {q}}_0)}{r_{k0}^3} -\frac{m_0({\mathbf {q}}_j-{\mathbf {q}}_0)}{r_{j0}^3} = {\bar{\lambda }} ({\mathbf {q}}_k-{\mathbf {q}}_j), \\&\frac{({\mathbf {q}}_k-{\mathbf {q}}_0)}{r_{k0}^3} -\frac{({\mathbf {q}}_j-{\mathbf {q}}_0)}{r_{j0}^3} = \frac{{\bar{\lambda }} -\lambda }{m_0}({\mathbf {q}}_k-{\mathbf {q}}_j)= \frac{({\mathbf {q}}_k-{\mathbf {q}}_0)-({\mathbf {q}}_j-{\mathbf {q}}_0)}{r_{k0}^3}, \end{aligned}$$

which implies that $|{\mathbf {q}}_k-{\mathbf {q}}_0|=|{\mathbf {q}}_j-{\mathbf {q}}_0|$. Thus, we obtain

$$\begin{aligned} \frac{1}{|{\mathbf {q}}_i-{\mathbf {q}}_0|^3}=\frac{{\bar{\lambda }} -\lambda }{m_0}= \frac{{\bar{\lambda }}}{{\bar{m}}},\quad i=1,\ldots , n. \end{aligned}$$

The equality $\frac{{\bar{\lambda }} -\lambda }{m_0}= \frac{{\bar{\lambda }}}{{\bar{m}}}$ implies that $\frac{ \lambda }{ m}= \frac{{\bar{\lambda }}}{{\bar{m}}}$, so we have $\frac{1}{|{\mathbf {q}}_i-{\mathbf {q}}_0|^3}= \frac{ \lambda }{ m}$ for $i=1,\ldots , n$.

The proof of the sufficient conditions: The first part of system (6) obviously holds. With the condition $\frac{1}{|{\mathbf {q}}_i-{\mathbf {q}}_0|^3}= \frac{ \lambda }{ m}, i=1,\ldots , n$, we obtain

$$\begin{aligned} \begin{aligned} \frac{{\bar{\lambda }}}{{\bar{m}}}&= {\bar{U}} /({\bar{m}} {\bar{I}}) = \frac{U + \sum _{i=1}^n \frac{m_0m_i}{r_{i0}}}{\sum _{0 \le i< j \le n} m_im_jr_{ij}^2} = \frac{U + \sum _{i=1}^n \frac{m_0m_i}{r_{10}} }{ mI + \sum _{i=1} ^n m_0m_ir_{i0}^2 } \\&= \frac{\lambda I + \frac{m_0 \lambda r_{10}^3}{r_{10}} }{ mI + m_0m r_{10}^2 } =\frac{ \lambda }{ m}. \end{aligned} \end{aligned}$$

The equality $\frac{ \lambda }{ m}= \frac{{\bar{\lambda }}}{{\bar{m}}}$ implies that $\frac{ \lambda }{ m} = \frac{{\bar{\lambda }} -\lambda }{m_0}= \frac{{\bar{\lambda }}}{{\bar{m}}}$, so we have

$$\begin{aligned} \frac{1}{|{\mathbf {q}}_i-{\mathbf {q}}_0|^3}=\frac{{\bar{\lambda }} -\lambda }{m_0}= \frac{{\bar{\lambda }}}{{\bar{m}}}, \quad i=1,\ldots , n. \end{aligned}$$

Thus, the second part of system (6) holds and the proof is completed. $\square$

Proof of Theorem 5

In the collinear case, Theorem 1 implies that it is possible if and only if $n=2$. For the non-collinear case, Theorems 2 and 3 implies that $r_{01}=\cdots =r_{0n}=r_{12}\cdots =r_{1n} \cdots = r_{n-1,n},$ which happens only if the $n+1$ bodies form a regular polytope. In $R^3$, that is, the equilateral triangle and the regular tetrahedron. On the other hand, it is well known that these configurations with arbitrary masses are central. This completes the proof. $\square$

Proof of Propositions 6 and 7

It is clear from Theorems 2 and 3. $\square$

Proof of Corollary 9

It is clear from the proof of Theorem 3. $\square$

Proof of Theorem 11

Assume that ${\mathbf {q}}_i=(\cos \theta _i, \sin \theta _i)$ and $0=\theta _1< \theta _2<\cdots< \theta _n<2\pi$. The configuration is central if and only if

$$\begin{aligned} \begin{aligned} \sum _{k\ne j} m_k \left( \frac{1}{r^3_{kj}} - \frac{\lambda }{m }\right) ({\mathbf {q}}_k -{\mathbf {q}}_j )&= \sum _{k\ne j} m_k S_{kj} ({\mathbf {q}}_k -{\mathbf {q}}_j )=0, \end{aligned} \end{aligned}$$

(10)

for $j=1,\ldots , n,$ where $S_{kj}= \frac{1}{r^3_{kj}} - \frac{1}{r_0^3}$. Here, we use the fact that $( m / \lambda )^{\frac{1}{3}}=r_0$.

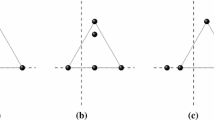
We first show that the two exterior sides incident with ${\mathbf {q}}_1$ are smaller than $r_0$ by contradiction. Note that the sequence $\{ r_{12}, r_{13},\ldots , r_{1n} \}$ is either monotonic or at first increasing and then decreasing.

Case I: $r_{12}\ge r_0, \ r_{n1} \ge r_0$. Then, we have

$$\begin{aligned} r _{k1}> \min \{r_{12}, r_{n1}\}\ge r_0, \ \frac{1}{r^3_{k1}} - \frac{1}{r_0^3} <0, \ k= 3,\ldots , n-1. \end{aligned}$$

That is, $S_{k1}\le 0$ for $k=2,\ldots , n$. Denote by l the line perpendicular with the tangent of the circle at ${\mathbf {q}}_1$ ( the dashed line), see Fig. 1, left, and by $P_l \mathbf{u}$ the orthogonal projection of vector $\mathbf{u}$ along the line l. Then, it is easy to see that

$$\begin{aligned} P_l \left( \sum _{k\ne 1} m_k S_{k1} ({\mathbf {q}}_k -{\mathbf {q}}_1 )\right) = \sum _{k\ne 1} m_k S_{k1} P_l ({\mathbf {q}}_k -{\mathbf {q}}_1 )\ne 0. \end{aligned}$$

Therefore, the first equation of system (10), $0= \sum _{k\ne 1} m_k S_{k1} ({\mathbf {q}}_k -{\mathbf {q}}_1 )$, cannot hold. This is a contradiction.

Fig. 1

Co-circular configuration with $r_{12}\ge r_0, \ r_{n1} \ge r_0$, left, and $r_{12}\ge r_0, \ r_{n1} < r_0$, right

Case II: Only one of the incident exterior sides is smaller than $r_0$, say, $r_{12}\ge r_0, \ r_{n1} < r_0$. Suppose that $\theta _2< \theta _k<\cdots< \theta _L<\theta _{L+1}<\cdots< \theta _n <2\pi$ and that

$$\begin{aligned} r_{1L}\ge r_0, \ r_{1, L+1} <r_0. \end{aligned}$$

That is, $S_{k1}\le 0$ for $k=2,\ldots , L$, and $S_{k1}>0$ for $k=L+1,\ldots , n$. Connect ${\mathbf {q}}_1$ and one point between ${\mathbf {q}}_L$ and ${\mathbf {q}}_{L+1}$ on the circle by the dashed line, and denote by l the line perpendicular with the dashed line, see Fig. 1, right. Then, it is easy to see that

$$\begin{aligned} \begin{aligned}&P_l \left( \sum _{k= 2}^L m_k S_{k1} ({\mathbf {q}}_k -{\mathbf {q}}_1 ) +\sum _{k= L+1}^n -m_k S_{k1} ({\mathbf {q}}_1 -{\mathbf {q}}_k ) \right) \ne 0. \end{aligned} \end{aligned}$$

Therefore, the first equation of system (10), $0= \sum _{k\ne 1} m_k S_{k1} ({\mathbf {q}}_k -{\mathbf {q}}_1 )$, cannot hold. This is a contradiction.

We conclude that the two exterior sides incident with ${\mathbf {q}}_1$ are smaller than $r_0$, i.e., $S_{12}>0, S_{1n}>0$. If the values $S_{12}, S_{13},\ldots , S_{1n}$ are all positive, the equation $0= \sum _{k\ne 1} m_k S_{k1} ({\mathbf {q}}_k -{\mathbf {q}}_1 )$ cannot hold neither, see Figure 1, left. Thus, there is at least a negative one that must correspond to a diagonal. Hence, there is at least one diagonal incident with ${\mathbf {q}}_1$ that is larger than $r_0$.

By symmetry, the statement made for the edges incident with ${\mathbf {q}}_1$ also holds for the edges incident with any other vertex. Therefore, we have proved that all the exterior sides are less than $r_0$ and that there is at least one incident diagonal larger than $r_0$ at each vertex. $\square$

Proof of Corollary 13

If a co-circular configuration lies entirely in a semi-circle, then there is one exterior side longer than all the diagonals. By Theorem 11, it is not central. $\square$

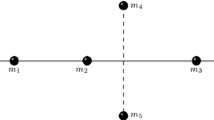
Proof of Corollary 15

We only prove for the six-body case. The other cases are similar. Order the six masses sequentially on the circle as in Fig. 2. First note that the center of the circle, O, must be in the convex hull of the six masses since the masses are not in a semi-circle. Assume that $r\ge r_0$. Then, Theorem 11 implies that

$$\begin{aligned} r_{12}, r_{23}, r_{34}, r_{45}, r_{56}, r_{61} < r. \end{aligned}$$

Fig. 2

An example of a co-circular configuration. The center of the circumscribing circle is marked with O

This implies that each of the six angles $\angle {\mathbf {q}}_1O {\mathbf {q}}_2, \angle {\mathbf {q}}_2O {\mathbf {q}}_3, \angle {\mathbf {q}}_3O {\mathbf {q}}_4,$ $\angle {\mathbf {q}}_4O {\mathbf {q}}_5$, $\angle {\mathbf {q}}_5O {\mathbf {q}}_6$, $\angle {\mathbf {q}}_6O {\mathbf {q}}_1$, is strictly less than $\pi /3$. It is a contradiction since the sum has to be $2\pi$. $\square$

Theorem 17 and Proposition 18 will be proved in Sect. 4.

Proof of Proposition 19

The proof of the necessary conditions: By Albouy (2003), Ouyang et al. (2004), the subconfiguration ${\mathbf {q}}$ must be central. Thus, both the pyramidal configuration and the subconfiguration are central and ${\mathbf {q}}_0\ne c$. Then, the other conditions follow easily from Theorem 3.

The proof of the sufficient conditions: By Theorem 3, if these conditions are satisfied, the pyramidal configuration ${\bar{{\mathbf {q}}}}$ must be central. $\square$

4 The Extensions of Two-, Three-, Four-, and More-Body Central Configurations

In this section, we discuss the $(n+1, 1)$-stacked central configurations for small n. If $n\le 4$, we understand thoroughly the extensions. For each n, we discuss the extensions to planar central configurations and spatial ones separately.

4.1 Two Bodies to Three

There is only one two-body central configuration, namely a segment with two arbitrary masses at the ends. The multiplier is $\lambda = U/I =m/r_{12}^3$, so $r_0=(\frac{m}{\lambda })^{\frac{1}{3}}=r_{12}$. It is obviously co-circular, and the circumscribed circle is not unique. The radius is in the range $[\frac{r_{12}}{2}, \infty )$.

• To planar: It is easy to see that the center of mass coincides with the geometric center if and only if the two masses are equal. In this case, we could extend it by adding an arbitrary mass $m_0$ at the center, which is a symmetric three-body collinear central configuration.

  Since $r_0=r_{12}$, the range of radius of the circumscribed circle is $[\frac{r_0}{2}, \infty )$. It is easy to see that we can extend it by adding one arbitrary mass $m_0$ on the orthogonal bisector of $\overline{{\mathbf {q}}_1{\mathbf {q}}_2}$ such that $r_{01}=r_{02}=r=r_0=r_{12}$. The three masses are all arbitrary and the triangle is equilateral. In other words, we have provided another proof of the well-known fact that the equilateral triangle with three arbitrary masses is central (Lagrange 1772).

• To spatial: Not exist.

Except the symmetric three-body collinear ones, there are other (3, 1)-stacked collinear central configurations. Assume that the central configuration is on the x-axis, with positions $x_1, x_2$, $x_1<x_2$. For any given mass $m_0$, it is easy to show that there is a unique position $x_0$ in each of the three intervals, $(-\infty , x_1), (x_1, x_2),$ and $(x_2, \infty )$, such that the configuration $(x_1, x_2, x_3)$ is central, which is the well-known three-body collinear Eulerian central configurations (Euler 1767).

For $n\ge 3$, by Theorem 1, an $(n+1, 1)$-stacked central configuration must be non-collinear. Recall that an n-body collinear configuration cannot extend to an $(n+1, 1)$-stacked non-collinear central configuration by the perpendicular bisector theorem (Moeckel 1990). Therefore, we only need to consider the extension of n-body non-collinear central configurations.

4.2 Three Bodies to Four

This has been considered by Hampton (2005b). In the three-body case, the only non-collinear central configuration is the equilateral triangle with three arbitrary masses, which is co-circular. It is easy to see that $r_0=(\frac{ m}{ \lambda })^{\frac{1}{3}}=r_{12}=r_{13}=r_{23}=\sqrt{3}r$.

• To planar: It is easy to see that the center of mass coincides with the geometric center if and only if the three masses are equal. In this case, we could extend it by adding an arbitrary mass $m_0$ at the center.

  There is no other (4, 1)-stacked planar central configurations since $r_0>r$.

• To spatial: As mentioned above, $r_0=\sqrt{3}r$ holds for any equilateral triangle central configuration. Thus, any equilateral triangle central configuration can extend to a pyramidal central configuration by adding one arbitrary mass $m_0$ such that $r_{10}=r_{20}=r_{30}=r_0=r_{12}$. In other words, we have provided another proof of the well-known fact that the regular tetrahedron with four arbitrary masses is a central configuration.

  There is no other (4, 1)-stacked spatial central configurations since the three-body central configurations are not co-spherical.

4.3 Four Bodies to Five

In the four-body case, the only spatial central configuration is the regular tetrahedron with arbitrary masses, which is co-spherical. On the other hand, the co-circular central configurations are very rich, and it has been studied thoroughly by Cors and Roberts (2012).

• To planar: By Hampton (2005a), the only one four-body co-circular central configuration with center of mass at the geometric center is the square with equal masses, which leads to a (5, 1)-stacked planar central configuration by adding an arbitrary mass $m_0$ at the center.

  There is no other (5, 1)-stacked planar central configurations since $r_0>r$ by Corollary 15.

• To spatial: Any four-body co-circular central configuration (Cors and Roberts 2012) could extend to a five-body pyramidal central configuration.

  It is easy to see that the center of mass of the regular tetrahedron central configuration coincides with the geometric center if and only if the four masses are equal. In this case, we could extend it by adding an arbitrary mass $m_0$ at the center.

  There is no other (5, 1)-stacked spatial central configurations since that $r_0=r_{12}=\frac{2\sqrt{6}}{3}r$ for any regular tetrahedron central configuration.

This discussion proves Theorem 17.

Remark 21

Fernandes–Mello in 2013 Fernandes and Mello (2013a) also announced that the four-body central configuration of a (5, 1)-stacked central configuration must be the square with equal masses. However, their original proof contains a flaw, which is fixed in Fernandes and Mello (2018). On page 302 of Fernandes and Mello (2013a), where the authors claim that the equation $r^3={\bar{m}} /{\bar{\lambda }}$, (with our notations), leads to a quadratic polynomial in $m_0$. But from the proof of Theorem 3, we see that if $r^3= m/\lambda$, in which no $m_0$ is involved, then $r^3={\bar{m}} /{\bar{\lambda }}$ is just an identity for any $m_0$. Chen-Hsiao pointed out this flaw in 2018 Chen and Hsiao (2018).

Cors and Roberts (2012) showed that the four-body co-circular central configurations form a two-dimensional surface parameterized by two of the edge lengths. Thus, the five-body pyramidal central configurations also form a two-dimensional surface. A direct corollary is as follows.

Proposition 22

Not all choices of five positive masses lead to a five-body pyramidal central configuration.

The property of the five-body pyramidal central configurations is really rich. We state some properties about them. They are straightforward corollaries of the results in Cors and Roberts (2012).

Proposition 23

For a five-body pyramidal central configuration, let $m_1, m_2, m_3, m_4$ be the four masses of the co-circular base. If just two of the four masses are equal, then the base configuration is symmetric, either a kite or an isosceles trapezoid. If any three of the four masses are equal, then the base configuration is a square and all four masses are necessarily equal.

4.4 Five and More Bodies

In the five- and more-body case, both the co-circular and co-spherical central configurations are rich, but much less research has been done in this direction. We only state some results known to us.

• To planar: Obviously, the regular n-gon $(n\ge 5)$ with equal masses leads to $(n+1, 1)$-stacked central configurations by adding one mass at the center. However, until now, we do not know any other co-circular central configuration whose center of mass is at the geometric center, since the question of Chenciner remains unsolved for $n\ge 5$, see the comment after Proposition 7.

  There is no other (6, 1)-stacked ((7, 1)-stacked) planar central configurations since $r_0>r$ by Corollary 15. For more bodies, we have not found any general example yet.

• To spatial: Any five-body (six-body) co-circular central configuration could extend to a six-body (seven-body) pyramidal central configuration. For more bodies, we have no general result, see Sect. 5.1.

  For the five to ten-body cases, We have some examples of co-spherical central configurations whose center of mass equals the geometric center, see Sect. 5.2. In those cases, we could extend it by adding an arbitrary mass $m_0$ at the center.

  For $n\ge 5$, we do not know that whether there exist n-body co-spherical central configurations with $r=r_0$ or not.

This discussion proves Proposition 18.

5 Regular Polygons and Some Examples of Co-spherical Central Configurations

In this section, we discuss the regular polygonal central configurations and construct some co-spherical central configurations. Some of them have center of mass at the sphere center. Thus, they can extend by adding one mass at the center.

5.1 Regular Polygons

Consider the regular n-gon with equal masses. Obviously, they can extend to planar central configurations by adding one mass at the center. Whether they can extend to pyramidal central configurations depends on the measurement of $r_0$ and r. The following result was first shown by Ouyang et al. (2004).

Proposition 24

The regular n-gon with equal masses can extend to pyramidal central configurations if and only if $n\le 472$.

We repeat the idea of their proof here. For the regular n-gon with equal masses, assume that the radius of the circle is 1. Direct computation leads to $r_0^3=\frac{n}{ A(n)}$, with $A(n)=\frac{1}{4}\sum _{ k=1} ^{n-1} \csc (\frac{k\pi }{n})$. It has been found by Moeckel and Simó (1995) that $\frac{ n}{A(n)}$ is decreasing, and $\frac{ n}{A(n)}\ge 1$ if and only if $n\le 472$.

5.2 Co-spherical Central Configurations

There are much less research on co-spherical central configurations, compared with the co-circular ones. Corbera et al. (2014) constructed three families of central configurations, each consisting of a regular polyhedron and its dual. In each family, there is a co-spherical one, and the center of mass equals its geometric center.

We construct some co-spherical central configurations by adding some bodies to some co-circular ones. Let us introduce some notations that will be used only in this subsection. For distinction, we denote by $r, r_0$ (resp. $R, R_0$) the radius of the circumscribing circle and the cube root of the ratio of total mass and the multiplier, respectively, for co-circular (resp. co-spherical)central configurations. In other words, $R^3_0=(\frac{m}{\lambda })$, but only for co-spherical central configurations. In this subsection, the mass at the top vertex of an $(n+1)$-body pyramidal configuration is denoted by $m_{n+1}$ and the position by ${\mathbf {q}}_{n+1}$.

We want to construct co-spherical central configurations that can extend as in case II and III of Proposition 7. That is, we want the center of mass to be at the sphere center, or, $R_0=R$.

5.2.1 Pyramidal Central Configurations

Recall that an $(n+1)$-body pyramidal central configuration is obtained by adding one arbitrary mass $m_{n+1}$ to a co-circular central configuration with the property $r_0>r$. The top vertex ${\mathbf {q}}_{n+1}$ is on the orthogonal axis passing through the center of the circle, and the height is $h= \sqrt{ r_0^2 -r^2}$. Obviously, pyramidal configurations are co-spherical.

Proposition 25

Let ${\mathbf {q}}$ be an $(n+1)$-body pyramidal central configuration. Assume that the center of mass of the co-circular base is at the center of the circumscribing circle. We can choose $m_{n+1}$ such that the center of mass of the pyramidal central configuration coincides with the circumscribing sphere center if and only if $r_0>\sqrt{2}r$.

Fig. 3

Slice of a pyramidal central configuration. The center of the circumscribing sphere is marked with O

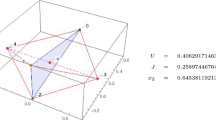
Proof

Obviously, the sphere center O is between the base and $m_{n+1}$ if and only if $h= \sqrt{ r_0^2 -r^2}>r$, see Fig. 3, left. That is, $r_0>\sqrt{2}r$. The center of mass is always between the base and $m_{n+1}$. Thus, to make the center of mass equals the sphere center, we must have $r_0>\sqrt{2}r$.

On the other hand, if $r_0>\sqrt{2}r$, it is easy to find $m_{n+1}$ such that the two centers equal. $\square$

Proposition 26

Let ${\mathbf {q}}$ be an $(n+1, 1)$-stacked pyramidal central configuration extended from an n-body co-circular central configuration. Then $R_0=R$ if and only if $r_0=\frac{2}{\sqrt{3}} r$.

Proof

By Corollary 9, we see that $R_0=r_0$. Note that $r_0 = R$ if and only if that $\alpha = 60^\circ$, or, $\sin \alpha = \frac{r}{r_0}= \frac{\sqrt{3}}{2}$, see Fig. 3, right. $\square$

Examples: Consider the central configurations of regular n-gon with equal masses. Suppose that the $m_1=1$, the radius of the circle is 1, and that the positions are ${\mathbf {q}}_k= e^{ \sqrt{-1} \theta _k}, \ \ \theta _k= \frac{2k\pi }{n}, \ k=1,\ldots , n.$ Recall that $\frac{r_0}{r}=(\frac{n}{ A(n)})^\frac{1}{3}$, and it is decreasing with respect to n.

Computation by MATLAB shows

$$\begin{aligned} \left( \frac{8}{ A(8)}\right) ^\frac{1}{3}>\sqrt{2}, \ \left( \frac{9}{ A(9)}\right) ^\frac{1}{3}<\sqrt{2}, \ \ \left( \frac{52}{ A(52)}\right) ^\frac{1}{3}> \frac{2}{\sqrt{3}}, \ \left( \frac{53}{ A(53)}\right) ^\frac{1}{3}< \frac{2}{\sqrt{3}}. \end{aligned}$$

We can draw two conclusions about the $(n+1, 1)$-stacked pyramidal central configurations extended from the regular n-gon central configurations $(n\le 472)$, see Fig. 4, left.

• (1) $R_0\ne R$;

• (2) Only for $n=3, 4, 5, 6, 7, 8$, we can choose a proper top mass to make that the center of mass of the pyramidal central configuration coincides with the sphere center. They lead to $(n+2, 1)$-stacked central configuration by adding one arbitrary mass at the center. As commented after Proposition 19, the total collision solutions associated with them are perverse solutions of the $(n+2)$-body problem (Chenciner 2004). This was noticed first by Ouyang et al. (2004).

5.2.2 Bipyramidal Central Configurations

By bipyramidal configurations, we mean configurations of $n+2$ bodies of which n bodies are coplanar and the other two being off the plane and in opposite directions. The regular n-gon with equal masses also generates $(n+2)$-body bipyramidal co-spherical central configurations. Similar construction has been considered by Zhang and Zhou (2001).

Place the n-gon with equal masses on the equator, and two equal masses at the north and south pole, see Fig. 4, right. Assume that the masses are $m_1=1,\ldots ,m_n= 1, m_{n+1}=m_{n+2}=a$, and the positions are ${\mathbf {q}}_k=( \cos \theta _k, \sin \theta _k, 0 ), \ \theta _k= \frac{2k\pi }{n}, k=1,\ldots , n, \ {\mathbf {q}}_{n+1}=( 0,0,1 ),\ {\mathbf {q}}_{n+2}=( 0,0,-1 ).$

Fig. 4

Examples of co-spherical central configuration generated from the equilateral triangle configuration

The center of mass is at the origin. The symmetry reduces the central configuration equations to the following system:

$$\begin{aligned}&-\lambda {\mathbf {q}}_1= \sum _{i=2}^n\frac{{\mathbf {q}}_k-{\mathbf {q}}_1}{r_{k1}^3} + a \frac{{\mathbf {q}}_{n+1} -{\mathbf {q}}_1}{r_{n+1,1}^3} +a \frac{{\mathbf {q}}_{n+2}-{\mathbf {q}}_1}{r_{n+1,1}^3}= -\left( A(n)+ \frac{a}{\sqrt{2}}\right) {\mathbf {q}}_1, \\&-\lambda {\mathbf {q}}_{n+1} =\sum _{i=1}^n\frac{{\mathbf {q}}_k-{\mathbf {q}}_{n+1}}{r_{n+1,k}^3} + a\frac{{\mathbf {q}}_{n+2}-{\mathbf {q}}_{n+1}}{r_{n+1,n+2}^3}= -\left( \frac{n}{2\sqrt{2}} +\frac{a}{4} \right) {\mathbf {q}}_{n+1}. \end{aligned}$$

Here we use the fact that $r_{n+1, 1}=\cdots =r_{n+1, n}=\sqrt{2}, r_{n+1, n+2}=2$ and that the subconfiguration on the equator is central:

$$\begin{aligned} \sum _{i=2}^n\frac{{\mathbf {q}}_k-{\mathbf {q}}_1}{r_{k1}^3} = - \frac{1}{r_0^3} \left( \sum _{i=1}^n m_i \right) {\mathbf {q}}_1= - \frac{A(n)}{n} n {\mathbf {q}}_1. \end{aligned}$$

The system holds for positive $a=m_{n+1}$ if and only if $\frac{n}{A(n)}> 2\sqrt{2}.$ We have shown that this happens if and only if $3\le n\le 8.$

Proposition 27

The bipyramidal $(n+2)$-body configurations constructed above are central with positive masses if and only if $3\le n\le 8$.

For all of them, the center of mass equals the sphere center. Thus, they extend to $(n+3, 1)$-stacked configurations by adding one arbitrary mass at the center. Direct computation shows $R_0=(\frac{ m}{ \lambda })^{\frac{1}{3}} >R=1$ for all of them.

6 Conclusions

We have classified the extensions of n-body central configurations to $(n+1)$-body central configurations in $R^3$. For the collinear case, the extensions happen only if $n= 2$, so it is well understood. For the non-collinear case, the n-body central configurations must be co-circular or co-spherical. The co-circular (co-spherical) central configurations can extend if the center of mass equals the geometric center, or $r_0\ge r$ ($r_0=r$ for the co-spherical case). We also obtain a property on the value of $r_0$ for co-circular central configurations. This enables us to prove the inequality $r_0>r$ for all four-, five-, and six-body co-circular central configurations. We solve the two questions of Hampton completely. It might be worth noting that most of our proof remains valid for more general potentials and higher dimensional spaces.

There exist many research works on co-circular central configurations. We hope that this work may spark similar interest to the co-spherical ones. The value $r_0=(\frac{ m}{ \lambda })^{\frac{1}{3}}$ has shown its importance in the study of four- and five-body planar convex central configurations (Chen and Hsiao 2018; MacMillan and Bartky 1932). Our work reveals its another role in the study of central configurations. Many questions arise for the value $r_0$. For example, except from the trivial case $n=2$, do there exist co-circular or co-spherical central configurations with the property $r_0=r$? Can one obtain some general property of $r_0$ for the co-spherical central configurations? We hope to explore some of these questions in future work.