Keywords

1 Introduction

Leon Chua in 1971 [1] depicted and named the fourth crucial electrical element by finishing a hypothetical group of the other three (resistor, capacitor, and inductor). The name of this element was memristor. A memristor is a non-direct two-terminal electrical element relating electric charge and magnetic flux linkage [2]. In a memristor, its resistance decreases when the current flows in a single way and the opposite [3]. At the point when the current stream is halted, memristor holds its last state.

The idea of memristive framework was subsequently summed up by Chua and Kang [4]. Such a framework contains a circuit, of various ordinary elements, which mirrors key properties of the ideal memristor element. The distinguishing proof of memristive properties in electronic elements has drawn in discussion. Tentatively, the ideal memristor is yet to be illustrated [5, 6]. Notwithstanding, a couple of executions interesting circuits have as of late utilized ReRAM memristive models [7,8,9]. Thus, a physical model of memristor is essential, to understand in depth this fourth circuit element.

Furthermore, while studying the semiconductor conduct of silver sulfide in 1833, Michael Faraday [10] discovered the concept of thermistors. As the temperature rose, he saw that the silver sulfides’ opposition decreased. Following it, in 1930, Samuel Ruben invented the basic commercial thermistor [11]. Also, Steinhart and Stanley Hart [12] discovered a capability that thermistor’s characteristics have, i.e., the resistance as a function of temperature, which turned out to be appropriate for a wide range of thermistors for ranges of a couple of degrees to two or three hundred degrees. Furthermore, Sah et al. [13] investigated a second-order memristor that depicts the model of a physical device known as a Positive Temperature Coefficient and Negative Temperature Coefficient thermistor coupled in series.

Thermistors are commonly employed as a linear resistor whose resistance fluctuates with temperature. A negative-temperature coefficient thermistor, in particular, is distinguished by Chua and Kang [4]

(11.1)

where β is the material constant, T is the thermistor temperature, and T 0 is the room temperature both in kelvin. The characteristic curve of the thermistor is modeled with the classical equation of Steinhart–Hart as shown in [14]. The constant R 0(T 0) denotes the cold temperature resistance at T = T 0. The instantaneous temperature T is a function of the power dissipated in the thermistor. Moreover, thermistor is governed by the heat transfer equation

$$\displaystyle \begin{aligned} p(T)=v_T(t)i(t)=\delta(T-T_0) + c\frac{dT}{dt}, \end{aligned} $$
(11.2)

where c is the heat capacitance and δ is the dissipation constant of the thermistor.

By combining Eqs. (11.1) and (11.2), it is obtained

$$\displaystyle \begin{aligned} \frac{dT}{dt}=-\frac{\delta}{c}(T-T_0) + \frac{R_0(T_0)}{c}exp\left[\beta \left(\frac{1}{T} - \frac{1}{T_0}\right)\right]i^2. \end{aligned} $$
(11.3)

As a result of Eq. (11.3), the thermistor is a first-order time-invariant current-controlled memristive. In this study, an autonomous three-dimensional system [14] with a thermistor was converted to a non-autonomous system by introducing an external alternating current source and a linear resistor into the model.

In this chapter, a detailed investigation of the dynamical behavior of the proposed non-autonomous circuit for different values of the capacitance of the capacitor, as well as the inductance of the inductor and the initial conditions, is presented. The capacitance is studied in the region of 0 and 2 F. Also, the inductance belongs between 0 and 15 H. This work is based on the simulation results, which are produced by using well-known numerical tools, such as Lyapunov exponents [15, 16], bifurcation diagrams [17], and Poincaré section. The calculation of the bifurcation diagrams is performed by computing the Poincaré map of the system. The sampling of the Poincaré map is done with the time being an integer multiple of the external period of the system, excluding the transient points. Also, the Lyapunov exponents are computed based on the algorithm from Sandri’s [18] package in Mathematica.

The work is organized as follows. In Sect. 11.2, the proposed circuit and its properties are introduced. In Sect. 11.3, the numerical investigation of the circuit’s dynamics is presented. Finally, the conclusions of this work are discussed in Sect. 11.4.

2 The Proposed Nonlinear Circuit

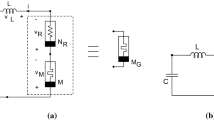
The proposed framework depends on the independent Muthuswamy–Chua–Ginoux circuit [14], which is changed over to a non-independent circuit by utilizing an external voltage source. The framework comprises a resistor R, a capacitor of capacitance C, an inductor of inductance L, a nonlinear resistor N R, a thermistor that is a nonlinear locally active memristor M, and an external AC voltage source. The previously mentioned circuit is displayed in Fig. 11.1.

Fig. 11.1
figure 1

Non-autonomous converted Muthuswamy–Chua–Ginoux circuit

Full size image

The nonlinear resistor is modeled [14] as a cubic function of the current and it is given by f(i) = αi + bi 3. Also as shown in [14] by using Kirchhoff’s law for voltages in the left and right loop of the system, the following equations for the voltages are produced:

$$\displaystyle \begin{aligned} V_S=V_R + V_C \end{aligned} $$
(11.4)
$$\displaystyle \begin{aligned} V_C + V_L + V_{N_R} + V_M = 0, \end{aligned} $$
(11.5)

where V L is the voltage of the inductor and it is given by \(V_L=L\frac {di_L}{dt}\).

In Eq. (11.4), \(V_S = V_0 \cos {}(2\pi ft)\) is the external ac voltage, V R is the voltage of the linear resistance, and V C is the voltage of the capacitor.

The voltage of the nonlinear resistor is modeled as a cubic function, and it is given by

$$\displaystyle \begin{aligned} V_{N_R}=f(i_L)=\alpha i+bi^3, \end{aligned} $$
(11.6)

where α and b are constants. The voltage of the thermistor is given by Ohm’s law and its equation is V M = R(T)i L. By taking Eq. (11.4) into account and since the current from the capacitor is given by \(i_C = C\frac {dV_C}{dt}\) and also from the equation of the currents which is Kirchhoff’s first law i R = i L + i C, the equations of the system are obtained.

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \frac{dV_c}{dt}& =&\displaystyle \frac{V_S}{RC}-\frac{i_L}{C}-\frac{V_c}{RC} \\ \frac{di_L}{dt}& =&\displaystyle -\frac{1}{L}\left(V_c+f(i_L)+R(T)i_L\right) \\ \frac{dT}{dt}& =&\displaystyle \frac{R(T)}{c}i_L^2-\frac{\delta}{c}(T-T_0). \end{array} \end{aligned} $$
(11.7)

By using the following approximation [14], R(T) is given:

$$\displaystyle \begin{aligned} R(T)=R_0\left[1 - \frac{\beta}{T_0^2}(T-T_0) + \frac{\beta(\beta + 2T_0)}{2T_0^4}(T-T_0)^2 + O((T-T_0)^3) \right]. \end{aligned} $$
(11.8)

To work on the investigation of system (11.7), a change to system’s variable is made as

$$\displaystyle \begin{aligned} x=V_C, y=i_L, z=T-T_0. \end{aligned}$$

Also, the following changes to equation’s (11.8) parameters have been used.

$$\displaystyle \begin{aligned} \theta=\frac{R_0}{c}, \gamma=-\frac{R_0}{c}\frac{\beta}{T_0^2}, \mu=\frac{R_0}{c}\frac{\beta(\beta+2T_0)}{2T_0^4}, \epsilon=\frac{\delta}{c}. \end{aligned}$$

Finally, the set of Eqs. (11.7) of system has been transformed to the following set of equations:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \frac{dx}{dt}& =&\displaystyle \frac{V_s}{RC}-\frac{x}{RC}-\frac{y}{C} \\ \frac{dy}{dt}& =&\displaystyle -\frac{1}{L}\left(x+f(y)+R(z)y\right) \\ \frac{dz}{dt}& =&\displaystyle R(z)y^2-\epsilon z, \end{array} \end{aligned} $$
(11.9)

where f(y) = αy + by 3 and R(z) = μz 2 + γz + θ. The basic difference of this system, from the system of equation (4) in [14], is the dependence of the time and the existence of more elements in the circuit. Also the units of the variables are in S.I. and especially the capacitance in F, the resistance in Ω, the voltage in V, the frequency in Hz, and the inductance in H.

3 Numerical Results

In this section, the dynamical behavior of the proposed, non-autonomous, system (11.9) with V 0 ≠ 0, C ≠ 0, and R ≠ 0 for different values of the capacitance of the capacitor C, the inductance L of the inductor, and the initial conditions is investigated. Generally, the system has rich dynamics that include regular (periodic and semi-periodic) and chaotic oscillations. Also, small changes in the inductance L and in the initial conditions produce a shift between chaotic and regular oscillations and the existence of coexisting attractors, respectively.

3.1 The Dynamics Related to the Capacitance C

Figure 11.2 presents the bifurcation diagram of the x variable, which is the voltage of the capacitor, in regard to the capacitance of the capacitor C. Moreover, the values of parameters of the system are V 0 = 1.0 V, R = 5 Ω, f = 0.5 Hz, \(\alpha =-6\,\Omega , b=3\frac {\Omega }{A^2}, L=12.2\,\text{H}, \mu =3 \frac {\Omega \text{kg}}{\text{J K}}, \gamma =-2 \frac {\Omega \text{kg}}{\text{J}}, \theta =3 \frac {\Omega \text{kg K}}{\text{J}},\) and \(\epsilon =0.6 \frac {\text{kg K}}{\text{J}}\). The parameters have been set to these values for two reasons. The first reason is because of the exponential behavior of R(T). More specifically, the resistance of the thermistor R(T) is supposed to be positive, and as a consequence, the right hand of Eq. (11.8) must be positive. The second reason is to find chaotic behavior. Also, the initial conditions are x 0 = 0.01, y 0 = 0, and z = 0. From this bifurcation diagram, a rich dynamical behavior of the system is investigated in regard to the capacitance C. There are regions where the system oscillates chaotically and regions where the system oscillates regularly. In more detail, system’s dynamic behavior is chaotic for C < 0.06 F. Then, the system goes to regular behavior (periodic) and finally to semi-periodic behavior. The maximal Lyapunov exponent diagram verifies this rich dynamical behavior and indicates that after the value of the capacitance (C = 0.38 F) the system goes to semi-periodic behavior for all the range of the bifurcation parameter. Figure 11.3 presents the maximal Lyapunov exponent, where when the exponent is positive, that means the existence of chaotic behavior (chaotic oscillations) and when it is not positive, that means the system has a regular behavior (periodic and semi-periodic oscillations).

Fig. 11.2
figure 2

(a) Bifurcation diagram of x versus the capacitance C and (b) zoom in specific region

Full size image
Fig. 11.3
figure 3

(a) Maximal Lyapunov exponent diagram and (b) zoom in specific region

Full size image

By taking a value of the capacitance (C = 1.0 F), the system is solved, and the time series of signals x, y and z and the respective phase portrait are presented in Fig. 11.4. Thus, from time series and from the phase, the portrait is observed that the orbit fills densely. So the conclusion is that the orbit is semi-periodic, which is also confirmed from the Poincaré section and maximal Lyapunov exponent of Fig. 11.5 where the maximal Lyapunov exponent is equal to mLCE = 0.000002. Also, the whole Lyapunov spectrum is (0.000002, 0, −0.0539074). Moreover, the Kaplan–Yorke conjecture [18,19,20] calculated from equation

$$\displaystyle \begin{aligned} D=j+\frac{\sum_{i=1}^{j} \lambda_i}{|\lambda_{j+1}|}, \end{aligned} $$
(11.10)

where λ i are the Lyapunov exponents, is equal to D = 2.0. This means that it is a torus of dimension 2.

Fig. 11.4
figure 4

(a), (b), (c) Time response for x,y and z variables and (d) phase portrait of system in x–y plane for V 0 = 1.0 V and C = 1.0 F

Full size image
Fig. 11.5
figure 5

(a) Poincaré section and (b) maximal Lyapunov exponent of system for V 0 = 1.0 V and C = 1.0 F

Full size image

3.2 The Dynamics Related to the Inductance L

In this section, the numerical results from the simulations regarding the value of inductance L are presented. The bifurcation diagram in regard to the parameter L for specific values of the capacitance of the capacitor C and the amplitude V 0 of the AC voltage source has been produced. In Fig. 11.6, the bifurcation diagram is presented in regard to the inductance L for C = 0.01 F and V 0 = 1.0 V, and in Fig. 11.7, the diagram of maximal Lyapunov exponent is depicted. From the bifurcation diagram of Fig. 11.6, it is observed that the dynamical behavior is changing between chaotic and regular as the inductance L increases, through period-doubling routes. This behavior is also confirmed from the maximal Lyapunov diagram of Fig. 11.7, where the maximal Lyapunov exponent is positive in chaotic regions and no positive in non-chaotic regions. Also, in Fig. 11.8, it is presented the time response of signal x, the phase portraits, and the Poincaré section of the system for L = 5 H and L = 4 H. It is observed that for L = 5 H the system has chaotic behavior, and for L = 4 H, the system’s behavior is regular and especially periodic with period 2.

Fig. 11.6
figure 6

Bifurcation diagram of system in regard to L for C = 0.01 F

Full size image
Fig. 11.7
figure 7

Maximal Lyapunov diagram of system in regard to L for C = 0.01 F

Full size image
Fig. 11.8
figure 8

(a, b) Time responses of x variable, (c, d) phase portraits, and (e, f) Poincaré section for L = 5 H and L = 4 H, respectively

Full size image

3.3 The Dynamics Related to the Initial Conditions x 0, y 0, z 0

In this subsection, the dynamical behavior of the system is investigated in regard to the initial condition x 0, y 0, z 0. More specifically, the parameters of the system are V 0 = 1.0 V, C = 0.01 F, and L = 12.2 H, and now the linear resistance is changed to a higher value and specially to R = 31 Ω. So, in Fig. 11.9, a bifurcation-like diagram and the maximal Lyapunov exponent diagram in regard to the initial conditions x 0, y 0, and z 0 have been produced.

Fig. 11.9
figure 9

Bifurcation-like diagram and maximal Lyapunov diagram of system in regard to (a, b) x 0, (c, d) y 0, and (e, f) z 0 for C = 0.01 F

Full size image

From the bifurcation-like diagram and the maximal Lyapunov exponent diagram, it is observed the dynamical behavior of the system changes in regard to the initial conditions x 0, y 0, and z 0. More specifically, there are regions where the behavior is only chaotic (2.7 < x 0 < 5.5) and regions where the behavior is only regular (7.7 < x 0 < 8.35). Also, except from these two regions, the behavior of the system is changing rapidly between chaotic and regular behavior, as it is observed from the bifurcation-like and maximal Lyapunov diagrams. Therefore, the existence of coexisting attractors for different initial conditions is observed. In Fig. 11.10, the phase portraits for x 0 = 0.06 (chaotic behavior) and for x 0 = 8.0 (regular behavior) are presented.

Fig. 11.10
figure 10

(a) Chaotic phase portrait of x–y plane for x 0 = 0.06 and (b) periodic phase portrait of x-y plane for x 0 = 8.0

Full size image

4 Conclusion

A three-dimensional non-autonomous chaotic circuit based on a physical memristor is examined, with a thermistor serving as a “local active” memristor. The thought was to consider the dynamical behavior of the autonomous system by embedding an external AC voltage source and a linear resistance R. Plenty of numerical tools to study the dynamical behavior, such as bifurcation and bifurcation-like diagrams, diagrams of maximal Lyapunov exponent, and the Poincaré map, were used.

The non-autonomous system (11.9) presented rich dynamical behavior. Chaotic and regular behavior were observed. More specifically, chaotic, periodic, and semi-periodic orbits were revealed. Moreover, the system presented route to chaos through the mechanism of period doubling as well as crisis phenomena. From bifurcation diagrams in regard to the capacitance C, it is observed that as the capacitance increases from C = 0.01 F to C = 2.0 F, the dynamical behavior of the system becomes regular (semi-periodic) in all the range as it is presented.

The second approach to our system was to change the inductance L and study the dynamical behavior. In this case, it is observed that, as the inductance increases, the dynamical behavior is changing between regular and chaotic as shown from the bifurcation diagram, as well as from the time responses for L = 5 H and L = 4 H. More specifically, periodic windows inside chaotic regions were observed.

Finally, the last approach was to change the initial conditions x 0, y 0, and z 0. In this approach, it is observed that as the initial conditions are increasing, the chaotic behavior is changing to the regular behavior rapidly. Also, the existence of coexisting attractors was presented. What is more, regions where the behavior is only chaotic and regions where the behavior is only regular were observed. As a recommendation, it would be interesting to investigate the dynamical behavior of the system, by changing the function that describes the nonlinear resistance, as well as by replacing the thermistor with a real memristor.