Integrating supplier selection decisions into an inventory location problem for designing the supply chain network

Abstract

This paper proposes a novel Inventory-Location problem that integrates supplier selection decisions to design a three-echelon supply chain network, under a continuous (s,Q) inventory control policy at the warehouses. In this problem, a set of warehouses must be selected within a set of potential locations to serve several customers or demand zones, additionally involving the selection of the suppliers for fulfilling incoming orders from the located warehouses. The optimal solution must be determined while minimizing total system costs including supplier selection, transportation (i.e., suppliers-warehouses and warehouses-customers), inventory (i.e., cycle and safety stock), and warehouse location costs. A key element of the problem is the consideration of variable lead-times for the warehouses, which are dependent on the selection of the supplier that serve them, thus increasing model complexity. Accordingly, an efficient algorithm based on the Generalized Benders Decomposition is developed and implemented to solve the proposed Mixed Integer, Nonlinear, Nonconvex, Programming Model. The proposed solution approach relies on a convenient model formulation and decomposition that yields a Mixed Integer Linear master problem and a continuous, convex subproblem. A wide set of medium-sized synthetic instances are optimally solved in affordable times, denoting the efficiency and effectiveness of the proposed model along with the proposed solution approach. Significant scientific and managerial insights are provided and discussed.

1 Introduction

Supply chain management (SCM) is a significant trend within modern administration and management, which aims at planning and controlling all the involved resources and activities in order to ensure that products and services are provided at the right times, quantities and places, while systemwide costs are minimized and established service levels are guaranteed (Escalona et al. 2015; Farahani et al. 2015; Melo et al. 2009; Simchi-Levi et al. 2003).

Within the scope of SCM, the network of facilities involved is of substantial significance, where decisions of warehouse and plant location, demand zone design and assignment, inventory deployment, and supplier selection, among others, are usually embraced, which may condition or determine the company’s success. In this context, supply chain network design (SCND) is a challenging and relevant problem in SCM and in strategic management for most companies nowadays. Thus, SCND consists in determining the number and location of facilities, such as plants, warehouses or distribution centers, and the manner in which these facilities are connected among each other, and serve external or end customers. In any supply chain network (SCN), supplying management and planning (for raw materials or spare parts) are crucial since an inappropriate way to deal with them may cause significant system failures and inefficiencies.

Traditionally, facility location problems (FLP), and more recently Inventory Location Problems (ILP), are suitable and well-known modeling structures for addressing SCND, where the latter explicitly integrates strategic/tactical inventory issues into FLP modelling structure. This integration of inventory issues allows to model a well-known phenomenon in SCM named Risk-Pooling (i.e., the more parallel warehouses operate the more total inventory level is required). Particularly, form a strategic perspective, the selection of the proper suppliers is a relevant decision to be addressed. Although some researches address supplier selection into FLP modeling structure (Benyoucef et al. 2013; Emirhüseyinoğlu and Ekici 2019; Kuderinova et al. 2021; Mota et al. 2018; Vanteddu et al. 2011), ILP literature still does not extensively address this issue. A similar situation occurs in the multilevel uncapacitated location problem (MULP), which can be used to model supply chain networks and an extension of FLP. The decisions to be made include determining which facilities are located on each level and which links are activated between them, but it does not involve inventory management at any level (Ortiz-Astorquiza et al. 2017; Şahin and Süral 2007).

Particularly, integrating these decisions into ILP directly affects inventory levels given the impact of lead-times upon safety stock levels. Consequently, and given the nature of ILPs modeling structure, particularly considering a continuous review-based inventory control policy, safety stocks are proportional to the square root of the multiplication between warehouse demand variance and the faced lead time, both are variables when customer and supplier assignments are modeled and optimized simultaneously. These arguments denote the higher complexity of the studied problem in contrast to previous ILP models without supplier selection decisions, and depicts the need for exact and efficient solution approaches, as proposed in this research.

It is worth pointing out that supplier selection decisions may significantly affect the optimal SCN topology, given the dependency of warehouse safety stocks on these decisions. Accordingly, the way in which supplier selection decisions affect the optimal SCN topology is still an open research and managerial question, which is addressed in this research.

Accordingly, this research aims at studying and modelling supplier selection decisions within an ILP modeling structure, where (s,Q) inventory control policy is considered. Specifically, this paper proposes a novel Inventory Location Problem that explicitly integrates supplier selection decisions, which directly affects the inventory management at each located warehouse. The proposed optimization model is Mixed Integer, Nonlinear, Nonconvex, Programming. Hence, this paper develops and applies a Generalized Benders Decomposition-based solution approach for the proposed novel formulation, which allows to effectively and efficiently deal with the observed high level of complexity. The novel proposed model and solution approach highly contribute to support supply chain (SC) decision makers in designing and planning the SCN configuration, by jointly solving at global optimality warehouse location, customer assignments, inventory control and supplier selection decisions, which is not possible only with existing literature. Particularly, most of previous ILP do not consider supplier selection decisions, while existing models that address supplier selection decisions are usually Mixed Integer Linear Programming formulations and do not consider inventory control issues.

From a managerial perspective, the utilization of the proposed methodology (model and solution approach) would naturally help in obtaining better global solutions instead of decoupling and solving the SCND problem separately. For example, a traditional FLP may be used to optimize warehouse location and customers assignment, and subsequently inventory decisions and supplier selection are addressed based on the previously obtained SCN structure (i.e., warehouse location and customers assignment). Alternatively, a more recent ILP can be employed after defining the suppliers that serve each potential warehouse. In any case, a sequential or hierarchical approach to address the whole problem may lead to more expensive solutions, compared to employing a unique simultaneous optimization problem, as proposed.

The paper is organized as follows. Section 2 provides a discussion of related literature, denoting the research gaps filled by this research. Section 3 presents the problem description along with the proposed model formulation. Section 4 presents the proposed GBD based solution approach. In Sect. 5 the computational implementation and obtained results are presented. In Sect. 6 the main managerial and research insights, and the final Section presents the conclusions and a future research discussion.

2 Literature review

Nowadays, companies are forced to effectively and efficiently manage all their operations, particularly under current fierce competition in global markets, being a significant trend within modern administration and management. SCM aims at coordinately planning and controlling all the involved participants, resources and activities in order to ensure that products and services are provided at the right times, quantities and places, while systemwide costs are minimized and the established system service levels are guaranteed. Moreover, it is required to align all the decisions and participants considering the SC goals (Escalona et al. 2015; Farahani et al. 2015; Melo et al. 2009; Simchi-Levi et al. 2003). SCM aims at efficiently and effectively managing decisions regarding activities, processes and resources throughout the supply chain (SC) system, i.e., suppliers, manufacturers, warehouses, wholesalers, retailers and end consumers (Christopher 2005; Coyle et al. 2003; Melo et al. 2009; Simchi-Levi et al. 2003; Tracey et al. 2005).

From a strategic perspective, the set of involved locations (e.g., suppliers, plants, warehouses, wholesalers, stores, and customers), the manner in which they are interconnected and interrelated, and the way in which inventories (e.g., raw materials, end products and spare parts) are located and managed throughout the SC almost fully define the SCN topology. Notice that the topology itself may condition the efficiency and effectivity, and finally the success of the SC and companies involved, and thus, developing and using systematic approaches to optimize the SCN are crucial. The SCND is a strategic problem where decisions and costs normally span in long term and may impact into the overall performance and competitiveness (Bhutta et al. 2003; Drezner 2014; Farahani et al. 2015; Melo et al. 2009).

Facility location problems (FLPs) have attracted the attention of researchers over the last 50 years (Baron et al. 2011; Current et al. 1990; Dönmez et al. 2021; Drezner 2014; Eiselt and Marianov 2011, 2015; Farahani et al. 2019; A. Geoffrion and McBride 1978; Lin et al. 2022; List et al. 1991; Melo et al. 2009; Ortiz-Astorquiza et al. 2018; Owen and Daskin 1998; ReVelle and Swain 1970; Tcha and Lee 1984; White and Case 1974). These models have been developed and applied in several industrial cases dealing with different types of facilities (de Vries et al. 2020; Drezner 2014; Eiselt and Marianov 2015; Kirschstein and Meisel 2019; Melo et al. 2009; Shahabi et al. 2018). However, supply chain management (SCM) aims at integrating decisions regarding all the supply chain (SC)-related issues, considering the still growing competitiveness of global markets generates pressure over the efficiency on managing the entire SC (Coyle et al. 2003; Simchi-Levi et al. 1997).

It is worth highlighting that the traditional FLP discussed above are consistent with a sequential scheme to address the SCND problem, where decisions belonging to different hierarchical levels are made separately without major concerns on the impacts that decisions may have over other decisions. In this context, facility location problems (FLPs) have captured the attention of several authors through the years. FLPs typically consider strategic decisions (e.g., warehouse location, customer assignment) determining the SCN structure (Emirhüseyinoğlu and Ekici 2019; Gebennini et al. 2009; Melo et al. 2009; Snyder 2006; Tapia-Ubeda et al. 2019; Tapia-Ubeda et al. 2018a, b; Thanh et al. 2008). Consequently, tactic and operational decision are made assuming a previously fixed SCN structure (Bradley and Arntzen 1999; Farahani et al. 2015; Miranda and Garrido 2004; Mourits and Evers 1995; Tapia-Ubeda et al. 2018a, b).

A generalization of FLP without inventory management is the multilevel uncapacitated location problem (MULP). This problem involves the transportation of materials from origin points to final clients through potential facilities of various levels. Şahin and Süral (2007) classify the set of hierarchical location problems as MULP. Ortiz-Astorquiza et al. (2017) extended the MULP by limiting the number of facilities to locate on each level (Multilevel Uncapacitated p-Location Problems, MUpLP). Later Ortiz-Astorquiza et al. (2019) include the link setup cost that connects two located facilities between two consecutive levels (The Multilevel Uncapacitated p-Location problem with Edge Setup Costs, MUpLP-E). Wang and Alidaee (2019) show a particular case for warehouse management for two levels, where each origin has to be assigned an unloading door (first level) while a destination point is assigned a loading door identifying the flow between two levels doors and minimizing the moving cost inside of the warehouse. Our problem can be modeled as an extension of 2-level Uncapacitated Location Problem to identify a single product flow from suppliers to the final client through warehouses incorporating inventory management to guarantee a server level. The suppliers are selected for the first level, while warehouses are located for the second level.

In contrast and based on traditional FLP modeling structure, Inventory Location Problems (ILPs) integrate tactical inventory control-related decisions and costs (Daskin et al. 2002a; Farahani et al. 2015; Jayaraman 1998; Melo et al. 2009; Miranda and Garrido 2004; Tapia-Ubeda et al. 2020). Although some authors also include other related issues on their researches, such as multi-period, multi-product, plant capacity, warehouse capacity, heterogeneous warehouses, ILPs mostly focus on integrating the key inventory control-related decisions aiming at determining a cost-efficient SCN design (Aǧrali et al. 2012; Diabat et al. 2015; Farahani et al. 2015; Pourhejazy and Kwon 2016). Particularly, a growing number of research has been developed in the last two decades (Farahani et al. 2015; Miranda et al. 2019).

Specifically, Jayaraman (1998) introduces a Mixed Integer Programming (MIP) integrating transportation, facility location and inventory decisions with deterministic demands. Erlebacher and Meller (2000), Daskin et al. (2002) and Miranda and Garrido (2004) introduce a Mixed Integer Nonlinear (MINL) problem integrating inventory and facility locations decisions with stochastic demands MINLP formulations, by incorporating safety stock into the analysis and the model, based on the variability of customers demand. Shen et al. (2003) proposes a set-covering reformulation. Miranda and Garrido (2006) and Miranda and Garrido (2008) integrates two capacity constraints obtained through a chance-constraint scheme (i.e., inventory and order size). Ozsen et al. (2009) introduces a MINL problem where retailers can be sourced by more than one source considering a centralized logistic system. Miranda and Garrido (2009) presents a model integrating inventory service level optimization considering unfilled demand related costs. In both Miranda and Cabrera (2010) and Cabrera et al. (2013) a MINP is presented, which integrates stochastic capacity constraints under a periodic inventory control policy (ICP). Kumar and Tiwari (2013), introduces a Mixed Integer Nonlinear Programming model incorporating location, production–distribution, and inventory decisions for designing the SCN and determining the capacity of the located facilities. Escalona et al. (2015) introduces a MINL problem considering differentiated service level considering two demand classes. Ross et al. (2017) and Amiri-Aref et al. (2018) presents MINL problems integrating multi-sourcing and reverse logistic strategies. Tapia-Ubeda et al. (2018a, b) presents a generic modelling structure for ILP considering inventory and facility location decisions for designing the spare parts SCN that is specified for three different suitable and widely used ICPs. Perez Loaiza et al. (2017) and Guerrero Campanur et al. (2018) present approximated methodologies for addressing a SCND problem with inventory and location decisions at two levels (i.e., plant and warehouse location), and sourcing from supplier related decisions. While Perez Loaiza et al. (2017) developed a genetic algorithm that heuristically solve the problem, Guerrero Campanur et al. (2018) proposed a linear approximation for its formulation. Tapia-Ubeda et al. (2019) presents a modelling structure integrating supplier selection, facility location and inventory control decisions considering two sourcing strategies (i.e., warehousing and cross-docking). Liu et al. (2020) introduces an inventory location problem model integrating different supply disruptions affecting operations throughout the SCN. Nasiri et al. (2021) presents a mixed integer nonlinear programming model to determine the optimal pricing of different products. Hajipour et al. (2021) presents a bi-objective mathematical model in order to plan the distribution and inventory of crucial items in the context of disasters.

Despite the several developments regarding ILPs models, most of the research is either made without considering suppliers or assuming that the suppliers are fixed and known. Supplier selection related issues have been studied by analyzing their impact over different SCM issues. Nonetheless, a reduced number of studies integrate SCN aspects (Amid et al. 2006, 2011; Burke et al. 2009; de Treville et al. 2014; Feng and Shi 2012; Georgiadis and Rajaram 2013; Ghassemi et al. 2018; Haq and Kannan 2006; Khalilzadeh and Derikvand 2018; Rienkhemaniyom 2015; Sajedinejad and Chaharsooghi 2018; Tanonkou et al. 2006; Vanteddu et al. 2011; Yu et al. 2014). For instance, Truong and Azadivar (2005) proposes a MIP model for determining the optimal SC configuration integrating different aspects, such as, location, inventory, transportation, production. Liao and Rittscher (2007) develops a multi-objective supplier selection model under stochastic decisions integrating costs and demand satisfaction related issues. Kumar and Tiwari (2013) introduces a two-stage algorithm where the first stage considers a piece-wise lineal function and the second phase enumerates the required capacity for all the located facilities. Mota et al. (2018) proposes a multi-objective MIP integrating sustainable issues into SCM. Emirhüseyinoğlu and Ekici (2019) proposes a dynamic facility location scheme considering an incremental quantity discount. Zhang et al. (2020) integrates reverse logistic issues considering criteria and methods for supplier selection. Lee and Ozsen (2020) introduces a Tabu Search algorithm for solving an Inventory Location model. Liu et al. (2020) presents a two-phase algorithm integrating queuing theory and a hybrid genetic algorithm. Nasiri et al. (2021) proposes a memetic algorithm based on evolutionary algorithm based on genetic algorithm scheme. Cárdenas-Barrón et al. (2021) proposes a multi-item inventory lot-sizing problem considering an extended formulating and valid inequalities. Recently Hajipour et al. (2021) introduces a metaheuristic called Multi-Objective Vibration Damping Optimization for solving the model.

It is worth pointing out that even considering that Perez Loaiza et al. (2017) and Guerrero Campanur et al. (2018) present more complex models compared to this research, they solve the proposed models in a approximated approach based on linearization and genetic algorithms. Tapia-Ubeda et al. (2019) is a related research that presents a preliminary modeling proposal and a generic GBD-based solution approach. However, the latter research does not consider computational implementations for solving problem and does not specify the ICPs employed for the models. Moreover, studying and solving the proposed model in Tapia-Ubeda et al. (2019) represents a further development for this research.

In terms of mathematical complexity, the integration of decisions from different hierarchical levels (e.g., strategic and tactical) may yield more complex optimization models. Particularly, within ILP literature, nonlinearity and nonconvexity usually arise in the proposed models. Thus, the increasing mathematical complexity requires effective and efficient solution approaches. Most of the authors have developed Lagrangian Relaxation-based algorithms (Araya-Sassi et al. 2018; Daskin et al. 2002; Diabat et al. 2015; Miranda and Garrido 2004; Ross et al. 2017; Snyder et al. 2007). However, according to Farahani et al. (2015), other methods for solving ILPs are based on Branch and Bound, Column Generation, Dynamic Programming, heuristic and meta-heuristics solution methods. Among the employed heuristic approaches are Tabu-Search, Genetic Algorithms, Particle Swarm Optimization (Bashiri and Tabrizi 2010; Chen et al. 2011; Gen and Syarif 2005; Guerrero et al. 2013; Shavandi and Bozorgi n.d.; Yao et al. 2010). Nevertheless, most of these solution approaches fails on ensuring optimality of the solutions obtained.

Recently, Tapia-Ubeda et al. (2018a, b) presents and GBD-based solution approach ensuring global optimality for the 160 tested instances. This research decomposes the studied ILP, where the SCN structure is considered as the master problem (MP) decisions (i.e., warehouse location and customer assignment) and the inventory control decisions and costs are associated to the sub-problem (SP). Afterward, Tapia-Ubeda et al. (2020) tailors the proposed solution approach for designing the internal spare parts SCN comparing different operation strategies.

Note that most of ILP models assume that safety stock at each location (e.g., plant, warehouse, retailer) is proportional to the square-root of the product between incoming lead-time and perceived demand variance at the location. In some cases, the suppliers of these location are previously determined and fixed, and then lead-time become fixed and known. If demand mean and variance depend on assignment scheme of downstream locations, such as warehouse or retailers, then demand mean and variance perceived at the specific location is actually a dependent variable. Therefore, the safety stock at each location is proportional to the square-root of a linear expression. In other cases, such as retailers, demand process is known usually involving fixed mean and variance, and suppliers have to be selected by the model. Then, the safety stock at each location is proportional to the square-root of a linear expression as well. In contrast, this research assumes that the suppliers for each warehouse have to be defined by the model and perceived demand is dependent of customer assignment scheme. Therefore, in contrast to the previous cases, safety stock at each warehouse is proportional to the square-root of a nonlinear expression, i.e., the product of a variable lead time and a variable demand variance. This fact yields a more complex optimization model. These facts denote the higher complexity of the proposed formulation in contrast to previous ILP in literature, and the need for advanced efficient solution approaches, as this research achieves.

This paper is focused on proposing a novel ILP integrating supplier selection decisions for designing a SCN. The proposed model considers a continuous inventory control review policy (r, Q), where r represents a reorder point and Q is the order quantity. The selection of suppliers for serving the located warehouses directly affects their inventory management (i.e., lead-times and safety stocks). Additionally, a GBD-based solution approach is proposed for solving a wide set of synthetic instances with different sizes. The proposed solution approach efficiently and effectively deals with the mathematical complexity of the model ensuring optimality for all the instances.

3 Problem description and mathematical model formulation

This section is focused on describing the problem addressed in this research (Sect. 3.1) and showing the mathematical formulation of the model (Sect. 3.2).

3.1 Problem description

We are proposing an ILP integrating supplier selection decisions for designing a SCN with three-echelons. This structure represents the flow of a single product from suppliers to customers using a warehousing strategy, where the product is stored. This research assumes a set of customers with a stochastic demand for a single item or product, which are served from a warehouse. While the warehouses are fulfilled from a set of suppliers. Each customer is served by only one warehouse and each warehouse is fulfilled by a single supplier. This assumption follows a practical service-level concern, in order to ensure a proper service for each warehouse from a single responsible supplier, and for each customer from a single responsible warehouse. In respect to the suppliers, selecting more than one source for each warehouse, increases lead-time variability, and thus increasing the safety stocks.

We need to identify the following SCN elements, for a single-period and single-commodity case: (1) Selection of suppliers, (2) Location of warehouses, (3) Assignation of located warehouse to selected suppliers, (4) Customers served by each located warehouse, and (5) Inventory control parameters for each selected warehouse. Figure 1 shows a SCN structure including sets of suppliers, warehouses, and customers.

Fig. 1

Three echelons SCN structure

Customers present high-volume stochastic demands, which are represented by their means and variances, affecting the inventory cost in each selected warehouse and the transportation cost with located warehouse. Selecting a supplier yields a fix cost and transportation cost between the supplier and the assigned warehouses. While warehouse location influence setting and operational fixed cost, and average cycle inventory (ordering and holding) and safety stock cost. The average cycle inventory cost is defined by the basic EOQ model due to the warehouses do not include capacitated constraints. While average safety stock cost of a located warehouse is computed based on the standard deviation of the demand during the lead time incurred by the selected supplier and considering a fixed and known service level (stockout probability). The problem is aimed to minimize a long-term estimation of the expected system costs including located warehouse settings, selected supplier, transportation, and inventory costs.

3.2 Mathematical formulation

The sets and parameters of the model are the following:

• S: Set of potential suppliers.

• N: Set of potential sites for locating warehouses.

• M: Set of customers.

• SFC_s: Fixed cost of selecting the supplier s.

• CIn_is: Inbound transportation cost of a warehouse on the location i from supplier s.

• COut_ij: Outbound transportation cost of a warehouse on location i to serve the customer j.

• FC_i: Setting and operational fixed cost of a warehouse on location i.

• LT_si: Lead time for an incoming order to the warehouse in the location i from supplier s.

• OC_i: Ordering cost of the warehouse i.

• HC_i: Unitary holding inventory cost of warehouse i

• μ_j: Mean of the demand of customer j

• σ²_j: Variance of the demand of customer j

• Z_1-αi: Standard normal distribution value that accumulates 1-α_i of warehouse i

The decision variables of the proposed mathematical formulation are as follows:

• Z_s: It is one if and only if the supplier s is selected, 0 otherwise.

• W_si: It is one if and only if the supplier s is selected for serving the warehouse i, 0 otherwise.

• X_i: It is one if and only if a warehouse is location on site i, 0 otherwise.

• Y_ij: It is one if the customer j is served from warehouse located on site i, 0 otherwise.

• D_i: Mean of the demand assigned to the warehouse i.

• V_i: Variance of the demand assigned to the warehouse i.

Given the previous notation, and following the most traditional ILP works (Erlebacher and Meller 2000; Miranda and Garrido 2004; Shen et al. 2003), it is assumed that each warehouse follows a continuous review ICP (r, Q), where the reorder point and the order size are constant in time but dependent on the SCND decisions of customer assignments and supplier selection. The order size Q is set to minimize the cycle inventory and fixed order costs, following the widely known EOQ model (Harris 1913; Wilson 1934). Then, in absence of capacity constraints, the minimum expected optimal cost for this optimal order size for each warehouse i can be expressed as in Eq. (1). Notice that, even that this expression is constant in time, it depends on assigned customers to each warehouse through variable D_i.

$$\sqrt {2 \cdot OC_{i} \cdot HC_{i} } \cdot \sqrt {D_{i} }$$

(1)

In addition, the reorder point r is set in order to ensure a maximum stockout probability of α, which yields an expected safety stock level as in Eq. (2). Notice that in this expression the lead time perceived by each warehouse i directly depends on the selected supplier, which is determined by the variable W_si. Additionally, this expression depends on the demand variance faced by the warehouse i that depends on the assigned customers through variable V_i. Thus, this expression presents two sources of nonlinearity, the square root of the served demand variance, and the product between two variable expressions. This expression entails the most significant mathematical complexity of the proposed model. For instance, a related work of Darmawan et al. (2021) considers supplier selection decisions for each retailer, however their demand process are known, and demand variance became a fixed and known parameter. Then, the resulting model presents a lower mathematical complexity compared to this research.

$$Z_{1 - \alpha } \cdot \left( {\sum\limits_{s \in S} {\sqrt {LT_{si} } \cdot W_{si} } } \right) \cdot \sqrt {V_{i} }$$

(2)

According to the previous notation and assumptions, the proposed Mixed Integer, Nonlinear, Nonconvex, Programming model is formulated as:

$$\begin{aligned} & Min\;\sum\limits_{s \in S} {SFC_{s} \cdot Z_{s} } + \sum\limits_{s \in S} {\sum\limits_{i \in N} {CIn_{si} \cdot D_{i} \cdot W_{si} } } \\ &\quad+ \sum\limits_{i \in N} {FC_{i} \cdot X_{i} } + \sum\limits_{i \in N} {\sum\limits_{j \in M} {COut_{ij} \cdot \mu_{j} \cdot Y_{ij}^{{}} } } \\ & \quad + \sum\limits_{i \in N} {\sqrt {2 \cdot OC_{i}^{{}} \cdot HC_{i}^{{}} } \cdot \sqrt {D_{i} } \cdot X_{i} } + \sum\limits_{i \in N} {HC_{i}^{{}} \cdot Z_{{1 - \alpha_{i} }}^{{}} \cdot \left( {\sum\limits_{s \in S} {\sqrt {LT_{si}^{{}} } \cdot W_{si} } } \right) \cdot \sqrt {V_{i} } } \\ \end{aligned}$$

(3)

s.t.:

$$\sum\limits_{i \in N} {Y_{ij}^{{}} } = 1\quad \quad \forall i \in N$$

(4)

$$Y_{ij}^{{}} \le X_{i} \quad \quad \forall i \in N,\forall j \in M$$

(5)

$$\sum\limits_{s \in S} {W_{si} } = X_{i} \quad \quad \forall i \in N$$

(6)

$$W_{si} \le Z_{s} \quad \quad \forall s \in S,\forall i \in N$$

(7)

$$Z_{s} \le \sum\limits_{i \in N} {W_{si} } \quad \quad \forall s \in S$$

(8)

$$X_{i} \le \sum\limits_{j \in M} {Y_{ij} } \quad \quad \forall i \in N$$

(9)

$$D_{i} = \sum\limits_{j \in M} {Y_{ij}^{{}} \cdot \mu_{j} } \quad \quad \forall i \in N$$

(10)

$$V_{i} = \sum\limits_{j \in M} {Y_{ij}^{{}} \cdot \sigma_{j}^{2} } \quad \quad \forall i \in N$$

(11)

$$Z_{s} \in \left\{ {0,1} \right\}\quad \quad \forall s \in S$$

(12)

$$W_{si} \in \left\{ {0,1} \right\}\quad \quad \forall s \in S,\forall i \in N$$

(13)

$$X_{i} \in \left\{ {0,1} \right\}\quad \quad \forall i \in N$$

(14)

$$Y_{ij}^{{}} \in \left\{ {0,1} \right\}\quad \quad \forall i \in N,\forall j \in M$$

(15)

The objective function (3) includes the total SCN design and operational expected costs. The first term represents the fixed costs related to the selected suppliers. The second term corresponds to the total transportation cost between suppliers and warehouses. The third term is the setting and operating fixed costs by the located warehouses. The fourth term is the total transportation costs between warehouses and customers.

The fifth term of the objective function represents the optimal holding and ordering costs for all warehouses as a function of the expected demand and parameters of holding costs and ordering costs, following the well-known EOQ model (Harris 1913; Wilson 1934). The last term in (3) is the expected safety stock costs at the warehouses, which are associated to the minimum reorder points that ensure a maximum stock-out probability α_i, for a given values of demand variances and lead-times (Axsäter 2015; Birge and Louveaux 2011; Porteus 2002). In this expression, lead-times are determined depending on the selection of the supplier serving each warehouse (i.e., variables W).

Equation (4) ensure that each customer must be served by a single warehouse. Constraints (5) guarantee that a customer is assigned to a single selected warehouse. Constraints (6) ensure that each located warehouse must be served from a single supplier. Constraints (7) ensure that warehouses are assigned only to selected suppliers. Constraints (8) ensure that at least a customer is assigned to a located warehouse. Constraints (8) define that each selected supplier must serve at least one located warehouse. Constraints (9) assure that a located warehouse serves at least one customer. Constraints (10) and (11) compute the means and the variances of the demand that must be served by each located warehouse. Constraints (12), (13), (14), and (15) define the domain of the decision variables.

4 Generalized Benders Decomposition based solution approach

In order to solve the proposed formulation, considering that it is a Mixed Integer, Nonlinear, Nonconvex, Programming problem, a GBD-based optimization algorithm is proposed. The original benders decomposition (BD) (Benders 1962) based algorithm, which was designed for linear programming (LP) formulations, exploits the decomposition of the set of decision variables into two disjoints sub-sets, usually named complicating and non-complicating variables. Based on this decomposition, a master problem (MP) that optimizes only the complicating variables is iteratively solved by integrating constraints or cuts obtained from solving a Sub-Problem (SP). Note that the SP only optimizes the non-complicating variables and assumes that the complicating variables are temporarily fixed at each algorithm iteration. The cuts integrated into the MP are obtained from the objective function of the equivalent dual formulation of the SP, which is a LP formulation. In contrast, the GBD (A. M. Geoffrion 1972) extends BD for addressing non-linear programming problems, where the cuts integrated into the MP are obtained based on the dual Lagrangian function of the SP. In this case strong duality is required to be satisfied by the SP (providing optimal solutions with 0 duality gap).

In this paper, the complicating variables are set to be all the binary variables of the problem (i.e., X, Y, Z, W), while the rest of the variables of continuous nature are considered as the non-complicating variables. In other words, the MP embraces the SCN design decisions variables, while inventory issues are addressed by the SP. Thus, temporarily fixing the complicating variables (i.e.,$\overline{X} ,\overline{Y} ,\overline{Z} ,\overline{W}$), the resulting SP is as follows:

$$\begin{aligned} & Min\sum\limits_{i \in N} {\left[ {\sqrt {2 \cdot OC_{i}^{{}} \cdot HC_{i}^{{}} } \cdot \sqrt {D_{i} } \cdot \overline{{X_{i} }} + HC_{i}^{{}} \cdot Z_{{1 - \alpha_{i} }}^{{}} \cdot \left( {\sum\limits_{s \in S} {\sqrt {LT_{si} } \cdot \overline{{W_{si} }} } } \right) \cdot \sqrt {V_{i} } } \right]} \\ & \quad + \sum\limits_{s \in S} {\sum\limits_{i \in N} {CIn_{si} \cdot D_{i} \cdot \overline{{W_{si} }} } } + \sum\limits_{s \in S} {SFC_{s} \cdot \overline{{Z_{s} }} } \\ &\quad+ \sum\limits_{i \in N} {FC_{i} \cdot \overline{{X_{i} }} } + \sum\limits_{i \in N} {\sum\limits_{j \in M} {COut_{ij} \cdot \mu_{j} \cdot \overline{{Y_{ij} }} } } \\ \end{aligned}$$

(16)

s.t.:

$$D_{i} = \overline{{D_{i} }} = \sum\limits_{j \in M} {\overline{{Y_{ij} }} \cdot \mu_{j} } \quad \quad \forall i \in N$$

(17)

$$V_{i} = \overline{{V_{i} }} = \sum\limits_{j \in M} {\overline{{Y_{ij} }} \cdot \sigma_{j}^{2} } \quad \quad \forall i \in N$$

(18)

Note that the proposed decomposition yields a SP that only computes total inventory system costs for the SCN structure provided by the solution defined the complicating variables.

Firstly, the SP is decoupled into one for each location i, and secondly, the optimal solution of each SP i (primal and dual optimality) is derived for two cases: (a) when $\overline{{X_{i} }} = 1$ and (b) when $\overline{{X_{i} }} = 0$.

$$\left( {\text{a}} \right)\quad \overline{{X_{i} }} = 1\quad \quad \left( {\overline{{X_{i} }} = 1 \Rightarrow \exists !s \in S \wedge \exists j \in M/\overline{{W_{si} }} = 1 \wedge \overline{{Y_{ij} }} = 1} \right)$$

The sub-problem for each location i can be written as follows:

$$\begin{aligned} & Min\quad \left[ {\sqrt {2 \cdot OC_{i} \cdot HC_{i} } \sqrt {D_{i} } + HC_{i} \cdot Z_{{1 - \alpha_{i} }}^{{}} \left( {\sum\limits_{s \in S} {\sqrt {LT_{si} } \cdot \overline{{W_{si} }} } } \right)\sqrt {V_{i} } } \right]\\ &\quad + \sum\limits_{s \in S} {\sum\limits_{i \in N} {CIn_{si} \cdot \overline{{W_{si} }} \cdot D_{i} } } \\ & s.t.:D_{i} = \overline{{D_{i} }} = \sum\limits_{j \in M} {\overline{{Y_{ij} }} \cdot \mu_{j} } \quad \quad \quad \forall i \in N \\ & V_{i} = \overline{{V_{i} }} = \sum\limits_{j \in M} {\overline{{Y_{ij} }} \cdot \sigma_{j}^{2} } \quad \quad \quad \quad \quad \forall i \in N \\ \end{aligned}$$

(19)

The optimal solution is $D_{i}^{*} = \overline{{D_{i} }} = \sum\limits_{j \in M} {\overline{{Y_{ij} }} \cdot \mu_{j} }$ and $V_{i}^{*} = \overline{{V_{i} }} = \sum\limits_{j \in M} {\overline{{Y_{ij} }} \cdot \sigma_{j}^{2} }$.

Thus, assigning $\lambda 1,\lambda 2$ to Eqs. (17) and (18) respectively, the Lagrangian dual problem can be written as follows:

$$Max\,L = \inf \left\{ \begin{gathered} \left[ {\sqrt {2 \cdot OC_{i} \cdot HC_{i} } \cdot \sqrt {D_{i} } + HC_{i}^{{}} \cdot Z_{{1 - \alpha_{i} }}^{{}} \cdot \left( {\sum\limits_{s \in S} {\sqrt {LT_{si} } \cdot \overline{{W_{si} }} } } \right) \cdot \sqrt {V_{i} } } \right] \hfill \\ + CIn_{si} \cdot \overline{{W_{si} }} \cdot D_{i} + \lambda 1_{i} \cdot \left( {\sum\limits_{j \in M} {\overline{{Y_{ij} }} \cdot \mu_{j} } - D_{i} } \right) + \lambda 2_{i} \cdot \left( {\sum\limits_{j \in M} {\overline{{Y_{ij} }} \cdot \sigma_{j}^{2} } - V_{i} } \right) \hfill \\ \end{gathered} \right\}$$

(20)

These dual variables must hold the Karush–Kuhn–Tucker optimality conditions, as follows:

$$\frac{\partial L}{{\partial D_{i} }} = \left[ {\frac{{\sqrt {2 \cdot OC_{i} \cdot HC_{i} } }}{{2 \cdot \sqrt {D_{i} } }}} \right] + \sum\limits_{s \in S} {CIn_{si} \cdot \overline{{W_{si} }} } - \lambda 1_{i} = 0$$

(21)

$$\frac{\partial L}{{\partial V_{i} }} = \frac{{HC_{i} \cdot Z_{{1 - \alpha_{i} }} \cdot \left( {\sum\limits_{s \in S} {\sqrt {LT_{si} } \cdot \overline{{W_{si} }} } } \right)}}{{2 \cdot \sqrt {V_{i} } }} - \lambda 2_{i} = 0$$

(22)

Then, optimal dual variables are obtained from (21) and (22):

$$\overline{{\lambda 1_{i} }}^{*} = \left[ {\frac{{\sqrt {2 \cdot OC_{i} \cdot HC_{i} } }}{{2 \cdot \sqrt {\overline{{D_{i} }} } }}} \right] + \sum\limits_{s \in S} {CIn_{si} \cdot \overline{{W_{si} }} }$$

(23)

$$\overline{{\lambda 2_{i} }}^{*} = \frac{{HC_{i}^{W} \cdot Z_{{1 - \alpha_{i} }}^{W} \cdot \left( {\sum\limits_{s \in S} {\sqrt {LT_{si}^{SW} } \cdot \overline{{W_{si} }} } } \right)}}{{2 \cdot \sqrt {\overline{{V_{i} }} } }}$$

(24)

$$\left( {\text{b}} \right)\quad \overline{{X_{i} }} = 0\quad \quad \left( {\overline{{X_{i} }} = 0 \Rightarrow \overline{{W_{si} }} = 0,\forall s \in S \wedge \overline{{Y_{ij} }} = 0,\forall j \in M} \right)$$

Considering that the warehouse i is not installed after solving the MP (i.e., $\overline{{X_{i} }} = 0$, $\overline{{W_{si} }} = 0$, $\overline{{D_{i} }} = 0$ and $\overline{{V_{i} }} = 0$), the underlying SP can be written as follows:

$$\begin{aligned} & Min\quad \sqrt {2 \cdot OC_{i}^{{}} \cdot HC_{i}^{{}} } \cdot \sqrt {D_{i} } \cdot \left( {\overline{{X_{i} }} = 0} \right) \\ &\qquad+ HC_{i}^{{}} \cdot Z_{{1 - \alpha_{i} }}^{{}} \cdot \left( {\sum\limits_{s \in S} {\sqrt {LT_{si} } \cdot \left( {\overline{{W_{si} }} = 0} \right)} } \right) \cdot \sqrt {V_{i} } = 0 \end{aligned}$$

(25)

s.t.:

$$D_{i} = \overline{{D_{i} }} = 0\quad \quad \forall i \in N$$

(26)

$$V_{i} = \overline{{V_{i} }} = 0\quad \quad \forall i \in N$$

(27)

Naturally, the optimal solution is:

$$\overline{{D_{i} }}^{*} = 0\,\,;\,\,\overline{{V_{i} }}^{*} = 0;$$

(28)

Thus, assigning $\lambda 1,\lambda 2$ to constraints (26) and (27) respectively, the dual Langrangian problem can be written as follows:

$$Max\,L = \inf \left\{ {\lambda 1_{i} \cdot \left( { - D_{i} } \right) + \lambda 2_{i} \cdot \left( { - V_{i} } \right)} \right\}$$

(29)

Establishing Karush–Kuhn–Tucker optimality conditions, as follows:

$$\frac{\partial L}{{\partial D_{i} }} = - \lambda 1_{i} = 0$$

(30)

$$\frac{\partial L}{{\partial V_{i} }} = - \lambda 2_{i} = 0$$

(31)

From (30) and (31), $\overline{{\lambda 1_{i} }}^{*} = 0\,$ and $\,\overline{{\lambda 2_{i} }}^{*} = 0$.

As can be observed SP is always feasible (it is only required to compute D_i and V_i for each location i, based on the values of variables Y), the proposed decomposition only considers the inclusion optimality cuts into the MP. Thus, once SP is solved for each location i, the optimality cut at iteration k is written as follows:

$$\begin{aligned} \eta & \ge \sum\limits_{s \in S} {SFC_{s} \cdot Z_{s} } + \sum\limits_{s \in S} {\sum\limits_{i \in N} {CIn_{si} \cdot \overline{{D_{i} }}^{k} \cdot W_{si} } } \\ &+ \sum\limits_{i \in N} {FC_{i} \cdot X_{i} } + \sum\limits_{i \in N} {\sum\limits_{j \in M} {COut_{ij} \cdot \mu_{j} \cdot Y_{ij} } } \\ & + \sum\limits_{i \in N} {\left[ {\sqrt {2 \cdot OC_{i} \cdot HC_{i} } \cdot \sqrt {\overline{{D_{i} }}^{k} } \cdot X_{i} + HC_{i}^{{}} \cdot Z_{{1 - \alpha_{i} }}^{{}} \cdot \left( {\sum\limits_{s \in S} {\sqrt {LT_{si} } \cdot W_{si} } } \right) \cdot \sqrt {\overline{{V_{i} }}^{k} } } \right]} \\ & + \sum\limits_{i \in N} {\overline{{\lambda 1_{i} }}^{k} \cdot \left( {\sum\limits_{j \in M} {Y_{ij} \cdot \mu_{j} } - \overline{{D_{i} }}^{k} } \right)} + \sum\limits_{i \in N} {\overline{{\lambda 2_{i} }}^{k} \cdot \left( {\sum\limits_{j \in M} {Y_{ij} \cdot \sigma_{j}^{2} } - \overline{{V_{i} }}^{k} } \right)} \\ \end{aligned}$$

(32)

In this expression, optimal subproblem solution (primal and dual) is fixed, and complicating variables are not-longer fixed, and $\eta$ is an auxiliary variable that represent the objective function of the MP.

By rearranging (32), a more compact version of the cut is written as in (33) and (34), where $\Gamma_{i}^{k}$ is an auxiliary parameter that accumulates the constant term of each of the optimality cuts added into the MP.:

$$\begin{aligned} \eta & \ge \sum\limits_{s \in S} {SFC_{s} \cdot Z_{s} } + \sum\limits_{s \in S} {\sum\limits_{i \in N} {\overline{{CIn_{si} }}^{k} \cdot W_{si} } } + \sum\limits_{i \in N} {\overline{{FC_{i} }}^{k} \cdot X_{i} } \\ & \quad + \sum\limits_{i \in N} {\sum\limits_{j \in M} {\overline{{COut_{ij} }} \cdot Y_{ij}^{W} } } + \sum\limits_{i \in N} {\Gamma_{i}^{k} } \\ \end{aligned}$$

(33)

where:

$$\begin{aligned} \overline{{CIn_{si} }}^{k} & = CIn_{si} \cdot \overline{{D_{i} }}^{k} + HC_{i}^{W} \cdot Z_{{1 - \alpha_{i} }}^{W} \cdot \sqrt {LT_{si}^{SW} } \cdot \sqrt {\overline{{V_{i} }}^{k} } \\ \overline{{FC_{i} }}^{k} & = FC_{i} + \sqrt {2 \cdot OC_{i}^{W} \cdot HC_{i}^{W} } \cdot \sqrt {\overline{{D_{i} }}^{k} } \\ \overline{{COut_{ij} }}^{k} & = COut_{ij} \cdot \mu_{j} + \overline{{\lambda 1_{i} }}^{k} \cdot \mu_{j} + \overline{{\lambda 2_{i} }}^{k} \cdot \sigma_{j}^{2} \\ \Gamma_{i}^{k} & = - \overline{{\lambda 1_{i} }}^{k} \cdot \overline{{D_{i} }}^{k} - \overline{{\lambda 2_{i} }}^{k} \cdot \overline{{V_{i} }}^{k} \\ \end{aligned}$$

(34)

Consequently, the master problem can be written as follows:

$$\begin{array}{*{20}l} {Min\quad \eta } & {} \\ {s.t.:} & {} \\ \begin{gathered} \eta \ge \sum\limits_{s \in S} {SFC_{s} \cdot Z_{s} } + \sum\limits_{s \in S} {\sum\limits_{i \in N} {\overline{{CIn_{si} }}^{r} \cdot W_{si} } } + \sum\limits_{i \in N} {\overline{{FC_{i} }}^{r} \cdot X_{i} } \hfill \\ \quad \; + \sum\limits_{i \in N} {\sum\limits_{j \in M} {\overline{{COut_{ij} }} \cdot Y_{ij} } } + \sum\limits_{i \in N} {\Gamma_{i}^{r} } \hfill \\ \end{gathered} & {\forall r = 1,....,k} \\ {\sum\limits_{i \in N} {Y_{ij} } = 1} & {\forall j \in M} \\ {Y_{ij} \le X_{i} } & {\forall i \in N,\forall j \in M} \\ {\sum\limits_{s \in S} {W_{si} } = X_{i} } & {\forall i \in N} \\ {X_{i} \le \sum\limits_{j \in M} {Y_{ij} } } & {\forall i \in N} \\ {W_{si} \le Z_{s} } & {\forall s \in S,\forall i \in N} \\ {Z_{s} \in \left\{ {0,1} \right\}} & {\forall s \in S} \\ {W_{si} \in \left\{ {0,1} \right\}} & {\forall s \in S,\forall i \in N} \\ {X_{i} \in \left\{ {0,1} \right\}} & {\forall i \in N} \\ {Y_{ij} \in \left\{ {0,1} \right\}} & {\forall i \in N,\forall j \in M} \\ \end{array}$$

(35)

In order to determine a first set of feasible solution for the complicating variables and being able to solve the first SP, a particular MP version is solved, which instead of considering the original cut the next constraints are considered:

$$\eta \ge \sum\limits_{s \in S} {SFC_{s} \cdot Z_{s} } + \sum\limits_{i \in N} {FC_{i} \cdot X_{i} } + \sum\limits_{i \in N} {\sum\limits_{j \in M} {COut_{ij} \cdot \mu_{j} \cdot Y_{ij} } }$$

(36)

$$\sum\limits_{i \in N} {FC_{i} \cdot X_{i} } = P$$

(37)

This modified MP version provides a feasible SCN configuration that minimizes supplier selection, warehouse location, and warehouse-customer transportations costs for a fixed value of P. Subsequently, once the SP is solved at the first iteration (considering the solution obtained by the modified MP as fixed), this cut is then aggregated in the MP by the original optimality cut in (36). This procedure is repeated independently for P = 1,…, |N|, providing |N| initial cuts for the MP.

Finally, the algorithm ends when the configuration obtained with the MP is the same at two consecutive iterations k and k + 1 (i.e., Z^k = Z^k+1, X^k = X^k+1, W^k = W^k+1, and Y^k = Y^k+1). Note that this criterion may be established without relying on any tolerance condition, given that decisions variables are binaries.

Appendix B provides a numerical example considering 2 suppliers, 5 potential warehouses, and 5 customers, for which the proposed formulation is solved by using the proposed GBD. In this case, after integrating the five initial cuts (P = 1, 2, 3, 4, 5), the algorithm took eight iterations for obtaining the final optimal solution, which is obtained by solving the MP in the last two iterations.

5 Computational implementation and results

This section is focused on presenting (1) computational implementation and (2) employed instances, in Sect. 5.1, and results obtained throughout the computational experimentation, and the underlying results analysis.

5.1 Computational implementation

The proposed algorithm was implemented on Microsoft Visual Studio using C++ language. The MP was solved with Cplex 12.9 on a computer with processor Intel Core I7 of 3.6 GHz and 32 GB of RAM in a 64-bit Operating System. Note that the proposed formulation is Mixed Integer, Nonlinear, Nonconvex, Programming Problem, which cannot be directly solved by Cplex. However, based on the proposed decomposition, the MP can effectively be solved by Cplex. Thus, the computational experimentation cannot consider Cplex as a benchmark solution approach.

The computational implementation was made considering 200 instances. These instances were created from 5 base instances; therefore, 40 instances were generated for each base instance. The coordinates of the potential suppliers, the potential warehouses and customers were randomly generated in a square area of 40,000 [km²]. Each base instance considers a |S|= 5 (potential suppliers), |N|= 10 (potential warehouses), and |M|= 20 (customers). Each of the 40 instances were obtained from full factorial combination of the sizes considering that S ranges within {1, 2, 3, 4, 5}, N ranges within {5, 10}, and M ranges in {5, 10, 15, 20}. All the generated instances consider a fixed customer demand variation coefficient of 0.2. The instances are named following the notation Inst_k_s_n_m where k represents the base instance number, s is the number of potential suppliers, n is the number of potential warehouses, and m represents the number of customers.

5.2 Results and discussion

Among the obtained results, one of the most relevant is that for all the 200 tested instances the optimal solution was found in competitive times where the 75.5% of the instances were solved in at most 1 min. Additionally, only a 3.5% of the instances were solved in more than 20 min, where the maximum time for solving an instance was 75 min. Considering the mathematical complexity of the proposed model (Mixed Integer, Nonlinear, Nonconvex, Programming), finding optimal solutions in affordable computing times is a relevant contribution for both researchers and practitioners. Figure 2i shows the computational times for all the 200 tested instances, while Fig. 2ii presents the computational times for the instances solved in less than 30 s (142 instances).

Fig. 2

Computational times for solving the problem

Figure 3 shows the relationship between the number of algorithm iterations and the computational times required for obtaining all the 200 optimal solutions. Moreover, Fig. 4 shows the evolution of the objective function of the SP (upper bound) and the MP (lower bund) for Instance Inst_2_10_15, which denotes algorithm behavior and convergence. It is worth highlighting that the upper bound (grey line, OF), which corresponds to the objective function of the feasible solution obtained once the SP is solved, converge to the optimal solution in an erratic way (rising/falling or zigzagging). In contrast, the lower bound (black line, ETA), which is the objective function of the MP (a maximization problem), converge monotonically (i.e., never decreasing), since it always includes additional constraints with iterations, worsening or holding the objective function. Additionally, the best upper bound (dashed line, BEST) at each iteration is also shown. It is remarkable that the best upper bound (primal convergence) reach near optimal solutions considerably faster than the lower bound (dual convergence). Notice that the instance Inst_2_10_15 is one of the instances that took more iterations to be solved (computational time 837,80 s).

Fig. 3

Relationship between iterations and computational time

Fig. 4

Convergence algorithm behavior for Inst_2_10_15

The detailed results for all the five Base Instances are shown in Appendix C. Considering that each Base Instance may represent the general behavior of the results, the results obtained from the Base Instance 3 will be analyzed in detail. Optimal values of the Objective Function (OF) obtained for each of the instances considering 5 and 10 potential warehouses (nW) are shown in Fig. 5i, ii, respectively.

Fig. 5

Optimal OF values for base instance 3

Based on Figs. 5i, ii, it should be clear that for a fixed number of customers (nC) the objective function is decreasing while the number of potential suppliers (nS) increases. Additionally, the objective function value increases for a fixed number of potential suppliers and warehouses while the number of customer increases. This is a natural consequence of having more customers that must be served, due to the increment of assignment and inventory costs.

Furthermore, while increasing the number of customers, potential warehouses and potential suppliers, the number of selected suppliers (NSS) and the number of located warehouses (NLW) also increases. The optimal number of selected suppliers considering 5 and 10 potential warehouses are shown in Fig. 6i, ii, respectively.

Fig. 6

Number of selected suppliers for the base instance 3

Additionally, the optimal number of located warehouses with 5 and 10 potential warehouses are shown in Fig. 7i, ii, correspondingly.

Fig. 7

Number of located warehouses the base instance 3

The optimal SCN structure for instances Inst_3_1_5_20, Inst_3_1_10_20, Inst_3_3_5_20, Inst_3_3_10_20, Inst_3_5_5_20, and Inst_3_5_10_20 are shown in Figs. 8i, ii, 9i, ii and 10i,ii, respectively. In these figures, circles represent the potential suppliers, squares represent the potential warehouses, and diamonds represent the customers. Through these figures it is possible to see how the number of potential suppliers and potential warehouses impact over the optimal SCN structure. All these elements in the figures (suppliers, warehouses and customers) are labeled with consecutive numbers starting in 1.

Fig. 8

Optimal SCN structure for instances with 1 supplier and 20 customers

Fig. 9

Optimal SCN structure for instances 3 with 3 suppliers and 20 customers

Fig. 10

Optimal SCN structure for instances 3 with 5 suppliers and 20 customers

In addition to the optimality reached for all the tested instances, the efficiency of the proposed GBD-based algorithm can be measured by analyzing the computing time for solving the instances. The computational times for the instances considering 5 and 10 potential warehouses (nW) are shown in Fig. 11i, ii, correspondingly.

Fig. 11

Computational times for base instance 3

In one hand, computational times tend to increase for a fixed number of suppliers while the number of customers also increases. On the other hand, computational times tend to decrease for a fixed number of customers while the number of potential suppliers increases. It should be clear that computational times are directly related to the number of iterations required for obtaining the optimal solution. The number of iterations for instances for 5 and 10 potential warehouses (nW) are shown in Fig. 12i, ii, respectively. Observing these figures, it is possible to note that the behavior of the number of iterations is very similar to the behavior of computational times shown in Fig. 11.

Fig. 12

Number of iterations for base instance 3

It is worth pointing out that the number of iterations is directly related to the number of cuts added into the MP. Despite considering that MP structure belongs to MIP, adding cuts into the MP implies that the size of the problems grows. It is easy assuming that the computational time tends to increase while the size of the problem grows. Considering the close relation between computational times and the number of iterations, it would be valuable to analyze the behavior of the ratio obtained by dividing computational time and the number of iterations. In this context this ratio is named as time-iterations ratio.

The behavior of the ratio is shown in Fig. 13i, ii, considering 5 and 10 number of potential warehouses. Observing these figures, it is possible to identify the behavior of the time-iterations ratio. The value of the ratio tends to increase for a fixed number of potential suppliers while the number of customers grows. Additionally, the value of the time-iterations ratio tends to decrease while the number of potential suppliers increases. It is valuable pointing out that Fig. 13i shows that time-iterations ratio for nW = 5 is bounded in less than 0.12. Even more, the effect is clearer analyzing the behavior shown in Fig. 13ii. Once the general behavior of the Base Instance 3, the analysis focuses on the impact of the variations of some of the critical parameters considered in the proposed mathematical model.

Fig. 13

Time-iterations ratio for the Base Instance 3

5.3 Sensitivity analysis

Despite the previous analysis was made only considering Base Instance 3, results and analysis made are replicable for each of the other four Base Instances. The following sensitivity analysis spotlights the impact that inbound transportation costs, outbound transportation costs, variance coefficient, and service level (i.e., stockout probability) has over the optimal SCN structure. Particularly, the sensitivity analysis is made considering instance I_3_5_10_20.

5.3.1 Inbound transportation costs (CIn)

The sensitivity analysis made considers variations ranges in {− 75%, − 50%, − 25%, 0, + 25%, + 50%, + 75%}, where 0 represents the base case (i.e., original inbound transportation costs). The results obtained are shown in Table 1.

Table 1 Results for CIn variations

It is relevant to be analyzed that the optimal number of located warehouses (NLW) whether increase or decrease while the Inbound transportation costs (CIn) varies for a fixed instance. Logically, while CIn costs increase their values the SCN structure should tend to centralize the network by decreasing the NLW, which is clearly observed from 0 to + 75%, in Table 1. Moreover, it can be observed that warehouse 9 is continuously reducing its size (i.e., assigned customer’s demands) from − 75% to 0, until to be completely closed for + 25%.

However, the observed results show that NLW may increase or decrease while CIn increase their values, between − 75%, and − 25%. Analyzing in detail the set of LW, the optimal solution for -50%, with warehouses {1,4,5,6,9,10}, can be considered an intermediate solution between the solutions for − 75% and − 25%. Initially, warehouse 1 is open for − 75%; next warehouse 5 is included for − 50%; and then, warehouse 1 is finally closed for − 25%. In other words, warehouse 5 tends to replace warehouse 1. It is worth to be mentioned that this replacement is not fully associated to serving the same customers through the recently located warehouse. It should be natural that these effects simultaneously occur while CIn increase their values. Figure 14 shows the variations of the optimal objective function value considering each of the variations above mentioned.

Fig. 14

Optimal OF values variations for different CIn costs

Beside the significant variations of the optimal objective function value, the considered variations generate significant variations on the optimal SCN structure. Figure 15 shows the variations on the number of located warehouses (NLW) and number of selected suppliers (NSS). Particularly, Fig. 16i, ii show the optimal SCN structure for the variations of − 75% and + 75% of the inbound transportation costs.

Fig. 15

NLW and NSS for different CIn costs

Fig. 16

Optimal SCN for different variation levels in CIn

Considering the relevance of CIn costs in the model, substantial variations in the values of this parameter generate significant variations in the optimal SCN structure. For lower CIn costs values it is efficient to decentralize (i.e., number of located warehouses) the operation allowing assignments of distant warehouses from selected suppliers. Furthermore, these changes imply that warehouses may be closer to customers implying potential improvements in performance (e.g., service level). The analysis for larger CIn costs values tend to generate the centralization of the optimal SCN structure. Consequently, locating more warehouses increases the fixed setting and operations costs.

5.3.2 Outbound transportation costs (COut)

The sensitivity analysis made considers variations ranges in {− 75%, − 50%, − 25%, 0, + 25%, + 50%, + 75%}, where 0 represents the base case (i.e., original outbound transportation costs). The results are shown in Table 2. Figure 17 shows the variations of the optimal objective function value considering each of the variations above mentioned.

Table 2 Results for COut variations

Fig. 17

Optimal OF values variations for different COut costs

It should be clear that the effect of these variations is relevant on the optimal objective function value. Moreover, it is possible to realize that the impact over the optimal OF values of COut is greater than the impact of CIn shown in the previous subsection. These variations generate relevant changes on the optimal SCN structure. Figure 18 shows the variations on the number of located warehouses (NLW) and number of selected suppliers (NSS).

Fig. 18

NLW and NSS for different COut costs

Moreover, Fig. 19i, ii show the optimal SCN structure for the variations of − 75% and + 75% of the outbound transportation costs. Similar to the previous case, the relevance of COut costs in the model implies that significant variations in the values of this parameter generate considerable variations in the optimal SCN structure. When COut costs values increase, it is efficient locating more warehouses for avoiding this type of costs. This decentralization tends to improve the response time between warehouse and customer. While COut cost values increase optimal SCN structure tends to be more centralized.

Fig. 19

Optimal SCN for variations in COut

5.3.3 Variation coefficient

The sensitivity analysis made considers variations ranges in {0,0001; 0,1; 0,2; 0,3; 0,4; 0,5}, where 0,2 represents the base case (i.e., original Variation Coefficient). The results are shown in Table 3. Figure 20 shows the variations of the optimal objective function value considering each of the variations mentioned above.

Table 3 Results for VC variations

Fig. 20

Optimal OF values variations for different CV levels

It is valuable pointing out that growing the VC generates the increment of demand variance values. Based on this, it should be natural that the SCN structure tends to centralize considering risk-pooling effect. Despite these variations do not generate considerable variations on the optimal OF value. However, these changes generate variations on the optimal SCN structure. Figure 21 shows the number of selected suppliers (NSS) and the number of located warehouses (NLW) for each of these variations.

Fig. 21

NLW and NSS for different CV levels

In this case, the optimal SCN structure for CV = 0.0001 is the same that in the base case (CV = 0.2). However, the optimal SCN structure for CV = 0.5.

5.3.4 Service level

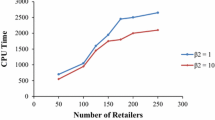
The sensitivity analysis made considers variations ranges in {80%, 85%, 90%, 95%, 99%, 99.99%}, where 95% represents the base case (i.e., original service level). The results are shown in Table 4.

Table 4 Results for Service Level variations

Figure 22 shows the variations of the optimal objective function value considering each of the service level variations.

Fig. 22

Optimal OF value variations for different SLs

It is valuable pointing out that the effect is stronger while the SL increases its value (SL → 1). With these values, lower values do not generate changes on the optimal SCN structure. However, when SL = 0,9999 the optimal SCN tends to centralize modifying the base optimal SCN structure.

5.3.5 Holding cost

The sensitivity analysis made considers variations ranges in {100, 250, 500, 750, 1000} where 500 represents the base case (i.e., original holding costs). The results are shown in Table 5. Figure 23 shows the variations of the optimal objective function value considering each of the holding cost variations. Despite the impact of the analyzed variations over the optimal OF value, only HC = 750 and HC = 1000 generate changes on the optimal SCN structure.

Table 5 Results for Holding Cost variations

Fig. 23

Optimal OF value variations for different HCs

5.3.6 Lead time

This subsection is focused on analyzing the impact of multiplying al lead times with the same factor. If the factor is greater than 1, all warehouses are relatively more distant to all potential suppliers. Clearly, varying the lead times affect the inventory control at each located warehouse, particularly, the variation impacts on the safety stocks. Table 6 shows the impact of increasing the Lead Time for all the warehouses. Results are clear about the potential impact of varying the Lead Times on the optimal SCN structure, by reducing the number of located warehouses and also the number of selected suppliers.

Table 6 Results for lead time variations

However, it is worth mentioning the extremely high values of lead time to observe these reductions, which is explain by lead times participate with square root in the safety stock costs, having a dimming impact on the optimal solution and costs. For example, by duplicating lead times the number of located warehouses and selected suppliers remain constant, and only multiplying lead times by 10,000 yield one warehouse and one supplier.

In addition, simultaneously increasing the values of the Holding Costs, Service Level and Lead Times would intensify the impact of safety stocks on optimal structure obtained. Accordingly, Table 7 present the results obtained when Service Level, Lead times and Holding Cost are varied jointly. It is observed a reduction in the number of located warehouses and selected suppliers, as can be expected, when these parameters increase individually and simultaneously.

Table 7 Simultaneous variation of service level, lead times and holding cost

5.3.7 Simultaneous variations for SL and VC

This Subsection is focused on analyzing the impacts of variating of Service Level (SL) and Variation Coefficient (VC) values simultaneously. This analysis is made considering SL values that ranges in {0,80; 0,95; 0,9999} and VC values that ranges in {0,0001; 0,2; 0,5}. Table 8 shows the results obtained for the nine potential combinations of values. The results of the optimal objective function (OF) values are shown in Fig. 24.

Table 8 Results for service level and variation coefficient variations

Fig. 24

Optimal OF values for different SL and VC levels

Based on the results shown in Fig. 24 it is possible identifying that the impact of considering higher service levels is greater while the VC values increase. Furthermore, the variations on the service level and variance coefficient also imply variations on the optimal SCN structure. Through all the results shown in Table 6, there are three SCN structures. These SCN structure considers NSS = 3 and NLW = 5, NSS = 2 and NLW = 4, and NSS = 2 and NLW = 3 and are shown in Fig. 25i–iii, respectively. These results reflect the impact of these two key parameters (i.e., Variation Coefficient and Service Level). Despite the optimal SCN structures shown in Fig. 25 are similar, they may imply relevant differences in the cost performance.

Fig. 25

Optimal SCN structure under VC and SL variations

6 Research and managerial insights

This section is focused on analyzing the results obtained through all the computational experimentation and providing managerial insights. Particularly, the analysis of the results is made considering the average among the 5 Base Instances. The detailed average results are shown in Appendix D. The results obtained for the optimal OF value, considering nW = 5 and nW = 10, are shown in Fig. 26i, ii respectively.

Fig. 26

Average optimal OF values

As can be expected, for a fixed number of customers, the optimal OF tends to decrease their values while additional suppliers are incorporated. Similarly, for a fixed number of available suppliers, the optimal OF values tends to increase while additional customers are added. In both cases, the larger set of customers and suppliers includes the customers and suppliers of the smaller instances.

Figure 27i, ii show the average Time/Iterations ratio behavior for nW = 5 and nW = 10 respectively. These figures confirm the behavior shown for Base Instance 3. Figures 28 and 29 confirm the expected behavior, where the number of selected suppliers and located warehouses tend to increase their value for a fixed number of potential suppliers while the number of customers increase their value.

Fig. 27

Average time/iterations ratio

Fig. 28

Average number of supplier selected

Fig. 29

Average number of located warehouses

Figure 28i, ii show the average NSS for nW = 5 and nW = 10 respectively, while Fig. 29i, ii show the average NLW for nW = 5 and nW = 10 respectively.

7 Conclusions and future research

This paper studies a novel problem that integrates decisions and costs regarding traditional ILP (i.e., warehouse location, customer assignments, and inventory control issues) with supplier selection. Thus, considering the proposed integration, it is possible to observe and analyze the impact of supplier selection over the SCN topology.

As may be expected, including supplier selection increases the mathematical complexity of the model, even compared to traditional ILPs. The proposed formulation, particularly considering the integration of supplier selection decisions, consists of a Mixed Integer, Nonlinear, Nonconvex, Programming Model, denoting a significantly higher complexity. Considering the combinatorial nature of the problem when including supplier selection decisions exponentially enlarges the set of feasible solutions. Despite the strategic-tactic nature of the decisions encompassed by the model, effective and efficient solution approaches are required for solving the model in reasonable times and yielding good quality solutions. Thus, a GBD-based solution approach is proposed and implemented in this paper. The proposed solution approach allows obtaining optimal solutions for all the tested instances in reasonable times. The tested instances represent a wide variety of sizes, thus representing different potential real-world scenarios where this problem may take place.

Besides the integration of supplier selection decisions impact in the mathematical model formulation, it significantly affects the optimal SCN structure. Particularly, the main aim of this research is understanding how selecting suppliers may impact the optimal configuration of the network. Analyzing the obtained results, it is possible to depict that while the number of available suppliers increases the number of located warehouses tends to increase. This effect may be generated considering the potential safety stock costs savings when opening new warehouses served from nearer supplier with lower lead-times that, despite the extra fixed costs, generates savings related to the supplier-warehouse and warehouse-customer transportation costs.

Another relevant aspect relates to the computational times for solving instances, where while the number of potential suppliers increases the computational time tends to decrease. This may be explained considering that the decision of which warehouses are select to open with fewer suppliers is more time consuming considering the relative distance between the suppliers and the warehouses. While the number of potential suppliers increases, then the set of suppliers may tend to be closer to the set of warehouses, considering the shortest distance between a supplier and a warehouse. This relative closeness may generate that it is simpler and faster to select a warehouse for serving customers considering fixed attractive supplier-warehouse pairs. Consequently, in these situations, the decision of selecting a warehouse implies the selection of a specific supplier, and the existence of these pairs positively impact on reducing the system transportation costs and computational times.

Other significant results are related to a combination of Risk-Pooling related effects observed when some significant parameters vary. The most intuitive is the reduction of warehouse number while holding costs, demand variance, lead-times or service level increases. However, additional SCN modifications appear, such as interchanging warehouse locations, in order to reach a new system cost balance, when some of these parameters change. For example, closing a warehouse and selecting an alternative location with shorter lead-times may help in reducing safety stock costs when demand variability significantly increases. Moreover, when parameter variation is not significant, this substitution may be preceded by another solution that involve both warehouses, representing a sort of intermediate solution. Despite these effects may be defined and observed independently, they may arise in combination and overlapping.

In terms of future research, natural extensions are multiperiod and multicommodity schemes. In the same line, it is worth analyzing how the integration of different capacity constraints may impact the optimal SCN structure (e.g., inventory capacity, dispatching capacity at warehouses). It is valuable integrating plant operations, production decision and raw material management. Additionally, it is valuable to integrate different inventory control policies. Finally, it may be crucial analyzing the impact of Bullwhip effect into the SCND. Finally, resilience and robustness may be integrated into SCN, where customers and warehouses have to be served by more than one warehouse and supplier respectively, to ensure continuous services under local disruptive events.

Appendices

Appendix A

This appendix provides a simple analysis to demonstrate the convenience of selecting a single supplier instead of two suppliers for serving a warehouse with known demand mean and variance. For this demonstration, we assume that, in cases of employing two suppliers with different lead times, the perceived lead time at the warehouse would be the average value, considering the proportion of demand served by each supplier as weighing parameter. Any other assumption may potently increase the perceived lead time at the warehouse, for example integrating the lead time variance, or considering the maximum lead time of the two values, yielding more advantages of selecting a single supplier.

Following the notation in Sect. 3, omitting the index i of the warehouse, and considering that θ is the proportion of demand served by supplier 2 respect to the demand served by supplier 1, the total costs perceived by the warehouse can be written as follows (all remaining costs does not depend on supplier selection):

$$\begin{aligned} G\left( \theta \right) & = HC \cdot Z_{1 - \alpha } \sqrt {\left( {\left( {1 - \theta } \right) \cdot LT_{1} + \theta \cdot LT_{2} } \right)} \cdot \sqrt V \\ & + CIn_{1} \cdot \left( {1 - \theta } \right) \cdot D + CIn_{2} \cdot \theta \cdot D \end{aligned}$$

(38)

This analysis aims at demonstrating that selecting one supplier (θ = 0 or θ = 1) always yield a lower cost compared to operating the two of them (0 < θ < 1). Without loss of generality, we assume that total cost of employing suppler 1 $(\theta = 0)$ is lower than selecting supplier 2 $(\theta = 1)$, i.e., the following expression holds.

$$HC \cdot Z_{1 - \alpha } \sqrt {LT_{1} } \cdot \sqrt V + CIn_{1} \cdot D < HC \cdot Z_{1 - \alpha } \sqrt {LT_{2} } \cdot \sqrt V + CIn_{2} \cdot D$$

(39)

The second derivative of G(θ) the expression is:

$$\frac{{\partial G^{2} \left( \theta \right)}}{{\partial \theta^{2} }} = - \frac{1}{4}HC \cdot Z_{1 - \alpha } \cdot \frac{{\left( {LT_{2} - LT_{1} } \right)^{2} }}{{\left( {\left( {1 - \theta } \right) \cdot LT_{1} + \theta \cdot LT_{2} } \right)^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} }} \cdot \sqrt V$$

(40)

Which is allays negative when LT₁ ≠ LT₂ and the costs function is strictly concave. Accordingly, any value of 0 < θ < 1 will always provide a more expensive cost than θ = 0 and selecting suppler 1 is always better than employing the two suppliers.

Notice that:

• When the lead times are the same, the selection would be driven by the transportation costs, and again one supplier will be better than two suppliers (except when the transportation costs are the same, where choosing one suppler is also optimum).

• If fixed cost of selecting suppliers are added in to the analysis, the costs function when 0 < θ < 1 is a vertical shift up, which does not affect the obtained result.

Appendix B

In this appendix, a numerical example is presented considering 2 suppliers, 5 potential warehouses, and 5 customers, for which the proposed formulation is solved by using the proposed GBD-based algorithm. In this case, after integrating the five initial cuts (P = 1, 2, 3, 4, 5), the algorithm employed 8 iterations for obtaining the final optimal solution. The MP solutions for all iterations are presented in Fig. 

Fig. 30

Solutions obtained with the MP at each iteration

30 (except for the iteration 4). In addition, Table 9 and Fig. 31 show information about solutions obtained at each iteration.

Table 9 Objective function values for each iteration

Fig. 31

Objective function evolution

The next is the set of cuts integrated into the MP, including the first five cuts obtained with the artificial or modified MP (i.e., P = 1, 2, 3, 4, 5), and the seven cuts obtained after solving the respective SP at each iteration.

Appendix C

			Base Instance 1				Base Instance 2
			#Customers (nC)				#Customers (nC)
			5	10	15	20	5	10	15	20
#Suppliers (nS) = 1	#Warehouses (nW) = 5	OF	1,653,895.92	2,860,993.11	4,572,433.18	6,162,400.77	1,341,407.58	2,548,128.58	3,857,099.02	5,184,189.95
		Time	3.67	7.56	6.73	7.31	0.42	0.95	1.58	2.34
		IT	21	19	20	20	18	21	20	21
		NSS	1	1	1	1	1	1	1	1
		NLW	1	1	2	2	2	3	3	4
	#Warehouses (nW) = 10	OF	1,653,895.92	2,860,993.11	4,572,433.18	6,162,400.77	1,334,676.43	2,523,856.89	3,833,785.20	5,173,655.55
		Time	154.73	640.28	2,444.92	4,336.02	15.47	364.33	951.34	2,163.33
		IT	137	237	438	476	90	194	264	382
		NSS	1	1	1	1	1	1	1	1
		NLW	2	1	2	2	2	3	3	5
#Suppliers (nS) = 2	#Warehouses (nW) = 5	OF	902,217.35	1,771,093.71	3,003,583.48	3,928,232.99	1,341,407.58	2,519,762.03	3,685,399.79	4,885,462.65
		Time	0.09	0.06	1.55	0.59	0.84	1.02	1.54	1.39
		IT	9	9	13	13	22	22	22	19
		NSS	2	2	2	2	1	2	2	2
		NLW	2	2	2	2	2	4	4	5
	#Warehouses (nW) = 10	OF	711,512.07	1,331,319.76	2,339,769.96	2,995,884.98	1,264,357.39	2,237,598.46	3,246,475.83	4,154,951.58
		Time	2.16	4.38	138.55	323.36	37.36	347.52	837.80	704.27
		IT	23	44	119	144	110	160	246	245
		NSS	2	2	2	2	2	2	2	2
		NLW	2	2	2	2	3	5	4	6
#Suppliers (nS) = 3	#Warehouses (nW) = 5	OF	902,217.35	1,771,093.71	3,003,583.48	3,928,232.99	1,127,656.11	2,116,536.19	3,269,642.37	4,373,393.58
		Time	0.02	0.08	0.72	0.34	0.30	0.28	0.61	1.73
		IT	9	9	13	13	16	15	18	17
		NSS	2	2	2	2	1	3	3	3
		NLW	2	2	2	2	2	4	4	4
	#Warehouses (nW) = 10	OF	711,512.07	1,331,319.76	2,339,769.96	2,995,884.98	1,064,691.21	1,884,622.88	2,888,657.25	3,687,404.66
		Time	1.72	4.61	161.25	312.48	11.09	87.61	598.34	393.86
		IT	24	43	116	146	70	122	203	160
		NSS	2	2	2	2	2	3	3	3
		NLW	2	2	2	2	3	5	4	5
#Suppliers (nS) = 4	#Warehouses (nW) = 5	OF	902,217.35	1,771,093.71	3,003,583.48	3,928,232.99	1,114,799.06	2,080,184.58	3,233,290.76	4,329,027.10
		Time	0.05	0.11	0.56	0.55	0.28	0.16	0.89	1.22
		IT	9	10	13	13	14	15	18	17
		NSS	2	2	2	2	2	4	4	4
		NLW	2	2	2	2	2	4	4	5
	#Warehouses (nW) = 10	OF	711,512.07	1,331,319.76	2,339,769.96	2,995,884.98	1,051,834.15	1,849,241.84	2,844,935.85	3,635,912.71
		Time	2.64	6.67	171.83	394.81	8.92	60.72	467.98	319.95
		IT	27	42	130	162	63	110	175	144
		NSS	2	2	2	2	3	4	4	4
		NLW	2	2	2	2	3	5	4	5
#Suppliers (nS) = 5	#Warehouses (nW) = 5	OF	796,223.69	1,588,750.60	2,715,683.21	3,534,363.11	1,114,799.06	2,064,311.57	3,182,573.28	4,260,916.25
		Time	0.16	0.44	0.41	0.89	0.19	0.31	0.64	0.77
		IT	8	9	11	13	14	15	16	15
		NSS	2	2	2	2	2	4	4	4
		NLW	2	2	2	2	2	4	4	5
	#Warehouses (nW) = 10	OF	686,625.76	1,295,891.76	2,246,120.38	2,883,470.01	1,051,834.15	1,847,216.18	2,837,172.63	3,635,912.71
		Time	2.38	4.25	105.48	239.78	12.80	64.20	498.11	435.16
		IT	27	41	108	141	70	113	178	157
		NSS	3	3	3	3	3	4	4	4
		NLW	3	3	4	4	3	5	5	5

			Base Instance 3				Base Instance 4
			#Customers (nC)				#Customers (nC)
			5	10	15	20	5	10	15	20
#Suppliers (nS) = 1	#Warehouses (nW) = 5	OF	995,112.73	2,515,167.29	4,200,934.27	5,258,949.57	1,238,599.35	2,832,975.75	4,325,107.64	5,424,879.07
		Time	0.16	0.44	0.75	2.03	0.30	0.14	1.20	1.75
		IT	12	16	19	19	13	13	17	17
		NSS	1	1	1	1	1	1	1	1
		NLW	1	2	2	2	2	2	2	2
	#Warehouses (nW) = 10	OF	947,693.14	2,429,290.47	4,037,254.73	5,065,233.24	1,057,054.89	2,046,949.19	3,262,833.68	4,198,252.61
		Time	3.92	367.42	1,088.72	1,667.41	10.47	38.22	254.28	352.20
		IT	63	208	296	320	73	84	137	160
		NSS	1	1	1	1	1	1	1	1
		NLW	2	2	2	3	2	2	2	2
#Suppliers (nS) = 2	#Warehouses (nW) = 5	OF	911,715.73	2,339,536.84	3,759,968.83	4,775,702.42	1,104,478.66	2,715,635.28	4,066,848.29	4,977,718.31
		Time	0.11	0.95	0.59	1.14	0.72	0.98	3.28	1.34
		IT	13	19	17	18	22	22	24	22
		NSS	2	2	2	2	2	2	2	2
		NLW	2	3	3	3	3	4	4	4
	#Warehouses (nW) = 10	OF	872,213.99	2,250,428.74	3,618,518.00	4,606,189.29	966,004.74	1,982,957.17	3,146,368.06	3,959,410.78
		Time	4.48	415.91	567.47	782.55	15.53	46.00	305.33	254.34
		IT	59	189	184	204	88	97	173	163
		NSS	2	2	2	2	2	2	2	2
		NLW	3	3	3	3	3	3	3	3
#Suppliers (nS) = 3	#Warehouses (nW) = 5	OF	712,827.76	1,802,342.72	2,797,581.10	3,669,264.02	1,104,478.66	2,715,635.28	4,066,848.29	4,977,718.31
		Time	0.09	0.14	0.30	0.44	0.77	1.05	2.41	1.80
		IT	9	12	12	12	22	21	22	21
		NSS	2	2	2	3	2	2	2	2
		NLW	2	2	2	3	3	4	4	4
	#Warehouses (nW) = 10	OF	646,117.64	1,611,471.85	2,551,847.98	3,369,148.32	923,324.60	1,939,914.68	2,914,593.43	3,715,791.39
		Time	2.97	27.83	43.02	139.97	14.38	36.25	35.56	44.16
		IT	32	70	82	103	76	85	77	71
		NSS	2	2	2	2	3	2	3	3
		NLW	4	4	4	4	3	3	3	3
#Suppliers (nS) = 4	#Warehouses (nW) = 5	OF	712,827.76	1,802,342.72	2,797,581.10	3,669,264.02	1,028,530.32	2,464,786.74	3,704,009.89	4,617,788.52
		Time	0.05	0.19	0.33	0.16	0.48	1.31	1.50	2.38
		IT	9	12	12	12	19	17	19	20
		NSS	2	2	2	3	2	3	3	3
		NLW	2	2	2	3	3	4	4	4
	#Warehouses (nW) = 10	OF	646,417.64	1,611,471.85	2,551,847.98	3,369,148.32	691,545.15	1,318,757.45	2,018,605.18	2,610,180.59
		Time	2.75	26.53	44.48	143.33	2.81	4.58	8.33	15.55
		IT	32	70	82	103	40	51	47	44
		NSS	2	2	2	2	3	3	3	3
		NLW	4	4	4	4	3	3	3	3
#Suppliers (nS) = 5	#Warehouses (nW) = 5	OF	712,827.76	1,802,342.72	2,797,581.10	3,669,264.02	997,555.19	2,359,739.83	3,574,912.38	4,482,864.95
		Time	0.05	0.33	0.34	0.27	0.28	0.70	1.91	1.69
		IT	9	12	12	12	17	18	20	18
		NSS	2	2	2	3	3	3	3	3
		NLW	2	2	2	3	3	3	3	4
	#Warehouses (nW) = 10	OF	641,973.51	1,610,049.60	2,538,434.70	3,357,335.96	691,545.15	1,318,757.45	2,018,605.18	2,610,180.59
		Time	2.91	29.30	52.64	130.23	2.72	5.88	7.22	16.08
		IT	32	72	77	104	43	49	40	43
		NSS	3	3	3	3	3	3	3	3
		NLW	4	5	5	5	3	3	3	3

			Base Instance 5
			#Customers (nC)
			5	10	15	20
#Suppliers (nS) = 1	#Warehouses (nW) = 5	OF	2,178,244.28	4,328,128.83	6,116,851.14	8,124,073.96
		Time	0.53	1.77	7.83	6.84
		IT	15	18	19	19
		NSS	1	1	1	1
		NLW	1	2	2	2
	#Warehouses (nW) = 10	OF	1,663,819.94	3,331,834.97	4,812,300.25	6,098,933.05
		Time	29.98	675.22	1,665.34	1,786.20
		IT	94	260	348	311
		NSS	1	1	1	1
		NLW	2	3	4	4
#Suppliers (nS) = 2	#Warehouses (nW) = 5	OF	1,935,285.14	3,788,038.48	5,311,398.25	7,204,257.02
		Time	0.66	3.77	7.09	4.11
		IT	19	23	23	22
		NSS	1	1	1	1
		NLW	2	2	2	2
	#Warehouses (nW) = 10	OF	1,293,913.57	2,617,644.85	3,838,034.86	4,996,407.90
		Time	9.78	159.97	502.75	457.14
		IT	52	95	172	146
		NSS	2	2	2	2
		NLW	2	3	4	4
#Suppliers (nS) = 3	#Warehouses (nW) = 5	OF	1,140,038.99	2,283,616.46	3,058,355.76	4,034,370.07
		Time	0.20	0.50	0.48	0.58
		IT	10	15	15	15
		NSS	1	1	1	1
		NLW	1	2	2	2
	#Warehouses (nW) = 10	OF	1,076,136.77	2,137,499.81	2,860,586.43	3,696,629.23
		Time	3.38	65.48	194.55	60.67
		IT	32	98	115	102
		NSS	2	3	3	3
		NLW	2	3	3	3
#Suppliers (nS) = 4	#Warehouses (nW) = 5	OF	1,140,038.99	2,255,318.32	3,015,394.18	3,991,818.42
		Time	0.08	0.41	0.92	1.66
		IT	10	15	17	17
		NSS	1	2	2	2
		NLW	1	2	2	2
	#Warehouses (nW) = 10	OF	964,500.00	1,925,217.76	2,593,771.64	3,430,290.72
		Time	1.41	9.94	24.81	9.19
		IT	20	53	57	51
		NSS	2	3	3	3
		NLW	2	3	3	3
#Suppliers (nS) = 5	#Warehouses (nW) = 5	OF	1,140,038.99	2,255,318.32	3,015,394.18	3,991,818.42
		Time	0.06	0.56	1.69	1.41
		IT	10	15	17	17
		NSS	1	2	2	2
		NLW	1	2	2	2
	#Warehouses (nW) = 10	OF	964,500.00	1,925,217.76	2,593,771.64	3,430,290.72
		Time	1.78	10.31	26.23	9.16
		IT	20	53	57	51
		NSS	2	3	3	3
		NLW	2	3	3	3

Appendix D

			AVERAGE
			#Customers (nC)
			5	10	15	20
#Suppliers (nS) = 1	#Warehouses (nW) = 5	OF	1.481.451,97	3.017.078,71	4.614.485,05	6.030.898,67
		Time	1,02	2,17	3,62	4,06
		IT	15,80	17,40	19,00	19,20
		NSS	1,00	1,00	1,00	1,00
		NLW	1,40	2,00	2,20	2,40
	#Warehouses (nW) = 10	OF	1.331.428,07	2.638.584,93	4.103.721,41	5.339.695,04
		Time	42,92	417,09	1.280,92	2.061,03
		IT	91,40	196,60	296,60	329,80
		NSS	1,00	1,00	1,00	1,00
		NLW	2,00	2,20	2,60	3,20
#Suppliers (nS) = 2	#Warehouses (nW) = 5	OF	1.239.020,89	2.626.813,27	3.965.439,73	5.154.274,68
		Time	0,48	1,36	2,81	1,72
		IT	17,00	19,00	19,80	18,80
		NSS	1,60	1,80	1,80	1,80
		NLW	2,20	3,00	3,00	3,20
	#Warehouses (nW) = 10	OF	1.021.600,35	2.083.989,80	3.237.833,34	4.142.568,91
		Time	13,86	194,75	470,38	504,33
		IT	66,40	117,00	178,80	180,40
		NSS	2,00	2,00	2,00	2,00
		NLW	2,60	3,20	3,20	3,60
#Suppliers (nS) = 3	#Warehouses (nW) = 5	OF	997.443,77	2.137.844,87	3.239.202,20	4.196.595,79
		Time	0,28	0,41	0,90	0,98
		IT	13,20	14,40	13,80	15,60
		NSS	1,60	2,00	2,00	2,20
		NLW	2,00	2,80	3,00	3,00
	#Warehouses (nW) = 10	OF	884.356,46	1.780.965,80	2.711.091,01	3.492.971,72
		Time	6,71	44,36	206,54	190,23
		IT	46,80	83,60	118,60	116,40
		NSS	2,20	2,40	2,60	2,60
		NLW	2,80	3,40	3,20	3,40
#Suppliers (nS) = 4	#Warehouses (nW) = 5	OF	979.682,70	2.074.745,21	3.150.771,88	4.107.226,21
		Time	0,19	0,43	0,84	1,19
		IT	12,20	13,80	15,80	15,80
		NSS	1,80	2,60	2,60	2,80
		NLW	2,00	2,80	2,80	3,20
	#Warehouses (nW) = 10	OF	813.161,80	1.607.201,73	2.469.786,12	3.208.283,47
		Time	3,71	21,69	143,49	176,57
		IT	36,40	65,20	98,20	100,80
		NSS	2,40	2,80	2,80	2,80
		NLW	2,80	3,40	3,20	3,40
#Suppliers (nS) = 5	#Warehouses (nW) = 5	OF	952.288,94	2.014.092,61	3.057.228,83	3.987.845,35
		Time	0,15	0,47	1,00	1,00
		IT	11,60	13,80	15,20	15,00
		NSS	2,00	2,60	2,60	2,80
		NLW	2,00	2,60	2,60	3,20
	#Warehouses (nW) = 10	OF	807.295,71	1.599.426,55	2.446.820,91	3.183.438,00
		Time	4,52	22,79	137,94	166,08
		IT	38,40	65,60	92,00	99,20
		NSS	2,80	3,20	3,20	3,20
		NLW	3,00	3,80	4,00	4,00