A multi-product dynamic supply chain inventory model with supplier selection, joint replenishment, and transportation cost

Abstract

The aim of this paper is to solve a multi-period supplier selection and inventory lot-sizing problem with multiple products in a serial supply chain. Compared to previous models proposed in the literature, our research incorporates a richer cost structure involving joint replenishment costs for raw material replenishment and production, and a more realistic description of the transportation costs represented as a vector of full-truck load costs for different size trucks. This problem can be displayed graphically as a time-expanded transshipment network defined by nodes and arcs that can be reached by feasible material flows. First, we propose an integrated mixed integer linear programming model that minimizes the cost over the entire supply chain for a given planning horizon. The model determines the optimal dynamic supplier selection, inventory lot-sizing, and production schedule simultaneously. Second, a sequential approach is proposed to solve the same problem. That is, a production schedule is determined first, and then a supplier selection and replenishment strategy is obtained according to that predetermined schedule. Sensitivity analysis comparing the two approaches is performed. Results show that, even though the integrated approach achieves the minimum cost, the sequential approach may be suitable for solving large-scale instances of the problem as it requires less information sharing and generates a near-optimal solution with shorter implementation time and computational effort.

1 Introduction

In today’s increasingly dynamic and complex business environment, responsiveness stands as one of the fundamental characteristics for competitive supply chains. According to Roy (2010), the new generation of supply chains are transforming processes and adding IT capabilities to reduce costs, improve responsiveness, and increase performance. In doing so, response to demand changes in real time is an essential task given that the build-to-forecast model has evolved into a demand-driven supply chain. Consequently, the shelf life of a typical operational plan is short and unforeseen changes in demand or supply may render the plan obsolete soon after it is released. Thus, it is necessary to be able to model integrated supply chains that consider existing customer orders and up-to-date inventory and in-transit inventory levels that can be used to generate operational plans to be executed in a relatively short time horizon.

Ravindran and Warsing (2013) indicate that one of the key drivers affecting supply chain responsiveness is inventory. Holding large quantities of inventory could make a supply chain more responsive to changes in demand. However, this could result in high holding costs. Therefore, an interesting problem to study in supply chain management is determining the proper inventory levels to hold at each stage of a supply chain network. Another critical driver in a supply chain is sourcing. Selecting the right suppliers can impact the overall purchasing cost, which accounts for a large percentage of the final product cost (Van Weele, 2005).

Given the importance of both inventory management and supplier selection for supply chain responsiveness, this paper expands prior research work developed by Ventura et al. (2013) and aims to solve a multi-period supplier selection and order quantity allocation problem with multiple products in a serial supply chain. In particular, the supplier selection process occurs in stage 1, where a manufacturing facility purchases raw materials from a set of potential vendors. These materials are then stored and processed into products at the manufacturing facility. Products may require additional processing in subsequent stages or are just stored at the manufacturer and transported to subsequent warehousing stages, where they are either stored or transported to the next stage until it reaches a final distribution center. The distribution center serves the demand for final products to the marketplace. The main contributions of our work can be summarized as follows:

• While modeling single-item lot sizing situations shed light on some structural elements of more complex problems, real problems mostly deal with multiple products. Therefore, we consider and study the multi-product case, where replenishment, production, inventory, and transportation operations are jointly considered to take advantage of potential economies of scale.

• We address the dynamic supply chain inventory lot-sizing problem in the presence of joint replenishment costs for purchasing raw materials from several suppliers and joint setup costs for production scheduling, with general time-varying costs and demand parameters.

• We consider a more realistic transportation cost structure modeled as a vector of full-truck load (TL) costs for different size trucks available for replenishment of raw materials and shipping final products between consecutive stages from the manufacturing facility to the marketplace.

• We also contemplate an all-unit quantity discount scheme on the purchased materials from suppliers. In real-life scenarios, most vendors offer price discounts to motivate manufacturers to order larger quantities and take advantage of economies of scale (Elmaghraby & Keskinocak, 2003).

• We propose an integrated mixed integer linear programming model to minimize the total cost over the entire supply chain for a given planning horizon in order to determine the optimal dynamic supplier selection and inventory planning strategy, simultaneously.

• Solving the integrated model to optimality can sometimes be hard in practical situations because of its size and complexity. Therefore, we also propose a sequential approach where the inventory plan is determined first, and then, a supplier selection and replenishment strategy is obtained according to that plan. The sequential approach is easier to implement to obtain a near-optimal solution in a more efficient fashion.

• While other papers with multiple products in similar settings propose heuristic approaches (e.g., Cárdenas-Barrón et al., 2015; and Alfares & Turnadi, 2018), including a partitioning heuristic for the joint replenishment problem over a finite time horizon that can guarantee an $\varepsilon$-optimal solution, for any $\varepsilon >0$ (Federgruen & Tzur, 1994), the current paper offers a method leading to an optimal solution.

The rest of this paper is organized as follows. Section 2 provides a literature review of related work. Section 3 shows the time-expanded transshipment network representation of the dynamic inventory problem in a serial supply chain with supplier selection. Section 4 introduces the general characterization of the transportation mode, joint replenishment cost, and all-unit quantity discount scheme considered in the problem formulation. In Sect. 5, mathematical models for the integrated and sequential versions of the problem are provided. In Sect. 6, we conduct a numerical analysis and discuss managerial insights. Finally, concluding remarks and possible future research directions are summarized in Sect. 7.

2 Literature review

This literature review is organized in three parts. First, the supplier selection problem is reviewed. Then, reviews of two cases of the joint supplier selection and inventory lot-sizing are provided: infinite planning horizon and finite planning horizon with time varying demand (Fiszeder & Orzeszko, 2018).

2.1 Supplier selection

Sourcing from multiple suppliers has numerous advantages as single sourcing exposes companies to disabled supply when interruptions occur due to material shortages, labor strikes, machine breakdowns, acute weather conditions, or natural disasters. Additionally, in the presence of demand uncertainty, multiple sourcing can improve customer service and reduce safety stocks (Yao & Minner, 2017).

Supplier selection is an important problem for single- and multi-sourcing environments, and usually depends on several factors, such as price, product quality, service level, and lead-time. Overtime, there has been a comprehensive effort to analyze the criteria used in this process, including the pioneer works by Dickson (1966) and Weber et al. (1991). Ghodsypour and O’Brien (1996) propose the integration of an analytical hierarchy process (AHP) and linear programming to consider both tangible and intangible factors in choosing the best suppliers and corresponding order quantities with the objective of maximizing the total value of purchasing. Degraeve et al. (2000) adopt the concept of total cost of ownership as a basis for comparing supplier selection models. This approach basically considers all relevant costs involved in the purchasing process of a good or service from each supplier. Talluri and Narasimhan (2003) propose a max–min productivity-based approach that derives vendor performance variability measures, which are then used in a nonparametric statistical technique in identifying supplier groups for effective selection and allowing the buyer to make the final decision considering other intangible factors. Ng (2008) suggests a weighted linear programming model for the multi-criteria supplier selection problem with the objective of maximizing the supplier score. Sawik (2014) conclude that a key issue in the supplier selection problem is a combination of performance on cost, quality, and service. More recently, Chai et al. (2013) provide a systematic literature review on articles published from 2008 to 2012 on the application of decision-making techniques for supplier selection. Due to the growing concern around sustainability in recent years, Luthra et al. (2017) propose a framework with 22 criteria to evaluate sustainable supplier selection in three dimensions: economic, environmental, and social. Moreover, provided the multicriteria nature of a supplier selection decision, recent studies review decision models considering green and social aspects with other performance criteria, simultaneously (Schramm et al., 2020; and Rashidi et al., 2020). Zhang et al. (2020) present a literature review on criteria utilized in reverse logistics supplier selection.

In our inventory management research, we consider capacity and quality as criteria for the supplier selection decision. On one hand, no company reaches 100% quality levels, and therefore is safe to consider that suppliers have restrictions on the quality of the products supplied (e.g., a minimum required quality level for the incoming parts, which should be satisfied as an aggregate performance measure from different suppliers). On the other hand, most of the times suppliers are constrained by actual capacity. Hence, when determining lot-sizing is appropriate to consider the supplier capacity. The availability, in addition to be something real, makes inventory cost trade-off an interesting effect to study (e.g., capacity also has implications for transportation decisions).

2.2 Integrated supplier selection and inventory lot-sizing over an infinite planning horizon

The literature shows extensive research on supplier selection and lot sizing in supply chain management as independent topics. However, research studies that consider both topics simultaneously are more limited. Chen and Zhang (2010) study the effect of demand disruptions on the production control policy and supplier selection decisions in a three-echelon supply chain. They use simulated annealing to search for the best production-inventory plan and AHP to select the best suppliers. Mendoza and Ventura (2010) consider a serial supply chain system with multiple suppliers. They propose a mixed integer nonlinear programming model aiming at determining an optimal inventory policy that coordinates the transfer of items between different stages of a serial supply chain, while properly allocating orders to selected suppliers in the first stage. In addition, a lower bound on the minimum total cost per time unit is provided and a 98% effective power-of-two algorithm is derived for the system under consideration. Parsa et al. (2013) also study the lot sizing and supplier selection problem for a two-stage supply chain. In this case, suppliers offered quantity discounts. The proposed mathematical model is solved using dynamic programming.

Choudhary and Shankar (2013), and Choudhary and Shankar (2014) address the integrated supplier selection, inventory lot-sizing, and carrier selection problem. Choudhary and Shankar (2013) propose an integer linear programming model to find lot-sizes, select carriers and suppliers, while minimizing the total cost over the planning horizon. They consider all-unit quantity discounts from potential suppliers. Choudhary and Shankar (2014) present a multi-objective integer linear programming model with the objective to minimize net rejected items, net costs, and net late delivered items. Taleizadeh and Noori-daryan (2014) study a supply chain formed by a supplier, a producer and some retailers. They optimize the total cost of the network. The decision variables of the model are supplier’s and producer’s price and the number of shipments received by the supplier and producer. Sawik (2014) consider a bi-objective stochastic mixed integer programming approach to integrate a supply, production, and distribution scheduling problem under disruption risks.

Taleizadeh et al. (2015) analyze a two-stage supply chain with one manufacturing vendor and multiple retailers. They consider a single product with a price-sensitive demand over an infinite horizon. They aim at maximizing the total profit of the network by employing the optimal pricing, lot-sizing and production policies. Purohit et al. (2016) propose an integer linear programming model for the inventory lot-sizing and supplier selection problem. They consider non-stationary stochastic demand, fill rate constraints, and all-unit quantity discounts from suppliers. Firouz et al. (2017) study the multi-sourcing supplier selection and inventory problem considering lateral transshipments. They suggest a decomposition based heuristic algorithm, powered with simulation. While the decomposition-based heuristic determines a solution with supplier selection and inventory decisions, the simulation model evaluates the objective function value corresponding to each generated solution. Adeinat and Ventura (2018) examine supplier selection, inventory, and pricing decisions in a two-stage supply chain consisting of a manufacturer followed by a retailer. The manufacturer periodically replenishes the retailer’s inventory, whose demand is sensitive to price changes. They propose a mixed integer nonlinear programming model designed to determine the size and frequency orders placed to the selected suppliers, the amount of inventory replenished at each stage, and the selling price that maximizes the profit per time unit. Noori-daryan et al. (2018) study optimal replenishment and pricing decisions for a two-stage supply chain. They consider three different transport modes. Additionally, the supplier offers both quantity and freight discounts as well as the so-called free shipping quantity (FSQ) strategy. They aim at optimizing the total profit concerning the selling prices and order quantities of the manufacturer and the retailers.

Noori-daryan et al. (2019) study a two-echelon multi-national supply chain with several multinational producers and a retailer. Market demand is assumed to be dependent on retail price and delivery lead time. Even though the retailer promises delivery times, the order response may vary due to uncertainty of demand and supply. Preliminary results show that the production and opportunity costs of the producers influence the profit of the supply chain. Duan and Ventura (2021) analyze the joint pricing, supplier selection, and inventory replenishment problem. They assess the effect of various price-sensitive demand functions on pricing and procurement decisions, and provide evidence that the logit demand function is a very good option for capturing the global change of the price in real-life applications. Recently, Ventura et al. (2021) examine the implications on the supplier selection and lot-sizing problem in a decentralized supply chain composed of a set of suppliers and a single buyer, when supplier production rates are finite. They evaluate generalized lot-sizing policies that are more dynamic than the classic lot-for-lot policy assumed in related papers. Although they optimize the performance of the supply chain, they also devise a profit-sharing contract that can possibly resolve the conflicting objectives of the firm within the decentralized system.

2.3 Integrated supplier selection and inventory lot-sizing over a finite planning horizon

Recently, researchers have integrated supplier selection and inventory control in supply chains operating under time-varying demand environments to reach global optimal operational plans over a finite time horizon aiming at minimizing purchasing cost and inventory holding cost simultaneously. Basnet and Leung (2005) develop a multi-period inventory lot-sizing model considering multiple products and multiple suppliers. They propose an enumerative search algorithm and a heuristic to solve their proposed mixed integer programming formulation. Ustun and Demirtas (2008) suggest an integration of the analytic network process and achievement scalarizing functions to select the best suppliers and identify optimal order quantities among the selected suppliers by assessing tangible–intangible criteria and the time horizon. Rezaei and Davoodi (2008) consider a multi-period multi-item supply chain with multiple suppliers. Suppliers have limited capacity and some items received from suppliers do not have perfect quality. They formulate the problem as a mixed integer programming and use genetic algorithms to find near-optimal solutions that could be suitable for real-world conditions. Moqri et al. (2011) develop a mathematical programming model to deal with a multi-period integrated supplier selection and lot sizing problem. They consider a single buyer and multiple suppliers and propose a forward dynamic programming approach to find the best solution. Ventura et al. (2013) analyze a multi-period supplier selection and lot-sizing problem for a single product in a serial supply chain. They formulate the problem as a mixed integer nonlinear program to determine an optimal inventory policy that coordinates the transfer of materials between consecutive stages while properly placing purchasing orders to selected suppliers and satisfying customer demand on time.

Lee et al. (2013) study the multi-period lot-sizing problem with multiple suppliers offering quantity discounts. They develop a mixed integer programming model and suggest a genetic algorithm solve the problem when it becomes too complicate. Mazdeh et al. (2015) investigate the dynamic lot sizing problem with supplier selection for a single item. Due to the complexity of the problem, they develop a heuristic based on the Fordyce-Webster algorithm (Fordyce & Webster, 1984). Cárdenas-Barrón et al. (2015) use a new heuristic approach, called “reduce and optimize” to solve the multi-item, multi-period supplier selection and inventory lot sizing problem. Their approach solves the problem over a small feasible space that contains near optimal solutions. The performance of the heuristic algorithm is satisfactory because it found higher quality solutions than those reported by Basnet and Leung (2005) on a set of benchmark instances.

Ghaniabadi and Mazinani (2017) formulate a mixed integer linear programming model to solve the dynamic lot sizing problem with supplier selection for a single item. They consider backlogging and two types of quantity discounts: all-unit and incremental. Alfares and Turnadi (2018) propose a mixed integer programming model to formulate the multi-item, lot-sizing problem with supplier selection considering multiple periods, quantity discounts, and backordering. They develop two heuristic solution methods to solve the problem. Duan and Ventura (2018) address the single-product, multi-period, multi-supplier, and multi-stage problem. They consider a novel supplier price break and discount scheme and propose a mixed integer linear programming formulation to solve the problem. Most recently, Cárdenas-Barrón et al. (2021) work on the multi-item inventory lot-sizing problem with supplier selection problem with dynamic demand and propose a facility location extended formulation which can be preprocessed considering the cost structure and introduce new valid inequalities in the original space of variables. They also develop a simple and effective mixed integer programming heuristic using the extended formulation. Computational results show that the preprocessing approach can significantly reduce the size of the formulation to be solved.

As stated by Brahimi et al. (2017), there is a growing interest in lot-sizing problems, both from scientific significance and practical application. So, Brahimi et al. (2006) and, most recently Brahimi et al. (2017), survey the literature on lot-sizing problems and conclude that single-item lot sizing problems are helpful in understanding some structural parts of more complex industrial problems. Though, real problems most often deal with multiple products. Yao and Minner (2017) also perform an extensive review of inventory models with multiple supply options with a focus on recent work since 2003, discuss their contributions from different managerial perspectives, and summarize key strategic aspects, including network design, supplier selection, competition, and contract coordination. They also identify gaps in the literature and suggest promising issues for future research, including multi-sourcing inventory models with multiple kinds of uncertainty, nonparametric approaches when a firm has no demand distribution information or historical demand data, supply chain performance evaluation based not only on metrics of cost, time and accuracy, but also on risk and sustainability, and new procedures for deriving optimal solutions or effective heuristic solutions.

The present paper contributes to the development of more realistic analytical approaches to generate operational plans for serial supply chain systems considering multiple suppliers, multiple products, and time varying demand over a finite-time horizon, and where replenishment, production, inventory, and transportation costs are jointly considered to take full advantage of potential economies of scale usually present in real-life scenarios.

3 Supply chain network model

In this section, a network model is employed to represent a serial supply chain with ${n}_{K}$ stages, a set of ${n}_{J}$ available suppliers available to procure ${n}_{M}$ types of raw materials to produce ${n}_{P}$ final products considering a deterministic time varying demand over ${n}_{T}$ planning periods. The following sets and notation are introduced to define the problem and understand the proposed network model:

3.1 Sets

$J$::

set of suppliers, $j\in J$, $J=\left\{1, 2,\cdots ,{n}_{J}\right\}$.

${J}_{2}$::

set of suppliers with positive delivery lead times, ${J}_{2}=\{ j\in J : {l}_{0,j}\ge 1\}$.

$K$::

set of supply chain stages, $k\in K, K=\left\{1, 2,\cdots ,{n}_{K}\right\}$.

$S$::

set of customers, $s\in S, S=\left\{1, 2,\cdots ,{n}_{S}\right\}$.

$T$::

set of planning periods, $t\in T, T=\left\{1, 2,\cdots ,{n}_{T}\right\}$.

${T}_{0j}$::

set of feasible time periods for raw material orders submitted to supplier $j, j\in J, {T}_{0j}\subseteq T$.

${T}_{k}$::

set of feasible time periods corresponding to stage $k, k\in K, {T}_{k}\subseteq T$.

$M$::

set of raw materials, $m\in M, M=\left\{1, 2,\cdots ,{n}_{M}\right\}$.

$P$::

set of final products, $p\in P, P=\left\{1, 2,\cdots ,{n}_{P}\right\}$.

${K}_{D}$::

set of intermediate stages that hold final products, $k\in {K}_{D}, {K}_{D}=\left\{2, 3, 4,\dots , {n}_{K}-1\right\}$.

3.2 Parameters

${l}_{0,j}$::

number of delivery lead time periods from supplier $j$ to stage 1, $j\in J$.

${l}_{1}$::

number of delivery lead time periods from stage 1 to stage 2 within the manufacturing facility.

${l}_{k}$::

number of delivery lead time periods from stage $k$ to stage $k+1$, $k\in {K}_{D}$.

${d}^{p,t}$::

total demand for product $p$ at time period $t, {d}^{p,t}=\sum_{s\in S}{d}_{s}^{p,t}, p\in P, t\in T$.

${I}_{1}^{m,0}$::

initial inventory of raw material $m$ in stage 1, $m\in M$.

${I}_{k}^{p,0}$::

initial inventory of product $p$ in stage $k, p\in P, k\in {K}_{D}\cup \left\{{n}_{K}\right\}$.

${q}_{0, j}^{m, 0}$::

pending order for raw material $m$ available from supplier $j$ at the beginning of the first period, $m\in M$,$j\in {J}_{2}$.

${I}_{1}^{m,{n}_{T}}$::

ending inventory of raw material $m$ in stage 1 at the end of time period${n}_{T}$. Assumption: ${I}_{1}^{m,{n}_{T}}=0, m\in M$.

${I}_{k}^{p,{n}_{T}}$::

ending inventory of product $p$ in stage $k$ at the end of time period${n}_{T}$. Assumption: ${I}_{k}^{p,{n}_{T}}=0, p\in P, k\in {K}_{D}\cup \left\{{n}_{K}\right\}$.

3.3 Continuous variables

${I}_{1}^{m,t}$::

inventory level of raw material $m$ at stage 1 at the end of period $t\in {T}_{1}, m\in M, t\in {T}_{1}$.

${I}_{k}^{p, t}$::

inventory level of product $p$ at stage $k$ at the end of period $t$, $p\in P$, $k\in {K}_{D}\cup \left\{{n}_{K}\right\}$, $t\in {T}_{k}$.

${Q}_{0,j}^{m, t}$::

quantity of raw material $m$ ordered to supplier $j\in J$ at the beginning of period $t, m\in M, j\in J, t\in {T}_{0,j}$.

${X}_{1}^{p,t}$::

production lot size (in units of product) ordered at the manufacturer stage (stage 1) of product $p\in P$ at the beginning of period $t, p\in P, t\in {T}_{1}$.

${Y}_{k}^{p,t}$::

order quantity for product $p$ to be shipped from stage $k$ to stage $k+1$ at the beginning of period $t, p\in P, k\in {K}_{D}, t\in {T}_{k}$.

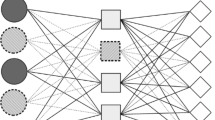
In this context, the several observations are in order. Stages 1 and 2 both represent the manufacturing facility. Stage 1 receives the raw materials purchased from suppliers. These raw materials are either stored or processed into products in stage 2. Additional processing or storage stages may be available after the second stage. The last stage, ${n}_{K}$, directly sells products to customers. Stage ${n}_{K}$ can be a retail distribution center (DC) where they fulfill retail or eCommerce orders, or a simple retail store where customers pick up their orders at the retail location. A simplified supply chain network model with ${n}_{K}=4$ stages is shown in Fig. 1.

Fig. 1

Simplified dynamic serial supply chain network

The network under study is dynamic because it allows changes in material flow between consecutive stages due to variations in demand from one period to the next. A time-expanded (static) supply chain network, corresponding to the dynamic network in Fig. 1, can be represented as a general (static) transshipment network, ${G}_{S}=\left({N}_{S},{A}_{S}\right)$, where the set of nodes ${N}_{S}$ and set of arcs ${A}_{S}$ are defined as follows:

$${N}_{S}=\left\{\left(0,j,t\right) :j\in J,t\in T\right\}\cup \left\{\left(k,t\right) :k\in K, t\in T\right\},$$

(1)

and

$$\begin{array}{*{20}l} {A_{s} = \left\{ {\left( {\left( {0,j,t} \right),\left( {1,t + l_{0,j} } \right)} \right):j \in J,t \in \left\{ {1,2, \ldots ,n_{T} - l_{0,j} } \right\}} \right\}} \hfill \\ {\,\,\,\,\,\,\,\quad\cup \left\{ {\left( {\left( {k,t} \right),\left( {k,t + 1} \right)} \right):k \in K,t \in T\backslash \left\{ {n_{T} } \right\}} \right\}} \hfill \\ {\,\,\,\,\,\,\,\quad \cup \left\{ {\left( {\left( {k,t} \right),\left( {k + 1,t + l_{k} } \right)} \right):k \in K\backslash \left\{ {n_{K} } \right\},t \in \left\{ {1,2, \ldots ,n_{T} - l_{k} } \right\}} \right\}}. \hfill \\ \end{array} $$

(2)

Observe that the definition of set ${N}_{S}$ in Eq. (1) contains neither the set of customers S nor node ${n}_{K}+1$ representing the customer market. Likewise, the definition of set ${A}_{S}$ in Eq. (2) excludes both initial and ending inventories. Figure 2 shows a time-expanded static supply chain network ${G}_{s}$ with three suppliers $({n}_{J}=3)$, four stages $({n}_{K}=4)$, and a planning horizon of five periods $\left({n}_{T}=5\right)$. Stages 1 and 2 represent the manufacturing facility, where raw materials can be processed into final products. Stage 3 is a centralized warehouse holding final products, and stage 4 stands for a distribution center that directly serves the customers’ demand. In this supply chain, two types of raw materials, $M=\left\{1, 2\right\}$, are used to manufacture two types of consumer products, $P=\left\{1, 2\right\}$. Lead times are positive for suppliers 2 and 3, where orders are delivered one period after they are submitted, i.e., ${l}_{\mathrm{0,2}}={l}_{\mathrm{0,3}}=1$. Notice that only supplier 1 can provide the order quantity ${Q}_{\mathrm{0,1}}^{m,t}, m\in M$, $t\in {T}_{\mathrm{0,1}}$, in the same requested period, i.e., ${l}_{\mathrm{0,1}}=0$. The lead times are zero between stages ($1, 2$) and ($2, 3$), and one period between states ($3, 4$), i.e., ${l}_{1}={l}_{2}=0, {l}_{3}=1$. Consequently, due to positive delivery lead times, raw materials and final products need to be ordered in advance or maintained in inventory to satisfy the demand in each period. In the graphical illustration of the network, flows are represented as two-dimensional vectors, indicating raw materials and final products. The raw material flow from supplier $j$ in period $t$ is represented as a directed arc connecting nodes $\left(0,j,t\right)$ and $\left(1,t+{l}_{0j}\right)$. Similarly, the inventory flow between consecutive time periods $t$ and $t+1$ at stage $k$ is characterized by a directed arc connecting nodes $\left(k,t\right)$ and $\left(k,t+1\right)$. Also, the product flow between consecutive stages $k$ and $k+1$ is shown by a directed arc that connects nodes $\left(k,t\right)$ and $\left(k+1,t+{l}_{k}\right)$.

Fig. 2

Time-expanded supply chain network ${G}_{s}$ (reduced network ${G}_{s}^{\mathrm{^{\prime}}}$ is circled with the dotted line)

The time-expanded network model allows for simultaneous coordination of inventory planning with the dynamic supplier selection strategy. One limitation of the model is the size of the network: $\left({n}_{J}+{n}_{K}\right)\times {n}_{T}$. The number of variables depends on the number of nodes: ${n}_{M}\times {n}_{T}$ variables for the raw material inventory level, (${I}_{1}^{m,t}$); ${n}_{P}\times {n}_{T}\times ({n}_{K}-1)$ variables for finished product inventory level (${I}_{k}^{p,t}, k\in {K}_{D}\cup \left\{{n}_{K}\right\}$); ${n}_{J}\times {n}_{M}\times {n}_{T}$ variables for raw material lot size (${Q}_{0,j}^{m,t}$); ${n}_{P}\times {n}_{T}$ variables for production lot size (${X}_{1}^{p,t}$); and ${n}_{P}\times {n}_{T}\times ({n}_{K}-1)$ variables for finished product order quantity (${Y}_{k}^{p,t}, k\in {K}_{D}\cup \left\{{n}_{K}\right\}$). Hence, the number of decision variables of the mathematical model is $\left({n}_{P}+{n}_{J}\right)\times {n}_{K}+\left({n}_{P}+1\right)\times {n}_{M}$.

However, the time-expanded supply chain network can be reduced in size by eliminating all the arcs and nodes that cannot be reached by any feasible raw material or product flow due to the positive lead times and finite planning horizon. Based on Theorem 1 in Ventura et al. (2013), for a given stage $k\in K$, let ${m}_{k}$ be either zero or the closest preceding stage with positive initial inventory or pending order, i.e.,

$${m}_{k}=\mathrm{max }\left\{0,{k}^{^{\prime}}: {Y}_{{k}^{^{\prime}}}^{p,0}+{I}_{k}^{p,0}>0,{k}^{^{\prime}}\in {K}_{D}\cup \left\{{n}_{K}\right\}, p\in P\right\}, k\in K.$$

(3)

Similarly, let ${m}_{k}^{*}$ be either ${n}_{K}$ or the closest succeeding stage with positive ending inventory, i.e.,

$${m}_{k}^{*}=\mathrm{min }\left\{{n}_{K},{k}^{^{\prime}}: {I}_{{k}^{^{\prime}}}^{p,{n}_{T}}>0,{k}^{^{\prime}}\in \left\{k,\cdots ,{n}_{K}-1\right\}, p\in P\right\}, k\in K.$$

(4)

Then, node $\left(k,t\right)$ is reachable in network ${G}_{S}=\left({N}_{S},{A}_{S}\right)$ if and only if $t\in {T}_{k}$, where ${T}_{k}$ is defined as follows:

$${T}_{k}=\left\{t :{l}_{0}+{\sum }_{{k}^{^{\prime}}={m}_{k}}^{k-1}{l}_{{k}^{^{\prime}}}\le t\le {n}_{T}-{\sum }_{{k}^{^{\prime}}=k}^{{m}_{k}^{*}-1}{l}_{{k}^{^{\prime}}}, t\in T\right\}, k\in K,$$

(5)

where

$$l_{0} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {m_{k} \ge 1,} \hfill \\ {1 + {\text{min}}\left\{ {l_{{0,j}} :j \in J} \right\},} \hfill & {m_{k} = 0.} \hfill \\ \end{array} } \right.$$

(6)

Note that, when ${m}_{k}=0$, initial inventory or pending orders for raw materials and products are zero. In this case, it is necessary to order raw material, initiate a production order, and move final products through several stages until certain stage $k$ can be reached.

Similarly, a raw material order submitted by the manufacturing stage to a given supplier $j\in J$ at time $t$ will be reachable if and only if $t\in {T}_{0,j},$ where

$${T}_{0,j}=\left\{t :1\le t\le max \left\{{T}_{1}\right\}-{l}_{0,j}\right\}, j\in J.$$

(7)

Hence, nodes $\left(0,j,{t}_{1}\right)$ and $\left(k,{t}_{2}\right)$ will be reachable if and only if ${t}_{1}\in {T}_{0,j}$ and ${t}_{2}\in {T}_{k}$. Consequently, a reduced network ${G}_{S}=\left({N}_{S},{A}_{S}\right)$ can be defined with the following sets of nodes and arcs:

$${N}_{s}^{^{\prime}}=\left\{\left(0,j,t\right) :j\in J, t\in {T}_{0,j}\right\}\cup \left\{\left(k,t\right) :k\in K, t\in {T}_{k}\right\},$$

(8)

and

$$\begin{array}{*{20}l} {A^{\prime}_{s} = \left\{ {\left( {\left( {0,j,t} \right),\left( {1,t + l_{0,j} } \right)} \right):j \in J,t \in T_{0,j} } \right\}} \hfill \\ {\,\,\,\,\,\,\,\,\, \cup \left\{ {\left( {\left( {k,t} \right),\left( {k + 1,t + l_{k} } \right)} \right):k \in K\backslash \left\{ {n_{K} } \right\},t \in T_{k} } \right\}} \hfill \\ \end{array} .$$

(9)

Given that the initial inventory ${I}_{1}^{m,0}=0$ for $m\in M$, ${I}_{k}^{p,0}=0$ for $k\in {K}_{D}\cup \left\{{n}_{K}\right\}$ and $p\in P$, pending orders ${q}_{0, j}^{m, 0}=0$ for $m\in M$ and $j\in J$, and ending inventory ${I}_{1}^{m,{n}_{T}}=0$ for $m\in M$, ${I}_{k}^{p,{n}_{T}}=0$ for $k\in {K}_{D}\cup \left\{{n}_{K}\right\}$ and $p\in P$, the subnetwork circled by the dotted line in Fig. 2 identifies the reduced network ${G}_{s}^{^{\prime}}$.

Since shortages are not allowed, demand at the distribution center, i.e., nodes $({n}_{K}, t)$ for $t\in {T}_{{n}_{K}}$, can be satisfied from initial inventory, pending orders, production orders, or a combination of these three sources (Graves, 1999). The following theorem establishes necessary feasibility conditions to satisfy customer demand of final products.

Theorem 1

Let ${IP}_{p}$ be the set of stages with positive initial inventory or a positive pending order for product $p, p\in P$ , i.e.,

$${IP}_{p}=\left\{ k\in {K}_{D}\cup \left\{{n}_{K}\right\} : {Y}_{k-1}^{p,0}+{I}_{k}^{p,0}>0 \right\}, p\in P.$$

(10)

Let $IM$ be the set of raw materials with positive initial inventory or a positive pending order at stage 1, i.e.,

$$IM=\left\{ m\in M : {I}_{1}^{m,0}+\sum_{ j\in {J}_{2}}\left({q}_{0,j}^{m,0}\right)>0 \right\}.$$

(11)

Additionally, let ${J}_{1}=\{ j\in J : {l}_{0,j}=0\}$ be the set of suppliers with zero lead time and ${J}_{2}=\{ j\in J : {l}_{0,j}\ge 1\}$ the set of suppliers with positive lead-time. In addition, let ${RM}_{p}\subseteq M$ be the set of raw materials used in product $p, p\in P$. Then, the following conditions for the demand of product$p\in P$, need to be satisfied for the supplier selection and inventory planning problem to be feasible:

• (i) If ${IP}_{p}\ne \mathrm{\varnothing }$, then ${d}^{p,t}=0$, for $t=1, 2,\dots , {\sum }_{k={\widehat{m}}_{p}}^{{n}_{K}-1}{l}_{k}$, where ${\widehat{m}}_{p}=\mathit{max }\left\{ k\in {IP}_{p}\right\}$.

• (ii) If ${IP}_{p}=\mathrm{\varnothing }$, and either ${J}_{1}\ne \mathrm{\varnothing }$ or $RM_{p} \subseteq IM$, then ${d}^{p,t}=0$, for $t=1, 2,\dots , {\sum }_{k=1}^{{n}_{K}-1}{l}_{k}$.

• (iii) Otherwise, if ${IP}_{p}=\mathrm{\varnothing }$,${J}_{1}=\mathrm{\varnothing }$, and RM_p ⊈ IM, then ${d}^{p,t}=0$, for $t=1, 2,\dots , {l}_{min}+{\sum }_{k=1}^{{n}_{K}-1}{l}_{k}$, where ${l}_{\mathit{min}}=\mathit{min }\left\{ {l}_{0,j} : j\in J\right\}$.

Proof

• (i) ${IP}_{p}\ne \mathrm{\varnothing }$ means there is some initial inventory or a positive pending order at the intermediate stages in period $1$. Then, the earliest time for this initial inventory or pending order to arrive at the last stage is $1+{\sum }_{k={\widehat{m}}_{p}}^{{n}_{K}-1}{l}_{k}$. Therefore, ${d}^{p,t}$ has to be zero for $t=1, 2,\dots , {\sum }_{k={\widehat{m}}_{p}}^{{n}_{K}-1}{l}_{k}$, for the problem to be feasible.

• (ii) From ${IP}_{p}=\mathrm{\varnothing }$, we know that there is no initial inventory or pending order within the intermediate stages at the beginning of period $1$. In the case of ${J}_{1}\ne \mathrm{\varnothing }$, there exists one or more suppliers with zero lead time; therefore, the total lead time for the product flow to reach the last stage is ${\sum }_{k=1}^{{n}_{K}-1}{l}_{k}$. Thus, for the time between period $1$ and $1+{\sum }_{k=1}^{{n}_{K}-1}{l}_{k}$, the system is not able to meet any demand, which means that ${d}^{p,t}=0$, for $t=1, 2,\dots , {\sum }_{k=1}^{{n}_{K}-1}{l}_{k}$. Now let us consider the condition of $RM_{p} \subseteq IM$. This condition indicates that there exists initial inventory of raw materials required for product $p$ at stage $1$. Consequently, the earliest time that the finished product $p$ can arrive at stage ${n}_{K}$ would be $1+{\sum }_{k=1}^{{n}_{K}-1}{l}_{k}$ as shown in condition (ii).

• (iii) In this case, we know that there is no initial inventory of raw materials, and at the same time, there is no initial inventory at the intermediate stages for product $p$. In addition, all suppliers have positive lead times for delivery. Note that ${l}_{min}$ is the minimum time that it takes for the raw materials to arrive to stage$1$. Then, ${\sum }_{k=1}^{{n}_{K}-1}{l}_{k}$ is the time that it takes for the final product $p$ to go from stage 1 to stage${n}_{K}$. Therefore, the least time that it takes for product $p$ to be available at stage ${n}_{K}$ would be $1+{l}_{min}+{\sum }_{k=1}^{{n}_{K}-1}{l}_{k}$. This proves the condition.

4 Some cost considerations

Our proposed models incorporate a broader cost structure involving joint replenishment costs and quantity discounts for raw material replenishment and production, and a more realistic description of the transportation costs.

4.1 Transportation cost structure

Third-party transportation providers are typically used to move products throughout the different stages of a supply chain. Freight can be transported using full-truck load (TL) or less-than-truckload (LTL) options. In this study, it is assumed that raw materials and products are moved from one stage to another using only TL as the available option. Raw materials and final products are measured in units of storage capacity. Let $R=\left\{\mathrm{1,2},\dots ,{n}_{R}\right\}$ be the set of truck types, mainly differentiated by their storage capacity (Samuelsson & Tilanus, 1997).

The TL transportation cost for a given shipment depends on the distance between origin and destination, and the mix of vehicles used with different storage capacities and costs. This type of functions takes the form of a step function (Cintron et al., 2010). For instance, Fig. 3 provides an example of the TL transportation cost, where ${LTC}_{r}$ is the cost of truck $r$ for a given travel distance and ${VC}_{r}$ is the capacity of truck $r\in R$.

Fig. 3

adapted from Cintron et al., 2010)

Stepwise transportation cost function (

4.2 Joint replenishment cost

As mentioned earlier, multi-product scenarios have a higher degree of applicability in real-world settings. When considering multi-product scenarios, Goyal and Satir (1989) recommend the use of joint replenishment strategies. Joint replenishment is considered whenever a number of different items are involved in a replenishment operation, and it is possible to share the fixed cost associated with such operation. Ordering items jointly reduces the ordering cost and may enable utilization of the same transportation vehicle.

Recall that in the dynamic joint replenishment problem under study, ${n}_{M}$ raw materials must be replenished to satisfy a deterministic time varying demand over a ${n}_{T}$ planning-period horizon. The ordering cost is comprised of a major ordering cost, denoted by ${s}^{t}$, incurred each time an order takes place at period $t$, and a minor ordering costs, denoted by ${s}^{m,t}$, charged each time raw material $m$ is included in an order placed at period $t$.

Let ${\widehat{M}}_{t}\subseteq M$ be the set of raw materials included in an order at time $t$. Hence, the joint-replenishment cost is ${s}^{t}+\sum_{m\epsilon {\widehat{M}}_{t}}{s}^{m,t}$. Let ${p}^{m,t}$ and ${Q}^{m,t}$ represent the unit price and order quantity of raw material $m$ at period $t$, so that the ordering cost is ${s}^{t}+\sum_{m\epsilon {\widehat{M}}_{t}}({s}^{m,t}+{p}^{m,t}{Q}^{m,t})$.

4.3 All-unit quantity discount scheme

Two discount schemes have been widely used in practice, all-unit and incremental quantity discounts. The fundamental idea behind is that suppliers provide a price discount to motivate manufacturers to order larger quantities and take advantage of economies of scale (Elmaghraby & Keskinocak, 2003). In this work, the all-unit quantity discount scheme is applied to raw materials ordered from suppliers. Let ${Q}_{m,j}=\left\{\mathrm{1,2},\cdots ,{n}_{{Q}_{m,j}}\right\}$ be the set of price intervals for raw material $m$ and supplier $j$, and $X$ the ordering quantity. Let ${\beta }^{0}=0<{\beta }^{1}<{\beta }^{2}<\cdots <{\beta }^{{n}_{{Q}_{m,j}}}$ represent the breakpoints, so that the ordering quantity always fall within one of these ranges, ${\beta }^{i-1}{\leq}X<{\beta }^{i}$, for some $i\in {Q}_{m,j}$. Also, let ${\alpha }_{i}$ denote the unit ordering cost for range ${\beta }^{i-1}{\leq}X<{\beta }^{i}$, such that ${\alpha }_{1}>{ \alpha }_{2}>\cdots >{\alpha }_{{n}_{{Q}_{m,j}}}>0.$ Then, the purchasing cost function $f(X)$ as a function of the order quantity X is defined as follows:

$$f\left( X \right) = \left\{ {\begin{array}{*{20}l} {\alpha _{1} X,\,\left( {0 \le X < \beta ^{1} } \right),} \hfill \\ {\alpha _{2} X,\,\left( {\beta ^{1} \le X < \beta ^{2} } \right),} \hfill \\ {\alpha _{3} X,\,\left( {\beta ^{2} \le X < \beta ^{3} } \right),} \hfill \\ \begin{gathered} \cdots \hfill \\ \cdots \hfill \\ \cdots \hfill \\ \end{gathered} \hfill \\ {\alpha _{{n_{{Q_{{m,j}} }} }} X,\,\left( {\beta ^{{n_{{Q_{{m,j}} }} - 1}} \le X < \beta ^{{n_{{Q_{{m,j}} }} }} } \right),} \hfill \\ \end{array} } \right.$$

(12)

An example of the mathematical representation of $f(X)$ is shown in Fig. 4.

Fig. 4

adapted from Ravindran & Warsing, 2013)

All-unit discount model (

5 Proposed mathematical models

In this section, two different approaches to solve the dynamic inventory problem under study are introduced: integrated and sequential. The list of additional parameters and decision variables used to formulate the mathematical models for the two approaches are provided below.

5.1 Additional parameters

$A$::

upper bound on the different types of raw material allowed in any replenishment order submitted to suppliers during the planning horizon.

$B$::

upper bound on the production lot size of any product during the planning horizon.

$C$::

upper bound on the total order quantity to be shipped from stage $k\in {K}_{D}$ to stage $k+1$ during the planning horizon, $k\in {K}_{D}$.

${w}^{m}$::

number of units of raw material m needed to fill one unit of storage capacity, $m\in M$.

${w}^{p}$::

number of units of final product p needed to fill one unit of storage capacity, $p\in P$.

${c}^{p}$::

relative production rate for product $p$ (in units/unit of capacity), $p\in P$.

${b}_{0,j}^{m,t}$::

capacity of supplier $j$ for raw material $m$ in period $t$ (in units/time unit), $j\in J, m\in M, t\in {T}_{0,j}$.

${b}_{1}^{t}$::

effective production capacity at stage 1 in period $t$ (in units/time unit), $t\in {T}_{1}$.

${b}_{k}^{p,t}$::

inventory capacity at stage $k$ for product $p$ in period $t$ (in units/time unit), $k\in {K}_{D}\cup \left\{{n}_{K}\right\}, t\in {T}_{k}$.

${b}_{1}^{m,t}$::

inventory capacity at stage $1$ for raw material $m$ in period $t$ (in units/time unit), $t\in {T}_{k}$.

${b}^{m,p}$::

bill of materials ratio. It is defined as the number of units of raw material $m$ required to produce one unit of final product $p$,  $m\in M, p\in P$.

${a}_{0,j}^{m}$::

perfect rate of supplier $j$ for raw material $m$ (probability that a unit is acceptable), $j\in J, m\in M$.

${a}^{m}$::

minimum acceptable perfect rate for raw material $m$, $m\in M$.

${h}_{1}^{m,t}$::

unit holding cost at the manufacturing stage for raw material $m$ from period $t$ to period $t+1$ (in $/unit/time unit), $m\in M, {t\in T}_{1}$.

${h}_{k}^{p,t}$::

unit holding cost at stage $k$ for final product $p$ from period $t$ to period $t+1$ (in $/unit/time unit), $k\in {K}_{D}\cup \left\{{n}_{K}\right\}, p\in P, {t\in T}_{k}$.

${u}_{1,j}^{m,t}$::

in-transit inventory holding cost for raw material $m$ shipped from supplier j (stage 0) to stage 1 during periods $t$ to $t+{l}_{0,j}-1$ (in $/unit/time unit), $j\in J, m\in M, t\in {T}_{0,j}$.

${u}_{k+1}^{p,t}$::

in-transit inventory holding cost of final product $p$ shipped from stage $k$ to stage $k+1$ during periods $t$ to $t+{l}_{k}-1$ (in $/unit/time unit), $k\in {K}_{D}, p\in P,t\in {T}_{k}$.

${p}_{0,j,q}^{m,t}$::

unit price of raw material $m$ for supplier $j$ at period $t$ in price interval $q$ (in $/unit), $j\in J, m\in M, q\in {Q}_{m,j}, t\in {T}_{0,j}$.

${s}_{0,j}^{t}$::

major ordering cost for each order submitted to supplier $j$ at period $t$ (in $/order), $j\in J,t\in {T}_{0,j}$.

${s}_{0,j}^{m,t}$::

minor ordering cost for raw material $m$ included in the order submitted to supplier $j$ at period $t$ (in $/order), $m\in M,j\in J,t\in {T}_{0,j}$.

${p}_{1}^{p,t}$::

variable production cost for final product $p$ at period $t$ (in $/unit), $p\in P, t\in {T}_{1}$.

${s}_{1}^{t}$::

major ordering cost at the manufacturing stage at period $t$ (in $/order), $t\in {T}_{1}$.

${s}_{1}^{p,t}$::

minor ordering cost for each final product $p$ manufactured on stage 1 at period $t$ (in $/order), $p\in P, t\in {T}_{k}$.

${s}_{k}^{t}$::

major ordering cost on stage $k$ at period $t$ (in $/order), $k\in {K}_{D}, t\in {T}_{k}$.

${\widehat{v}}_{0,j,r}^{t}$::

fixed charge rate for one shipment from supplier $j$ to stage 1 using truck type $r$ (in $/truck), $j\in J,t\in {T}_{0,j}, r\in R$.

${\widehat{v}}_{k,r}^{t}$::

fixed charge rate for one shipment from stage $k$ to stage $k+1$ using truck type $r$ (in $/truck), $k\in {K}_{D},t\in {T}_{k}, r\in R$.

${VC}_{r}$::

capacity of truck type r (in units of storage capacity/truck), $r\in R$.

${Q}_{j,q}^{m}$::

boundary quantity of raw material $m$ ordered from supplier $j$ (in units), $j\in J, m\in M, q\in {Q}_{m,j}$.

5.2 Additional continuous variables

${Q}_{0,j,q}^{m,t}$::

quantity of raw material $m$ ordered from supplier $j$ in price interval $q$ at period $t$ (in units/price interval/order/time unit), $j\in J, m\in M, q\in {Q}_{m,j}, t\in {T}_{0,j}$.

5.3 Integer variables

${L}_{0,j,r}^{t}$::

number of full truck loads assigned to transport raw materials from supplier $j$ to stage 1 at period $t$ using truck $r, j\in J, t\in {T}_{0,j}, r\in R$.

${L}_{k,r}^{t}$::

number of full truck loads assigned to transport final products from stage $k$ to stage $k+1$ at period $t$ using truck $r, k\in {K}_{D}, t\in {T}_{k}, r\in R$.

5.4 Binary variables

${\updelta }_{0,j}^{t}$::

1 if a replenishment order is submitted to supplier $j$ at period $t$; otherwise, 0; $j\in J,t\in {T}_{0,j}$.

${\updelta }_{0,j}^{m,t}$::

1 if a replenishment order for raw material $m$ is submitted to supplier $j$ at period $t$; otherwise, 0; $j\in J,m\in M,t\in {T}_{0,j}$.

${\updelta }_{k}^{t}$::

1 if a replenishment order is placed to stage $k$ at period $t$; otherwise,$0; k\in {K}_{D}\cup \left\{{n}_{k}\right\}, t\in {T}_{k}$.

${\updelta }_{1}^{p,t}$::

1 if a manufacturing order for final product $p$ is placed to stage 1 in period $t$; otherwise, 0; $p\in P, t\in {T}_{k}$.

${\varphi }_{0,j,q}^{m,t}$::

1 if raw material $m$ is ordered from supplier $j$ to stage 1 at period $t$ falls in price interval $q$; otherwise, 0;$j\in J, m\in M, q\in {Q}_{m,j},t\in {T}_{0,j}$.

${\updelta }_{1}^{t}$::

1 if a replenishment order is placed at manufacturing stage at period $t$; otherwise, 0; $t\in {T}_{1}$.

5.5 Integrated approach

The integrated dynamic supplier selection and inventory planning problem, where raw material procurement, manufacturing, and distribution decisions are considered simultaneously, can be formulated as a mixed integer linear programming model as follows:

5.5.1 Model (INT)

Minimize

$$\begin{array}{*{20}l} {Z = \sum\nolimits_{j \in J} {\sum\nolimits_{{t \in T_{o,j} }} {\left( {s_{0,j}^{t} \delta_{0,j}^{t} + \sum\nolimits_{m \in M} {\left( {s_{0,j}^{m,t} \delta_{0,j}^{m,t} + \sum\nolimits_{{q \in Q_{m,j} }} {p_{0,j,q}^{m,t} Q_{0,j,q}^{m,t} } } \right)} } \right)} } } \hfill \\ {\,\,\,\,\,\,\,\, + \sum\nolimits_{{t \in T_{1} }} {\left( {s_{1}^{t} \delta_{1}^{t} + \sum\nolimits_{p \in P} {\left( {s_{1}^{p,t} \delta_{1}^{p,t} + p_{1}^{p,t} X_{1}^{p,t} } \right)} } \right) + \sum\nolimits_{{k \in K_{D} }} {\sum\nolimits_{{t \in T_{K} }} {s_{k}^{t} \delta_{k}^{t} } } } } \hfill \\ {\,\,\,\,\,\,\,\, + \sum\nolimits_{m \in M} {\sum\nolimits_{{t \in T_{1} }} {h_{1}^{m,t} I_{1}^{m,t} + \sum\nolimits_{{k \in K_{D} \cup \left\{ {n_{K} } \right\}}} {\sum\nolimits_{p \in P} {\sum\nolimits_{{t \in T_{k} }} {h_{k}^{p,t} I_{k}^{p,t} } } } } } } \hfill \\ {\,\,\,\,\,\,\,\, + \sum\nolimits_{j \in J} {\sum\nolimits_{m \in M} {\sum\nolimits_{{t \in T_{0,j} }} {u_{1,j}^{m,t} Q_{0,j}^{m,t} + \sum\nolimits_{{k \in K_{D} }} {\sum\nolimits_{p \in P} {\sum\nolimits_{{t \in T_{k} }} {u_{k + 1}^{p,t} Y_{k}^{p,t} } } } } } } } \hfill \\ {\,\,\,\,\,\,\,\, + \sum\nolimits_{j \in J} {\sum\nolimits_{{t \in T_{0,j} }} {\sum\nolimits_{r \in R} {\hat{v}_{0,j,r}^{t} L_{0,j,r}^{t} + \sum\nolimits_{{k \in K_{D} }} {\sum\nolimits_{{t \in T_{k} }} {\sum\nolimits_{r \in R} {\hat{v}_{k,r}^{t} L_{k,r}^{t} } } } } } } } \hfill \\ \end{array} ,$$

(13)

subject to

$$\sum_{j\in J}{Q}_{0,j}^{m,t-{l}_{0,j}}+{I}_{1}^{m,t-1}={I}_{1}^{m,t}+\sum_{p\in P}{b}^{m,p} {X}_{1}^{p,t}, \quad m\in M,t\in {T}_{1}\backslash \left\{1\right\}$$

(14)

$$\sum_{q\in {Q}_{m,j}}{Q}_{0,j,q}^{m,t}={Q}_{0,j}^{m,t}, \quad m\in M, j\in J, t\in {T}_{0,j}$$

(15)

$${X}_{1}^{p,t}+{I}_{2}^{p,t-1}={I}_{2}^{p,t}+{Y}_{2}^{p,t}, \quad p\in P, t\in {T}_{2}$$

(16)

$${Y}_{k-1}^{p,t-{l}_{k-1}}+{I}_{k}^{p,t-1}={I}_{k}^{p,t}+{Y}_{k}^{p,t}, k\in {K}_{D}\backslash \left\{2\right\}, \quad p\in P, t\in {T}_{k}$$

(17)

$${Y}_{{n}_{K-1}}^{p,t-{l}_{{n}_{K-1}}}+{I}_{{n}_{K}}^{p,t-1}={d}^{p,t}{+ I}_{{n}_{K}}^{p,t}, \quad p\in P, t\in {T}_{{n}_{k}}$$

(18)

$$\sum_{j\in J}{a}_{0,j}^{m} {Q}_{0,j}^{m,t-{l}_{0,j}}\ge {a}^{m}\sum_{j\in J}{Q}_{0,j}^{m,t-{l}_{0,j}}, \quad m\in M, t\in {T}_{1}$$

(19)

$${Q}_{0,j}^{m,t}\le {b}_{0,j}^{m,t} {\delta }_{0,j}^{m,t}, \quad j\in J, m\in M, t\in {T}_{0,j}$$

(20)

$$\sum_{m\in M} {\delta }_{0,j}^{m,t}\le A{ \delta }_{0,j}^{t}, \quad j\in J, t\in {T}_{0,j}$$

(21)

$${X}_{1}^{p,t}\le {B \delta }_{1}^{p,t}, \quad p\in P, t\in {T}_{1}$$

(22)

$$\sum_{p\in P}\frac{{X}_{1}^{p,t}}{{c}^{p}}\le {{b}_{1}^{t} \delta }_{1}^{t}, \quad t\in {T}_{1}$$

(23)

$$\sum_{p\in P}{Y}_{k}^{p,t}\le {C \delta }_{k}^{t}, k\in {K}_{D}, \quad t\in {T}_{k}$$

(24)

$${{w}^{m} I}_{1}^{m,t}\le {b}_{1}^{m,t}, m\in M, \quad t\in {T}_{1}$$

(25)

$${{w}^{p} I}_{k}^{p,t}\le {b}_{k}^{p,t}, k\in {K}_{D}\cup \left\{{n}_{K}\right\}, \quad p\in P, t\in {T}_{k}$$

(26)

$$\sum_{m\in M}{w}^{m}{ Q}_{0,j}^{m,t}\le \sum_{r\in R}{{VC}_{r} L}_{0,j,r}^{t}, \quad j\in J, t\in {T}_{0,j}$$

(27)

$$\sum_{m\in M}{w}^{p} {Y}_{k}^{p,t}\le \sum_{r\in R}{{VC}_{r} L}_{k,r}^{t}, k\in {k}_{D}, \quad p\in P, t\in {T}_{k}$$

(28)

$${\varphi }_{0,j,q}^{m,t}{ Q}_{j,q-1}^{m}<{Q}_{0,j}^{m,t}\le {\varphi }_{0,j,q}^{m,t} {Q}_{j,q}^{m}, \quad j\in J, m\in M, q\in {Q}_{m,j}, t\in {T}_{0,j}$$

(29)

$$\sum_{q\in {Q}_{m,j}}{\varphi }_{0,j,q}^{m,t}\le 1, \quad j\in J, m\in M, t\in {T}_{0,j}$$

(30)

$${Q}_{0,j}^{m,t}\ge 0, {\delta }_{0,j}^{m,t} \in \left\{\mathrm{0,1}\right\}, \quad j\in J,m\in M,t\in {T}_{0,j}$$

(31)

$${Q}_{0,j,q}^{m,t}\ge 0, \quad j\in J, m\in M,q\in {Q}_{m,j}, t\in {T}_{0,j}$$

(32)

$${X}_{1}^{p,t}\ge 0, \quad p\in P,t\in {T}_{1}$$

(33)

$${I}_{1}^{m,t}\ge 0, \quad m\in M, t\in {T}_{1}$$

(34)

$${Y}_{k}^{p,t}\ge 0, k\in {K}_{D}, \quad p\in P,t\in {T}_{k}$$

(35)

$${I}_{k}^{p,t}\ge 0, k\in {K}_{D}\cup {n}_{K}, \quad p\in P,t\in {T}_{k}$$

(36)

$${L}_{0,j}^{t}\ge 0, {\text{integer}}, {\delta }_{0,j}^{t}\in \left\{\mathrm{0,1}\right\}, \quad j\in J, t\in {T}_{0,j}$$

(37)

$${L}_{k}^{t}\ge 0, {\text{integer}}, {\delta }_{k}^{t}\in \left\{\mathrm{0,1}\right\}, \quad k\in {K}_{D},t\in {T}_{k}$$

(38)

$${\varphi }_{0,j,q}^{m,t}\in \left\{\mathrm{0,1}\right\}, \quad j\in J, m\in M, q\in {Q}_{m,j}, t\in {T}_{0,j}$$

(39)

$${\delta }_{1}^{p,t}\in \left\{\mathrm{0,1}\right\}, \quad p\in P, t\in {T}_{1}$$

(40)

This model has been formulated with respect to the reduced network ${G}_{s}^{^{\prime}}$ with the objective of minimizing the total cost while satisfying all the demand on time. Equation (13) represents the total cost function, including purchasing, manufacturing, inventory, and transportation costs during the ${n}_{T}$ periods. No transportation cost is considered between stages 1 and 2 because all flows occur within the manufacturing facility. In-transit inventory holding cost is considered in this model and represented by a linear cost function.

The flow balance between raw materials and final products in stage 1 is enacted through Equation set (14). To correctly calculate the requirements of each type of raw material, each production lot size ${X}_{1}^{p,t}$ is multiplied by the respective bill of materials ratio ${b}^{m,p}$. Equation set (15) determines raw material quantities purchased from each supplier by adding the quantities in each price interval for each type of raw material. Sets of Eqs. (16–18) assure the balance of final products between consecutive stages, from stage 2 to the final stage. This guarantees complete fulfillment of customer demand in each planning period. Constraint set (19) guarantees that, at each period, the average minimum acceptable perfect rate for raw materials is satisfied. Given the effect of delivery lead times, these requirements are imposed when raw materials are received at the first manufacturing (stage 1). Constraint set (20) activates binary variable ${ \delta }_{0,j}^{m,t}$, associated with each type of raw material $m$ included in each order from specific supplier $j$ in period $t$ to assure that the supplier capacity is satisfied. Constraint set (21) activates binary variable ${\delta }_{0,j}^{t}$, which identifies specific period $t$ when a replenishment order is submitted to supplier $j$; $A$ is an upper bound on the different types of raw material allowed in the order. Constraint set (22) triggers binary variable ${\delta }_{1}^{p,t}$, which is activated each time a production order is scheduled for product $p$ in period $t$; $B$ is an upper bound on the production lot size of any product. Constraint set (23) requires the joint production capacity in each period to be satisfied, where changeover times between products are assumed to be imperceptible. Constraint set (24) is used as a trigger for variable ${\delta }_{k}^{t}$, which is activated each time a shipment of products is scheduled from stage $k\in {K}_{D}$ to stage $k+1$ in period $t$, where $C$ is a large value representing an upper bound on the total order quantity to be shipped. Sets of inequalities (25) and (26) correspond to inventory capacities counted in equivalent units of raw materials and final products at different stages. Sets of Eqs. (27) and (28) provide upper bounds on the number of units of raw materials and final products that can be transported by trucks between consecutive stages. Sets of Eqs. (29) and (30) guarantee raw material ordering quantities fall in the corresponding price intervals. Notice that at most one of the order quantities ${Q}_{0,j,q}^{m,t}$ can become positive for a given $\left(j, m, q, t\right)$ combination. Finally, sets of Eqs. (31–40) describe variable characteristics.

As discussed in Sect. 3, the time-expanded supply chain network is feasible only if the demand at any demand node $({n}_{K}, t)$ can be satisfied. If accumulated initial inventory and pending orders cannot satisfy the demand requirements, the network would be infeasible. It is reasonable to check whether inventory capacities are large enough to hold raw materials and final products and if production and supplier capacities are large enough so that sufficient products can be manufactured to meet demand requirements (Graves, 1999). Feasible solutions can be obtained either by increasing the initial inventory, or by increasing inventory and production capacities, as well as the overall supplier capacity. Inventory capacity can be augmented by subcontracting warehouse space, production capacity can be improved by enabling overtime schedules, and supplier capacity can be enhanced by considering additional suppliers and allowing increased raw material purchasing cost.

5.6 Sequential approach

Model (INT) can be hard to solve in some practical situations due to its size and complexity. In related cases, sequential approaches have been widely used in solving real-world applications (Seuring, 2008). In a sequential approach, a large-scale problem is split into subproblems that are solved separately in a sequential manner. In our sequential approach, raw material supply decisions are made in response to the manufacturing and inventory decisions: the production scheduling and inventory management subproblem (Scenario 1) is solved first, and the raw material procurement schedule for the entire planning horizon (Scenario 2) is generated accordingly. The vertical dashed line between stages 1 and 2 in Fig. 2 splits the time-expanded network into two subnetworks corresponding to the two subproblems identified in the sequential approach. The subnetwork defined by stages 2–4 corresponds to the subproblem in Scenario 1 that considers the demand requirements to determine the production lot-sizes, shipments of products between consecutive stages, and the raw material requirements in each period. These raw material requirements are inputs to the supplier selection and raw material procurement subproblem in Scenario 2, which is represented by the subnetwork defined by stage 1.

The production and inventory planning subproblem in Scenario 1 is solved using the following model:

5.6.1 Model (SEQ-IP)

Minimize

$$\begin{aligned}\begin{array}{*{20}l} {Z = \sum\nolimits_{{t \in T_{1} }} {\left( {s_{1}^{t} \delta_{1}^{t} + \sum\nolimits_{p \in P} {\left( {s_{1}^{p,t} \delta_{1}^{p,t} + p_{1}^{p,t} X_{1}^{p,t} } \right)} } \right) + \sum\nolimits_{{k \in K_{D} }} {\sum\nolimits_{{t \in T_{k} }} {s_{k}^{t} \delta_{k}^{t} } } } } \hfill \\ {\,\,\,\,\,\,\, + \sum\nolimits_{{k \in K_{D} \cup \left\{ {n_{K} } \right\}}} {\sum\nolimits_{p \in P} {\sum\nolimits_{{t \in T_{k} }} {h_{k}^{p,t} I_{k}^{p,t} } } } + \sum\nolimits_{{k \in K_{D} }} {\sum\nolimits_{p \in P} {\sum\nolimits_{{t \in T_{k} }} {u_{k + 1}^{p,t} Y_{k}^{p,t} } } } } \hfill \\ {\,\,\,\,\,\,\, + \sum\nolimits_{{k \in K_{D} }} {\sum\nolimits_{{t \in T_{k} }} {\sum\nolimits_{r \in R} {\hat{v}_{k,r}^{t} L_{k,r}^{t} } } } } \hfill \\ \end{array} \end{aligned}$$

(41)

subject to.

Constraints (16–18), (22–24), (26), (28), (33), (35), (36), (38) and (40).

The objective function in (41) represents the total production, in-transit inventory, and holding cost for final products, and transportation cost for the ${n}_{T}$ periods. In this scenario, the procurement schedule of raw materials is assumed to be irrelevant.

Once Scenario 1 is solved using Model (SEQ-IP), raw material requirements are obtained:${ q}^{m,t}=\sum_{p\in P}{b}^{m,p}{X}_{1}^{p,t}$, $m\in M$, $t\in {T}_{1}$, where ${X}_{1}^{p,t}$ is the production lot size for product $p$ in period $t$. Then, the optimal raw material procurement schedule in Scenario 2 is obtained by solving the following model:

5.6.2 Model (SEQ-SS)

Minimize

$$\begin{array}{*{20}l} {Z = \sum\nolimits_{j \in J} {\sum\nolimits_{{t \in T_{0,j} }} {\left( {s_{0,j}^{t} \delta_{0,j}^{t} + \sum\nolimits_{m \in M} {\left( {s_{0,j}^{m,t} \delta_{0,j}^{m,t} + \sum\nolimits_{{q \in Q_{m,j} }} {p_{0,j,q}^{m,t} Q_{0,j,q}^{m,t} } } \right)} } \right)} } } \hfill \\ {\,\,\,\,\,\, + \sum\nolimits_{m \in M} {\sum\nolimits_{{t \in T_{1} }} {h_{1}^{m,t} I_{1}^{m,t} } } + \sum\nolimits_{j \in J} {\sum\nolimits_{m \in M} {\sum\nolimits_{{t \in T_{0,j} }} {u_{1,j}^{m,t} Q_{0,j}^{m,t} } } } } \hfill \\ {\,\,\,\,\,\, + \sum\nolimits_{j \in J} {\sum\nolimits_{{t \in T_{0,j} }} {\sum\nolimits_{r \in R} {\hat{v}_{0,j,r}^{t} L_{0,j,r}^{t} } } } } \hfill \\ \end{array}$$

(42)

subject to

$$\sum_{j\in J}{Q}_{0,j}^{m,t-{l}_{0,j}}+{I}_{1}^{m,t-1}={I}_{1}^{m,t}+{ q}^{m,t}, m\in M, t\in {T}_{1}$$

(43)

and constraints (15), (19–21), (25), (27), (29–32), (34), (37) and (39).

The objective function in (42) represents the total raw material replenishment, in-transit inventory and inventory holding, and transportation cost between selected suppliers and the manufacturing stage (stage 1) for the ${n}_{T}$ periods.

6 Numerical analysis and managerial insights

A numerical example is presented below to compare the results of the integrated and sequential approaches used to solve the dynamic inventory problem under study. Then, sensitivity analysis is performed to examine the effect of key cost parameters on raw material replenishment decisions. Lastly, managerial insights are provided based on the results of our numerical analysis.

6.1 Illustrative example

Let us consider a four-stage serial supply chain. Stages 1 and 2 are located at the manufacturing facility. Raw materials are procured from a set of three potential suppliers to stage 1. Then, these raw materials are processed into two final products in stage 1 and sent to stage 2 to be stored. Suppliers 2 and 3 offer all-unit quantity discounts on raw materials. Stage 3 stands for a regional warehouse and Stage 4 for a distribution center close to customer locations. This distribution center satisfies customer demand requirements for the two types of final products during a five-month planning horizon. Raw materials and final products are represented in units of storage capacity and are shipped using TL transportation. Three types of trucks are available.

Relative production rates in stage 1 are assumed to be ${c}^{1}=8.0$ units/unit of capacity for product 1 and ${c}^{2}=6.0$ units/unit of capacity for product 2. A unit of capacity is defined as an hour. The total production capacity from one period to the next may change depending on resource availability. Inventory capacities, however, are assumed to be constant for the four stages during the entire planning horizon. Equivalent units are expressed in cubic meters (${m}^{3}$). Therefore, the storage capacity is mainly limited by the space occupied by raw materials and final products. As far as raw materials, their minimum acceptable perfect rate is ${\alpha }^{m}=$ 0.955, for $m\in M.$

Table 1 shows bill of material ratios. Table 2 defines demand from customers in each period. Table 3 provides production capacity and inventory capacity at each stage.

Table 1 Bill of material ratios (expressed in units of raw material per unit of final products)

Table 2 Customer demand

Table 3 Production and inventory capacities

Table 4 defines prices for raw materials and the price intervals corresponding to the all-unit quantity disc

Table 4 Raw material prices and price intervals

ounts provided by suppliers 2 and 3. Table 5 provides further information for each supplier.

Table 5 Additional information of suppliers

Table 6 defines variable production and inventory holding costs for each stage. Table 7 describes equivalent amounts of raw materials and final products measured in cubic meters per unit. Table 8 provides information on setup costs during the manufacturing process.

Table 6 Inventory holding and production costs through all periods

Table 7 Equivalence factors ${w}^{m}$ and ${w}^{p}$ (expressed in ${m}^{3}$/unit)

Table 8 Setup costs during manufacturing process, warehousing, and distribution stages

Table 9 defines initial and ending inventory for raw materials or final products at each stage.

Table 9 Initial and ending inventory levels required at each stage (expressed in units)

Table 10 shows information on the three types of trucks used for shipping raw materials and final products. Finally, Table 11 presents in-transit inventory holding costs.

Table 10 Truck information for shipping raw materials and final products

Table 11 In-transit inventory holding cost (expressed in $/unit/shipment)

Models (INT), (SEQ-IP) and (SEQ-SS) were solved in SAS 9.4 by means of the optimization package with the “MILP” (mixed integer linear programming) solver using the “Branch and Cut” algorithm with solution status “Optimal within Relative Gap”. SAS was run on an Intel Core i7-4790S CPU at 3.2 GHZ 16 GB RAM.

The results of the sequential approach were obtained by solving first the inventory planning scenario with Model (SEQ-IP). Then, the raw material procurement schedule was generated by solving Model (SEQ-SS). An optimal solution for the original problem was obtained by the integrated approach and a suboptimal solution by the sequential approach. The results are compared in Figs. 5 and 6, and Table 12.

Fig. 5

Optimal raw material allocation: integrated vs sequential approaches

Fig. 6

Inventory levels at each stage for both integrated and sequential approaches

Table 12 Optimal solutions for the integrated and sequential approaches

Figure 5 compares the raw material allocation (supplier selection) between the two approaches. The results of the integrated approach show that 46% of raw material 1 and 32% of raw material 2 are ordered from supplier 1, remaining (higher) proportions of raw materials are allocated to supplier 3, and supplier 2 is not a choice. In this example, supplier 3 as compared to supplier 1, not only offers lower joint replenishment costs and transportation costs, but higher quality rates that, in combination with those of supplier 1, help to achieve the minimum acceptable perfect rate required for the raw materials. Note that, expensive and low-quality suppliers, as supplier 1 in this case, are only used as needed if they have short delivery lead times.

Under the sequential approach, Fig. 5 shows that higher proportions of raw materials are procured from supplier 1: 73% of raw material 1 and 67% of raw material 2. This can be explained by the fact that the positive delivery lead times of suppliers 2 and 3 represent an advantage for supplier 1, which delivers raw materials instantaneously, to satisfy the demand generated when solving Model (SEQ-IP). That is, the optimal solution for the production/distribution Model (SEQ-IP) forces the selection of a relatively expensive supplier among the available alternatives. In the case of raw material 2, supplier 2 becomes a good option, mainly because it offers lower minor cost, lower transportation cost, and higher quality.

Figure 6 provides a graphical representation of inventory levels at each stage for all periods. It is easy to see by inspection that the inventory levels of the sequential approach are much higher than those of the integrated approach, especially in stages 1 and 4. Table 12 shows that the integrated approach achieves an overall reduction of 30.37% in inventory holding cost in the 5-month planning horizon.

Table 12 shows the optimal solutions for the two approaches. Notice that, when the integrated approach is used, an overall 6% cost reduction is achieved. Even though the sequential approach takes advantage of the economies of scale achieved by larger production and distribution lot sizes, the integrated approach can generate a better solution by considering the effects of raw material procurement decisions at the same time. In spite that the sequential approach generates a more competitive alternative (0.09% cost savings) on the fixed costs (major and minor ordering, and shipping costs), the integrated approach achieves important savings (6.84%) coming from the total variable costs (raw material procurement, production, and inventory holding costs). As expected, the integrated approach is able to account for all the factors that finally produce a superior solution for the entire problem. However, in many important real applications of this type of problems, generating an optimal solution for the problem in an efficient manner could be burdensome. Thus, dividing the problem and solving it in a sequential fashion may help to achieve near-optimal solutions in a reasonable time.

6.2 Sensitivity analysis

To study the effect of holding and joint replenishment costs (major and minor setup costs) over raw material supply decisions, thirteen different scenarios under both approaches were run and analyzed. Results are shown in Table 13. Note that “major setup cost”, “minor setup cost” and “inventory holding cost” for each scenario were maintained (100%), decreased to (0 or 50%), or increased to (150%) with respect to the original values. Holding costs include on-stage and in-transit inventory holding costs. It is shown that changes in holding and major setup costs affect all stages in the supply chain, whereas changes in minor setup cost only affect supplier selection and manufacturing stages. In order to avoid neutralization of setup and inventory holding costs, when holding costs were increased or decreased, major and minor setup costs were maintained. Similarly, if major and minor setup costs were changed simultaneously, they should follow the same direction (decrease or increase). Percentages of raw materials allocated to suppliers are rounded to the closest second decimal.

Table 13 Sensitivity analysis under the integrated and sequential approaches

Table 13 shows that the sequential approach always entails shorter running times, and the supplier selection strategy is always different between the two approaches. Considering the effect of key factors over the integrated approach, when holding cost is decreased individually (Scenarios 3 and 12), supplier 1 becomes more competitive and delivers a higher volume of raw materials. When major setup cost is decreased (Scenarios 8 and 9), the volume of raw material 2 allocated to supplier 2 is increased, while the volume allocated to supplier 3 is decreased. This is because supplier 2, with relatively higher ordering cost, becomes more attractive than before.

Similar results can be observed in Scenarios 11 and 13, where major and minor setup costs are decreased simultaneously. In Scenario 12, when major and minor setup costs are increased, and inventory holding cost is decreased, cheaper inventory holding cost helps suppliers 1 and 2 become more attractive than before by obtaining more orders originally allocated to supplier 3. For the sequential approach, supplier selection changes significantly in Scenarios 2, 11, 12 and 13. This happens when inventory holding cost is modified, or major and minor ordering costs are decreased simultaneously. In general, it can be concluded that setup and inventory holding costs play a very important role in supplier selection in both approaches.

6.3 Managerial insights

In an era where supply chains have become increasingly globalized and extended, there has been a substantial increase in the number of materials and products. Products manufactured in one part of the globe can be transported to another part of the globe and indeed, components of a product can be made in different countries. As a result, manufacturing and supply issues have created considerable challenges in modern supply chains; thus, managers need to plan ahead to keep operational plans flowing smoothly (Feng et al., 2021; Kim & Chai, 2017; Gerefi & Lee, 2012; and Singh et al., 2012). Therefore, the integrated model studied in this paper may become a useful tool to enable managers make sound decisions with respect to supplier selection, raw materials procurement, production, and inventory. Additionally, the proposed model can easily be extended to a more general supply chain setting with multiple facilities in each stage. It can also be extended by considering other types of constraints (e.g., space utilization and environmental factors).

As shown through the numerical example, the proposed sequential approach can ease the computational burden of solving a complex mathematical model in cases where the number of stages, materials, products, or available suppliers increases. That is, the sequential approach can easily be implemented, though the deviation from the optimal (integrated) approach may be around 6%.

Under the setting studied in this research, it is readily observed that supplier selection decisions are very sensitive to setup and inventory holding costs. Therefore, in real life situations it is important for manufacturing stages to work together with potential suppliers to develop and share proper information that would lead to optimal selection and replenishment plans. For managers, centralizing these types of decisions offers a way to reduce inventories and costs simultaneously (Huggins & Olsen, 2003).

In accordance with Roy (2010), modern supply chains need to be responsive to demand changes in real time, requiring real time planning to make optimal decisions based on real demand, e.g., customer orders, and accessible raw materials from reliable suppliers. To be precise, the build-to-forecast model is evolving into a demand-driven supply chain that can achieve a higher service level at a lower operational cost. Given the dynamic environments in which supply chains operate, an operational plan may become obsolete shortly after its release or even before the plan is run. Therefore, the responsiveness of a supply chain becomes a vital measurement of supply chain performance and efficiency. In this context, the proposed integrated and sequential models should be useful to supply chain managers, not only to coordinate decisions on procurement, production, and inventory management, but also to respond quickly to real time demand changes to adapt to increasingly challenging environments.

7 Conclusions and future research

In this work, we have proposed a new mixed integer linear programming formulation for the multi-period inventory multi-product lot-sizing problem in a serial supply chain with multiple suppliers and customers. Our research incorporates a richer cost structure involving joint replenishment costs for raw material replenishment and production, and a more realistic description of the transportation costs, represented as a vector of full-truck load costs for different size trucks. Supplier selection, raw material procurement, production, and distribution decisions are analyzed using two approaches: integrated and sequential. The integrated approach solves the problem to optimality, while the sequential approach provides near optimal solutions in a timely manner. As stated before, since we consider multiple products, it is advantageous to consider joint replenishment costs, where major and minor ordering costs are incurred every time that an order is placed at the raw material procurement and manufacturing stages. In addition, it is assumed that suppliers offer all-unit quantity discounts for raw materials, and materials are moved between adjacent stages using the TL transportation mode.

We have illustrated our proposed approaches, integrated and sequential, using a numerical example. The analysis shows that the sequential approach is efficient in terms of time and computational effort, but the integrated approach provides a better solution quality. The sensitivity analysis shows that, as far as the total cost obtained, the main difference resides in variable costs. For instance, the sequential approach might reduce ordering costs by increasing production and distribution lot sizes. However, this might increase inventory holding costs as well as material purchasing costs given that supplier selection decisions are not made integrally. In those cases, dividing the problem and solving it in a sequential fashion may help to achieve near-optimal solutions in a reasonable time. Additionally, results of thirteen different cost scenarios in sensitivity analysis indicate that inventory holding cost and joint replenishment costs play an important role in supplier selection.

Future research could consider the effect of variability in some key parameters like supplier lead time, inventory capacity, and transportation costs under both integrated and sequential approaches. Besides the all-unit discount strategy, the piecewise-unit discount strategy could also be considered in these models. A new supplier price break and discount scheme taking into account order frequency and lead time introduced by Duan and Ventura (2018) could also be incorporated in the models. Under this scheme, each supplier claims his/her own supply schedule with several price break points. Every price break point is paired with the cumulative amount of available quantity as well as the earliest delivery time. Finally, the LTL transportation mode could also be incorporated as part of the analysis.