Modeling the effect of transcriptional noise on switching in gene networks in a genetic bistable switch

Abstract

Gene regulatory networks in cells allow transitions between gene expression states under the influence of both intrinsic and extrinsic noise. Here we introduce a new theoretical method to study the dynamics of switching in a two-state gene expression model with positive feedback by explicitly accounting for the transcriptional noise. Within this theoretical framework, we employ a semi-classical path integral technique to calculate the mean switching time starting from either an active or inactive promoter state. Our analytical predictions are in good agreement with Monte Carlo simulations and experimental observations.

1 Introduction

Variability of gene expression can be used to develop a quantitative understanding of the underlying gene regulation [1]. Single-cell observations and stochastic analyses have revealed qualitative and quantitative features of gene regulation in both prokaryotes [2] and eukaryotes [3]. Biochemical noise drives stochastic switching between bistable states in genetic networks [4]. Such switching can hence lead to different phenotypic changes for a cellular population. Theoretical modeling of stochastic gene expression [5–7] has been a subject of intense studies in the last few years and has helped us to develop our understanding of the effect of noise on gene regulation. Such models mostly focus on describing intrinsic fluctuations that arise from randomness in time of individual chemical reactions. Theoretical methods such as generating functions [6–8], Langevin and Fokker-Planck equations [9], linear noise approximation [10], many-body theory [11], as well as stochastic simulations using the Gillespie algorithm [12] have been used to study such models of gene expression. Shahrezaei and Swain [6] developed an analytical theory of gene expression to calculate the steady-state protein distributions for a three-stage model where the gene containing the promoter fluctuates between active and inactive states at a constant rate. By considering the protein burst model, which is based under the assumption that mRNA lifetimes are shorter than protein lifetimes, they could derive the master equation for proteins, which implicitly includes mRNA fluctuations. Recently, it has been shown that including mRNA noise in master equations plays a strong role in determining switching rates [13, 14]. Employing the WKB theory [15] to treat the underlying chemical master equations, Assaf et al. [16] provided a theoretical framework to obtain the quasi-stationary probability distributions of mRNA/protein copy numbers for a genetic network with positive feedback and also to calculate the mean switching time from either of these active/inactive states.

In this work, we present a different analytical method to investigate the stability of genetic switches in gene expression. We apply this method to a simple gene expression model where the two-state promoter switches between the active and inactive states and the switching rate depends on the transcription factor, which in this case is the protein. We calculate the noise characteristics for the mRNA/protein distribution as well as the switching time between the active and inactive states of the promoter. Lastly, we extend our calculations to noise in more complex promoter architectures by introducing more than two promoter states using our proposed theoretical recipe.

2 Methods

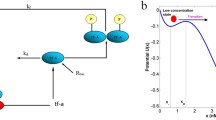
We start by considering a simple two-state gene expression model as shown in Fig. 1a. In this model, the transition between the inactive and active states of the promoter gene is no longer constant but is controlled by protein number n via positive feedback, the protein thereby inducing its own expression. This two-state model with positive feedback is identical to the model treated by Assaf et al. [16]. This two-state positive feedback switch has been shown to describe biological switching experimentally [17]. The transition rates between active and inactive states are k _on(n) ≡ f(n), k _off(n) ≡ g(n) where n is the protein copy number. f(n) and g(n) are considered to be Hill-type functions, $f(n)={k}_0^{\min }+\left({k}_0^{\max }-{k}_0^{\min}\right){n}^{h_1}/\left({n}_{50}^{h_1}+{n}^{h_1}\right)$ and $g(n)={k}_1^{\max }-\left({k}_1^{\max }-{k}_1^{\min}\right){n}^{h_2}/\left({n}_{50}^{h_2}+{n}^{h_2}\right)$ where n ₅₀ is the curve’s midpoint and h ₁ = h ₂ = h. To account for the stochastic behavior of the genetic switches, Assaf et al. [16] used this simple model and employed two coupled chemical master equations that can describe the probability distribution functions, P ^˙ _m,n and ${\dot{Q}}_{m,n}$ of having m mRNAs and n proteins at time t with the promoter DNA being in the inactive and active state, respectively. They used the WKB approximation method [18] to obtain a quasi-stationary solution to the master equation. The WKB ansatz [15] is given as P _m,n  ≃ exp[−S(m, n)], where S is the action. This ansatz has been used extensively to study population switches between metastable states [19–21]. Then, by considering stationary distributions ${\overset{\cdotp }{P}}_{m,n}={\overset{\cdotp }{Q}}_{m,n}=0$ and employing the WKB ansatz they arrived at the stationary Hamiltonian Jacobi equation, $H=H\left(m,\frac{\partial S}{\partial m},n,\frac{\partial S}{\partial n}\right)=0$. Here we can draw an analogy to classical mechanics and introduce momenta ${\chi}_m=\frac{\partial S}{\partial m}$ and ${\chi}_n=\frac{\partial S}{\partial n}$ such that $\overset{\cdotp }{m}=\frac{\partial H}{\partial {\chi}_m}$, $\overset{\cdotp }{n}=\frac{\partial H}{\partial {\chi}_n}$, $\overset{\cdotp }{\chi_m}=-\frac{\partial H}{\partial m}$, $\overset{\cdotp }{\chi_n}=-\frac{\partial H}{\partial n}$.

Fig. 1

a Model for the positive feedback network derived from [16]. Transcription, translation, mRNA decay, and protein degradation are modeled as first-order processes with rates a, γb, γ, and 1, respectively (rates are rescaled by the protein decay rate). The feedback functions k _on(n) and k _off (n) regulate promoter transitions. b χ _n versus n showing bistability at ab = 2,400, b = 22.5, h = 2, n ₅₀  = 1,000, k ^min₀  = k ^min₁  = a/100, k ^max₀  = k ^max₁  = a

Assuming that the mRNA lifetimes are much shorter than the protein degradation rates (γ > > 1), one can eliminate the mRNA degrees of freedom [22] $\left(\overset{\cdotp }{m},{\overset{\cdotp }{\chi}}_m=0\right)$ and obtain a reduced rather effective Hamiltonian, H = H(n, χ _n ), which describes the evolution of slow variables only. Such a kind of separation of variables has been applied earlier in biochemical networks consisting of reactions operating at multiple time scales [23]. Time-scale separation between variables allows one to coarse-grain the system by integrating over fast degrees of freedom without loss of much information about mesoscopic fluctuations of the slow variables. For example, in the context of modeling viral infection kinetics, we eliminated the virus-related variables and calculated the extinction rate by considering the virus clearance rate to be faster than the infected cell dynamics [24].

In our present study, we consider the same model for the positive feedback network as discussed in [16] but propose a different theoretical method that employs the stochastic semi-classical path integral technique to explicitly account for the mRNA noise along with protein fluctuations. This semi-classical method has been used earlier to calculate rare event statistics in reaction diffusion systems [25] and it has been applied to various epidemiological stochastic models [24, 26, 27]. In this method, we start with the eikonal ansatz:

$$ Z\left(\chi, t\right)={e}^{S\left(\chi, t\right)}={\displaystyle \sum_{n=0}^{\infty }{P}_n(t){e}^{in\chi }} $$

(1)

where Z is the generating function for the number of molecules n that are formed during a chemical process in time t. χ is a variable conjugated to n number of molecules and appears as a ‘Lagrange multiplier’ that takes care of conservation laws during the derivation of path integrals (see supporting information Text S1 of [24]). This eikonal approximation is used to solve master equations and it can recast the problem in terms of an effective classical Hamiltonian system. Here we do not provide the derivation of the semi-classical path integral approach and refer the reader to Text S1 in [24].

By considering the trajectories that dominate the dynamics, it was found that S(χ, t) is given by [25]:

$$ S\left({\chi}_C,t\right)={\displaystyle \underset{0}{\overset{t_f}{\int }}\left(\overset{\cdotp }{\chi }(n)+H\left(n,\chi \right)\right)dt} $$

(2)

where H is the Hamiltonian that can be obtained following the general method discussed in [24]. Such a path integral representation has been derived for the case of a Michaelis-Menten enzyme attached to the membrane of a eukaryotic cell and later generalized to a network of reactions [23]. This theory is valid in the limit of short-lived mRNA [16–28]. Our first step is to consider the process of mRNA generation. Let P ^G _m and P ^G * _m be the probabilities to generate m mRNA molecules at time t in the inactive and active state of the promoter, respectively. The master equations for their evolution are [16]:

$$ \begin{array}{l}\frac{d}{dt}{P}_m^G=-{k}_{on}(n){P}_m^G+{k}_{off}(n){P}_m^{G*}\hfill \\ {}\frac{d}{dt}{P}_m^{G*}={k}_{on}(n){P}_m^G-\left({k}_{off}(n)+a\right){P}_m^{G*}+a{P}_{m-1}^{G*}\hfill \end{array} $$

(3)

Assuming that the mRNA is short-lived compared to the protein, we can solve these master equations by introducing the generating function:

$$ {Z}^g\left({\chi}_R\right)={\displaystyle \sum_{m=0}^{\infty }{P}_m^g{e}^{i{\chi}_Rm}} $$

(4)

with g ∈ {G, G *} and the total generating function is Z(χ _R ) = Z _G  + Z _G *. The cumulants are given by:

$$ \begin{array}{l}\left\langle m\right\rangle =-i\frac{\partial \ln Z\left({\chi}_R\right)}{\partial {\chi}_R}{\left|{}_{\chi_R=0},{\sigma}_m^2=\left\langle {m}^2\right\rangle -{\left\langle m\right\rangle}^2={\left(-i\right)}^2\frac{\partial^2 \ln Z\left({\chi}_R\right)}{\partial {\chi}_R^2}\right|}_{\chi_R=0}\hfill \\ {}F=\frac{\sigma_m^2}{\left\langle m\right\rangle}\hfill \end{array} $$

(5)

The Fano factor F is a ratio of the variance to mean and is a measure of the noise strength due to stochastic switching between different on and off states.

In terms of this generating function, the master equation can be written as [29]:

$$ \begin{array}{l}\frac{d}{dt}{Z}^G=-{k}_{on}(n){Z}^G+{k}_{off}(n){Z}^{G*}\hfill \\ {}\frac{d}{dt}{Z}^{G*}={k}_{on}(n){Z}^G-\left({k}_{off}(n)+a\right){Z}^{G*}+a{e}^{i{\chi}_R}{Z}^{G*}\hfill \end{array} $$

(6)

Equation (6) can be considered as a Schrödinger equation:

$$ \frac{d}{dt}\left(\begin{array}{c}\hfill {Z}^G\hfill \\ {}\hfill {Z}^{G*}\hfill \end{array}\right)=\widehat{H}\left({\chi}_R\right)\left(\begin{array}{c}\hfill {Z}^G\hfill \\ {}\hfill {Z}^{G*}\hfill \end{array}\right) $$

(7)

where

$$ H\left({\chi}_R\right)=\left(\begin{array}{l}-{k}_{on}(n)\kern3em {k}_{off}(n)\hfill \\ {}{k}_{on}(n)\kern1em a\left({e}^{i{\chi}_R}-1\right)-{k}_{off}(n)\hfill \end{array}\right). $$

(8)

Assuming that the switching rates between the inactive and active transcriptional state are faster than the time of a substantial change of protein number n or order of $\sqrt{n}$, Eq. (7) can be solved as an eigenvalue problem with:

$$ Z\left({\chi}_R\right)={e}^{\lambda_0t} $$

(9)

where λ ₀ is the eigenvalue of the least negative real part. By diagonalizing, |H − λI| = 0, we have:

$$ Z\left({\chi}_R\right)={e}^{\frac{t}{2}\left\{K\left({\chi}_R\right)+\sqrt{K\left({\chi}_R\right)+4{k}_{on}{H}_0\left({\chi}_R\right)}\right\}}. $$

(10)

where $K\left({\chi}_R\right)={H}_0\left({\chi}_R\right)-\left({k}_{on}(n)+{k}_{off}(n)\right)$

We also assume that when the gene is in the on state, mRNAs are generated according to a Poisson process and hence:

$$ {H}_0\left({\chi}_R\right)=a\left({e}^{i{\chi}_R}-1\right) $$

(11)

Following Eq. (5), for this two-state promoter model, we can compute the first two moments of the mRNA distribution and calculate the Fano factor:

$$ \begin{array}{l}\left\langle m\right\rangle =\frac{a{k}_{on}(n)}{\gamma \left({k}_{on}(n)+{k}_{off}(n)\right)},{\sigma}_m^2=\left\langle {m}^2\right\rangle -{\left\langle m\right\rangle}^2=\left\langle m\right\rangle \left(1+\frac{2a{k}_{off}(n)}{\gamma {\left({k}_{off}(n)+{k}_{on}(n)\right)}^2}\right)\hfill \\ {}{F}_{mRNA}=1+\frac{a}{\gamma}\varDelta .\hfill \end{array} $$

(12)

where γ is the degradation rate of each mRNA molecule and $\varDelta =\frac{2{k}_{off}(n)}{{\left({k}_{on}(n)+{k}_{off}(n)\right)}^2}$

This Fano factor is larger than unity and depends on the concentration of the regulatory factor binding to the promoter, which here is the protein copy number n.

The next step is to combine Eq. (10) with the generating function of proteins translated from a single mRNA.

Let P(τ) = γe ^− γτ be the probability for the mRNA to live during time τ. Then the probability P(n|1 _R ) to have n proteins generated by one mRNA is:

$$ P\left(\left.n\right|{1}_R\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}d\tau P\left(\tau \right)}p\left(n\left|\tau \right.\right). $$

(13)

where $p\left(\left.n\right|\tau \right)={\displaystyle \int d{\chi}_0{e}^{- in{\chi}_0+\tau H\left({\chi}_0\right)}}$

The total generating function of probabilities to have n proteins generated by any single mRNA is given by:

$$ Z\left({\chi}_1\left|{1}_R\right.\right)={\displaystyle \sum_{n=-\infty}^{\infty }P\left(n\left|{1}_R\right.\right){e}^{in{\chi}_1}}=\frac{1}{1-H\left({\chi}_1\right)/\gamma } $$

(14)

where we have performed the integration over τ. Summation over n then produces a delta function δ(χ ₁ − χ ₀), which is then removed by integration over χ ₀.

If we assume that all mRNAs generate proteins independently, then the generating function of protein distribution due to m mRNA is [Z(χ ₁|1 _R )]^m. Then the probability to have n proteins generated during time t, where t > > τ is given by:

$$ \begin{array}{l}P\left(n,t\right)=\frac{1}{2\pi }{\displaystyle \sum_{m=0}^{\infty }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}d{\chi}_1}{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}d{\chi}_R}{\left[Z\left({\chi}_1\left|{1}_R\right.\right)\right]}^m{e}^{- in{\chi}_1-im{\chi}_R+tH\left({\chi}_R\right)}}\hfill \\ {}=\frac{1}{2\pi }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}d{\chi}_1}{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}d{\chi}_R}\frac{1}{1-{e}^{-i{\chi}_R}Z\left(\left.{\chi}_1\right|{1}_R\right)}{e}^{in{\chi}_1+tH\left({\chi}_R\right)}\hfill \end{array} $$

(15)

Then the moment generating function to generate n proteins in time t > > τ is as follows:

$$ {Z}_p\left({\chi}_n\right)={\displaystyle \sum_{n=-\infty}^{\infty }P\left(\left.n\right|t\right){e}^{in{\chi}_n}}. $$

(16)

Substituting Eq. (15) into Eq. (16) and writing ${\displaystyle \sum_{n=-\infty}^{\infty }{e}^{in\left({\chi}_n-{\chi}_1\right)}}$ as a delta function δ(χ _n  − χ ₁), we have:

$$ {Z}_p\left({\chi}_n\right)={\displaystyle \underset{-\pi }{\overset{\pi }{\int }}d{\chi}_1}{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}d{\chi}_R}\frac{1}{1-{e}^{-i{\chi}_R}Z\left(\left.{\chi}_1\right|{1}_R\right)}{e}^{tH\left({\chi}_R\right)}\delta \left({\chi}_n-{\chi}_1\right) $$

(17)

By integration over χ ₁ and using properties of the delta function, we have a path integral over the χ _n variable that can be written as:

$$ {Z}_p\left({\chi}_n\right)={\displaystyle \oint d\frac{\left({e}^{i{\chi}_{\left\{R\right\}}}\right)}{2\pi }}\frac{-i}{e^{-i{\chi}_R}-Z\left(\left.{\chi}_n\right|{1}_R\right)}{e}^{tH\left({\chi}_R\right)}={e}^{tH\left({\chi}_R\right)}\left|{e}^{i\chi R}=Z\left({\chi}_n\left|{1}_R\right.\right)\right.. $$

(18)

Using the above equations, the Hamiltonian for protein generation and degradation can be written as:

$$ {H}_p\left({\chi}_n\right)=\frac{1}{2}\left\{{K}_1\left({\chi}_n\right)\pm \sqrt{K_1{\left({\chi}_n\right)}^2+4{k}_{on}{H}_1\left({\chi}_n\right)}\right\}+n\left({e}^{-i{\chi}_n}-1\right) $$

(19)

where ${H}_1\left({\chi}_n\right)=\frac{a}{\gamma}\frac{H\left({\chi}_n\right)}{1-H\left({\chi}_n\right)/y}$ and $H\left({\chi}_n\right)=b\gamma \left({e}^{i{\chi}_n}-1\right)$ where b is the burst size, i.e., the average number of proteins translated from one mRNA molecule. It is assumed that generation of a protein from a single mRNA is also a Poisson process.

From Eqs. (5) and (19) and using the relation ${Z}_p\left({\chi}_n\right)={e}^{t{H}_p\left({\chi}_n\right)}$, the Fano factor for protein distribution is given by:

$$ {F}_{protein}=1+2b+b{\varDelta}^{\hbox{'}} $$

(20)

where $\varDelta \hbox{'}=\frac{a}{\gamma}\varDelta$.

The switching between the on and off states occurs along a trajectory in the phase space of the classical Hamiltonian known as the optimal path trajectory. The mean switching time along the Hamiltonian trajectories that start from the metastable state and end either in the off or on state has the form:

$$ {\tau}_{on/ off\to off/ on}=\sigma \exp \left[{S}_{on/ off\to off/ on}\right] $$

(21)

where S is known as ‘action’ in classical physics. A precise estimation of the prefactor σ is a hard task, although it can be obtained for one-dimensional systems; however it is not important because Eq. (21) is dominated by the exponent, when the system is not too close to the bifurcation point [25, 30]. Strong fluctuations drive the system from its equilibrium metastable state to the on/off states along an optimal path that minimizes the action S. The optimal Hamiltonian trajectory that describes S starts from the metastable state and ends either at the on or off state. Since the probability of extinction is found by minimizing the action, we compute such trajectories satisfying the zero energy condition, i.e., H _p (χ _n ) = 0 as discussed in [24]. This simplifies our calculations because, from H _p (χ _n ) = 0, one can find how χ _n depends on n along this trajectory and then the action has the form:

$$ S={\displaystyle \underset{n_{off}/{n}_{on}}{\overset{n_0}{\int }}{\chi}_ndn}. $$

(22)

If n _on and n _off are the average protein number in the on and off states respectively, then at the metastable state these points are separated by a repeller n ₀ such that n _off < n ₀ < n _on and is obtained from the solution:

$$ {\overset{\cdotp }{n}}_{{}_0}=\frac{\partial {H}_P\left({\chi}_n\right)}{\partial {\chi}_n}\left|{\chi}_n=0\right. $$

(23)

and χ _n as a function of n along the zero energy trajectory of the Hamiltonian can be obtained at H _p (χ _n ) = 0 such that:

$$ {\chi}_n= \ln \left[\frac{-B+\sqrt{B^2-4 AC}}{2A}\right] $$

(24)

where B = − n{n(1 + 2b) + ab + (1 + b)(k _off(n) + k _on(n))}, A = nbk _off(n) + (ab + bn(n + k _on(n))), C = n ²(1 + b). Figure 1b shows this trajectory as a function of the protein number n.

The probability of switching from the off to on state and vice versa along this trajectory is given by P _{on/off → off/on}(n) ~ exp[−S _{on/off → off/on}(n)].

3 Results and discussion

To check our theoretical predictions, we compare our results for MST prediction to Monte Carlo simulations (MC) using the Gillespie algorithm [12]. Figure 2 shows the functional dependence of τ _{off → on} on the translation rate b at small and large gamma values. The numerical results are fitted with MC simulations using suitable values of the prefactor σ in Eq. (21). The MST has a superexponential dependence on b. In Fig. 2a, the burst size ranges from 1 to 4 for large values of gamma, whereas in Fig. 2b the burst size varies from 10 to 35 for small values of gamma. This suggests that the most important parameter in this theory is bγ instead of γ. This is the reason for obtaining good agreement with the simulation results for small values of gamma because in that case b> > 1. Figure 3 shows the MST from on to off states for a high value of gamma and off to on states for a low value of gamma as a function of n ₅₀ . In Fig. 3a, as n ₅₀ increases, k _off becomes smaller. This indicates that the switching rate from the on to off state decreases. Conversely, in Fig. 3b as n ₅₀ increases, k _on increases and the mean switching time from the off to on state becomes faster. In both Figs. 2 and 3, the numerical results are fitted with MC simulation by adjusting the value of the prefactor σ.

Fig. 2

MST from off to on state as a function of b for (a) γ = 50 (b) γ = 2. The solid lines are the numerical results with preexponents while (●) are from MC simulations. Prefactors are 17.08 and 300 for a and b, respectively. Here ab = 2,400, h = 2, k ^min₀  = k ^min₁  = a/100, k ^max₀  = k ^max₁  = a. For ,a, n ₅₀  = 720, b n ₅₀  = 1,000

Fig. 3

a MST as a function of Hill-type function curve’s midpoint n ₅₀ for a on to off state, γ = 50, b off to on state, γ = 2. The solid lines are the numerical results with preexponents while (●) are from MC simulations. Prefactors are 4.8 and 230 for a and b, respectively. Here ab = 2,400, h = 2, k ^min₀  = k ^min₁  = a/100, k ^max₀  = k ^max₁  = a. For a, b = 15, b b = 22.5

We can use our analytical model to determine a relationship between gene expression and noise, which is defined as the ratio of variance to the square of the mean, μ _mRNA  = σ ² _m /〈m〉² or μ _n  = σ ² _n /〈n〉². From Eqs. (3) and (15), we have:

$$ {\mu}_n=\frac{1+2b}{\left\langle n\right\rangle }+\frac{b\varDelta^{\prime }}{\left\langle n\right\rangle }. $$

(25)

The second term in Eq. (25) captures the effect of the promoter architecture. The same form of noise is also obtained for mRNA distributions, ${\mu}_{mRNA}=\frac{1}{\left\langle m\right\rangle }+\frac{\varDelta }{\left\langle m\right\rangle }$, where both Δ and Δ ′ have been defined earlier. In Fig. 4, we plot the protein noise μ _n as a function of the gene expression 〈n〉. We find that for this protein feedback loop where the on-off switching rate is controlled by the unbinding and binding of the protein to the promoter region, the expression increases and the noise decreases with the increase in the protein copy number n. This relationship between mean expression and noise in response to binding of the transcription factor (TF) to binding sites containing the promoter has also been observed experimentally by Segal et al. [31]. The gene expression and noise were measured as a function of the TF Zap1, which can act both as an activator and a repressor. For the experimental scenario of a Zap1-activated target gene, we can easily make a direct comparison with our two-state model (Fig. 1a) where the positive protein feedback loop essentially acts as an activator. Our calculations show that having a positive protein feedback loop causes an increase in gene expression along with a decrease of noise. This in fact agrees with the experimental predictions [31] of increased gene expression and decreased noise with the increased binding of TF Zap1 to the promoter region of the gene. The observed parallelism between our calculated results and reported experimental observations clearly implies the practical utility of our proposed theoretical methodology.

Fig. 4

Mean expression versus noise for the positive feedback model as shown in Fig. 1a for b = 15 (solid line) and b = 12 (dashed line), ab = 2,400, h = 2, k ^min₀  = k ^min₁  = a/100, k ^max₀  = k ^max₁  = a , n ₅₀   = 720, γ = 1

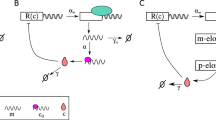
To test the robustness of our theoretical framework, we used our theory of stochastic transcriptional regulation to handle further complexity in promoter architectures. Such complexity can be introduced by varying the strength, number, and position of the transcription factor binding sites and also the strength of the repressors or activators. It has been reported earlier both in experiments and in theoretical studies that the promoter architecture of the gene regulatory network affects cell-to-cell variability in gene expression [32–35]. Thermodynamic models of gene expression have been used earlier to calculate the mean mRNA number and the protein copy number per cell [36–38]. However, these simple thermodynamic models can only compute the mean and not the higher moments of protein/mRNA distributions. As shown in the previous section, we can not only use our approach to calculate the mean and the variance of the protein/mRNA distributions but to also obtain the mean switching time between active and inactive promoter states for a complex promoter architecture such as the three-state promoter model [39–41] as shown in Fig. 5. State 1 refers to the inaccessible promoter (repressor bound) that makes a reversible transition to the DNA in the inactive state. The DNA then undergoes stochastic switching between the on and off states. For this birth-death mechanism the master equation for the mRNA probability distribution in terms of generating functions can be written as:

Fig. 5

Three-state promoter model for positive feedback. State 1 is the inaccessible promoter that may be bound to a repressor and k ₁ and k _-1 are the transition rates between state 1 and inactive state of the promoter, DNA _inactive. The rest is the same as in Fig. 1a

$$ \begin{array}{l}\frac{\partial }{\partial t}{Z}^1=-{k}_1{Z}^1+{k}_{-1}{Z}^G\hfill \\ {}\frac{\partial }{\partial t}{Z}^G=-\left({k}_{-1}+{k}_{on}(n)\right){Z}^G+{k}_1{Z}^1+{k}_{off}(n){Z}^{G*}\hfill \\ {}\frac{\partial }{\partial t}{Z}^{G*}=-\left(a+{k}_{off}(n)\right){Z}^{G*}+a{e}^{i{\chi}_R}{Z}^{G*}+{k}_{on}(n){Z}^G\hfill \end{array} $$

(26)

As shown previously in Eq. (6), one can recast this in the form of a Schrödinger equation such that:

$$ \frac{d}{dt}\left(\begin{array}{l}{Z}^1\hfill \\ {}{Z}^G\hfill \\ {}{Z}^{G*}\hfill \end{array}\right)=H\left({\chi}_R\right)\left(\begin{array}{l}{Z}^1\hfill \\ {}{Z}^G\hfill \\ {}{Z}^{G*}\hfill \end{array}\right) $$

(27)

where $H\left({\chi}_R\right)=\left(\begin{array}{l}-{k}_1\kern4em {k}_{-1}\kern6.1em 0\hfill \\ {}{k}_1\kern2em -\left({k}_{-1}+{k}_{on}(n)\right)\kern2em {k}_{off}(n)\hfill \\ {}0\kern4em {k}_{on}(n)\kern3em -\left(a+{k}_{off}(n)-a{e}^{i{\chi}_R}\right)\hfill \end{array}\right)$

Using the same argument used earlier, we can solve this eigenvalue problem and obtain the generating function for mRNA production:

$$ Z\left({\chi}_R\right)={e}^{\frac{t\left({K}_2\left({\chi}_R\right)+\sqrt{K_2\left({\chi}_R\right)+4{H}_2\left({\chi}_R\right)}\right)}{2}} $$

(28)

where K ₂(χ _R )  =  − (k ₁ + A + B), H ₂(χ _R )  =  k _on(n)k _off(n)  +  k ₁ AB  −  k ₁(A + B + k _on(n)k _off(n))  − AB

and A and B is given by $A=\left({k}_{off}(n)+a\left(1-{e}^{i{\chi}_R}\right)\right)$ and B = k _on(n) + 2k _− 1, respectively.

Using Eq. (5) and from Eq. (28) we can compute the Fano factor that is given by:

$$ {F}_{mRNA}=1+\frac{a}{\gamma }{\varDelta}_1 $$

(29)

where: ${\varDelta}_1=2\frac{k_{on}(n)/{k}_{off}(n)}{1+{k}_{on}(n)/{k}_{off}(n)+{k}_{-1}/{k}_1}\left(\left(\frac{1/{k}_{on}(n)}{1+{k}_{on}(n)/{k}_{off}(n)+{k}_{-1}/{k}_1}\right)+\left(\frac{k_{-1}/{k}_1}{1+{k}_{on}(n)/{k}_{off}(n)+{k}_{-1}/{k}_1}\right)\left(\frac{1}{k_1}+\frac{2+{k}_{-1}/{k}_1}{k_{on}(n)}\right)\right)$

In the absence of a repressor, this noise is identical to Eq. (10), which corresponds to a two-state promoter model. We find that Δ ₁ is a function of the switching rates between different promoter states. This clearly shows that although the expression of the Fano factor has the same structural form, it will be different for different promoter architectures and is a measure of the variability of the gene expression level in different cells. Similar findings were reported in [40] where it was found that DNA-looping that acts as a third transcriptional state changes the bistability properties of this stochastic model of gene expression in the lac operon. Also it was shown in [41] that the transmission of genetic information was affected for generic promoter models with multiple internal states including the one described in [40]. Further, we can use our semi-classical path integral technique to obtain the on-off switching times between different promoter states in this particular three-state promoter model.

4 Conclusions

In this work we presented an analytical method to understand the role of mRNA fluctuations in switching stability. We find that that this semi-classical path integral is a suitable method to coarse-grain the system and obtain an effective model for protein/mRNA fluctuations. Also, our technique can be used to calculate switching times, in the limit of short-lived mRNA. The considered model is only the minimal model of protein production. However, our theoretical model is quite unique and diverse in the sense that it can be applied to more complex models of gene expression with multiple promoter sites. We illustrated the effective use of our theoretical framework for a complex system, namely the three-state promoter model as shown in Fig. 5. As reported earlier [39–41], our analysis of the three-state promoter model shows that the gene expression level is strongly affected by the promoter architecture. Also, in the two-state promoter model, one can introduce a non-exponential protein degradation step instead of a simple Poisson process. It is practically impossible to capture such variations in the model using previously known theoretical techniques but we show that these can be easily incorporated into our proposed theoretical method. As reported experimentally in the literature, we find that promoter architecture has the same qualitative effect on cell-to-cell variability in the noise and gene expression for both mRNA and protein distributions. In this work we only focus on describing intrinsic noise but, in the high copy-number regime, extrinsic noise that arises from the interactions of the system of interest with its environment is equally significant. Extension of this theory to describe the combined effect of intrinsic and extrinsic noise on the dynamics of stochastic genetic switches is underway.