1 Introduction

Gene regulation is one of the most fundamental processes in living systems. The experimental systems of lac operon in bacteria E. coli and the genetic switch of bacteriophage lambda virus allowed to unravel the basic molecular mechanisms of how a gene is turned on and off. These were followed by a molecular-level explanation of stochastic switching between lysis and lysogeny of phage [22], all the way to more complex logic gate formalisms that attempt to abstract more complex biological behaviour [6, 12, 21]. To date, synthetic biology has demonstrated remarkable success in engineering simple genetic circuits that are encoded in DNA and perform their function in vivo. However, significant conceptual challenges remain, related to the still unsatisfactory quantitative but also qualitative understanding of the underlying processes [19, 30]. Partly, this is due to the unknown or unspecified interactions in experiments in vivo (crosstalk, host-circuit interactions, loading effect). Another major challenge towards rational and rigorous design of synthetic circuits is computational modelling: gene regulation has a combinatorial number of functional entities, it is inherently stochastic, exhibits multiple time-scales, and experimentally measuring kinetic parameters/rates is often difficult, imprecise or impossible. In such context, predicting the transient profile - how gene expression in a population of cells evolves over time - becomes a computationally expensive task. However, predicting how the transient phenotype emerges from the mechanistic, molecular interactions, is crucial both for engineering purposes of synthetic biology (e.g. when composing synthetic systems), as well as for addressing fundamental biological and evolutionary questions (e.g. for understanding whether the cell aims to create variability by modulating timing).

Mechanistically, the transcription of a single gene is initiated whenever a subunit of RNA polymerase binds to that gene’s promoter region at the DNA [35]. While such binding can occur spontaneously, it is typically promoted or inhibited through other species involved in regulation, such as proteins and transcription factors (TFs). Consequently, the number of possible molecular configurations of the DNA grows combinatorially with the number of operator sites regulating the gene in question. For instance, one hypothesised mechanism in lambda-phage, containing only three left and three right operators, leads to 1200 different DNA configurations [31]. The combinatorial explosion of the number of possible configurations makes the model tedious to even write down, let alone execute and make predictions about it. The induced stochastic process enumerates states which couple the configuration of the DNA, with the copy number of the protein, and possibly other species involved in regulation, such as mRNA and transcription factors. In order to faithfully predict the stochastic evolution of the gene product (protein) over time, the modelled system can be solved numerically, by integrating the Master equation of the stochastic process. This is often prohibitive in practice, due to large dimensionality and a combinatorial number of reachable states. For this reason, modelling practice often abstracts away details and adds assumptions. One popular approach is simulating the system by Gillespie simulation [7] and statistically inferring the protein expression profile, hence trading off accuracy and precision. Other approaches are based on mean-field approximations (e.g. deterministic limit [17] and linear-noise approximation [5]), significantly reducing the computational effort. However, mean-field models do not capture the inherent stochasticity, which is especially prominent in gene regulation. Further model reduction ideas exploit multi-scaleness of the system: fast subsystems are identified (possibly dynamically), and assumed to be reaching an equilibrium fast, relative to the observable dynamics [2, 13, 29, 34]. A special class of reductions based on steady-state assumption is the experimentalists’ favourite approach of statistical thermodynamics limit. This widely and successfully used method (e.g. [3, 24, 33]) estimates the probability of being in any of the possible DNA binding configurations from their relative binding energies (Boltzmann weights) and the protein concentrations, both of which can often be experimentally accessed. The statistical thermodynamics limit model is rooted in the argument that, when the switching rates among DNA configurations are fast, the probability distribution over the configurations is rapidly arriving at its stationary distribution. While this model takes into account the stochasticity inherent to the DNA binding configurations, it neglects the transient probabilities in the DNA switching, before the equilibrium is reached. It abstracts away the relative speed of rates of different reactions at the DNA, and how they connect to one another. The question arises: how does the transient gene expression - its shape and duration - depend on the topology and scale of the rates of reactions involving the DNA? Is it justifiable, in this context, to consider sufficiently fast propensities as an argument for applying a (quasi-)steady-state assumption?

In this paper, we investigate how the transient gene expression depends on the topology and scale of the rates of reactions involving the DNA. In Sect. 2, we introduce reaction networks, a stochastic process assigned to it, and the equations for the transient dynamics. In Sect. 3, we describe a generic example where a single protein is regulated through a number of arbitrarily connected DNA configurations, without feedback. This means that any transition between two states of the network is possible. In our first result, we analytically show that, if all switching rates are uniformly speeded up, then, as expected, the protein transient is faster and the noise is smaller. In Sect. 3.1, we introduce concrete parameter instances to illustrate the phenomenon numerically. Then, in Sect. 4, we present our main result: counter-intuitively, if all rates are fast but some more than others (two orders of magnitude vs. one order of magnitude), the opposite effect may emerge: time to equilibration is slower and protein noise increases. We use singular perturbation analysis to systematically show that, in general, the fast chain with some rates even faster, exactly reduces to a slow-switching chain. We conclude the paper by discussing the implications of our results in Sect. 5.

1.1 Related Works

Timing aspects of gene regulation are gaining increasing attention, such as explicitly modelling delays in gene expression [28], showcasing dramatic phenotypic consequences of small delays in the arrival of different TFs [11], resolving the temporal dynamics of gene regulatory networks from time-series data [10], as well as the study of transient hysteresis and inherent stochasticity in gene regulatory networks [27]. Following the early works on examining the relation between topology and relaxation to steady states of reaction networks [9], stochastic gene expression from a promoter model has been studied for multiple states [14]. Singular perturbation analysis has been used for lumping states of Markov chains arising in biological applications [4, 34]. To the best of our knowledge, none of these works showcases the phenomenon of obtaining slower dynamics through faster rates, or, more specifically, slowing down gene expression by speeding up the reactions at the DNA.

2 Preliminaries

The default rate of gene expression, also referred to as the basal rate, can be modified by the presence of transcriptional activators and repressors. Activators are transcription factors (TFs) that bind to specific locations on the DNA, or to other TFs, and enhance the expression of a gene by promoting the binding of \({\mathsf {RNAP}}\). Repressors reduce the expression of gene g, by directly blocking the binding of \({\mathsf {RNAP}}\), or indirectly, by inhibiting the activators, or promoting direct repressors. The mechanism of how and at which rates the molecular species are interacting is transparently written in a list of reactions. Reactions are equipped with the stochastic semantics which is valid under mild assumptions [7]. In the following, we will model gene regulatory mechanisms with the standard Chemical Reaction Network formalism (CRN).

Definition 1

A reaction system is a pair \(({\mathsf S},\mathsf R)\), such that \({\mathsf S}=\{S_{1},\ldots ,S_{s}\}\) is a finite set of species, and \(\mathsf R=\{\mathsf {r}_1,\ldots ,\mathsf {r}_{r}\}\) is a finite set of reactions. The state of a system can be represented as a multi-set of species, denoted by \(\varvec{x}=(x_1,...,x_{s})\in \mathbb {N}^{s}\). Each reaction is a triple \(\mathsf {r}_j\equiv ({\varvec{a}}_{j},\varvec{\nu }_{j},c_j)\in \mathbb {N}^{s}\times \mathbb {N}^{s}\times {\mathbb {R}}_{\ge 0}\), written down in the following form:

$$\begin{aligned} a_{1j}S_{1},\ldots ,a_{sj}S_{s} {\mathop {\rightarrow }\limits ^{{c_{j}}}}{a}'_{1j}S_{1},\ldots ,{a}'_{sj}S_{s}, \text { such that } \forall i.{a}'_{ij}=a_{ij}+\nu _{ij}. \end{aligned}$$

The vectors \({\varvec{a}}_{j}\) and \({\varvec{a}}_{j}'\) are often called respectively the consumption and production vectors due to jth reaction, and \(c_j\) is the respective kinetic rate. If the jth reaction occurs, after being in state \(\varvec{x}\), the next state will be \(\varvec{x}' = \varvec{x}+\varvec{\nu }_j\). This will be possible only if \(x_i\ge a_{ij}\) for \(i=1,\ldots ,s\).

Stochastic Semantics. The species’ multiplicities follow a continuous-time Markov chain (CTMC) \(\{X(t)\}_{t\ge 0}\), defined over the state space \( S=\{\varvec{x}\mid \varvec{x}\) is reachable from \(\varvec{x}_0\) by a finite sequence of reactions from \(\{\mathsf {r}_1,\ldots ,\mathsf {r}_{r}\}\}\). In other words, the probability of moving to the state \(\varvec{x}+{\varvec{\nu }}_j\) from \(\varvec{x}\) after time \(\varDelta \) is

$$ \mathsf {P}(X(t+\varDelta ) = \varvec{x}+\varvec{\nu }_j\mid X(t)=\varvec{x}) = \lambda _{j}(\varvec{x})\varDelta +o(\varDelta ), $$

with \(\lambda _{j}\) the propensity of jth reaction, assumed to follow the principle of mass-action: \(\lambda _{j}(\varvec{x})= c_j\prod _{i=1}^{s}{x_i\atopwithdelims ()a_{ij}} \). The binomial coefficient \({x_i\atopwithdelims ()a_{ij}}\) reflects the probability of choosing \(a_{ij}\) molecules of species \(S_i\) out of \(x_i\) available ones.

Computing the Transient. Using the vector notation \(\mathbf {X}(t)\in {\mathbb {N}}^n\) for the marginal of process \(\{X(t)\}_{t\ge 0}\) at time t, we can compute this transient distribution by integrating the chemical master equation (CME). Denoting by \(p_{\varvec{x}}(t):=\mathsf {P}(\mathbf {X}(t)=\varvec{x})\), the CME for state \(\varvec{x}\in {\mathbb {N}}^{s}\) reads

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t} p_{\varvec{x}}(t) = \sum _{j=1, \varvec{x}-\varvec{\nu }_{j}\in {\mathsf S}}^{r} \lambda _{j}(\varvec{x}-\varvec{\nu }_{j}) p_{(\varvec{x}-\varvec{\nu }_{j})}(t) - \sum _{j=1}^{r} \lambda _{j}(\varvec{x})p_{\varvec{x}}(t). \end{aligned}$$
(1)

The solution may be obtained by solving the system of differential equations, but, due to its high (possibly infinite) dimensionality, it is often statistically estimated by simulating the traces of \(\{X_t\}\), known as the stochastic simulation algorithm (SSA) in chemical literature [7]. As the statistical estimation often remains computationally expensive for desired accuracy, for the case when the deterministic model is unsatisfactory due to the low multiplicities of many molecular species [18], different further approximation methods have been proposed, major challenge to which remains the quantification of approximation accuracy (see [32] and references therein for a thorough review on the subject).

3 Moment Calculations

We consider a generic example with m different \({\mathsf {DNA}}\) states regulating a single protein, without feedback. The configurations of the \({\mathsf {DNA}}\) are indexed by \(1,2\ldots m\), and we denote the transition rates between them (reaction propensities) by \(q_{ij}\) (we additionally define \(q_{ii}=-\sum _{j=1}^m q_{ij}\)). We assume that the gene chain is irreducible, justified by the reversibility of all reactions at the \({\mathsf {DNA}}\). The dynamics of the protein copy number is modelled as usually by a birth–death process (with gene-state-dependent birth rate \(k_i\) and linear death rate \(\delta \) per protein). The respective reaction system is schemed in Table 1, left.

The underlying stochastic process \(\{X(t)\}\) takes values in the state space \(S\subseteq \mathbb {N}^{m+1}\), such that the first m components represent the \({\mathsf {DNA}}\) states, and the last one is the protein count.

In the following, we will use notation \(\varvec{X}_{1:m}(t)\in \{0,1\}^m\), to denote the projection of the marginal process at time t, to the \({\mathsf {DNA}}\)-regulatory elements, and, for better readability, we introduce \(N(t):=\varvec{X}_{m+1}(t)\) to denote the protein count at time t.

In total, since there is exactly one copy of the \({\mathsf {DNA}}\), any state in S can be seen as a gene state coupled with the protein copy number, i.e. \(S\cong \{1,2,\ldots ,m\}\times \mathbb {N}\). We introduce short-hand notation \(s_{(i,n)}\) for state \(\varvec{x}=(\underbrace{0,\ldots ,1}_{i},\ldots ,0,n) \in S\). Allowable transitions and their rates are summarised in Table 1, right.

Table 1. Two equivalent formulations of a multi-state gene expression model. Left: a reaction system with \(m+1\) reaction species S\(_1\), \(\ldots \), S\(_m\) (gene states) and S\(_{m+1}=\,\)P (protein) with copy numbers \(X_1(t)\), \(\ldots \), \(X_m(t)\) and \(X_{m+1}(t)=N(t)\), whereby \(X_1(t)+\ldots +X_m(t)=1\) holds initially (and throughout time). Right: a two-component Markov chain in which the first component indexes the gene state and the second component gives the protein copy number.
Full size table

We arrange the probabilities \(p_{n,i}(t):=\mathsf {P}(\mathbf {X}(t)=s_{(i,n)})\) of being in gene state i and having n protein into a column vector

$$ \varvec{p}_n(t) = (p_{n,1}(t),\ldots , p_{n,m}(t))^T. $$

The probability vector satisfies a system of difference–differential equations

$$\begin{aligned} \frac{\mathrm {d}\varvec{p}_n}{\mathrm {d}t} = \varvec{A} \varvec{p}_n + \varvec{\varLambda }_{\varvec{k}} (\varvec{p}_{n-1} - \varvec{p}_n) + \delta ( (n+1) \varvec{p}_{n+1} - n \varvec{p}_n), \end{aligned}$$
(2)

where \(\varvec{A}=\varvec{Q}^\intercal \) is the Markovian generator matrix and \(\varvec{\varLambda }_{\varvec{k}}\) is a diagonal square matrix with the elements of the vector \(\varvec{k} = (k_1, \ldots ,k_m)^T\) placed on the main diagonal. We study (2) subject to the initial condition

$$\begin{aligned} \varvec{p}_n(0) = \delta _{n,n_0} \varvec{e}_{j_0} \end{aligned}$$
(3)

in which \(n_0\) is the initial protein copy number, \(j_0\) is the initial gene state, \(\delta _{n,n_0}\) represents the Kronecker delta, \(\varvec{e}_{j_0}\) is the \(j_0\)-th element of the standard basis in the m-dimensional Euclidean space.

Let us introduce the variables

$$\begin{aligned}&\varvec{p}(t) = \sum _{n=0}^\infty \varvec{p}_n(t),\quad \langle N(t) \rangle = \sum _{n=0}^\infty n \varvec{1}^T \varvec{p}_n(t),\end{aligned}$$
(4)
$$\begin{aligned}&\varvec{f}(t) = \left( \sum _{n=0}^\infty n \varvec{p}_n(t) \right) - \langle N(t) \rangle \varvec{p}(t),\end{aligned}$$
(5)
$$\begin{aligned}&\sigma ^2(t) = \left( \sum _{n=0}^\infty n^2 \varvec{1}^T \varvec{p}_n(t)\right) - \langle N(t) \rangle ^2. \end{aligned}$$
(6)

Note that \(\varvec{1}^T \varvec{p}_n(t) = p_{n,1}(t)+\ldots +p_{n,m}(t)\), where \(\varvec{1}^\intercal =(1,\ldots ,1)\) is the m-dimensional row vector of ones, gives the marginal protein probability mass function. It is instructive to interpret the variables \(\varvec{p}(t)\) and \(\varvec{f}(t)\) from the standpoint of the reaction-network formulation of the model (Table 1, left). The elements of the copy-number vector \(\varvec{X}_{1:m}(t) ^\intercal \) of gene states can be zero or one, with exactly one of them being equal to one; the gene-state copy-number statistics can be expressed in terms of (4)–(6) as

$$\begin{aligned} \langle \varvec{X}_{1:m}(t) \rangle&= \varvec{p}(t),\\ \langle N(t) \varvec{X}_{1:m}(t) \rangle - \langle N(t) \rangle \langle \varvec{X}_{1:m}(t) \rangle&= \varvec{f}(t),\\ \langle \varvec{X}_{1:m}(t) \varvec{X_{1:m}}(t)^\intercal \rangle - \langle \varvec{X}_{1:m}(t) \rangle \langle \varvec{X}_{1:m}(t) \rangle ^\intercal&= \varvec{\varSigma }(t) = \varvec{\varLambda }_{\varvec{p}(t)} - \varvec{p}(t)\varvec{p}(t)^T. \end{aligned}$$

The variables (4)–(6) thus fully describe the mean and covariance of the reaction system in Tabl  1, right. In particular, \(\varvec{f}(t)\) is the covariance between the gene state and protein copy number; \(\varvec{\varSigma }(t)\) is the covariance matrix of the gene state (with itself).

The variables (4)–(6) satisfy a system of differential equations (see Appendix B for derivation)

$$\begin{aligned}&\frac{\mathrm {d}\varvec{p}}{\mathrm {d}t} = \varvec{A} \varvec{p},\quad \frac{\mathrm {d}\langle N(t) \rangle }{\mathrm {d}t} = \varvec{k}^T \varvec{p}- \delta \langle N(t) \rangle ,\end{aligned}$$
(7)
$$\begin{aligned}&\frac{\mathrm {d}\varvec{f}}{\mathrm {d}t} = \varvec{A} \varvec{f} - \delta \varvec{f} + \varvec{\varSigma }\varvec{k},\quad \text {where}\quad \varvec{\varSigma } = \varvec{\varLambda }_{\varvec{p}} - \varvec{p}\varvec{p}^T,\end{aligned}$$
(8)
$$\begin{aligned}&\frac{\mathrm {d}\sigma ^2}{\mathrm {d}t} = 2 \varvec{k}^T \varvec{f} + \varvec{k}^T \varvec{p}+ \delta \langle N(t) \rangle - 2 \delta \sigma ^2 \end{aligned}$$
(9)

subject to initial conditions

$$\begin{aligned} \varvec{p}(0) = \varvec{e}_{j_0},\quad \langle N(0)\rangle = n_0, \quad \varvec{f}(0) = \varvec{0},\quad \sigma ^2(0) = 0, \end{aligned}$$
(10)

where \(\varvec{e}_{j_0}\) is the \(j_0\)-th element of the standard basis in m-dimensional Euclidean space.

Equating the derivatives in (7)–(9) to zero, we obtain steady state protein mean and Fano factor in the form

$$\begin{aligned} \langle N(t) \rangle = \frac{\varvec{k}^T \bar{\varvec{p}}}{\delta },\quad \frac{\sigma ^2}{\langle N(t) \rangle } = 1 + \frac{\varvec{k}^T \bar{\varvec{f}}}{\varvec{k}^T \bar{\varvec{p}}}, \end{aligned}$$
(11)

where \(\bar{\varvec{p}}\) and \(\bar{\varvec{f}}\) satisfy algebraic equations

$$\begin{aligned} \varvec{A} \bar{\varvec{p}} = 0,\quad (\varvec{A} - \delta ) \bar{\varvec{f}} + \varvec{\varSigma } \varvec{k} = 0. \end{aligned}$$
(12)

We note that the solution \(\bar{\varvec{f}}\) to (12) can be represented as

$$\begin{aligned} \bar{\varvec{f}} = \int _0^\infty \mathrm {e}^{-\delta t} \left( \mathrm {e}^{t \varvec{A}} - \bar{\varvec{p}} \varvec{1}^T \right) \mathrm {d}t \varvec{\varSigma } \varvec{k}. \end{aligned}$$
(13)

Equation (13) connects the magnitude of \(\bar{\varvec{f}}\) to the equilibration timescale of the gene-state Markov chain (note that \(\bar{\varvec{p}}\varvec{1}^\intercal = \lim _{t\rightarrow \infty } \mathrm {e}^{t \varvec{A}}\)). Specifically, if \(\varvec{A}=\tilde{\varvec{A}}/\varepsilon \), where \(\varepsilon \ll 1\), i.e. the gene transition rates are \(O(1/\varepsilon )\) large, then substituting \(t=\varepsilon s\) into (13) implies that

$$ \bar{\varvec{f}} = \varepsilon \int _0^\infty \left( \mathrm {e}^{s \tilde{\varvec{A}}} - \bar{\varvec{p}} \varvec{1}^T \right) \mathrm {d}s \varvec{\varSigma } \varvec{k}+O(\varepsilon ^2), $$

which is \(O(\varepsilon )\) small. Correspondingly, the (steady-state) protein Fano factor (11) will differ from the Poissonian value of 1 by an \(O(\varepsilon )\) quantity. This concludes the argument that, in agreement with intuition, if all rates are faster by an order of magnitude (\(\varepsilon ^{-1}\)), then, as expected, the magnitude of equilibration time-scale of the whole chain scales down with the same factor. The fast fluctuations of the gene chain are thereby averaged out at the downstream level of the protein.

However, as will be demonstrated in the next section with a specific example of a four state chain, the largeness of transition rates does not guarantee, on its own, fast equilibration, and the connectivity of the chain can play a crucial role. Indeed, we will show that one can slow down equilibriation (and hence increase protein noise) by increasing some of the transition rates.

Fig. 1.
figure 1

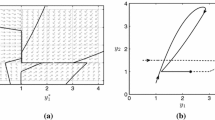
Dependence of \(\langle N(t)\rangle \,\pm \,\sigma (t)\) on t for a value of \(\varepsilon = 0.01\), using two regimes. Left: “fast” scaling regime where all transition rates are \(O(1/\varepsilon )\). Right: “slow by fast” scaling regime, where the backward rates are speeded up to \(O(1/\varepsilon ^2)\). ODE results (dashed line) are cross-validated by Gillespie simulations (solid line). The chain is initially at state \(j_0 = 2\), and the amount of protein is set to \(n_0 = 50\). The transition matrix parameters are set to \({\tilde{a}}_{\mathrm {g}}={\tilde{b}}_{\mathrm {g}}={\tilde{a}}_{\mathrm {r}}={\tilde{b}}_{\mathrm {r}}={\tilde{\tilde{a}}}_{\mathrm {b}}={\tilde{\tilde{b}}}_{\mathrm {b}}=1\).

Full size image

3.1 Four-State Chain

We specifically focus on a case with four gene states, with transition matrix

$$\begin{aligned} \varvec{A} = \begin{pmatrix} -{a}_{\mathrm {r}} &{} {a}_{\mathrm {b}} &{} 0 &{} 0 \\ {a}_{\mathrm {r}} &{} -{a}_{\mathrm {b}} - {a}_{\mathrm {g}} &{} {b}_{\mathrm {g}} &{} 0 \\ 0 &{} {a}_{\mathrm {g}} &{} -{b}_{\mathrm {g}} - {b}_{\mathrm {b}} &{} {b}_{\mathrm {r}}\\ 0 &{} 0 &{} {b}_{\mathrm {b}} &{} -{b}_{\mathrm {r}} \\ \end{pmatrix} \end{aligned}$$
(14)

(recall that the matrix \(\varvec{A}\) is shown as a transpose of the graph of connections, the respective graph is depicted in Fig. 2, left). We investigate two alternative, different scaling regimes with respect to a small dimensionless parameter \(\varepsilon \):

  • Fast. We assume that all transition rates are \(O(1/\varepsilon )\), i.e.

    $$ {a}_{\mathrm {g}} = \frac{{\tilde{a}}_{\mathrm {g}}}{\varepsilon },\quad {a}_{\mathrm {b}} = \frac{{\tilde{a}}_{\mathrm {b}}}{\varepsilon },\quad {a}_{\mathrm {r}} = \frac{{\tilde{a}}_{\mathrm {r}}}{\varepsilon },\quad {b}_{\mathrm {g}} = \frac{{\tilde{b}}_{\mathrm {g}}}{\varepsilon },\quad {b}_{\mathrm {b}} = \frac{{\tilde{b}}_{\mathrm {b}}}{\varepsilon },\quad {b}_{\mathrm {r}} = \frac{{\tilde{b}}_{\mathrm {r}}}{\varepsilon }, $$

    where \({\tilde{a}}_{\mathrm {g}}\), \({\tilde{a}}_{\mathrm {b}}\), \({\tilde{a}}_{\mathrm {r}}\), \({\tilde{b}}_{\mathrm {g}}\), \({\tilde{b}}_{\mathrm {b}}\), and \({\tilde{b}}_{\mathrm {r}}\) are O(1).

  • Slow by fast. We speed up the backward rates by making them \(O(1/\varepsilon ^2)\), i.e.

    (15)

    where \({\tilde{a}}_{\mathrm {g}}\), , \({\tilde{a}}_{\mathrm {r}}\), \({\tilde{b}}_{\mathrm {g}}\), , and \({\tilde{b}}_{\mathrm {r}}\) are O(1).

We first numerically analyse the transient protein dynamics for these two scaling scenarios. In Fig. 1, we plot the average protein count and the standard deviation. Increasing the speed of rates from states 2 (resp. 3) to state 1 (resp. 4) not only does not increase the scale and decrease the protein noise, but significantly slows down the protein dynamics and increases noise. In the next section, we systematically derive that the case ‘slow by fast’ regime is approximated by a slow-switching 2-state chain (shown in Fig. 2, right).

4 Singular-Perturbation Analysis of the Slow-by-fast Regime

The probability dynamics generated by the transition matrix (14) in the slow-by-fast scaling regime (15) is given by a system of four differential equations

(16)
(17)
(18)
(19)

Equations such as (16)–(19) whose right-hand sides depend on a small parameter \(\varepsilon \) are referred to as perturbation problems. Additionally, problems in which, like in (16)–(19), the small parameter multiplies one or more derivatives on the left-hand side, are classified as singularly perturbed [16, 23]. We study solutions to system (16)–(19) that satisfy an intial condition

$$\begin{aligned} p_i(0) = p_i^\mathrm {init},\quad i=1,2,3,4, \end{aligned}$$
(20)

where the right-hand side of (20) is a prescribed probability distribution. The aim of what follows is to characterise the behaviour as \(\varepsilon \rightarrow 0\) of the solution to (16)–(19) subject to (20).

We look for a solution to (16)–(19) in the form of a regular power series

$$\begin{aligned} p_i(t;\varepsilon ) = p_i^{(0)}(t) + \varepsilon p_i^{(1)}(t) + O(\varepsilon ^2),\quad i=1,2,3,4. \end{aligned}$$
(21)

Inserting (21) into (16) and (19) and collecting terms of same order yields

(22)
(23)
(24)

Equations (22) imply that the probability of states 2 or 3 is \(O(\varepsilon )\)-small. Equation (23) means that, at the leading order, the probability of state 2 is proportional to that of state 1; equation (24) establishes the analogous for states 3 and 4. Adding (16) to (17), and (18) to (19), yield

$$\begin{aligned} \varepsilon \frac{\mathrm {d}}{\mathrm {d}t}(p_1 + p_2)&= - {\tilde{a}}_{\mathrm {g}} p_2 + {\tilde{b}}_{\mathrm {g}} p_3, \end{aligned}$$
(25)
$$\begin{aligned} \varepsilon \frac{\mathrm {d}}{\mathrm {d}t}(p_3 + p_4)&= {\tilde{a}}_{\mathrm {g}} p_2 - {\tilde{b}}_{\mathrm {g}} p_3. \end{aligned}$$
(26)

Inserting (21) into (25)–(26) and collecting \(O(\varepsilon )\) terms gives

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}(p_1^{(0)} + p_2^{(0)})&= - {\tilde{a}}_{\mathrm {g}} p_2^{(1)} + {\tilde{b}}_{\mathrm {g}} p_3^{(1)}, \end{aligned}$$
(27)
$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}(p_3^{(0)} + p_4^{(0)})&= {\tilde{a}}_{\mathrm {g}} p_2^{(1)} - {\tilde{b}}_{\mathrm {g}} p_3^{(1)}. \end{aligned}$$
(28)

Inserting (22)–(24) into (27)–(28) yields

(29)
(30)

Equations (29)–(30) describe the probability dynamics of a two-state (or random-telegraph) chain with states 1 and 4 and transition rates and between them. Intriguingly, the emergent dynamics of (29)–(30) occurs on the \(t=O(1)\) scale although the original system (16)–(19) featured only \(O(1/\varepsilon )\) rates (or faster).

4.1 Inner Solution and Matching

In singular-perturbation studies, the leading-order term of a regular solution (21) is referred to as the outer solution [15, 23]. As is typical in singularly perturbed problems, the outer solution satisfies a system, here (29)–(30), that is lower-dimensional than the original system (16)–(19); the remaining components of the outer solution are trivially given by (22). Therefore, the initial condition (20) cannot be immediately imposed on the outer solution. In order to formulate an appropriate initial condition for (29)–(30), we need to study (16)–(19) on the fast timescale, find the so-called inner solution, and use an asymptotic matching principle [15, 23] to connect the two asymptotic solutions together.

Fig. 2.
figure 2

(left) Four-state chain at the \({\mathsf {DNA}}\): all rates are faster than O(1): some by order or magnitude \(\varepsilon ^{-1}\), and some even faster, by order of magnitude \(\varepsilon ^{-2}\). (left) The emergent dynamics is approximated by a two-state chain. Intriguingly, the emergent dynamics of occurs on the \(t=O(1)\) scale although the original system featured only \(O(1/\varepsilon )\) rates and faster.

Full size image

In order to construct the inner solution, we focus on the fast dynamics of system (16)–(19) by means of a transformation

$$\begin{aligned} t = \varepsilon ^2\,T,\quad p_i(t) = P_i(T). \end{aligned}$$
(31)

Inserting (31) into (16)–(19) yields a time-rescaled system

$$\begin{aligned}&\end{aligned}$$
(32)
$$\begin{aligned}&\end{aligned}$$
(33)
$$\begin{aligned}&\end{aligned}$$
(34)
$$\begin{aligned}&\end{aligned}$$
(35)

Note that in the time-rescaled system (32)–(35), the time derivative is no longer multiplied by a small parameter.

$$\begin{aligned} P_i(T;\varepsilon ) = P_i^{(0)}(T) + \varepsilon P_i^{(1)}(T) + O(\varepsilon ^2),\quad i=1,2,3,4. \end{aligned}$$
(36)

into (32)–(35) and collecting the O(1) terms yield

(37)

Since the reduced problem (37) retains the dimensionality of the original problem (32)–(35), we can solve it subject to the same initial condition

$$\begin{aligned} P_i^{(0)}(0) = p_i^\mathrm {init}, \end{aligned}$$
(38)

which yields

(39)
(40)

Thus, on the inner timescale, there occurs a fast transfer of probability mass from the states 2 and 3 into the states 1 and 4, respectively.

Fig. 3.
figure 3

The inner, outer, and composite approximations (solid curves) to the first component of the exact solution (dashed curve) to (16)–(20) (time is shown at logarithmic scale). The timescale separation parameter is set to \(\varepsilon =0.01\). The chain is initially at state 2, i.e. \(p_2^\mathrm {init}=1\), \(p_1^\mathrm {init}=p_3^\mathrm {init}=p_4^\mathrm {init}=0\). The transition matrix parameters are set to \({\tilde{a}}_{\mathrm {g}}={\tilde{b}}_{\mathrm {g}}={\tilde{a}}_{\mathrm {r}}={\tilde{b}}_{\mathrm {r}}={\tilde{\tilde{a}}}_{\mathrm {b}}={\tilde{\tilde{b}}}_{\mathrm {b}}=1\).

Full size image

According to the asymptotic matching principle [15, 23], the large-T behaviour of the inner and the small-t behaviour of the outer solution overlap, i.e.

$$\begin{aligned} p_1^{(0)}(0)&= P_1^{(0)}(\infty ) = p_1^\mathrm {init} + p_2^\mathrm {init},\end{aligned}$$
(41)
$$\begin{aligned} p_4^{(0)}(0)&= P_4^{(0)}(\infty ) = p_3^\mathrm {init} + p_4^\mathrm {init}. \end{aligned}$$
(42)

Equations (41)–(42) establish the relationship between the original initial condition (20) and the initial condition that needs to be imposed for the outer solution; solving (29)–(30) subject to (41)–(42) yields

(43)
(44)

We note that the second and third components of the outer solution are trivially given by \(p_2^{(0)}(t) = p_3^{(0)}(t)=0\) by (22). The outer solution (43)–(44) provides a close approximation to the original solution for \(t=O(1)\) but fails to capture the behaviour of the initial transient; the inner solution (39)–(40) provides a close approximation for \(T=O(1)\), i.e. \(t=O(\varepsilon ^2)\), but disregards the outer dynamics. A uniformly valid composite solution can be constructed by adding the inner and outer solutions up, and subtracting the matched value, i.e.

(45)
(46)

Figure 3 shows the exact solution to (16)–(20), the inner solution (39)–(40), the outer solution (43)–(44), and the composite solution (45)–(46).

5 Discussion and Future Work

The key ingredient of our analysis is the separation of temporal scales at the level of the gene state chain. If all gene transition rates are of the same order, say \(O(1/\varepsilon )\), then the chain equilibrates on a short \(O(\varepsilon )\) timescale (the O(1) timescale is assumed to be that of protein turnover). This situation has been widely considered in literature, e.g. [25, 34]. In the example on which we focused in our analysis, however, some transition rates are of a larger order, \(O(1/\varepsilon ^2)\). These faster rates generate an \(O(\varepsilon ^2)\) short timescale in our model. Importantly (and counterintuitively), the acceleration of these rates drives an emergent slow transitioning dynamics on the slow O(1) timescale. This means, in particular, that the transient behaviour, as well as stochastic noise, is not averaged out but retained at the downstream level of protein dynamics. We expect that more general networks of gene states can generate more than two timescales (fast and slow). Results from other works can be used to compute approximations for multiple timescales [9]. In particular, we note that although our example retains some \(O(1/\varepsilon )\) transition rates, no distinguished dynamics occurs on the corresponding \(O(\varepsilon )\) timescale. We expect, however, the intermediate \(O(\varepsilon )\) timescale can play a distinguished role in more complex systems.

The possibility of realistic GRNs implementing slow gene expression dynamics by accelerating reactions at the DNA, opens up fundamental biological questions related to their regulatory and evolutionary roles. For modelling, the uncertainty about even the magnitude of biochemical reaction rates pressures us to account for the potentially emerging slow-by-fast phenomenon: approximations resting on the argument that all rates are ‘sufficiently fast’, while not accounting for the topology of interactions at the DNA, can lead to wrong conclusions. The key feature of the 4-state example presented in this paper are very fast rates towards two different states which are poorly connected and consequently hard to leave. This situation will likely be seen in larger, realistic gene regulatory networks, because the rate of forming larger functional complexes typically depends on the order of TF’s binding at the DNA. For instance, in a biologically realisable gene regulatory circuit shown in [11], a pair of activators and a pair of repressors compete to bind the DNA, so to rapidly transition to highly stable conformational change at the DNA. One of the interesting directions for future work is automatising the derivation of singular perturbation reduction shown in Sect. 4. Such a procedure would allow us to systematically explore reductions for larger gene regulatory networks. Additionally, we want to examine different topologies and sizes of networks to generalize our results. This could reveal if the backward reactions are always the crucial factor in causing the slow-by-fast phenomenon.

Slow-by-fast phenomena we show here, could appear in application domains beyond gene regulation, i.e., wherever nodes over a weighted network regulate a collective response over time. For instance, in network models used to predict the spread of information or spread of disease, among coupled agents [26, 36], or in network-models for studying the role of communication in wisdom of the crowds (known to be enhanced by interaction, but at the same time hindered by information exchange [1, 20]). Finally, networks of neurons are known to have different intrinsic time-scales, in addition to the time-scales that arise from network connections [8].