Using MKT measures for cross-national comparisons of teacher knowledge: case of Slovakia and Norway

Abstract

The measures of mathematical knowledge for teaching developed at the University of Michigan in the U.S., have been adapted and used in studies measuring teacher knowledge in several countries around the world. In the adaptation, many of these studies relied on comparisons of item parameters and none of them considered a comparison of raw data. In this article, we take advantage of having access to the raw data from the adaptation pilot studies of the same instrument in Norway and Slovakia (149 practicing elementary teachers in Norway, 134 practicing elementary teachers in Slovakia) that allowed us to compare item parameters and teachers’ ability estimates on the same scale. Statistical analysis showed no significant difference in the mean scores between the Norwegian and the Slovak teachers in our samples and the paper provides further insight into the issues of cross-national adaptations of measures of teachers’ knowledge and the limitations of the methods commonly applied in the item adaptation research. We show how item adaptations can be refined by combining robust quantitative methods with qualitative data, how decisions on adaptation of individual items depend on context and purpose of the adaptation, and how comparability and heterogeneity of samples affects interpretation of the results.

Introduction

Teachers play an important role in student learning but identifying quality teaching is not straightforward. A large study involving more than 3000 U.S. teachers revealed that teachers identified as more effective by measures of effective teaching achieved higher student gains throughout a school year than teachers identified as less effective (Kane et al., 2013). These researchers also found that gains persisted when the same teachers were randomly assigned new students the following school year. Taken together, these findings demonstrate that effective teaching can be measured.

In mathematics, Hoover’s review of research articles (Hoover et al., 2016) that focus on the distinct mathematical knowledge needed in the work of teaching mathematics and published in English in international peer-reviewed journals between 2006 and 2013, revealed 190 published articles. In 99 of these articles, researchers used an instrument to measure teachers’ knowledge, and in 56 of these cases, the instrument employed was non-standardized. Among the authors that used a standardized instrument, the LMT instrument¹ was most prevalent (31 articles), including articles dealing with adaptations of the LMT instrument (Hoover et al., 2016, p. 7).

One reason for the popularity of the LMT instrument are good correlations between teachers’ MKT score and the mathematical quality of their instruction (Hill, Ball, et al., 2008; Hill, Blunk, et al., 2008), and student achievement (Hill et al., 2005). Delaney’s adaptation of the LMT instrument for use in Ireland (Delaney et al., 2008) was the first attempt to use the LMT instrument outside the U.S. His study served as a general guidance to other international researchers in their efforts to adapt the instrument, and numerous facets of the adaptation process have been described in literature since then. Delaney et al. (2008) and researchers from Ghana (Cole, 2012) discussed various aspects of adapting and validating the instrument. Five other research teams have explored the linguistic issues of item translation in Indonesia (Ng, 2012), Malawi (Kazima et al., 2016), Norway (Mosvold et al., 2009), Slovakia (Marcinek & Partová, 2011), and South Korea (Kwon et al., 2012). The goals of the cross-national LMT studies have been to explore and describe proper translation and validation procedures, to analyze item performance in different settings, and to collect qualitative data to reveal cultural differences and nuances. One problem with commonly used quantitative methods is that item parameters in different settings refer to different scales and can sometimes falsely flag items as problematic (false positives) or miss potentially problematic ones (false negatives). Furthermore, as our review of literature shows, even though the LMT instrument is the most frequently used measure of MKT around the world (Hoover et al., 2016), no studies—to our knowledge—involve collecting and analyzing data using the same form in two different cultural contexts.

The aim of this paper is to fill the gap in existing literature by exploring the challenges of using the LMT items for cross-national comparisons of teacher’s MKT. We will do so by examining raw data obtained by the adaptation of the same instrument in two cultural educational contexts—Norway (NW) and Slovakia (SK). The rationale for choosing these two countries is threefold. Firstly, the selection of countries available for such research is limited to countries in which local researchers have already adapted LMT items or had access to such adaptation. Secondly, among such countries, Norway and Slovakia exhibit the most favorable demographic similarities: their official languages are different from English and are being spoken by a relatively small population of almost the same size (5.36 million in NW, 5.45 million in SK (Eurostat, 2019)). These similarities make a comparison of the technical issues of item adaptation and form performance easier. Thirdly, despite demographic similarities, the two countries have considerably different system of elementary teacher education and certification, which will allow us to better model and explore the issues of cross-national comparisons of teacher knowledge around the world.

The primary goal of our study is to use the same LMT form for a cross-national comparison of teachers’ MKT. The focus is on exploring the feasibility and meaningfulness of such comparisons rather than producing generalized rankings. To this end, we will have to review the methods of identifying ill-performing items used in the LMT items adaptation literature and thoroughly investigate the performance of LMT items in the cultural context of the two participating countries. Raw data available for both countries allow us to employ robust statistical methods that can shed more light on the methods commonly used in the literature.

The contribution of our study will therefore have three related aspects. (1) The technical aspect involves reviewing quantitative methods of assessing item performance commonly applied in the literature, discussing their limitations, and using them to identify items that may perform differently in our two countries. (2) The local aspect includes the use of qualitative data to scrutinize problematic items with the goal of capturing cultural nuances in the LMT items and informing decisions as to which items to exclude from the form. The technical and local aspects of our work helped us produce Norwegian and Slovak versions of the original form with very similar psychometric properties. And finally, (3) the global aspect involves the application of the forms with the goal of comparing Norwegian and Slovakia teachers’ MKT and discussing the challenges and pitfalls of using the LMT form for such an endeavor.

We will start by reviewing literature about comparison of teacher knowledge, and methods used in the translation, adaption, and validation of instruments for teacher knowledge around the world, with a focus on the LMT instrument. Cultural variables specific for Norway and Slovakia are also explained, and a description of the sample is given. Because we have used the same form, we can examine the performance of the individual items and the form as a whole. This was done by performing separate sample analyses for Norway (N = 149) and Slovakia (N = 134) along with combined sample analyses using the raw data from both countries (N = 283). We finally use the raw data and information on item performance to attempt a cross-national comparison of MKT of Norwegian and Slovak teachers and discuss the issues and challenges entailed in such an endeavor.

Mathematical knowledge for teaching and measures of teachers’ knowledge

The works of Shulman and colleagues (Shulman, 1986, 1987; Wilson et al., 1987) have triggered a considerable attention of researchers around the world. Shulman’s proposal of categories that constitute the knowledge base of teaching (Shulman, 1987) appealed too many in the field. He introduced the idea of special content knowledge in teaching, and this category of teacher knowledge has been further specified in many subject areas including Social Studies and History (Wilson & Wineburg, 1988), English and Literature (Grossman, 1990), Science (Gess-Newsome & Lederman, 1999), etc. He also introduced the term Pedagogical Content Knowledge (PCK) as “content knowledge that embodies the aspects of content most germane to its teachability” (Shulman, 1986, p. 9). This term is now adopted in the field and according to Google scholar, his 1986 publication has been cited in more than 25,000 articles.²

Despite a shared interest in the work of teaching mathematics, researchers perceive teachers’ knowledge in diverse ways, which eventually led to the development of different conceptualizations of teachers’ knowledge. The Knowledge Quartet, or Knowledge in Teaching (Rowland et al., 2005), Knowledge for Teaching (Davis & Simmt, 2006), Didactic-Mathematical Knowledge, DMK (Pino-Fan et al., 2015) or Mathematics Teacher’s Specialized Knowledge, MTSK (Scheiner et al., 2019) expemplify the diversity of perspectives All these conceptualizations are aimed at understanding the nature of such knowledge: Teachers’ knowledge can be seen as dynamically emerging in various teaching situations (knowledge in teaching), or as a less dynamic part of teacher’s knowledge structure that evolves as the teacher learns (knowledge for teaching) or viewed through the complexity of interactions of knowledge structures, teaching situations and other aspects of teaching (DMK, MTSK). Some frameworks, such as the conceptualizations focused on pedagogical content knowledge (Baumert et al., 2010) and mathematical knowledge for teaching (Ball et al., 2008), included development of instruments for measuring such specialized knowledge.

Among these frameworks, the MKT conceptualization of teacher knowledge, with the associated LMT instrument, tends to be predominantly used in studies of teacher mathematical knowledge for teaching, at least when it comes to studies focused on measuring such knowledge (Blömeke & Delaney, 2012; Hoover et al., 2016). As MKT is a practice-based framework, the knowledge domains are defined in relation to the work of teaching (Ball et al., 2008). By observing classroom teaching in the U.S., Ball and colleagues identified recurrent tasks and problems involved in the work of teaching mathematics and thus “framed knowledge in terms of its use—in terms of particular tasks of teaching” (p. 399). They provided a list of recurrent tasks teacher do as a part of their work of teaching mathematics—tasks that are specific to the work of teaching—and this helped them in developing the LMT items to measure this kind of knowledge. The items gave them a way to investigate further the different domains of mathematical knowledge for teaching.

The LMT project is not the only one that employed rigorous item and form design. Other measures of mathematics teacher knowledge spanning various grade levels have been proposed. The COACTIV instrument was designed to study how secondary teachers’ competence affects classroom practice and student learning outcomes (Kunter et al., 2013), and the Diagnostic Science Assessments for Middle School Teachers (DTAMS) captures knowledge of middle school teachers to study its strengths, weaknesses and growth (Saderholm et al., 2010). Measures that focus on a specific content topic or facet of teacher’s work have also been developed (Chick, 2009; Herbst & Kosko, 2012; Hoover et al., 2014; Izsak et al., 2012; McCrory et al., 2012; Thompson, 2015; Zodik & Zaslavsky, 2008).

With respect to our study, The Teacher Education and Development Study in Mathematics (TEDS-M) deserves special attention as it is the only project that attempted to use measures of teacher knowledge for cross-national comparisons (Tatto et al., 2012). TEDS-M was conducted in 17 countries in 2008 and provides a review of educational systems, conditions for teachers’ work, teacher education programs and practices, and the characteristics of teacher candidates in each of the 17 countries. The TEDS-M framework for measuring knowledge shares commonalities with the TIMSS studies (for example, the descriptions of the cognitive domains) and some items were obtained from the LMT project (Döhrmann et al., 2012; Tatto et al., 2012). The TEDS-M team designed the items to address two major knowledge areas—mathematics content knowledge (MCK) and mathematics pedagogical content knowledge (MPCK) that were further elaborated into seven subdomains.

Instrument translations, adaptations, and validations

The arguments made for teaching being a cultural activity (Stigler & Hiebert, 1998) underscore the importance of questioning the validity and utility of MKT measures adapted for use in new settings. Research has shown that the characteristics of the work of teaching differ across countries. Variations have been documented in the content covered and the way new concepts are introduced, in procedural complexity, individual student work, blackboard use, homework and listening practices, to name a few (Andrews, 2011; Hiebert et al., 2003; Pepin, 2011; Santagata & Stigler, 2000). Validity studies are thus an important segment of the LMT instrument adaptations research aimed at addressing crucial questions: Are the adapted LMT items measuring the same construct as in the U.S.? Can they be used in other settings to measure the MKT—its level or growth—the same way they are used in the U.S.?

The literature on the design and adaptation of the LMT instrument offers several approaches to addressing the validity concerns. In designing the LMT instrument, Schilling and Hill (2007) referred to Kane’s (2008) argument-based approach to validation and they described a framework consisting of three assumptions that need to be addressed. First, designers and adapters of MKT measures need to ensure that individual items properly tap into the MKT, i.e., knowledgeable respondents will choose a correct answer while respondents who lack the knowledge will not (the elemental assumption). Second, they need to ensure that MKT forms capture an adequate image of the entire MKT domain or its subdomains, so that a respondent’s score obtained from an MKT form can be interpreted as the respondent’s overall MKT score or a respective subdomain score (structural assumption). Third, test designers and adapters need to ensure that the respondents’ MKT scores are related to their effectiveness in the classroom (ecological assumption). In testing the elemental assumption, the LMT instrument designers used cognitive interviews to explore how answering the LMT items relates to the respondents’ underlying knowledge. The designers addressed the structural assumption by the interpretation of factors revealed in a factor analysis (Hill, 2007; Hill, Ball, et al., 2007; Hill, Dean, et al., 2007; Schilling & Hill, 2007). Finally, to test the ecological assumption, they used criterion-based validity checks. Video validation study, for example, explored if teachers’ MKT scores correlate with mathematical quality of their instruction (MQI) and the analysis of student gains was used to reveal how higher MKT scores correlate with student learning (Hill, 2007; Hill et al., 2007a; Hill, Ball, et al., 2008; Hill, Blunk, et al., 2008; Hill, Dean, et al., 2007).

In his validation study of the LMT instrument adapted for the use in Ireland, Delaney (2012) employed three methods to investigate the validity issues. He interviewed five teachers to explore the consistency of their thinking and chosen answers and reported that teachers’ interview responses were consistent with the answers they gave on the test (elemental assumption). He also performed a factor analysis on the responses from 501 Irish teachers to explore how the structure of factors supports the notion of the MKT domains, concluding that the revealed factors are similar to those found in the U.S. (structural assumption). Finally, Delaney used the MQI protocol to analyze video recordings of lessons taught by 10 teachers to capture the relationship between the teachers’ MKT and MQI scores and reported that only half of the video-recorded teachers showed a positive relationship between MKT and MQI scores (ecological assumption). He thus concluded that although items “appeared to elicit the kind of thinking about mathematics and about teaching that was anticipated,” the inconsistent MKT and MQI relationship illustrated the “challenges in validating the use of test results when measures are adapted and transferred to a new setting” (Delaney, 2012, p. 439).

In her validation study of the use of LMT items in Ghana, Cole (2012) focused on the elemental assumption and interviewed three teachers to reveal the knowledge they used when responding to the LMT items. Similarly to Delaney’s findings, most of the items were eliciting the intended kind of knowledge and could be used in Ghana. Yet, some items provided evidence of “cultural incongruence” Invalid source specified. of the contexts in which these items were presented. In summarizing her study, Cole argued that the LMT items, as originally adapted, may be better at identifying high-scoring Ghanaian teachers, while the LMT items may be a less valid measure for low MKT levels.

The validity considerations in the TEDS-M project pertain to the content validity of their MCK and MPCK measures. The TEDS-M team employed statistical methods, such as reliability analysis, factor analysis, and Item Response Theory (IRT) items parameters analysis, to support the MCK/MPCK conceptualization and evidence the validity of their measures. They also commissioned expert panels to examine the content and appropriateness of items (Tatto et al., 2013). Addressing the elemental and ecological assumptions, such as how the responses relate to the respondents’ actual knowledge or how MCK and MPCK measures correlate with some external criteria that speak to the teacher candidates’ success in their teaching career, was not among the TEDS-M objectives. This can be viewed as unproblematic as the interpretation of their results does not go beyond the specific purpose, for which the MCK and MPCK measures were designed. According to Tatto et al. (2012), the specific project aim was to explore the correlation between the opportunities to learn offered to teacher candidates across teacher education institutions with the knowledge for teaching mathematics that the candidates possess at the end of their teacher education.

Researchers from non-English speaking countries face additional challenges, as the validity of the instruments strongly depends on the translation quality, i.e., linguistic equivalence (Peña, 2007). To this end, the TEDS-M team designed specific translation and adaptation guidelines and employed rigorous external translation verification process (International Association for the Evaluation of Educational Achievement (IEA), 2007; Malak-Minkiewicz & Berzina-Pitcher, 2013). Mosvold et al. (2009) referred to the PISA Technical Reports (Adams, 2014) as a guide to ensure linguistic equivalence of the adapted LMT items. They emphasized the importance of two independent translations followed by reconciliation.

The validity of the LMT instrument, as it relates to our study, has several aspects. Unlike large international comparative studies, the motivation for the adaptation of the form, and data processing and interpreting, was local and independent of other countries. The fact that the decisions to adapt the instrument were made locally indicate that the national experts who reviewed the instrument arrived at a conclusion that the adaptation efforts are worthwhile, and the instrument is likely to capture important aspects of the work of teaching in our specific settings. Local data processing and interpreting implies that the primary focus of the pilot studies was on a thorough review of the instrument performance in the new setting. A local focus marks a clear distinction between studies such as ours and international comparative studies commissioned by supranational organizations or consortia. Such studies have been criticized for ignoring many local aspects and concerns (Keitel & Kilpatrick, 2001).

We examined the LMT items included on our form to reveal the differences in their performance in two cultural settings and shed light on the meaningfulness of cross-national comparisons of teachers’ knowledge. Our aim was not to make any inferences about how effective Slovak and Norwegian teachers are and, in this regard, our validation methods were similar to those in the TEDS-M study, focusing on the content and linguistic equivalence.

Cultural variables: primary education and teacher education

In this section, we outline major similarities and differences in school and teacher education systems in our two countries. As the discussion in this paper cannot comprise all cultural nuances, we will focus on those that are either important for understanding our later discussions (grade spreads and content differences) or can further describe the diversity of our samples and understand the basis for cultural specificity of the measures of teachers’ knowledge (the scope of mathematics teacher education and its historical trajectory).

In the TEDS-M international report (Tatto et al., 2012), the challenges posed by different grade spreads covered in teacher education have been described. Such challenges are clearly present in our study as well. Using the TEDS-M program-type group classification, the Norwegian primary teachers are classified as “Primary/lower-secondary generalists (grade 10 maximum)”, while the Slovak primary teachers are “Lower-primary generalists (grade 4 maximum)” (p. 36).

Content and standards for primary mathematics in Slovakia and Norway are set forth by national institutions (The Norwegian Directorate for Education and Training in Norway, Ministry of Education in Slovakia) and show many similarities. The Norwegian standards (Utdannings direktorated, 2019) are, however, more general, while the Slovak ones (Štátny pedagogický ústav, 2014) provide greater details. Textbook market in Slovakia is regulated and textbooks have to be approved by the Ministry of Education for compliance with the Program. Such regulations are absent in Norway and primary mathematics textbooks show a greater diversity. As a consequence, some topics have more consistent coverage in Slovakia and most teachers spend significant time teaching them, while the same topic may not be taught by many Norwegian teachers at all. For example, the competence aims after 4th grade in the Norwegian curriculum that relate to synthetic geometry state that students should be able to “draw, build, explore and describe geometric shapes and models in practical contexts, including technology and design”. On the other hand, 4th grade Slovak standards specify elements of synthetic geometry that students need to master: Using compass to construct a circle with a given center and radius; Using straightedge and compass to construct a triangle given three sides; Finding a graphical sum and difference of two line segments, and a multiple of a given line segment; Constructing a triangle perimeter, etc. Elements of synthetic geometry is an example of a topic that is very explicit in Slovak standards, assumes considerable instructional time and, as we will discuss later, Slovak teachers perceive it as an important part of the Slovak mathematics curriculum.

Mathematics teacher education in Norway

One factor that has shaped the requirement for teachers and teacher education in Norway is the development of compulsory schooling. While compulsory schooling was introduced in Norway in 1736, the current format with ten years compulsory school and school start at age six was introduced in 1997 (Jakobsen & Munthe, 2020). The changes in teacher education have been tremendous. Only a couple of decades ago, it was possible to become a qualified mathematics teacher in primary education grades 1 − 9, with only a short course in the didactics of mathematics as part of teacher education (Hoover et al., 2016). This contrasts with the most recent reform of Norwegian primary and lower secondary teacher education implemented in 2017, where teacher education is a five-year master’s program guided by national curriculum regulations (National Council for Teacher Education., 2016a, b).

All teachers that participated in this study were educated under the teacher education program that was in place prior to 2010. At that time, there were three major tracks for pre-service teacher education in Norway. The largest track (in terms of number of students) was a general teacher education program (ALU) for teachers in the compulsory school (grades 1–10). This was a four-year concurrent program that educated and certified teachers to teach children in all school subjects both in primary school (grades 1–7) and lower secondary school (grades 8–10). The ALU program included teaching practicum every year (20–22 weeks divided over four years), and all students had to complete a minimum of 30 ECTS³ mathematics credits (Mathematics 1, equivalent to half a year of study). This was an integrated mathematics and education course, strongly linked to the school content. It was also possible to opt for additional 30 + 30 ECTS credits mathematics (Mathematics 2 and Mathematics 3). For teacher education prior to 1992—when it was made by law into a four-year program—the amount of compulsory mathematics was even less than 30 ECTS credits.

There were also two additional tracks that qualified candidates to teach in lower and upper secondary schools (grades 8–13). Track two was a consecutive path, where students first studied mathematics and another subject, obtaining a master’s degree in mathematics or in the other subject. It required a minimum of 60 ECTS of mathematics as part of the master’s program. After gaining the master’s degree, these students had to take a one-year postgraduate course which consisted of pedagogy (30 ECTS credits), subject matter methods (didactics), and field practice (30 ECTS credits) in order to become qualified as teachers. Finally, around 2000, some universities started offering concurrent master’s programs that upon completion qualified the graduates to teach in grades 8–13, but none of the teachers in our sample completed this track.

Mathematics teacher education in Slovakia

Lower primary education in Slovakia comprises grades 1 − 4 (age 6 − 10). The National Educational Program sets forth the standards for each content area (Numbers and Operations, Geometry and Measurement, Applications of mathematics and mathematical literacy). The teacher education in Slovakia was also shaped by several reforms, but unlike in Norway, more recent reforms generally reduced the mathematics coursework needed for graduation and teacher certification.

The education reform in 1976 introduced a nationally unified mathematics teacher education. The structure of the mathematical preparation of primary teachers (grades 1 − 4) included a fixed combination of (an equivalent of) 12 ECTS of Elementary Arithmetic, 4 ECTS of Elementary Geometry, 10 ECTS of Didactics of Mathematics, and 3 ECTS of Capstone Mathematics seminar. The total of 29 ECTS was equivalent to around 17% of all hours required for graduation.

After 1989, teacher education colleges were allowed to diversify their mathematical course offerings. For example, primary (1 − 4 grade) programs replaced the required capstone seminar with electives, the content of which varied across colleges and reflected what teacher education programs valued: Remedial mathematics, State Examination review courses, or coverage of underrepresented mathematical disciplines such as data and probability, graph theory, functions, etc. In general, total mathematics ECTS ranged from 27 to 31 and made up about 12% of all hours required for graduation.

The Slovak University Act in 2001 brought about the adoption of the ECTS credit system. Fixed course sequence was replaced with required courses, a range of required electives, and free electives for students to choose from. Required courses, together with the minimum required electives, comprised about 12% of all credits required for graduation.

Prior to enacting a three-stage college education (Bachelor’s, Master’s and Doctoral) in 2005, all teacher education program graduates were awarded the master’s degree (four years for 1 − 4 and five years for 5 − 12 teaching programs). Since 2005, 3-year bachelor’s programs (Pre-school and Elementary pedagogy) and 2-year master’s program (Primary Education and Teaching) were introduced. Credit hours for mathematical courses also changed. Bachelor’s programs focus on pre-school mathematics and mathematics pre-requisites for the master’s degree programs, as only graduates with a master’s degree can be certified teachers. Required mathematics courses and the minimum required electives made up 8% of all credits required for graduation in bachelor’s programs. In Master’s programs, students needed to obtain 23 − 29 credits in mathematics and didactics, which amounts to 12 − 17% of all credits required for graduation. This does not include practicums and student teaching.

After the complex accreditation process in 2009, many colleges started to emphasize pre-school pedagogy in bachelor’s elementary education programs and hours for mathematical courses declined. Mathematical courses in bachelor’s programs range from 11 to 21 semester hours, and master’s programs range from 8 to 24 semester hours, depending on the institution. Thus, certified teachers could have as few as 19 ECTS of mathematics and didactics of mathematics, but often have more.

Examples of the differences in the mathematics teacher education and their historical trajectories in our two countries help us understand the diversity of our teacher populations and the importance of careful consideration of the cultural specificity of measures of teacher knowledge. Contrast in certification grade bands, different composition of teacher education and requirements for mathematics coursework, and overall trends in mathematics education of primary teachers brought about by reforms illustrate important cultural differences that exist in our two countries and outline a basis for cultural differences in the practice of teaching mathematics.

Methods

A complete form with LMT items was chosen for translation and adaptation in Norway and Slovakia. The form⁴ was selected because it contained items for all three content areas, for which the LMT project had developed items—number concept and operation (26 items), geometry (19 items), and patterns, functions, and algebra (16 items)—61 items in total, distributed over 30 item stems. All three content areas are important for both the Norwegian and the Slovak primary school curriculum. Both research teams included researchers properly trained for the administration of the LMT form.

Both Norway and Slovakia are situated in Europe—Norway in the north and Slovakia in the central part of Europe. In Norway, the spoken language is Norwegian—a north-Germanic language, and in Slovakia the Slovak language is used—a Slavic language. The items were first translated and adapted independently from U.S. English to the Norwegian and Slovak language. This was followed by independent pre-pilot studies with five practicing teachers in Norway and six practicing elementary teachers and one teacher educator in Slovakia. The teachers had different teaching experiences and reflected on items’ content, context, wording, or other aspects of the translation.

Discussions of content validity of the adapted LMT form have been separately reported for the Norwegian and Slovakian case (Fauskanger et al., 2012; Fauskanger & Mosvold, 2012, 2015; Jakobsen et al., 2011; Marcinek & Partová, 2011, Mosvold et al., 2009). In both countries, four aspects that speak to the content validity and linguistic equivalence of our adaptations of the form were reported. First, local experts in mathematics teacher education thoroughly reviewed all items, focusing on content and context appropriateness, before the decision was made to adapt the instrument. Second, the rigorous translation and adaptation process involved independent translators and expert reviewers of the translated items (Mosvold et al., 2009, Marcinek & Partová, 2011) and provides compelling case for quality translations of our instruments. As these efforts were taking place independently in Norway and Slovakia, we compared the Norwegian and Slovak version of the translated items to document any deviations in the items as a result of adaptations. Third, after piloting the items, interviews with a subsample of teachers in both Norway and Slovakia provided qualitative data for assessing various aspects of our form, such as content coverage and test parameters (format, length, clarity of questions and distractors). The Norwegian researchers also analyzed response patterns to explore the elemental assumption (Jakobsen et al., 2011; Fauskanger & Mosvold, 2012, 2015). Fourth, IRT psychometric analysis provided statistical indicators of the instrument performance and allowed for comparison of these parameters with the original U.S. form.

Upon the pre-pilot completion, 149 teachers in Norway and 134 teachers in Slovakia participated in a pilot study. The Norwegian sample was a convenience sample (Bryman, 2004) comprising of teachers recruited from 19 schools in the region close to the researchers’ university. In Slovakia, efforts were made to sample different geographical areas, including areas where minority languages are used alongside the official Slovak language. However, the representation of these areas may not satisfy the requirements of a truly national sample. A demographic survey administered at the beginning of the testing session contained various questions regarding respondents’ education, grades they teach currently and have taught in the past, years of experience, professional development completed, etc.

Table 1⁵ summarizes years of experience of the Norwegian and Slovak respondents and grades in which they teach.

Table 1 Current Grades Taught and Years of Experience of the Norwegian and Slovak Sample

All respondents in Norway completed a paper-and-pencil test at their respective schools proctored by one researcher. In 7 of the 19 schools, semi-structured interviews with 15 of the participating teachers took place immediately after the teachers had finished the test. In Slovakia, most teachers took a computer-based test at a proctored location, with some teachers taking a proctored paper-and-pencil version of the test at their schools. Thirteen teachers in one school participated in a semi-structured interview after finishing the test and five additional teachers from different schools were interviewed within a week of taking the test either in person or through Skype. After analyzing the pilot results, ten additional teachers were asked to answer only the flagged items and were subsequently interviewed. The analysis of the test answers and interviews obtained in the pilot study in Slovakia verified that the test mode (computer-based vs. paper-and-pencil) did not significantly affect response patterns.

In this study, we applied two separate analyses to examine the methods of identifying ill-performing items typically used in the LMT items adaptation literature. First, our pilot studies employed a two-parameter IRT model⁶—the same model as originally used in the U.S. (see, for example, Hill, 2007; Hill, Ball, et al., 2007, 2008; Hill, Dean, et al., 2007; Hill, Blunk, et al., 2008) to recover items’ difficulties. The difficulty parameter b is calculated on the same scale as the respondent’s ability⁷ θ (MKT score in our case). A person with the ability θ has a 50% chance to correctly answer a question with difficulty b = θ. The parameters are scaled so that the average θ for the entire population is 0 and the population standard deviation is 1. The slope parameter, sometimes referred to as discrimination parameter, describes how well an item discriminates among respondents with similar ability. We used the IRT parameters recovered in the pilot phase to calculate the differences of item difficulties in NW and SK. In the LMT item adaptation literature, items with large differences in difficulty were flagged as potentially problematic. This method does not require an access to raw data for both countries.

Second, we took advantage of having raw data for both national samples (N = 283) and applied a robust differential item functioning (DIF) analysis. DIF methods originated in the efforts of test designers to control test bias. Zieky explains that “Differential item functioning (DIF) occurs when people of approximately equal knowledge and skill in different groups perform in substantially different ways on a test question.” (Zieky, 2003, p. 2) For example, an item might be problematic if top-scoring respondents in one group answer an item incorrectly, while top-scoring respondents in the other group answer it correctly. DIF analysis evaluates such differences for various ability levels and an item that exhibits DIF is a candidate for a biased item.

The performance of DIF methods is typically examined with at least 100 − 200 cases per group Invalid source specified.. Although our national samples satisfy these conditions, some of our subgroups are much smaller. In a recent simulation study, Belzak (2020) explored the usability of these methods on smaller samples. He showed that “moderate levels of intercept DIF can be consistently recovered in sample sizes as low as 50 − 100 cases (25 − 50 in each group)” if parsimonious (less complex) models are used Invalid source specified.. We applied a one-parameter DIF analysis in our study to be consistent with these findings.

These methods helped us (1) identify items that may perform differently in Norway and Slovakia and (2) examine the effectiveness of the methods of identification of ill-performing items typically used in the LMT items adaptation literature. Qualitative data collected as part of the pre-pilot and pilot studies assisted us in the interpretation of the result of these quantitative analyses. Teachers who responded to the form were asked to elaborate on selected items that they perceived as either “too hard”, or “too easy”, or that exhibited different difficulty profiles when compared to the U.S. original. Slovak respondents were also asked to comment on items with different difficulty profiles between our two countries. After we identified problematic items, we interviewed ten teachers in Slovakia who were not part of the pilot study and asked them to solve the problematic items as part of the interview. These interviews gave us an insight that turned out to be indispensable for our understanding of how these items trigger our teachers’ responses and how these triggers relate (or do not relate) to knowledge of mathematics for teaching.

After careful consideration of item performance, we compared Norwegian and Slovak respondents’ MKT scores. Instead of focusing on generalized inferences about the performance of the two groups, we carried out several data simulations to explore how items that do not perform comparably and heterogeneity in our populations affect the ability estimates and their interpretation.

Results and discussion

We start by first presenting what we learned from examining adaptation methods used by researchers around the world, and what we can conclude about the performance of problematic items from a robust DIF analysis followed by the examination of our qualitative data. We then compare the performance of the Norwegian and Slovak teachers, with the goal of assessing the feasibility of such comparisons.

Instrument and item performance

No matter how accurate, the translation, localization, and adaptation process cannot guarantee that the translated items will be measuring teachers’ MKT in a new cultural setting the same way they do in the U.S. To explore the performance of translated and adapted items, researchers around the word have pilot-tested the items with practicing teachers on samples ranging from 60 teachers in Ghana (Cole, 2012) to 210 in Indonesia (Ng, 2012). A common practice has been to retrieve psychometric (IRT) properties of individual items and compare them to the parameters of the original U.S. items. Point-biserial correlation is another parameter widely used to assess item performance. However, one disadvantage with this method not mentioned in the literature is that the psychometric parameters are not reported on the same scale, as the authors did not have access to the U.S. raw data and estimation of psychometric parameters is done relatively to the two samples. Raw data from both our countries enables us to investigate the effect of this disadvantage on the evaluation of item performance and bias.

Point-biserial correlation

In Classical Test Theory (CTT), the point-biserial correlation (r_pbi) is an item discrimination parameter as it allows to evaluate the degree to which an item can discriminate between more knowledgeable and less knowledgeable respondents. Negative r_pbi values of an item indicate that knowledgeable teachers are likely to answer this item incorrectly (and vice versa) and the item may not measure the intended construct. Items with r_pbi values around zero show no correlation between how the respondents answer the item and their overall knowledgeability. In other words, by singling out such an item, we cannot say if the teacher who answered it correctly is indeed more knowledgeable overall than the one who provided an incorrect answer.

Researchers who analyzed LMT item properties flagged all items with negative r_pbi values as poorly functioning (Fauskanger et al., 2012; Marcinek & Partová, 2016; Delaney et al., 2008; Kwon et al., 2012; Ng, 2012). Additionally, some authors provided scatter plots, performed a Fisher Z transformation on the r_pbi values to place them on the interval scale, identified outliers and reported the correlations between r_pbi values of the items in the U.S. and those used in their country (Delaney et al., 2008; Ng, 2012).

As none of our items exhibited negative r_pbi values (either for separate or combined samples), we extended the analysis and scrutinized items with r_pbi ≤ 0.1. This method flagged one item in Norway (Item 39, r_pbi = 0.094) and two in Slovakia (Item 21, r_pbi = 0.063 and Item 37, r_pbi = 0.1), which will be discussed in a greater detail later. Correlation between r_pbi values of Slovak and Norwegian items is moderate, although markedly higher than the correlations reported in the pertinent literature (Table 2). When performing the same analysis on the combined sample, all items had r_pbi > 0.1.

Table 2 Point-biserial Correlation Values Reported in the Literature on Adaptations of the LMT Items

IRT parameters

The original LMT items and forms designed in the U.S. were calibrated using a two-parameter IRT model. IRT has therefore been used as the primary tool for statistical assessment of the adaptation quality. Depending on the size of their pilot study sample, researchers use either one- or two-parameter IRT models. Even if two-parameter models are used, only the difficulty parameters are analyzed, and the discussion of the slope parameters is rare (Jakobsen et al., 2011), mostly due to the limits posed by sample sizes.

Distribution of item difficulties across the ability spectrum is an important indicator of instrument performance. Ideally, an instrument should contain items ranging from very easy to very difficult, with higher frequencies between the extremes. If the translated items have their difficulty parameters distributed in a narrow interval or if the interval is shifted toward one end of the ability spectrum, the instrument will not be able to distinguish between more and less knowledgeable respondents in some parts of the ability spectrum. Results from the separate samples analyses in Norway and Slovakia shows that both adapted instruments (Norwegian and Slovak) are appropriately distributed over the ability spectrum (see Fig. 1).

Fig. 1

Distribution of Item Difficulties in Norwegian and Slovak Adaptations

Distributions of item difficulties, however, do not compare the performance of specific items in the two separate samples. An attractive feature of IRT is item parameter invariance (Rupp & Zumbo, 2016), indicating that the item parameters do not depend on the respondent group. Of course, in practice, a perfect invariance is rarely achievable, and researchers have used item difficulty correlation and scatter plot to evaluate the “closeness” in instrument performance. A good correlation between the reported item difficulties in the U.S. and the item difficulties estimated in the adapted country is used as an indication that the adapted instrument is performing similarly in the new context (e.g., Fauskanger et al., 2012; Delaney et al., 2008; Ng, 2012). This has been done even if the item difficulties reported are not referring to the same scale, and it was initially done in separate sample analyses by the Norwegian and Slovak researchers (see e.g., Fauskanger et al., 2012; Marcinek & Partová, 2011). They reported a correlation of r = 0.812 (p < 0.005) (Norway-U.S.) and r = 0.671 (p < 0.005) (Slovakia-U.S.). The correlation between Norwegian and Slovak item difficulty is r = 0.766 (p < 0.005) for all items or r = 0.883 (p < 0.005) after removing the items identified as problematic.

Discussion of critical items

Our data allow us to apply the separate sample analysis methods of identification of problematic items commonly used in the LMT adaptation literature and compare them to the DIF method afforded by the raw data. In DIF analysis, Norwegian and Slovak respondents are arranged in groups according to their ability and then Norwegian and Slovak respondents with similar ability are compared. If respondents with similar ability answer an item differently, then DIF flag is raised, and the item needs to be scrutinized for a possible bias. Such stratification of respondents with respect to their ability provides a much more robust way of identifying biased items than a simple comparison of item difficulties commonly used in LMT adaptation research. To illustrate problems that may arise by applying methods based on difficulty differences, we provide a scatter plot (Fig. 2) showing the relationship between the difference of Norwegian and Slovak item difficulties and total $\chi^{2}$, a common indicator of DIF.⁸

Fig. 2

Scatter plot of IRT difficulty difference vs. DIF

The plot helped us identify groups of potentially problematic items:

• Problematic items Items with large differences in IRT difficulties and large DIF. These items are strong candidates for incongruent items—items with underlying cultural differences. After a thorough review, these items were listed for removal from the form. Problematic items are marked with .

• Potentially problematic items Items with higher DIF values relative to most of the items on the form. Relatively higher DIF values may indicate potential bias and these items also needed to be reviewed. Their review, however, did not result in a definite consensus whether they should be removed from the form. These items are marked with .

• False positives Items with large differences in difficulties and small DIF. This indicates that the methods based on comparing IRT difficulties flag these items as incongruent, yet the DIF does not corroborate this evidence. Qualitative analysis is needed to gain further insight. These items are marked with .

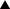• False negatives The methods based on comparing IRT difficulties do not indicate problems (the difference in difficulties is small), yet DIF shows that these items can potentially be problematic (relatively large DIF). Item 50 landed in this region and requires further attention. It is marked with .

All items not included in the above groups were identified by the quantitative or qualitative methods as unproblematic. Criteria for inclusion into the above groups involved both quantitative indicators (position of items in the scatter plot) as well as qualitative data to further inform the decision. Thus, the boundaries between the categories cannot be unambiguously delineated based solely on quantitative thresholds, and some items were considered unproblematic despite their proximity to items included in the discussion.

False positives

False positives are the items that were flagged as problematic by the difficulty difference method although DIF values do not suggest problems. Items 10, 27, 36, 38 and 55 appear in the false positive area, and the analysis of the qualitative data confirmed that their large difficulty differences are caused by different difficulty scales rather than underlying cultural differences in the practice of teaching mathematics. The DIF analysis supports this conclusion. Items 39, 21 and 37 also fall into the false positives area but we will discuss these items in greater detail as they also exhibit near zero r_pbi values and may involve some other issues. We will also discuss Item 15 as it shows an interesting case for the teachers’ knowledge of fractions.

Item 39 was one of four items from an item stem⁹ that focused on polygon definitions and properties, but only Item 39 exhibited r_pbi < 0.1 in the Norwegian sample (0.094; r_pbi of the remaining three items ranged from 0.22 to 0.36). Fauskanger et al.Invalid source specified. discussed the poor performance of Item 39 in the context of the stem and concluded that Norwegian teachers rely on definitions provided by textbooks and consequently tend to label items involving polygon definitions and hierarchy as hard. Our interpretation is a bit more complicated. If these items were indeed hard as suggested by teachers in the interviews, then it would be reflected in difficulty values and success rate. This, however, is not the case. The difficulty values of all items in the stem are negative (“easier than the average”) and success rates are high (56%—91%). It is possible, however, that such items do not correlate well with the rest of the form simply because they tap to the knowledge that is used inconsistently in school mathematics. For example, some Norwegian textbooks discuss inclusive definitions of quadrilaterals while some stick to the exclusive ones. If this is the case, then the success of teacher’s response to such items reflects their exposure to different perspectives on quadrilateral definitions and may not be correlated with their overall MKT as measured by the remaining items on the form.

Item 21 and Item 37 show a rather low r_pbi for the Slovak sample (0.063 and 0.1, respectively). Appendix (Item 21) shows an item similar to Item 21. More than a half of Slovak teachers chose an incorrect answer (3). When interviewed, many of them saw 15 + 15 + 15 in both diagrams and ignored other important properties. When told that diagram A represents 3 × 15, they readily understood their error but pointed out that they were not familiar with such representation of multiplication and simply overlooked the differences. On the other hand, about one quarter of teachers answered this item correctly, including teachers who scored low overall. Interviewed teachers who answered the item correctly understood the difference between the representations and were able to pick a correct one.

Item 37 is illustrated with a similar item in the Appendix (Item 37). It turns out that the term used in the Slovak form for a “rectangle” (pravouholník)—defined hierarchically to include squares—teachers do not always understand as a quadrilateral or quadrilateral with all right angles. For example, a right triangle and right trapezoid were also incorrectly mentioned as examples of a “rectangle” in the interviews. When talking about rectangles, many interviewed teachers (including highly knowledgeable ones) used a different term, which includes rectangles but not squares (obdĺžnik, the term can be described as a “rectangular oblong”). If the term “rectangle” (pravouholník) was substituted with “rectangular oblong” (obdĺžnik) in the item, these teachers would be more likely to choose a correct answer. On the other hand, 44% of Slovak teachers (including low scoring ones), were likely aware of the proper rectangle definition and answered the question correctly.

The awareness (knowledge) of the Slovak inclusive definition of a rectangle (Item 37), and the area representation of the distributive property (Item 21) appear to be “randomly distributed” among knowledgeable and less knowledgeable teachers. This may indicate inconsistent exposure to these concepts and models, and opportunities to learn them. Slovak experts who reviewed these items agreed that these items are unproblematic as they tap into important pieces of professional knowledge that teachers should have. The r_pbi flags were therefore considered false positives and further investigation into possible factors, such as treatment of the topics across teacher education programs or in school textbooks, was recommended (Marcinek & Partová, 2016).

Item 15, together with Items 17 and 25 that exhibit relatively larger DIF, make an interesting case for teachers’ knowledge of fractions. Elementary mathematics standards (grades 1 − 4) set forth by the Slovak National Education Program refer only to propaedeutics of fractions (focusing on visual representations) without any expectations for symbolic manipulation or operations. This was clearly reflected in the surveys, where the Slovak teachers indicated undue emphasis on “working with fractions” at the expense of other parts that are more relevant to teaching elementary mathematics in Slovakia, such as synthetic geometry.

It is therefore natural to expect that these problems will be harder for Slovak teachers. Interestingly, items 17 and 25 (Appendix, Item 17 and 25) confirm this hypothesis, but item 15 (Appendix, Item 15) shows the opposite effect. Although rather difficult in both countries, it turns out to be easier for Slovak teachers. This item asks teachers to reflect on a fraction division procedure that is very unusual. Albeit mathematically correct, it is rarely discussed in primary classrooms as it often results in fractions with non-integers in the numerator or denominator.

Distribution of answers (Fig. 3) suggests an explanation. Only a small portion of teachers thought the answer is incorrect (d). But while the majority of Norwegian teachers selected that the method does not work (c), answers of Slovak teachers are almost equally distributed among the three remaining options (a − c). As fraction operations are not taught in elementary mathematics in Slovakia, Slovak teachers seem to have an advantage of not being influenced by the “standard textbook” division procedure and seem to be trying to reason about the answer. This echoes the concerns of Norwegian researchers who noticed that for Norwegian teachers, perceived authority of the textbook supersedes appropriate reasoning.

Fig. 3

Distribution of answers to item 15

Problematic items

Analysis of Item 16 confirms the adaptation concerns raised by Slovak researchers (Marcinek & Partová, 2011). The item asks teachers to interpret a subtraction algorithm from a student’s artifact. The original U.S. item contains an algorithm that is uncommon in the U.S. and Norway but is a standard one in Slovakia (students learn it that way). The Slovak researchers, therefore, decided to adapt the item and change the algorithm to the one typically taught in the U.S., yet uncommon in Slovakia. However, the Slovak pre-pilot indicated that the “U.S. algorithm” posed little interpretation difficulties for Slovak teachers, as they were either familiar with it or they did not have problems to link the algorithm to base-10 modeling. The quantitative analysis clearly confirms this concern. While the item ranks 17th in the item difficulty ranking in Slovakia (i.e., relatively easy for Slovak teachers), it ranks 59th in Norway (the 3rd most difficult item for Norwegian teachers) and the item exhibits considerable DIF.

Lack of explicitly stated item intent also played a role in adaptation problems in Slovakia. The general intent is clear as the teachers are asked to interpret an algorithm that is not typically taught in schools. Yet, it is less clear if the item is meant to measure teachers’ ability to interpret an alternative common algorithm used elsewhere (i.e., teachers can be familiar with it from the literature or their teacher education and professional development) or simply an algorithm unfamiliar to the teachers (i.e., including artificially constructed algorithms, potentially a work of a student, that are valid but rarely encountered). Similarly, Delaney et al. (2008) noted that the adaptation of some items can be ambiguous, as the items’ intent is not explicitly documented, and researchers have to infer it from the item itself.

Appendix (Item28) illustrates the nature of Item 28. This item ranked 18th in Slovakia, but 56th in Norway (6th most difficult item). Interestingly, the misconception of Slovak teachers about rectangles described above (Item 37) helped them answer Item 28 correctly. For example, a teacher who thinks that right triangles or right trapezoids belong to rectangles will choose the correct answer (“some rectangles can have two or more congruent adjacent sides”). In Norway, many teachers use the word “rectangle” (rektangel) exclusively for “rectangles that are not squares”—a misconception often reinforced by illustrations in children’s mathematics books. Hence, those teachers are likely to choose an incorrect answer. This item is problematic as it gives the Slovak teachers an unfair advantage. Many Slovak teachers answer it correctly not based on their knowledge, but because the item is unable to flag their misconception as incorrect.

Potentially problematic items

We reviewed items 11 and 46, that exhibit relatively higher DIF and difficulty differences when compared to the rest of the form. Item 46 taps to the same content area as the item flagged as false negative and will be discussed there. Item 11 (Appendix, Item 11) asks teachers to reason about multiplication and its effects. Unlike in Norway, operations in Slovak elementary school do not go beyond the set of whole numbers, in which the statement “multiplication makes numbers bigger” is considered true by many teachers who ignore the effect of multiplying by 0 and 1. But whether this item shows a cultural bias is much less clear. Slovak experts agree that knowing that multiplication can sometimes make numbers smaller is critical. For example, when students come up with similar statements on their own, teachers should be able to respond appropriately, hinting what students will learn in later grades. On the other hand, when this item was discussed for inclusion on an instrument for cross-national comparison of teachers’ knowledge, issues of “fairness” were raised: Although this item is an important piece of professional knowledge and provides us with a valuable information of where our teachers are, comparing their knowledge to a different group of teachers who routinely teach operations in number sets beyond the whole numbers, may give that other group an “unfair” advantage and thus our teachers can unfairly be viewed as inferior with regards to this item.

False negatives

False negatives are the items that were flagged as problematic by the DIF method although the methods based on examining the difficulty differences, commonly used in the MKT adaptation literature, would not indicate issues. Item 50 landed closer to the false negatives area than any other item. The item was a part of an item stem and all other items from the same stem (47, 48, 49) appear in the adjacent region. The discussion below also includes Items 46 and 61 that deal with the same content area and exhibit relatively larger DIF.

These items focus on discovering and describing linear patterns and representing them by equations. Experts in Norway agreed that such knowledge firmly belongs to teachers’ professional knowledge base. The consensus was not that clear among Slovak mathematics educators. Some of them argued that, although discovering and describing linear patterns is an important task of teaching at elementary level, the relationships beyond direct proportion (y = kx) and their representation by linear equations is less relevant. Teachers are not expected to teach it in grades 1 − 4 and their exposure to algebraic equations in their teacher education may also be limited. In other words, although we can expect elementary teachers to be familiar with algebraic representation of linear functions from their high school studies, such knowledge may not necessarily be a valid predictor of how these teachers perform as elementary teachers in Slovakia.

Such lack of expert consensus illustrates an important challenge of identifying problematic items. Expert discussions led to a realization that whether an item is problematic or not depends on the purpose of its use. For example, if the use of the form is meant to be local (e.g., benchmarking teacher’s knowledge to gage its changes), then most Slovak experts did not see the items 46 − 50 and 61 as problematic. However, concerns were raised if they were to be used globally for cross-national ranking as these items could create unfair disadvantage for Slovak teachers.

The described IRT analysis indicated potential cultural differences in the items on the form. Yet, it could not reveal the differences in topics and content areas not represented on the form. For example, synthetic geometry was almost unanimously mentioned by Slovak teachers as the most important curricular area absent from the form. Synthetic geometry is devoted a considerable amount of instructional time (and teacher education coursework) in Slovakia, while it is not represented in Norway until higher grades. This does not indicate problems with the form itself—after all, we want to exclude items that would favor one group over the other—but it poses problems with the interpretation of the comparison results, as we will discuss in the conclusion.

Comparison of teachers’ MKT

Our data allowed us to go beyond item and form analyses that has been previously reported in the literature and compare the performance of the Norwegian and Slovak respondents. Primary teachers in Slovakia teach in grades 1 − 4 while the Norwegian ALU teachers—at the time when this study was conducted—were certified to teach beyond the grade 4 (up to grade 10). To illustrate the challenges in comparing the MKT of such populations, we removed the two problematic items (Items 16 and 28) from the analysis, and compared the following groups of teachers:

• 1. Primary teachers in Slovakia (N = 105). Teachers certified to teach and with experience in teaching grades 1 − 4.

• 2. ALU teachers in Norway (N = 103). Teachers certified to teach and with experience in teaching grades 1 − 10. We segregated this group of teachers further:

  • 2a. Norwegian ALU teachers who have taught only in grades 1 − 4 (N = 33).

  • 2b. Norwegian teachers who teach or have at some point taught beyond the grade 4 (N = 70).

  • 2c. Norwegian ALU teachers who recently taught in grades 1 − 4 but had experience teaching beyond grade 4 in the past (N = 16). This is a subsample of Group 2b.

  • 2d. Norwegian ALU teachers who recently taught in grades 1 − 4 (N = 49). This is Group 2a and Group 2c combined.

Figure 4 provides a visual comparison of the average θ for these groups (plotted with 95% confidence intervals). It shows that although the average θ for NW primary teachers is 0.141 higher than for SK in our two samples (Group 1 and 2), they are not statistically significantly different (p = 0.152¹⁰). Norwegian teachers who currently teach in grades 1 − 4 but had experience teaching in higher grades (Group 2c) have their θ average closest to that of the Slovak primary teachers (the difference is 0.096). Controlling for the same experience and comparing Slovak teachers with Norwegian ones whose experience has been limited to grades 1 − 4 (Group 2a) suggests 0.399 higher average θ for SK teachers, although still within the statistical insignificance (p = 0.103).

Fig. 4

Comparison of average θ of SK primary teachers and selected subgroups of NW teachers

The different θ averages of SK and different groups of NW teachers relative to each other are noticeable and demonstrate the effects of population heterogeneity on statistical measures. Our example thus underscores the importance of careful selection of groups for a meaningful comparison. But the choice of groups for a meaningful and “fair” cross-border comparison is ambiguous at best and exemplifies another challenge of capturing country differences in a single quantitative measure (a country average or “score”). For example, Slovak teachers and teacher educators voiced concerns that it is not “fair” to compare Slovak primary teachers to Norwegian teachers who have had experience teaching above grade 4, due to their different exposure to mathematical concepts in higher grades, i.e., limiting experience to grades 1 − 4 (Group 1 and Group 2a) is the only “fair” option. On the other hand, excluding subgroups from the group of Norwegian teachers who teach in grades 1 − 4 is also problematic, as such exclusion can result in a subsample that is not representative of Norwegian teachers or Norwegian ALU teachers who teach in grades 1 − 4. Small size of Group 2a indicates that such concern is real.

Limitations of the study

Our study took advantage of the availability of raw data from pilot studies of two countries using the same LMT form. The form went through a rigorous process of translation, adaptation, and validation in our respective countries. In Norway, this process was guided solely by local interests and our current study was designed only after the data in Norway had been collected. Data collection in Slovakia was designed to allow for both the local and global purposes.

This specificity of our design leads to several important considerations. On the first hand, Norwegian researchers did not segregate their sample into groups as described in 6.2; such segregation was only needed to allow for meaningful NW − SK comparisons. Moreover, sample distributions (grades, experience, etc.) could only be adjusted in the Slovak sample to match the Norwegian one, which explains why most of the Norwegian subgroups ended up with fewer than 50 respondents. This reduced the sensitivity of some of the statistical methods and, for example. Relatively large confidence intervals for several NW groups seen in Fig. 4 prevented us from making statistically significant inferences.

On the other hand, the process of communication and negotiations between Norwegian and Slovak researchers led us to the realization that even if we increased the size of Norwegian subgroups to carry out statistically more sensitive comparisons, the questions of the “fairness” of such comparisons would still be relative and perceived differently in Norway and Slovakia. This echoes and underscores the concerns of fairness discussed in 6.2: Selecting national samples with proper representation of different groups of teachers who teach in primary grades in our two countries leads to different representation of groups across the two countries and raise concerns in the country, where the experience of primary teachers is strictly limited to grades 1 − 4 (SK). Still, selecting groups with matching grade and experience distributions would greatly underrepresent some groups of Norwegian teachers who teach in primary grades. Thus, it appears that the limitations of this study are not a simple consequence of the research design but rather deeply rooted in the challenges inherent to the cross-national comparisons of MKT. This will likely be the case for any comparison of MKT between countries with differences in primary grade banding, teacher education or certification.

Conclusion

The overarching goal of our study—using raw data from adaptations of the same LMT form in Norway and Slovakia to shed light on potential challenges of comparing teachers’ MKT across the borders—helped us formulate several observations pertinent to such cross-national endeavors.

On the technical level, our investigation of the adaptation of the LMT instrument around the world revealed that quantitative methods of evaluating item and instrument performance that have commonly been applied in previous studies, can potentially be problematic depending on the use of the adapted measures. Methods relying on comparing item difficulties are specifically prone to misidentification of problematic items. In our case, such methods identified nine items as false positives—the items were flagged as problematic, yet the subsequent quantitative and qualitative analysis did not corroborate such evidence. One item was identified as a false negative, meaning the methods applied in the LMT item adaptation literature would overlook it while this and similar items require a careful analysis and consideration for removal.

Availability of raw data allowed us to employ the DIF analysis, which turned out to be a robust tool that yielded results consistent with the qualitative data. This, however, does not diminish the importance of using both quantitative and qualitative methods when making item selection or removal decisions. Quantitative methods sometimes flag items because they are sensitive to differences in what teachers in each country know, while teachers and mathematics education experts agreed that these items are unproblematic for the local use as they tap into important knowledge that teachers should know. This finding was in line with the results reported by Ng (2012), who noticed the implications of the rift between what teachers are required to know and what they should know.

On the local level, we have demonstrated that a thorough review of the LMT items that perform differently in different cultural settings has its own value and merit. Apart from the imperfections of the quantitative methods used in the literature, identification of gaps in teacher knowledge and comparing them to what teachers in other countries know or should know, is one of the most valuable contributions of the literature on the cross-national adaptations of LMT items. Such cross-national application is still local in nature: Researchers in one country compare their results in specific knowledge areas with another country, provide explanations for the knowledge differences and discuss implications for their own local educational practice.

The situation is quite different when an adapted form is used globally to produce a generalized country “MKT score” for comparing teachers’ MKT internationally. Our attempt to do so showed that, after the exclusion of problematic items, the adapted Norwegian and Slovak forms exhibit similar psychometric properties, and the forms could technically be used to compare MKT possessed by Norwegian and Slovak teachers. As presented in Sect. 6.2, we did not find statistically significant differences, and this result seems to be in line with some other measures, such as international comparisons of students’ knowledge: TIMSS 2015 showed no significant difference between the mathematics score of Slovak 4th grade students (M = 498, SD = 2.5) and Norwegian 4^th grade benchmarking population (M = 493, SD = 2.3) (Mullis et al., 2016).

However, we learned that the psychometric congruence of the forms may not suffice to make a comparison of teachers’ MKT in two countries meaningful. The interpretation of the results of such a comparison can be problematic with the challenges stemming from the nature of the knowledge being measured and populations being compared.

One of the challenges concerns the process of decision making regarding the removal of problematics items. We removed items 16 and 28 from the form as there was a broad consensus for their removal. We saw, however, that some Slovak experts raised concerns that items discussed in the False Negatives section may unfairly favor Norwegian teachers and should also be removed. This lack of consensus among Slovak experts was apparent only when these items were considered for cross-national comparisons. Their local use was not seen as problematic.

Achieving broad expert consensus for cross-national comparison would in our case require further removal of items, which in turn would further limit the scope of the form and the richness and diversity of knowledge it elicits. In general, the notion of a cross-national core knowledge base is needed to eliminate the cross-national variability in school mathematics and allow for comparisons (see also Delaney et al., 2008; Döhrmann et al., 2012). Such a notion, however, may turn out to be problematic in comparisons of the MKT as the teachers’ professional knowledge. If we consider Tamir’s (1991) definition that “By professional knowledge we commonly refer to that body of knowledge and skills which is needed in order to function successfully in a particular profession” (p. 263), any “core” teacher knowledge that could be agreed on internationally would constitute necessary knowledge base for being successful in mathematics teaching profession but may not be sufficient. The concern raised by Slovak teachers that our form does not cover synthetic geometry exemplifies the problem: A teacher from one country who receives a very high MKT score on our form may still be unsuccessful in teaching a topic that is specific to the other country’s curriculum and was thus excluded from the form. Benefits of comparing teachers’ core knowledge include identification of areas of strengths and weaknesses and measuring growth in core knowledge in individual countries. However, item removal driven solely by a universal consensus of core knowledge may compromise richness and diversity of knowledge triggered through such items and lead to a loss of some (if not most) of the test’s predictive power as to how successful teachers are overall in their teaching profession. This puts into the question the ecological assumption and thus the very validity of the instrument conceived to measure MKT as the professional knowledge.

Finally, we have shown that heterogeneity in our teacher populations impacted the results and their interpretation, relativized the perception of “fairness” and imposed limits on the research design, especially with respect to the quantitative methods. We have seen that the population of primary mathematics teachers can be heterogeneous and the difference in average ability between primary teachers in Slovakia and Norway can range from positive to negative, depending on other characteristics of the groups. The challenge of selecting “right” groups for comparison is thus real and we saw it manifested in different perceptions of what’s a “fair” comparison. If the purpose of comparison is to produce a generalized country ranking on the international scale, Slovak teachers and teacher educators voiced concerns that comparing Slovak 1 − 4 teachers to some groups of Norwegian teachers is unfair due to different teaching bands and a greater exposure of these NW teachers to more advanced mathematics in their teacher education and practice. On the other hand, constraining the comparison to groups with experience strictly limited to grades 1 − 4 can also hardly be seen as “fair” as such a subgroup of NW teachers would not be representative of the population of NW teachers who teach in grades 1 − 4. The challenge of selecting “right” groups is similarly manifested in the methodological limitations: Quantitative methods rely on the appropriate size and comparable distributions of the groups being compared, while the composition of and distributions in the national teacher populations can be very different in different countries.

Several general aspects of measuring teachers’ knowledge emerge from the above discussions. Validation studies in our and other countries indicate that it is possible to design valid measures of teachers’ knowledge that correlate with other indicators of teachers’ effectiveness, such as the quality of their instruction or knowledge gain of their students. The use of such measures across cultural boundaries can, however, be problematic. Differences in curriculum, standards, grade spreads, teacher education and certification, and other aspects of practice of teaching mathematics, and efforts to mitigate these differences through core knowledge may negatively impact knowledge diversity elicited by such measures, thus compromise their interpretation in terms of teachers’ performance and effectiveness. Moreover, as validation studies are statistical in nature, they rely on adequate sizes of groups to be compared. Consequently, the statistical power of MKT measures is also limited by group sizes and, for example, their application to individual teachers is clearly problematic, as in the case of examinations for teacher education or certification.

Cross-cultural use of MKT measures brings the question of the rationale for such a use to the forefront of the discussions. As we have seen in our study, the intended use of the LMT instrument greatly affected the perception of “fairness”. On one hand, local use of the LMT instrument is unproblematic and, as the literature on LMT items adaptations demonstrated, provides a very valuable insight into the cultural nuances of teachers’ MKT. Problematic items call for an analysis of reasons for incongruence and a deep inquiry into teaching practice, which in turn enhances the ecological assumption. On the other hand, even if equivalent adapted forms that exhibit the same psychometric properties in two settings can be designed, they do not imply meaningful comparisons of teachers’ MKT, and the perceptions of “fairness” of such comparisons can be viewed very differently in different settings.

Appendix

Items in the appendix illustrate the nature of the items mentioned in the text. The actual items may incorporate different concepts and distractors and can be easier or harder than the ones given here.

Item 11

If you multiply “z” by a number, the result.

(Mark one answer).

• (a) Will always be bigger than z

• (b) Will never be bigger than z

• (c) Will only sometimes be bigger than z

• (d) I don’t know

Item 15

The original Item 15 talks about a fraction division procedure. To avoid revealing the original item, we are illustrating the nature of this problem by using a different content area.

Decide if the following procedure for finding percent.

8% of 25 = 25% of 8 = 2.

(Mark one answer) a) Always works, b) Sometimes works, c) This method is incorrect; The correct answer 2 is just a coincidence, d) Answer 2 is incorrect.

Item 17

Can the following scenario be represented by the division $5\div\frac{1}{3}$ ?

If you share a third of 5 cookies with your friend, how much will your friend get?

(Mark one answer) a) Yes b) No c) I don’t know.

Item 21

Sally explains how she calculated 5 × 9: “I know that 5 × 3 is 15 and there are three of those in 5 × 9 because 9 = 3 + 3 + 3. Therefore, 5 × 9 is 45”. Which diagram in Fig. 5 would you draw on the board to illustrate solving 5 × 9 using Sally’s method?

Fig. 5

Sally's method (Diagrams for Item 21)

Mark one answer: (1) Diagram A, (2) Diagram B, (3) Both diagrams, (4) Neither diagram.

Item 25

Read the following explanation for why $12\div\frac{4}{7}$ = 25 is incorrect.

The answer 25 is not correct because if we add $\frac{4}{7}$ twenty-one times, we will get 12.

(Mark one answer).

• (a) The answer is not 25 and the explanation is valid.

• (b) The answer is not 25 but the explanation is invalid.

• (c) The answer is 25, explanation is incorrect.

• (d) I’m not sure

Item 28

During a unit on polygons, Mr. Jackson asked his students to describe properties of quadrilaterals that may or may not hold. Alex came up with the following property:

At least two adjacent sides of a rectangle are congruent.

How should students respond? (Mark one answer) (1) Always true (2) Sometimes true (3) Always false.

Item 37

During the same unit on polygons, Mr. Jackson asked his students to try to stump each other by describing figures that may or may not exist. Jordan came up with the following description:

A rectangle that has at most three right angles.

Mark one answer: (1) Such a polygon exists, (2) Such a polygon does not exist.