National organizations in the USA have called for instructional change in undergraduate Science, Technology, Engineering, and Mathematics (STEM) in general, and mathematics in particular, with growing urgency in recent years (Fairweather 2008; PCAST 2012; Braun et al. 2016). Current research leaves little doubt that student-centered approaches to instruction are related to greater student interest, persistence, and learning gains in STEM fields when compared with more traditional, lecture-based modes of instruction (e.g., Freeman et al. 2014; Laursen et al. 2014). In a recent meta-analysis of 225 studies in undergraduate STEM, Freeman et al. (2014) documented drastically different student outcomes between courses that actively involve students as learners and those that do not; students in lecture-based classes were 1.5 times more likely to fail than students in classes with active learning, and students in active learning classes outperformed those in lecture-based classes by almost half a standard deviation on concept inventories designed to measure student understandings of core ideas.

Encouragingly, there appears to be awareness, support, and movement toward more student-centered instructional approaches in the USA. For instance, Hurtado et al. (2012) found in a national survey that while 61% of STEM faculty report using extensive lecturing when they teach, a promising 49% of STEM faculty report incorporating cooperative learning into their courses. Furthermore, research indicates that even instructors who do report extensive use of lecture sometimes also report misgivings about the practice. As an example, in a survey study conducted with undergraduate abstract algebra instructors, Johnson et al. (2018) found that 64% of the respondents who think lecture is not the best way to teach still lecture. Additionally, Iannone and Nardi (2005) found that university mathematics instructors in their study acknowledged shortcomings of lecture but saw it as an inherent element of their institutional setting. These instructors viewed interaction as important for students’ learning and identified sites where interaction with instructors could occur outside lecture (e.g., seminars, tutorials, and in homework feedback).

As these shifts in awareness and attitudes toward lecturing occur, undergraduate mathematics education researchers have been developing more student-centered instructional approaches. Research into these approaches has documented greater conceptual learning gains, as well as more productive student attitudes and dispositions, when compared with classes in which lecture is the dominant instructional practiceFootnote 1 (e.g., Kogan and Laursen 2013; Kwon et al. 2005; Larsen et al. 2013; Bouhjar et al. 2018). These findings are well aligned with the efforts of strong and growing communities of mathematicians in the USA working toward sustained instructional change (e.g., The Academy of Inquiry-Based Learning and the Mathematical Association of America’s Project NExT).

Even with these positive trends, we know that instructional change is difficult to achieve at scale (Henderson et al. 2011). Thus, we view the question of how to effectively support instructional change at scale as one of the most critical questions facing education researchers. This challenge is heightened in undergraduate math, as instructors’ reasoning about pedagogical issues has, until recently, been largely unexamined (Speer et al. 2010). As such, our work in this study informs the broader goal of understanding and achieving instructional change at scale by examining efforts to support instructors’ understanding of specific research-based, student-centered instructional materials for undergraduate mathematics courses.

In particular, the instructional materials at the center of this study are inquiry-oriented materials developed for undergraduate mathematics courses. The implementation of such materials offers a host of challenges for instructors. These challenges include interpreting students’ idiosyncratic mathematical reasoning (Johnson 2013; Johnson and Larsen 2012; Speer and Wagner 2009), determining the potential of students’ contributions, and then leveraging those contributions to advance the mathematical agenda (Johnson 2013; Speer and Wagner 2009; Rasmussen and Marrongelle 2006). Given that undergraduate mathematics instructors typically have limited pedagogical training, coupled with mounting pressure at the undergraduate level to shift toward student-centered pedagogies, we argue that learning to support instructors effectively in relation to the aforementioned challenges is particularly important and thus implies a need for professional development programs that foster the development of undergraduate mathematics instructors’ pedagogical reasoning.

Here, we analyze data from a professional development program designed to support instructors as they engaged with inquiry-oriented instructional materials. In the context of this program, we examine instructors’ pedagogical reasoning as evidenced by conversations in two different content area breakout groups with two different facilitators. The nature of conversations and pedagogical reasoning differed between the two groups in ways we believe to be consequential. We explore the origins of these differences through the following research questions:

  1. 1.

    What is the nature of mathematicians’ talk when asked to engage in mathematical problem-solving tasks designed to support student learning, to consider student reasoning, and to speculate about instructional choices in relation to mathematical goals of said tasks?

  2. 2.

    What patterns of talk support rich pedagogical reasoning about inquiry-oriented instruction?

Literature review and theoretical perspective

In 2010, Speer, Smith, and Hovarth conducted a literature review on collegiate mathematics teaching. This review concluded that instructors’ practice (i.e., their pedagogical actions and reasoning related to those actions in the context of instructional activities) remains largely unexamined in the research literature. In the last decade, there have been a number of research articles on the development of inquiry-oriented instructional materials and their implementation at the undergraduate level (e.g., Andrews-Larson and 2017; Johnson and Larsen 2012; Larsen et al. 2013; Rasmussen and Kwon 2007; Speer and Wagner 2009; Wawro et al. 2012; Zandieh et al. 2017). However, research on professional development in undergraduate mathematics education is still sparse, especially when the focus is on instructors and tenure-track faculty (as opposed to programs for graduate teaching assistants).

Speer and Hald (2008) reviewed findings on teacher learning from elementary and secondary mathematics education literature and suggested ways in which this literature can inform the training of mathematics graduate students who are learning to teach—yet few studies have examined this further, as highlighted by Florensa et al. (2017). Nardi et al. (2005) delineated a framework for a spectrum of pedagogical awareness by drawing on interview data collected from a set of six undergraduate mathematics tutors. This framework organizes these tutors’ conceptualizations of student difficulties and how they address those in their teaching. While Nardi et al. (2005) examined the reasoning of tutors, others have examined the reasoning of mathematicians with regard to the ways in which they motivate topics, structure explanations, and pose questions (Viirman 2015), or decide how to present proofs (Lai and Weber 2014). However, we are specifically interested in the reasoning of instructors working to teach in ways that are responsive to student reasoning—particularly that leverage student reasoning as a resource (rather than a deficit) to inform their instruction. Thus, we decided to ground our professional development work in the research literature about the implementation of inquiry-oriented instruction at the undergraduate level. In particular, we attend to the pedagogical reasoning presented in that research base.

The context of this study was a professional development workshop designed to support the implementation of three sets of inquiry-oriented instructional materials that had been developed for undergraduate mathematics courses in linear algebra (Wawro et al. 2013), differential equations (Rasmussen et al. 2018), and abstract algebra (Larsen et al. 2016). Each of these curricula were informed by the instructional design heuristics of Realistic Mathematics Education and were designed to leverage students’ informal and intuitive ways of reasoning as starting points from which to build more sophisticated and formal mathematical understandings (Freudenthal 1991). These cycles of inquiry and formalization, supported by the task sequence and guided by the instructor, are usually carried out in collaborative small groups and whole-class discussions. The commonalities in the design and instructional intentions of these materials serve as the foundation for what we refer to as inquiry-oriented instruction (IOI).

In order to theorize the pedagogical reasoning that may be particularly relevant for IOI, we grounded our work in the IOI research base to include literature that characterizes IOI (e.g., Kuster et al. 2018; Kuster et al. 2019) and research that examines the implementation of IOI (e.g., Andrews-Larson et al. 2017; Johnson 2013; Johnson and Larsen 2012; Rasmussen and Marrongelle 2006; Speer and Wagner 2009; Wagner et al. 2007). In our theorizing, we leverage Horn and Little (2010) ideas about examining pedagogical reasoning relative to the instructional triangle (i.e., content, students, and teacher). In particular, we attend to how the IOI research literature discusses implementation related to mathematical content, engaging with student thinking (especially in the moment), and instructional decision making. This theorizing about the pedagogical reasoning needed to implement IOI served as the foundation for the design and analysis of our professional development.

In inquiry-oriented instructional materials, the mathematical content may be developed in ways that are unfamiliar to the instructor. As a result of the novel mathematical trajectory presented in the materials, some instructors have difficulty understanding how the subject matter fits together to form a coherent whole. Wagner et al. (2007) described this challenge in the following way:

By examining the materials, an instructor could discern the general direction of the curriculum, but without actually working through all the problems and activities ahead of time, it might be difficult to discern the “hidden agenda” supported by those activities that revealed how they are connected across the semester. (p. 262)

Thus, when considering the mathematical demands placed on the instructors, we see a need for “working through all the problems” in order to fully appreciate the mathematical rationale and trajectory of the tasks/lessons/units. However, this is only one form of mathematical activity that supports the implementation of IOI.

One of the defining characteristics of IOI is the notion that instructors must use student contributions and reasoning to inform the direction of their lesson (Kuster et al. 2018). Therefore, instructors must make sense of, and use, student thinking in the moment. Johnson (2013) documented a number of mathematical activities that support an instructor in being responsive to their students’ emerging reasoning while implementing IOI. This teachers’ mathematical activity includes interpreting students’ mathematical reasoning and contributions (Johnson and Larsen 2012); analyzing student work, contributions, and proofs (Johnson and Larsen 2012); figuring out the potential of student ideas to advance the mathematical agenda (Speer and Wagner 2009); and leveraging student ideas to advance the mathematical agenda (Rasmussen and Marrongelle 2006). The idea that instructors must attend to student thinking in the moment is not specific to IOI. In fact, similar ideas have been discussed extensively in the elementary and secondary mathematics education literature. This includes the work on teacher noticing (e.g., Jacobs et al. 2010; Mason 2002; van Es and Sherin 2008) and research that aims at unpacking the knowledge that teachers draw upon while teaching (e.g., Ball et al. 2008; Rowland et al. 2005).

Moreover, it is not enough for instructors to understand the mathematical content, the way in which that content is developed in the context of the materials, and to be able to make sense of, and engage with, student contributions. Instructors must also coordinate the intended mathematical goals and the emerging student understanding to inform their instructional decisions. The literature has several examples of instructional practices that support such coordination. These practices include: engaging in generative listening wherein a teacher revises a lesson trajectory in response to a student’s contribution (Johnson and Larsen 2012); selecting student ideas to pursue (Speer and Wagner 2009); using transformational records in which instructors annotate student contributions in ways that help establish links to conventional mathematical language and notation (Rasmussen and Marrongelle 2006); and using generative alternatives in which instructors present students with a set of possible ideas related to a task and ask students to make arguments for, against, and/or relating the set of ideas to one another (Rasmussen and Marrongelle 2006).

Such coordination practices have been shown to be quite complex and challenging for instructors. For example, in an inquiry-oriented classroom, it is crucially important for the instructor to become skilled at identifying potentially productive approaches to a problem (which are often partially correct or expressed in idiosyncratic, informal, and imprecise ways), selecting which approaches should be shared and/or discussed, and deciding how to orient those contributions so that they might be made sense of and leveraged mathematically by all students in the class. As such, what the teacher notices in an inquiry-oriented classroom determines what they are able to interpret and how they choose to respond instructionally (see Johnson and Larsen 2012 for an example). Additionally, given the research literature on IOI (e.g., Johnson and Larsen 2012; Speer and Wagner 2009; Wagner et al. 2007), we have reason to believe that the teacher’s understanding of the mathematics may be related both to what they notice in students’ mathematical reasoning and the extent to which they are able to leverage that understanding to inform pedagogical decisions. Thus, in the context of this study, we are interested in how instructors engage with the mathematics, what instructors notice about students’ mathematical reasoning, and instructors’ own ideas about the instructional choices they might make based on their understanding of students’ reasoning.

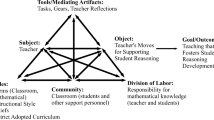
With the research literature on the implementation of IOI as our foundation, we define rich pedagogical reasoning in IOI as reasoning that is grounded in the mathematical goals of the lesson and informed with an understanding of students’ mathematical reasoning. Accordingly, we propose the hypothetical model for supporting rich pedagogical reasoning among mathematicians shown in Fig. 1. Encapsulated in this figure is our conjecture that both reasoning about mathematics and an understanding of students’ mathematical reasoning are equally important components of rich pedagogical reasoning. This model informed the design of our professional development as well as our analysis; it focused our attention on the kinds of talk that we theorized to be important. It also supported us in identifying patterns in talk that ultimately allowed a revised model to emerge from the results of our analysis.

Fig. 1
figure 1

Hypothetical model for supporting rich pedagogical reasoning about IOI

Full size image

Study design

The analysis presented in this paper draws on data from a broader NSF-funded project, < BLINDED >investigating what is needed to support instructors interested in learning to teach in inquiry-oriented ways. To test (and ultimately refine) our hypothetical model, we examined conversations from participants in two content area breakout groups from the same professional development program. The data for this analysis come from a summer workshop offered at a national mathematics conference. The workshop lasted a total of 4 h and was split across two 2-hour sessions. On each day, about half of the time was spent discussing issues of inquiry-oriented instruction that cut across content areas, and the other half of the time was devoted to work in content-specific breakout groups. The two content areas we present here are abstract algebra and linear algebra.

Data sources and participants

Our primary data source in this analysis was a set of audio/video recordings from the workshop sessions. The workshop included 25 participants, 21 of whom responded to a workshop pre-survey that provided us with information about their teaching background and home institutions. Of those participants that provided pre-survey data, all but one were housed in mathematics departments, and the group represented a variety of institutions and positions (see Fig. 2). Less than a third of survey respondents reported that they prefer to lecture most of the time, more than 70% reported that they like to have students work in groups on problems in class, and more than 60% reported they frequently ask students to explain their thinking to the whole class when they teach.

Fig. 2
figure 2

Position and institution types of survey respondents

Full size image

Study context: workshop activities and mathematical content

Workshop facilitators designated time in each of the breakout groups for participants to focus on three main activities, each of which corresponded to the vertices of the instructional triangle and to the components of our hypothesized model. Our plan for the workshop was for the participants to first work through selected mathematical tasks from the inquiry-oriented curricular materials, then examine evidence of student reasoning on these tasks as documented through classroom video and/or written work, and finally discuss related implementation considerations and in-the-moment instructional decisions.

In the USA, introductory abstract algebra (AA) courses are normally taught to upper division mathematics majors in small classes, typically less than 40 students. During the summer workshop, the AA group worked through a set of tasks designed to introduce the idea of subgroups and support the development of a “subgroup criteria” conjecture—i.e., to conjecture about the minimal criteria needed to ensure that a subset of a group is itself a group. The task sequence begins by defining a subgroup as a subset of a group that is itself a group. Subsequent tasks ask the students—or, in this case, workshop participants—to (1) verify that 5 \({\mathbb{Z}}\) is a subgroup of \({\mathbb{Z}}\) (under addition), (2) determine a smaller set of conditions that are sufficient (and necessary) to ensure that a subset of a group is a subgroup (i.e., reinvent the subgroup criterion), and (3) in anticipation of difficulties with the last task, show the identity of a subgroup is the same as the identity in the ambient group and that the inverse of any element in the subgroup must be the same as that element’s inverse in the ambient group. (See Larsen and Zandieh 2008 for a comprehensive discussion of this task sequence. Notes about task rationale and student thinking are also provided in the online appendix.)

There were three professional development activities planned around this task. To set up the activities, the participants were first to be asked to take a few minutes to write down how they typically teach subgroups and/or how they were taught subgroups. After that private reflection, the mathematics instructors were going to be asked to engage with the tasks as written—i.e., to solve the tasks as if they were students. The facilitator planned to structure the discussion of these tasks much as she does when she teaches these materials: after the participants had a few minutes to think privately, they were to collaborate in pairs or small groups, there would then be a whole group discussion around the mathematics in which the participants would share their mathematical thinking and the group would come to a consensus around a reduced list of axioms.

In the second session, the plan was for the participants to watch classroom video of these tasks being implemented. To frame this activity, the facilitator planned to share a tension inherent to implementing IOI—that instructors are expected to build on the students’ informal ideas to help them construct the formal mathematics while ensuring that the students maintain ownership of the emerging mathematical ideas (Johnson et al. 2013). As the participants watched the video, they were to be asked to try to track the students’ mathematical contributions and the evolution of the classroom’s subgroup criteria conjecture. After the video, there was a discussion that focused on “where the students are” and “where we want them to be” in relation to the evolving mathematical agenda. Finally, in the last session, the participants were to be asked, if they were the instructor, “what might you do next?” After a discussion of ideas, the group would finish watching the classroom video data to see what the instructor decided to do in the moment, followed with a discussion of pros and cons about that decision.

In the USA, introductory linear algebra (LA) courses are typically taught after students have completed two semesters of calculus. Class sizes for this course in the USA usually range from 20 to 80 students, with 45 or fewer being typical. The LA group worked on activities from a sequence of tasks intended to help students develop and coordinate geometric and algebraic ways of symbolizing linear combinations of vectors as they learn about span and linear independence. The context for this work is shown in Fig. 3. The sequence of four tasks involves: (1) determining if and how a given pair of vectors in \({\mathbb{R}}^{2}\) can be weighted and combined to “reach” a particular location in the plane, (2) determining if there is any location in the plane that cannot be reached using that pair of vectors (this primes the formalization of span), (3) determining if three given vectors in \({\mathbb{R}}^{3}\) can be combined to make a journey that starts and ends at the origin (this primes the formalization of linear dependence), and (4) generate examples of sets of vectors that satisfy particular properties (e.g., “Give an example of two vectors in \({\mathbb{R}}^{2}\) that form a linearly dependent set”) in order to motivate more general conjectures about linearly (in)dependent sets. (See Wawro et al. 2012 for a comprehensive discussion of this task sequence. Notes about task rationale and student thinking are also provided in the online appendix.)

Fig. 3
figure 3

Context for the linear algebra group’s task sequence

Full size image

Similar to the AA group, the professional development plan for the LA group was to be to first ask the participants to reflect on how they typically teach, or how they were taught, span and linear independence. The facilitator then planned to provide an overview of the task sequences, before asking the participants to work through the second task in the sequence. As they worked on the second task, the facilitator planned to ask them to: solve the task themselves, think about how a student might approach it, and think about how they might introduce the concepts of span and linear independence based on how they imagine the students will approach these tasks. Then, there was to be a discussion about the different solutions/approaches elicited by the tasks, how the mathematical concepts emerge from the task sequence, and things participants think might be challenging for students. The facilitator brought six samples of student work that featured a variety of approaches; these were to be used to offer insight into how students might reason about the task, and to discuss how participants might sequence approaches in whole-class discussion.

In the second day’s session, the plan was to watch a class video in which several student groups presented their approaches to the second task prior to formalization of the definition of span. Participants would similarly be asked to keep track of students’ contributions to support a discussion of their current reasoning and how it could be leveraged to link to the formal definition of span; the plan was similarly to then watch how the instructor did this in the video.

In looking across the two content areas, there are a few differences in the nature of the tasks. In the abstract algebra task sequence, the main mathematical activity is conjecturing, whereas there is a stronger emphasis on notating and generalizing in the linear algebra tasks. Relatedly, in the abstract algebra group, the goal of the guided reinvention is a conjecture and theorem, whereas the goal in the linear algebra group is the reinvention of intuitive notions of span and linear (in)dependence that serve as a basis for the instructor to introduce formal definitions of those constructs. However, the structure of the professional development for the two content areas was largely consistent. Generally speaking, the plan was to have the participants focus on the mathematics, then consider examples of student thinking, and finally think about instructional decisions.

Methods of analysis

Immediately following the workshop, the facilitators (and members of the authorship team) noted and discussed perceived differences in terms of the participants’ level of mathematical engagement. In order to more systematically investigate the nature of mathematicians’ pedagogical reasoning about inquiry-oriented instruction in the context of our workshop, we conducted a qualitative content analysis (Elo and Kyngäs 2008). As we were working from a hypothesized model for pedagogical reasoning, we conducted a deductive content analysis with the vertices of the instructional triangle serving as our initial codebook. However, in order to test and refine this hypothesized model, we decided to use an unconstrained characterization matrix. Because it was an unconstrained matrix, we had the flexibility to refine the codes following the principles of inductive content analysis.

Using our initial codebook, the authors analyzed complete transcripts of the abstract algebra and linear algebra breakout sessions (a total of approximately 2 h of video for the abstract algebra group and 2 h of audio for the linear algebra group). The authors made a first attempt to code participants’ talk relative to the instructional triangle via the rough codes mathematics, students, and teaching. In discussions that followed, the research team agreed on a number of refinements that were needed to capture variation in participant talk that was relevant to our research questions and related to the research literature more precisely. This subsequent inductive phase (detailed below) allowed us to refine our initial theory-driven codes, in a data-driven way (DeCuir-Gunby et al. 2011).

With regard to the “Mathematics” vertex, after reflecting on our data and the initial phase of analysis we decided it was important to differentiate between talk in which participants were actually doing mathematics and talk that was merely about mathematics. As such, the mathematics code became “Doing Mathematics” (DM). This reflection also indicated a need to distinguish between the depths of mathematical reasoning discussed. Within the DM code, each turn of talk was therefore assigned a High Depth sub-code if the speaker described his or her solution method or reasoning about a particular mathematical task with relative specificity, or a Low Depth sub-code if the speaker described what he or she would do without rationale or specific evidence of actually working through mathematical details (see Table 1).

Table 1 Abbreviated codebook for “Doing Mathematics”
Full size table

Moreover, the decision to use the code DM, as opposed to mathematics, allowed us to distinguish whose mathematics was being discussed (students’ mathematics versus the participant’s own mathematics). Accordingly, a new data-driven code was developed—“Engaging with Students’ Mathematical Reasoning” (ESMR)—to capture many of the comments that were previously associated with the Student vertex of the instructional triangle. Some statements related to students’ mathematical reasoning were based on empirical evidence, while others were based on what participants speculated students might do or think. To capture this nuance, sub-codes were developed to reflect whether or not participants’ comments about student thinking were empirically based (referring to evidence of what students had said or done) or hypothetical (what students might do or think) and to assign depth to a statement (High or Low) based on specificity regarding the mathematics (see Table 2). Here, we arrived at four ESMR codes: ESMR—Hypothetical—Low, ESMR—Hypothetical—High, ESMR—Empirical—Low, and ESMR—Empirical—High.

Table 2 Abbreviated codebook for “Engaging in Students’ Mathematical Reasoning”
Full size table

Finally, participant comments related to the original “Instruction” code were grouped into three main categories: Instructional Principle, Instructional Choice, or Instructional Observation (examples are given in Table 3) and classified as either Instruction—High Depth or Instruction—Low Depth. We considered instructional comments that were explicitly linked by participants to their own mathematical thinking, or their explanations of students’ thinking, to be indicative of rich pedagogical reasoning. Thus, we considered an Instruction code to be High Depth precisely when it appeared in combination with another code (either DM, ESMR, or a second type of Instruction code) and we considered turns of talk to be Instruction—Low Depth if only a single instructional code was assigned in isolation. Our rationale for this is aligned with our theorization of rich pedagogical reasoning as that which attends to mathematical goals and students’ reasoning—with a broadening to acknowledge that in the patterns of talk observed, articulations of rationale often attended to other broader issues that are also of instructional value. Thus, we viewed multiple codes together as evidence of richly connected rationale about instruction. It is these “Instruction—High Depth” turns of talk that capture our notions of rich pedagogical reasoning.

Table 3 Abbreviated codebook for “Instruction”
Full size table

Two researchers independently coded transcripts for the linear algebra and abstract algebra groups. Codes were assigned at the level of turns of talk, though not every turn of talk received a code, and some turns of talk received multiple codes. Coding discrepancies were resolved by discussing and coming to consensus on a final code. We then quantified differences in talk between the LA and AA group using our coding scheme.

Findings

To offer the reader a sense of the context and focus of conversations in which we examine mathematicians’ pedagogical reasoning, we provide an overview of the conversations that took place in the two breakout groups over the 2 days. We then provide representative examples of the participant talk in each content group in relation to each of our three codes. In order to identify patterns of talk that supported rich, inquiry-oriented pedagogical reasoning, we examine the results of our coding quantitatively.

Examples of participant talk and coding scheme: linear algebra

As previously mentioned, facilitators of the breakout groups collaborated to structure workshop activities so as to focus on each vertex of the instructional triangle in turn, starting with mathematics, building to consider student thinking, and ultimately, examining the role of the teacher. On the first day of the workshop, after introducing themselves, LA participants were asked to engage in specific tasks from the curricular materials and were encouraged to work through the math together. Participants spent some time speculating about what students might do and discussing logistical aspects of task implementation before eventually completing the task and then examining some samples of student work. On the second day of the workshop, participants watched video of students explaining their approaches in class and considered how they would introduce the concept of span to build on these ideas. In the following subsections, we characterize in greater detail the participants’ engagement as it relates to our coding scheme.

Doing Mathematics

The first mathematical task the linear algebra participants were asked to engage in was whether it was possible to use two specific vectors in \({\mathbb{R}}^{2}\) to get anywhere in the plane by traveling on each for different amounts of time (see Fig. 3). Here is an excerpt from the transcript:

LA-P1:

They can generate any vector that is on opposite sides of the parallelogram… pretty easily, because all they have to do is restate this and add this and…in two-dimensions if they remember… they would not solve a system…

LA-P2:

Do they have problems with dealing with the fractional parts of time? Cause it might be possible that they need to ride one of these for a fractional amount of time to get some place

Facilitator:

I am going to ask you guys to entertain the notion, like actually work through it as a student. Does that make sense?

LA-P3:

I can’t think of any other way than how I would do it…

Facilitator:

So that’s fine as a starting point

Notice that in the first two comments the participants did not focus on their own thinking, and instead focused on how students might approach this task (i.e., “they can generate any vector”). Thus, these comments were not coded as Doing Math—rather they were coded as ESMR—Hypothetical—Low. The facilitator then attempted to redirect participants to actually work through the mathematics as a student, and a participant remarked that he did not know how students would do it, only how he would do it. This comment was coded as Doing Math—Low Depth, and the conversation subsequently turned to a discussion of prerequisite coursework. Another participant made the following remark (which was also coded as Doing Math—Low Depth) that explicitly acknowledged the difficulty in trying to solve the problem without using the full breadth of their mathematical background:

LA-P2:

I know no matter where we go, I know I can come up with a linear combination that will get me there, I’m trying to, I don’t know, it’s hard for me to pull away my knowledge

Eventually, most members of the linear algebra group worked through the task more or less completely on Day 1. They came together for a more focused discussion about participants’ own mathematical strategies, but the conversation repeatedly turned toward issues of implementation as they related to student thinking. Below we highlight turns of talk from several participants that were coded as Doing Math—High Depth. It is noteworthy that the prompt by the facilitator at the outset of this conversation is the third such invitation for participants to share their mathematical thinking—and it was in this exchange that most of the Doing Math—High Depth codes for the linear algebra groups were assigned.

Facilitator:

Let’s start by discussing strategies because they were actually different when people solved it for themselves.

LA-P3:

I immediately put the numbers in a matrix and solved for an arbitrary vector x, y

LA-P4:

So, I am rusty on my linear algebra so I went back to the analogy, if I am given a location x, y that I need to get to, how long using each mode of transportation. And so I built a linear combination and then turned it into a matrix and row-reduced by hand. That way, given x and given y, I knew how long to ride this and how long to ride that.

LA-P1:

I did a more geometric approach. I drew the two vectors and then just kind of built the lattice of if you take integer combinations and then…I first looked at positives because I didn’t hear any of the discussion about time and with negatives you can see how this extends over the whole plane and fractional parts and non-integer coefficients.

LA-P2:

Since the pre-req for my class is precalc and we go over systems of equations, I turned it into a system of equations, but I don’t think my students would do that because it is a system with two unknowns and that would probably freak them out.

All four of these participant turns of talk were coded as Doing Math—High Depth (and the final comment also received an ESMR—Hypothetical—Low code). The final quote is indicative of the mathematical conversations in the LA group: when participants did speak about their own solutions to the mathematical tasks, their statements about math were often tied either to student thinking or to instructional decision making. More broadly, linear algebra participants’ engagement with the mathematics tended to be framed in terms of what students (“they”) might do, rather than in terms of their own (“our/my”) mathematical reasoning.

Engaging in students’ mathematical reasoning

After discussing the mathematical underpinnings of the task sequence and potential approaches, the LA group engaged in two activities related to students’ mathematical reasoning: looking at student work (which took place on day 1) and watching video where students explain their approaches in class (which took place on day 2). About 44 min into the first day’s session, the facilitator distributed copies of students’ work with six different mathematical approaches to the problem they had discussed (the second problem in the task sequence). Below are comments made as participants examined this student work:

Facilitator:

So what things are people noticing that are surprising?

LA-P3:

This tangent approach is kind of off the wall for me. I am not sure how I would respond to that group

Facilitator:

I think that they may have abandoned that. Sometimes you get things on a white board that were part of an attempt, but ended up not being productive so that might have been part of that… I am curious about Group 6 and what people interpret that diagram to be indicating

LA-P2:

I would want to know more about their reasoning but it looks like they are saying you can get to anywhere in here but the coefficients of both vectors is positive. Over here both of the coefficients are negative and here that one is positive negative and this one is negative–positive

LA-P1:

And that is why 1 and then 2 builds on that by adding something to that, and the, I think in terms of the geometry, 6 is really what completes the geometric picture and then 3 and 5 add in algebra in slightly different ways

The first participant comment in this exchange was coded as ESMR—Empirical—Low, as they were referring to the sample student work, but only by giving a general characterization of the student’s approach (i.e., “this tangent approach”). This comment was also coded as instructional choice as it raised the question of what to do with a particular approach. The other two participant comments were both coded as ESMR—Empirical—High Depth because they involve some degree of specificity, though we note that neither delved into student rationale nor reasoning related to their observations. In general, the LA group’s engagement in students’ mathematical reasoning was consistent with the ways in which they discussed the mathematics. Overall, we saw a frequent focus on issues of implementation, varying depth of talk (with High Depth talk rarely occurring in a sustained way), and often surface-level descriptions of mathematical details.

Instruction

It was the intention of the facilitators of both the LA and AA groups to host a discussion on the second day of the workshop regarding issues of implementation after watching classroom video. After the LA group watched video in which students explained their approaches to the task, participants were asked to describe how they would introduce the concept of span if their students were reasoning in the ways shown in the video they had just watched. One participant responded in terms of what conclusions the class had made about what locations in the plane can be reached with (linear combinations of) the given pair of vectors. Below is transcript including both the facilitator’s prompt and participants’ responses.

Facilitator:

Turn to the person sitting next to you and see if you can brainstorm the mathematical approaches and ideas that have been brought out so far and in terms of thinking about the sequencing of the tasks, think about how do you think if you were teaching, that you would introduce the concept of span because they still haven’t heard that word…if you were teaching this and you knew that you wanted to use this to introduce span, how would you do it?

LA-P2:

So it seems as though there’s been the geometric approach a couple geometric approaches that come out, both with the vectors and with the equations.

LA-P5:

Well, the big thing that’s come out, although they haven’t called it this yet, is the idea of independence.

LA-P1:

…. they could combine the geometric approach and the algebraic… They could go directly to symbols. They haven’t used trig. Do they know vectors? Or do they just know. oh, they have to know vectors to write even 3,1 and 1,2—

Facilitator:

Right, and on the first day she gave sort of an overview of vectors, linear combinations of vectors and she already introduced the language for scalars

LA-P5:

We noticed that there were geometric and algebraic and you could kind of take a geometric or an algebraic point of view (inaudible) lines shifting and intersecting and then also the algebraic way you could actually solve…

LA-P6:

If the consensus becomes “everything” then you set the tone, you can go into the animation, and the definition can be using linear combinations and… all possible ways of scaling the first one and adding the second, and then scaling the second one and adding the first one… then you’re primed to talk about… all possible linear combinations and it spans \({\mathbb{R}}^{2}\) in this case

Many of the statements in this exchange focused on mathematical representations and topic order without explicit connection to student reasoning or learning goals (e.g., how to sequence the introduction of independence and dependence). This suggests that participants were still wrestling with what students knew about the mathematics—which may relate to the way in which participants’ themselves had been positioned to reason through the mathematics in the task sequence. As such, the only turn of talk in this exchange coded as being explicitly about instruction was the final one. This last turn of talk was assigned a single code of instructional choice; since there is no explicit evidence of taking on a student’s perspective or doing any mathematics, it was considered to be Instruction—Low Depth. All other participant remarks in this exchange received ESMR codes. More broadly, instructional codes from the linear algebra group tended to be evaluative comments about the quality of a solution or explanation (without attending to student reasoning or how that would affect instructional choices).

Examples of participant talk and coding scheme: abstract algebra

On the first day of the workshop, abstract algebra participants spent nearly the entire one-hour breakout session discussing how to apply the definition of a “subgroup” (i.e., a subset of a group that is itself a group) in various contexts. First, they used the definition of “subgroup” to demonstrate that \(5{\mathbb{Z}}\) is a subgroup of \({\mathbb{Z}}\) under addition by checking to verify that all of the group axioms were still satisfied in \(5{\mathbb{Z}}\). They then drew on this definition in order to develop a different, more efficient method (i.e., the subgroup criterion) for deciding when a subset of a group is a subgroup. On the second day of the workshop, the abstract algebra breakout group was shown a video of students explaining their partial progress in thinking about ways to develop a more efficient way to check if a subset of a group is a subgroup. Following this video, participants reasoned about how students in the video were making sense of the mathematics, proximal mathematical goals given students’ current reasoning, and what they would do next if they were the instructor.

Doing Mathematics

In contrast with the linear algebra group who frequently discussed aspects of instruction and student reasoning as they worked through the mathematics, the abstract algebra participants spent nearly the entire one-hour breakout session on the first day deeply engaged directly in the mathematical tasks. As an example, consider the following exchange that took place after workshop participants were asked to consider the closure axiomFootnote 2 in the subgroup setting.

Facilitator:

I have a question for you, what does the check on closure mean? [points to paper with a check mark] Can you write that out formally for me, please? More importantly can you write out formally the check on inverses? Is it the same thing you would check if you are checking a group? …

AA-P1:

Like you know this would be in H automatically by the first condition… by closure.

AA-P2:

We don’t know that. That isn’t what the identity is.

AA-P1:

What you’re saying is—Sorry—once we have both conditions, because you have h and g−1 in H then its product is, but we’re trying to get identity from inverses. So assuming those two and let this element be in H and therefore the identity of G lies in H to prove that it is the same operation for H.

AA-P2:

Well, it is an identity for H. We still don’t know-

AA-P1:

And then so either you need to know uniqueness of identities.

AA-P2:

That’s not part of our definition.

In this exchange, the participants are themselves reasoning through the mathematical tasks. They are constructing mathematical arguments, they are trying to verify group axioms, and they are questioning what they know and what they have to prove. In short, they are engaging in the task directly, from their own points of view, with great specificity. The turns of talk in this exchange, as well as 70 of the 76 coded turns of talk from the first day, were coded as Doing Math—High Depth.

Engaging in students’ mathematical reasoning

To start the second day of the workshop, the AA breakout group was shown video from a whole-class discussion. These students were working through the same set of tasks that the participants worked through on Day 1, and in the video they were discussing their progress in determining the minimal criteria needed to determine that a subset of a group was itself a group. After watching, the participants were asked to comment on the students’ mathematical reasoning.

Facilitator:

I’m going to bring you guys together now. So, do people feel comfortable with the statement about where the class’ mathematics was? Do you think you could answer that question? Where the class was in the process?

AA-P1:

I don’t think it’s super clear. I don’t think everybody has the same thing in their mind from what people were saying. We were getting the impression that there was still a real tension between some of the ideas that had been expressed and where the discussion was going right at the end. There were still unresolved tensions, I thought, between different ideas of what the task was even

Facilitator:

Can you elaborate on what those tensions were?

AA-P1:

Well, the same kind of tensions we experienced yesterday in some of the groups, where, is the task to take this list of four axioms and just strike off things from that list, but keep them exactly as the statement or is it to actually produce something where those statements get revised into something rather different, and simpler and shorter. The discussion started with something that really had to do with revising in terms of “is eG equal to eH” and things like that. And then just at where you stopped it if you looked at the board the bottom of the board was simply a list of four things with some stuff struck off. I think that was just an artifact that it was really very much still in the middle of the discussion, but if I were a student in the class at that moment I think I would have been quite possibly rather confused and I know that that would be okay, as to what the eventual product is that we’re going to come up with here and what’s the real issue

Here, we see an abstract algebra participant trying to make sense of the students’ mathematical reasoning based on a classroom video. This participant’s turns of talk were coded ESMR—Empirical—High Depth. It was coded as Empirical because the participant was making explicit reference to the evidence of students’ reasoning presented in the video clip. In particular, this participant was commenting that they saw the students in the clip struggling with one of the key mathematical subtleties of this task sequence—“is the task to take this list of four axioms and just strike off things from that list, but keep them exactly as the statement or is it to actually produce something where those statements get revised into something rather different, and simpler and shorter.” The specificity of this comment, which was further elaborated on by referencing a particular axiom that the students were discussing in the video (“is eG equal to eH?”), is indicative of a “High Depth” code.

We also note that the mathematics the students are reasoning about in the video is the same mathematics that the participants had engaged in during the previous day of the workshop, and that this was acknowledged by this participant. This is captured in the comment “the same kind of tensions we experienced yesterday in some of the groups.”

Instruction

Day 2 of the AA breakout concluded with the workshop participants being asked to consider what they would do next if they were the instructor of the class whose discussion they had just watched. The comments made by several participants evidenced a layering of reasoning that drew both on their own mathematical reasoning and the student reasoning they had just discussed. The exchange below highlights this layering of reasoning:

AA-P3:

I’m assuming they have already shown the identity is unique.

Facilitator:

They have shown the identity is unique.

AA-P3:

So, and I’m, if they haven’t shown that the inverse is unique, then I would ask can an element have more than one inverse. And then I would ask what can you say about a subset of a group if it is closed under inverses.

This participant’s comment shows evidence of pedagogical reasoning that attends to the mathematics (“the identity is unique”), what students know (“if they haven’t shown that the inverse is unique”), and what the instructor might do next to advance students’ reasoning about that mathematics (“I would ask what you can say about a subset of a group if it is closed under inverses”). The third turn of talk from this exchange was coded as Instruction—High Depth, as it was an instructional choice paired with an ESMR code.

Overall, instructional talk in the AA group tended to focus on two primary issues: how to help students refine conjectures into mathematically provable statements (as see in the previous exchange) and how to maintain student authority over notation (e.g., who is doing the symbolizing and how). We posit that participants’ own deep engagement with this mathematics themselves on the first day of the workshop supported this nuanced coordination of the vertices of the instructional triangle. This was especially clear in moments when the participants referenced ways in which they saw similarities in how they had worked through the mathematics and how the students were talking about the mathematics.

Comparison of linear algebra and abstract algebra groups’ talk: by the numbers

Our initial impressions that the mathematical focus of the two groups differed sharply were supported by the quantitative results of our coding. As shown in Fig. 4, nearly half of all participants’ turns of talk in the abstract algebra group were coded as “Doing Mathematics” compared to only 23% of the linear algebra turns of talk.Footnote 3 In contrast, many more turns of talk in linear algebra (39%) were focused on ESMR than were in abstract algebra (22%). These quantities alone might suggest that the abstract algebra group conversed primarily about mathematics, while the linear algebra group placed greater emphasis on student reasoning. Differences in the nature of talk between the two groups, however, suggest a more nuanced interpretation.

Fig. 4
figure 4

Percentage of turns of talk assigned each code (across both days)

Full size image

Doing Mathematics

In addition to having a larger portion of talk coded as Doing Mathematics, when compared to the linear algebra group, more of the abstract algebra group’s mathematical talk was of High Depth (see Fig. 5). In the abstract algebra group, 93% of the 72 turns of talk coded as Doing Mathematics were of High Depth. In contrast, in the linear algebra group only about 65% of the 23 turns of talk coded as Doing Mathematics were of High Depth.

Fig. 5
figure 5

DM codes, by content area and depth

Full size image

Engaging in students’ mathematical reasoning

As shown in Fig. 4, a larger portion of talk in the LA group was coded as Engaging in Students’ Mathematical Reasoning (ESMR) as compared with the AA group (approximately 39% and 22%, respectively). Our coding, however, also indicates important differences in the nature of this talk. Recall that a turn of talk coded as ESMR was considered to be High Depth if it attended to specific details of students’ mathematical reasoning and Low Depth if it provided only a generic description of students’ mathematics without details of their process or reasoning. Further, ESMR comments were coded as Empirical if they referenced evidence explicitly (e.g., from video data or student artifacts) and Hypothetical if they referenced what a student might do or think without empirical evidence.

Table 4 shows a breakdown of ESMR codes for each group by depth and use of evidence (empirical versus hypothetical). The abstract group exhibited more sophisticated ESMR at a higher rate than the linear algebra group as indicated by the proportion of Empirical—High ESMR codes when talking about students’ mathematical thinking. More than half (53.2%) of the abstract algebra group’s ESMR codes were of High Depth, whereas only 42.5% of ESMR codes were of High Depth in the linear algebra group. Furthermore, we see that when the abstract algebra participants engaged in students’ mathematical reasoning, they drew on empirical evidence nearly 72% of the time, whereas linear algebra participants did so only 60% of the time. Considering the intersection of these categories, we find 43.8% of the ESMR codes for the abstract algebra group were High Depth—Empirical as compared to 27.5% in linear algebra. Thus, the abstract algebra group not only focused more on what students actually did (empirical), but these participants were engaging in this evidence in greater mathematical depth.

Table 4 Percentage breakdown of ESMR codes
Full size table

When we look within the ESMR codes for the two groups, we see evidence that the AA participants’ prolonged work with the mathematics appeared to support talk surrounding ESMR as they connected student reasoning that resembled mathematicians’ reasoning in their own mathematical talk. This is contrasted with the LA group in which many of their participants’ ESMR codes, even those of High Depth, made much less explicit connection to their own mathematical thinking and instead focused on what students might do given situational factors (e.g., prerequisite coursework).

Instruction

As a reminder, we grouped instructional comments made by participants during the workshop breakout sessions into three broad categories: statements of instructional principles, statements of instructional choices, and instructional observations. We considered instructional comments that were explicitly linked by participants to their own mathematical thinking, or their explanations of students’ thinking, to be indicative of rich pedagogical reasoning. Thus, we considered an instructional code to be High Depth precisely when it appeared in combination with another code (either DM, ESMR, or a second type of instructional code) and we considered turns of talk to be Instruction—Low Depth if only a single instructional code was assigned in isolation.

Both linear algebra and abstract algebra groups had similar proportions of talk explicitly focused on instructional issues. As shown previously in Fig. 4, the linear algebra participants produced 21 turns of talk that were assigned some instructional code and the abstract algebra participants produced 33 turns of talk coded as either instructional choice, principle, or observation (21% and 22.6%, respectively). Figure 6 shows the breakdown of High and Low Depth for each group.

Fig. 6
figure 6

Instructional codes by depth

Full size image

In the linear algebra group, 28.57% of the 21 turns of talk receiving an instructional code were High Depth. In the abstract algebra group, 57.58% of the 33 turns of talk receiving an instructional code were High Depth. From this, we conclude that the abstract algebra group engaged in richer pedagogical reasoning.

Discussion, facilitation, and limitations

Regarding our research questions, we highlight the following findings. First, we found that the mathematicians in our context engaged in talk about mathematics in two primary ways: as doers of mathematics and as instructors of mathematics. When engaged as doers of mathematics, participants typically engaged with mathematical tasks at a high level of depth. When engaged as instructors of mathematics, participants typically engaged with mathematical tasks at a low level of depth (e.g., describing the kinds of approaches or representations they might anticipate rather than working through the task themselves) or engaged in the tasks based on hypothesized student knowledge, often at a similar level of mathematical depth. We found that mathematicians engaged in student reasoning at varying levels of depth, and that they tended to rely on either empirical evidence or hypothesized student understandings. Further, our analysis indicates a relationship between the depth of the instructors’ own mathematical engagement with the tasks and the depth with which they engage with empirical evidence of student reasoning.

Second, we found that mathematicians engaged in talk about instruction in different ways as related to prior conversations about mathematics and student reasoning. Those who had engaged in talk about mathematics and student reasoning at lower levels of depth tended to focus on describing representational choices and evaluation of student contributions. In contrast, those who had engaged in talk about mathematics and student reasoning in greater depth focused on supporting students in refining their conjectures into mathematically provable statements and how to maintain student authority with regard to notation and symbolizing.

Our findings provide connections to documented pedagogical conceptions among those who teach undergraduate mathematics. There is a strong research base in elementary and secondary mathematics education showing that teachers can learn more about student thinking, and that this knowledge is related to improved instruction (e.g., Jacobs et al. 2010; Carpenter et al. 1996). Our findings provide empirical evidence in support of Speer and Hald’s (2008) conjecture that this finding generalizes to the post-secondary mathematics instructors—and particularly highlights the importance of the work of solving innovative mathematical tasks as an important entry point for undergraduate instructors to learn about student thinking. Further, our data show that this kind of entry point can generate conversations in which post-secondary mathematics instructors quickly come to engage in some of the higher levels of pedagogical awareness featured in Nardi et al.’s (2005) framework. The lowest levels of pedagogical awareness in this framework are marked by tendencies to describe student difficulties in general rather than specific ways (and to blame student difficulties on lack of effort). Intermediate levels of pedagogical awareness are characterized by efforts to analyze student difficulties and speculate on their origins, by monitoring student progress, and by adjusting instruction. At the highest levels of pedagogical awareness, instructors empathized with student difficulties, and linked those difficulties to pedagogical issues in detailed and nuanced ways. Not only did participants in our study engage in reasoning in ways aligned with the most sophisticated forms of pedagogical awareness highlighted in Nardi and colleagues’ work, but they did so in a framing that focused on an asset-based view of student reasoning rather than a deficit-based view.

This analysis has informed an emergent model for an entry point for mathematicians to engage in rich pedagogical reasoning about IOI (see Fig. 7). A primary distinction between this model and our initial hypothetical model (Fig. 1) came from observing how deep engagement in students’ mathematical reasoning built on participants’ own prior mathematical engagement. We argue that this revised model better captures the patterns of talk found in our data. In particular, in the abstract algebra group we saw ways in which the participants explicitly drew on their own mathematical engagement with the tasks as they worked to make sense of student reasoning. Then, when discussing possible instructional decisions, these participants were able to coordinate their own mathematical work, the mathematical goals of the lesson, and their understanding of the students’ reasoning. In contrast, in the linear algebra group, we saw that the participants did not have the same level of mathematical engagement. Without that deep mathematical engagement, we also saw this group rarely attending deeply to empirical evidence of student reasoning, and we saw fewer instances of instructional talk that coordinated student reasoning and mathematical goals. We speculate that, for mathematicians, mathematics (rather than issues more intertwined with pedagogy) may serve as a more productive common entry point for examining student reasoning and related instructional choices. It is reasonable to assume that a group of mathematicians are more likely to hold a common set of shared disciplinary (i.e., content-based) understandings and commitments than they are to hold a common set of shared pedagogical (i.e., instruction-based) knowledge and commitments.

Fig. 7
figure 7

Emergent model for supporting rich pedagogical reasoning about IOI

Full size image

Additionally, the act of making sense of, and utilizing, student contributions is itself a mathematical activity (Johnson 2013). Thus, we argue that the revised model—which forefronts the ways in which teachers must draw on their own mathematical understanding in order to make sense of their students’ mathematical reasoning—better speaks to the teachers’ mathematical activity (Johnson 2013) that is central to implementing IOI. However, we also believe that more research needs to be done to test this model in order to better understand how instructors coordinate, and draw on, their own mathematical reasoning and their students’ mathematical reasoning in order to inform their pedagogical reasoning. A need remains to examine the role of the mathematical tasks themselves in shaping mathematicians’ pedagogical reasoning. In our data set, the two groups engaged in tasks that were notably different with regard to their mathematical framing—with one more oriented toward refining provable criteria, and the other more oriented toward modeling a situation. However, we have no reason to believe the participating mathematicians were differently equipped to engage in the two types of mathematical tasks, yet they did engage in the mathematics differently. Additionally, both groups were given access to empirical data that offered insights into student reasoning, yet the group with deep mathematical engagement was more attentive to that empirical data. Further research is needed to explore issues related to the nature of the mathematical tasks, as well as the nature of empirical evidence highlighting student reasoning, that productively support rich pedagogical reasoning about IOI.

Given the importance of deep mathematical engagement for rich pedagogical reasoning found in our data set, we believe professional development facilitators may need to pay careful attention to how they shape instructors’ engagement in mathematics. In order to consider how our results may inform the design and facilitation of professional development, we want to note some important differences we saw in how the facilitators positioned the workshop participants. After highlighting and exemplifying these differences in facilitation, we discuss some study limitations and present practical implications and conclusions.

Facilitation of Doing Mathematics: disciplinary versus instructional orientations

In reflecting on the facilitation of the workshop, we noted important differences in how the participants in the two groups were positioned for the mathematics tasks. In the abstract algebra group, we see more direct language asking the participants to reason through task sequences from their own mathematical perspective:

AA Facilitator:

I have a question for you, what does the check on closure mean? [points to paper with a check mark] Can you write that out formally for me, please? More importantly can you write out formally the check on inverses? Is it the same thing you would check if you are checking a group? …

In contrast, the linear algebra facilitator opened the session with a discussion that foregrounded participants’ teaching contexts, provided an overview of the task sequence, and tended to prompt participants to engage with the mathematics from more of an instructional perspective:

LA Facilitator:

I am going to ask you guys to entertain the notion, like actually work through it as a student. Does that make sense?

We argue that these subtle differences in facilitation likely influenced participants of the two groups to engage with the mathematics from different perspectives.

Asking participants to “think about it from the perspective of a student” likely primed the linear algebra participants to approach these tasks as a teacher. This could account for why participants, when the facilitator was trying to get them to do the mathematics, speculated about how their students might respond (i.e., ESMR—hypothetical codes) and asked how the tasks played out in classrooms for different student populations (e.g., “how long did they work?” and “can I ask what the prerequisites are for your linear algebra classes?”). This is in contrast to the AA group, where the participants were treated very much like students in an inquiry-oriented classroom. They were asked to work on mathematical tasks in pairs, while the “teacher” (facilitator) circulated through the room asking questions and holding whole group discussions.

As a result, the AA participants engaged from a disciplinary perspective as doers of mathematics, with the vast majority of coded turns of talk on the first day being Doing Mathematics—High. In contrast, the linear algebra participants’ engagement was framed from an instructional lens and, pursuant to that, requests to approach mathematical tasks as their students might create barriers that functioned to obscure their mathematical engagement. We posit that LA participants’ more limited mathematical engagement subsequently interfered with their ability to engage in students’ mathematical reasoning and thus link instructional choices to mathematical goals and student reasoning.

Limitations

Our study carries some limitations. First, our discussion of differences in facilitation is speculative in nature. Other factors could contribute to differences in participant engagement, such as differences in the mathematics and nature of the task sequences and differences in participants’ orientation and prior experiences. Secondly, it is plausible that mathematicians’ prior engagement in the math tasks could lead mathematicians to project their experience onto students. Third, our analytic methods relied on coding turns of talk and thus did not capture the length of turns of talk or attend to key points that were addressed across larger or smaller numbers of turns of talk. Finally, the context for this study—a professional development seminar held for volunteers who were interested in implementing IOI and had reason to believe this would fit their institutional context—likely meant that some of the decision-making factors typically discussed in instructional change literature were alleviated. Thus, the findings presented here largely ignore other situational and individual factors such as resources, values, biases, and institutional context (Schoenfeld 2011; Winsløw et al. 2014). However, even when considering these other factors, we would argue that instructors’ mathematical reasoning and the extent to which they attend to student mathematical reasoning, are necessary for pedagogical decision making in IOI.

Recommendations and concluding remarks

Overall, our findings suggest that when mathematicians’ pedagogical reasoning is engaged through a content-specific mathematical lens, rich and layered connections among their own mathematical reasoning, students’ mathematical reasoning, and possible instructional moves can be forged in a relatively short period of time. We saw this layering evidenced more richly in comments from abstract algebra participants, who: (1) articulated specifics of their own mathematical reasoning at a high level of depth, (2) drew on empirical evidence to engage in students’ mathematical reasoning with a high level of depth, and (3) linked in-the-moment instructional comments with rationales rooted in mathematics and student reasoning about mathematics.

Based on our analysis, we offer two recommendations for designing professional development aimed at supporting rich pedagogical reasoning about inquiry-oriented instruction. First, we propose deep mathematical engagement is better achieved by asking participant to work through task sequences from a disciplinary perspective (their own mathematical lens) rather than from an instructional perspective. Second, we propose that a productive way of engaging participants in students’ mathematical reasoning is to present empirical evidence that emphasizes partially formed student understandings rather than students’ presentations of their final solutions. We conjecture that this approach helps to generate an intellectual need for identifying and discussing possible in-the-moment instructional goals and decisions that an instructor might make to leverage students’ ideas in ways that move forward their mathematical understandings. These recommendations are consistent with the research design employed in other substantial projects that have similarly engaged mathematicians and examined their pedagogical reasoning (e.g., Iannone and Nardi 2005; Nardi et al. 2005).

The data presented in this paper offer a glimpse into the thinking of mathematicians interested in instructional change, and points toward what is possible when mathematics education researchers work with such mathematicians. To that end, this work expands research on pedagogical reasoning to include mathematicians’ reasoning about a particular form of student-centered instruction, namely inquiry-oriented instruction. This is important for informing efforts designed to scale up instructional change in undergraduate teaching (particularly for those interested in designing workshops for mathematicians to learn about student-centered instructional innovations rooted in student reasoning). We further argue that a way to move toward achieving instructional change at scale is by forging sustainable alliances between instructors of undergraduate mathematics and mathematics education researchers, and that these alliances should be structured so as to leverage mathematicians’ deep disciplinary knowledge and teaching experience in ways that can support robust instructional change. By leveraging the unique resources and insights brought to collaborative efforts by both undergraduate mathematics instructors and mathematics education researchers, we as a field will be better equipped to implement changes that support students’ mathematical learning.