Introduction

As typical granular materials, geotechnical materials have crushing characteristics. Rockfill, gravel, calcareous sand, and other easily broken particles [1,2,3] are widely used as main building materials in dam construction, foundation filling of high-speed railways, and offshore engineering, which are related to the long-term safety of the project. The crushing of granular materials will significantly affect the overall strength and deformation characteristics of the soil. Therefore, it is of great significance for related engineering research to explain the crushing laws and their macro- and micro-characteristics responses.

At present, the traditional method of obtaining the stress–strain and shear band changes of samples through experiments and the Discrete Element Method (DEM), which was originally described by Cundall et al. [4] in the 1970s, are applied to the study of particle crushing. Coop et al. [5] conducted a series of ring shear tests to study the variation of calcareous sand breaking with strain. Ghafghazi [6] and Yu [7] investigated characteristics of particle breakage with different stress levels in triaxial shear. Although the results of the experimental method are more intuitive, the method has the disadvantage that the specimens and experimental conditions cannot be accurately replicated, which will inevitably lead to unnecessary errors. The DEM allows precise control of external stress conditions while satisfying the reproducibility of samples. It is well suited to understand the motion between a given combination of particles during loading and is applied to develop and verify the intrinsic relationships of soils, providing an important avenue for particle fragmentation studies. There are mainly two DEM methods to simulate particle breakage: one is the Bonded-Particle Method (BPM) [8], in which multiple small particles are bound into one large particle through contact connections. The large particle will be broken, when the force is greater than the set binding force. Cheng et al. [9] applied BPM to simulate single-particle crushing as well as triaxial tests on cubical samples made of 389 agglomerates, which provided valuable insights into plasticity on crushable soils from micromechanics. McDowell and Harireche [10, 11] et al. simulated the fracture of granular materials by this method and further investigated the yield stress of sand based on oedometer tests. BPM is suitable for simulating particles of different shapes and can reflect the strength characteristics of particle breakage and complex interactions between particles to a certain extent. However, the strength and size effects can only be well reflected if the premise of large-scale particle aggregate crushing is satisfied, which leads to a significant reduction in computational efficiency. And most critically, the internal sub-particles cannot be crushed multiple times. Another method is the Fragment Replacement Method (FRM), which replaces the parent particle with a series of inner-filled daughter particles when fragmentation occurs. Lobo-Guerrero and Vallejo [12] obtained the sub-particle evolution law by simulating two-dimensional particle fragmentation, but the discussion of critical void fraction under two-dimensional conditions is very limited. Marketos and Bolton [13] investigated the particle cementation bond strength and fragmentation condition for the compacted region by three-dimensional DEM, which provided an idea for the study of compaction band initiation and propagation. FRM has the advantage of high computational efficiency, but the accuracy of the simulation results depends on the determination of particle failure criterion and arrangement of the daughter particles. De Bono and McDowell [14, 15] performed a series of one-dimensional normal compression simulations of granular materials but did not address the mass loss problem in crushing. The two main problems of the FRM are the mass conservation (volume conservation) and the number of the generated daughter fragments, which have been studied by many scholars on these two points [16,17,18]. Bun-Nun et al. [19] used a self-organized form of split particles without mutual overlap, which can avoid additional inter-particle forces, but the discriminant condition for fragmentation is still the characteristic strength of individual particles and does not fully consider the effect of local stress concentration in the particles. To ensure mass conservation, Shi et al. [20] used BPM for the first crushing and FRM method for subsequent crushing. But this method still has a non-negligible mass loss for the re-crushing of particles with larger particle size. Cleary [21] and Sinnott [22] improved the organization pattern of sub-particles to reduce the mass loss to some extent, but their results were not the actual grade change. Li [23] et al. used overlapped particles to substitute, which ensured the conservation of mass and volume and reflected the real gradation change. But additional work is introduced in the process of breakage, which changes the condition of contact force and results in the change of crushing amount. While most of the existing studies on the conservation of mass focus on the fragmentation evolution law after the improved self-organization pattern, and rarely study the effect of volume loss on macroscopic properties under the change of confining pressure. However, the effect of volume differences on the macroscopic mechanical properties and the accuracy of simulation results is unclear. Therefore, it is necessary to study the volume conservation problem.

Breakage is defined as the process of turning large particles into small ones under the action of external forces. The problem of volume conservation mainly arises from the form of self-organization of daughter particles during the fragmentation of parent particles to secondary particles. The contact rupture between BPM clusters can visually reflect the particle crushing state, but the accuracy of the results is limited by the particle base. While the breakage of FRM reflects the real crushing situation. The triaxial compression process of fracturable materials is accomplished by both particle rearrangement and particle breakage. Cracking occurs when the local force state of the particles exceeds a given threshold during compaction, and the crack extends from the contact point leading to crushing. The existing failure criteria can be divided into two categories, respectively, the overall particle stress state and the maximum contact force acting on the particle as a criterion to discriminate crushing. The overall stress of the particles is mostly based on the classical fracture criterion, and the average particle stress is usually considered. Such as McDowell et al. [15, 24, 25] applying the Von Mise criterion, Zhou et al. [26] applying the Mohr–Coulomb criterion, and Ben-Nun et al. [27] applying the Drucker-Prager criterion are from this perspective. However, it is also therefore necessary to introduce additional factors to consider the stress concentration in the formulation. When the overall stress does not meet the crushing conditions, the local stress exceeding the ultimate strength of the particle may still cause crushing. Because of the phenomenon of stress concentration, using the maximum contact force of the particles as the limit condition for judging crushing [20] is more in line with the actual crushing situation. Jaeger [28] suggested that the tensile strength of an individual particle can be defined as its failure tensile stress. Therefore, it is more reasonable to use the maximum contact force as the criterion for breakage.

To sum up, this paper combines the discrete element method with different FRM daughter particle self-organization modes to consider the effect of newly spawned particles' volume loss introduced by breakage. By establishing a discrete element triaxial compression model, the role of the volume effect in the variation of specimen grain size distributions (GSDs), the stress–strain characteristics, and the critical state is further discussed. The effect of the particle motion law on the macroscopic properties is analyzed from the microscopic point of view, and then the rationality of using the expansion method to maintain volume conservation is verified.

DEM model of particle breakage

Particle failure criteria

The particle failure criteria need to relate the limitation on certain characteristic strengths to the contact forces acting on the particles. In this paper, the stress concentration in the particle contact process is considered, and the simulation is carried out using the maximum contact force. Fracturing and compression simulations performed by De Bono and Mcdowell [14, 15, 29] for silica sand used two different particle failure criteria and investigated in detail their correctness under normal compression conditions. Russell et al. [30] obtained a two-parameter maximum contact force breakage criterion by performing point load tests on a single spherical particle, which provided a more reliable estimate of compressive strength, and extended it to compression tests with different particle sizes. He [31] then proved that the criterion is also applicable to spherical particle groups with different coordination numbers and indicates that rupture occurs when the maximum contact force exceeds a threshold particle strength value. Under the assumption that the sphere is elastic, \(\kappa_{{{\text{mob}}}}\) at any point will be proportional to the applied load. As the applied load is increased, the maximum \(\kappa_{{{\text{mob}}}}\) attains a value equal to the available strength \(\kappa\).Therefore, the relationship between the limit condition can be expressed as

$$\kappa_{{{\text{mob}}}} \le \kappa$$
(1)

where \(\kappa_{{{\text{mob}}}}\) is the mobilized strength and \(\kappa\) is the intrinsic strength, which is related to the uniaxial tensile and compressive strengths.

When a sphere is subjected to contact forces, a certain amount of this available strength, denoted by mobilized strength \(\kappa_{{{\text{mob}}}}\), will use up. The forces are assumed to act normal with a small area on the surface of the sphere defined by the subtended angle θ0 and radius R (Fig. 1). The symmetrical maxima of \(\kappa_{{{\text{mob}}}}\) is located on and near the diameter of the connecting load center. Under the above stress conditions, the value of mobilized strength \(\kappa_{{{\text{mob}}}}\) can be expressed as Eq. (2). When θ0 is small, ρ given by Hiratsu and Oka [32] can be approximately regarded as the average pressure obtained by dividing the contact force F by the action area Af.

$$\kappa_{{{\text{mob}}}} = f(\chi ,\nu )\frac{F}{{\pi R^{2} \sin \theta_{0} }}$$
(2)
$$f(\chi ,\nu ) = \frac{{\sqrt 3 (1 + \chi^{2} }}{\chi } \cdot \frac{{\left[ {\frac{3}{32} + \frac{\sqrt 2 }{{24}}\left( {\frac{\sqrt 2 }{{12}} - \frac{1}{4}} \right)\nu + \left( {\frac{1}{2} - \frac{\sqrt 2 }{3}} \right)} \right]\nu^{2} }}{{\left( {2 - \sqrt 2 } \right)(1 + \nu )}}$$
(3)
$$A_{f} = \pi R^{2} \sin^{2} \theta_{0}$$
(4)
$$\rho = \frac{F}{{A_{f} }}$$
(5)

where ν is the Poisson ratio; χ is a parameter that reflects the microstructural properties of the material, f(χ,ν) is shown in Eq. (3) as a function of the Poisson ratio of the material and its own properties[30], and its value is between 10 and 170, proposed by Christensen [33]; F is the load value of the particle; R is the radius of sphere; θ0 is the central angle enclosed by the edge point radius and the normal radius through the action of the normal force F. In general, the stresses acting on a given particle can be defined as a second-order tensor in discrete element method. The stress tensor can be expressed as

$$\sigma_{ij} = \frac{1}{V}\sum\limits_{{N_{c} }} {I_{i}^{c} J_{j}^{c} }$$
(6)

where V is the volume of the particle, Nc is total number of contacts on the particle, Iic is the i-th component of contact vector, and Ji is the force acting on j-th component of the contact point. The critical contact force can be obtained from the limit condition

$$F^{\prime } \ge \frac{\kappa }{f(\chi ,\nu )}A_{f} \Rightarrow \sigma_{\lim } = \frac{\kappa }{f(\chi ,\nu )}$$
(7)
Figure 1
figure 1

Range of spherical particles affected by point load and induced equivalent stress

Full size image

From Eq. (7), it can be seen that the ultimate force F′ is affected by the ultimate strength σlim of the particle and the contact area of the force Af.σlim is related to the experimental material and its value increases with decreasing particle size. As the ultimate strength of single particle follows Weibull statistics distribution [34, 35], the relationship between the σlim and the tensile strength of the particle σn under diametrical loading can be related to size by:

$$\sigma = \sigma_{0} \left( {\frac{d}{{d_{0} }}} \right)^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} m}} \right. \kern-0pt} m}}}$$
(8)
$$\sigma_{\lim } = 0.9\sigma_{n}$$
(9)

where σ0 is the characteristic particle strength at diameter d0, which is a value of the distribution such that 37% of the particles survive, m is the Weibull modulus, which decreases with increasing strength.

Self-organization form of fragments

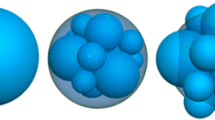
The fragment spawning procedure is another important issue related to particle fragmentation DEM modelling in addition to the particle breakage criterion. The spawned particles are assembled according to the Apollonian sphere packings proposed by Borkovec et al. [36] after a fragmentation event. The limiting fractal dimension of the apollonian packings in most geotechnical materials is close to that found by Coop et al. [5] for particle fragmentation, with a final value of 2.47. Ciantia et al. [17, 37] studied the number of filled daughter particles in a 3D model and showed that 14 non-overlapping spheres satisfy the accuracy condition while ensuring computational efficiency. But the 14 inscribed daughter spheres of the mother particle, which is called the direct filling method (DFM) here, lost more than 40% of the original particle volume after the first crushing. This results in a mass loss of up to 47% at constant sphere density. To ensure the two conservation principles, the method of linear expansion of the volume of the daughter fragments to satisfy the mass conservation after the original crushing and filling are adopted. An overlap-free spawned particles layout by the expansion method is achieved (Fig. 2), the algorithm is shown in Table 1.

Figure 2
figure 2

Sub-particle layouts of FRM after breaking with apollo filling

Full size image
Table 1 Sub-particle expansion algorithm
Full size table

In case of particle fragmentation, the radius and position of the sub-particles can be determined based on Apollo filling. The sub-particles expand as individuals until volume conservation before and after fragmentation is satisfied. In the expansion phase, to avoid local breakage effects caused by excessive sub-particle velocity, a zeroing setting is performed when the velocity exceeds the limit, and multiple expansions are also used to reduce local disturbances.

Crushing causes a local imbalance in the contact of the particles. In this case, the combined forces on the daughter particles can rise abruptly and the force chain including the mother particle breaks, resulting in local collapse. To solve the local imbalance and sub-particle diameter expansion problem, a reduced critical time step in a global–local framework is needed to ensure its stable operation. By means of two discrete dynamic time steps-local time step and global time step, the effects of excessive local stresses between particles as well as internal stress variations can be eliminated by multiple low-velocity expansion in local time step. Thus, the conservation of mass, the conservation of volume and the non-overlapping sub-particle layout are realized. Simplified breakage algorithm is shown in Fig. 3. The particles are discriminated according to the contact force and particle position under the global time step. If no fragmentation occurs, the particle remains under the global time step. If fragmentation occurs, the IDs and positions of sub-particles are updated in the local time step. The sub-particles undergo iterative expansion. In particular, under the expansion process, the values of spin and velocity are set to 0 in order to avoid the extra kinetic energy caused by expansion. After the expansion is completed, the parent particle is replaced by the sub-particle cluster and the parent particle is deleted.

Figure 3
figure 3

Simplified breakage algorithm

Full size image

Discrete element model validation

A series of numerical triaxial tests were performed to simulate drained shear conditions. In this paper, a cylindrical particle aggregate with a height of 40 mm and a diameter of 20 mm was used as the specimen in the numerical model, and the minimum particle size that could be crushed was set at dlim = 0.25 dmin, which dminwas the minimum particle size of the initial material. Both physical test and numerical simulations use specimens with the same gradation distribution. Physical triaxial tests are irregularly shaped particles, while numerical simulations are spherical particles. The particle size of the assembly ranges from 1 to 3 mm. The initial specimen particle size is adopted from the test gradation in Fig. 4. Percentage passing is the percentage of the total mass of the specimen by the mass of a particle passing through a certain millimeter mesh sieve. Since the study of the effect of volume loss on the simulation was the main purpose, the stress variation of the numerical method was calibrated mainly using the results of triaxial tests of calcareous sand in Fig. 5 to determine the corresponding particle parameters and particle fragmentation criterion parameters. In the soil mechanics, the compression direction is taken as the positive direction. The ratio of \({\sigma }_{1}\)- \({\upsigma }_{3}\) to \({\upsigma }_{3}\) is the deviatoric stress ratio and the difference between the deformation length and the original length of the specimen axially divided by the original length is the axial strain. It can be seen that the discrete element model is in general agreement with the macroscopic stress–strain characteristics of the physical tests under different confining pressures. In critical state soil mechanics, the state in which shear drives granular soil toward a state of constant volume and constant shear stress at a constant mean stress is called the critical state. [38] In the triaxial compression test, the critical state needs to be reached at a larger axial strain. 30% of the termination strain is selected in the text. The average value in the strain range of 29%-30% is chosen as the representative value of the critical state.

Figure 4
figure 4

Initial gradation curve of different crush methods

Full size image
Figure 5
figure 5

Simulation of triaxial test results of calcareous sand

Full size image

To validate the DEM model, the input parameters are shown in Table 2.The Hertzian contact model was used [15, 17]. In the plane of void ratio and spherical stress, the critical state line needs to be determined by sufficient critical state points. Therefore, in this paper, five confining stress levels, i.e., 50 kPa, 100 kPa, 500 kPa, 1 MPa, and 2 MPa are used and 0.63 is used as the initial void ratio. The model tests aim to reveal the effect of volume conservation on the deformation characteristics, macroscopic gradation differences, and critical state of the specimens.

Table 2 Input parameters of FRM method for simulation
Full size table

Analysis of numerical test results

To explore the role of volume effects in two forms of daughter particles’ self-organization, a numerical model without particle fragmentation is combined. And the comparison is mainly made in three aspects of grain size distributions, change of stress–strain difference and critical state, and the particle microscopic motion mechanism is analyzed in depth.

Variation of GSDs

Many scholars have proposed different fragmentation parameters by physical experiments to trace the changes in gradation curves [39,40,41,42], and the relative breakage ratio (Br) used in this paper is the concept of relative fragmentation proposed by Hardin to quantitatively describe the GSDs [41], which is shown in Fig. 6 to describe the gradation distribution quantitatively,

$$B_{r} = \frac{{B_{t} }}{{B_{p} }}$$
(10)

where Bt is the total breakage potential, defined as the area enclosed by the 0.074 mm size line, the current grading, and the initial grading curve, Bp is the initial breakage potential, which can be expressed as the area surrounded by the initial grading curve and 0.074 mm particle size line.

Figure 6
figure 6

Illustration for relative breakage ratio of particle crushing amount

Full size image

In the past, the FRM focused more on changes in the number of crushed particles and paid less attention to the post-crushing gradation changes. However, it is worth noting that microscopic volume change has a two-way effect on the macroscale. Figure 7 shows the changes in GSDs in the two methods. At low confining pressure, the crushing amount of both methods is small and has little effect on the gradation. As the confining pressure increases, both gradation curves shift upward, and the difference between the methods is getting bigger, and the expansion method is obviously higher than the directly filling method. Under 2 MPa confining pressure, the difference in grading between the two methods becomes smaller again. Figure 8 shows the volume change after shearing at different confining pressures. It can be seen that the difference in volumetric strain between the two methods is small at low perimeter pressure. The difference between the volumetric strains becomes as the confining pressure increases. At high confining pressures, the difference between volumetric strains becomes smaller again. The reduction of the volume of the filled particles by the Apollo method leads to an upward shift of the grading curve; at the same time, due to the reduction of the sub-particle volume, the ultimate strength of the single-particle increases and further prevents the crushing, which in turn reduces the magnitude of the upward shift of the grading curve. In this paper, while counting the number of crushed and uncrushed particles, the effect of volume loss on the relative breakage ratio is investigated, which in turn quantitatively describes the different patterns reflected by the two filling methods in terms of gradation changes.

Figure 7
figure 7

Grain size distributions of two kind of samples under triaxial tests

Full size image
Figure 8
figure 8

Relationship between volumetric strain and confining pressure after shear completion

Full size image

The relative breakage ratios caused by the two methods are shown in Fig. 9 and Table 3. Br of specimens filled directly by the Apollo method under 50 kPa confining pressure is slightly lower than that of the expansion method specimens following volume conservation. By counting the number of particles, it is clear that the volume loss leads to an increase in the ultimate particle strength with little difference in the number of uncrushed particles. At the same time, the crushing volume is less than the volume conserving specimens obtained by the expansion method due to the limitation of the lower confining pressure level. The differences in the gradation curves at this stage are mainly influenced by the ultimate strength of the sub-particles. However, due to the small amount of crushing, little difference is reflected in the gradation curves. When the confining pressure increases to 100–500 kPa, the difference between the grading curves of different methods is more obvious, and the volume loss of the Apollo method is larger than the volume conservation expansion method. The stress concentration phenomenon caused by the volume reduction of daughter particles due to the change of the confining pressure conditions promotes the fragmentation of adjacent particles in the Apollo method. The particle volume expansion causes the stress concentration effect to be reduced, but the number of broken particles is much higher than that of the directly filling method shown in Table 4, due to the volume effect of the expanded particles reducing the ultimate strength of individual particles, which are the main source of the number of broken particles. The difference in the number of crushed particles at this stage is greater than that at the previous stage. While the number of uncrushed particles for the directly filling method is significantly less than that for the expansion method. Therefore, the main factor causing the upward shift of the grading curve at this stage originates from the number of uncrushed particles. When confining pressure increases to 1–2 MPa, the expansion method specimens upward shift more than the direct Apollo filled specimens. The variability of the grading curves again decreases with the increase of the surrounding pressure. A further increase in stress level leads to more initial particle fragmentation. Larger volume sub-particles have a higher fragmentation probability. With these two effects, the expansion method far exceeds the Apollo direct filling method in terms of the number of crushed particles. Therefore, there exists the equilibrium point of the volume loss effect mentioned before, which leads to the alternating position of the grading curve. And there is a volume loss point that makes the maximum difference in the gradation curves. Beyond this point, as the confining pressure increases, the two gradation curves start to approach each other and converge to the ultimate crushing curve at the same time.

Figure 9
figure 9

Relationship between Br and confining pressure

Full size image
Table 3 Br of two samples under different confining pressures
Full size table
Table 4 Statistics of broken particles and unbroken particles of samples
Full size table

Characteristics of strength and deformation

Previous studies have concluded that the Apollo layout has a small effect on the strength properties of the particles. Figure 10 shows the results of the volumetric strain and stress–strain simulation considering the volume loss factor in this paper. The specimens reached the peak strength at the beginning of shear at a small shear displacement. As the confining pressure increases, the shear strain required to reach the peak strength increases. The post-peak strength undergoes different degrees of stress drop, which is consistent with strain softening characteristics. Under the condition of lower confining pressure, the amount of particle breakage is very small. The unbroken particles play a major role, and the main skeleton of the sample still dominates the stress maintenance. The stress curve is therefore not subject to mass loss. The stress variation trends of the two forms of self-organization are almost the same, but both strengths are lower than that of unbroken particles. The crushing of the direct filling method specimens surges with increasing confining pressure. The effect of mass loss on stress variation starts to come to the fore. The volume loss effect due to the direct filling method is further enhanced at 500 kPa confining pressure. The difference between the two stress variation curves is more obvious, and even the difference between strain-softened and strain-hardened types appears. This is due to the reduction in the volume of the replacement sub-particles resulting in larger voids in the specimen. The stress concentration phenomenon tends to be obvious, and more initial particles produce crushing. However, their volume loss leads to a larger single-particle ultimate strength, which has an inverse effect on the amount of crushing. At low confining pressure levels, this crushing equilibrium effect is not sufficient to affect the stress trend. As the confining pressure level increases, it causes the crushing difference to be accentuated. From the simulation results, it can be concluded that there is a volume loss effect equilibrium point. Exceeding this point leads to a divergence of stress trends. Its positive promotion effect on the crushing volume starts to gradually exceed the negative hindrance effect. In contrast, the replacement sub-particles by expansion do not affect their ultimate strength and do not change the force conditions of the surrounding initial particles. This directly leads to the difference in the trend of stress change between the two. The particles in Fig. 11 are crushed particles. The crushed particles produced by the directly filling method are more dispersed, while the crushed particles produced by the expansion method are mostly concentrated within the circle. Meanwhile, it can be seen that the expansion method results in volume conserved specimen following a pattern of fragmentation along with the shear band.

Figure 10
figure 10

Stress–strain curves of two different crush

Full size image
Figure 11
figure 11

Comparison of broken bond of two samples under triaxial tests

Full size image

The stress changes of the expansion method and the direct filling method converge again for the cases of 1 and 2 MPa of the confining pressure. This is since the fact that the ultimate strength of the latter sub-particles is higher than that of the former at high confining pressure levels. The reverse hindrance of crushing is enhanced by the direct filling method.

From the strain curves of the three specimens, it is clear that the volumetric strain of the unbroken specimens is only related to the degree of void compression. The dilatancy phenomenon eventually appeared in the specimens under each confining pressure condition. However, as the force level increases, the shear contraction is significantly enhanced while the shear dilatation is weakened. The shear contraction of the expansion method specimens is further enhanced compared to the uncrushed specimens. This is due to the filling of voids by small crushed particles, resulting in a further reduction of the volumetric strain. It is noteworthy that under the 500 kPa confining pressure condition, there is still a tendency for shear dilatation in the expanded specimens. The direct filling method is more fully crushed, resulting in increased porosity, smaller sub-particles, and more adequate filling of the voids. Affected by these two aspects, the shear contraction of the specimens is more obvious compared with the expansion method. With the increase of the confining pressure to more than 1 MPa, both crushed specimens were contracted, which also proved the existence of the equilibrium point of the volume loss effect.

Critical state lines

The critical state lines in the q–p plane are shown in Fig. 12 were obtained by critical state point fitting. The critical state lines of all three simulated specimens in this plane pass through the coordinate origin. All three fitting coefficients R2 are up to 0.99 or more, which can be expressed by the equation q = Mp. The critical state stress ratio of unbroken particles is Munbroken = 1.762, the critical state stress ratio of volume loss particles is Mloss = 1.853, and the critical state stress ratio of volume conserved particles is Mequal = 1.851. The critical state stress ratios of the two broken specimens are approximately equal. Therefore, it can be seen that volume loss does not affect the final critical state stress ratio.

Figure 12
figure 12

Critical state line in q-p plane

Full size image

Figure 13a shows the distribution of the critical void ratio state points for the numerical tests of three different samples. Since the gradation and initial void ratio of the three are the same, the shift of the critical state line mainly comes from the difference in fragmentation. The state line where particle breakage does not occur is called the initial critical state line. From the fitting curve results of the critical state point, the initial critical state line gradually decreases with the increase of the confining pressure. The compression causes the critical void ratio to drop. The curve of the expansion method shifts overall to below the initial critical state line. The change of the critical void ratio is influenced by the initial void being compressed. At the same time, the filling of the specimen by crushed sub-particles leads to further compression. The specimens of the direct filling method did not affect the critical state line under the initial confining pressure. As the force level increases, the critical state line gradually shifts downward. The larger the confining pressure is, the larger the downward shift is. The volume loss has two effects on the critical state. On one hand, the particle volume reduction causes the porosity to be elevated and the compressibility to become stronger. The volumetric strain thus increases and there exists a positive effect on the compression. On the other hand, sub-particle volume loss and filling of voids by fine particles make the specimen denser and prevents the volume from being compressed. The reduction in daughter particle volume leads to increased difficulty in crushing. This creates resistance to continued filling and produces a negative effect. However, the negative effect gradually decreases at large shear displacements. And the effect on the void ratio diminishes as the stress level increases.

Figure 13
figure 13

Critical state line in e-p plane

Full size image

Li et al. [43] found that the critical state lines in the e − lgp plane of sandy soils are irregular curves. However, it can be approximated by a straight line in the \(e - \left( {{p \mathord{\left/ {\vphantom {p {p_{a} }}} \right. \kern-0pt} {p_{a} }}} \right)^{\xi }\) plane, which is given by

$$e_{c} = e_{\Gamma } - \lambda_{c} \left( {\frac{p}{{p_{a} }}} \right)^{\xi }$$
(11)

where ec is the critical void ratio, eΓ is the critical void ratio when the effective spherical stress is 0, λc is the slope of the critical line, ξ is the material parameter, which is taken as 0.7 in this paper, and Pa is the atmospheric pressure. The slopes of the fitted curves for the expansion method and the unbroken samples were 0.0431 and 0.0411, respectively, which were approximately parallel. While the slope of the direct filling method fitted straight line is 0.0812 and the fitting accuracy is lower than the other two lines as shown in Fig. 13b.

Microscale responses

The trajectory of particle motion, as well as the particle motion velocity vector center profiles of the specimens under 1 MPa confining pressure, are given in Figs. 14 and 15. Both methods have intense motion in the particle crushing zone, while the motion at the initial particles is not obvious. The trajectory of the direct filling method is mainly concentrated in the particle crushing region and shows disorder. While the overall motion trend of the expansion method is extended from the upper and lower loading plates to the middle of the specimen. The trajectory covers the broken particles, and the end triangle region is obviously broken. From the velocity vector, it can be seen that the sub-particles of the direct filling method are affected by the plunge at replacement and cannot maintain the original motion direction. The expansion method makes the upper and lower end tapered sections move approximately vertically, which can be identified as the elastic region. In the middle of the profile the velocity turns horizontally and the closer to the middle the more obvious the deflection is, showing a symmetrical decreasing phenomenon.

Figure 14
figure 14

Particle trajectory of samples under 1 MPa confining pressure

Full size image
Figure 15
figure 15

The particle velocity vector figure of samples under 1 MPa confining pressure

Full size image

Figure 16 gives the displacement nephogram in the central longitudinal section under different strains of the two specimen numerical models. The comparison shows that the initial displacement development is approximately the same. As the axial strain increases, the difference in particle displacement is gradually accentuated. The direct filling method shows a certain regularity in shear morphology at the time of damage. That is, the end effect is obvious, but the particle displacement variability in the middle of the specimen is small and always shows uniform expansion. The overall displacement variation of the expansion method is more clear. Its nephogram better reflects the formation of the shear zone. The particles in the middle part of the specimen exhibit non-uniform dilatation when the specimen is damaged. This leads to a difference in displacement, which results in an “X” shaped distribution of the shear zone.

Figure 16
figure 16

Numerical simulation displacement nephogram at different axial strains

Full size image

As the mechanism of force transmission in discrete elements, the evolution and distribution of the force chain play a crucial role. Figure 17 shows the central profile of force chain development under different axial strains. With the increase of axial strain, the force chain appears to develop gradually from an initial more uniform distribution toward the end. In combination with Figs. 15 and 16, the application of the expansion method results in a more regular movement of the end particles. The axial force chains are transferred early through the contact generated by the particle motion. The number of force chains is significantly more than that of the direct filling method specimens. With increasing shear displacement, the force chain development tends to be consistent for the specimens of both methods. In addition, the coordination number, as an index to evaluate the overall contact stability of the specimens, is also important for the distribution of force chains. The critical coordination number of the volume conserved specimen is 5.212189, and the critical coordination number of the volume lost specimen is 5.154938. The difference between them is very small. The force chain distribution and the coordination number together determine that the critical stress ratios of the two methods are approximately equal.

Figure 17
figure 17

Development of contact force chain in the center section of samples under 1 MPa confining pressure

Full size image

Comparative analysis with physical tests

The effect of model parameters has a great influence on the simulation results, but the final simulation law obtained needs to be consistent with the triaxial experiment (Fig. 18). The triaxial test materials and test conditions are shown in Table 5. Based on the consideration of the correctness of the numerical model, the influence of the expansion method on the simulation results is analyzed.

Figure 18
figure 18

Triaxial test specimen

Full size image
Table 5 Test scheme
Full size table

Figure 19 shows the comparison between the results of the expansion method and the physical experimental method under 400 kPa confining pressure, respectively. It can be seen that for the stress variation trend, the variability between the numerical simulation results and the experimental results is relatively small. However, the volume of the sub-particles plays a crucial role in the axial strain versus the volumetric strain. Both physical experiments and expansion method simulation results show significant shear dilatation. However, the direct filling method continuously maintains shear contraction with volume loss due to crushing. Although the stress changes of both the direct filling method and the expansion method meet the experimental results at lower envelope pressures, the difference in volumetric strains between the two is significant as the crushing proceeds. Therefore, the expansion method ensured the reasonableness of the volume change.

Figure 19
figure 19

Results obtained by simulation methods and physical experiment

Full size image

Conclusions

A three-dimensional discrete element model is established based on the mass conservation and volume conservation considerations of daughter particle’s self-organization. The response of volume effect to macroscopic properties such as deformation characteristics, GSDs, and critical line variation is analyzed and concluded as follows.

  1. 1.

    The existence of the equilibrium point of the volume loss effect is verified. This point affects the stress–strain variability and is directly related to the stress level of the specimen. The softening curve is converted to hardening by the influence of this point. The volumetric strain is also influenced by this point from shear dilatation to shear contraction.

  2. 2.

    It can be seen that the difference in GSDs originates from the bidirectional influence of the volume loss of sub-particles on the crushing through quantitative analysis of the crushing rate and the number of particles. At a low-stress level, the volume loss promotes the crushing, and the gradation difference becomes larger with increasing stress levels. At a high-stress level, the volume loss hinders crushing and the gradation curve tends to move to the ultimate crushing curve and the difference becomes smaller.

  3. 3.

    The effect of volume loss on the critical state line is complex. Although the volume loss has a significant effect on the stress change during shear, it don’t affect the critical stress ratio. The decrease in the critical void ratio due to volume loss increases with the increase in the confining pressure.

  4. 4.

    From the microscopic displacement development, particle motion, and force chain development, it is clear that the microscopic characteristics of the expansion method are more consistent with the crushing law. Its macroscopic mechanical characteristics reflect more reasonably.

The expansion method is verified by the results of triaxial tests. The application of this method needs to be further research on experimental comparison studies. This study was only performed in same GSD. The macro and micro characteristics due to particle breakage needs to be investigated in other conditions.