Introduction

The weight reduction in airplanes is one of the big challenges in aerospace industry. In order to achieve the ambitious goals considering fuel consumption and emission reduction, new airplanes with more than 50 wt% of composite materials, mainly carbon fiber reinforced plastics (CFRP), were introduced to the market [1]. Future efforts are to be focused on manufacturing efficiency as well as on breakthrough solutions for damage tolerance and function integration. Compared to aluminum alloys, contemporary CFRP solutions for airframe structures offer poor electrical and thermal conductivities. In order to improve these properties, the outer airplane structure is covered with an expanded copper foil according to lightning zoning requirements. Moreover, CFRP shows brittle failure behavior, limiting the structural integrity in crash load cases. The limited damage tolerance against impact events leads to a minimum wall thickness criterion. Against this background, a new hybrid composite material, consisting of reinforcing carbon and steel fibers embedded in an epoxy matrix, is investigated. Basic idea of this material concept is to combine electrical and load-bearing functions by incorporating highly conductive and ductile stainless steel fibers. The increased density of the composite is overcompensated by eliminating the need for additional electrical system installation items and the enhanced damage tolerance, resulting in a reduced minimum wall thickness. Within this topic, the mechanical strength of these new hybrid materials is an important property. Because of the anisotropy of fiber reinforced plastics (FRP), the mechanical strength has to be determined by a multitude of experimental techniques (tensile/compression tests in fiber direction and transversal to fiber direction as well as tests for several combined tension/compression and shear loads). Thus, it is desirable to model and simulate the strength of hybrid composites in order to reduce the experimental efforts and costs. The present study focuses on determining the effective strength of hybrid steel/carbon fiber reinforced plastics (SCFRP) for unidirectional plies. A representative volume element (RVE) and a homogenization approach are used to calculate the effective material properties based on micromechanical models.

Homogenization and representative volume element

For transversally isotropic and linear approximable materials like CFRP, the prediction of some effective material properties is possible by using simple rules of mixture [2]. However, the prediction of effective strength by rule of mixtures is not accurate enough, because of the oversimplification of the micromechanical stress states. This is particularly true for loadings transverse to the fiber direction and for shear loadings. Thus, homogenization methods that rely on the identification of a representative volume element (RVE) [3] have to be used. The RVE is a finite-sized sample from the heterogeneous material which characterizes its macroscopic behavior [4,5,6,7,8]. A general requirement for a RVE is that the typical dimension of the heterogeneities should be much smaller than that of the RVE. This is true for RVEs that are generated using the geometrical data such as the volume fraction as well as using the mechanical information such as strain and stress. Moreover, the size of the RVE should be much smaller than the typical dimension of the macrostructures. This is known as the micro–meso–macro principle, where micro, meso and macro refer to the microstructure, RVE size and macrostructure, respectively [9, 10]. Generally, the size of the RVE is given by the smallest unit cell in the case of heterogeneous materials that possess local or global periodicity, provided that appropriate boundary conditions are used in the homogenization analysis [11,12,13]. However, this procedure might fail when deviations from periodicity or material instabilities occur on the microscale [14,15,16]. For the numerical simulations, three different types of boundary conditions for the RVE might be used: linear displacement, uniform traction and mixed type [4, 5, 17, 18]. The periodic boundary conditions belong to the mixed type and are the preferred choice, particularly for materials with linear properties [12, 19, 20]. The homogenization approach is well established for linear material properties [7, 12]. The nonlinear, inelastic issues have been studied for infinitesimal and finite deformation as well [21,22,23,24,25,26,27,28].

The homogenization procedure is based on the assumption that an arbitrary physical quantity \( f\left( x \right) \) of a considered volume V (e.g., stress, strain and conductivity) can be split in their macroscopic mean value \( \bar{f}_{V} \) and a microscopic fluctuation \( f^{\prime } \left( x \right)_{V} \). Moreover, it is assumed that the averaged microscopic fluctuations are negligible small for a sufficiently large representative volume element (RVE). Therefore, the physical quantities on macroscopic scale can be determined by means of the volume integral shown in Eq. (1) [29].

$$ f\left( x \right) = \bar{f}_{V} + \underbrace {{f^{\prime } \left( x \right)_{V} }}_{ = 0} = \frac{1}{V}\int\limits_{V} {f\left( x \right)} \;{\text{d}}x. $$
(1)

In order to determine the size of a sufficiently large RVE, it has to be considered that the RVE needs to represent the volume fraction and the topology of the given hybrid composite. That means that the fiber and matrix volume fractions and the fiber arrangements should represent the composite as accurately as possible [30].

Within this study, carbon fibers with a diameter of d c = 7 µm and steel fibers with a diameter of d s = 8 µm are used. Based on this basic geometric dimension, the generated RVEs of the hybrid composites fulfill the following requirements:

  • Square- and hexagonal-packed RVEs are investigated

  • The epoxy resin volume fraction (C E) is around 40%

  • The steel fiber volume fraction (C S) is varied between approximately 10 and 30% volume ratios in at least three steps

  • RVEs for pure CFRP and pure steel fiber reinforced plastics (SFRP) should be built in order to compare their effective properties with those of the hybrid composites.

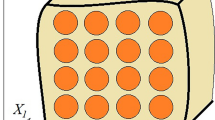
The smallest RVE that fulfills all requirements contains 16 fibers for square arrangements (Fig. 1a) and 18 fibers for hexagonal arrangements (Fig. 1b). In respect of the fiber diameters, this leads to RVEs of a cross-sectional size between 1026 and 1341 μm2 for square arrangements and 1154 and 1508 μm2 for hexagonal arrangements. The depth for both kinds of ideal-packed RVE is 2.5 μm. Additionally, recorded micrographs exist for non-hybrid SFRP (Fig. 1c) and non-hybrid CFRP (Fig. 1d), which allow to build RVE with a quadratic cross-sectional size of 10000 μm2. The depth of such real RVEs is 4 μm. The coordinate system for all RVEs is chosen in such a way that the 1-direction is the fiber direction and the 2- and 3-directions are the directions transverse to the fiber. For the ideal-packed RVEs (Fig. 1a, b), the origin of each coordinate system is placed in the center of volume of the RVE.

Figure 1
figure 1

Different RVEs: a square arrangement; b hexagonal arrangement; RVE based on micrographs for SFRP (c) and CFRP (d)

Full size image

Modeling and simulation

The macroscopic effective material properties of hybrid polymer composites reinforced by carbon and steel fibers, which represent the behavior of the whole composite, are determined from the properties and material models selected for each individual phase. This study restricts to the investigation of tensile and shear loadings using the finite element program ANSYS. In order to simulate the effective strength, it is necessary to take the nonlinear material behavior into account. Therefore, the flowchart shown in Fig. 2 is implemented in ANSYS Parametric Design Language (APDL).

Figure 2
figure 2

Program flowchart to calculate the effective strength of fiber reinforced composites

Full size image

In a first step, the material properties, the geometry and the mesh are defined. All RVEs are meshed with second-order 3D SOLID186 elements. The fiber matrix contact is assumed to be ideal and is modeled by sharing their nodes at the interface. According to the components of the hybrid composite, three different material models are used. All components are assumed to be isotropic. For the carbon fiber a linear elastic model and for the steel fiber a bilinear elastic–plastic material model are applied. For the epoxy resin, the stress–strain curve measured in Hobbiebrunken et al. [31] is adopted. The used material parameters are listed in Table 1.

Table 1 Material parameters for the steel fiber, the carbon fiber and the epoxy resin
Full size table

Afterward, a predefined strain state of ε i  = 0 is chosen which is increased sequentially. Based on a given strain state, the boundary conditions (BC) are calculated. Taking into account that a RVE can only represent a small part of a composite material, periodic BCs representing the predefined strain state are used. The ideal-packed RVEs used in this study are modeled with center-based coordinate systems and are at least orthotropic; see Fig. 1a, b. Due to orthotropic symmetry, the model size for tensile and compression loadings can be reduced to 1/8 of the original RVE. This means that all nodes, which are initially placed at the coordinate planes, remain at the coordinate plane as shown in Eq. (2).

$$ {\text{at}}\;x_{1} = 0, u_{1} = 0;\quad {\text{at}}\;x_{2} = 0, u_{2} = 0;\quad {\text{at}}\;x_{3} = 0, u_{3} = 0 $$
(2)

Nodes at the outer faces are coupled in the direction perpendicular to the plane.

$$ {\text{at}}\;x_{1} = \frac{{L_{1} }}{2}, u_{1}^{i} = u_{1}^{j} = \cdots ;\quad {\text{at}}\;x_{2} = \frac{{L_{2} }}{2}, u_{2}^{i} = u_{2}^{j} = \cdots ;\quad {\text{at}}\; x_{3} = \frac{{L_{3} }}{2}, u_{3}^{i} = u_{3}^{j} = \cdots $$
(3)

The lengths L 1,2,3 are the side length of the full RVE, and i and j are representative, local node numbers of nodes on the plane. At the three planes shown in (3), a displacement BC can be applied additionally, which is calculable out of the given strain state [see Eq. (4)]. If no strain is given, the faces are only coupled as seen in Eq. (3). So the transverse contraction is not hindered macroscopically in this direction and the homogenized stress in this direction is zero.

$$ {\text{at}}\;x_{1} = \frac{{L_{1} }}{2}, u_{1} = \varepsilon_{1} \cdot \frac{{L_{1} }}{2};\quad {\text{at}}\;x_{2} = \frac{{L_{2} }}{2}, u_{2} = \varepsilon_{2} \cdot \frac{{L_{2} }}{2};\quad {\text{at}}\; x_{3} = \frac{{L_{3} }}{2}, u_{3} = \varepsilon_{3} \cdot \frac{{L_{3} }}{2} $$
(4)

This approach is also applicable for RVEs based on micrographs (Fig. 1c, d), since their material behavior can be assumed as quasi-orthotropic for sufficiently large RVEs. For this, the coordinate system is shifted to the RVEs corner and the 1/8 boundary conditions are applied analogous; see Eqs. (2), (3) and (4).

With the 1/8 method, only tensile and compression loadings can be applied. For shear loadings, the assumption that nodes can remain within the coordinate planes is not valid. Hence, the full RVE has to be used and the nodes at opposing sides are coupled with constrain equations (CE). Therefore, the displacement difference u of these nodes in each direction is constant. The constant value is determined from the given strain state ε ij and the side length of the RVE L i . Equations (5)–(7) show the used CEs in vector notation.

$$ {\text{at}}\;x_{1} = \pm \frac{{L_{1} }}{2}, \quad \varvec{u}\left( {\frac{{L_{1} }}{2},x_{2} ,x_{3} } \right) - \varvec{u}\left( { - \frac{{L_{1} }}{2},x_{2} ,x_{3} } \right) = L_{1} \left[ {\varepsilon_{11} \varepsilon_{21} \varepsilon_{31} } \right]^{\text{T}} $$
(5)
$$ {\text{at}}\;x_{2} = \pm \frac{{L_{2} }}{2},\quad \varvec{u}\left( {x_{1} ,\frac{{L_{2} }}{2},x_{3} } \right) - \varvec{u}\left( {x_{1} , - \frac{{L_{2} }}{2},x_{3} } \right) = L_{2} \left[ {\varepsilon_{21} \varepsilon_{22} \varepsilon_{23} } \right]^{\text{T}} $$
(6)
$$ {\text{at}}\;x_{3} = \pm \frac{{L_{3} }}{2}, \quad \varvec{u}\left( {x_{1} ,x_{2} ,\frac{{L_{3} }}{2}} \right) - \varvec{u}\left( {x_{1} ,x_{2} , - \frac{{L_{3} }}{2}} \right) = L_{3} \left[ {\varepsilon_{31} \varepsilon_{23} \varepsilon_{33} } \right]^{\text{T}} $$
(7)

To guarantee a statically determined system, the node in the center of the RVE has to be fixed. These BCs, which allow a periodical deformation of the RVE, are set automatically within an APDL macro. To reduce computational time, only the constant term of the CE is changed, if the strain state changes.

In the next step, the finite element problem is solved by the ANSYS implicit solver using the Newton–Raphson method. The macroscopic stresses are determined from the microscopic ones following the described homogenization technique; see “Homogenization and representative volume element” section. Due to the discretization, the volume integral [cf. Eq. (1)] can be replaced by a discrete finite sum, as shown in cf. Eq. (8). Each component of the homogenized stress tensor σ hom for the whole RVE can be calculated out of the total volume V tot of the RVE, the volume of each finite element V el,i and the corresponding component of the element stress tensor σ el,i of each element. The element stress tensor σ el,i is the mean value of all integration point values of this element.

$$ \sigma_{\hom } = \frac{1}{{V_{\text{tot}} }} \mathop \sum \limits_{i = 1}^{n} \sigma_{{{\text{el}},i}} \cdot V_{{{\text{el}},i}} $$
(8)

After each homogenization step, the hybrid composite is checked for failure states. Therefore, different failure criteria are considered for each constituent. For the brittle carbon fibers the maximum principal stress criterion and for the ductile steel fiber the von Mises criterion are used. For the epoxy resin, both equivalent stresses are applied to evaluate the influence of the criteria for inter-fiber failure. If failure occurs, a stiffness degradation strategy is used inside the corresponding finite elements. For tensile loadings, the simulation stops if a predefined maximum strain ε max (cf. Fig. 2) is reached. ε max is chosen 10% higher than the highest breaking elongation of all the composite components (cf. Table 1). For loadings transversal to fiber direction and for shear loadings, it is assumed that the composite fails due to inter-fiber failure and the simulation stops, if the first failure is detected. To simulate failure curves and 3D failure surfaces, a similar procedure including a second iteration loop is considered. The first outer iteration loop is used to vary the strain state, and the second loop iterates over the magnitude of the chosen strain state as explained above. In this case, the simulation stops when the first outer iteration loop ends, after all defined strain states are sampled.

Results and discussion

For the investigation of the stress–strain behavior in fiber direction and transversal to fiber direction 1/8 RVEs and for shear loadings full RVEs are used. The failure envelopes are computed by using the extended program sequence consisting of the inner and the outer iteration loop. The failure envelopes are compiled for different superposed tensile loadings. A comparable analysis for different arrangements and other failure criterions is feasible.

Uniaxial tensile loading in fiber direction

For uniaxial tensile loading in fiber direction, the stress–strain diagrams for different C S are displayed in Fig. 3 (left). The results for CFRP (C S = 0%) show a linear material behavior with a brittle fracture when the breaking strain (ε = 2.13%) is reached. The stress–strain diagram for SCFRP shows a bilinear material behavior with a kink at ε = 0.25% and decreasing strength with higher C S. This bilinear behavior is caused by the plastic deformation of the stainless steel fibers which decreases their load carrying capacity for uniaxial strain states higher than ε = 0.25%. After the degradation of the carbon fiber at ε = 2.13%, the steel fibers are still intact. This behavior is caused by the used stiffness degradation strategy, which reduces the stiffness of all affected finite elements. In this case, the remaining load carrying capacity of the steel fibers increases for high CS up to the load carrying capacity of pure SFRP (C S = 60%), which shows no break at ε = 2.13%.

Figure 3
figure 3

Stress–strain curves for tensile loadings in fiber direction of hexagonal RVE with different C S (left); stress–strain curves for tensile loadings in fiber direction of hexagonal RVE with C S = 30.7% using full degradation and degradation at coordinate plane (right)

Full size image

Another degradation strategy reduces the stiffness only for the affected finite elements at the symmetry plane; see Fig. 3 (right). In this case, a load transfer occurs between the carbon and the steel fibers. The elastic energy previously carried by the carbon fibers now must be carried by the steel fibers. In dependency of C S (it is assumed that the steel fibers still remain intact after the degradation of the carbon fibers for significantly higher C S), the resulting strain state leads to the failure of the steel fibers, too. Due to the chosen static analysis, the influence of the dynamic effects of the load transfer between the carbon fibers and the steel fibers can be neglected.

Table 2 shows that the use of hexagonal-, square- and real-packed RVEs has no impact on the strength results in fiber direction R 1,FEM because all results show a relative deviation of less than 0.1% compared to the strength calculated by simple rules of mixtures R 1,analytic. This verifies that the chosen RVEs represent the properties in fiber direction for the tested composite (see “Experimental verification” section) sufficiently.

Table 2 Comparison of the simulation results in fiber direction with simple rules of mixtures
Full size table

Uniaxial tensile loading transversal to fiber direction

The stress–strain diagram for tensile loadings transversal to fiber direction is shown in Fig. 4 (left). To visualize the strength results, the end of the stress–strain curves is connected to the x-axis with a vertical line. The curves show a nonlinear hardening behavior. The strength in 2-direction is on average 37% higher than in 1-direction. For pure CFRP and pure SFRP, the strengths reach their maximum. For hybrid composites, the strength values are lower and decrease with higher CS. This is mainly caused by the decreasing distances between the fibers within the corresponding RVEs resulting in the higher fiber diameter of the steel fibers. Due to the assumed isotropic material behavior of the carbon fiber and the resulting very small difference between the stiffness of the carbon and the steel fiber in transverse direction of the fiber, the influence of the stiffness on the tensile strength transversal to fiber direction is not investigated. Square-packed RVEs show the same dependence of the steel fiber content. As it was expected, the behavior in 2- and 3-directions is identical.

Figure 4
figure 4

Stress–strain curves for tensile loadings transverse to fiber direction of hexagonal RVE in 2-direction (continuous line) and in 3-direction (dashed line) with different C S (left); stress–strain curves of hexagonal RVE, square RVE and RVE based in micrographs using the von Mises criterion (continuous line) and the maximal principle stress criterion (dashed line) for pure SFRP in 2-direction (right)

Full size image

Figure 4 (right) shows the result of the comparison between the hexagonal-, square- and real-packed RVEs for an SFRP in 2-direction. It can be observed that the stiffness depends on the fiber arrangement of RVE (19.4 GPa for square RVEs, 13.65 GPa for hexagonal RVEs and 15.32 GPa for RVE based on recorded micrographs). On average, the predicted strength based on the von Mises criterion is 98% higher than the strength based on the maximum principal stress criterion. The strength for the real arrangement is at least two times lower than the strength of the ideal arrangements (R 2,real = 18.3 MPa; R 2,hex = 63.6 MPa; R 2,square = 39.6 MPa) when using the maximum principal stress criterion. For the von Mises criterion, the strength is also reduced for the real arrangement (R 2,real = 53.6 MPa; R 2,hex = 88.6 MPa; R 2,hex = 98.16 MPa).

Shear loading

For shear loadings, the resulting stress state leads to an inter-fiber failure. For the failure criterion and the yield criterion, the von Mises stress is taken into account. For shear loadings, the von Mises criterion is more conservative than the maximum principal stress criterion. As soon as the end of the stress–strain curve of the epoxy resin is reached, the material behaves ideally plastic and the maximum principal stress can never reach the strength. For this reason, the maximum principal criterion is not considered in this study.

Figure 5 shows the stress–strain curves of RVEs with hexagonal and square arrangements for pure CFRP (C s = 0%). The stress–strain curves show a typical hardening behavior. The shear stiffness G 12 and the shear stiffness G 13 are for hexagonal (4.3 GPa) and square (4.7 GPa) arrangements in the same dimension. The shear stiffness G 23 is for square (3.1 GPa) arrangements 26% lower than for hexagonal (4.2 GPa) ones. The strength R 23 shows in mean 3.2% higher values than the strengths R 12 and R 13 for square arrangements. Hexagonal RVEs show 22.6% higher strengths for loadings in 1–2- or 1–3-directions than for loadings in 2–3-directions.

Figure 5
figure 5

Results for hexagonal and square RVE out of CFRP for shear loading

Full size image

Failure envelopes

In general arbitrary, external loads generate a complex stress states inside a composite. In such cases, failure envelopes are needed to indicate the failure behavior for these multiaxial loadings. Figure 6 (right) shows the failure behavior for CFRP (black), SFRP (magenta) and hybrid SCFRP with different fiber volume fractions (red, green, turquoise and blue).

Figure 6
figure 6

3D failure surface for CFRP with hexagonal RVEs (left) and 2D failure curves for square RVEs with different steel fiber fractions (right)

Full size image

The strength in 1-direction is in mean 35 times higher than in 2-direction. In order to visualize this difference, the 2-axis is scaled. Because the strength in 1-direction is mainly influenced by the carbon fiber volume fraction and the strength in 2-direction is mostly influenced by the C S, the different failure curves intersect each other. The 3D failure surface, shown in Fig. 6 (right), visualizes the failure behavior of pure CFRP according to the three stress components σ 1, σ 2 and σ 3. From these results, it is possible to identify the areas where the fiber fails (blue) and where inter-fiber failure occurs (rest of 3D failure surface). The color of the inter-fiber failure surface indicates the distance to the 1-axis. It is shown that the strength in 3-direction can be enhanced, if there is a non-negligible stress in 2-direction for ideally hexagonal RVE.

Experimental verification

Hannemann’s et al. [32, 33] experimental investigations on hybrid composites reinforced by carbon and steel fibers allow a validation of the simulation results. In order to assess the electrical and mechanical properties of carbon and steel fiber reinforced epoxy resin, Hannemann manufactured various uniaxial reinforced hybrid composites with various fiber proportions and fiber arrangements by a combination of tape deposition and filament winding technology. The laminates had a thickness of approximately 1 mm. Examples are shown in Fig. 7.

Figure 7
figure 7

Architecture and fiber volume fractions of manufactured laminate SCFRP 1 and SCFRP 2 (C C = carbon fiber volume fraction; C S = steel fiber volume fraction)

Full size image

These laminates were analyzed with regard to their tensile properties in parallel with the fiber direction. For this purpose, tensile tests were carried out in dependence on DIN EN ISO 527-5 with a hydraulic tensile testing machine of type Zwick Roell HTM 50/20. The specimens were sized 250 mm by 15 mm and provided with 3-mm-thick, chamfered aluminum end tabs. The specimen was clamped with a free gauge length of 150 mm and loaded to failure with a constant crosshead speed of 3 mm/s. The test forces were metered by a piezoelectric load cell with a calibrated range of 50 kN. In order to determine the elongation of the specimen, all tests were captured by a high-speed camera system (sample rate 200 Hz) and evaluated by a digital image correlation system of type GOM ARAMIS v6.3.0. Among others, two material configurations with a homogenous steel fiber distribution and 10 vol% (SCFRP 1) or 19 vol% (SCFRP 2) of stainless steel fibers were considered. For each material configuration, five specimens were analyzed. The obtained characteristics (arithmetic mean and standard deviation of modulus of elasticity, ultimate tensile strength, elongation at break) are summarized in Table 3.

Table 3 Results of the experimental tests on hybrid composites
Full size table

It should be pointed out that the steel fiber diameters and arrangements used in [32, 33] differ from those of this study. However, as shown in “Uniaxial tensile loading in fiber direction” section this has no impact on the results for tensile loadings in fiber direction. For these reasons, the material properties as well as the fiber volume fractions of the numerical investigations were adapted to the experimental study. In Fig. 8, the nominal stress–strain curves of each sample are plotted (depicted in blue) and compared with the results of the numerical simulation (marked in red).

Figure 8
figure 8

Comparison between simulation and experimental results [32, 33] for tensile loadings in fiber direction (SCFRP 1 C s = 10%/SCFRP 2 C s = 18%)

Full size image

The comparison proves a good agreement of the measured and simulated stiffness. Despite incorporation of highly ductile steel fibers, a post-failure behavior (after fracture of the carbon fibers) cannot be observed, which indicates that the element degradation at coordinate plane (see “Uniaxial tensile loading in fiber direction” section) leads to more realistic results. The simulated strength value is larger than the experimental one (SCFRP 1: +6.3%, SCFRP 2: +8.3%). This difference between theoretical and measured values is, however, already known and presented in Schürmann [30]. The main reason is the preexisting microscopic damage in each composite. The fiber strength is in general not consistent for each fiber, but it can be assumed that it is rather a normally distributed value. If certain fibers fail early, the applied load has to be carried by the remaining, intact fibers. As a consequence, strength of unidirectional layers is determined mainly on the microscopic scale [30].

Summery and outlook

In the present study, a micromechanical approach is used to estimate the effective strength of hybrid composites consisting of carbon and stainless steel fibers. As expected, the predicted strength agrees well with simple rules of mixtures in fiber direction. In addition, the strength in fiber direction does not depend on the choice of the RVE, supposing that the volume contents of the fibers remain unchanged. In order to predict the residual load capability after carbon fiber failure due to their lower breaking elongation, a degradation strategy is used. In case that the stiffness of the finite elements in the symmetry plane is reduced, the residual load capability of the hybrid composite is rather negligible. This behavior agrees well with the experimental results obtained for hybrid carbon and stainless steel fiber composites. Furthermore, the calculated values of the stiffness agree well with the experimental ones. However, the measured strength values are generally smaller by about 8% than the calculated ones. This behavior is observed for pure carbon fibers composites as well [30].

The present simulations show that the shape of the RVE and the used failure criterion influence the results strongly for loadings transversal to fiber direction and for shear loadings. Moreover, it is shown that the strength values depend on the distribution of the fibers within a given RVE. Significant lower strength values are obtained for RVEs based on micrographs where higher stress concentration areas are present. For a further analysis of this phenomenon, the effect of fiber matrix adhesion should be considered. In the subsequent study, the crack initiation and the delamination process at the constituent’s interfaces will be investigated using cohesive zone models.

The proposed modeling approach allows analyzing 2D failure envelopes and 3D failure bodies of the hybrid composites for complex, multiaxial stress states. For the different composite’s constituents, linear and nonlinear failure criteria can be applied. Moreover, the adhesion concerns at the constituent’s interfaces can be investigated as well by implementing appropriate models. The used approach allows identifying the different failure modes of the hybrid composites. Thus, for the design of hybrid composite structures physical-based models instead of empirical-based assumptions can be used.