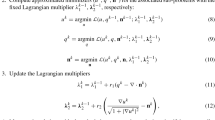Image Reconstruction by Minimizing Curvatures on Image Surface

Abstract

The curvature regularities are well-known for providing strong priors in the continuity of edges, which have been applied to a wide range of applications in image processing and computer vision. However, these models are usually non-convex, non-smooth, and highly nonlinear, the first-order optimality condition of which are high-order partial differential equations. Thus, numerical computation is extremely challenging. In this paper, we estimate the discrete mean curvature and Gaussian curvature on the local $3\times 3$ stencil, based on the fundamental forms in differential geometry. By minimizing certain functions of curvatures over the image surface, it yields a kind of weighted image surface minimization problem, which can be efficiently solved by the alternating direction method of multipliers. Numerical experiments on image restoration and inpainting are implemented to demonstrate the effectiveness and superiority of the proposed curvature-based model compared to state-of-the-art variational approches.

1 Introduction

Curves and surfaces are important geometric elements in image processing and analysis, which can be ideally measured by quantities such as arc length, area and curvatures [12]. Let $u:\Omega \rightarrow {\mathbb {R}}$ be an image defined on an open-bounded subset $\Omega \subset {\mathbb {R}}^2$ with Lipschitz continuous boundary. For each gray level $\lambda$, by taking the length energy as the curve model, it yields the well-known total variation (TV) regularization [42]

$$\begin{aligned} \mathrm {TV}(u) = \int _{-\infty }^\infty \mathrm {Length}(\varGamma _\lambda )\mathrm{d}\lambda =\int _{\Omega }|\nabla u|\mathrm{d}x, \end{aligned}$$

(1)

where $\varGamma _\lambda = \{x\in \Omega | u(x)=\lambda \}$. Curvatures can depict the amount of a curve from being straight as in the case of a line or a surface deviating from being a flat plane, which have also been applied to various image processing tasks [1, 23, 43]. Suppose we take the curvature curve model, then the image model becomes

$$\begin{aligned} \mathrm E(u) = \int _{{\Omega }}g(\kappa )|\nabla u|\mathrm{d}x=\int _{{\Omega }}g\Big (\Big |\nabla \cdot \Big (\frac{\nabla u}{|\nabla u|}\Big )\Big |\Big )|\nabla u|\mathrm{d}x, \end{aligned}$$

(2)

where $g(\kappa ) = 1+\alpha \kappa ^2$, $\alpha >0$, yielding the Euler’s elastica image model [36]. Nitzberg, Mumford and Shiota [39] observed that line energies such as Euler’s elastica can be used as regularization for the completion of missing contours in images by providing strong priors for the continuity of edges. Since then, Euler’s elastica has been successfully used for image denoising [47, 56], inpainting [35, 45, 54], segmentation [3, 18, 61], segmentation with depth [22, 59] and illusory contour [28].

However, the numerical minimization of Euler’s elastica is highly challenging due to its non-smoothness, nonlinearity and non-convexity. The gradient flow was used to solve a set of coupled second-order partial differential equations in [4, 45] for minimizing the Euler’s elastica energy, which usually takes high computational cost in imaging applications. Schoenemann, Kahl and Cremers [43] solved the associated linear programming relaxation and thresholded the solution to approximate the original integer linear program regarding curvature regularization. Discrete algorithms based on graph cuts methods have been studied for Euler’s elastica models in [2, 21]. Thanks to the development of operator splitting technique and augmented Lagrangian algorithm, fast solvers for Euler’s elastica models have been presented in [3, 19, 47, 52, 54]. Recently, Deng, Glowinski and Tai [15] proposed a Lie operator-splitting-based time discretization scheme, which is applied to the initial value problem associated with the optimality system. A convex, lower semi-continuous, coercive approximation of Euler’s elastica energy via functional lifting was discussed in [8]. Later, Chambolle and Pock [11] used a lifted convex representation of curvature depending variational energies in the roto-translational space and yielded a natural generalization of the total variation to the roto-translational space.

By considering the image surface or graph in a high-dimensional space, the image denoising problem turns to find a piecewise smooth surface to approximate the given image surface. Both mean curvature and Gaussian curvature can be used as the regularizer to preserve geometric features of the image surface for different image processing tasks. The mean curvature was first introduced for noise removal problems as the mean curvature-driven diffusion algorithms [20, 55], which evolved the image surface at a speed proportional to the mean curvatures. Zhu and Chan [58] proposed to employ the $L^1$-norm of mean curvature over the image surface as follows

$$\begin{aligned} \mathrm H(u)=\int _{\Omega }\bigg |\nabla \cdot \bigg (\frac{\nabla u}{\sqrt{1+|\nabla u|^2}}\bigg )\bigg |\mathrm{d}x, \end{aligned}$$

(3)

which was proven to be able to keep corners of objects and greyscale intensity contrasts of images and remove the staircase effect. Originally, the smoothed mean curvature regularized model was numerically solved by the gradient descent method, which involves high-order derivatives and converges slowly in practice. To deal with this difficulty, some effective and efficient numerical algorithms for mean curvature regularized models were proposed based on the augmented Lagrangian method [37, 60]. However, there exist some inevitable problems in this kind of method, such as the choices of the algorithm parameters and the slow convergence rate.

Gaussian curvature-driven diffusion was studied in [30] for noise removal problems, which was shown superior in preserving image structures and details. Lu, Wang and Lin [32] proposed an energy functional based on Gaussian curvature for image smoothing, which was solved by a diffusion process. Gong and Sbalzarini [25] presented a variational model with local weighted Gaussian curvature as the regularizer, which was solved by the splitting techniques. In [9], the authors minimized the following $L^1$-norm of Gaussian curvature of the image surface

$$\begin{aligned} \mathrm K(u)=\int _{\Omega }\frac{|\text{ det } \nabla ^2 u|}{(1+|\nabla u|^2)^2}\mathrm{d}x, \end{aligned}$$

(4)

with $\nabla ^2 u$ being the Hessian of function u and

$$\begin{aligned} \text{ det } \nabla ^2 u = \frac{\partial ^2u}{\partial x^2}\frac{\partial ^2u}{\partial y^2}-\Big |\frac{\partial ^2u}{\partial x\partial y}\Big |^2. \end{aligned}$$

Similarly, Gaussian curvature regularizer can also preserve image contrast, edges and corners very well. However, the minimization of (4) is even harder due to the determinant of Hessian, which was solved by a two-step method based on the vector filed smoothing and gray-level interpolation.

Recently, efficient methods are proposed to directly estimate curvatures in the discrete setting. Ciomaga, Monasse and Morel [13] evaluated the curvatures on the level lines of the bilinearly interpolated images, where a smoothing step depending on affine erosion of the level lines is implemented on the images to remove pixelization artifacts. Gong and Sbalzarini [26] presented a filter-based approach to use the pixel-local analytical solutions to approximate the TV, mean curvature and Gaussian curvature by enumerating the constant, linear and developable surfaces in the discrete $3\times 3$ neighborhood. Although the curvature filter avoids solving the high-order partial differential equations associated with the curvature-based variational models, it lacks rigorous definition and accurate estimation of the curvatures. Zhong et al. [57] introduced the total curvature regularization by minimizing all the normal curvatures over image surface, in which the normal curvatures are well-defined in a pixel-wise local neighborhood.

Fig. 1

The estimated curvature maps of a simple image ‘Cat’ estimated by image curvature microscope (ICM) [13] and our approach, where yellow denotes zero curvature, and green and red represent positive and negative curvatures, respectively (Color figure online)

1.1 Our Contributions

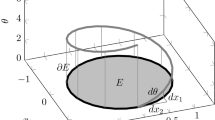
Assume an image surface (x, y, u(x, y)) is defined on $\Omega$. We define a level set function $\phi (x,y,z) = u(x,y)-z$, the zero level set of which corresponds to the surface $z = u(x,y)$. By integrating over $\Omega$, it gives the surface area energy as follows

$$\begin{aligned} A(u){=}\int _{\Omega }\sqrt{\Big (\frac{\partial z}{\partial x}\Big )^2{+}\Big (\frac{\partial z}{\partial y}\Big )^2+1}\mathrm{d}x {=} \int _\Omega \sqrt{1 {+} |\nabla u|^2}\mathrm{d}x,\nonumber \\ \end{aligned}$$

(5)

which has been used as the efficient regularization for image smoothing [46, 55] and blind deblurring [31], etc. We formulate a new curvature regularized model by minimizing either the mean curvature or Gaussian curvature over image surfaces. Taking image denoising as an example, we define the curvature energy as follows

$$\begin{aligned} \min _{u}~ \int _{\Omega } g(\kappa )\sqrt{1 + |\nabla u|^2}dx + \frac{\lambda }{2} \int _{\Omega }(u-f)^2dx, \end{aligned}$$

(6)

where $\kappa$ denotes either mean curvature or Gaussian curvature and $g(\cdot )$ is a certain function of the curvature. According to [11], the following three typical energies are considered and extended to the graph, where $\alpha$ is a positive parameter to balance the curvature and surface area.

• (1) Total absolute curvature (TAC): measures the sum of the surface area and absolute curvature

  $$\begin{aligned} g_1(\kappa (u))&= 1+\alpha |\kappa (u)|. \end{aligned}$$

  (7)

• (2) Total square curvature (TSC): penalizes the surface area and the squared curvature

  $$\begin{aligned} g_2(\kappa (u))&= 1+\alpha |\kappa ^2(u)|. \end{aligned}$$

  (8)

• (3) Total roto-translational variation (TRV): measures the surface area and curvature through an Euclidean metric

  $$\begin{aligned} g_3(\kappa (u))&= \sqrt{1+\alpha |\kappa ^2(u)|}. \end{aligned}$$

  (9)

Both mean curvature and Gaussian curvature are estimated based on normal curvatures, which can be defined on a $3\times 3$ neighborhood of each pixel followed our previous work [57]. As long as the curvatures being computed explicitly, we can use the operator splitting technique and ADMM-based algorithm to iteratively solve the curvature minimization problem (6). We prove the existence of a solution and discuss the convergence of the ADMM algorithm under certain assumptions. Numerical applications to image denoising and inpainting show the superiority of the proposed method, which can provide better restoration qualities with lower computational cost compared to several state-of-the-art variational models. To sum up, our method presents the following advantages:

• (1) We develop a new discrete method to estimate both mean curvature and Gaussian curvature on image surfaces. Different from the discrete curvature in [13], which is designed for 2D level lines and strongly relies on the smoothness of the level lines, our approach makes use of 3D level sets information. As shown in Fig. 1, the curvature maps are different on image edges due to the intrinsic differences among the curvatures, and our method performs better on the original image by producing fewer outliers.

• (2) By computing the normal curvatures in the $3\times 3$ neighborhood, we can estimate both mean curvature and Gaussian curvature in terms of principal/normal curvatures. Thus, our model can be regarded as a re-weighted minimal surface model, where the weights are automatically updated using curvature information. It can not only achieve good image restoration results but also preserve the geometric properties, such as edges, corners, etc., very well.

• (3) Because we only introduce one artificial variable, our ADMM has fewer parameters than other curvature-based models. More specifically, our algorithm has one parameter of the augmented term while the ADMMs for Euler’s elastica model in [47] and mean curvature model in [60] have three and four such kinds of parameters, respectively.

• (4) Our formulation is more flexible to adapt to the different combinations of the function-type and curvature-type without affecting the way of the operator-splitting and the associated ADMM-based algorithm. The proposed curvature regularization can be easily applied to other image processing tasks such as segmentation [18, 33], reconstruction [52, 56], etc.

1.2 Organizations

This paper is organized as follows. We introduce the estimation of curvatures based on differential geometry theory in Sect. 2. The ADMM-based algorithm and convergence analysis are discussed in Sect. 3. Section 4 is dedicated to numerical experiments on image reconstruction problem to demonstrate the efficiency and superiority of the proposed approach. Finally, we draw some conclusions in Sect. 5.

To summarize this section, we would like to mention that the proper functional frameworks to formulate the curvature-based variational models involving aforementioned curvature regularizations (2)–(4) have not been identified yet. Therefore, we do not know much about the function space of our model (6), which has to be a subspace of $L^2(\Omega )$. Obviously, the discrete problems largely ignore these functional analysis considerations. Thus, we discuss our model under the discrete setting in the followings.

2 Curvature Estimation

Fig. 2

Curvature vector

Fig. 3

The projection distance of a neighboring point to the tangent plane

2.1 Notations and Definitions

Let ${{\varvec{r}}} = {{\varvec{r}}}(x,y): {\Omega }\subset {\mathbb {R}}^2\rightarrow {{\mathbb {R}}}^3$ be a regular parametric surface ${\mathcal {S}}$ and (x, y) be the coordinates on ${\Omega }$. In order to quantify the curvature of a surface ${\mathcal {S}}$, we consider a curve ${\mathcal {C}}$ on ${\mathcal {S}}$ passing through point O shown in Fig. 2. The curvature vector is used to measure the rate of change of the tangent along the curve, which can be defined using the unit tangent vector ${\varvec{t}}$ and the unit normal vector ${\varvec{n}}$ of the curve ${\mathcal {C}}$ at point O as

$$\begin{aligned} {\varvec{\kappa }} = \frac{\mathrm{d}{\varvec{t}}}{\mathrm{d}s} = {\varvec{\kappa }}_n + {\varvec{\kappa }}_g \end{aligned}$$

with ${\varvec{\kappa }}_n$ being the normal curvature vector and ${\varvec{\kappa }}_g$ being the geodesic curvature vector. Let ${\varvec{N}}$ be the surface unit normal vector, which is defined as

$$\begin{aligned} {\varvec{N}} = \frac{{{\varvec{r}}}_x \times {{\varvec{r}}}_y}{|{{\varvec{r}}}_x \times {{\varvec{r}}}_y|}. \end{aligned}$$

By differentiating ${\varvec{N}}\cdot {\varvec{t}} =0$ along the curve with respect to s, we obtain

$$\begin{aligned} \frac{d{\varvec{t}}}{\mathrm{d}s}\cdot {\varvec{N}} + {\varvec{t}}\cdot \frac{d{\varvec{N}}}{\mathrm{d}s} =0. \end{aligned}$$

Thus, the normal curvature of the surface at O in the direction ${\varvec{t}}$ can be expressed as

$$\begin{aligned} \kappa _n= & {} \frac{\mathrm{d}{\varvec{t}}}{\mathrm{d}s}\cdot {\varvec{N}}=-{\varvec{t}} \cdot \frac{\mathrm{d}{\varvec{N}}}{\mathrm{d}s} = -\frac{\mathrm{d}{\varvec{r}}}{\mathrm{d}s}\cdot \frac{d{\varvec{N}}}{\mathrm{d}s}\nonumber \\= & {} \frac{L\mathrm{d}x^2+2M\mathrm{d}x\mathrm{d}y+N\mathrm{d}y^2}{E\mathrm{d}x^2+2F\mathrm{d}x\mathrm{d}y +G\mathrm{d}y^2}, \end{aligned}$$

(10)

which is the quotient of the second fundamental form and the first fundamental form. The denominator of (10) is the first fundamental form, which is the square of the arc length

$$\begin{aligned} \mathrm{I} = \mathrm{d}s^2 =\mathrm{d}{\varvec{r}}\cdot \mathrm{d}{\varvec{r}} = E\mathrm{d}x^2 + 2F \mathrm{d}x\mathrm{d}y + G \mathrm{d}y^2, \end{aligned}$$

with the first fundamental form coefficients $E = {\varvec{r}}_x\cdot {\varvec{r}}_x$, $F= {\varvec{r}}_x\cdot {\varvec{r}}_y$, $G = {\varvec{r}}_y\cdot {\varvec{r}}_y$. On the other hand, the numerator of (10) is the second fundamental form such that

$$\begin{aligned} \mathrm{II} = - \mathrm{d}{\varvec{r}} \cdot \mathrm{d}{\varvec{N}} = \mathrm{d}^2{\varvec{r}} \cdot {\varvec{N}} = L\mathrm{d}x^2 + 2M\mathrm{d}x\mathrm{d}y + N\mathrm{d}y^2, \end{aligned}$$

with the second fundamental form coefficients $L = {\varvec{r}}_{xx}\cdot {\varvec{N}}$, $M = {\varvec{r}}_{xy}\cdot {\varvec{N}}$, $N = {\varvec{r}}_{yy}\cdot {\varvec{N}}$.

Table 1 List of notations used in the this work

Proposition 2.1

Suppose ${\mathcal {S}}$: ${{\varvec{r}}} = {{\varvec{r}}}(x,y)$ is a regular parametric surface, $O(x_0,y_0)$ being an arbitrary point on ${\mathcal {S}}$, then the second fundamental form at point O can be estimated by

$$\begin{aligned} \mathrm{II}\approx 2 d, \end{aligned}$$

(11)

where d denotes the projection distance of its neighboring point $P(x_0+\Delta x,y_0+\Delta y)$ to the tangent plane of O.

Proof

As shown in Fig. 3, the projection distance of the neighboring point $P(x_0+{\Delta x},y_0+{\Delta } y)$ to the tangent plane is obtained as follows

$$\begin{aligned} d({\Delta } x,{\Delta } y) = ({{\varvec{r}}}(x_0+{\Delta } x,y_0+{\Delta } y)-{{\varvec{r}}}(x_0,y_0)) \cdot {{\varvec{N}}}. \end{aligned}$$

By Taylor’s expansion, we have

$$\begin{aligned}&{{\varvec{r}}}(x_0+{\Delta } x,y_0+{\Delta } y)-{{\varvec{r}}}(x_0,y_0) \\&\quad =({{\varvec{r}}}_x {\Delta } x + {{\varvec{r}}}_y {\Delta } y)+\frac{1}{2}({{\varvec{r}}}_{xx} ({\Delta } x)^2+2{{\varvec{r}}}_{xy}{\Delta } x{\Delta } y\\&\qquad +{{\varvec{r}}}_{yy} ({\Delta } y)^2) +\, {{\varvec{o}}}(({\Delta } x)^2+({\Delta } y)^2), \end{aligned}$$

and

$$\begin{aligned} \lim _{({\Delta } x)^2+({\Delta } y)^2 \rightarrow 0} \frac{{{\varvec{o}}}(({\Delta } x)^2+({\Delta } y)^2)}{({\Delta } x)^2+({\Delta } y)^2} = 0. \end{aligned}$$

Owing to ${{\varvec{r}}}_x \cdot {{\varvec{N}}} = {{\varvec{r}}}_y \cdot {{\varvec{N}}} = 0$, it follows that

$$\begin{aligned}&d({\Delta } x,{\Delta } y) = \frac{1}{2}[L({\Delta } x)^2+2M{\Delta } x{\Delta } y+N({\Delta } y)^2] \\&\quad +{{\varvec{o}}}(({\Delta } x)^2+({\Delta } y)^2), \end{aligned}$$

the first term on the right-hand side of which gives the second fundamental form. Thus, as long as $\sqrt{({\Delta } x)^2+({\Delta } y)^2} \rightarrow 0$, there is

$$\begin{aligned} \mathrm{II}\approx 2 d({\Delta } x,{\Delta } y), \end{aligned}$$

which completes the proof. $\blacksquare$

With the normal curvatures, we can further define the two principal curvatures of point O to measure how the surface bends by different amounts in different directions at that point, which are

$$\begin{aligned} \kappa _\mathrm{max}&:= \mathrm{the}\, \mathrm{maximum}\, \mathrm{normal}\, \mathrm{curvature}\, \mathrm{at} O,\\ \kappa _{\mathrm{min}}&:= \mathrm{the}\, \mathrm{minimum}\, \mathrm{normal}\, \mathrm{curvature}\, \mathrm{at} O. \end{aligned}$$

Now we are ready to define the mean curvature and Guassian curvature based on the principal curvatures as follows.

Fig. 4

Calculate the normal curvature on image surface, the gray triangle in which represents a tangent plane of center point O

Definition 2.2

The mean curvature and Gaussian curvature of ${\mathcal {S}}$ at point O are defined as

$$\begin{aligned} \mathrm H = \frac{1}{2}(\kappa _{\mathrm{max}}+\kappa _{\mathrm{min}}),~ \text{ and }~~ \mathrm K = \kappa _{\mathrm{max}}\kappa _{\mathrm{min}}. \end{aligned}$$

(12)

The Gaussian curvature is also known as the curvature of a surface, which is an intrinsic measure of the curvature, depending only on distances that measured on the surface, not on the way that isometrically embedded in Euclidean space. Although the mean curvature is not intrinsic, a surface with zero mean curvature at all points is called the minimal surface, which is widely used in shape analysis, high-dimensional data processing, etc. For convenience, the important notations used in this paper are summarized in Table 1.

2.2 Calculation of Normal Curvatures

Without loss of generality, we represent a gray image as a $m\times n$ matrix and the grid ${\Omega }=\{(ih,jh):1\le i\le m,1\le j\le n\}$ with h being the grid step size fixed as the same value in the x-axis and the y-axis. In the following, we use the notation $u(i,j)=u(ih,jh)$ and (i, j) denotes a discrete point. Similarly to Euler’s elastica energies [11, 45, 47], we use the staggered grid in the $x-y$ plane, where an example with $3\times 3$ pixels is displayed in Fig. 4a. The $\triangle$-nodes express half grids and $\Box$-nodes represent middle points, which are used as the neighboring points in the calculation of normal curvatures. The intensity values on $\triangle$-nodes are estimated as the mean of its two neighboring $\bullet$-nodes, while on $\Box$-nodes are estimated as the mean of the four surrounding $\bullet$-nodes.

Now we discuss how to estimate the discrete normal curvatures locally. As shown in Fig. 4b, we use the triangular plane $\mathrm {T}_{XYZ}$ to approximate tangent plane of point O. Since the 3D coordinates of point X, Y and Z are known, the normal vector ${{\varvec{N}}}$ of $\mathrm T_{XYZ}$ can be decided by the cross-product of the vector $\overrightarrow{XY}$ and $\overrightarrow{XZ}$ as follows

$$\begin{aligned} {{\varvec{N}}} = \overrightarrow{XY} \times \overrightarrow{XZ} = (2u_{i,j}-u_{i,j-1}-u_{i,j+1},u_{i,j-1}-u_{i,j+1},2). \end{aligned}$$

In order to implement Proposition 2.1 to approximate the second fundamental form, we use the half point $P(i-\frac{1}{2},j,u_{i-\frac{1}{2},j})$ in Fig. 4b for estimating the projection distance d of P to its tangent plane $\mathrm {T}_{XYZ}$, which gives

$$\begin{aligned} d&= \mathsf {dist}(P, \mathrm T_{XYZ}) = \overrightarrow{QP}\cdot {{\varvec{N}}}\nonumber \\&=\frac{2u_{i,j}-u_{i,j-1}-u_{i,j+1}}{2\sqrt{(2u_{i-1,j}-u_{i,j-1}-u_{i,j+1})^2+(u_{i,j-1}-u_{i,j+1})^2+4}}. \end{aligned}$$

(13)

On the other hand, the first fundamental form can be estimated using the arc length ${\widehat{OP}}$, which is approximated by the length of the line segment, i.e., |OP|. Based on the Pythagorean theorem, we have

$$\begin{aligned} \mathrm{d}s={\widehat{OP}} \thickapprox \sqrt{(u_{i-\frac{1}{2},j}-u_{i,j})^2+h^2}, \end{aligned}$$

(14)

where $u_{i-\frac{1}{2},j}$ can be estimated as the mean of its two neighboring points $u_{i-1,j}$ and $u_{i,j}$. Therefore, according to formula (10), the normal curvature of point O in direction $\overrightarrow{OP}$ can be expressed as follows

$$\begin{aligned} \kappa _n \thickapprox \frac{2d}{\mathrm{d}s^2} \thickapprox \frac{2u_{i,j}-u_{i,j-1}-u_{i,j+1}}{((u_{i-\frac{1}{2},j}-u_{i,j})^2+h^2) \sqrt{(2u_{i-1,j}-u_{i,j-1}-u_{i,j+1})^2+(u_{i,j-1}-u_{i,j+1})^2+4}}. \end{aligned}$$

(15)

Fig. 5

The eight tangent planes of the center point in a $3\times 3$ local window and the representatives of the two different kinds of projections

Proposition 2.3

The approximation of the normal curvature by (15) is ${{\varvec{o}}}(h^2)$.

Proof As shown in Fig. 4b, $P(i-\frac{1}{2},j,\frac{u_{i-1,j}+u_{i,j}}{2})$ is a neighboring point of $O(i,j,u_{i,j})$ used to calculate the normal curvature. Obviously, when $h \rightarrow 0$, we obtain $\lim \limits _{h \rightarrow 0} \frac{{\widehat{OP}}}{|OP|}=1$. As a result, the approximate error of first fundamental form using the square of |OP| is ${{\varvec{o}}}(h^2)$. On the other hand, according to Proposition 2.1, the approximate error of second fundamental form using the projection distance d is also ${{\varvec{o}}}(h^2)$. Thus, the estimation of the normal curvature by (15) is a second-order approximation. $\blacksquare$

2.3 Mean Curvature and Gaussian Curvature

In order to estimate the mean and Gaussian curvatures t each point of the image surface, we compute the normal curvatures along eight directions in the local $3\times 3$ window. As shown in Fig. 5a, eight triangular planes (i.e., T1-T8) are defined as the approximate tangent planes, which locate physically nearest to the center point O and pairwise centrosymmetric to avoid the grid bias. We can simply divide these tangent planes into two categories such that T1-T4 use the half points and T5-T8 use the middle points to compute the projections. The examples of each type (i.e., T2 and T8) are also presented in Fig. 5b, c, which illustrate the tangent planes and the corresponding projections.

Given the eight neighboring points being either the half points or the middle points, we can estimate the second fundamental form by calculating the distance from the neighboring point P as depicted in Fig. 5b, c to the corresponding tangent plane. More specifically, we calculate $d_\ell =\mathsf {dist}(P_\ell , T_\ell )$, $\ell =1,\ldots ,8$, which are defined as

$$\begin{aligned}&d_1 = \frac{2u_{i,j}-u_{i,j-1}-u_{i,j+1}}{2\sqrt{(2u_{i-1,j}-u_{i,j-1}-u_{i,j+1})^2+(u_{i,j-1}-u_{i,j+1})^2+4}};\\&d_2 = \frac{u_{i,j-1}+u_{i,j+1}-2u_{i,j}}{2\sqrt{(2u_{i+1,j}-u_{i,j-1}-u_{i,j+1})^2+(u_{i,j+1}-u_{i,j-1})^2+4}};\\&d_3 = \frac{u_{i-1,j}+u_{i+1,j}-2u_{i,j}}{2\sqrt{(u_{i+1,j}-u_{i-1,j})^2+(u_{i-1,j}+u_{i+1,j}-2u_{i,j-1})^2+4}};\\&d_4 = \frac{2u_{i,j}-u_{i-1,j}-u_{i+1,j}}{2\sqrt{(u_{i-1,j}-u_{i+1,j})^2+(u_{i-1,j}+u_{i+1,j}-2u_{i,j+1})^2+4}};\\&d_5 = \frac{u_{i-1,j-1}+u_{i-1,j+1}+u_{i+1,j-1}-u_{i,j}-u_{i-1,j}-u_{i,j-1}}{2\sqrt{(u_{i+1,j-1}-u_{i-1,j-1})^2+(u_{i-1,j+1}-u_{i-1,j-1})^2+4}};\\&d_6 = \frac{u_{i,j}+u_{i+1,j}+u_{i,j+1}-u_{i+1,j+1}-u_{i-1,j+1}-u_{i+1,j-1}}{2\sqrt{(u_{i-1,j+1}-u_{i+1,j+1})^2+(u_{i+1,j-1}-u_{i+1,j+1})^2+4}};\\&d_7 = \frac{u_{i,j}+u_{i-1,j}+u_{i,j+1}-u_{i-1,j-1}-u_{i+1,j+1}-u_{i-1,j+1}}{2\sqrt{(u_{i-1,j+1}-u_{i+1,j+1})^2+(u_{i-1,j-1}-u_{i-1,j+1})^2+4}};\\&d_8 = \frac{u_{i-1,j-1}+u_{i+1,j+1}+u_{i+1,j-1}-u_{i,j}-u_{i+1,j}-u_{i,j-1}}{2\sqrt{(u_{i+1,j-1}-u_{i-1,j-1})^2+(u_{i+1,j+1}-u_{i+1,j-1})^2+4}}. \end{aligned}$$

On the other hand, we estimate the arc length of the central point $O(i,j,u_{i,j})$ to the neighboring points $P_\ell$, $\ell =1,\ldots ,8$, in the local $3\times 3$ neighborhood, which is computed by the square root of the quadratic sum of the intensity differences and the grid size between two points according to (14). As a result, eight normal curvatures can be calculated using (15) as

$$\begin{aligned} \kappa _\ell&\thickapprox {\left\{ \begin{array}{ll} \frac{2d_\ell }{(u^\vartriangle _\ell -u_{i,j})^2+h^2}, &{}\quad \ell = 1,~2,~3,~4,\\ \frac{2d_\ell }{(u^\square _\ell -u_{i,j})^2+2h^2},&{}\quad \ell = 5,~6,~7,~8, \end{array}\right. } \end{aligned}$$

(16)

where $u^\vartriangle _\ell$ and $u^\square _\ell$ denote the intensities of the two types of neighboring points as shown in Fig. 4a. The normal curvatures are well-defined and applicable to every point on the image surface.

With all normal curvatures, we are ready to obtain the two principal curvatures $\kappa _{\mathrm{max}}$ and $\kappa _{\mathrm{min}}$ from

$$\begin{aligned} \kappa _{\mathrm{max}} = \mathrm{{max}}\{\kappa _\ell \},~~ \kappa _{\mathrm{min}} = \mathrm{{\mathrm{min}}}\{\kappa _\ell \},\quad \text{ for }~{\ell =1,2,\ldots ,8}.\nonumber \\ \end{aligned}$$

(17)

According to Definition 2.2, both mean and Gaussian curvatures are evaluated on each point of the image surface, which only involve simple arithmetic operations.

3 The Curvature-Based Variational Model and Numerical Algorithm

3.1 ADMM-Based Numerical Algorithm

Now we discuss the numerical algorithm for solving the minimization problem (6) by firstly rewriting it into the following discrete form

$$\begin{aligned} \min _{u} \sum _{i,j} g(\kappa (u_{i,j})) \sqrt{1+|\nabla u_{i,j}|^2} +\frac{\lambda }{2}\Vert u-f\Vert ^2, \end{aligned}$$

(18)

where $\kappa (u_{i,j})$ denotes either the mean curvature or Gaussian curvature, $|\cdot |$ is the usual Euclidean norm in ${\mathbb {R}}^2$ and $\Vert \cdot \Vert$ is the $l^2$ norm. Note that all matrix multiplication and divisions in this paper are element-wise. The discrete gradient operator $\nabla :{\mathbb {R}}^{mn}\rightarrow {\mathbb {R}}^{mn\times mn}$ is defined by

$$\begin{aligned} (\nabla u)_{i,j} {=} ((\nabla u)^x_{i,j}, (\nabla u)^y_{i,j})\quad \text{ for }~i{=}1,\ldots ,m,~j{=}1,\ldots ,n \end{aligned}$$

with

$$\begin{aligned}&(\nabla u_{i,j})^x = {\left\{ \begin{array}{ll} u_{i+1,j}-u_{i,j} ,&{}\quad \mathrm {if}~{1 \le i<m}\\ u_{1,j}-u_{i,j} ,&{}\quad \mathrm {if}~{i=m} \end{array}\right. },\quad \text{ and }\quad \\&(\nabla u_{i,j})^y = {\left\{ \begin{array}{ll} u_{i,j+1}-u_{i,j} ,&{}\quad \mathrm {if}~{1 \le j<n}\\ u_{i,1}-u_{i,j} ,&{}\quad \mathrm {if}~{j=n} \end{array}\right. }. \end{aligned}$$

As can be seen, when the mean and Gaussian curvatures are given, the curvature regularized model (18) becomes a weighted minimal surface model, for which fast algorithms can be used as the numerical solver, for instance the split Bregman method [24], primal-dual splitting method [10] and augmented Lagrangian method [50]. Therefore, we solve the weighted minimal surface model based on the ADMM algorithm and then evaluate the curvatures separately using the most recent update of u in an iterative way. To be specific, we introduce an auxiliary variable ${\varvec{v}}$ and rewrite the minimization problem (6) into a constrained minimization as follows

$$\begin{aligned} \begin{aligned} \min _{u,{\varvec{v}}}~&\sum _{i,j}g(\kappa (u_{i,j}))\sqrt{1+|{\varvec{v}}_{i,j}|^2} + \frac{\lambda }{2}\Vert u-f\Vert ^2 \\ ~~\mathrm {s.t.,}~&~~{\varvec{v}}_{i,j}=\nabla u_{i,j}. \end{aligned} \end{aligned}$$

(19)

Given some $(u^k,{\varvec{v}}^k)\in {\mathbb {R}}^{mn} \times {\mathbb {R}}^{mn\times mn}$, the proximal augmented Lagrangian of above-constrained minimization problem can be defined as

$$\begin{aligned} {\mathcal {L}}(u,{\varvec{v}}; {\varvec{\varLambda }})&= \sum _{i,j} g(\kappa (u_{i,j}^k))\sqrt{1+|{\varvec{v}}_{i,j}|^2} +\frac{\lambda }{2}\Vert u-f\Vert ^2 \\&\quad +\, <{\varvec{\varLambda }},{\varvec{v}}-\nabla u> + \frac{\mu }{2}\Vert {\varvec{v}}-\nabla u\Vert ^2\\&\quad + \frac{\tau }{2}\Vert u-u^k\Vert ^2 +\, \frac{\sigma }{2}\Vert {\varvec{v}}-{\varvec{v}}^k\Vert ^2, \end{aligned}$$

where ${\varvec{\varLambda }}$ represents the Lagrangian multiplier, and $\mu ,\tau ,\sigma$ are positive parameters. Then, we iteratively and alternatively solve the u-subproblem and ${\varvec{v}}$-subproblem until reaching the terminating condition; see Algorithm 3.1.

3.1.1 The ${\varvec{v}}$-Subproblem

The sub-minimization problem w.r.t. ${\varvec{v}}$ is a typical nonlinear minimization problem, which can be solved by Newton’s method. Assume ${\varvec{v}}^{k+1,0} = {\varvec{v}}^{k}$, we compute

$$\begin{aligned} {\varvec{v}}^{k+1,\ell +1} = {\varvec{v}}^{k+1,\ell } -\, \frac{g(\kappa (u^{k})){\varvec{v}}^{k+1,\ell } (1+{|{\varvec{v}}^{k+1,\ell }|^2})^{-\frac{1}{2}}+\mu ({\varvec{v}}^{k+1,\ell } - \nabla u^{k}) + {\varvec{\varLambda }}^k + \sigma ({\varvec{v}}^{k+1,\ell }-{\varvec{v}}^{k,\ell })}{g(\kappa (u^{k}))(1+{|{\varvec{v}}^{k+1,\ell }|^2})^{-\frac{3}{2}} + \mu + \sigma }, \end{aligned}$$

for $\ell =0, 1, \ldots , L-1$. Then, the update of variable ${\varvec{v}}$ is given as ${\varvec{v}}^{k+1} = {\varvec{v}}^{k+1,L}$.

3.1.2 The u-Subproblem

The first-order optimality condition of (21) gives us a linear equation as follows

$$\begin{aligned} \big ((\lambda +\tau ){\mathcal {I}}-\mu \Delta \big ) u^{k+1} = \lambda f +\tau u^k-\nabla \cdot (\mu {\varvec{v}}^{k+1}+{\varvec{\varLambda }}^k) \end{aligned}$$

with ${\mathcal {I}}$ being the identity matrix. Under the periodic boundary condition, we can solve the above equation by the fast Fourier Transform (FFT), i.e.,

$$\begin{aligned} u^{k+1}= {\mathcal {F}}^{-1} \bigg (\frac{{\mathcal {F}}\big ({\lambda f}-\nabla \cdot (\mu {\varvec{v}}^{k+1}+{\varvec{\varLambda }}^k)+\tau u^k\big )}{(\lambda +\tau ){\mathcal {I}}-\mu {\mathcal {F}}({\Delta })} \bigg ), \end{aligned}$$

(23)

where ${\mathcal {F}}$ and ${\mathcal {F}}^{-1}$ denote the Fourier transform and inverse Fourier transform, respectively.

3.2 Convergence Analysis

In this subsection, we discuss the convergence of Algorithm 3.1. Firstly, we prove that a solution of our curvature-based regularization model (18) exists.

Lemma 3.1

There exists a minimizer $u^*\in {\mathbb {R}}^{mn}$ for the discrete minimization problem (18).

Proof

By the definitions of g in (7), (8) and (9), $g(\kappa (u))\ge 1$. According to Lemma 3.8 of [27], we have $\sum \limits _{i,j}|\nabla u_{i,j}| +\frac{\lambda }{2}\Vert u-f\Vert ^2$ is coercive. Then, there is

$$\begin{aligned}&\sum _{i,j}g(\kappa (u_{i,j}))\sqrt{1+|\nabla u_{i,j}|^2} +\frac{\lambda }{2}\Vert u-f\Vert ^2\nonumber \\&\quad > \sum \limits _{i,j}|\nabla u_{i,j}| +\frac{\lambda }{2}\Vert u-f\Vert ^2 \end{aligned}$$

(24)

is also coercive. By definition of $\kappa =\{\mathrm {H,K}\}$ as defined in (12) and continuity of the min/max functions, $\kappa =\kappa (\{\kappa _{\min },\kappa _{\max }\})$ is continuous on $\{\kappa _\ell :\ell =1,\ldots ,8\}$. Moreover by (16), $\kappa _\ell$ ($\ell =1,\ldots ,8$) are continuous functions on u. Therefore, $\sum \limits _{i,j}g(\kappa (u_{i,j}))\sqrt{1+|\nabla u_{i,j}|^2} +\frac{\lambda }{2}\Vert u-f\Vert ^2$ is continuous on u. Together with coercivity and continuity, we have that the discrete minimization problem (18) has a minimizer $u^*\in {\mathbb {R}}^{mn}$. $\blacksquare$

The convergence analysis of the proximal ADMM scheme has been widely studied [6, 14, 16, 44]. We follow the work [54] to give some theoretical analysis of Algorithm 3.1. We first prove the monotonic decrease of the error sequence and the convergence of the residuals under certain assumption. Then, we show the iterative sequences generated by Algorithm 3.1 converges to a limit point that satisfies the first-order optimality conditions.

Theorem 3.2

Let $\{(u^k, {\varvec{v}}^k; {\varvec{\varLambda }}^{k})\}_{k \in {\mathbb {N}}}$ be the sequence generated by proposed ADMM-based Algorithm 3.1 and $({{\bar{u}}}, \bar{{\varvec{v}}}; \bar{{\varvec{\varLambda }}})$ be a point satisfying the first-order optimality conditions

$$\begin{aligned} \left\{ \begin{array}{ll} g(\kappa (u))\frac{{\varvec{v}}}{\sqrt{1+|{\varvec{v}}|^2}}+{\varvec{\varLambda }}=0,\\ \lambda (u-f)+\nabla \cdot {\varvec{\varLambda }}=0,\\ {\varvec{v}}-\nabla u=0. \end{array} \right. \end{aligned}$$

(25)

Suppose $u_e^k=u^k-\bar{u}$, ${\varvec{v}}_e^k={\varvec{v}}^k-\bar{{\varvec{v}}}$ and ${\varvec{\varLambda }}_e^k={\varvec{\varLambda }}^k-\bar{{\varvec{\varLambda }}}$ denote the error sequence. If the quantity

$$\begin{aligned} {\Delta }^{k}:= & {} \big \langle g(\kappa (u^{k-1}))\frac{{\varvec{v}}^{k}}{\sqrt{1+|{\varvec{v}}^{k}|^2}} -\, g(\kappa ({\bar{u}}))\frac{\bar{{\varvec{v}}}}{\sqrt{1+|\bar{{\varvec{v}}}|^2}},\nonumber \\&\quad {\varvec{v}}^k- \bar{{\varvec{v}}}\big \rangle \ge 0,~ \forall k\in {\mathbb {N}}, \end{aligned}$$

(26)

then the followings hold:

(1) The sequence $\{e^k\}_{k\in {\mathbb {N}}}$ defined by

$$\begin{aligned} e^k: = \frac{\tau }{2}\Vert u_e^k\Vert ^2+\frac{\mu }{2}\Vert \nabla u_e^k\Vert ^2+\frac{\sigma }{2}\Vert {\varvec{v}}_e^k\Vert ^2+\frac{1}{2\mu }\Vert {\varvec{\varLambda }}_e^k\Vert ^2 \end{aligned}$$

(27)

is monotonically decreasing.

(2) The sequence $\{(u^k, {\varvec{v}}^k; {\varvec{\varLambda }}^{k})\}_{k \in {\mathbb {N}}}$ converges to a limit point $(u^*, {\varvec{v}}^*; {\varvec{\varLambda }}^{*})$ that satisfies the first-order optimality conditions (25).

Proof

(1) The optimality conditions of subproblems in proposed ADMM-based algorithm are

$$\begin{aligned} \left\{ \begin{array}{ll} g(\kappa (u^{k}))\frac{{\varvec{v}}^{k+1}}{\sqrt{1+|{\varvec{v}}^{k+1}|^2}}+\mu ({\varvec{v}}^{k+1}-\nabla u^{k})\\ +{\varvec{\varLambda }}^k+\sigma ({\varvec{v}}^{k+1}-{\varvec{v}}^{k})=0,\\ \lambda (u^{k+1}-f)-\mu \nabla \cdot (\nabla u^{k+1}-{\varvec{v}}^{k+1})\\ +\nabla \cdot {\varvec{\varLambda }}^k+\tau (u^{k+1}-u^{k})=0,\\ {\varvec{\varLambda }}^{k+1}={\varvec{\varLambda }}^k+\mu ({\varvec{v}}^{k+1}-\nabla u^{k+1}). \end{array} \right. \end{aligned}$$

(28)

We express (28) in the form of the error differences $u_e^k$, ${\varvec{v}}_e^k$ and ${\varvec{\varLambda }}_e^k$ and obtain

$$\begin{aligned} \left\{ \begin{array}{ll} g(\kappa (u^{k}))\frac{{\varvec{v}}^{k+1}}{\sqrt{1+|{\varvec{v}}^{k+1}|^2}}-g(\kappa ({\bar{u}}))\frac{\bar{{\varvec{v}}}}{\sqrt{1+|\bar{{\varvec{v}}}|^2}}\\ +\mu ({\varvec{v}}_e^{k+1}-\nabla u_e^{k})+{\varvec{\varLambda }}_e^k+\sigma ({\varvec{v}}_e^{k+1}-{\varvec{v}}_e^{k})=0,\\ \lambda u_e^{k+1}-\mu \nabla \cdot (\nabla u_e^{k+1}-{\varvec{v}}_e^{k+1})+\nabla \cdot {\varvec{\varLambda }}_e^k\\ +\tau (u_e^{k+1}-u_e^{k})=0,\\ {\varvec{\varLambda }}_e^{k+1}={\varvec{\varLambda }}_e^k+\mu ({\varvec{v}}_e^{k+1}-\nabla u_e^{k+1}). \end{array} \right. \end{aligned}$$

Taking the inner product of each of the above equations, respectively, with ${\varvec{v}}_e^{k+1}$, $u_e^{k+1}$ and ${\varvec{\varLambda }}_e^{k}$, we obtain

$$\begin{aligned} \left\{ \begin{array}{ll} \big \langle g(\kappa (u^{k}))\frac{{\varvec{v}}^{k+1}}{\sqrt{1+|{\varvec{v}}^{k+1}|^2}}-g(\kappa ({\bar{u}}))\frac{\bar{{\varvec{v}}}}{\sqrt{1+|\bar{{\varvec{v}}}|^2}},{\varvec{v}}_e^{k+1}\big \rangle \\ +\mu \langle {\varvec{v}}_e^{k+1}-\nabla u_e^{k},{\varvec{v}}_e^{k+1}\rangle +\sigma \langle {\varvec{v}}_e^{k+1}-{\varvec{v}}_e^{k},{\varvec{v}}_e^{k+1}\rangle \\ = -\langle {\varvec{\varLambda }}_e^k,{\varvec{v}}_e^{k+1}\rangle ,\\ \lambda \Vert u_e^{k+1}\Vert ^2+\mu \langle \nabla u_e^{k+1}-{\varvec{v}}_e^{k+1},\nabla u_e^{k+1}\rangle \\ +\tau \langle u_e^{k+1}-u_e^{k},u_e^{k+1}\rangle =\langle {\varvec{\varLambda }}_e^k,\nabla u_e^{k+1}\rangle ,\\ \langle {\varvec{\varLambda }}_e^{k+1}-{\varvec{\varLambda }}_e^k,{\varvec{\varLambda }}_e^k\rangle =\mu \langle {\varvec{v}}_e^{k+1}-\nabla u_e^{k+1},{\varvec{\varLambda }}_e^k\rangle . \end{array} \right. \end{aligned}$$

Then, applying $\langle x-y,x\rangle =\frac{1}{2}(\Vert x\Vert ^2+\Vert x-y\Vert ^2-\Vert y\Vert ^2)$ to the above equations yields

$$\begin{aligned} \left\{ \begin{array}{ll} \big \langle g(\kappa (u^{k}))\frac{{\varvec{v}}^{k+1}}{\sqrt{1+|{\varvec{v}}^{k+1}|^2}}-g(\kappa ({\bar{u}}))\frac{\bar{{\varvec{v}}}}{\sqrt{1+|\bar{{\varvec{v}}}|^2}},{\varvec{v}}_e^{k+1}\big \rangle \\ +(\frac{\sigma +\mu }{2})\Vert {\varvec{v}}_e^{k+1}\Vert ^2+\frac{\mu }{2}\Vert {\varvec{v}}_e^{k+1}-\nabla u_e^{k}\Vert ^2 \\ \quad +\frac{\sigma }{2}\Vert {\varvec{v}}^{k+1}-{\varvec{v}}^{k}\Vert ^2=\frac{\mu }{2}\Vert \nabla u_e^{k}\Vert ^2+\frac{\sigma }{2}\Vert {\varvec{v}}_e^{k}\Vert ^2-\langle {\varvec{\varLambda }}_e^k,{\varvec{v}}_e^{k+1}\rangle ,\\ \lambda \Vert u_e^{k+1}\Vert ^2 +\frac{\mu }{2}\Vert \nabla u_e^{k+1}\Vert ^2 + \frac{\mu }{2}\Vert \nabla u_e^{k+1}-{\varvec{v}}_e^{k+1}\Vert ^2 \\ \quad + \frac{\tau }{2}\Vert u_e^{k+1}\Vert ^2 + \frac{\tau }{2}\Vert u^{k+1}-u^k\Vert ^2 \\ \quad =\frac{\tau }{2}\Vert u_e^{k}\Vert ^2 +\frac{\mu }{2}\Vert {\varvec{v}}_e^{k+1}\Vert ^2 + \langle {\varvec{\varLambda }}_e^k,\nabla u_e^{k+1}\rangle ,\\ \frac{1}{2\mu }\Vert {\varvec{\varLambda }}_e^{k+1}\Vert ^2=\frac{1}{2\mu }\Vert {\varvec{\varLambda }}_e^k\Vert ^2+\frac{\mu }{2}\Vert {\varvec{v}}_e^{k+1}-\nabla u_e^{k+1}\Vert ^2\\ \quad +\langle {\varvec{v}}_e^{k+1}-\nabla u_e^{k+1},{\varvec{\varLambda }}_e^k\rangle . \end{array} \right. \end{aligned}$$

(29)

Moreover, summing of the equations in (29), it follows that

$$\begin{aligned}&\frac{\tau }{2}\Vert u_e^{k+1}\Vert ^2+\frac{\mu }{2}\Vert \nabla u_e^{k+1}\Vert ^2+\frac{\sigma }{2}\Vert {\varvec{v}}_e^{k+1}\Vert ^2+\, \frac{1}{2\mu }\Vert {\varvec{\varLambda }}_e^{k+1}\Vert ^2\\&\quad + \frac{\tau }{2}\Vert u^{k+1}-u^k\Vert ^2 +\, \frac{\mu }{2}\Vert {\varvec{v}}_e^{k+1}-\nabla u_e^{k}\Vert ^2 \\&\quad +\frac{\sigma }{2}\Vert {\varvec{v}}^{k+1}-{\varvec{v}}^{k}\Vert ^2 +\, \lambda \Vert u_e^{k+1}\Vert ^2 +\big \langle g(\kappa (u^{k}))\frac{{\varvec{v}}^{k+1}}{\sqrt{1+|{\varvec{v}}^{k+1}|^2}}\\&\quad -\, g(\kappa ({\bar{u}}))\frac{\bar{{\varvec{v}}}}{\sqrt{1+|\bar{{\varvec{v}}}|^2}},{\varvec{v}}_e^{k+1}\big \rangle = \frac{\tau }{2}\Vert u_e^{k}\Vert ^2 +\frac{\mu }{2}\Vert \nabla u_e^{k}\Vert ^2\\&\quad +\, \frac{\sigma }{2}\Vert {\varvec{v}}_e^{k}\Vert ^2+ \frac{1}{2\mu }\Vert {\varvec{\varLambda }}_e^{k}\Vert ^2. \end{aligned}$$

By the assumption of the theorem, we have $\big \langle g(\kappa (u^{k}))\frac{{\varvec{v}}^{k+1}}{\sqrt{1+|{\varvec{v}}^{k+1}|^2}}-g(\kappa ({\bar{u}}))\frac{\bar{{\varvec{v}}}}{\sqrt{1+|\bar{{\varvec{v}}}|^2}},{\varvec{v}}_e^{k+1}\big \rangle ={\Delta }^{k+1}\ge 0$. By dropping the nonnegative terms $\lambda \Vert u_e^{k+1}\Vert ^2$ and ${\Delta }^{k+1}$, there is

$$\begin{aligned}&e^{k+1}+\frac{\tau }{2}\Vert u^{k+1}-u^k\Vert ^2 + \frac{\mu }{2}\Vert {\varvec{v}}_e^{k+1}- \nabla u_e^{k}\Vert ^2\nonumber \\&\quad +\,\frac{\sigma }{2}\Vert {\varvec{v}}^{k+1}-{\varvec{v}}^{k}\Vert ^2 \le e^k. \end{aligned}$$

(30)

Since $\frac{\tau }{2}\Vert u^{k+1}-u^k\Vert ^2 + \frac{\mu }{2}\Vert {\varvec{v}}_e^{k+1}-\nabla u_e^{k}\Vert ^2+\frac{\sigma }{2}\Vert {\varvec{v}}^{k+1}-{\varvec{v}}^{k}\Vert ^2\ge 0$, then $\{e^k\}_{k\in {\mathbb {N}}}$ is a monotonically decreasing sequence.

(2) By the sequence $\{e^k\}_{k\in {\mathbb {N}}}$ being monotonically decreasing, we add the inequality (30) from $k=0$ to $\infty$ to obtain

$$\begin{aligned}&\sum _{k=0}^\infty \bigg (\frac{\tau }{2}\Vert u^{k+1}-u^k\Vert ^2+\frac{\mu }{2}\Vert {\varvec{v}}_e^{k+1} -\nabla u_e^{k}\Vert ^2\\&\quad +\frac{\sigma }{2}\Vert {\varvec{v}}^{k+1}-{\varvec{v}}^k\Vert ^2\bigg )\le \sum _{k=0}^\infty e^k-e^{k+1}<\infty . \end{aligned}$$

This indicates

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert u^{k+1}-u^k\Vert= & {} \lim _{k\rightarrow \infty }\Vert {\varvec{v}}_e^{k+1} -\nabla u_e^{k}\Vert \nonumber \\= & {} \lim _{k\rightarrow \infty } \Vert {\varvec{v}}^{k+1}-{\varvec{v}}^k\Vert =0. \end{aligned}$$

(31)

In addition, using (31) and the Minkowski’s inequality, we also obtain

$$\begin{aligned} \Vert {\varvec{\varLambda }}^{k+1}-{\varvec{\varLambda }}^k\Vert\le & {} \big (\mu \Vert {\varvec{v}}_e^{k+2} -{\varvec{v}}_e^{k+1}\Vert \\&+\mu \Vert {\varvec{v}}_e^{k+2}-\nabla u_e^{k+1}\Vert \big )=0, \end{aligned}$$

thus

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert {\varvec{\varLambda }}^{k+1}-{\varvec{\varLambda }}^k\Vert =\lim _{k\rightarrow \infty }\Vert {\varvec{v}}^{k+1}-\nabla u^{k+1}\Vert =0. \end{aligned}$$

Based on part (1), the error term $\{e^k\}_{k\in {\mathbb {N}}}$ is a monotone decreasing sequence for any point $({{\bar{u}}}, \bar{{\varvec{v}}}; \bar{{\varvec{\varLambda }}})$ that satisfies (25) in ${\mathbb {R}}^+$, this shows the sequence $\{(u^k,{\varvec{v}}^k;{\varvec{\varLambda }}^k)\}_{k\in {\mathbb {N}}}$ generated by Algorithm 3.1 is a Cauchy sequence and has a weakly convergent subsequence. We denote the subsequence as $\{(u^{k_\ell },{\varvec{v}}^{k_\ell };{\varvec{\varLambda }}^{k_\ell })\}_{\ell \in {\mathbb {N}}}$ and the limit point as $(u^*, {\varvec{v}}^*; {\varvec{\varLambda }}^{*})$.

Therefore, the sequence $\{(u^{k_\ell },{\varvec{v}}^{k_\ell };{\varvec{\varLambda }}^{k_\ell })\}_{\ell \in {\mathbb {N}}}$ satisfies the optimality conditions (28) such that

$$\begin{aligned} \left\{ \begin{array}{ll} g(\kappa (u^{k_\ell }))\frac{{\varvec{v}}^{{k_\ell }+1}}{\sqrt{1+|{\varvec{v}}^{{k_\ell }+1}|^2}}+\mu ({\varvec{v}}^{{k_\ell }+1}-\nabla u^{k_\ell })+{\varvec{\varLambda }}^{k_\ell }\\ \quad + \sigma ({\varvec{v}}^{{k_\ell }+1}-{\varvec{v}}^{k_\ell }) = 0, \\ {\lambda }(u^{{k_\ell }+1}-f)-\mu \nabla \cdot (\nabla u^{{k_\ell }+1}-{\varvec{v}}^{{k_\ell }+1})+\nabla \cdot {\varvec{\varLambda }}^{k_\ell }\\ \quad + \tau (u^{{k_\ell }+1}-u^{k_\ell }) = 0,\\ {\varvec{\varLambda }}^{{k_\ell }+1}={\varvec{\varLambda }}^{k_\ell }+\mu ({\varvec{v}}^{{k_\ell }+1}-\nabla u^{{k_\ell }+1}). \end{array} \right. \end{aligned}$$

(32)

By taking the limit of the convergent sequence, it yields

$$\begin{aligned} \left\{ \begin{array}{l} g(\kappa (u^{*}))\frac{{\varvec{v}}^{*}}{\sqrt{1+|{\varvec{v}}^{*}|^2}}+{\varvec{\varLambda }}^{*}=0,\\ \lambda (u^{*}-f)+\nabla \cdot {\varvec{\varLambda }}^{*}=0,\\ {\varvec{v}}^{*}-\nabla u^{*}=0, \end{array} \right. \end{aligned}$$

for almost every point in $\Omega$. This implies that the limit point $(u^*, {\varvec{v}}^*; {\varvec{\varLambda }}^{*})$ of the sequence $\{(u^{k},{\varvec{v}}^{k};{\varvec{\varLambda }}^{k})\}_{k\in {\mathbb {N}}}$ satisfies the first-order optimality conditions (25). $\blacksquare$

Remark 3.3

Similarly to the $\kappa \mathrm {TV}$ method in [54], we introduce the proximal terms to gain the theoretical convergence of Algorithm 3.1 and simply set $\sigma =0$ and $\tau =0$ in the numerical experiments. Although it is difficult to validate the lower bound of ${\Delta }_k$, we observe that ${\Delta }_k\ge 0$ holds for $k\ge 0$ numerically as shown in Fig. 6.

4 Experiments

In this section, comprehensive experiments on both synthetic and real image reconstruction problems are implemented to verify the effectiveness and efficiency of our curvature-based model. All numerical experiments are performed utilizing MATLAB R2016a on a machine with 3.40GHz Intel(R) Core(TM) i7-6700 CPU and 32GB RAM.

In our experiments, we use both peak signal-to-noise ratio (PSNR) and structural similarity (SSIM) [48] to quantitatively evaluate the qualities of the reconstruction results. The PSNR is defined explicitly as

$$\begin{aligned} \mathrm{PSNR}(u_0,u) = 10 \mathrm log{\frac{255^2}{MSE}}, \end{aligned}$$

where $u_0$ denotes the clean image, u denotes the recovery image and MSE denotes the mean squared error between $u_0$ and u. We further define the SSIM as follows

$$\begin{aligned} \mathrm{SSIM}(u_0,u) = \frac{(2\mu _{u_0}\mu _u+c_1)(2\sigma _{u_0u}+c_2)}{(\mu ^2_{u_0}+\mu ^2_{u}+c_1)(\sigma ^2_{u_0}+\sigma ^2_{u}+c_2)}, \end{aligned}$$

where ${\mu _{u_0}}$ and ${\mu _{u}}$ express the local mean values of images $u_0$ and u, ${\sigma _{u_0}}$ and ${\sigma _{u}}$ signify the respective standard deviations, ${\sigma _{{u_0}u}}$ is the covariance value between the clean image $u_0$ and recovered image u, and ${c_1}$ and ${c_2}$ are two constants to avoid instability for near-zero denominator values. Theoretically, higher PSNR and SSIM values indicate better performance of the restoration methods.

Fig. 6

The behavior of ${\Delta }^{k}$ with iteration numbers in TAC method on different test images with $\tau =0$ and $\sigma =0$. Note that ${\Delta }^{k}\ge 0$ for all iterations

Fig. 7

The PSNR evolutions of ‘Cameraman’ obtained by different combinations of the parameter $\mu$ and $\alpha$ with fixed regularized parameters $\lambda$ in TAC-K method

Fig. 8

The PSNR evolutions of ‘Cameraman’ obtained by different combinations of the parameter $\mu$ and Iter with fixed regularized parameters $\alpha$ in TAC-K method

Fig. 9

The PSNR evolutions of ‘Cameraman’ obtained by different inner Newton iterations (L) in TAC-H and TAC-K methods

Fig. 10

Evaluations of ‘Cameraman’ obtained by the proposed methods. From left to right: Relative error in $u^k$, numerical energy, PSNR and SSIM, respectively (Color figure online)

Table 2 The PSNR and SSIM of Gaussian noise removal for the Euler’s elastica and our curvature-based models

4.1 Computational Complexity

In this subsection, we analyze the computational complexity of Algorithm 3.1. The main computationally expensive components include the calculation of H or K, the FFT, inverse FFT and Newton iterations. Generally speaking, calculating the H or K on image surface costs $\varvec{O}(mn)$. The computational complexity of FFT, inverse FFT in u-subproblem is well-known as $\varvec{O}(mn\log (mn))$ at each iteration. The ${\varvec{v}}$-subproblem with two components can be computed at the cost $\varvec{O}(2mn)$ using the Newton iterations. Therefore, the total computational complexity of Algorithm 3.1 is $\varvec{O}(2mn\log (mn)+3mn)$. On the other hand, the augmented Lagrangian method (ALM) of the Euler elastica model in [47] has four subproblems, which are solved by the FFT, inverse FFT and shrinkage operators. Its total computational complexity can be expressed as $\varvec{O}(6mn\log (mn)+4mn)$ per iteration. Besides, the augmented Lagrangian method for mean curvature regularization model in [60] has five subproblems, whose total computational complexity can be denoted as $\varvec{O}(6mn\log (mn)+8mn)$ per iteration. Therefore, our algorithm has lower computational complexity per iteration compared to the other two curvature-based models.

4.2 Parameters Discussion

There are a total of three parameters in the proposed algorithm, i.e., $\lambda$, $\alpha$ and $\mu$. Both $\lambda$ and $\mu$ are model parameters, such that $\lambda$ balances the contributions between the data fidelity and the regularization term, and $\alpha$ tradeoffs the influences between the curvature regularization and area minimization. The parameter $\mu$ is the penalty parameter, which affects the convergent speed and stability of the proposed algorithm. In the paragraphs below, we use the total absolute Gaussian curvature (TAC-K) as the regularization term to discuss the impacts of the parameters in more details.

We first evaluate the impact of the parameter $\lambda$ with regard to $\alpha$ and $\mu$ on image ‘Cameraman’, where $\lambda$ is chosen from $\lambda \in \{0.045, 0.09, 0.18\}$. For each $\lambda$, we vary the parameters $(\alpha ,\mu ) \in \{\alpha ^0\times 2^{-\delta }, \alpha ^0\times 2^{-\delta +1},\ldots , \alpha ^0\times 2^{\delta -1}, \alpha ^0\times 2^{\delta }\}\times \{\mu ^0\times 2^{-\delta }, \mu ^0\times 2^{-\delta +1},\ldots , \mu ^0\times 2^{\delta -1}, \mu ^0\times 2^{\delta }\}$ with $\alpha ^0=12$, $\mu ^0=2$ and $\delta =9$. In Fig. 7, we plot the values of PSNR versus different combinations of $\lambda$ and $(\alpha ,\mu )$, together with the best recovery results for $\lambda = \{0.045, 0.09, 0.18\}$, respectively. For a fixed $\lambda$, the value of PSNR drops as $\alpha$ and $\mu$ become too large, but there are relatively large intervals for both $\alpha$ and $\mu$ to produce satisfactory results. In addition, too small $\lambda$ results in over smooth recovery result with some details missing, while too large $\lambda$ leads to non-smooth recovery results with some noises remaining. Thus, $\lambda$ needs to be manually tuned according to the noise levels and image structures in practice.

We further analyze the impact of $\alpha$ relating to $\mu$ and the convergence with a fixed $\lambda = 0.09$. Different values of $\alpha \in \{3,12,48\}$ and $(\mu ,\mathrm{Iter})\in \{2^{-8},2^{-7},\ldots ,2^{7},2^{8}\} \times \{0,30,\ldots ,570,600\}$ are used to evaluate the denoising performance. As shown in Fig. 8, for a fixed $\alpha$, we notice that the value of $\mu$ affects the numerical convergence such that a relatively large $\mu$ yields faster convergence and a too small $\mu$ usually results in using more iterations to reach convergence. Therefore, we use $\mu =2$ as its default value unless otherwise specified. With the default $\mu$, the plots reveal that the number of iterations $\mathrm{Iter}=300$ is enough for different $\alpha$. We also observe that a too small $\alpha$ (e.g., $\alpha = 3$ for ‘Cameraman’) leads to non-smooth results and a too large $\alpha$ (e.g., $\alpha = 48$ for ‘Cameraman’) results in over-smooth results. Thus, $\alpha$ should be properly chosen according to image structures and noise levels to smooth out the homogenous regions as well as preserve the image details.

Moreover, the iteration number of inner Newton’s method also affects the efficiency of the proposed algorithm. Under the same stopping condition $\epsilon =2\times 10^{-5}$, Fig. 9 displays the values of PSNR versus CPU time with three different options of the iteration number L, i.e., $L=1$, 5 and 10. It can be seen that a too large L results in higher computational cost and a too small L leads to a lower PSNR. Therefore, we fix $L=5$ for all applications. Lastly, we fix the spatial step size h as $h=0.5$ in all experiments for the best balance between the smoothness and fine details.

4.3 Numerical Convergence

The decays of the relative error and numerical energy are provided to illustrate the convergence of the ADMM algorithm versus the iterations

$$\begin{aligned} \mathrm {ReErr}(u^k)=\frac{\Vert u^k-u^{k-1}\Vert _1}{\Vert u^{k-1}\Vert _1}, \end{aligned}$$

and

$$\begin{aligned} \mathrm {E}(u^k) =\sum _{i,j} g\big (\kappa (u^{k-1}_{i,j})\big )\sqrt{1+|\nabla u_{i,j}^k|^2} + \frac{\lambda }{2}\Vert u^k-f\Vert ^2. \end{aligned}$$

With the optimal parameters $\lambda =0.09$, $\mu =2$, $\alpha =\{0.3,12\}$ for TAC-H and TAC-K models, respectively, we track the decays of the relative errors and the numerical energies, as well as the values of PSNRs and SSIMs for ‘Cameraman’, which are displayed using log-scale in Fig. 10. These plots demonstrate the convergence of the iterative process and the stability of the proposed methods. Note that the TAC-K model usually converges to a comparable larger relative error due to a relatively larger $\alpha$ is used in the Gaussian curvature-based model to achieve the best restoration results.

Fig. 11

The denoising results of the smooth images A1, A2 and A3 (from top to bottom) obtained by the Euler’s elastica and our TAC-H model

Fig. 12

The numerical mean curvature of the clean images and denoising images obtained by the Euler’s elastica and TAC-H model

Fig. 13

The image surfaces of the clean images and reconstructed images by the Euler’s elastica and our TAC-H model

4.4 Gaussian Denoising

In the first place, we compare the proposed models relying on TAC, TSC and TRV, with the Euler’s elastica model on image denoising examples. Three smooth images (i.e., A1, A2 and A3) corrupted by Gaussian noise with zero mean and the standard deviation 10 are used in the evaluation. We fix the parameters $\lambda =0.11$ and $\mu = 2$ for our model, and set $\alpha = 0.3$ for the mean curvature-based variational models (i.e., TAC-H, TSC-H and TRV-H) and $\alpha = 12$ for the Gaussian curvature-based models (i.e., TAC-K, TSC-K and TRV-K). In particular, we implement the ALM algorithm in [47] with the same parameters as the ones used in the original paper such that $\alpha =10$, $\lambda =10^2$, $r_1=1$, $r_2=2\cdot 10^2$, $r_4=5\cdot 10^2$ and $\epsilon =10^{-2}, 1.3\cdot 10^{-3}, 8\cdot 10^{-3}$ for image A1 to A3, respectively.

In Table 2, we detail the comparison results in terms of PSNR and SSIM. It can be observed that our curvature-based model always achieves higher PSNR and SSIM than the Euler’s elastica method for all combinations of curvature functions and curvature types. Moreover, the TAC-H model gives the best recovery results for all three images among the combinations. In Fig. 11, we display the restoration results obtained by the Euler’s elastica model and our TAC-H model, which clearly shows our model can ideally preserve image structures such as edges and corners. The numerical mean curvatures of the image A1 and A2 are exhibited in Fig. 12, which are computed using Eqs. (12)–(17) on the clean images, denoising images obtained by the Euler’s elastica model and our TAC-H model. For a fair comparison, we min-max scale all images into [0, 1] in advance of the calculation. It can be observed the numerical mean curvature is relatively small in the homogeneous regions, and jumps across the edges, which demonstrates that mean curvature regularization can well preserve sharp jumps in images. The image surfaces of the clean images and restored images of Euler’s elastica and TAC-H models in Fig. 13 also accord with our conclusion such that our mean curvature regularization has an advantage in preserving the edges and sharp corners over the Euler’s elastica.

Fig. 14

The denoising results of ‘Cameraman’ (top) and the corresponding residual images (bottom) generated by the comparative methods

Fig. 15

The denoising results of ‘Triangle’ (top) and the corresponding residual images (bottom) generated by the comparative methods

Fig. 16

The denoising results of ‘Lena’ (top) and the corresponding local magnification views (bottom) generated by the comparative methods

Fig. 17

The denoising results of ‘Plane’ (top) and the corresponding local magnification views (bottom) generated by the comparative methods

Table 3 The PSNR and SSIM of Gaussian noise removal for comparative methods

Table 4 The CPU time(s) comparison of Gaussian noise removal for comparative methods, where underline represents the lowest computational cost, bold and italics denote the computational cost of our TAC-H and TAC-K models, respectively

To further demonstrate the effectiveness and efficiency of our curvature-based model, we evaluate the performance on more synthetic and natural images by comparing with several state-of-the-art variational denoising methods including the total variation (TV) model in [53], Euler’s elastica (Euler) model in [47], the second-order total generalized variation (TGV) model in [7] and mean curvature regularizer (MEC) model in [60]. Four test images (i.e., ‘Cameraman’, ‘Triangle’, ‘Lena’ and ‘Plane’) are explored and degraded by the Gaussian noise with zero mean and the standard deviation 20. To set up the experimental comparison as fair as possible, the parameters of the comparative methods are selected as suggested in the corresponding papers, which are given as (a) TV: $r_1=10$ and $\lambda =15$; (b) Euler’s elastica: $\alpha =10$, $r_1=1$, $r_2=2\cdot 10^2$, $r_4=5\cdot 10^2$ and $\lambda =2\cdot 10^2$; (c) TGV: $\alpha _0=1.5$, $\alpha _1=1.0$, $r_1=10$, $r_2=50$ and $\lambda =10$; (d) MEC: $r_1=40$, $r_2=40$, $r_3=10^5$, $r_4=1.5\cdot 10^5$ and $\lambda =10^2$. The experience-dependent parameters are set as $\lambda =0.09$, $\mu =2$, $\alpha =0.3$ for TAC-H model and $\alpha =12$ for TAC-K model.

We compare the restoration results both quantitatively and qualitatively. The recovery results and the residual images $f-u$ of ‘Cameraman’ and ‘Triangle’ are visually exhibited in Figs. 14 and 15, while the denoising images and the selected local magnified views of ‘Lena’ and ‘Plane’ are shown in Figs. 16 and 17. In general, all methods can remove the noises and recover the major structures and features quite well. However, the TV model suffers from obvious staircase-like artifacts and lots of image details and textures can be observed in the residual images. As representatives of high-order regularities, the Euler’s elastica, TGV and MEC models can overcome the staircase effects and preserve image details to a certain extent. And our TAC-H and TAC-K models always give the best recovery results, which can not only keep the smoothness in the homogeneous regions but also preserve fine details in the texture regions. Table 3 records the values of PSNR and SSIM for all the algorithms, which also convinces our TAC-K model and gives the overall best recovery results.

The CPU time recorded in Table 4 illustrates that our TAC-H and TAC-K models are more efficient than other high-order methods, which are significantly faster than the Euler’s elastica and mean curvature models. To better visualize the convergence of the comparative methods, we plot the relative errors in $u^k$ of these methods for ‘Lena’ and ‘Plane’ in Fig. 18. Although the relative error of the Euler’s elastica model drops faster at the beginning, our curvature-based models can attain smaller relative errors as the number of iterations increases. Thus, our proposal usually converges faster than others when a stringent relative error is used as the stopping criterion.

The visual illustrations of the numerical mean and Gaussian curvatures of ‘Cameraman’ and ‘Lena’ estimated on the noisy images, restoration images, and the clean images are presented in Fig. 19. Significant noises can be observed in the curvature maps of noisy images, while the curvature maps of the recovery images are noiseless and only jump on edges. Indeed, the curvature maps of the restorations are much alike to the ones obtained on the clean images in visual perceptions. It reveals that the TAC-H and TAC-K models successfully reduce the noises contained in the mean curvature and Gaussian curvature maps, which indicates the reasonability and effectiveness of our proposed models. Through an in-depth comparison between the curvature maps of the recovery images and clean images, we have the following two observations:

• Only main edges are presented in the Gaussian curvature maps. The Gaussian curvature has a small magnitude, as long as one principal curvature is small. It well explains why the Gaussian curvature-based model gives lower numerical energy; see Fig. 10b. Thus, minimizing Gaussian curvature allows for fine details and structures, which is more suitable for natural images such as ‘Lena’ and ‘Cameraman’ etc.

• More details and small edges exist in the mean curvature maps. By minimizing the total mean curvature of the noisy image, some tiny structures in the mean curvature maps will be smoothed out. Thus, the mean curvature regularization works better for images containing large homogeneous or slowly varying regions e.g., the smooth images in Fig. 11.

Fig. 18

Relative errors in $u^k$ of ‘Lena’ and ‘Plane’ obtained by the comparative methods

Fig. 19

The numerical mean curvature and Gaussian curvature maps of the noisy images (N), the restoration results (R) obtained by our proposals and clean images (C) on the first, second and third row, respectively

Fig. 20

The salt & pepper denoising results of ‘House’ and ‘Realtest’ obtained by the Euler’s elastica, TGV and TAC-K methods

Table 5 The evaluations of salt & pepper noise removal for the Euler’s elastica, TGV and TAC-K methods

Fig. 21

The Poisson denoising results of ‘Hill’ and ‘Boats’ obtained by the Euler’s elastica, TGV and TAC-K methods

Table 6 The evaluations of Poisson noise removal for the Euler’s elastica, TGV and TAC-K methods

Fig. 22

The denoising results of ‘Airplane’ generated by the Euler’s elastica and TAC-K methods

Fig. 23

The denoising results of ‘Fruits’ generated by the Euler’s elastica and TAC-K methods

Fig. 24

The denoising results of ‘Flower’ generated by the Euler’s elastica and TAC-K methods

Table 7 The evaluations of color image noise removal for the Euler’s elastica and TAC-K methods

Fig. 25

The inpainting results (top) and local magnification views (bottom) of synthetic image obtained by TV, Euler’s elastica, TAC-H and TAC-K methods, where the parameters are adopted as $\lambda =5$, $\alpha =\{0.5,10\}$, $\mu _1=2$, $\mu _2=0.2$

Fig. 26

The inpainting results of real images obtained by TV, Euler’s elastica, TAC-H and TAC-K methods

4.5 Salt & Pepper and Poisson Denoising

In this subsection, both the salt & pepper and Poisson denoising examples are operated to further illustrate the advantages of our curvature regularized model. According to the statistical properties of the salt & pepper noise, we adopt the $l^1$-norm data fidelity term instead of the $l^2$-norm one [17, 24, 38], which gives

$$\begin{aligned} \min _{u} \sum _{i,j} g(\kappa (u_{i,j}))\sqrt{1+|\nabla u_{i,j}|^2} + {\lambda }\Vert u-f\Vert _1. \end{aligned}$$

(33)

To deal with the above minimization problem, two auxiliary variables are introduced to rewrite it into the following constrained minimization problem

$$\begin{aligned} \begin{aligned} \min _{u,{\varvec{v}},w}~&\sum _{i,j}g(\kappa (u_{i,j}))\sqrt{1+|{\varvec{v}}_{i,j}|^2} + {\lambda }\Vert w\Vert _1 \\ ~\mathrm {s.t.}~~~&~~{\varvec{v}}_{i,j}=\nabla u_{i,j},~~w=u-f. \end{aligned} \end{aligned}$$

More details of the numerical algorithm for solving such constrained minimization problem can be referred to [24, 53].

Table 8 The evaluations of image inpainting for TV, Euler’s elastica, TAC-H and TAC-K methods

We use two grayscale test images ‘House’ $(256\times 256)$ and ‘Realtest’ $(400\times 420)$, both of which are corrupted by $30\%$ salt & pepper noise. The parameters are set as $\lambda =1.8$, $\alpha =2$, and $\mu _1=2$, $\mu _2=0.1$. Figure 20 shows the recovery results and the selected magnified views obtained by the Euler’s elastica, TGV and our TAC-K methods. It can be observed that all methods can avoid the staircase-like artifacts in smooth regions. Table 5 illustrates that our TAC-K model gives slightly higher PSNR and SSIM than the Euler’s elastica and TGV models. Simultaneously, our TAC-K model can save much computational cost compared to the other two high-order methods on both images for meeting the same stopping criteria.

We also conduct examples on Poisson noises removal, the variational model of which can be formalized by integrating with the Kullback-Leibler (KL) distance as follows

$$\begin{aligned}&\min _{u} \sum _{i,j} g(\kappa (u_{i,j}))\sqrt{1+|\nabla u_{i,j}|^2} \nonumber \\&\quad + \lambda \sum _{i,j}(u_{i,j}-f_{i,j}\log u_{i,j}). \end{aligned}$$

(34)

More detailed implementation of the operator splitting and ADMM-based algorithm for the above minimization problem (34) can be found in [29, 51].

In Fig. 21, Poisson noises are introduced into two clean images, i.e., ‘Hill’ $(256\times 256)$ and ‘Boats’ $(512\times 512)$. We set the parameters in our model as $\lambda =25$, $\alpha =15$, $\mu _1=2$ and $\mu _2=4$. As shown in Fig. 21, the TAC-K model can preserve more image details and features than both Euler’s elastica and TGV models, e.g., the window area in ‘Hill’ and the mast area in ‘Boats’, which are further verified by the PSNR and SSIM in Table 6. Similarly to the previous experiment, our TAC-K method outperforms the other two methods by significantly reducing the calculation time.

4.6 Color Images Denoising

In this subsection, we extend our TAC-K model to color image restoration [34, 49]. Without loss of generality, we consider a vectorial function $\mathbf{u}=(u^r,u^g,u^b):{{\Omega }}\rightarrow {\mathbb {R}}^3$. For the sake of simplicity, we propose to independently recover each RGB channel of color images (channel by channel), and then generate the final restored image by combining the RGB channels together. Thus, the corresponding color image denoising model for Gaussian noise removal can be described as

$$\begin{aligned}&\min _\mathbf{u} \sum _{c \in \{r,g,b\}}\sum _{i,j} g(\kappa (u^c_{i,j}))\sqrt{1+|\nabla u^c_{i,j}|^2}\nonumber \\&\quad + \frac{\lambda }{2}\sum _{c \in \{r,g,b\}}\Vert u^{c}-f^{c}\Vert ^2. \end{aligned}$$

(35)

We plan to extend our curvature regularized models to the color TV model [5] and Beltrami color image model [40, 41] in the future.

Three different color images are selected as examples to demonstrate the efficiency and superiority of our TAC-K model, which are ‘Airplane’, ‘Fruits’ and ‘Flower’ degraded by the Gaussian noise with zero mean and the standard deviation $\theta =\{20, 30, 40\}$, respectively. The parameters are set as $\lambda =\{0.09, 0.06, 0.03\}$, $\alpha =10$ and $\mu =2$ for different noise levels accordingly to guarantee satisfactory restoration results can be achieved. On the other hand, the parameters of the Euler’s elastica model are set as $\lambda =\{2\cdot 10^2, 1.5\cdot 10^2, 10^2\}$, $\alpha =10$, $r_1=1$, $r_2=2\cdot 10^2$ and $r_4=5\cdot 10^2$ for the three images, respectively. As shown in Figs. 22, 23 and 24, the proposed TAC-K model can provide sharper image edges and smoother homogenous regions. The energy curves demonstrate that our algorithm converges well for the vectorial image problems. To further evaluate the denoising performance, quantitative results with different degradations are summarized in Table 7, which shows the TAC-K model outperforms the Euler’s elastica model in both recovery quality and computational efficiency.

4.7 Image Inpainting

Last but not least, we demonstrate some examples of our curvature regularized model on the applications of color image inpainting [45]. In general, the task of image inpainting is to reconstruct missing parts of an image using information from the given regions, where the missing parts are called the inpainting domain and denoted by $D\subset {\Omega }$. For a given image $\mathbf{f}=(f^r,f^g,f^b)$, we formulate the curvature-based inpainting model as follows

$$\begin{aligned}&\min _\mathbf{u}~ \sum _{c \in \{r,g,b\}}\sum _{i,j} g(\kappa (u_{i,j}^{c}))\sqrt{1+|\nabla u_{i,j}^{c}|^2}\nonumber \\&\quad + \frac{\lambda }{2}\sum _{c \in \{r,g,b\}}\Vert u^{c}-f^{c}\Vert ^2_{{{\Omega }\setminus D}}, \end{aligned}$$

(36)

which is also implemented channel by channel. More details of the numerical implementation of the above model can be found in [54].

In Figs. 25 and 26, we present several convincing examples obtained by the TV, Euler’s elastica, and our TAC-H, TAC-K models on both color synthetic and real image inpainting applications. It is obviously shown that the results of the TV model tend to fill in the inpainting domain with the piecewise constant values, which are unnatural for large missing domains. The Euler’s elastica, TAC-H and TAC-K models have the capability of connecting the large gap as well as protecting image structures owing to the minimization of the curvatures. Moreover, it can be observed that the TAC-K model gives the visually best inpainting results, which can well recover the inpainting domain and preserve fine details. Table 8 records the evaluations of the inpainting results in terms of PSNR, SSIM and CPU time, which further verifies the efficiency and superiority of our curvature regularized models in providing significantly better PSNR and SSIM using only 2/3 of the CPU time of the Euler’s elastica model.

5 Conclusions

In this work, we introduced novel curvature regularizers for image reconstruction problems, where both mean curvature and Gaussian curvature were derived and investigated using the normal curvatures according to differential geometry theory. The proposed curvature regularized model was regarded as a re-weighted image surface minimization model and efficiently solved by the ADMM-based algorithm. We discussed the existence of the minimizer and provided the convergence analysis for the proposed ADMM-based algorithm. Numerical experiments on both gray and color images have illustrated the efficacious and superior performance of our proposed method in terms of quantitative and qualitative evaluations. The proposed method can be used for other practical applications in image processing and computer vision, for instance, image segmentation, image registration, image super-resolution, etc.