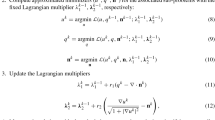Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Image denoising is to remove noise while keeping meaningful vision information such as object edges and boundaries. It is a crucial step in image processing with a wide range of applications in medical image analysis, video monitoring, and others. During the last three decades, numerous models have been proposed to deal with this problem [3, 4, 7, 19–21, 23–25, 28]. One of the most popular variational models was proposed by Rudin, Osher, and Fatemi in their seminal work (ROF model) [25], where the cleaned image corresponds to the minimizer of the following functional

$$\begin{aligned} E(u)&= \lambda \int _{\varOmega }|\nabla u|+ \int _{\varOmega }(f-u)^{2}, \end{aligned}$$
(1)

where \(f: \varOmega \rightarrow \mathbb {R}\) is a given noisy image defined on \(\varOmega \) (always a rectangle in \(\mathbb {R}^{2}\)) and \(\lambda >0\) is a positive tuning parameter controlling how much noise will be removed. The remarkable feature of the ROF model lies in its effectiveness in preserving object edges while removing noise. This is due to the total variation based regularizer. In fact, the total variation has been widely employed in accomplishing other image tasks such as deblurring, segmentation, and registration. However, as pointed out in [6], the ROF model has several unfavorable features. The main caveat is the stair case effect, that is, the resulting clean image would present blocks even though the desired image could be smooth, such as human face. Other undesirable properties include corner smearing and loss of image contrast. To remedy these drawbacks, quite a few high order variational models have been proposed [1, 2, 9, 16–18, 31]. Despite of the effectiveness of these models in removing the staircase effect, it is often a challenging issue to minimize the corresponding functionals. Note that the models contain second order derivatives, the related Euler-Lagrange equations are fourth-order, which raises a nontrivial problem of developing effective and efficient algorithms to solve them. Indeed, as more and more high order models were used in image processing [5, 7, 8, 12–15, 22, 27, 30, 32], it is an imperative need to explore efficient numerical algorithms for these models.

Recently, augmented Lagrangian methods have been successfully employed in the minimization of nondifferentiable or high order functionals [26, 29]. For instance, the minimization of the ROF model suffers from the presence of its nonlinear and nondifferentiable term. In [29], the authors proposed an efficient and accurate algorithm using augmented Lagrangian method to minimize the ROF functional. In [26], the technique was extended to functionals related to Euler’s elastica with applications in image denoising, inpainting, and zooming [1, 2, 8, 17, 18], where the original minimization problem was converted to several subproblems of low order functionals. Therefore, augmented Lagrangian method becomes a suitable technique to handle curvature related functionals.

Inspired by these works, in [33], we constructed an augmented Lagrangian method based fast algorithm for the mean curvature based image denoising model [31], whose functional can be expressed as follows:

$$\begin{aligned} E(u)&= \lambda \int \left| \nabla \cdot \left( \frac{\nabla u}{\sqrt{1+|\nabla u|^2}}\right) \right| +\frac{1}{2}\int (f-u)^2, \end{aligned}$$
(2)

where \(\lambda \) is a tuning parameter and the term \(\nabla \cdot \left( \frac{\nabla u}{\sqrt{1+|\nabla u|^2}}\right) \) is the mean curvature of the surface \(\phi (x,y,z)=u(x,y)-z=0\) (see [10]). The model tries to fit the given noisy image surface \((x,y,f(x,y))\) with a surface \((x,y,u(x,y))\) that bears small magnitude of mean curvature. As demonstrated in [31], the model is able to sweep noise while keeping object edges, and it also ameliorates the staircase effect. More importantly, the model is also capable of preserving image contrasts as well as geometry of object shapes, especially object corners. As detailed in [33], by using augmented Lagrangian method, the original minimization problem was reformulated as a constrained optimization, and with the specially designed constraints, the pursuit of saddle points of the optimization problem amounts to minimizing several functionals alternatively, some of which have closed form solutions while the other ones can be solved using FFT. Note that FFT yields exact solutions to those equations, in this work, we want to check whether these exact solutions in each iteration can be replaced by some approximations in order to further reduce the computational cost.

This paper is organized as follows. In Sect. 2, we present a short review of the mean curvature denoising model and recall the augmented Lagrangian method developed for this model [33]. Section 3 presents the details of the minimization of the associated subproblems. In Sect. 4, numerical results obtained using the two methods as well as the efficiency will be compared, which is then followed by a conclusion in Sect. 5.

2 The Image Denoising Model and the Augmented Lagrangian Method

In this section, we first review the mean curvature based image denoising model and then sketch the augmented Lagrangian method developed for this model [33].

2.1 The Mean Curvature Based Image Denoising Model

For a given image \(f: \varOmega \rightarrow \mathbb {R}\) defined on a domain \(\varOmega \subset \mathbb {R}^{2}\), one can regard it as a surface \((x,y,f(x,y))\) in \(\mathbb {R}^{3}\). The denoising task amounts to finding a piecewisely smooth surface that approximates that noisy surface while also keeping its sharp gradients, since these sharp transitions determine important vision clues such as edges and corners. To single out those piecewisely smooth surfaces, one needs to choose an appropriate regularizer. In [31], the \(L^{1}\)-norm of mean curvature of an image surface was employed as the regularizer.

Specifically, let \(u: \varOmega \rightarrow \mathbb {R}\) be a function. Its image surface is just the zero level set of the function \(\phi (x,y,z)=u(x,y)-z\). Then the mean curvature of this surface can be expressed as \(\nabla \cdot \left( \frac{\nabla \phi }{|\nabla \phi |}\right) =\nabla \cdot \left( \frac{\nabla u}{\sqrt{1+|\nabla u|^2}}\right) \), denoted by \(\kappa _{u}\). Using the \(L^{1}\)-norm of mean curvature as the regularizer, the mean curvature denoising model can be written as the minimization of the following functional:

$$\begin{aligned} E(u)&= \lambda \int |\kappa _{u}|+\frac{1}{2}\int (f-u)^2, \end{aligned}$$
(3)

which gives the Eq. (2).

Due to the non-differentiable term in this functional, numerically, one often considers its regularized version [22, 32]

$$\begin{aligned} E(u)&= \lambda \int \varPhi (\kappa _{u})+\frac{1}{2}\int (f-u)^2, \end{aligned}$$
(4)

with

$$\begin{aligned} \varPhi (x) = \left\{ \begin{array}{l} x^{2}, \, {|x| \le 1}\\ |x|, \, {|x| > 1,} \end{array} \right. \end{aligned}$$
(5)

and derives the following fourth order Euler-Lagrange equation:

$$\begin{aligned} \lambda \nabla \cdot [\frac{1}{\sqrt{1+|\nabla u|^{2}}}(\mathbf {I}-\mathbf {P})\nabla \varPhi '(\kappa _{u})]-(f-u)&= 0, \end{aligned}$$
(6)

where \(\mathbf {I}, \mathbf {P}:\mathbb {R}^{2}\rightarrow \mathbb {R}^{2}\) with \(\mathbf {I}(\mathbf {x})=\mathbf {x}\) and \(\mathbf {P}(\mathbf {x})=\left( \mathbf {x}\cdot \frac{\nabla u}{\sqrt{1+|\nabla u|^{2}}}\right) \frac{\nabla u}{\sqrt{1+|\nabla u |^{2}}}\). This equation is often solved by considering the steady state of the following time-dependent one:

$$\begin{aligned} \frac{\partial u}{\partial t}&= -\lambda \nabla \cdot \left[ \frac{1}{\sqrt{1+|\nabla u|^{2}}}(\mathbf {I}-\mathbf {P})\nabla \varPhi '(\kappa _{u})\right] +(f-u), \end{aligned}$$
(7)

with time \(t\) being an evolution parameter.

The above modification surely affects the outcome of the model. However, as shown later, by using augmented Lagrangian method, the functional (2) can be exactly treated. This is one of the most important merits of augmented Lagrangian method, which has been shown in the treatment of the non-differentiable total variation norm of the ROF model in [29].

2.2 Augmented Lagrangian Method

In [33], following a similar idea for treating Euler’s elastica based functionals [26], we converted the minimization of functional (Eq. 2) to be the following constrained problem;

$$\begin{aligned} \nonumber \mathrm{min }_{u,q,\mathbf {n},\mathbf {p}} \left[ \lambda \int _{\varOmega }|q|+\frac{1}{2}\int (f-u)^2 \right] ,\\ \text{ with } q=\nabla \cdot \mathbf {n}, \mathbf {n}=\frac{\mathbf {p}}{|\mathbf {p}|}, \mathbf {p}=\langle \nabla u,1\rangle , \end{aligned}$$
(8)

and developed the associated augmented Lagrangian functional:

$$\begin{aligned} \nonumber {\mathcal {L}}(u,q,\mathbf {p},\mathbf {n},\mathbf {m};\lambda _{1},\varvec{\lambda }_{2},\lambda _{3},\varvec{\lambda }_{4})&= \lambda \int |q|+\frac{1}{2}\int (f-u)^2\\ \nonumber&+ r_{1}\int (|\mathbf {p}|-\mathbf {p}\cdot \mathbf {m})+\int \lambda _{1}(|\mathbf {p}|-\mathbf {p}\cdot \mathbf {m})\\ \nonumber&+ \frac{r_{2}}{2}\int |\mathbf {p}-\langle \nabla u,1\rangle |^{2}+\int \varvec{\lambda }_{2}\cdot (\mathbf {p}-\langle \nabla u,1\rangle )\\ \nonumber&+ \frac{r_{3}}{2}\int (q-\partial _{x}n_{1}-\partial _{y}n_{2})^{2}+\int \lambda _{3}(q-\partial _{x}n_{1}-\partial _{y}n_{2})\\&+ \frac{r_{4}}{2}\int |\mathbf {n}-\mathbf {m}|^{2}+\int \varvec{\lambda }_{4}\cdot (\mathbf {n}-\mathbf {m})+\delta _{\mathcal {R}}(\mathbf {m}), \end{aligned}$$
(9)

where \(\mathbf {n}, \mathbf {m}, \mathbf {p}\in \mathbb {R}^{3}\) are auxiliary vectors and \(\lambda _{1},\lambda _{3}\in \mathbb {R}\), \(\varvec{\lambda }_{2}, \varvec{\lambda }_{4}\in \mathbb {R}^{3}\) are Lagrange multipliers. Note that in this Lagrangian functional, we used \(\mathbf {p}=\langle \nabla u,1\rangle \) instead of \(\mathbf {p}=\nabla u\) as in [26]. This substitution was chosen purposely to treat the mean curvature term since it is nonhomogeneous in \(u\). Just as in [26], the introduction of the variable \(\mathbf {m}\) is to relax the variable \(\mathbf {n}\) that is supposed to connect with the variable \(\mathbf {p}\) in terms of \(\mathbf {n}=\mathbf {p}/|\mathbf {p}|\), and the variable \(\mathbf {m}\) is required to lie in the set \(\mathcal {R}=\{\mathbf {m}\in L^{2}(\varOmega ): |\mathbf {m}|\le 1 \text{ a.e. } \text{ in } \varOmega \}\) through the characteristic function \(\delta _{\mathcal {R}}(\cdot )\) defined as follows:

$$\begin{aligned} \delta _{\mathcal {R}}(\mathbf {m}) = \left\{ \begin{array}{l} 0, \quad \,\, {{\mathbf {m}\in \mathcal {R};}} \\ +\infty , \; {\hbox {otherwise,}} \end{array} \right. \end{aligned}$$

so that the term \(|\mathbf {p}|-\mathbf {p}\cdot \mathbf {m}\) is always non-negative. The benefit of this non-negativeness is that the \(L^{2}\) penalization is unnecessary and we just use \(|\mathbf {p}|-\mathbf {p}\cdot \mathbf {m}\) as a penalization, which simplifies the associated subproblems when finding saddle points of the above Lagrangian functional (Eq. 9).

Note that saddle points of the functional (9) correspond to minimizers of the constrained minimization problem (8), and equivalently, minimizers of the mean curvature model (2), one just needs to find saddle points of (9). To this end, as in [26], we apply an iterative algorithm. Specifically, for each variable in (9), we fix all the other variables and seek a critical point of the induced functional to update this variable. Once all the variables are updated, the Lagrange multipliers will then be advanced accordingly. Then we repeat this process until the variables converge to steady state.

To find saddle points of the functional (9), we consider the following subproblems and need to obtain minimizers for all of them.

$$\begin{aligned} \varepsilon _{1}(u) =&\; \frac{1}{2}\int (f-u)^{2}+\frac{r_{2}}{2}\int |\mathbf {p}-\langle \nabla u,1\rangle |^{2}+\int \varvec{\lambda }_{2}\cdot (\mathbf {p}-\langle \nabla u,1\rangle ), \end{aligned}$$
(10)
$$\begin{aligned} \varepsilon _{2}(q) =&\; \lambda \int |q|+\frac{r_{3}}{2}\int (q-\partial _{x}n_{1}-\partial _{y}n_{2})^{2}+\int \lambda _{3}(q-\partial _{x}n_{1}-\partial _{y}n_{2}),\end{aligned}$$
(11)
$$\begin{aligned} \nonumber \varepsilon _{3}(\mathbf {p}) =&\; r_{1}\int (|\mathbf {p}|-\mathbf {p}\cdot \mathbf {m})+\int \lambda _{1}(|\mathbf {p}|-\mathbf {p}\cdot \mathbf {m})+\frac{r_{2}}{2}\int |\mathbf {p}-\langle \nabla u,1\rangle |^{2}\\&\;+\int \varvec{\lambda }_{2}\cdot (\mathbf {p}-\langle \nabla u,1\rangle ),\end{aligned}$$
(12)
$$\begin{aligned} \nonumber \varepsilon _{4}(\mathbf {n}) =&\; \frac{r_{3}}{2}\int (q-\partial _{x}n_{1}-\partial _{y}n_{2})^{2}+\int \lambda _{3}(q-\partial _{x}n_{1}-\partial _{y}n_{2})+\frac{r_{4}}{2}\int |\mathbf {n}-\mathbf {m}|^{2}\\&\;+\int \varvec{\lambda }_{4}\cdot (\mathbf {n}-\mathbf {m}),\end{aligned}$$
(13)
$$\begin{aligned} \nonumber \varepsilon _{5}(\mathbf {m}) =&\; r_{1}\int (|\mathbf {p}|-\mathbf {p}\cdot \mathbf {m})+\int \lambda _{1}(|\mathbf {p}|-\mathbf {p}\cdot \mathbf {m}) +\frac{r_{4}}{2}\int |\mathbf {n}-\mathbf {m}|^{2}\\&\; +\int \varvec{\lambda }_{4}\cdot (\mathbf {n}-\mathbf {m})+\delta _{\mathcal {R}}(\mathbf {m}). \end{aligned}$$
(14)

The functionals \(\varepsilon _{2}(q)\), \(\varepsilon _{3}(\mathbf {p})\), and \(\varepsilon _{5}(\mathbf {m})\) have closed-form solutions for their minimizers, while the minimizers of the functionals \({\varepsilon _{1}(u)}\) and \({\varepsilon _{4}(\mathbf {n})}\) are determined by the associated Euler-Lagrange equations. Specifically, as discussed in [33], the minimizers of \(\varepsilon _{2}(q)\), \(\varepsilon _{3}(\mathbf {p})\), and \(\varepsilon _{5}(\mathbf {m})\) read

$$\begin{aligned} \mathrm{Argmin }_{q} \varepsilon _{2}(q) = \text{ max }\left\{ 0,1-\frac{\lambda }{r_{3}|\widetilde{q}|}\right\} \widetilde{q},\quad \widetilde{q}=\partial _{x}n_{1}+\partial _{y}n_{2}-\frac{\lambda _{3}}{r_{3}}, \end{aligned}$$
(15)
$$\begin{aligned} \mathrm{Argmin }_{\mathbf {p}}\varepsilon _{3}(\mathbf {p}) = \text{ max }\left\{ 0,1-\frac{r_{1}\!+\!\lambda _{1}}{r_{2}|\widetilde{\mathbf {p}}|}\right\} \widetilde{\mathbf {p}},\quad \widetilde{\mathbf {p}}=\langle \nabla u,1\rangle -\frac{\varvec{\lambda }_{2}}{r_{2}}\!+\!\frac{(r_{1}\!+\!\lambda _{1})\mathbf {m}}{r_{2}},\end{aligned}$$
(16)
$$\begin{aligned} \mathrm{Argmin }_{\mathbf {m}}\varepsilon _{5}(\mathbf {m}) = \left\{ \begin{array}{ll} \widetilde{\mathbf {m}}, &{} {|\widetilde{\mathbf {m}}|\le 1;} \\ \widetilde{\mathbf {m}}/|\widetilde{\mathbf {m}}|, &{} {|\widetilde{\mathbf {m}}|> 1.} \end{array} \right. \quad \widetilde{\mathbf {m}}=\mathbf {n}+\frac{\varvec{\lambda }_{4}}{r_{4}}+\frac{(r_{1}\!+\!\lambda _{1})\mathbf {p}}{r_{4}}, \end{aligned}$$
(17)

and the Euler-Lagrange equations associated with \(\varepsilon _{1}(u)\) and \(\varepsilon _{4}(\mathbf {n})\) are given as follows:

$$\begin{aligned} -r_{2}\Delta u + u&= f-\partial _{x}(r_{2}p_{1}+\lambda _{21})-\partial _{y}(r_{2}p_{2}+\lambda _{22}), \end{aligned}$$
(18)

and

$$\begin{aligned} \nonumber -r_{3}\partial _{x}(\partial _{x}n_{1}+\partial _{y}n_{2}) + r_{4}n_{1}&= r_{4}m_{1}-\lambda _{41}-(r_{3}q+\lambda _{3})_{x},\\ \nonumber -r_{3}\partial _{y}(\partial _{x}n_{1}+\partial _{y}n_{2}) + r_{4}n_{2}&= r_{4}m_{2}-\lambda _{42}-(r_{3}q+\lambda _{3})_{y},\\ n_{3}&= m_{3}-\lambda _{43}/r_{4}, \end{aligned}$$
(19)

where \(\mathbf {p}=\langle p_{1},p_{2},p_{3}\rangle \), \(\mathbf {m}=\langle m_{1},m_{2},m_{3}\rangle \), \(\mathbf {n}=\langle n_{1},n_{2},n_{3}\rangle \), \(\varvec{\lambda }_{2}=\langle \lambda _{21},\lambda _{22},\lambda _{23}\rangle \), and \(\varvec{\lambda }_{4}=\langle \lambda _{41},\lambda _{42},\lambda _{43}\rangle \). To update the variables \(u\) and \(\mathbf {n}\), one needs to solve these Euler-Lagrange equations. In the subsequent section, we discuss how to solve them using Gauss-Seidel method. Indeed, in [33], we employed FFT and thus got the exact numerical solutions of the two equations for each iteration. This is often expensive but may be unnecessary since it is enough to have some good approximations of \(u\) and \(\mathbf {n}\) for each iteration. To this end, in this work, we apply the Gauss-Seidel method for the two equations. The later experiments demonstrate that this numerical method yield very similar results but with much less computational cost, especially for large size images. A related work can also be found in [11].

Besides the above variables, the Lagrange multipliers \(\lambda _{1},\varvec{\lambda }_{2},\lambda _{3},\varvec{\lambda }_{4}\) also need updates for each iteration:

$$\begin{aligned} \nonumber \lambda _{1}^{new}&= \lambda _{1}^{old} + r_{1}(|\mathbf {p}|-\mathbf {p}\cdot \mathbf {m}),\\ \nonumber \varvec{\lambda }_{2}^{new}&= \varvec{\lambda }_{2}^{old} + r_{2}(\mathbf {p}-\langle \nabla u,1 \rangle ),\\ \nonumber \lambda _{3}^{new}&= \lambda _{3}^{old} + r_{3}(q-\partial _{x}n_{1}-\partial _{y}n_{2}), \\ \varvec{\lambda }_{4}^{new}&= \varvec{\lambda }_{4}^{old} + r_{4}(\mathbf {n}-\mathbf {m}), \end{aligned}$$
(20)

where \(\lambda _{1}^{old}\) denotes the value of \(\lambda _{1}\) at the previous iteration while \(\lambda _{1}^{new}\) represents that of the current one.

3 Numerical Implementation

In this section, we present the details of solving Eqs. (18) and (19) using one sweeping of the Gauss-Seidel method as well as updating the variables \(q\), \(\mathbf {p}\), and \(\mathbf {m}\) for each iteration.

As discussed in [33], we emphasize that the spatial mesh size is needed when considering the discretization of derivatives. This is because the mean curvature is not homogeneous in \(u\), which is one of the most important features that distinguishes this mean curvature denoising model from other ones such as the ROF model [25] and the Euler’s elastica based model [1, 2].

Let \(\varOmega =\{(i,j)| 1\le i \le M, 1\le j \le N \}\) be the discretized image domain and each point \((i,j)\) is called a pixel point. All the variables are defined on these pixel points. We then introduce the discrete backward and forward differential operators with periodic boundary condition and the spatial mesh size \(h\) as follows:

$$\begin{aligned} \nonumber \partial _{1}^{-}u(i,j)&= \left\{ \begin{array}{ll} (u(i,j)-u(i-1,j))/h, &{} {1<i \le M;} \\ (u(1,j)-u(M,j))/h, &{} {i=1.} \end{array} \right. \\ \nonumber \partial _{1}^{+}u(i,j)&= \left\{ \begin{array}{ll} (u(i+1,j)-u(i,j))/h, &{} {1\le i < M-1;} \\ (u(1,j)-u(M,j))/h, &{} {i=M.} \end{array} \right. \\ \nonumber \partial _{2}^{-}u(i,j)&= \left\{ \begin{array}{ll} (u(i,j)-u(i,j-1))/h, &{} {1< j \le N;} \\ (u(i,1)-u(i,N))/h, &{} {j=1.} \end{array} \right. \\ \nonumber \partial _{2}^{+}u(i,j)&= \left\{ \begin{array}{ll} (u(i,j+1)-u(i,j))/h, &{} {1\le j < N;} \\ (u(i,1)-u(i,N))/h, &{} {j=N.} \end{array} \right. \end{aligned}$$

For Eq. (18), a detailed discussion on how to solve it using FFT can be found in [33], and we here employ one sweeping of the Gauss-Seidel method and get

$$\begin{aligned} \nonumber \left( 1+\frac{4r_{2}}{h^{2}}\right) u^{new}(i,j) = \\ \, g(i,j)+\frac{r_{2}}{h^{2}}[u^{new}(i-1,j)+u^{old}(i+1,j)+u^{new}(i,j-1)+u^{old}(i,j+1)], \end{aligned}$$
(21)

where \(u^{new}(i,j)\) denotes the updated value of \(u\) and \(g(i,j)\) represents the value of the right-hand side of Eq. (18) at the pixel point \((i,j)\). In the experiments, we just use one sweeping of the Gauss-Seidel method. Moreover, periodic condition is imposed. This boundary condition is often employed for the image denoising problem. In fact, this condition won’t affect too much the result obtained by the denoising model under consideration since it is able to preserve jumps and image contrasts.

Similarly, for Eq. (19), one gets the following

$$\begin{aligned} \left( r_{4}+\frac{2r_{3}}{h^{2}}\right) n^{new}_{1}(i,j)&= g_{1}(i,j)+\frac{r_{3}}{h^{2}}[n^{new}_{1}(i-1,j)+n^{old}_{1}(i+1,j)],\end{aligned}$$
(22)
$$\begin{aligned} \left( r_{4}+\frac{2r_{3}}{h^{2}}\right) n^{new}_{2}(i,j)&= g_{2}(i,j)+\frac{r_{3}}{h^{2}}[n^{new}_{2}(i,j-1)+n^{old}_{2}(i,j+1)], \end{aligned}$$
(23)

where \(g_{1}\) and \(g_{2}\) denote the right-hand side of Eq. (19).

We then discuss the update of the variables \(q\), \(\mathbf {p}\), \(\mathbf {m}\) as well as the Lagrange multipliers. As \(q\) is a scalar defined on the pixel point \((i,j)\), based on the formulation (15), one gets

$$\begin{aligned} \nonumber q(i,j)&= \text{ max }\left\{ 0,1-\frac{\lambda }{r_{3}|\widetilde{q}(i,j)|} \right\} \widetilde{q}(i,j), \end{aligned}$$

with \(\widetilde{q}_{i,j}=\partial ^{-}_{1}n_{1}(i,j)+\partial ^{-}_{2}n_{2}(i,j)-\lambda _{3}/r_{3}\).

As for the variable \(\mathbf {p}\), we first calculate the three components of \(\widetilde{\mathbf {p}}\), the length of \(\widetilde{\mathbf {p}}\), and then the updated \(\mathbf {p}\). Specifically,

$$\begin{aligned} \nonumber \widetilde{\mathbf {p}}(i,j)&= \langle \partial ^{+}_{1}u,\partial ^{+}_{2}u,1\rangle (i,j)-\frac{\langle \lambda _{21},\lambda _{22},\lambda _{23}\rangle +(r_{1}+\lambda _{1})\langle m_{1},m_{2},m_{3}\rangle }{r_{2}}(i,j), \end{aligned}$$

and based on the formulation (16)

$$\begin{aligned} \nonumber \mathbf {p}(i,j)&= \text{ max }\left\{ 0,1-\frac{r_{1}+\lambda _{1}(i,j)}{r_{2}|\widetilde{\mathbf {p}}(i,j)|}\right\} \widetilde{\mathbf {p}}(i,j). \end{aligned}$$

Similarly, we calculate

$$\begin{aligned} \nonumber \widetilde{\mathbf {m}}(i,j)&= \mathbf {n}(i,j)+\frac{\varvec{\lambda }_{4}(i,j)}{r_{4}}+\frac{(r_{1}+\lambda _{1}(i,j))\mathbf {p}(i,j)}{r_{4}}, \end{aligned}$$

and get the new \(\mathbf {m}(i,j)\) using the formulation (17).

Moreover, based on the formulations (20), we may update all the Lagrange multipliers:

$$\begin{aligned} \nonumber \lambda _{1}^{new}(i,j)&= \lambda _{1}^{old}(i,j) + r_{1}(|\mathbf {p}|(i,j)-\mathbf {p}(i,j)\cdot \mathbf {m}(i,j)), \end{aligned}$$

with \(|\mathbf {p}|(i,j)=\sqrt{p_{1}^{2}(i,j)+p_{2}^{2}(i,j)+p_{3}^{2}(i,j)}\), and

$$\begin{aligned} \nonumber \lambda _{21}^{new}(i,j)&= \lambda _{21}^{old}(i,j) + r_{2}(p_{1}(i,j)-\partial ^{-}_{1}u(i,j)),\\ \nonumber \lambda _{22}^{new}(i,j)&= \lambda _{22}^{old}(i,j) + r_{2}(p_{2}(i,j)-\partial ^{-}_{2}u(i,j)),\\ \nonumber \lambda _{23}^{new}(i,j)&= \lambda _{23}^{old}(i,j) + r_{2}(p_{3}(i,j)-1),\\ \nonumber \lambda _{3}^{new}(i,j)&= \lambda _{3}^{old}(i,j) + r_{3}(q(i,j)-\partial ^{-}_{1}n_{1}(i,j)-\partial ^{-}_{2}n_{2}(i,j)),\\ \nonumber \lambda _{41}^{new}(i,j)&= \lambda _{41}^{old}(i,j) + r_{4}(n_{1}(i,j)-m_{1}(i,j)),\\ \nonumber \lambda _{42}^{new}(i,j)&= \lambda _{42}^{old}(i,j) + r_{4}(n_{2}(i,j)-m_{2}(i,j)),\\ \nonumber \lambda _{43}^{new}(i,j)&= \lambda _{43}^{old}(i,j) + r_{4}(n_{3}(i,j)-m_{3}(i,j)). \end{aligned}$$

4 Numerical Experiments

In this section, we present numerical experiments to compare the results obtained using Gauss-Seidel method and FFT respectively and also to illustrate the efficiency of the proposed algorithm.

For each experiment, as in [33], we monitor the following relative residuals in order to check whether the iteration converges to a saddle point:

$$\begin{aligned} (R_{1}^{k},R_{2}^{k},R_{3}^{k},R_{4}^{k})&= \frac{1}{|\varOmega |}(\Vert \widetilde{R}_{1}^{k}\Vert _{L^{1}},\Vert \widetilde{R}_{2}^{k}\Vert _{L^{1}},\Vert \widetilde{R}_{3}^{k}\Vert _{L^{1}}, \Vert \widetilde{R}_{4}^{k}\Vert _{L^{1}}), \end{aligned}$$
(24)

with

$$\begin{aligned} \nonumber \widetilde{R}_{1}^{k}&= |\mathbf {p}^{k}|-\mathbf {p}^{k}\cdot \mathbf {m}^{k},\\ \nonumber \widetilde{R}_{2}^{k}&= \mathbf {p}^{k}-\langle \nabla u^{k},1\rangle ,\\ \nonumber \widetilde{R}_{3}^{k}&= q^{k}-\partial _{x}n_{1}^{k}-\partial _{y}n_{2}^{k},\\ \nonumber \widetilde{R}_{4}^{k}&= \mathbf {n}^{k}-\mathbf {m}^{k}, \end{aligned}$$

and \(|\varOmega |\) is the domain area. We use these relative residuals (24) as the stopping criterion, that is, for a given threshold \(\epsilon _{r}\), once \(R_{i}^{k}<\epsilon _{r}\) for \(i=1,...,4\) and some \(k\), the iteration process will be terminated. To determine the convergence of the iteration process, we also check the relative errors of Lagrange multipliers:

$$\begin{aligned}&\nonumber (L_{1}^{k},L_{2}^{k},L_{3}^{k},L_{4}^{k}) \\&= \left( \frac{\Vert \lambda _{1}^{k}-\lambda _{1}^{k-1}\Vert _{L^{1}}}{\Vert \lambda _{1}^{k-1}\Vert _{L^{1}}}, \frac{\Vert \varvec{\lambda }_{2}^{k}-\varvec{\lambda }_{2}^{k-1}\Vert _{L^{1}}}{\Vert \varvec{\lambda }_{2}^{k-1}\Vert _{L^{1}}}, \frac{\Vert \lambda _{3}^{k}-\lambda _{3}^{k-1}\Vert _{L^{1}}}{\Vert \lambda _{3}^{k-1}\Vert _{L^{1}}}, \frac{\Vert \varvec{\lambda }_{4}^{k}-\varvec{\lambda }_{4}^{k-1}\Vert _{L^{1}}}{\Vert \varvec{\lambda }_{4}^{k-1}\Vert _{L^{1}}} \right) , \end{aligned}$$
(25)

and the relative error of the solution \(u^{k}\)

$$\begin{aligned} \frac{\Vert u^{k}-u^{k-1}\Vert _{L^{1}}}{\Vert u^{k-1} \Vert _{L^{1}} }. \end{aligned}$$
(26)

We also observe how the energy (2) is evolving during the iteration by tracking the amount \(E(u^{k})\). For the presentation purpose, all the above quantities are shown in \(log\)-scale. Moreover, to illustrate what signals are removed as noise, we present the associated residual image \(f-u\), besides the given noisy image \(f\) and the cleaned one \(u\).

To compare the results using FFT and Gauss-Seidel method respectively, we calculate the quantity \(\Vert u_{GS}-u_{FFT}\Vert _{L^{1}}/|\varOmega |\) and also present the iteration numbers needed for a given threshold \(\epsilon _{r}\) for these two methods.

Two numerical experiments are considered to test the effectiveness of the proposed algorithm. The first example is a synthetic image inside which there are several shapes with straight or curvy edges as well as sharp corners; the second one is the real image “Lenna”. The original noisy images, denoised images, and their differences \(f-u\) are presented in Fig. 4. The results for the synthetic image demonstrate that besides removing noise and keeping edges, the model also preserves sharp corners and image contrasts, which can be visualized from the difference image in which there is almost no meaningful signals. For the real image “Lenna”, the noise part is effectively removed while edges are kept. An important feature worthy of emphasizing is the improvement of the staircase effect. The cleaned image, especially at the face and shoulder, illustrates that the model produces smooth patches instead of blocky ones.

Table 1. The comparison of the iteration numbers needed for \(\epsilon _{r}=2.5\times 10^{-3}\) using Gauss-Seidel and FFT respectively and the difference quantity \(\Vert u_{GS}-u_{FFT}\Vert _{L^{1}}/|\varOmega |\).
Full size table
Table 2. The image sizes, the SNRs, the iteration numbers needed for the given threshold \(\epsilon _{r}\), and the computational times using Gauss-Seidel and FFT for the experiments.
Full size table
Fig. 1.
figure 1

The denoising results for a synthetic image and a real image “Lenna”. The noisy, denoised, and residual images are listed from the first row to the third row respectively. For the synthetic image, we set the spatial step size \(h=5.0\), and choose \(\lambda =2\times 10^{3}\), \(r_{1}=40\), \(r_{2}=40\), \(r_{3}=10^{5}\), \(r_{4}=2.0\times 10^{5}\), and \(\epsilon _{r}= 2.5\times 10^{-3}\). For the real image, we set the spatial step size \(h=5.0\), choose \(\lambda = 10^{3}\), \(r_{1}=40\), \(r_{2}=40\), \(r_{3}=10^{5}\), \(r_{4}= 10^{5}\), and \(\epsilon _{r}=2.5\times 10^{-3}\).

Full size image
Fig. 2.
figure 2

The first row lists the plots of relative residuals (a1), relative errors in Lagrange multipliers (b1), relative error in \(u^{k}\) (c1), and energy (d1) versus iterations for the example “shape” using Gauss-Seidel method; the second row presents the corresponding plots when using FFT. The plot (e) shows the difference between the two cleaned images \(u_{GS}\) and \(u_{FFT}\).

Full size image
Fig. 3.
figure 3

The first row lists the plots of relative residuals (a1), relative errors in Lagrange multipliers (b1), relative error in \(u^{k}\) (c1), and energy (d1) versus iterations for the example “Lenna” using Gauss-Seidel method; the second row presents the corresponding plots when using FFT. The plot (e) shows the difference between the two cleaned images \(u_{GS}\) and \(u_{FFT}\).

Full size image
Fig. 4.
figure 4

The denoising results for real images. Each row presents the original image, the cleaned one, and the difference image from the left to the right.

Full size image

Figure 4 lists the plots of the relative residuals (Eq. 24), relative errors of the Lagrange multipliers (Eq. 25), relative error of the iterative \(u^{k}\) (Eq. 26), and the energy \(E(u^{k})\) versus iterations for the synthetic image “shape”. The first row presents the plots obtained using Gauss-Seidel method while the second row shows those ones obtained using FFT. Firstly, these plots demonstrate the convergence of iteration and therefore a saddle point of the augmented Lagrangian functional (9) and thus a minimizer of the functional (2) is achieved for each case. Secondly, the plots also illustrate the efficiency of the proposed augmented Lagrangian method. In general, it only needs a few hundred of iterations to approach minimizers with reasonable accuracy. In fact, in the experiments, for each iteration, one needs to use two times of Gauss-Seidel sweeping and three times of the application of closed-form solutions. Thirdly, the plots in these two rows present almost no difference for each corresponding quantity versus iteration, indicating that the substitution of FFT with one sweeping of Gauss-Seidel for solving the equations of \(u\) and \(\mathbf {n}\) is feasible. To further compare these two methods, we present in the third row with the difference \(u_{GS}-u_{FFT}\), each of which is obtained with the same iteration number. This plot illustrates that the two cleaned images only differ in small magnitudes around some parts on the edges of the shapes.

Besides these, the iteration numbers needed for the stopping threshold and the difference quantity \(\Vert u_{GS}-u_{FFT}\Vert _{L^{1}}/|\varOmega |\) are also compared for the two methods in Table 1. From this table, when the threshold \(\epsilon _{r}\) is achieved, less iterations are needed using FFT than Gauss-Seidel method, which is reasonable since FFT gives exact solutions to those equations. However, as shown in Table 2, this cannot save too much the computational cost for the utilization of FFT.

Figure 4 presents the comparison of the two methods for the example “Lenna”. In summary, these two examples demonstrate that replacing FFT by Gauss-Seidel method won’t affect the final results considerably and thus this replacement is applicable when using the mean curvature denoising model.

In Fig. 4, we consider more experiments for real images using Gauss-Seidel method. These examples again demonstrate the features of the mean curvature based denoising model, including the amelioration of the staircase effect and the preservation of image contrasts. To show the efficiency of the proposed algorithm as well as the comparison of the Gauss-Seidel method and FFT that are used for solving Eqs. (18) and (19), we present in Table 2 for all the experiments with the image sizes, the SNRs, the numbers of total iteration needed to satisfy the given threshold \(\epsilon _{r}\), and the computational times using Gauss-Seidel and FFT respectively. From this table, when compared with FFT, the utilization of Gauss-Seidel method reduces the computational cost, and the larger the image size, the more this reduction will be. Here, we omit the comparison of the proposed algorithm with the standard gradient descent method that is used to solve Eq. (7), which can found in [33]. Moreover, all computations were done using Matlab R2011a on an Intel Core I5 machine (Figs. 1, 2 and 3).

5 Conclusion

Recently, the augmented Lagrangian method has been successfully used to minimize the classical ROF functional [29] and Euler’s elastica based functionals [26]. In [33], inspired by the idea in [26], we developed a special technique to treat the mean curvature based image denoising model [31] using augmented Lagrangian method, and thus converted the original challenging minimization problem to be several tractable ones, some of which have closed form solutions while the other of which can be solved using FFT. In this work, we consider to use Gauss-Seidel method to substitute FFT for solving those equations in order to further reduce the computational cost. The numerical experiments demonstrate that the substitution is feasible and saves considerable computational effort especially for images of large sizes.