A Measure of Q-convexity for Shape Analysis

Abstract

In this paper, we study three basic novel measures of convexity for shape analysis. The convexity considered here is the so-called Q-convexity, that is, convexity by quadrants. The measures are based on the geometrical properties of Q-convex shapes and have the following features: (1) their values range from 0 to 1; (2) their values equal 1 if and only if the binary image is Q-convex; and (3) they are invariant by translation, reflection, and rotation by 90 degrees. We design a new algorithm for the computation of the measures whose time complexity is linear in the size of the binary image representation. We investigate the properties of our measures by solving object ranking problems and give an illustrative example of how these convexity descriptors can be utilized in classification problems.

1 Introduction

Techniques of shape analysis are widely applied in various fields of computer vision, e.g., in object classification, image segmentation, and simplification. The use of shape descriptors and the development of new measures for descriptors in shape analysis is a current topic of broad interest [15]. Recent works develop sophisticated recognition methods and powerful machine learning approaches for dealing with the challenge of classification of deformation, occlusion and view variation of the images [1, 26]. Differently from these approaches, in this paper, we propose a very easy shape representation by a scalar convexity measure. The advantage of this approach is that it is computationally extremely efficient. Our method can be used for classification of suitable datasets as well as a basic step of solving more complex issues.

Convexity measures and their applications are studied in several papers which can be grouped into different categories: area-based measures form one popular category [8, 24, 25], while boundary-based ones [27] are also frequently used. Other methods use simplification of the contour [19], a probabilistic approach [22, 23] or fuzzy set theory and mathematical morphology [21] to measure convexity. In discrete geometry, and especially in discrete tomography, a natural notion of convexity is provided by the horizontal and vertical convexity (shortly, hv-convexity), arising inherently from the pixel-based representation (and the notion of neighborhood) of the digital image (see, e.g., [6, 12]). A first attempt to define a measure of directional (horizontal or vertical) convexity was studied in detail in [2]. Independently, the authors of [16, 17] came to the same idea, to use the degree of directional convexity as a shape prior in image segmentation. However, in [2], the authors showed also that the aggregation of the horizontal and vertical convexity measures to obtain a combined hv-convexity measure is challenging. On the other hand, a one-dimensional measure can be derived easily from a two-dimensional convexity measure, being the former a special case of the latter.

A fruitful approach, introduced in [3], was to define an immediate “two-dimensional” convexity measure, based on the concept of Q-convexity (see, e.g., [11]). Mostly studied in discrete tomography, this kind of convexity permits to generalize hv-convexity to any two directions. Moreover, for the class of Q-convex binary images analogue properties and results can be proven to those of the class of convex binary images. In [3], the basic idea to define Q-convexity estimators was to exploit the geometrical description of the binary image provided by so-called salient and generalized salient points [13, 14], and the notion of “Q-convex hull.” Then, in [4], the authors extended their work by including weighting of the generalized salient points, while in [5] they investigate a vector descriptor for the hierarchy of generalized salient points.

In this paper, we define four descriptors based on [3], and we focus on the algorithmic aspects. Based on a better understanding of the properties of (generalized) salient points (see Sect. 3), we design a new one-scan algorithm (implementation details are given in Sect. 4) to compute the measure of Q-convexity with respect to the horizontal and vertical directions, which runs in linear time in the size of the image and thus outperforms the algorithm in [3] and speeds up also the computation of the descriptor in [4] and [5]. In addition, we generalize the algorithm to compute measures of Q-convexity with respect to any couple of directions.

In Sect. 5, we test our shape descriptors on the datasets in [23]. This choice allows us to evaluate our shape descriptors in view of another one measuring similar characteristics, since that of [23] is based on a (total) convexity measure. In particular, we assess sensitivity using a set of synthetic polygons with rotation and translation of intrusions/protrusions and global skew; we investigate a ranking issue using a variety of shapes; and finally, we conduct an image classification experiment using a dataset of 43 algae (taxon Micrasterias). In these experiments, our shape measures correctly incorporate the Q-convexity property (even if the rankings present some differences) and they are sensitive to small details of the shape, robust to noise, and, except one of them, they are also scale tolerant. In the small-scale classification task, we first preprocess the images to align principal axes of the original images to the coordinate axes. This step allows us to deal with possible rotations of the shapes. Results confirm a good performance of the proposed measures, and a combination of these shape descriptors reaches an accuracy of $76.74\%$ in this illustrative example. Moreover, we show that the combination of the proposed shape descriptors together with an additional couple of directions can permit to improve the performance of our approach.

2 Notation and Definitions

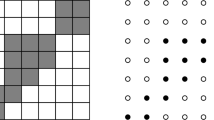
In this section, we introduce the necessary notations and recall main definitions from [3, 13] for the reader convenience. We restrict the treatment to two dimensions, since we consider (non-empty) 2D-objects. The definitions can be easily extended to higher dimensions. Any binary image $\mathcal {F}$ is an $m\times n$ binary matrix and can be represented by a set of black (foreground) and white (background) cells/pixels (unit squares) (see Fig. 1 left). Equivalently, black pixels can be regarded as points of $\mathbb {Z}^2$; thus, any binary image $\mathcal {F}$ can be viewed as a finite lattice set, denoted by F, delimited by its minimum bounding rectangle R (see Fig. 1 right). Throughout the paper, we will use both representations, since the set notation is more suitable to describe geometrical properties. Images are illustrated as sets of black and white pixels. For our convenience, we use $\mathcal {F}$ for both the image and its representation when not confusing. In this context, the complement of $\mathcal {F}$ (denoted by $\mathcal {F}^c$) is defined as the complement of its pixel values reversing foreground and background pixels and corresponds in the lattice representation to $\mathcal {F}^c = R\setminus {F}$.

Fig. 1

[5] A binary image $\mathcal {F}$ represented as black and white pixels (left) and by a lattice set (right). The binary image $\mathcal {F}$ is Q-convex. For example, all the four quadrants around M contain points of $\mathcal {F}$, and in the same time $M\in \mathcal {F}$. Salient points are marked with red borders

Even if our results hold for any pair of lattice directions, in order to simplify our explanation, let us consider the horizontal and vertical directions, and denote the coordinates of any point M of $\mathbb {Z}^2$ by $(x_M,y_M)$. Then, M and the directions determine the following four quadrants (see Fig. 1):

$$\begin{aligned} Z_0(M)=&\{ N\in \mathbb {Z}^2:\; x_N\le x_M, \; y_N\le y_M\}\ ,\\ Z_1(M)=&\{ N\in \mathbb {Z}^2:\; x_M\le x_N, \; y_N\le y_M\}\ ,\\ Z_2(M)=&\{ N\in \mathbb {Z}^2:\; x_M\le x_N, \; y_M\le y_N\}\ ,\\ Z_3(M)=&\{ N\in \mathbb {Z}^2:\; x_N\le x_M, \; y_M\le y_N\}\ .\\ \end{aligned}$$

Definition 1

[13] A binary image $\mathcal {F}$ is Q-convex if and only if $Z_p(M)\cap {F}\ne \emptyset$ for all $p=0,\ldots ,3$ implies $M\in F$.

By definition, if F is Q-convex and $M\notin F$, a quadrant $Z_p(M)$ exists such that $Z_p(M)\cap {F}= \emptyset$. Figure 1 illustrates the above concepts. There, the image $\mathcal {F}$ is Q-convex, while removing point M from F, $F\setminus \{M\}$ is no longer Q-convex, as all four quadrants around M are then non-empty, and still $M\not \in F$. Note that a Q-convex image is also convex along the horizontal and vertical directions. On the other hand, if $\mathcal {CH}({F})$ denotes the convex hull of a Q-convex lattice set F, then $\mathcal {CH}({F})\cap \mathbb {Z}^2 = {F}$ does not always hold, i.e., F (or equivalently, $\mathcal {F}$) is not necessarily digitally convex. For an arbitrary point M, if $Z_p(M)\cap {F}= \emptyset$, we say that $Z_p(M)$ is a background quadrant (in M) of F.

2.1 A Measure Based on the Q-convex Hull

The Q-convex hull of $\mathcal {F}$ can be found by studying the minimal set of points to be added to the lattice set F in order to obtain a Q-convex image:

Definition 2

[13] The Q-convex hull $\mathcal {Q}(\mathcal {F})$ of a binary image $\mathcal {F}$ is the set of points $M\in \mathbb {Z}^2$ such that $Z_p(M)\cap {F}\ne \emptyset$ for all $p=0,\ldots ,3$.

Therefore, if $\mathcal {F}$ is Q-convex then ${F}=\mathcal {Q}({F})$. On the other hand, if $\mathcal {F}$ is not Q-convex, then $\mathcal {Q}({F})\setminus {F}\ne \emptyset$. Moreover, if ${F}\subseteq \mathcal {G}\subset \mathbb {Z}^2$, then $\mathcal {Q}({F})\subseteq \mathcal {Q}(\mathcal {G})$.

Denote the cardinality of F and $\mathcal {Q}({F})$ by $\alpha _{\mathcal {F}}$ and $\alpha _{\mathcal {Q}(\mathcal {F})}$, respectively. Inspired by the classical area-based convexity measure proposed in the literature, we can define a Q-convexity measure as follows:

Definition 3

[3] For a given binary image $\mathcal {F}$, its Q-convexity measure $\varTheta (\mathcal {F})$ is defined to be $\varTheta (\mathcal {F})=\alpha _{\mathcal {F}}/\alpha _{\mathcal {Q}(\mathcal {F})}$.

Figure 2a and b shows a binary image F and its Q-convex hull, respectively. For this image $\varTheta (F) = 32/40 = 0.8$.

Since $\varTheta (\mathcal {F})$ equals 1, if $\mathcal {F}$ is Q-convex, and $\alpha _{\mathcal {Q}(\mathcal {F})}\ge \alpha _{F}$, this measure ranges in (0, 1]. A major drawback of this area-based measure is that it does not detect defects in the shape which do not affect the size of $\alpha _{\mathcal {F}}$ and $\alpha _{\mathcal {Q}(\mathcal {F})}$. For example, the images presenting intrusions in Fig. 16 receive the same score since they have the same number of object points and their Q-convex hulls are also of the same size. However, the skew intrusion has a different impact from the viewpoint of Q-convexity than other intrusions have. Therefore, we define a new measure in between region- and boundary-based measures.

2.2 Measures Based on Salient Points

Definition 4

[13] Let $\mathcal {F}$ be a binary image. A point $M\in {F}$ is a salient point of F if $M \notin \mathcal {Q}({F} \setminus \{M\})$.

By definition, there follows that M is a salient point of F if and only if there exists $p\in \{0,1,2,3\}$ such that $Z_p(M)\cap {F}=\{M\}$ (see [13]). Consequently, every salient point M identifies background quadrants of $\mathcal {Q}({F})$ minus M itself. Denote the set of salient points of F by $\mathcal {S}(\mathcal {F})$. Of course $\mathcal {S}(\mathcal {F})=\emptyset$ if and only if ${F}=\emptyset$. In particular, Daurat proved in [13] that the salient points of $\mathcal {F}$ are the salient points of the Q-convex hull $\mathcal {Q}(\mathcal {F})$ of $\mathcal {F}$, i.e., $\mathcal {S}(\mathcal {F})=\mathcal {S}(\mathcal {Q}(\mathcal {F}))$. Therefore, if $\mathcal {F}$ is Q-convex, its salient points completely characterize $\mathcal {F}$ [13]. If it is not, then there are points belonging to the Q-convex hull of $\mathcal {F}$ but not to $\mathcal {F}$ that “track” the non-Q-convexity of $\mathcal {F}$. These points are called generalized salient points (abbreviated by g.s.p.) [13]. The set of g.s.p. $\mathcal {S}_g(\mathcal {F})$ of $\mathcal {F}$ is obtained by iterating the definition of salient points on the sets obtained each time by discarding the points of the set from its Q-convex hull, i.e., using the set notation:

Definition 5

[13] If $\mathcal {F}$ is a binary image, then the set of its generalized salient points $\mathcal {S}_g(\mathcal {F})$ is defined by $\mathcal {S}_g(\mathcal {F})=\bigcup _{k=1}^{{k}_{\mathrm{max}}} \mathcal {S}({\mathcal {F}}_k)$, where ${{F}}_1={F}$, ${{F}}_{k+1}=\mathcal {Q}({{F}}_k)\setminus {{F}}_k$, and $k_{\mathrm{max}}$ is the smallest integer for which $\mathcal {Q}({{F}}_{{k}_{\mathrm{max}}})\setminus {{F}}_{{k}_{\mathrm{max}}}=\emptyset$ (i.e., ${\mathcal {F}}_{{k}_{\mathrm{max}}}$ is Q-convex).

Note that $\mathcal {Q}({F}_k)\supset \mathcal {Q}({{F}}_{k+1})$, since $\mathcal {Q}({F}_{k+1})=\mathcal {Q}(\mathcal {Q}({F}_{k})\setminus {F}_{k})$ and $\mathcal {S}(F_{k})=\mathcal {S}(\mathcal {Q}({F}_{k}))$. By definition, $\mathcal {S}({F})\subseteq \mathcal {S}_g({F})$ and equality holds when F is Q-convex. Moreover, the points of $\mathcal {S}_g({F})$ are points of subsets of $\mathcal {Q}({F})$, thus $\mathcal {S}_g({F})\subseteq \mathcal {Q}({F})$.

Fig. 2

a A binary image F, b its Q-convex hull $\mathcal {Q}({\mathcal {F}})$ as a set of dark and light gray pixels, c the salient points $\mathcal {S}(\mathcal {F})$ of F colored red, and d the set $\mathcal {S}_g(\mathcal {F})$ of the generalized salient points of F (see also Fig. 10)

We now define two Q-convexity measures. The first one, $\varPsi _1(\mathcal {F})$, measures the Q-convexity of $\mathcal {F}$ in terms of proportion between salient points and g.s.p.

Definition 6

[3] For a given binary image $\mathcal {F}$, its Q-convexity measure $\varPsi _1(\mathcal {F})$ is defined by $\varPsi _1(\mathcal {F})= \alpha _{\mathcal {S}(\mathcal {F})}/\alpha _{\mathcal {S}_g(\mathcal {F})}$, where $\mathcal {S}(\mathcal {F})$ and $\mathcal {S}_g(\mathcal {F})$ denote the sets of its salient and generalized salient points, respectively.

Figure 2 presents a binary image F together with its salient points and generalized salient points. In this case, $\varPsi _1(F) = 8/20 = 0.4$.

Note that the measure $\varPsi _1$ is purely qualitative, since it is independent from the size of the image. For instance, consider a frame which is defined as a binary matrix having items equal to 1 in the first row and column, and in the last row and column, and 0 elsewhere: it has always measure equal to $4/8=1/2$, regardless its size. Moreover we will experimentally show in Sect. 5 that it is scale invariant. If most of the g.s.p. are also salient points, then $\mathcal {F}$ is close to be Q-convex.

The second measure, $\varPsi _2(\mathcal {F})$, takes salient points and g.s.p. with respect to the Q-convex hull of the image into account.

Definition 7

[3] For a given binary image $\mathcal {F}$, its Q-convexity measure $\varPsi _2(\mathcal {F})$ is defined by

$$\begin{aligned} \varPsi _2(\mathcal {F})= \frac{\alpha _{\mathcal {Q}(\mathcal {F})}-\alpha _{\mathcal {S}_g(\mathcal {F})}}{\alpha _{\mathcal {Q}(\mathcal {F})}-\alpha _{\mathcal {S}(\mathcal {F})}}\ , \end{aligned}$$

where $\mathcal {Q}(\mathcal {F})$ denotes its Q-convex hull and $\mathcal {S}(\mathcal {F})$ and $\mathcal {S}_g(\mathcal {F})$ denote the set of its salient points and g.s.p., respectively.

Taking again a look at Fig. 2, we can calculate that $\varPsi _2(F) = (40-20)/(40-8) = 0.625$.

The Q-convexity measure $\varPsi _2(\mathcal {F})$ can be rewritten as

$$\begin{aligned} 1- \frac{\alpha _{\mathcal {S}_g(\mathcal {F})}-\alpha _{\mathcal {S}(\mathcal {F})}}{\alpha _{\mathcal {Q}(\mathcal {F})}-\alpha _{\mathcal {S}(\mathcal {F})}}\, \end{aligned}$$

that is, in fact it measures the defect of Q-convexity. We point out that we must have $\mathcal {S}(\mathcal {F})\subset \mathcal {Q}(\mathcal {F})$ in the definition of $\varPsi _2(\mathcal {F})$. Notice that $\mathcal {S}(\mathcal {F})= \mathcal {Q}(\mathcal {F})$ can hold only for binary images of size $2\times 2$ or smaller and in these cases, evidently, $\mathcal {S}_g(\mathcal {F})= \mathcal {Q}(\mathcal {F})$; thus, $\varPsi _2(\mathcal {F})$ would be undefined. In these cases, the images are Q-convex; therefore, we set $\varPsi _2(\mathcal {F})=1$.

Since $\mathcal {S}(\mathcal {F})\subseteq \mathcal {S}_g(\mathcal {F}) \subseteq \mathcal {Q}(\mathcal {F})$, both $\varPsi _1$ and $\varPsi _2$range from 0 to 1 and they are equal to 1 if and only if $\mathcal {F}$is Q-convex. In particular, for $\varPsi _1(\mathcal {F})$, there are examples where $\mathcal {S}_g(\mathcal {F})=\mathcal {Q}(\mathcal {F})$ (for instance in the chessboard configuration); thus, the ratio decreases in inverse proportion of the size of $\mathcal {Q}(\mathcal {F})$. For $\varPsi _2(\mathcal {F})$, in the same case, we get exactly 0. Moreover, since $\alpha _{\mathcal {S}(\mathcal {F})},\; \alpha _{\mathcal {S}_g(\mathcal {F})}$, and $\alpha _{\mathcal {Q}(\mathcal {F})}$ are invariant under translation, reflection, and rotation by 90 degrees for the horizontal and vertical directions, the measures are also invariant.

In order to incorporate quantitative information involving also the number of foreground pixels of the image, we propose in addition to make the previous measure dependent on $\varTheta (\mathcal {F})$. Among the possible ways to do this, we note that

$$\begin{aligned} \varTheta (\mathcal {F})- \varTheta (\mathcal {F})\frac{\alpha _{\mathcal {S}_g(\mathcal {F})}-\alpha _{\mathcal {S}(\mathcal {F})}}{\alpha _{\mathcal {Q}(\mathcal {F})}-\alpha _{\mathcal {S}(\mathcal {F})}}\, \end{aligned}$$

is a defect measure on $\varTheta$. Therefore, we decided to study $\varPsi _2'(\mathcal {F})=\varTheta (\mathcal {F}) \varPsi _2(\mathcal {F})$, and analogously, $\varPsi _1'(\mathcal {F})=\varTheta (\mathcal {F}) \varPsi _1(\mathcal {F})$.

3 Properties

By definition, the set of generalized salient points is computed by iterating the computation of salient points on $\mathcal {Q}({F}_k)\setminus {F}_k$ until the set reduces to the empty set. A naive algorithm requires to compute the salient points of an image, its Q-convex hull and set difference, to determine the successive $\mathcal {F}_k$. Fixed the iteration, this can be done in linear time in the size of the image but using a storage of two-dimensional arrays for each of the four quadrants $Z_p$, for $S_p$, and for each point of the image $\mathcal {F}_k$ (see Section 3 of [3]). Moreover the number of iterations is bounded by the size of $\mathcal {Q}(\mathcal {F})$, so that the computation of generalized salient points is quadratic in the worse case. In this section, we detect properties of the Q-convex hull, not studied anywhere else before. Based on these properties, we design a new algorithm that is efficient in time and space.

Let $\mathcal {F}$ be a binary image. Let us recall that, by Definition 1, $\mathcal {F}$ is Q-convex iff there exists at least one background quadrant $Z_p(M)$ for every pixel M in the background of $\mathcal {F}$ (i.e., in $\mathcal {F}^c$).

Proposition 1

The Q-convex hull of a binary image $\mathcal {F}$ is the complement of the union of the background quadrants of $\mathcal {F}$.

Proof

If $P\in \mathcal {Q}({F})$, then it cannot belong to any background quadrant of F. Indeed it is trivial if $P\in F$. Else if $P\in \mathcal {Q}({F})\setminus F$, by definition all the quadrants for P have non-empty intersection with F. There follows that $\mathcal {Q}({F})$ is contained in the complement of the union of the background quadrants of F. Vice versa, if $P\not \in \mathcal {Q}({F})$, then P belongs to $\mathcal {F}^c$ and there exists $p\in \{0,\ldots ,3\}$ such that $Z_p(P)$ is a background quadrant. This implies that $\mathcal {Q}(\mathcal {F})$ contains the complement of the union of the background quadrants. $\square$

By Proposition 1, the Q-convex hull of a binary image can be computed by looking at the background quadrants of the image.

By definition of the quadrants, if $N\in Z_p(M)$, then $Z_p(N)\subset Z_p(M)\ (p=0,1,2,3)$. In particular, we can define the set of the two neighbors of M which maximize the inclusion. More precisely, for $p=0$, we define $\hbox {Neigh}_0(M)$ as the set of points $\{(x_M,y_M-1),(x_M-1,y_M)\}$, where $M=(x_M,y_M)$. Analogously, we can define $\hbox {Neigh}_1(M)$, $\hbox {Neigh}_2(M)$, $\hbox {Neigh}_3(M)$. Denote $\mathcal {S}_p(\mathcal {F})=\{M\in F: Z_p(M)\cap F=\{M\}\}\ (p=0,1,2,3)$.

Proposition 2

The point $M\in F$ belongs to $\mathcal {S}_0(\mathcal {F})$ if and only if $Z_0(N_1)\cap {F}=\emptyset$ and $Z_0(N_2)\cap {F}=\emptyset$, where $N_1,N_2\in$$\hbox {Neigh}_0(M)$.

Proof

By definition, M is a salient point of F if and only if $Z_0(M)\cap F=\{M\}$. Therefore, we have that $M\in \mathcal {S}_0(\mathcal {F})$ if and only if $Z_0(x_M,y_M-1)\cap {F}=\emptyset$ and $Z_0(x_M-1,y_M)\cap {F}=\emptyset$ with $M\in F$. Note that $N_1=(x_M,y_M-1)$ and $N_2=(x_M-1,y_M)$ are in $\hbox {Neigh}_0(M)$, i.e., the neighbors in $\hbox {Neigh}_0(M)$ belong to background quadrants of F. $\square$

Analogously, it can be proven that the set of salient points $\mathcal {S}_p(\mathcal {F})=\mathcal {S}_p(\mathcal {Q}(\mathcal {F}))$ of a binary image $\mathcal {F}$ is constituted by the points of F such that their neighbors in $\hbox {Neigh}_p$ belong to background quadrants of $F\ (p=0,1,2,3)$. We get $\mathcal {S}(\mathcal {F})=\mathcal {S}_0(\mathcal {F})\cup \mathcal {S}_1(\mathcal {F})\cup \mathcal {S}_2(\mathcal {F})\cup \mathcal {S}_3(\mathcal {F})$. By Proposition 2 immediately follows:

Corollary 1

If M is a salient point in $\mathcal {S}_0(\mathcal {F})$ (resp., $\mathcal {S}_1(\mathcal {F})$), then $Z_0(x_M,y)$ (resp., $Z_1(x_M,y)$) cannot be a background quadrant of F for $y>y_M$. Similarly, if M is a salient point in $\mathcal {S}_2(\mathcal {F})$ (resp., $\mathcal {S}_3(\mathcal {F})$), then $Z_2(x_M,y)$ (resp., $Z_3(x_M,y)$) cannot be a background quadrant of F for $y<y_M$.

Corollary 2

If M is a salient point in $\mathcal {S}_0(\mathcal {F})$ (resp., $\mathcal {S}_3(\mathcal {F})$), then $Z_0(x,y_M)$ (resp., $Z_3(x,y_M)$) cannot be a background quadrant of F for $x>x_M$. Similarly, if M is a salient point in $\mathcal {S}_1(\mathcal {F})$ (resp., $\mathcal {S}_2(\mathcal {F})$), then $Z_1(x,y_M)$ (resp., $Z_2(x,y_M)$) cannot be a background quadrant of F for $x<x_M$.

In the next section, we will design a procedure to compute salient points by means of background quadrants, processing the image row by row, based on Proposition 2 and Corollary 1 (Corollary 2 could be used in case of processing the image column by column).

In the rest of this section, we focus on the problem of iterating the search of salient points on the successive $\mathcal {F}_{k}$.

Proposition 3

Let $\mathcal {F}_{k}$ be defined as in Definition 5. The following two statements are equivalent:

• 1. The Q-convex hull of the foreground pixels of $\mathcal {F}_{k}$ contains the Q-convex hull of the foreground pixels of $\mathcal {F}_{k+1}$.

• 2. The union of the background quadrants of $\mathcal {F}_{k}$ are contained in the union of background quadrants of $\mathcal {F}_{k+1}$.

Proof

Consider statement 1: the foreground pixels of ${\mathcal {F}}_k$ are the black (resp., white) pixels, and its background pixels are the white (resp., black) pixels, if k is odd (resp., even). Therefore, passing to the lattice set representation, we have that $\mathcal {Q}({F}_{k+1})=\mathcal {Q}(\mathcal {Q}({F}_{k})\setminus {F}_{k})= \mathcal {Q}(\mathcal {S}(\mathcal {Q}({F}_{k})\setminus {F}_{k}))$. Since $\mathcal {S}(F_{k})=\mathcal {S}(\mathcal {Q}({F}_{k}))$, we deduce that $\mathcal {Q}({F}_k)\supset \mathcal {Q}({{F}}_{k+1})$, or, equivalently, $\mathcal {Q}({\mathcal {F}}_k)\supset \mathcal {Q}({\mathcal {F}}_{k+1})$.

By Proposition 1, statement 2 follows. $\square$

By Proposition 3 (2.), we can design an algorithm that computes generalized salient points by scanning $\mathcal {F}$ just once as illustrated in Fig. 10 (see next section). Indeed pixels of the background quadrants of $\mathcal {F}_{k}$ visited at iteration k of the algorithm are in the background of $\mathcal {F}_{k+1}$ and can be discarded by any further consideration.

4 The Algorithm

The binary image $\mathcal {F}$ is represented by an $m\times n$ binary matrix ($\mathcal {F}=(f_{ij})$). Therefore, in this section, we use the order of the items in a matrix and $0\le i\le m-1$ for indexing the rows, and $0\le j\le n-1$ for indexing the columns.¹ The algorithm outputs the g.s.p. of the image ${\mathcal {F}}$ and stores them in the $m\times n$ integer matrix $\mathcal {S}=(s_{i j})$ such that $s_{i j}=k$ if and only if the item $f_{i j}$ is a salient pixel of ${\mathcal {F}}_k$.

Fig. 3

Two examples of $\mathcal {Q}$-convex hulls with the relative positions of the four background quadrants. The arrows illustrate the order of processing of the rows and columns for each quadrant

4.1 Preliminaries

The row and column indices which limit the set of pixels of $\mathcal {F}$ to be considered at a certain iteration are stored in up, down, and left, right, respectively. Initially, they are set to $up=0$, $down=m-1$, $left=0$, and $right=n-1$, according to the size of the initial matrix $\mathcal {F}=\mathcal {F}_1$. At each iteration k, the algorithm determines the g.s.p. of the image ${\mathcal {F}}$ by searching foreground pixels of ${\mathcal {F}}_k$ in order to compute $\mathcal {S}_p(\mathcal {F}_{k})$ for $p=0,1,2,3$. This is performed by scanning the matrix row by row. The boundary of ${\mathcal {F}}_k$ is described by column indices for each row: they depend on p and are stored in the vectors $j^p_{start}$ and $j^p_{end}$, i.e., $j^p_{start}(i)$ is the start-column index, and $j^p_{end}(i)$ is the end-column index, for row i at the current iteration. They are initialized as follows:

• $j^{\,0}_{start}:=j^{\,3}_{start}:=\{0\};\;j^{\,0}_{end}:=j^{\,3}_{end}:=\{n\}$;

• $j^{\,1}_{start}:=j^{\,2}_{start}:=\{n-1\};\;j^{\,1}_{end}:=j^{\,2}_{end}:=\{-1\}$;

and updated in the procedures for the computation of salient points in any row since they bound the searching region. At the end of each iteration k, they are recalculated in the procedure SetNewLimits to provide the new boundary values for the next iteration (see Fig. 10).

The order in which considering the rows and the items in any row depends on the background quadrant taken into consideration to compute $\mathcal {S}_p(\mathcal {F}_{k})$ and the order for processing the latter is $p=0,1,2,3$ (see Fig. 3 and flowchart in Fig. 9).

4.2 Computation of $\mathcal {S}$

The computation of g.s.p. on row i is realized based on Proposition 2. Let us focus on $p=0$: rows are processed from the bottom to the top. We are going to describe the main procedure SearchRow$\_0$ to compute $\mathcal {S}_0(\mathcal {F}_{k})$ on row i. Proof of correctness is shown in Theorem 1 at the end of the section.

The execution of the procedure is illustrated in Fig. 4.

Fig. 4

Illustrative example of the execution of the procedure SearchRow$\_0$ iterated in the pseudocode of Fig. 5. Each image shows the configuration after processing row i: items visited at the current iteration are drawn italic, and the identified g.s.p. are drawn bold; $j^{\,p}_{start}$ and $j^{\,p}_{end}$ are colored with blue and red, respectively, green when they coincide

The procedure SearchRow$\_0$.

For a fixed iteration k, and row i, the procedure searches the column index $j^{0}(i)$ of the first foreground pixel, with $j^{0}_{start}(i)\le j^{0}(i)<j^{0}_{end}(i)$ (steps 3–5 of Procedure SearchRow$\_0$). By the inclusion property of the quadrants, the search is performed by visiting pixels in the specified interval from left to right until a foreground pixel is reached—and in this case, the corresponding item of $\mathcal {S}_0$ is set to k (step 7 of Procedure SearchRow$\_0$)—or no foreground pixel is found. Visited pixels are counted and their number is stored in count² (see step 4 of Procedure SearchRow$\_0$). Then, the new endpoints for the next processed row $i-1$ are set using Corollary 1: If a foreground pixel is found, $j^{\,0}_{end}(i-1):=j^{0}(i)$ (step 7 of Procedure SearchRow$\_0$), otherwise it remains the same as in the current row, i.e., $j^{\,0}_{end}(i-1):=j^{\,0}_{end}(i)$ (step 9 of Procedure SearchRow$\_0$). In both cases, the procedure adds all the pixels on row i with indices lower than or equal to $j^{\,0}(i)$ to the background quadrant (step 11 of Procedure SearchRow$\_0$): they have been already visited and discarded by any further consideration since, in the next iteration, the row will be scanned starting from $j^{\,0}_{start}(i)$, leftmost column index on row i. Finally, if the left-top corner of the boundary is reached and a foreground pixel is found there, the procedure returns TRUE and the algorithm proceeds by searching salient points in $\mathcal {S}_1$ ($p=1$) since no other g.s.p can be found in the successive rows by Corollary 1. Figure 5 shows the fragment of pseudocode for the computation of $\mathcal {S}_0(\mathcal {F}_k)$. After the call to the procedure (step 4), $j^{\,1}_{end}$ and $j^{\,2}_{end}$ are updated at step 5, and, if the stop condition is not satisfied, the procedure is called on the successive row $i-1$ (step 13) unless all the rows have been already checked (i.e., $i=up$, step 2).

Fig. 5

Computation of $\mathcal {S}_0(F_k)$

It remains to comment the case handled in steps 6–12 of the pseudocode in Fig. 5. Indeed, because of the updating of $j^{\,0}_{end}$ in the procedure (for a fixed iteration k), we can have that $j^{\,0}_{start}(i)=j^{\,0}_{end}(i)$. In this case, if a foreground pixel was found so far (at the current iteration), the algorithm updates $j^{\,0}_{end}(i-1)$ or sets STOP to true if a stop condition is satisfied.

Fig. 6

Possible cases for boundary stop conditions. In blue, the part of two consecutive rows not already visited during the current step. Left-top: the left-bottom corner has been reached in the search for $\mathcal {S}_3$; Right-top: the right-bottom corner has been reached in the search for $\mathcal {S}_2$; Left-bottom: the left-top corner has been reached in the search for $\mathcal {S}_0$; Right-bottom: the right-top corner has been reached in the search for $\mathcal {S}_1$

4.2.1 Notes on the Computation of $\mathcal {S}_1,\mathcal {S}_2,\mathcal {S}_3$

Procedures analogous to SearchRow$\_0$ can be written for computing $\mathcal {S}_1(\mathcal {F}_{k}),\; \mathcal {S}_2(\mathcal {F}_{k})$, and $\mathcal {S}_3(\mathcal {F}_{k})$ in a row, we refer to them as SearchRow$\_1$, SearchRow$\_2$ and SearchRow$\_3$, accordingly. We point out that if $p=1,2$ the search interval is $j^{p}_{end}(i)< j^{p}(i)\le j^{p}_{start}(i)$, visited from right to left, and the successor of row i in the order of processing is $i-1$ for $p=1$ and $i+1$ for $p=2$. If $p=3$ the search interval is $j^{3}_{start}(i)\le j^{3}(i)<j^{3}_{end}(i)$ scanned from left to right, and the successor of row i in the order of processing is $i+1$.

The stop conditions, for every case, are illustrated in Fig. 6 and the pseudocodes are listed in Fig. 7. For example, in the case of the computation of $\mathcal {S}_0$, the left-top corner of the boundary $\mathcal {F}_k$ is reached when the configuration shown in the left-bottom hand happens: rows $i-1$ and i are illustrated and the arrow links the two considered items of column j. Indeed no salient pixels can be found on the right of j, i.e., if $j^{\,0}_{start}(i-1)>j^{\,0}_{end}(i)$ for $j=j^{\,0}_{end}(i)$, or $s_{i j}=k$ AND $j=left$, by Corollary 1. Similarly the other cases can be explained.

Fig. 7

Stop conditions to the search of a forward pixel in any row. Left-top: instructions used in the computation of $\mathcal {S}_0$; right-top: instructions used in the computation of $\mathcal {S}_1$; left-bottom: instructions used in the computation of $\mathcal {S}_2$; right-bottom: instructions used in the computation of $\mathcal {S}_3$

For completeness, we report the updating of the end-limits for row i during the current iteration k in Fig. 8. We can recognize the instruction at step 5 of the pseudocode in Fig. 5 for the computation of $\mathcal {S}_0(\mathcal {F}_k)$.

Fig. 8

Update end-limits for row i during the current iteration k. First instruction is used in the computation of $\mathcal {S}_0$, second in the computation of $\mathcal {S}_1$, third in the computation of $\mathcal {S}_2$, and fourth in the computation of $\mathcal {S}_3$

Finally, let us focus on the conditions of the while-loop iterating the procedure SearchRow$\_p$, for $p=1,2,3$. In case of $p=0$, the condition is $i\ge up$ (see Fig. 5 step 2). Same condition holds for the procedure SearchRow$\_1$, since rows are considered from down to up. Differently, rows are considered in the opposite order for the computation of $\mathcal {S}_2$ and $\mathcal {S}_3$. So, in these cases $i\le down$. Actually, since the computation of $\mathcal {S}_2$ and $\mathcal {S}_3$, follow the computation of $\mathcal {S}_0$ and $\mathcal {S}_1$ (see the flowchart in Fig. 9), rows already visited provide an upper bound to the repetition of the calls of the procedure SearchRow$\_2$ and SearchRow$\_3$. To this aim, row-indices $i_0,\;i_1$ store the index of the last g.s.p. found at the current iteration k during the computation of $\mathcal {S}_0$ and $\mathcal {S}_1$, respectively. Therefore, the conditions of the while-loops are $i>i_1$ for the repetition of SearchRow$\_2$, and $i>i_0$ for the repetition of SearchRow$\_3$. Indices $i_2,\;i_3$ store the index of the last row already visited during the last computation of $\mathcal {S}_2,\;\mathcal {S}_3$, respectively, with the constraint that $i_3<i_0$ and $i_2<i_1$.

4.3 Setting New Limits

At the end of each iteration, the algorithm sets the new limits for the next iteration.

Fig. 9

Flowchart of the algorithm

During a current iteration k, the case in which all the items in a row have been visited can arise. The indices of the aforementioned rows are in correspondence with the indices of a Boolean vector empty_row such that empty_$\hbox {row}_i$=TRUE if and only if all the items of row i have been visited. This permits to easily compute the row-limits up and down of $\mathcal {F}_{k+1}$ since if empty_row(up)=TRUE, then up is increased, and if empty_row(down)=TRUE, then down is decreased.

Then, the algorithm sets the endpoints bounding $\mathcal {Q}(\mathcal {F}_{k+1})\subset \mathcal {Q}(\mathcal {F}_{k}\setminus \mathcal {S}(\mathcal {F}_{k}))$ by $j^p_{start}$ and $j^p_{end}$. More precisely, leftmost items are indexed by columns:

• $j^3_{start}(i)$, with $up\le i \le i_3$,

• left, with $i_3<i<i_0$, possibly empty,

• $j^0_{start}(i)$, with $i_0\le i\le down$;

while rightmost items are indexed by columns:

• $j^2_{start}(i)$, with $up\le i \le i_2$,

• right, with $i_2<i<i_1$ possibly empty,

• $j^1_{start}(i)$, with $i_1\le i \le down$,

since $i_3<i_0$ and $i_2<i_1$. The procedure SetNewLimits assigns the values of $j^p_{start}(i)$ in the whole interval, i.e., $j^0_{start}(i)=j^3_{start}(i)$, and $j^1_{start}(i)=j^2_{start}(i)$, and sets $j^0_{end}(i)=j^3_{end}(i)=j^1_{start}(i)+1$ and $j^1_{end}(i)=j^2_{end}(i)=j^0_{start}(i)+1$, $up\le i \le down$, and reset values for $i_0,\;i_1,\;i_2,\;,i_3$ for next iteration $k+1$. This is necessary, since the end-limits must be set for every row in between [up, down].

Fig. 10

Illustrative example of the algorithm for finding g.s.p. in the iterations ($k=0,1,2,3,4,5$) in case of the image shown in Fig. 2a. Each image shows the configuration at the end of iteration k: identified g.s.p. in the current iteration are drawn bold; $j^{\,p}_{start}$ and $j^{\,p}_{end}$ are colored with blue and red, respectively, and they provide the boundary for next iteration ($k+1$)

As a summary, we report in Fig. 9 the flowchart of the algorithm described: after the initialization step, the algorithm iteratively performs the search of g.s.p. in $\mathcal {S}_p(\mathcal {F}_k)$ in the order $p=0,1,2,3$ until all the items of $\mathcal {F}$ have been visited ($count=mn$). Figure 10 illustrates the execution of the algorithm.

Fig. 11

Binary image constituted by one row. The g.s.p. are marked by red borders, the iteration step they are found in are given under the pixels

4.4 A Toy Example

For a complete toy example of a binary image of size $1\times 22$ consider Fig. 11. We use the notation $j^{\,k,p}_{start}(i)$, $j^{\,k,p}_{end}(i)$, $j^{\,k,p}(i)$ to follow the evolution for k and p. In the first iteration ($k=1$), the algorithm starts with $p=0$, and sets $j^{\,1,0}_{start}(i)=0$, and $j^{\,1,0}_{end}(i)=22$. In this case, $i=down=up=0$, and the procedure SearchRow$\_0$ determines $j^{\,1,0}(0)=2$ (corresponding to the first g.s.p. found in the row), and sets $j^{\,2,0}_{start}(0)=j^{\,1,0}(0)+1=3$ (step 11). Then the algorithm updates the end-limit $j^{\,1,1}_{end}(0)=j^{\,2,0}_{start}(0)-1=2$ (step 5 in Fig. 5, or Fig. 8). Since there is only one row, the while-loop of Fig. 5 stops with $i=-1<up=0$, and the algorithm proceeds by processing $p=1$: we have $j^{\,1,1}_{start}(0)=21$ and the procedure SearchRow$\_1$ finds $j^{\,1,1}(0)=20$, and sets $j^{\,2,1}_{start}(0)=j^{\,1,1}(0)-1=19$. Then, the end-limit is updated $j^{\,2,0}_{end}(0)=j^{\,2,1}_{start}(0)+1=20$ (Fig. 8). Since the image is constituted by just one row, $i_3<i_0=0$ and $i_2<i_1=0$, so that the algorithm skips the blocks for the computation of $\mathcal {S}_2$ and $\mathcal {S}_3$, and then updates $left=2$ and $right=20$. In the next iteration ($k=2$), $j^{\,2,0}(0)=3$ and $j^{\,2,1}(0)=19$, and so on, until all the pixels have been visited. We point out that the algorithm does not execute the while-instructions for $p=2,3$ (on the same row) to avoid visiting the same pixels twice.

4.5 Correctness and Complexity

Theorem 1

The algorithm computes $\mathcal {S}_g(\mathcal {F})$ in linear time in the size of the binary image $\mathcal {F}$.

Proof

In a generic iteration k, the algorithm computes $\mathcal {S}({F}_k)=\mathcal {S}(\mathcal {Q}({F}_k))$. This can be done by determining, based on Proposition 1, the background quadrants of ${F}_k$ to get $\mathcal {Q}({F}_k)$. Background quadrants of ${F}_k$ permit to get $\mathcal {S}(\mathcal {Q}({F}_k))$ based on Proposition 2, since the salient points of $F_k$ are the foreground pixels with neighbors in $\hbox {Neigh}_p$ which belong to background quadrants of $F_k$. The algorithm computes them by processing the matrix row by row. Let $p=0$: we prove that for every row i, if a foreground pixel is found on column j, then it is a g.s.p., i.e., $Z_0(i+1,j)\cap F_k=\emptyset$, and $Z_0(i,j-1)\cap F_k=\emptyset$. We prove the statement by induction on i.

Base step: consider the first processed row of index $i=down$:

• If the procedure finds a foreground pixel in column j, $Z_0(down,j-1)$ is a background quadrant since it is the interval $[j^0_{start}(down),j)$ of row down which contains only items in the background (as j is the first foreground pixel). In this case $Z_0(down+1,j)=\emptyset$, and there follows that the item in position (down, j) is a g.s.p. of $F_k$.

• If no foreground pixel is found, $Z_0(down,j^0_{end}(down))\cap F_k=\emptyset$.

By induction hypothesis, consider row $i=h$:

• If a foreground pixel is found in column j, it is a g.s.p. and $Z_0(h+1,j)\cap F_k=\emptyset$, and $Z_0(h,j-1)\cap F_k=\emptyset$. By $j^0_{end}(h-1)=j$, we get $Z_0(h,j^0_{end}(h-1)-1)\cap F_k=\emptyset$.

• If no foreground pixel is found, $j^0_{end}(h-1)=j^0_{end}(h)$, and so $Z_0(h,j^0_{end}(h-1)-1)\cap F_k=Z_0(h,j^0_{end}(h)-1)\cap F_k=\emptyset$.

Consider now the successive row $i=h-1$: If a foreground pixel is found in column $j<j^0_{end}(h-1)$ we have for its neighbors in $\hbox {Neigh}_0$: $Z_0(h,j-1)\subset Z_0(h,j)\subset Z_0(h,j^0_{end}(h-1)-1)$ that is a background quadrant by the induction assumption, and $Z_0(h-1,j-1)\setminus Z_0(h,j-1)=[j^0_{start}(h-1),j-1)$ contains only items in the background (since j is the first foreground pixel) so that $Z_0(h-1,j-1)\cap F_k=\emptyset$. There follows that the item in position $(h-1,j)$ is a g.s.p. of $F_k$.

Moreover notice that for every row i we can easily show that, by Corollary 1, no g.s.p. in $\mathcal {S}_0$ can exist in the columns with indices greater than j (if j is the foreground pixel found on row i) or $j^0_{end}(i)$ (if no foreground pixel is found in the given interval) for all row $i'<i$, so that all the g.s.p. are determined.

Analogously, it can be proven that the algorithm computes correctly $\mathcal {S}_1(F_k)$, $\mathcal {S}_2(F_k)$, and $\mathcal {S}_3(F_k)$.

At the end of each iteration k, by Proposition 1, the subset of items not already visited constitute the Q-convex set $\mathcal {Q}(F_k)\setminus \mathcal {S}(F_k)$ bounded by the row- and column-limits up, down, left and right, and by the column-indices in vectors $j^p_{start}\ (p=0,1,2,3)$. By Proposition 3, the search proceeds visiting the items in $\mathcal {Q}(F_k)\setminus \mathcal {S}(F_k)\supset F_{k+1}$ so that, in the next iteration $k+1$, the algorithm computes the salient points of $F_{k+1}$. Finally, the algorithm stops when all the items have been visited ($count=mn$) corresponding to $F_{k+1}=\emptyset$.

By the previous description, the algorithm is correct.

The time complexity of the algorithm is linear in the image size. Indeed, the algorithm iteratively executes the blocks for the computations of $\mathcal {S}_p(\mathcal {F}_k)$ until $count<mn$ (see the flowchart in Fig. 9). The complexity of each block is given by the complexity of the procedure for searching forward pixels in any row, that, in turn, depends on the visited pixels. The key point is that for each visited item a fixed number of operation is done, and it is sufficient to scan the image just once. To see that each pixel is investigated only once, fix p, and for any row index i, starting from $j^p_{start}(i)$, the column index j is incremented for $p=0,3$ (resp., decremented for $p=1,2$) until a g.s.p is found, i.e., $j'=j^p(i)$ or $j'=j^p_{end}(i)-1$ (resp., $j'=j^p_{end}(i)+1$) is reached; then $j^p_{start}(i)$ is updated to $j'$ so that, in the next iteration, items with column index $j>j'$ (resp., $j<j'$) are considered. Since count is incremented in the procedures computing salient points and never decremented, the algorithm runs in linear time in the size of the binary image. Note that the procedure SetNewLimits scans consecutive items in [up, down] of a monodimensional array so that globally the complexity is also bound by O(mn). $\square$

There follows that the measures $\varPsi _1$ and $\varPsi _2$ can be computed in the same time complexity.

4.6 General Directions

Here, we treat the general case of measuring Q-convexity along two arbitrary prescribed lattice directions $r=\lambda _rx+\mu _ry$ and $q=\lambda _qx+\mu _qy$. Let us denote by $\langle i,j\rangle _{r,q}$ the point M which satisfies $r(M)=i$ and $q(M)=j$. We point out that if $\delta =|\det (r,q)|=|\lambda _r\mu _q-\lambda _q\mu _r|\ne 1$, the intersection of an r-line and a q-line is not always in $\mathbb {Z}^2$ so that $\langle i,j\rangle _{r,q}$ may be a point of $\mathbb {Q}^2$. The definition of the four quadrants for the two directions r and q in $M=\langle i,j\rangle$ becomes the following:

$$\begin{aligned}&Z_0(\langle i,j\rangle )=&\{ \langle i',j'\rangle \in \mathbb {Z}^2 :\, i'\le i\, \text{ and }\, j'\le j)\}\ ,\\&Z_1(\langle i,j\rangle )=&\{\langle i',j'\rangle \in \mathbb {Z}^2 :\, i'\ge i\, \text{ and }\, j'\le j\}\ ,\\&Z_2(\langle i,j\rangle )=&\{\langle i',j'\rangle \in \mathbb {Z}^2 :\, i'\ge i\, \text{ and }\, j'\ge j\}\ ,\\&Z_3(\langle i,j\rangle )=&\{\langle i',j'\rangle \in \mathbb {Z}^2 :\, i'\le i\, \text{ and }\, j'\ge j\}\ . \end{aligned}$$

Let us define

$$\begin{aligned} rmin=&\min \{i\,:\, r(M)=i, \;M\in \mathcal {F}\}\ ,\\ rmax=&\max \{i\,:\, r(M)=i, \;M\in \mathcal {F}\}\ ,\\ qmin=&\min \{j\,:\, q(M)=j, \;M\in \mathcal {F}\}\ ,\\ qmax=&\max \{j\,:\, q(M)=j, \;M\in \mathcal {F}\}\ .\\ \end{aligned}$$

Then, $\mathcal {F}$ is contained in

$$\begin{aligned} \{\langle i,j\rangle _{r,q}\in \mathbb {Z}^2 \,:\,pmin\le i \le pmax,\ qmin\le j\le qmax\}. \end{aligned}$$

Let $m'=rmax-rmin+1,\; n'=qmax-qmin+1$. We implement the binary image as an enhanced matrix of size $m'\times n'$, where r-lines and q-lines are the rows and the columns of the matrix, the foreground pixels are 1 items, the background pixels are 0 items and all the other items are $-1$’s. Note that $-1$ items correspond to points not in $\mathbb {Z}^2$ which, in turn, do not correspond to any pixel of the image. Thus, they can be simply omitted during the processing. This trick permits to extend the previous algorithms in a straightforward way.

5 Experimental Results

We implemented the algorithm in C language. The program is available at http://www.inf.u-szeged.hu/~pbalazs/ImageAnalysis/Q-convexity.htm.

To investigate the properties of our measures, we conducted different kinds of experiments following tests and datasets in [23]. We refer to [23] because our measures present similar properties to the descriptors proposed by Rosin and Žunić, and in that way, similar experiments are suitable for testing and comparison. In all the experiments, we used the images with original sizes, however, we rescaled them in the figures for better presentation quality. The convexity values were calculated up to six digits. In the figures and tables, these are rounded to four digits.

For a ranking problem and to investigate scale invariance and robustness to noise, we used the 14 shapes in Fig. 12. These images have varying sizes in both dimensions between 100 and 500 pixels. In the second experiment, we used the 9 synthetic shapes of Fig. 16 presenting rotation and translation of intrusions/protrusions and global skew for assessing sensitivity. The shapes are of sizes between $315\times 315$ and $315\times 555$, except the skew image (last shape in the first row of Fig. 16) which is of size $734\times 1095$. Finally, we used a dataset of 43 algae (taxon Micrasterias) images with varying squared sizes between $258\times 258$ and $957\times 957$, for a classification problem (see Fig. 17).

5.1 Sensitivity, Robustness, Scale Invariance

In this experiment, we computed the directional convexity measures (see Fig. 12) and the (two dimensional) Q-convexity measures (see Fig. 13) to a variety of shapes. The directional convexity measures can be directly obtained restricting the measures to lines and dividing by the number of lines for normalization. We ranked the shapes into ascending order to highlight the behavior of the measures. As clearly shown in the figures, the Q-convexity measures do not just average the values of the directional measures. Indeed, they yield a more complex combination of them.

Fig. 12

Shapes ranked into ascending order by the horizontal ($\varPsi _1^h$ and $\varPsi _2^h$) and vertical ($\varPsi _1^v$ and $\varPsi _2^v$) directional convexity measures, from top to bottom, respectively

Fig. 13

Shapes ranked into ascending order by the Q-convexity measures $\varPsi _1$, $\varPsi _1'$, $\varPsi _2$, and $\varPsi _2'$, from top to bottom, respectively

Let us notice that all the measures assign correctly value 1 to the rectangle and leg images, even if there are some differences in the ranking. The wiggle rectangle image (12-th shape in the first row of Fig. 12)—which is horizontally convex but vertically not—receives a high (1) or lower score accordingly, and lower values also in Fig. 13 where Q-convexity is evaluated. In general, since the measures are based on the boundary and the interior of the image, they are sensitive to deep intrusions (see also next subsection) by assigning lower values to them (see first and second shapes in the first row of Fig. 13). Finally, note that $\varPsi _1'$ and $\varPsi _2'$ depend on the quantitative factor $\varTheta$. This is less evident (in this case) for $\varPsi _1'$ as the corresponding order consists in a small rearrangement of the shapes with respect to $\varPsi _1$, whereas for $\varPsi _2'$ this results clearly in the corresponding order (see, e.g., the second image in the last row of Fig. 13).

For investigating robustness to noise, we also generated distorted versions of the original images following exactly the same strategy as in [22], for the same size of images. We added salt-and-pepper noise to the images where a parameter p controlled the probability an image pixel is inverted. Then, we kept only the largest connected black component and filled all the white components (holes) having area less than 20 pixels. In this way, there is only a very low probability of changing the interior of the object or creating small components in the background. Thus, with a high probability, only the boundary of the object is affected (see Fig. 14).

Fig. 14

The spiral image of Fig. 12 with a moderate ($p=0.05$, left) and a high amount ($p=0.25$, right) of noise

We ranked the images according to the Q-convexity values of their noisy versions. To compare the rankings achieved in different ways, we used the Spearman rank defined as

$$\begin{aligned} 1-\sum \frac{6(r_o(X)-r_d(X))^2}{n(n^2-1)}\ , \end{aligned}$$

where $r_o(X)$ and $r_d(X)$ are the rank of the original and distorted image, respectively. Spearman rank is always a value in $[-1,1]$ and it is close to 1 when the two compared rankings are similar. Table 1 reports the results. We found all four measures to be robust against a moderate amount of noise. Especially, $\varPsi _2'$ turned out to be extremely tolerant of even a high amount of noise. The reason that $\varPsi _1'$ and $\varPsi _2'$ achieved in this test better values than $\varPsi _1$ and $\varPsi _2$, respectively, is that the former measures take into account also the area of the object, thus they are less sensitive to perturbations on the border of the object.

Table 1 Spearman ranks of the different Q-convexity measures according to the noise level

We also investigated scale invariance. This time, we omitted the two fully convex images (they are clearly scaleable without loosing convexity). Taking the vectorized versions of the remaining 12 original images, we digitized them on different scales ($64\times 64$, $128\times 128$, $256\times 256$, $512\times 512$, and $1024\times 1024$). Then, for each image, we computed the Q-convexity values. Figure 15 shows the trends of the convexity values for each image. The trend lines belonging to the measures $\varPsi _1$ and $\varPsi _1'$ are close to horizontal from which we deduce scale invariance of these measures. Indeed, their definition is based on the ratio of salient and generalized salient points of an image (calculated by quadrants) which does not significantly change during scaling.

Taking a look at the graph of $\varPsi _2$, we observe that the trend is not horizontal, in higher resolutions the values are generally close to 1. The reason is that, by definition, $\varPsi _2$ is affected by the ratio of the size of the Q-convex hull, and the number of (generalized) salient points. The higher the resolution is, the bigger (in terms of number of points) the Q-convex hull is, whereas the number of (generalized) salient points do not drastically change. By definition, $\varPsi _2$ provides small values for images such that the number of pixels of the Q-convex hull and the number of g.s.p. are close. This happens for configurations like chessboard ($\varPsi _2 =0$), and for example, for salt-and-pepper noisy images.

Thus, in general, $\varPsi _2$ is not scale-invariant. However, this property can be even beneficial as it allows us to measure convexity on different scales, and thus to distinguish between images by using image pyramids. Nevertheless, $\varPsi _2'$ can compensate scale-sensitivity, by taking also the area of shape into account, and, in the same time, it also mitigates the problem that the values of $\varPsi _2$ are close to 1.

Fig. 15

Trends of convexity values of images in Fig. 12 as they depend on the resolution of the image

5.2 Sensitivity to Rotation, Translation of Intrusions/Protrusions

In this experiment, we use the set of synthetic polygons to show how the measures behave in case of rotation, translation of intrusions/protrusions and global skew. Results are illustrated in Fig. 16 and give evidence that the measures are invariant under translation of intrusions and protrusions (see, e.g., the third and fourth images, and the sixth and seventh images, with respect to $\varPsi _1$), and are sensitive to rotations of angles different from 90 degrees (compare, e.g., the first image to the third one, and the sixth image to the eighth one, with respect to $\varPsi _1$).

Fig. 16

Synthetic shapes ranked into ascending order by shape measures $\varPsi _1$, $\varPsi _2$, and $\varTheta$ (from top to bottom, respectively)

Concerning $\varPsi _2$, we may notice in addition that the values are close to each other so that just a small difference may change the order. The $\varTheta$ descriptor gives a quantitative information of the images and assigns the same value to all the intrusions images, since they have same sizes and also their Q-convex hulls are of the same size. Although the measures rank differently the shapes, we can observe that they assign in general a low value to images with intrusions and higher values to images with protrusions.

Fig. 17

Some of the 43 desmids, one for each class, ordered by $\varPsi _1$

For this dataset, the ranking obtained by $\varPsi _1'$ is the same as that for $\varPsi _1$. Measure $\varPsi _2'$ gives also the same ranking as $\varPsi _1$, except that it swaps the fifth and eight image of the first row of Fig. 16.

5.3 A Classification Problem

Table 2 Classification accuracy for 43 desmids

In the last experiment, we illustrate how to use the shape measures to perform an image classification task, on the dataset of images in [23] constituted by 43 types of algae, called desmids (taxon Micrasterias) with 4–7 drawings for each of eight classes. In this small-scale classification task, the desmid images present several narrow indentations to show the sensitivity and effectiveness of our descriptors. One shape for each class is illustrated in Fig. 17. We use again the images in their original sizes and preprocess them to deal with rotation dependency: first we compute the orientation of the principal axis by the second central moment, and then we rotate the image accordingly to obtain an image having the coordinate axes as principal axes. After, we extract one or more convexity measures as features from the image and form a feature vector of them.

Following the same strategy as in [23], for evaluating shape classification performance we applied a nearest neighbor (1NN) classifier on the feature vectors with Mahalanobis distance. To avoid overfitting, we used leave-one-out cross validation: for each image, we use the current one for testing and the rest for training. We report the average classification accuracies giving the best results for a single measure, or a combination of two or three descriptors (rows 1–3 of Table 2). In addition, we computed the measures with respect to the diagonal directions $d_1=(1,1),\, d_2=(1,-1)$ as in Sect. 4.6, denoted by $\varPsi _1(d_1,d_2),\varPsi _1'(d_1,d_2),\varPsi _2(d_1,d_2),\varPsi _2'(d_1,d_2)$. Best results combining the measures in the horizontal, vertical, and the diagonal directions are reported in rows 4–6 of Table 2.

We observe that increasing the number of descriptors used in the combination results in a better worst case accuracy. By an exhaustive search, we also computed all combinations of the above 8 shape measures w.r.t. the two couple of directions, and we found the best combination to ensure $76.74\%$ classification accuracy (see row 7 of Table 2, for one of them).

We repeated the classification task with the horizontal and vertical convexity measures given in [2] (rows 8–10 of Table 2), as well as with some conventional low-level shape descriptors: the area ratio of the shape and its convex hull, the shape circularity measure, and the first moment invariant of Hu [18]. With a combination of these latter three descriptors and the second Hu moment, we could reach an accuracy of $69.76\%$ (see rows 11–14 of Table 2). No combinations including also any (or even all) of the 7 Hu moments could outperform this result. We also point out that the accuracy of the descriptor $\mathcal {C}_{0,0}$ in [23] was $55.81\%$ (row 15 of Table 2), on the same classification problem. Finally, the best accuracy in this test reached in [5] (see Table 4, there) is $58.48\%$.

This illustrative example reveals that using a combination of the proposed shape descriptors and additional couple of directions could be a good strategy to improve classification accuracy. Of course, the best set of measures (including also the best directions) depends on the classification issue, and can be found, e.g., by feature selection methods, like those of [20].

6 Conclusion

In this paper, we studied new shape descriptors based on the notion of Q-convexity. The descriptors incorporate region-based information and are sensitive to intrusions in the images as shown in the experiments. In addition, we studied robustness to noise and scale invariance. The small-scale classification task we conducted showed that a combination of these descriptors seems to be appropriate for solving classification issues.

The designed algorithm runs in linear time in the size of the image, and it is suitable for a parallel implementation. Furthermore, it works also if the image is constituted by disconnected parts, whereas, as far as we know, in other approaches like for example those based on combinatorics on words (see for successful examples [7, 9, 10]), images are supposed to be 8-connected or 4-connected. Finally, the shape descriptors can be easily generalized and implemented to any couple of lattice directions.