A Q-Convexity Vector Descriptor for Image Analysis

Abstract

Shape representation is a main problem in computer vision, and shape descriptors are widely used for image analysis. In this paper, based on the previous work Balázs, P., Brunetti, S.: A New Shape Descriptor Based on a Q-convexity Measure, Lecture Notes in Computers Science 10502, 20th Discrete Geometry for Computer Imagery (DGCI) (2017) 267–278, we design a new convexity vector descriptor derived by the notion of the so-called generalized salient points matrix. We investigate properties of the vector descriptor, such as scale invariance and its behavior in a ranking task. Moreover, we present results on a binary and a multiclass classification problem using k-nearest neighbor, decision tree, and support vector machine methods. Results of these experiments confirm the good behavior of our proposed descriptor in accuracy, and its performance is comparable and, in some cases, superior to some recently published similar methods.

1 Introduction

As shape is an intrinsic feature of the object, shape representation is a main problem in computer vision and shape descriptors are widely used for image understanding [13, 25]. One class of descriptors captures single geometrical or topological characteristics of shapes, like moments [10], orientation and elongation [30], circularity [18], just to mention a few. Among them, convexity is studied in several papers [17, 20]. Depending on whether the interior or the boundary of the shape is investigated in order to determine the degree of convexity, these measures can be grouped into area-based [4, 25, 27] and boundary-based [29] categories. Other works use a probabilistic approach (see, for example, [19, 21]) and exploit convexity for shape decomposition [15, 22]. Closely related questions are extensions for classification of shapes [23] (providing corner and shape parameters to study the abrasion process) and the use of some kind of convexity to deal with complex spatial relationships [3, 8] (like enlacement, interlacement, and surrounding).

In [1], we proposed a shape descriptor (scalar) which used both boundary and area information and based on the concept of Q-convexity [6, 7], mostly studied in Discrete Tomography [14] (it generalizes so-called hv-convexity to any two or more directions and has interesting connections with “total” convexity). The notion of salient points of a Q-convex image has been introduced in [9] as the analog of extremal points of a convex set. Salient points can be generalized for any binary image, and they have been studied to model the “complexity” of a binary image which lead to the convexity measure of [1, 5].

In [2], we extended the Q-convexity measure by weighting differently the generalized salient points—depending on “how” far they are from the boundary—in calculating the measure. For this purpose, we introduced the matrix of generalized salient points g.s.p. of a binary image, shortly, GS matrix (see Sect. 2 for the definition).

Unfortunately, how to choose the proper weights for a given image processing issue is by far not trivial. Therefore in this paper, we provide a more flexible descriptor extension of [1] and [2] derived directly from the GS matrix. Indeed, a GS matrix characterizes its binary image by means of its g.s.p. maintaining the information about their “depth” (see Sects. 4 and 5 for details). A vector descriptor is now considered instead of a scalar descriptor to get additional flexibility. Since the size of the vector depends on the image itself, we introduce the concept of “maximal sequence” to impose an upper bound to the number of components of the vector descriptor. This theoretical bound is then used in the experiments for dealing with the classification of images.

We investigate properties of the new vector descriptor, such as scale invariance and its behavior in a ranking task. Moreover, we conduct image classification (a binary and a multiclass classification problem) and robustness-to-noise tests on two different suitable datasets: the datasets DRIVE [26], CHASEDB1 [12] of fundus photographs of the retina, and the dataset of algae (desmids taxon Micrasterias) in [21]. The choice of these datasets allows us to evaluate and compare our shape descriptor to the descriptors defined in [8] and in [21] also based on a convexity measure. As classifiers, we use k-nearest neighbor with Euclidean distance (kNN), decision tree (DT), and support vector machine with linear kernel (SVM). Results of these experiments confirm the good behavior of our proposed descriptor: it reaches an accuracy comparable and, in some cases, superior to the methods in [8, 21], and it is computationally more efficient (as it is linear in the size of the image).

The structure of the paper is the following. In Section 2, we present the background. In Sect. 3, the concept of maximal sequences is introduced. In Sect. 4, we define the matrix of generalized salient points (GS matrix, for short) and describe a linear-time algorithm for the construction of the binary image from its GS matrix. The aim of Sect. 5 is to briefly show how the GS matrix can be efficiently computed, in linear time in the size of the image. In Sect. 6, we give the definition of the new shape descriptor. In Sect. 7, we report on the experiments we conducted. Finally, Sect. 8 is for the conclusion.

2 Background

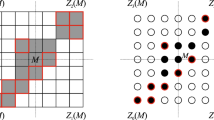
Any binary image$\mathcal {F}$ is a $m\times n$ binary matrix, and it can be represented by a set of black, foreground pixels denoted by F, and white, background pixels (unit squares) (see Fig. 1 left). Equivalently, foreground pixels can be regarded as points of $\mathbb {Z}^2$ contained in a finite lattice grid $\mathcal {G}$ (rectangle of size $m\times n$), up to a translation, and background pixels can be viewed as points in $\mathcal {G}\setminus F$. In this view, the non-empty finite set F is called lattice set (see Fig. 1 right). Throughout the paper, we will use both representations for binary images as interchangeable, even if the order of the points in the lattice and the order of the items in a matrix are different. For our convenience when not confusing, we use $\mathcal {F}$ for both the image and its representations, and we denote by $\mathcal {F}^c$ the complement of $\mathcal {F}$, i.e., the image obtained as the complement of its pixel values reversing foreground and background pixels. In the lattice representation, $\mathcal {F}^c$ corresponds to the lattice set $\mathcal {G}\setminus {F}$.

Fig. 1

A binary image represented as black and white pixels (left), and by a lattice set (right)

Let us introduce the main definitions concerning Q-convexity [6, 9]. In order to simplify our explanation, let us consider the horizontal and vertical directions and denote the coordinate of any point M of the grid $\mathcal {G}$ by $(x_M,y_M)$. Then, M and the directions determine the following four quadrants:

$$\begin{aligned} Z_0(M)= & {} \{ N\in \mathcal {G}:\quad 0\le x_N\le x_M, \quad 0\le y_N\le y_M\}\\ Z_1(M)= & {} \{ N\in \mathcal {G}:\quad x_M\le x_N< m, \quad 0\le y_N\le y_M\}\\ Z_2(M)= & {} \{ N\in \mathcal {G}:\quad x_M\le x_N< m, \quad y_M\le y_N< n\}\\ Z_3(M)= & {} \{ N\in \mathcal {G}:\quad 0\le x_N\le x_M, \quad y_M\le y_N< n\}. \end{aligned}$$

Definition 1

A lattice set F is Q-convex if $Z_p(M)\cap {F}\ne \emptyset$ for all $p=0,\ldots ,3$ implies $M\in F$.

We say that the binary image $\mathcal {F}$ is Q-convex, if F is Q-convex. We also say that $Z_p(M)$ is a background quadrant, if $Z_p(M)\cap {F}= \emptyset$. Thus, in other words, a binary image is Q-convex if there exists at least a background quadrant $Z_p(M)$ for every pixel M in the background of $\mathcal {F}$. Figure 2 illustrates the above concepts.

Fig. 2

Illustration of the concept of Q-convexity. A Q-convex (left) and a non-Q-convex (right) lattice set. Note that the image on the left is the Q-convex hull of the image on the right

The Q-convex hull of F can be defined as follows:

Definition 2

The Q-convex hull $\mathcal {Q}({F})$ of a lattice set F is the set of points $M\in \mathcal {G}$ such that $Z_p(M)\cap {F}\ne \emptyset$ for all $p=0,\ldots ,3$.

Equivalently, the Q-convex hull $\mathcal {Q}({F})$ of a lattice set F is the intersection of all the Q-convex sets containing F. By Definitions 1 and 2, if F is Q-convex, then ${F}=\mathcal {Q}({F})$. Conversely, if F is not Q-convex, then $\mathcal {Q}({F})\setminus {F}\ne \emptyset$ (see Fig. 2, again, where for the lattice set F on the right, $\mathcal {Q}({F})\setminus {F}=\{M\}$).

Definition 3

Let F be a lattice set. A point $M\in {F}$ is a salient point of F if $M \notin \mathcal {Q}({F} \setminus \{M\})$.

We may speak about the salient points of a binary image, accordingly. Let us denote the set of salient points of $\mathcal {F}$ by $\mathcal {S}({F})$. Of course $\mathcal {S}({F})=\emptyset$ if and only if ${F}=\emptyset$. Moreover, $\mathcal {Q}(F)=\mathcal {Q}(\mathcal {S}(F))$. Daurat proved in [9] that the salient points of $\mathcal {F}$ are the salient points of the Q-convex hull $\mathcal {Q}({F})$ of F, i.e., $\mathcal {S}({F})=\mathcal {S}(\mathcal {Q}({F}))$. This means that if F is Q-convex, its salient points completely characterize F. If it is not, there are other points belonging to the Q-convex hull of F but not in F that “track” the non-Q-convexity of F. These points are called generalized salient points (abbreviated by g.s.p.). The set of generalized salient points $\mathcal {S}_g({F})$ of F is obtained by iterating the definition of salient points on the sets obtained each time by discarding the points of the set from its Q-convex hull, i.e., using the set notation:

Definition 4

If F is a lattice set, then the set of its generalized salient points (g.s.p.) $\mathcal {S}_g({F})$ is defined by $\mathcal {S}_g({F})=\bigcup _i \mathcal {S}({{F}}_i)$, where ${{F}}_1={F}$, ${{F}}_{i}=\mathcal {Q}({{F}}_{i-1})\setminus {{F}}_{i-1}$.

We may denote the binary images related to $\mathcal {Q}(F)$, $\mathcal {S}(F)$, and $F_i$ by $\mathcal {Q}(\mathcal {F})$, $\mathcal {S}(\mathcal {F})$, and $\mathcal {F}_i$, respectively. Figure 3 illustrates the definition in the lattice representation. Last set in the sequence is $\mathcal {F}_4$, since $\mathcal {F}_4$ is Q-convex and so $F_5=\mathcal {Q}(F_4)\setminus F_4=\emptyset$. We notice that ${\mathcal {F}}_{i}$ is contained in ${\mathcal {F}}_{i-1}^c$ (more precisely, in $\mathcal {Q}({{F}}_{i-1})\setminus {{F}}_{i-1}$), and if i is even, ${\mathcal {F}}_{i}$ is contained in ${\mathcal {F}}_{1}^c$, else if i is odd ${\mathcal {F}}_{i}$ is contained in ${\mathcal {F}}_{1}$. In the pixel representation, this corresponds to say that foreground and background pixels in $\mathcal {F}_i$ correspond to white and black pixels for i even and to black and white pixels for i odd, respectively. In this view, the Q-convex hull of the foreground pixels of $\mathcal {F}_{i-1}$ contains the Q-convex hull of the foreground pixels of $\mathcal {F}_{i}$.

Fig. 3

Generalized salient points are in black. Top left: $\mathcal {F}_1$. Top right: $\mathcal {F}_2$. Bottom left: $\mathcal {F}_3$. Bottom right: $\mathcal {F}_4$

3 Maximal Sequences

Let $\mathcal {F}$ be a binary image of size $m\times n$ (or equivalently, $F\subset \mathcal {G}$ and $\mathcal {G}$ is of size $m\times n$). By Definition 4, we obtain a sequence of sets $(F_1,\ldots ,F_k)$, k being the index such that ${F}_{k+1}=\emptyset$. Fixed $\mathcal {G}$, there can be another image $\mathcal {E}$ which gives rise to the sequence of sets $(E_1,\ldots ,E_{k'})$, with $k'\ne k$.

Definition 5

We say that a sequence$(F_1,\ldots ,F_k)$is maximal for $\mathcal {G}$, if k is maximum among all the lattice subsets in $\mathcal {G}$.

Proposition 1

Let $\mathcal {G}$ be given. A maximal sequence $(F_1,\ldots ,F_k)$ for $\mathcal {G}$ exists such that $\mathcal {Q}(F_i)\setminus \mathcal {Q}(F_{i+1})=\mathcal {S}(F_i)$, for $i=1,\ldots ,k$.

Proof

If there exists a maximal sequence $(F_1,\ldots ,F_k)$ such that $\mathcal {Q}(F_i)\setminus \mathcal {Q}(F_{i+1})\supset \mathcal {S}(F_i)$, we may ”remove” pixels other than g.s.p to construct another maximal sequence (corresponding to a different binary image): indeed, $\mathcal {Q}(F_i)\supset \mathcal {Q}(F_{i+1})$, and we may change $F_{i+1}$ by adding the pixels in $\mathcal {Q}(F_i)\setminus \mathcal {Q}(F_{i+1})$ which are not g.s.p., i.e., $E_{i+1}=F_{i+1} \cup (\mathcal {Q}(F_i)\setminus (\mathcal {S}(F_i)\cup \mathcal {Q}(F_{i+1})))$. This change reflects on $F_1,\ldots ,F_{i}$ accordingly. Let $k'$ be the index of the new sequence $(E_1,\ldots ,E_{i+1},\ldots ,E_{k'})$; since $\mathcal {Q}(E_{i+1})\supset \mathcal {Q}(F_{i+1})$, we have that $k'\ge k$. $\square$

Proposition 2

Let $(F_1,\ldots ,F_k)$ be a maximal sequence for a given $\mathcal {G}$. $\mathcal {Q}(F_i)\setminus \mathcal {Q}(F_{i+1})=\mathcal {S}(F_i)$, for $i=1,\ldots ,k-1$ if and only if all the pixels in $\mathcal {Q}(F_1)$ are g.s.p.

Proof

Let $\mathcal {Q}(F_i)\setminus \mathcal {Q}(F_{i+1})=\mathcal {S}(F_i)$ and $\mathcal {Q}(F_{k})=\mathcal {S}(F_k)$; then, $\mathcal {Q}(F_1)=\mathcal {S}(F_1)\cup \ldots \cup \mathcal {S}(F_k)$. If all the pixels in $\mathcal {Q}(F_1)$ are g.s.p., $\mathcal {Q}(F_1)=\mathcal {S}(F_1)\cup \ldots \cup \mathcal {S}(F_k)$. There follows $\mathcal {Q}(F_{1})\setminus \mathcal {S}(F_1)=\mathcal {S}(F_2)\cup \ldots \cup \mathcal {S}(F_k)$ is Q-convex because by definition, the set obtained by removing salient points from a Q-convex set is Q-convex. So, $\mathcal {Q}(F_2)= \mathcal {S}(F_2)\cup \ldots \cup \mathcal {S}(F_k)$, and $\mathcal {Q}(F_1)\setminus \mathcal {Q}(F_{2})=\mathcal {S}(F_1)$. By induction on i, the thesis follows. $\square$

By inspection, it is easy to see that the chessboard configuration is such that all its pixels are g.s.p. We now prove by construction that it is the unique image having this property.

Proposition 3

The unique binary image such that all its pixels are g.s.p. is the chessboard.

Proof

Consider a pixel M to be in $\mathcal {S}(F_i)$, and $Z_0(M)\cap (\mathcal {Q}(F_i)\setminus \{M\})=\emptyset$. Since all the pixels in F are g.s.p., $P=(x_M+1,y_M)$ and $Q=(x_M,y_M+1)$ are in $\mathcal {S}(F_{i+1})$. In the same way, we deduce that $(x_P+1,y_P)$ and $(x_P,y_P+1)=(x_Q+1,y_Q)$ and $(x_Q,y_Q+1)$ are in $\mathcal {S}(F_{i+2})$. This construction gives rise to a chessboard configuration. $\square$

From this proposition, we can claim that

Theorem 1

Let $\mathcal {G}$ be given. The chessboard image gives rise to the maximal sequence for $\mathcal {G}$.

As a consequence, it is easy to prove:

Remark 1

Let $\mathcal {G}$ of size $m\times n$ be given. The maximal sequence $(F_1,\ldots ,F_k)$ for $\mathcal {G}$ is such that $k\le min(m,n)$.

This remark is useful to theoretically upper bound the length of the sequences and will be used in the experimental section.

4 The GS Matrix

In this section, we present a characterization of a binary image based on its g.s.p. Consider the matrix representation of $\mathcal {F}=(f_{ij})$. We may associate $\mathcal {F}$ with the $m\times n$ integer matrix B of its generalized salient points defined as follows: $b_{ij}=h$, if and only if $f_{ij}$ is a g.s.p. of $\mathcal {F}_h$; $b_{ij}=0$ otherwise. Informally, items $0<h(\le k)$ of the integer matrix B correspond to g.s.p in $\mathcal {S}(\mathcal {F}_h)$; items 0 do not correspond to any g.s.p. of $\mathcal {F}$. For example, the matrix in Fig. 4 is the GS matrix associated with the first image in Fig. 3. We call B, the GS matrix associated with $\mathcal {F}$, where GS stands for “generalized salient”. The GS matrix is well defined since by Definition 4, we have that $\cap _i \mathcal {S}(\mathcal {F}_i)=\emptyset$.

Fig. 4

GS matrix of the image in Fig. 3

Theorem 2

Any two binary images are equal if and only if their GS matrices are equal.

Proof

Let B be the GS matrix associated with the binary image $\mathcal {F}$. The following construction permits to determine $\mathcal {F}$ by B. For all items i in B considered in decreasing order (of i), compute the Q-convex hull of the pixels corresponding to the items i and fill the corresponding pixels not already considered with the foreground w.r.t. i.

To show that this construction is correct, let k be the maximum value in the GS matrix; then, ${F}_{k+1}=\emptyset$, and $\mathcal {F}_k$ is Q-convex. Therefore, in the first step $i=k$, the construction determines $F_k=Q(\mathcal {S}(F_k))$. Suppose at step $i+1$ the construction determines $\mathcal {F}_{i+1}$, we show by induction step i: the construction computes the Q-convex hull of the pixels corresponding to the items i in the GS matrix, i.e., $Q(\mathcal {S}({F}_{i}))=Q({F}_{i})$, and fills the corresponding pixels not already considered with the foreground w.r.t. i, i.e., $Q({F}_{i})\setminus {F}_{i+1}$. By definition, ${F}_{i+1}=Q({F}_{i})\setminus {F}_{i}$, and since $Q({F}_{i})={F}_{i}\cup {F}_{i+1}$ and ${F}_{i}\cap {F}_{i+1}=\emptyset$, we have ${F}_{i}=Q({F}_{i})\setminus {F}_{i+1}$. By induction, the construction determines $\mathcal {F}={F}_1=Q({F}_{1})\setminus {F}_2$. Therefore, starting from B we obtain F.

Finally, since two different binary images have different GS matrices, there is a one-to-one correspondence between images and matrices. $\square$

In order to design an efficient algorithm based on the constructive proof of the theorem, we extend the definition of Q-convex hull as follows:

Definition 6

The Q-convex hull $\mathcal {Q}({F}_i)$ of the lattice set ${F}_i$ is the set of points $M\in \mathcal {G}$ such that $Z_p(M)\cap {F}_i\ne \emptyset$ for all $p=0,\ldots ,3$.

Remark 2

Since $\mathcal {Q}(F_i)=\mathcal {Q}(\mathcal {S}(F_i))$, pixel M belongs to the Q-convex hull of ${F}_i$ if $Z_p(M)\cap \mathcal {S}({F}_i)\ne \emptyset$ for all p, or equivalently, if there is an item i in the GS matrix associated with $\mathcal {F}_i$ in each zone of M. Since the Q-convex hull of the foreground pixels of $\mathcal {F}_i$ contains the Q-convex hull of the foreground pixels of $\mathcal {F}_{i+1}$, pixel M belongs to $Q({F}_i)\setminus Q({F}_{i+1})$, if i is the minimum among the maximum items in the GS matrix in each zone in M, $i=1,\ldots ,k$. Therefore if i is odd, then $f_{M}=1$ (i.e., $M\in F$), else if i is even, then $f_{M}=0$ (i.e., $M\notin F$). This also ensures that every pixel can be considered once.

Let us extend the definition of the four zones $Z_0,\;Z_1$, $Z_2,\; Z_3$ to the items (viewed as weighted lattice points) of the GS matrix B, i.e., $Z_0(b_{ij})$ is the submatrix of B with items $b_{i'j'}$ such that $i'\ge i$ and $j'\le j$, $Z_1(b_{ij})$ is the submatrix of B with items $b_{i'j'}$ such that $i'\ge i$ and $j'\ge j$, $Z_2(b_{ij})$ is the submatrix of B with items $b_{i'j'}$ such that $i'\le i$ and $j'\ge j$, and $Z_3(b_{ij})$ is the submatrix of B with items $b_{i'j'}$ such that $i'\le i$ and $j'\le j$. Moreover, let $Z^t=(z^t_{ij})$ denote the integer matrix such that $z^t_{ij}=h$ if and only if $b_{ij}=0$ and h is the maximum item in the submatrix $Z_t(b_{ij})$, for $t\in \{0,1,2,3\}$ ($z^t_{ij}=0$ if $b_{ij}\ne 0$). We design the following procedure reconstructing F from its associated GS matrix B.

For example, starting from the GS matrix B in input,

$$\begin{aligned} B= \begin{bmatrix} 0&1&2&2&1&0\\ 0&0&3&3&0&0\\ 1&0&0&0&0&1\\ 0&0&0&0&3&2\\ 2&3&0&4&0&1\\ 1&0&0&0&0&0\\ 0&0&0&4&0&0\\ 0&0&0&3&0&0\\ 0&0&1&2&1&0 \end{bmatrix}. \end{aligned}$$

The procedure computes $Z_0(B),Z_1(B),Z_2(B)$ and $Z_3(B)$ (lines 2–7):

$$\begin{aligned} {\scriptscriptstyle Z^0= \begin{bmatrix} 2&0&0&0&0&4\\ 2&3&0&0&4&4\\ 0&3&3&4&4&0\\ 2&3&3&4&0&0\\ 0&0&3&0&4&0\\ 0&1&1&4&4&4\\ 0&0&1&0&4&0\\ 0&0&1&0&3&0\\ 0&0&0&0&0&0 \end{bmatrix}, \ Z^1= \begin{bmatrix} 4&0&0&0&0&2\\ 4&4&0&0&4&4\\ 0&4&4&4&3&0\\ 4&4&4&4&0&0\\ 0&0&4&0&1&0\\ 0&4&4&4&1&0\\ 4&4&4&0&1&0\\ 3&3&3&0&1&0\\ 2&2&0&0&0&0 \end{bmatrix}\ .} \\ {\scriptscriptstyle Z^2= \begin{bmatrix} 2&0&0&0&0&0\\ 3&3&0&0&1&0\\ 0&3&3&3&1&0\\ 3&3&3&3&0&0\\ 0&0&4&0&3&0\\ 0&4&4&4&3&2\\ 4&4&4&0&3&2\\ 4&4&4&0&3&2\\ 4&4&0&0&0&2 \end{bmatrix}, \ Z^3= \begin{bmatrix} 0&0&0&0&0&2\\ 0&1&0&0&3&3\\ 0&1&3&3&3&0\\ 1&1&3&3&0&0\\ 0&0&3&0&4&0\\ 0&3&3&4&4&4\\ 2&3&3&0&4&4\\ 2&3&3&0&4&4\\ 2&3&0&0&0&4 \end{bmatrix}\ .} \end{aligned}$$

If we consider, for instance, $b_{22}=0$, since $\min \{z_{22}^0=3,z_{22}^1=4,z_{22}^2=3,z_{22}^3=3\}=3$, then $f_{22}$ is in $\mathcal {Q}({F}_3)\setminus \mathcal {Q}({F}_4)$ and so $f_{22}=1$ (lines 8–13). Moreover, since item $b_{02}=2$, then pixel associates with $f_{02}$ is a g.s.p. in ${F}_2$ and so $f_{02}=0$ (lines 14–18). Note the procedure reconstructs $\mathcal {F}$ of Fig. 3.

Theorem 3

The procedure computes the binary image from its GS matrix in linear time.

Proof

Let $B=(b_{ij})$ be the $m\times n$GS matrix in input, and $\mathcal {F}=(f_{ij})$ be the binary matrix representation of the image associated with B. Initially, $f_{ij}=0$, for all i, j. The correctness of the algorithm comes from Remark 2, since $f_{ij}=h \pmod {2}$, where h is the minimum (line 9) among the maximum items in the GS matrix in each zone in M, $i=1,\ldots ,k$ (lines 3–6).

We show that the complexity of the algorithm is O(mn). The computation of the maximum in any zone for each item $b_{ij}=0$ (statements 2-7) can be done in linear time in the size of the image. Indeed, consider zone $Z_0$: for $b_{ij}$, by definition, $Z_0(b_{ij})=Z_0(b_{i-1 j})\cup Z_0(b_{i j-1})$. Therefore, the maximum in $Z_0(b_{ij})$ can be computed by previous computations for $Z_0(b_{i-1 j})$ and $Z_0(b_{i j-1})$ and stored in a matrix $Z^0$. (Analogous relations hold for $Z_1,\,Z_2,\,Z_3$.) For any item $b_{ij}$, the minimum among four corresponding values stored in the four matrices $Z^0,Z^1,Z^2,Z^3$ (statement 9), and the determination of the parity of the minimum cost O(1) (statements 10, 14). Hence, the complexity of the algorithm is linear in the size of matrix B. $\square$

5 Computation of GS Matrix

The GS matrix can be computed in linear time in the size of the binary image by the algorithm designed in [5] for the determination of generalized salient pixels.

Here we briefly describe the algorithm. The basic idea is that salient points and generalized salient points of a binary image $\mathcal {F}$ can be determined by implicit computation of $Q(\mathcal {F})$. Indeed, the authors in [5] proved that $Q(\mathcal {F})$ is the complement of the union of maximal background quadrants. At each step i, the algorithm finds the foreground (generalized) salient pixels of $\mathcal {F}_i$ by computing the maximal background quadrants of $\mathcal {F}_i$. Pixels in the background quadrants are discarded, and the remaining complemented image is considered in the next step being the Q-convex hull of $\mathcal {F}_i$ (recall that $\mathcal {F}_{i+1}=Q({F}_{i})\setminus {F}_i$).

During the computation of generalized salient points, the algorithm constructs the GS matrix $B=(b_{ij})$. Indeed, $b_{ij}=h$, if $f_{ij}$ is a g.s.p. in $\mathcal {F}_h$ and the algorithm finds it at step h (and $b_{ij}=0$ for any item which is not a g.s.p.). Therefore, B is the matrix of the steps at which every g.s.p. is found.

In Fig. 5, we illustrate the GS matrix associated with the second image in Fig. 7, and in Fig. 6, the GS matrix associated with the fourth image in Fig. 7. In particular, g.s.p. is represented in grayscale colors depending on the iteration at which the g.s.p. has been found (darker color indicates later iteration).

Fig. 5

The GS matrix associated with the second image in Fig. 7 and represented as a grayscale image

Fig. 6

The GS matrix associated with the fourth image in Fig. 7 and represented as a grayscale image

6 The New Descriptor

Since the GS matrix characterizes the binary image it is associated with, we exploit information to define a shape descriptor. In [1], we defined a shape measure in terms of proportion between salient points and generalized salient points, and in [2] we generalized the measure by providing a parametrized version. In this paper, the idea is to investigate a vector descriptor based on the GS matrix. Denoting the cardinality of an arbitrary set $\mathcal {P}$ of points by $|{\mathcal {P}}|$, here we extend the measure as follows:

Fig. 7

Shapes ranked into ascending order by $||\varPsi (.)||_2$. Values are rounded to four digits

Definition 7

Let $\mathcal {F}$ and B be any binary image and its GS matrix, respectively. The Q-convexity descriptor $\varPsi (\mathcal {F})$ of $\mathcal {F}$ is defined by

$$\begin{aligned} \varPsi (\mathcal {F})= \left( \frac{|{B}|_{b_{ij}=1}}{|{B}|_{b_{ij}>0}},\frac{|{B}|_{b_{ij}=2}}{|{B}|_{b_{ij}>0}},\ldots , \frac{|{B}|_{b_{ij}=k}}{|{B}|_{b_{ij}>0}}\right) . \end{aligned}$$

By definition of GS matrix, we also have that

$$\begin{aligned} \varPsi (\mathcal {F})= \left( \frac{|{\mathcal {S}(\mathcal {F}_1)}|}{|{\mathcal {S}_g(\mathcal {F})}|}, \frac{|{\mathcal {S}(\mathcal {F}_2)}|}{|{\mathcal {S}_g(\mathcal {F})}|},\ldots , \frac{|{\mathcal {S}(\mathcal {F}_k)}|}{|{\mathcal {S}_g(\mathcal {F})}|}\right) . \end{aligned}$$

Each component of the vector is in (0, 1], and if the binary image is Q-convex, then its vector descriptor reduces to one non-null component which equals 1. For comparing images of the same size, we fix the dimension of the vector descriptor. Indeed, due to Remark 1, the upper bound for the maximal index k in the sequence is obtained by the chessboard image. Finally, the descriptor needs only to compute the GS matrix, which—as mentioned in Sect. 5—can be done in linear time in the number of pixels of the image.

7 Experiments

To examine the properties of our shape descriptor, we conducted experiments of different kinds for the study of ranking a variety of shapes and investigating scale invariance.

At first, we consider a variety of shapes in [21] of size $512\times 512$, and we rank them simply according to the Euclidean norm of the vector descriptor. Note that we prescribe $k=512$ components for the vector descriptor due to Remark 1. In Fig. 7, the ranking in ascending order and the values are illustrated. Note that the measure correctly assigns value 1 to the “L” and rectangular shapes. Moreover, the ranking is very similar to the one obtained in [2] (with parameters equal to 1) and we achieve lower values for shapes with many narrow and/or deep intrusions (see the first four elements of the first row of Fig. 7) than for shapes with wider intrusions (see the second to fifth element of the second row of Fig. 7). At first glance, the value assigned to the rectangle with lozenges could seem too low (in comparison with the rectangle), but the lozenges give rise to many g.s.p.. We stress that this configuration cannot be considered at all as a noisy version of the rectangle, and indeed, we will show in the experiments that the measure is robust to (a reasonable amount of) noise (see, later, 2nd paragraph of Sect. 7.3).

Secondly, we test scale tolerance. This time we omit the fully Q-convex images as their convexities are naturally scale invariant. Taking the vectorized version of the remaining 12 images, we digitize them on different scales ($32\times 32$, $64\times 64$, $128\times 128$, $256\times 256$). Then, for each image, we compute the normalized difference with the original sized image as

$$\begin{aligned} {\frac{||\varPsi (\mathcal {F}^o)-\varPsi (\mathcal {F}^r)||_2}{||\varPsi (\mathcal {F}^o)||_2}}\ , \end{aligned}$$

(1)

where $\mathcal {F}^o$ and $\mathcal {F}^r$ are the original and rescaled image, respectively. Table 1 shows the average and variance of the values found for the 12 images for each size. Of course, in lower resolutions, the small details of the shapes disappear; therefore, the differences are higher. Nevertheless, for higher resolutions the values are small, from which we can deduce that scaling has no significant impact, from the practical point of view.

Table 1 Average normalized difference and variance of the convexity vector of the original and rescaled images

7.1 Datasets for Classification

In the experiments, we use the following datasets for the classification issues. The datasets from DRIVE [26] and CHASEDB1 [12] databases contain images of fundus photographs of the retina. In particular, our datasets are composed by the segmented images. First dataset is constituted by 20 binary images where the optic disk is shifted from the center, whereas second dataset is constituted by 20 binary images where the optic disk is centered. Figure 8 shows a sample from both dataset.

Fig. 8

Examples of two retinal images. Left: from the DRIVE dataset. Right: from the CHASEDB1 dataset

For the second classification test, we use the dataset of images in [21] constituted by 43 types of algae, called desmids (taxon Micrasterias) with 4–7 drawings for each of eight classes. Some shapes, one for each class, are illustrated in Fig. 9. Finally, in the third classification experiment we use the well-known KIMIA-99 dataset consisting of 9 classes of images, with 11 representatives from each class (see Fig. 10) [24].

Fig. 9

Some of the 43 desmids, one for each class

Fig. 10

The KIMIA-99 dataset. The class Fish, Rabbit, Aircraft, Greeble, Tool, Hand, Doll, Four-legged animal, Sea-animal, from top to bottom, respectively

7.2 Classifiers

In all three experiments, we attempt to classify the images of the datasets into the correct classes by using three different types of classifiers: k-nearest neighbor with Euclidean distance (kNN), decision tree (DT), and support vector machine with linear kernel (SVM). We decided to use the kNN classifier for comparison with descriptors in [8] and [21]. Moreover, we exploit the power of SVM to weighting the components of the vector shape descriptor to reach additional flexibility. Finally, decision trees allow us to better understand the results of kNN and SVM and can help in selecting the proper vector components for classification. For the implementation of the classifiers, we choose the WEKA Toolbox [11]. We use leave-one-out cross-validation to evaluate the accuracy of the methods.

Table 2 Classification accuracy (in percentage) of CHASEDB1 and DRIVE images in the noiseless case, for different resolutions

7.3 Experimental Protocol and Results

At first, we tested scale invariance in binary classification. Results are reported in Table 2. We scaled the images of the CHASEDB1 and DRIVE datasets to different sizes from $128\times 128$ up to $1024\times 1024$ and set the maximal number of vector components, accordingly. We performed the classification using just the first $10-20-30-40-50$ and also with all the components of the vector descriptor (“all” in the table). We observe this problem can be solved with high accuracy even when only a small number (say, 20) of components are taken into account. We also notice that taking more than 50 components no better results are found. We can deduce that 5NN seems the best choice for this problem; nevertheless, SVM performs similarly well. Knowing that kNN is a lazy learner, when classification speed is an issue SVM may be prioritized. However, one must take into account that this latter classifier tends to overfit, especially when many vector components are used for bigger sized images (see the drop in the accuracy for all the components in case of $512\times 512$ and $1024\times 1024$). DT is not considered as a useful alternative here; it is more sensitive to scaling. Indeed, SVM and 5NN are robust to scaling, as their classification is based on the Euclidean distance, by which scale tolerance was measured in (1), whereas DT uses the information content of the attributes (vector components).

Following the strategy of [8], we gradually added different types of random noise to the images of size $1024\times 1024$ (which can be interpreted as increasingly strong segmentation errors) and repeated the experiments with 5NN. Gaussian and speckle noise were added with 10 increasing variances $\sigma ^2\in [0,2]$, while salt and pepper noise was added with 10 increasing amounts in [0, 0.1]. Some example images are shown in Fig. 11, while the results are presented in Table 3. We can observe that in case of speckle noise we need at least 40 components of the feature vector to ensure similar classification accuracy as in the noiseless case. Salt and pepper noise can also be beaten when the complete feature vector is used. The same holds for a moderate amount of Gaussian noise. However, further increasing the amount of Gaussian noise results a drop in classification accuracy. In [8], the authors reported to reach an average accuracy of $97.75\%$, $99.25\%$, and $98.75\%$ for speckle, Gaussian, and salt and pepper noise, respectively, on the same dataset with 5NN. Their results are surprisingly good (the images are completely distorted by the high levels of noise, in case of Gaussian) and slightly better than ours. Notice that they employ the so-called interlacement descriptor using $d=180$ discrete directions along with measuring directional convexity, which has a computational complexity of $\mathcal {O}(dN^2)$, where N is the number of image pixels. By comparison, our vector descriptor uses the information of Q-convexity w.r.t. two directions, and it is computationally more efficient since it can be computed in $\mathcal {O}(N)$ time. Finally, the authors of [8] also report better results in comparison with force histograms [16] and generic Fourier descriptors [28]. In turn, our results are slightly better than force histograms and competitive with generic Fourier descriptors for speckle and salt and pepper noise, whereas they are worse for Gaussian.

Fig. 11

Retina images with moderate (top row) and high (bottom row) amount of noise. Speckle, salt and pepper, and Gaussian noise, from left to right, respectively

Table 3 5NN classification accuracy (in percentage) of CHASEDB1 and DRIVE images for different types and levels of noise (first column)

For the more complex multiclass separation problem (desmids), the results are given in Table 4. Since the image classes in this case are rather small (they may contain less than 5 elements), 5NN could be misleading here. For this reason and also for a further comparison with the results in [21], we present here the accuracy of 1NN classification instead of the 5NN. Notice that 1NN reaches the best accuracy when only the first 20 components are used, whereas the other two (more sophisticated) methods use 40 components for the best classifications. Using less components, clearly, results in underfitting. On the other hand, taking more components can lead to overfitting. Both phenomena of machine learning are clearly observable from the entries of the table and should be avoided. Overall, we can say that nearest neighbor is, again, a good choice for this problem. However, to avoid overfitting it is desirable to provide a strategy to select the proper vector components for classification. Here, DT can come to our help. Knowing that it positions the most informative attributes (in our case, vector components) close to the root of the model tree built, we can select the vector components that are preserved in the pruned tree to expect a good classification rate. Indeed, taking all the components, building a DT, and pruning it, yields a tree that only contains the $\{1,8,28,113\}$ set of components. Feeding these four vector components to 1NN, we achieve the accuracy of $58.13\%$ (best value in the table). Of course, since the algorithm building the tree is greedy, the solution could be not optimal, and indeed, we also found that for the first 16 components we may reach the accuracy of $62.79\%$. We also point out that in comparison with the performance of the convexity measure $C_{0,0}$ in [21] (with an accuracy of $55.81\%$ for 1NN), our result is slightly better.

Table 4 Classification accuracy (in percentage) of the desmid images

In the last classification experiment, we deal with the KIMIA-99 dataset for testing the behavior of our vector descriptor on a dataset not suitable for the features extracted by shape descriptors based on convexity. Indeed, as far as we know, we do not find in the literature comparable descriptors tested on this dataset. This is particularly difficult because images present two types of occlusions. The results are reported in Table 5 with the best accuracy of $70.70\%$ reached using 10 components. Here, the pruned decision tree contains the component set $\{1,2,4,8,9\}$ by which we can reach $71.71\%$ and $66.66\%$ accuracy, with the 1NN and 5NN classifier, respectively. Taking a look at the confusion matrix in case of 1NN for this special attribute set, we notice that classes Sea-animal, Doll, Aircraft, and Tool are easy (10–11 hits per classes), while Greeble is the hardest to classify (only 3 of the 11 instances get the correct class label, and in six cases, the wrong class label is Rabbit). In the remaining classes, 6–7 instances are correctly classified.

Table 5 Classification accuracy (in percentage) of the KIMIA-99 images

8 Conclusion

In this paper, we presented a more flexible vector descriptor, extension of [1] and [2], derived directly from the GS matrix. First we proved how to upper bound the dimension of the vector descriptor by introducing the concept of maximal sequences. This theoretical bound is then used in the experiments for dealing with the classification of images. Then, we tested for scale invariance, ranking, and binary and multiclass classification problems using kNN, decision tree, and support vector machine methods. Results of these experiments confirmed the good behavior of our proposed descriptor in accuracy, and its performance is comparable and, in some cases, superior to some recently published similar methods. Moreover, our vector descriptor can be computed in linear time in the size n of the image, and this makes our method even more competitive with respect to the compared descriptors which depend quadratically on n [8], or require at least O(nlog(n)) time (see [21] and the implementations for force histograms and generic Fourier descriptors). Therefore, our approach is computationally efficient in contrast to other time-consuming shape-recognition methods.