Joint Contours, Corner and T-Junction Detection: An Approach Inspired by the Mammal Visual System

Abstract

We introduce a new algorithm that allows the detection of line segments, contours, corners and T-junctions. The proposed model is inspired by the mammal visual system. The detection of corners and T-junctions plays a role as part of the process in contour detection. This method unifies tasks that have been traditionally worked apart. An a-contrario validation is applied to select the most meaningful contours without the need of fixing any critical parameter.

1 Introduction

Contour, corner and T-junction detection in digital images is a fundamental problem in computer vision. These features provide important and necessary information for more complex tasks as object detection and segmentation [27], object recognition [31] and depth ordering [12, 36], among others.

The detection of contours and corners has been an intensive research area since the pioneering works by Canny [9] and Harris [23]. The Canny contour detector models edges as sharp discontinuities in the brightness, adding nonmaximum suppression and hysteresis thresholding steps. The use of anisotropic kernels [46, 50] or local thresholding [43] has been proposed to overcome some of Canny’s algorithm limitations. Structure tensor-based methods have been used for contour identification. For instance, Köthe [30] jointly computes edges and corners from the defined tensor. More complete image representations, as the response to a family of filters at different scales and orientations, have been considered to improve the detection [18, 40]. More recent approaches take into account color and texture information and make use of learning techniques [2, 34].

A particular instance of contour detection is line segment detection. Most algorithms use the edge information to identify line segments. Pixels are either grouped in the image plane if they lie in the same direction [8, 22] or accumulated in a parametric space using methods based on the Hough transform [1, 19]. A combination of these techniques has been proposed by Nieto et al. [37].

The corner detector introduced by Harris [23] is widely used as a feature detector. This method analyzes the matrix of local derivatives around each point. It is neither able to identify the geometry around corner points, nor to differentiate a corner of a T-junction. For that reason, it is commonly used as a general feature detector and has been thoroughly studied and improved [16, 29]. More recent methods identify corners as points, lying on a detected boundary or edge, which have a high curvature [33, 35]. In [35], an additional analysis on different scales is performed to achieve an accurate localization. Other methods analyze the principal directions of directional derivatives on contours [47, 49].

The aim of this work is to jointly identify contours, line segments, corners and T-junctions. It is inspired by the first stages of the mammal visual system. Hubel and Wiesel [25, 26] studied the organization and functionality of the primary visual cortex (V1) in macaques. The authors characterized the functionality of the neurons in V1, their interaction and its relationship with their spatial organization in the visual cortex. In the particular case of the hypercolumn system of the V1, proximity in the system relates to spatial closeness in the view and similar dominant orientation. The basic operations made by the neurons in V1 are equivalent to directional derivatives of the image. The same calculations were also the main atom suggested for representing images in Field et al. [17]. They also appear naturally in image processing when computing an Independent Component Analysis (ICA) of image patches [4]. The introduction of normalization on patch space before applying ICA [32] makes high level features appear, for example corner detectors.

The second motivation for this work is using the a-contrario validation, introduced into digital imaging by Desolneux, Moisan and Morel [13]. The authors defined those geometrical configurations that cannot be observed by chance as meaningful. Desolneux et al. [14] applied this formulation for the detection of contrasted boundaries and Cao et al. [10] for detecting good continuation of contours. In both cases, the level lines of the image are employed as potential candidates to be meaningful edges or contours. The Line Segment Detection algorithm (LSD) [21] performs state-of-the-art line contour detection using the a-contrario validation. This algorithm groups close pixels sharing a similar orientation. Thus, it is valid only for detecting line segments or short edges. An extension of LSD was introduced in [39] to detect elliptic arcs by joining small segments. A-contrario validation has shown to be effective for hierarchical image segmentation, Cardelino et al. [11], and for T-junction detection, Xia et al. [48]. For junction detection, a measure is associated with each candidate depending on the number and strength of gradient branches meeting the point. A meaningful analysis on this measure permits to select the detected junctions.

We propose a new method capable of dealing efficiently with line segment and contour detection, as well as corner and T-junction identification. Traditionally, these tasks are performed independently and with a very different formulation. Since these features are complementary, we believe that a unified procedure should identify all at once. Indeed, corners and T-junctions separate continuous curves into different edges, and edges are the main feature used for identifying corners and T-junctions. In [41, 42], the authors build junction and symmetry detectors based on 2D steerable wavelets. Their algorithm is able to detect M-fold junctions in different scales and orientations. The work in [42] is the most similar to ours, in the sense that it permits to detect junctions and contours at the same time. Indeed, edges are detected as a particular case of M-fold junctions with $M=2$. The main purpose of [42] is the detection of $M>2$ folds; for $M=2$ edges are not differentiated from corners. While their algorithm detects junction points, our aim is to group pixels with a continuity in orientation, giving as output entire contours, clearly differentiated from corners.

Our approach groups spatially close pixels which share a similar orientation. These two notions are embedded in a 3D system that computes the response to an oriented filter for each particular pixel position (x, y) and orientation $\theta$. This representation depends on a prefixed scale $\sigma$. The theoretical analysis of such 3D system has been performed by Sarti et al. [44, 45] and Zucker et al. [5, 6]. However, no specific implementation for contour detection exploiting such a structure has been accomplished yet. We also investigate the geometric relationships among curves using this representation, starting with parallelism. The detection of orthogonality and amodal completion will be the object of future research.

The paper is organized as follows. In Sect. 2, the detection algorithm is introduced, and the a-contrario validation is elaborated along Sect. 3. A comparison between our method and state-of-the-art contour and segment detection is discussed in Sect. 4. Finally, Sect. 5 contains a brief summary with the main conclusions and relevance of this work.

2 Detection Algorithm

The algorithm is divided into two parts. The first part builds and processes the responses of the image to several oriented filters. The responses are organized in a 3D volume depending on the pixel coordinates and the orientation of the filter. We call this 3D volume the cube. Then, inhibition and filtering stages help to enhance the structures. The second part is a grouping process in the cube which identifies contours, corners and T-junctions. Figure 1 shows a block diagram of the algorithm.

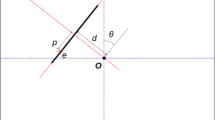
Orientation response The first stage of the algorithm is the convolution, at each scale $\sigma$, of the image with several directional filters. We compute $d_{\sigma }(x,y,\theta )$: the response of the image u at any point (x, y) to the directional derivative of a Gaussian of standard deviation $\sigma$. The direction is indicated by the angle $\theta \in [0,2\pi ]$, meaning that directions with a difference of $\pi$ are taken as different, even when their response at a particular pixel differs only in the sign. We retain only positive values,

$$\begin{aligned} d_{\sigma }(x,y,\theta ) \leftarrow \max \big (0,d_{\sigma }(x,y,\theta )\big ), \end{aligned}$$

and the $2\pi$ range is sampled with p different angles.

Fig. 1

Block diagram of the novel algorithm

In order to reduce the computational cost of the detection algorithm, only points having $d_{\sigma }(x,y,\theta )$ larger than a certain threshold $\tau$ are retained. Generally, we are able to distinguish a contour when its gradient is larger than 8, for images with range in [0, 255]. In order to be conservative, we set this threshold to a low value $\tau =2.5$. Flat points are thus easily discarded, making the algorithm faster, thanks to the reduction in the number of points for which the further processing must be applied.

The responses at each scale are processed independently. That is, interactions only occur in a 3D volume of fixed scale $\sigma$. The data organization is similar to the hypercolumn geometry of the V1 visual cortex [38]. Close points in the volume have close pixel coordinates and similar orientation. This permits to combine points with similar orientation and pixel coordinates by 3D convolution.

Fig. 2

Left: association field. Right: inhibition or lateral field. For each reference point, neighbors in its association field reinforce its response while the ones in the inhibition field cancel it. Points in the association field share a similar orientation and are spatially located according to this direction

Lateral inhibition The next step is to identify meaningful points to be candidates for edges. This is achieved by a lateral inhibition process. That is, we suppress the points that have lateral neighbors with larger responses. Lateral inhibition is a pervasive mechanism in the visual nervous system [38]. The aim of this step is to reduce lateral redundancy by selecting the set of points that best follow the ridge of the edge. Again, each scale $\sigma$ is processed separately. A point $(x,y,\theta )$ is retained only if

$$\begin{aligned} d_{\sigma }(x,y,\theta ) > e^{-\frac{(x-x')^2+(y-y')^2}{8\sigma ^2}} \cdot d_{\sigma }(x',y',\theta ') \end{aligned}$$

for $(x',y',\theta ')$ in the lateral neighborhood as shown in Fig. 2 (center). The lateral neighborhood is defined as

$$\begin{aligned} \{(x',y',\theta ') \ \mid \ | \mathbf {d} \cdot \theta | > | \mathbf {d} \cdot \theta ^\perp | \text{ and } |\theta -\theta '| < \theta _0 \}, \end{aligned}$$

where $\mathbf {d} = (x-x',y-y')$ and $\theta _0$ is fixed empirically to 15 degrees. This lateral neighborhood is the complementary of the association field well studied in visual perception. The neurones in the association field enforce the response of the current one, while neurones in the lateral field inhibit its response. A simplified scheme is provided in Fig. 2. In practice, the association and inhibition fields form a 3D structure in the cube, since they might react to different orientations.

Retained points are set to one and nonretained ones to zero. The response to the oriented filter is no longer used. This means the contrast information is not considered for detecting contours apart from the initial threshold. We will denote the output of this process by $d_{\sigma }^\mathrm {th}(x,y,\theta )$.

Filtering/density computation After the inhibition process, points in the cube mutually reinforce by averaging their responses. We want responses to interact if they are linked by the association field displayed in Fig. 2 (left). The exact solution leads to the computation of geodesics in a space with sub-Riemannian geometry [44, 45].

Two points $(x_0,y_0,\theta _0)$ and $(x_1,y_1,\theta _1)$ are linked if orientations $\theta _0$ and $\theta _1$ are similar, pixel coordinates $(x_0,y_0)$ and $(x_1,y_1)$ are close and the segment joining them has similar orientation to $\theta _0$. We write such an operation as a linear convolution in the cube. Each point of the cube is convolved with a 3D Gaussian oriented according to the current point orientation. Since this operation is separable, each 2D component $(\cdot , \cdot , \theta )$ is convolved with a directional Gaussian kernel of orientation $\theta$. The resulting response is filtered with a 1D convolution in the third dimension $\theta$.

Since $(d_{\sigma }^\mathrm {th}(x,y,\theta ))$ has only zeros and ones, the output of the current filtering stage can be interpreted as an anisotropic local density around each point. We will denote the output of this process by $d_{\sigma }^{f}(x,y,\theta )$.

High curvature point detection We define a high curvature point as a pixel that responds meaningfully to a representative set of orientations. For each pixel coordinate (x, y), we compute the indicator function,

$$\begin{aligned} {\varGamma }_{\sigma }(x,y) = \big |\{\theta \mid d_{\sigma }^{f}(x,y,\theta ) >\gamma \}\big |. \end{aligned}$$

Recall that the orientations were quantized into p different values. The compared response is obtained after the inhibition and filtering processes; after these two stages, only meaningful orientations have a nonzero value, so $\gamma$ is set to a small value, $\gamma =0.01$.

The indicator function ${\varGamma }_{\sigma }(\cdot ,\cdot )$ is convolved with a 2D Gaussian of standard deviation $\sigma$. The high curvature points are defined as local maxima of this convolved image and larger than a certain threshold parameter $\rho$. This parameter is proportional to the sampling rate of the $[0, 2\pi ]$ orientation range, actually $\rho =0.3 p$. That is, a point has to respond to at least the 30% of directions to be considered as possible corner. This percentage is fixed experimentally.

Fig. 3

Comparison of detection for different length parameters $\lambda$ and different scales $\sigma$

The detection of corners and T-junctions is by itself one of the objectives of our algorithm. In addition, it will serve as part of the contour integration algorithm. Contours will not be allowed to pass through a corner/T-junction, thus stopping the grouping of points in the cube. The analysis on the number of edges arriving at a particular high curvature point permits to differentiate between corners and junctions.

Second lateral inhibition The same inhibition process of the first stage is now computed on the local densities $d_{\sigma }^{f}$ to obtain $d_{\sigma }^{p}$. With this second inhibition, the prominent points are detected, highlighting the skeleton of each contour.

Grouping A $5\times 5\times 5$ connectivity grouping is applied to the output of the previous inhibition stage. The detected corners/T-junctions serve to stop the grouping process, thus separating a contour in two edges if it goes through a high curvature point.

Finally, only long enough contours are retained as meaningful. A threshold $\lambda$ on the length must be applied. Figure 3 illustrates a detection example for different threshold values and scales. As one can see, this length-based threshold turns out to be the main parameter of the algorithm. The next section describes an a-contrario formulation for automatically selecting such threshold considering the length and density of points of each curve.

Corner update and T-junctions We retain only the points identified with high curvature when at least two detected curves of different orientation join in them. At this point, we can differentiate between corners and T-junctions based on the number of different edges arriving at a high curvature point. More than two arriving contours with different orientations indicate a junction.

Once we updated the high curvature points, we re-apply the grouping algorithm with the updated high curvature points mask.

3 A-Contrario Validation

This section describes the statistical setting used to automatically select the relevant curves, that is, getting rid of the threshold on the curve length.

We follow the a-contrario framework introduced in [13] and developed further in [15]. This method is based on the nonaccidentalness principle, according to which, an observed geometric structure is perceptually meaningful only when its expectation is low under random conditions. This principle guarantees the absence of false positives in the following weak sense: Only one false detection would be made on average in a white noise image of the same size. For the control of the expected number of false detections, a geometrical structure is validated only when a test rejects the noise hypothesis. Because a big amount of structures are tested, we need to consider the problem of multiple testing, well known in statistics [24]. The a-contrario setting corresponds to the formulation of Gordon et al. [20].

We use the length of the curve and the computed density at each point to compute the meaningfulness of a curve. The density $d_\sigma ^f(x,y,\theta )$ implicitly encodes the local curvature. The result is compatible with the fact that one generally perceives line segments as more important than curved contours.

The closest approach to ours is the one introduced by Desolneux et al. [14]. The authors proposed an a-contrario method for contour extraction based on the contrast of the level lines. The meaningfulness of a level line depends on the magnitude of the gradient of their points, $|\nabla u(x,y)|$. The gradient of pixels at a distance larger than two was assumed to be independent. Then, the probability that all points in a line of length l have a contrast larger than $\mu$ is $H(\mu )^l$. Here $H(\mu )$ is the probability for a point on any level line to have a contrast larger than $\mu$. An important issue arising in a-contrario validations is the choice of the null hypothesis distribution $H(\mu )$. This distribution can be given beforehand or estimated from the image itself. The authors of [14] decided to learn this probability from the image itself computing the histogram of $|\nabla u(x,y)|$.

Our meaningfulness approach will be based on the grouped curves and will depend on the evaluated density instead of the contrast. In contrast to Desolneux et al. [14], an a priori probability distribution will be used for the null hypothesis.

3.1 A Priori Model

It seems appropriate to define the a priori noise model $H(\mu )$ computing the density $d_{\sigma }^{f}(x,y,\theta )$ on a noise sample image. This a priori probability must be estimated for each scale at which contours will be evaluated. In order to do so, we first generate a noise image of large size (we used an image of width and height equal to 2048). We then apply the inhibition/filtering strategy introduced in Sect. 2. In order to make the process independent of the noise standard deviation, we set $\tau =0$. This means we compute the density for all points in the cube.

Finally, we compute the histogram of the density of nonzero points. The values are normalized by the total number of points with nonzero density. The accumulated histogram gives a valid estimate of $H_\sigma (\mu )$.

3.2 Detection

Our model does not require the whole curve to have large density. Such assumption would suppress many meaningful curves, because the density decreases near its end points. Instead, we count the number of points for which the contrast is higher than a given threshold $\mu$.

Given a curve L of length l and a density threshold $\mu$, the number k will be evaluated as

$$\begin{aligned} k = \#\{ (x,y,\theta ) \in L : d_{\sigma }^{f}(x,y,\theta ) \ge \mu \}. \end{aligned}$$

The probability P of observing one such point under the noise hypothesis is $P=H_\sigma (\mu )$. Given the independence assumption, the probability of observing at least k of such points is given by the tail of a binomial distribution of parameter P:

$$\begin{aligned} B(l,k,P) = \sum _{i=k}^{l} {{l}\atopwithdelims (){i}} P^i (1-P)^{l-i}. \end{aligned}$$

We define then the quantity

$$\begin{aligned} \mathrm {NFA}(L) = N_T \cdot B\Big (l,k,H_\sigma (\mu )\Big ), \end{aligned}$$

where $N_T$ is the number of tests to be performed and corresponds to the Bonferroni correction term in multiple testing [20]. The $\mathrm {NFA}(L)$ is an upper bound to the expected number of detections under the noise model. The larger the NFA value, the more common it is to observe by chance a curve similar to L in the noise model, making it less interesting. Inversely, a curve with small NFA value does not appear frequently in noise images and would require a rare accident to be observed. When the $\mathrm {NFA}(L)<\varepsilon$, the curve is validated. It can be shown [15, 20] that this formulation guarantees on average no more than $\varepsilon$ detections on noise. As it is common in the a-contrario literature, we will set $\varepsilon =1$, since obtaining one or less false detections per image is a good compromise.

In this formulation, one needs to choose the value of $\mu$. Instead of selecting a particular value, we propose to test several values $\mu _i$. A curve will be declared valid if its NFA is less than $\varepsilon$ for any of the $\mu _i$. Formally, this is equivalent to increasing the number of tests, so $N_T$ must be multiplied by a factor M corresponding to the number of tested $\mu$. We do not choose arbitrary values for $\mu$; we rather fix probability values $P_i$ and derive the corresponding $\mu _i$ from $P_i=H_\sigma (\mu _i)$. We selected the values $\{0.1,0.2,0.3,0.4,0.5\}$ for $P_i$.

To complete the formulation, we need to specify the number of tests $N_T$. This value depends on the scale parameter $\sigma$. The proposed inhibition stage limits the distance between detected curves, thus reducing the area of the image that can be occupied by a contour. This suggests that the number of tests can be written as $\frac{N^2}{\kappa \sigma ^2}$, N being the number of pixels in the image. We chose $\kappa =4$, as the exact theoretical number of curves is not computable. This number of tests is multiplied by M, the number of tested probabilities yielding the family of tests

$$\begin{aligned} M \cdot N_T \cdot B\Big (l,k,H_\sigma (\mu _i)\Big ) < \epsilon . \end{aligned}$$

for $i=1,\ldots ,M$. To conclude the process, the corners are updated and the grouping applied again, replacing the length criterion by the above-mentioned a-contrario validation.

Computational complexity We cannot estimate the complexity of the algorithm. It depends on the image being processed since only contrasted points are taken into account during the detection. The most time-consuming parts are the lateral inhibition and the directional filtering, having order $O((4\sigma +1)^2 p)$ for each point in the cube, where p is the number of different orientations. If all points in the cube were processed, the total complexity would be of the order $O((4\sigma +1)^2 p^2 N$), N being the number of pixels in the image. The algorithm is, however, highly parallelizable, which is indeed the strategy applied in the visual cortex. The execution time for a $600 \times 500$ natural image, as those in Fig. 9, with $\sigma =2$ is in average 20 s in a 3.3 GHZ 6-Core Intel Xeon.

Fig. 4

Comparison of detection with fixed length and a-contrario method with scale parameter $\sigma =2.0$. From left to right: original image, length threshold $\lambda = 0, 10, 50$ and a-contrario validation. This figure illustrates the need to get rid of the length parameter. For too small values of this threshold, spurious curves are detected while for larger values short, but well-contrasted segments are not detected. The use of the a-contrario validation allows to remove spurious short curves while maintaining meaningful short segments

Fig. 5

Comparison of detection with fixed length and a-contrario method with scale parameter $\sigma =2.0$. From top to bottom and left to right: original image, length threshold $\lambda = 0, 10, 50$ and a-contrario validation. Spurious contours created by noise are detected if a length criterion is used. Long curves might be created in nearly constant areas by chance. Fixing a threshold on contrast or length does not contribute to get rid of these false detections. The nonregularity of these curves, interpreted as a fast change in curvature, actually allows to discard these detections. This is naturally performed by our directional density computation, since slowly varying curvatures associate with larger density values. In such a scenario, for the same length, segments or slightly varying curves will be detected, while false alarms in noise will be discarded

Fig. 6

Joint visualization of different scale detection. Top: original image and unified visualization of detection for scales $\sigma =1, 1.5, 2, 2.5$ and 3. Bottom: detection for each of the scales. The unified visualization of all scales is achieved by drawing all detected curves at the same scale with the same color and width proportional to the value of $\sigma$ (Color figure online)

Fig. 7

Comparison with three structure detectors on figures from Gestalt experiments. Desolneux et al. [14] aim at detecting well-contrasted contours by selecting parts of image level lines, but one obtains some spurious curves and most contours are represented by multiple level line segments. Köthe [30] detects edges and junctions from a structure tensor, with no distinction made between corners and junctions. The detected edges are irregular and not well defined. LSD [22] is a line segment detector, and therefore, curved contours are rendered as a chain of line segments. The proposed method extracts all the relevant information, keeping curves as such, while also detecting corners (red dots) and junctions (blue dots) (Color figure online)

4 Experimentation and Discussions

We illustrate the performance of the proposed algorithm with different tests. We evaluate and compare our approach with state-of-the-art methods for contour and T-junction detection. We also study the property of parallelism among the detected contours.

4.1 Contour Detection

The performance of the a-contrario validation is illustrated in Figs. 4 and 5. We compare this criterion with the length-based thresholding of the grouped curves. For low values of the length threshold, spurious curves are detected, whereas for larger values, short, but well-contrasted line segments are missed. The length-based criterion may also validate long grouped curves created by chance in noisy parts of the image. The nonregularity of these curves, interpreted as a fast change in curvature, allows to discard these false detections. This feature is implicitly considered by the a-contrario validation. Indeed, slowly varying curvatures are associated with large density values. In such a scenario, segments or slightly varying curves of the same length will be detected by the a-contrario criterion, while false alarms in noise will be discarded.

Figure 6 displays the application of the current algorithm at several scales $\sigma =1, 1.5, 2, 2.5, 3$. The detected curves are nearly identical for all the scales tested. A unified visualization is proposed by drawing all detected curves at the same scale with the same color and width proportional to the value of $\sigma$. Small scales are displayed in the foreground, while larger scales are drawn thicker in the back.

Figure 7 compares our detector with Köthe [30], Desolneux et al. [14] and the LSD [22] on figures from Gestalt experiments. The approach by Desolneux et al. [14] identifies well-contrasted pieces of image level lines as contours. An image contour may create many close parallel level lines. In such case, this algorithm represents the contour by multiple lines. Since regularity is not taken into account, false detections are distinguished in noisy regions. Köthe [30] detects edges and junctions with a structure tensor. The detected edges are irregular and not well defined. LSD [22] is a line segment detector. The method correctly identifies straight contours, but curves are rendered as a chain of small line segments. The proposed method ($\sigma =2$) extracts all the relevant information, keeping curves as such. It also detects corners (red dots) and junctions (blue dots). We display these features since they take an active part in our curve detection algorithm.

Figure 8 compares our method with the state of the art [2, 14, 22, 30] on several natural images. Arbeláez et al. [2] bring together all contour identification cues in a single strategy. This algorithm, as well as Köthe’s algorithm [30], needs to fix a threshold on the estimated contour density, thus identifying candidate points rather than complete structures. The rest of the algorithms provide a contour description. Due to these different contour representations, the algorithms are not directly comparable. Nevertheless, all results show similar detections at roughly the same regions of the images.

Fig. 8

A comparison of the proposed method ($\sigma =2$) with the detection of contrasted level lines [14], Köthe [30], Arbeláez et al. [2] and LSD [22]

Fig. 9

Visual results on the Bowyer et al.’s dataset [7]

Fig. 10

Quantitative comparison with Canny [9]. Aggregated ROC curve using the 50 images of the Objects dataset from [7]. A ROC curve standing to the lower left of another curve is preferred

Finally, we have evaluated our method on the dataset with annotated ground truth edges introduced by Bowyer et al. in [7]. Figure 9 compares the proposed model with Canny [9] and Köthe [30] edge detectors. Our method shows to be less sensitive to texture oscillations and has very few false detections compared to the other two methods. The contour image provided by our approach is more similar to the ground truth.

Fig. 11

Corner and junction detection. Junctions are plotted in blue while corners are plotted in red. From left to right, top to bottom: original image, Harris detector [23], CSS [35], Köthe [30], Püspöki et al.’s [42], Xia et al.’s [48] and the proposed method (Color figure online)

A quantitative comparison with Canny [9] is illustrated in Fig. 10. The empirical ROC curve proposed in [7] is plotted using the 50 images of the Objects dataset. The curve represents, at different parameter settings, the points (% Unmatched GT edges, % FP edges). These are,

$$\begin{aligned} \% \text {Unmatched GT edges} = 1-\frac{C_\mathrm {TP}}{C_\mathrm {P}},\, \% \text {FP edges} = \frac{C_\mathrm {FP}}{C_\mathrm {N}}, \end{aligned}$$

where $C_\mathrm {TP}$ stands for true positives, $C_\mathrm {P}$ for positives, $C_\mathrm {FP}$ for false positives and $C_\mathrm {N}$ for negatives. The different parameters are selected to vary the sensitivity of the result. In Canny, these parameters are the scale and lower and upper thresholds. In our method, the sensitivity can be adjusted by tuning the minimum contrast $\tau$, the allowed number of false alarms $\epsilon$ and the scale $\sigma$. Under this format, the ideal point is (0, 0) and a ROC curve standing to the lower left of another curve is preferred. As shown in Fig. 10, our method yields better results than Canny in terms of ROC curve.

4.2 Corner and T-Junction Identification

In Fig. 11, we compare our corner and junction detection algorithm with the classical Harris detector [23], the wavelet-based detection by Püspöki et al. [42], the a-contrario algorithm by Xia et al. [48], the curvature scale space (CSS) method by Mokhtarian et al. [35] and the structure tensor approach by Köthe [30]. The Harris, CSS and Köthe methods do not differentiate corners from junctions. For that reason, we plot all their detections in red. The detector presented in Püspöki et al. [42] aims at the identification of M-fold junctions: $M = 2$ corresponds to an edge, $M=3$ depicts a T-junction, $M=4$ goes for an X-junction, etc. It therefore does not distinguish between edges and corners as both are twofold symmetries. Then, for this method we only plot results with $M>2$ and all its detections are in blue. Our method, as well as Xia et al.’s, additionally differentiates T-junctions from X-junctions. For simplicity, we plot all junctions detected by these methods in blue. Harris and CSS algorithms identify many false corners, whereas Köthe’s method misses many feature points in the second example of the figure. Püspöki et al.’s approach produces many false detections, essentially at edge points, with a low amount of true positives in both images. Xia et al.’s algorithm produces some false positives at high curvature points. The proposed method does not have any false positive and identifies nearly all corners and junctions.

Fig. 12

Set of images considered for quantitative evaluation on corner detection

We test the robustness of our method to noise and geometrical deformations using the average repeatability and localization error measures proposed in [3]. We initially consider seven images (see Fig. 12) from which we create two different datasets. The first set is obtained by rotating each image at angles from $-\,90^{\circ }$ to $90^{\circ }$ with steps of $10^{\circ }$. This procedure provides 18 test images for each initial one. For the second dataset, we add zero-mean white Gaussian noise with variances ranging from 0.005 to 0.05 with steps of 0.005 (for images in range [0, 1]), creating ten additional noisy images.

Let $N_o$ be the total number of detected corners in the initial image, $N_t$ the number of detected corners in a test image and $N_r$ the number of repeated corners (detected in both initial and test images). Then, the average repeatability is defined as

$$\begin{aligned} R_\mathrm {avg} = \frac{N_r}{2}\left( \frac{1}{N_o}+\frac{1}{N_t}\right) . \end{aligned}$$

An average repeatability equal to one means that all corners detected in the original image have also been detected in the test image. Besides, the localization error stands for the distance between repeated corners:

$$\begin{aligned} L_e =\sqrt{\frac{1}{N_r}\sum _{i=1}^{N_r}(x_{oi}-x_{ti})^2+(y_{oi}-y_{ti})^2}, \end{aligned}$$

$(x_{oi}, y_{oi})$ and $(x_{ti},y_{ti})$ being the pixel positions of the repeated corner i in the initial and test images, respectively. Notice that the initial corners are rotated using the same parameters to compute these measures. A maximum pixel distance of 3 is set as valid to consider a corner repetition. Figure 13 reports the performance of the proposed method in comparison with Harris [23], Köthe [30], CSS [35] and Xia et al. [48] detectors. Figures 14 and 15 detail the repeatability and localization error measures for each value of the tested rotation and noise parameters. Our method performs the best in terms of repeatability while being competitive in localization error under both noise and rotation.

Fig. 13

Quantitative evaluation of the proposed corner detector compared to Harris [23], Köthe [30], CSS [35] and Xia et al. [48]. Average repeatability (left) and localization error (right) under white Gaussian noise and rotations

Fig. 14

Comparison between the proposed method and Harris [23], Köthe [30], CSS [35] and Xia et al. [48], for corner detection evaluation. Left: average repeatability. Right: localization error under rotation with different angles

Fig. 15

Comparison between the proposed method and Harris [23], Köthe [30], CSS [35] and Xia et al. [48], for corner detection evaluation. Left: average repeatability. Right: localization error under zero-mean white Gaussian noise with different variances

Fig. 16

Example for identification of parallel curves. Curves represented with the same color are detected as parallel by our algorithm. We used $\eta =5$ for all the experiments (Color figure online)

4.3 Identification of Parallel Curves

We study the notion of parallelism among the set of detected contours C, $|C|=n$. Notice that any curve $\mathbf {c}\in C$ belongs to the three-dimensional cube, that is, each point $\mathbf {x} \in \mathbf {c}$ actually writes as $\mathbf x =(x,y,\theta )$ .

Let us define $\hat{\delta }: C\times C\rightarrow \mathbb {R}^+$ the distance between two curves as

$$\begin{aligned} \hat{\delta }(\mathbf {c_1}, \mathbf {c_2}) = \max \big (\delta (\mathbf {c_1},\mathbf {c_2}), \delta (\mathbf {c_2}, \mathbf {c_1})\big ), \end{aligned}$$

$\mathbf {c_1}, \mathbf {c_2}\in C$ being curves of length $l_1$ and $l_2$, respectively, and

$$\begin{aligned} \delta (\mathbf {c_1}, \mathbf {c_2}) = \frac{1}{l_1} \sum _{\mathbf {x_1}\in \mathbf {c_1}}\min _{\mathbf {x_2}\in \mathbf {c_2}} \Vert \mathbf {x_1-x_2}\Vert ^2. \end{aligned}$$

with

$$\begin{aligned} ||\mathbf {x_1}- \mathbf {x_2}||^2 = ||x_1-x_2||^2+||y_1-y_2||^2 + ||\theta _1-\theta _2||^2. \end{aligned}$$

For each pair of curves $\mathbf {c_i}, \mathbf {c_j}\in C$ of lengths $l_i$ and $l_j$, respectively, with $i, j = 1, 2, \dots , n$, $i\ne j$, we compute the barycenter of the points forming the curve taking into account only spatial coordinates. That is,

$$\begin{aligned} \mathbf {b_{c_i}} = \frac{1}{l_i}\sum _{(x,y,\theta )\in \mathbf {c_i}}(x,y)\quad \text {and}\quad \mathbf {b_{c_j}} = \frac{1}{l_j}\sum _{(x,y,\theta )\in \mathbf {c_j}}(x,y). \end{aligned}$$

Now, we translate the curve $\mathbf {c_i}$ by the vector $\mathbf {v} = (\mathbf {b_{c_j}-b_{c_i}, 0)}$. We then consider the translated curve $\mathbf {Tc_i} = \mathbf {c_i+v}$. Note that if curves $\mathbf {c_i}$ and $\mathbf {c_j}$ are parallel, $\mathbf {Tc_i}$ and $\mathbf {c_j}$ will be the same curve. Therefore, we will say that curves $\mathbf {c_i}$ and $\mathbf {c_j}$ are parallel if the distance between $\mathbf {Tc_i}$ and $\mathbf {c_j}$ is lower than a certain threshold, i.e.,

$$\begin{aligned} \hat{\delta }(\mathbf {Tc_i}, \mathbf {c_j}) < \eta , \end{aligned}$$

with $\eta >0$. Curves are compared in the three-dimensional system; this means taking into account the orientation, even when only the spatial coordinates are shifted.

Figure 16 illustrates the detection of curve parallelism with several examples. We have used a value of $\eta =5$ for all the images. Parallel curves are plotted using the same color. The algorithm performs correctly for both line segments (see a–e) and circular contours (see a, d, e). Notice that line segments with the same orientation and different length are not identified as parallel, since the distance implicitly takes into account the length of the curve. Circular contours with different curvature are neither identified as parallel as illustrated in (a). The method is also capable of identifying circles of the same radius; see, for instance, (e).

5 Conclusion

We proposed a method for joint contour, corner and T-junction detection on digital images. Inspired by the mammal visual cortex, a 3D space is computed integrating the spatial and orientation information. After lateral inhibition and filtering steps, a unified grouping process in the 3D space extracts contours, corners and T-junctions. An a-contrario validation allows to get rid of the main threshold parameter, resulting in an algorithm that merely depends on the scale of detection. The experimental results show performances comparable to state-of-the-art methods, with the advantage of a richer structure by the addition of the corners and T-junctions. Parallelism among detected contours has also been studied.

Future work will concentrate on the integration of contours and corners across different scales. The role of T-junctions in the occlusion phenomenon and the amodal completion, introduced by the Gestalt school, represent challenging/interesting investigations to address [28].