Accurate Junction Detection and Characterization in Natural Images

Abstract

Accurate junction detection and characterization are of primary importance for several aspects of scene analysis, including depth recovery and motion analysis. In this work, we introduce a generic junction analysis scheme. The first asset of the proposed procedure is an automatic criterion for the detection of junctions, permitting to deal with textured parts in which no detection is expected. Second, the method yields a characterization of L-, Y- and X- junctions, including a precise computation of their type, localization and scale. Contrary to classical approaches, scale characterization does not rely on the linear scale-space. First, an a contrario approach is used to compute the meaningfulness of a junction. This approach relies on a statistical modeling of suitably normalized gray level gradients. Then, exclusion principles between junctions permit their precise characterization. We give implementation details for this procedure and evaluate its efficiency through various experiments.

1 Introduction

Junctions are of primary importance for visual perception and scene understanding. They are parts of the well known primal sketch, the schematic representation of images introduced by (Marr 1982). Recent approaches to the computation of this sketch, as proposed by (Guo et al. 2007), show the key role played by junctions. Depending on the number of edges they connect, junctions are often classified into L-, Y- (or T-) and X-junctions. In particular, the role of T-junctions as cues for the perception of occlusions has been thoroughly studied by (Kanizsa 1979). Later, it has been shown in (Rubin 2001) that junctions are essential local cues to initiate contour completion and that their specific configuration (e.g. T- or Y-junction) has to be taken into account in this process. The distinct roles of L- and T-junctions for the perception of motion, in particular through the aperture phenomenon, has been known for long (Wallach 1935). Junction types and positions are also shown to have a strong impact on the perception of brightness and transparency, as investigated in (Metelli 1974; Adelson 2000).

Junctions are therefore naturally used as important cues for various computer vision tasks. Since they reveal important occlusion relationships between objects, they are involved in figure/ground separation (Geiger et al. 1996; Ren et al. 2006; Leichter and Lindenbaum 2009; Dimiccoli and Salembier 2009). Junctions are also used for grouping edges and regions to achieve image segmentations (Fuchs and Förstner 1995; Lindeberg and Li 1997; Ishikawa and Geiger 1998). The role of junction for object recognition has been studied since the early works on automatic scene analysis, see (Guzmán 1968; Bolles and Cain 1982; Lin et al. 2007).

In the present work, we propose a principled and automatic method for the detection, localization and characterization of junctions. We define junctions as local or semi-local structures at the center of which at least two dominant and different edge directions meet. Junctions are defined locally, and not for instance as a by-product of a global image segmentation, mostly to achieve precise description of the junction. Following observations from psychophysics (McDermott 2004), we nevertheless consider large regions for the assessment of a junction. This is made possible by an automatic scale selection rule. It should be noticed that not all perceived junctions enter this framework, and that some of them are only detected while performing scene analysis (McDermott 2004). Nevertheless, as advocated above, we believe that a precise and accurate description of junction makes them valuable information in view of a more global scene analysis.

More precisely, we take interest in a junction detection method meeting several requirements. First, junctions have to be clearly related to the geometry of the image. In particular, the description of the junction branches should be accurate. This is in strong contrast with the classical corner detectors such as Harris, that are commonly used as keypoint detectors. Second, an automatic validation rule will be derived. For this, we rely on the a contrario methodology (Desolneux et al. 2000), in which structures are validated by controlling the number of false detections. A key advantage of this approach is the automatic setting of detection parameters in a way that will prevent the numerous junctions that are usually detected in textured areas. Third, the position and scale of the junctions should be detected precisely and be closely related to the image geometry. This will be achieved thanks to a competition between junctions relying on a sound quality measure, the number of false alarms associated with a junction. A shorter version of this work has appeared in (Xia et al. 2012).

1.1 Related Works

1.1.1 Corner Detectors

Automatic junction detection has been a very active research field over the last four decades. Some of the earliest methods were introduced by (Hannah 1974) and (Moravec 1977), both considering interest points as points which are not similar to their neighbors, the similarity being assessed either by correlation or by a quadratic distance between patches. It has then been proposed, in (Förstner 1986) and (Harris and Stephens 1988), to compute derivative of similarity measures, and therefore to rely on the so-called Harris matrix to detect corners. Such approaches are widely used in practice and a large number of detectors rely on similar ideas, the detection of corners boiling down to the analysis of the eigenvalues of this matrix, see e.g. (Shi and Tomasi 1994; Förstner 1994; Kovesi 2003; Kenney et al. 2005). In particular, in order to achieve contrast invariance, (Kovesi 2003) uses phase congruency to derive cornerness measurement. In this work, the image gradient is normalized over small wedges. Alternative measurements of self-similarity have also been proposed, such as the univalue segment assimilating nucleus (USAN) (Smith and Brady 1995) and its variants (Trajkovic and Hedley 1998; Rosten et al. 2010). Observe that such methods relying on a measure of cornerness actually do not distinguish between different types of junctions. They are therefore usually used to compute generic interest points and their use as local cues for occlusion analysis or figure/ground separation is less clear. Also observe that in order to identify the characteristic scale of a corner, corner detectors usually make use of the linear scale-space (Deriche and Giraudon 1993; Lindeberg 1994; Schmid et al. 2000; Lowe 2004; Mikolajczyk and Schmid 2004). One of the main shortcomings of such approaches is that they quickly lose precision both in localization and scale. A notable exception is the work of (Förstner et al. 2009) where the keypoint locations are optimized and their type are identified. For an overview of the use of linear scale-space for keypoint detection, one may consult (Dickscheid et al. 2011). An other approach is to rely on some contrast invariant multi-scale analysis. In this direction, (Alvarez and Morales 1997) analyze junctions in images using an affine morphological scale space.

1.1.2 Boundary Based Methods

A second popular and efficient way to detect corners relies on explicit boundaries in images. Corners are interpreted as points in the image where a boundary changes direction rapidly and points with high curvature are selected. Many works have concentrated on different and efficient ways to compute the curvature of curves for detecting corners, see (Rosenfeld and Johnston 1973; Teh and Chin 1989; Rattarangsi and Chin 1992; Wang and Brady 1995; Mokhtarian and Suomela 1998; Mohammad and Lu 2008). In a different way, it has been proposed in (Beymer 1991) to detect junctions by extending disconnected edges and by filling gaps at junctions. Junction detection can also rely on the grouping of edges in the neighborhood of a candidate junction (Freeman 1992; Rohr 1992; Perona 1992; Bergevin and Bubel 2004). In a related direction, it is proposed in (Rosenthaler et al. 1992) to combine the responses of several oriented filters to detect junctions. Several works have proposed to rely on the contrast invariant level lines of images to detect junctions. (Caselles et al. 1996) have proposed a method based on a level-set representation, detecting junctions as points where two level lines meet. Cao (2003) detects corners as points along level lines where a good continuation criterion is broken. Corners are detected as points where the curvature along a level line is abnormally high, in an a contrario framework. In other approaches, a global segmentation of the image is first performed, followed by a heuristic grouping of edges to form junctions (Wu et al. 2007; Maire et al. 2008). It should there be emphasized that the segmentation process in itself is a very challenging task. For instance, before detecting junctions, (Maire et al. 2008) finds contours by the global probability of boundary (gPb) detector learned from a human-annotated database. Such approaches permit to benefit from global image interpretation to find junctions. On the other hand, boundary are often imprecise in the neighborhood of a junction, so that such approaches do not enable an accurate characterization of junctions, that in turn can be used to refine edges.

1.1.3 Template-based Methods

Among existing approaches, the model-based or template-based ones are the most suitable for accurate local junction detection. Deriche and Blaszka (1993) presents computational approaches for a model-based detection of junctions. A junction model is a 2D intensity function depending on several parameters. Starting from a poorly localized initialization (e.g. from the Harris detector) parameters are then optimized in view of a precise localization. Parida et al. (1998) suggest a region-based model for simultaneously detecting, classifying and reconstructing junctions. A junction is defined as an image region containing piecewise constant wedges meeting at the central point. This work relies on a template deformation framework and uses minimum description length principle and dynamic programming to obtain the optimal parameters describing the model. This work also involves junction candidates provided by a preliminary corner detector. Ruzon and Tomasi (2001) model junctions as points in images where two or more image regions meet. Regions are described by their color distributions, which allows textured objects with the same average color to be distinguished. Following the model of Parida et al. (1998), (Cazorla and Escolano 2003; Cazorla et al. 2002) propose both a region-based and an edge-based model for junction classification by using Bayesian methods. The region-based one formalizes junction detection as a radial image segmentation problem under a regions competition framework and the edge-based one detects junctions as radial edges minimizing some Bayesian classification error. In this work, the edge-based approach is shown to yield more accurate junction detections, but at the price of a large number of false detections, especially in textured regions. More recently, the work of (Sinzinger 2008) first detects a set of junction candidates by using a preliminary detector (for instance the Harris detector) and then refines those candidates by relying on a radial edge energy.

The different approaches for junction detection, as well as their properties, are summarized in Table 1.

Table 1 Classification of junction detection methods

1.2 Contributions and Outline

As explained earlier in the introduction, the goal of this paper is to design a junction detection procedure involving an automatic decision step and permitting a geometrically accurate description of junction properties, including type, localization and scale. This is made possible thanks to the use of an a contrario methodology (Desolneux et al. 2000). The resulting detection method will be coined ACJ (for a contrario junction detection). In short, we first define (in Sect. 2) junctions as geometrical structures in discrete images and we associate to each candidate junction a quantity called strength, which is designed to be high at locations where several edges (called branches) meet in the image. This strength relies on a well chosen normalization of the gradient, which makes the whole approach robust to local contrast changes. We then rely in Sect. 3 on a statistical framework in order to decide automatically which junctions deserve to be detected or not in a given image. More precisely, meaningful junctions are detected as those which are very unlikely under some null hypothesis $\mathcal{H }_0$. This detection step is followed by several exclusion criteria, designed to rule out redundant junctions and to identify precisely the correct scales, positions and complexities (number of branches) of junctions. As a by-product of the scale estimation, the whole approach is robust to resolution changes. Finally, in Sect. 4, details about implementation and parameter settings are provided. Section 5 analyzes the proposed algorithm experimentally.

2 Contrast Invariant Junctions

The aim of this section is to define junctions in discrete images (Sect. 2.2) and to associate to each candidate junction a strength (Sect. 2.3). The strength of a junction is defined through both the gradient orientation and magnitude. Robustness to local contrast changes is achieved by normalizing the gradient magnitude, as explained in Sect. 2.1. The strength of junctions will be used in Sect. 3 to decide whether junctions are meaningful or not in a given image.

2.1 Gradient Normalization

Let us start with some definitions and vocabulary that will be used throughout the paper. A discrete image is a function $I: \varOmega \rightarrow \mathbb{R }$, where $\varOmega$ is a rectangular subset of $\mathbb{Z }\times \mathbb{Z }$. We write $\nabla I = (I_x, I_y)$ for the discrete gradient of the image $I$.¹ For a pixel $\mathbf{q }$ in $\varOmega$, we define $\phi (\mathbf{q }) = (\arctan \frac{{I_y}(\mathbf{q }) }{{I_x}(\mathbf{q }) } + \pi /2) modulo (2\pi )$, the direction perpendicular to the gradient at $\mathbf{q }$ (and set $\phi (\mathbf{q }) = \pi$ when $I_x(\mathbf{q }) = 0$). We call this angle the direction of the pixel q.

In order to be robust to local contrast changes, we locally normalize the gradient magnitude by dividing it by its average on a small neighborhood. That is, for $\mathbf{q }= (x,y)$, we define ${\widehat{\nabla I}} = ({\widehat{I_x}}, {\widehat{I_y}})$ as

$$\begin{aligned} {\widehat{I_x}}(\mathbf q ) = \frac{I_x(\mathbf{q })}{\langle \sqrt{I_x^2 + I_y^2}\rangle _{\mathcal{N }_\mathbf{q }}} \;\; \text { and }\;\; {\widehat{I_y}}(\mathbf q ) = \frac{I_y(\mathbf{q })}{\langle \sqrt{I_x^2 + I_y^2}\rangle _{\mathcal{N }_\mathbf{q }}},\nonumber \\ \end{aligned}$$

(1)

where ${\mathcal{N }_\mathbf{q }}$ is a small neighborhood around q and $\langle . \rangle _{\mathcal{N }_\mathbf{q }}$ is the linear average operator on ${\mathcal{N }_\mathbf{q }}$. The resulting gradient is robust to contrast changes that can be approximated by affine transformations on each neighborhood ${\mathcal{N }_\mathbf{q }}$. An example of the gradient and normalized gradient of an image, obtained with a square neighborhood of size $5 \times 5$ around each pixel, is shown in Fig. 1. Observe that the phase of the normalized gradient is the same as the phase of the plain gradient.

Fig. 1

Gradient $\nabla I$ and normalized gradient ${\widehat{\nabla I}}$ on an image patch

In Sect. 3, we will rely on the empirical distribution of the gradient to detect meaningful junctions. More precisely, we will consider the globally normalized gradient

$$\begin{aligned} {\widetilde{I_x}} = \frac{{\widehat{I_x}} - \mu _x}{\sigma _x}\;\;\text { and } {\widetilde{I_y}} = \frac{{\widehat{I_y}} - \mu _y}{\sigma _y}, \end{aligned}$$

(2)

where $\mu _x$ (resp. $\mu _y$) and $\sigma _x$ (resp. $\sigma _y$) are the empirical mean and standard deviation of ${\widehat{I_x}}$ (resp. ${\widehat{I_y}}$) over the whole image. In the following paragraphs, this globally normalized gradient will be used to weight the contribution of local orientations in order to define the strength of a junction. As we will see, the distribution of the norm $\Vert {\widetilde{\nabla I}}\Vert = \sqrt{{\widetilde{I_x}}^2 + {\widetilde{I_y}}^2}$ in natural images is well approximated by a standard Rayleigh distribution outside of 0.

2.2 Discrete Junction Definition

A junction is defined as a discrete image structure $\jmath : \Big \{ \mathbf{p }, r, \{\theta _m\}_{m=1}^{M}\Big \}$, characterized by its center pixel $\mathbf{p }$, its scale $r \in \mathbb{N }$ and a set of branch directions $\{\theta _1, \dots \theta _M\}$ around $\mathbf{p }$. The number $M$ of branches in the junction is called the order of the junction : when $M = 2$, 3 or 4, we speak respectively of $L, Y$ or $X$-junctions. The discrete set $\mathcal{D }(r)$ of possible directions at a given scale $r$ is defined as

$$\begin{aligned} \mathcal{D }(r) :=\left\{ \frac{2\pi k}{K(r)}\; ; \; k \in \{1,\dots K(r) \} \right\} . \end{aligned}$$

(3)

In this definition, $K(r)$ is a prescribed number of discrete directions on the circle. In the experimental part, $K(r)$ will be chosen as $K(r) = \lfloor 2\pi r \rfloor$.²

For a given scale $r$ and a given direction $\theta$ in $\mathcal{D }(r)$, we define the branch of direction $\theta$ at $\mathbf{p }$ as the disk sector

$$\begin{aligned} S_{\mathbf{p }}(r,{\theta })&{:=} \Big \{\mathbf{q } \!\in \! \varOmega ;\! \; \mathbf{q }\!\ne \! \mathbf{p }, \;\! \Vert \overrightarrow{\mathbf{pq }} \Vert \nonumber \\&\le r, d_{2\pi }(\alpha (\overrightarrow{\mathbf{pq }}), \theta ) \le \varDelta (r) \Big \}, \end{aligned}$$

(4)

where $\varDelta (r)$ is a precision parameter, $\alpha (\overrightarrow{\mathbf{pq }})$ is the angle of the vector $\overrightarrow{\mathbf{pq }}$ in $[0,2\pi ]$ and where $d_{2\pi }$ is the distance along the unit circle, defined as $d_{2\pi } (\alpha , \beta ) = \min (|\alpha - \beta |, 2\pi - |\alpha - \beta | )$. We note $J(r, \theta )$ the number of pixels in a sector of direction $\theta$ at scale $r$. This size depends on the scale $r$ but also slightly changes with the direction $\theta$ since the image is defined on a discrete grid.

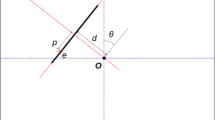
Finally, we require that two branches of a given junction do not intersect. It follows that the angle between two directions in a junction $\jmath$ must be larger than $2\varDelta (r)$. As a consequence, the number of possible directions in a junction at scale $r$ is smaller than $\frac{\pi }{\varDelta (r)}$. An example of a junction with three branches is shown on Fig. 2.

Fig. 2

A junction with three branches. Each branch is represented by a disk sector $S_{\mathbf{p }}(r,{\theta })$ with an angular aperture of $2\varDelta (r)$

2.3 Junction Strength

The strength of a junction will be defined from the strength of its branches. The strength of a branch is a measure of how well the corresponding angular sector agrees with the pixels it contains. A pixel $\mathbf{q }$ contributes all the more to the strength as its direction $\phi (\mathbf{q })$ is in agreement with the direction $\alpha (\overrightarrow{\mathbf{pq }})$ and as the normalized gradient $\Vert \widetilde{\nabla I}(\mathbf{q })\Vert$ is large. Precisely, the strength of a branch is defined as

Definition 1

(Strength of a branch) Let $\mathbf{p }$ be a pixel, $r$ a positive scale and $\theta$ a direction in $\mathcal{D }(r)$. The strength of the branch $S_{\mathbf{p }}(r,{\theta })$ is defined as the quantity

$$\begin{aligned} \omega _{\mathbf{p }}(r,\theta ) = \sum _{\mathbf{q }\in S_{\mathbf{p }}(r,{\theta })} \gamma _{\mathbf{p }}(\mathbf{q }), \end{aligned}$$

(5)

where

$$\begin{aligned} \gamma _{\mathbf{p }}(\mathbf{q })&= \Vert {\widetilde{\nabla I}}(\mathbf{q })\Vert \cdot \max \Big (|\cos (\phi (\mathbf{q }) - \alpha (\overrightarrow{\mathbf{pq }})| \nonumber \\&-|\sin (\phi (\mathbf{q }) - \alpha (\overrightarrow{\mathbf{pq }}))|, 0 \Big ). \end{aligned}$$

(6)

The max operator has been chosen so that the contribution of the pixel is equal to zero if the difference between $\alpha$ and $\phi$ is larger than $\pi /4$. Other choices could be made. The larger the strength of a branch, the more likely it is that the branch corresponds to an edge. Figure 3c shows the values of $\gamma _{\mathbf{p }}(\mathbf q )$ for the image patch shown in Fig. 3a.

Fig. 3

Computation of junction candidates at scale $r=12$, when $\mathbf{p }$ is the center of the original image (a). The blue curve in (d) shows the strength $\omega _{\mathbf{p }}(r,\theta )$ as a function of the direction $\theta$ along the circle. The directions that remain after the NMS procedure are shown in red. For $r=12, K(r)=75$, and $2\varDelta (r) = 0.289$ (see Sect. 4.1) (Color figure online)

The strength of a junction is then derived from the strength of its branches as follows:

Definition 2

(Strength of a junction) The strength of a junction $\jmath : \Big \{ \mathbf p , r, \{\theta _m\}_{m=1}^{M}\Big \}$ is defined as

$$\begin{aligned} t(\jmath ) := \min _{m = 1\dots M} \omega _{\mathbf{p }}(r,\theta _m). \end{aligned}$$

(7)

Starting from this definition, a first naive algorithm for junction detection can be developed. The idea is to detect, for a fixed scale $r$ and a given threshold $t$, all the junctions in $I$ having a strength greater than $t$. In practice, testing all possible junctions for every point $\mathbf{p }$ in $\varOmega$ is computationally heavy. Among all the potential branches at a given point $\mathbf{p }$, we restrict ourselves to the directions $\theta$ in the discrete set $\mathcal{D }(r)$ where the periodic function $\omega _{\mathbf{p }}(r,.)$ reaches a local maximum. Moreover, in order for branches not to intersect, we impose that the local maximality holds over a length $2 \varDelta (r)$, that is $\omega _{\mathbf{p }}(r,\theta )$ is greater than $\omega _{\mathbf{p }}(r,\theta ^{\prime })$ for $\theta -\varDelta (r)\le \theta ^{\prime }\le \theta +\varDelta (r)$. The set of these local maxima can be computed quickly, for instance by using a non-maximum suppression (NMS) procedure (see Kitchen and Rosenfeld 1982; Neubeck and Van Gool 2006). In practice, if two local maxima are equal and located at a distance smaller than $\varDelta (r)$, one of them is discarded.

The Case of L-junctions   In order not to detect all edge points as $L$-junctions, junctions for which $M=2$ and whose branches are opposite (that is, with two directions $\theta _1$ and $\theta _2$ such that $d_{2\pi }(\theta _1,\theta _2+\pi ) \le 2\varDelta (r)$) are discarded.

The overall detection procedure is summarized in Algorithm 1.

The first parts of the procedure are illustrated in Fig. 3. In this example, the pixel $\mathbf{p }$ is chosen as the center of Fig. 3a. Figure 3d shows in blue the values of $\omega _{\mathbf{p }}(r,\theta )$ when the angle $\theta$ spans the periodic set $\mathcal{D }(r)$ and shows in red the semi-local maxima kept after the NMS procedure (step (2) of the loop in Algorithm 1). Figure. 3e represent respectively a candidate $L$-junction, a candidate $Y$-junction and a candidate $X$-junction at $\mathbf{p }$. The main drawback of this detection algorithm is that the threshold $t$ on the junction strength remains the same whatever the junction scale and order and whatever the image size. Setting such a threshold globally is not easy and can lead to over-detect at some scales and under-detect at others. The goal of the next section is to provide detection thresholds that adapt to the junction scale and order, as well as to the image size. For this purpose, we resort to an a contrario methodology.

3 An a contrario Approach for Junction Detection

The a contrario detection theory has been primarily proposed by (Desolneux et al. 2000). This methodology is inspired by geometric grouping laws governing low-level human vision, known as Gestalt laws (Kanizsa 1979), and states that meaningful structures in images are structures which are very unlikely under some hypothesis of randomness. The method has been extensively tested and successfully applied to various problems in image processing and computer vision, see e.g. (Cao 2003; Moisan and Stival 2004; Musé et al. 2006; von Gioi et al. 2010). A complete overview of these methods can be found in (Desolneux et al. 2008). In this section, this methodology is adapted to the detection of meaningful junctions in images.

3.1 Null Hypothesis

The goal of the following sections is to set detection thresholds on junction strengths in such a way that no junction will be detected under a given null hypothesis $\mathcal{H }_0$. Let us precise what “null hypothesis” stands for here. For each pixel $\mathbf{q }$ of $\varOmega$, write $\Vert {\widetilde{\nabla \mathbf{I }}}(\mathbf{q })\Vert$ and $\phi _{\mathbf{I }}(\mathbf{q })$ the random variables corresponding to the value and orientation at this pixel. We say that these variables follow the null hypothesis $\mathcal{H }_0$ if

• 1. $\forall \mathbf{q }\in \varOmega , \Vert {\widetilde{\nabla \mathbf{I }}}(\mathbf{q })\Vert$ follows a Rayleigh distribution with parameter $1$ ;

• 2. $\forall \mathbf{q }\in \varOmega , \phi _{\mathbf{I }}(\mathbf{q })$ is uniformly distributed over $[0,2\pi ]$ ;

• 3. The family $\{\Vert {\widetilde{\nabla \mathbf{I }}}(\mathbf{q })\Vert , \phi _{\mathbf{I }}(\mathbf{q })\}_{\mathbf{q }\in \varOmega }$ is made of independent random variables.

Let us comment on the first assumption. In Ruderman and Bialek (1994), observe that if we normalize the logarithm of the intensity of an arbitrary natural image by its local mean and standard deviation in a neighborhood $\mathcal{N }_p$ around each pixel, “the histogram of pixel values has Gaussian tails, and the distribution of gradients in the‘variance-normalized’ image is almost exactly the Rayleigh distribution”. A similar behavior may be observed on our case on the modified derivatives ${\widehat{I_x}}$ and ${\widehat{I_y}}$: except on a small neighborhood around $0$, their distribution is well approximated by a Gaussian distribution. This is illustrated for a particular image $I$ in Fig. 4. In this figure, the empirical distributions of ${\widehat{I_x}}$ and ${\widehat{I_y}}$ are drawn in blue, and the best Gaussian fits are drawn in red. If we except a peak around 0, the fit is very good (the poor approximation for large values is a numerical effect: probabilities smaller than $\frac{1}{|\varOmega |}$ are not attainable empirically). It follows from this observation that ${\widetilde{I_x}}$ and ${\widetilde{I_y}}$ are well approximated by the standard normal distribution (that is, a Gaussian distribution with zero mean and unit variance) and the norm $\Vert {\widetilde{\nabla I}}\Vert$ in natural images approximately follows a central chi-distribution with 2 degrees of freedom (also known as the Rayleigh distribution of parameter 1). This is confirmed experimentally by the example shown in Fig. 4. Moreover, we performed a small scale experiment whose results are shown on Fig. 5a. In blue are displayed the empirical distributions of $\Vert {\widetilde{\nabla I}}\Vert$ for 50 different natural images, as well as the density of the Rayleigh distribution of parameter 1 (in red). Again, probabilities smaller than $\frac{1}{|\varOmega |}$ cannot be reached empirically, which explains the poor fit for large values. Eventually, observe that the Gaussian approximation used for the normalized gradients ${\widehat{I_x}}$ and ${\widehat{I_y}}$ would not be adequate for the classical gradients $I_x$ and $I_y$, whose distributions are highly non-Gaussian and accurately modeled by generalized Gaussian distributions.

Fig. 4

Approximations of the distributions of ${\widetilde{I_x}}, {\widetilde{I_y}}$ and $\Vert {\widetilde{\nabla I}}\Vert$ (given by Eqs. (1) and (2)). The blue curves represent the empirical histograms and the red curves are the corresponding Gaussian and Rayleigh distributions. Plots are displayed in a semi-log scale. The poor approximation for large gradient values is due to a numerical effect: small probabilities cannot be reached with the available number of observations (Color figure online)

Fig. 5

Distributions of $\Vert {\widetilde{\nabla I}}\Vert$ (blue curves in (a)) and $\gamma _{\mathbf{p }}(\mathbf{q })$ (blue curvesin (b)) for 50 different natural images. $Rayleigh(1)$ density (red curve in (a)) and density of the corresponding strength distribution $\mu$ (red curve in (b)) are displayed for comparison (Color figure online)

3.2 Distribution of $\mathbf{t }(\jmath )$ Under $\mathcal{H }_0$

Let ${\jmath }: \Big \{ \mathbf{p }, r, \{\theta _m\}_{m=1}^{M}\Big \}$ be a junction in $I$ and assume that the normalized gradients and directions of $I$ follow the null hypothesis $\mathcal{H }_0$. Then the strengths $\omega _{\mathbf{p }}(r,\theta _m)$ of the different branches $S_{\mathbf{p }}(r,\theta _m)$ are independent random variables (since branches do not intersect). Recall also that the strength of a junction is the minimum of the strengths of its branches. Thus, if we note $\mathbf{t }(\jmath )$ the random variable measuring the strength of $\jmath$,

$$\begin{aligned} \mathbb{P }_{\mathcal{H }_0}[\mathbf{t }(\jmath ) \ge t]&= \mathbb{P }_{\mathcal{H }_0}[\forall m, \;\mathbf \omega _{\mathbf{p }}(r,\theta _m) \ge t] \nonumber \\&= \prod _{m=1}^{M}\mathbb{P }_{\mathcal{H }_0}[\omega _{\mathbf{p }}(r,\theta _m) \ge t]. \end{aligned}$$

(8)

Now, the strength of each branch, $\omega _{\mathbf{p }}(r,\theta _m)$, is itself a sum (over the angular sector $S_{\mathbf{p }}(r,\theta _m)$) of i.i.d. random variables $\gamma _{\mathbf{p }}(\mathbf{q })$. For two given points $\mathbf{p }$ and $\mathbf{q }$ in $\varOmega$, the direction $\alpha (\overrightarrow{\mathbf{pq }})$ is a constant in $[0,2\pi ]$. This implies that under the hypothesis $\mathcal{H }_0$, the random angle $\phi _\mathbf{I }(\mathbf{q }) - \alpha (\overrightarrow{\mathbf{pq }})$ is still uniformly distributed on $[0,2\pi ]$. As a consequence, each $\gamma _{\mathbf{p }}(\mathbf{q })$ can be written as a product $X \cdot \max (|\cos \theta |- |\sin \theta |, 0)$, where $X$ and $\theta$ are independent, $X$ follows a Rayleigh distribution and $\theta$ is uniformly distributed on $[0,\pi ]$. Finally, it can be shown that under the hypothesis $\mathcal{H }_0$, each random variable $\gamma _{\mathbf{p }}(\mathbf{q })$ follows the distribution (see Appendix 2 for a proof)

$$\begin{aligned} \mu = \frac{1}{2} \left( \delta _0 + R.\mathcal{L } \right) , \end{aligned}$$

(9)

where $\delta _0$ is a Dirac measure centered at 0 and $\mathcal{L }$ is the Lebesgue measure on the real line. The function $R$ can be written

$$\begin{aligned} R(z) = \frac{2}{\sqrt{\pi }} e^{-\frac{z^2 }{4}}\cdot \mathrm {erfc} \left( \frac{z}{2}\right) 1\!\!1_{z\ge 0}, \end{aligned}$$

(10)

with erfc the complementary error function, $\mathrm {erfc} (z) = \frac{2}{\sqrt{\pi }}\int _z^{\infty } e^{-s^2}ds$.

The empirical distribution of $\gamma _{\mathbf{p }}(\mathbf{q })$ on 50 natural images is displayed in Fig. 5b, along with its theoretical distribution $\mu$, showing very good fit to the model. It remains to compute the distribution (under $\mathcal{H }_0$) of the strength of a branch. Recall that under $\mathcal{H }_0$, branches are mutually independent. Therefore, the law of the strength of a branch $\omega _{\mathbf{p }}(r,\theta _m)$ (that is, of the sum of pixel contributions given by Formula (5)) is obtained by convolving $J(r,\theta _m)$ copies of the distribution $\mu$, where $J(r,\theta _m)$ is the size of a sector of orientation $\theta _m$ at scale $r$. Finally,

Proposition 1

Let ${\jmath }: \Big \{ \mathbf{p }, r, \{\theta _m\}_{m=1}^{M}\Big \}$ be a junction and suppose that the hypothesis $\mathcal{H }_0$ is satisfied, then the probability that the random variable $\mathbf{t }(\jmath )$ is larger than a given threshold $t$ is

$$\begin{aligned} F_{\jmath }(t):=\mathbb{P }_{\mathcal{H }_0}[\mathbf{t }(\jmath ) \ge t] =\prod _{m=1}^M \mathop \int \limits _t^{+\infty } d\left( \mathop {\star }_{j=1}^{J(r,\theta _m)} \mu \right) , \end{aligned}$$

(11)

where $J(r,\theta _m)$ is the size of a sector of orientation $\theta _m$ at scale $r$ and where $\mathop {\star }$ denotes the convolution operator.

3.3 Meaningful Junctions

Thanks to the previous computations, we are now in a position to automatically fix detection thresholds on junction strengths. Indeed, thresholds are set so that the average number of false detections under the null hypothesis is controlled. This is obtained by thresholding the probability (11) and by taking into account the number of possible discrete junctions in the image.

3.3.1 Number of Tests

In this paragraph, we assume that the order $M$ is fixed, and we call $\mathcal{J }(M)$ the set of all possible (possibly overlapping) junctions of order $M$ in the discrete image $I$. The size of $\mathcal{J }(M)$ depends on several parameters: the minimum and maximum authorized scales $r_{min}$ and $r_{max}$, the size $N$ (number of pixels) of $I$ and the precision $\varDelta (r)$ of branches at each scale $r$. The practical setting of these parameters will be discussed in Sect. 4.1.

At a given location $\mathbf{p }$, once the first branch is chosen among the $K(r)$ possible directions, the second direction must be chosen in such a way that the two branches of width $2\varDelta (r)$ do not intersect (in the sense that their sectors do not overlap), which means that only $K(r)(1-2\frac{\varDelta (r)}{\pi })$ directions are authorized. Therefore, at each location $\mathbf p \in \varOmega$, and for a given scale $r$, the number of possible junctions of order $M$ is always smaller than

$$\begin{aligned} \frac{1}{M!}\prod _{m=1}^{M} K(r) \left( 1-2(m-1)\frac{\varDelta (r)}{\pi } \right) . \end{aligned}$$

It follows that the size of the set $\mathcal{J }(M)$ is upper bounded by

$$\begin{aligned} \#\mathcal{J }(M) =\frac{N}{M!} \cdot \sum _{r = r_{min}}^{r_{max}} \prod _{m=1}^{M} K(r) \left( 1-2(m-1)\frac{\varDelta (r)}{\pi } \right) .\nonumber \\ \end{aligned}$$

(12)

3.3.2 $\epsilon$-meaningful Junctions

The next definition and the following proposition explain how to fix thresholds on junctions strengths in order to control the average number of false detections.

Definition 3

($\epsilon$-meaningful junction) Let $I$ be a discrete image. For $\epsilon >0$, a junction $\jmath$ of order $M$ and at scale $r$ is said to be $\epsilon$-meaningful if its number of false alarm (NFA) under the hypothesis $\mathcal{H }_0$ satisfies

$$\begin{aligned} {\mathrm{NFA}}(\jmath ) := \#\mathcal{J }(M) \cdot F_{\jmath }(t(\jmath ) )\le \epsilon , \end{aligned}$$

(13)

The quantity $\mathrm {NFA} (\jmath )$ is a measure of the meaningfulness of the junction: the smaller it is, the more meaningful the junction $\jmath$. A junction of order $M$ and scale $r$ is detected as $\epsilon$-meaningful in $I$ if its strength $t(\jmath )$ is larger than the threshold

$$\begin{aligned} t(r,{\epsilon }) := \min \Big \{t;\;\ F_{\jmath }(t) \le \frac{{\epsilon }}{\#\mathcal{J }(M)} \Big \}. \end{aligned}$$

(14)

Notice that for a fixed ${\epsilon }$, this formula yields a different threshold on $t(\jmath )$ for each value of the scale $r$. The value ${\epsilon }$ is easy to interpret: it corresponds to an expected number of false detections under the hypothesis $\mathcal{H }_0$. Indeed,

Proposition 2

Assume that the null hypothesis $\mathcal{H }_0$ is satisfied in image I. Let $M$ be a positive integer. The expectation of the number of ${\epsilon }$-meaningful junctions of order $M$ in $I$ is smaller than ${\epsilon }$.

This proposition is an obvious consequence of the fact that if $X$ is a random variable and if we define $F(t) = \mathbb{P }[X \ge t]$, then for all $\beta$ in $[0,1], \mathbb{P }[F(X) \le \beta ] \le \beta$.

Observe that in the definition of the $\mathrm {NFA}$, the correcting factor $\#\mathcal{J }(M)$ is independent of the scale $r$. We could have used different correcting factors, depending on the junction scale $r$, in order to favor some particular scales in the detection, and still have a result similar to Proposition 2.

As can be seen from Formula (13), the quantity $\mathrm{NFA} (\jmath )$ is computed from the number of tests (12) and the probability (11). Its practical computation is detailed in Appendix 1.

3.4 Junctions or Nearby Edges?

In images, some structures may appear as junctions at large scales without being detected as such when the scale is small. For instance, when three straight edges have close endpoints and are supported by concurring lines, a $Y$-junction may be detected even if the actual edges do not physically meet, when the possible junction contains a gap at its center. Deciding between a real junction and interacting edges is actually far from trivial. Psychophysical experiments (Rubin 2001) suggest that human may find junctions although there is a small gap at the center. In practice, we got qualitatively better results when removing junctions with large gaps at their center. This restriction is imposed by computing for each ${\epsilon }$-meaningful junction $\jmath : \{ \mathbf{p },r,\{ \theta _m \}_{m \in \{1,\dots ,M \} } \}$ a minimum scale of detection $r_d[\jmath ]$ and by removing all ${\epsilon }$-meaningful junctions such that $r_d[\jmath ]$ is strictly larger than a fixed threshold $r_{gap}$. This minimum scale of detection is defined as the smallest scale $r_d$ such that there exists ${\epsilon }$-meaningful junctions of order $M$ centered at $\mathbf{p }$ for all scales between $r_d$ and $r$ (see Fig. 6),

$$\begin{aligned} r_d[\jmath ]&= \min \Big \{r^{\prime }\le r;\; \forall s\in [r^{\prime },r],\;\; \exists \jmath ^{\prime }: \{ \mathbf{p },s,\{ \theta ^{\prime }_m \}_{m=1}^M \}\; \nonumber \\&\text { s.t. } \jmath ^{\prime } \text { is }{\epsilon }\hbox {-}\text {meaningful.} \Big \}. \end{aligned}$$

(15)

In practice and for all experiments in this paper, the threshold $r_{gap}$ is chosen as $r_{gap}=12$. In order to be fully scale invariant, this threshold could be replaced by a value proportional to the junction scale $r$.

Fig. 6

Scale of a junction. Left image $I$. The point $\mathbf{p }$ is chosen as the center of $I$. Middle for each scale $r$ (in abscissa) is displayed the smallest $\mathrm {NFA} (\jmath )$ observed for a junction $\jmath$ of order 3 centered at $\mathbf{p }$. Right the smallest scale of detection $r_d = 8$ in magenta and the scale corresponding to the smallest $\mathrm{NFA}$ in red (found for $r=13$), represented on top of the strength $\gamma _{\mathbf{p }}(\mathbf{q })$ (Color figure online)

3.5 Redundant Detections and Maximality

3.5.1 Redundancy: Scale and Location

As it is common when analyzing geometrical structures in images, junctions are usually detected in a redundant way. A single structure in the image may yield many detections. First, junctions are detected over a range of scale. For a single ideal junction in the image, meaningful junctions will be detected for scales both smaller and larger than the one of the underlying structure, see Fig. 7, middle, where several junctions having the same center but different scales, and corresponding to the same ideal $Y$-junctions, are displayed. Second, several junctions with slightly different locations are detected for a single underlying structure. This is all the more strong as there is blur in the image. An example of such redundant detections is displayed in Fig. 7, right. Moreover, both type of over-detections (multiple scales and multiple locations) are usually combined in images. These redundancies are addressed in the next paragraph thanks to an exclusion principle.

Fig. 7

Redundancy of junction detection. For the sake of clarity, each junction is represented by a circle and its center, the radius of the circle is equal to the scale of the junction, and the color of the circle depends on the NFA value (red corresponds to small values, i.e. very meaningful junctions and blue corresponds to high values). Left a junction $\jmath : \{ \mathbf{p },r,\{ \theta _m \}_{m \in \{1,\dots ,3 \} } \}$, with $r=20$. Mid all junctions detected at the same point $\mathbf p$, with different scales. Right all $Y$-junctions detected in the neighborhood of $\mathbf{p }$, with the same directions and scale (Color figure online)

3.5.2 Maximal Junctions

In order to choose the right representative among all redundant detections, we use an exclusion principle, called maximality. We assign to each junction $\jmath$ a neighborhood $\mathcal{N }^{\prime }_{\jmath }$. For a given order $M$, we only keep the junctions not containing any more meaningful junction in its neighborhood. That is, we only keep junctions that are maximal in the following sense.

Definition 4

(Maximal ${\epsilon }$-meaningful junction of order $M$) A junction $\jmath :\{ \mathbf{p }, r, \{\theta _m\}_{m=1}^{M}\}$ is said to be a maximal ${\epsilon }$-meaningful junction of order $M$ if $\jmath$ is ${\epsilon }$-meaningful and if $\mathrm{NFA} (\jmath ) \le \mathrm NFA (\jmath ^{\prime })$ for any junction $\jmath ^{\prime }: \{ \mathbf p ^{\prime }, r^{\prime }, \{\theta _m^{\prime }\}_{m=1}^{M}\}$, with $\mathbf p ^{\prime }\in \mathcal{N }^{\prime }_{\jmath }$.

Observe that in this definition the use of the NFA is the keypoint. Indeed, it permits to compare structures at different scales. Using the strengths $t(\jmath )$ to carry out this comparison would require a well chosen normalization depending on the scale.

In order to select maximal meaningful junctions, the most meaningful junction is first considered. All junctions having it as a neighbor are then removed. Then we proceed to the next most meaningful junction and iterate the same procedure until all junctions have been treated.

A result of these selection rules is illustrated in Fig. 8 for $M=3$. In practice, the spatial neighborhood $\mathcal{N }^{\prime }_p$ used for maximality is chosen as a disk centered at $\mathbf{p }$, with a radius $r_d[\jmath ]$, the minimum scale of detection of $\jmath$ as defined by Formula (15).

Fig. 8

Maximal meaningful junctions of order 3. Each $Y$-junction is represented by a circle and its center. The radius of the circle indicates the junction scale $r$, and the color of the circle corresponds to the NFA of the junction (the cooler the color, the larger the NFA). Left all $\epsilon$-meaningful $Y$-junctions, with $\epsilon =1$. Mid the maximal meaningful $Y$-junctions. Right the maximal meaningful $Y$-junctions displayed over the image (Color figure online)

3.5.3 Masking and Junction Order

When a $Y$-junction is perceived in a image, the underlying $L$-junctions are usually not perceived and we decided not to detect them. This masking phenomenon (for a given junction, no junction made of a subset of its branches should be detected) is easily implemented by the following second exclusion principle: locally, only the more complex junction (the one with the largest order) is kept.

Definition 5

(Maximal ${\epsilon }$-meaningful junction) A junction $\jmath :\{ \mathbf{p }, r, \{\theta _m\}_{m=1}^{M}\}$ is said to be a maximal ${\epsilon }$-meaningful junction if $\jmath$ is a maximal ${\epsilon }$-meaningful junction of order $M$ and if there is no maximal ${\epsilon }$-meaningful junction of order $M^{\prime }$ located at $\mathbf{p }^{\prime }$ with $M^{\prime } > M$ and $p^{\prime } \in \mathcal{N }^{\prime }_{\jmath }$.

3.6 The Three Algorithmic Steps for Junction Detection

The different steps of the junction detection procedure are summarized in Algorithms 2 (the a contrario detection), 3 (maximality of order $M$) and 4 (maximality). The complete algorithm pipeline includes a speed-up step and an optional precision refinement and will be described in Sect. 4 and summarized in Algorithm 7.

Algorithm 2 does not include the two maximality steps (described in Algorithms 3 and 4). Notice however that line 11 of Algorithm 2 is a first step towards maximality, since only the best junction of a given order $M$ is tested at each point. This permits to speed-up the algorithm by excluding junctions that will obviously not be maximal. If we wish to compute all ${\epsilon }$-meaningful junctions in an image, and not only maximal junctions, lines 11 to 22 should be replaced by Algorithm 5.

4 Implementation

The goal of this section is to provide all necessary information for the practical implementation of junction detection. First, the setting of parameters is addressed in Sect. 4.1. An optional refinement step to improve the accuracy of the detected branch directions is described in Sect. 4.2. A pre-selection of the junction candidates for speeding up the method is detailed in Sect. 4.3. Eventually, the complete detection algorithm pipeline is given in Sect. 4.4. A practical issue regarding the numerical computation of the NFA is also given in Appendix 1.

4.1 Parameter Choices

Recall that in the definition of discrete junctions, $K(r)$, the number of possible directions for junction branches as defined by Formula (3), was chosen as $K(r) = \lfloor 2\pi r \rfloor$, in order to have a precision of roughly one pixel along the circle of radius $r$. The choice of the precision $\varDelta (r)$ relies on similar considerations. Visual experiments show that the perceived precision of an angle between two crossing segments in an image is better for long segments than short ones. Now, recall that $2\varDelta (r)$ is the angle of a branch (or sector) in a junction at scale $r$. We consider that the length of the arc defined by this sector should be a constant $w$ and should not depend on $r$. This length is exactly $2\varDelta (r)\times r$, which implies that $\varDelta (r)$ should be chosen as inversely proportional to $r$. In practice, we choose $w=5$. Thus

$$\begin{aligned} 2\varDelta (r) = \frac{w}{r} = \frac{5}{r}. \end{aligned}$$

(16)

Figure 9 illustrates the corresponding angular sectors for two different scales.

Fig. 9

$\varDelta (r)=\omega /r$ for two distinct $r$ values. Observe that the length of the arc defined by a sector, $w$, is a constant and does not depend on $r$

It follows that for a given order $M$, the number of tests $\#\mathcal{J }(M)$ can be computed as

$$\begin{aligned} \#\mathcal{J }(M) = \frac{N}{M!} \sum _{r = r_{min}}^{r_{max}} \prod _{m=1}^{M} \lfloor 2\pi r \rfloor \left( 1-\frac{5(m-1)}{r\pi } \right) , \end{aligned}$$

(17)

where $N$ is the total number of pixels in the image. In the experimental section, the maximum order of junctions will be $M = 4$ and the smallest possible radius is $r_{min} = 1$ for all experiments. The maximal scale $r_{max}$ is chosen as 5% of the diagonal of the natural image. For synthetic images, $r_{max}$ can be set with a prior. The threshold on the minimum scale of detection is set to $r_{gap}=12$ for all experiments in this paper.

4.2 Optional Direction Refinement

Since directions in a junction are bisectors of angular sectors (see Eq. (4) for the definition of $S_{\mathbf{p }}(r,\theta )$) and since the set of possible directions is discrete, it may happen that the directions of some branches in a detected junction remain slightly imprecise. In the following, we describe a simple refinement in the computation of junction directions.

For a branch of direction $\theta$ centered at $\mathbf{p }$, a refined direction ${\widehat{\theta }}$ is computed as follows

$$\begin{aligned} {\widehat{\theta }}&= \arctan \frac{\mathcal{O }_y}{\mathcal{O }_x},\end{aligned}$$

(18)

$$\begin{aligned} \hbox {with }\quad \mathcal{O }_x&= \sum _\mathbf{q \in S_{\mathbf{p }}(r,\theta )} \gamma _{\mathbf{p }}(\mathbf{q }) \cos \psi _\mathbf{q }; \nonumber \\ \mathcal{O }_y&= \sum _\mathbf{q \in S_{\mathbf{p }}(r,\theta )} \gamma _{\mathbf{p }}(\mathbf{q }) \sin \psi _\mathbf{q }; \nonumber \\ \hbox {and}\quad \psi _\mathbf{q }&= \left\{ \begin{array}{ll} \phi _{\mathbf{q }}&{} \text { if } d_{2\pi }(\phi _{\mathbf{q }}, {\theta }) < \frac{\pi }{2} \\ \phi _{\mathbf{q }} + \pi &{} \text { otherwise. } \end{array} \right. \end{aligned}$$

(19)

Notice that after this refinement, two sectors of a given junction may overlap. If this happens, the detected junction is removed. The refinement process is described in Algorithm 6.

Let us stress that an extra refinement on the spatial position of the junction could be added to the algorithm. However we decided not to make any specific assumptions about the image structure. Therefore, our method does not yield sub-pixel positions, as may be achieved by e.g. the detector from (Deschenes et al. 2004) or the SFOP detector from (Förstner et al. 2009).

4.3 Speed Up

In order to speed-up the algorithm, and following (Parida et al. 1998; Cazorla et al. 2002; Cazorla and Escolano 2003; Sinzinger 2008), we propose to apply a pre-processing step to select potential junction candidates.

We take advantage of a fast segment detector, the Line Segment Detector (LSD) as introduced in (von Gioi et al. 2010),³ whose complexity is linear in the size of the image. In order to make sure that we won’t miss some junction candidates, the detection threshold $\lambda$ of the LSD is set to a large value. The value $\lambda = 10^4$ has been used for all experiments in this paper. Once all possible line segments have been found, potential junction locations are restricted to a small neighborhood around each endpoint of those line segments. Figure 10 displays all line segments detected with $\lambda = 10^4$ for a given image and shows the corresponding junction candidates in red.

Fig. 10

Junction candidates using LSD. Left the input image; mid all line segments detected with $\lambda = 10^4$; right all junction candidates

Table 2 shows the number of detections and the running time of the complete junction detection procedure, with and without use of the LSD preprocessing. The comparisons are implemented on three types of images: images containing both geometry and texture, images containing mostly textures and photographs of abstract paintings (see Fig. 11). Using candidates from LSD clearly reduces the computing time, while the quantity of detections is not affected. Notice that this reduction strongly depends on image structures. The simpler the structures contained within the images, the larger the achieved reduction.

Fig. 11

Test images for the speed up evaluation. Top house, Lena and window; mid autumn, park and branches; bottom: images of geometric paintings: Geometric by John Cooper, Composition by Charmion von Wiegand, and Suprematism by Kazimir Malevich

Table 2 Number of detections and running time when using or not the LSD pre-selection

4.4 Algorithm Pipeline

The pipeline of the whole a contrario junction detection algorithm is summarized in Algorithm 7. Remark that the parameters to be set in this algorithm are: the detection threshold $\epsilon$, the maximum order of junctions $M^{\prime }$ and the radiuses $r_{min}, r_{max}, r_{gap}$ (see Sect. 4.1).

In the rest of the paper, we refer to this algorithm by the acronym ACJ (for A Contrario Junction detection).

5 Experimental Analysis

This section gathers experiments illustrating the performances of the a contrario junction detection (ACJ). When possible, performances will be compared with the classical Harris detector (Harris and Stephens 1988) and the recent “Pj on gPb” method (Maire et al. 2008) and “SFOP” method (Förstner et al. 2009). For the Harris detector, the “cornerness” is defined as $det(H)-k\cdot Tr(H)^2$, where $H$ is the Harris matrix and the default value $k=0.06$ is chosen. For Pj on gPb and SFOP, the codes kindly provided by the authors are used.

Section 5.1 illustrates the stability of the detection for different images and the control of the number of false detections in a random noise image. We then investigate the invariance properties of the method: scale and contrast changes are respectively studied in Sects. 5.2 and 5.3. In particular, we show the ability of the method to accurately detect both the scale and the position of a junction. Evaluation on a benchmark is given and discussed in Sect. 5.4 and some more results are displayed in Sect. 5.5.

5.1 Stability and Control of the Number of False Detections

One great quality of a contrario detection methods relies in the fact that the threshold ${\epsilon }$ has an intuitive meaning: it is an upper bound of the average number of false detections in an image following $\mathcal{H }_0$. In this section, we first check that the average number of false detections in Gaussian noise images is less than ${\epsilon }$ (Proposition 2). We then illustrate how the threshold $\epsilon$ controls the number of detections in natural images.

5.1.1 False Alarms Under Hypothesis $\mathcal{H }_0$

In order to test the a contrario model, we first consider 1000 large Gaussian noise images $J$ (pixel values are i.i.d. random variables following a standard normal distribution). Each of these images has a size $700 \times 700$. The gradient of these images is then normalized locally (on $5 \times 5$ windows) and globally, as described in Sect. 2.1. In such images, the norm of the gradient at each pixel follows approximately a Rayleigh distribution and the orientation of the gradient is uniformly distributed. However, the values of the gradient norms and directions at neighboring pixels are not independent. We thus downsample each $\nabla J$ by a factor of 7 to obtain a new gradient image $\nabla I$. This ensures that the values of $\Vert \nabla I\Vert$ are independent and follow approximately a Rayleigh distribution. The gradient orientations are also independent and follow a uniform distribution on $[0,2\pi [$.

On each of these gradient images, the validation experiment consists of the following procedure: for different values of the detection threshold $\epsilon$ and for all images, all $\epsilon$-meaningful L-, Y- and X-junctions are detected. This is done thanks to a slight modification of Algorithm 2 : in the algorithm, all possible junctions of order $M$ are tested, and not only the best one at each point, since we wish to count all $\epsilon$-meaningful junctions and not only maximal ones. Table 3 illustrates the results of this experiment, averaged over the 1,000 images, with $\epsilon$ changing from $10^{-3}$ to $10^3$. Observe that the average number of detections is always smaller than $\epsilon$.

Table 3 Average numbers of ${\epsilon }$-meaningful junctions when $\mathcal{H }_0$ is satisfied

Observe that the previous experiment is actually independent of the noise level, since we globally normalize gradients in the algorithm. Invariance to the noise level is actually stronger. Indeed, the local normalization of gradients makes the detection invariant to local affine contrast transforms, thus to local variations in noise level, as may for instance be observed with Poisson photon noise. A similar property may be obtained by locally estimating the noise variance, as in (Förstner 1994).

5.1.2 Stability and Choice of ${\epsilon }$

The control of the number of false alarms makes the setting of ${\epsilon }$ quite easy in practice: by default, and unless otherwise indicated, ${\epsilon }$ is set to 1 in all experiments.

The real strength of the ACJ approach comes from the fact that the value ${\epsilon }=1$ yields very satisfying detections in natural images, whatever their content, size or resolution. In contrast, other approaches such as Harris or “Pj on gPb” tend to strongly over-detect in textured areas when using a fixed parameter, see Fig. 12. This stability property is all the more interesting as it remains valid through scales. For a given choice of ${\epsilon }$, Formula (14) yields different thresholds $t(r,{\epsilon })$ that adapt to the scales of the junctions. As a consequence, by choosing ${\epsilon }=1$, results are simultaneously satisfying at all scales. This would not be possible with a fixed threshold on junction strengths.

Fig. 12

Junctions obtained by ACJ (top row), Harris (mid row) and “Pj on gPb” (bottom row). Parameters are fixed for the three images, yielding the same number of detections on the house image (this correspond to $\epsilon =1$). Observe that only ACJ prevent from over-detection in textured areas. The color of the junction depends on the $\mathrm{NFA}$ value (red corresponds to small values, i.e. very meaningful junctions and blue corresponds to high values) (Color figure online)

5.2 Scale Invariance

This section focus on the behavior of our approach with respect to scale changes. Recall that the scale of a junction is defined as the scale at which the junction is most meaningful and therefore strongly differs from classical approaches relying on the linear scale space. In Sect. 5.2.1, we show that such scales change linearly with the resolution of images, a clearly desirable property. In Sect. 5.2.2, we discuss the interpretation of these scales in images.

5.2.1 Scale and Resolution

In order to investigate the coherence of detections through scale changes,we apply the proposed junction detection algorithm to a sequence of images with different resolutions. An original image $I$ is resized with eight different zoom factors $s_0 > \dots > s_7$, using a bilinear interpolation. The set of factors is chosen as $\{1, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3 \}$. Algorithm 7 is then applied to each image $s_i I$ of the sequence and yields a junction list $\mathcal{J }_{s_i}$. Then, each junction $\jmath _0$ of $\mathcal{J }_{s_0}$ is tracked through resolutions. For this purpose, we define an angular distance between two junctions:

$$\begin{aligned} \mathcal{S }(\jmath , \jmath _0) = \max _{ \theta \in \{\theta _m\}_{m=1}^{M}} \min _{\theta ^{\prime } \in \{\theta _m^0\}_{m=1}^{M_0}} d_{2\pi }( \theta , \theta ^{\prime }). \end{aligned}$$

(20)

A junction $\jmath _0$ in $\mathcal{J }_{s_0}$ is then matched with $j_i$ in $\mathcal{J }_{s_i}$ if they have the same order $M_0$, if their centers are close enough, in the sense that ${\Vert \mathbf{p } - s_i \cdot \mathbf{p }_0 \Vert }_2 < 3$, and if their angular distance $\mathcal{S }(\jmath _0, \jmath )$ is smaller than $\frac{\pi }{20}$. If several junctions in $\mathcal{J }_{s_i}$ satisfy these properties, $\jmath _0$ is matched with the one minimizing the angular distance $\mathcal{S }(\jmath _0, \jmath )$. If there is no junction in $\mathcal{J }_{s_i}$ satisfying these properties, no junction in $\mathcal{J }_{s_i}$ is matched with $\jmath _0$. For each junction $\jmath _0$ in the original image, we call trajectory the list of its corresponding junctions through the different resolutions.

Several such trajectories are shown on Fig. 13b. In this experiment, we only consider junctions potentially having complete trajectories in the scale space. Therefore, the maximal scale considered in the coarsest image is $r_{max}\times 0.3 = 30 \times 0.3 = 9$. The red curves show the scales of junctions along all the trajectories as functions of $s_i/0.3$. The baselines $\{y= r \cdot s_i\}$, where $r$ changes from 1 to 90, are displayed in blue. These correspond to an ideal behavior with respect to resolution changes. Notice that the red curves remain close to the baselines: this implies that the scales of maximal meaningful junctions are quite robust to resolution changes. Figure 14a gives some concrete examples of junctions detected by the ACJ algorithm along their trajectories. Once more, their scales increase linearly with resolution. To the best of our knowledge, the only approaches which permit to obtain a similar coherence between scale detection and resolution are those which rely on linear scale-spaces (Lindeberg 1998; Luo et al. 2007). However, it should be underlined that the use of linear scale-spaces inevitably leads to poor location precisions at large scales. Figure 14b illustrates the aforementioned dilemma (see Sect. 3.4) to detect or not a junction in the presence of nearby edges. In these examples, junctions are not detected at large scale because of the constraint $r_{gap}$ (see Sect. 3.5). This behavior seems consistent with human perception: when several edges meet around a large gap, we probably disregard it as a junction.

Fig. 13

Illustration of the scale invariance along the scale space. The first row shows the tested images. The second row shows the scales of junctions detected by ACJ along all the trajectories (curves in red) as a function of the zoom factor $s_i$ (the abscissa is $s_i/0.3$). The baselines $\{y= r \cdot s_i\}$, where $r$ changes from 1 to 90, are displayed in blue. The bottom row presents the repeatability rate of the junctions as a function of the zoom factor

Fig. 14

Examples of detected junctions along several junction trajectories: each row shows a list of junctions detected at the same relative locations in images, from the coarsest to the finest resolution. (a) In these examples, junctions can be followed along complete trajectories, and their scales remain roughly proportional to the image resolution. (b) These two examples illustrate the difficulty of junction detection in the presence of nearby edges. Observe that as shown in (b), a T-junction might be split into two L-junctions with the increasing of scale

In a second experiment, shown on Fig. 13c, we compute the repeatability rate of detections with respect to image resolution. More precisely, if we note $\mathcal{J }_{s_0}(s_0I \rightarrow s_i I)$ the list of junctions that are matched for all intermediate resolutions between ${s_0}I$ and ${s_i}I$, the repeatability rate is defined as

$$\begin{aligned} R(s_i) = \frac{\# \mathcal{J }_{s_0}(s_0I \rightarrow s_i I)}{\#\mathcal{J }_{s_0}}. \end{aligned}$$

(21)

Observe that, for the three images, the repeatability rate always remains above 60 %.

5.2.2 How to Interpret the Detected Scales ?

Most of the junction detection approaches in the literature do not provide characteristic scales for their junctions. One notable exception is the Harris-Laplace interest point detector, which makes use of a linear scale space in order to detect keypoints at different scales. Detected points are those which maximize the Laplacian of Gaussian (LoG) in the scale-space and the Harris corner measure in a local space neighborhood. Some results of this detector on a synthetic and a real image are given in Fig. 15b, e. Observe that the scales of junctions do not have a clear interpretation in these images. Another recent approach addressing the scales of junctions is the SFOP detector (Förstner et al. 2009). This method, which draws on a junction model, extends the detector of (Förstner 1994) in a scale-space framework. Results of this detector are shown on Fig. 15c, f. Although the junctions obtained are less redundant and far easier to interpret than with Harris-Laplace, the detected scales are still difficult to link with the underlying geometry of images. In contrast, the scales detected by ACJ (see Fig. 15a, d) arguably correspond to the optimal size at which one can observe the junction in the image. For instance, the scale of the L-junctions located at the corner of a rectangle is generally chosen as the length of the smaller side of the rectangle, see Fig. 15a. More generally, we observed that the scale of a junction usually corresponds to the length of its shortest branch. The fact that the use of the $NFA$ as a tool to select the most prominent scale yields such simple geometric behavior is a strong asset of the proposed approach. The same coherence between the characteristic scales of junctions and the sizes of local structures can be observed in the examples of Fig. 14.

Fig. 15

Scale selection. (a) shows the characteristic scale of L-, Y- and X-junctions given by the proposed approach, and (b), c show the characteristic scale of junctions given by Harris-Laplace and SFOP (Förstner et al. 2009) on a synthetic image, respectively. (d), (f) show the same comparison on the house image. The location of each junctions is indicated by a red cross and circles have a radius equal to the corresponding scale. Refer to the text for more explanations (Color figure online)

5.3 Contrast Invariance

The goal of this section is to evaluate the robustness to contrast changes of different junction detection approaches. To this aim, we create a sequence of images by applying different gamma corrections to an original image $I$, with $\gamma$ in $\big \{\frac{1}{4}, \frac{1}{3}, \frac{2}{5}, \frac{1}{2}, \frac{2}{3}, 1, 1.5, 2, 2.5, 3, 4\big \}$. For each image in the sequence, we detect junctions with

• our ACJ approach, with ${\epsilon }= 1$,

• Harris corner detector, with a threshold 0.06 on local maxima,

• Maire’s approach using “Pj on gPb” (Maire et al. 2008),

• the SFOP detector from (Förstner et al. 2009)

• a totally contrast invariant version of ACJ (denoted TACJ), obtained by removing the normalized gradient amplitudes in the definitions (5),(6) of the branch strength.⁴

For both “Pj on gPb” and the SFOP detector, we use the default values of the codes provided by the authors.⁵ In order to evaluate the different results, we compute the repeatability rate of each method on the image sequence. More specifically, if $\mathcal{J }_0$ is the list of junctions in the original image ($\gamma = 1$), and $\mathcal{J }_i$ the list of junctions in the $i$-th image, we note $\mathcal{J }_0 \cap \mathcal{J }_i$ the set of junctions in $\mathcal{J }_i$ that can be matched with junctions in $\mathcal{J }_0$, where the matching criterion is the one defined in Sect. 5.2.1. Following the same protocol as in (Schmid et al. 2000), the repeatability rate of the $i$-th image is then calculated as

$$\begin{aligned} Repeat(i) = \frac{ \#\{\mathcal{J }_0 \cap \mathcal{J }_i \}}{\#\mathcal{J }_0}. \end{aligned}$$

(22)

The curves of repeatability rates for the different methods are shown on Fig. 16. Results are averaged on the 100 first images from the natural image database provided by (Rabin et al. 2009).⁶ We can see that the Harris detector has the worst performance with respect to contrast changes, which could be expected since it is the most contrast dependent. Maire’s approach (Maire et al. 2008) gives better results, possibly because it relies on an edge detector that is tuned to match boundaries annotated by humans, which may somehow eliminate contrast variations. The three other approaches perform better, SFOP and TACJ providing slightly better results than ACJ. This could advocate for the choice of TACJ in practice. The good performances of the SFOP detector are inherited from a local estimation of the noise variance, used to set the detection parameter. The good performances of the ACJ and TACJ detectors are obtained by design and inherited from invariance property of the gradient orientation. In practice, the totally contrast invariant approach appears to be less robust than ACJ to small image modifications, such as those created by JPEG compression. A more in depth study of the specific impact of compression procedures on contrast invariant detection would be of interest. The choice of ACJ results in a compromise between contrast invariance requirements and robustness.

Fig. 16

Repeatability rate of different approaches regarding contrast changes. The curves are averaged over 100 image sequences. Each sequence is obtained by applying different gamma corrections (as specified in the text) to a test image. Each position on the $x$-axis corresponds to a given $gamma$ correction

5.4 Junction Benchmark

A practical way to evaluate the consistency of our approach with human perception would be to rely on a human annotated junction database. To the best of our knowledge, such a database does not exist. Nevertheless, the well known Berkeley segmentation dataset⁷ has been used by the authors of (Maire et al. 2008) in order to evaluate different junction detectors. In their paper, Maire et al. use the human annotated boundaries to create a ground truth of junctions in the following way: L-junctions are locations of high curvature along these boundaries and $Y$-junction are locations where more than three regions intersect.

As mentioned before, these authors also propose a procedure called Pj to detect junctions from any given set of boundaries. This procedure is applied to the results of different edge detectors, including their detectors Pb and gPb. The quality of the resulting junctions is assessed by comparing them to the previously created ground truth. We applied the same protocol to the ACJ method proposed in this paper. In order to overcome the strong compression artifacts of the Berkeley database, to which we are sensitive because of strong contrast robustness, we apply a small amount of blur and noise to images before proceeding. Figure 17 presents the results for several junction detection algorithms on the benchmark. The ACJ approach yields a performance of $F= 0.38$,⁸ which is better than the baseline Harris detector ($F=0.28$), the SFOP detector ($F=0.29$) and Pj on Canny ($F=0.35$), but remains below the performance of Pj on Pb ($F=0.38$) and Pj on gPb ($F=0.41$). The human agreement on the database yields $F=0.47$. The performance of our approach in comparison to Pj on gPb has to be tempered by two facts. First the junctions of the ground truth stem from a set of human annotated boundary, and the junctions detected by Pj stem from a computer segmentation. Therefore, both are boundary-based. It is likely that any detector using a more local junction definition (including ACJ or even Harris) will be penalized in the benchmark. As explained in the introduction and shown by psychophysical studies Rubin (2001), both local and global cues are at play for the perception of junctions. Second, and most important, the parameters of Pb and gPb are optimized in order to match human detected edges on the same database, which introduces a bias in favor of these methods.

Fig. 17

The precision-recall curves of different methods on the BSDS-based junction benchmark

5.5 More Results

This last section aims at illustrating the proposed approach with several more visual experiments. Figure 18 presents all the junction detected on a synthetic image. We can observe that the junctions are found with high accuracy and are mostly correctly classified. Figures 19 and 20 present the results on two natural images. Observe that junctions are accurately characterized through their type, localization and scale. Again, we emphasize that the proposed ACJ algorithm yields very few detections in texture areas, see Fig. 20.

Fig. 18

Some results of the proposed ACJ approach, with ${\epsilon }=1$. From left to right L-, Y- and X- junctions. On this simple synthetic image (from E. H. Adelson), junctions are well detected and classified. The color of the junction depends on the $\mathrm{NFA}$ value (red corresponds to small values, i.e. very meaningful junctions and blue corresponds to high values) (Color figure online)

Fig. 19

Specific junction detections on a natural image. The color of the junction depends on the $\mathrm{NFA}$ value (red corresponds to small values, i.e. very meaningful junctions and blue corresponds to high values) (Color figure online)

Fig. 20

Specific junction detections on a natural image. The color of the junction depends on the NFA value (red corresponds to small values, i.e. very meaningful junctions and blue corresponds to high values) (Color figure online)

6 Conclusion and Perspectives

In this work, we have introduced a generic and principled approach for the detection and characterization of junctions in digital images. The proposed procedure is able to inhibit junction detection in textured areas, in contrast with classical approaches. Junctions are accurately characterized through their type, localization and scale. In particular, the method does not rely on the linear scale-space for scale computation, permitting geometric precision.

This work opens several perspectives. First, the accuracy of junction characterization is of importance for depth recovery or motion interpretation. The characterization of junction’s type, the difference between T- and Y- junctions or their precise localization claim to be tested in the framework of such applications. Second, and as advocated in the introduction, several psychophysical studies show that the perception of junctions relies on both local and global cues. Therefore the proposed, local, procedure for junction detection could benefit from more global image analysis schemes. The modeling of interactions between junction detection and segmentation procedures is far from trivial, but similar principled approaches could be applied to junction definitions building from color and textured-based region analysis. In the opposite direction, segmentation methods can benefit from meaningful junction detections. Preliminary tests show that the boundary saliency, as for instance defined in (Golubchyck and Lindenbaum 2006), can benefit from a meaningful detection of junctions, in particular by solving ambiguities in boundary connections near these junctions. The characterization of junctions also shows potentials in the automatic interpretation of high-resolution remote sensing images, for instance, in the analysis of built-up areas (Liu et al. 2013).

Appendices

Appendix 1: Computing NFA in Practice

The NFA of a junction $\jmath :\Big \{ \mathbf{p }, r, \{\theta _m\}_{m=1}^{M}\Big \}$ has been defined as $\mathrm{NFA} (\jmath ) := \#\mathcal{J }(M) \cdot F_{\jmath }(t(\jmath ) )$, where

$$\begin{aligned} F_{\jmath }(t)=\prod _{m=1}^M \int \limits _t^{+\infty } d\left( \mathop {\star }_{j=1}^{J(r,\theta _m)} \mu \right) , \end{aligned}$$

with

$$\begin{aligned} \mu = \frac{1}{2} \delta _0 + \frac{1}{2}R.\mathcal{L }, \end{aligned}$$

where $\mathcal{L }$ is the Lebesgue measure and where $R$ is the function

$$\begin{aligned} R(z) = \frac{2}{\sqrt{\pi }} e^{-\frac{z^2 }{4}}\cdot \mathrm{erfc} \left( \frac{z}{2}\right) 1\!\!1_{z\ge 0}. \end{aligned}$$

In practice, the numerical values taken by $F_{\jmath }(t(\jmath ))$, as a product of $M$ possibly small values, can become smaller than the precision of the computer when the strength $t(\jmath )$ is too high. In order to overcome this limitation, we compute instead $\log (\#\mathcal{J }(M)) + \log ( F_{\jmath }(t(\jmath ) ))$ and compare this expression to $\log (\epsilon )$. The quantity $\log ( F_{\jmath }(t(\jmath ) ))$ can indeed be rewritten

$$\begin{aligned} \log ( F_{\jmath }(t(\jmath ) )) = \sum _{m=1}^M \log \left( \mathop \int \limits _t^{+\infty } d\left( \mathop {\star }_{j=1}^{J(r,\theta _m)} \mu \right) \right) . \end{aligned}$$

In order to compute these terms, we discretize $\mu$ on the interval $[0,6]$ (the weight of the distribution $\mu$ above $6$ being negligible), with a precision of 120 bins. Each term of the sum is then computed thanks to a discrete convolution of the distribution $\mu$, followed by a discrete integration.

Appendix 2: Distribution of $\gamma _{\mathbf{p }}(\mathbf{q })$ Under the Null Hypothesis $\mathcal{H }_0$

The goal of this appendix is to compute the distribution of the random variable $\gamma _{\mathbf{p }}(\mathbf{q })$ under the hypothesis $\mathcal{H }_0$. Recall that

$$\begin{aligned} \gamma _{\mathbf{p }}(\mathbf{q })&= \Vert \widetilde{\nabla I}(\mathbf{q })\Vert \cdot \max \Big (|\cos (\phi (\mathbf{q }) - \alpha (\overrightarrow{\mathbf{pq }})|\nonumber \\&-|\sin (\phi (\mathbf{q }) - \alpha (\overrightarrow{\mathbf{pq }}))|, 0 \Big ). \end{aligned}$$

(23)

In the following, we first derive the distribution of $\max (|\cos \theta |-|\sin \theta |, 0)$ when $\theta$ is a random variable following a uniform distribution on $[0, 2\pi [$, then the full distribution of $\gamma _{\mathbf{p }}(\mathbf{q })$.

1.1 Distribution of $\max (|\cos \theta |-|\sin \theta |, 0)$

Assume that $\theta$ is a random variable following a uniform distribution on $[0, 2\pi [$. If $Y = \max (|\cos \theta |-|\sin \theta |, 0)$, we have $Y \in [0, 1]$ with probability $1$ and

$$\begin{aligned} Y \!=\! \left\{ \begin{array}{ll} |\cos \theta |-|\sin \theta | &{}\quad \mathrm {if} \theta \!\in \! [0, \frac{\pi }{4}]\cup [\frac{3\pi }{4}, \frac{5\pi }{4}]\cup [\frac{7\pi }{4}, 2\pi ],\\ 0 &{}\quad {\mathrm{otherwise}}.\\ \end{array}\right. \nonumber \\ \end{aligned}$$

(24)

Note $\varTheta = [0, \frac{\pi }{4}]\cup [\frac{3\pi }{4}, \frac{5\pi }{4}]\cup [\frac{7\pi }{4}, 2\pi ]$, then $(|\cos \theta |-|\sin \theta |)^2 = 1- |\sin 2\theta |$ for $\theta \in \varTheta$. The cumulative distribution function $F_Y$ of $Y$ can then be computed as follows.

$$\begin{aligned} \begin{array}{ll} \mathrm {For} y<0,F_Y(y) = 0&{},\;\;\mathrm for y>1,F_Y(y) = 1.\\ \mathrm For 0\le y\le 1,F_Y(y) &{}= \mathbb P \Big ( \max (|\cos \theta |-|\sin \theta |, 0) \le y \Big ) \\ &{}= \frac{1}{2} + \mathbb P \Big ( 0 < |\cos \theta |-|\sin \theta | \le y \Big ) \\ &{}= \frac{1}{2} + \mathbb P \Big ( \theta \in \varTheta \;\text { and } \; |\sin 2\theta | \ge 1 - y^2 \Big )\\ &{}= \frac{1}{2} + 4\cdot \frac{1}{2\pi }\cdot \Big ( \frac{\pi }{4} - \frac{1}{2}\arcsin (1-y^2) \Big ) \\ &{}= 1 + \frac{1}{\pi }\arcsin (y^2 - 1). \nonumber \\ \end{array}\\ \end{aligned}$$

(25)

Finally,

$$\begin{aligned} F_Y(y) = \Big ( 1 + \frac{1}{\pi }\arcsin (y^2 - 1) \Big )1\!\!1_{0\le y \le 1}. \end{aligned}$$

(26)

The distribution of the random variable $Y$ is obtained by differentiating this expression, which gives

$$\begin{aligned} \mu _Y = \frac{1}{2}\delta _0+ \frac{2}{\pi } \frac{1}{\sqrt{2 - y^2}}1\!\!1_{0\le y \le 1}\mathcal{L }, \end{aligned}$$

(27)

where $\delta _0$ is the Dirac mass centered at $0$ and where $\mathcal{L }$ is the Lebesgue measure on $\mathbb{R }$.

1.2 Distribution of $|{\widetilde{\nabla I}}| \cdot \max (|\cos \theta |-|\sin \theta |, 0)$

We compute in this section the distribution of the product $Z=XY$ when $X$ and $Y$ are two independent random variables, $X$ following a Rayleigh distribution of parameter $1$ and $Y$ following the distribution (27). We recall that the density of the Rayleigh distribution is

$$\begin{aligned} f_X(x) = \chi (x,2) = xe^{-x^2/2}, ~x \in [0, \infty ). \end{aligned}$$

(28)

Now, notice that if $Z = XY$, then $Z \in [0, +\infty )$ with probability $1$ and the cumulative distribution function $F_{Z}(z)$ can be computed as follows,

$$\begin{aligned} \begin{array}{ll} \mathrm {For} z < 0, ~F_{Z}(z) &{}= 0. \\ \mathrm For z = 0, ~F_{Z}(z) &{}= \frac{1}{2}. \\ \mathrm For z > 0, ~F_{Z}(z) &{}=\mathbb{P }(0 \le XY \le z)\\ &{} = \int \limits _{0}^{1} \int \limits _{0}^{z/y} f_{X}(x)dx \mu _Y(dy) \\ &{} = \frac{1}{2} + \frac{2}{\pi } \int \limits _{0}^{1} (1-e^{-\frac{z^2}{2y^2}}) \frac{1}{\sqrt{2 - y^2}}dy. \end{array} \end{aligned}$$

We differentiate this expression with respect to $z$ to obtain the distribution of the random variable $Z$ :

$$\begin{aligned} \mu _{Z} = \frac{1}{2}\delta _0 +1\!\!1_{z\ge 0} \cdot \frac{2z}{\pi } \left( \int \limits _{0}^{1} e^{-\frac{1}{2} (\frac{z}{y})^2} \frac{1}{y^2\sqrt{2 - y^2}}\, dy\right) \mathcal{L }. \end{aligned}$$

(29)

In addition,

$$\begin{aligned} \begin{array}{ll} \int \limits _{0}^{1} &{} \frac{1}{y^2} e^{-\frac{1}{2} (\frac{z}{y})^2} \frac{1}{\sqrt{2 -y^2}}\, dy \\ &{} = \int \limits _{1}^{\infty } e^{-\frac{z^2 x^2}{2}} \frac{x}{\sqrt{2x^2 - 1}}\, dx, ~\mathrm {with} ~x=\frac{1}{y}, \\ &{} = \frac{1}{2}\int \limits _{1}^{\infty } e^{-\frac{z^2 }{4} \cdot (t^2 +1)}\, dt, ~\mathrm {with} ~t= \sqrt{2x^2 -1}, \\ &{} = \frac{\sqrt{\pi }}{2z} e^{-\frac{z^2 }{4}}\cdot \Big ( 1- \mathrm erf (\frac{z}{2})\Big ) = \frac{\sqrt{\pi }}{2z} e^{-\frac{z^2 }{4}}\cdot \mathrm{ erfc} (\frac{z}{2}), \end{array} \end{aligned}$$

(30)

where $\mathrm {erf} (z) = \frac{2}{\sqrt{\pi }} \int \limits _0^z e^{-t^2}\, dt$ is the error function and where $\mathrm {erfc} (z) = 1 -erf(z)$ is the complementary error function. Finally,

$$\begin{aligned} \mu _{Z} = \frac{1}{2} \delta _0 + \frac{1}{2}R.\mathcal{L }, \end{aligned}$$

(31)

where $\mathcal{L }$ is the Lebesgue measure and where $R$ is the function

$$\begin{aligned} R(z) = \frac{2}{\sqrt{\pi }} e^{-\frac{z^2 }{4}}\cdot \mathrm {erfc} \left( \frac{z}{2}\right) 1\!\!1_{z\ge 0}. \end{aligned}$$

Observe that the measure $\mu _{Z}$ is a mixture between a Dirac mass function and an absolutely continuous distribution.