Introduction

Polytetrafluoroethylene (PTFE) is a fluoropolymer that has many excellent properties such as high hydrophobicity, high oleophobicity, high chemical resistance, high antifouling property, high sliding property, high thermal resistance, high weather resistance, low relative permittivity, and low dielectric loss tangent. It has been used in many applications including polymer bearing, gaskets, gears, valve seats, piston rings, seals, bushes, hose assemblies, high voltage switches, extension joints, cook wears, clinical, containers and pipework for reactive and corrosive chemicals. It has also been used in biomedical applications such as oxygenator membrane, vascular graft and catheter coating. The virgin PTFE rods or components are manufactured through sintering or compression molding. The specific grade of PTFE which has the greater dielectric strength is frequently used in wire and cable wrap, and to separate conductive surfaces in capacitors.

As an instance, thick walled close tolerance extruded PTFE can be machined into standoff insulators and can also be used in high voltage encapsulation devices for miniature components with high dimensional accuracy and integrity. These components may require further machining operations to have net shape, suitable for the specific application. The accuracy of the machining process is decided by the control parameters such as feed, depth of cut, speed, nose radius etc. The poorly set control parameters do increase the surface roughness and lead to the poor net shape. The current research is aimed to determine the optimum control parameters for obtaining the minimum surface roughness and maximum material removal rate of material during machining of PTFE. The minimization surface roughness increases the quality of the products and the maximization of material remove rate increases the production rate (quantity) of the products.

In most existing literatures, the regression models were developed as nonlinear functions consisting of several input process parameters with boundary limits. Although the idea of utilizing optimization method to solve a given regression model is proven feasible to obtain the optimum machining parameters, the solutions produced by traditional optimization algorithms (e.g., nonlinear programming, quadratic programming, dynamic programming and etc.) tend to stagnate into local optima due to the difficulty of achieving good guess of initial solutions (Mukherjee and Ray 2006). The emergence of new metaheuristic search algorithms (Lim and Isa 2015; Ji et al. 2017; Al-Omoush et al. 2019; Hu et al. 2019; Fan and Yan 2016) has become the popular alternative to overcome these challenges. Because, these algorithms do not strongly rely on the quality of initial solutions and the gradient information of objective functions to solve an optimization problem. The substantial amounts of real-world optimization problems have been tackled using the metaheuristic search algorithms due to their promising search robustness. These include the energy management optimization (Yao et al. 2015, 2017; Mathew et al. 2018; Zhao et al. 2013; Zhao et al. 2012), robust control system design (Tang et al. 2013, 2014; Solihin et al. 2009, 2010), machine vision and image processing (Senthilnath et al. 2016; Li et al. 2011; Jiao and Pan 2019; Mistry et al. 2017; Van and Kang 2016), just to name a few.

Majority of machining problems are formulated as the multi-objective optimization problems (MOPs) due to the simultaneous consideration of multiple performance characteristics. There could be three to four control parameters involved in the optimization of response variables. There are generally two popular approaches used to tackle the MOPs, namely the priori method and the posterior method (Collette and Siarry 2003). In contrast to the priori method that only be able to produce one optimum solution at each trial of simulation by considering the predefined relative importance levels of objective functions, the posterior method is able to produce a complete set of trade-off optimal solutions with single run. Referring to the relative importance of objective functions that normally not known in advance, the process planner can choose a unique solution from the complete set of trade-off solutions obtained (Abbas et al. 2016). Due to its excellent capability to cater the frequent changes of customer requirements in real-world scenario of machining process, the posterior method is considered as a more promising approach than the priori method to address the machining problems with MOP characteristic. In addition, the performance selection index method for solving machining multi-criteria decision making problems was discussed by Petković et al. (2017).

Substantial research works have been reported to design various posterior version of multi-objective evolutionary algorithms (MOEAs), aiming to effectively optimize different multi-objective machining problems. These MOEAs can be generally categorized under two different frameworks known as the Pareto-dominance-based (Deb et al. 2005; Corne et al. 2001; Zitzler et al. 2001) and decomposition-based (Zhang and Li 2007; Deb and Jain 2014). The micro-Electric Discharge Machining (microEDM) of Stainless Steel (SS) 316L was modelled with response surface methodology (RSM). Three machining parameters known as discharge current, pulse-on and pulse-off times were optimized by a multi-objective genetic algorithm (Suresh et al. 2014) in order to achieve the maximization of material removal rate and the minimization of tool wear rate simultaneously. Three process parameters for the electrochemical machining (ECM) of die tool steel with nanofluid coolant (i.e., tool feed rate, applied voltage and electrolyte discharge rate) were optimized using a multi-objective genetic algorithm developed by Sathiyamoorthy et al. (2015a). Sathiyamoorthy et al. (2015b) also attempted to optimize the machining of AISI 202 Austenitic stainless steel by considering multiple objectives. A regression model was developed by Viswanathan et al. (2017) to correlate the response variable of cutting temperature for AZ91 Magnesium alloy with three process parameters knowns as the depth of rate, cutting speed and feed rate. Notably, the cutting speed was reported to play significant role in minimizing the cutting zone temperature. The multi-objective ultrasonic machining process was addressed by Teimouri et al. (2015) with an imperialist competitive algorithm (ICA), while the particle swarm optimization was employed by Mohanty et al. (2016) to address the multi-response optimization of electric discharging machining process. Recently, the cuckoo optimization algorithm and hoopoe heuristic were employed by Mellal and Williams (2016) to optimize the process parameters of two traditional machining processes (i.e., drilling process and grinding process) and four modern machining processes (i.e., abrasive jet machining, abrasive water jet machining, ultrasonic machining and water jet machining). A multi-objective version of Jaya algorithm has been proposed by Rao et al. (2017b) to optimize four non-traditional machining processes, i.e., focused ion beam (FIB) micro-milling, laser cutting, wire-electric discharge machining (WEDM) and ECM. Similar multi-objective Jaya algorithm was further applied by Rao et al. (2019) to optimize the process parameters of abrasive waterjet machining process and a multi-objective decision making method was incorporated to select a preferred solution from Pareto front based on the predefined requirements of process planner. The electrical discharge machining (EDM) of polycrystalline diamond (PCD) was modelled by Ong et al. (2018) using a radial basis function neural network. A multi-objective moth search algorithm was then applied to determine the optimal machining parameters, aiming to maximize the material removal rate and minimize the electrode wear rate simultaneously. The teaching–learning-based optimization (TLBO) and most of its modified versions have emerged as the popular optimizers to solve various traditional and modern machining processes, because these approaches do not require the fine tuning of any algorithm-specific control parameters. For instance, the simultaneous minimization of operation time incurred and carbon emission produced from a turning process were achieved with the multi-objective TLBO (MOTLBO) proposed by Lin et al. (2015). A nonlinear regression was used by Abhishek et al. (2017) to formulate the machining model of carbon fibre reinforced polymer (CFRP) composite using single point high-speed steel cutting tool. A prior method developed using TLBO was then applied to optimize four machining parameters known as the spindle speed, feed rate, depth of cut and fibre orientation angle, aiming to achieve satisfactory machining performances in terms of material removal rate, surface roughness and cutting force. A non-dominated sorting TLBO (NSTLBO) was designed to find the optimum parameters settings of four non-traditional machining processes of FIB micro-milling, laser cutting, ECM and WEDM (Rao et al. 2018). An enhanced multi-objective TLBO (EMOTLBO) was proposed by Natarajan et al. (2018) to achieve the maximization of material removal rate and the minimization of surface roughness for the machining process of Delrin material. Apart from the machining process, other practical applications of MOTLBO and its variants can be found in existing literatures (Sultana and Roy 2014; Rao and Waghmare 2015; Yu et al. 2015; Li et al. 2016; Rao et al. 2016, 2017a).

This research aims to address the multi-response optimization of machining of PTFE. Given its overwhelming demands for industrial applications, substantial works related to investigation of mechanical and wear properties of unfilled PTFE and reinforced PTFE have been conducted. Nevertheless, the investigation on the machining characteristics of PTFE has yet to be conducted based on the best of the authors’ knowledge. In order to bridge this research gap, the first major contribution of this paper, as presented in Sect. 2, focused on the experimental design, derivation of regression model of PTFE based on the experimental results. The second major contribution (in Sect. 3) focused on designing an enhanced version of multi-objective algorithm known as the non-dominated sorting modified teaching–learning-based optimization (NSMTLBO), aiming to optimize the machining parameters of PTFE that respond to the minimum surface roughness and maximum material removal rate simultaneously. Some modifications were incorporated into the proposed NSMTBLO in order to solve the MOPs effectively. For instance, a teacher selection mechanism based on the nearest Euclidean distance and the derivation of weighted mean position for each learner were introduced into the modified teacher phase to enhance the exploitation search capability of algorithm. A self-learning mechanism was also integrated into the modified learner phase, aiming to enhance the exploration search of algorithm through a probabilistic mutation. Finally, a fuzzy decision maker (Aghaei et al. 2011) was also applied to determine the most suitable machining parameters from the Pareto front obtained, based on the relative importance of all objective functions that may change frequently. Comprehensive simulation and experimental studies were performed and discussed in Sect. 4, followed by the concluding remarks in Sect. 5.

Experimental design and modelling of PTFE

Experimental details

The virgin PTFE rod in 30 mm diameter, prepared by sintering process was used for experimental analysis. The virgin PTFE is a pure and higher grade material which does not have recycled or reclaimed materials. It is in white colour and preferred to use in industries for its hygienic, better frictional resistance, excellent chemical resistance, outstanding electrical properties and excellent flexural properties. Table 1 shows the physical and mechanical properties of the material. Three levels of cutting speed (Vc), feed rate (f), depth of cut (ap) and nose radius (Nr) were used in design of experiments (DOE) to design L27 orthogonal array (4 × 27). The nose radius of Nr = 0.4, 0.8 and 1.2 mm as per the guidance from the cutting tool manufacture was used. The machining parameters and levels used for DOE is shown in Table 2. The surface roughness \( \left( {R_{a} } \right) \) and material removal rate (MRR) were considered as response variables. The CNC turning centre (Model: Sprint 16TC Fanuc 0i T Mate Model C) was used for machining. The experiments were carried out with servo super cut coolant 32t according to DOE. The time taken for each pass of the required length was recorded. Each sample’s surface roughness was instantaneously measured with Mitutoyo make surf tester. Four trials were done for each experiment and the average of the measurements was recorded. The MRR value was computed by referring to the rate of material’s volume removed from the sample as specified in Eq. (1) shown below:

$$ MRR = \frac{{\frac{\pi }{4}\left( {D_{initial} - D_{final} } \right)^{2} \times L}}{T} $$
(1)

where MRR refers to material removal rate (cm3/min); \( D_{initial} \) and \( D_{final} \) refer to the initial and final diameters of PTFE sample (cm) before and after machining processes, respectively; L refers to the length of cut (cm); T refers to the time taken to cut the sample (min). The experimental design involved three (3) center runs which vary from low to high (− 1 is low, 0 is medium and + 1 is high). The values − 1, 0 and 1 represent the first level, second level and third level of each control parameter respectively. Figure 1 shows the machined sample, while Table 3 presents the control parameters and the corresponding response variables for each experiment conducted.

Table 1 Mechanical properties of PTFE
Full size table
Table 2 Three levels of input machining parameters
Full size table
Fig. 1
figure 1

Machined PTFE sample

Full size image
Table 3 Control parameters and experimental results of PTFE machining
Full size table

Response surface methodology (RSM)

Response surface methodology (RSM) is a common modelling technique used to investigate the effects of several input control variables and one or more output response variables. In this study, RSM was used to explore the relationship between four input machining parameters known as cutting speed \( \left( {V_{c} } \right) \), feed rate (f), depth of cut (ap) and nose ratio \( \left( {N_{r} } \right) \) on two output response variables of surface roughness \( \left( {R_{a} } \right) \) and material removal rate (MRR).

Without loss of generality, a second-degree polynomial RSM model is represented as follows:

$$ Y = \alpha_{0} + \sum\limits_{i = 1}^{I} {\beta_{i} X_{i} } + \sum\limits_{i = j}^{I} {\beta_{ij} X_{i} X_{j} } + \sum\limits_{i = 1}^{I} {\beta_{ii} X_{i}^{2} } $$
(2)

where Y represents the response term;\( \alpha_{0} \) represents the free term of regression equation; \( X_{1} ,X_{2} , \ldots ,X_{I} \) represent the set of control variable terms; \( \beta_{i} ,\;\beta_{ii} \) and \( \beta_{ij} \) refer to the linear coefficient, quadratic coefficient and interacting coefficient terms, respectively. In this research, the response variable Y is associated with the four control variables, viz. \( V_{c} \), f, ap and \( N_{r} \), hence the function denoted as \( \psi \left( { \cdot , \cdot , \cdot , \cdot } \right) \) is,

$$ Y = \psi \left( {V_{c} ,\;f,\;ap,\;N_{r} } \right) $$
(3)

Let \( \psi_{1} \left( { \cdot , \cdot , \cdot , \cdot } \right) \) and \( \psi_{2} \left( { \cdot , \cdot , \cdot , \cdot } \right) \) be the operators used to return the output response variables of \( R_{a} \) and MRR, respectively, based on the four control variables of \( V_{c} \), f, ap and \( N_{r} \), where:

$$ R_{a} = \psi \left( {V_{c} ,\;f,\;ap,\;N_{r} } \right) $$
(4)
$$ MRR = \psi \left( {V_{c} ,\;f,\;ap,\;N_{r} } \right) $$
(5)

The regression models represented by Eqs. (4) and (5) are the second-degree polynomial regression model which can be determined with RSM-Box-Behnken design-uncoded units in Design Expert software. The coefficients of \( \alpha_{0} \),\( \beta_{i} \),\( \beta_{ii} \) and \( \beta_{ij} \) in Eq. (2) were determined from the measured experimental data, which further used for obtaining quadratic regression models (Mia 2018; Chabbi et al. 2017; Natarajan et al. 2018). The quadratic regression models of \( R_{a} \) and MRR are expressed as:

$$ \begin{aligned} R_{a} = & 5.95983 + 0.057355 \times V_{c} + 2.93750 \times f + 7.43219 \times ap + 2.99103 \times N_{r} \\ & \quad - 0.079688 \times V_{c} \times f - 0.036660 \times V_{c} \times ap + 7.20000 \times f \times ap + 2.90625 \times f \times N_{r} \\ & \quad - 1.75000 \times ap \times N_{r} - 2.49455 \times ap^{2} - 1.44817 \times N_{r}^{2} \\ \end{aligned} $$
(6)
$$ \begin{aligned} MRR = & 124.84157 + 0.16068 \times V_{c} - 298.32469 \times f - 333.61027 \times ap + 67.27500 \times N_{r} \\ & \quad + 399.65000 \times f \times ap - 85.25000 \times f \times N_{r} - 50.00000 \times ap \times N_{r} \\ & \quad + 240.99254 \times f^{2} + 193.44869 \times ap^{2} \\ \end{aligned} $$
(7)

Problem formulation of PTFE machining

The objective functions for solving the multiobjective optimization machining optimization of PTFE were developed based on the regression models stated in Eqs. (6) and (7). The four input parameters to be optimized in the multiobjective machining model of PTFE include the cutting speed, feed rate, depth of cut and nose ratio denoted as \( V_{c} \), f, ap, and \( N_{r} \), respectively. Meanwhile, the surface roughness and material removal rate, represented by \( R_{a} \) and MRR, respectively, are two contradict objective functions to be optimized because these output responses imply the quality and quantity of products, respectively.

The mathematical formulation of multi-response optimization of PTFE machining process was presented in Eq. (8). The optimal parameters of \( V_{c} \), f, ap, and \( N_{r} \) were solved using the proposed NSMTLBO as explained in the following sections. For sake of convenience, the maximization problem of MRR was converted into the minimization of negative MRR so that both objective functions can be expressed as the minimization problems.

$$ \begin{aligned} & \left\{ {\begin{array}{*{20}l} {\mathop {\text{Minimize}}\limits_{{V_{c} ,f,ap,N_{r} }} } \hfill & {R_{a} } \hfill \\ {\mathop {\text{Maximize}}\limits_{{V_{c} ,f,ap,N_{r} }} } \hfill & {MRR} \hfill \\ \end{array} } \right. \\ & \begin{array}{*{20}l} {{\text{s}} . {\text{t}} .} \hfill & { 8 0\;{\text{mm/minute}} \le V_{c} \le 200\;{\text{mm/minute}}} \hfill \\ {} \hfill & { 0. 1\;{\text{mm/revolution}} \le f \le 0. 5\;{\text{mm/revolution}}} \hfill \\ {} \hfill & { 0. 5\;{\text{mm}} \le ap \le 1. 0\;{\text{mm}}} \hfill \\ {} \hfill & { 0. 4\;{\text{mm}} \le N_{r} \le 1.2\;{\text{mm}}} \hfill \\ \end{array} \\ \end{aligned} $$
(8)

Proposed methodology

Teaching–learning-based optimization

The teaching–learning-based optimization (TLBO) algorithm was inspired by the classical teaching and learning processes in school (Rao et al. 2011). A group of learners with the population size of N are randomly initialized at the beginning stage of optimization. Each of the n-th learner, denoted as \( X_{n} = \left[ {X_{n,1} , \ldots ,X_{n,d} , \ldots ,X_{n,D} } \right] \), is assumed to be the candidate solution of a given optimization problem, where \( d \in \left[ {1,D} \right] \) and D represent the index and the total dimensional size of problem, respectively. Let \( \varPsi \left( {X_{n} } \right) \) be the objective function value of each n-th solution and it is used to represent the knowledge level of each n-th learner in a classroom that can be enhanced via the teacher or learner phases.

During the teacher phase, all learners can improve their knowledge by learning from the teacher denoted as \( X^{teacher} \), i.e., an individual with the best fitness in population, by considering the average knowledge level of all learners in the population represented as \( X^{mean} \), where:

$$ X^{mean} = \frac{1}{N}\sum\limits_{n = 1}^{N} {X_{n} } $$
(9)

Let \( r_{1} \in \left[ {0,1} \right] \) be a random number obtained from uniform distribution; \( T_{f} \in \left\{ {1,2} \right\} \) be a teaching factor used to emphasize the importance of learner’s average quality \( X^{mean} \). During the teacher phase, a new solution of n-th learner, denoted as \( X_{n}^{new} \), can be obtained as:

$$ X_{n}^{new} = X_{n} + r_{1} \left( {X^{teacher} - T_{f} X^{mean} } \right) $$
(10)

For learner phase, each of the n-th learner aims to improve its knowledge level (i.e., fitness) by interacting with its peers in the population. Let s be the index of a learner randomly selected by the n-th learner from population for peer learning, where \( s \in \left[ {1,N} \right] \) and \( s \ne n \); \( r_{2} \in \left[ {0,1} \right] \) is a random number generated from the uniform distribution. If the learner \( X_{s} \) that is randomly selected from the population has better fitness than \( X_{n} \), the latter learner is attracted towards the former one as shown in Eq. (11). Otherwise, a repel mechanism is introduced in Eq. (12) to prevent the convergence of a learner \( X_{n} \) towards the peer learner \( X_{s} \) with inferior fitness.

$$ X_{n}^{new} = X_{n} + r_{2} \left( {X_{s} - X_{n} } \right) $$
(11)
$$ X_{n}^{new} = X_{n} + r_{2} \left( {X_{n} - X_{s} } \right) $$
(12)

If the new solution \( X_{n}^{new} \) generated from the teacher or learner phases has better fitness than the n-th learner, the latter solution will be replaced by the former one. Both of the teacher and learner phases are repeated in until the termination criteria of TLBO are met. The teacher solution \( X^{teacher} \) is considered as best solution obtained from the optimization process.

Non-dominated sorting modified teaching–learning-based optimization

In this section, the non-dominated sorting modified teaching–learning-based optimization (NSMTLBO) is proposed as an improved posterior approach to solve the multi-objective optimization problems. The modified versions of teacher phase and learner phase are introduced into NSMTLBO to enhance its exploration and exploitation capabilities while searching for the optimal solutions in the parameter spaces. Two core concept known as the fast non-dominated sorting and crowding distance (Deb et al. 2002) are also incorporated into NSMTLBO to ensure that the proposed work can solve multi-objective optimization problems effectively and efficiently. Without loss of generality, the minimization problems are considered in the remaining subsections, while explaining the search mechanisms of NSMTLBO in detail here.

Pareto dominance concept

Suppose that a total M objective functions are considered in a given multi-objective optimization problem. Let \( \varPsi_{m} \left( {X_{n} } \right) \) be the objective function value of the n-th learner \( X_{n} \) for the m-th objective function. For a single objective optimization, it is intuitive to compare the quality of different solutions based on its objective function values. Nevertheless, it is nontrivial to rank all solutions from the best to worst for multi-objective optimization problems due to the presence of multiple conflicting objectives.

Pareto dominance concept is a commonly used approach to overcome the challenges of multi-objective optimization problems (Deb et al. 2002). For the self-contained purpose, the definitions of Pareto dominance are presented as follows:

Definition 1

A solution \( X_{n} \) is considered to dominate another solution \( X_{s} \) if \( X_{n} \) shows better or equal objective values on all objectives and produce a better result in at least one objective function. In other words,\( X_{n} \succ X_{s} \) if and only if \( \varPsi_{i} \left( {X_{n} } \right) \le \varPsi_{i} \left( {X_{s} } \right) \) for \( \forall i \in \left\{ {1,2, \ldots ,M} \right\} \) and \( \varPsi_{j} \left( {X_{n} } \right) < \varPsi_{j} \left( {X_{s} } \right) \) for \( \exists j \in \left\{ {1,2, \ldots ,M} \right\} \), or vice versa.

Definition 2

A solution denoted as \( X^{*} \) is considered as a Pareto optimal solution if there is no existence of another solution X such that \( X^{*} \succ X \). A Pareto optimal set can be determined from these Pareto optimal solutions.

Definition 3

Pareto front can be obtained by mapping the Pareto optimal set in the objective space.

Fast non-dominated sorting and crowding distance

An initial population of NSMTLBO denoted as \( {\mathbf{P}} = \left[ {X_{1} , \ldots ,X_{n} , \ldots ,X_{N} } \right] \) consisting of N learners is randomly generated. Similar with majority posteriori version of multi-objective algorithms, NSMTLBO aims to generate an approximated Pareto front consisting of a set of non-dominated solutions that are evenly distributed. In order to solve the multi-objective optimization problems effectively and efficiently, both of the fast non-dominated sorting approach and the crowding distance mechanism are incorporated into NSMTLBO to determine the ranking of all learners.

The fast non-dominated sorting approach is employed in NSMTLBO to ensure that only non-dominated solutions are selected to guide the learners during the search process in order to ensure the population can converge towards the true Pareto front. During the fast non-dominated sorting process, two entities are computed for each n-th learner \( X_{n} \), i.e., (i) the domination count denoted as \( C_{n} \) to indicate the number of solutions that dominate the learner \( X_{n} \) and (ii) a set denoted as \( S_{n} \) to store the solution sets that are dominated by the learner \( X_{n} \)-. All non-dominated solutions with \( C_{n} = 0 \) found in the first round of sorting process are allocated in the first front denoted as \( F_{1} \). For every n-th learner with \( C_{n} = 0 \) stored in the first front \( F_{1} \), each of the s-th learner \( X_{s} \) stored in the set \( S_{n} \) is visited to reduce its domination count by one. If the domination count \( C_{s} \) of any s-th learner is reduced to zero, it is stored into a new list denoted as Q to form the second front \( F_{2} \). The same process is repeated for all members stored in list Q to identify the third front \( F_{3} \). From Fig. 2, the fast non-dominated sorting process continues until the non-domination rank \( {\mathbf{Rank}} = \left[ {Rank_{1} , \ldots ,Rank_{n} , \ldots ,Rank_{N} } \right] \) and fronts \( {\mathbf{F}} = \left[ {F_{1} , \ldots ,F_{r} , \ldots ,F_{R} } \right] \) of all N learners are found, where r and R represent the index and upper limit of front counters, respectively.

Fig. 2
figure 2

The pseudo-code of fast non-dominated sorting approach

Full size image

In order to prevent premature convergence, it is crucial for NSMTLBO to maintain the diversity of its Pareto optimal solution sets by choosing the non-dominated solutions from sparse regions as teacher in guiding the search process of remaining learners. The crowding distance (Deb et al. 2002) denoted as \( \Delta_{n} \) is a metric used to measure the density of solution \( X_{n} \) around the n-th learner in population by calculating the average distance of two nearest solutions on both sides of \( X_{n} \) along each of the M objectives. Suppose that \( \left| {F_{r} } \right| \) is to the number of members allocated to the r-th front. The initial crowding distance of each a-th member is set as \( \Delta_{a,r} = 0 \), where \( a = 1, \ldots ,\left| {F_{r} } \right| \). For every m-th objective function, a sorting process is performed on all members allocated to the r-th front in ascending manner by referring to their respective objective values and a list represented as Lm,r is used to store all sorted members. Suppose that for the r-th front, the a-th member is sorted to become the j-th element denoted as \( L_{m,r} \left[ j \right] \) for the m-th objective, where \( j = 1, \ldots ,\left| {F_{r} } \right| \). Then, the crowding distance for every j-th sorted member with the objective function value denoted as \( \varPsi_{m} \left( {X_{{L_{m,r} \left[ j \right]}} } \right) \) can be calculated as:

$$ \Delta_{{L_{m,r} \left[ j \right]}} = \left\{ {\begin{array}{*{20}l} {\infty ,\quad if\;j = 1\;or\;j = \left| {F_{r} } \right|} \hfill \\ {\Delta_{{L_{m,r} \left[ j \right]}} + \frac{{\varPsi_{m} \left( {X_{{L_{m,r} \left[ {j + 1} \right]}} } \right) - \varPsi_{m} \left( {X_{{L_{m,r} \left[ {j - 1} \right]}} } \right)}}{{\varPsi_{m} \left( {X_{{L_{m,r} \left[ {\left| {F_{r} } \right|} \right]}} } \right) - \varPsi_{m} \left( {X_{{_{{L_{m,r} \left[ 1 \right]}} }} } \right)}},} \hfill \\ {\quad if\;j = 2, \ldots ,\left( {\left| {F_{r} } \right| - 1} \right)} \hfill \\ \end{array} } \right. $$
(13)

From Eq. (13), the front members with larger crowding distances are located on the more sparse regions of objective space and vice versa. For every m-th objective function, the boundary solutions stored in the sorted list \( L_{m,r} \) are assigned with infinite crowding distance values. Similar procedures are repeated for all M objective functions and all R fronts as shown in Fig. 3. A set denoted as \( {\varvec{\Delta}} = \left[ {\Delta_{1} , \ldots ,\Delta_{n} , \ldots ,\Delta_{N} } \right] \) used to store the overall crowding-distance value of each n-th learner is then computed as the sum of individual distance values corresponding to each m-th objective function value.

Fig. 3
figure 3

The pseudo-code of computing the crowding distance value of each learner

Full size image

Referring to the non-domination rank \( Rank_{n} \) and the crowding distance \( \Delta_{n} \) of each n-th learner, a crowding-comparison operator denoted as \( \prec_{cco} \) is used to compare the superiority of two solutions during the selection process so that a uniformly spread-out optimal Pareto front can be generated to solve the given multi-objective optimization problem. From Eq. (14), if both learners of \( X_{n} \) and \( X_{s} \) have different non-domination ranks,\( X_{n} \) is preferred over \( X_{s} \) if the former solution has better (i.e., lower) rank than the latter one. If both learners belong to the same rank, the solution located in the less crowded regions with larger \( \Delta_{n} \) value is preferred as follow:

$$ X_{n} \prec_{cco} X_{s} ,\;{\text{if }}\left( {Rank_{n} < Rank_{s} } \right)\;{\text{or}}\;\left( {Rank_{n} = Rank_{s} } \right)\;{\text{and}}\;\left( {\Delta_{n} > \Delta_{s} } \right) $$
(14)

Modified teacher phase

During the teacher phase of TLBO, each of the n-th learner adjusts its position \( X_{n} \) based on the differences between the teacher \( X^{teacher} \) and the mainstream knowledge of population denoted as a mean value \( X^{mean} \) as shown in Eq. (10). For single objective optimization problem, the selection of teacher is intuitive and can be achieved by identifying the learner with best objective function value from population. On the other hand, the existance of mutually contradictory objectives in the multi-objective optimization problems tends to produce multiple non-dominated learners that are able to guide other learners as teachers in searching for the Pareto front.

A modified teacher selection scheme is introduced for teacher phase of NSMTLBO, aiming to leverage the expertise of multiple teachers in solving the multi-objective optimization problems. In contrast to the conventional TLBO where a same teacher is assigned to guide the search processes of all learners, the nearest non-dominated learner stored in the Pareto front \( F_{1} \) is assigned as the teacher for every n-th learner during the teacher phase of NSMTLBO. Let \( \left| {F_{1} } \right| \) be the number of candidate teachers contained in the Pareto front \( F_{1} \) and D represents total numbers of design variables that need to be optimized. Let \( X_{d}^{U} \) and \( X_{d}^{L} \) be the d-th dimensional component of the upper and lower limits, respectively, where \( d = 1, \ldots ,D \). Denote \( X_{a,d}^{Cand} \) and \( X_{n,d} \) as the d-th dimension of the a-th candidate teacher and n-th learner, where \( a = 1, \ldots ,\left| {F_{1} } \right| \) and \( n = 1, \ldots ,N \), respectively. Then, the normalized Euclidean distance between the n-th learner and the a-th candidate teacher represented with \( E_{n,a} \) are computed as follow:

$$ E_{n,a} = \sqrt {\sum\limits_{d = 1}^{D} {\left( {\frac{{X_{a,d}^{Cand} - X_{n,d} }}{{X_{d}^{U} - X_{d}^{L} }}} \right)}^{2} } $$
(15)

As shown in Fig. 4, the computation of normalized Euclidean distances between the n-th learner and all \( \left| {F_{1} } \right| \) candidate teachers are repeated using Eq. (15). Based on the \( E_{n,a} \) values, the closest candidate teacher denoted as \( X_{n}^{teacher} \) is identified as the teacher for the n-th learner during the teacher phase. The adopted teacher selection mechanism is anticipated to enhance the exploitation capability of NSMTLBO because each learner is guided by its closest teacher. The diversity of Pareto front can also be preserved due to the employment of different teachers in guiding different learners during the teacher phase of NSMTLBO.

Fig. 4
figure 4

The pseudo-code of finding the closest teacher for each learner in the teacher phase

Full size image

For conventional TLBO, the contributions of all learners are equal in determining the mean value of population \( X^{mean} \). It is anticipated that the conventional TLBO is susceptible to premature convergence because the same values of \( X^{teacher} \) and \( X^{mean} \) are used to update all of the learners in each generation. If the most knowledgeable teacher is trapped in a local optimum, it tends to misguide the rest of learners searching towards the local optimum and produce the same mean position \( X^{mean} \). When both of the \( X^{teacher} \) and \( X^{mean} \) becomes undistinguishable, the position of learners cannot be updated and stuck at local optimum because the second term of Eq. (10) tends to approach zero value when teaching factor obtained by all learners are \( T_{f} = 1 \).

In order to address this issue, an alternate approach in obtaining the mean knowledge of population is proposed for the teacher phase of NSMTLBO. Unlike TLBO, the proposed NSMTLBO only leverages the benefits of useful information carried by the non-dominated learners stored in Pareto front \( F_{1} \) as the source of influences in guiding the search process of other learners. In order to prevent the diversity loss in second component of Eq. (10), each a-th non-dominated learner from \( F_{1} \) is assigned with different weightage to reflect its unique contribution in constructing the weighted mean position of the n-th learner. Denote \( r_{a} \in \left[ {0,1} \right] \) as the random number obtained from a uniform distribution for each a-th non-dominated learner in \( F_{1} \) with the position value of \( X_{a} \). Suppose that \( \tilde{X}_{n}^{mean} \) represents the weighted mean position of n-th learner, then

$$ \tilde{X}_{n}^{mean} = \frac{{\sum\nolimits_{a = 1}^{{\left| {F_{1} } \right|}} {r_{a} X_{a} } }}{{\sum\nolimits_{a = 1}^{{\left| {F_{1} } \right|}} {r_{a} } }} $$
(16)

Given the closest teacher \( X_{n}^{teacher} \) and weighted mean \( \tilde{X}_{n}^{mean} \), the new position of each n-th NSMTLBO learner is updated through the modified teacher phase, where

$$ X_{n}^{new} = X_{n} + r_{3} \left( {X_{n}^{teacher} - T_{f1} X_{n} } \right) + r_{4} \left( {\tilde{X}_{n}^{mean} - T_{f2} X_{n} } \right) $$
(17)

where \( r_{3} \) and \( r_{4} \) are the random number with the range of 0 to 1 generated from uniform distribution;\( T_{f1} \) and \( T_{f2} \) are the teaching factors with the range of 1 to 2 generated from uniform distribution, where \( T_{f1} ,T_{f2} \in \left[ {1,2} \right] \) (Rao and Patel 2013; Lin et al. 2015). As shown in Fig. 5 and Eq. (17), each of the n-th NSMTLBO learner can learn directly from multiple teachers by updating its knowledge based on the differences between its current knowledge and (i) the closest teacher’s knowledge and (ii) weighted mean knowledge of other teachers in classroom. These uniform distributions of \( T_{f1} \) and \( T_{f2} \) are used to emulate a more realistic classroom paradigm by generating the learners with different levels of learning tendency from the teachers. Particularly, the NSMTLBO learner is assumed to learn everything from the teachers successfully when \( T_{f1} \) and \( T_{f2} \) are equal to 2, while the learner fails to learn anything when \( T_{f1} = T_{f2} = 1 \) (Rao and Patel 2013; Lin et al. 2015).

Fig. 5
figure 5

The pseudo-code of modified teacher phase in NSMTLBO

Full size image

Modified learner phase

The learner phase of TLBO promotes the exploration search of algorithm by introducing the repelling mechanism in Eq. (12) when the n-th learner is randomly assigned to an inferior peer. As the iterative generation of TLBO becomes larger, the changes in population tends to be stabilized because all learners tend to converge towards a particular region of search space. Without the notable changes of population diversity, it becomes challenging for a randomly selected learner to assist the particular learner to break out from sub-optimal region, especially if the optimization problem consists of a complicated Pareto front. It is also more difficult for the learner in a multi-objective algorithm to randomly choose another peer that is completely dominated by it, hence the likelihood of triggering repelling mechanism in Eq. (12) is reduced further.

In order to address these challenges, a modified learner phase is proposed for NSMTLBO. A probabilistic mutation scheme is first designed as an alternative learning strategy in the learner phase of NSBTLBO, aiming to perturb the learners with a mutation probability represented as \( P_{mut} = {1 \mathord{\left/ {\vphantom {1 D}} \right. \kern-0pt} D} \). From the perspective of classroom teaching–learning paradigm, different types of learners exist in the same classroom and some learners might prefer to improve their knowledge level via self-learning rather than interacting with their peers. The inclusion of this mutation operator is to facilitate the self-learning of some NSMTLBO learners during the learner phase after they complete the teacher phase. When the self-learning mechanism is triggered for the n-th learner with probability \( P_{mut} \), a random dimensional component of n-th learner, denoted as \( d_{r} \in \left[ {1,D} \right] \), is selected for perturbation, where

$$ X_{{n,d_{r} }}^{new} = X_{{n,d_{r} }} + r_{5} \left( {X_{{d_{r} }}^{U} - X_{{d_{r} }}^{L} } \right) $$
(18)

where \( r_{5} \in \left[ { - 1,1} \right] \) is a random number obtained from uniform distribution;\( X_{{n,d_{r} }}^{new} ,\;X_{{n,d_{r} }}^{U} \) and \( X_{{n,d_{r} }}^{L} \) are the \( d_{r} \)-th dimensional component of the n-th learner, the upper and lower boundary limits of decision variables, respectively. The pseudocode of self-learning mechanism is described in Fig. 6.

Fig. 6
figure 6

The pseudo-code of self-learning mechanism in the modified learner phase

Full size image

For the n-th learner that prefer to improve its knowledge by interacting with other peers, a random peer learner denoted as \( X_{s} \) is chosen from population to update \( X_{n} \) using Eq. (11) or Eq. (12), where \( n,s \in \left[ {1,N} \right] \) and \( s \ne n \). If the randomly chosen peer learner \( X_{s} \) dominates the learner \( X_{n} \), the latter learner is attracted towards the former one as shown in Eq. (11). On the other hand, the learner \( X_{n} \) tends to be driven away from the inferior peer learner \( X_{s} \) using Eq. (12) to prevent the premature convergence of population in sub-optimal regions of fitness lanscapes. If both of the learner \( X_{n} \) and peer \( X_{s} \) are non-dominated with each other, one of the learning strategy expressed using Eq. (11) or Eq. (12) will be randomly selected with an equal chance for updating the n-th learner at the modified learner phase of NSMTLBO as shown in Fig. 7.

Fig. 7
figure 7

The pseudo-code of modified learner phase in NSMTLBO

Full size image

Fuzzy decision maker

After obtaining the Pareto front \( F_{1} \) of a given multi-objective optimization problem, a fuzzy decision maker is then used by NSMTLBO to determine the most suitable solution from the Pareto front obtained by referring to the relative importance levels of all objective functions stated by the stakeholders.

Denote \( {\varvec{\Psi}}^{{\mathbf{U}}} = \left[ {\varPsi_{1}^{U} , \ldots ,\varPsi_{m}^{U} , \ldots ,\varPsi_{M}^{U} } \right] \) as the utopia point of a given multi-objective optimization problem consisting of M objective functions. Utopia point is a specific point located in objective space with all objective function values demonstrate the best possible values. On the other hand, the pseudo nadir point denoted as \( {\varvec{\Psi}}^{{{\mathbf{SN}}}} = \left[ {\varPsi_{1}^{SN} , \ldots ,\varPsi_{m}^{SN} , \ldots ,\varPsi_{M}^{SN} } \right] \) is another extreme point in objective space that consisting of the worst values for all objective functions. In order to select the most preferred optimal solution from Pareto front \( F_{1} \), the membership value of every a-th Pareto front member with \( a = 1, \ldots ,\left| {F_{1} } \right| \) for the m-th objective function is computed by calculating the relative distances between the objective function value of a-th Pareto front member, denoted as \( \varPsi_{m} \left( {X_{a} } \right) \), and both of the utopia and pseudo nadir points in each m-th objective function. For any m-th objective function, if the a-th Pareto optimal solution is closer to the utopia point, the higher membership value denoted as \( \mu_{a}^{m} \) is assigned to indicate the higher degree of optimality for the a-th Pareto front member in the m-th objective function and vice versa.

For minimization problem, the fuzzification process used to determine the membership value \( \mu_{a}^{m} \) of each a-th Pareto front member with the objective function value \( \varPsi_{m} \left( {X_{a} } \right) \) in the m-th objective function is shown as follow:

$$ \mu_{a}^{m} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\varPsi_{m} \left( {X_{a} } \right) < \varPsi_{m}^{U} } \hfill \\ {\frac{{\varPsi_{m}^{SN} - \varPsi_{m} \left( {X_{a} } \right)}}{{\varPsi_{m}^{SN} - \varPsi_{m}^{U} }},} \hfill & {\varPsi_{m}^{U} \le \varPsi_{m} \left( {X_{a} } \right) \le \varPsi_{m}^{SN} } \hfill \\ {0,} \hfill & {\varPsi_{m} \left( {X_{a} } \right) > \varPsi_{m}^{SN} } \hfill \\ \end{array} } \right. $$
(19)

The value of \( \mu_{a}^{m} \) for maximization problem is computed as:

$$ \mu_{a}^{m} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {\varPsi_{m} \left( {X_{a} } \right) < \varPsi_{m}^{SN} } \hfill \\ {\frac{{\varPsi_{m} \left( {X_{a} } \right) - \varPsi_{m}^{SN} }}{{\varPsi_{m}^{U} - \varPsi_{m}^{SN} }},} \hfill & {\varPsi_{m}^{SN} \le \varPsi_{m} \left( {X_{a} } \right) \le \varPsi_{m}^{U} } \hfill \\ {1,} \hfill & {\varPsi_{m} \left( {X_{a} } \right) > \varPsi_{m}^{U} } \hfill \\ \end{array} } \right. $$
(20)

Assume that \( w_{m} \) represents the relative importance level of every m-th objective function given by stakeholders, while \( \mu_{a} \) refers to the total degree of optimality for every a-th Pareto front member. Then,

$$ \mu_{a} = \sum\limits_{m = 1}^{M} {w_{m} \mu_{a}^{m} } $$
(21)

From Fig. 8, the a-th Pareto front member with the largest value of \( \mu_{a} \) is selected from \( F_{1} \) as the most preferred Pareto optimal solution denoted as \( X^{preferred} \) because it produces better optimization on all objective functions of a given multi-objective optimization problem as compared with other Pareto front members by referring to the relative importance of all objective functions.

Fig. 8
figure 8

The pseudo-code of fuzzy decision maker

Full size image

The complete NSMTLBO algorithm

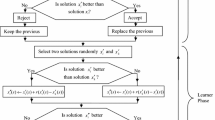
The complete procedures of NSMTLBO are presented in Fig. 9, where \( \gamma \) and \( \varGamma \) denote the counter of function evaluations and maximum fitness evaluation numbers, respectively. During the initialization stage of NSMTLBO, a population P consists of N learners is randomly generated, followed by the function evaluation of these N learners in all M objective functions. The front number, non-domination rank and crowding distance of all learners are then computed, followed by the sorting of members of population P from the best to worst by referring to these metrics.

Fig. 9
figure 9

The pseudo-code of complete NSMTLBO

Full size image

During the search process, the new solution \( X_{n}^{new} \) of each n-th learner is generated via the modified teacher or learner phases and stored in an offspring population denoted as \( {\mathbf{P}}^{{{\mathbf{off}}}} \) with the population size of N. A combined population denoted as \( {\mathbf{P}}^{{{\mathbf{comb}}}} = {\mathbf{P}} \cup {\mathbf{P}}^{{{\mathbf{off}}}} \) with the population size of 2 N is constructed and all members of \( {\mathbf{P}}^{{{\mathbf{comb}}}} \) are sorted from the best to worst based on their non-domination ranks and crowding distances. An operator denoted as \( Trunc\left( { \cdot , \cdot } \right) \) is then applied to truncate the best N members with the lowest \( Rank_{n} \) and largest \( \Delta_{n} \) in \( {\mathbf{P}}^{{{\mathbf{comb}}}} \), aiming to create a new population of P for the next phase or next generation. These procedures are repeated until the termination condition is satisfied, i.e., when the values of fitness evaluation counter exceed the maximum fitness evaluation numbers, i.e.,\( \gamma > \varGamma \). When the proposed NSMTLBO is terminated, the preferred optimal solution denoted as \( X^{preferred} \) is determined from the Pareto front of \( F_{1} \) with the fuzzy decision maker based on the relative importance level specified for each objective function.

Performance metrics

Two evaluation metrics are adopted in this study to compare the optimization performances of all algorithms in tackling the multi-response optimization of PTFE machining problem. The first metric used for performance comparison of two Pareto fronts is a coverage operator of two sets by computing the percentage of members of one Pareto front to be dominated by those of another Pareto front (Zitzler et al. 2000). Denote \( C\left( { \cdot , \cdot } \right) \) as the coverage operator used to compare two Pareto fronts of \( F_{1}^{A} \) and \( F_{1}^{B} \), then

$$ C\left( {F_{1}^{A} ,F_{1}^{B} } \right) = \frac{{\left| {\left\{ {b \in F_{1}^{B} ;\exists a \in F_{1}^{A} :a \prec = b} \right\}} \right|}}{{\left| {F_{1}^{B} } \right|}} $$
(22)

If \( C\left( {F_{1}^{A} ,F_{1}^{B} } \right) = 1 \), it implies that all members of the Pareto front \( F_{1}^{B} \) are dominated or perform equally to all members from \( F_{1}^{A} \). In contrary,\( C\left( {F_{1}^{A} ,F_{1}^{B} } \right) = 0 \) means that none of the solution in \( F_{1}^{B} \) are covered by those of \( F_{1}^{A} \). Notably, it is not guarantee that \( C\left( {F_{1}^{A} ,F_{1}^{B} } \right) \) must be equal to \( 1 - C\left( {F_{1}^{B} ,F_{1}^{A} } \right) \), therefore it is crucial to obtain both results during performance comparisons.

Spacing metric (Coello et al. 2004) is the second metric used for performance comparison by measuring the uniformity of Pareto fronts distribution obtained by different algorithms. Suppose that M refers to the numbers of objective functions to be optimized, while \( \left| {F_{1} } \right| \) represents the number of non-dominated solutions obtained from Pareto front. Then, the smallest Euclidean distance between the a-th and b-th Pareto optimal solutions for each m-th objective function in the objective space is:

$$ d_{a} = \mathop {\hbox{min} }\limits_{a,a \ne b} \sum\limits_{m = 1}^{M} {\left| {\varPsi_{m} \left( {X_{a} } \right) - \varPsi_{m} \left( {X_{b} } \right)} \right|} ,\quad a,b = 1, \ldots ,\left| {F_{1} } \right| $$
(23)

The average value of all \( d_{a} \) is then computed as:

$$ \bar{d} = \frac{{\sum\limits_{a = 1}^{{\left| {F_{1} } \right|}} {d_{a} } }}{{\left| {F_{1} } \right|}} $$
(24)

Define S as the spacing measure to quantify the distance variance of neighbouring Pareto optimal solutions, then

$$ S = \sqrt {\frac{1}{{\left| {F_{1} } \right| - 1}}\sum\limits_{a = 1}^{{\left| {F_{1} } \right|}} {\left( {\bar{d} - d_{a} } \right)^{2} } } $$
(25)

The spacing measure of \( S = 0 \) is the best possible value produced by a compared algorithm because it implies that all of the Pareto front members are equidistant from each other.

Experimental studies

In this section, the capability of the proposed PTFE regression model to fit in the given experimental data is first investigated. The quantitative and qualitative analyses of Pareto fronts produced by NSMTLBO and another six well-established algorithms are then conducted and compared thorough simulation studies. Based on the optimized machining parameters obtained from simulations, the performance deviations between the actual and simulated results were then investigated through further validation experiments in order to confirm the practicability NSMTLBO in solving the PTFE machining problem.

Evaluation of PTFE modelling using analysis of variances (ANOVA)

The goodness-of-fit of the measured data and model was done using a statistical tool known as ANOVA. SD, R2 and P are the output parameters of ANOVA that represent the standard deviation, percentage of variation of data and significance of the control variable (adequacy), respectively. The parameter SD represents how far the date values fall from the fitted values, which seems to be an indicator to show how good of a model in describing the response. The percentage of data variation in the response is qualified using the parameter R2 with the range of 0–100%, where greater values of R2 implies for better fitting in modelling. The probability P is used to check if the tested parameters are essential in determining the responses of model. If \( P < 5\% \), it indicates that the parameters are significant on responses of an adequate model. On the other hand, the parameter is concluded to be insignificant on the responses of an adequate model for \( P > 5\% \).

The Box-Behnken uncoded units were used in this study and the 95% confidence interval was set to find the variance among input machining parameters (Vc, f, ap and Nr) and output responses \( R_{a} \) and MRR. The contribution of each process parameter on the output responses were calculated as shown in Tables 4 and 5. Table 6 shows the parameter R2 which is used to assess the percentage of data variance to the response. It is seen that 97% variability of data of MRR and 95% variability data of surface roughness are around the mean. In other words, the higher R2 shown above, reveals the strength of the relationship between the model and the dependent variable. It is the evidence of the fitness of the models.

Table 4 ANOVA results for modelling the surface roughness of PTFE
Full size table
Table 5 ANOVA results for modelling the material removal rate of PTFE
Full size table
Table 6 Fit statistics (R2) values for material removal rate and surface roughness
Full size table

Performance analysis of NSMTLBO in PTFE machining problem

The parameter settings of all involved multi-objective optimization algorithms considered in solving the proposed PTFE machining optimization problem are first presented. It is followed by the presentation and discussion of simulation results obtained by all algorithms. Both of the qualitative and quantitative analyses are used to compare the optimization performance demonstrated by each compared methods. Finally, the performance deviations between the simulated and experiment results obtained for the surface roughness and material removal rate are compared based on the selected optimized machining parameters.

Parameter settings for simulation and experimental studies

Extensive performance evaluation of NSMTLO was conducted by comparing it with another six well-established algorithms. This included the multi-objective particle swarm optimization (MOPSO) (Coello et al. 2004), non-dominated sorting genetic algorithm II (NSGA-II) (Deb et al. 2002), multi-objective grey wolf optimizer (MOGWO) (Mirjalili et al. 2016), multi-objective teaching–learning based optimization (MOTLBO) (Lin et al. 2015), multi-objective improved teaching–learning based optimization (MO-ITLBO) (Patel and Savsani 2016) and non-dominated sorting teaching–learning based optimization (NSTLBO) (Rao et al. 2018). The concept of external archive is used by MOPSO, MOGOW and MO-ITLBO to store the non-dominated solution found during the optimization. Meanwhile, both mechanisms of fast non-dominated sorting and crowding distance are incorporated into NSGA-II, MOTLBO and NSTLBO for determining the quality of solutions obtained in solving the multi-objective optimization problems. The excellent performances of these six selected algorithms in handling different multi-objective optimization problems were verified in their literatures, hence the performance comparison between NSMTLBO and these peer algorithms are expected to be convincing.

The parameter settings of all compared algorithms were tuned as shown in Table 7 based on the recommendations of their respective literatures. The inertia weight \( \omega \) of MOPSO was set to be reduced from 0.9 to 0.4 in linear manner, while the parameter settings of both acceleration coefficients were given as c1 = c2 = 2.05. For MOPSO and MOGWO, the parameters of grid inflation and number of grid per dimension that are crucial in constructing the external archive were set as \( \alpha = 0.1 \) and \( nGrid = 10 \), respectively. The teaching factor \( T_{f} \) of NSTLBO was randomly generated as 1 or 2, while the NSGA-II has a crossover rate of \( P_{cr} = 0.9 \). A multiple group learning approach with the group number of \( nGroup = 4 \) was adopted by MO-ITLBO during the teaching phase and its archive was managed by epsilon-dominance method with \( \varepsilon = 0.007 \) (Patel and Savsani 2016). For NSMTLBO, the mutation probability were set similar as MOPSO and NSGA-II, i.e., \( P_{mut} = {1 \mathord{\left/ {\vphantom {1 D}} \right. \kern-0pt} D} \) (Deb et al. 2002; Coello et al. 2004). The teaching factors of MOTLBO, MO-ITLBO and NSMTLBO were generated as the values between 1 and 2 to show the different capabilities of learners to improve their knowledge level from the teachers.

Table 7 The parameter settings of all involved multi-objective optimization algorithms
Full size table

Different population sizes of N = 20, 30 and 40 were set to investigate the effect of population sizes on the optimization performances of all compared algorithms based on the recommendation of selected previous works (Natarajan et al. 2018; Rao et al. 2017b). For MOPSO, MOGWO and MO-ITLBO, the archive size \( \left| A \right| \) was set equal to N. Based on most official documents that specify the rules of competition among optimization algorithms the same maximum fitness evaluation number needs to be used as the termination condition of all compared algorithms for the sake of fair performance comparison (Suganthan et al. 2005; K. Tang et al. 2010; Liang et al. 2013). In this study, the maximum fitness evaluation number is set as \( \varGamma = 20,000 \). All algorithms were implemented with a Matlab 2017a software on the workstation consisting of Intel ®Core i7-7500 CPU @ 2.70 GHz. Each compared algorithm was run 20 times independently to obtain their average results.

Results and discussions

Table 8 presents the mean and standard deviation (SD) values of coverage metric obtained by all compared algorithms for N = 20, 30 and 40. The proposed NSMTLBO is reported to have the most competitive optimization performance because of its capability to produce the Pareto fronts with larger percentages of non-dominated solutions as compared with the remaining six peer algorithms in all population sizes. For instance, it is observed that 32.9% of the members of Pareto front obtained by NSGA-II are inferior to those of NSMTLBO for N = 40, whereas only 0.8% of the Pareto front members of NSMTLBO are inferior to those of NSGA-II. There are 17.5% and 6.5% of Pareto front members of MOPSO and MOGWO, respectively, in N = 20 are worse than those of NSMTLBO. In contrary, all Pareto optimal solutions obtained by NSMTLBO are non-dominated by those of MOPSO and MOGWO. For all three TLBO variants considered in benchmarking, MOTLBO demonstrates the worst results because the percentages of its Pareto optimal solutions dominated by NSMTLBO increase with population sizes, i.e., 5.0%, 10.3% and 16.9% for N = 20, 30 and 40, respectively. In contrary, the Pareto optimal solutions of NSMTLBO that are dominated by those of MOTLBO are at least ten times lesser for all population sizes. It is also observed that the performance differences between NSTLBO and NSMTLBO are relatively small because not more than 2.5% of NSTLBO’s Pareto optimal solutions are dominated by NSMTLBO, while there are not more than 0.5% of the Pareto front members produced by NSMTLBO are worse than those of NSTLBO for the population sizes of N = 20, 30 and 40.

Table 8 Performance comparison of coverage metrics of all algorithms for different population sizes
Full size table

Remark

The Pareto fronts generated by NSMTLBO, MOPSO, NSGA-II, MOGWO, MOTLBO, MO-ITLBO and NSTLBO algorithms are represented with RP, SP, TP, UP, VP, Wp and Xp respectively.

The mean and SD values of spacing metric obtained by MOPSO, NSGA-II, MOGWO, MOTLBO, MO-ITLBO, NSTLBO and NSMTLBO for the 20 independent runs in all population sizes are summarized in Table 9. It is reported that the quality of Pareto fronts generated by NSMTLBO are the best for having the non-dominated solution sets that are diversified and yet uniformly distributed as indicated by the lowest spacing values obtained for N = 20, 30 and 40. Among all compared algorithms, the Pareto fronts obtained by NSGA-II in solving the PTFE machining problem has the worst quality because not only majority of the Pareto front members are dominated by those of NSMTLBO, but they also have the poorest distributions. While the MOPSO, MOGWO and MOTLBO can produce lesser Pareto optimal solutions dominated by NSMTLBO, the uniformity and diversity of their Pareto fronts are at least two times worse than those of NSMTLBO according to the spacing metric. It is noteworthy that the Pareto fronts generated by MO-ITLBO and NSTLBO have shown different observations. For MO-ITLBO, the Pareto fronts generated have second best spacing values but they consist of more inferior solutions dominated by NSMTLBO. In contrary, the Pareto fronts produced by NSTLBO have much higher spacing values although it can produce more non-dominated solutions. The poor quality of Pareto fronts obtained by NSTLBO reveals the existence of duplicated non-dominated solutions and this explains the better coverage and yet inferior spacing values. As compared with MO-ITLBO and NSTLBO, the proposed NSMTLBO has more competitive performance in producing the Pareto fronts with better quality and well distributed solutions.

Table 9 Performance comparison of spacing metric of all algorithms for different population sizes
Full size table

In order to evaluate the computational efficiency of each compared algorithm, the mean computation time incurred by MOPSO, NSGA-II, MOGWO, MOTLBO, MOITLBO, NSTLBO and NSMTLBO in 20 independent runs in all population sizes are presented in Table 10. The proposed NSMTLBO has demonstrated promising computation efficiency because the computational time incurred to optimize the PTFE multi-objective machining problems is lesser than those of NSGA-II, MOGWO, MOTLBO and NSTLBO for all population sizes of N = 20, 30 and 40. Although the mean computational time incurred by MOPSO and MO-ITLBO are lower than NSMTLBO in most population sizes, the performance differences of computational efficiency between these three algorithms are not significant. In addition, the proposed NSMTLBO has better performance than MOPSO and MO-ITLBO for being able to produce the Pareto fronts consisting of higher percentages of non-dominated solutions and more uniformly distributed of solution sets. Based on the simulation results shown in Table 10, it is suggested that the proposed modifications incorporated into NSMTLBO can achieve better tradeoff between the extra computational overheads consumed and performance enhancement achieved as compared with majority of peer algorithms.

Table 10 Performance comparison of mean computation times of all algorithms for different population sizes
Full size table

The Pareto-fronts of PTFE machining problem obtained by MOPSO, NSGA-II, MOGWO, MOTLBO, MO-ITLBO, NSTLBO and NSMTLBO for N = 30 are illustrated in Fig. 10. In general, the qualitative results of Fig. 10 are aligned with the quantitative performance analyses reported in Tables 2 and 3. NSGA-II shows the worst optimization performance not only because it has Pareto-front with uneven distribution of solutions, but some solutions obtained are also dominated by the other compared algorithms. For instance, the material removal rate of solution produced by NSGA-II is around 20 cm3/mm when the surface roughness value is 1.6 μm, while other peer algorithms such as MOGWO, MOTLBO, MO-ITLBO, NSTLBO and NSMTLBO can produce the material removal rates higher than 40 cm3/mm with same surface roughness. In addition, it is observed that the Pareto-fronts generated by MOPSO, MOGWO, MOTLBO, MO-ITLBO and NSTLBO are inferior than that of NSMTLBO because the proposed approach can produce higher percentages of non-dominated solutions, especially those at the boundary regions of objective space. For instance, the proposed NSMTLBO is able to obtain five Pareto solutions when surface roughness changes from 1.4 to 1.6 μm, while the MOPSO, MOGWO, MOTLBO and NSTLBO can only produce one, four, four and three Pareto solutions, respectively, for the same range of surface roughness. In contrast to NSMTLBO, the Pareto fronts of MOTLBO, MO-ITLBO and NSTLBO fail to detect a Pareto front member with the surface roughness of 2.7 μmand the material removal rate of 98 cm3/mm. The capability of NSMTLBO in identifying the Pareto optimal solutions located in the boundary regions of objective space is attributed to the promising exploitation strength offered by the modified teacher phase. The mechanism of assigning the nearest non-dominated solution as teacher of each learner allows the refinement of search process around a promising solution. Meanwhile, the unique mean positions generated for each learner by considering different weight contributions of all non-dominated solutions allow the learners to search the regions slightly beyond the promising solutions in order to reach other unvisited non-dominated solutions. Finally, the proposed NSMTLBO also outperforms the MOPSO, MOGWO, MOTLBO and MO-ITLBO for being able to produce the Pareto front with better uniformity. The extra momentum offered by the probabilistic self-learning mechanism in the modified learner phase during the search process can prevent the stagnation of NSMTLBO at the local Pareto-front as well as maintaining the diversity of solutions in Pareto-front.

Fig. 10
figure 10

The Pareto fronts of (a) MOPSO, b NSGA-II, c MOGWO, d MOTLBO, e MO-ITLBO, f NSTLBO and g NSMTLBO

Full size image

After completing the quantitative and qualitative analyses of Pareto-fronts obtained by NSMTLBO, it is equally crucial to validate the optimal process parameters obtained by considering relative importance levels of all objective functions with those actual values of surface roughness (Ra) and material removal rate (MRR) obtained from experiments. Define \( w_{1} \) and \( w_{2} \) as the weightage to imply the importance levels of objectives in minimizing Ra and maximizing MRR, respectively, where \( w_{1} + w_{2} = 1 \). In this section, the weightage setting of \( w_{1} = w_{2} = 0.5 \) are considered on both contradict objectives. This implies that the equal emphasis levels were considered in maximizing the quality and quantity of PTFE product simultaneously during the machining process. The proposed NSMTLBO was first executed with a population size of N = 30 to produce a Pareto-front similar to that of in Fig. 10g. A fuzzy decision maker was then applied to determine the preferred optimum machining parameters based on the predefined weights of \( w_{1} \) and \( w_{2} \) using Eqs. (19) to (21). The predicted and experimental values of \( R_{a} \) and MRR obtained based on the optimum machining parameters were presented in Table 11 together with their error values.

Table 11 Comparison between the predicted and experimental values
Full size table

Given the equal weightage values of \( w_{1} = w_{2} = 0.5 \), the optimum machining parameters obtained by the proposed NSMTLBO are Vc = 160 m/min, f = 0.50 mm/rev, ap = 0.98 mm and Nr = 0.8 mm. The predicted values of surface roughness and material removal rate based on the simulation with these machining parameter settings are \( R_{a} \)= 2.2347 μm and MRR = 96.8347 cm3/mm, respectively. By referring to the validation results presented in Table 11, it is observed that the deviations between the predicted and experimental values of \( R_{a} \) and MRR are 3.26% and 3.7%, respectively. Referring to these negligibly small performance deviations, it can be concluded that the good consistency between the simulated and actual experimental results is achieved.

Conclusions

The experimental design was done and the L27 orthogonal array consisting of three-level of cutting speed \( \left( {V_{c} } \right) \), feed (f), depth of cut (ap) and nose radius \( \left( {N_{r} } \right) \) was formulated. The experiments were performed using a CNC turning machine with cemented carbide tool at an insert angle of 80°. The surface roughness was measured and material removal rate was computed instantly in each experiment. The response surface model (RSM) was rendered from the experimental results and the minimization function of surface roughness and maximization function of material removal rate were derived. ANOVA was applied to determine the relationship between the dependent variable and independent variables.

Apart from developing the regression model of PTFE, an enhanced version of multi-objective optimization algorithm abbreviated as NSMTLBO was designed to tackle the multi-objective machining problem. Some notable modifications were introduced into the proposed NSMTLBO, including: (i) a modified teacher phase consisting of the teacher selection mechanism based on the nearest Euclidean distance and the derivation of weighted mean position for each learner, (ii) a modified learner phase consisting of the probabilistic mutation operator to emulate the self-learning mechanism of learner and (iii) a fuzzy decision maker to determine the preferred non-dominated solution from Pareto front based on the predefined importance levels of objective functions. The optimization performance of NSMTLBO was evaluated through extensive simulation studies and it was proven that the proposed approach can outperform the other six peer algorithms due to its excellent capability in generating the Pareto fronts with better uniformity and higher numbers of non-dominated solutions. Finally, the simulation results obtained by NSMTLBO were validated and it was reported that the performance deviations between the simulated and experimental results of both surface roughness and material removal rates for PTFE are less than 3.70%, implying the applicability of proposed work in machining of PTFE.