Multi-objective optimization of abrasive waterjet machining process using Jaya algorithm and PROMETHEE Method

Abstract

In this work, the process parameters optimization problems of abrasive waterjet machining process are solved using a recently proposed metaheuristic optimization algorithm named as Jaya algorithm and its posteriori version named as multi-objective Jaya (MO-Jaya) algorithm. The results of Jaya and MO-Jaya algorithms are compared with the results obtained by other well-known optimization algorithms such as simulated annealing, particle swam optimization, firefly algorithm, cuckoo search algorithm, blackhole algorithm and bio-geography based optimization. A hypervolume performance metric is used to compare the results of MO-Jaya algorithm with the results of non-dominated sorting genetic algorithm and non-dominated sorting teaching–learning-based optimization algorithm. The results of Jaya and MO-Jaya algorithms are found to be better as compared to the other optimization algorithms. In addition, a multi-objective decision making method named PROMETHEE method is applied in this work in order to select a particular solution out-of the multiple Pareto-optimal solutions provided by MO-Jaya algorithm which best suits the requirements of the process planer.

Introduction

Abrasive waterjet machining (AWJM) process is a widely used modern machining process which is characterized by a number of input process parameters which significantly influence the process output parameters. The input parameters are classified into four groups namely hydraulic parameters, mixing and acceleration parameters, abrasive parameters and cutting parameters. The hydraulic parameters are: pump pressure, water-orifice diameter, water flow rate, etc. The mixing and acceleration parameters are: focus diameter and focus length, workpiece material composition and hardness. The abrasive parameters are: particle hardness, particle shape, particle size distribution, particle diameter and mass flow rate. The cutting parameters are: impact angle, stand-off distance, number of passes, traverse rate, etc.

The performance of AWJM process is measured in terms of the amount of material removed from the work-piece per unit time, smoothness of the cut surface, geometry of the cut in terms of kerf and taper angle, degree of accuracy achieved, satisfying the prescribed geometrical tolerances while machining, rate of wear of orifice and focusing tube. These performance measures are significantly influenced by the input process parameters. For instance, the depth of cut is mainly influenced by abrasive flowrate, waterjet pressure, traverse speed and stand-off distance. Increase in abrasive flow rate increases the number of abrasive particles striking on the workpiece which increases the depth of cut. The velocity of abrasive particles increases with the increase in water jet pressure which increases the depth of cut. At high stand-off distance the kinetic energy of the abrasive particles decreases which reduces the depth of cut.

The waterjet pressure, stand-off distance and traverse speed have a synergistic effect on kerf. At high waterjet pressure and low stand-off distance the diameter of jet is almost equal to the diameter of the orifice which results in low kerf. A low waterjet pressure and high stand-off distance flaring increase the diameter of jet which increases the kerf. Increase in the traverse speed decreases the jet interaction on a given area of material, which leads to material erosion by fewer abrasive particles. This reduces the depth of cut and increases the kerf. However, very low traverse speed increases the production time.

The surface roughness is mainly influenced by abrasive flow rate, waterjet pressure, stand-off distance and size of abrasive particles. As the stand-off distance increases the cutting ability of the abrasive particles decreases due to decrease in the kinetic energy and this increases the surface roughness. Increase in abrasive flow rate reduces the surface roughness because more number of impacts and cutting edges are available per unit area. As the size of the abrasives increases the surface roughness increases due to formation of large size crater on the surface of the work piece surface. Similarly, the other performance measures of AWJM process such as taper angle, geometry of cut, machining accuracy, etc. are influenced by the input process parameters.

Thus, in the presence of multiple input process parameters, selecting the best combination based only on the past experience and judgement is difficult for the process planner. The improper selection of input process parameters may result in poor material removal rate (MRR), low depth of cut, poor geometrical accuracy, poor surface finish and high wear rate of orifice and focusing tube. This may affect the quality of the machined workpiece, effectiveness and efficiency of the process. Therefore, selection of optimal combination of input parameters for AWJM process is a matter of concern for process engineers and researchers. Thus, there arises a need to apply optimization algorithms for determining the optimal combination of input process parameters.

The output process parameters of AWJM process are expressed by means of regression models which are developed by the researchers based on the data gathered by means of actual experimentation on AWJM process. These regression models are mathematical functions of input process parameters which help in precise mapping of the output process parameters corresponding to a particular set of input parameters. Therefore, the researchers have identified the strong need for developing such rigorous mathematical models which form a relationship between input process parameters and output process parameters. Furthermore, these models can be effectively used to form optimization models. These optimization models may be solved using a number of optimization techniques. However, traditional optimization techniques tend to provide a local optimum solution in scenarios where the size of the search space is large, a number of variables are to be handled, multiple objectives are to be achieved and a number of constraints are to be satisfied simultaneously. Therefore, researchers have developed a number of population based optimization algorithms known as the advanced optimization algorithms such as genetic algorithm (GA), particle swarm optimization (PSO) algorithm, simulated annealing (SA), cuckoo search (CS) algorithm, fire fly (FF) algorithm, black hole (BH) algorithm, biogeography based optimization (BBO) algorithm, cuckoo search algorithm (CSA), teaching–learning-based optimization (TLBO) algorithm, etc. These algorithms are found to perform well in such complex optimization scenarios which involve a number of variables, multiple objectives and a number of constraints (Rao and Kalyankar 2014). AWJM process is a multi-input process which requires optimization of multiple objectives. Therefore, it is observed that number of researchers have used the advanced modeling techniques such as response surface methodology (RSM), Taguchi’s method, artificial neural networks (ANN), fuzzy logic, etc. in order to formulate the process models and advanced optimization algorithms to optimize the input process parameters of AWJM processes. Such works carried out by various researchers are summarized in Table 1.

Table 1 Summary of AWJM process parameters optimization review

It is observed that a number of nature-inspired population based optimization algorithms such as GA, SA, ABC, PSO, CS, COA, FF, BH, BBO, TLBO, etc. have been applied by the researchers for optimizing the input process parameters of AWJM process. However, the main limitation of these nature-inspired population based optimization algorithms is the need for setting of common control parameters like population and number of generations. In addition to common control parameters, these nature-inspired optimization algorithms require setting of their own algorithm-specific parameters. For instance, the GA requires tuning of algorithm specific parameters such as cross-over probability, mutation probability, selection operator, etc. The PSO algorithm requires tuning of algorithm-specific parameters such as inertia weight, cognitive and social coefficients. The SA algorithm requires tuning of initial temperature and cooling rate. The ABC algorithm requires algorithm-specific parameters such as number of scout bees, number of onlooker bees, number of employed bees, limit, etc. The CS algorithm requires tuning of levy flight constant and selection probability. The BBO algorithm requires tuning of algorithm-specific parameters such as habitat modification probability, mutation probability, maximum species count, maximum migration rates and maximum mutation rate. The FF algorithm requires tuning of algorithm-specific parameters such as attractiveness at source, randomness coefficient and absorptivity index.

The common control parameters and algorithm-specific parameters for any algorithm are required to be selected meticulously to achieve effective performance of the algorithm, to avoid convergence at local optima and to minimize the computational effort. In order to determine the best combination of common control parameters and algorithm-specific parameters for any optimization algorithm the user is required to perform a number of computational trials. Therefore, there is a need to develop an advanced optimization algorithm which is free from algorithm-specific parameters.

Recently, Rao (2016) has proposed a new metaheuristic optimization algorithm which does not require tuning of any algorithm-specific parameters for its working and it is named as Jaya algorithm. In order to implement the Jaya algorithm the user is only required to tune the common control parameters like population size and number of generations. In addition to algorithm specific parameter-less control, other distinctive features of Jaya algorithm are simplicity and ease of implementation, as the solutions are updated using a single equation. The effectiveness of Jaya algorithm was proved on a number of constrained and unconstrained benchmark functions and engineering optimization problems (Rao 2016; Rao and Waghmare 2016).

The AWJM process is a multi-input process requiring simultaneous optimization of the multiple responses. (Rao 2011; Rostami and Neri 2017). Therefore, there arises a need to formulate the multi-objective optimization problems (MOOPs) and determine the Pareto-efficient set of solutions. These MOOPs can be effectively solved using a priori approach such as weighted sum, $\varepsilon$-constraint method, achievement scalarizing function, etc. However, in a priori approach, in order to obtain a set of distinct solutions, it is required to run the algorithm independently for each set of weights. Another approach to solve MOOPs is, a posteriori approach, in such approach it is not required to assign the weights to the objective functions prior to the simulation run and multiple tradeoff (Pareto-efficient) solutions for a MOOP is obtained in a single run of simulation. The decision maker can then select one solution from the set of Pareto-efficient solutions based on the requirement or order of importance of objectives. Keeping in view of the advantages of the posteriori approach, researchers have developed posteriori versions of well-known optimization algorithms such as multi-objective differential evolution (MODE), non-dominated sorting genetic algorithm (NSGA), multi-objective particle swarm optimization (MOPSO), etc. These posteriori multi-objective optimization algorithms have been widely applied by the researchers to solve the multi-objective optimization problems in the field of engineering and science (Zhou et al. 2011). Chandrasekaran et al. (2010) proposed a posteriori multi-objective optimization algorithm based on clonal selection for solving engineering optimization problems. Falco et al. (2016) used multi-objective evolutionary algorithm for optimizing personalized touristic itineraries. Yu et al. (2016) proposed a prediction-based multi-objective evolutionary algorithm (MOEA) with NSGA-II for oil purchasing and distribution.

In this work a posteriori population based multi-objective version of the Jaya algorithm is applied to solve the MOOP of abrasive water-jet machining processes and is named as “Multi-objective Jaya algorithm (MO-Jaya)” algorithm. Similar to the Jaya algorithm, the MO-Jaya algorithm does not require tuning of any algorithm-specific parameters for its working. This averts the risk of algorithm getting trapped into local optima or slow convergence rate due to improper tuning of algorithm-specific parameters by the user. Furthermore, in the MO-Jaya algorithm the solutions are updated only in a single phase using a single equation. Therefore, the MO-Jaya algorithm is simple in implementation. The MO-Jaya algorithm has already proved its effectiveness in improving the performance of a number of modern machining processes and has shown better performance as compared to other optimization algorithms such as GA, NSGA, NSGA-II, BBO, NSTLBO, PSO, SQP and Monte Carlo simulations (Rao et al. 2017). Therefore, in the present work the MO-Jaya algorithm is applied to solve the input process parameters optimization problems of AWJM process.

The Jaya and MO-Jaya algorithms are described in “Optimization methodology” section. A computer code for MO-Jaya algorithm is developed in MATLAB R2009a. A computer system with a 2.93 GHz processor and 4 GB RAM is used for execution of the program.

Optimization methodology

Jaya algorithm

The Jaya algorithm mimics the behavior exhibited by bio-logical species to survive and succeed in their respective habitats. There are a million of different species available in our eco-system. However, a common behavior exhibited by most of the species is to imitate the most successful member in the group at the same move away from the unsuccessful member of the group. Similarly, in the Jaya algorithm the solutions in the current population are analogous to a group of certain species. The most successful member in the group is analogous to the best solution, while, the most unsuccessful member in the group is analogous to the worst solution.

In the Jaya algorithm P initial solutions are randomly generated obeying the upper and lower bounds of the process variables. Thereafter, each variable of every solution is stochastically updated using Eq. (1). The best solution is the one with maximum fitness (i.e. best value of objective function) and the worst solution is the one with lowest fitness (i.e. worst value of objective function).

$$\begin{aligned} O_{p+1, q, r}= & {} O_{p, q, r} + \alpha _{p, q, 1} (O_{p, q, best} - abs(O_{p, q, r} )) \nonumber \\&-\, \alpha _{p, q, 2} (O_{p, q, worst} - abs(O_{p, q, r} ) ) \end{aligned}$$

(1)

Here best and worst represent the index of the best and worst solutions among the population. p, q, r are the index of iteration, variable, and candidate solution. $O_{p, q, r}$ means the $q{\mathrm{th}}$ variable of $r{\mathrm{th}}$ candidate solution in $p{\mathrm{th}}$ iteration. $\alpha _{p, q, 1}$ and $\alpha _{p, q, 2}$ are numbers generated randomly in the range of [0, 1]. The random numbers $\alpha _{p, q, 1}$ and $\alpha _{p, q, 2}$ act as scaling factors and ensure exploration. The absolute value of the variable (instead of a signed value) also ensures exploration. Figure 1 shows the flowchart for Jaya algorithm.

Fig. 1

Flowchart for Jaya algorithm

An improtant feature of the Jaya algorithm which ensures convergence is the selection procedure. Once every solution is modified based on Eq. (1), the fittness of new solutions $(O_{p+1})$ is evaluated based on the objective function. Thereafter, the fitness of every new solution is compared with its respective parent solution $(O_{p})$ and the new solution is selected for the next iteration, if and only if its fitness is better than the parent solution. If the fitness of the new solution is better than the parent solution then the parent solution is discared and replaced by the new solution. However, if the fitness of the new solution is not better than the parent solution then it is discarded and the parent solution is kept as it is and taken to the next iteration. This type of selection procedure ensures selection of only superior solutions in every iteration of the Jaya algorithm. Therefore, in each iteration of Jaya algorithm the solutions always move closer to the best solution and thus convergence is achieved.

MO-Jaya algorithm

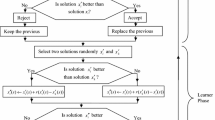
The MO-Jaya algorithm is a posteriori version of Jaya algorithm for solving MOOPs. The solutions in the MO-Jaya algorithm are updated in the similar manner as in the Jaya algorithm based on Eq. (1). In the interest of handling problems in which more than one objective co-exist the MO-Jaya algorithm is embedded with dominance ranking approach and crowding distance evaluation approach (Deb et al. 2002; Rao 2015).

In the MO-Jaya algorithm, the superiority among the solutions is decided according to the non-dominance rank and value of the density estimation parameter i.e. crowding distance ($\xi$). The solution with highest rank (i.e. rank = 1) and largest value of $\xi$ is chosen as the best solution. On the other hand the solution with the lowest rank and lowest value of $\xi$ is selected as the worst solution. Such a selection scheme is adopted so that solution in less populous region of the objective space may guide the search process. Once the best and worst solutions are selected, the solutions are updated based on the Eq. (1).

After all the solutions are updated, the updated solutions are combined with the initial population so that a set of 2P solutions (where P is the size of initial population) is formed. These solutions are again ranked and the $\xi$ value for every solution is computed. Based on the new ranking and $\xi$ value P good solutions are chosen. The flowchart of MO-Jaya algorithm is given in Fig. 2.

Fig. 2

Flowchart for MO-Jaya algorithm

In the case of MO-Jaya algorithm, in each iteration, all the initial solutions in the population are updated according to Eq. (1) to obtain the new solutions. Thereafter, a combined population is formed by combining initial solutions and the new solutions. Now from the combined population, good solutions are selected based on the non-dominance rank and crowding distance value and only the good solutions are taken to the next iteration. Such a selection procedure prevents the inferior solutions (i.e. lower rank solutions) from entering into the next iteration. As the algorithm progresses, the number of non-dominated solutions in the population increases. This ensures that, in every iteration of MO-Jaya algorithm, the solutions always move towards the Pareto-optimal set in every iteration. Finally, the algorithm converges at the Pareto-optimal set.

For every candidate solution the MO-Jaya algorithm evaluates the objective function only once in each iteration. Therefore, the total no. of function evaluations required by MO-Jaya algorithm = population size $\times$ no. of iterations. However, when the algorithm is run more than once, then the number of function evaluations is to be calculated as: no. of function evaluations = no. of runs $\times$ population size $\times$ number of iterations. The methodology used for ranking of solutions, computing the crowding distance and crowding comparison operator are described in the following subsections.

Ranking methodology

The approach used for ranking of solutions is based on the non-dominance relation between solutions and is described as follows. In an M objective optimization problem, P is the set of solutions to be sorted and $n = {\vert } P{\vert }$.

Domination A solution $x_{1}$ is said to dominate another solution $x_{2}$ if and only if $f_{i}$ ($x_{1}) \le f_{i}$ ($x_{2})$ for all 1 $\le i \le M$ and $f_{i}$ ($x_{1}) <f_{i}$ ($x_{2})$ for at least one i, where $i \in \{1,{\ldots }., M\}$ (when all objectives are to be minimized).

Non-domination A solution $x^{*}$ in P is non-dominated if there does not exist any solution $x_{j}$ in $P_{-}$ which dominates x*

Similarly, every solution in P is competes with every other solution and the not dominated solution are removed from P and assigned rank one. The remaining solutions in P are again sorted in the same way and the not dominated solutions are removed and assigned rank two. Unless all the solutions in P receive a rank this procedure is continued. A group of solutions with same rank is known as front (F)

Computing the crowding distance

The crowding distance $(\xi _{j})$ is an estimate of the density of the solutions in the vicinity of a particular solution j. For a particular front F, let $l ={\vert }F{\vert }$ then for each member in F, $\xi$ is calculated as follows.

Step 1: Initialize $\xi _{j} = 0$

Step 2: Sort all solutions in F the set in the worst order of objective function value $f_{m}$.

Step 3: In the sorted list of $m\mathrm{th}$ objective assign infinite crowding distance to solutions at the extremes of the sorted list (i.e. $\xi _{1} = \xi _{l}=\infty )$, for $j = 2$ to ($l-1$), calculate $\xi _{j}$ as follows:

$$\begin{aligned} \xi _j = \xi _j +\frac{ {f}_{m}^{j+1} - {f}_{m}^{j-1} }{{f}_{m}^{\max } -{f}_{m}^{\min } } \end{aligned}$$

(2)

where, j represents a solution in the sorted list, $f_{m}$ is the objective function value of $m\mathrm{th}$ objective of $j\mathrm{th}$ solution, and are the highest and the lowest values of the $m\mathrm{th}$ objective function in the current population. Likewise, $\xi$ is computed for all the solutions in all Fs

In the case of MOOPs there exists more than one optimal solution. Therefore, the aim is to find a set of Pareto-efficient solutions. In MO-Jaya algorithm in order to avoid clustering of solutions about a single good (higher rank) solution, the good solutions in the isolated region of the search space are identified based on the $\xi$ value, and a solution with a higher rank and higher $\xi$ value is considered as the best solution in the next generation. Thus, the other solutions in the population will be directed towards the good solution which lies in the less populous (isolated) region of the search space in the next generation. This will prevent the algorithm from converging to single optimum solution and ensure diversity among the solutions. For this purpose a solution from the more isolated region of search space is given more preference than the solution in the crowded region of the search space. In the MO-Jaya algorithm, among the two competing solutions i and j, primarily, the solution with a higher rank is preferred. If the two solutions have equal rank then the solution with a higher $\xi$ value is preferred.

Improved preference ranking organization method for enrichment evaluations

Selecting one solution out-of the multiple Pareto-optimal solutions provided by the MO-Jaya algorithm, based on the decision maker’s order of importance to the objectives, is a multi-criteria decision making (MCDM) problem. The multiple Pareto-optimal solutions are treated as alternatives and the objectives form the selection criteria. Rao and Patel (2010) proposed a multi-criteria decision making method named as improved preference ranking organization method for enrichment evaluations (improved PROMETHEE) and demonstrated its effectiveness in solving various decision making problems in the manufacturing environment.

Now in this work the improved PROMETHEE method is employed to select the best solution out-off the set of multiple solutions provided by MO-Jaya algorithm for optimization problems of modern machining processes. Like other MCDM techniques, the improved PROMETHEE method also employs pairwise comparison of the alternatives with respect to a particular criterion. If a1 and a2 are the two alternatives, then, the improved PROMETHEE method uses a preference function $(P_{i})$ to translate the difference between the evaluations obtained by two alternatives (a1 and a2) in terms of a particular criterion into a preference degree ranging from 0 to 1 which is mathematically expressed by Eqs. (3) and (4).

$$\begin{aligned}&P_{i,a1 a2} =G_i [c_i (a1)-c_i (a2)] \end{aligned}$$

(3)

$$\begin{aligned}&0 \le P_{i,a1,a2} \le 1 \end{aligned}$$

(4)

where,$G_{i}$ is a non-decreasing function of the observed deviation $(c_i (a1)-c_i (a2))$ between two alternatives a1 and a2 over the criterion $c_{i}$; i represents a particular criterion. Further, the multiple criteria preference index is evaluated as the weighted average of preference functions $P_{i}$ which is mathematically expressed by Eq. (5).

$$\begin{aligned} \Pi _{a1 a2} = \sum _{i=1}^M {w_i P_{i,a1,a2} } \end{aligned}$$

(5)

where, $w_{i}$ is the weights assigned by the decision maker to each criterion and M is the total number of selection criteria. $\prod _{a1 a2}$ is the overall preference index of alternative a1 over alternative a2. The next step is to evaluate the leaving flow, entering flow and the net flow for a particular alternative a, which belongs to the set of alternatives A, using the following equations.

$$\begin{aligned}&\varphi ^{+}(a)=\sum _{x \in A} {\prod _{xa} } \end{aligned}$$

(6)

$$\begin{aligned}&\varphi ^{{-}}(a)=\sum _{x \in A} {\prod _{xa} } \end{aligned}$$

(7)

$$\begin{aligned}&\varphi (a)= \varphi ^{+}(a) -\phi ^{-}(a) \end{aligned}$$

(8)

where, $\varphi ^{+}(a)$is called the leaving flow, $\varphi ^{{-}}(a)$ is called the entering flow and $\varphi (a)$ is called net flow. An alternative a1 out-ranks alternative a2 if $\varphi (a1) >\varphi (a2)$. The improved PROMETHEE method provides complete ranking of alternatives from best to worst using the net flows.

Performance measure

In order to compare the quality of Pareto-fronts obtained by optimization algorithms the hypervolume metric is used in this work. Hypervolume gives the volume (area in the case of bi-objective optimization problems) of the search space which is dominated by a Pareto-front obtained by a particular algorithm with respect to a given reference point. Therefore for a particular algorithm a higher value of hypervolume is desirable which indicates the quality of the Pareto-front obtained by the algorithm.

Mathematically, for a Pareto-front containing Q solutions, for each solution i belongs to Q, a hypervolume $v_{i}$ is constructed with reference point W and the solution i as the diagonal corners of the hypercube. Thereafter the union of these hypercubes is found and its hypervolume is calculated as follows.

$$\begin{aligned} { HV} ={ volume} \left( {\bigcup _{{\mathrm{i}=1}}^{\left| {Q} \right| } {{v}_{\mathrm{i}} } } \right) \end{aligned}$$

(9)

A superior Pareto-front is characterized by three important criteria which are as follows: (1) quality of solutions i.e. solutions in a Pareto-front should be superior in terms of objective function values, (2) diversity among the solutions i.e. the solutions in a Pareto-front must be uniformly distributed as much as possible and (3) pertinence i.e. a Pareto-front must contain as many number of solutions as possible so as to give maximum possible choices to the decision maker. The hypervolume is one such performance indicator which compares two sets of Pareto-optimal solutions on the basis of the all three aforementioned performance criteria simultaneously (Zitzler and Thiele 1999; Rostami and Neri 2017). Therefore, in the present work, the hypervolume indicator is used for comparison of Pareto-fronts obtained by MO-Jaya algorithm with the Pareto-fronts obtained by other optimization algorithms.

Case studies

This section describes three optimization case studies of AWJM process. Single objective and multi-objective optimization problems are formulated based on the regression models developed by previous researchers and the same are solved using Jaya algorithm and multi-objective Jaya algorithm, respectively, and the results are reported.

Case study 1

In the case of AWJM process, Kerf is an important performance characteristic as it directly governs the geometry of the cut produced by the abrasive waterjet. For superior quality of the machined components it is required to achieve a uniform cut within the prescribed geometrical tolerances. Thus, the minimization of Kerf is desirable. On the other hand a superior surface finish in the machined components is desirable in order to minimize the effect of wear and friction. For this purpose minimization of mean surface roughness $R_{a}$ in machined components is desirable. Kechagias et al. (2012) showed that Kerf andRa are mutually conflicting in nature and are largely influenced by input process parameters such as material thickness ‘A’ (mm), nozzle diameter ‘B’ (mm), stand-off distance ‘C’ (mm), traverse speed ‘D’ (mm/min). Kechagias et al. (2012) developed precise regression models based on actual experimental data in order to map the relationship between the input process parameters with Kerf and Ra. However, as Kerf and Ra govern the quality of the machined components in AWJM process, besides developing regression models, it is important to determine the combination of input process parameters that will provide a trade-off between Kerf and Ra. For this purpose, in the present case study, the regression models developed by Kechagias et al. (2012) are used to formulate a multi-objective optimization problem and the same is solved using MO-Jaya algorithm.

Objective functions

$$\begin{aligned} { Minimize\,\,Kerf}= & {} 0.86068{-}0.068333\times {A}+0.61131\times {B}\nonumber \\&+\,0.0021518\times {C-}0.0020416\times {D} \nonumber \\&{-}\,0.3596\times {A}\times {B}+0.0030106\nonumber \\&\times {B}\times {C}+\,0.0019143\nonumber \\&\times {B}\times {D} {-}1.0143E-5\times {C}\times {D} \end{aligned}$$

(10)

$$\begin{aligned} { Minimize}\,\,{R}_a= & {} {-}11.106+10.211\times {A}+15.169\nonumber \\&\times {B}+\,0.0047057\times {C}+0.011813\times {D} \nonumber \\&{-}\,10.331\times {A}\times {B}+0.01012\times {B}\nonumber \\&\times \,{C-}0.0074535\nonumber \\&\times \,{B}\times {D}+7.1924E-6\times {C}\times {D} \end{aligned}$$

(11)

Process parameters

$$\begin{aligned}&0.9 \le A \le 1.25 \end{aligned}$$

(12)

$$\begin{aligned}&0.95 \le B \le 1.5 \end{aligned}$$

(13)

$$\begin{aligned}&20 \le C \le 96 \end{aligned}$$

(14)

$$\begin{aligned}&200 \le D \le 600 \end{aligned}$$

(15)

The Kerf and $R_{a}$ are mutually conflicting performance measures as the process parameter setting which may give a minimum value of Kerf may increase $R_{a}$. The process parameter setting which may lead to minimum $R_{a}$ may simultaneously increase Kerf. Therefore, it is necessary to achieve a trade-off between Kerf and $R_{a}$ in order to achieve the best performance of the AWJM process. Therefore, in this work MO-Jaya algorithm is applied to simultaneously optimize Kerf and $R_{a}$ and achieve multiple trade-off solutions.

In order to set the population size for MO-Jaya algorithm, computational experiments are conducted by varying the population size from 10 to 70 in a step size of 10. It is observed that the population size of 50 and maximum number of iterations equal to 100 provided the best result for MO-Jaya algorithm (i.e. maximum number of function evaluations = $50 \times 100 = 5000$). The Pareto-efficient set of solutions obtained by MO-Jaya algorithm in a single simulation run is reported in Table 2. Fifty optimal combinations of input process parameters like material thickness, nozzle diameter, stand-off distance and traverse speed are provided in Table 2 along with the corresponding values of Kerf and Ra.

Table 2 Pareto-efficient solutions obtained using MO-Jaya algorithm for case study 1

Now, in order to show the effectiveness of MO-Jaya algorithm, the results of MO-Jaya algorithm are compared with the non-dominated sorting teaching–learning-based optimization algorithm (NSTLBO) algorithm. The NSTLBO algorithm is a posteriori version of TLBO algorithm. Similar, to the MO-Jaya algorithm the NSTLBO algorithm does not require tuning of any algorithm-specific parameters and provides a set of multiple Pareto-optimal at the end of every simulation run. Furthermore, the NSTLBO algorithm has been found successful in solving the multi-objective optimization problems of machining processes such as turning process, wire-electric-discharge machining process, focused ion beam micro-milling process, micro wire-electric discharge machining process and laser cutting process (Rao et al. 2016). The NSTLBO algorithm had provided better results as compared to the other well-known optimization algorithms such as GA, PSO, NSGA-II and iterative search method (Rao et al. 2016). Therefore, considering the effectiveness of NSTLBO algorithm in solving the multi-objective optimization problems of machining processes, in this work the NSTLBO algorithm is applied to solve the optimization problems of AWJM process and the results are compared with the results of MO-Jaya algorithm.

For the purpose of comparison, the same problem is solved using NSTLBO algorithm with a population size of 50 and maximum number of function evaluations equal to 5000. The Pareto-fronts obtained by MO-Jaya and NSTLBO algorithms are shown in Fig. 3. The MO-Jaya algorithm achieved a higher hypervolume as compared to NSTLBO algorithm (HV$_{MO{\text{- }}Jaya}$ = 1.4235; HV$_{NSTLBO}$ = 1.352). The MO-Jaya and NSTLBO algorithms required 1800 and 2200 function evaluations, respectively to converge at the Pareto-optimal set of solutions. The CPU time required by MO-Jaya and NSTLBO algorithms is 5.822 and 8.6183 s, respectively to perform 5000 function evaluations.

The MO-Jaya algorithm has provided 50 Pareto-optimal solutions for the optimization problem considered in this case study. The user is now required to choose one solution out-of the 50 solutions provided by MO-Jaya algorithm based on his order of preference to Kerf and $R_{a}$. This forms a decision making problem with 50 alternatives and two selection criteria i.e. Kerf and $R_{a}$. Both the criteria are considered as non-beneficial criteria. To demonstrate the applicability of the improved PROMETHEE method, three different sets of weights are considered and the best choice corresponding to each of the considered set of weights provided by improved PROMETHEE method is shown in Table 3. The steps of the improved PROMETHEE method for evaluating the alternatives are shown in the “Appendix A”. In Table 3, three optimal combinations of input process parameters are provided which correspond to different sets of weights; $w_{1}$ and $w_{2}$ represent the weights assigned to Kerf and $R_{a}$, respectively. By changing the values of weights three decision making scenarios are formed. Scenario 1 and scenario 2 are formed by assigning high importance to Kerf and $R_{a}$, respectively. Scenario 3 is formed by assigning equal importance to both the criteria. The choice of the best alternative provided by improved PROMETHEE method out-of the 100 alternatives in each of the decision making scenario is shown in Table 3. The weights assigned to the criteria in this work are only for the purpose of demonstration. However, the decision maker may choose any set of weights based on his interests and may select the best alternative using the improved PROMETHEE method.

Fig. 3

Pareto-fronts obtained by MO-Jaya and NSTLBO algorithms for case study 1

Table 3 The best choice provided by PROMTHEE method corresponding to different set of weights for case study 1

Case study 2

In the case of AWJM process, depth of penetration ‘DOP’ and surface roughness ‘$R_{a}$’ are considered as important performance parameters. This is mainly because DOP directly corresponds to the material removal rate which governs the machining time and efficiency. On the other hand, $R_{a}$ of the machined components governs the production quality. Therefore, maximization of depth of penetration and minimization of surface roughness is desirable in order to achieve production efficiency and product quality. However, Liu et al. (2014) showed that depth of penetration and surface roughness are mutually conflicting in nature and depend upon a number of process parameters such as traverse speed ‘A’ (mm/s), pressure ‘B’ (MPa), stand-off distance ‘C’ (mm), tilt angle ‘D’ (degree), surface speed ‘E’ (m/s) and abrasive flow rate ‘F’ (g/s). Liu et al. (2014) had developed precise regression models for DOP($\upmu$m) and $R_{a}(\upmu$m) considering the aforementioned process parameters based on actual experimental data. Now considering the importance of DOP and $R_{a}$ and their mutually conflicting nature, it is important to achieve a trade-off between the two. Therefore, in the present work, a multi-objective optimization problem is formulated based on the regression models developed by Liu et al. (2014) and the same is solved using MO-Jaya algorithm in order to obtaine trade-off between DOP and $R_{a}$.

Objective functions

$$\begin{aligned} { Maximize\,\,DOP}= & {} 671.17-1107.08 {A-}1.03{B-}8.49{D}\nonumber \\&+\,13.27{F}-2.11{AB}-35.74{AC} \nonumber \\&-\,42.93{AF}+0.028{BD}+0.89{CF}\nonumber \\&+\,2666.77{A}^{{2}}\end{aligned}$$

(16)

$$\begin{aligned} { Minimize\,\,R}_a= & {} 33.17+0.023 E\nonumber \\&+\,1.53 F-1.49{AC-}0.12{AD-}1.87{AF} \nonumber \\&+\,0.00084{BD}-0.0029{BE-}0.0051{BF}\nonumber \\&+\,0.0086{CD}+0.066{CE}\nonumber \\&+\,0.061{CF}+0.011{DE} \nonumber \\&-\,0.014{DF-}0.081{EF}+8.23{A}^{{2}}\nonumber \\&-\,0.00019{B}^{{2}}-0.029{C}^{{2}}+0.0027D^{2} \nonumber \\&+\,0.079F^{2} \end{aligned}$$

(17)

Process parameters

$$\begin{aligned}&0.1 \le A \le 0.5 \end{aligned}$$

(18)

$$\begin{aligned}&200 \le B \le 320 \end{aligned}$$

(19)

$$\begin{aligned}&2 \le C \le 10 \end{aligned}$$

(20)

$$\begin{aligned}&60 \le D \le 90 \end{aligned}$$

(21)

$$\begin{aligned}&2 \le E \le 8 \end{aligned}$$

(22)

$$\begin{aligned}&5 \le F \le 11.67 \end{aligned}$$

(23)

Desirability function approach was used by Liu et al. (2014) in order to optimize DOP and $R_{a}$ simultaneously and two trade-off solutions were provided. In the present work the MO-Jaya algorithm is applied for simultaneous optimization of DOP and $R_{a}$. In order to see whether any improvement in the results is obtained, the solutions obtained by Liu et al. (2014) using desirability approach are considered as it is and the same are compared with the solutions obtained using MO-Jaya algorithm. In order to select a population size for MO-Jaya algorithm computational experiments are conducted by varying the population size from 20 to 70 with a step size of 10. A population size of 50, a maximum number of iterations equal to 100 (i.e. maximum number of function evaluations equal to 50,000)is chosen for MO-Jaya algorithm. The Pareto-efficient set of solutions obtained using MO-Jaya algorithm in a single simulation run is shown in Table 4.

For the purpose of comparison the same problem is solved by NSTLBO algorithm. The Pareto-fronts obtained by MO-Jaya and NSTLBO algorithms are shown in Fig. 4 and the quality of the Pareto-fronts is judged based on the hypervolume metric. Although, the Pareto-fronts obtained by MO-Jaya and NSTLBO algorithms overlap each other The MO-Jaya algorithm obtained a higher value of hypervolume ($\hbox {HV}_{\mathrm{MO}{\text{- }}\mathrm{Jaya}}=15,335$) as compared to NSTLBO algorithm $(\hbox {HV}_{\mathrm{NSTLBO}}= 15{,}100)$. MO-Jaya and NSTLBO algorithms required 1250 and 1500 function evaluations, respectively, to converge at the Pareto-efficient set of solutions. The MO-Jaya and NSTLBO algorithms required a CPU time of 9.305 and 10.789 s, respectively, to perform 5000 function evaluation.

Table 4 Pareto-efficient solutions obtained using MO-Jaya algorithm for case study 2

Table 5 gives optimum process parameter combination suggested by desirability approach and its comparison with the results of MO-Jaya algorithm. It is observed that the results of MO-Jaya algorithm are better than the results obtained using desirability approach in terms of DOP and $R_{a}$.

Fig. 4

Pareto-fronts obtained by MO-Jaya and NSTLBO algorithms for case study 2

The MO-Jaya algorithm has provided 50 Pareto-optimal solutions for the multi-objective optimization problem considered in this case study. The decision maker is now required to choose one out-of the 50 alternative solutions with DOP and $R_{a}$ as selection criteria. This forms a decision making problem with two criteria and 50 alternatives where DOP is the beneficial criteria and $R_{a}$ as non-beneficial criteria. To demonstrate the applicability of improved PROMETHEE method, three different set of weights are considered. The steps in the improved PROMETHEE method are similar to those discussed in “Optimization methodology” section. The best choice corresponding to each of the considered set of weights provided by improved PROMETHEE method is shown in Table 6.

Table 5 Comparison of results obtained by desirability approach and MO-Jaya algorithm for case study 2

Table 6 The best choice provided by PROMTHEE method corresponding to different set of weights for case study 2

Table 7 Results of single objective optimization for case study 3

Case study 3

In the case of AWJM process, in order to improve the quality of the machined components it is important to achieve a uniform cut within the prescribed geometrical tolerances. The geometry of the cut is mostly governed by Kerf top width ‘Ktw’ and taper angle. Thus, in order to achieve a uniform cut it is important to maximize the Ktw and minimize the taper angle. Shukla and Singh (2016a) studied the influence of input process parameters such as traverse speed ‘$x_{1}$’ (mm/min), stand-off distance ‘$x_{2}$’ (mm), and mass flow rate ‘$x_{3}$’ (gm/sec) on Ktw and taper angle and developed regression models. Shukla and Singh (2016a) used these regression models to formulate an optimization problem. Shukla and Singh (2016a) optimized Ktw and taper angle separately using PSO, SA, FA, BH, CSA and BBO algorithms. Furthermore, Shukla and Singh (2016a) optimized Ktw and taper angle, simultaneously, using NSGA algorithm. Now in order to see whether any further improvement in the results can be achieved this case study is considered in the present work. The same optimization problem is solved using Jaya and MO-Jaya algorithms and the results are compared with the results reported by Shukla and Singh (2016a).

Objective functions

$$\begin{aligned} { Maximize\,\,Ktw}= & {} 12.7538-0.0974 {x}_{1} +0.0913x_2 \nonumber \\&-\,1.0424 {x}_{3} + 0.0002x_1^2 - 0.0289 {x}_{2}^{2} \nonumber \\&+\,0.12011x_3^2 +0.0016x_1 x_2 \nonumber \\&+\,0.0032x_1 x_3 \end{aligned}$$

(24)

$$\begin{aligned} { Minimize\,\,taperangle}= & {} 26.0879-0.2401 {x}_{1} +0.5024x_2 \nonumber \\&-\,2.2168 {x}_{3} + 0.0006x_1^2 - 0.0884 {x}_{2}^{2} \nonumber \\&0.3657x_3^2 +0.0024x_1 x_2 \nonumber \\&+\,0.0028x_1 x_3 \end{aligned}$$

(25)

Process parameter bounds

$$\begin{aligned}&160 \le x_{1} \le 200 \end{aligned}$$

(26)

$$\begin{aligned}&1 \le x_{2} \le 5 \end{aligned}$$

(27)

$$\begin{aligned}&1.5 \le x_{3} \le 3.5 \end{aligned}$$

(28)

Shukla and Singh (2016a) optimized Ktw and taper angle individually using PSO, SA, FA, BH, CSA and BBO algorithms. Now Jaya algorithm is applied to individually optimize Ktw and taper angle. For this purpose a population size of 25, maximum number of iterations equal to 20 (i.e. maximum number of function evaluations equal to 500) and the number of independent runs equal to 10 are selected for Jaya algorithm. Shukla and Singh (2016a) did not provide the size of initial population used for PSO, FA, BH, CSA and BBO algorithms, therefore, the maximum number of function evaluations required by these algorithms cannot be determined.

The results of Jaya algorithm are compared with the results of algorithms such as PSO, FA, BH, CSA and BBO (Shukla and Singh 2016a) and are reported in Table 7.The optimal combination of input process parameters such as traverse speed, stand-off distance and mass flow rate obtained by different algorithms are shown in Table 7 along with the corresponding optimum values of Ktw and taper angle. It can be observed that the Jaya algorithm could achieve the best value of Ktw in only 2 iterations which is much better as compared to the number of iterations required by PSO, SA, FA, BH, CSA and BBO algorithms.

The Jaya algorithm could achieve a value of taper angle which is better than the best value of taper angle obtained by Shukla and Singh (2016a). The Jaya algorithm required only 6 iterations to obtain the minimum value of taper angle which is much better as compared to the number of iterations required by PSO, SA, FA, BH, CSA and BBO algorithms (refer Table 7). Furthermore, the Jaya algorithm was executed 10 times independently and the mean, standard deviation (SD) and CPU time required by Jaya algorithm for 10 independent runs is recorded and the same is compared with mean, SD and CPU time required by BBO algorithm in Table 8. It is observed that the Jaya algorithm achieved the same value of Ktw and taper angle for all 10 independent runs. Therefore, Jaya algorithm has shown more consistency and robustness and required less CPU time as compared to BBO algorithm. Figures 5 and 6 give the convergence graph of Jaya algorithm for Ktw and taper angle, respectively.

In order to achieve multiple trade-off solutions for Ktw and taper angle in AWJM process Shukla and Singh (2016a) used NSGA considering a population size of 50 and maximum number of iterations as 1000 (i.e. maximum number of function evaluations as 50,000). The algorithm specific parameters required by NSGA were chosen by Shukla and Singh (2016a) as follows: sharing fitness 1.2, dummy fitness 50. However, the values of crossover and mutation parameters required by NSGA were not reported by Shukla and Singh (2016a). Now, the same problem is solved using MO-Jaya algorithm and NSTLBO algorithm (Rao et al. 2016). For fair comparison of results the maximum number of function evaluations for MO-Jaya and NSTLBO algorithms are maintained same as that of NSGA. For this purpose a population size of 100 and maximum number of iterations equal to 500 and 250 are chosen for MO-Jaya and NSTLBO algorithms, respectively. The Pareto-efficient set of solutions obtained by MO-Jayaalgorithm in a single simulation runis reported in Table 9. In Table 9, optimal combinations of input process parameters such as traverse speed, stand-off distance and mass flow rate are provided, each solutions corresponds to a trade-off between Ktw and taper angle. Figure 7 shows the Pareto-front obtained by NSGA, MO-Jaya and NSTLBO algorithms. In order to judge the quality of the Pareto-front obtained by the three algorithms the hypervolume (HV) metric is used (Zitzler and Thiele 1999). The value of HV metric achieved by MO-Jaya algorithm is higher than the NSTLBO and NSGA ($\hbox {HV}_{\mathrm{MO}{\text{- }}\mathrm{Jaya}}= 2.6028$; $\hbox {HV}_{\mathrm{NSTLBO}}= 2.5995$ and $\hbox {HV}_{\mathrm{NSGA}}= 2.5516$).

Table 8 Mean, standard deviation and CPU time required by BBO and Jaya algorithms for case study 3

Fig. 5

Convergence graph of Jaya algorithm for maximization of Ktw (case study 3)

Fig. 6

Convergence graph of Jaya algorithm for minimization of taper angle (case study 3)

Table 9 Pareto-efficient solutions obtained using MO-Jaya algorithm for case study 3

NSGA used 50,000 function evaluations to converge at the Pareto-efficient set of solutions. Only for fair comparison of results the maximum number of function evaluations for MO-Jaya and NSTLBO algorithms are maintained as 50,000. However, the MO-Jaya and NSTLBO algorithms required 700 and 1600 function evaluations, respectively to converge at the Pareto-efficient set of solutions. The CPU time required by MO-Jaya and NSTLBO algorithms to perform 50,000 function evaluations is 77.086 and 80.67 s, respectively. However, the CPU time required NSGA is not reported by Shukla and Singh (2016a).

The MO-Jaya algorithm has provided 100 Pareto-optimal solutions for the multi-objective optimization problem of AWJM process. The decision maker is now required to choose one out-of the 100 alternative solutions with Ktwand taper angle as selection criteria. This forms a decision making problem with two criteria and 100 alternatives considering Ktw and beneficial criteria and taper angleas non-beneficial criteria. To demonstrate the applicability of improved PROMETHEE method, three different set of weights are considered. The steps in the improved PROMETHEE method are similar to those discussed in“Optimization methodology” section. The best choice corresponding to each of the considered set of weights provided by improved PROMETHEE method is shown in Table 10.

Results and discussion

In the first case study, the results provided by MO-Jaya algorithm are justifiable and analogous with the working of AWJM process. In the AWJM process, at constant pressure as the nozzle diameter increases the kinetic energy of the abrasive particles decreases. Therefore, the surface roughness and Kerf increases with the increase in nozzle diameter. Therefore in order to obtain a lower value of surface roughness and Kerf the MO-Jaya algorithm has maintained the nozzle diameter to its lower bound value in order to ensure that the abrasive particles are discharged with a higher kinetic energy from the nozzle.

Fig. 7

Pareto-fronts obtained by NSGA (Shukla and Singh 2016a), MO-Jaya and NSTLBO for case study 3

Table 10 The best choice provided by PROMTHEE method corresponding to different set of weights for case study 3

As the traverse speed increase the faster passing of waterjet results in less number of abrasive particles impinging on the workpiece surface, resulting into formation of a narrow slot which reduces the Kerf. However, at low traverse speed more number of abrasive particles are available for eroding the material from the workpiece which results in a lower surface roughness. Accordingly, the MO-Jaya algorithm has selected the lower bound value of traverse speed (i.e. 200 mm/min) to achieve a minimum value of Kerf (i.e. 0.691 mm) and the MO-Jaya algorithm has selected the upper bound value of traverse speed (i.e. 600 mm/min) to achieve minimum value of surface roughness (i.e. 4.9247 $\upmu$m). In order to obtain the intermediate trade-off solutions the MO-Jaya algorithm has appropriately selected the values of traverse speed within the working range.

Shukla and Singh (2016b) developed their own regression models for Kerf and $R_{a}$ using the experimental of Kechagias et al. (2012). However, the regression model developed by Shukla and Singh (2016b) for Kerf provides negative value of Kerf for the certain combination of process parameters the values which lie on their respective bounds which is practically incorrect. In the case of $R_{a}$ the regression model developed by Shukla and Singh (2016b) is solved using Jaya algorithm. The Jaya algorithm minimum value of $R_{a}$ obtained by Jaya algorithm is $4.431729\,\upmu \hbox {m}$ which is lower than the value of $R_{a}$ obtained by Shukla and Singh (2016b) which is $4.443\,\upmu$m. Furthermore, Shukla and Singh (2016b) did not report the number of iterations and computational time required by firefly (FA) algorithm to achieve the minimum value of $R_{a}$. However, Jaya algorithm required only 6 iterations with a population size of 25 and maximum number of iterations equal to 20 and a computational time of 0.052 s was required by Jaya algorithm to obtain the minimum value of $R_{a}$ (i.e. for $x_{1} = 0.9000$ mm; $x_{2} = 0.9500$ mm; $x_{3} = 20$ mm; $x_{4}$ = 200 mm/min,; $R_{a-} = 4.431729\,\upmu$m) using regression model developed by Shukla and Singh (2016b).

In the second case study, the results of MO-Jaya algorithm show that, DOP increases as the traverse speed decreases. This is mainly because at higher value of traverse speed the abrasive particles that impinge on a target area are very less which tend to reduce the DOP. Therefore to achieve maximum value of DOP (i.e. 405.194 $\upmu$m) the MO-Jaya algorithm has maintained the traverse speed to its lower bound (i.e. 0.1 mm/s).According to Bernoulli’s principle as the waterjet pressure increases the energy also increase which results in higher DOP. Therefore to achieve the higher value of DOP the MO-Jaya algorithm as maintained the waterjet pressure to its upper bound value (i.e. 320 MPa). At lower value of stand-off distance the particle interference increases which reduces the energy and velocity of the particles impinging on the workpiece surface. Therefore, in order to achieve a high DOP the MO-Jaya algorithm has maintained the stand-off distance to its upper bound value (i.e. 10 mm).

As the abrasive flow rate increases the number of abrasive particles available for material removal also increases. Therefore to achieve a higher DOP the MO-Jaya algorithm has maintained the abrasive flow rate mostly close to the upper bound. Although, the effect of surface speed and tilt angle seems to be negligible on DOP. However, tilt angle and waterjet pressure have a synergistic effect on DOP. It is observed from the results of MO-Jaya algorithm that maximum DOP is achieved at higher tilt angle and higher pressure.

At higher peripheral speed the workpiece chips are cleaned effectively. This reduces the damage caused to the workpiece surface due to formation of chips. Therefore, to achieve minimum surface roughness the MO-Jaya algorithm has maintained a higher value of peripheral speed (i.e. 7.99 m/s). As the pressure increases the jet diameter increases, and the overlapping of larger effective jet produces smoother surface. As waterjet pressure is beneficial for a DOP as well as $R_{a}$ the Mo-Jaya algorithm has maintained waterjet pressure to its upper bound value (i.e. 320 MPa). The traverse speed and abrasive flow rate have a synergistic effect on $R_{a}$. The results of MO-Jaya algorithm show that minimum value of $R_{a}$ is achieved at higher value of traverse speed and higher abrasive flow rate (refer Table 4).

In the third case study, the results provided by MO-Jaya algorithm are logical and analogous with the working of AWJM process. In the AWJM process, as the stand-off distance increases the divergence of jet before impingement on the work-piece also increases due to the external drag from the surrounding environment. Therefore, the kinetic energy of the abrasive particles at the periphery of the jet is less as compared to abrasive particles at the centerline of the jet. Therefore, the material removal at the centerline is higher as compared to the material removal at the periphery. Thus, the kerf top width and taper angle increases with increase in stand-off distance. Accordingly, the results of MO-Jaya algorithm in Table 9 show that as the taper angle and Ktw increases stand-off distance increases from 1 to 5 mm.

At a constant nozzle diameter, as the mass flow rate increases the kinetic energy of the abrasive particles increases. This reduces flaring of abrasive waterjet and a jet of uniform diameter is produced. High kinetic energy results in a narrow slot of uniform width. Therefore, as the mass flow rate increases the kerf top width and taper angle decrease. However, as the mass flow rate increases beyond a certain critical value kerf top width and taper angle increase with the increase in mass flow rate. Therefore, in order to achieve a trade-off between kerf top width and taper angle the MO-Jaya algorithm has appropriately varied the mass flow rate within the given range.

In the AWJM process as the traverse speed increases the faster passing of waterjet allows less number of abrasive particles to strike on the target material generating a narrow slot which reduces the kerf top width and taper angle. As the traverse speed decreases the number of abrasive particles striking the target material also increases. This increases the erosion of the workpiece material at the walls of the slot especially near the top surface which increases the Ktw and taper angle. The results of MO-Jaya algorithm (refer Table 9) show that minimum value of taper angle is achieved for the value of traverse speed close to the upper bound and a maximum value of kerf top width is achieved for the value of traverse speed close to the lower bound.

The maximum value of Ktw achieved by NSGA is 2.8768 mm. However, the maximum value of Ktw achieved by MO-Jaya algorithm is 2.9168 mm which is 1.39% higher than NSGA. The minimum value of taper angle achieved by NSGA is 1.0884. The minimum value of taper angle achieved by MO-Jaya algorithm is 1.054 which is 3.16% lower than NSGA.

Conclusions

The single-objective and multi-objective optimization aspects of abrasive waterjet machining process are considered in this work. Three optimization case studies are formulated based on the regression models developed by previous researchers. The performance measures such as depth of cut, surface roughness, kerf geometry and taper angle are optimized using Jaya and MO-Jaya algorithms.

The Jaya algorithm and MO-Jaya algorithm have provided better results as compared to other optimization algorithms such as SA, PSO, FA, CSA, BH, BBO, NSGA and NSTLBO algorithms. In the case of multi-objective optimization problems the Pareto-fronts provided by MO-Jaya algorithm are compared with the Pareto-fronts provided by NSGA and NSTLBO algorithms. The MO-Jaya algorithm achieved a higher value of hypervolume metric as compared to NSGA and NSTLBO algorithms. Thus the quality of Pareto-fronts provided by MO-Jaya algorithm is better than that of NSGA and NSTLBO algorithms for the optimization problems considered in this work.

In case study 1, the MO-Jaya algorithm obtained better results as compared to the NSTLBO algorithm requiring less CPU time for its execution. In case study 2, the MO-Jaya algorithm obtained better solutions as compared to NSTLBO algorithm and desirability function approach. The CPU time required by the MO-Jaya algorithm is less as compared to NSTLBO algorithm. In case study 3, the Jaya algorithm obtained better results as compared to BBO algorithm and the CPU time required by the Jaya algorithm is lower than that of BBO algorithm. The MO-Jaya algorithm obtained a better Pareto-front as compared to NSGA within a very less computational time.

It is observed that, the working of Jaya and MO-Jaya algorithms is dependent only on common control parameters like population size and number of generations and there is no need of tuning of any algorithm-specific parameters. The computational complexity of MO-Jaya algorithm is less as compared to NSTLBO, NSGA and BBO algorithms because in these algorithms the solutions are updated in multiple phases. However, in the Jaya and MO-Jaya algorithms the solutions are updated in a single phase using a single equation. Therefore, the two main advantages of Jaya and MO-Jaya algorithms are: (1) the Jaya and MO-Jaya algorithms do not burden the user with the task of tuning the algorithm-specific parameters. (2) The Jaya and MO-Jaya algorithms are simple in implementation and require less CPU time for their working.

The effects of the best and worst solutions in the current population are considered simultaneously which gives a high convergence speed to MO-Jaya algorithm without trapping into local optima. The ranking mechanism based on the concept of non-dominance relation between the solutions helps MO-Jaya algorithm to maintain the good solutions in every generation and guides the search process towards the Pareto-optimal set.

Furthermore, an improved PROMETHEE method is used to select a suitable solution from multiple Pareto-optimal solutions provided by MO-Jaya algorithm based on his/her order of preference. The improved PROMETHEE is a more objective and logical selection approach as it allows the decision maker to systematically assign the values of relative importance to the criteria based on his/her preferences. In the improved PROMETHEE method the alternatives are evaluated with better accuracy as the values of the criteria and their relative importance are considered simultaneously.

The Pareto optimal set of solutions provided by MO-Jaya algorithm for the three case studies considered in this work are helpful to the process planner as it contains a wide range of optimal values. This enables the process planner to choose a particular solution from the Pareto optimal set that corresponds to a specific order of importance of objectives, in order to achieve the desired outcome from the machining process even in situations where the order of importance of objectives is subjected to frequent changes. Thus, the results presented in this work are useful for real production systems.

Appendices

Appendix A

Now the steps of the improved PROMETHEE method for selection of an optimal solution from the set of Pareto-optimal solution based on the order preference of the decision maker are demonstrated. For the purpose of demonstration the multi-objective optimization problem of AWJM process described in “Optimization methodology” section is considered.

Step 1 :

A multi-objective decision making problem for AWJM process is formulated by considering the 50 Pareto-optimal solutions provided by MO-Jaya algorithm as alternatives and the multiple objectives such as Kerf and $R_{a}$ are considered as selection criteria. Both the criteria are considered as non-beneficial criteria. Table 11 shows the objective data for multi-objective decision problem of AWJM process. In Table 11, the fifty solutions are considered as alternatives while Kerf and $R_{a}$ are considered as two attributes.

Step 2 :

The next step is to assign the weights of the criteria based on the order preference of decision maker. For the purpose of demonstration equal importance is assigned to all the criteria (i.e. $w_{1}=w_{2} = 0.5$).However, if a decision maker wants to assign unequal weights of relative importance to the criteria then he/she may use the analytical hierarchy process (AHP) method for determining weights of relative importance, explained by Rao and Patel (2010).

Table 11 Objective data for multi-objective decision making problem of AWJM process (case study 1)

Step 3 :

After assigning the weights of relative importance to the criteria next step is to select a preference function. Rao and Patel (2010) had suggested six preference functions namely, usual function, U-shape function, V-shape function, level function, linear function and Gaussian function. In this work the V-shape function is used as the preference function. For more details about calculating the values of preference indices using V-shape preference function the readers may refer to Rao and Patel (2010).

Step 4 :

Now each alternative is to be compared with every other alternative and the preference indices are to be calculated considering each criterion separately. For the purpose of demonstration, the preference indices resulting from pairwise comparison of 50 alternative solutions with respect to the criteria Kerf and $R_{a}$ are shown in Tables 12 and 13, respectively.

Step 5 :

Once the preference values resulting from pairwise comparison of each alternative with every other alternative is calculated for each criteria separately, the next step is to determine the weighted average of the preference functions according to Eq. (5). The weighted average of preference function values are shown in Table 14.

Step 6 :

The values of leaving flow, entering flow and net flow are calculated for each alternative according to Eqs. (6), (7) and (8). Considering, the values of net flow rank is assigned to each alternative following the higher-the-better approach.The values of leaving flow, entering flow, net flow and rank of each alternative is shown in Table 14.

Table 12 The preference values resulting from pairwise comparison of 50 alternative solutions with respect to the criterion Kerf

Table 13 The preference values resulting from pairwise comparison of 50 alternative solutions with respect to the criterion $R_{\mathrm{a}}$

Table 14 Leaving, entering, net flow values and ranking of fifty alternatives

Table 14 shows that for equal importance to both the criteria (i.e. $w_{1}=w_{2}= 0.5$) the improved PROMETHEE method has suggested alternative solution no. 40 as the first choice. Mainly for the purpose of demonstration equal weights are considered for all the criteria. However, if a decision maker wants to assign unequal weights to the criteria then he/she may use the analytical hierarchy process (AHP) method for determining weights of relative importance, explained by Rao and Patel (2010).

Appendix B

In order to demonstrate the working of MO-Jaya algorithm, the multi-objective optimization problem formulated in “Optimization methodology” section is considered in this work. The objective functions are expressed by Eqs. (10) and (11). The input process parameters and their respective upper and lower bounds are expressed by Eqs. (12) to (15). For the purpose of demonstration, a population size of five is considered and two iterations of MO-Jaya algorithm are shown now. The randomly generated initial population is shown in Table 15. The ranks are assigned to each solution based on the ranking methodology discussed in “Ranking methodology” section and crowding distance (CD) is computed as discussed in “Computing the crowding distance” section. The solution with the highest rank and highest CD value is the best solution and the solution with the lowest rank is selected as the worst solution.

Now the new values of the variables are calculated according to Eq. (1). For the purpose of demonstration, the random numbers $\alpha _{1}$ and $\alpha _{2}$ for variable A are considered as 0.91 and 0.15, respectively. The random numbers $\alpha _{1}$ and $\alpha _{2}$ for variable B are considered as 0.67 and 0.5, respectively. The random numbers $\alpha _{1}$ and $\alpha _{2}$ for variable C are considered as 0.25 and 0.65, respectively. The random numbers $\alpha _{1}$ and $\alpha _{2}$ for variable D are considered as 0.36 and 0.75, respectively. The new values of variables A, B, C and D are calculated and are shown in Table 16 along with the corresponding values of Kerf and $R_{a}$.

Now the new solutions are combined with the initial solutions and a combined population is formed. The combined population is shown in Table 17. The ranks and CD value are determined for all the solutions in the combined population. Now based on the ranks and CD value five good solutions are selected from the combined population. These five solutions which are shown in Table 18 will act as initial population for the next iteration.

Iteration 2

The solutions selected at the end of the first iteration, shown in Table 18 are used as initial population for the second iteration. Now in the second iteration, the initial solutions (Table 18) are modified according to Eq. (1) and are shown in Table 19. For the purpose of demonstration the random numbers $\alpha _{1}$ and $\alpha _{2}$ for variable A are considered as 0.54 and 0.29, respectively. The random number $\alpha _{1}$ and $\alpha _{2}$ for variable B are considered as 0.48 and 0.37, respectively. The random numbers $\alpha _{1}$ and $\alpha _{2}$ for variable C are considered as 0.62 and 0.14, respectively. The random numbers $\alpha _{1}$ and $\alpha _{2}$ for variable D are considered as 0.73 and 0.55, respectively.

The combined population is shown in Table 20. Five good solutions are selected from the combined population based on the ranks and CD which are shown in Table 21. These five solutions will act as initial solutions for the third iteration of MO-Jaya algorithm.

Table 15 Initial population

Table 16 New values of the variables and objective functions

Table 17 Combined population

Table 18 Selection of candidate solutions based on non-dominance rank and crowding distance

Table 19 New values of the variables and objective functions

Table 20 Combined population

Table 21 Selection of candidate solutions based on non-dominance rank and crowding distance