1 Introduction

Rolling bearings play a paramount role in machine tools and are primarily employed to support rotations and carry the radical dynamic loads of spindles [1,2,3]. As a safety–critical component, rolling bearings usually work under harsh operating conditions, and are therefore prone to various failures, which may lead to production efficiency reduction and economic losses in the manufacturing industry [4]. Accurate fault diagnosis of rolling bearings is thus of great importance for ensuring the high safety and high-efficiency operation of manufacturing equipment. When a localised bearing fault occurs, the defect passes its mating surface resulting in a short force pulse. As the bearing rotates in a continuous fashion, the transient pulse repeatedly arises, and thus, periodic impulse features take place in the vibration signal. Hence, the bearing fault diagnosis technique based on vibration signal analysis has attracted significant attention in recent years [5,6,7,8]. Nevertheless, vibration signals are normally contaminated by noise and harmonic interference due to poor operating conditions.

Numerous effective methods have sprung up for extracting periodic fault features from vibration signals. Commonly applied vibration signal analysis methods include the short-time Fourier transform (STFT) [9, 10], wavelet transform [11, 12], ensemble empirical mode decomposition (EEMD) [13], and tuneable Q-factor wavelet transform (TQWT) [14, 15]. However, these methods suffer from threshold setting and high computational costs, as well as the requirement of abundant human expertise. Recently, sparse representation, emerging as an active and valid signal analysis approach, has garnered considerable attention because of its outstanding performance in feature extraction.

Sparse representation has two key components: dictionary construction, and the determination of sparse coefficients. The matching pursuit (MP) [16] and basis pursuit (BP) algorithms [17] are two typical approaches employed to determine sparse coefficients. The advantage of the MP algorithm over the BP algorithm is that the former is computationally simpler and easier to implement [18]. The orthogonal matching pursuit (OMP) algorithm is an improved derivate of the MP algorithm, which has been extensively utilised in the determination of sparse coefficients. For example, Li et al. [19] applied the OMP algorithm and a self-adaptive complete dictionary to obtain a sparse signal. Song et al. [20] proposed a cluster contraction stagewise OMP (CcStOMP) algorithm to detect the fault features of rolling bearings. In fact, the coefficient solving algorithm mainly affects the speed of feature reconstruction, whereas it is the dictionary which truly underlies the accuracy of feature extraction [21]. Hence, designing an appropriate dictionary is essential to fault feature extraction.

Among the existing dictionaries, wavelet parameter dictionaries are extensively explored because of the flexibility and variability of wavelet waveforms. Notably, the similarity between the dictionary atoms and fault impulse directly determines the performance of feature extraction [21]. The unit impulse response, Laplace wavelet, and Morlet wavelet are widely used as mathematical models of wavelet dictionary atoms, where the first two are both single-sided and damped exponential functions. By coincidence, a bearing fault-induced impulse response is generally acknowledged to be single-sided attenuation, which leads a wide application of such two wavelets to bearing fault feature extraction. For instance, Jiang et al. [21] used a unit impulse response function as the mathematical model of atoms to design a dictionary, which was employed in conjunction with the MP algorithm to realise fault feature extraction for bearings. Li et al. [22] applied the Laplace wavelet dictionary and a secondary selection-based OMP (SS-OMP) algorithm to successfully detect the fault features of rolling bearings, whilst Sun et al. [23] also utilised the Laplace wavelet parametric dictionary to extract fault features of rolling bearings. Meanwhile, Qin et al. [24] constructed a new impulsive wavelet as the dictionary atom model for a sparse representation of rolling bearing fault-induced impulses. On the contrary, the distinctive feature of the Morlet wavelet is that its waveform has a shape similar to that of a gear fault-induced impulse response with double-sided attenuation. Hence, Fan et al. [25] constructed a parameter dictionary to diagnose gearboxes based on Morlet wavelets, whereas Wang et al. [26] used the Morlet wavelet as a transient model and identified the model parameters via a correlation filtering algorithm (CFA) to diagnose gear faults within rotating machinery. In the case of compound faults where gear and bearing faults co-exist, Deng et al. [27] introduced the Laplace and Morlet wavelets as the mathematical models of dictionary atoms to design corresponding dictionaries for diagnosing bearing and gear faults simultaneously. He et al. [28] designed two types of dictionaries for the sparse representation of gear and bearing faults, where the mathematical models of their dictionary atoms were a steady harmonic and unit impulse response function.

The review of the previous literature indicates that the wavelet mathematical model used for sparse representation has a significant effect on the fault feature extraction. However, the commonly used wavelet functions exhibit single-sided attenuation or bilateral symmetric attenuation because of a single damping ratio. In fact, the impulse response components in the real-life faulty bearing vibration signal generally exhibit bilateral asymmetric attenuation because of the influence of such factors as fault mechanism, transmission paths, and sensor characteristics. Therefore, such wavelet functions fail to be used to good effect when serving as mathematical models for dictionary atoms in practical engineering applications. To address the above issues, this work makes use of a bi-damped wavelet as the mathematical model of an atom to construct an initial parameter dictionary, where the bi-damped wavelet is able to take an asymmetric bilateral shape resembling the fault-induced impulse response [29]. As such, this initial dictionary is expected to achieve a global match with the fault-induced impulses in vibration signals.

Most wavelet dictionaries are paved by changing the time-shift parameter of an optimal wavelet basis, so that the waveforms of all the atoms are essentially identical. This is also the case of the bi-damped wavelet parameter dictionary. However, the fault-induced impulses in the vibration signals are not identical in terms of amplitudes and oscillation characteristics. A data-driven learning dictionary can automatically update each column of the dictionary according to the fault-induced impulses in the signal at hand. As a typical dictionary learning model, K-singular value decomposition (K-SVD) has been applied widely in fault diagnosis [30,31,32]. However, when the noise and harmonic components are intensive, the K-SVD algorithm is prone to learning components that are unrelated to fault-induced impulse features.

To improve the global and local matching of the initial dictionary to the fault-induced impulse, we developed a cascaded dictionary construction method. In this approach, a bi-damped wavelet is first employed as the wavelet mathematical model of the atom, which globally matches the fault-induced impulses. Motivated by the periodicity characteristic of the impulses in the vibration signal, the parameter dictionary atom is constructed with period-assisted bi-damped wavelets. Next, the initial bi-damped wavelet parameter dictionary is substituted into the K-SVD algorithm to adjust the amplitude and oscillation characteristics of each atom to achieve a local match with the fault impulses. Thus, a cascaded dictionary is obtained that takes into account the global and local features of the vibration signals.

The main contributions of this paper are as follows: (1) The cascaded dictionary is proposed to merge the parametric dictionary and the learning one, integrating the power of individual dictionary and overcomes their own shortcomings simultaneously. (2) Period-assisted bi-damped wavelets are employed as the dictionary atoms, considering not only the shape of the impulse response but also the periodicity in real vibration signals. (3) The proposed method can achieve excellent performance in the fault feature extraction of an actual locomotive wheel-set bearing.

The structure of this paper is arranged as follows. In Section 2, the individual methods utilised in the developed approach are briefly described. The implementation details of the proposed approach are introduced in Section 3. In Section 4, the effectiveness of the proposed method is validated by simulation analysis. In Section 5, the performance and superiority of the proposed method are analysed using experimental and actual engineering signals. Finally, concluding remarks are summarised in Section 6.

2 Methods

2.1 Sparse representation and OMP algorithm

A bearing fault vibration signal typically consists of periodic transient impulse components and background noise. Thus, the observed fault signal y can be described as.

$$y=h+e$$
(1)

where \(h\) represents the periodic transient impulse components and \(e\) denotes the background noise. In accordance with the theory of sparse decomposition, the signal \(y\in {{\varvec{R}}}^{n\times 1}\) can be expanded with an over-complete dictionary \(D\in {{\varvec{R}}}^{n\times M}\), \(D=[{d}_{1},{d}_{2},\dots ,{d}_{M}]\). Then, the signal \(y\) can be modelled as.

$$y=Dx+\varepsilon$$
(2)

where \(x\in {{\varvec{R}}}^{M\times 1}\) denotes the sparse coefficient vector and \(\varepsilon\) is the reconstruction error. The purpose of sparse representation is to use as few atoms as possible from the over-complete dictionary D to represent the vibration signal \(y\) with the minimum \({l}_{0}\) norm \({\Vert x\Vert }_{0}\). The sparse representation is defined as.

$${}_x^{min}\left\|x\right\|_0,\;s.t.\;\left\|y-Dx\right\|_2^2<\varepsilon$$
(3)

Determining the minimum \({l}_{0}\) norm \({\Vert x\Vert }_{0}\) is a non-deterministic polynomial hard problem. The OMP algorithm can transform the \({l}_{0}\)-minimisation problem into an \({l}_{1}\)-minimisation problem, as follows:

$${}_x^{min}\left\|x\right\|_1,\;s.t.\;\left\|y-Dx\right\|_2^2<\varepsilon$$
(4)

To ensure that the solution is optimal, the OMP algorithm performs a Gram-Schmidt orthogonalisation operation on all selected atoms during each iteration. For clarity, a basic description of the OMP algorithm is presented in Table 1.

Table 1 Description of OMP algorithm
Full size table

2.2 Cascaded sparse dictionary

For better extraction of the transient impulse responses from a vibration signal submerged in noise and harmonic components, the construction of a dictionary that allows atoms to follow impulse changes and not easily be affected by noise interference is a subject worthy of attention. This paper proposes a cascaded dictionary construction method that satisfies the aforementioned demands and the accuracy of rolling bearing feature extraction is expected to be improved. Considering the asymmetric bilateral attenuation and periodicity of the real-life impulse responses, a period-assisted bi-damped wavelet is employed as the atom to design an initial parameter dictionary. Then, the K-SVD algorithm is utilised to refine the initial parameter dictionary locally. Finally, a cascaded dictionary can be obtained that matches the real impulse response globally and locally.

2.2.1 Bi-damped wavelet

Some researchers consider that the transient impulses generated by a bearing fault exhibit strictly single-sided attenuation characteristics [33, 34], with the impulse model described as Eq. (5):

$${\varphi }_{imp}\left(\omega ,\xi ,\tau ,t\right)={e}^{\frac{-\xi }{\sqrt{1-{\xi }^{2}}}\omega \left(t-\tau \right)}sin\omega \left(t-\tau \right),t\geq\tau$$
(5)

where \(\omega =2\pi f\) represents the oscillation frequency, which is denoted by \(f\) in the following equations. Meanwhile, \(\tau\) denotes the time shift; \(\xi\) represents the damping ratio, which is used to control the rate of wavelet attenuation; and \(t\) is the signal duration.

Figure 1 illustrates the commonly used wavelet functions, from which we can see that the Laplace wavelet with single-sided attenuation and the Morlet wavelet with double-sided symmetric attenuation match poorly with the fault-induced double-sided asymmetric attenuation impulses as shown in Fig. 2, which come from the bearing vibration signals provided by the Western Reserve University. Therefore, based on the characteristics of the bearing fault impulses, and considering the weaknesses of commonly used wavelet functions, this study uses a bi-damped wavelet \({g}_{imp}(\omega ,\xi ,\zeta ,\tau ,t)\) as the atom mathematical model to construct an initial parameter dictionary, which is expressed as Eq. (6):

$$\begin{array}{c} g_{imp}\left(\omega,\xi,\zeta,\tau,t\right)=\left\{\begin{array}{lc} K_{imp}\left(t-\tau,0\right)\cdot e^{\frac{-\xi}{\sqrt{1-\xi^2}}\omega\left(t-\tau\right)}&\cos\left(\omega\left(t-\tau\right)\right)-K_{imp}\left(\tau-t,0\right)\cdot e^{\frac\zeta{\sqrt{1-\zeta^2}}\omega\left(t-\tau\right)}\cos\left(\omega\left(t-\tau\right)\right),t\epsilon\lbrack\tau-W_s,\tau+W_s\rbrack\\0,&else\end{array}\right.\\K_{imp}\left(t,\;0\right)=\left\{\begin{array}{ll}1,&t>0\\0,&else\end{array}\right.\end{array}$$
(6)

where by carefully adjusting the two damping ratios \(\xi\) and \(\zeta\), we can refine the oscillation attenuations on the left and right sides of the wavelet respectively, so as to match the inherent impulse responses in faulty bearing vibration signals. Figure 3 displays three bi-damped wavelets with the parameter combinations of \({g}_{imp}\left(1000, 0.5, 0.2, 0.01\right)\), \({g}_{imp}(1500, 0.15, 0.15, 0.03)\), and \({g}_{imp}(1800, 0.2, 0.5, 0.05)\). It is seen that a suitable selection of wavelet parameters has the potential to yield a bi-damped wavelet matching perfectly with the fault-induced impulse response.

Fig. 1
figure 1

Commonly used wavelet functions: (a) db4 wavelet; (b) Morlet wavelet; (c) Laplace wavelet

Full size image
Fig. 2
figure 2

Bearing fault signals: a outer ring fault signal; b inner ring fault signal

Full size image
Fig. 3
figure 3

Waveforms of bi-damped wavelet with different parameter combinations

Full size image

2.2.2 Building bi-damped wavelet dictionary

  1. (1)

    Optimise the bi-damped wavelet by CFA with respect to the parameters \((\omega ,\xi ,\zeta ,\tau )\) (\(\omega =2\pi f)\) to approximate fault-induced impulses in the processed signal. First, in accordance with Ref. [34], let \(f\epsilon[0,\) \({f}_{s}/2\)], \(\tau\epsilon [0, { T}_{c}]\), and both \(\xi \mathrm{and} \zeta \epsilon [0, 1]\), where \({f}_{s}\) is the sampling frequency, and \({T}_{c}\) is the signal time series used for correlation filtering.

    Next, the inner products of the wavelets of various parameter combinations and the signal of interest are calculated by CFA. The inner product measures the correlation degree between the wavelet atom and the signal, which can be defined as Eq. (7).

    $$\langle {g}_{imp}\left(t\right),y(t)\rangle ={\Vert {g}_{imp}(t)\Vert }_{2}{\Vert y(t)\Vert }_{2}\mathrm{cos}\left(\theta \right)$$
    (7)

    As can be seen from Eq. (7), the inner product is affected by the amplitude of the wavelet \({g}_{imp}\left(t\right)\) and the signal \(y\left(t\right)\), as well as the angle \(\theta\). Actually, the smaller the angle \(\theta\) is, the more similar of \({g}_{imp}(t)\) and \(y\left(t\right)\) will be. To eliminate the amplitude effect of the wavelet and signal, a correlation coefficient \({K}_{r}\) can be defined to quantify the magnitude of the angle, i.e., the similarity level of the wavelet to the signal. The correlation coefficient \({K}_{r}\) is described as Eq. (8).

    $${K}_{r}=cos\theta =\sqrt{2}\frac{\mid\langle {g}_{imp}(t),y(t)\rangle \mid}{{\Vert {g}_{imp}(t)\Vert }_{2}\cdot{\Vert y(t)\Vert }_{2}}$$
    (8)

    Considering that the process of identifying the optimal parameters is computationally expensive, the CFA is performed in conjunction with the particle swarm optimisation (PSO) algorithm to speed up the optimisation process. The correlation coefficient \({K}_{r}\) is employed as the fitness function in the PSO algorithm, as shown in Eq. (9). Finally, the optimal parameters are selected as those maximising \({K}_{r}\). In the PSO algorithm, the main parameters are the particle swarm size \(A\), maximum number of iterations \(M\), and acceleration factors \({c}_{1}\) and \({c}_{2}\), prescribed as \(A=50\), \(M=10\), and \({c}_{1}={c}_{2}=1.49445\).

    $$fitness=\begin{array}{c}max\\ \left\{f,\xi ,\zeta ,\tau \right\}\end{array}\left({K}_{r}\right)$$
    (9)
  2. (2)

    Construct the initial bi-damped wavelet parameter dictionary. After the above parameter optimisation, the optimal bi-damped wavelet \({g}_{imp}(i)\) is obtained for the subsequent dictionary atom construction. The length of the optimal wavelet is set to \({L}_{w}=\mathrm{round} ({f}_{s}/{f}_{i})\) (where \({f}_{i}\) is the fault characteristic frequency of the bearings). Inspired by the periodicity of fault impulses, period-assisted optimal wavelets are employed as the dictionary atoms. The period number of the optimal wavelet in an atom is set to 4 [29]. Thus, the length of an atom is \({L}_{a}=4\times {L}_{w}\). Meanwhile, we can observe from Fig. 3 that the parameter \(\tau\) controls only the position of the bi-damped wavelet on the time axis and has no effect on the wavelet waveform. Thus, paving the optimal wavelet with varied time-shift parameter \(\tau\) gives rise to an initial bi-damped wavelet parameter dictionary.

2.2.3 K-SVD algorithm

At present, K-SVD is the most widely used dictionary learning algorithm which can effectively reduce the sparsity of the coefficient matrix. That is to say, the bi-damped wavelet dictionary can represent signal features more effectively, if the K-SVD is further utilised. The K-SVD can be defined as an objective optimisation problem:

$${}_{D,X}^{min}{\Vert Y-DX\Vert }_{F}^{2} s.t.{\Vert {x}_{i}\Vert }_{0}\le {T}_{0},\,for\; i=\mathrm{1,2},\dots , n$$
(10)

where \(Y\) denotes the training sample, \({x}_{i}\) is the column vector of the coefficient matrix \(X\), and \({T}_{0}\) represents the sparsity constraint factor. The K-SVD algorithm first fixes the dictionary D and then updates the sparse coefficients \(X\) using the OMP algorithm. Each column of the dictionary is then sequentially updated during the above optimisation process with reference to the signal features to be extracted. The mathematical formula for updating the dictionary is as follows:

$${\Vert Y-DX\Vert }_{2}^{2}={\Vert Y-{\sum }_{j=1}^{P}{d}_{j}{x }_{T}^{j}\Vert }_{2}^{2}={\Vert \left(Y-{\sum }_{j\ne l}{d}_{j}{x }_{T}^{j}\right)-{d}_{l}{x }_{T}^{l}\Vert }_{2}^{2}={\Vert {E}_{l}-{d}_{l}{x }_{T}^{l}\Vert }_{2}^{2}$$
(11)

where \({E}_{l}\) denotes the residual matrix. Then, the residual matrix is decomposed into various singular values via the singular value decomposition (SVD) method.

$${E}_{l}=U\Delta {V}^{T}={\sum }_{j=1}^{m}{E}_{lj}$$
(12)

where \({E}_{lj}={o}_{j}{u}_{j}{v}_{j}^{T}\) denotes the j-th singular component. Meanwhile, \({o}_{j}\) denotes the j-th singular value and \({u}_{j}\) represents the j-th column vector of the singular matrix \(U\). Besides, \({v}_{j}\) is the j-th column vector of the singular matrix \(V\), and \(\Delta =diag({o}_{1},{o}_{2}, \dots , {o}_{n})\) is the diagonal matrix. According to the principle of K-SVD, \({d}_{l}\) is updated by the columns of U, and the solution to \({x}^{l}\) is \({o}_{1}{v}_{1}^{T}\). All the atoms \({d}_{l}\) (l = 1, 2, …, L) in D are updated sequentially.

The K-SVD has been recognised as an effective tool to detect inherent fault features. However, the updating principle of the K-SVD algorithm is based on the maximum singular value. When the noise and harmonic components are intense, it will learn some features unrelated to fault impulses [29]. Therefore, through substituting the bi-damped wavelet parameter dictionary into the K-SVD dictionary, the influence of unrelated features can be avoided, and the dictionary atoms can be learned in the way of a secondary learning to obtain a cascaded dictionary that further suits the local features of the fault vibration signals. Consequently, the cascaded dictionary is promising in the sense that it can achieve better feature extraction in bearing fault diagnosis.

3 Proposed procedures for feature extraction

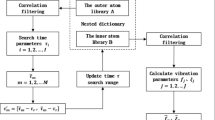
Based on the theory of sparse representation, this paper presents a novel cascaded dictionary construction method using a bi-damped wavelet and the K-SVD algorithm. The steps of the proposed approach are provided in detail as follows, with the corresponding flowchart presented in Fig. 4.

  • Step 1: Input the original fault vibration signal of a rolling bearing. First, a cascaded dictionary is constructed based on the method mentioned in Section 2.2, which can reduce noise and harmonic interference and learn the characteristics of fault impulses.

  • Step 2: Determine the sparse coefficients. The fault vibration signal is divided into several segments with the lengths equal to those of the atoms in the cascaded dictionary. The OMP algorithm is then applied to obtain a sparse coefficient matrix \(\widehat{x}=({\widehat{x}}_{1}, {\widehat{x}}_{2},\dots ,{\widehat{x}}_{i})\).

  • Step 3: Detect the fault feature frequency. The fault vibration signals are recovered using the sparse coefficient matrix and the cascaded dictionary. The recovered signal is then demodulated by the Hilbert transform to get the envelope spectra. Finally, bearing fault can be diagnosed by identifying the fault characteristic frequency in the envelope spectra.

Fig. 4
figure 4

Flowchart of the proposed approach for fault diagnosis

Full size image

4 Simulation verification and result analysis

To validate the effectiveness and adaptiveness of the proposed approach to feature extraction, a quasi-periodic signal \(y(t)\) is simulated, which is composed of three kinds of impulse responses \({g}_{imp}(t)\) and a random noise \(n(t)\). The simulated signal \(y(t)\) is formulated as follows:

$$y\left(t\right)=\sum_{i}{A}_{i}{g}_{imp}(t-i{T}_{r})+{A}_{0}n\left(t\right)$$
(13)

where the cyclic period \({T}_{r}=0.1 s\), and \({A}_{i}\) and \({A}_{o}\) represent the amplitude of the impulse response and noise, respectively. The parameters for the three types of impulse responses are predefined as \({g}_{imp}(\mathrm{80,0.35,0.15,0.05})\),\({g}_{imp}(\mathrm{80,0.25,0.25,0.35})\), and \({g}_{imp}(80, \mathrm{0.15,0.35,0.65})\), and their amplitudes are set as 1, 0.5, and 1, respectively. The sampling frequency is 12 kHz. Figure 5a and b show the waveforms of pure signal and polluted signal with noise level \({A}_{0}=0.4\), respectively.

Fig. 5
figure 5

Simulation signal: a pure signal; b noisy signal

Full size image

According to the procedure shown in Fig. 4, the first step is to search for the optimal bi-damped wavelet atom using the CFA-PSO method by maximising the correlation coefficient \({K}_{r}\) (Eq. 8). For the polluted signal in Fig. 5b, the identified optimal parameters of the bi-damped wavelet are \(\widetilde{f}=62\), \(\widetilde{\xi }=0.1058\), \(\widetilde{\zeta }=0.2419\), and \(\widetilde{\tau }=0.8568\), with the corresponding atom shown in Fig. 6a. From a global perspective, the optimal wavelet atom has a waveform similar to the impulse responses in the simulated signal. An initial bi-damped wavelet dictionary is then paved by changing the time-shift parameter \(\tau\) to form a period-assisted optimal wavelet. Figure 6b shows the signal reconstructed by the initial wavelet dictionary and original pure signal. It can be observed that there is a large difference between the impulse responses in the two signals in terms of both amplitude and decay characteristics, but the impulse locations are correctly identified. Next, the initial bi-damped wavelet dictionary is substituted into the K-SVD algorithm to perform a secondary learning to form a cascaded dictionary, where the initial wavelet atoms are locally adjusted to match globally and locally with the fault features of interest. Finally, with the help of the OMP algorithm, Fig. 6c and d present the recovered signal resultant from the cascaded dictionary and its envelope spectrum. As shown in Fig. 6c, almost all impulse responses are perfectly recovered. More specifically, the locations, amplitudes, and decay characteristics of the impulse responses in the recovered signal are extremely identical to those of the pure signal. It is noteworthy that the reconstructed signal is almost completely free of noise. In the envelope spectrum (Fig. 6d), the spectrum peaks indicative of fault frequency and its harmonics are prominent.

Fig. 6
figure 6

The representation results of the simulated signal by using the proposed method: a the optimal wavelet atom; b the result of wavelet dictionary; c the result of cascaded dictionary; d the envelope spectrum

Full size image

For comparison, a Laplace wavelet parameter dictionary is also applied to analyse the polluted signal. The Laplace wavelet is a complex wavelet being single-sided and damped exponential as shown in Fig. 1c. It is reported that the Laplace wavelet perform well on bearing fault feature extraction due to the fact that its waveform resembles the impulses induced by bearing faults. The Laplace wavelet is defined as.

$$\psi \left(t\right)=\left\{\begin{array}{ll}{e}^{\frac{-\xi }{\sqrt{1-{\xi }^{2}}}2\pi f(t-\tau )}&{e}^{-j2\pi f(t-\tau )}, t\in [\tau ,\tau +{W}_{s}]\\ 0,& else\end{array}\right.$$
(14)

The Laplace wavelet is determined by three parameters, i.e., \((f,\xi ,\tau )\). To test the validity of the Laplace wavelet as a mathematical model for dictionary atoms, the CFA is also employed to choose its optimal parameters. With the help of the OMP algorithm, Fig. 7a and b show the recovered signal and its envelope spectrum obtained by using the Laplace wavelet dictionary with optimal parameters \(\widetilde{f}=100\), \(\widetilde{\xi }=0.2000\), and \(\widetilde{\tau }=0.0600\). We can see from Fig. 7a that the impulse period cannot be easily observed from the time-domain signal and the shape of the impulses differentiates greatly from the pure signal, although relatively obvious spectral peaks appear at the fault frequencies (see Fig. 7b).

Fig. 7
figure 7

a, b The processing results of the Laplace wavelet dictionary; c, d the processing results of the K-SVD algorithm

Full size image

To further demonstrate the superiority of the cascaded dictionary with a secondary learning, the K-SVD algorithm is employed individually to handle the polluted simulation signal. Figure 7c and d illustrate the results of the K-SVD algorithm. In Fig. 7c, the periodic impulses are severely masked by noise. The feature extraction by the single use of the K-SVD algorithm is absolutely inferior to the proposed approach (Fig. 6d), which is also manifested in its envelope spectrum shown in Fig. 7d. In fact, the K-SVD algorithm along may be unsuited for extracting features directly as it is extremely susceptible to noise and harmonic interferences. Based on the analysis above, it can be inferred that the quality of the recovered signal using the cascaded dictionary is distinctly superior to those obtained by the single use of the Laplace dictionary or K-SVD algorithm.

To validate the anti-noise performance of the proposed approach, we increase the amplitude \({A}_{o}\) of the random noise from 0.4 to 1.2 with a step of 0.2, resulting in five simulated signals. The reconstructed signals using the cascaded dictionary are shown in Fig. 8a. In addition, the root-mean-square error (RMSE) is employed to evaluate the quality of the recovered signals with the results listed in Table 2.

Fig. 8
figure 8

Recovered signals at various noise intensities (i.e., the noise amplitudes A0 = 0.4, 0.6, …, 1.2): a cascaded dictionary; b Laplace dictionary

Full size image
Table 2 Comparative analysis of reconstructed signals at different SNRs
Full size table

In the forgoing comparative study (Fig. 7), the performance of the Laplace wavelet dictionary is obviously superior to that of the K-SVD algorithm. Therefore, the reconstruction results of the Laplace wavelet dictionary other than the K-SVD in various signal-to-noise ratio (SNR) scenarios are shown in Fig. 8b, and the RMSE of the recovered signals are presented in Table 2. It is evident in Fig. 8a that the periodic impulse responses are clearly revealed with a good noise interference cancellation. In contrast, the shape and periodicity of the impulse responses are poorly captured by the Laplace wavelet dictionary (Fig. 8b). From Table 2, we can observe that the RMSEs of the cascaded dictionary are significantly lower than those of the Laplace dictionary. Therefore, the proposed approach has excellent anti-noise performance, and the feature extraction effect of the cascaded dictionary is significantly superior to that of the Laplace dictionary.

5 Application validation

5.1 Case 1: inner race fault from laboratory

The experimental signal was obtained from the fault simulation test bench (COINV-1618) shown in Fig. 9, which is provided by the China Orient Institute of Noise & Vibration. Different faulty bearings can be installed on this bench to conduct vibration experiments. The platform includes a base plate, motor, gearbox, rotor, rolling bearings, and acceleration sensor. The bearing type used in the test was 6200Z with eight rolling elements. There was a fracture in the inner raceway of the bearing. The acceleration signals were sampled at the frequency of 19,692.3 Hz as the bearing rotates at 1000 rpm. Correspondingly, the inner race fault characteristic frequency (\({f}_{i})\) is 75 Hz. The signal and its spectrum of the inner race fault are shown in Fig. 10a and b, respectively, although \({f}_{i}\) and its harmonics can be identified from the envelope spectra (Fig. 10c), where substantial noise components remain.

Fig. 9
figure 9

COINV-1618 test bench

Full size image
Fig. 10
figure 10

Inner race fault signal: a time-domain waveform; b spectra; c envelope spectra

Full size image

Next, the proposed approach is employed to enhance the fault feature information. The identified optimal parameters of the bi-damped wavelet are \(\widetilde{f}=1140\), \(\widetilde{\xi }=0.1688\), \(\widetilde{\zeta }=0.5095\), and \(\widetilde{\tau }=0.1271\). The recovered signal from the cascaded dictionary sparse representation and its envelope spectrum are shown in Fig. 11a and b respectively, where the fault-induced impulses as well as the characteristic frequency and its harmonics are clearly evident.

Fig. 11
figure 11

Analysis results of cascaded dictionary: a recovered signal; b envelope spectra

Full size image

To illustrate the advantage of the proposed approach in fault feature enhancement, three other signal reconstruction methods involving the Laplace dictionary, K-SVD algorithm, and fast kurtogram (FK) method were applied to analyse the experimental signal. The optimal parameters of the Laplace wavelet are identified as \(\widetilde{f}=1968\), \(\widetilde{\xi }=0.02\), and \(\widetilde{\tau }=0.01\). Figure 12a and b present the results using the Laplace dictionary. We can observe from Fig. 12a that noise is essentially reduced, but some impulse responses are absent and the characteristic frequencies deviate considerably in Fig. 12b. The results of the K-SVD are shown in Fig. 13. From the envelope spectra in Fig. 13b, the fault characteristic frequencies can be observed but submerged in rather heavy noise.

Fig. 12
figure 12

Analysis results of Laplace dictionary: a recovered signal; b envelope spectra

Full size image
Fig. 13
figure 13

Analysis results of K-SVD dictionary: a recovered signal; b envelope spectra

Full size image

Meanwhile, the results of the FK method are shown in Fig. 14. The fault characteristic frequency \({f}_{i}\) and its harmonics up to \(4{f}_{i}\) can be observed but with certain noise interference in Fig. 14b. Based on the results, the FK method demonstrates no superiority to the proposed approach. The investigations on the experimental signal prove that the cascaded dictionary can effectively enhance fault-induced impulses and thus has great potential to improve the extraction accuracy of fault features.

Fig. 14
figure 14

Analysis results of FK method: a FK; b envelope spectra

Full size image

5.2 Case 2: outer race fault from engineering

The fault impulses of the experimental signal presented above are easily observable because of an artificial defect and a relatively low external interference. However, in real engineering applications, the working environment is much more complicated than that in a laboratory, resulting in more noise components in vibration signals.

To verify the practicality of the proposed approach, the signal from a wheel-set bearing with a real outer ring fault dismantled from a DF4 diesel locomotive was studied. The bearing testing platform is shown in Fig. 15 with the tested bearing presented in Fig. 16. Meanwhile, Table 3 lists the main parameters of the testing platform and the bearing. Figure 17a implies that the fault impulse responses in the real-life signal are masked by severe noise. Figure 17b shows the spectra of the signal. The envelope spectra in Fig. 17c indicate that the fault characteristic frequency is completely overwhelmed by noise.

Fig. 15
figure 15

JL-501 locomotive bearing dynamic testing platform

Full size image
Fig. 16
figure 16

Wheel-set bearing with outer race fault

Full size image
Table 3 Parameters of NJ2232WB bearing
Full size table
Fig. 17
figure 17

Signal of locomotive bearing: a waveform; b spectra; c envelope spectra

Full size image

Next, the proposed approach is applied to the real-life outer race fault signal. The identified bi-damped wavelet parameters are \(\widetilde{f}=3333\), \(\widetilde{\xi }=0.0473\), \(\widetilde{\zeta }=0.0334\), and \(\widetilde{\tau }=0.1045\). Figure 18a and b show the analysis results using the cascaded dictionary. It can be inferred from Fig. 18a that the fault impulse responses are clearly recovered in time domain without any interference components. The fault characteristic frequency and its harmonics appear distinctly in the envelope spectra shown in Fig. 18b. Undoubtedly, this reliable evidence demonstrates the practicality of the proposed approach in engineering applications.

Fig. 18
figure 18

Locomotive bearing analysis results of cascaded dictionary: a recovered signal; b envelope spectra

Full size image

For comparison, the Laplace dictionary, K-SVD, and FK methods are applied to the same signal. The parameters of the Laplace wavelet are ascertained to be \(\widetilde{f}=4100\), \(\widetilde{\xi }=0.025\), and \(\widetilde{\tau }=0.33\). The results of the Laplace dictionary are shown in Fig. 19. No periodicity of fault impulses is observed in the recovered signal of the Laplace dictionary (Fig. 19a). Accordingly, there is no distinctive fault characteristic frequency in the envelope spectra (Fig. 19b). In addition, the results from the K-SVD are given in Fig. 20. Limited by the atom updating principle, K-SVD is extremely susceptible to interference components. Thus, in the envelope spectra, a great deal of irrelevant noise interference is retained. Meanwhile, the results obtained using the FK method, which is known to be an effective tool for feature extraction, are shown in Fig. 21. As shown in Fig. 21b, although the fault characteristic frequency \({f}_{o}\) is presented in the envelope spectra, it is heavily disturbed by noise, and thus, this method is weak to extract fault features from a vibration signal in case of low SNRs.

Fig. 19
figure 19

Locomotive bearing analysis results of Laplace dictionary: a recovered signal; b envelope spectra

Full size image
Fig. 20
figure 20

Locomotive bearing analysis results of K-SVD dictionary: a recovered signal; b envelope spectra

Full size image
Fig. 21
figure 21

Locomotive bearing analysis results of FK method: a FK; b envelope spectra

Full size image

Therefore, the cascaded dictionary outperforms the other three leading methods in terms of fault feature extraction, and therefore provides an effective tool for bearing fault detection.

6 Conclusions

Based on the properties of the wavelet parameter dictionary and learning dictionary, we designed a cascaded dictionary, which performs better in sparse representation than the Laplace dictionary, K-SVD algorithm, and FK method. In addition, inspired by the characteristics of the fault-induced impulses in real-life vibration signals, period-assisted bi-damped wavelets are adopted as the atoms for the initial parameter dictionary, which is then substituted into the K-SVD for a secondary learning, so as to achieve a much better agreement with the fault features and an effective noise reduction. The main conclusions can be summarised as follows.

  1. (1)

    The anti-noise performance of the cascaded dictionary was verified by simulation signals at different SNRs. Investigations on experimental signals confirm that the cascaded dictionary can effectively enhance impulse features, thus improving the accuracy of bearing fault diagnosis. The engineering application results indicate that the cascaded dictionary has outstanding performance in handling signals with heavy background noise, which poses challenging to most existing sparse representation dictionaries.

  2. (2)

    The effectiveness of the proposed approach was validated on a simulated signal, an experimental signal, and an actual engineering signal. Meanwhile, the superiority of the proposed approach was verified by comparing it with three other leading methods. In addition, the proposed approach is quite suited for practical engineering applications.

Form all the results in this paper, we can observe that there are large fluctuations in the amplitudes of the recovered signals. Investigation into this issue is to be conducted in the future.